1 Introduction

Microstrip patch antennas are extensively used in mobile communication systems and wireless since of their merits, like low profile, ease of fabrication and light weight, respectively. Normally, the elementary antenna topology can be preferred as per to the desired antenna presentation. The huge challenge is to conclude the regular constraints of the antenna, including the feed position and the patch dimensions, to attain the best design that satisfies convinced conditions. Noticeably, a trial-and-error procedure is time-consuming and will not necessarily give the optimum patch constants or parameters. Then, the most robust MHAs are needed which will assist the antenna designer to design a definite antenna that meets exact necessities. The best training–testing stratification proportions have been thoroughly examined consuming the forecast of porosity and permeability of petroleum reservoirs as a trial circumstance by [1]. The fair performances of seven traditional and advanced machine learning methods were measured by [2].Further, an inclusive research has been lead on the forecast of the bubble point pressure and oil formation volume factor using two hybrid of soft computing methods. Experimental outcomes of the proposed methods have been compared with commonly used regression correlations, including standard artificial neural networks.

To meet the present demand, the issues in designing of microstrip patch antenna can be resolved using optimization functions, i.e., if we need to find efficient patch antenna specifications. The metaheuristic algorithms (MHAs) are most powerful techniques for these kinds of issues, because these involve the strong and powerful tools which help in designing the efficient patch antenna. Hence, day by day, the researchers are trying to develop more enhanced evolutionary algorithms for tracking of highly complex issues. These are refined optimization techniques, and they are often an enhanced substitute to traditional MHAs, giving an outstanding trade off between the optimal solution’s quality and computing time, particularly for complex issues or large dimension optimization functions. Usually, the MHAs can be distributed into dissimilar stages as per sources of motivation [3]:(1) swarm intelligence (SI) methods, including population-based methods that mimic the social behavior of animals or insects, (2) evolutionary algorithms that follow the natural evolution processes found in nature, and (3) natural phenomena (NP) algorithms that imitate the principles of physics and chemistry. In detail, MHAs have delivered extraordinary performances in several practical problems of a broad domain of applications, such as engineering [4, 5], feature selection [6], wireless sensor networks [7, 8], optimization problems [9], biomedical [10], drug design [11] and microstrip patch antenna [12]. For superior efficiency of the MHAs, various robust population-based algorithms have been developed in the last few decades.

A newly physical inspired optimizer algorithm is developed by [13].To assess the robustness and effectiveness of the algorithm, it is tested through other recent optimizers. On the basis of outcomes, it has been shown that the proposed method is very powerful with other deliberated state-of-the-art metaheuristics. Greedy–Levy ant colony optimization method has been originally developed by [14] with the help of levy flight mechanism and greedy policy. The computational testing shows the supremacy of the presented method. It has been observed that the proposed method can reach the best outcomes with the least number of generations. A newly hybrid physics-based optimization algorithm has been originally developed by [15]. In this strategy, atom search and tree-seed method have been merged together. And further, the levy flight random walk and chaos theory were merged with it. To assess the robustness of the presented method, it has been tested on 23-standard functions. This rising attention in MHAs coincides with the needed for additional efficient MHAs for searching the best optima’s of the complex issues. Several of these MHAs include particle swarm optimization (PSO) [16], genetic algorithms (GAs) [17], simulated annealing algorithm (SA) [18], Henry gas solubility optimization (HGSO) [19], Cuckoo search (CS) algorithm [20], sine cosine algorithm (SCA) [21], Archimedes optimization algorithm (AOA) [22], Chimp optimizer algorithm (ChoA) [23], Lévy flight distribution (LFD) [24], one half personal best position particle swarm optimizations (OHGBPPSO) [25], personal best position particle swarm optimization (PBPPSO) [26], half mean particle swarm optimization algorithm (HMPSO) [27], HAGWO [28], hybrid particle swarm optimization (HPSO) [29], HPSOGWO [30], hybrid MGBPSO-GSA [31], HGWOSCA [32], MGWO [33], MVGWO [34], HSSAPSO [35], SChoA [36], HSSASCA [37], respectively. In addition, the researchers of different areas are using the robust optimizers for addressing the challenges such as efficient mechanical performance [38], feature selection [39], structural damage detection problem [40], FMC green scheduling problem [41], random projection-based feature transformation [42], structural damage identification problem [43] and constraint and unconstrained problems [44], respectively.

Nowadays, patch antenna is a huge challenging optimization problem. It is worth revealing that with the help of the MHAs, the numerous shortcomings of the microstrip patch antenna’s have been determined such as design of microstrip patch antenna in the communication systems like Wi-Fi, Wi-MAX, Telemedicine , UWB applications, to cover Bluetooth operations as light, cheap, small size and low profile, [45]. In [46], the newly enhanced version of central force optimization (CFO) is introduced for designing and optimizing the two different patch antennas such as microstrip line fed E-shaped and a coaxial line-fed double E-shaped patch antennas. Robustness of the proposed method have been verified through different MHAs. [47] presented a new method for minimizing the size or dimension of the planar MPA and to achieve inferior frequencies. The dimension decrease method was constructed on slicing the antenna into dissimilar slots mostly in saw teeth shape (STS). As the demand of mobile devices was exceeding, the miniaturization methods were commonly applied besides the dimension decrease in devices. This work is divided into two categories; firstly, the MPA was designed; then, to achieve STS, these lots were separated. On the basis of this strategy, the MPA was compact to 87.88% with an operation frequency same to 1.7 GHz. [48] presents a circular MPA design for UWB issues. The MPA has been designed on FR-4 substrate with size same to \(0.9\,\mathrm{mm} \times 30\,\mathrm{mm} \times 35\,\mathrm{mm}\). To develop the impedance alike, a thin strip line 1.8 mm has been introduced amid the circular radiating patch and feed port. Various constants have been carried out such as inner and outer radius, feed size, substrate size and ground plane through applying the HFSS simulator. A planar monopole MPA is designed by [49] with U-shaped patch and slantwise cut partial ground plane for MSS (mobile satellite services). By optimizing the cut in patch and partial ground plane length, the designed antenna has been reduced. During this work, frequency stable radiation patterns and bands have been obtained. Experimental solutions shows that the extreme radiation competence attained has 13 % for 2–2.1 GHz frequency, and competence has 75% for 4–4.7 GHz. MFO algorithm has been used by [12] for designing the high performance and inexpensive MPA during this work. The return loss cost of developed algorithm is 20 dB with a bandwidth of 3.1 GHz. The newly existing approach robustness is examined based on return loss as well as antenna gain.

In particular, Archimedes optimization algorithm (AOA) [22] is a new metaheuristic that has already started attracting attention. The purpose of the present-day study is the enhanced application of a novel modified MHAs based on the mixture of AOA with levy flight called Levy Flight Archimedes optimization algorithm (LAO) for considering the microstrip patch antenna issues. All experimental efforts proves that the LAO algorithm robustness is better to other well-known MHAs in the literature. In summary, the main contributions of this work are:

  • A novel enhanced method called LAO algorithm that includes features from AOA and levy flight is proposed.

  • proposed method is developed for solving 29-CEC 2017 standard test suites.

  • The proposed strategy is developed for the design of microstrip patch antenna’s.

  • Statistical and qualitative experimental analyses assess the robustness of the LAO algorithm compared to recent competitive MHAs.

The remainder of this paper is as follows: An overview about the Archimedes optimization algorithm (AOA) is given in Sect. 2. Section 3 describes the mathematical model of the proposed LAO algorithm. Section 4 presents the results and their analyses obtained by the proposed strategy and the competitor algorithms. Brief details of the optimal solutions of antenna design issues are given in Sect. 5. Lastly, Sect. 6 concludes the paper.

2 Archimedes optimization algorithm (AOA)

The AOA is a recent population-based method, and it has been developed by Hashim et al. [22], which mimics the Archimedes’ principle. In this methodology, the search process of each member of crowd in the complex domain starts with accelerations, densities and random volumes, respectively. Here, the object is also re-modified with its random location in fluid. After testing fitness of each object, this method works in generations until stopping criteria are not met. This method also updates the volume and density for each object in all iterations during the whole search process. The acceleration of each object has been modified based on the conditions of its collision with the nearest object. The reorganized acceleration, density and volume defines the new update location of an object. Further, the mathematical formulation of AOA method has been illustrated in the following steps:

  • Initialization For initializing the location or position of the each object in the search domain during the search process, Eq. 2.1 is applied:

    $$\begin{aligned} o_{i} = \mathrm{low}_{i}+r \times (\mathrm{up}_{i}-\mathrm{low}_{i}); \, \, i=1,2,...,N \end{aligned}$$
    (2.1)

    where \(o_{i}\), \(\mathrm{low}_{}\) and \(\mathrm{up}_{i}\) illustrate the \(i^{th}\) object in a crowd, lower and upper bound of the search area.

    For initializing the volume and density for the each object in the search domain during the search process, Eqs. (2.2–2.3) are applied:

    $$\begin{aligned} d_{i}&=\mathrm{rand} \end{aligned}$$
    (2.2)
    $$\begin{aligned} v_{i}&=\mathrm{rand}. \end{aligned}$$
    (2.3)

    Further, initialize the acceleration of the each object by Eq. (2.4):

    $$\begin{aligned} a_{i}=\mathrm{low}_{i}+r \times (\mathrm{up}_{i}-\mathrm{low}_{i}). \end{aligned}$$
    (2.4)

    During this stage, it assesses the initial crowd and identifies the best object with the help of best fitness score.

  • Modify volume and densities The volume and density of object have been modified by Eqs. (2.5–2.6);

    $$\begin{aligned} v_{i}^{t+1}&=v_{i}^{t} +r \times (v_\mathrm{best}-v_{i}^{t}) \end{aligned}$$
    (2.5)
    $$\begin{aligned} d_{i}^{t+1}&=v_{i}^{t} +r \times (d_\mathrm{best}-d_{i}^{t}) \end{aligned}$$
    (2.6)

    where r, \(d_\mathrm{best}\) and \(v_\mathrm{best}\) illustrate the random number, density and volume linked with the best object found so far, respectively.

  • Density factor and transfer operator The following mathematical equations have been used for transform search from exploration to exploitation:

    $$\begin{aligned} T_{f}=\mathrm{exp}\left( \frac{t-t_\mathrm{max}}{t_\mathrm{max}} \right) \end{aligned}$$
    (2.7)

    where t and \(t_\mathrm{max}\) illustrate iteration number and maximum iterations. Similarly, the density factor has calculated by the following mathematical equation:

    $$\begin{aligned} d^{t+1}=\mathrm{exp}\left( \frac{t-t_\mathrm{max}}{t_\mathrm{max}} \right) -\left( \frac{t}{t_\mathrm{max}} \right) . \end{aligned}$$
    (2.8)

  • Exploration stage If \(t_\mathrm{max}\leqslant 0 \), then object’s acceleration updated by the following mathematical equation is:

    $$\begin{aligned} a_{i}^{t+1}=\frac{d_{mr}+v_{mr} \times a_{mr}}{d_{i}^{t+1} \times v_i^{t+1}} \end{aligned}$$
    (2.9)

    where \(d_{i}\), \(a_{i}\) and \(v_{i}\) illustrate the density, acceleration and volume of object i.

  • Exploitation stage If \(t_{max}>0\), then the acceleration updated by the following mathematical equation is:

    $$\begin{aligned} a_{i}^{t+1}=\frac{d_\mathrm{best}+v_\mathrm{best} \times a_\mathrm{best}}{d_{i}^{t+1} \times v_i^{t+1}} \end{aligned}$$
    (2.10)

    where \(a_\mathrm{best}\) is denoted the acceleration of the superior object.

  • Normalize acceleration For evaluating the % of change, the normalize acceleration equation is applied:

    $$\begin{aligned} a_{i-\mathrm{norm}}^{t+1}=u\times \frac{a_{i}^{t+1}-\mathrm{min}\left( a \right) }{\mathrm{max}\left( a \right) -\mathrm{min}\left( a \right) }+l \end{aligned}$$
    (2.11)

    where u and l denote the constant parameters; generally, these range set amid 0.9 to 0.1, respectively.

  • Modified location of object If \(t_{F}\le 0.5\), then the next position of object’s is updated by the following equation:

    $$\begin{aligned} x_{i}^{t+1}=x_{i}^{t}+c_{1}\times r \times a_{i-\mathrm{norm}}^{t+1}\times d \times \left( x_{r}-x_{i}^{t} \right) \end{aligned}$$
    (2.12)

    where \(c_{1}=2\) denotes the constant value. Similarly if \(t_{F}>0.5\), then the location of the each object’s is replaced or modified by the following equation:

    $$\begin{aligned} x_{i}^{t+1}=x_\mathrm{best}^{t}+F \times c_{2}\times r \times a_{i-\mathrm{norm}}^{t+1}\times d \times \left( t \times x_\mathrm{best}-x_{i}^{t} \right) \end{aligned}$$
    (2.13)

    where \(c_{2}=6\) denotes the parameter value. F denotes the flag, and it is applied for replacing the position of motion using following equation:

    $$\begin{aligned} F=\left\{ \begin{matrix} +1 &{}\quad \mathrm{if} &{} p\le 0.5 \\ -1 &{} \quad \mathrm{if} &{} p>0.5 \end{matrix}\right. \end{aligned}$$
    (2.14)

    where \(p=2\times r-c_{4}\).

  • Calculation The fitness function is used for identifying the best solution so far, and select \(x_\mathrm{best}\), \(d_\mathrm{best}\),\(v_\mathrm{best}\) and \(a_\mathrm{best}\), respectively.

2.1 Pseudo-code of AOA

The pseudo-code of AOA is illustrated by Algorithm 1.

figure a

3 Modified Archimedes Optimization Algorithm with Levy Fight (LAO)

The AOA is the most recent algorithm. It is developed for tackling the complex issues of the different domains. But due to some shortcomings, it faced some issues such as premature convergence, and producing incompetent solutions is still persisting. The levy flight phase has been applied in the position update equation of the object of AOA which can handle these issues. The levy flight is most famous for its own long jumps, so it helps in improving the position of each object in the search area. Additionally, it also helps to ignore the local optima for finding the best score globally. Hence, the enhanced methodology traps the best optima solutions in the search space during the search process without being trapped in local optima. Further, the modification steps are illustrated through the followings sub-sections.

3.1 Constant Settings

During the implementation of the code of the evolutionary algorithms, various constant have been fixed such as crowd size (\(N=30\)), total number of iterations (\(t_{\max }=500\)) and constants (\(c_{3}=1\) & \(c_{4}=2\)). In literature, it could be seen that the performance and robustness of the algorithm depend on the parameter settings. The above parameter settings are most famous due to their best balance. With this fact, in this research, the same parameter settings have been taken.

3.2 Initialization

Under implementation, the value of each variable of problem denotes the location of each object in the search domain. Here, the position of each object is assigned by equations (2.1–2.4).

3.3 Fitness Evaluation

The best and worst fitness of each object at every iteration has been calculated by the following equations:

$$\begin{aligned} F_\mathrm{best}&=\mathrm{Min} (\mathrm{fit}_{j}(z)) \, \, j \varepsilon (1,2,...,n) \end{aligned}$$
(3.1)
$$\begin{aligned} F_\mathrm{worst}&=\mathrm{Max} (\mathrm{fit}_{j}(z)) \, \, j \varepsilon (1,2,...,n) \end{aligned}$$
(3.2)

where \(F_\mathrm{best}\) and \( F_\mathrm{worst}\) illustrate the best and worst fitness for minimization functions.

3.4 Lévy Flight

The lévy flight [50] is a random walk in which the step lengths have a Lévy distribution and is a non-Gaussian r process. This is simple power law mathematical formula \(L(s)\sim \left| s \right| ^{-1-\beta }\), where \(0<\beta <2\) is an index. Generally, it is most famous for its long jump, which helps in improving the premature convergence of the evolutionary algorithms. Mathematical formulation of lévy flight has been illustrated in the following forms [51] and [52]:

$$\begin{aligned} L\left( s,\gamma ,\mu \right) =\left\{ \begin{array}{lll} \sqrt{\frac{\gamma }{2\pi }}\times exp\left[ -\frac{\gamma }{2(s-\mu )} \right] \frac{1}{(s-\mu )^{\tfrac{3}{2}}} &{}\quad \mathrm{if} &{} 0< \mu< s < inf \\ 0 &{}\quad \mathrm{if} &{} s \le 0 \end{array}\right. \end{aligned}$$
(3.3)

where \(\mu \) and \(\gamma >0\) illustrate the scale factor or parameters. This distribution can be formulated in the form of Fourier transform as :

$$\begin{aligned} F(k)=exp\left[ -\alpha \left| k \right| ^{\beta }\right] , \,\, 0<\beta \le 2 \end{aligned}$$
(3.4)

where \(\alpha \) shows the scale factor, and it lies amid \(\left[ -1,1 \right] \) interval, and \(\beta \epsilon (0,2]\) denotes the index of stability. In some special case for \(\beta =1\), the integral can be carried out analytically, and it is also called Cauchy distribution. Mathematically, it can be formulated in the following form:

$$\begin{aligned} F(k)=exp\left[ -\alpha \left| k \right| \right] , \,\, 0<\beta \le 2. \end{aligned}$$
(3.5)

Similarly, when \(\beta =2\), the distribution corresponds to Gaussian probability distribution as

$$\begin{aligned} F(k)=exp\left[ -\alpha k^{2} \right] . \end{aligned}$$
(3.6)

Here, \(\alpha \), \(\beta \), \(\mu \) and \(\gamma \) show the major and minor part in determination of the probability distribution. The \(\beta \) plays a role for controlling the shape of prob-distribution and to make longer jumps because there will be a big tail [53]. Other side, the \(\alpha \) denotes the skew position. When \(\alpha =0\), it indicates the prob-distribution is symmetric. The \(\gamma \) and \(\mu \) illustrate the width and shift of the prob-distribution peaks [54].The distinct values of \(\beta \) work to change the prob-distribution. It makes big jumps for least constant value, whereas it makes smaller jumps for large constant value.

Modified Position of Object

After studying the details that how probability distribution performed by applying levy flight, here, we are applying the levy phase for enhancing the following position update Eq. (2.13) of AOA for finding the location values of new object. When generating the new outcome or solution \( x_{i}^{t+1}\) for the \(i^th\) outcome \(x_\mathrm{best}^{t}\) by performing levy flight, the new search agent \( x_{i}^{t+1}\) is illustrated as follows:

Here, if \(t_{F}>0.5\), then

$$\begin{aligned} x_{i}^{t+1}=x_\mathrm{best}^{t}+F \times c_{2}\times r \times a_{i-\mathrm{norm}}^{t+1}\times d \times \left( t \times x_\mathrm{best}-x_{i}^{t} \right) \oplus Levy(\beta ) \end{aligned}$$
(3.7)

where \(c_{2}=6\) and \(\oplus \) denote the parameter value and entry-wise multiplications.

In Mantegna Algorithm, the step size s can be defined as follows:

$$\begin{aligned} s=\mathrm{random}(\mathrm{size}(d))\oplus \mathrm{levy}(\beta )\sim 0.01\frac{u}{\left| v \right| ^{1/\beta }} \times \left( t \times x_\mathrm{best}-x_{i}^{t} \right) \end{aligned}$$
(3.8)

where random(size(d)) is a random step size parameter, \(\beta \) is a Levy Flight distribution parameter,t represents the number of iterations, and v and u are drawn form normal probability distribution, such as

$$\begin{aligned} u\sim N(0,\sigma _{u}^{2})v \sim N(0,\sigma _{v}^{2}) \end{aligned}$$
(3.9)

with

$$\begin{aligned} \sigma _{u}=\left\{ \frac{\Gamma (1+\beta )sin(\frac{\pi \beta }{2})}{\Gamma [(\frac{1+\beta }{2})]\beta ^{(\beta -1)/2} } \right\} \,\,\, \sigma _{v}=1. \end{aligned}$$
(3.10)

Here, \(\Gamma \) and s illustrates the standard gamma function and step size sample.

The F denotes the flag, and it is applied for replacing the position of motion using Eq. (2.14). If \(t_{F}\le 0.5\), then the next position of each object’s is updated by Eq. (2.12).

3.5 Stopping condition

At the end, stopping condition has been utilized for updating the new location of each object. These criteria are continuously repeated until it satisfies the criteria of prevention for example whether it reaches the highest no. of generations or the output is found earlier.

And the rest of the operations are same as AOA algorithm.

3.6 Pseudo-Code of LAO

The pseudo-code of LAO is illustrated by Algorithm 2.

figure b

4 Results Analysis and Discussion of CEC 2017 Test Suites

For verifying the robustness and accuracy of the LAO method, a comprehensive simulation has been executed. For assessment, numerous recent robust optimizers such as SCA [21], Chimp [23], SBPO [55] and AOA [22] algorithms have been compared with the proposed LAO method.

Table 1 Summary of the CEC 2017 test suite
Full size table

4.1 Constant Settings and CEC 2017 Test Suites

The code of all evolutionary methods have been coded in R2018a for testing the robustness of the algorithms. Under the implementation of the evolutionary algorithms, the various constant settings have been fixed such as total number of objects (30) and maximum iterations (500).

To examine the robustness of the proposed LAO method, a well-known 29-CEC 2017 test suite has taken [56] and shown in Table 1. The 3D graphs of these test suites are also shown in Fig. 1. In CEC 2017, 29-test suites involved, which have been divided into four categories such as unimodal, simple multimodal, hybrid and composition test suites. Multimodal test suites are applied to testing competing evolutionary algorithms to ignore adaptation as these suites have various local optima values. Additionally, composite test suites have applied to examine the balance amid the exploration and exploitation phases (Table 2; Fig. 2).

Experimental optimal solutions of the evolutionary algorithms on 29-CEC 2017 standard test suites are given in Tables (3, 4 and 5) in terms of min and max objective values, average and standard scores, etc. The convergence graphs have been plotted of evolutionary methods through Figs. 3, 4, 5 and 6. In these graphs, the x-axis and y-axis illustrate the number of iterations and best solutions so far, etc.

The least and maximum score of the objective function represents the best outputs of the evolutionary algorithms. Results of tables show that the LAO method is able to find the best optima for 29-CEC 2017 standard test functions as compared to others. The least average and standard scores are proved the superior stability and fast convergence speed of the LAO method as compared to others. Hence, all simulations have proven that the LAO method is able to provide best global optima solutions in the complex domains as compared to SCA, Chimp, SBPO and AOA methods.

In addition, the more explanation of the LAO results have been illustrated through the following sub-sections.

Fig. 1
figure 1

Graphs of CEC 17 standard test suites

Full size image

4.2 Discussion

To examine the robustness of the LAO algorithm, 29-CEC 2017 test suites have been used which are shown in Tables 3–5. These test suites have been divided into three distinct phases, such as: Firstly, unimodal test suites, which have been used for evaluating the exploitation capability; secondly, the multimodal test suites, which have been used to find the best score on many local optima which verified the capability of the algorithms; and at the end, hybrid and composite test suites which have been used to verify the exploitation performance of the evolutionary algorithms.

4.3 Exploitation Ability

Unimodal test suites have only one global compatibility which is used to evaluate the exploitation phase. Experimental results of evolutionary algorithms in tables show that the proposed method is competent to give better optima than others. Hence, results reveal that the LAO method has demonstrated superior exploitation abilities that outperform than others. The objective of these best results is that the modification of algorithms allowed the problem to reach the optima. Hence, the experimental output shows that the LAO method has a better exploitation behavior which is significant for numerous issues of compatibility that are essential to be addressed. As stated formally, unimodal CEC 2017 standard test suites are more appropriate for the benchmarking evolutionary algorithms. Experiments prove that the proposed method is highly functional. In addition, this modification shows that it is most effective and successful for finding the solution of complex issues in the complex domains.

4.4 Capability Assessment

Multimodal test suites contain various variables and local global optima which exceeds exponentially with the size of function as compared to these unimodal test suites. In general, these are used for testing the suitability of the evolutionary methods. Hence, simulation concluded that the LAO method reaches a sophisticated finding competency.

4.5 Exploration and Exploitation

Hybrid and composition test suites are normally utilized to assess the capability of local optima survivors and the stability amid exploitation and detection, which comprises a huge amount of local and global optima. Results show that the LAO method is able to create a best balance during exploitation or detection. Due to that fact, LAO method provides a huge amount of optima in the complex domain due to the levy flight. Levy flight helps in creating a new location for all objects at each generation and amend the current position of each object to the highest position in many aspects that make it possible for the LAO method to reach the optima solution. In these test suites, a huge level of complex search spaces are involved, while this high exploration is needed for finding the accurate optima outputs. The solutions of these test suites prove that the LAO method has an high scan ability which leads this to the best global optimizer.

Additionally, the LAO method involves the high-level local optima avoidance capacity. This quality helps the proposed method to reach up to the best optima fastly. So the proposed method can enhance the search space and find areas of ease of discovery by improving the number of local optimas.

4.6 Exactness

Evolutionary method exactness on 29-CEC 2017 test suites is given in Table 2.This performance has been designed through the results of Table (4). Average scores in Table 2 have been divided into two different phases such as worst (W) and best (B), respectively. In general, least average scores show the exactness of the algorithms for the best optima’s. Experiments prove that the LAO method is able to find the best optima on maximum standard suites against least average scores as compared to others. These efforts show the exactness of the proposed method, and results provide strong evidence that proposed method is able to provide accurate solutions for highly complex space issues.

Table 2 Average values of algorithms on CEC 2017 standard test suites
Full size table
Fig. 2
figure 2

Standard deviation (sd) scores algorithms on 29-CEC 2017 standard test suites

Full size image
Table 3 Numerical performance of evolutionary algorithms on the 29-CEC 2017 test suits
Full size table
Table 4 Average values (\(\mu \)) of evolutionary algorithms on the 29-CEC 2017 test functions
Full size table
Table 5 Standard deviation values (sd) of evolutionary algorithms on the 29-CEC 2017 test functions
Full size table
Fig. 3
figure 3

Convergence graphs of evolutionary algorithms on unimodal test functions

Full size image
Fig. 4
figure 4

Convergence graphs of evolutionary algorithms on simple multimodal test functions

Full size image
Fig. 5
figure 5

Convergence graphs of evolutionary algorithms on hybrid test functions

Full size image
Fig. 6
figure 6

Convergence graphs of evolutionary algorithms on composition test functions

Full size image

4.7 Stability

As in the literature, the stability of the algorithms have been verified through standard deviation (sd) scores. So the stability of the algorithms has been discussed statistically. Each (sd) score of all algorithms on 29-CEC 2017 standard test suites is plotted in Fig. 2. These graphs show that the proposed method is able to find the best optima against least (sd) scores, and these sd scores are near to zero on maximum standard suites, and it means that the LAO is stable on the CEC suites that were performed. These efforts show the fast convergence performance of the proposed method against the others. Hence, on the basis of these solutions, we can say that this strategy can trap the best optima’s fastly as compared to others.

4.7.1 Convergence Performance

Now, we are describing the performance of the algorithms through the convergence graphs on 29-CEC 2017 standard test suites. All these graphs are shown in Figs. 3, 4, 5 and 6. Graphs have been plotted through x-axis and y-axis, where x-axis illustrates the number of iterations and y-axis shows the obtained best global optima so far. In these graphs, we can easily see how much each algorithm takes the number of periods to find the best optima against the number of generations. As per study of Berg et al. [57], this behavior can assure that the algorithms ultimately converge to a point and are found locally.

With these reasons, further we can discuss how to trap the optima by LAO method in the search space. Each object moves from high value to low value, so with the assumption of strength of LAO, all objects and their fitness are modified during generations. With this strategy, we save the best optima for searching the next best optima which helps the objects to find the next new position or best optima’s. Based on these graphs, we concluded that the LAO method can provide the best optima against the least number of iterations as compared to others. This proposed methodology also can help in saving time for complex issues and is able to resolve very difficult problems.

Summing up, on the basis of all simulations, we concluded that the proposed methodology can tackle the complex issues strongly.

5 Antenna Design Problems

5.1 Microstrip Patch Antenna-I

Nowadays, it is widely accepted that growing societies are increasingly distinguished by—more aged, less mobile/healthy, rising cost of medical processes and even the declining financial assets. To tackle all these problems, telemedicine/telecare including primitive measures to observe patients in a timely fashion within their own home is just the beginning to provide a cost-effective and less painful solution in comparison with treatment in hospitals/other institutions. Moreover, it is generally found that most of the patients in such critical situations prefer to be monitored within their own home environment. To solve all such issues, wearable textile antennas attracted more attention in past few years. Their rapid growth of wireless body area networks has increased its scope in applications like medical, sports, emergency services like firefighters, detectives and police, etc. In all these applications, wearable antenna is integrated in clothes which transfer the data from the sensors that are placed on body to central database/station. Traditional wearable systems were bulky due to large size of batteries and antenna. But due to the latest advancements in fabrication technologies, nowadays, size of wearable systems is getting miniaturized, and textile materials are being used in fabrication of antennas. The various features like effective cost, low profile, lightweight, easy realization and its bending and crumbling features make textile microstrip patch antennas more suitable candidate for WBAN applications.

Based on research point of view, the motive of this work is to design a wearable textile microstrip patch antenna, which will operate in 2.3 GHz band. The fitness function to be maximized is illustrated in Eq. (5.1):

$$\begin{aligned} F=-S_{11} \,\, \, \, (2.3 \, \, \mathrm{GHz}) \end{aligned}$$
(5.1)

The performance parameters like return loss, gain, bandwidth and VSWR of the antenna are measured. Finally, the performance of antenna is enhanced by applying the improved LAO optimization algorithm.

5.1.1 Antenna Design Material

The conductive material used for designing and fabrication of proposed antenna is copper foil tape (CFT). It is used as it has flexibility, high conductivity, i.e., \(5.88 \times 107\) and low thickness of 0.14 mm. The textile materials polyester is chosen to make substrate of antenna because of its availability, durability and inelasticity. Moreover, textile substrate-based antennas can be easily integrated into clothes without interfering with the user’s comfort. The textile material used along with its properties is given in Table 6.

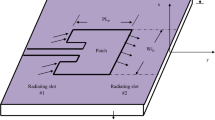
5.1.2 Proposed Antenna Geometry

The proposed antenna details are shown in Fig. 7. The overall size of the antenna is \(32 \mathrm{mm} \times 40\,\mathrm{mm}\), while the thickness of the substrate varies with the type of textile fabric. The permittivity of 1.6 and loss tangent 0.02 have been taken during this design. The feed to antenna is provided by a microstrip feed whose width is taken as \((W_{f}=2.52)\) mm and length \((L_{f}=19.5)\) to match the impedance properly. There is no ground metallization underneath the radiator for appropriate procedure. The proposed antenna’s design is quite simple which is modified from rectangular patch shape. The radiating patch is glass-shaped geometry with partial ground plane that results in wider bandwidth coverage, and it is below the feed line on other side of the substrate. The initial geometry of patch is shown in Fig. 7 and Eq. 5.2.

$$\begin{aligned} P_{0}&=(x_{0},y_{0}) \nonumber \\ P_{1}&=(x_{1},y_{0}+\Delta y_{1}) \nonumber \\ P_{2}&= (x_{2},y_{0}+\Delta y_{1}+\Delta y_{2}) \nonumber \\ P_{3}&= (x_{3},y_{0}+\Delta y_{1}+\Delta y_{2}+\Delta y_{3}) \nonumber \\ P_{4}&= (x_{4},y_{0}+\Delta y_{1}+\Delta y_{2}+\Delta y_{3}+\Delta y_{4}) \nonumber \\ P_{5}&= (x_{5},y_{0}+\Delta y_{1}+\Delta y_{2}+\Delta y_{3}+\Delta y_{4}+\Delta y_{5}) \nonumber \\ P_{6}&= (-x_{5},y_{0}+\Delta y_{1}+\Delta y_{2}+\Delta y_{3}+\Delta y_{4}+\Delta y_{5}) \nonumber \\ P_{7}&= (-x_{4},y_{0}+\Delta y_{1}+\Delta y_{2}+\Delta y_{3}+\Delta y_{4}) \nonumber \\ P_{8}&= (-x_{3},y_{0}+\Delta y_{1}+\Delta y_{2}+\Delta y_{3}) \nonumber \\ P_{9}&= (-x_{2},y_{0}+\Delta y_{1}+\Delta y_{2}) \nonumber \\ P_{10}&=(-x_{1},y_{0}+\Delta y_{1}) \nonumber \\ P_{11}&=(x_{0},y_{0}) \end{aligned}$$
(5.2)
Table 6 Textile material used for designing proposed antenna
Full size table
Fig. 7
figure 7

Geometry of antenna

Full size image
Fig. 8
figure 8

Reflection coefficient (dB) versus frequency and imaginary graphs of LAO and AOA algorithms on microstrip patch antenna

Full size image
Fig. 9
figure 9

Reflection coefficient (dB) versus frequency and imaginary graphs of PSO algorithm on microstrip patch antenna

Full size image

5.1.3 Discussion on Results of Antenna-I

In this work, we have optimized ten constants (\(x_{1}\) to \(x_{5}\) and \(\Delta y_{1}\) to \(\Delta y_{5}\)) for designing the polyester patch antenna. For designing the antenna, three different algorithms have been applied. Computer simulation tool (CST) software is used for designing and simulation of the antennas. The results of polyester-based antenna is given in Table 12 in terms of resonant frequency return loss, bandwidth and gain. This polyester patch antenna has been designed in the following form.

Simulated and optimized solutions are given in Table 12. The performance of the metaheuristics is shown in Figs. (8, 9, 10, 11, 12, 13 and 14). The tabulated results of Table 12 shows that the robustness of LAO algorithms in giving best solutions such as the resonant frequency (2.257 GHz), return loss (\(-\,\)44.68335), band width (589.684161 MHz) and gain (2.23 dB), respectively. All simulations proved that the proposed method is able to give the best optimal values to design a new antenna as compared to AOA algorithm (Fig. 15).

Fig. 10
figure 10

Simulated and measured VSWR of the antenna

Full size image
Fig. 11
figure 11

Performance efficiency of metaheuristics

Full size image
Fig. 12
figure 12

Admittance/s performance of metaheuristics

Full size image
Fig. 13
figure 13

Impedance/Ohm performance of metaheuristics

Full size image
Fig. 14
figure 14

S-parameters balance for designing the antenna

Full size image

5.2 Microstrip Patch Antenna (MPA)-II

The basic structure of microstrip patch antenna (MPA) is shown in Fig. 16. The Shield lt super is a rugged rip-stop fabric which used to design the patch antenna ground plane and conductive element. This fabric is manufactured by less EM Incorporated, USA [58] with weight 30 \(g/m^{2}\), thickness (t) of 0.17 mm, conductivity of \(6.67 \times 10^{5}\) and \(R_{s} < 0.5 \Omega \) and a surface resistivity, respectively. During this work, we are using the sheildlt super and jeans fabric to design the antenna. During this work, I have taken permittivity (\(\varepsilon _{r}\)) of 1.70, thickness (h) of 1.00 mm and loss tangent of 0.025 [59]. If (\(\varepsilon _{r}\)) is < 2.0, then MPA can create a higher gain with effective efficiency [60].

The ground dimension and line feed values have been optimized by the metaheuristics, and gain graphs have been plotted by ADS software on the basis of obtained optimized values.

R-MATLAB-2018a and ADS (Keysight Advanced design system software) have been used for optimizing and plotting the graphs. The main objective is to minimize the return loss and maximize the gain of the following function (\(S_{11}\)) (5.3):

$$\begin{aligned} \mathrm{Fitness} = -S_{11} \,\,\, 2.35\,GHz \leqslant f \leqslant 2.45\,GHz \end{aligned}$$
(5.3)

Figure 17 illustrates the layout of the wearable MPA fed by an edge. Figure 18 shows the structure of the wearable MPA with jeans and Shield lt super fabrics (Tables 7, 8). The simulated and optimized values are given in the Table 9. The MPA performance have been verified in the terms of gain, impedance matching, three 3d-dim radiation pattern and return loss (\(S_{11}\)), respectively. Here, the least loss and maximum gain values of the fitness function show the best optima result for the wearable MPA, while the reflection coefficient of \(S_{11}\) should be less than \(-\,10\) dB [60].

The simulated, optimized, return loss and maximum gain solutions of wearable MPA are given in Tables 9 and 10. The return loss and gain of the wearable MPA is plotted by Figs. 19 and 20. These results have been obtained in the form of total return loss and maximum gain (in dB), respectively. Here for wearable MPA antenna-II, the LAO algorithm gives the total return loss \(-\,35\) and gain 2.7 at \(f_{c}\)=2.40 GHz, AOA shows total return loss \(-\,34.1023\) and gain 2.601 at \(f_{c}\)=2.40 GHz while [61] used jeans and denim fabric and clearly gives that the return loss \(-\,34.4530\) with maximum gain 2.689. The optimized results of the proposed LAO method is more superior than the output found by [61], in [62] using polyester fabric where return loss was \(-\,30.1520\) at \(f_{c}\)=2.4 GHz, in [60] using wash cotton fabric where return loss was \(-\,26.4300\) at \(f_{c}\)=2.4 GHz, \(f_{c}\)=2.45 GHz, in [59] using jeans fabric where the return loss was \(-\,18.7741\) at \(f_{c}\)=1.58 GHz and felt fabric shows return loss \(-\,17.3900\) at \(f_{c}\)=2.39 GHz by [58]. All simulation shows that the proposed LAO method is able to find the best optima results for wearable MPA as compared to others.

5.3 Microstrip E-Shaped Patch Antennas

In this section, we are trying to optimize the E-shaped patch antenna. This antenna was optimized by [63] by particle swarm optimization (PSO). During implementation on the dual-frequency antenna, it operated at 1.8–2.4 GHz frequency, while the antenna had a bandwidth from 1.79–2.43 GHz (30.5 %). Similarly, this antenna was also optimized by the MPSO algorithm by [64]. During the designing of these antennas, we had taken dielectric constant 2.55, microstrip line at (W/2,\(L_{f}\)), fixed width (\(W_{l}\)=5.6 mm), respectively.

In [46], the enhanced version of central force optimization (CFO) has been proposed for optimizing the E-shaped patch antennas. The performance of the modified version has been compared with the differential evolution (DE) algorithm. On the behalf of all simulation, it has been shown that the CFO optima solutions are near DE solutions. Here, we are implementing new proposed LAO and AOA algorithms on microstrip line-fed E-shaped patch antennas in order to evaluate the robustness of the proposed algorithm in such real antenna issues.

For ignoring the overlap issue in IE3D simulations, the following restrictions have been taken for this antenna: [64].

$$\begin{aligned}&P_{s}+2W_{s}<W \nonumber \\&L_{s}<L, \,\, L_{f}<L \nonumber \\&P_{s}>W_{l}+2W_{f} \, or \, P_{s}+2W_{s}<W_{l} \nonumber \\&when\,\, L_{s}+L_{f}>=L \end{aligned}$$
(5.4)
Fig. 15
figure 15

Polyester patch antenna

Full size image
Fig. 16
figure 16

Shapes of MPA antenna-II

Full size image

The proposed LAO and AOA algorithms have been applied on the following two different fitness functions to evaluate the robustness of the algorithms. Under this implementation, the resonance frequencies have been fixed such as \(f_{r}\)=2.4 GHz) and (\(f_{r}\)=2.4 GHz to 2.484 GHz).

$$\begin{aligned} Fitness&= -S_{11}(2.4 GHz) \end{aligned}$$
(5.5)
$$\begin{aligned} Fitness&= -S_{11} \,\,\, 2.4 GHz \leqslant f \leqslant 2.484 GHz \end{aligned}$$
(5.6)

Experimental results of the algorithms are illustrated in tables. During the comparison of the optima solutions of the algorithms in tables, results show that the proposed method gives highly effective solution on these functions in comparison with CFO, DE and MPSO algorithms. For first function, the proposed method provides return loss \(-\,\)88 dB, bandwidth 45.76 and for second function the fitness value \(-\,\)0.15432, return loss \(-\,\) 16.44 dB and SWR < 1.32 respectively.

Table 7 Optimized values
Full size table

Simulated results proved that the proposed method gives larger bandwidth, best fitness, SWR and return loss than the CFO, DE and MPSO algorithms. Hence, all the evidences shows that the proposed method is able to gives the best solutions for these real antenna issues (Tables 11, 12).

Summing up, the proposed method is able to provide the best solutions to the complex space functions and real antenna issues.

Fig. 17
figure 17

Edge feeding method of MPA antenna-II

Full size image
Fig. 18
figure 18

Wearable MPA antenna-II with Jeans and Shield lt super fabrics

Full size image
Table 8 Simulated and optimized results of polyester-based textile antenna-I
Full size table
Table 9 Simulated and optimized results of wearable MPA antenna-II
Full size table
Table 10 Return loss and Gain (in dB) results of Wearable MPA antenna-II
Full size table
Fig. 19
figure 19

LAO return loss graph for wearable MPA

Full size image
Table 11 Simulated and optimized results of E-shaped patch antenna on Eq. (5.5)
Full size table
Table 12 Simulated and optimized results of E-shaped patch antenna on Eq. (5.6)
Full size table
Fig. 20
figure 20

LAO gain graph for wearable MPA

Full size image

6 Conclusion and Future Work

In order to overcome the shortcomings of AOA method such as trap in local optima and incompetent to achieve well global optima due to initial convergence, AOA is merged with levy flight in this effort. This modification is known as the LAO method. The performance of the AOA and LAO method has been verified on 29-CEC 2017 standard test suites. The LAO is in competence to provide superior quality of optima’s in almost each standard test suite and is more influential in utmost of them. In addition, to confirm the robustness of the LAO, it is compared with the most latest algorithms such as SCA, SBPO, Chimp and AOA. The numerical and statistical efforts gives strong evidence that the LAO is more robust than others.

Fig. 21
figure 21

Geometry of E-shaped antenna

Full size image

Additionally, the proposed method has been successfully implemented to design four different microstrip patch antennas. The performance of LAO method has been compared with various metaheuristics in terms of total return loss, maximum bandwidth, total gain, fitness score and SWR. Experiments give strong evidence that the accuracy of the LAO method is able to validate their potential application in antenna design issues (Fig. 21).

In future work, we shall develop various enhanced algorithms for real world and antenna design issues. In the end, we expect this work will encourage the young scientists of different domains, who are recently working on recent evolutionary algorithms and patch antenna issues.