1 Introduction

In modern era, there are a number of industrial and biological situations where we come across the domains that exhibit dilating and squeezing motion. From filling machines to expanding and contracting arteries, this type of situation is very common. Also, in most of the cases, the boundaries moving together or apart are permeable. To understand the flow in such domains can help in understanding the mechanisms precisely. For this purpose, researchers from all over the world have turned their heads toward the study of the flows between dilating and squeezing channels.

The brains behind initiating the study regarding the flow between parallel and permeable plates are Berman. In his pioneering work [1], he studied laminar flow in porous channels. After him, many others followed his footsteps and extended his journey. Some of the most recent and relevant efforts are cited here [2–7]. In the flows between dilating and squeezing walls, the resulting equation is inherently nonlinear. For these equations, the exact solutions are very unlikely. In the studies mentioned above, several analytical as well as numerical methods have been opted to obtain the solutions of the problems.

The study of heat transfer in different equipment, instruments and mechanisms is essential to develop such methods that not only ensure the proper working, but also, the enhancements in the current gear. Thermal analysis of the physical systems gives us such information that can be very handy to increase the performance, reliability and the durability of these systems. Some of such mechanisms are involved in processes like the production of glass sheets, automobile engines, combustion chambers, paper manufacturing and wire coating [8–16].

In the situations where the convective heat transfer plays a less dominant role, the heat transfer through radiation takes control of the total heat transfer and its actions are more dominant. Even in the presence of free or forced convection, the radiation has its own part to play and it affects the total heat transfer in such a way that cannot easily be neglected. Due to this reason, several researchers dedicated their efforts to study and model the radiative heat transfer in different geometries and situations. Some of them can be found here [17–21].

In our literature exploration, we have come to know that the effects of thermal radiation have not been studied for the flows through dilating and squeezing domains. In this article, we have studied the effect of nonlinear thermal radiation in the flow of a viscous fluid between two infinite plates. The lower plate is fixed, solid and heated, while the upper plate is permeable and moving up and down yet remaining parallel to the lower plate. After obtaining the governing system of ordinary differential equations, we have solved it by using a finite element method known as Galerkin method. The results are compared with the solution obtained by a mathematical software Maple. A good agreement between the solutions has been found that is displayed in the form of tables. The effects of relevant physical parameters on the temperature distribution are highlighted with the help of graphs. An appropriate explanation of the events presented in the graphical results is also provided.

2 Mathematical exploration

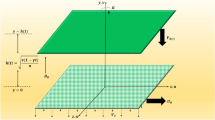
We intend to explore the effects of nonlinear thermal radiation on the flow of a Newtonian fluid between two infinite parallel plates. The lower plate is solid, fixed and heated, while the upper plate is permeable and is moving uniformly toward, or away from the lower plate at a time (t) dependent rate \(\dot{h}\left( t \right)\). The Cartesian coordinate system is considered in such a way that the horizontal axis coincides with the lower plate. The configuration of the axes in presented in Fig. 1.

Fig. 1
figure 1

Geometrical description of the problem

Full size image

The components of velocity along \({\grave{x}}\) and \({\grave{y}}\) axes are denoted by \({\grave{u}}\) and \({\grave{v}}\), respectively. To cool down the lower plate, a coolant is injected through the porous plate at a uniform speed v w . We shall also be interested in examining the case when the fluid is sucked out from the same plate at the same speed. The conduction fluxes as well as the dissipative disturbance, along the tangential direction, are neglected.

For the current problem, Navier–Stokes equations take the following form [3, 4];

$$\frac{{\partial \grave{u}}}{{\partial \grave{x}}} + \frac{{\partial\grave{v}}}{{\partial \grave{y}}} = 0,$$
(1)
$$\frac{{\partial \grave{u}}}{\partial t} + \grave{u} \frac{{\partial \grave{u}}}{{\partial \grave{x}}} + \grave{v} \frac{{\partial \grave{u}}}{{\partial \grave{y}}} = - \frac{1}{{\grave{\rho}}}\left({\frac{{\partial \grave{p}}}{{\partial \grave{x}}}} \right) + \upsilon\,\left({\frac{{\partial^{2} \grave{u}}}{{\partial \grave{x}^{2}}} + \frac{{\partial^{2} \grave{u}}}{{\partial \grave{y}^{2}}}} \right),$$
(2)
$$\frac{{\partial \grave{v}}}{\partial t} + \grave{u} \frac{{\partial \grave{v}}}{{\partial \grave{x}}} + \grave{v} \frac{{\partial \grave{v}}}{{\partial \grave{y}}} = - \frac{1}{{\grave{\rho}}}\left({\frac{{\partial \grave{p}}}{{\partial \grave{y}}}} \right) + \upsilon\,\left({\frac{{\partial^{2} \grave{v}}}{{\partial \grave{x}^{2}}} + \frac{{\partial^{2} \grave{v}}}{{\partial \grave{y}^{2}}}} \right),$$
(3)
$$\frac{{\partial \grave{T}}}{\partial t} + \grave{u}\frac{{\partial \grave{T}}}{{\partial \grave{x}}} + \grave{v}\frac{{\partial \grave{T}}}{{\partial \grave{y}}} = \beta \left({\frac{{\partial^{2} \grave{T}}}{{\partial \grave{x}^{2}}} +\frac{{\partial^{2} \grave{T}}}{{\partial \grave{y}^{2}}}}\right) - \frac{1}{{\grave{\rho} c_{\text{p}}}}\left({\frac{{\partial\grave{q}_{r}}}{{\partial \grave{x}}} + \frac{{\partial\grave{q}_{r}}}{{\partial \grave{y}}}} \right),$$
(4)

where \(\upsilon,\,\grave{p},\,T\) and c p represent kinematic viscosity, dimensional pressure, dimensional temperature and the specific heat under constant pressure, respectively. Besides, \(\beta = k/\grave{\rho}c_{\text{p}}\) is thermal diffusivity that depends on thermal conductivity (k), density (\(\grave{\rho}\)) and c p. Furthermore, the term \(\grave{\rho}_{r}\) in Eq. (4) represents the net heat radiation flux. The expression, approximating the radiative diffusion, is proposed by Rosseland and is given by [22]

$$\grave{q}_{r} = - \frac{{16\grave{\sigma}\grave{T}^{3}}}{{3a_{\text{R}}}}\frac{{\partial \grave{T}}}{{\partial \grave{y}}},$$
(5)

In above equation, \(\grave{\sigma}\) symbolizes Stefan–Boltzmann constant and a R denotes Rosseland mean absorption coefficient.

By following [4], the auxiliary conditions can be written as follows:

$$\begin{aligned}{\text{at}}\,\grave{y}&=0,\hfill\\ \grave{u} &= \grave{v} = 0\quad {\text{and}}\quad \grave{T} =\grave{T}_{\text{l}},\end{aligned}$$
(6)
$$\begin{aligned} {\text{at}}\,\grave{y} &= h\left(t \right), \hfill \\ \grave{u} &= 0,\quad \grave{v} = - A_{\text{u}} \dot{h} = - v_{w}\quad {\text{and}}\quad \grave{T} = \grave{T}_{\text{u}}, \hfill \\ \end{aligned}$$
(7)

where \(\grave{T}_{\text{l}}\) is the temperature of the heated plate. Moreover, \(\grave{T}_{\text{u}}\) is the temperature at the upper wall where the coolant is injected from.

Equations (1)–(3) can be reduced to a single, fourth-order, ordinary differential equation (ODE). It can be achieved by implementing the similarity transform proposed by [2] and [23]. The transformation is given as under

$$\varpi = \grave{y}/h,\quad \grave{u} = \upsilon \,\grave{x}\grave{F}_{\varpi}/h^{2},\quad \grave{v} = - \upsilon\grave{F} \left({\varpi, t} \right)/h.$$
(8)

In Eq. (8), the subscript ϖ represents the differentiation with respect to ϖ. As the process of this transition has been explained in many studies [2–4], so we feel appropriate to mention only the essential ingredients and skip the details about the process of reduction. The ultimate result is a non-dimensional ODE that is given as follows:

$$\grave{f}^{{\left({iv}\right)}} + \alpha \left({\zeta\,\grave{f}^{\prime\prime\prime} + 3\grave{f}^{\prime\prime}}\right) + R\left({\grave{f} \grave{f}^{\prime\prime\prime} -\grave{f}^{\prime} \grave{f}^{\prime\prime}} \right) = 0,$$
(9)

where \(\alpha = h \dot{h}/\upsilon\) and \(R = h v_{w} /\upsilon\) denote the dimensionless wall reformation rate and the permeation Reynolds number, respectively. As customary, the positive value of α represents the parting motion of the upper plate and the positive value of R represents the injection of the fluid. Besides, the primes denote the differentiation with respect to ϖ. It is worth mentioning that Boutros et al. [24] obtained a similar equation by using the Lie group symmetries.

The non-dimensional variables have been obtained by using the following normalizing scales:

$$\grave{u} = \grave{u}/\dot{h},\quad \grave{v} =\grave{v}/\dot{h},\quad \grave{x} = \grave{x}/h,\quad \grave{f} =\grave{F}/R.$$
(10)

The supporting conditions for the velocity profile, after being non-dimensionalized, can be written as [4]

$$\grave{f} \left(0 \right) = \grave{f}^{\prime} \left(0 \right) =\grave{f}^{\prime} \left(1 \right) = 0;\,\grave{f} \left(1\right) = 1,$$
(11)

The Eq. (4), representing the conservation of energy, can be reduced to an ODE by using the following transformation:

$$\grave{T} = \grave{T}_{\text{u}} + \left({\grave{T}_{\text{l}} - \grave{T}_{\text{u}}} \right)\theta \left(\varpi \right).$$
(12)

Equation (12), also transforms the part of the boundary conditions, in Eqs. (6) and (7), associated with the temperature profile. The consequent ODE and the boundary condition are presented, respectively, in the next two equations to follow (see Eqs. 13 and 14).

$$\left({1 + Rd\left({1 + \left({\theta_{w} - 1} \right)\theta}\right)^{3} \theta^{\prime}} \right)^{\prime} + \Pr \left({\alpha\varpi + R\grave{f}} \right)\theta^{\prime} = 0.$$
(13)
$$\theta \left( 0 \right) = 1;\quad \theta \left( 1 \right) = 0.$$
(14)

In Eq. (13), \(\Pr = \beta/\upsilon,\, Rd =16\grave{\sigma}\grave{T}_{\text{u}}^{3}/3a_{\text{R}} k\) and \(\theta_{w} = \grave{T}_{\text{l}}/\grave{T}_{\text{u}}\) represent Prandtl number, radiation parameter and the temperature ratio (between lower and upper plates), respectively.

The dimensionless expression, representing the local rate of heat transfer also known as Nusselt number, can be obtained by using the following relation:

$${\text{Nu}} = \frac{h}{{k\left({\grave{T}_{\text{l}} - \grave{T}_{\text{u}}} \right)}}\left({\grave{q}_{r} + \grave{q}_{w}} \right),$$
(15)

where,

$$\grave{q}_{r} = - k\frac{{\partial \grave{T}^{3}}}{\partial\grave{y}}.$$
(16)

By making use of Eqs. (5), (12), (15) and (16), Nusselt number at lower and upper plates is given as:

$${\text{Nu}} = - \left[ {1 + Rd\left( {\theta_{w} } \right)^{3} } \right]\theta^{{\prime }} \left( 0 \right),$$
(17)
$${\text{Nu}} = - \left[ {1 + Rd } \right]\theta^{{\prime }} \left( 1 \right).$$
(18)

3 Solution of the problem

The system of ordinary differential equation (Eqs. 9 and 13) with the boundary conditions (Eqs. 11 and 14) has been solved by two methodologies. One, using a finite element algorithm known as Galerkin method (GM), and the other, by using built-in methods provide by a mathematical software Maple. It is done to see the relative accuracy of the calculated solutions. Galerkin method as other methods of weighted residual (MWRs) requires a trial solution to initiate the solution process. The trial solution is forged with the help of basis function chosen from a set of orthonormal basis. The residual is calculated by plugging the trail solution into the differential equation. The trail function contains some undermined constants that can be calculated by minimizing the weighted residual in an average sense.

To explain the procedure, let us consider a deferential operator D acting upon a function f(ϖ) to yield a function \(g\left( x \right)\), i.e.,

$$D\left( {f\left( \varpi \right)} \right) = g\left( \varpi \right).$$
(19)

To find the solution of above problem, we consider a trial solution \(\check{f}\left(\varpi \right)\) which is a linear combination of linearly independent base functions. i.e.,

$$f\left(\varpi \right) \cong \check{f} \left(\varpi \right) =\phi_{0} + \sum\limits_{1}^{n} c_{i} \phi_{i},$$
(20)

where ϕ 0 satisfies the essential boundary conditions and c i s are the constants to be determined. These constants are obtained by minimizing the residual error in an average sense. The residual for Eq. (19) after substituting Eq. (20) can be written as

$$R\left(x\right) = D\left({\check{f}} \left(\varpi \right)\right)- g\left(\varpi \right) \ne 0,$$
(21)

If the trail solution is an exact solution the residual vanishes. In fact, it is very rare and mostly we end up with a nonzero residual.

The next step is to construct a weighted residual error with appropriate weights and minimize it to get the values of c i s, that is,

$$\int_{x} {R\left( x \right) W_{i} \left( x \right) = 0} \quad i = 1,2,3, \ldots n,$$
(22)

The above equation, after the selection of proper weight functions, gives us a system of algebraic equation consisting of unknown constants. After solving the resulting system, we get the values of c i s against which the residual error is minimum. By using these values of constants in the trial solution, we get an approximated solution for the original differential equation.

To solve the problem at hand, we can use the following couple of trail solutions.

$$\check{F}\left(\varpi \right) = 3\varpi^{2} - 2\varpi^{3} +\sum\limits_{i = 1}^{5} c_{i}\,\left(\varpi \right)\left({\varpi- 1} \right)^{i}.$$
(23)
$$\check{\theta}\left(\varpi\right) = \varpi + \sum\limits_{i =1}^{5} d_{i} \left(\varpi \right)\left({\varpi - 1} \right)^{i}.$$
(24)

By using these as trial functions and following the steps stated above, we can find the approximated solution of the original problem. The following equations display the solution of the problem for a particular set of values of the parameters. i.e., \(R = 1.5:\, \alpha = 1.0: \,\theta_{w} = 1.1: \,Rd = 0.1:\,{ \Pr } = 4.5.\)

$$\begin{aligned}\grave{f} \left(\zeta\right)\cong\check{F}\left(\zeta \right) &=-0.1954653365x^{6} + 0.8756651867x^{5} - 0.737389047x^{4} \hfill\\&\quad -2.370356119x^{3} + 3.427545316x^{2} - 0.0000000001x \hfill \\\end{aligned}$$
(25)
$$\begin{aligned} \theta \left(\zeta \right) \cong\check{\theta}\left(\zeta \right) &= - 1.485749312x^{6} +2.144382664x^{5} + 2.38518252x^{4} \hfill \\ &\quad - 4.92411405x^{3}+ 0.515476060x^{2} + 2.364822102x \hfill \\ \end{aligned}$$
(26)

To compare the results with Maple solutions, we present the following tables. The values of the parameters remain the same as stated above. Table 1 shows the comparison for the velocity profile while the Table 2 does the same for the temperature profile. A very good agreement between both the solutions is clearly visible.

Table 1 Comparison of the results for the velocity profile
Full size table
Table 2 Comparison of the results for temperature profile
Full size table

4 Results and discussion

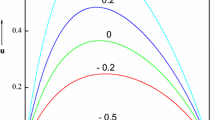
We dedicate this section to explore and analyze the variations in the temperature distribution caused by the relevant physical parameters. The graphs to follow provide a pictorial description of the behavior of the temperature profile under the influence of involved parameters. Figures 2 and 3 display the influence of varying α on the temperature profile ϑ(ϖ) for the suction (R < 0) and injection (R > 0) cases, respectively. It is worth mentioning again that the positive values of α represent the parting motion of the upper plate and the negative values of α describes the case when the upper plate moves toward the lower plate of the channel. Besides, the fixed upper plate is described by the value α = 0. For the suction case (see Fig. 2), the temperature of the fluid increases when the upper plate moves toward the lower plate (α < 0), as the upper plate comes closer to the lower heated plate and the fluid is sucked out from the upper plate, a rise in temperature is logically sane. On the other hand, when the plates go apart, a temperature drop is also evident from the same figure. A lager area of the channel perhaps is a reason behind this drop. For injection case, a similar behavior is shown in the next figure (see Fig. 3); however, this time the temperature has lesser values. These lesser values are a result of injection of a coolant fluid from the upper plate.

Fig. 2
figure 2

Temperature variations due to changing α: suction case

Full size image
Fig. 3
figure 3

Temperature variations due to changing α: injection case

Full size image

Figures 4 and 5 display the effects of permeation Reynolds number R on the temperature profile for contraction and expansion cases, respectively. The behavior is similar as far as the variations due to the suction or injection are concerned; with increasing suction, the temperature of the fluid increases, and for increasing injection, the temperature falls. This is expected as the injection of coolant is supposed to drop the temperature of the fluid. It is also appropriate to mention that the contracting channel has higher temperature values as compared to the expanding channel. It is due to the decrement and increment in the area of the channel, respectively.

Fig. 4
figure 4

Temperature variations due to changing R: contraction case

Full size image
Fig. 5
figure 5

Temperature variations due to changing R: suction case

Full size image

The variations in the temperature profile, caused by increasing θ w , are captured in next two figures (see Figs. 6, 7). Two cases are considered, the injection combined with contraction, and the injection combined with expansion. The temperature in both the cases rises due to increasing θ w . As θ w increases, the temperature difference between the lower and upper plate increases. Due to the increasing temperature difference, more heat flows toward the upper plate, and in results, the temperature of the fluid rises.

Fig. 6
figure 6

Temperature variations due to θ w varying: injection/contraction

Full size image
Fig. 7
figure 7

Temperature variations due to θ w varying: injection/expansion

Full size image

Figures 8 and 9 display that the temperature distribution rises with increasing Rd. As Rd increases, the mean absorption decreases; therefore, a temperature surge is most likely. It can also be seen from the same figures that the deviation in the temperature distribution is more prominent in the expansion/injection case.

Fig. 8
figure 8

Temperature variations due to Rd varying: injection/contraction

Full size image
Fig. 9
figure 9

Temperature variation du to Rd varying: injection/expansion

Full size image

In Fig. 10, an increment in the rate of heat transfer, at upper and lower plates, is portrayed. This increment is caused by increasing the values of θ w . The local rate of heat transfer (Nusselt number) is plotted against the increasing values of Rd. It is also evident that an increase in Rd increases the Nusselt number. The case considered, involves expansion combined with injection.

Fig. 10
figure 10

Nusselt number for θ w varying: expansion/injection

Full size image

We keep the same setup as was in Fig. 10, but now the case considered is contraction combined with suction (see Fig. 11). For this case, Nusselt number at lower plate behaves in a similar manner as it did in the expansion/injection case; however, the behavior is opposite at upper plate, and there a decrease in Nu is observed for increasing both Rd and θ w .

Fig. 11
figure 11

Nusselt number for θ w varying: contraction/suction

Full size image

5 Conclusion

This manuscript deals with the study of effects of nonlinear thermal radiation on the flow of a viscous fluid between two infinite plates. The lower plate is fixed, solid and heated, while the upper plate is porous and it is moving to or away from the lower plate. Appropriate similarity transformations have been used to obtain a system of ordinary differential equations from the laws of conservation of mass, momentum and energy. The nonlinear radiation effects have been incorporated in energy equation by using Rosseland approximation [22]. The solution of the problem is found by using Galerkin method. The Galerkin solution is also supported by a numerical solution obtained by using built-in routines of the mathematical software Maple. A summary of conclusive remarks is presented in the form of bullet points as follows:

  • The temperature of the fluid rises when the plates come closer to each other and it drops when they go apart (see Figs. 2, 3). This happens for both suction and injection cases.

  • For a fixed contraction or expansion rate, the injection of coolant decreases the temperature. The temperature increases when the suction takes place. (see Figs. 4, 5).

In all the cases considered, the temperature rises with increasing Rd and θ w . It means that the thermal radiation increases the temperature of the fluid.

Nusselt number, at lower and upper plates, increases with increasing Rd and θ w in all the cases, except at upper wall when the contraction is combined with suction.