Hyperbolic is the only Hilbert geometry having circumcenter or orthocenter generally

Abstract

A Hilbert geometry is hyperbolic if and only if the perpendicular bisectors or the altitudes of any trigon form a pencil. We also prove some interesting characterizations of the ellipse.

1 Introduction

Hilbert geometries, introduced by David Hilbert in 1899 (Hilbert 1971), are natural generalizations of hyperbolic geometry, and hence the question immediately arises if some properties of a Hilbert geometry are specific to the hyperbolic geometry.

For a recent survey on the results see Guo (2014).

To place our subject in a broader context we mention that it can also be considered as a so-called ellipsoid characterization problem in Euclidean space, which is often treated as characterization of Euclidean spaces (inner product spaces) among the normed spaces [see (Amir 1986) and (Martini et al. 2001; Martini and Swanepoel 2004)]. Further, the unitary imaginary unit sphere in generalized space-time model (Horváth 2010, 2011) can also be considered as a Hilbert geometry.

In this article we prove two results: the existence of a circumcenter in every trigon (Theorem 5.1) or the existence of an orthocenter in every trigon (Theorem 5.2) renders Hilbert geometry hyperbolic. Moreover, we also prove two characterizations of ellipses in Sect. 4.

2 Preliminaries

Points of $\mathbb R^n$ are denoted as $\mathbf {a} , \mathbf {b} , \dots$; the line through different points $\mathbf {a}$ and $\mathbf {b}$ is denoted by $\mathbf {a} \mathbf {b}$, the open segment with endpoints $\mathbf {a}$ and $\mathbf {b}$ is denoted by $\overline{\mathbf {a} \mathbf {b} }$. Non-degenerate triangles are called trigons.

For given different points $\mathbf {p}$ and $\mathbf {q}$ in $\mathbb R^n$, and points $\mathbf {x},\mathbf {y}\in \mathbf {p}\mathbf {q}$ one has the unique linear combinations $\mathbf {x} =\lambda _1 \mathbf {p} + \mu _1 \mathbf {q},\, \mathbf {y} =\lambda _2 \mathbf {p} + \mu _2 \mathbf {q}$ which allows to define the cross ratio

$$\begin{aligned} (\mathbf {p} ,\mathbf {q};\;\mathbf {x} ,\mathbf {y} ) =\frac{\mu _1\lambda _2}{\lambda _1\mu _2}, \end{aligned}$$

(2.1)

of the points $\mathbf {p} ,\mathbf {q}, \mathbf {x}$ and $\mathbf {y}$, provided that $\lambda _1\mu _2\ne 0$ [see ((Busemann and Kelly 1953, page 243))].

Definition 2.1

((Busemann and Kelly 1953, page 297)) Let $\mathcal H\subset \mathbb R^n$ ($n\ge 2$) be an open and convex set with boundary $\partial {\mathcal H}$. The metric $d_{\mathcal H}:\mathcal H\times \mathcal H\rightarrow \mathbb R_{0\le }^{}$ defined by

$$\begin{aligned} d_{\mathcal H}(\mathbf {x},\mathbf {y} ) ={\left\{ \begin{array}{ll} \frac{1}{2}\bigl |\ln |(\mathbf {p} ,\mathbf {q};\;\mathbf {x} ,\mathbf {y} )|\bigr |,&{}\quad \text {if }\;\mathbf {x}\ne \mathbf {y},\quad \text { where }\;\{\mathbf {p},\mathbf {q}\}=\mathbf {x}\mathbf {y}\cap \partial \mathcal H,\\ 0,&{}\quad \text {if }\;\mathbf {x}=\mathbf {y}, \end{array}\right. } \end{aligned}$$

(2.2)

is called the Hilbert metric on $\mathcal H$. The pair $(\mathcal H,d_{\mathcal H})$ is called Hilbert geometry.

Note that as all the defining conditions of a Hilbert geometry $(\mathcal H,d_{\mathcal H})$ is projective invariant, two Hilbert geometries are isomorphic if there is a projective map between their sets of points.

Further, the generalized Cayley–Klein model of the hyperbolic geometry $\mathbb H^n$ is, in fact, a special kind of Hilbert geometry $(\mathcal E,d_{\mathcal E})$ given by an ellipsoid $\mathcal E$.

Let $\mathbf {a} , \mathbf {b}$ be different points in $\mathcal H$. For any $\mathbf {c}\in \mathcal H\cap (\mathbf {a}\mathbf {b}{\setminus }\{\mathbf {b}\})$ the hyperbolic ratio ¹ of the triple $\mathbf {a} ,\mathbf {b}, \mathbf {c}$ is defined by

$$\begin{aligned} \langle \mathbf {a} ,\mathbf {b};\;\mathbf {c}\rangle _{\mathcal H} = {\left\{ \begin{array}{ll} -\frac{\sinh d_{\mathcal H}(\mathbf {c},\mathbf {a})}{\sinh d_{\mathcal H}(\mathbf {b},\mathbf {c})}, &{} \quad \text {if }\; \mathbf {c} \in \overline{\mathbf {a} \mathbf {b} } ,\\ \frac{\sinh d_{\mathcal H}(\mathbf {c},\mathbf {a})}{\sinh d_{\mathcal H}(\mathbf {b},\mathbf {c})}, &{}\quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

(2.3)

Perpendicularity of $\mathcal H$-lines, non-empty intersections of Euclidean lines with $\mathcal H$, in Hilbert geometry is defined in (Busemann and Kelly (1953), pp. 119–121).² It is based on the notion of the foot of a point of $\mathcal H$ on an $\mathcal H$ -line.

Let $\ell$ be an $\mathcal H$-line and let the point $\mathbf {g}\in \mathcal H$ be outside of $\ell$. The point $\mathbf {f}\in \ell$ is the $\ell$ -foot of $\mathbf {g}$, if $d_{\mathcal H}(\mathbf {g},\mathbf {x})\ge d_{\mathcal H}(\mathbf {g},\mathbf {f})$ for every $\mathbf {x}\in \ell$.³

A line $\ell '$ intersecting the line $\ell$ in a point $\mathbf {f}$ is said to be $\mathcal {H}$ -perpendicular to $\ell$ if $\mathbf {f}$ is an $\ell$-foot of $\mathbf {g}$ for every $\mathbf {g}\in \ell '{\setminus }\{\mathbf {f}\}$. We denote this relation by $\ell '\perp _{\mathcal H}\ell$.⁴

It is proved in Busemann and Kelly (1953, (28.11)) that, if $\mathcal H$ is strictly convex, then for any given point $\mathbf {f}\in \mathcal H$ and $\mathcal H$-line $\ell$ there exists a unique $\mathcal H$-line $\ell '$ such that it goes through $\mathbf {f}$ and $\ell '\perp _{\mathcal H}\ell$. Moreover, the Euclidean line containing $\ell '$ is the one that connects $\mathbf {f}$ and the intersection of those tangents of $\mathcal H$ that touch $\mathcal H$ at the points $\partial \ell$.

A set of lines is said to form a pencil if they have a common (maybe ideal) point. This point is called the center of the pencil. We say that a set of $\mathcal H$-lines forms a pencil with center $\mathbf {c}$, if the corresponding euclidean lines form a pencil with center $\mathbf {c}$.

Thus the set of those lines that are $\mathcal H$-perpendicular to an arbitrary fixed line $\ell$ is a pencil.

Based on the foregoing, one can speak about the

• $\mathcal {H}$ -perpendicular bisector of a segment $\overline{\mathbf {a}\mathbf {b}}$, as the unique line through the midpoint of $\overline{\mathbf {a}\mathbf {b}}$, that is $\mathcal {H}$-perpendicular to the line ${\mathbf {a}\mathbf {b}}$, and the

• $\mathcal {H}$ -altitude of a triangle $\triangle {\mathbf {a}\mathbf {b}\mathbf {c}}$, as a line through one of the vertices of $\triangle {\mathbf {a}\mathbf {b}\mathbf {c}}$, that is $\mathcal {H}$-perpendicular to the corresponding opposite edge of $\triangle {\mathbf {a}\mathbf {b}\mathbf {c}}$.

These definitions⁵ extend the respective notion of the perpendicular bisector of a segment and the altitude of a triangle, as defined in hyperbolic geometry.

From now on, we assume that $\mathcal H$ is strictly convex and has $C^2$ boundary.

3 Utilities

The useful notations $\mathbf {u}_\tau =(\cos \tau ,\sin \tau )$ and $\mathbf {u}_\tau ^\perp =(-\sin \tau ,\cos \tau )$ are used all over this article. Also the following technical lemmas and the notations will be used in proving our main results.

Lemma 3.1

((Kozma and Kurusa 2014, Lemma 2.3)) Let $\mathbf {a},\mathbf {b}$ and $\mathbf {c}$ be collinear points in a Hilbert geometry $\mathcal H$, and let $\mathbf {a}\mathbf {b}\cap \partial \mathcal H=\{\mathbf {p},\mathbf {q}\}$, such that $\mathbf {a}$ separates $\mathbf {p}$ and $\mathbf {b}$. Set a Euclidean coordinate system on $\mathbf {a}\mathbf {b}$ such that the coordinates of $\mathbf {p}$ and $\mathbf {a}$ are $0$ and $1$, respectively. Let $q,b$ and $c$, with assumptions $q>b>1$ and $0<c<q$, be the coordinates of $\mathbf {q}$, $\mathbf {b}$ and $\mathbf {c}$, respectively, in this coordinate system. Then we have

$$\begin{aligned} |\langle \mathbf {a},\mathbf {b};\;\mathbf {c}\rangle _{\mathcal H}| =\frac{|c-b|}{|c-1|\sqrt{b}}\sqrt{1+\frac{b-1}{q-b}} .\end{aligned}$$

(3.1)

Lemma 3.2

((Busemann and Kelly 1953, Lemma 12.1, pp. 226)) A bounded open convex set $\mathcal H$ in $\mathbb R^n$ $(n\ge 2)$ is an ellipsoid if and only if every section of it by any 2-dimensional plane is an ellipse.

Lemma 3.3

Let $\mathcal {H}$ be a convex body in the plane. Then

• (i) there exists an ellipse $\mathcal E$ circumscribed around $\mathcal {H}$ with at least three different contact points $\mathbf {e}_1,\mathbf {e}_2,\mathbf {e}_3$ lying in $\partial \mathcal {H}\cap \partial \mathcal {E}$ such that the closed triangle $\triangle \mathbf {e}_1\mathbf {e}_2\mathbf {e}_3$ contains the center $\mathbf {c}$ of $\mathcal E$, and

• (ii) if $\mathcal {H}\not \equiv \mathcal {E}$, then these contact points can be chosen so that in every neighborhood of one of them $\partial \mathcal {H}{\setminus }\partial \mathcal {E}\ne \emptyset$.

Let $t_1, t_2, t_3$ be the common support lines at $\mathbf {e}_1, \mathbf {e}_2, \mathbf {e}_3$, respectively. Then

• (iii) $\mathbf {c}$ is in the interior of $\triangle \mathbf {e}_1\mathbf {e}_2\mathbf {e}_3$ if and only if $t_1, t_2, t_3$ form a trigon with vertices $\mathbf {m}_1=t_2\cap t_3$, $\mathbf {m}_2=t_3\cap t_1$ and $\mathbf {m}_3=t_1\cap t_2$;

• (iv) $\mathbf {c}$ is in one of the edges of $\triangle \mathbf {e}_1\mathbf {e}_2\mathbf {e}_3$, say $\mathbf {c}\in \overline{\mathbf {e}_2\mathbf {e}_3}$, if and only if $t_1, t_2, t_3$ form a half strip with vertices $\mathbf {m}_2=t_1\cap t_3$, $\mathbf {m}_3=t_2\cap t_1$ and the ideal point $\mathbf {m}_1=t_2\cap t_3$.

If$~\,\mathbf {b}_1, \mathbf {b}_2, \mathbf {b}_3$ are the midpoints of the segments $\overline{\mathbf {e}_2\mathbf {e}_3}$, $\overline{\mathbf {e}_3\mathbf {e}_1}$ and $\overline{\mathbf {e}_1\mathbf {e}_2}$, respectively, then

• (v) the straight lines $\mathbf {m}_i\mathbf {b}_i$ $(i=1,2,3)$ meet in $\mathbf {c}$.

Proof

Take the unique minimal area ellipse $\mathcal E$ containing $\mathcal {H}$ and let the center $\mathbf {c}$ of $\mathcal E$ be the origin $\mathbf {o}$.

(i) By Gruber and Schuster (2005, Theorem 2 (ii)) there is an integer $(5{\ge })m\ge 3$ such that there are contact points $\mathbf {e}_1,\dots ,\mathbf {e}_m$ lying in $\partial \mathcal {H}\cap \partial \mathcal {E}$ such that a positive linear combination of the contact points vanishes. This means that the origin is in the convex hull of these contact points, hence a (closed) trigon of three of them, say $\triangle \mathbf {e}_1\mathbf {e}_2\mathbf {e}_3$, also contains the origin.

(ii) Transform the configuration given in (i) with a linear affinity $\mu$ so that $\mathcal D=\mu (\mathcal E)$ is the unit disc centered to $\mathbf {o}$. Let $\mathbf {e}_i'=\mu (\mathbf {e}_i)$ ($i=1,2,3$) and $\mathcal H'=\mu (\mathcal H)$.

By (i) the center $\mathbf {o}$ is in the trigon $\triangle \mathbf {e}_1'\mathbf {e}_2'\mathbf {e}_3'$. Let $\varepsilon _i\in (-\pi ,\pi ]$ be such that $\mathbf {e}_i'=\mathbf {u}_{\varepsilon _i}$ and let the support function of ${\mathcal H'}$ be denoted by $h_{\mathcal H'}$. Define $\alpha _i:=\limsup \{\alpha :h_{\mathcal H'}([\varepsilon _i,\varepsilon _i+\alpha ])=\{1\}\}$ ($i=1,2,3$). If $\alpha _i$ is infinite, then $\mathcal H\equiv \mathcal E$, that is excluded. Assume that $\alpha _k=\min _{i=1,2,3}\alpha _i$ for some $k\in \{1,2,3\}$. Set $\mathbf {f}_i=\mu ^{-1}(\mathbf {u}_{\varepsilon _i+\alpha _k})$ ($i=1,2,3$). Then $\mathbf {f}_1,\mathbf {f}_2,\mathbf {f}_3$ are contact points of $\partial \mathcal {H}$ and $\partial \mathcal {E}$, the trigon $\mathbf {f}_1,\mathbf {f}_2,\mathbf {f}_3$ contains the center $\mathbf {o}$, and in every neighborhood $\mathcal N$ of $\mathbf {f}_k$ $(\partial \mathcal {H}{\setminus }\partial \mathcal {E})\cap \mathcal N\ne \emptyset$.

(iii) and (iv) are easy consequences of the strict convexity of the ellipse $\mathcal E$.

(v) This readily follows if one transforms the ellipse into a circle by a linear affinity. $\square$

Lemma 3.4

For a small $\varepsilon >0$ let $\mathbf {r},\mathbf {p}:(-\varepsilon ,0]\rightarrow \mathbb R^2$ be twice differentiable convex curves such that $\mathbf {p}(\tau )=p(\tau )\mathbf {u}_\tau$ and $\mathbf {r}(\tau )=r(\tau )\mathbf {u}_\tau$, where $p,r:(-\varepsilon ,0]\rightarrow \mathbb R_+$, $\lambda (\tau ):=r(\tau )/p(\tau )$ takes its minimum value $1$ at $\tau =0$, and $\max _{(-\delta ,0]}\lambda >1$ for every $\delta \in (0,\varepsilon )$.

Let $\tau _n$ be a sequence in $(-\varepsilon ,0]$ tending to $0$ such that $\lambda (\tau _n)>1$ for every $n\in \mathbb N$. Then the tangent lines of $\mathbf {r}$ and $\mathbf {p}$ at $\mathbf {r}(\tau _n)$ and $\mathbf {p}(\tau _n)$, respectively, intersect each other in a point $\mathbf {m}(\tau _n)$ that tends to $\mathbf {p}(0)$ as $\tau _n\rightarrow 0$ so that it is on the same side of the line $\mathbf {0}\mathbf {p}(\tau _n)$ as $\mathbf {p}(0)$ is.

Proof

First we prove the statement with the assumption that $\lambda$ takes its minimum value $1$ uniquely at $\tau =0$. This means that $\dot{\lambda }(0)=0$, $\ddot{\lambda }(0)>0$ and we have to prove that

$$\begin{aligned} \begin{array}{ll} &{}\text {the tangent lines of }\mathbf {r}\text { and }\mathbf {p} \text { at }\mathbf {r}(\tau )\text { and }\mathbf {p}(\tau ), \text {respectively, intersect}\\ &{}\text {each other in a point }\mathbf {m}(\tau ) \text { that tends to }\mathbf {p}(0)\text { as }\tau \rightarrow 0\text { so that it}\\ &{}\text {is on the same side of the line } \mathbf {0}\mathbf {p}(\tau )\text { as }\mathbf {p}(0)~\text {is}. \end{array}\quad \end{aligned}$$

(3.2)

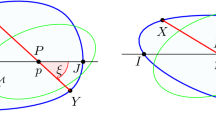
Since $\dot{\mathbf {r}} =\lambda \dot{\mathbf {p}}+\dot{\lambda }{\mathbf {p}}$, $\dot{\mathbf {p}}\parallel \dot{\mathbf {r}}$ if and only if $\dot{\lambda }=0$, therefore $\mathbf {m}(\tau )$ exists uniquely for every $\tau \ne 0$ (see Fig. 1).

Fig. 1

The crossing of the tangent lines

We clearly have

$$\begin{aligned} \pm |\mathbf {m}-\mathbf {p}|\frac{\dot{\mathbf {p}}}{|\dot{\mathbf {p}}|}+\mathbf {p} =\mathbf {m} =\pm |\mathbf {m}-\mathbf {r}|\frac{\dot{\mathbf {r}}}{|\dot{\mathbf {r}}|}+\mathbf {r}, \end{aligned}$$

(3.3)

that is $\pm |\mathbf {m}-\mathbf {p}||\dot{\mathbf {r}}|\dot{\mathbf {p}}+|\dot{\mathbf {r}}||\dot{\mathbf {p}}|\mathbf {p} =\pm |\mathbf {m}-\mathbf {r}||\dot{\mathbf {p}}|\dot{\mathbf {r}}+|\dot{\mathbf {p}}||\dot{\mathbf {r}}|\mathbf {r} .$

Since $\dot{\mathbf {p}}=\dot{p}\mathbf {u}_\tau +p\mathbf {u}_\tau ^\perp$, $\dot{\mathbf {r}}=\dot{r}\mathbf {u}_\tau +r\mathbf {u}_\tau ^\perp$ and $\mathbf {u}_\tau \perp \mathbf {u}_\tau ^\perp$, we obtain

$$\begin{aligned} |\mathbf {m}-\mathbf {p}||\dot{\mathbf {r}}|p&=|\mathbf {m}-\mathbf {r}||\dot{\mathbf {p}}|r \end{aligned}$$

(3.4)

and

$$\begin{aligned} \pm |\mathbf {m}-\mathbf {p}||\dot{\mathbf {r}}|\dot{p}+p|\dot{\mathbf {p}}||\dot{\mathbf {r}}|&=\pm |\mathbf {m}-\mathbf {r}||\dot{\mathbf {p}}|\dot{r}+r|\dot{\mathbf {r}}||\dot{\mathbf {p}}|. \end{aligned}$$

(3.5)

Multiplying (3.5) by $p$ then substituting (3.4) into the product results in

$$\begin{aligned} \pm |\mathbf {m}-\mathbf {r}||\dot{\mathbf {p}}|r\dot{p}+p^2|\dot{\mathbf {p}}||\dot{\mathbf {r}}| =\pm |\mathbf {m}-\mathbf {r}||\dot{\mathbf {p}}|p\dot{r}+pr|\dot{\mathbf {r}}||\dot{\mathbf {p}}| ,\end{aligned}$$

hence

$$\begin{aligned} \pm |\mathbf {m}-\mathbf {r}|&=\frac{p|\dot{\mathbf {r}}|(r-p)}{r\dot{p}-p\dot{r}} =\frac{|\dot{\mathbf {r}}|p^2(\lambda -1)}{\lambda p\dot{p}-p(\dot{\lambda }p+\lambda \dot{p})} =|\dot{\mathbf {r}}|\frac{\lambda -1}{-\dot{\lambda }}. \end{aligned}$$

(3.6)

This implies $\lim _{\tau \rightarrow 0}|\mathbf {m}(\tau )-\mathbf {r}(\tau )|=0$ via l’Hôspital’s rule.

On the other hand, using (3.4) and putting (3.6) into (3.3) gives

$$\begin{aligned} \frac{\lambda (\lambda -1)}{-\dot{\lambda }}\dot{\mathbf {p}}+\mathbf {p} =\mathbf {m} =\frac{\lambda -1}{-\dot{\lambda }}\dot{\mathbf {r}}+\mathbf {r}. \end{aligned}$$

As $\lambda \ge 1$, this implies that $\mathbf {m}$ is on the same side of $\mathbf {0}\mathbf {r}$ and $\mathbf {0}\mathbf {p}$ as $\mathbf {m}(0)=\mathbf {r}(0)=\mathbf {p}(0)$.

This proves claim (3.2).

For the proof of the statement in the lemma we take the broken line $\bar{\mathbf {q}}$ with vertices $\mathbf {p}(\tau _n)$ and edges $\overline{\mathbf {p}(\tau _n)\mathbf {p}(\tau _{n+1})}$. It is clearly convex and can easily be deformed into a twice differentiable convex curve $\mathbf {q}$ so that ${\mathbf {q}}(\tau _n)={\mathbf {p}}(\tau _n)$, $\dot{\mathbf {q}}(\tau _n)=\dot{\mathbf {p}}(\tau _n)$ and $r(\tau )/|{\mathbf {q}}(\tau )|$ takes its minimum value $1$ uniquely at $\tau =0$. Using claim (3.2) for $\mathbf {q}$ and $\mathbf {r}$ therefore immediately implies the lemma. $\square$

4 Characterizations of ellipses

The following configuration, construction, theorems, and the notations they introduce, are used in the next sections, but are interesting on their own too.

Definition 4.1

If a strictly convex body $\mathcal {H}$ is given in the plane, and the points $\mathbf {e}_1,\mathbf {e}_2,\mathbf {e}_3$ are placed on its border $\partial \mathcal H$, then the following configuration is defined (see Fig. 2).

Fig. 2

Construction for Definition 4.1

For every $i=1,2,3$, $\ell _i$ denotes the line $\mathbf {e}_j\mathbf {e}_k$, $t_i^\mathcal {H}$ denotes the tangent line of $\mathcal H$ at the point $\mathbf {e}_i$, and $f_i^\mathcal {H}$ denotes the straight line through $\mathbf {e}_i$ that forms a harmonic pencil with the lines $\ell _j,\ell _k,t_i^\mathcal {H}$, where $\{i,j,k\}=\{1,2,3\}$.

Theorem 4.2

Take a configuration given in Definition 4.1.⁶

• (i) For any ellipse $\mathcal E$ the lines $f_1^\mathcal {E},f_2^\mathcal {E},f_3^\mathcal {E}$ form a pencil.

• (ii) If the lines $f_1^\mathcal {H},f_2^\mathcal {H},f_3^\mathcal {H}$ form a pencil for any points $\mathbf {e}_1,\mathbf {e}_2,\mathbf {e}_3\in \partial \mathcal H$, then $\mathcal H$ is an ellipse.

Proof

First note that not only keep projectivities the cross ratio, but takes any tangent line of a curve into a tangent line of the image curve.

(i) Taking a suitable affinity we may assume that ellipse $\mathcal H$ is a disc $\mathcal D$. The projective group is three-transitive⁷ on every conic, hence we may assume that $\mathbf {e}_1,\mathbf {e}_2,\mathbf {e}_3$ forms a regular triangle on the circle $\partial \mathcal D$. Then, obviously, the lines $f_1,f_2,f_3$ meet in the center of $\mathcal C$ that proves statement (i) (see Fig. 3).

Fig. 3

Transforming the ellipse $\mathcal {E}$ into a disc $\mathcal D$ and the triangle $\triangle \mathbf {e}_1\mathbf {e}_2\mathbf {e}_3$ into a regular one

(ii) The condition remains unchanged if the configuration is transformed by a projective map, therefore we may assume that the points $\mathbf {e}_{1},\mathbf {e}_2$ and $\mathbf {H}$ are such that $\mathbf {e}_{1}=(0,1)$, $\mathbf {e}_2=(0,-1)$, $\mathbf {e}_3=(1,0)$ and $\mathbf {f}=(\sqrt{2}-1,0)$.

Then, the straight lines $f_1^{\mathcal H}, f_2^{\mathcal H}$ and $f_3^{\mathcal H}$ are determined and from the conditions $-1=(\ell _1,\ell _2;\;t_{3}^{\mathcal H},f_{3}^{\mathcal H}) =(\ell _2,\ell _3;\;t_{1}^{\mathcal H},f_{1}^{\mathcal H}) =(\ell _3,\ell _1;\;t_{2}^{\mathcal H},f_{2}^{\mathcal H})$, we get the equations $y=1$, $y=-1$ and $x=1$ for $t_1^\mathcal {H},t_2^\mathcal {H}$ and $t_3^\mathcal {H}$, respectively.

Now choose a general point $\mathbf {h}\in \partial \mathcal H$ different from $\mathbf {e}_{1},\mathbf {e}_2$, and let $\partial \mathcal E_{\mathbf {h}}$ be the unique ellipse through the points $\mathbf {e}_{1},\mathbf {e}_2,\mathbf {h}$ with tangents $t_{1}^{\mathcal E}:=t_{1}^{\mathcal H}$ and $t_{2}^{\mathcal E}:=t_2^{\mathcal H}$ at $\mathbf {e}_{1}$ and $\mathbf {e}_2$, respectively.

Let us introduce some new notations (see Fig. 4):

• $t_{\mathbf {h}}^{\mathcal H}$ is the tangent of ${\mathcal H}$ at $\mathbf {h}$;

• $\overline{\ell _i}$ is the line $\mathbf {h}\mathbf {e}_i$ for $i=1,2$; $\overline{\ell _3}$ is the line $\mathbf {e}_1\mathbf {e}_2$;

• $f_i^\mathcal {H}$ is the line through $\mathbf {e}_i$ for $i=1,2$ such that $-1=(\overline{\ell }_j,\overline{\ell }_k;\;t_i^\mathcal {H},f_i^\mathcal {H})$, where $\{i,j,k\}=\{1,2,3\}$;

• $f_{\mathbf {h}}^\mathcal {H}$ is the line through $\mathbf {h}$ such that $-1=(\overline{\ell }_1,\overline{\ell }_2;\;t_{\mathbf {h}}^\mathcal {H},f_{\mathbf {h}}^\mathcal {H})$.

We denote the analogous objects for the ellipse $\mathcal E_{\mathbf {h}}$ in the same way except that the superscript $\mathcal H$ is exchanged to $\mathcal E$.

Fig. 4

Introducing harmonic pencils

Since $t_{1}^{\mathcal E}=t_{1}^{\mathcal H}$ and $t_{2}^{\mathcal E}=t_2^{\mathcal H}$ we clearly have $f_i^\mathcal {H}=f_i^\mathcal {E}$ for $i=1,2$.

As the lines $f_1^{\mathcal E},f_2^{\mathcal E}$ and $f_{\mathbf {h}}^{\mathcal E}$ form a pencil by (i), and $f_1^{\mathcal H},f_2^{\mathcal H}$ and $f_{\mathbf {h}}^{\mathcal H}$ form a pencil by the condition in (ii), we deduce that the lines $f_{\mathbf {h}}^{\mathcal H}$ and $f_{\mathbf {h}}^{\mathcal E}$ intersect each other not only in $\mathbf {h}$, but also in $f_1^{\mathcal H}\cap f_2^{\mathcal H}=f_1^{\mathcal E}\cap f_2^{\mathcal E}$, hence they coincide.

Thus, we have $t_{\mathbf {h}}^{\mathcal H}=t_{\mathbf {h}}^{\mathcal E}$. So it makes sense to introduce the notations $t_{i}:=t_{i}^{\mathcal E}=t_{i}^{\mathcal H}$ for $i=1,2$ and $t_{\mathbf {h}}:=t_{\mathbf {h}}^{\mathcal E}=t_{\mathbf {h}}^{\mathcal H}$.

Let   $r:(-\pi ,\pi ]\rightarrow \mathbb R_+$ be such that $\mathbf {h}(\varphi )=r(\varphi )\mathbf {u}_\varphi$ is in $\partial \mathcal H$, for every $\varphi \in (-\pi ,\pi ]$.

Then a tangent vector of $\partial \mathcal H$ at $\mathbf {h}(\varphi )$ is $\dot{\mathbf {h}}(\varphi ) =\dot{r}(\varphi )\mathbf {u}_\varphi +r(\varphi )\mathbf {u}_\varphi ^\perp$ which is parallel to the tangent of the unique ellipse $\partial \mathcal E_{\mathbf {h}(\varphi )}$ (see Fig. 5).

Fig. 5

Parametrization of $\partial \mathcal {H}$

The ellipse $\partial \mathcal E_{\mathbf {h}(\varphi )}$ goes through the points $\mathbf {e}_1,\mathbf {e}_2,\mathbf {h}(\varphi )$ and it has tangents $t_1$ and $t_2$ at $\mathbf {e}_1$ and $\mathbf {e}_2$, respectively, therefore its equation is $\frac{x^2}{a^2}+y^2=1$ for some $a=a(\mathbf {h}(\varphi ))$. Putting the coordinate of $\mathbf {h}(\varphi )$ into this equation we get

$$\begin{aligned} 1=r^2(\varphi )\left( \frac{\cos ^2\varphi }{a^2}+\sin ^2\varphi \right) , \ \text { that is, }\ a^2=\frac{r^2(\varphi )\cos ^2\varphi }{1-r^2(\varphi )\sin ^2\varphi } . \end{aligned}$$

(4.1)

On the other hand, the slope of the tangent of the ellipse at $(x,y)$ is $\tfrac{dy}{dx}=\tfrac{-x}{ya^2}$ which at the point $\mathbf {h}(\varphi )$ is

$$\begin{aligned} \frac{\dot{r}(\varphi )\sin \varphi +r(\varphi )\cos \varphi }{\dot{r}(\varphi )\cos \varphi -r(\varphi )\sin \varphi } =\frac{dy}{dx}=\frac{-x}{ya^2} =\frac{-\cos \varphi }{a^2\sin \varphi }. \end{aligned}$$

This implies

$$\begin{aligned} \frac{\dot{r}(\varphi )}{r(\varphi )}&=\frac{(1-a^2)\sin \varphi \cos \varphi }{a^2\sin ^2\varphi +\cos ^2\varphi } =\frac{\left( 1-\frac{r^2(\varphi )\cos ^2\varphi }{1-r^2(\varphi )\sin ^2\varphi }\right) \sin \varphi \cos \varphi }{\frac{r^2(\varphi )\cos ^2\varphi }{1-r^2(\varphi )\sin ^2\varphi } \sin ^2\varphi +\cos ^2\varphi } =(1-r^2(\varphi ))\tan \varphi . \end{aligned}$$

At every $\varphi$, where $r(\varphi )\ne 1$, this gives

$$\begin{aligned} \frac{\dot{r}(\varphi )}{r(\varphi )(1-r^2(\varphi ))}=\tan \varphi \end{aligned}$$

which, by integration, yields

$$\begin{aligned} \frac{-1}{2}\ln \frac{|1-r^2(\varphi )|}{r^2(\varphi )}=-\ln |\cos \varphi |+c_0 \end{aligned}$$

for a constant $c_0$. An equivalent reformulation of this is

$$\begin{aligned} r(\varphi )=\frac{1}{\sqrt{1\pm c_1\cos ^2\varphi }}, \end{aligned}$$

where $c_1$ is a constant. Substituting this into (4.1), $a^2(1\pm c_1)=1$ follows, hence $a$ is the same constant for all ellipses $\partial \mathcal {E}_{\mathbf {h}(\varphi )}$, which are therefore a fixed ellipse $\partial \mathcal {E}$. This means that $\partial \mathcal {H}$ is a subset of $\partial \mathcal {E}$ having equation $(1\pm c_1)\cdot x^2+y^2=1$.

However, $\partial \mathcal H$ contains the point $\mathbf {e}_3=(1,0)$ too, hence $c_1=0$ and therefore $\partial \mathcal H$ is the unit circle centered at the origin. This proves statement (ii). $\square$

Definition 4.3

Take a configuration according to Definition 4.1. We construct a set of geometric object in the following way: Chose a point $\mathbf {x}_i$ close to $\mathbf {e}_i$ on the open segment $\sigma _i=\overline{\mathbf {e}_j\mathbf {e}_k}$ for every $i=1,2,3$, where $\{j,k\}=\{1,2,3\}{\setminus }\{i\}$.

Let the lines $\mathbf {e}_2\mathbf {x}_3$, $\mathbf {e}_3\mathbf {x}_1$ and $\mathbf {e}_1\mathbf {x}_2$ be denoted by $\ell _1',\ell _2',\ell _3'$, respectively.

Take the points $\mathbf {v}_1=\ell _2'\cap \ell _3'$, $\mathbf {v}_2=\ell _3'\cap \ell _1'$, $\mathbf {v}_3=\ell _1'\cap \ell _2'$, and denote the open segments $\overline{\mathbf {v}_2\mathbf {v}_3}$, $\overline{\mathbf {v}_3\mathbf {v}_1}$ and $\overline{\mathbf {v}_1\mathbf {v}_2}$, by $\sigma _1'$, $\sigma _2'$ and $\sigma _3'$, respectively.

Further, we take the points $\mathbf {x}_1^t=t_1\cap \ell '_2$, $\mathbf {x}_2^t=t_2\cap \ell '_3$, $\mathbf {x}_3^t=t_3\cap \ell '_1$, and $\mathbf {x}_1^\mathcal {H}=\partial \mathcal {H}\cap (\ell '_2{\setminus }\{\mathbf {e}_3\})$, $\mathbf {x}_2^\mathcal {H}=\partial \mathcal {H}\cap (\ell '_3{\setminus }\{\mathbf {e}_1\})$, $\mathbf {x}_3^\mathcal {H}=\partial \mathcal {H}\cap (\ell '_1{\setminus }\{\mathbf {e}_2\})$. These points of intersection do exist if $\mathbf {x}_i$ are chosen close enough to $\mathbf {e}_i$ ($i=1,2,3$) (see Fig. 6).

Fig. 6

A construction for the triple asymptotic $\mathcal H$-triangle

Finally, let the magnitude of the angles $\angle \mathbf {x}_2\mathbf {e}_1\mathbf {e}_2$, $\angle \mathbf {x}_3\mathbf {e}_2\mathbf {e}_3$, $\angle \mathbf {x}_1\mathbf {e}_3\mathbf {e}_1$ be denoted by $\xi _1$, $\xi _2$, $\xi _3$, respectively, that of the angles $\angle \mathbf {x}_1^t\mathbf {e}_1\mathbf {e}_2$, $\angle \mathbf {x}_2^t\mathbf {e}_2\mathbf {e}_3$, $\angle \mathbf {x}_3^t\mathbf {e}_3\mathbf {e}_1$ be denoted by $\alpha _1$, $\alpha _2$, $\alpha _3$, respectively, and that of the angles $\angle \mathbf {e}_3\mathbf {e}_1\mathbf {e}_2$, $\angle \mathbf {e}_1\mathbf {e}_2\mathbf {e}_3$, $\angle \mathbf {e}_2\mathbf {e}_3\mathbf {e}_1$ be denoted by $\beta _1$, $\beta _2$, $\beta _3$, respectively.

Theorem 4.4

Take a construction according to Definition 4.3. For every $i=1,2,3$ denote the Euclidean midpoint of the segment $\sigma _i$ by $\mathbf {b}_i$ and the $\mathcal H$-midpoint of the segment $\sigma _i'$ by $\mathbf {b}_i^\mathcal {H}$

The lines $f_1^\mathcal {H},f_2^\mathcal {H},f_3^\mathcal {H}$ form a pencil if and only if the points $\mathbf {x}_1$, $\mathbf {x}_2$ and $\mathbf {x}_3$ can be chosen for any $\varepsilon ,\delta >0$ so that

$$\begin{aligned} \begin{aligned} |\mathbf {b}_1^\mathcal {H}-\mathbf {b}_1|+|\mathbf {b}_2^\mathcal {H}-\mathbf {b}_2| +|\mathbf {b}_3^\mathcal {H}-\mathbf {b}_3|&<\varepsilon , \\ |\mathbf {x}_1-\mathbf {e}_1|+|\mathbf {x}_2-\mathbf {e}_2|+|\mathbf {x}_3-\mathbf {e}_3|&<\delta . \end{aligned} \end{aligned}$$

Proof

Since $d_{\mathcal H}(\mathbf {v}_j,\mathbf {b}_i^\mathcal {H}) = d_{\mathcal H}(\mathbf {b}_i^\mathcal {H},\mathbf {v}_k)$, where $\{i,j,k\}=\{1,2,3\}$, (2.2) implies $(\mathbf {e}_j,\mathbf {x}_k^\mathcal {H};\mathbf {v}_j,\mathbf {b}_i^\mathcal {H}) =(\mathbf {e}_j,\mathbf {x}_k^\mathcal {H};\mathbf {b}_i^\mathcal {H},\mathbf {v}_k)$, hence

$$\begin{aligned} 1&= \frac{(\mathbf {e}_j,\mathbf {x}_k^\mathcal {H};\mathbf {v}_j,\mathbf {b}_i^\mathcal {H})}{(\mathbf {e}_j,\mathbf {x}_k^\mathcal {H};\mathbf {b}_i^\mathcal {H},\mathbf {v}_k)} =\frac{ (\mathbf {e}_j,\mathbf {x}_k^\mathcal {H},\mathbf {v}_j) /(\mathbf {e}_j,\mathbf {x}_k^\mathcal {H},\mathbf {b}_i^\mathcal {H})}{ (\mathbf {e}_j,\mathbf {x}_k^\mathcal {H};\mathbf {b}_i^\mathcal {H}) /(\mathbf {e}_j,\mathbf {x}_k^\mathcal {H},\mathbf {v}_k)} \nonumber \\&= \frac{(\mathbf {e}_j,\mathbf {x}_k^\mathcal {H},\mathbf {v}_k)(\mathbf {e}_j,\mathbf {x}_k^\mathcal {H},\mathbf {v}_j)}{(\mathbf {e}_j,\mathbf {x}_k^\mathcal {H};\mathbf {b}_i^\mathcal {H})^2} =\frac{|\mathbf {e}_j-\mathbf {v}_k||\mathbf {e}_j-\mathbf {v}_j|}{|\mathbf {x}_k^\mathcal {H}-\mathbf {v}_k||\mathbf {x}_k^\mathcal {H}-\mathbf {v}_j|} \frac{1}{(\mathbf {e}_j,\mathbf {x}_k^\mathcal {H};\mathbf {b}_i^\mathcal {H})^2} \end{aligned}$$

(4.2)

From now on, assume that $\xi _i\rightarrow 0$ for every $i=1,2,3$. Then $\mathbf {x}_k^\mathcal {H}\rightarrow \mathbf {e}_k$, hence the affine midpoint of $\overline{\mathbf {e}_j\mathbf {x}_k^\mathcal {H}}$ converges to $\mathbf {b}_i$, and therefore $\mathbf {b}_i^\mathcal {H}\rightarrow \mathbf {b}_i$ if and only if $(\mathbf {e}_j,\mathbf {x}_k^\mathcal {H};\mathbf {b}_i^\mathcal {H})\rightarrow 1$.

As we have $\frac{|\mathbf {e}_j-\mathbf {v}_k|}{|\mathbf {x}_k^\mathcal {H}-\mathbf {v}_j|}\rightarrow 1$, (4.2) implies the asymptotic equation

$$\begin{aligned} (\mathbf {e}_j,\mathbf {x}_k^\mathcal {H};\mathbf {b}_i^\mathcal {H})^2 \sim \frac{|\mathbf {e}_j-\mathbf {v}_j|}{|\mathbf {x}_k^\mathcal {H}-\mathbf {v}_k|} \end{aligned}$$

which, in the light of the previous reasoning, means that

$$\begin{aligned} \mathbf {b}_i^\mathcal {H}\rightarrow \mathbf {b}_i\text { if and only if } {|\mathbf {e}_j-\mathbf {v}_j|}\sim {|\mathbf {x}_k^\mathcal {H}-\mathbf {v}_k|}. \end{aligned}$$

(4.3)

Fig. 7

The construction with the midpoints

Using the law of sines (see Fig. 7) we obtain

$$\begin{aligned} \frac{|\mathbf {x}_k^\mathcal {H}-\mathbf {v}_k|}{|\mathbf {e}_j-\mathbf {v}_j|}&= \frac{|\mathbf {x}_k^t-\mathbf {e}_j|-|\mathbf {v}_k-\mathbf {e}_j|-|\mathbf {x}_k^\mathcal {H}-\mathbf {x}_k^t|}{|\mathbf {e}_i-\mathbf {e}_j|\sin \xi _i/\sin (\beta _j-\xi _j+\xi _i)}\\&= \frac{\frac{|\mathbf {e}_j-\mathbf {e}_k|}{\sin (\beta _k+\alpha _k+\xi _j)}\sin (\beta _k+\alpha _k) -\frac{|\mathbf {e}_j-\mathbf {e}_k|}{\sin (\beta _k-\xi _k+\xi _j)}\sin (\beta _k-\xi _k) -|\mathbf {x}_k^\mathcal {H}-\mathbf {x}_k^t|}{\frac{|\mathbf {e}_i-\mathbf {e}_j|}{\sin (\beta _j-\xi _j+\xi _i)}\sin \xi _i}\\&= \frac{\sin (\beta _j-\xi _j+\xi _i)}{\sin \xi _i} \frac{|\mathbf {e}_j-\mathbf {e}_k|}{|\mathbf {e}_i-\mathbf {e}_j|}\\&\quad \quad \times \left( \frac{\sin (\beta _k+\alpha _k)}{\sin (\beta _k+\alpha _k+\xi _j)} -\frac{\sin (\beta _k-\xi _k)}{\sin (\beta _k-\xi _k+\xi _j)} -\frac{|\mathbf {x}_k^\mathcal {H}-\mathbf {x}_k^t|}{|\mathbf {e}_j-\mathbf {e}_k|}\right) \\&= \frac{\sin (\beta _j-\xi _j+\xi _i)}{\sin \xi _i} \frac{|\sigma _i|}{|\sigma _k|}\\&\quad \quad \times \left( \frac{\tan (\beta _k+\alpha _k)}{\sin \xi _j+\cos \xi _j\tan (\beta _k+\alpha _k)} -\frac{\tan (\beta _k-\xi _k)}{\sin \xi _j+\cos \xi _j\tan (\beta _k-\xi _k)} -\frac{|\mathbf {x}_k^\mathcal {H}-\mathbf {x}_k^t|}{|\mathbf {e}_j-\mathbf {e}_k|}\right) \\&= \frac{\sin (\beta _j-\xi _j+\xi _i)}{\sin \xi _i} \frac{|\sigma _i|}{|\sigma _k|}\\&\quad \quad \times \left( \frac{\sin \xi _j(\tan (\beta _k+\alpha _k)-\tan (\beta _k-\xi _k))}{(\sin \xi _j+\cos \xi _j\tan (\beta _k+\alpha _k)) (\sin \xi _j+\cos \xi _j\tan (\beta _k-\xi _k))} -\frac{|\mathbf {x}_k^\mathcal {H}-\mathbf {x}_k^t|}{|\mathbf {e}_j-\mathbf {e}_k|}\right) \\&= \frac{\sin \xi _j}{\sin \xi _i} \frac{|\sigma _i|}{|\sigma _k|}\\&\quad \quad \times \left( \frac{\sin (\beta _j-\xi _j+\xi _i)(\tan (\beta _k+\alpha _k)-\tan (\beta _k-\xi _k))}{(\sin \xi _j+\cos \xi _j\tan (\beta _k+\alpha _k)) (\sin \xi _j+\cos \xi _j\tan (\beta _k-\xi _k))} \right. \\&\quad \quad \quad \quad \quad \left. - \frac{\sin (\beta _j-\xi _j+\xi _i)|\mathbf {x}_k^\mathcal {H}-\mathbf {x}_k^t|}{|\mathbf {e}_j-\mathbf {e}_k|\sin \xi _j}\right) \\&\sim \frac{\sin \xi _j}{\sin \xi _i} \frac{|\sigma _i|}{|\sigma _k|} \frac{\sin \beta _j(\tan (\beta _k+\alpha _k)-\tan \beta _k)}{\tan (\beta _k+\alpha _k)\tan \beta _k} = \frac{\sin \xi _j}{\sin \xi _i} \frac{|\sigma _i|}{|\sigma _k|} \frac{\sin \beta _j\sin \alpha _k}{\sin (\beta _k+\alpha _k)\sin \beta _k}. \end{aligned}$$

Putting this into (4.3) results in

$$\begin{aligned} \mathbf {b}_1^\mathcal {H}\rightarrow \mathbf {b}_i \&\Longleftrightarrow \ \frac{\sin \xi _1}{\sin \xi _2} \sim \frac{|\sigma _1|}{|\sigma _3|} \frac{\sin \beta _2\sin \alpha _3}{\sin (\beta _3+\alpha _3)\sin \beta _3}, \\ \mathbf {b}_2^\mathcal {H}\rightarrow \mathbf {b}_2 \&\Longleftrightarrow \ \frac{\sin \xi _2}{\sin \xi _3} \sim \frac{|\sigma _2|}{|\sigma _1|} \frac{\sin \beta _3\sin \alpha _1}{\sin (\beta _1+\alpha _1)\sin \beta _1}, \\ \mathbf {b}_3^\mathcal {H}\rightarrow \mathbf {b}_3 \&\Longleftrightarrow \ \frac{\sin \xi _3}{\sin \xi _1} \sim \frac{|\sigma _3|}{|\sigma _2|} \frac{\sin \beta _1\sin \alpha _2}{\sin (\beta _2+\alpha _2)\sin \beta _2}. \end{aligned}$$

Having arbitrary $\xi _2\rightarrow 0$, $\xi _1\rightarrow 0$ and $\xi _3\rightarrow 0$ can be so chosen, that the first two of these asymptotic equations are satisfied, and the fulfillment of the third one then depends exactly on their product. Such angles $\xi _1,\xi _2,\xi _3$ can be chosen therefore if and only if

$$\begin{aligned} \sin \alpha _1\sin \alpha _2\sin \alpha _3 =\sin (\beta _1+\alpha _1)\sin (\beta _2+\alpha _2)\sin (\beta _3+\alpha _3). \end{aligned}$$

(4.4)

Denote the magnitude of the angles $\angle f_1^\mathcal {H}\ell _2$, $\angle f_2^\mathcal {H}\ell _3$, $\angle f_3^\mathcal {H}\ell _1$ by $\psi _1$, $\psi _2$, $\psi _3$, respectively, and the angles $\angle f_1^\mathcal {H}\ell _3$, $\angle f_2^\mathcal {H}\ell _1$, $\angle f_3^\mathcal {H}\ell _2$ by $\phi _1$, $\phi _2$, $\phi _3$, respectively (see Fig. 7). We clearly have $\psi _i+\phi _i=\beta _i$ for every $i=1,2,3$.

Observe that

$$\begin{aligned} \begin{aligned} -1&=(\ell _3,\ell _2;t_1,f_1^\mathcal {H}) =\frac{-\sin \alpha _1/\!\sin (\beta _1+\alpha _1)}{\sin \phi _1/\!\sin \psi _1}, \\ -1&=(\ell _1,\ell _3;t_2,f_2^\mathcal {H}) =\frac{-\sin \alpha _2/\!\sin (\beta _2+\alpha _2)}{\sin \phi _2/\!\sin \psi _2}, \\ -1&=(\ell _2,\ell _1;t_3,f_3^\mathcal {H}) =\frac{-\sin \alpha _3/\!\sin (\beta _3+\alpha _3)}{\sin \phi _3/\!\sin \psi _3}, \end{aligned} \end{aligned}$$

hence (4.4) is equivalent to

$$\begin{aligned} 1=\frac{\sin \phi _1}{\sin \psi _1} \frac{\sin \phi _2}{\sin \psi _2} \frac{\sin \phi _3}{\sin \psi _3}. \end{aligned}$$

Let $f_i^\mathcal {H}\cap \sigma _i=\mathbf {f}_i$ for every $i=1,2,3$. Then the law of sines gives

$$\begin{aligned} (\mathbf {e}_1,\mathbf {e}_2;\mathbf {f}_3) =\frac{|\sigma _2|}{|\sigma _1|}\frac{\sin \phi _3}{\sin \psi _3},\ \! (\mathbf {e}_2,\mathbf {e}_3;\mathbf {f}_1) =\frac{|\sigma _3|}{|\sigma _2|}\frac{\sin \phi _1}{\sin \psi _1} ,\ \text { and }\ \! (\mathbf {e}_3,\mathbf {e}_1;\mathbf {f}_2) =\frac{|\sigma _1|}{|\sigma _3|}\frac{\sin \phi _2}{\sin \psi _2}. \end{aligned}$$

By Ceva’s theorem the product of these ratios equals to $1$ if and only if the lines $f_1^\mathcal {H},f_2^\mathcal {H}$ and $f_3^\mathcal {H}$ form a pencil. This proves the theorem. $\square$

5 Circumcenter and orthocenter in Hilbert geometry

Existence of the circumcenter of a trigon, the common point of the three perpendicular bisectors, is a well known property in Euclidean plane. It can be formulated also for the hyperbolic plane (Martin (1975), p. 350): In hyperbolic geometry the perpendicular bisectors of any trigon form a pencil.

Theorem 5.1

If the $\mathcal {H}$-perpendicular bisectors of any trigon in the Hilbert geometry $\mathcal {H}$ form a pencil, then $(\mathcal H,d_{\mathcal H})$ is the hyperbolic geometry.

Proof

We need to show that $\mathcal H$ is an ellipsoid. By Lemma 3.2 we only need to work in the plane, therefore from now on in this proof $\mathcal H$ is in a plane $\mathcal P$.

Suppose that $\mathcal {H}$ is not an ellipse. We shall have to arrive at a contradiction.

By (i) of Lemma 3.3 there exists an ellipse $\mathcal E$ circumscribed around $\mathcal {H}$ with at least three different contact points $\mathbf {e}_1,\mathbf {e}_2,\mathbf {e}_3$ lying in $\partial \mathcal {H}\cap \partial \mathcal {E}$ such that the closed triangle $\triangle \mathbf {e}_1\mathbf {e}_2\mathbf {e}_3$ contains the origin.

Suppose we have the configuration described in (iv) of Lemma 3.3.

Choose a plane $\mathcal P'$ such that one of its open halfspace $\mathcal S$ contains $t_1$ and $\mathcal {E}$. Now choose a point $P$ out of $\mathcal P'\cup \mathcal P\cup \mathcal S$. Let $\pi$ be the perspective projection of $\mathcal P$ into $\mathcal P'$ through the point $P$. This projection $\pi$ clearly maps the configuration in $\mathcal P$ into a configuration in $\mathcal P'$ that is described in (iii) of Lemma 3.3. Thus, since the statement of the theorem is of projective nature, it is enough to validate it for configurations described in (iii) of Lemma 3.3.

Take a construction defined by Definition 4.3 (see Fig. 8), and let $\varepsilon =|\mathbf {x}_1-\mathbf {e}_1|+|\mathbf {x}_2-\mathbf {e}_2|+|\mathbf {x}_3-\mathbf {e}_3|$.

By (v) of Lemma 3.3 the straight lines $\mathbf {m}_i\mathbf {b}_i$ $(i=1,2,3)$ meet in the center $\mathbf {o}$ of the ellipse $\mathcal E$, which is in the interior of the trigon $\triangle \mathbf {e}_1\mathbf {e}_2\mathbf {e}_3$, therefore the center $\mathbf {o}$ of the ellipse $\mathcal E$ is in the interior of the trigon $\triangle \mathbf {v}_1\mathbf {v}_2\mathbf {v}_3$ too, if $\varepsilon$ is small enough, which we assume from now on.

According to Lemma 3.1 the lines $\ell _1',\ell _2',\ell _3'$ contain the points

$$\begin{aligned} \begin{aligned} \mathbf {e}_2&\prec \mathbf {v}_2\prec \mathbf {b}_1^\mathcal {H}\preceq \mathbf {b}_1^\mathcal {E}\prec \mathbf {v}_3 \prec \mathbf {x}_3\prec \mathbf {x}_3^\mathcal {H}\preceq \mathbf {x}_3^\mathcal {E}, \\ \mathbf {e}_3&\prec \mathbf {v}_3\prec \mathbf {b}_2^\mathcal {H}\preceq \mathbf {b}_2^\mathcal {E}\prec \mathbf {v}_1 \prec \mathbf {x}_1\prec \mathbf {x}_1^\mathcal {H}\preceq \mathbf {x}_1^\mathcal {E}, \\ \mathbf {e}_1&\prec \mathbf {v}_1\prec \mathbf {b}_3^\mathcal {H}\preceq \mathbf {b}_3^\mathcal {E}\prec \mathbf {v}_2 \prec \mathbf {x}_2\prec \mathbf {x}_2^\mathcal {H}\preceq \mathbf {x}_2^\mathcal {E}, \end{aligned} \end{aligned}$$

(5.1)

respectively, in the given order (see Fig. 8).

Fig. 8

Constructions of circumcenters in $\mathcal H$ and $\mathcal E$

Take the tangent lines $t_i^{\mathcal H}$ and $t_i^{\mathcal E}$ of $\mathcal H$ and $\mathcal E$ at the points $\mathbf {x}_i^{\mathcal H}$ and $\mathbf {x}_i^{\mathcal E}$, respectively, for every $i\in \{1,2,3\}$. Let $\mathbf {m}_1^{\mathcal H}=t_2^{\mathcal H}\cap t_3$, $\mathbf {m}_2^{\mathcal H}=t_3^{\mathcal H}\cap t_1$, $\mathbf {m}_3^{\mathcal H}=t_1^{\mathcal H}\cap t_2$, and $\mathbf {m}_1^{\mathcal E}=t_2^{\mathcal E}\cap t_3$, $\mathbf {m}_2^{\mathcal E}=t_3^{\mathcal E}\cap t_1$ and $\mathbf {m}_3^{\mathcal E}=t_1^{\mathcal E}\cap t_2$ (see Fig. 8).

According to Lemma 3.4, the tangents $t_1,t_2,t_3$ contain the points

$$\begin{aligned} \begin{aligned} \mathbf {m}_2 \prec \mathbf {e}_1&\prec \mathbf {m}_3\prec \mathbf {m}_3^\mathcal {E}\preceq \mathbf {m}_3^\mathcal {H}, \qquad \mathbf {m}_3 \prec \mathbf {e}_2\prec \mathbf {m}_1\prec \mathbf {m}_1^\mathcal {E}\preceq \mathbf {m}_1^\mathcal {H}, \\&\quad \quad \mathbf {m}_1 \prec \mathbf {e}_3\prec \mathbf {m}_2\prec \mathbf {m}_2^\mathcal {E}\preceq \mathbf {m}_2^\mathcal {H}, \end{aligned} \end{aligned}$$

(5.2)

in the given order, respectively (see Fig. 8).

Notice, that for well-chosen $\mathbf {x}_1,\mathbf {x}_2,\mathbf {x}_3$ we have $\mathbf {x}_i^\mathcal {H}\not =\mathbf {x}_i^\mathcal {E}$ for some $i\in \{1,2,3\}$, say $\mathbf {x}_1^\mathcal {H}\not =\mathbf {x}_1^\mathcal {E}$, and then we also have $\mathbf {m}_3^\mathcal {E}\not =\mathbf {m}_3^\mathcal {H}$ and $\mathbf {b}_2^\mathcal {E}\not =\mathbf {b}_2^\mathcal {H}$ by (ii) of Lemma 3.3.

While the triangle $\triangle \mathbf {v}_1\mathbf {v}_2\mathbf {v}_3$ is in ${{\mathrm{Int}}}\mathcal H\cap {{\mathrm{Int}}}\mathcal E$, letting $\varepsilon$ tend to $0$, it tends to the triangle $\triangle \mathbf {e}_1\mathbf {e}_2\mathbf {e}_3$ in Euclidean meaning, hence Lemma 3.4 implies

$$\begin{aligned} \mathbf {m}_i^\mathcal {H}\rightarrow \mathbf {m}_i\ \text { and }\ \mathbf {m}_i^\mathcal {E}\rightarrow \mathbf {m}_i \quad \text { for every }i\in \{1,2,3\}. \end{aligned}$$

(5.3)

On the other hand, for well-chosen $\mathbf {x}_1,\mathbf {x}_2,\mathbf {x}_3$, Theorems 4.2 and 4.4 imply that

$$\begin{aligned} \mathbf {b}_i^\mathcal {E}\rightarrow \mathbf {b}_i\ \text { and }\ \mathbf {b}_i^\mathcal {H}\rightarrow \mathbf {b}_i \quad \text { for every }i\in \{1,2,3\} \end{aligned}$$

(5.4)

as $\varepsilon \rightarrow 0$.

By (5.3) and (5.4) the hyperbolic circumcenter $\mathbf {c}$ of the triangle $\triangle \mathbf {v}_1\mathbf {v}_2\mathbf {v}_3$ tends to the center $\mathbf {o}$ of $\mathcal E$ as $\varepsilon \rightarrow 0$, and therefore the circumcenter $\mathbf {c}$ is in the interior of the triangle $\triangle \mathbf {v}_1\mathbf {v}_2\mathbf {v}_3$ if $\varepsilon$ is small enough.

Suppose that the triangle $\triangle \mathbf {v}_1\mathbf {v}_2\mathbf {v}_3$ has also an $\mathcal H$-circumcenter, say $\mathbf {c}'$. By (5.3) and (5.4) the $\mathcal H$-circumcenter $\mathbf {c}'$ tends also to the center $\mathbf {o}$ of $\mathcal E$ as $\varepsilon \rightarrow 0$, hence it is in the interior of the triangle $\triangle \mathbf {v}_1\mathbf {v}_2\mathbf {v}_3$ if $\varepsilon$ is small enough.

On account of (5.1) and (5.2), for every $i\in \{1,2,3\}$ the closed segments $\overline{\mathbf {m}_i^\mathcal {H}\mathbf {b}_i^\mathcal {H}}$ and $\overline{\mathbf {m}_i^\mathcal {E}\mathbf {b}_i^\mathcal {E}}$ have $k(i)\ge 1$ points in common, which is on the same side of $\ell _i'$ as $\mathbf {m}_i$ is. By the notice after the relations (5.1) and (5.2), we may assume that $k(2)=1$ and $k(3)=1$.

This implies that $\mathbf {c}'$ is in the left open half plane of the lines $\mathbf {m}_i^\mathcal {E}\mathbf {b}_i^\mathcal {E}$ directed from $\mathbf {m}_i^\mathcal {E}$ to $\mathbf {b}_i^\mathcal {E}$ for every $i\in \{2,3\}$ and it is in the left closed half plane of the lines $\mathbf {m}_1^\mathcal {E}\mathbf {b}_1^\mathcal {E}$ directed from $\mathbf {m}_1^\mathcal {E}$ to $\mathbf {b}_1^\mathcal {E}$.

This contradicts the fact that the intersection of these half planes are empty, therefore the supposition of the existence of $\mathbf {c}'$ was wrong, and the theorem is proved. $\square$

Existence of the orthocenter of a trigon, the common point of the three altitudes, is well known in Euclidean plane. It is also known for the hyperbolic plane (Ivanov (2011), Theorem 3): In hyperbolic geometry the altitudes of any trigon form a pencil.

Theorem 5.2

If the altitudes of any trigon in a Hilbert geometry $\mathcal {H}$ form a pencil, then $(\mathcal H,d_{\mathcal H})$ is the hyperbolic geometry.

Proof

Following the proof of Theorem 5.1 we have the very same construction of the tangents and points, but without the midpoints for now (see Fig. 9).

Fig. 9

A triangle with altitudes intersecting in inner points

According to (5.3), the intersection $\mathbf {a}$ of the hyperbolic altitudes $\mathbf {v}_i\mathbf {m}_i^{\mathcal E}$ ($i=1,2,3$) of the triangle $\triangle \mathbf {v}_1\mathbf {v}_2\mathbf {v}_3$ tends to the center $\mathbf {o}$ of $\mathcal E$ as $\varepsilon \rightarrow 0$, and therefore $\mathbf {a}$ is in the interior of the triangle $\triangle \mathbf {v}_1\mathbf {v}_2\mathbf {v}_3$ if $\varepsilon$ is small enough.

Suppose that the $\mathcal H$-altitudes $\mathbf {v}_i\mathbf {m}_i^{\mathcal H}$ ($i=1,2,3$) of the triangle $\triangle \mathbf {v}_1\mathbf {v}_2\mathbf {v}_3$ also intersect in a point $\mathbf {a}'$.

By (5.3) the point $\mathbf {a}'$ also tends to the center $\mathbf {o}$ of $\mathcal E$ as $\varepsilon \rightarrow 0$, hence it is in the interior of the triangle $\triangle \mathbf {v}_1\mathbf {v}_2\mathbf {v}_3$ if $\varepsilon$ is small enough.

On account of relations (5.2), $\mathbf {v}_i=\mathbf {v}_i\mathbf {m}_i^\mathcal {H}\cap \mathbf {v}_i\mathbf {m}_i^\mathcal {E}$ for every $i\in \{1,2,3\}$, and therefore $\mathbf {a}'$ is in the left open half plane of the lines $\mathbf {v}_i\mathbf {m}_i^\mathcal {E}$ directed from $\mathbf {v}_i$ to $\mathbf {m}_i^\mathcal {E}$ for every $i\in \{1,2,3\}$.

This contradicts the fact that the intersection of these halfplanes are empty, therefore the supposition of the existence of $\mathbf {a}'$ was wrong, and the theorem is proved. $\square$