Locating damage to structures using incomplete measurements

Abstract

In situ measured data concerning a large civil engineering structure, such as a building, a bridge or a dam, are often incomplete because of the cost of their acquisition. To overcome the spatial incompleteness of a measured mode shape, many modal expansion methods have been developed. However, the accuracy of the expanded mode shapes corresponding to high frequencies that are obtained using traditional modal expansion methods, such as Guyan expansion, IRS, and spline interpolation is not good enough. To overcome this difficulty, this work proposes an approach of spline interpolation using a pseudo-story for modal expansion. Based on the expanded first mode shape, the damage location index (DLI) is defined for locating damage. Two structures, a uniform structure (a cantilever beam) and a non-uniform structure (a seven-story shear building), are used to demonstrate the feasibility of using the proposed approach for locating damage to structures.

1 Introduction

Structural health monitoring is the in situ nondestructive sensing and analysis of the characteristics of a structure, including the structural response to external excitations, for the purpose of detecting changes that may indicate damage or degradation. However, detecting structural damage and identifying damaged elements in a large complex structure is challenging because in situ measurements of a large civil engineering structure, such as a building, a bridge or a dam, are invariably imprecise (because of noise corruption) and commonly incomplete (for reasons of cost).

Among structural health monitoring techniques [1], mode shape-based methods [2, 3] and flexibility-based methods [4–6] have the potential to locate structural damage. Mode shapes or flexibility can only be obtained using many sensors. However, even when a large number of sensors are utilized, the measurement of modal characteristics is typically incomplete. Issues of optimal sensor placement (OSP) and modal expansion thus arise, particularly if the intention is to monitor a network of structures.

OSP techniques use information from sensing nodes that are sufficiently sensitive to detect changes in modal parameters [7, 8]. The effective independence (EI) method, proposed by Kammer [9], is one of the most widely used OSP techniques. EI searches sensor locations based on the quantitative information (Fisher Information) about target modes and eliminates less significant locations from the candidate sensing locations.

Modal expansion is a technique for overcoming the spatial incompleteness of measured mode shapes. Guyan [10] developed the static expansion method in which the mass and stiffness matrices are partitioned into sub matrices relating to the master and slave degrees of freedom (DOFs). This method is widely used because it is simple and provides accurate results for lower-order mode shapes; the errors increase with the order of the mode shapes. The type and number of master DOFs significantly influences modal expansion. As an extension of the Guyan reduction process, the improved reduced system (IRS) [11] takes into account some of the effects of the eliminated DOFs that cause distortion in the Guyan reduction process.

The objective of this paper is to develop an approach for locating damage to structures using incomplete measurements. Two OSP methods, EI and the uniform spacing method, were studied and compared. Based on the sensor configuration, the mode shapes are expanded using the Guyan expansion, IRS, and the proposed approach (spline interpolation using a pseudo-story). Modal assurance criteria [12] between the expanded mode shape from the optimal sensor configuration and the targeted mode shape are then used to examine the performance of the modal expansion methods. Based on the expanded first mode shape, the damage location index (DLI), is defined for the purpose of locating damage. Additionally, two structures, a uniform structure (a cantilever beam) and a non-uniform structure (a seven-story shear building), are used to demonstrate the feasibility of the proposed method for locating damage to structures.

2 Optimal sensor placement

The objective of the optimal sensor placement (OSP) problem is to minimize the number of sensors and to locate them to estimate target dynamic modes of structures such that the sensor management cost is minimized and the structural modal parameters are accurately estimated.

2.1 Effective independence method

Effective independence (EI) method [9] is one of the most widely used OSP techniques for optimally locating N sensors. The Fisher information matrix [13] associated with candidate sensor locations is evaluated to quantify the contribution to the independence of the target modes and, then, used to maximize the spatial independence of the target modes by ranking the contribution of each sensor location.

The measured response, y, of the structure to vibration can be estimated by combining the contributions of m target modes as,

$$ y = {\varvec{\Phi}}q + w $$

(1)

where ${\varvec{\Phi}} \in R^{n \times m}$ is the target mode shape matrix for n candidate sensor locations; q is the modal contribution factor that is associated with m target modes, and w is the stationary random noise vector with a mean of zero.

An unbiased estimator $\widehat{q} = ({\varvec{\Phi}}^{T} {\varvec{\Phi}})^{ - 1} {\varvec{\Phi}}^{T}$ is utilized to evaluate the error in the estimation of the response to vibration. The covariance of the error between the modal contribution factor q and the unbiased estimator $\widehat{q}$ is identical to the inverse of the Fisher information matrix F:

$$ J = E[(q - \widehat{q})(q - \widehat{q})^{T} ] = \left( {\frac{1}{{\sigma^{2} }}{\varvec{\Phi}}^{T} {\varvec{\Phi}}} \right)^{ - 1} = {\mathbf{F}}^{ - 1} $$

(2)

where $\sigma$ is the standard deviation of the stationary random noise vector, w. The Fisher information matrix measures the amount of information that the mode shape matrix conveys for a specific sensor set. Therefore, the best estimate $\widehat{{\mathbf{q}}}$ is achieved when the Fisher information matrix, F, is maximized.

The EI method solves this optimization problem by examining the contribution of the candidate sensor nodes to the independence of the target modes and eliminating sensor positions that reduce the determinant of F. To evaluate the contribution of the candidate sensor locations to the independence of the target modes, the effective independence distribution (EID) vector, $E_{D} ,$ is introduced as [9].

$$ E_{D} = [{\varvec{\Phi}}\psi ] \otimes [{\varvec{\Phi}}\psi ]\lambda^{ - 1} t $$

(3)

where $\psi$ and $\lambda$ are the eigenvector and eigenvalue of F, respectively; t is a column vector of m unity values to sum all fractional contributions to the independence of the target modes at each sensor location, and $\otimes$ denotes a term-by-term matrix multiplication, which transforms the dot product ${\varvec{\Phi}}\psi$ into absolute identification space, to quantify the contribution to the independence of the target modes at each sensor location.

The ith element of $E_{D}$ represents the fractional contribution to the independence of the target modes at the ith sensor location. A candidate sensor location that has the lowest value of the index $E_{D}$ is eliminated, and this procedure is repeated until the number of remained sensors equals to a preset value.

3 Modal expansion methods

Modal expansion is a technique for overcoming the spatial incompleteness of a measured mode shape. Three modal expansion approaches, Guyan expansion, the improved reduced system (IRS), and spline interpolation, were compared. The performance of the modal expansion approach was studied using the modal assurance criteria (MAC) value between the expanded mode shape that is obtained with the optimal sensor configuration and the targeted mode shape.

3.1 Guyan expansion

Guyan expansion [10] may be the most popular and simplest modal expansion approach. State and force vectors, x and f, and mass and stiffness matrices, M and K, are split into sub vectors and matrices that are related to the master DOFs, which are retained, and the slave DOFs, which are eliminated. If no force is applied to the slave DOFs, then

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{M}}_{mm} } & {{\mathbf{M}}_{ms} } \\ {{\mathbf{M}}_{sm} } & {{\mathbf{M}}_{ss} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\ddot{x}_{m} } \\ {\ddot{x}_{s} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{mm} } & {{\mathbf{K}}_{ms} } \\ {{\mathbf{K}}_{sm} } & {{\mathbf{K}}_{ss} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {x_{m} } \\ {x_{s} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {f_{m} } \\ {\mathbf{0}} \\ \end{array} } \right] $$

(4)

The subscripts m and s specify master and slave coordinates, respectively. Neglecting the inertia terms in the second set of equations yields,

$$ {\mathbf{K}}_{sm} x_{m} + {\mathbf{K}}_{ss} x_{s} = 0 $$

(5)

which may be used to eliminate the slave DOFs, yielding,

$$ \left\{ {\begin{array}{*{20}c} {x_{m} } \\ {x_{s} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\mathbf{I}} \\ { - {\mathbf{K}}_{ss}^{ - 1} {\mathbf{K}}_{sm} } \\ \end{array} } \right]x_{m} = {\mathbf{T}}_{s} x_{m} $$

(6)

where ${\mathbf{T}}_{s}$ is the static transformation between the full state vector and the master coordinates, so the expanded mode shapes are,

$$ \left\{ {\begin{array}{*{20}c} {\varPhi_{m} } \\ {\varPhi_{s} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {\mathbf{I}} \\ { - {\mathbf{K}}_{ss}^{ - 1} {\mathbf{K}}_{sm} } \\ \end{array} } \right]\varPhi_{m} = {\mathbf{T}}_{s} \varPhi_{m} . $$

(7)

Importantly, the master DOFs remain unchanged as seen in the upper part of this equation:

$$ \varPhi_{m} = {\mathbf{I}}\varPhi_{m} $$

(8)

and the deleted DOFs are estimated as

$$ \varPhi_{s} = - {\mathbf{K}}_{ss}^{ - 1} {\mathbf{K}}_{sm} \varPhi_{m} $$

(9)

However, since this technique is based only on the static stiffness of the system, the mode shape expansion may not be accurate. Of course, the Guyan expansion process will not yield acceptable results unless the DOFs suffice to specify the mass inertia of the system. If enough DOFs are available, then the Guyan expansion process will yield reasonably good results but will never yield exact results because the formulation of the transformation matrix is approximate.

3.2 Improved reduced system

As an extension of the Guyan reduction process, the improved reduced system (IRS) [11] takes into account knowledge of system inertial effects. The development is based on the fact that the static structural model that incorporates distributed forces can be condensed to a reduced system and solution. The displacements of the reduced system are then expanded and adjusted for the eliminated forces, yielding an exact static solution for the complete system. A first-order approximation of the eigensystem is obtained using a Guyan/Irons reduced model approach, which is based on the static condensation, with no adjustment for the eliminated distributed inertia forces. The modal vectors of the approximate solution can be adjusted in a similar manner as in the static solution, yielding an improved set of eigenvectors. Finally an estimate of the transformation matrix from full space to reduced space can be obtained for the IRS system. The resulting equations are summarized below but are not detailed herein.

$$ {\mathbf{T}}_{IRS} = {\mathbf{T}}_{s} + {\mathbf{T}}_{l} $$

(10)

Where

$$ {\mathbf{T}}_{l} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{K}}_{ss}^{ - 1} } \\ \end{array} } \right]{\mathbf{M}}_{n} {\mathbf{T}}_{s} {\mathbf{M}}_{R}^{ - 1} {\mathbf{K}}_{R} $$

(11)

$$ {\mathbf{M}}_{R} = {\mathbf{T}}_{S}^{T} {\mathbf{M}}_{n} {\mathbf{T}}_{S} $$

(12)

$$ {\mathbf{K}}_{R} = {\mathbf{T}}_{S}^{T} {\mathbf{K}}_{n} {\mathbf{T}}_{S} $$

(13)

${\mathbf{M}}_{n}$ and ${\mathbf{K}}_{n}$ are the mass and stiffness matrices of the system, respectively; ${\mathbf{M}}_{R}$ and ${\mathbf{K}}_{R}$ are the reduced mass and stiffness matrices of the system, respectively. The expanded mode shapes are

$$ \left\{ {\begin{array}{*{20}c} {\varPhi_{m} } \\ {\varPhi_{s} } \\ \end{array} } \right\} = {\mathbf{T}}{}_{IRS}\varPhi_{m} $$

(14)

3.3 Spline interpolation

Spline interpolation is an extensively used curve-fitting method that minimizes total curvature and maximizes the straightness of an approximate curve [14]. The modal ordinates of the non-measurable or non-measured locations are interpolated using the piecewise pth order (p = 3 is used herein) of the spline, which minimizes the residual sum of squares, S, defined as

$$ S = \sum {_{i} } \left[ {y_{i} - s(x_{i} )} \right]^{2} $$

(15)

where $x_{i}$ is the ith sensing location; $y_{i}$ is the sensor data obtained at the ith sensing location, and s is the polynomial function of order p for each segment of an approximate curve. The compatibility equations are defined using the continuities of the all derivatives up to the (p−1)th derivative of the whole shape function at sensor locations. To handle the unknown coefficients for piecewise polynomial functions, additional modal ordinates are extrapolated linearly outside the investigated span. The continuous piecewise functions are determined using the continuity of modal ordinates and their derivatives.

Notably, the accuracy of spline interpolation is not good enough for mode shapes corresponding to high frequencies. To overcome this difficulty, this work proposes an approach that combines spline interpolation with a pseudo-story to obtain mode shapes; it extends mode shapes to the location of the pseudo-story to reduce the spline interpolation error. The pseudo-story is not a real part of a structure, which is located above the top story for a shear building and beside the free end for a cantilever beam. The distance between the pseudo-story and the first sensor (counting from the sensor closest to the pseudo-story to that farthest) is assumed to be equal that between the first two sensors. The location of the pseudo-story is assumed to be $x_{\text{ps}}.$ Therefore, the ith mode shape vector, extended to the location of the pseudo-story, becomes

$$ \varPhi_{i} = \left[ {\begin{array}{*{20}c} {\varPhi_{i} (x_{1} )} & {\varPhi {}_{i}(x_{2} )} & { \cdots \varPhi_{i} (x_{m} )} & {\varPhi_{i} (x_{ps} )} \\ \end{array} } \right]^{T}. $$

Based on the assumption that the first mode shape vector

$$ \varPhi_{1} = \left[ {\begin{array}{*{20}c} {\varPhi_{1} (x_{1} )} & {\;\varPhi_{1} (x_{2} )} & { \cdots \varPhi_{1} (x_{m} )\;} & {\varPhi_{1} (x_{ps} )} \\ \end{array} } \right]^{T} $$

is known, $\varPhi_{i} (x_{ps} )$ (for i = 2,…, m) can be obtained by exploiting the orthogonality relations between the ith mode and the first mode. That is, $\varPhi_{i} (x_{ps} )$ (for i = 2,…, m) can be obtained by minimizing the following objective function ${\mathbf{\mathcal{G}}}$.

$$ {\mathcal{G}}\left( {\varPhi_{i} (x_{pf} )} \right) = {\text{abs}}\left( {\varPhi_{1}^{T} \varPhi_{i} } \right)\;\left( {{\text{for}}\;i = 2, \ldots ,m} \right) $$

(16)

After $\varPhi_{i} (x_{\text{ps}} )$ is obtained, the second to the mth mode shapes can be obtained by spline interpolation. Remarkably, compared with Guyan expansion and IRS, mode (shape) expansion by spline interpolation in cases of incomplete measurement requires no approximate mass and (or) stiffness matrices. Objective function ${\mathcal{G}}$ in Eq. (16) was minimized herein using the line search algorithm, which is briefly introduced as follows.

In optimization algorithms, for given $x_{k}$, the iterative scheme is

$$ x_{k + 1} = x_{k} + \alpha_{k} d_{k} $$

(17)

where $\alpha_{k}$ and $d_{k}$ are the step size and direction vector, respectively. Line search finds $\alpha_{k}$ such that the objective function f in the direction $d_{k}$ is minimized, so

$$ f(x_{k} + \alpha_{k} d_{k} ) = \min_{\alpha > 0} f(x_{k} + \alpha d_{k} ) $$

(18)

This line search is called an exact line search or an optimal line search, and $\alpha_{k}$ is called the optimal step size. If $\alpha_{k}$ set such that the objective function has an acceptable descent so satisfies

$$ f(x_{k} ) - f(x_{k} + \alpha_{k} d_{k} ) > 0 $$

(19)

then this line search is called an inexact line search, an approximate line search, or an acceptable line search.

Since, in practice, a theoretically exact optimal step size generally cannot be found, and finding a step size that is very close to exact step size is very expensive, an inexact line search with a lower computational load is greatly favored.

The framework for the line search is as follows. First, determine or specify an initial search interval that contains the minimizer; then iteratively apply some section techniques or interpolations to reduce the interval until the size of the interval is less than some specified tolerance.

3.4 Modal assurance criterion

One of the most popular tools for quantitatively comparing modal vectors is the modal assurance criterion (MAC) [12]. The MAC for the ith target mode between an estimated mode shape vector with expansion $(\overline{\varPhi }_{i} )$ and an exact mode shape $(\widehat{\varPhi }_{i} )$ is calculated as,

$$ MAC_{i} = \frac{{\left( {\overline{\varPhi }_{i}^{T} \widehat{\varPhi }_{i} } \right)^{2} }}{{\left( {\overline{\varPhi }_{i}^{T} \overline{\varPhi }_{i} } \right)\left( {\widehat{\varPhi }_{i}^{T} \widehat{\varPhi }_{i} } \right)}} $$

(20)

The MAC takes value between 0 (representing no consistent correspondence) and 1 (representing a consistent correspondence).

4 Damage location strategy

Among all structural properties, the mode shape may be the most useful for locating structural damage because it is related to the locations of structural elements. The accuracy of the first mode shape that is obtained by the aforementioned modal expansion approaches greatly exceeds those of other such shapes. Therefore, locating structural damage using the difference between the first mode shapes in undamaged and damaged states may be feasible. The normalized difference between the first mode shapes in undamaged and damaged states, called the first mode difference function $\left( {\varPhi^{diff,k} } \right)$, is defined as

$$ \varPhi^{diff,k} = \frac{{\left( {\varPhi_{1}^{U} - \varPhi_{1}^{D,K} } \right)}}{{\hbox{max} \left( {{\text{abs}}(\varPhi_{1}^{U} - \varPhi_{1}^{D,K} )} \right)}} $$

(21)

where $\varPhi_{1}^{U}$ and $\varPhi_{1}^{D,k}$ are the first mode shapes in undamaged and damaged (damaged at element k) states, respectively. A sequence of trial reveals that the first mode difference function varies little with the extent of damage to a structure at a fixed location. However, it varies considerably with the location of damage to a structure. This important characteristic applies to the first mode shape that is obtained by spline interpolation. Accordingly, Eq. (21) can be rewritten as follows for the first mode shape that is obtained by spline interpolation.

$$ \varPhi_{spline}^{diff,k} = \frac{{\left( {\varPhi_{spline,1}^{U} - \varPhi_{spline,1}^{D,k} } \right)}}{{\hbox{max} \left( {{\text{abs}}\left( {\varPhi_{spline,1}^{U} - \varPhi_{spline,1}^{D,k} } \right)} \right)}} $$

(22)

A database of the first mode difference function, which is called the basis matrix of the first mode difference, can be constructed as a basis for locating damage. If a shear building structure has n stories (or n lateral translation DOFs), then the basis matrix of the first mode difference $(\varOmega )$ is given by,

$$ \varOmega = \left[ {\begin{array}{*{20}c} {\varOmega_{spline,basis}^{diff,1} } & {\varPhi_{spline,basis}^{diff,2} } & \cdots & {\varPhi_{spline,basis}^{diff,n} } \\ \end{array} } \right] $$

(23)

The kth column of $\varOmega$ is the first mode difference function for damage to the kth story of the shear building. Comparing the first mode difference function for damage to an unknown story of the shear building $\left( {\varPhi_{spline,case}^{diff} } \right)$ with those in each column of $\varOmega$ allows the damage to the shear building to be located. Based on the difference between $\left( {\varPhi_{spline,case}^{diff} } \right)$ and $\varPhi_{spline,basis}^{diff,j}$ (for j = 1, …, n), a damage location index (DLI) is defined as follows.

$$ {\text{DLI}}(k) = \sum\nolimits_{j = 1}^{n} {{\text{abs}}\left( {\varPhi_{spline,basis}^{diff,k} (j) - \varPhi_{spline,case}^{diff} (j)} \right)\;(for\;k = 1, \ldots n)} $$

(24)

Theoretically, DLI should reach its minimum value at the exact damage location. Figure 1 schematically depicts the proposed method for locating damage.

Fig. 1

Schematic diagram of the proposed damage location approach

5 Simulation examples

To confirm the feasibility of the proposed approach for locating damage, two structures—a uniform structure (a cantilever beam) and a non-uniform structure (a seven-story shear building)—were numerically studied.

5.1 Description of example structures

5.1.1 Cantilever beam

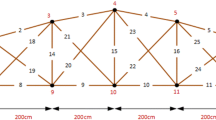
As presented in Fig. 2, the assumed structural properties of the analytical model of a massless cantilever beam are as follows; lumped mass m _j  = 2000 kg (j = 1, …, 10) and stiffness k _j  = 290 kN/m (j = 1, …, 10). Axial and shear deformations of the beam are neglected. Table 1 presents the effective modal masses of the cantilever beam. Generally, the constructed (real) structural properties differ from the designed ones. The designed cantilever beam is specified as CB1. The structural properties (mass and stiffness) of CB1 are assumed to be those that were specified above. Two constructed (real) cantilever beams, CB2 and CB3, are considered. The structural properties of CB2 and CB3 are assumed to be as follows: the structural properties [the masses m _j (j = 1,…, 10) and the stiffness values k _j (j = 1,…, 10)] of CB2 and CB3 equal those of CB1, but randomly increased or decreased by 10 and 20%, respectively.

Fig. 2

The cantilever beam model

Table 1 The effective modal mass of the cantilever beam

5.1.2 The seven-story shear building

The structural properties of the seven-story shear building, as presented in Fig. 3, are assumed to be as follows: the first six story masses are 2000 kg; the seventh story mass is 1000 kg; the first story stiffness is 2000 kN/m; the second story stiffness is 1800 kN/m, and the third to the seventh story stiffness values are 600 kN/m. Table 2 presents the effective modal masses of the seven-story shear building. The designed seven-story shear building is specified as SB1. The structural properties (mass and stiffness) of SB1 are assumed to be those specified above. Two constructed shear buildings, SB2 and SB3, are considered. The structural properties of SB2 and SB3 are assumed to be as follows: the structural properties [the masses m _j (j = 1,…,7) and the stiffness values k _j (j = 1,…,7)] of SB2 and SB3 equal those of SB1, but randomly increased or decreased by 10 and 20%, respectively.

Fig. 3

The seven-story shear building model

Table 2 The effective modal mass of the seven-story shear building model

5.2 Modal expansion

5.2.1 Performance comparison of EI method and uniform spacing method

First, the performances of the two OSP methods, the EI method and the uniform spacing method, are studied. The mode shapes of CB1 and SB1 that are obtained by spline interpolation are investigated. Figures 4, 5, and 6 compare the first three mode shapes of CB1 that are obtained by spline interpolation with two, three, and four sensors, respectively. Table 3 compares the MAC values for the first three modes of CB1. Figures 7, 8, and 9 compare the first three mode shapes of SB1, obtained using spline interpolation with two, three, and four sensors, respectively. Table 4 compares the MAC values for the first three modes of SB1. The results reveal that the interpolation more accurately approximates the target mode shape when the sensors are located uniformly. However, uniform spacing is not always better for non-uniform structures for all possible numbers of sensors. The EI method performs worse because it considers overall modal information in determining OSP, so the sensors are placed too close to, or too far from, each other. Therefore, accurate modal information at a location without a nearby sensor cannot be obtained. Based on these findings, the uniform spacing method is used in the following to locate sensors.

Fig. 4

Comparison of the first three mode shapes of CB1 estimated by using spline interpolation with two sensors a the first mode b the second mode c the third mode

Fig. 5

Comparison of the first three mode shapes of CB1 estimated by using spline interpolation with three sensors a the first mode b the second mode c the third mode

Fig. 6

Comparison of the first three mode shapes of CB1 estimated by using spline interpolation with four sensors a the first mode b the second mode c the third mode

Table 3 Case CB1: best sensor configuration of EI method to observe mode shape using spline interpolation and comparison of MAC to uniformly spaced method

Fig. 7

Comparison of the first three mode shapes of SB1 estimated by using spline interpolation with two sensors a the first mode b the second mode c the third mode

Fig. 8

Comparison of the first three mode shapes of SB1 estimated by using spline interpolation with three sensors a the first mode b the second mode c the third mode

Fig. 9

Comparison of the first three mode shapes of SB1 estimated by using spline interpolation with four sensors a the first mode b the second mode c the third mode

Table 4 Case SB1: best sensor configuration of EI method to observe mode shape using spline interpolation and comparison of MAC to uniformly spaced method

5.2.2 Performance of spline interpolation with a pseudo-story in determining mode shapes

Second, the performance of the spline interpolation with a pseudo-story in determining mode shapes was studied. Tables 5 and 6 present the MAC values between exact mode shapes and estimated ones of CB1 and SB1, respectively. The results reveal that the MAC values between the exact second and third mode shapes and estimated ones that are estimated using spline interpolation with a pseudo-story exceed those without a pseudo-story for both CB1 and SB1. The MAC value is a measure of the accuracy of the estimated mode shape. The accuracy of the mode shape that is estimated by spline interpolation is increased using a pseudo-story. The minimum number of required sensors can be determined from minimum MAC value. The results reveal that the minimum number of sensors is sometimes reduced when using spline interpolation with a pseudo-story to estimate mode shapes. Comparing Table 5 with Table 6 reveals that MAC values between exact mode shapes and estimated ones that are estimated by spline interpolation with a pseudo-story of CB1 are larger than those of SB1 in most situations. One possible reason may be that the uniformity of structural properties (including stiffness and mass) strongly affects the convergence of line search. The performance of spline interpolation with a pseudo-story in estimating mode shapes of a uniform structure is better than that in estimating those of a non-uniform structure. A larger variance of structural properties (stiffness and mass) corresponds to poorer performance of spline interpolation with a pseudo-story in estimating mode shapes.

Table 5 Case CB1 with sensor configuration of uniform spacing: comparison of MAC values between actual mode shapes and estimated ones using spline interpolation with and without a pseudo-story

Table 6 Case SB1 with sensor configuration of uniform spacing: comparison of MAC values between actual mode shapes and estimated ones using spline interpolation with and without a pseudo-story

5.2.3 Comparison of modal expansion methods

The performance of the proposed modal expansion approach (spline interpolation with a pseudo-story) is compared with those of Guyan expansion and IRS. Herein, the structural properties of CB1 are taken as the approximate structural properties in the mode shape expansion for a cantilever beam (uniform structure). Table 7 lists the MAC values between the actual mode shapes and estimated ones that are expanded using Guyan expansion, IRS, and the proposed modal expansion approach for the first three mode shapes of CB2 and CB3. The results reveal that the IRS method performs best for CB2. However, the proposed modal expansion approach performs best for CB3. Since the stiffness values of CB2 and CB3 are those of CB1 but randomly increased or decreased by 10 and 20%, respectively, the results reveal that, for uniform structures, the proposed modal expansion approach is much more effective when the difference between the designed (approximate) structural properties and the real ones is large.

Table 7 Comparison of Guyan expansion, IRS, and the proposed modal expansion approach for CB1

Similarly, the structural properties of SB1 are taken as the approximate structural properties in the mode shape expansion for the seven-story shear building. Table 8 lists the MAC values between the actual mode shapes and estimated ones that are expanded using Guyan expansion, IRS, and the proposed modal expansion approach for the first three mode shapes of SB2 and SB3. The results indicate that the IRS method performs best for both SB2 and SB3. In fact, the performances of the proposed modal expansion approach and the IRS method are approximately the same for SB3. Therefore, for non-uniform structures, the proposed modal expansion approach is also effective when the difference between the designed (approximate) structural properties and the real ones is large. Remarkably, the mode shape can be expanded using the proposed modal expansion approach even when the structural properties are unknown; neither Guyan expansion nor IRS has this ability.

Table 8 Comparison of Guyan expansion, IRS, and the proposed modal expansion approach for SB1

5.3 Locating structural damage

5.3.1 Verification of the first mode difference function to be a baseline for damage localization

After obtaining mode shape using spline interpolation with pseudo-story, these mode shapes can be used for damage localization. The first mode difference function is used as a baseline for locating damage in this study. At first whether the changes of the first mode difference function for different damage extent at a certain location of a structure are slight is verified. In this study, damage was simulated by reducing the stiffness (k _i ) of the affected ith element and single damage location was considered. The MAC threshold is set to be 0.99 to determine the minimum number of sensors. From Tables 7 and 8, we can see that MAC values between the true mode shapes and the expanded ones that are expanded by the proposed modal expansion approach for CB2, CB3, SB2, and SB3 are larger than 0.99 when the number of sensor is 3. Therefore, the minimum number of sensors is set to be 3. Uniform spacing method is used for sensor placement. Figure 10 shows the first mode difference functions of CB1 for stiffness reduction of the 3rd, 5th, and 8th elements. Stiffness reduction of each element varies from 10 to 90 percent every 10 percent. Likewise, Fig. 11 shows the first mode difference functions of SB1 for stiffness reduction of the 3rd, 5th, and 7th stories (represent low, medium, and high stories, respectively). Stiffness reduction of each floor varies from 10 to 90 percent every 10 percent. Except Fig. 11a, Figs. 10 and 11 indicate that the first mode difference function has only a slight variance with damage (stiffness reduction) for the same damage location and a large variance with damage location. Figure 11a shows that the first mode difference function of SB1 damaged at the third story has a large variance for the first two DOFs (or stories) and a slight variance for other DOFs (or stories); thus, the result of the first mode difference function of SB1 damaged at the third story is still acceptable.

Fig. 10

The first mode difference function of CB1 for a reduction of the stiffness of a the 3rd element b the 5th element c the 8th element

Fig. 11

The first mode difference function of SB1 for a reduction of the stiffness of a the 3rd story b the 5th story c the 7th story

Mode shapes that are obtained by spline interpolation with a pseudo-story can be used for locating damage to a structure. The first mode difference function is used as a baseline for locating damage in this work. First, whether the first mode difference function varies with the extent of structural damage at a fixed location is studied. In this work, damage was simulated by reducing the stiffness (k _i ) of the affected ith element at a single damage location. The MAC threshold is set to be 0.99 to determine the minimum number of sensors. From Tables 7 and 8, the MAC values between the actual first mode shapes and the expanded ones that are expanded using the proposed modal expansion approach for CB2, CB3, SB2, and SB3 exceed 0.99 when three sensors are used. Therefore, the minimum number of sensors is set to three. The uniform spacing method is used for placing the sensors. Figure 10 plots the first mode difference functions of CB1 for a reduction of the stiffness of the 3rd, 5th, and 8th elements. The stiffness reduction of each element varies from 10 to 90 percent in steps of 10 percent. Likewise, Fig. 11 plots the first mode difference functions of SB1 for a reduction of the stiffness of the 3rd, 5th, and 7th stories (representing low, medium, and high stories, respectively). The stiffness of each story is reduced by 10–90 percent in steps of 10 percent. Figures 10 and 11 (excluding Fig. 11a) show that the first mode difference function varies only slightly with extent of damage (stiffness reduction) at a fixed location but varies considerably with damage location. Figure 11a reveals that the first mode difference functions of SB1 with different extent of damage at the third story differ from each other greatly for the first two degrees (stories) but slightly for other degrees (stories), so the first mode difference function of SB1 with different extent of damage at the third story is acceptable.

5.3.2 Damage location

Constructed (real) structural parameters are unknown, whereas designed ones are known. Therefore, in this work, to locate damage, the basis matrix of the first mode difference is computed for various degrees of damage from the designed structural parameters. Then, the first mode difference function was computed from the first mode shape of the damaged structure to locate the damage. The DLI can be computed and the damage located from the minimum DLI value. To confirm the feasibility of using DLI for locating damage, 15 and 20% damage to each of the elements of CB2, CB3, SB2, and SB3 were simulated. Tables 9 and 10 present the DLI values for 15 and 20% damage, respectively, to each element of CB2. Tables 11 and 12 present the DLI values for 15 and 20% damage, respectively, to each element of CB3. The results reveal that DLI can successfully locate all locations of damage to CB2 and CB3. Tables 13 and 14 present the DLI values for 15 and 20% damage, respectively, to each element of SB2. Tables 15 and 16 present the DLI values for 15 and 20% damage, respectively, to each element of SB3. The results reveal that DLI can successfully locate damage to SB2 and SB3 in most cases, but not when the first story or the sixth story of SB2 or SB3 is damaged, because the mode shape that is estimated by spline interpolation with a pseudo-story is not close to the actual mode shape at the location where the structural property of interest (mass or stiffness) is changed.

Table 9 Damage location index values for 15% damage to each element of CB2

Table 10 Damage location index values for 20% damage to each element of CB2

Table 11 Damage location index values for 15% damage to each element of CB3

Table 12 Damage location index values for 20% damage to each element of CB3

Table 13 Damage location index values for 15% damage to each element of SB2

Table 14 Damage location index values for 20% damage to each element of SB2

Table 15 Damage location index values for 15% damage to each element of SB3

Table 16 Damage location index values for 20% damage to each element of SB3

To simulate a situation in the real world, the assumption is made that the mode shape of CB3 is contaminated by measurement noise with an error of 1, 0.1, 0.02, and 0.01%. Tables 17, 18, 19 and 20 present DLI values for 20% damage to each element of CB3 with mode shape errors of 1, 0.1, 0.02, and 0.01%, respectively. The results reveal that DLI is effective in locating damage only when the mode shape error is less than 0.01%. Since responses of real structures are supposed to be high noise corrupted, further research could investigate how to improve DLI method to locate damage for the real structures using high noise corrupted measurements. Because the first mode shape is not sensitive to damage, so it must be accurately obtained for DLI to be used to locate damage.

Table 17 Damage location index values for 20% damage to each element of CB3 with 1% mode shape error

Table 18 Damage location index values for 20% damage to each element of CB3 with 0.1% mode shape error

Table 19 Damage location index for 20% damage to each element of CB3 with 0.02% mode shape error

Table 20 Damage location index for 20% damage to each element of CB3 with 0.01% mode shape error

6 Conclusions

The work develops an approach for locating damage to structures from incomplete measurements. Two structures, a uniform structure (a cantilever beam) and a non-uniform structure (a seven-story shear building), are presented to demonstrate the feasibility of using the proposed approach to locate damage to structures. The following important conclusions are drawn from the results herein.

• 1. The performance of uniform spacing method is better than the EI method for uniform structures, but not always better for non-uniform structures. The EI method performs worse because it considers overall modal information in determining OSP, so the sensors are placed too close to, or too far from, each other. Therefore, accurate modal information at a location without a nearby sensor cannot be obtained.

• 2. The accuracy of the mode shape that is estimated by spline interpolation is increased using a pseudo-story.

• 3. The first mode difference function varies only slightly with the degree of damage (stiffness reduction) at a fixed location but greatly with the location of damage, and so can be used for locating damage.

• 4. DLI can successfully locate damage to uniform structures but it does not work in locating some damage to non-uniform structures because the mode shape that is obtained using spline interpolation with a pseudo-story does not closely fit the exact mode shape where structural property of interest (mass or stiffness) is changed.

• 5. DLI is effective for locating damage only when the mode shape error is less than 0.01%. Therefore, the first mode shape must be obtained with high accuracy for the use of DLI to locate damage to a structure.

• 6. The proposed approach is only applicable to structures with “|” or “−” shape, for example, structures in simulation examples. How the proposed approach is applicable to more complicated real structures would be investigated on the basis of this research.