Abstract
The topics of structural proof theory and logic programming have influenced each other for more than three decades. Proof theory has contributed the notion of sequent calculus, linear logic, and higher-order quantification. Logic programming has introduced new normal forms of proofs and forced the examination of logic-based approaches to the treatment of bindings. As a result, proof theory has responded by developing an approach to proof search based on focused proof systems in which introduction rules are organized into two alternating phases of rule application. Since the logic programming community can generate many examples and many design goals (e.g., modularity of specifications and higher-order programming), the close connections with proof theory have helped to keep proof theory relevant to the general topic of computational logic.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Both symbolic logic and the theory of proof have been applied successfully in the foundations of mathematics. For example, Gentzen’s early work on the sequent calculus (Gentzen 1935, 1938) was used to show the consistency of classical and intuitionistic logic and arithmetic. The last several decades have demonstrated that logic has a significant and continuing impact on computer science, possibly rivaling its impact on mathematics. For example, there are major journals that cover the general topic of computational logic—the ACM Transactions on Computational Logic, Logical Methods in Computer Science, the Journal on Automated Reasoning, and the Journal of Logic and Computation—to name a few. Similarly, there are several major conferences (e.g., CADE, CSL, FSCD, LICS, IJCAR) that address various uses of logic in computational settings. This topic also has its own “unreasonable effectiveness” paper, namely “On the Unusual Effectiveness of Logic in Computer Science” (Halpern et al. 2001).
As computer science moves forward, researchers and practitioners occasionally design new programming languages. Usually, the first demands asked of the designers of programming languages are short term, such as the need to support effective implementations and to support interoperability with existing code and hardware. While such short-term demands can always be realized, poor language designs can lead to long-term costs. On this point, it is useful to be reminded of the following, oft-cited quote.
Beauty is the first test: there is no permanent place in the world for ugly mathematics. — G. H. Hardy, A Mathematician’s Apology (Hardy 1940)
The computer scientist sees in this quote a parallel in their own field: a poorly designed computer system, even one that might be working, may have no permanent place in the world since many additional demands usually appear and these will likely force ugly systems to be replaced by those based on better designs. Such additional demands are numerous and include the requirement that code should be modular to support maintainability; programs should be compilable so that they work on a single processor as well as on multiple processors; or that some properties of code may need to be formally proved before that code is used in critical systems. Satisfying such additional demands requires a deep understanding of the semantics of a programming language: quickly hacked languages do not generally support deep understanding or establishing formal properties.
When looking to articulate and exploit deep principles in computing, researchers are often led to exploit existing mathematically well-understood concepts or to develop new frameworks. For example, finite state machines and context-free grammars have been employed to provide a strong foundation for parsing strings into structured data. When needing to deal with communications and shared resources in computer networks, process calculi, such as CSP (Hoare 1985) and CCS (Milner 1980), have been developed, studied, and shaped into programming languages (e.g., the Occam programming language (Burns 1988)). Occasionally, syntactic systems that are not traditionally considered logics are so well studied and found to be of such high quality that they can be used as frameworks for programming languages: the λ-calculus (Barendregt 1997; Church 1985) and the π-calculus (Milner 1999; Milner et al. 1992; Sangiorgi and Walker 2001) are two such examples.
In this paper, I show how various features of some well-studied logical systems directly influenced aspects of programming. At the same time, I provide some examples where attempts to deal with various needs of computing directly lead to new designs and results in logic. Logic is a challenging framework for computation: much can be gained by rising to that challenge to find logical principles behind computation.
I should make it clear before proceeding that I am a participant in the several-decade-long story that I give in this paper: I am not a detached and objective historian. I have two goals in mind in telling this story. First, I want to give specific examples of the mutual influence that has occurred between the abstract and formal topic of proof theory and the concrete and practical topic of computer programming languages. Second, I want to show how a part of computer science can be attached to the foundations of formal proof that was pioneered by Hilbert, Gödel, and Gentzen: the foundation that they and many others provided in the first half of the twentieth century has had significant and immediate impact on computer science today.
2 Logic and Computation: the Different Uses of Logic
Early in the twentieth century, some logicians invented various computational systems, such as Turing machines, Church’s λ-calculus, and Post correspondence systems, which were shown to all compute the same set of recursive functions. With the introduction of high-level programming languages, such as LISP, Pascal, Ada, and C, it was clear that any number of computation systems could be designed to compute these same functions. Eventually, the large number of different programming languages were classified via the four paradigms of imperative, object-oriented, functional, and logic programming. The latter two base computational systems on various aspects of symbolic logic. Unlike most programming languages, symbolic logic is a formal language that has well-defined semantics and which has been studied using model theory (Tarski 1954), category theory (Lambek and Scott 1986; Lawvere 1963), recursion theory (Gödel 1965; Kleene 1935), and proof theory (Gentzen 1935; Girard 1987). As we now outline, logic plays different roles when it is applied to computation.
The earliest and most popular use of logic in computer science views computation as something that happens independently of logic, e.g., registers change, tokens move in a Petri net, messages are buffered and retrieved, and a tape head advances along a tape. Logics (often modal or temporal logics) are used to make statements about such computations. Model checkers and Hoare proof systems employ this computation-as-model approach.
Another use of logic is to provide specification and programming languages with syntax and semantics tied directly to logic. The computation-as-deduction approach to programming languages takes as its computational elements objects from logic, namely types, terms, formulas, and proofs. Thus, instead of basing computation on abstractions of existing technology, e.g., characters on a Turing machine’s tape or tokens in a Petri net, this approach to programming makes direct use of items found in symbolic logic. One hope in making this choice is that programs that rely heavily on logic-based formalisms might be able to exploit the rich meta-theory of logic to help prove properties of specific programs and of entire programming languages.
There are, however, two strikingly different ways to apply the computation-as-deduction approach to modeling computation: these different avenues rely on different roles of proof in the design and analysis of computation.
- Proof normalization::
-
Natural deduction proofs can be seen as describing both functions and values. For example, when a proof of the implication \(B\supset C\) is combined with a proof of the formula B using the rule of modus ponens (also known as \(\supset \)-elimination in natural deduction), the result is a proof of C. That proof, however, is generally not a proof in normal form. The steps involved to normalize such a proof (as described by, for example, Prawitz (1965)) are similar to β-reductions in typed λ-calculi. In that way, a proof of \(B\supset C\) can be seen as a function that takes a proof of B to a proof of C (employing modus ponens and normalization). This computational perspective of (natural deduction) proofs is often used as a formal model of functional programming.
- Proof search::
-
Formulas can be used to encode both programs and goals (think to rules and queries in database theory). Sequents are used to encode the state of a computation and (cut-free) proof search is used to provide traces in computation: changes in sequents denote the dynamics of computation. Cut-elimination is not part of computation but can be used to reason about computation. This view of computation is used to provide a foundation for logic programming.
Although both of these frameworks put formal proofs at their core, the difference between these two approaches is a persistent one. Indeed, advances in understanding the proof theory of higher-order quantification and of linear logic have resulted in different advances in both of these paradigms separately. No current advances in our understanding of proof have forced a convergence of these two paradigms.
The connections between functional programming and proof theory are well documented and celebrated in the literature as the Curry-Howard Isomorphism: see, for example, Ong and Stewart (1997) and Sørensen and Urzyczyn (2006). The connection between logic programming and proof theory is less well documented, and it is the focus of this article.
The field of proof theory covers many topics, including consistency proofs, ordinal inductions, reverse mathematics, proof mining, and proof complexity. Here, we focus instead on structural proof theory, a topic initiated by Gentzen’s introduction of sequent calculus and natural deduction (Gentzen 1935). The sequent calculus is particularly appealing since Gentzen explicitly preferred it over natural deduction as a setting for developing the meta-theory of proofs for both classical and intuitionistic logics simultaneously. Later, Girard showed that the sequent calculus provides a natural account proofs in linear logic as well (Girard 1987). As we shall document, this feature of the sequent calculus provides logic programming with a natural framework in which proof search is described for much richer logics (first-order and higher-order versions of classical, intuitionistic, and linear logics) than the underlying Prolog. Another feature of sequent calculus is its support for abstraction: that is, it provides mechanisms for allowing some aspects of a program’s specification to be hidden while other aspects are made explicit. In programming language terminology, such abstractions provide logic programming with modularity, abstract data types, and higher-order programming. The use of abstractions can significantly aid in establishing formal properties of programs (Miller 1990).
3 Why Turn to Logic to Design a Programming Language?
In many early programming systems, it was specific compilers (and interpreters) that determined the meaning of programs. Since computer processors were rapidly changing and since compilers map high-level languages to these evolving processors, compilers needed to evolve in order to exploit new processor architectures. Since the new compilers did not commit to preserving the same execution behavior of programs as earlier compilers, the meaning of programs would also change. For the many people writing high-level code, the fact that their code could break when moving it between computer systems or to higher version numbers eventually became a serious problem. This situation became untenable when programs also grew dependent on the services—such as memory management, file systems, and network access—offered by operating systems: now programs could also break whenever there were changes to operating systems.
Early efforts to formalize the meaning of programs employed the computation-as-model paradigm mentioned above. For example, logical expressions could be attached to program phrases in order to define pre- and post-conditions. In this setting, the expression {P}S{Q} is used to denote the judgment that “if the formula P holds and the program phrase S executes and terminates, then the formula Q holds.” For example, the expression:
should be true for most notions of while-loops and variable assignments. While this approach to reasoning about the meaning of programs has had some success and is used in several existing systems today, it has also had some significant failures. In fact, the topic of model checking, in which the search for counterexamples (bugs) replaced the search for formal proofs, arose from frustration that it was too difficult to use pre- and post-condition reasoning in many systems, particularly those that had elements of distributed and concurrent execution (Emerson 2008).
Other mathematical frameworks for specifying the meaning of programming languages were given by denotational semantics (Stoy 1977), where the meaning of program phrases is compositionally mapped into well-defined and understood mathematical objects, and operational semantics (Milner et al. 1990; Plotkin 2004), in which program execution is modeled using inference rules to build proof-tree-like structures.
Still another approach to providing a formal semantics to a programming language is to accept as a programming language a formal system that already has a mathematical and well-understood semantics. Here, quantificational classical and intuitionistic logics have well-developed theories of proofs and models: soundness and completeness theorems relate these two remarkably different means of attributing meaning to logical expressions. Logic programming is an approach to programming where programs elements are logical formulas. While this approach can solve the problem of giving a formal semantics to programs, one must recognize that there is a tension between the needs of programming and solutions offered by logic. For example, classical logic views formulas as either true or false and the search for a proof might establish a given formula as true: in that case, it will always be true. Of course, many situations need such permanence: for example, once a (sub)proof establishes that the atomic formula (p l u s 2 3 5) holds (encoding the fact that 2 + 3 is equal to 5) then this fact is, of course, always true. On the other hand, computing needs to deal with situations where a memory cell contains one value now, but in the future, it contains another value. Modeling such memory cells in classical logic cannot be done as simply as by using a predicate of the form “the memory location l contains value x.”
Resolving this tension has generally gone along two different avenues. The first avenue added various features to a programming language, such as Prolog, that were difficult or impossible to provide a logical description. In these cases, the resulting features can be useful but the underlying programming language drifts more and more from its basis in logic. The second avenue attempted to use more expressive logics than first-order classical logic in order to gain some expressive strengths. This paper describes several milestones along this particular avenue for resolving the tension between what logic and proof theory offers and what programming languages need. As we shall see, this particular journey starts with classical logic and then moves to intuitionistic and linear logics in order to provide more expressive programs.
4 A Quick Primer: Terms and Formulas of Predicate Logic
We shall assume that the reader has at least some familiarity with first-order predicate logic. In this section, we simply review a few concepts that will help anchor our later discussions.
In order to define term and formula structures, we need to know which symbols denote predicates and function symbols and what is their arity. Many first-order logic systems (including most Prolog languages) only declare the arity of such symbols. For example, the constructors for natural numbers and lists of natural numbers can be written as:
Thus, cons (the non-empty list constructor) takes two arguments while append (the relation between two lists and the result of appending them) takes three arguments. Some first-order logics are sorted: that is, there are primitive sorts, say, nat (for natural numbers) and list (for lists of natural numbers), and constructors are declared to take their arguments from certain sorts. For example, the declaration displayed above could be made more explicit using sorts such as:
Above only term constructors are given declarations in which the first member of their associated tuple is the list of argument types it expects and the second member is the type of the object that the constructor builds. Predicates could be declared separately using the declaration {append : 〈list,list,list〉} which associates a predicate with the list of argument types it expects.
So that we can also comment on higher-order logic and syntax later, we use the conventions introduced by Church’s Simple Theory of Types (Church 1940). In particular, a type is either a primitive type (these are introduced as we need them and correspond to primitive sorts) and an arrow type which is an expression of the form \(\tau _{1}\rightarrow \tau _{2}\). The arrow associates to the right: thus, \(\tau _{1}\rightarrow \tau _{2}\rightarrow \cdots \rightarrow \tau _{n}\rightarrow \tau _{0}\) reads as \(\tau _{1}\rightarrow (\tau _{2}\rightarrow \cdots \rightarrow (\tau _{n}\rightarrow \tau _{0})\cdots )\). A function symbol with the sort declaration 〈〈τ 1,…,τ n〉,τ 0〉 would correspond to the type \(\tau _{1}\rightarrow \tau _{2}\rightarrow \cdots \rightarrow \tau _{n}\rightarrow \tau _{0}\). A predicate symbol with the sort declaration 〈τ 1,…,τ n〉 is encoded as the type \(\tau _{1}\rightarrow \tau _{2}\rightarrow \cdots \rightarrow \tau _{n}\rightarrow o\), where we follow Church’s convention to use the primitive type o to denote the (syntactic category of) formulas. Thus, the declarations above can be revised to be:
While the arrow type is natural for presenting first-order logic, its presence will also make it easy to generalize the syntax of terms and formulas to accommodate higher-order logic (in Section 9).
A signature is a set containing pairings of tokens with their declared type so that all tokens are declared to have at most one type. Informally, a Σ-term of type τ is a (closed) term all of whose tokens are taken from the signature Σ and which respects the typing declarations. For example, if \({\Sigma }^{\prime }\) is the signature declared at the end of the previous paragraph, then (s (s z)) and (cons (s z) (cons z n i l)) are valid Σ-terms of type nat and list, respectively. The \({\Sigma }^{\prime }\)-term:
has type o which means that it is also a formula. In Prolog syntax, the latter expression corresponds to the (more compact) append([0], [1], [0,1]), which in turn denotes the assertion that [0,1] is the result of appending the lists [0] and [1]. In general, we intend the token append to stand for the three-place relation such that (append L K M) holds if and only if the concatenation of the list L with the list K is the list M (a formal definition for this predicate is given in the next section).
The terms described above are examples of closed terms in the sense that they contain no free variables. Let \({\mathscr X}\) be an infinite set of token-type pairs of the form x : τ where τ is restricted to a primitive type. Assume that the two signatures Σ (of constants) and \({\mathscr X}\) (of first-order variables) do not contain the same token: in that case, a term over the combined signature \({\Sigma }\cup {\mathscr X}\) are terms with possible free variables.
Predicate symbols are introduced as a means to collect together some terms and to yield an atomic formula (such as the assertion about appending lists above). Non-atomic formulas are created using the following propositional constants (along with their declared types): ⊤ : o (truth), ⊥ : o (false), \(\neg : o\rightarrow o\) (negation), \(\vee : o\rightarrow o\rightarrow o\) (disjunction), \(\wedge : o\rightarrow o\rightarrow o\) (conjunction), and \(\supset : o\rightarrow o\rightarrow o\) (implication). The two quantifiers are parameterized by a type: ∀τx.B and ∃τ x.B denote the universal and existential quantifiers (respectively) of the variable x of type τ within the formula B. If a quantifier is written without a subscript type expression, then that type either is unimportant or is easy to infer from its context.
5 Early Foundations of Logic Programming
The logic programming paradigm had a beginning within the artificial intelligence community dating back to the 1960s and 1970s. We start our story here with the first systematic development of a proof procedure by Kowalski (1974), which provided a (non-deterministic) procedural interpretation of logic that lines up well with the nearly simultaneous development of the first Prolog system by Colmerauer and Roussel (1993).
5.1 Declarative vs Procedural Programs
A central and early question about Prolog was how it might be possible to turn declarative information about a desired computation into an actual procedure or program. For example, consider the simple problem of concatenating two lists to get a third list. A declarative treatment of concatenation can be given by stating the following two facts.
-
1.
Concatenating an empty list on the front of a list L yields the list L.
-
2.
If the result of concatenating list L to the front of list K is the list M, then the result of concatenating list (cons X L) to the front of list K is the list (cons X M) for any X (of type nat).
Of course, there are many other statements about concatenation that one could make (for example, that concatenation is associative). The two facts above can be captured easily in first-order logic. Using the predicate symbol append introduced in Section 4, the above two facts about concatenation can be encoded as the two formulas:
(Here, the type of X is nat and of L, K, and M is list.) Following standard Prolog-inspired conventions, we shall write variables as tokens with an initial capital letter and we shall drop all quantifiers assuming that all variables are universally quantified around such formulas. Another convention used by Prolog is to reverse the direction of the implication and to use an ASCII approximate :- to a turnstile (⊩). Following these conventions, we have the following Prolog-style program definition: Footnote 1
append nil L L. append (cons X L) K (cons X M) :- append L K M.
For a second example of a declarative specification written using Prolog syntax, Fig. 1 contains a small graph along with the specification of both the adjacency relation of that graph and a specification of the notion of a path between two points in that graph. In the last line of that specification, another Prolog convention is used: the comma denotes conjunction. That last line can be read as follows: if there is a step from X to Z and a path from Z to Y then there is a path from X to Y. We have also assumed that the signature for these formulas contains the following items:
where n o d e is a primitive type denoting nodes in the graph.
In general, the logical formulas that underlie the Prolog programming language are formulas generally referred to as Horn clauses. These formulas are of the form:
where the formulas A 0,A 1,…,A m are atomic formulas all of whose free variables are in the set {x 1,…,x n}. If n = 0, then we do not write any universal quantifiers and if m = 0, then we do not write the implication. In classical logic, it is possible to convert all formulas to a logically equivalent formula (of essentially the same size) in which implication \(\supset \) is not present and where all occurrences of negation ¬ are applied only to atomic formulas. Such formulas are in negation normal form. In particular, the negation normal form of the Horn clause above is:
If we let \({\mathscr P}\) be the set containing the five formulas displayed in Fig. 1, it would seem natural to expect that provability from \({\mathscr P}\) and computing with this logic program might be related. For example, it is the case that \({\mathscr P}\) proves (in classical and intuitionistic logics) the atomic formula (path a c) (i.e., that there is a path from node a to node c) and that the formula (path a d) has no proof. While one might expect this connection to be rather immediate, the early history of Prolog obfuscated this connection with provability by describing logic programming computation as a refutation, as we shall now illustrate.
5.2 Refutation and Skolemization
In the late 1960s and early 1970s, the resolution refutation procedure of Robinson (1965) was applied in various areas of computational logic. For example, Green (1969) showed that resolution refutations could be used to provide answers within question-answering systems. Given the dominance of resolution, it was natural for Kowalski to have adopted it to provide a description of the operational behavior of Prolog.
On one hand, the choice of resolution was natural for this purpose since term unification was needed to describe Colmerauer’s Prolog and since unification was built into the principle inference rule of resolution. On the other hand, this choice was unfortunate since it required turning what is most naturally considered a problem of searching for a proof into the problem of searching for a refutation. Since classical logic has an involutive negation, it is the case that proving A from \({\mathscr P}\) is equivalent to proving ⊥ from \({\mathscr P}\cup \{A\supset \perp \}\): that is, building a refutation of \({\mathscr P}\cup \{A\supset \perp \}\). Note that this latter step is not valid in intuitionistic logic: in general, resolution is not a sound procedure for intuitionistic logic (without significant modifications to that procedure).
There seems to be only one reason why refutation and not proof dominated the early years of theorem proving in classical logic, and that was the use of skolemization to simplify quantifier structures in formulas. The process of skolemizing a first-order formula, say B (in negation normal form), involves repeatedly replacing a subformula occurrence ∃y.C(y) in B with C(f(x 1,…,x n)), where f is a new function symbol (an extension to the formula signature) and where x 1,…,x n is the list of universally quantified variables of B that contain the occurrence ∃y.C(y) in their scope. A Skolem normal form of B is then a formula that arises from repeatedly removing existential quantifiers in this manner until no occurrences of existential quantifiers remain. The main theorem that relates a formula B with a Skolem normal form of B is that they are equisatisfiable: that is, there is a model of B if and only if there is a model of a Skolem normal form of B. Since skolemization can introduce new constants (Skolem function symbols), the models of B are necessarily different from the models of a Skolem normal form of B. Thus, the stage is set for introducing refutations: in order to prove B is a theorem, we can show instead that ¬B is unsatisfiable. This restatement is, of course, equivalent to showing that the skolemized form of ¬B is unsatisfiable. It is this latter property that the resolution refutation framework is designed to demonstrate.
There are at least a couple of reasons why basing the theory of logic programming on skolemization and refutation was not a good idea, at least in hindsight. First, Horn clauses do not contain quantifier alternations and, hence, skolemization is not a needed processing step. Since skolemization is not required, the motivation to use refutations as outlined loses its force. Second, a couple of the extensions to the design of logic programming that we shall cover soon do not work simply with either skolemization or refutations. In particular, intuitionistic logic plays an important role in the development of logic programming, but skolemization and resolution refutation are both not a sound process in intuitionistic logic. It is also the case that higher-order quantification plays an important role in the development of logic programming and in that setting, and when higher-order substitutions are present, skolemization is a more complex and problematic process. For example, since higher-order instantiations can introduce new instances of quantifiers, the result of a higher-order instantiation of a formula in Skolem normal form may result in a formula that is no longer Skolem normal (something that cannot happen in the first-order setting). More seriously, in higher-order logic, Skolem functions can give rise to uses of the Axiom of Choice even for situations (such as logic programming) where one does not intend for the Axiom of Choice to be a relevant logical feature. For example, Andrews (1971) has described a generalization of resolution refutation for a higher-order logic that can dynamically re-skolemize after the application of a higher-order substitution, but his system was not sound. If the Axiom of Choice was admitted, his system became sound but no longer complete. While an improvement to unification (a key component of resolution) was found that can make skolemization sound (Miller 1987), many computer systems that use unification in a higher-order intuitionistic logic setting, such as λ Prolog (Miller and Nadathur 2012), Twelf (Pfenning and Schürmann 1999), and the Isabelle theorem prover (Paulson 1989), have found ways to avoid both resolution and skolemization entirely.
5.3 SLD-resolution
There were two main ingredients in resolution refutations. The first ingredient is clauses, which are formulas of the form:
where x 1,…,x n is a (possibly empty) list of first-order variables and L 1,…,L m is a (possibly empty) list of literals (atomic formulas or their negation). From what we noted above, Horn clauses can be seen as clauses in which exactly one literal is an atomic formula (instead of the negation of an atomic formula). In general, however, a clause can have any mixture of atomic formulas and negated atomic formulas.
The second ingredient is inference rules that take clauses as their premises and conclusion. The only one of these rules that interest us here is the so-called resolution rule which can be written as:
Here, L and K are atomic formulas, M and N are (possibly empty) disjunctions of literals, and the proviso for this rule is that L and K are unifiable and that θ is set to the most general unifier L and K. A resolution refutation of the set of clauses {C 1,…,C q} is a tree of such inference rules (plus another rule called factoring) in which the leaves come from the set of clauses and the root is the empty clause. When such a tree exists, the fact that the empty disjunction is clearly unsatisfiable can then be transferred to the collection of clauses in its leaves.
The resolution rule is rather remote from Gentzen’s rules for sequent calculus. While Gentzen’s introduction rules process exactly one logical connective per rule, the resolution rule above will deal with n + m + p universal quantifiers along with a number of disjunctions. Furthermore, the operation of unification is not contained in sequent calculus presentations (although the implementation of theorem provers based on the sequent calculus often uses unification).
Kowalski and Kuehner developed a specialized form of resolution based on linear resolution with selection function (SL-resolution) (Kowalski and Kuehner 1971). When this variant of resolution is applied to Horn clauses, it was called SLD-resolution (D for definite, since Horn clauses have also been called definite clauses) (Apt and van Emden 1982). In this setting, attempting to prove the conjunctive goal A 1 ∧… ∧ A n from the Horn clauses in \({\mathscr P}\) results in attempting to refute the clauses in \({\mathscr P}\) together with the clause ¬A 1 ∨… ∨¬A n: this latter clause is distinguished in that the literals it contain are all negated atoms. In this setting, SLD resolution is essentially the restriction of resolution so that one of the clauses being used in the premise of a resolution is always the most recently produced such distinguished clause. This greatly restricted version of resolution could be seen as forming the basis of the engine used in Prolog. Effective implementations of SLD resolution were developed, with the most popular one based on the Warren abstract machine (Aït-Kaci 1991; Warren 1983).
Several variations on Horn clauses have been considered: these include disjunctive logic programs (Lobo et al. 1992; Minker and Seipel 2002) and constraint logic programs (Jaffar and Lassez 1987). In the latter variation, equality of terms is generalized to be a richer relation (e.g., greater-than and non-equal-to) than syntactic equality: such constraints do not normally have most general solutions so one should not choose to solve them immediately but rather delay them until additional constraints are discovered. Most of these extensions were limited to features that could either be seen as retaining the basic characteristics of SLD resolution or which could be compiled into the Warren Abstract Machine. While some extensions, such as HiLoG (Chen et al. 1993), proved useful in some circles, they often exerted no influence on the topics of logic and proof theory.
There are, however, many downsides of using resolution as the core explanation of how logic programming languages should work.
-
Refuting is an odd choice in a setting where proving seems more natural.
-
In order to present formulas as Horn clauses, one may need to transform a formula into its conjunction normal form, and this can cause an exponential increase in formula sizes or require the introduction of new predicate constants in order to keep that size from exploding.
-
First-order unification maintains the normal form of clauses while this is not the case with higher-order quantification since predicate substitutions can transform a formula in normal form into one that is not in normal form. This particular problem could be addressed by re-normalizing after predicate substitutions (Andrews 1971; Huet 1973).
-
More importantly, resolution does not naturally fit with intuitionistic and linear logics although it is possible to develop them based on the structure of sequent calculus proofs (Fitting 1987; Tammet 1996).
These limitations with resolution refutations were then limitations to the designs of new logic programming languages. At roughly the same time as this framework was being designed for logic programming, researchers in functional programming languages were embracing many features of computational logic and proof theory that go well beyond the theory of first-order Horn clauses. In particular, higher-order programming, intuitionistic-logic based typing, and linear logic where all being considered as central and powerful themes in the design of modern functional programming languages. Guided by the Curry-Howard Isomorphism, the proof theory of higher-order intuitionistic logic helped guide the design of many functional programming and reasoning systems (Coquand and Huet 1988; Martin-Löf 1985) and linear logic was seen as offering new features (Wadler 1990).
6 Proof Theory Characterization of Horn Clauses
Gentzen’s sequent calculus provides a natural setting for describing the operational behavior of proof search. Instead of building a refutation, one could instead attempt a proof. When attempting the proof of a goal G from a set of program clauses \({\mathscr P}\), we can consider the problem of building a Gentzen-style proof system with the sequent \({\mathscr P}\vdash G\). For example, let \({\mathscr P}\) be a set of Horn clauses and let one of them be:
The following backchaining rule of inference is then admissible in Gentzen’s LK calculus:
where it is the case that θ is a substitution such that ΘA 0 = A. Admissibility of this rule is easy to see since it is the combination of one occurrence of a contraction, n occurrences of ∀-left introduction, one occurrence of \(\supset \)-left, and one occurrence of the initial rule. A stronger statement is also possible: this is the only inference rule that is required. That is, \({\mathscr P}\vdash A\) is provable in classical logic implies that there is a proof of that sequent in which only instances of the BC rule are needed.
Let A be a syntactic variable that ranges over first-order atomic formulas. Let \({\mathscr G}_{1}\) and \({\mathscr D}_{1}\) be the sets of all first-order G- and D-formulas defined inductively by the following rules:
For the rest of this paper, the formulas of \({\mathscr D}_{1}\) are called first-order Horn clauses.
For the reader familiar with Church’s treatment of higher-order logic, we define also a higher-order generalization to first-order Horn clauses. Let \({\mathscr H}_{1}\) be the set of all λ-normal terms that do not contain occurrences of the logical constants \(\supset , \forall \), and ⊥. Let A and A r be syntactic variables denoting, respectively, atomic formulas and rigid atomic formulas (atomic formulas with a constant as its head symbol) in \({\mathscr H}_{1}\). Let \({\mathscr G}_{2}\) and \({\mathscr D}_{2}\) be the sets of all higher-order G and D-formulas defined inductively by the following rules:
Note that the type of quantified variables in this definition can be at any type including higher-order (predicate) types. The formulas of \({\mathscr D}_{2}\) are called higher-order Horn clauses. Notice that \({\mathscr G}_{2}\) is precisely the set of formulas contained in the set of terms \({\mathscr H}_{1}\).
The proof theory surrounding the higher-order version of Horn clauses has some challenges. In particular, higher-order (predicate) instantiations of higher-order Horn clauses may no longer yield higher-order Horn clauses. Nadathur was able to prove (Nadathur 1987; Nadathur and Miller 1990), however, that in the restricted setting of logic programming, whenever there was a proof involving higher-order Horn clauses, it was also possible to restrain higher-order substitutions so that the only instances of Horn clauses were other Horn clauses.

Notice that goal formulas (G-formulas in the definitions above) are not necessarily limited to atomic formulas: in the Horn clause setting, they can also be conjunctions, disjunctions, and existential quantifiers. Thus, backchaining is not the only inference rule that can be used in this setting. In fact, one can prove the following: when a sequent contains a non-atomic right-hand side (i.e., a goal formula with a logical connective) then the proof of that sequent can be assumed to be a right-introduction rule. Thus, provability with respect to this presentation of Horn clauses builds proofs divided into two phases: when the goal formula is atomic, the backchaining inference rule is used but when the goal formula is non-atomic, then the goal is reduced by using a right-introduction rule (reading proofs from the conclusion to premises).
This two-phase aspect of proof search has a natural appeal. The processing of logical connectives in the goal is fixed (by the right-introduction rules). It is only when a non-logical symbol (the predicate at the head of an atomic formula) is encountered as the goal that we need to consult the (logic) program.
Now that we have a firm basis for logic programming using Horn clauses in sequent calculus, we can ask a natural question: What is the dynamics of proof search? More precisely, if \({\mathscr P}\vdash A\) is a root of a sequent calculus proof and \({\mathscr P}^{\prime }\vdash A^{\prime }\) is any other sequent in that proof (where A and \(A^{\prime }\) are atomic formulas), then how are \({\mathscr P}\) and \({\mathscr P}^{\prime }\), and A and \(A^{\prime }\) related. In the case of Horn clauses, we know that there are rather natural proof systems for classical logic in which \({\mathscr P}={\mathscr P}^{\prime }\). Thus, during the search for a goal, there is no change to the left and, thus, the logic program is global and flat: every part of it is present at all times. Another way to describe this is to say that the only dynamics—the changing of atomic formulas—takes place within non-logical contexts, that is, in the scope of the non-logical symbols that are the predicates of atoms. Putting the dynamics of computation outside of logical contexts certainly seems to diminish the potential of logic to encode and reason about computational dynamics.
This characterization of Horn clauses has important implications for the structuring of programs: if a program clause is ever needed during a computation, it must be available at the beginning of that computation. Thus, Horn clauses do not support directly any hiding of one part of a program from other parts of a program: such a lack is a significant problem for a modern programming language (Miller 1990).
7 What’s Past is PROLOGue: Intuitionistic Logic Extensions
Working from this last observation about how the left-hand side of sequents using Horn clauses is a fixed and global value, the simple suggestion to use goals that are implications would allow contexts to grow as one moves up a proof from the conclusion to premises. In particular, Gentzen’s right-introduction rule for implication:
can be interpreted as adding the new program element D (which might be a Horn clause) to the logic program \({\mathscr P}\). Thus, an attempt to prove the query \((D_{1}\supset A_{1})\land (D_{2}\supset A_{2})\) from the logic program \({\mathscr P}\) would be expected to yield the attempts to prove A 1 from \({\mathscr P}\cup \{D_{1}\}\) and to prove A 2 from \({\mathscr P}\cup \{D_{2}\}\). Thus, attempts to prove the two goals A 1 and A 2 are performed with different logic programs.
While this approach to adding a form of modularity to logic programming is rather immediate, one must confront the fact that classical logic does not provide the proper foundations for this notion of modularity. For example, one expects that attempting to prove \((D_{1}\supset A_{1})\lor (D_{2}\supset A_{2})\) from \({\mathscr P}\) would result in an attempt to prove A 1 from \({\mathscr P}\cup \{D_{1}\}\) or to prove A 2 from \({\mathscr P}\cup \{D_{2}\}\). But this interpretation is not supported by classical logic. Since the classical interpretation of the implication \(D\supset G\) is the same as (¬D) ∨ G, then \((D_{1}\supset A_{1})\lor (D_{2}\supset A_{2})\) is logically equivalent to both \((D_{2}\supset A_{1})\lor (D_{1}\supset A_{2})\) and \((D_{1}\supset (D_{2} \supset (A_{1}\lor A_{2}))\). That is, classical logic does not support the intended scoping interpretation.
In the mid-1980s, the author was developing just such a scheme for providing λ Prolog (Miller and Nadathur 2012; Nadathur and Miller 1988) with a form of modularity: the theory quickly settled on the need to use intuitionistic logic and not classical logic in order to achieve this approach to modularity (Miller 1986, 1989). By the mid-1980s, intuitionistic logic and its proof theory had had a long development, much of that was in the general area of the Curry-Howard Isomorphism (proofs-as-programs). As it turns out, at about this same time, there was nearly simultaneous development of computational uses of large parts of intuitionistic logic that fell outside the Curry-Howard Isomorphism and more squarely in the proof-search framework. These various developments include the following.
-
The N-Prolog language of Gabbay (1985) and Gabbay and Reyle (1984) was designed to allow hypothetical implications in a Prolog-like setting.
-
McCarty (1988a, 1988b) explored using intuitionistic logic to extend the expressiveness of logic programs.
-
Miller, Nadathur, Pfenning, and Scedrov (Miller et al. 1991, 1987) developed a higher-order version of hereditary Harrop formulas in order to support within logic programming rich notions of abstractions, such as modules, abstract datatypes, and higher-order programming.
-
Paulson employed an intuitionistic logic to maintain proof states within the Isabelle theorem prover (Paulson 1989).
-
Hällnais and Schroeder-Heister applied proof-theoretic considerations to extend Horn clause programming in ways similar to these other approaches (Hallnȧs and Schroeder-Heister 1991).
The simultaneous development of similar uses of intuitionistic logic within the logic programming (proof search) setting provided a great deal of confidence that intuitionistic logic and formulas with logical complexity much richer than Horn clauses could have important applications in computational logic. Since resolution refutations fundamentally rely on classical logic principles, the familiar framework on SLD resolution needed to be rejected as a framework for these newly extended logic programming proposals. The sequent calculus provided just such a new starting point.

A uniform proof (Miller et al. 1991, 1987) is a single conclusion (cut-free) sequent proof in which each occurrence of a sequent whose right-hand side contains a non-atomic formula is the conclusion of a right-introduction rule. In other words, a uniform proof is a sequent proof such that, for each occurrence of a sequent Γ ⊩ G in it, the following conditions are satisfied:
-
1.
If G is ⊤, then that sequent is immediately proved.
-
2.
If G is B ∧ C, then that sequent is inferred from Γ ⊩ B and Γ ⊩ C.
-
3.
If G is B ∨ C, then that sequent is inferred from either Γ ⊩ B or Γ ⊩ C.
-
4.
If G is \(\exists x{\kern 2.8pt}!B\), then that sequent is inferred from Γ ⊩ [t/x]B for some term t.
-
5.
If G is \(B\supset C\), then that sequent is inferred from B,Γ ⊩ C.
-
6.
If G is \(\forall x{\kern 2.8pt}!B\), then that sequent is inferred from Γ ⊩ [c/x]B, where c is a variable (parameter) that does not occur free in \(\forall x{\kern 2.8pt}!B\) nor in the formulas in Γ. Gentzen referred to such variables used in this manner as eigenvariables of the proof (Gentzen 1935).
The notion of a uniform proof reflects the search instructions associated with the logical connectives. The logic program is only examined (via left-introduction rules) in the case that a non-logical symbol rises to the top of the query: such non-logical symbols are predicates and these are given meaning (axiomatized) by the logic program on the left-hand side of a sequent. An abstract logic programming language is a triple \(\langle {\mathscr D},{\mathscr G},\vdash \rangle \) such that for all finite subsets \({\mathscr P}\) of \({\mathscr D}\) and all formulas G of \({\mathscr G}\), \({\mathscr P}\vdash G\) holds if and only if there is a uniform proof of G from \({\mathscr P}\). It is in the following sense that uniform proofs are intended to capture the notion of goal-directed search. The impact on the search for proofs is fixed by the top-level logical connective of the goal. We only examine the program when there is a non-logical symbol at the head of the sequent.
One example of an abstract logic programming language is the one based on Horn clauses. In particular, both the triples \(\langle {\mathscr D}_{1},{\mathscr G}_{1},\vdash _C\rangle \) (capturing first-order Horn clauses) and \(\langle {\mathscr D}_{2},{\mathscr G}_{2},\vdash _C\rangle \) (capturing higher-order Horn clauses), are abstract logic programming languages. This statement is also true if classic provability is replaced by intuitionistic provability in both of these triples.
The following is a more complex example of an abstract logic programming language. Let A be a syntactic variable that ranges over first-order atomic formulas. Let \({\mathscr G}_{3}\) and \({\mathscr D}_{3}\) be the sets of all first-order G- and D-formulas defined by the following rules:
Formulas in \({\mathscr D}_{3}\) are called first-order hereditary Harrop formulas. It is proved in Miller et al. (1991) that the triple \(\langle {\mathscr D}_{3},{\mathscr G}_{3},\vdash _I\rangle \) is an abstract logic programming language.
Let \({\mathscr H}_{2}\) be the set of all λ-normal terms that do not contain occurrences of the logical constants \(\supset \) and ⊥. Let A and A r be syntactic variables denoting, respectively, atomic formulas and rigid atomic formulas in \({\mathscr H}_{2}\). Let \({\mathscr G}_{4}\) and \({\mathscr D}_{4}\) be the sets of G- and D-formulas that are defined by the following mutual recursion:
The formulas of \({\mathscr D}_{4}\) are called higher-order hereditary Harrop formulas and it is proved in Miller et al. (1991) that the triple \(\langle {\mathscr D}_{4},{\mathscr G}_{4},\vdash _I\rangle \) is an abstract logic programming language.
As in the case of Horn clauses, proof search with hereditary Harrop formulas yields uniform proofs that are organized into alternating phases: one phase reduces goal formulas (using right-introduction rules), and one phase performs backchaining steps (using left-introduction rules and the initial rule) (Miller 1991; Miller et al. 1991).
The λ Prolog programming language was designed to implement most of the intuitionistic theory of higher-order hereditary Harrop formulas: a key design goal of that language was to demonstrate the abstraction mechanisms that those formulas provide (Miller and Nadathur 2012; Nadathur and Miller 1988). Since there is a significant gap between having a description of a logic programming language in a sequent calculus and an actual implementation of that language, there were a number of significant developments that needed to be made prior to having comprehensive implementations of that language, of which there are two currently, namely Teyjus (Nadathur and Mitchell 1999; Qi et al. 2015) and ELPI (Dunchev et al. 2015). The description of a unification algorithm that works well in the sequent calculus where eigenvariables are present was one of those challenges (Miller 1991, 1992; Nadathur et al. 1995): such unification made it possible to avoid the problematic use of Skolem terms.
At the end of Section 6, we described the dynamics of proof search with Horn clauses as flat since the logic program used during proof search never changes during a computation. When we examine the dynamics of change using hereditary Harrop formulas, we note that the left-hand side of sequents (the logic program) can grow monotonically as we move from the conclusion to premises.
The overview of structuring mechanisms for logic programming given in Bugliesi et al. (1994) provides still additional examples of how proof theory considerations can provide or can influence this aspect of designing logic programming languages.
8 Linear Logic and Logic Programming
As we noted in the previous section, the use of intuitionistic logic and hereditary Harrop formulas allowed logic programs to be seen as a structure that grows in a stack-based discipline as the search for proofs moves from the conclusion to premises. While such growth in logic programs is an improvement over what was available using only Horn clauses, many additional problems existed in computational logic that were just out of reach of having an elegant solution using intuitionistic logic.
For example, in the area of natural language, a good treatment of filler-gap dependencies (used to characterize such natural language constructs as questions and relative clauses) was hard to achieve using standard Horn clause-based logic grammars and lead to the development of the slashed non-terminal in the framework of Generalized Phrase Structure Grammar (GPSG) (Gazdar et al. 1985). A different approach using intuitionistic logic made it possible to identify the linguistic notion of gap introduction with hypothesis introduction that arises from an implicational goal. As reported by Pareschi (1989) and Pareschi and Miller (1990), that technique provided an elegant new perspective to that linguistic phenomenon but it also failed to treat known restrictions on the distribution and use of gaps-as-hypotheses: in particular, gaps needed to be used and they could not appear in certain parts of phrases.
For another example, Hodas and Miller (1990) and Hodas (1994) described how it was possible to capture partially the notion of objects-with-state within logic programming. Again, intuitionistic logic provides a partial solution. In particular, it is possible to store the value of a register as an atomic formula among the other clauses of a logic program. For example, the atomic formula r e g(4) can encode the fact that a register has a value of 4. Unfortunately, there is no way to have that atomic formula replaced with, say, r e g(5) within intuitionistic logic. More specifically, it is not possible to write a logic program clause such that backchaining on it would justify the following inference:
where both A and \(A^{\prime }\) are atomic formulas. The best one can do within intuitionistic logic is to move to a context in which both atoms r e g(4) and r e g(5) are present: that is, the following inference is possible.
Unfortunately, this situation (where a register has two different values) does not provide a proper model of a register.
With the appearance of Girard’s linear logic (Girard 1987), it was possible to extend the design of previous logic programming languages so that they could solve the cited problems in both the gap-threading and the state-encapsulation situations. Logic programming provided other important examples that helped convince a number of computer scientists of the value of linear logic to computational logic: beyond the two examples mentioned above, additional examples appeared in the areas of concurrency (Kobayashi and Yonezawa 1993; Miller 1993), Petri nets (Engberg and Winskel 1990; Kanovich 1995), and theorem proving (Hodas and Miller 1994).

Linear logic also provided a richer analysis of the role of structural rules in Gentzen’s sequent calculus and, as a result, greatly improved our understanding of proof search. For example, if one can restrict the uses of the structural rule of contraction (which can be done in linear logic), one can often turn a naive proof-search mechanism into a complete decision procedure.
After Girard’s introduction of linear logic in 1987, it became clear that there should be linear logic programming languages: the logic programming paradigm lacked certain features (e.g., side effects and communications) which linear logic seems capable of capturing.
Among the first linear logic programming languages designed, there was a divergence along two axes. One of the most challenging connectives in linear logic for computer scientists to appreciate was the multiplicative disjunction
 . For the proof theorist, this connective was not a challenge since it could be identified with the comma appearing on the right of Gentzen’s multiple conclusion sequents. It could also be seen as the de Morgan dual of the multiplicative conjunction ⊗. In computational logic, however, intuitions coming from intuitionistic logic can make it difficult to find computational meaning for
. For the proof theorist, this connective was not a challenge since it could be identified with the comma appearing on the right of Gentzen’s multiple conclusion sequents. It could also be seen as the de Morgan dual of the multiplicative conjunction ⊗. In computational logic, however, intuitions coming from intuitionistic logic can make it difficult to find computational meaning for  since Gentzen identified intuitionistic logic with single conclusion sequents. While an early proposal for a linear logic programming language avoided using
since Gentzen identified intuitionistic logic with single conclusion sequents. While an early proposal for a linear logic programming language avoided using  , the first linear logic programming language actually made prominent use of that connective.
, the first linear logic programming language actually made prominent use of that connective.
8.1 Linear Objects
Historically speaking, the first proposal for a linear logic programming language was LO (Linear Objects) by Andreoli and Pareschi (1991a, b). LO is an extension to the Horn clause paradigm in which, roughly speaking, the role of atomic formulas in Horn clauses is generalized to multisets (built using  ) of atomic formulas. In LO, backchaining captures multiset rewriting and the dominant examples of LO were taken from those domains where multiset rewriting had proved useful, namely object-oriented programming and the coordination of processes. Program clauses in LO are formulas of the form:
) of atomic formulas. In LO, backchaining captures multiset rewriting and the dominant examples of LO were taken from those domains where multiset rewriting had proved useful, namely object-oriented programming and the coordination of processes. Program clauses in LO are formulas of the form:

Here, p > 0 and m ≥ 0; occurrences of ↪ are either occurrences of − ∘ (linear implication) or ⇒ (intuitionistic implication); G
1,…G
m are built from  , &, and ∀; and A
1,…A
m are atomic formulas. The two implications are related by the familiar linear logic equivalence between B ⇒ C and \((\mathop {!} B)\mathbin {-\hspace {-0.70mm}\circ } C\). By applying (uncurrying) equivalences, the displayed formula above can be rewritten as:
, &, and ∀; and A
1,…A
m are atomic formulas. The two implications are related by the familiar linear logic equivalence between B ⇒ C and \((\mathop {!} B)\mathbin {-\hspace {-0.70mm}\circ } C\). By applying (uncurrying) equivalences, the displayed formula above can be rewritten as:

where §G
i is either G
i if G
i is to the immediate left of a − ∘ or is \(\mathop {!} G_{i}\) if G
i is to the immediate left of a ⇒. Note that if this displayed formula contained no occurrences of  and ⇒ then it is an easy matter to view that formula as a simple Horn clause.
and ⇒ then it is an easy matter to view that formula as a simple Horn clause.
8.2 Lolli
The Lolli logic programming language was introduced by Hodas and the author as a linear logic extension to the intuitionistic theory of hereditary Harrop formulas. In particular, Lolli can be seen as a revision and small extension to the logic of hereditary Harrop formulas (Section 7). For our purposes here, the following definitions of goal formulas and program clauses are simplified slightly from the definition found in Hodas and Miller (1994).
Note that the intuitionistic conjunction used in hereditary Harrop formulas corresponds here to &. A more significant difference is that both − ∘ and ⇒ are available in the positions where only occurrences of the intuitionistic implication appear in hereditary Harrop formulas. (Note that there is no difference here between G-formulas and D formulas: they are both formulas freely generated using &, − ∘, ⇒, and ∀.)
For the benefit of the reader familiar with the sequent calculus, we briefly describe a proof system for Lolli since it illustrates two innovations that arise from accounting for proofs in linear logic. The inference rules for Lolli are presented in Fig. 2. This proof system differs from those used by Gentzen (1935) and Girard (1987) in two important ways.
-
1.
The left-hand context is divided into two parts Ψ;Δ (where both Ψ and Δ are multisets of D formulas). The context Ψ denotes those formulas that can be used any number of times during the search for a proof while those in Δ are controlled is the sense that the structural rules of contraction and weakening are not applicable to them. As a result, the context Ψ is often called the unbounded context and Δ is often called the bounded context.
-
2.
There are two kinds of sequents written as Ψ;Δ ⊩ G and
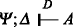 (where, A is restricted to being an atomic formula). These sequents can be mapped into the more usual linear logic sequents by rewriting:
(where, A is restricted to being an atomic formula). These sequents can be mapped into the more usual linear logic sequents by rewriting:

(Here, !Ψ is defined to be the multiset \(\{! D{\kern 2.8pt}!|{\kern 2.8pt}! D\in {\Psi }\}\).) The formula that is placed on top of the turnstile in the second class of sequents is the formula involved with backchaining. The left-introduction rules are only applied to the formula that labels such a turnstile.
In every inference rule, it is the case that the unbounded context of the conclusion is a subset of the unbounded contexts over every premise sequent. Such an invariant is not true of the bounded context: in particular, when the inference rule is one of the left-introduction rules for − ∘ and ⇒. In the case of the left-introduction for − ∘, the bounded context in the conclusion must be divided into two multisets Δ1 and Δ2 and the two premises use each one of these splits. Thus, as one moves from a conclusion to a premise, the bounded contexts of sequents can reduce. In the case of the left introduction for ⇒, the bounded context in the conclusion must again be split but the only legal split is one where the left premise must have an empty bounded context: that is, the entire bounded context must move to the right premise.
The use of two different kinds of sequents allows for a succinct presentation of the two-phase construction of proofs that we have already mentioned. Sequents of the form Ψ;Δ ⊩ G, where G is not atomic, can only be proved by a right-introduction rule: hence, such sequents are used to describe the goal-directed phase. The sequent Ψ;Δ ⊩ A, where A is an atomic formula, can only be proved by first choosing a formula D from either Ψ or from Δ. In the d e c i d e rule, D is chosen from the unbounded context and D remains in the unbounded context of the premise sequent. In the d e c i d e rule, D is chosen from the bounded context and that occurrence of D no longer remains in the bounded context of the premise. In effect, the d e c i d e rule contains a built-in application of the contraction rule: note also that this rule is the only explicit occurrence of contraction in this proof system.
The form of the i n i t rule in Fig. 2 reveals that it can only apply in the backchaining phase, only when the bounded context is empty, and only when the formula labeling the sequent arrow must be the same atomic formula as the conclusion of the sequent.
We can now illustrate how we can model the change in a register’s value. Assume that Ψ contains the formula:
Using the proof rules in Fig. 2, we can write the following partial derivation.

Here, \(D^{\prime }\) is the formula (reg(5) − ∘ G) − ∘inc(G). Thus, the inference that this derivation gives rise to is simply:
Critical for the correct modeling of the change in state of this register is the splitting of the linear context in the − ∘ left-introduction rule between its two premises and the fact that the linear context must be empty in the initial rules.
8.3 Goal-Directed Search with Multiple Conclusion
A natural question is whether or not it is possible to view LO and the Lolli as sublanguages of a larger linear logic programming language. While Lolli contains occurrences of many linear logic connectives, it does not allow occurrences of  , its unit ⊥, and its associated exponential \(\mathop {?}\). One thing to note is that if one adds to Lolli just ⊥, all connectives of linear logic can then be defined. For example,
, its unit ⊥, and its associated exponential \(\mathop {?}\). One thing to note is that if one adds to Lolli just ⊥, all connectives of linear logic can then be defined. For example,  can be defined as (B − ∘⊥) − ∘ C and \(\mathop {?} B\) can be defined as (B − ∘⊥) ⇒⊥. In Miller (1994, 1996), the author proposed a new logic programming language, called Forum, which results from adding
can be defined as (B − ∘⊥) − ∘ C and \(\mathop {?} B\) can be defined as (B − ∘⊥) ⇒⊥. In Miller (1994, 1996), the author proposed a new logic programming language, called Forum, which results from adding  , and \(\mathop {?}\) to Lolli. Thus, Forum is essentially a presentation of all of linear logic as a logic programming language.
, and \(\mathop {?}\) to Lolli. Thus, Forum is essentially a presentation of all of linear logic as a logic programming language.
The most direct way to view all of linear logic as a logic programming language suggests attempting to generalize the notion of uniform proof from single-conclusion to multiple-conclusion sequents. This can be done if we insist that goal-reduction should continue to be independent of not only the logic program but also other goals, i.e., multiple goals should be reducible simultaneously. Although the sequent calculus does not directly allow for simultaneous rule application, it can be simulated easily by referring to permutations of inference rules (Kleene 1952). In particular, we can require that if two or more right-introduction rules can be used to derive a given sequent, then all possible orders of applying those right-introduction rules can be obtained from any other order simply by permuting right-introduction inferences. It is easy to see that the following definition of uniform proofs for multiple-conclusion sequents generalizes that for single-conclusion sequents: a cut-free, sequent proof Ξ is uniform if for every subproof Ψ of Ξ and for every non-atomic formula occurrence B in the right-hand side of the end-sequent of Ψ, there is a proof \({\Psi }^{\prime }\) that is equal to Ψ up to permutation of inference rules and is such that the last inference rule in \({\Psi }^{\prime }\) introduces the top-level logical connective occurring in B (Miller 1993, 1996). The notion of an abstract logic programming language can be generalized to include this extended notion of uniform proof.
8.4 Focusing
As it turns out, the completeness of multiple conclusion uniform proofs for Forum had actually been proved a couple of years before the introduction of Forum. The Ph.D. dissertation of Andreoli (1990) introduced a new sequent calculus proof system for linear logic, called a focused proof system, that was composed of two kinds of sequents and two phases of proof construction. That proof system resembles the proof system in Fig. 2 and the formula that is placed over the turnstile in that figure corresponds to the focus that exists in one of the phases of focused proofs. The completeness of focused proofs (see also Andreoli 1992) provided the completeness result for Forum (Miller 1996) (see also Bruscoli and Guglielmi 2006). However, Andreoli’s presentation of a focused proof system of linear logic provided important and deeper insights into the structure of proof search in the sequent calculus. In particular, Andreoli’s analysis of the two phases of rule application was based on a notion of polarity of logical connectives and that polarity is flipped by de Morgan duality. (Polarity of a logical connective is related to whether or not its right introduction rule is invertible or not.) The use of two phases of proof construction was a powerful addition to the results of pure proof theory. Several subsequent efforts have been made to provide focused proof systems for classical and intuitionistic logic all of which appear to be captured by the LKF and LJF focused proofs system of Liang and the author (Liang and Miller 2009).

8.5 Other Linear Logic Programming Languages
Besides LO, Lolli, and Forum, various other subsets of linear logic have been studied as logic programming languages. The Lygon system of Harland et al. (1996) is based on a notion of multiple-conclusion goal-directed proof search different from the one described above (Pym and Harland 1994). The operational semantics for proof search in Lygon is different and more complex than the alternating of goal reduction and backchaining found in, say, Forum. Various other specification logics have also been developed, often designed directly to deal with specific application areas. In particular, the language ACL by Kobayashi and Yonezawa (Kobayashi and Yonezawa 1993, 1994) captures simple notions of asynchronous communication by identifying the primitives for sending and receiving of messages with two complementary linear logic connectives. Lincoln and Saraswat have developed a linear logic version of concurrent constraint programming (Lincoln and Saraswat 1993; Saraswat 1993), and Fages, Ruet, and Soliman have analyzed similar extensions to the concurrent constraint paradigm (Fages et al. 1998; Ruet and Fages 1997).
Let G and H be formulas composed of  , and ∀. Closed formulas of the form \(\forall \bar x [ G \mathbin {-\hspace {-0.70mm}\circ } H]\) (where H is not ⊥) have been called process clauses in Miller (1993) and are used there to encode a calculus similar to the π-calculus: the universal quantifier in goals are used to encode name restriction. These clauses, when written in their contrapositive form (replacing, for example,
, and ∀. Closed formulas of the form \(\forall \bar x [ G \mathbin {-\hspace {-0.70mm}\circ } H]\) (where H is not ⊥) have been called process clauses in Miller (1993) and are used there to encode a calculus similar to the π-calculus: the universal quantifier in goals are used to encode name restriction. These clauses, when written in their contrapositive form (replacing, for example,  with ⊗), have been called linear Horn clauses by Kanovich and have been used to model computation via multiset rewriting (Kanovich 1994). A generalization of process clauses was presented in Miller (2003) and was applied to the description of security protocols.
with ⊗), have been called linear Horn clauses by Kanovich and have been used to model computation via multiset rewriting (Kanovich 1994). A generalization of process clauses was presented in Miller (2003) and was applied to the description of security protocols.
Some aspects of dependent typed λ-calculi overlap with notions of abstract logic programming languages. Within the setting of intuitionistic, single-side sequents, uniform proofs are similar to β η-long normal forms in natural deduction and typed λ-calculus. The LF logical framework (Harper et al. 1993) can be mapped naturally (Felty 1991) into a higher-order extension of hereditary Harrop formulas (Miller et al. 1991). Inspired by such a connection and by the design of Lolli, Cervesato, and Pfenning developed a linear extension to LF called Linear LF (Cervesato and Pfenning 2002).
An overview of linear logic programming up until 2004 can be found in Miller (2004b).

9 First-order and Higher-order Quantification
While most work in proof theory and logic programming has addressed only first-order quantification, several researchers have defined and implemented logic programming languages that include higher-order quantification.
Church, the inventor of the λ-calculus, is also the inventor of the most popular version of higher-order logic in use in computational logic presently. In particular, Church’s Simple Theory of Types (STT) (Church 1940) defines the syntax of both terms and formulas using simply typed λ-terms (simple types have been introduced in Section 4). STT used only one form of binding, and that is the one used to form λ-abstractions: all other bindings—for example, the universal and existential quantifiers—are built using the λ-binder. In STT, it was possible to quantify over variables of primitive type (first-order quantification) as well as types—such as \(\textit {list}\rightarrow \textit {list}\), \(\textit {nat}\rightarrow o\), and \((\textit {list}\rightarrow o)\rightarrow o\)—that contain the arrow constructor and the primitive type o (higher-order quantification).
When implementing computer systems that need to manipulate syntactic expressions in artificial and natural languages, the strings containing those syntactic expressions need to be parsed. The result of such a parse is generally a parse tree or abstract syntax tree representation capturing the structure of the parsed expression. Most traditional programming languages—functional, imperative, logic—have convenient and flexible means to process tree structures. However, a majority of syntactic expressions that need to be parsed and manipulated contain more than recursive tree structures: they also contain binding structures. While binding structures can, of course, be encoded in tree structures (using techniques such as de Bruijn’s nameless dummies (de Bruijn 1972)), no traditional programming language contains direct support for such an important feature of many syntactic expressions.
A good starting point for treating bindings in logic programming would then seem to involve a proper merging of Church’s logic with Gentzen’s sequent calculus. Such a merging also involves continuing Church’s identification of bindings to one additional level. That is, term-level bindings (λ-abstractions) and formula-level bindings (quantifiers) need to also be merged with proof-level bindings, which are the eigenvariables of the sequent calculus. It is possible to consider eigenvariables to be bindings around sequents: that is, if \({\mathscr V}\) is a set of distinct variables then the expression \({\mathscr V} \colon {\Gamma }\vdash {\Delta }\) can be interpreted as the formal binding of the variables in \({\mathscr V}\) over the formulas in both Γ and Δ.
To illustrate this merging of bindings at these three levels, consider specifying the binary predicate typeof whose arguments are encodings of an untyped λ-term and of a simple type, respectively. The intended meaning of this predicate is that (typeof ⌈B⌉ ⌈τ⌉) holds if and only if the untyped λ-term B can be typed with τ. For this example, we will write ⌈t⌉ to denote some encoding of untyped λ-terms into simply typed terms: the key for this encoding is that bindings in the untyped terms are encoded as binders in the encoded terms. We also assume that there is some encoding, also written ⌈τ⌉, of simple type expressions into (first-order) terms. Consider the following derivation involving the specification of typeof:
Informally, this partial derivation can be seen as reducing the attempt to show that the term λ x.B has type \(\alpha \rightarrow \beta \) to the attempt to show that if (the eigenvariable) x has type α then B has type β. In this case, the binder named x moves from term-level (λ x) to formula-level (∀x) to proof-level (as an eigenvariable in \({\mathscr V},x\)). Thus, an integration of Church’s STT and Gentzen’s sequent calculus supports the mobility of binders.

λ Prolog was the first programming language to embraced this notion of binder mobility (Miller 2004a; 2018), although this notion is also present in specification languages based on dependently typed λ-calculus (Coquand and Huet 1988; Harper et al. 1993; Pfenning and Schürmann 1999). The Isabelle theorem prover (Paulson 1989) also supports binder mobility using the technical device of ∀-lifting to link proof-level bindings to formula-level quantification.
10 Conclusion
There have been significant reciprocal influences between researchers working on structural proof theory and those working on logic programming. While it is not surprising to find that the older and more mature topic of proof theory provided the bulk of that influence, it is still the case that problems identifies within logic programming forced proof theorists to deepen and extend their results. The development of two-phase proof constructions that resulted in focused proof systems might be the most prominent example; the encoding of binder mobility has been a second such example.
Notes
We use the syntax of λ Prolog instead of Prolog: for simple programs, the difference between these languages is small.
References
Aït-Kaci, H. (1991). Warren’s abstract machine: a tutorial reconstruction. Logic Programming Research Reports and Notes. Cambridge: MIT Press. http://wambook.sourceforge.net/.
Andreoli, J.M. (1990). Proposal for a synthesis of logic and object-oriented programming paradigms. Ph.D. Thesis University of Paris VI.
Andreoli, J.M. (1992). Logic programming with focusing proofs in linear logic. Journal of Logic and Computation, 2(3), 297–347. https://doi.org/10.1093/logcom/2.3.297.
Andreoli, J.M., & Pareschi, R. (1991). Communication as fair distribution of knowledge. In: Proceedings of OOPSLA 91 (pp. 212–229).
Andreoli, J.M., & Pareschi, R. (1991). Linear objects: logical processes with built-in inheritance. New Generation Computing, 9(3-4), 445–473.
Andrews, P.B. (1971). Resolution in type theory. Journal of Symbolic Logic, 36, 414–432.
Apt, K.R., & van Emden, M.H. (1982). Contributions to the theory of logic programming. Journal of the ACM, 29(3), 841–862.
Barendregt, H. (1997). The impact of the lambda calculus in logic and computer science. Bulletin of Symbolic Logic, 3(2), 181–215.
de Bruijn, N.G. (1972). Lambda calculus notation with nameless dummies, a tool for automatic formula manipulation, with an application to the Church-Rosser theorem. Indagationes Mathematicae, 34(5), 381–392.
Bruscoli, P., & Guglielmi, A. (2006). On structuring proof search for first order linear logic. Theoretical Computer Science, 360(1-3), 42–76.
Bugliesi, M., Lamma, E., Mello, P. (1994). Modularity in logic programming. Journal of Logic Programming, 19(/20), 443–502.
Burns, A.R. (1988). Programming in OCCAM 2. Addison-Wesley.
Cervesato, I., & Pfenning, F. (2002). A linear logical framework. Information & Computation, 179(1), 19–75.
Chen, W., Kifer, M., Warren, D.S. (1993). HILOG: A foundation for higher-order logic programming. Journal of Logic Programming, 15(3), 187–230.
Church, A. (1940). A formulation of the simple theory of types. Journal of Symbolic Logic, 5, 56–68. https://doi.org/10.2307/2266170.
Church, A. (1985). The calculi of lambda conversion. (AM-6) (Annals of Mathematics Studies). Princeton: Princeton University Press.
Colmerauer, A., & Roussel, P. (1993). The birth of Prolog. SIGPLAN Notices, 28(3), 37–52.
Coquand, T., & Huet, G. (1988). The calculus of constructions. Information and Computation, 76(2/3), 95–120.
Dunchev, C., Guidi, F., Coen, C.S., Tassi, E. (2015). ELPI: fast, embeddable, λ Prolog interpreter. In Davis, M., Fehnker, A., McIver, A., Voronkov, A. (Eds.) Logic for programming, artificial intelligence, and reasoning - 20th International Conference, LPAR-20 2015, Suva, Fiji, November 24-28, 2015, Proceedings, LNCS, (Vol. 9450 pp. 460–468). Berlin: Springer.. https://doi.org/10.1007/978-3-662-48899-7_32
Emerson, E.A. (2008). The beginning of model checking: a personal perspective. In Grumberg, O., & Veith, H. (Eds.) 25 years of model checking - history, achievements, perspectives, lecture notes in computer science, (Vol. 5000 pp. 27–45). https://doi.org/10.1007/978-3-540-69850-0_2. Berlin: Springer.
Engberg, U., & Winskel, G. (1990). Petri nets and models of linear logic. In Arnold, A. (Ed.) CAAP’90, LNCS 431 (pp. 147–161). Springer.
Fages, F., Ruet, P., Soliman, S. (1998). Phase semantics and verification of concurrent constraint programs. In Pratt, V. (Ed.) 13th symp.on logic in computer science. IEEE.
Felty, A. (1991). Transforming specifications in a dependent-type lambda calculus to specifications in an intuitionistic logic. In Huet, G., & Plotkin, G.D. (Eds.) Logical Frameworks. Cambridge University Press.
Fitting, M. (1987). Resolution for intuitionistic logic. In: Proc. International Symposium of Methodologies for Intelligent Systems ISMIS’87 (pp. 400–407).
Gabbay, D.M. (1985). N-prolog: An extension of Prolog with hypothetical implication II—logical foundations, and negation as failure. Journal of Logic Programming, 2(4), 251–283.
Gabbay, D.M., & Reyle, U. (1984). N-Prolog: an extension of Prolog with hypothetical implications. I. Journal of Logic Programming, 1, 319–355.
Gazdar, G., Klein, E., Pullum, G., Sag, I. (1985). Generalized Phrase Structure Grammar. Cambridge: Harvard University Press.
Gentzen, G. (1935). Investigations into logical deduction. In Szabo, M. E. (Ed.), The Collected Papers of Gerhard Gentzen (pp. 68–131), North-Holland, Amsterdam. https://doi.org/10.1007/BF01201353.
Gentzen, G. (1938). New version of the consistency proof for elementary number theory. In Szabo, M. E. (Ed.) Collected papers of Gerhard Gentzen (pp. 252–286). North-Holland, Amsterdam, Originally published 1938.
Girard, J.Y. (1987). Linear logic. Theoretical Computer Science, 50 (1), 1–102. https://doi.org/10.1016/0304-3975(87)90045-4.
Gödel, K. (1965). On formally undecidable propositions of the principia mathematica and related systems. I. In Davis, M. (Ed.) The undecidable. Raven press.
Green, C. (1969). Theorem proving by resolution as a basis for question-answering systems. Machine Intelligence 4.
Hallnȧs, L., & Schroeder-Heister, P. (1991). A proof-theoretic approach to logic programming. II. Programs as definitions. Journal of Logic and Computation, 1(5), 635–660.
Halpern, J.Y., Harper, R., Immerman, N., Kolaitis, P.G., Vardi, M.Y., Vianu, V. (2001). On the unusual effectiveness of logic in computer science. Bulletin of Symbolic Logic, 7(1), 213–236.
Hardy, G.H. (1940). A mathematician’s apology. Cambridge University Press.
Harland, J., Pym, D., Winikoff, M. (1996). Programming in lygon: an overview. In Proceedings of the Fifth International Conference on Algebraic Methodology and Software Technology (pp. 391–405).
Harper, R., Honsell, F., Plotkin, G. (1993). A framework for defining logics. Journal of the ACM, 40(1), 143–184.
Hoare, C.A.R. (1985). Communicating sequential processes. Prentice-Hall.
Hodas, J., & Miller, D. (1990). Representing objects in a logic programming language with scoping constructs. In Warren, D.H.D., & Szeredi, P. (Eds.) 1990 International Conference in Logic Programming (pp. 511–526). MIT Press.
Hodas, J., & Miller, D. (1994). Logic programming in a fragment of intuitionistic linear logic. Information and Computation, 110(2), 327–365.
Hodas, J.S. (1994). Logic programming in intuitionistic linear logic: theory, design, and implementation. Ph.D. thesis, University of Pennsylvania Department of Computer and Information Science.
Huet, G.P. (1973). A mechanization of type theory. In Proceedings of the 3rd International Joint Conference on Artificial Intelligence (pp. 139–146).
Jaffar, J., & Lassez, J.L. (1987). Constraint logic programming. In Proceedings of the 14th ACM Symposium on the Principles of Programming Languages.
Kanovich, M. (1994). The complexity of Horn fragments of linear logic. Annals of Pure and Applied Logic, 69, 195–241.
Kanovich, M.I. (1995). Petri nets, Horn programs, linear logic and vector games. Annals of Pure and Applied Logic, 75(1–2), 107–135. https://doi.org/10.1017/S0960129500001328.
Kleene, S.C. (1935). A theory of positive integers in formal logic, part I. American Journal of Mathematics, 57, 153–173.
Kleene, S.C. (1952). Permutabilities of inferences in Gentzen’s calculi LK and LJ. Memoirs of the American Mathematical Society, 10, 1–26.
Kobayashi, N., & Yonezawa, A. (1993). ACL - A concurrent linear logic programming paradigm. In Miller, D. (Ed.) Logic programming - Proceedings of the 1993 International Symposium (pp. 279–294). MIT Press.
Kobayashi, N., & Yonezawa, A. (1994). Asynchronous communication model based on linear logic. Formal Aspects of Computing, 3, 279–294.
Kowalski, R.A. (1974). Predicate logic as a programming language. Information Processing, 74, 569–574.
Kowalski, R.A., & Kuehner, D. (1971). Linear resolution with selection function. Artificial Intelligence, 2, 227–260.
Lambek, J., & Scott, P.J. (1986). Introduction to higher order categorical logic. Cambridge University Press.
Lawvere, F.W. (1963). Functorial semantics of algebraic theories. Proceedings National Academy of Sciences USA, 50, 869–872.
Liang, C., & Miller, D. (2009). Focusing and polarization in linear, intuitionistic, and classical logics. Theoretical Computer Science, 410(46), 4747–4768. https://doi.org/10.1016/j.tcs.2009.07.041.
Lincoln, P., & Saraswat, V. (1993). Higher-order, linear, concurrent constraint programming. ftp://parcftp.xerox.com/pub/ccp/lcc/hlcc.dvi.
Lobo, J., Minker, J., Rajasekar, A. (1992). Foundations of disjunctive logic programming. MIT Press.
Martin-Löf, P. (1985). Constructive mathematics and computer programming. In Hoare, C.A.R., & Shepherdson, J.C. (Eds.) Mathematical logic and programming languages (pp. 167–184). Prentice-Hall.
McCarty, L.T. (1988). Clausal intuitionistic logic I. Fixed point semantics. Journal of Logic Programming, 5, 1–31.
McCarty, L.T. (1988). Clausal intuitionistic logic II. Tableau proof procedure. Journal of Logic Programming, 5, 93–132.
Miller, D. (1986). A theory of modules for logic programming. In Keller, R.M. (Ed.) Third Annual IEEE Symposium on Logic Programming (pp. 106–114). Salt Lake City.
Miller, D. (1987). A compact representation of proofs. Studia Logica, 46(4), 347–370.
Miller, D. (1989). A logical analysis of modules in logic programming. Journal of Logic Programming, 6(1-2), 79–108.
Miller, D. (1990). Abstractions in logic programming. In Odifreddi, P. (Ed.) Logic and Computer Science (pp. 329–359): Academic Press. http://www.lix.polytechnique.fr/Labo/Dale.Miller/papers/AbsInLP.pdf.pdf.
Miller, D. (1991). A logic programming language with lambda-abstraction, function variables, and simple unification. Journal of Logic and Computation, 1(4), 497–536.
Miller, D. (1992). Unification under a mixed prefix. Journal of Symbolic Computation, 14(4), 321–358.
Miller, D. (1993). The π-calculus as a theory in linear logic: preliminary results. In Lamma, E., & Mello, P. (Eds.) 3rd Workshop on Extensions to Logic Programming, no. 660 in LNCS. http://www.lix.polytechnique.fr/Labo/Dale.Miller/papers/pic.pdf (pp. 242–265). Bologna: Springer.
Miller, D. (1994). A multiple-conclusion meta-logic. In Abramsky, S. (Ed.) 9Th symp.on Logic in Computer Science (pp. 272–281). Paris: IEEE Computer Society Press.
Miller, D. (1996). Forum: a multiple-conclusion specification logic. Theoretical Computer Science, 165(1), 201–232.
Miller, D. (2003). Encryption as an abstract data-type: an extended abstract. In Cervesato, I. (Ed.) Proceedings of FCS’03: Foundations of Computer Security (pp. 3–14).
Miller, D. (2004). Bindings, mobility of bindings, and the ∇-quantifier. In Marcinkowski, J., & Tarlecki, A. (Eds.) 18th International Conference on Computer Science Logic (CSL) 2004, LNCS, (Vol. 3210 p. 24). https://doi.org/10.1007/978-3-540-30124-0_4.
Miller, D. (2004). Overview of linear logic programming. In Ehrhard, T., Girard, J.Y., Ruet, P., Scott, P. (Eds.) Linear Logic in Computer Science, London Mathematical Society Lecture Note, (Vol. 316 pp. 119–150). Cambridge: Cambridge University Press.
Miller, D. (2018). Mechanized metatheory revisited. Journal of Automated Reasoning. https://doi.org/10.1007/s10817-018-9483-3.
Miller, D., & Nadathur, G. (2012). Programming with higher-order logic. Cambridge University Press. https://doi.org/10.1017/CBO9781139021326.
Miller, D., Nadathur, G., Pfenning, F., Scedrov, A. (1991). Uniform proofs as a foundation for logic programming. Annals of Pure and Applied Logic, 51 (1–2), 125–157.
Miller, D., Nadathur, G., Scedrov, A. (1987). Hereditary Harrop formulas and uniform proof systems. In Gries, D. (Ed.) 2nd symp.on Logic in Computer Science (pp. 98–105). Ithaca.
Milner, R. (1980). A calculus of communicating systems LNCS Vol. 92. New York: Springer.
Milner, R. (1999). Communicating and systems: the π-calculus. New York: Cambridge University Press.
Milner, R., Parrow, J., Walker, D. (1992). A calculus of mobile processes, Part I. Information and Computation, 100(1), 1–40.
Milner, R., Tofte, M., Harper, R. (1990). The definition of standard ML. MIT press.
Minker, J., & Seipel, D. (2002). Disjunctive logic programming: a survey and assessment. In Computational logic: logic programming and beyond, (Vol. 2407 pp. 472–511). Berlin: Springer.
Nadathur, G. (1987). A higher-order logic as the basis for logic programming. Ph.D. thesis, University of Pennsylvania.
Nadathur, G., Jayaraman, B., Kwon, K. (1995). Scoping constructs in logic programming: implementation problems and their solution. Journal of Logic Programming, 25(2), 119–161. https://doi.org/10.1016/0743-1066(95)00037-K.
Nadathur, G., & Miller, D. (1988). An overview of λ Prolog. In Fifth International Logic Programming Conference (pp. 810–827). Seattle: MIT Press. http://www.lix.polytechnique.fr/Labo/Dale.Miller/papers/iclp88.pdf.
Nadathur, G., & Miller, D. (1990). Higher-order Horn clauses. Journal of the ACM, 37(4), 777–814.
Nadathur, G., & Mitchell, D.J. (1999). System description: Teyjus— a compiler and abstract machine based implementation of λ prolog. In Ganzinger, H. (Ed.) 16Th Conf.on Automated Deduction (CADE), no. 1632 in LNAI (pp. 287–291). Trento: Springer.
Ong, C.L., & Stewart, C.A. (1997). A Curry-Howard foundation for functional computation with control. In Conference record of POPL’97: the 24th ACM SIGPLAN-SIGACT Symposium on Principles of Programming Languages, Paris, France, 15-17 January 1997 (pp. 215–227). https://doi.org/10.1145/263699.263722.
Pareschi, R. (1989). Type-driven natural language analysis. Ph.D. thesis, University of Edinburgh.
Pareschi, R., & Miller, D. (1990). Extending definite clause grammars with scoping constructs. In Warren, D.H.D., & Szeredi, P. (Eds.) 1990 International Conference in Logic Programming (pp. 373–389): MIT Press.
Paulson, L.C. (1989). The foundation of a generic theorem prover. Journal of Automated Reasoning, 5, 363–397.
Pfenning, F., & Schürmann, C. (1999). System description: Twelf — a meta-logical framework for deductive systems. In Ganzinger, H. (Ed.) 16th Conf.on Automated Deduction (CADE), no. 1632 in LNAI (pp. 202–206). Trento: Springer. https://doi.org/10.1007/3-540-48660-7_14.
Plotkin, G.D. (2004). A structural approach to operational semantics. Journal of Logic and Algebraic Programming, 60-61, 17–139.
Prawitz, D. (1965). Natural deduction. Uppsala: Almqvist & Wiksell.
Pym, D.J., & Harland, J.A. (1994). The uniform proof-theoretic foundation of linear logic programming. Journal of Logic and Computation, 4(2), 175–207.
Qi, X., Gacek, A., Holte, S., Nadathur, G., Snow, Z. (2015). The Teyjus system – version 2. http://teyjus.cs.umn.edu/.
Robinson, J.A. (1965). A machine-oriented logic based on the resolution principle. JACM, 12, 23–41.
Ruet, P., & Fages, F. (1997). Concurrent constraint programming and non-commutative logic. In Proceedings of the 11t h Conference on Computer Science Logic, LNCS. Springer.
Sangiorgi, D., & Walker, D. (2001). π-calculus: a theory of mobile processes Cambridge University Press.
Saraswat, V. (1993). A brief introduction to linear concurrent constraint programming. Tech. rep., Xerox Palo Alto Research Center. ftp://parcftp.xerox.com/pub/ccp/lcc/lcc-intro.dvi.Z.
Sørensen, M.H., & Urzyczyn, P. (2006). Lectures on the Curry-Howard Isomorphism, Studies in Logic, vol. 149 Elsevier.
Stoy, J.E. (1977). Denotational semantics: the Scott-Strachey approach to programming language theory. Cambridge: MIT Press.
Tammet, T. (1996). A resolution theorem prover for intuitionistic logic. In Automated deduction — CADE-13, LNCS, (Vol. 1104 pp. 2–16).
Tarski, A. (1954). Contributions to the theory of models. I. Indagationes Mathematicae, 16, 572–581.
Wadler, P. (1990). Linear types can change the world!. In Programming Concepts and Methods (pp. 561–581). North holland.
Warren, D.H.D. (1983). An abstract Prolog instruction set. Tech. Rep. 309 SRI International.
Acknowledgments
I thank the participants of the “Fourth Symposium on the History and Philosophy of Programming” (HaPoP 2018) meeting and the members of the ANR project PROGRAMme (ANR-17-CE38-0003-01) for their comments on a talk based on an earlier version of this paper.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Miller, D. Reciprocal Influences Between Proof Theory and Logic Programming. Philos. Technol. 34, 75–104 (2021). https://doi.org/10.1007/s13347-019-00370-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13347-019-00370-x




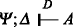 (where, A is restricted to being an atomic formula). These sequents can be mapped into the more usual linear logic sequents by rewriting:
(where, A is restricted to being an atomic formula). These sequents can be mapped into the more usual linear logic sequents by rewriting:

