Abstract
While model checking has often been considered as a practical alternative to building formal proofs, we argue here that the theory of sequent calculus proofs can be used to provide an appealing foundation for model checking. Since the emphasis of model checking is on establishing the truth of a property in a model, we rely on additive inference rules since these provide a natural description of truth values via inference rules. Unfortunately, using these rules alone can force the use of inference rules with an infinite number of premises. In order to accommodate more expressive and finitary inference rules, we also allow multiplicative rules but limit their use to the construction of additive synthetic inference rules: such synthetic rules are described using the proof-theoretic notions of polarization and focused proof systems. This framework provides a natural, proof-theoretic treatment of reachability and non-reachability problems, as well as tabled deduction, bisimulation, and winning strategies.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Model checking was introduced in the early 1980’s as a way to establish properties about (concurrent) computer programs that were hard or impossible to do then using traditional, axiomatic proof techniques of Floyd and Hoare [11]. In this paper, we show that despite the early opposition to proofs in the genesis of this topic, model checking can be given a proof-theoretic foundation using the sequent calculus of Gentzen [14] that was later sharpened by Girard [16] and further extended with a treatment of fixed points [3, 5, 24, 41]. The main purpose of this paper is foundational and conceptual. Our presentation will not shed new light on the algorithmic aspects of model checking but will present a declarative view of model checking in terms of proof theory. As a consequence, we will show how model checkers can be seen as having a proof search foundation shared with logic programming and (inductive) theorem proving.
By model checking, we shall mean the general activity of deciding if certain logical propositions are either true or false in a given, specified model. Various algorithms are used to explore the states of such a specification in order to determine reachability or non-reachability as well as more logically complex properties such as, for example, simulation and bisimulation. In many circles, model checking is identified with checking properties of temporal logic formulas, such as LTL and CTL: see the textbook [6] for an overview of such a perspective to model checking. Here, we focus on an underlying logic that emphasizes fixed points instead of temporal modalities: it is well known how to reduce most temporal logic operators directly into logic with fixed points [11].
Since the emphasis of model checking is on establishing the truth of a property in a model, a natural connection with proof theory is via the use of additive connectives and inference rules. We illustrate in Sect. 3 how the proof theory of additive connectives naturally leads to the usual notion of truth-table evaluation for propositional connectives. Relying only on additive connectives, however, fails to provide an adequate inference-based approach to model checking since it only rephrases truth-functional semantic conditions and requires rules with potentially infinite sets of premises.
In addition to the additive connections and inference rules, sequent calculus also contains the multiplicative connectives and inference rules which can be used to encode algorithmic aspects used to determine, for example, reachability, simulation, and winning strategies. In order to maintain a close connection between model checking and truth in models, we shall put additive inference rules back in the center of our framework but this time these rules will be additive synthetic inference rules. The synthesizing process will allow multiplicative connectives and inference rules to appear inside the construction of synthetic rules while they will not appear outside such synthetic rules. The construction of synthetic inference rules will be based on the proof-theoretic notions of polarization and focused proof systems [1, 18].
We summarize the results of this paper as follows.
-
We provide a declarative treatment of several basic aspects of model checking by using a proof search semantics of a fragment of multiplicative additive linear logic (MALL) extended with first-order quantification, equality, and fixed points. The notion of additive synthetic inference rule and the associated notion of switchable formula are identified (Sect. 8).
-
Given the faithful encoding of a core aspect of model checking within sequent calculus proofs, we illustrate how familiar model checking problems such as reachability, non-reachability, simulations, and winning strategies are encoded within sequent calculus (Sects. 7 and 8). This encoding makes it possible to turn evidence generated by a model checker—paths in a graph, bisimulations, winning strategies—into fully formal sequent calculus proofs (see [20]).
-
The sequent calculus also provides for the cut-rule which allows for the invention and use of lemmas. We illustrate (Sect. 10) how tables built during state exploration within a model checker can be captured as part of a sequent calculus proof.
Finally, this paper reveals interesting applications of aspects of proof theory that have been uncovered in the study of linear logic: in particular, the additive/multiplicative distinction of proposition connectives, the notion of polarization, and the use of focusing proof systems to build synthetic inference rules.
2 The Basics of the Sequent Calculus
Let \(\varDelta \) and \(\varGamma \) range over multisets of formulas. A sequent is either one-sided, written \(~\mathbin {\vdash }\varDelta \), or two-sided, written \(\varGamma \mathbin {\vdash }\varDelta \) (two-sided sequents first appear in Sect. 5). An inference rule has one sequent as its conclusion and zero or more sequents as its premises. We divide inference rules into three groups: the identity rules, the structural rules, and the introduction rules. The following are the two structural rules and two identity rules we consider.

The negation symbol \(\lnot (\cdot )\) is used here not as a logical connective but as a function that computes the negation normal form of a formula. The remaining rules of the sequent calculus are introduction rules: for these rules, a logical connective has an occurrence in the conclusion and does not have an occurrence in the premises. (We shall see several different sets of introduction inference rules shortly.)
When a sequent calculus inference rule has two (or more) premises, there are two natural schemes for managing the side formulas (i.e., the formulas not being introduced) in that rule. The following rules illustrate these two choices for conjunction.

The choice on the left is the additive version of the rule: here, the side formulas in the conclusion are the same in all the premises. The choice on the right is the multiplicative version of the rule: here, the various side formulas of the premises are accumulated to be the side formulas of the conclusion. Note that the cut rule above is an example of a multiplicative inference rule. A logical connective with an additive right-introduction rule is also classified as additive. In addition, the de Morgan dual and the unit of an additive connective are also additive connectives. Similarly, a logical connective with a multiplicative right-introduction rule is called multiplicative; so are its de Morgan dual and their units.
The multiplicative and additive versions of inference rules are, in fact, inter-admissible if the proof system contains weakening and contraction. In linear logic, where these structural rules are not available, the conjunction and disjunction have additive versions \( \mathbin { \& }\) and \(\mathbin {\oplus }\) and multiplicative versions \(\mathbin {\otimes }\) and  , respectively, and these different versions of conjunction and disjunction are not provably equivalent. Linear logic provides two exponentials, namely the \(\mathop {!}\) and \(\mathop {?}\), that permit limited forms of the structural rules for suitable formulas. The familiar exponential law \(x^{n+m}=x^n x^m\) extends to the logical additive and multiplicative connectives: in particular, \( \mathop {!}(B\mathbin { \& }C)\equiv \mathop {!}B\mathbin {\otimes }\mathop {!}C\) and
, respectively, and these different versions of conjunction and disjunction are not provably equivalent. Linear logic provides two exponentials, namely the \(\mathop {!}\) and \(\mathop {?}\), that permit limited forms of the structural rules for suitable formulas. The familiar exponential law \(x^{n+m}=x^n x^m\) extends to the logical additive and multiplicative connectives: in particular, \( \mathop {!}(B\mathbin { \& }C)\equiv \mathop {!}B\mathbin {\otimes }\mathop {!}C\) and  .
.
Since we are interested in model checking as it is practiced, we shall consider it as taking place within classical logic. One of the surprising things to observe about our proof-theoretical treatment of model checking is that we can model almost all of model checking within the proof theory of linear logic, a logic that sits behind classical (and intuitionistic) logic. As a result, the distinction between additive and multiplicative connectives remains an important distinction for our framework. Also, weakening and contraction will not be eliminated completely but will be available for only certain formulas and in certain inference steps (echoing the fact that in linear logic, these structural rules can be applied to formulas annotated with exponentials).
We start with the logic MALL as introduced by Girard in [16] but consider two major extensions to it. In Sect. 5, we extend MALL with first-order quantification (via the addition of the universal and existential quantifiers) and with logical connectives for term equality and inequality. To improve the readability of model checking specifications, we shall also use the linear implication (written here as simply \(\mathrel {\supset }\)) instead of the multiplicative disjunction (written as  ): details of this replacement are given in Sect. 7.3. The resulting logic, which is called MALL\(^=\), is not expressive enough for use in model checking since it does not allow for the systematic treatment of terms of arbitrary depth. In order to allow for recursive definition of relations, we add both the least and greatest fixed points. The resulting extended logic is \(\mu \hbox {MALL}^=\) and is described in Sect. 6.
): details of this replacement are given in Sect. 7.3. The resulting logic, which is called MALL\(^=\), is not expressive enough for use in model checking since it does not allow for the systematic treatment of terms of arbitrary depth. In order to allow for recursive definition of relations, we add both the least and greatest fixed points. The resulting extended logic is \(\mu \hbox {MALL}^=\) and is described in Sect. 6.
The important proof systems of this paper are all focused proof systems, a style of sequent calculus proof that is first described in Sect. 7.2. The logic \(\mu \hbox {MALL}^=\) will be given a focused proof system which is revealed in three steps. In Sect. 7, the proof system \(\mu \hbox {MALLF}^=_{0}\) contains just introduction rules and the structural rules normally associated to focused proof systems (the rules for store, release, and decide). In particular, the least and greatest fixed points are only unfolded in \(\mu \hbox {MALLF}^=_{0}\), which means, of course, that there is no difference between the least and greatest fixed point with respect of that proof system. In Sect. 9, the proof system \(\mu \hbox {MALLF}^=_{0}\) is extended with the rules for induction and coinduction to yield the proof system \(\mu \hbox {MALLF}^=_{1}\) so now least and greatest fixed points are different logical connectives. Finally, in Sect. 10, the proof system \(\mu \hbox {MALLF}^=_{1}\) is extended to yield the proof system \(\mu \hbox {MALLF}^=_{2}\) with the addition of the familiar rules for cut and initial.
3 Additive Propositional Connectives
Let \(\mathcal{A}\) be the set of formulas built from the propositional connectives \(\{\wedge ,t,\vee ,f\}\) (no propositional constants included). Consider the proof system given by the following one-sided sequent calculus inference rules.

Here, \(t\) is the unit of \(\wedge \), and \(f\) is the unit of \(\vee \). Note that \(\vee \) has two introduction rules while \(f\) has none. Also, \(t\) and \(\wedge \) are de Morgan duals of \(f\) and \(\vee \), respectively. We say that the multiset \(\varDelta \) is provable if and only if there is a proof of \(~\mathbin {\vdash }\varDelta \) using these inference rules. Also, we shall consider no additional inference rules (that is, no contraction, weakening, initial, or cut rules): in other words, this inference system is composed only of introduction rules and all of these introduction rules are for additive logical connectives.
The following theorem identifies an important property of this purely additive setting. This theorem is proved by an induction on the structure of proofs.
Theorem 1
(Strengthening) Let \(\varDelta \) be a multiset of \(\mathcal{A}\)-formulas. If \(~\mathbin {\vdash }\varDelta \) has a proof, then there is a \(B\in \varDelta \) such that \(~\mathbin {\vdash }B\).
This theorem essentially says that provability of purely additive formulas is independent of their context. Note that this theorem immediately proves that the logic is consistent, in the sense that the empty sequent \(~\mathbin {\vdash }\cdot \) is not provable. Another immediate conclusion of this theorem: if \(\mathcal{A}\) has a classical proof (allowing multiple conclusion sequents) then it has an intuitionistic proof (allowing only single conclusion sequents).
The following three theorems state that the missing inference rules of weakening, contraction, initial, and cut are all admissible in this proof system. The first theorem is an immediate consequence of Theorem 1. The remaining two theorems are proved, respectively, by induction on the structure of formulas and by induction on the structure of proofs.
Theorem 2
(Weakening & contraction admissibility) Let \(\varDelta _1\) and \(\varDelta _2\) be multisets of \(\mathcal{A}\)-formulas such that (the support set of) \(\varDelta _1\) is a subset of (the support set of) \(\varDelta _2\). If \(~\mathbin {\vdash }\varDelta _1\) is provable then \(\mathbin {\vdash }\varDelta _2\) is provable.
Theorem 3
(Initial admissibility) Let B be an \(\mathcal{A}\)-formula. Then \(~\mathbin {\vdash }B,\lnot B\) is provable.
Theorem 4
(Cut admissibility) Let B be an \(\mathcal{A}\)-formula and let \(\varDelta _1\) and \(\varDelta _2\) be multisets of \(\mathcal{A}\)-formulas. If both \(~\mathbin {\vdash }B,\varDelta _1\) and \(~\mathbin {\vdash }\lnot B,\varDelta _2\) are provable, then there is a proof of \(~\mathbin {\vdash }\varDelta _1,\varDelta _2\).
These theorems lead to the following truth-functional semantics for \(\mathcal{A}\) formulas: define \(v(\cdot )\) as a mapping from \(\mathcal{A}\) formulas to booleans such that \(v(B)\) is \(t\) if \(~\mathbin {\vdash }B\) is provable and is \(f\) if \(~\mathbin {\vdash }\lnot B\) is provable. Theorem 3 implies that \(v(\cdot )\) is always defined and Theorem 4 implies that \(v(\cdot )\) is functional (does not map a formula to two different booleans). The introduction rules can then be used to show that this function has a denotational character: e.g., \(v(A\wedge B)\) is the truth-functional conjunction of \(v(A)\) and \(v(B)\) (similarly for \(\vee \)).
While this logic of \(\mathcal{A}\)-formulas is essentially trivial, we will soon introduce much more powerful additive inference rules: their connection to truth-functional interpretations (a la model checking principles) will arise from the fact that their provability is not dependent on other formulas in a sequent.
4 Additive First-order Structures
We move to first-order logic by adding terms, equality on terms, and quantification.
We shall assume that some ranked signature\(\varSigma \) of term constructors is given: such a signature associates to every constructor a natural number indicating that constructor’s arity. Term constants are identified with signature items given rank 0. A \(\varSigma \)-term is a (closed) term built from only constructors in \(\varSigma \) and obeying the rank restrictions. For example, if \(\varSigma \) is \(\{a/0, b/0, f/1, g/2\}\), then a, (f a), and (g (f a) b) are all \(\varSigma \)-terms. Note that there are signatures \(\varSigma \) (e.g., \(\{f/1, g/2\}\)) for which there are no \(\varSigma \)-terms. The usual symbols \(\forall \) and \(\exists \) will be used for the universal and existential quantification over terms. We assume that these quantifiers range over \(\varSigma \)-terms for some fixed signature.
The equality and inequality of terms will be treated as (de Morgan dual) logical connectives in the sense that their meaning is given by the following introduction rules.

Here, t and s are \(\varSigma \)-terms for some ranked signature \(\varSigma \).
Consider (only for the scope of this section) the following two inference rules for quantification. In these introduction rules, [t / x] denotes capture-avoiding substitution.

Although \(\forall \) and \(\exists \) form a de Morgan dual pair, the rule for introducing the universal quantifier is not the standard one used in the sequent calculus (we will introduce the standard one later). This rule, which is similar to the \(\omega \)-rule [38], is an extensional approach to modeling quantification: a universally quantified formula is true if all instances of it are true.
Consider now the logic built with the (additive) propositional constants of the previous section and with equality, inequality, and quantifiers. The corresponding versions of all four theorems in Sect. 3 holds for this logic. Similarly, we can extend the evaluation function for \(\mathcal{A}\)-formulas to work for the quantifiers: in particular, \(v(\forall x. B x)=\bigwedge _t v(B t)\) and \(v(\exists x. B x)=\bigvee _t v(B t)\). Such a result is not surprising, of course, since we have repeated within inference rules the usual semantic conditions. The fact that these theorems hold indicates that the proof theory we have presented so far offers nothing new over truth functional semantics. Similarly, this bit of proof theory offers nothing appealing to model checking, as illustrated by the following example.
Example 1
Let \(\varSigma \) contain the ranked symbols z / 0 and s / 1 and let us abbreviate the terms z, (s z), (s (s z)), (s (s (s z))), etc by 0, 1, 2, 3, etc. Let A and B be the set of terms \(\{\mathbf{0}, \mathbf{1}\}\) and \(\{\mathbf{0}, \mathbf{1}, \mathbf{2}\}\), respectively. These sets can be encoded as the predicate expressions \(\lambda x. x=\mathbf{0}\vee x=\mathbf{1}\) and \(\lambda x. x=\mathbf{0}\vee x=\mathbf{1}\vee x=\mathbf{2}\). The fact that A is a subset of B can be denoted by the formula \(\forall x. A\,x\mathrel {\supset }B\,x\) or, equivalently, as
Proving this formula requires an infinite number of premises of the form \((t\not =\mathbf{0}\wedge t\not =\mathbf{1})\vee t=\mathbf{0}\vee t=\mathbf{1}\vee t=\mathbf{2}\). Since each of these premises can, of course, be proved, the original formula is provable, albeit with an “infinite proof”.
While determining the subset relation between two finite sets is a typical example of a model checking problem, one would not use the above-mentioned inference rule for \(\forall \) except in the extreme cases where there is a finite and small set of \(\varSigma \)-terms. As we can see, the additive inference rule for \(\forall \)-quantification generally leads to “infinitary proofs” (an oxymoron that we now avoid at all costs).
5 Multiplicative Connectives
Our departure from purely additive inference rules now seems forced and we continue by adding multiplicative inference rules.
5.1 Implication and Another Conjunction
Our first multiplicative connective is implication. Since the most natural treatment of implication uses two-sided sequents, we use them now instead of one-sided sequents. (We introduce various inference rules incrementally in this section: all of these rules are accumulated into Fig. 1.) The introduction rules for implication are now split between a left-introduction and a right-introduction rule and are written as follows.

The left-introduction rule is a multiplicative rule and the right rule is the first rule we have seen where the components of the introduced formula (here, the two schema variables A and B) are both in the same sequent. Note that context matters in these rules: in particular, the right-introduction of implication provides the familiar hypothetical view of implication: if we can prove a sequent with A assumed on the left and with B on the right, then we can conclude \(A\mathrel {\supset }B\).
Note that if we add to these rules the usual initial rule, namely

we have a proof system that violates the strengthening theorem (Sect. 3): for example, the sequent \(~\mathbin {\vdash }p\mathrel {\supset }q,p\) is provable while neither \(~\mathbin {\vdash }p\mathrel {\supset }q\) nor \(~\mathbin {\vdash }p\) are provable.
Along with the implication, it is natural to add a conjunction that satisfies the curry/uncurry equivalence between \(A\mathrel {\supset }B\mathrel {\supset }C\) and \((A\wedge B)\mathrel {\supset }C\). In our setting, the most natural version of conjunction introduced in this way is not the conjunction satisfying the additive rules (that we have seen in Sect. 3) but rather the multiplicative version of conjunction. To this end, we add the multiplicative conjunction \(\mathbin {\wedge ^+}\) and its unit \(t^+\) and, for the sake of symmetry, we rename \(\wedge \) as \(\mathbin {\wedge ^-}\) and \(t\) to \(t^-\). Exactly the relevance of the plus and minus symbols will be explained in Sect. 7 when we discuss polarization. These two conjunctions and two truth symbols are logically equivalent in classical and intuitionistic logic although they are different in linear logic where it is more traditional to write \( \mathbin { \& }\), \(\top \), \(\mathbin {\otimes }\), \(\mathbf {1}\) for \(\mathbin {\wedge ^-}\), \(t^-\), \(\mathbin {\wedge ^+}\), \(t^+\), respectively.
5.2 Eigenvariables
The usual proof-theoretic treatment for introducing universal quantification on the right uses eigenvariables [14]. Eigenvariables are binders at the sequent level that align with binders within formulas (i.e., quantifiers). Binders are an intimate and low-level feature of logic: their addition requires a change to some details about formulas and proofs. In particular, we need to redefine the notions of term and sequent.
Let the set \(\mathcal{X}\) denote first-order variables and let \(\varSigma (\mathcal{X})\) denote all terms built from constructors in \(\varSigma \) and from the variables in \(\mathcal{X}\): in the construction of \(\varSigma (\mathcal{X})\)-terms, variables act as constructors of arity 0. (We assume that \(\varSigma \) and \(\mathcal{X}\) are disjoint.) A \(\varSigma (\mathcal{X})\)-formula is one where all term constructors are taken from \(\varSigma \) and all free variables are contained in \(\mathcal{X}\). Sequents are now written as \(\mathcal{X}\,;\,\varGamma \;\mathbin {\vdash }\; \varDelta \): the intended meaning of such a sequent is that the variables in the set \(\mathcal{X}\) are bound over the formulas in \(\varGamma \) and \(\varDelta \). We shall also assume that formulas in \(\varGamma \) and \(\varDelta \) are all \(\varSigma (\mathcal{X})\)-formulas. All inference rules are modified to account for this additional binding: see Fig. 1. The variable y used in the \(\forall \) introduction rule is called an eigenvariable.
5.3 Term Equality
The left-introduction rule for equality and the right-introduction rule for inequality in Fig. 1 significantly generalize the inference rules involving only closed terms given in Sect. 4: they do this by making reference to unifiability and to most general unifiers. In Fig. 1, the domain of the substitution \(\theta \) is a subset of \(\mathcal{X}\), and the set of variables \(\theta \mathcal{X}\) is the result of removing from \(\mathcal{X}\) all the variables in the domain of \(\theta \) and then adding back all those variables free in the range of \(\theta \). This treatment of equality was developed independently by Schroeder-Heister [37] and Girard [19] and has been extended to permits equality and inequality for simply typed \(\lambda \)-terms [24].
The strengthening theorem does not apply to this logic. In particular, let \(\varSigma \) be any signature for which there are no ground \(\varSigma \)-terms, e.g., \(\{ f/1 \}\). It is the case that neither \(~\mathbin {\vdash }\forall x.x\not = x\) nor \(~\mathbin {\vdash }\exists y.t^+\) is provable: the latter is not provable since there is no ground \(\varSigma \)-term that can be used to instantiate the existential quantifier. However, the following sequent does, in fact, have a proof.

While the use of eigenvariables in proofs allows us to deal with quantifiers using finite proofs, that treatment is not directly related to model theoretic semantics. In particular, since the strengthening theorem does not hold for this proof system, the soundness and completeness theorem for this logic is no longer trivial.
Using the inference rules in Fig. 1, we now find a proper proof of the theorem considered in Example 1.
Example 2
Let \(\varSigma \) and the sets A and B be as in Example 1. Showing that A is a subset of B requires showing that the formula \(\forall x. A x\mathrel {\supset }B x\) is provable. That is, we need to find a proof of the sequent \( ~\mathbin {\vdash }\forall x.(x=\mathbf{0}\vee x=\mathbf{1}) \mathrel {\supset }(x=\mathbf{0}\vee x=\mathbf{1}\vee x=\mathbf{2}). \) The following proof of this sequent uses the rules from Fig. 1: a double line means that two or more inference rules might be chained together.

Note that the proof in this example is actually able to account for a simple version of “reachability” in the sense that we only need to consider checking membership in set B for just those elements “reachable” in A.
The proof system MALL\(^=\): The introduction rules for MALL are extended with first-order quantifiers and term equality. The \(\exists \) right-introduction rule and the \(\forall \) left-introduction rules are restricted so that t is a \(\varSigma (\mathcal{X})\)-term. The \(\forall \) right-introduction rule and the \(\exists \) left-introduction rules are restricted so that \(y\not \in \mathcal{X}\)
5.4 The Units From Equality and Inequality
Although we have not introduced the “multiplicative false” \(f^-\) (written as \(\perp \) in linear logic), it and the other units can be defined using equality and inequality. In particular, the positive and negative versions of both true and false can be defined as follow:
Note that equality can sometimes be additive (\(f^+\)) and multiplicative (\(t^+\)) and that inequality can sometimes be additive (\(t^-\)) and multiplicative (\(f^-\)).
5.5 Single-conclusion Versus Multi-conclusion Sequents
Given that the inference rules in Fig. 1 are two sided, it is natural to ask if we should restrict the sequents appearing in those rules to be single-conclusion, that is, restrict the right-hand side of all sequents to contain at most one formula. Such a restriction was used by Gentzen [14] to separate intuitionistically valid proofs from the more general (possibly using multiple-conclusion sequents) proofs for classical logic.
Since our target is the development of a proof theory for model checking, we can, indeed, restrict our attention to single-conclusion sequents in Fig. 1. We shall not impose that restriction, however, since the we shall eventually impose an even stronger restriction: in Sect. 8, we introduce a restriction (involving switchable formulas) in which synthetic inference rules involve sequents that have at most one formula in their entire sequent (either on the left or the right). Such sequents necessarily are single-conclusion sequents.
6 Fixed Points
A final step in building a logic that can start to provide a foundation for model checking is the addition of least and greatest fixed points and their associated rules for unfolding, induction, and coinduction. Given that computational processes generally exhibit potentially infinite behaviors and that term structures are not generally bounded in their size, it is important for a logical foundation of model checking to allow for some treatment of infinity. The logic described by the proof system in Fig. 1 is a two-sided version of MALL\(^=\) (multiplicative additive linear logic extended with first-order quantifiers and equality) [3, 5]. There appears to be no direct way to encode in MALL\(^=\) predicates that can compute with first-order terms that are not bounded in size. For that, we need to extend this logic.
Girard extended MALL to full linear logic by adding the exponentials \(\mathop {!}\), \(\mathop {?}\) [16]. The standard inference rules for exponentials allows for some forms of the contraction rule (Sect. 2) to appear in proofs. A different approach to extending MALL with the possibility of having unbounded behavior was proposed in [5]: add to MALL\(^=\) the least and greatest fixed point operators, written as \(\mu \) and \(\nu \), respectively. The proof theory of the resulting logic, called \(\mu \hbox {MALL}^=\), has been developed in [3] and exploited in the design of the Bedwyr model checker [4, 42].
The logical constants \(\mu \) and \(\nu \) are each parameterized by a list of typed constants as follows:
where \(n\ge 0\) and \(\tau _1,\ldots ,\tau _n\) are simply types. (Following Church [8], we use o to denote the type of formulas.) Expressions of the form \(\mu ^n_{\tau _1,\ldots ,\tau _n} B t_1\ldots t_n\) and \(\nu ^n_{\tau _1,\ldots ,\tau _n} B t_1\ldots t_n\) will be abbreviated as simply \(\mu B \bar{t}\) and \(\nu B \bar{t}\) (where \(\bar{t}\) denotes the list of terms \(t_1\ldots t_n\)). We shall also restrict fixed point expressions to use only monotonic higher-order abstraction: that is, in the expressions \(\mu ^n_{\tau _1,\ldots ,\tau _n} B t_1\ldots t_n\) and \(\nu ^n_{\tau _1,\ldots ,\tau _n} B t_1\ldots t_n\) the expression B is equivalent (via \(\beta \eta \)-conversion) to
and where all occurrences of the variable P in \(B'\) occur to the left of an implication an even number of times.
In this setting, the unfolding of the fixed point expressions \(\mu B\,\bar{t}\) and \(\nu B\,\bar{t}\) are \(B(\mu {}B)\,\bar{t}\) and \(B(\nu {}B)\,\bar{t}\), respectively. In both cases, unfoldings like these yield logically equivalent expressions.
Horn clauses (in the sense of Prolog) can be encoded as fixed point expressions, as illustrated by the following example.
Example 3
The adjacency graph in Fig. 2 and its transitive closure can be specified using the Horn clause logic program below. (We use \(\lambda \)Prolog syntax here: in particular, the sigma Z\({\backslash }\) construction encodes the quantifier \(\exists {}Z\).)

We can translate the step relation (sometimes written as the infix binary predicate \({\cdot }\buildrel {}\over \longrightarrow {\cdot }\)) defined by
which only uses positive connectives. Likewise, path can be encoded as the fixed point expression (and binary relation)
To illustrate unfolding of the adjacency relation, note that unfolding the expression \({a}\buildrel {}\over \longrightarrow {c}\) yields the formula \( (a=a\mathbin {\wedge ^+}c=b)\mathbin {\vee }(a=b\mathbin {\wedge ^+}c=c)\mathbin {\vee }(a=c\mathbin {\wedge ^+}c=b)\) which is not provable. Unfolding the expression \({ path}(a,c)\) yields the expression \( {a}\buildrel {}\over \longrightarrow {c}\mathbin {\vee }(\exists {}y.\,{a}\buildrel {}\over \longrightarrow {y}\mathbin {\wedge ^+}{}{ path}\,y\,c).\)
In \(\mu \hbox {MALL}^=\), both \(\mu \) and \(\nu \) are treated as logical connectives in the sense that they will have introduction rules. They are also de Morgan duals of each other. The inference rules for treating fixed points are given in Fig. 3. The rules for induction and coinduction (\(\mu L\) and \(\nu R\), respectively) use a higher-order variable S which represents the invariant and coinvariant in these rules. As a result, it will not be the case that cut-free proofs will necessarily have the sub-formula property: the invariant and coinvariant are not generally subformulas of the rule that they conclude. The following unfolding rules are also admissible since they can be derived using induction and coinduction [5, 24].

Since \(\mu \hbox {MALL}^=\) is based on MALL, it does not contain the contraction rule: that is, there is no rule that allows replacing a formula B on the left or right of a conclusion with B, B in a premise. Instead of the contraction rule, the unfolding rules allow replacing \(\mu B \bar{t}\) with \((B (\mu B) \bar{t})\), thus copying the (\(\lambda \)-abstracted) expression B.
The introduction rules in Figs. 1 and 3are exactly the introduction rules of \(\mu \hbox {MALL}^=\), except for two shallow differences. The first difference is that the usual presentation of \(\mu \hbox {MALL}^=\) is via one-sided sequents and not two-sided sequents. The second difference is that we have written many of the connectives differently (hoping that our set of connectives will feel more comfortable to those not familiar with linear logic). To be precise, to uncover the linear logic presentation of formulas, one must translate \(\mathbin {\wedge ^-}\), \(t^-\), \(\mathbin {\wedge ^+}\), \(t^+\), \(\vee \), and \(\supset \) to \( \mathbin { \& }\), \(\top \), \(\mathbin {\otimes }\), \(\mathbf {1}\), \(\oplus \), and \(\mathbin {-\circ }\) [16].
The following example shows that it is possible to prove some negations using either unfolding (when there are no cycles in the resulting state exploration) or induction.
Example 4
Below is a proof that the node a is not adjacent to c: the first step of this proof involves unfolding the definition of the adjacency predicate into its description.

A simple proof exists for \({ path}(a,c)\): one simply unfolds the fixed point expression for \({ path}(\cdot ,\cdot )\) and (following the two step path available from a to c) chooses correctly when presented with a disjunction and existential on the right of the sequent arrow. Given the definition of the path predicate, the following rules are clearly admissible. We write \(\langle t,s \rangle \in Adj\) whenever \(~\mathbin {\vdash }{t}\buildrel {}\over \longrightarrow {s}\) is provable.

The second rule has a premise for every pair \(\langle t,s \rangle \) of adjacent nodes: if t is adjacent to no nodes, then this rule has no premises and the conclusion is immediately proved. (We describe in Sect. 8 how these two inference rules are actually synthetic inference rules that are computed directly from the definition of the path and adjacency expressions.) A naive attempt to prove that there is no path from c to a gets into a loop (using these admissible rules): an attempt to prove \({ path}(c,a)\mathbin {\vdash }\cdot \) leads to an attempt to prove \({ path}(b,a)\mathbin {\vdash }\cdot \) which again leads to an attempt to prove \({ path}(c,a)\mathbin {\vdash }\cdot \). Such a cycle can be examined to yield an invariant that makes it possible to prove the end-sequent. In particular, the set of nodes reachable from c is \(\{b,c\}\) (a subset of \(N=\{a,b,c,d\}\)). The invariant S can be described as the set which is the complement (with respect to \(N\times N\)) of the set \(\{b,c\}\times \{a\}\), or equivalently as the predicate \(\lambda x\lambda y. \bigvee _{\langle u,v \rangle \in S} (x=u\mathbin {\wedge ^+}y=v)\). With this invariant, the induction rule (\(\mu L\)) yields two premises. The left premise simply needs to confirm that the pair \(\langle c,a \rangle \) is not a member of S. The right premise sequent \(\bar{x}\,;\,BS\bar{x}\;\mathbin {\vdash }\; S\bar{x}\) establishes that S is an invariant for the \(\mu {}B\) predicate. In the present case, the argument list \(\bar{x}\) is just a pair of variables, say, x, z, and B is the body of the \({ path}\) predicate: the right premise is the sequent \( \ x,z\; ;\; {x}\buildrel {}\over \longrightarrow {z}\mathbin {\vee }(\exists {}y.\,{x}\buildrel {}\over \longrightarrow {y}\mathbin {\wedge ^+}{}S\,y\,z)\mathbin {\vdash }S\,x\,z. \) A formal proof of this follows easily by blindly applying applicable inference rules.
While the induction and coinduction rules for fixed points are strong enough to prove non-reachability and (bi)simulation assertions in the presence of cyclic behaviors, these rules are not strong enough to prove other simple truths about inductive and coinductive predicates. Consider, for example, the following two named fixed point expressions used for identifying natural numbers and computing the ternary relation of addition.
The following formula, stating that the addition of two numbers is commutative,
is not provable using the inference rules we have described. This failure is not because the induction rule (\(\mu L\) in Fig. 3) is not strong enough or that we are actually situated close to a weak logic such as MALL: it is because an essential feature of inductive arguments is missing. To motivate that missing feature, consider attempting a proof by induction that the property P holds for all natural numbers. Besides needing to prove that P holds of zero, we must also introduce an arbitrary integer j (corresponding to the eigenvariables of the right premise in \(\mu L\)) and show that the statement \(P(j+1)\) reduces to the statement P(j). That is, after manipulating the formulas describing \(P(j+1)\) we must be able to find in the resulting proof state, formulas describing P(j). Up until now, we have only “performed” formulas (by applying introduction rules) instead of checking them for equality. More specifically, while we do have a logical primitive for checking equality of terms, the proof system described so far does not have an equality for comparing formulas. As a result, many basic theorems are not provable in this system. For example, there is no proof of \(\forall n.({ nat} ~n \supset { nat} ~n)\). The full proof system for \(\mu \hbox {MALL}^=\) contains the following two initial rules

as well as the cut rule. For now, we shall concentrate on using only the introduction rules of \(\mu \hbox {MALL}^=\).
Example 5
With its emphasis on state exploration, model checking is not the place where proofs involving arbitrary infinite domains should be attempted. If we restrict to finite domains, however, proofs appear. For example, consider the less-than binary relation defined as
The formula \((\forall n. { lt} ~n~\mathbf{10}\supset { lt} ~n~\mathbf{10})\) has a proof that involves generating all numbers less than 10 and then showing that they are, in fact, all less than 10. Similarly, a proof of the formula \( \forall n\forall m\forall p( { lt} ~n~\mathbf{10}\supset { lt} ~m~\mathbf{10}\supset { plus} ~n~m~p\supset { plus} ~m~n~p) \) exists and consists of enumerating all pairs of numbers \(\langle n,m \rangle \) with n and m less than 10 and checking that the result of adding \(n+m\) yields the same value as adding \(m+n\).
7 Synthetic Inference Rules
As we have illustrated, the additive treatment of connectives yields a direct connection to the intended model-theoretic semantics of specifications. When reading such additive inference rules proof theoretically, however, the resulting implied proof search algorithms are either unacceptable (infinitary) or naive (try every element of the domain even if they are not related to the specification). The multiplicative treatments of connectives are, however, more “intensional” and they make it possible to encode reachability aspects of model checking search directly into a proof.
We now need to balance these two aspects of proofs if we wish to provide a foundation for model checking. We propose to do this by allowing both additive and multiplicative inference rules to be used to build synthetic inference rules and to require that these synthetic inference rules be essentially additive in character. Furthermore, we will be able to build rich and expressive inference rules that can be tailored to capture directly rules that are used to specify a given model.
Proof theory has a well developed method for building synthetic inference rules and these use the notions of polarization and focused proof systems that were introduced by Andreoli [1] and Girard [18] shortly after the introduction of linear logic [16].
7.1 Polarization
All logical connectives are assigned a polarity: that is, they are either negative or positive. The connectives of MALL\(^=\) whose right-introduction rule is invertible are classified as negative. The polarity of the least and greatest fixed point connectives is actually ambiguous [3] but we follow the usual convention of treating the least fixed point operator as positive and the greatest fixed point operator as negative [29]. In all cases, the de Morgan dual of a negative connective is positive and vice versa. In summary, the negative logical connectives of \(\mu \hbox {MALL}^=\) are \(\not =\), \(\mathbin {\wedge ^-}\), \(t^-\), \(\mathrel {\supset }\), \(\forall \), and \(\nu \), while the positive connectives are \(=\), \(\mathbin {\wedge ^+}\), \(t^+\), \(\vee \), \(\exists \), and \(\mu \). Furthermore, a formula is positive or negative depending only on the polarity of the top-level connective of that formula.
A formula is purely positive (purely negative) if every occurrence of logical connectives in it are positive (respectively, negative). Horn clause specifications provide natural examples of purely positive formulas. For example, assume that one has several Horn clauses defining a binary predicate p (as in Example 3). A standard transformation of such clauses leads to a single clause of the form
where the expression (B p x y) contains only positive connectives as well as possible recursive calls (via reference to the bound variable p). If we now mutate this implication to an equivalence (following, for example, the Clark completion [9]) then we have
or more simply the equality between the binary relations (B p) and p. Using this motivation, we shall write the predicate denoting p not via a (Horn clause) theory but as a single fixed point expression, in this case, \((\mu \lambda p\lambda x\lambda y. B~p~x~y)\). (In this way, our approach to model checking does not use sets of axioms, i.e., theories.) If one applies such a translation to the Horn clauses (Prolog clauses in Example 3) one gets the fixed point expressions for both the step and path predicates. It is in this sense that we are able to capture arbitrary Horn clause specifications using purely positive expressions.
As is well-known (see [5], for example), if B is a purely positive formula then one can prove (in linear logic) that \(\mathop {!}B\) is equivalent to B and, therefore, that \(B\mathbin {\wedge ^+}B\) is equivalent to B.
7.2 A Focused Proof System
Figure 4 provides a two-sided version of part of the \(\mu \)-focused proof system for \(\mu \hbox {MALL}^=\) that is given in [5]. Here, y stands for a fresh eigenvariable, s and t for terms, N for a negative formula, P for a positive formula, C for the abstraction of a variable over a formula, and B the abstraction of a predicate over a predicate. The \(\dag \) proviso requires that \(\theta \) is the mgu (most general unifier) of s and t, and the \(\ddag \) proviso requires that s and t are not unifiable. This collection of inference rules may appear complex but that complexity comes from the need to establish a particular protocol in how \(\mu \hbox {MALL}^=\) synthetic inference rules are assembled.
The \(\mu \hbox {MALLF}^=_{0}\) proof system: A subset of the two sided version of part of the \(\mu \)-focused proof system from [3]. This proof system does not contain rules for cut, initial, induction, and coinduction
Sequents in our focused proof system come in the following three formats. The asynchronous sequents are written as  . The left asynchronous zone of this sequent is \(\varGamma \) while the right asynchronous zone of this sequent is \(\varDelta \). There are two kinds of focused sequents. A left-focused sequent is of the form \(\mathcal{X}:\mathcal {N} \mathbin {\Downarrow }B\mathbin {\vdash }\mathcal {P}\) while a right-focused sequent is of the form \(\mathcal{X}:\mathcal {N}\mathbin {\vdash }B\mathbin {\Downarrow }\mathcal {P}\). In all three of these kinds of sequents, the zone marked by \(\mathcal {N}\) is a multiset of negative formulas, the zone marked by \(\mathcal {P}\) is a multiset of positive formulas, \(\varDelta \) and \(\varGamma \) are multisets of formulas, and \(\mathcal{X}\) is a signature of eigenvariable as we have seen before. Focused sequents are also referred to as synchronous sequents. The use of the terms asynchronous and synchronous goes back to Andreoli [1].
. The left asynchronous zone of this sequent is \(\varGamma \) while the right asynchronous zone of this sequent is \(\varDelta \). There are two kinds of focused sequents. A left-focused sequent is of the form \(\mathcal{X}:\mathcal {N} \mathbin {\Downarrow }B\mathbin {\vdash }\mathcal {P}\) while a right-focused sequent is of the form \(\mathcal{X}:\mathcal {N}\mathbin {\vdash }B\mathbin {\Downarrow }\mathcal {P}\). In all three of these kinds of sequents, the zone marked by \(\mathcal {N}\) is a multiset of negative formulas, the zone marked by \(\mathcal {P}\) is a multiset of positive formulas, \(\varDelta \) and \(\varGamma \) are multisets of formulas, and \(\mathcal{X}\) is a signature of eigenvariable as we have seen before. Focused sequents are also referred to as synchronous sequents. The use of the terms asynchronous and synchronous goes back to Andreoli [1].
Note that the number of formulas in a sequent remains the same as one moves from the conclusion to a premise within synchronous rules but can change when one moves from the conclusion to a premise within asynchronous rules.
We shall now make a distinction between the term proof and derivation. A proof is the familiar notion of a tree of inference rules in which there are no open premises, while derivations are trees of inference rules with possibly open premises (these could also be called incomplete proofs). A proof is a derivation but not conversely. One of the applications of focused proof systems is the introduction of interesting derivations that may not be completed proofs. As we shall see, synthetic inference rules are examples of such derivations.
Sequents of the general form  are called border sequents. A synthetic inference rule (also called a bipole) is a derivation of a border sequent that has only border sequents as premises and is such that no \(\Uparrow \)-sequent occurrence is below a \(\Downarrow \)-sequent occurrence: that is, a bipole contains only one alternation of synchronous to asynchronous phases. We shall use polarization and a focused proof system in order to design inference rules (the synthetic ones) from the (low-level) inference rules of the sequent calculus. We shall usually view synthetic inference rules as simply inference rules between border premises and a concluding sequent: that is, the internal structure of synthetic inference rules are not part of their identity.
are called border sequents. A synthetic inference rule (also called a bipole) is a derivation of a border sequent that has only border sequents as premises and is such that no \(\Uparrow \)-sequent occurrence is below a \(\Downarrow \)-sequent occurrence: that is, a bipole contains only one alternation of synchronous to asynchronous phases. We shall use polarization and a focused proof system in order to design inference rules (the synthetic ones) from the (low-level) inference rules of the sequent calculus. We shall usually view synthetic inference rules as simply inference rules between border premises and a concluding sequent: that is, the internal structure of synthetic inference rules are not part of their identity.
The construction of the asynchronous phase is functional in the following sense.
Theorem 5
(Confluence) We say that a purely asynchronous derivation is one built using only the store and the asynchronous rules of \(\mu \hbox {MALLF}^=_{0}\) (Fig. 4). Let \(\varXi _1\) and \(\varXi _2\) be two such derivations that have  as their end-sequents and that have only border sequents as their premises. Then the multiset of premises of \(\varXi _1\) and of \(\varXi _2\) are the same (up to alphabetic changes in bound variables).
as their end-sequents and that have only border sequents as their premises. Then the multiset of premises of \(\varXi _1\) and of \(\varXi _2\) are the same (up to alphabetic changes in bound variables).
Proof
Although there are many different orders in which one can select inference rules for introduction within the asynchronous phase, all such inference rules permute over each other (they are, in fact, invertible inference rules). Thus, any two derivations \(\varXi _1\) and \(\varXi _2\) can be transformed into each other without changing the final list of premises. Thus, as is common, computing with “don’t care nondeterminism” is confluent and, hence, it can yield (partial) functional computations. \(\square \)
In various focused proof systems for various logics without fixed points (for example, [1, 22]), the left and right asynchronous zones (written using \(\varGamma \) and \(\varDelta \) in Fig. 4) are sometimes lists instead of multisets. In this case, proving the analogy of Theorem 5 is immediate. As the following example illustrates, when there are fixed points, the function that maps the sequent  to a list of border premises can be partial: the use of multisets of formulas instead of lists allows more proofs to be completed.
to a list of border premises can be partial: the use of multisets of formulas instead of lists allows more proofs to be completed.
Example 6
Recall the definition of the natural number predicate \({ nat} \) from Sect. 6, namely,
Any attempt to build a purely asynchronous derivation with endsequent
will lead to a repeating (hence, unbounded) attempt. As a result, the implied computation based on this sequent is partial. On the other hand, there is a purely asynchronous derivation of
that maps this sequent to the empty list of border sequents. If a list structure in used in the \(\varGamma \) zone and only the first formula in such lists were selected for introduction, then this computation of border sequents would not terminate.
Many of the inference rules in the synchronous phase require, however, making choices. In particular, there are three kinds of choices that are made in the construction of this phase.
-
1.
The \(\mathbin {\wedge ^-}\) left-introduction rules and the \(\vee \) right-introduction rule require the proper selection of the index \(i\in \{1,2\}\).
-
2.
The right-introduction of \(\exists \) and left-introduction of \(\forall \) both require the proper selection of a term.
-
3.
The multiplicative nature of both the \(\mathrel {\supset }\) left-introduction rules and \(\mathbin {\wedge ^+}\) right-introduction rules requires the multiset of side formulas to be split into two parts.
With our emphasis on the proof theory behind model checking, we are not generally concerned with the particular algorithms that are used to search for proofs (which is, of course, a primary concern in the model checking community). Having said that, we comment briefly on how the nondeterminism of the synchronous phase can be addressed in implementations. Generally, the first choice above is implemented using backtracking search: for example, try setting \(i=1\) and if that does not lead eventually to a proof, try the setting \(i=2\). The second choice is often resolved using the notion of “logic variable” and unification: that is, when implementing the right-introduction of \(\exists \) and left-introduction of \(\forall \), instantiate the quantifier with a new variable (not an eigenvariable) and later hope that unification will discover the correct term to have used in these introduction rules. Finally, the splitting of multisets can be very expensive: a multiset of n distinct formulas can have \(2^n\) splits. In the model checking setting, however, where singleton border sequents dominate our concerns, the number of side formulas is often just 0 so splitting is trivial.
7.3 Two-sided Versus One-sided Sequent Proof System
At the start of Sect. 7.2, we claimed that Fig. 4 provides a two-sided version of part of the \(\mu \)-focused proof system for \(\mu \hbox {MALL}^=\) that is given in [2, 5]. That claim needs some justification since the logic given in [2, 5] does not contain implications and its proof system uses one-sided sequents. Consider the two mutually-recursive mapping function given in Fig. 5. These functions translate from formulas using  to formulas using \(\mathrel {\supset }\) instead. The familiar presentation of MALL has a negation symbol that can be used only with atomic scope: since \(\mu \hbox {MALL}^=\) does not contain atomic formulas, it is possible to remove all occurrences of negation by using de Morgan dualities. Thus, if we set \({\bar{B}}\) to be the de Morgan dual of B, the we can translation
to formulas using \(\mathrel {\supset }\) instead. The familiar presentation of MALL has a negation symbol that can be used only with atomic scope: since \(\mu \hbox {MALL}^=\) does not contain atomic formulas, it is possible to remove all occurrences of negation by using de Morgan dualities. Thus, if we set \({\bar{B}}\) to be the de Morgan dual of B, the we can translation  to \({\bar{B}}\mathrel {\supset }C\). Note that since all fixed point expressions are monotone (see [5] and Sect. 6), the translation of recursive calls within fixed point definitions are actually equal and not de Morgan duals (or negations): \([[p\bar{t}]]_+=[[p\bar{t}]]_-=p\bar{t}\). This apparent inconsistency is not a problem since recursively defined variables have only positive (and not negative) occurrences within a recursive definition.
to \({\bar{B}}\mathrel {\supset }C\). Note that since all fixed point expressions are monotone (see [5] and Sect. 6), the translation of recursive calls within fixed point definitions are actually equal and not de Morgan duals (or negations): \([[p\bar{t}]]_+=[[p\bar{t}]]_-=p\bar{t}\). This apparent inconsistency is not a problem since recursively defined variables have only positive (and not negative) occurrences within a recursive definition.
Returning to the proof system for \(\mu \hbox {MALLF}^=_{0}\), it is now easy to observe that the two-sided sequents can be translated to one-side sequents using the inverse of the mapping defined in Figure 5.

This mapping will also cause two inference rules in Fig. 4 to collapse to one inference rules from the original one-sided proof system. While the one-sided presentation of proof for linear logic, especially MALL, is far more commonly used among those studying proofs for linear logic, the presentation using implication and two-sided sequents seems more appropriate for an application involving model checking. The price of using a presentation of linear logic that contains implication is the doubling of inference rules.
7.4 Deterministic and Nondeterministic Computations Within Rules
Let \(\mu B \bar{t}\) be a purely positive fixed point. As we have noted earlier, such a formula can denote a predicate defined by an arbitrary Horn clause (in the sense of Prolog). Attempting a proof of the sequent \(\mathcal{X}:\cdot \mathbin {\vdash }\mu B \bar{t}\mathbin {\Downarrow }\) will only lead to a sequence of right synchronous inference rules to be attempted. Thus, this style of inference models completely (and abstractly) captures Horn clause based computations. The construction of such proofs are, in general, nondeterministic (often implemented using backtracking search and unification). On the other hand, a sequent of the form \(\mathcal{X}\mathbin {:}\cdot \mathbin {\Uparrow }\mu B\bar{t}\mathbin {\vdash }\cdot \mathbin {\Uparrow }P\) yields a deterministic computation and phase.
Example 7
Let move be a purely positive least fixed point expression that defines a binary relation encoding legal moves in a board game (think to tic-tac-toe). Let wins denote the following greatest fixed point expression.
Attempting a proof of \(\cdot \mathbin {:}\cdot \mathbin {\Uparrow }\cdot \mathbin {\vdash }\hbox {wins} (b_0) \mathbin {\Uparrow }\cdot \) leads to attempting a proof of
The asynchronous phase with this as it root will explore all possible moves of this game, generating a new premise of the form \(\cdot \mathbin {:}\cdot \mathbin {\Uparrow }\cdot \mathbin {\vdash }\exists u.\hbox {move} (b_i,u) \mathbin {\wedge ^+}\hbox {wins} (u) \mathbin {\Uparrow }\cdot \) for every board \(b_i\) that can arise from a move from board \(b_0\). Note that computing all legal moves is a purely deterministic (functional) process. The only rules that can be used to prove this sequent are the release and decide rules, which then enters the synchronous phase. Note that this reading of winning strategies exactly corresponds to the usual notion: the player has a winning strategy if for every move of the opponent, the player has a move that leaves the player in a winning position. Note also that if the opponent has no move then the player wins.
This example illustrates that synthetic inference rules can encode both deterministic and nondeterministic computations. The expressiveness of the abstraction behind synthetic inference rules is strong enough that their application is not, in fact, decidable. We see this observation as being no problem for our intended application to model checking: if the model checking specification uses primitives (such as move) that are not decidable, then the entire exercise of model checking with them is questionable.
8 Additive Synthetic Connectives
As we illustrated in Sect. 3, a key feature of additive inference rules is the strengthening theorem (Theorem 1): that is, additive rules and the proofs built from them only need to involve sequents containing exactly one formula. As was also mentioned in Sect. 3, the strengthening feature, along with the initial and cut admissibility rules, makes it possible to provide a simple model-theoretic treatment of validity for each such inference rules. In this section, we generalization the notion of additive inference rules to additive synthetic inference rule.
A border sequent  in which \(\mathcal{X}\) is empty and \(\mathcal {P}\mathrel {\cup }\mathcal {N}\) is a singleton multiset is called a singleton border sequent. Such a sequent is of the form \(\cdot \mathbin {:}N\mathbin {\Uparrow }\cdot \mathbin {\vdash }\cdot \mathbin {\Uparrow }\cdot \) or \(\cdot \mathbin {:}\cdot \mathbin {\Uparrow }\cdot \mathbin {\vdash }\cdot \mathbin {\Uparrow }P\): in other words, these sequents represent proving the negation of N (for a negative formula N) or proving P for a positive formula P. The only inference rule in Fig. 4 that has a singleton sequent as its conclusion is either the decide left or decide right rule: in both cases, the formula that is selected is, in fact, the unique formula listed in the sequent. An additive synthetic inference rule is a synthetic inference rule in which the conclusion and the premises are singleton border sequents.
in which \(\mathcal{X}\) is empty and \(\mathcal {P}\mathrel {\cup }\mathcal {N}\) is a singleton multiset is called a singleton border sequent. Such a sequent is of the form \(\cdot \mathbin {:}N\mathbin {\Uparrow }\cdot \mathbin {\vdash }\cdot \mathbin {\Uparrow }\cdot \) or \(\cdot \mathbin {:}\cdot \mathbin {\Uparrow }\cdot \mathbin {\vdash }\cdot \mathbin {\Uparrow }P\): in other words, these sequents represent proving the negation of N (for a negative formula N) or proving P for a positive formula P. The only inference rule in Fig. 4 that has a singleton sequent as its conclusion is either the decide left or decide right rule: in both cases, the formula that is selected is, in fact, the unique formula listed in the sequent. An additive synthetic inference rule is a synthetic inference rule in which the conclusion and the premises are singleton border sequents.
Our goal now is to identify a sufficient condition that guarantees that when a decide rule is applied (that is, a synthetic inference rule is initiated), the bipole that arises must be an additive synthetic inference rule. Our sufficient condition requires using two notions which we present next: switchable formulas and predicate-typing.
8.1 Switchable Formulas
In order to restrict the multiplicative structure of formulas so that we will be building only additive synthetic connectives, we need to restrict some of the occurrences of the multiplicative connectives \(\mathrel {\supset }\) and \(\mathbin {\wedge ^+}\). The following definition achieves such a restriction.
Definition 1
A \(\mu \hbox {MALL}^=\) formula is switchable if
-
whenever a subformula \(C\mathbin {\wedge ^+}{}D\) occurs negatively (to the left of an odd number of implications), either C or D is purely positive;
-
whenever a subformula \(C\mathrel {\supset }{}D\) occurs positively (to the left of an even number of implications), either C is purely positive or D is purely negative.
An occurrence of a formula B in a sequent is switchable if it appears on the right-hand side (resp. left-hand side) and B (resp. \(B\mathrel {\supset }f^-\)) is switchable.
Note that both purely positive formulas and purely negative formulas are switchable.
Example 8
Let P be a set of processes, let A be a set of actions, and let \({\cdot }\buildrel {\cdot }\over \longrightarrow {\cdot }\) be a ternary relation defined via a purely positive expression (that is, equivalently as the least fixed point of a Horn clause theory). If \(p,q\in P\) and \(a\in A\) then both \({p}\buildrel {a}\over \longrightarrow {q}\) and \({p}\buildrel {a}\over \longrightarrow {q}\mathrel {\supset }f^-\) are switchable formulas. The following two greatest fixed point expressions define the simulation and bisimulation relations for this label transition systems.
Let \({ sim}\) denote the first of these expressions and let \({ bisim}\) denote the second and let p and q be processes (members of P). The expressions \({ sim}(p,q)\) and \({ bisim}(p,q)\) as well as the expressions \({ sim}(p,q)\mathrel {\supset }f^-\) and \({ bisim}(p,q)\mathrel {\supset }f^-\) are switchable.
Note that the bisimulation expression contains both the positive and the negative conjunction: this choice of polarization gives focused proofs involving bisimulation a natural and useful structure (see Example 10).
The following example illustrates that deciding on a switchable formula in a sequent may not necessarily lead to additive synthetic inference rules since eigenvariables may “escape” into premise sequents.
Example 9
Let \({{ bool}}\) be a primitive type containing the two constructors \({ tt}\) and \({ ff}\). Also assume that N is a binary relation on two arguments of type \({\hbox { bool}}\) that is given by a purely negative formula. For example, \(N(u,v)\) can be \(u\not =v\). The following derivation of the singleton border sequent \(\cdot \mathbin {:}\forall x_{\hbox { bool}}\;\exists y_{\hbox { bool}}\; N x y\mathbin {\Uparrow }\cdot \mathbin {\vdash }\cdot \mathbin {\Uparrow }\cdot \) has a premise that is not a singleton sequent.

Let B be the expression \(\lambda x. x={ tt}\mathbin {\vee }x={ ff}\) which encodes the set of booleans \(\{{ tt}, { ff}\,\}\). If we double up on the typing of the bound variable \(y_{\hbox { bool}}\) by using the B predicate, then the above derivation changes to the following derivation which has singleton border sequents as premises.

This latter derivation justified the following additive synthetic inference rule.

8.2 Predicate-typed Formulas
As Example 9 suggests, it is easy to introduce defined predicates that capture the structure of terms of primitive type and then exploit those predicates in the construction of synthetic inference rules. We now describe the general mechanism for capturing primitive types as \(\mu \)-expressions for a first-order signature (we follow here the approach described in [25, Section 3]).
Assume that we are given a fixed set S of primitive types and a first-order signature \(\varSigma \) describing the types of constructors over those primitive types. For the sake of simplifying our presentation, we assume that the pair S and \(\varSigma \) are stratified in the sense that we can order the primitive types S as a list such that whenever \(f:\tau _1\rightarrow \cdots \rightarrow \tau _n\rightarrow \tau _0\) is a member of \(\varSigma \), every primitive types \(\tau _1,\ldots ,\tau _n\) is either equal to \(\tau _0\) or come before \(\tau _0\) in that list. Such stratification of typing occurs commonly in, say, many functional programming languages where the order of introducing datatypes and their associated constructors is, in fact, a stratification of types.
For every primitive type \(\tau \in S\), we next introduce a new predicate \({\hat{\tau }}:\tau \rightarrow o\). These predicates are axiomatized by the theory \(\mathcal{C}(\varSigma )\) that is defined to be the collection of Horn clauses \(\mathcal{C}(f)\) such that
where f has type \(\tau _1\rightarrow \cdots \rightarrow \tau _n\rightarrow \tau _0\). As described in Sect. 7.1, such a set of Horn clauses can be converted to \(\mu \)-expressions that formally define the predicates \({\hat{\tau }}\) for every \(\tau \) in S. Stratification of types is needed for this particular way of defining such predicates.
Finally, we define the function \((B)^o\) by recursion on the structure of the formula B: this function leaves all propositional constants unchanged by mapping quantified expressions as follow.
We note that the restriction to first-order types and to stratified definitions of types can be removed by making use of simple devices that have been developed in the work surrounding the two-level logic approach to reasoning about computation [13, 25]. Using the terminology of [13], predicates denoting primitive types would be introduced into the specification logic along with the logic programs (as hereditary Harrop formulas) that describes the typing judgment. The encoding of \((\cdot )^o\), which translates among reasoning logic formulas would then be written as follows:
Here, the curly brackets are a reasoning-level predicate used to encode object-level provability. Note also that the \(\nabla \) quantifier [12, 30] would be invoked in the reasoning logic in order to treat any type containing terms with bound variables: such a type would involve constructors of higher-order type.
The following theorem is proved by an induction on the structure of first-order formulas.
Theorem 6
Let S be a set of primitive types, let \(\varSigma \) be a first-order signature, and let B be a first-order formulas all of whose non-logical constants are in \(\varSigma \). If the formula B is switchable then so is \((B)^o\).
While it is the case that B and \((B)^o\) may not be equivalent formulas, there is a sense that the formula \((B)^o\) is, in fact, the formula intended when one writes B. It is always the case, however, that the formulas \((B)^o\) and \(((B)^o)^o\) are logically equivalent since all expressions of the form \({\hat{\tau }}~t\) are purely positive and, hence, \({\hat{\tau }}~t\) and \({\hat{\tau }}~t \mathbin {\wedge ^+}{\hat{\tau }}~t\) are logically equivalent (see the end of Sect. 7.1).
8.3 Sufficient Condition for Building Additive Synthetic Inference Rules
The following theorem implies that switchable formulas and predicate-typing leads to proofs using only additive synthetic rules.
Theorem 7
Let \(\varPi \) be a \(\mu \hbox {MALLF}^=_{0}\) derivation of either \(\mathcal{X}\mathbin {:}(B)^o\mathbin {\Uparrow }\cdot \mathbin {\vdash }\cdot \mathbin {\Uparrow }\cdot \) or \(\mathcal{X}\mathbin {:}\cdot \mathbin {\Uparrow }\cdot \mathbin {\vdash }\cdot \mathbin {\Uparrow }(B)^o\) where the occurrence of \((B)^o\) is switchable. Then every sequent in \(\varPi \) that is the conclusion of a rule that switches phases (either a decide or a release rule) contains exactly one occurrence of a formula and that occurrence is switchable.
Proof
This proof proceeds by induction on the structure of \(\mu \hbox {MALLF}^=_{0}\) focused proofs. A key invariant dealing with predicate-typing is given as follows: in any asynchronous sequent with a variable \(x:\tau \) in the signature, there must be a formula in the left asynchronous context of the form \({\hat{\tau }}~t\) in which x is free in t. Thus, if the left asynchronous context is empty, the signature is empty. \(\square \)
It is interesting to note that the structure of focused proofs based on switchable formulas is similar to the structure of proofs that arises from examining winning strategies using the simple games from [10, Section 4].
Example 10
Consider attempting a proof of \({ sim}(p_0,q_0)\), where \(p_0,q_0\in P\). This proof must have the structure displayed here.

Double lines denote (possibly) multiple inference rules. In particular, the group of rules labeled by A contain exactly two introduction rules for \(\forall \) and one for \(\mathrel {\supset }\). The group labeled by B consists entirely of asynchronous rules that completely generates all possible labeled transitions from the process \(p_0\). In general, there can be any number of pairs \(\langle a_i,p_i \rangle \) such that \({p_0}\buildrel {a_i}\over \longrightarrow {p_i}\): if that number is zero, then this proof succeeds at this stage (if \(p_0\) can make no transitions then it is simulated by any other process). (We shall make the common assumption that the transition is finitely branching in order to guarantee that the number of premises at stage B is finite.) Above B is the \(store_R\) and \(decide_R\) rules. The group of rules labeled by C is a sequence of right-synchronous rules that prove that \({p_i}\buildrel {a_i}\over \longrightarrow {q_i}\). Finally, the top-most inference rule is a release rule. (See [26] for a similar project on encoding simulation in the sequent calculus.)
As this example illustrates, the specification of \({ sim}\) as a greatest fixed point expression (see Example 8) generates singleton sequents at every change of phase. In particular, the focused derivation with conclusion \({ sim}(p_0,q_0)\) leads to a derivation with premises \({ sim}(p_1,q_1),\ldots ,{ sim}(p_n,q_n)\), where the complex side conditions regarding the relationships between \(p_0,\ldots ,p_n,q_0,\ldots ,q_n\) are all internalized into the phases. The focused proof rules for simulation are so natural that if one takes a \(\mu \hbox {MALLF}^=_{0}\) proof of \(\cdot \mathbin {:}\cdot \mathbin {\Uparrow }\cdot \mathbin {\vdash }{ sim}(p_0,q_0)\mathbin {\Uparrow }\cdot \) and collects into a set all the pairs \(\langle p',q' \rangle \) such that \({ sim}(p',q')\) appears in that proof (hence, as the right side of the singleton border sequents) then the resulting set of pairs is a simulation in the sense of Milner [32]. Furthermore, if one has a proof of the negation of a simulation, that is, a proof of \(\cdot \mathbin {:}\cdot \mathbin {\Uparrow }{ sim}(p_0,q_0)\mathbin {\vdash }\cdot \mathbin {\Uparrow }\cdot \) then one can easily extract from the sequence of synthetic rules in that proof a Hennessy-Milner formulas that satisfies \(p_0\) but not \(q_0\) [20].
One of the values of using model checkers is they are often able to discover counter-examples to proposed theorems. Just as a formula can be either true or false, we can attempt to find a proof of a given formula or of its negation. In the latter case, we can have proofs of counterexamples. For example, the formula \(\forall n.~{ nat} ~n \mathrel {\supset }\hbox { prime}~n \mathrel {\supset }\hbox { odd }~n\) (for suitable definitions of primality and odd as purely positive fixed point expressions) is not true. There is, in fact, a proof in \(\mu \hbox {MALLF}^=_{0}\) of the formula
Such a proof would need to choose, of course, 2 as the existential witness.
9 Induction and Coinduction
As the previous examples and results suggest, the proof theory of \(\mu \hbox {MALL}^=\) allows us to build familiar inference rules that both allow us to explore a model (given by a collection of fixed point definitions) as well as retain a traditional truth-functional interpretation since the synthetic inference rules are additive. The logic \(\mu \hbox {MALL}^=\) allows for more that just state exploration. In this section and the next, we add to \(\mu \hbox {MALLF}^=_{0}\) more inference rules and illustrate the possibilities for model checking.
There appears to be two natural ways to add to sequent calculus rules for induction. One approach uses an induction rule similar to the one used by Gentzen in [15], namely,

This rule is not an introduction rule since there is no logical symbol appearing in the conclusion that does not also appear in the premise.
A second approach captures the induction rule as a left-introduction rule for \(\mu \)-expressions and the coinduction rule as a right-introduction rule for \(\nu \)-expressions (as in Fig. 3). The right-introduction rule for \(\mu \)-expressions and the left-introduction rule for \(\nu \)-expressions will remain unchanged: that is, they are simply unfolding rules. This approach to induction and coinduction was developed in [3, 24, 41]. In particular, the proof system \(\mu \hbox {MALLF}^=_{1}\) results from accumulating the inference rules in Figs. 4 and 6. Such induction principles are expressive and require insights to apply since they involve picking the instantiation of the higher-order relational variable S which acts as an invariant and coinvariant.
In the following example, we illustrate how to formally prove the non-existence of a path within the \(\mu \hbox {MALLF}^=_{1}\) proof system.
Example 11
Consider again the graph in Fig. 2 and the related encoding of it in Example 3. The \(\mu \hbox {MALLF}^=_{1}\) proof system is strong enough to provide a formal proof that there is no path from node b to node d. Let the invariant \(S\) be the complement of the set \(\{b,c\}\times \{d\}\): that is, S is the binary relation \(\lambda {}x\lambda {}y.\,((x=b\mathbin {\wedge ^+}{}y=d)\mathbin {\vee }(x=c\mathbin {\wedge ^+}{}y=d))\mathrel {\supset }f^-. \) The proof of unreachability can be written as follows.

Here, the proof \(\varXi _1\) simply requires a use of the right introduction rules for disjunction, (positive) conjunction, and equality. By expanding abbreviations, the proof \(\varXi _2\) has the following shape.

The proofs \(\varXi _3\) and \(\varXi _4\) involve only asynchronous inference rules and are left to the reader to complete. (This example has not needed to use predicate-types.)
As this example illustrates, if a model checker is capable of computing the strongly connected component containing, say, node b, (in this case the set \(\{b,c\}\)), then it is an easy matter to produce the invariant that allows proving non-reachability.
The following example, taken from [20], illustrates a proof using a coinduction.
Example 12
According to Fig. 7, the set \(\{(r_0,s_0),(r_1,s_1)\}\) is a simulation and, therefore, the process \(r_0\) is simulated by the process \(s_0\). In a formal proof of \({ sim}(r_0,s_0)\), the binary relation written as \(\lambda {}x\lambda {}y.\,(x=r_0\mathbin {\wedge ^+}{}y=s_0)\mathbin {\vee }(x=r_1\mathbin {\wedge ^+}{}y=s_1)\) can be used as the coinvariant to complete the proof.
While the two examples in this section illustrate the role of invariants and coinvariants in building proofs, these examples were simple and require only small invariants and coinvariants. In general, invariants and coinvariants are difficult of discover and to write down. Even when some clever model checking algorithm has established some inductive or coinductive property, it might be difficult to extract from the results of that algorithm’s execution an actual invariant or coinvariant that could allow for the completion of a formal (sequent calculus) proof. Of course, considerable interest has been applied to the problem of extracting invariants from model checking procedures: see, for example, [23, Chapter 1]. Various bisimulation-up-to techniques have been designed to make it possible to prove various coinvariant-like properties that are easier to discover and write down than attempting to discover an actual coinvariant for the bisimulation definition itself that is required by the coinduction rule (Fig. 6). For example, it is often much easier to exhibit an actual bisimulation-up-to-contexts than to exhibit an actual bisimulation (i.e., a coinvariant): considerable meta-theory is required to justify the fact that, for example, a bisimulation-up-to-contexts actually implies the existence of a bisimulation [32, 35, 36]. In general, invariants and coinvariants are not always given explicitly: instead, various meta-theoretic properties are usually used to show that certain kinds of surrogate relations are both easier to extract from model checkers and guarantee the existence of the needed invariants and coinvariants.
10 Tabled Deduction
An important aspect of model checking is the incorporation of previously proved statements and possible consequences of those statements. For example, the process of proof search might create the same goal to prove multiple times: obviously, once a subgoal is proved, it does not need to be re-proved. One proof search technique used to avoid reproving subgoals is tabled deduction (see, for example, [33, 34]). The implementer of tabled deduction, when given a new subgoal to prove, first checks to see if that subgoal already appears in the table: if it is found in the table then the goal is marked as proved. If the goal is not in the table, then the attempt to find a proof continues. If that attempt is eventually successful, the goal is then added to the table.
10.1 Tabling as Unfocused Proof
Once a proof using tabled deduction is successful, the table must be considered as part of the proof. A description of how to transform a table built into an actual proof is provided in [28, 31], which we repeat here briefly in a non-focused fashion.
A proof-theoretic approach to tabled deduction will make use of both instances of the initial rule and the cut rule. Assume that the formula B is proved with respect to a table containing the formulas \(A_1,\ldots ,A_n\), where we assume that this enumeration of the table follows the order in which those formulas are proved: that is, when \(i<j\) the \(A_i\) entered the table before \(A_j\), and, as a result, the proof of \(A_j\) may have depended on the proof of \(A_i\). Given this ordering of the table, we can build the following proof (in, say, a standard single conclusion sequent calculus for intuitionistic logic).

Here, \(\varXi _1\) is a (cut-free) proof of \(A_1\) while \(\varXi _2\) is a (cut-free) proof of \(A_1\vdash A_2\). That is, this proof of \(A_2\) may or may not use the assumption \(A_1\), reflecting the fact that \(A_1\) was entered into the table before the attempt to proof \(A_2\). Proceeding in this fashion, the entire table can be “loaded” into the assumption of the sequent used to prove B by means of the cut inference rule. The final proof of B can now make use of all the items in the table directly and without the need to reprove them.
We cannot, however, view tables-as-proofs in \(\mu \hbox {MALL}^=\) since entailments such as \(A_1\vdash A_2\) and \(A_1,\ldots ,A_n\vdash B\) are not intended to be linear in the sense that all assumption must be accounted for exactly once. The items placed in the table are intended to be used any number of times (including not being used at all). What is needed here (also for the first time in this paper) is the linear logic exponential \(\mathop {!}\): that is, the deduction that we intend is \(\mathop {!}A_1,\ldots ,\mathop {!}A_n\vdash B\) (from which we can conclude \(\mathop {!}A_1,\ldots ,\mathop {!}A_n\vdash \mathop {!}B\) using the promotion rule of linear logic).

Of course, for the proofs \(\varXi _2,\ldots ,\varXi _{n+1}\) to actually use the additional assumptions available to them from the table, the initial rule must also be added to the proof system. Both the initial and cut rules are multiplicative rules since they express relationships between elements within a sequent.
Since we have mentioned explicitly in this section the linear logic exponential \(\mathop {!}\), it is worth noting that one can prove (by induction) that \(\vdash (\mu B \bar{t})\equiv \mathop {!}(\mu B \bar{t})\) whenever the expression \(\mu B \bar{t}\) is purely positive [5]. Thus, in this case, the implication \(P\mathrel {\supset }C\), where P is purely positive, can be seen as either linear (as is the default in this paper) or as intuitionistic. Thus, the distinction between linear and intuitionistic logics diminishes in this situation.
10.2 Tabling as Focused Proof
We will illustrate here how it is possible to use the techniques just presented within the setting of \(\mu \hbox {MALL}^=\). As we motivated above, a table can be converted to a proof if we allow for both the initial and the cut rules. Figure 8 contains a version of these two inference rules for a focused proof system. This figure also contains a left and right version of the freeze rule. The schematic variable \(\mathcal {N}_\mu \) ranges over multisets of formulas which can be either negative or (positive) \(\mu \)-expressions. Dually, the schematic variable \(\mathcal {P}_\nu \) ranges over multisets of formulas which can be either positive or (negative) \(\nu \)-expressions. In the initial rule, the \(\mathcal {P}\) variable will range only over multisets of \(\mu \)-formulas and the \(\mathcal {N}\) variable will range only over multisets of \(\nu \)-formulas.
The proof system \(\mu \hbox {MALLF}^=_{2}\) results from accumulating the inference rules in Figs. 4, 6, and 8. Up to this point in our story about inference in \(\mu \hbox {MALL}^=\), a fixed point expression in a sequent was either unfolded or used in an induction or coinduction. The treatment of tables, however, requires the third option of using a fixed point expression as simply an expression that might be equal to another such expression. For example, if we have an assumption of the form \({ path}(a,d)\) (there is a path from node a to d), then we wish to prove the \(\mu \)-expression \({ path}(a,d)\) without doing either an unfolding or an induction. The usual initial inference rule (in their two versions within the focused proof system in Fig. 8) will achieve this as is witnessed by the derivation in Fig. 9: if in the proof \(\varXi _{n+1}\) there is an attempt to prove \(A_j\) (\(1\le j\le n\)), that proof can simply be justified using the init\(_R\) rule.
11 Conclusions
Linear logic is usually understood as being an intensional logic whose semantic treatments are remote from the simple model theory considerations of first-order logic and arithmetic. Thus, we draw the possibly surprising conclusion that the proof theory of linear logic provides a suitable framework for certifying some of the results of model checking. Many of the salient features of linear logic—lack of structural rules, polarization, and two conjunctions—play important roles in this framework. The role of linear logic here seems completely different and removed from, say, the use of linear logic to encode multiset rewriting and Petri nets [21] or to provide a new analysis of computation as is done with the Geometry of Interactions [17]. These wide ranging applications of linear logic illustrate the status of linear logic as the logic behind computational logic, especially when linear logic embraces fixed points and term equality.
The use of fixed points also allows for the direct and natural application of the induction and coinduction principles. The work by Baelde in [2, 5] illustrated that several model checking examples can be described well using \(\mu \hbox {MALL}^=\). In this paper, we extend that observation by exploiting the interplay between additive and multiplicative rules in order to provide a proof theory for model checking. After identifying additive rules as the main inferences used to build proofs from model specifications, we systematically allow aspects of multiplicative inference to enter the broader framework in order to capture more aspects of deduction in model checking. In particular, we first allow multiplicative linear logic inferences within synthetic additive rules (via the restriction to switchable formulas) and then we added the multiplicative initial and cut rules so that we can build and use tables. A natural next step in this process would be to capture constraints: these would naturally be assumptions which are not treated within one phase but are delayed for treatment in some later phase. Thus, border sequents would contain one switchable formula plus some collection of constraint formulas.
The ability to tightly link aspects of model checking to proof theory can have an impact on both of these topics. For example, this link helps to bolster the claims that linear logic is the logic behind computational logic since model checking is such a successful and popular instance of computational logic. Similarly, because model checking is a mature and often implemented task, the underlying algorithms for search and invariant generation that are implemented in model checkers should be transferable to the domain of proof search.
Conversely, there should be some impacts on the general framework of model checking. We conclude with a list of four such possible and known impacts.
-
1.
Given that there can be a common proof theory for both model checking and inductive theorem proving, using these two tools together can be natural (and certified). For example, consider proving that fib(n), the \(n^{th}\) Fibonacci number, is equal to \(n^2\) if and only if \(n\in \{0,1,12\}\). An attempt at proving this theorem could invoke the automatic search features of a model checker to search for solutions to \(fib(n)=n^2\) where \(n\le 12\) while using standard inductive techniques to prove that \(n>12\) implies that \(fib(n)>n^2\). For another example, consider using a model checker to prove that there is no winning strategy in tic-tac-toe starting from the empty board. An inductive theorem prover could be used to prove that if two board positions are symmetric then one admits a winning strategy if and only if the other admits a winning strategy. Such a theorem could be used (say, within the tabling mechanism) by a model checker to greatly reduce its search space.
-
2.
This proof-theoretic framework for model checking can lead to the design of proof certificates for some of the conclusions made by a model checking system and these certificates can be independently checked by theorem provers and proof assistants which might be interested in having model checkers as untrusted subsystem. The authors have taken the foundational proof certificate (FPC) framework from [7, 27] and have extended it to this setting with fixed point expressions: in particular, they have defined proof certificates for reachability, non-reachability, bisimulation, and non-bisimulation [20].
-
3.
There are a number of other computational logic topics—for example, logic programming, databases, modal logics, and type theories—that can use proof theory to describe at least parts of their foundations. As a result, the links between these topics and model checking should be facilitated by the encodings used in this paper. Also, some applications to which model checking might be applied are sensitive to the differences between classical and intuitionistic logic: a proof theoretic foundations should greatly help in justifying when a model checking result can be viewed as intuitionistically valid.
-
4.
Proof theory supports rich abstractions, including term-level abstractions, such as bindings in terms. As a result, lifting model checking from using first-order terms to using simply typed \(\lambda \)-terms is natural in a proof-theoretical setting. In particular, the Bedwyr model checker [4] has been built on using proof theory principles [12, 30] and, as a result, it is capable of performing model checking tasks with linguistic structures including binders. Various model checking problems related to the \(\pi \)-calculus have particularly clean and elegant treatments within proof theory and using the Bedwyr system [39, 40].
References
Andreoli, J.-M.: Logic programming with focusing proofs in linear logic. J. Logic Comput. 2(3), 297–347 (1992)
Baelde, D.: A linear approach to the proof-theory of least and greatest fixed points. PhD thesis, Ecole Polytechnique, (2008)
Baelde, D.: Least and greatest fixed points in linear logic. ACM Trans. Comput. Logic (2012). https://doi.org/10.1145/2071368.2071370
Baelde, D., Gacek, A., Miller, D., Nadathur, G., Tiu, A.: The Bedwyr system for model checking over syntactic expressions. In: Pfenning F. (ed.) 21th Conference on Automated Deduction (CADE), number 4603 in Lecture Notes in Artificial Intelligence, pp. 391–397, New York, (2007). Springer
Baelde, D., Miller, D.: Least and greatest fixed points in linear logic. In: Dershowitz N., Voronkov A. (eds.) International Conference on Logic for Programming and Automated Reasoning (LPAR), volume 4790 of Lecture Notes in Computer Science, pp. 92–106, (2007)
Baier, C., Katoen, J.-P.: Principles of model checking. MIT Press, Cambridge (2008)
Chihani, Z., Miller, D., Renaud, F.: A semantic framework for proof evidence. J. Autom. Reason. 59, 287–330 (2017). https://doi.org/10.1007/s10817-016-9380-6
Church, A.: A formulation of the simple theory of types. J. Symb. Logic 5, 56–68 (1940)
Clark, K.L.: Negation as failure. In: Gallaire, J., Minker, J. (eds.) Logic and Data Bases, pp. 293–322. Plenum Press, New York (1978)
Delande, O., Miller, D., Saurin, A.: Proof and refutation in MALL as a game. Ann. Pure Appl. Logic 161(5), 654–672 (2010)
Emerson, E. A.: The beginning of model checking: A personal perspective. In: Grumberg O., Veith H. (eds.) 25 Years of Model Checking–History, Achievements, Perspectives, volume 5000 of Lecture Notes in Computer Science, pp. 27–45. Springer, (2008)
Gacek, A., Miller, D., Nadathur, G.: Combining generic judgments with recursive definitions. In Pfenning F. (ed.) 23th Symposium on Logic in Computer Science, pp. 33–44. IEEE Computer Society Press (2008)
Gacek, A., Miller, D., Nadathur, G.: A two-level logic approach to reasoning about computations. J. Autom. Reason. 49(2), 241–273 (2012)
Gentzen, G.: Investigations into logical deduction. In: Szabo, M.E. (ed.) The Collected Papers of Gerhard Gentzen, pp. 68–131. North-Holland, Amsterdam (1935)
Gentzen, G.: New version of the consistency proof for elementary number theory. In Szabo M. E. (ed.) Collected Papers of Gerhard Gentzen, pp. 252–286. North-Holland, Amsterdam, 1938. Originally published (1938)
Girard, J.-Y.: Linear logic. Theoret. Comput. Sci. 50, 1–102 (1987)
Girard, J.-Y.: Towards a geometry of interaction. In: Categories in Computer Science, volume 92 of Contemporary Mathematics, pp. 69–108. AMS, (1987)
Girard, J.-Y.: A new constructive logic: classical logic. Math. Struct. Comp. Sci. 1, 255–296 (1991)
Girard, J.-Y.: A fixpoint theorem in linear logic. An email posting to the mailing list linear@cs.stanford.edu, (1992)
Heath, Q., Miller, D.: A framework for proof certificates in finite state exploration. In: Kaliszyk C., Paskevich A. (eds.) Proceedings of the Fourth Workshop on Proof eXchange for Theorem Proving, number 186 in Electronic Proceedings in Theoretical Computer Science, pp. 11–26. Open Publishing Association, (2015)
Kanovich, M.I.: Petri nets, Horn programs, Linear Logic and vector games. Ann. Pure Appl. Logic 75(1–2), 107–135 (1995)
Liang, C., Miller, D.: Focusing and polarization in linear, intuitionistic, and classical logics. Theoret. Comput. Sci. 410(46), 4747–4768 (2009)
Manna, Z., Pnueli, A.: Temporal verification of reactive systems: safety. Springer, Berlin (2012)
McDowell, R., Miller, D.: Cut-elimination for a logic with definitions and induction. Theoret. Comput. Sci. 232, 91–119 (2000)
McDowell, R., Miller, D.: Reasoning with higher-order abstract syntax in a logical framework. ACM Trans. Comput. Logic 3(1), 80–136 (2002)
McDowell, R., Miller, D., Palamidessi, C.: Encoding transition systems in sequent calculus. Theoret. Comput. Sci. 294(3), 411–437 (2003)
Miller, D.: Foundational proof certificates. In: Delahaye D., Paleo B. W. (eds.) All about Proofs, Proofs for All
Miller, D., Nigam, V.: Incorporating tables into proofs. In: Duparc J., Henzinger T. A. (eds.) CSL 2007: Computer Science Logic, volume 4646 of Lecture Notes in Computer Science, pp. 466–480. Springer, (2007)
Miller, D., Saurin, A.: A game semantics for proof search: Preliminary results. In: Proceedings of the Mathematical Foundations of Programming Semantics (MFPS05), number 155 in Electronic Notes in Theoretical Computer Science, pp. 543–563, (2006)
Miller, D., Tiu, A.: A proof theory for generic judgments. ACM Trans. Comput. Logic 6(4), 749–783 (2005)
Miller, D., Tiu, A.: Extracting proofs from tabled proof search. In: Gonthier G., Norrish M. (eds.) Third International Conference on Certified Programs and Proofs, number 8307 in Lecture Notes in Computer Science, pp. 194–210, Melburne, Australia, (2013). Springer
Milner, R.: Communication and Concurrency. Prentice-Hall International, Englewood Cliffs (1989)
Ramakrishna, Y. S., Ramakrishnan, C. R., Ramakrishnan, I. V., Smolka, S. A., Swift, T., Warren, D. S.: Efficient model checking using tabled resolution. In: Proceedings of the 9th International Conference on Computer Aided Verification (CAV97), number 1254 in Lecture Notes in Computer Science, pp. 143–154, (1997)
Ramakrishnan, C.: Model checking with tabled logic programming. ALP News Lett. (2002)
Sangiorgi, D., Milner, R.: The problem of “weak bisimulation up to”. In: CONCUR, volume 630 of Lecture Notes in Computer Science, pp. 32–46. Springer, (1992)
Sangiorgi, D., Walker, D.: \(\pi \)-Calculus: A Theory of Mobile Processes. Cambridge University Press, Cambridge (2001)
Schroeder-Heister, P.: Rules of definitional reflection. In: Vardi M. (ed.) 8th Symposium on Logic in Computer Science, pp. 222–232. IEEE Computer Society Press, IEEE, (1993)
Schwichtenberg, H.: Proof theory: Some applications ofcut-elimination. In: Barwise J. (ed.) Handbook ofMathematical Logic, volume 90 of Studies in Logic and theFoundations of Mathematics, pp. 739–782. North-Holland,Amsterdam, (1977)
Tiu, A., Miller, D.: A proof search specification of the \(\pi \)-calculus. In: 3rd Workshop on the Foundations of Global Ubiquitous Computing, volume 138 of ENTCS, pp. 79–101, (2005)
Tiu, A., Miller, D.: Proof search specifications of bisimulation and modal logics for the \(\pi \)-calculus. ACM Trans. Comput. Logic (2010). https://doi.org/10.1145/1656242.1656248
Tiu, A., Momigliano, A.: Cut elimination for a logic with induction and co-induction. J. Appl. Logic 10(4), 330–367 (2012)
Tiu, A., Nadathur, G., Miller, D.: Mixing finite success and finite failure in an automated prover. In: Empirically Successful Automated Reasoning in Higher-Order Logics (ESHOL’05), pp. 79–98, (2005)
Acknowledgements
We thank the anonymous reviewers of an earlier draft of this paper for their valuable comments. This work was funded by the ERC Advanced Grant ProofCert.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Heath, Q., Miller, D. A Proof Theory for Model Checking. J Autom Reasoning 63, 857–885 (2019). https://doi.org/10.1007/s10817-018-9475-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10817-018-9475-3




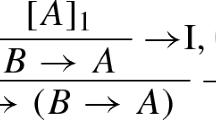





 into formulas containing
into formulas containing 


