Performance of Genetic Algorithm and Levenberg Marquardt Method on Multi-Mother Wavelet Neural Network Training for 3D Huge Meshes Deformation: A Comparative Study

Abstract

We propose, in this paper, a novel technique for large Laplacian boundary deformations using estimated rotations. The introduced method is used in the domain of Region of Interest (ROI) to align features of mesh based on Multi Mother Wavelet Neural Network (MMWNN) structure found in several mother wavelet families. The wavelet network allows the alignment of the characteristic points of the original mesh towards the target mesh. The key component of our correspondence scheme is a deformation energy that penalizes geometric distortion, encourages structure preservation and simultaneously allows mesh topology changes. To ensure the design of wavelet neural network architecture, an optimization algorithm should be applied to estimate and optimize the network parameters. Therefore, we compare our approach of 3d mesh deformation using MMWNN architecture based on genetic algorithm and our approach relying on Levenberg-Marquardt Method. We also discuss the existing comparison metrics for static and deformed triangle meshes employing the two mentioned approaches. Besides, we enumerate their strengths, weaknesses and relative performance.

1 Introduction

With technological advances in multimedia, telecommunication, hardware and computer design, the use of 3D data is now well established in several industrial domains, such as scientific visualization, entertainment, computer-aided design, etc. Mesh-based deformation has recently developed, which allowed the interactive deformation of the objects while preserving various types of constraints. The deformation of 3D surface mesh starts by the displacement of the control vertices. It consists in setting the target positions of the control vertices (directly or by using an affine transformation applied to a control vertex or a range of control vertices). Then, a rotation or a translation of a control vertex is constantly applied on its last target position set. In this technique, the object is encoded, using differential equations, and the mesh is deformed by modifying the boundary conditions of the differential equations. In fact, it is a fundamental modeling operation used to change the local shape of a mesh. Deformation transfer applies the deformation showed by a source triangle mesh onto a different target triangle mesh. It computes the set of transformations induced by the deformation of the source mesh and maps the transformations through the correspondence from the source to the target. In the area of function approximation, 3D system modelling the wavelet network and the neural network are generally used as non-parametric estimators. Mostly, the neural network modeling consists of two steps: determining the network structure and adjusting the network parameters using back-propagation (BP) algorithms. For example, in [1,2,3] wavelet networks represent an implementation of wavelet decomposition. This recently-developed technique, is an efficient tool utilized in many applications applied in the signal processing domain; such as function approximation and 3D data modeling [4, 5]. The wavelet network structure has also been applied in nonlinear system identification [6,7,8]. In the last decades, many research studies on the wavelet network algorithms have been carried out. We proposed in [9] a novel and an efficient framework of 3D mesh deformation, based on multi-mother wavelet neural network architecture and trust region spherical parameterization to edit the mesh, was proposed. These processes were considered, as an approximation tool for feature alignment between the source and the target models considered in the deformation process. To initialize the weights of wavelet neural network [10], many algorithms were developed. The main goal of these algorithms is to accelerate the convergence [11, 12] and to adapt the wavelet network architecture [11] when the error back-propagation is applied to the training algorithms. To train the wavelet network, other techniques, such as Kalman filter [13], genetic algorithms [14,15,16] and immune algorithms [17], were developed. These methods stem mainly from the typical neural network. Some other studies used the excellent wavelets properties [18] in the frequency domain though they have accelerated convergence, avoided local minimum and overcome over fitting to some extent.

In [9] we, we proposed a 3D mesh deformation technique based on multi-mother wavelet neural network architecture relying on Gradient-based Optimization methods, to estimate the network parameters, optimize them and maximize the probability of selecting the best wavelets that approximates better the signal. The first step of applying the classic forming algorithms consists in using a predetermined network architecture that may be insufficient or too complicated. In addition, the resolution of wavelet neural network training problems is described by their perceived inability to escape local optima. In the current manuscript, we develop new learning algorithms using the improved version of Levenberg–Marquardt technique and genetic algorithm to solve the problem of best wavelet selection and that of determining the wavelets number to be selected to construct the network, So, we present a comparative study between our results obtained in [9] and those provided by applying our proposed deformation technique based on multi-mother wavelet neural network architecture using Genetic Algorithm and Levenberg–Marquardt method. The main objective of our work is to overcome the inability to escape of local optima when implemented on high dimensional meshes, and to estimate more advanced visual similarity measures for meshes with noise or large-scale deformations. The key component of our correspondence scheme is a deformation energy that penalizes geometric distortion, encourages structure preservation and simultaneously allows mesh topology changes.

2 Wavelet Networks

Wavelet networks combine some of the useful classification properties of neural networks with the localization and feature extraction properties of wavelets. They replace the global sigmoidal activation units of the classic feedforward wavelet network with wavelets, while preserving the networks universal approximation property. For function approximation and 3D modelling, both wavelet network and neural network are extensively used as non-parametric estimators. Generally, the wavelet network modeling consists of two steps: determining the network structure and adjusting the network parameters using a back-propagation algorithm. A new mapping network, called wavelet neural network or wavenets (WNN), is proposed by combining the wavelet transform theory with the basic concept of neural networks as an alternative to feedforward neural networks for approximating arbitrary nonlinear functions. The fundamental idea behind applying wavelets is to analyze the signal at different scales or resolutions, which is called multiresolution analysis [19, 20]. Wavelets are a class of functions used to localize a given signal in both space and scaling domains. A family of wavelets can be constructed from a mother wavelet. Compared to Windowed Fourier analysis, a mother wavelet is stretched or compressed to change the size of the window. In this case, large wavelets give an approximate image of the signal, while smaller wavelets zoom in on small details. Therefore, wavelets can be automatically adapted to both high-frequency and low-frequency components of the signal having different window sizes. A wavelet network with one output y, $N_{i}$ inputs $x1, x2,\ldots , x_{N_{i}}$ and N wavelets can be parameterized as follows:

$$\begin{aligned} {\hat{y}}(x)=\sum _{i=1}^{N_{p}}\omega _{i}\varPsi _{i}(x)+\sum _{k=0}^{N_{i}}a_{k}x_{k}+b \end{aligned}$$

(1)

where $\varPsi _{i}(x)=\varPsi \left( \frac{x-b_{i}}{a_{i}}\right)$

$x=[x_{1},x_{2},\ldots ,x_{Ni} ]^T$ is the input vector ($x_{k}$ is the sampled input). The network parameters are $\omega _{i} \in \mathfrak {R}$, $d_{i}\in \mathfrak {R}^{*}$ and $t_{i}\in \mathfrak {R}$, correspond respectively to the wavelet coefficient, dilation parameter and translation parameter. Concerning the other parameters: $a_{k}\in \mathfrak {R}$, $b\in \mathfrak {R}$ are the linear coefficients and the biais term. The Wavelets $\varPsi _{i}$ are dilated and translated versions of a single function $\varPsi$ termed the “mother wavelet”: $\mathfrak {R}^{d}\rightarrow \mathfrak {R}$

$$\begin{aligned} \varPsi _{i}(x)=\varPsi (d_{i}(x-t_{i})) \end{aligned}$$

(2)

with

$$\begin{aligned} \varPsi (d_{i}(x-t_{i}))= \frac{1}{\sqrt{d_{i}}}\varPsi \left( \frac{x-t_{i}}{d_{i}}\right) \end{aligned}$$

(3)

The role of the wavelet network is to construct a discretized wavelet family by adapting the network parameters to the displacement data. To obtain the best set of wavelets to be used in the network, these steps are followed. Firstly, an initial set of wavelets is defined on the basis of the available data. Secondly, considering the wavelets as regression candidates, a regressor selection algorithm is applied to identify the members of the wavelet set. Finally, to further enhance the quality of the used model [21], a training algorithm can be applied to adjust the network parameters.

The latter is estimated by an optimization algorithm. The wavelet network learning implements then iterative methods such as back-propagation.

3 Training Algorithms: Multi-Mother Wavelet Neural Network (MMWNN)

Wavelet neural networks which employ wavelets as basis function have various interesting properties including fast training and good generalization performance. Several approaches have been recently proposed for structure selection and wavelet neural networks training based on the limited band of wavelet networks, in which the input weights are determined by the sampling period or the frequency band of the target function (if available). This approach has shown global convergence and has allowed avoiding overfitting for non-noisy equi-spaced samples. In many practical situations, a finite number of samples of the target function are known and there is not a priori information about the frequency contents and frequency band of the target function. Without using information about the target signal and relying on the sampling period to find the input weights of neural network causes complex structure and a serious overfitting. To overcome this problem, a suitable model selection approach for complexity control and overfitting prevention should be used.

Once the initialization set W of wavelet basis functions has been constructed, the next step is to select the best M-size subset (M < L) of wavelet basis functions in W to estimate f(x). However, in general, a search through all the M-size subsets is a computationally expensive procedure suffering from a combinatorial optimization problem [4].

One nonlinear optimization technique consists in using genetic algorithms which have been utilized successfully by Echauz et al. in [4], for radial wavelet networks, and Chen in [22] for RBF networks. In fact, genetic algorithms can provide optimal or near-optimal network topologies, at the expense of extensive computational requirements [22]. The proposed network structure is similar to that of the classic network, but it has some differences. Indeed, the classic network uses dilation and translation versions of only one mother wavelet and it is constructed by the new version by implementing several mother wavelets in the hidden layer [23, 24]. The objective of the new architecture is to maximize the potentiality of wavelet selection [25] that approximates better the signal.

The new wavelet network structure with one output f, can be expressed by the following equation:

$$\begin{aligned} {\hat{y}}(x)=\sum _{i=1}^{N_{1}}W_{i}^{1}\varPsi _{i}^1(x)+\sum _{i=1}^{N_{2}}W_{i}^{2}\varPsi _{i}^2(x)+\cdots +\sum _{i=1}^{N_{M}}W_{i}^{M}\varPsi _{i}^M(x)+\sum _{k=0}^{N_{i}}a_{k}x_{k} \end{aligned}$$

(4)

we propose a new training procedure that permits to make:

• The initialization of weights, as well as translations and dilations of the wavelet network (generation of the Multi-mother).

• An automatic selection and increment of the wavelet in the hidden layer.

• The choice of the optimal wavelet numbers opt $N_{opt}$.

• The update and construction of the wavelet network. Since the new wavelet network structure based on several mother wavelets families is defined, we can ask the question of model construction, consisting of wavelet network for a given process. The parameters that determine the network construction are:

• The values that give the different network parameters: the structural parameters of wavelets, and the linear coefficient.

• The necessary wavelet numbers to reach a wanted performance.

The essential difficulty resides in the determination of the network parameters. Since these parameters take discreet values, conceive wavelets selection methods can be applied in a discreet wavelets library. The performance depends on the initial choice of the wavelets library as well as on a discriminating selection in this library. Thus, the problem of selecting the number of wavelets in the hidden layer is presented here. The criteria considered to calculate the parameters already proposed in the literature are often developed for a particular modeling framework under restrictive hypotheses and using important approximations. The improvement of the developed learning algorithms can provide good solutions to solve the problem of best wavelet selection and that of determining the wavelets number to be selected to construct the network. The multi wavelet families library is constructed by forming several mother wavelet families for the network construction (M wavelets). The library elements, generated by distributing the parameters on a dyadic grid, are grouped in levels according to the dilation and translation parameters. This architecture is to maximize the potentiality of wavelet selection that approximates better the signal. This choice allows not only enriching the library, but also getting a better performance for a given wavelet number, by using regressor selection techniques to choose the best wavelets is often shorter than the training of the dilations and translations. Therefore, the supplementary cost introduced by different versions can be acceptable.

In the current study our proposed architecture has a new structure, made up of multi-mother wavelet families, a hidden layer formed by N wavelets of M mother wavelets. The components of each mother wavelet families belong to a family of wavelets having different sizes.

To design our wavelet neural network architecture, an optimization algorithm should be applied to estimate and optimize the network parameters.

In this context, the genetic algorithm is considered as an optimization algorithm used to treat important research spaces, while the Levenberg–Marquardt algorithm is one of the most efficient training algorithms utilized in neural network modeling. Gradient-based Optimization Methods have been applied with the improved version of Levenberg–Marquardt technique. It is based on steepest descent principle which is relatively easy to implement. However, the error surface of wavelet network training usually contains planes with a gentle dope due to the squashing functions commonly used in wavelet networks. This gradient is too small for weights to move rapidly on these planes, which reduces the rate of convergence. The rate of convergence could also be very slow when the steepest descent method encounters “narrow valley” in the error surface where the direction of gradient is close to the perpendicular direction of the valley. The update direction oscillates back and forth along the local gradient. Since supervised learning of wavelet networks can be viewed as a function optimization problem, higher order optimization methods employing gradient information can be adopted in wavelet network training to enhance convergence rate. The genetic algorithm is a global search technique (i.e. stochastic metaheuristics) utilized to find approximate solutions to optimization and search problems. It is also an efficient, and effective techniques employed in both optimization and machine learning applications. In our experiments, we used the genetic algorithm to overcome the inability of the signal to escape local optima when implemented on high dimensional data set and to ensure the design of wavelet neural network meshes. This algorithm minimized the error between the original object and the target object and gave good results in several cases. Our main objective is to present a genetic algorithm that makes it possible to decrease or to increase the dimension of the multi-mother wavelet library and to evade local minima; thanks to the ability of genetic algorithm to examine the entire search space. This method may plainly initialize the wavelet network facilitating the employment of the gradient descent.

4 Our Training MMWNN Using Levenberg–Marquardt Algorithm for 3D Mesh Deformation

Lately, various,researchers applied a newly developed wavelet neural network, to function approximations [2, 5, 26] and, more recently, to nonlinear time series predictions [27,28,29]. All these studies indicated that wavelet network structures were better than either back-propagation neural network (BPNN) and radial basis function neural network (RBFNN) structures at approximating nonlinearities, generated better prediction and approximation results. In this study, we introduce a novel multi-mother wavelet neural network based on Levenberg method for 3D huge mesh deformation technique. The Levenberg–Marquardt algorithm is used to train the wavelet network structure. This training process can be considered as an unconstrained nonlinear optimization problem that can be founded by several optimization tools. In our study the Levenberg–Marquardt method is used to train the presented wavelet network prediction architectures. The Levenberg–Marquardt algorithm is founded on the standard Newton method and has been exposed to be a very powerful optimization technique [30, 31]. In [30] Hagan et al. found that the Levenberg–Marquardt algorithm is more efficient than the popular conjugate gradient algorithm, and in various cases it can converge when the conjugate gradient algorithm cannot. Our preliminary experiment also shows that the Levenberg–Marquardt algorithm is the most efficient algorithm among those, such as gradient descent, gradient descent with momentum, and gradient descent with adaptive learning rate.

The Levenberg–Marquardt (LM) algorithm is an iterative technique that locates the minimum of a multivariate function that is expressed as the sum of squares of non-linear real-valued functions. It has become a standard technique for non-linear least-squares problems, widely adopted in a broad spectrum of disciplines. LM can be thought of as a combination of steepest descent and the Gauss-Newton method. When the current solution is far from the correct one, the algorithm behaves like a steepest descent method, slow, but guaranteed to converge. When the current solution is close to the correct solution, it becomes a Gauss-Newton method.

The Levenberg–Marquardt Optimization algorithm is a virtual standard in nonlinear optimization that notably outperforms gradient descent and conjugate gradient methods for medium sized problems. It is a pseudo-second order algorithm which means that it works with only function evaluations and gradient information but it estimates the Hessian matrix using the sum of outer products of the gradients.

Gradient-based optimization algorithms were used with the improved version of Levenberg–Marquardt method.

It is founded on steepest descent principle which is comparatively easy to implement. The only variance is in the introduction of a parameter $\lambda$ , called Levenberg–Marquardt parameter, enabling to stabilize the Newton method. This parameter $\lambda$ is updated automatically, based on the convergence of every iteration. Stabilization is feasible through a reiterative process (if one iteration diverges, it starts again by increasing the parameter $\lambda$ to obtain a convergent iteration). However, this process has a strong divergence when approaching the optimum inherent in Newton method. The divergence can be reduced. Succeeding Newton method, it is suggested to switch automatically to the conjugate gradient method when the phenomenon of divergence appears.

First, we must note that initialization step is so necessary: that if we have a good initialization, the local minimum problem can be avoided, it is sufficient to select the best regressions (the best based on the training data) from a finished set of regressors. The initialization of weights, as well as translations and dilations of the wavelet network (generation of the Multi-mother), Now, the wavelet network is considered with the linear coefficients $a_{k}$ and the biais term. In order to more easily capture linear properties in regressions, the terms $a_{k}$ and the biais are always first selected. One $a_{jm}$ and $b_{jm}$ are obtained from the initialization by a dyadic grid, they are used in computing a least squares solution.

Training the wavelet network models is to determine $\beta =\{ w(0), w(m), u(j), a_{jm}, b_{jm} \}$ where w(0) is the biais; w(m) is the weights connecting input layer and output layer, $m =1, 2,\ldots , In$; u(j) is the weights connecting hidden layer and output layer, $j = 1, 2,\ldots , Hd$; $a_{jm}$ is the dilation coefficient for the jth hidden neuron and the mth input neuron; $b_{jm}$ is the translation coefficient for the jth hidden neuron and the mth input neuron such that the discrepancy between the observed data and the predictions is minimized. This training process may be regarded as an unconstrained nonlinear optimization problem that can be solved by various optimization tools.

For training our multi-mother wavelet network architecture, we want to minimize the training error represented by Eq. 5.

$$\begin{aligned} E(\beta )=\frac{1}{2}\sum _{i=1}^{M}e_{i}^{2}=\frac{1}{2}\sum _{i=1}^{M}(y(i)-{\hat{y}}(i))^{2} \end{aligned}$$

(5)

where ${\hat{y}}(i)$, y(i) is the predicted and observed outputs respectively for the ith input, M is the number of training inputs; and $E(\beta )$ is the training error to be minimized. The variables to be optimized are the parameters in vector $\beta$. The training error $E(\beta )$ is minimized by refining these parameters. The Levenberg–Marquardt algorithm uses Eq. 6 to search for the best parameters [30, 31].

$$\begin{aligned} \beta _{k+1}= \beta _{k}-(J^{T}J+\lambda _{k}I)^{-1}J^{T}e \end{aligned}$$

(6)

where I is the identity matrix that has the same size as $J^{T}J$, $\lambda _{k}$ is the constant parameter, $e= [e_{1} e_{2} e_{3},\ldots , e_{M}]^{T}$ is the error vector and the Jacobian matrix is:

$$\begin{aligned} J = \begin{bmatrix} \frac{\partial _{e_{1}}}{\partial _{w(0)}} &{}\frac{\partial _{e_{1}}}{\partial _{w(m)}} &{} \frac{\partial _{e_{1}}}{\partial _{u(j)}} &{} \frac{\partial _{e_{1}}}{\partial _{a_{jm}}} &{} \frac{\partial _{e_{1}}}{\partial _{b_{jm}}}\\ \frac{\partial _{e_{2}}}{\partial _{w(0)}} &{}\frac{\partial _{e_{2}}}{\partial _{w(m)}} &{} \frac{\partial _{e_{2}}}{\partial _{u(j)}} &{} \frac{\partial _{e_{2}}}{\partial _{a_{jm}}} &{} \frac{\partial _{e_{2}}}{\partial _{b_{jm}}}\\ \cdots &{} \cdots &{} \cdots &{} \cdots &{} \cdots \\ \frac{\partial _{e_{M}}}{\partial _{w(0)}} &{}\frac{\partial _{e_{M}}}{\partial _{w(m)}} &{} \frac{\partial _{e_{M}}}{\partial _{u(j)}} &{} \frac{\partial _{e_{M}}}{\partial _{a_{jm}}} &{} \frac{\partial _{e_{M}}}{\partial _{b_{jm}}} \end{bmatrix} \end{aligned}$$

(7)

We require to calculate the Jacobian matrix and define the parameter $\lambda _{k}$ in Eq. 6. Based on the proposed wavelet network structure, using mother wavelet, the expression for every element in the Jacobian matrix are:

$$\begin{aligned}&\frac{\partial _{e_{i}}}{\partial _{w(0)}}=-1,\nonumber \\&\frac{\partial _{e_{i}}}{\partial _{w(m)}}=-x(m),\nonumber \\&\frac{\partial _{e_{i}}}{\partial _{u(j)}}=-\varPsi _{j}(X(i)),\nonumber \\&\frac{\partial _{e_{i}}}{\partial _{b_{jm}}}=-u(j)\varPsi _{j}(X(i))\left( \frac{1}{Z_{jm}}-Z_{jm}\right) \left( \frac{-1}{a_{jm}}\right) , \nonumber \\&\frac{\partial _{e_{i}}}{\partial _{a_{jm}}}=\frac{\partial _{e_{i}}}{\partial _{b_{jm}}}Z_{jm}, \nonumber \\&Z_{jm}=\frac{x_{m}(i)-b_{jm}}{a_{jm}}, and \nonumber \\&\quad i=1,2, \ldots , M, \quad j=1,2, \ldots , Hd, \quad m=1,2, \ldots , In \end{aligned}$$

(8)

By the defined Jacobian matrix, our multi-mother wavelet network prediction structure can be trained for 3D mesh deformation following the process exposed in Fig. 1. In this figure, Mu, $Mu_{Inc}$, and $Mu_{max}$ are parameters used to control the training process. The training process of our multi mother wavelet neural networks can appropriate the underlying nonlinear trend in the training data set, but it can also learn the noise contained in the data and lead to overfitting. This training is based on the formation of a training set consisting of pairs inputs/outputs $(x_{k},y_{k})$. The training algorithm aims to reduce the error of the wavelet network on the training set examples, adjusting the network parameters. It then implements iterative methods such as back-propagation. Besides the choice of selection method, we must choose an optimization algorithm to optimize the parameters. From the Levenberg method, originally scheduled for solving linear systems by least squares. Marquart modifies the algorithm to enable solving nonlinear systems of statistical problems.The method combines two algorithms into one. The simple gradient method (the steepest descent method) which is merely a less accurate estimate but has a slow convergence and the Gauss-Newton which has a quadratic convergence but requires an initial vector near to the solution. Thus, leading the gradient method to a local optimum makes the Gauss-Newton ineffective since the Jacobian becomes singular. One frequently used way of preventing overfitting and improving generalization is to present a validation error term, and the best network parameters in vector $\beta$ are selected founded on validation errors rather of training errors. With a good initialization of the network parameters and with the proposed optimization scheme using LM algorithm to adjusting the network parameters the efficiency of training increases to have a good 3D mesh deformation process. As we previously noted, classical approaches begin often with predetermined wavelet networks. Consequently, the network is often insufficient. After that, new works are used to construct a several mother wavelets families library for the network construction every wavelet has different dilations following different inputs. This choice has the advantages of enriching the library, and offering a better performance for a given wavelets number. Supervised learning of wavelet networks can be viewed as a function optimization problem, higher order optimization methods using gradient information can be adopted in wavelet network training to improve the rate of convergence.

Fig. 1

Multi-mother wavelet neural network training based Levenberg–Marquardt method

5 Our Training MMWNN Using Genetic Algorithm for 3D Mesh Deformation

In our work we presents the implementation of the genetic algorithm in the multi-mother wavelet network training which aims at searching for an optimal or near optimal solution to the 3D objects deformation problem. The idea is to integrate genetic algorithms into the wavelet network to avoid both insufficiency and local minima in the 3D mesh deformation technique. Our wavenet learning algorithms consist of two processes: the self-construction of networks and the minimization error.

5.1 Network Initialization Parameter

Once $t_{i}$ and $d_{i}$ are obtained from the initialization by a dyadic grid, they are used in computing a least square solution for w, a, b. The variable Ni represents the number of displacement pairs data. Using families of wavelets, we have a library that contains Nl wavelets. To every wavelet $\varPsi _{ji}$ we associate a vector whose components are the values of this wavelet according to the examples of the training sequence. Now, the wavelet network is considered with the linear coefficients $a_{k}$ and the biais term b. In order to more easily capture linear properties in regressions, the terms $a_{k}$ and b are always first selected. One $t_{i}$ and $d_{i}$ are obtained from the initialization by a dyadic grid, they are used in computing a least squares solution for w, a, b.

$$\begin{aligned} \begin{bmatrix} \varPsi _{1}^{1}(X_{1}) &{} \cdots &{}\varPsi _{N}^{M}(X_{1}) &{} x_{1} &{} 1\\ . &{}\cdots &{} . &{} . &{} . \\ . &{}\cdots &{} . &{} . &{} . \\ . &{}\cdots &{} . &{} . &{} . \\ . &{}\cdots &{} . &{} . &{} . \\ \varPsi _{1}^{1}(X_{N_{i}}) &{} \cdots &{}\varPsi _{N}^{M}(X_{N_{i}}) &{} x_{N_{i}} &{} 1 \end{bmatrix} . \begin{bmatrix} w_{1} \\ .\\ .\\ w_{L}\\ a\\ b \end{bmatrix} = \begin{bmatrix} y_{1} \\ . \\ .\\ .\\ .\\ y_{N_{i}} \end{bmatrix} \end{aligned}$$

(9)

where $y_{1},\ldots ,y_{Ni}$ are the sampled outputs in Z and $L=M*N$.

5.2 Selection of the Best Wavelets

A wavelet library having several wavelet families is more voluminous than the one that possesses the same wavelet mother. It implies a more elevated calculation cost during the selection process. Because the model size M is usually excessively large, the subset model selection is required. The optimal subset selection techniques are computationally prohibitive and impractical. The practical method is the forward selection, and the OLS procedure (Orthogonal Least Squares) which are an efficient implementation of this subset selection procedure. For the best selection, we propose an improved version of OLS procedure for the subset model selection. Nevertheless, using regressor selection techniques to choose the best mother wavelets is often shorter than the training of the dilations and translations; the supplementary cost introduced by different versions can be therefore acceptable. The library being constructed, a selection method is applied in order to determine the most meaningful wavelet for modelling and deforming 3D mesh. Generally, the wavelets in W are not all meaningful to estimate the signal. Lets suppose that we want to construct a wavelets network with M wavelets, the problem is to select M wavelets from the wavelet library W. The proposed selection is based on Orthogonal Least Square (OLS) [32, 33]. A selection method is applied in order to determine the most meaningful wavelet to model the considered signal. Generally, the regressors in $V_{MW}$ are not all meaningful to estimate the signal. Let’s suppose that we want to construct a wavelet network f(x) with $N_{MW}$ wavelets, the problem is how to select $N_{MW}$ wavelets from $V_{MW}$. To the first iteration, the signal is defined as $Y= [y_{1}, \ldots ,y_{Ni}]$ and the regressors vectors are the $V_{MW}(t,d)$ defined by Eq. 10. The selected regressor is the one for which the absolute value of the cosine with the signal Y is maximal. We constitute a matrix that is constituted of $V_{MW}$ of blocks of the vectors representing the wavelets of every mother wavelet where the expression is:

$$\begin{aligned} V_{MW}=\{{V_{i}^{j}}\}_{i=[1,\ldots ,N], j=[1,\ldots ,M[} \end{aligned}$$

(10)

The $V_{MW}$ matrix is defined as follows:

$$\begin{aligned} V_{MW}= \begin{vmatrix} V_{1}^{1}(x_{1})&\cdots&V_{N}^{1}(x_{1})&\cdots&V_{1}^{M}(x_{1})&\cdots&V_{N}^{M}(x_{1}) \\ \vdots&\cdots&\vdots&\cdots&\vdots&\cdots&\vdots \\ \vdots&\cdots&\vdots&\cdots&\vdots&\cdots&\vdots \\ \vdots&\cdots&\vdots&\cdots&\vdots&\cdots&\vdots \\ V_{1}^{1}(x_{Ni})&\cdots&V_{N}^{1}(x_{Ni})&\cdots&V_{1}^{M}(x_{Ni})&\cdots&V_{N}^{M}(x_{Ni}) \end{vmatrix} \end{aligned}$$

(11)

5.3 Change of the Library Dimension

5.3.1 Crossover Operators

This algorithm used two crossover operators: One of them changes the number of columns of chromosome so it changes the number of mother wavelets and introduce in the library a new version of wavelets issued of the new mother wavelet. The second operator does not change the number of columns of each chromosome.

The Crossover1 Operator: After the selection of the two chromosomes to which we will apply this operator, we choose an arbitrary position a in the first chromosome and a position b in the second according to a. After that, we exchange the second parts of the two chromosomes (Fig. 2).

Fig. 2

Crossover1 operator

The Crossover2 Operator: For the second operator, we choose an arbitrary position c in the first chromosome and a position d in the second chromosome according to c. Let $Min_{point}= Min(c,d)$. First, we change the values of c and d to $Min_{point}$. Then, we exchange the second parts of the two chromosomes. In this case, we have necessarily first children having the same length as the second chromosome and the second children having the same length as the first chromosome.

5.3.2 Mutation Operator

Generally, the initial population does not have all the information that is essential to the solution. The goal of applying the mutation operator is to inject some new information (wavelets) into the population. Mutation consists in changing one or more gene(s) in chromosome chosen randomly according to a mutation probability pm. Nevertheless, the muted gene may be the optimal one therefore, the new gene will not replace the old but it will be added to this chromosome.

5.4 Change of Settings Wavelets

In this step, we have a uniform crossover operator and a mutation operator applied to structural parameters of wavelet network (translations and dilatations).

5.4.1 Uniform Crossover Operator

Let $T=(t_{1},t_{2},\ldots ,t_{N})$ the vector representing the translations: A coefficient is chosen and a vector $T=(t_{1}^{\prime },t_{2}^{\prime },\ldots ,t_{N}^{\prime })$ is constructed as follows:

$$\begin{aligned}&t_{1}=\alpha .t_{1}+(1-\alpha ).t_{2} \end{aligned}$$

(12)

$$\begin{aligned}&t_{2}=\alpha .t_{2}+(1-\alpha ).t_{1} \end{aligned}$$

(13)

where $\alpha$ is a real random value chosen in [-1 1]. The same operator is applied to the vector dilation D.

5.4.2 Mutation Operator

After crossing operation, the string is subject to mutation. We consider the optimal wavelet, we reset the network with these wavelets that will replace the old in the library and the optimization algorithm will be continued using new wavelets.

Finally, after N iterations, we construct a wavelets network for the approximation signal Y.

A genetic algorithm that allows you to both reduce or increase the size of the mother wavelet library and then escape local minima.

This approach therefore makes it possible to properly initialize the wavelet network, which then facilitates the task for the gradient.

Our proposed algorithm is resumed in Fig. 3.

Fig. 3

Multi-mother wavelet neural network training based genetic algorithm

6 Results and Simulation

To ensure the design of our multi-mother wavelet neural network architecture, we used an optimization algorithm and performed a comparative study between genetic algorithm and Levenberg–Marquardt algorithm. We employed a multi-mother library wavelet network based on the Levenberg–Marquardt algorithm and on genetic algorithm for 3D mesh approximation and deformation.

6.1 3D Mesh Modeling Results

We further demonstrated and evaluate our approach in the 3D mesh modeling context. The complexity of 3D modeling object is directly related to the number of wavelets selected and the iterations to build the network.

To assess the performance of the two approaches, we utilized the mean square error (MSE) and the normalized square root of the mean square error (NSRMSE) for 3D mesh modelling which is defined as follows:

$$\begin{aligned} MSE= & {} \frac{1}{N_{i}}\sum _{k=1}^{N_{i}}(O_{N}(x_{NK},y_{NK},z_{NK})-O(x_{K},y_{K},z_{K}))^{2} \end{aligned}$$

(14)

$$\begin{aligned} NSRMSE= & {} \sqrt{\frac{\sum \nolimits _{k=1}^{N_{i}}(O_{N}(x_{NK},y_{NK},z_{NK})-O(x_{K},y_{K},z_{K}))^{2}}{\sum \nolimits _{k=1}^{N_{i}}({\bar{O}}-O(x_{K},y_{K},z_{K}))^{2}}} \end{aligned}$$

(15)

O is the approximate object, K is the number of observation and ${\bar{O}}=\sum _{k=1}^{N_{i}}{O(x_{K},y_{K},z_{K})}$ is the results of the 3D representation, from the multi mother wavelet library. The 3D wavelet can be constructed as the separable 1D wavelet product by applying a 1D wavelet analysis in three directions of space:

$$\begin{aligned} \varPsi _{i}^{j}(x,y,z)=\varPsi _{i}^{j}(x)*\varPsi _{i}^{j}(y)*\varPsi _{i}^{j}(z) \end{aligned}$$

(16)

The following figures represent the approximations of vertex X, Y and Z of bunny object by our MMWNN (Fig. 4):

Fig. 4

Approximations of X, Y and Z vertex of bunny object

We compare, in this section, some experimental results of obtained by applying the genetic algorithm MMWNN-GA with those provided by the Levenberg–Marquardt algorithm MMWNN-LM to ensure the design of wavelet neural network for 3D mesh approximation and modeling.

Tables 1 and 2 give the mean square error and the final normalized square root of the mean square error respectively after 20 training iterations using MMWNN, MMWNN-LM and MMWNN-GA constructed with 15 wavelets in hidden layer and based on several wavelets (Beta, Polywog1, Mexican Hat, Slog1 and Polywog1). The optimal wavelet number was fixed by our MMWNN algorithm. In fact, MMWNN structure is as an interesting alternative to classic wavelet network. It is effectively used to construct the network by several mother wavelets and solve the problem of choosing the best wavelet mother that can better approximate the signal.

For the MMWNN-GA solution, we applied the genetic algorithm to overcome the inability of the signal to escape local optima when implemented on high dimensional data set and to ensure the design of wavelet neural network meshes. For MMWNN-LM, the Levenberg–Marquardt algorithm is used to train the wavelet network models because it is more efficient than the other algorithms based on gradient descent and it is one of the most efficient training algorithms for neural network modeling. Having the updating rule, the Jacobian matrix needs to be computed and a training process should be designed. A good method used for weights adaptation is the Levenberg–Marquardt algorithm. It is a combination of the gradient descendent rule and the Gauss-Newton method.

Table 1 MSE for different activation wavelet functions using MMWNN, MMWNN and MMWNN-GA

Table 2 NSRMSE for different activation wavelet functions using MMWNN, MMWNN and MMWNN-GA

We can see, in tables 1 and 2, that MMWNN-GA are more suitable for 3D approximation, compared to the Levenberg method and MMWNN structure. For example, to approximate Horse object using MMWNN-GA after 20 iterations over 1.95420e – 4, the Levenberg method gave an MSE equal to 1.47022e – 4; whereas MMWNN structure provided 4.74990e – 2. The genetic algorithm has a sound theoretical basis and guarantee convergence for most of the smooth functions, which may reduces divergence.

we applied genetic algorithm to improve the robustness of gradient-descent algorithms. We also presented a genetic algorithm for the design of wavelet network in [34, 35]. The problem was to find the optimal network structure and parameters. In order to determine the optimal network, the developed algorithm modified the number of wavelets in the library. In MMWNN-LM structure, Gradient-based optimization methods were applied with the improved version of Levenberg–Marquardt technique, this gradient is too small for weights to move rapidly on these plans, which minimizes the rate of convergence. The rate of convergence can also be very slow when the steepest descent method encounters “narrow valley” in the error surface where the direction of gradient is close to the perpendicular direction of the valley. The good performance of the algorithm is achieved by evolving the initial population and by using operators that alter the structure of the wavelets library. Comparing our algorithm with the classical ones, our results show significant improvement either with MMWNN-GA or with MMWNN-LM in the resulting performance and topology.

Figure 5 represents the evolution of the MSE when the number of wavelets in the hidden layer is increased from 15 to 100 wavelets using MMWNN, MMWNN-LM and MMWNN-GA.

Fig. 5

Evolution of the MSE according to the number of wavelets by MMWNN, MMWNN-LM and MMWNN-GA

From the simulation results we see that increasing the wavelet number in the hidden layer increases not only the approximation capacity, but also time cost and algorithm complexity increase considerably. The procedure allows to specify the selected wavelets for every mother wavelet. Therefore, when we increase the number of wavelets the MSE given by the MMWNN-GA network are weaker than those obtained by the MMWNN and very close to the MSE by MMWNN-LM .

In addition to that, to ameliorate these criteria :MSE and NSRMSE, we can increase the iterations number in the training stage.

Figure 6 gives the evolution of the MSE according to the number of iterations:

Fig. 6

Evolution of the MSE according to the number of iterations

6.2 3D Mesh Deformation Results

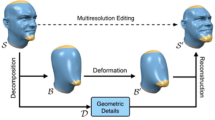
For 3D mesh deformation the interpolation between objects can be realised by determining the trajectory of the corresponding vertices on the representation obtained in the previous step. The simplest way to interpolate between these points is a linear interpolation.

The interpolation in the wavelet domain makes it possible to control interpolation starting time and speed at various resolutions. In fact, multi-mother wavelet neural network have achieved great success in different areas of computer science. Compared with 2D images, 3D shapes are more difficult to process, due to their irregular connectivity and limited data availability.

The 3D deformation sequence consists of a large number of frames; each of which represents a large static 3D object.

A deformed mesh with fixed connectivity can be represented by a $3F\times N$ matrix A, where F is the number of frames and N the number of vertices:

$$\begin{aligned} A=\begin{pmatrix} v_{1}^{(1)}&{}\cdots &{} v_{N}^{(1)} \\ \vdots &{}\ddots &{}\vdots \\ v_{1}^{(F)}&{}\cdots &{}v_{N}^{(F)} \end{pmatrix} \end{aligned}$$

(17)

The approximation error is typically reported in terms of the following error metric:

$$\begin{aligned} 100\%.\frac{||A-A_{approx}||_{F} }{||A-A_{timeAverage}||_{F}} \end{aligned}$$

(18)

where $A_{timeAverage}\in \mathfrak {R}^{3F\times N}$ is a matrix indicating a static mesh (average of all keyframes). Unfortunately, this metric is sensitive to global motion applied to the entire mesh.

For example, adding linear motion increases the denominator ${||A-A_{timeAverage}||_{F}}$ but leaves the numerator

${100\%.||A-A_{approx}||_{F} }$ unchanged because skinning can trivially reproduce translation (by simply adding the translation to all bone transformations). For example, an on-spot walking sequence will have higher error than exactly the same animation where the character moves forward.

Therefore, we propose to simply use $\sqrt{3NF}$ as the normalizing factor, obtaining:

$$\begin{aligned} E_{RMS}=100\%.\frac{||A-A_{approx}||_{F} }{\sqrt{3NF}} \end{aligned}$$

(19)

A deformed mesh with fixed connectivity can be represented by a $3\hbox {F}\times \hbox {N}$ matrix A, where F is the number of frames and N the number of vertices. Since 3NF is the total number of elements of matrix A, $E_{RMS}$ is simply the average error per element (scaled by 1000 for convenience). To be able to compare $E_{RMS}$ between objects with different proportions, we uniformly scale every animation so that its first frame is tightly enclosed by a unit ball.

To evaluate the effectiveness of our proposed method, we use the $E_{RMS}$ generalization ability error (root mean square) to ensure the comparison on the set of tests of our method with several state-of-the-art methods in term of 3D mesh deformation process, including sparse localized deformation component (SPLOCS) with edge lengths and dihedral angles [36], SPLOCS with the feature from [37], and Mesh-Based Autoencoders for Localized Deformation Component Analysis [38]. The Variation of $E_{RMS}$ in terms of 3D mesh deformation is presented in Table 3.

Table 3 $E_{RMS}$ using MMWNN-LM and MMWNN-GA

Obviously, the existing methods cannot cope with such dataset with large deformations and they suffer from artifacts. As a solution, our deformation algorithm presents a good reconstructed object and has better quantitative reconstruction results than the deformation techniques presented in the literature, with lower reconstruction errors when sufficient components are used. It is clear that the obtained error rate was remarkably reduced and the performance of Levenberg–Marquardt and genetic algorithm on the synthesized deformed mesh allowed minimizing the distortion without losing the initial data, reaching the control mesh. We can see also that the error was minimized when we used the wavelet network by the genetic algorithm MMWNN-GA and MMWNN-LM, compared to state-of-the-art methods.

Besides, it is obvious that the error rate decreased by applying the wavelet network and the genetic algorithm MMWNN-GA, in comparison with MMWNN-LM. However, it is almost the same when the two methods were applied, except for the horse object for which we obtained an $E_{RMS}$ of 10.0321, using MMWNN-LM, against an $E_{RMS}$ equal to 6.4412 using MMWNN-GA. We may conclude that the horse object contains considerable deformations and suffers from artifacts with large scale rotations. To solve these limitations, the genetic algorithm is a good alternative solution that may treat better this type of objects, compared to Levenberg–Marquardt method.

Generally, our deformation algorithm based on MMWNN-GA and MMWNN-LM provides a good reconstructed object and allows obtaining better quantitative reconstruction results than the existing deformation techniques, with lower reconstruction errors when sufficient components are used.

Table 4, reveals that MMWNN-LM clearly minimizes the time necessary to ensure the deformation process, in comparison with the MMWNN-GA architecture. For example, for Elephant object, the simulation time is reduced from 2875.004(s), using MMWNN-GA architecture, to 410.552(s), employing MMWNN-LM. In our approach, the 3D deformation sequence consists of a large number of frames; each of which represents a large static 3D mesh, characterized by a search space with an increasing number of dimensions. The wavelet network permitted the characteristic points of the original mesh to be aligned towards the target mesh.

Table 4 Comparative study of the execution time between our approach with MMWNN-GA and MMWNN-LM architectures

The genetic algorithm is an optimization algorithm applied to treat important research spaces. However, it requires more calculations than the other meta-heuristic algorithms (notably the evaluation function).

On the other hand, the Levenberg–Marquardt algorithm is one of the most efficient training algorithms for neural network modeling, and therefore for training a feed-forward neural network with the Levenberg–Marquardt algorithm. Having the updating rule, the Jacobian matrix needs to be computed and a training process should be designed. This algorithm combines the ability of both methods (i.e., convergence from any initial state as in the case of gradient descent, and rapid convergence near the vicinity of the minimum error as in the case of Gauss-Newton method) while avoiding their drawbacks.

We used the genetic algorithm to ensure the deformation of the 3D meshes and we got good results. However, for 3D huge meshes genetic algorithm requires less information about the problem and designing an objective function and getting the representation and operators right can be difficult and computationally expensive. In this case, we talk about time-consuming modeling. The Levenberg–Marquardt method, that can handle noisy objective function values as well as random models, provided sufficient accuracy. As the probability of accurate function estimates and models is sufficiently large, we assume that the proposed algorithm converges globally to a first-order stationary point of the objective function with probability one. For this reason, local optimization techniques, such as the Levenberg method, are used mainly for their computational and processing time. However, due to the slowness of the execution time, in many cases, the genetic algorithm diverged and did not give accepted reconstructions when the search space of the best wavelet was enlarged. Thus, gradient-based optimization methods were applied with the improved version of Levenberg–Marquardt technique.

Figures 7, 8, 9 and 10 represent our training results obtained using 15 wavelets in the hidden layer for the 3D deformation of the four objects (Scape, Horse, Elephant and Flamingo). These findings were provided by the MMWNN-GA and MMWNN-LM.

Fig. 7

Comparison of deformation components located in similar areas for Horse object by MMWNN-GA (first row) and MMWNN-LM (second row)

Fig. 8

Comparison of deformation components located in similar areas for Flamingo object by MMWNN-GA (first row) and MMWNN-LM (second row)

Fig. 9

Comparison of deformation components located in similar areas for Scape object by MMWNN-GA (first row) and MMWNN-LM (second row)

Fig. 10

Comparison of deformation components located in similar areas for Elephant object by MMWNN-GA (first row) and MMWNN-LM (second row)

7 Conclusion

In our approach, the 3D deformation sequence consists of a large number of frames; each of which represents a large static 3D mesh. We used a wavelet network to align the characteristic points of the original mesh and to aligned towards the target mesh. To ensure the design of wavelet neural network architecture, an optimization algorithm was used to estimate and optimize the network parameters. The applied genetic algorithm, which is an optimization algorithm, allowed treating important research spaces, and the Levenberg Marquardt algorithm showed its efficiency in neural network modeling. A comparative study between genetic algorithm and Levenberg–Marquardt algorithm was also presented in this article. Experimental results reveal that MMWNN-GA and MMWNN-LM provided a good reconstructed object and better quantitative reconstruction results, compared to the existing deformation techniques, with lower reconstruction errors when sufficient components were used. For object containing considerable deformations and suffering from artifacts with large scale rotations, the genetic algorithm treated better this type of objects, in comparison with Levenberg–Marquardt method. On the other hand, genetic algorithm requires more calculations than Levenberg–Marquardt algorithm and it is computationally expensive, i.e. it is time-consuming modelling algorithm. So, MMWNN-LM minimized more remarkably the time necessary to ensure the deformation, in comparison with the MMWNN-GA architecture.

In our future work, using MMWNN-GA structure, we will apply a simplification method to reduce the simulation time of deformation for all high-resolution objects.