1 Introduction

With superior mechanical properties and the advantage of adapting to complex configurations, cast steels have become a promising solution for joints and connectors in steel constructions. In reticulated spatial structures, cast steel joints were often adopted to connect steel members from multiple spatial directions (Chen et al., 2016; Haldimann-Sturm & Nussbaumer, 2008). In different structure systems for high rise buildings, cast steel connectors were adopted as yielding braces (Gray et al., 2014), steel beam-to-column connections (Han et al., 2015; Sumer et al., 2007; Tong et al., 2016), and shear link beams (Tong et al., 2018). With cast steels, smooth transitions can be easily fabricated to reduce the stress concentration and achieve a better structural performance of the joints. However, the resistance of cast steels to the ductile fracture may be weakened considerably by cast defects. The ductile fracture is then a possible failure mode of cast steel joints and connectors under complex stress states.

Various micromechanical models are vital tools to address the ductile fracture of structural steels. In micromechanics of fracture, the ductile fracture of porous materials is related to the evolution of microvoids in the materials during load actions. In the late 1960s, Rice and Tracey (1969) found that the growth of microvoids is dependent on the stress triaxiality (T), which is the ratio of the hydrostatic pressure to von Mises stress. They deduced the relationship between the void growth rate and the plastic strain for the situation of high stress triaxiality (T ≥ 0.7). Hancock and Mackenzie (1976) simplified this relationship by ignoring the variation of the stress triaxiality during the loading process. Based on these researches, Kanvinde (2004) established the void growth model (VGM) and the stress modified critical strain (SMCS) model, in which the ductile fracture of the material was explained by the nucleation, growth and coalescence of the microvoids. In 1977, Gurson (1977) coupled the material degradation caused by the void development to the constitutive equation and proposed the Gurson model. In 1984, Needleman and Tvergaard (1984) modified Gurson’s criterion by taking into account the interaction between adjacent voids, and formed the GTN model. With these models, the ductile fracture can be predicted successfully for materials at high stress triaxiality regions. Chi et al. (2006), Wang et al. (2011) and Liao et al. (2015) adopted the VGM and the SMCS model to simulate the ductile fracture of welded steel connections of different steels. Qian et al. (2005) and Huang et al. (2013) used the GTN model to predict ductile fracture of circular hollow section joints and beam-to-column welded joints. Recently, micromechanical fracture models were extended to ductile fracture analysis of high strength steels. Yang et al. (2020) predicted the ductile fracture of S690Q, S700MC and S960Q steels based on the void growth equation proposed by Rice and Tracey (1969). Yan et al. (2021) calibrated parameters in the GTN model for cold-formed S700 steels.

In 2004, Bao and Wierzbicki (2004) found that the stress triaxiality is not the only parameter controlling the ductile fracture of materials under pure shear states. For such low stress triaxiality situations, deviatoric stresses, which can be measured by the Lode angle or the Lode parameter, also have considerable effects on the ductile fracture of materials. Many researchers have proposed different micromechanical models considering the effect of the Lode angle or the Lode parameter for the prediction of ductile fracture of materials under shear stresses. Xue (2007) combined deviatoric state parameters to fracture envelope. Bai and Wierzbicki (2008) defined fracture locus by considering three kinds of stress states: compression, tension and shear, then Liu et al. (2019) replaced Lode angle in the Bai-Wierzbicki model with Lode parameter. Lou et al. (2012) showed that shear fracture of material was controlled by the normalized maximal stress. Wen and Mahmoud (2016), and Zhu and Engelhardt (2018) extended the void growth equation proposed by Rice and Tracey (1969) to low triaxiality situations by adding a Lode angle multiplier. Wang et al. (2020) proved the necessity of considering the Lode parameter in ductile fracture analysis of high strength steel under multi-axial loadings. Li et al. (2021) modified the GTN model to consider shear factor and size effect, while Jiao et al. (2021) proposed a dimensionless quantity to evaluate shear-dominated fracture initiation and propagation. With all these models, the accuracy of ductile fracture prediction for materials under shear stresses was significantly improved. Danas and Ponte Castañeda (2012), and Kiran and Khandelwal (2014) described the evolution of microvoids in materials under shear stresses as a successive procedure of nucleation, growth, elongation and collapse, which would result in the localized shear bands. Based on the behavior of microvoids under shear stresses, Yan and Zhao (2018) proposed an equation for the calculation of critical plastic strain for ductile fracture of materials under shear stresses which is quite attractive due to its simple formulation.

Material parameters in the VGM and SMCS model have been calibrated for G20Mn5QT cast steels under ambient and low temperatures by Yin et al., 2020a and Yin et al., 2020b. These calibrated models are applicable to ductile fracture analysis of the cast steels in high stress triaxiality regions. This paper aims to establish a micromechanical model to address the ductile fracture caused by shear for G20Mn5QT cast steels in low stress triaxiality regions. For this purpose, a new formula was deduced for the critical plastic strain of ductile fracture by shear under the framework of Yan and Zhao (2018) and calibrated for G20Mn5QT cast steels by tests on six shear specimens. A new criterion was stipulated for the onset of the void collapse according to scanning electron microscopes of the fracture surfaces of the test specimens. With this criterion and the reformulated equations, the influences of the stress triaxiality and the Lode parameter on the void collapse and the ductile fracture by shear were reasonably evaluated.

2 Parameters for Stress State Definition

2.1 Stress Triaxiality

The stress triaxiality, T, plays an important role in ductile fracture of materials. As a measurement of the stress concentration, it is defined as the ratio of the hydrostatic stress, σm, to the von-Mises stress, σeq, as shown in Eq. 1.

$$T = \frac{{\sigma_{m} }}{{\sigma_{eq} }}$$
(1)

The hydrostatic stress and the von-Mises stress can be calculated by Eqs. 2 and 3.

$$\sigma_{m} = \frac{{\sigma_{1} + \sigma_{2} + \sigma_{3} }}{3}$$
(2)
$$\sigma_{eq} = \sqrt {\frac{{(\sigma_{1} - \sigma_{2} )^{2} + (\sigma_{1} - \sigma_{3} )^{2} + (\sigma_{2} - \sigma_{3} )^{2} }}{2}}$$
(3)

where σ1, σ2 and σ3 are three principal stresses. The sign of the stress triaxiality is determined by the hydrostatic stress, which is positive for tension and negative for compression. The high stress triaxiality (T ≥ 0.7) usually represents the stress state of restricted tension, such as that at the crack tip, while the low stress triaxiality (T < 0.4) generally represents the specific stress states dominated by shear. When the stress triaxiality equals zero, the material is under the action of pure shear.

2.2 Equivalent Plastic Strain

Equivalent plastic strain describes the extent of plastic deformation. It is an invariant of plastic strain tensor, representing its total cumulant, the increment form of which can be expressed by Eq. 4.

$$d\varepsilon_{p} = \sqrt {\frac{2}{3}d\varepsilon_{p}^{ij} \cdot d\varepsilon_{p}^{ij} }$$
(4)

The equivalent plastic strain is an important index for the ductile fracture of materials, based on which many criteria have been established.

2.3 Lode Angle

The Lode angle describes the deviatoric stress state, which may affect the ductile fracture of materials in low stress triaxiality regions. In the principal stress space, the plane perpendicular to the hydrostatic pressure denotes the deviatoric plane, and the Lode angle θ is defined as the angle between the principal deviatoric stress axis and the projection of the stress on the deviatoric plane, as shown in Fig. 1. The Lode angle ranges from \(- \pi {/3}\) to \(\pi {/}3\), and θ = 0 represents the pure shear state.

Fig. 1
figure 1

Definition of the Lode angle

Full size image

2.4 Lode Parameter

The Lode parameter, L, is an alternative variable to describe the state of deviatoric stresses. A stress circle is shown in Fig. 2, where OP1 = σ1, OP2 = σ2 and OP3 = σ3. The circles with diameters of P1P3 are termed as Circle A. Then, taking the distance of OM as σm, and τ’ axis is made through point M. Therefore,

$$MP_{1} = \sigma_{1} - \sigma_{m} = s_{1}$$
(5)
$$MP_{2} = \sigma_{2} - \sigma_{m} = s_{2}$$
(6)
$$MP_{3} = \sigma_{3} - \sigma_{m} = s_{3}$$
(7)

The center of the Circle A is taken as O1, the diameter as P1P3, then

$$OO_{1} = \frac{1}{2}(\sigma_{1} + \sigma_{3} )$$
(8)
$$O_{1} P_{1} = \frac{1}{2}(\sigma_{1} - \sigma_{3} )$$
(9)
Fig. 2
figure 2

Definition of Lode parameter

Full size image

The Lode parameter, L, is defined as the ratio of O1P2 to O1P1, representing the relative position of P1, P2 and P3, which is the characteristic of the stress state. The Lode parameter can be calculated by Eq. 10 and ranges from -1 to 1. For the monotonic tension stress state, σ1 > 0, σ2 = σ3 = 0 and L = -1; for the pure shear stress state, σ2 = 0, σ1 = -σ3 and L = 0; for the plane stress state, 2σ2 = σ1 + σ3 and L = 0.

$$L = \frac{{O_{1} P_{2} }}{{O_{1} P_{1} }} = \frac{{OP_{2} - OO_{1} }}{{O_{1} P_{1} }} = \frac{{\sigma_{2} - (\sigma_{1} + \sigma_{3} )/2}}{{(\sigma_{1} - \sigma_{3} )/2}} = \frac{{2\sigma_{2} - \sigma_{1} - \sigma_{3} }}{{\sigma_{1} - \sigma_{3} }}$$
(10)

3 A New Micromechanical Criterion for Ductile Fracture Under Shear

3.1 Evolution of Microvoids Under Shear

In the ductile fracture dominated by shear, the bonding interface between particles is mainly subject to shear stresses, which makes it harder for voids to nucleate. Therefore, the process of void nucleation plays a more critical role in the ductile fracture. After nucleation, voids will be elongated along the direction of maximum shear stress. Then, the elongated voids may collapse under the shear action and form the localized shear bands.

3.2 Void nucleation Strain

It is assumed that the nucleation of microvoids occurs under the critical local stress that is the internal stress caused by the discordant deformation between the inclusions and the matrix (Goods & Brown, 1979). The process of the void nucleation can be described by continuum medium model proposed by Argon et al. (Argon et al., 1975), in which the critical local stress, σc, at the nucleation of the voids is expressed as the summation of the hydrostatic pressure, σm, and the von-Mises stress, σeq, as shown in Eq. 11.

$$\sigma_{c} = \sigma_{m} + \sigma_{eq}$$
(11)

By introducing the stress triaxiality, T, Eq. 11 can be written as:

$$\sigma_{eq} = \frac{{\sigma_{c} }}{T + 1}$$
(12)

According to the plastic constitutive relation of the material: σ = Kεpn (K is the strength parameter; n is the hardening exponent), void nucleation strain, εnc, the equivalent plastic strain for the nucleation of the voids, can be obtained, as shown in Eq. 13 (Yan & Zhao, 2018).

$$\varepsilon_{nc} = \varepsilon_{eq} = \frac{{\varepsilon_{c} }}{{(T + 1)^{\frac{1}{n}} }}$$
(13)

3.3 Void Collapse Strain

The initial void volume fraction of ductile metals is usually tiny. Therefore, each void evolved almost independently after its nucleation (Bonora et al., 2005). The shear stress may cause the collapse of the ellipsoidal voids before the void coalescence, and result in oval-shaped dimples on the fracture surface of the material. Therefore, the void compression ratio, λc, is introduced to quantify the ellipsoidal configuration of the voids. The void compression ratio is defined as the ratio between lengths of the axis perpendicular to the fracture surface and the longest axis of the void. When λc reaches its critical value, the void is considered to collapse. Kiran and Khandelwal (2014) proposed that the expansion of the voids was mainly caused by the stress triaxiality, while the deformation of the voids was controlled by the Lode parameter. Thus, the critical void compression ratio, \(\lambda_{c}^{critical}\), can be regarded as a function of the Lode parameter, as shown in Eq. 14, and the function can be determined based on the scanning electron microscope of fracture surfaces of test specimens.

$$\lambda_{c}^{critical} = f(L)$$
(14)

The equivalent plastic strain corresponding to the critical compression ratio is the void collapse strain, εcl, which is affected significantly by both the stress triaxiality and the Lode parameter. The relationship between εcl and these two parameters adopted in this paper is as shown in Eq. 15. This equation was obtained by removing the constant term of the equation proposed by Yan and Zhao (2018).

$$\varepsilon_{cl} = p_{1} e^{{p_{2} T - p_{3} L}}$$
(15)

where \({p}_{1}\), \({p}_{2}\) and \({p}_{3}\) are material parameters. It would be illustrated in Sec. 4.4 that the removal of the constant term has little effect on the agreement of the equation with the results of the unit cell analysis since a new criterion was adopted for the onset of the void collapse in this paper. In addition, the removal of the constant term will add convenience for the following deductions.

3.4 The Micromechanical Criterion for Ductile Fracture Under Shear

Based on the study of the evolution of microvoids, a new micromechanical criterion was proposed for ductile fracture under shear, in which the fracture criterion was expressed by the critical equivalent plastic strain, \(\varepsilon_{f}^{s}\), as shown in Eq. 16.

$$\varepsilon_{f}^{s} = \varepsilon_{nc}^{{c_{1} }} \cdot \varepsilon_{cl}^{{c_{2} }}$$
(16)

where εnc, and εcl are void nucleation strain and void collapse strain respectively; c1 and c2 are both material parameters. It should be noted that the new formula for the critical equivalent plastic strain, as shown in Eq. 16, was proposed by reformulating the counterpart equation in Yan and Zhao (2018), in which the critical equivalent plastic strain was calculated as the product of the void nucleation strain and the void collapse strain, as shown in Eq. 17.

$$\varepsilon_{f}^{s} = c_{1} \varepsilon_{nc} \cdot c_{2} \varepsilon_{cl}$$
(17)

Substituting Eqs. 13 and 15 into Eq. 16 and setting \(\varepsilon_{c}^{{c_{1} }} p_{1}^{{c_{2} }} = c\), the critical plastic strain for the shear fracture can be expressed as the function of the stress triaxiality and the Lode parameter, as shown in Eq. 18.

$$\varepsilon_{f}^{s} = \frac{{c \cdot e^{{(p_{2} T - p_{3} L) \cdot c_{2} }} }}{{(T + 1)^{{\frac{1}{n} \cdot c_{1} }} }}$$
(18)

where n is the hardening exponent in the plastic constitutive relation of the material; p2, p3, c, c1 and c2 are all parameters; p2 and p3 can be obtained by unit cell analysis with the determination of the critical void compression ratio, \(\lambda_{c}^{critical}\), based on the scanning electron microscope of fracture surfaces of shear specimens; c, c1 and c2 can be calibrated by tests and complementary finite element analysis on shear specimens.

It should be noted that several similar formats have been tried for the critical equivalent plastic strain, including Eq. 16 and Eq. 17. It was found that the reformulated equation, Eq. 16, led to a more concise expression of the critical equivalent plastic strain (Eq. 18) and will add convenience in the calibration of material parameters in Sec. 4.5.

4 Calibration of the Proposed Micromechanical Criterion for G20Mn5QT Cast Steels

4.1 Experimental Study on Shear Specimens

Six shear specimens were tested to calibrate the proposed micromechanical criterion for G20Mn5QT cast steels. A “butterfly” gauge section was used in the design of the specimens, which was originally proposed by Bao and Wierzbicki (2004). Various shear specimens containing similar configurations have been widely adopted by many researchers (Jia et al., 2016; Kong et al., 2020; Liu et al., 2019; Yan & Zhao, 2018). Three different configurations (S0, S30 and S60, each with two repetitions), as shown in Fig. 3, were designed in this paper for different combinations of the stress triaxiality and the Lode parameter. These specimens were all machined from a 30 mm thick plate of G20Mn5QT cast steels and numbered after the angle θ between the central line of the thinned part of the specimen and the loading direction.

Fig. 3
figure 3

Configuration of shear specimens

Full size image

The tests were carried out on the universal testing machine in the Structure Laboratory of Tianjin University, and the typical test setup is as shown in Fig. 4. All the specimens were tested under uniaxial tension, and the loading procedure was controlled by the extensometer shown in Fig. 4. In order to obtain the ideal shear stress state, all the specimens were loaded through pin connections at both ends. The gauge length of the extensometer was 50 mm and the measuring range was ± 10%. All test specimens were loaded monotonically until the ductile fracture occurred at the thinned part of the specimens.

Fig. 4
figure 4

Test setup

Full size image

Load-deformation curves obtained by tests for these specimens are as shown in Fig. 5. The initiation of the ductile fracture was identified by the sudden change in the slope of these curves, which is also consistent with the observation during the tests. It was observed that ductile fracture initiated on the surfaces of the thinned part for all test specimens and the fractured specimens were shown in Fig. 6. For all three groups of specimens, the load-deformation curves exhibited considerable differences, especially for specimen S30. Possible reasons for these differences were attributed to the variability of the cast steel materials and the manufacturing error.

Fig. 5
figure 5

Load-deformation curves for all shear specimens

Full size image
Fig. 6
figure 6

Fractured shear specimens

Full size image

4.2 Scanning Electron Microscopes

Dimples on scanning electron microscopes (SEM) of the fracture surfaces are illustrated for the shear specimens in Fig. 7. Since the ductile fracture occurred due to shear or combined action of shear and tension, the shape of most dimples on the fracture surfaces of the specimens was elliptical, as shown in Fig. 7. Obvious elongation along the direction of the maximum shear stress was observed.

Fig. 7
figure 7

Dimples in SEM of the fracture surfaces of shear specimens

Full size image

The shapes of dimples on the fracture surfaces of the shear specimens were compared. With the measured long axis (D1) and short axis (D2) of the elongated dimples, as shown in Fig. 7 (a), the elongation ratios (λe = D1/ D2) of these dimples were calculated. Twenty dimples were selected randomly at the center of the scanning electron microscopes shown in Fig. 7 for the determination of the elongation ratios. The maximum, minimum and average elongation ratios were listed in Table 1 for all shear specimens. The average values were adopted to determine the critical void compression ratio, λc, for triggering the void collapse in Sect. 4.4.

Table 1 Elongation ratios for shear specimens
Full size table

Stepped cleavage planes formed by shear action were also noticed on the fracture surfaces of the specimens. Two types of cleavage plane distributions can be distinguished by the observation of SEM, as shown in Fig. 8 (a) for specimen S0. Large and concentrated cleavage planes (Types A), as shown in Fig. 8 (b), were found in limited areas along the top and bottom edges of the fracture surface. Small and dispersed cleavage planes (Type B), as shown in Fig. 8 (c), interlaces with dimples areas in the center area of the fracture surface.

Fig. 8
figure 8

Cleavage planes in SEM of the fracture surfaces of specimen S0-1

Full size image

4.3 Determination of the Hardening Exponent \({\varvec{n}}\)

Tension coupon tests had been conducted for this batch of G20Mn5QT cast steels by Yin et al., 2020b. The true stress–strain curve obtained based on the test results was shown in Fig. 9.

Fig. 9
figure 9

True stress–strain relationship of G20Mn5QT cast steels

Full size image

This true stress–strain relationship can be expressed by the Holloman formula, as shown in Eq. 19.

$$\sigma = K\varepsilon_{p}^{n}$$
(19)

where K is the strength parameter and n is the hardening exponent. Obviously, the true stress has linear relationship with the true strain in the double logarithmic coordinate according to the Holloman formula. By linear regression analysis, it was obtained that K = 879.1 and n = 0.16.

4.4 Determination of Parameters p 1, p 2 and p 3 by the Simulation of Void Elongation

Assuming that the nucleate voids are initially spherical and are scattered randomly in the material, a macroscopic material point can be simulated by a unit cell with a spherical cavity at the center. This unit cell has often been employed in the analysis of the evolution of the microvoid (Bonora et al., 2005; Kuna & Sun, 1996; Yan & Zhao, 2018). By the unit cell analysis, the elongation of the microvoid can be simulated to determine the critical collapse strain for the void under low positive or slightly negative stress triaxiality. The unit cell analyzed in this section was shown in Fig. 10 (a). The length of all the edges of the unit cell is 2L0 and the radius of the spherical cavity was set to be r0 = L0/3.74 so that the initial void volume fraction (f0) was 0.01 (Kiran & Khandelwal, 2013).

Fig. 10
figure 10

Finite element model setup for unit cell analysis

Full size image

The finite element model was established for the unit cell with general finite element software ABAQUS, as shown in Fig. 10 (b). In consideration of the symmetricity, only 1/8 of the unit cell was modeled. 8-node linear brick element with reduced integration, C3D8R, implemented in ABAQUS, was adopted for model discretization. All the outer surfaces of the unit cell were kinematically constrained, and only the uniform deformation along their normal direction was allowed. Material properties were set according to test data on G20Mn5QT cast steels in Yin et al. (2020b).

A total number of 48 groups of principal stresses (σ1, σ2 and σ3) were adopted in the unit cell analysis to produce different combinations of the stress triaxiality and the Lode parameter. The influences of these two parameters on the void evolution were investigated based on the results of the unit cell analysis. Three principal stresses were calculated from the specified values of the stress triaxiality and the Lode parameter by Eqs. 20 and 21, which were deduced from Eqs. 1 and 10. The variation range of the stress triaxiality was [-0.3, 0.4] with the interval of 0.1 and that of the Lode parameter was [-1, 0] with the interval of 0.2.

$$\sigma_{2} = \frac{1}{2}(1 + L)\sigma_{1} + \frac{1}{2}(1 - L)\sigma_{3}$$
(20)
$$\sigma_{3} = \frac{{18T\sqrt {3 + L^{2} } + L^{2} - 27T^{2} - 9T^{2} L^{2} - 9}}{{(3 - L)^{2} - 9T^{2} (3 + L^{2} )}}\sigma_{1}$$
(21)

Typical shapes of the deformed void obtained by the unit cell analysis for different combinations of the stress triaxiality and the Lode parameter were illustrated in Table 2. The stress triaxiality almost has no influence on the shape-changing of the void, and the shape of the deformed void depends only on the Lode parameter. With the increase of the Lode parameter from -1 to 0, the shape of the deformed void changed gradually from prolate ellipsoids (D1 > D2≈D3) to oblate ones (D1≈D2 > D3) (Zhu & Engelhardt, 2018), where D1 and D2 are as shown in Fig. 7 (a) and D3 is the length of the axis perpendicular to the fracture surface. For the loading conditions with zero Lode parameter, the shear stress would squeeze the void to a very flat configuration, which facilitated the deformed void to collapse. For the loading conditions with the Lode parameter being -1, the length of the two short axes of the deformed void remained equal, which made the void rather difficult to collapse.

Table 2 Evolution of the void in different stress states
Full size table

As shown in Fig. 11, a void deformed and was about to collapse under the stress state of T = 0.4 and L = − 0.2. Though D1 and D2 can be measured on the fracture surface for the calculation of the elongation ratio (λe = D1/ D2), the stability of the void is more related to D3, the length of the shortest axis perpendicular to the fracture surface. Therefore, the compression ratio, defined as λc = D3/D1 in Sect. 3.3, was adopted to trigger the collapse of the void for the determination of the void collapse strain.

Fig. 11
figure 11

Typical deformation of a void (T = 0.4 and L = − 0.2)

Full size image

Two criteria were investigated for the onset of the void collapse based on the unit cell analysis of the three shear specimens tested in Sec. 4.1. One is the complete vanishment of the void (Yan & Zhao, 2018), i.e., \(\lambda_{c}^{critical} { = }0\). Unit cell analysis showed that, based on this criterion, the elongation ratios of the collapsed void were λe = 2.3, 3.0 and 12.5 for specimens S0, S30 and S60, respectively. These elongation ratios were inconsistent with those obtained by measurements on the scanning electron microscopes in Sect. 4.2, especially for specimen S60. Therefore, a new criterion was proposed that void collapse occurs when the compression ratio, λc = D3/D1, was squeezed to specific values. The elongation ratios measured on the scanning electron microscopes were λe = 2.1, 2.6 and 3.3 for specimens S0, S30 and S60, respectively. The corresponding compression ratios obtained by unit cell analysis were λc = 0.13, 0.15 and 0.20, which were the critical compression ratios for the void collapse of these specimens. The critical compression ratio, \(\lambda_{c}^{critical}\), varied with the Lode parameter almost linearly, as shown in Fig. 12 and the linear relationship, defined by Eq. 22, was adopted for the calculation of the critical compression ratios for all the 48 loading conditions in unit cell analysis.

$$\lambda_{c}^{critical} = - 0.12L + 0.12$$
(22)
Fig. 12
figure 12

Variation of the critical compression ratio with the Lode parameter

Full size image

In unit cell analysis, when the compression ratio reached its critical value, the void collapse strain εcl can be calculated by Eqs. 23 and 24.

$$\varepsilon_{i} = \ln \left(\frac{{L_{0} + U_{i} }}{{L_{0} }}\right)$$
(23)
$$\varepsilon_{cl} = \frac{1}{3}[(\varepsilon_{1} - \varepsilon_{2} )^{2} + (\varepsilon_{2} - \varepsilon_{3} )^{2} + (\varepsilon_{3} - \varepsilon_{1} )^{2} ]$$
(24)

where Ui (i = 1, 2, 3) is the normal displacement for the surface at xi = Li; εi is the strain in xi direction.

The void collapse strains obtained by unit cell analysis for all the 48 loading conditions were illustrated in the stress triaxiality and the Lode parameter space, as shown in Fig. 13. According to the regression analysis, the parameters in Eq. 15 were determined as p1 = 0.47, p2 = 1.1 and p3 = -0.1. The determination coefficient, R2, was calculated by Eq. 25 to evaluate the precision of the regression analysis.

$$R^{2} = 1 - \frac{SSE}{{SST}}$$
(25)
Fig. 13
figure 13

The void collapse strain in the stress triaxiality and the Lode parameter space

Full size image

where SSE is the residual sum of squares; SST is the total sum of squares. It was obtained that the determination coefficient was 0.982, which indicated that the surface defined by Eq. 15 was in good agreement with the results of the unit cell analysis, as also observed from Fig. 13.

It should be noted that parameters p2 and p3 reflect how the void collapse depends on the stress triaxiality and the Lode parameter. The two parameters were determined reasonably with the reformulated equation for the void collapse strain and the critical compression ratio for the onset of the void collapse. These parameters can be substituted into Eq. 18 directly for the calculation of the critical plastic strain of the ductile fracture by shear for G20Mn5QT cast steels.

4.5 Calibration of Parameters c, c 1 and c 2

Parameters c, c1 and c2 were calibrated by complementary finite element simulations of the tests on the shear specimens. Finite element models were set up with general finite element software ABAQUS, as shown in Fig. 14 for specimen S0. Though the dimensions of all specimens were measured before tests, it was found very difficult to measure the thickness of the specimens at the fracture location with high precision. Therefore, all FE models were established based on the nominal dimensions of the specimens. Eight-node linear brick element with reduced integration, C3D8R, was adopted for model discretization except for the 4-node linear tetrahedron element, C3D10, for the transition zone. Extremely fine meshes with element sizes of 0.2 mm, which is approximately the characteristic length of G20Mn5QT cast steels, were generated around the potential fracture locations and transited gradually to relatively coarse meshes in other regions of the specimens. The characteristic length is a length scale introduced in VGM and SMCS model (Kanvinde & Deierlein, 2006) for ductile fracture of materials. Micromechanical fracture criteria should be met over the characteristic length to initiate the ductile fracture. Therefore, in ductile fracture analysis, the mesh size of the finite element model at the potential fracture location should be approximately the characteristic length of the material. The characteristic length depends on the microstructure of the material and can be determined for particular material through scanning electron microscopy of its fracture surfaces. In Yin et al., 2020b, the characteristic length of G20Mn5QT cast steel was determined as 0.214 mm by SEM analysis. To ensure the accuracy of the calculation, there were at least four elements along the thickness direction. The boundary and loading conditions of all the finite element models were set in consistency with the corresponding tests. The elastic and plastic material properties obtained by tension coupon tests on the same batch of G20Mn5QT cast steels (Yin et al., 2020b) were adopted in all finite element analysis.

Fig. 14
figure 14

Typical finite element model of the shear specimens

Full size image

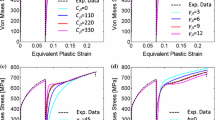
Load–displacement curves obtained by finite element simulations agreed with the corresponding test results, as shown in Fig. 5Fig., which verified the rationality of the finite element analysis. The reasons for the differences between finite element simulations and the test results were also the variability of the cast steel materials and the test errors. Calibration of the parameters based on test results of all the six specimens would make for the decrease of the influence of errors.

According to finite element simulations, the maximum equivalent plastic strain occurred on the surface of the thinned region for all shear specimens, as shown in Fig. 15, which was consistent with the observations during the tests. The deformations obtained by FEA for the shear specimens under different loadings were also consistent with the test observation, as shown in Fig. 16 for specimen S0.

Fig. 15
figure 15

Equivalent plastic strain contours at the crack initiation of the shear specimens

Full size image
Fig. 16
figure 16

Comparison of deformations by FEA with test observations for specimen S0-1

Full size image

The stress state at the fracture location of the specimens varied with the loading process. Accordingly, the average stress triaxiality Tav and average Lode parameter Lav were calculated by Eqs. 26 and 27 respectively to represent the ‘average’ stress state during the loading process.

$$T_{av} = \frac{1}{{\varepsilon_{f} }}\int_{0}^{{\varepsilon_{f} }} {Td\overline{\varepsilon } }$$
(26)
$$L_{av} = \frac{1}{{\varepsilon_{f} }}\int_{0}^{{\varepsilon_{f} }} {Ld\overline{\varepsilon } }$$
(27)

Fracture displacements, Δf, were determined from the sudden change in the slope of the load–displacement curves obtained by tests, as shown in Fig. 5. The maximum equivalent plastic strain corresponding to the fracture displacement was the critical plastic strain, \(\varepsilon_{f}^{test}\), which can be determined based on the results of finite element simulations. The fracture displacement (Δf), the critical plastic strain (\(\varepsilon_{f}^{test}\)), the average stress triaxiality (Tav) and the average Lode parameter (Lav) were summarized in Table 3 for all the six shear specimens. Based on these data, the last three parameters in Eq. 18 were then obtained as c = 0.97, c1 = 1.65 and c2 = 18.75 by regression analysis.

Table 3 Critical equivalent plastic strains for shear specimens
Full size table

All the determined parameters were then substituted into Eq. 18 and the critical equivalent plastic strain for ductile fracture under shear can be expressed by the stress triaxiality and the Lode parameter for G20Mn5QT cast steels, as shown in Eq. 28.

$$\varepsilon_{f}^{s} = \frac{{0.97 \cdot e^{1.8T - 0.17L} }}{{(T + 1)^{3} }}$$
(28)

The critical equivalent plastic strains calculated by Eq. 28 were compared with the test results for all shear specimens, as shown in Table 3. The differences between the results of Eq. 28 and the tests were all less than 9%, which verified the applicability of the proposed micromechanical criterion and the accuracy of the material parameters calibrated for G20Mn5QT cast steels in the section.

The surface defined by Eq. 28 illustrated the variation of the critical plastic strain with the stress triaxiality and the Lode parameter, as shown in Fig. 17. The data points for the six shear specimens in Table 3 scattered on the surface, as shown in the figure, which indicated again that the critical equivalent strains calculated by Eq. 28 were in good agreement with the test results. It should be noted that this equation is only applicable to situations with -1 ≤ L ≤ 0 because only specimens with the Lode parameter in this range were tested.

Fig. 17
figure 17

Variation of critical plastic strain with stress triaxiality and Lode parameter

Full size image

5 Discussion on Different Fracture Mechanisms of G20Mn5QT Cast Steels

In the previous two sections of this paper, a new micromechanical criterion was proposed and calibrated for G20Mn5QT cast steels to predict the ductile fracture under shear. A formula (as shown in Eq. 28) has been set up for the calculation of the critical plastic strain that is corresponding to the ductile fracture occurred in the region of low stress triaxiality. For the material in the region of high stress triaxiality, ductile fracture tends to occur under tension. For such situation, the stress modified critical strain (SMCS) model has been calibrated for G20Mn5QT cast steels (Yin et al., 2020b). Based on the SMCS model, the critical plastic strain for the ductile fracture under tension can be calculated by Eq. 29, where α represents the material’s resistance to ductile fracture and α = 1.4 for G20Mn5QT cast steels as calibrated by Yin et al. (2020b).

$$\varepsilon_{f}^{t} = \alpha e^{ - 1.5T}$$
(29)

The surface defined by Eq. 29 intersected with that by Eq. 28 in the stress triaxiality and the Lode parameter space, as shown in Fig. 17. Only the lower parts of the two surfaces were plotted, which formed a failure surface for ductile fracture of G20Mn5QT cast steels. Data points representing tests on smooth notched tensile (SNT) specimens of G20Mn5QT cast steels (Yin et al., 2020b) were also summarized and labeled in Table 4 and Fig. 17, respectively.

Table 4 Stress states for SNT specimens (Yin et al., 2020b)
Full size table

Ductile fracture under tension and under shear are two competing failure mechanisms for different combinations of the stress triaxiality and the Lode parameter (Barsoum & Faleskog, 2007; Li et al., 2011; Pardoen & Brechet, 2004). The smaller value of the critical plastic strains calculated by Eqs. 28 and 29 determines whether the final ductile fracture is caused by tension or shear. The intersecting curve between the two surfaces was projected onto the T - L coordinate system, as shown in Fig. 18. For combinations of the stress triaxiality and the Lode parameter on the left side of this curve, the ductile fracture will be caused by tension; for those on the right side, the ductile fracture will be caused by shear. It can be seen that the fracture mechanism depends mainly on the stress triaxiality, and the Lode parameter has limited influence on it. Ignoring this minor influence of the Lode parameter, fracture mechanism can be determined for G20Mn5QT cast steels approximately based on the stress triaxiality: tension fracture occurs when T > 0.371 and shear fracture occurs when T ≤ 0.371, as shown in Fig. 18. The critical plastic strain can then be calculated by Eq. 28 or Eq. 29 accordingly.

Fig. 18
figure 18

Determination of fracture mechanism for G20Mn5QT cast steels

Full size image

Critical plastic strains for both fracture mechanisms were calculated for the shear specimens and the STN specimens in (Yin et al., 2020b) by Eq. 28 and Eq. 29, respectively. Then the fracture displacements were predicted based on complementary finite element simulations of tests on these specimens. The predicted fracture displacements were compared with the test results for the two fracture mechanisms in Fig. 19. For the shear specimens with stress triaxiality lower than 0.371, the proposed micromechanical fracture criterion (Eq. 28) gave more accurate predictions; for SNT specimens with stress triaxiality higher than 0.371, the SMCS model (Eq. 29) was more applicable. It should be noted that, for specimen S60 with relatively large stress triaxiality, the accuracy of the SMCS model is also acceptable. However, for specimen S0 with very small stress triaxiality, the SMCS model predicted the fracture displacement about 30% larger than the test result, and for negative stress triaxiality, the accuracy of the SMCS model will be even poorer.

Fig. 19
figure 19

Comparison of predictions by the proposed criterion and the SMCS model

Full size image

6 Conclusions

A new micromechanical criterion was proposed for ductile fracture caused by shear in low stress triaxiality regions, in which the influences of both the stress triaxiality and the Lode parameter were reasonably considered. Six shear specimens of G20Mn5QT cast steels were tested under monotonic tension. Scanning electron microscopes of the fracture surfaces of the test specimens were studied. It was illustrated that shear action played a more dominating role with the decrease of the stress triaxiality and the Lode parameter. The critical void compression ratio for the void collapse was determined in accordance with the shape of the dimples observed on the fracture surfaces of the test specimens. Parameters in the proposed criterion were then calibrated for G20Mn5QT cast steels based on unit cell analysis, scanning electron microscopes, and results of the tests and complementary finite element analysis on the shear specimens. The critical equivalent plastic strains predicted by the proposed micromechanical criterion agreed very well with the test results for all shear specimens, which verified the applicability of the proposed criterion and the accuracy of the material parameters calibrated for G20Mn5QT cast steels. Different fracture mechanisms of G20Mn5QT cast steels were discussed. Fracture mechanism can be determined for G20Mn5QT cast steels approximately based on the stress triaxiality: fracture by tension when T > 0.371 and fracture by shear when T ≤ 0.371.