1 Introduction

Bracing systems have been broadly used in designing structures to limit drift and ensure stability (Sardari, Dehkordi, Eghbali, & Samadian, 2020). Lateral drift in tall structures increases as an exponent of structure height. For this reason, a high amount of steel is necessary to control the lateral drift. It is also complicated to determine the optimal position of braces in these systems (Alhaddad, Halabi, Xu, & Lei, 2020). While X-braces are usually used for one story, single-, double-, V-shaped and diagonal braces are commonly considered for all stories of a structure. On the other hand, the use of trial and error is, in many cases, cumbersome and impossible. Therefore, there is a need for a method that appropriately performs the optimization process with reasonable accuracy and the use of time (Yang, Yan & Qi, 2019).

Optimization is the art of finding the best response among the existing ones (Ramly, 2018). Optimization has been used in the design and maintenance of many engineering, economic, and even social systems to minimize the required cost and maximize the profit (Mohammadhosseini & Ghadiri, 2019). Due to the vast application of optimization in different sciences, this topic has been highly developed and used in mathematics, management, industries, and several science branches with different titles as mathematical planning and operation research in order to hint optimization topics (Rosenblueth, 1986). There are various methods to solve the optimization problems, but they lose their application by the increase of problem dimension and existence of nonlinear and non-convex functions in the optimization model of mathematical optimization methods (Weihmann, Martins, de Andrade Bernert, & dos Santos Coelho, 2012). Generally, there is a large number of designs that provide the accepted criteria of designing, but choosing an economical design is not easily possible. For this reason, there are new innovative and exploratory methods under development.

The optimization methods and algorithms are divided into two categories of exact and approximate algorithms. Although the exact algorithms can find the optimized solution accurately, they are not efficient enough in complex optimization problems, and the execution time depends exponentially on the dimensions of the problem. The approximate algorithms can find good solutions (near-optimal) for the hard optimization problems in a short time. The approximate algorithms are also divided into three categories of heuristic, meta-heuristic, and hyper-heuristic. The two main problems of the heuristic algorithms are sticking in the optimized local points and early convergence in these points. The meta-heuristic algorithms have been developed to solve these problems. The meta-heuristic algorithm is one type of approximate optimization algorithms, which has the strategies to exit from the optimal local point and have applicability in a wide range of problems. Various classes of this type of algorithm have been developed in recent decades, all of which are subsets of the meta-heuristic algorithm (De Stefani, Scotta & Lazzari, 2015; Kaur, Singh & Josan, 2017).

The well-known population-based meta-heuristic algorithms include evolutionary algorithms (genetic algorithm, genetic planning, and so on), the ant colony optimization algorithm, bee colony, particle swarm optimization method, league championship algorithm, optics inspired optimization, runner root algorithm, and intelligent water drops algorithm. New meta-heuristic algorithms have been developed in recent years inspired by living creatures in nature, the most famous of which are the grey wolf optimization algorithm, the dragonfly algorithm, the flower pollination algorithm, the whale optimization algorithm, locust optimization algorithm, and emperor penguin colony algorithm. The conventional single-solution-based meta-heuristic algorithms are the Tabu search algorithm and simulated annealing algorithm (Kaveh & Javadi, 2014; Saka & Kameshki, 1998).

A study entitled "Semi-rigid steel frame design with the minimal cost" investigated the applicability of genetic algorithms with the objective function of cost minimization and using Load and Resistance Factor Design (LRFD) and Allowable Stress Design (ASD) methods. The results showed that the design obtained by the LRFD method was almost 8% more economical than that of the ASD method (Hayalioglu & Degertekin, 2005). The optimization of the steel frames was done by three meta-exploration methods of genetic, colony, and particle swarm algorithms. According to the obtained results, it was found that the particle swarm algorithm gives better results than the other two algorithms (Hasançebi, Çarbaş, Doğan, Erdal & Saka, 2010).

Another study investigated the determination of damage position and intensity in structure using different optimization algorithms and the changes in modal strain energy of structural elements. The algorithms investigated in this study include the particle swarm optimization algorithm, the harmony search algorithm (HS), the cuckoo search algorithm (CS), and the gravitational search algorithm (GSA) (Zhang, Zhou & Shih, 2020). Damage usually reduces the stiffness of the structure and thereby changing the modal properties of the structure. In this study, the damage position and intensity have been determined using the changes of strain energy in the element modal damage index for each element. These changes are measured using only a few modes of shape and an element stiffness matrix. The difference in structural damage index between the real and modeled structure has been used as the objective function of optimization algorithms. This method was implemented numerically on truss structures (Ghiasi, Fathnejat & Torkzadeh, 2019). The results of the suggested method showed that these methods can successfully determine the position and intensity of damage in structure with good precision. However, the CS algorithm has better capability among the proposed algorithms in space searching and as a result has higher accuracy in detecting damage in structures (Ghiasi, Ghasemi, Binaee & Ghafari, 2016).

It is worth noting that in the optimization problems under frequency constraint, the method for obtaining the response of the structure, which is that of structure's frequency in these cases, is very important in addition to the importance of the selected optimization algorithm. In the study, the optimal weight design of structures has been presented under several constraints of frequency and drift. Frequency constraints are highly nonlinear and are non-convex and implicit for design variables (Lieu, Do & Lee, 2018). Optimization has been performed in a heuristic algorithm, which has discrete variables. A modified colliding bodies optimization algorithm has been selected as the optimization algorithm in this study. SAP2000 is an applicable and almost accurate software, which has many users among the structural engineers. The connection capability of this software to MATLAB has been used in this research to decrease the analysis time and increase simplicity. In this research, two 2D-braced frames under frequency and drift constraints have been optimized and the results have been compared to the previous ones. The results showed less optimized structure weights, better convergence, and better satisfaction of the constraints (Baghlani, Dehghan & Ebrahimi Tavani, 2016). An experimental study of three steel rings made of two half-rings was reported by Andalib et al. (Andalib, Kafi, Kheyroddin & Bazzaz, 2014). The results showed that the connection type significantly affects the ring performance. Some numerical methods were also performed using ANSYS software to supplement the findings. The hysteresis curve of the steel specimen made of steel plates was wide and a tensile ductility factor of 8.68 was achieved. They also conducted another research to analyze the nonlinear and linear behaviors of the steel frames coupled with ductile element and off-centre bracing system to get the best position of the bracing elements. The modeling was done using ANSYS software. The optimum eccentricity was obtained by modeling three steel frames with different eccentricities. The analytical findings confirmed that the model OBS-C with 0.3 eccentricities has the highest performance (Bazzaz, Kheyroddin, Kafi & Andalib, 2012). Bazzaz et al. proposed a new bracing system using circular element (circular dissipater) to replace the damaged part without an overhaul. For this, the nonlinear software package of ANSYS was used to design two frames; one with a off-centre bracing system and optimum eccentricity (OBS-C-O) and the other with the same specifications and without circular element (OBS). This was the first time that the performance of the general system was studied. The two frames were also compared in terms of linear and nonlinear behaviors. The analytical results and comparison between the plots of the two models showed that the first model has a higher performance than the others (Bazzaz, Kafi, Kheyroddin, Andalib & Esmaeili, 2014).

Various studies have also been done on the pattern and arrangement of different braces. Kumar and Jie studied the braced frames and the energy dissipation capacity (Kumar, Kumar & Kalyanaraman, 2007; Xie, 2005). The results showed that the bracing arrangement and pattern type significantly affect the behavior of the structure. In another research, they also examined the behavior of a 20-story structure with different arrangements of convergent braces and k-braces. They reported that the integration of x-brace with other braces gives better performance in terms of base shear force-drift of the floors (Shinde, Galatage, & Kulkarni, 2017).

This research also tries to present an influential and applicable algorithm for optimizing bracing steel frame with the approach of decreasing structure weight (consequently, the base shear force on the structure and reducing the seismic responses of the structure with the help of artificial intelligence and topological optimization technique of braces). Based on an optimization problem, the study mainly focuses on designing and identifying the best topology and number of spans in the structural steel bracing for resiting against earthquakes. The parallel processing method is used for problem analysis. Parallel computing refers to the simultaneous implementation of one program (divided into smaller parts) on several processors to reach a higher speed. The main idea is that solving a problem is usually divided into minor duties. By simultaneous implementation of the sub-duties and their coordination, the main problem will be solved in a shorter time. Parallel computing for the concurrent execution of a process is usually performed by dividing the processing operation into several processors to increase efficiency and accelerate the solution-finding. The idea behind this is that each problem is usually divided into several smaller problems, which can simultaneously be solved and integrated to reach the final result quickly. Shorter calculation time, the possibility of solving larger problems, overcoming the memory limitations, economic efficiency, and using novel technologies are among the superiorities mentioned for parallel processing compared to serial processing (the traditional information processing method). (Kaveh, Kalatjari, Talebpour, Torkamanzadeh, 2013). This research uses this method to optimize the topology of braces in low-, mid-, and high-rise metallic structures. The different types of CBF braces (X-bracing, Multi-story X-bracing) are among the designing variables in this study. Accordingly, after defining the objective function, the problem constraints (including frequency, design of members, drift, and the allowed values of the tensile forces in braces) and developing an algorithm based on a parallel island model, a method will be suggested for the optimal topology of the braces in three types of steel structures. The research seeks the optimal location of bracing spans with reasonable accuracy and the best topology of bracing to improve seismic indices of the structures. The primary motivation of this paper is to introduce an innovative method based on a parallel processing pattern (island method) and with several meta-heuristic algorithms. The technique examines each frame at a time with several algorithms. Finally, the general optimal design of the frame is presented that is free from the common optimization problems with single meta-heuristic algorithms.

2 Methodology

Despite the efforts made in recent years to improve the performance of ultra-innovative algorithms, they still have significant drawbacks. One of the problems with the conventional structures is the long running time of the program. In a genetic algorithm, the number of generations required to achieve convergence is usually high, and a large number of chromosomes must be analyzed in each generation. One of the conventional methods to solve this problem is parallel processing. Many studies have recently been done on parallel meta-heuristic algorithms. The studies mainly proposed parallel processing in two ways (Tanimura, Hiroyasu & Miki, 2001; Rajan & Nguyen, 2004) of direct parallelism (Ghazi, Banan, Ashrafizadeh, 2003) and island parallelism (Miki, Hiroyasu, Kaneko, & Hatanaka, 1999; Haupt & Haupt, 2004). The first system, known as the Master–Slave, consists of a main processor and an n − 1 secondary processor. These processors work in parallel and independently and send the results to the main processor. In the second system (island method used in this paper), the initial population is first divided into several sub-populations (islands) and each island is optimized directly by a processor.

2.1 Multi Meta-Heuristic Based Search Method (MHSM)

In the multi meta-heuristic-based search method, the population is divided into different parts (the islands in this study include the algorithms of particle swarm, genetics, charged system search, big bang-big crunch). Each part has an individual structure and environment and a specific algorithm has been used in each island.

The method is similar to the island model genetic algorithm (Kalatjari & Talebpour, 2011) such that first, the primary population is divided into different parts and sub-populations are organized in the existing islands. Each island has its optimization method, as were explained by the algorithms mentioned in the continuation of this section. Then, the best islands are specified based on the existing designs of islands during the migration interval (number of repetitions for each algorithm which is considered 150–250 for each algorithm). Then, the relations governing the best island of optimization will govern the entire system, and the process will continue based on the algorithm in Fig. 2. Figure 1 shows a schematic view of the suggested meta-heuristic search method.

Fig. 1
figure 1

Migration of the selected designs to the best island in multi meta-heuristic-based search method (MHSM)

Full size image

It is worth noting in algorithm of Fig. 2 and during the stage of transmitting the best island designs to the selected island, the migration rate has been considered to be 25%. The point is that the migrants must change based on the condition and structure of the members of (selected) destination island. This change is an adaptation to the destination environment. For example, if GA is the destination island, the migrants are mapped to the genetic space, and if CSS and PSO are the destination islands, the migrants are mapped to the vector space. In this research, a computer network consisting of 4 computers was designed, each computer was assigned to an island, and each island was optimized with its parameters and relationships.

Fig. 2
figure 2

Algorithm of multi meta-heuristic-based search method (MHSM)

Full size image

2.2 Introducing Island Algorithms

  1. 1.

    Genetic algorithm (GA) is a meta-heuristic method following the biological laws of nature. The algorithm is an intelligent search method based on the structure of genes and chromosomes and begins with a set of random answers (strings), called populations, used to construct the next population. Accordingly, the best populations have a better chance of reproduction and survival. This process is repeated until a suitable and optimal design is obtained based on the convergence criterion (Goldberg & Samtani, 1986).

  2. 2.

    Another meta-heuristic algorithm used by engineering researchers in the last decade is the Particle Community Search (PSO) method, inspired by the lifestyle of group organisms, as one of the meta-heuristic algorithms in optimal science. Like other meta-heuristic algorithms, the method uses an initial population that includes possible designs to start the optimization process. Each design in this population is known as a particle in the group. Each particle moves in proportion to the corresponding velocity in the design space. The velocity of each particle depends on the best position of the particle from the beginning to the present, as well as the position of the best particle among all the particles. Therefore, the motion of any particle in space is possible in two directions: 1. moving to the best position that the particle has been observed from the beginning until now and 2. moving to the best position that other particles have been observed from the beginning until now (Kennedy, 1997).

  3. 3.

    The Big Bang Algorithm is one of two well-known theories about how the universe began and will be ended; (1) Big Bang theory, addressing how the universe came into being, and (2) Big Crunch theory, dealing with the combination of the sinking of the universe and the end of its life. The algorithm is similar to the genetic and PSO algorithm in terms of initial population generation. Generally, it consists of two phases of the Big Bang and Big Crunch. The production stage of the initial population is called the Big Bang phase, in which the population is randomly and uniformly distributed over the entire search space. Once the initial population is generated, the fitness level of each volunteer will be calculated according to the objective function. After the Big Bang phase, a contraction phase is applied by a contraction operator, during which a parameter called the Center of Mass is obtained by considering the fitness and current position of each candidate (Erol & Eksin, 2006).

  4. 4.

    In the charged particle search algorithm, the optimization of the algorithm is performed according to the laws of charged particles and Newtonian Mechanics. For this purpose, each vector of the design variables is considered a charged particle in the design space. Each particle has an electric field, which is defined by the amount of electric charge and based on Each particle is then affected by the electric field of other particles in proportion to the amount of electrical force caused by other particles, moves in the design space, and thus acquires a new position. The manner particles move in the exploration space is based on Newton's laws of motion. In this way, each particle moves towards a new position based on its previous position, as well as the speed and acceleration caused by the force exerted by other particles to obtain the best position in space. The best position for each particle is the place that has the most electric field due to its position. Accordingly, each particle, together with other particles, tries to reach its best location (Kaveh & Talatahri, 2010).

2.3 Formulation of the Optimization Problem in the Islands of the Multi Meta-heuristic Algorithm for Analysis and Design

In this research, the optimization of bracing topology is investigated according to the meta-heuristic island algorithm when the design variables are distinct and must be selected from the available “section” list, “node coordinates”, and “one of the convergent bracing type including multi-story X-bracing or X bracing”. The formulation of the problem is defined as follows:

Finding “the optimal coordinate and arrangement” appropriate for each bracing type in a steel frame with certain dimensions and spans.

Problem parameters:

Node coordinates for the two sides of bracing (Eq. 1), Cross-section (Eq. 2) and Bracing type (Eq. 3).

$$\left[ {\left( {X_{1} ,Y_{1} } \right),\left( {X_{2} ,Y_{2} } \right)} \right] = \left[ {\left( {x_{1} ,y_{1} } \right),\left( {x_{2} ,y_{2} } \right),\left( {x_{3} ,y_{3} } \right), \ldots \ldots \ldots \left( {x_{Nos} ,y_{Nos} } \right)} \right]^{T}$$
(1)
$$\begin{aligned} & \left( {x_{i} ,y_{i} } \right) \in S;\quad i = 1, \ldots Nos \\ & \left[ A \right] = \left[ {a_{1} ,a_{2} , \ldots \ldots ,a_{Nos} } \right]^{T} ;\quad a_{1} \in S;\quad i = 1, \ldots Nos \\ \end{aligned}$$
(2)
$$\left[ {BT} \right] = \left[ {b_{1} ,b_{2} , \ldots ..,b_{Nos} } \right]^{T} ;\quad b_{1} \in S;\quad i = 1, \ldots ,Nos$$
(3)

Finally, the analysis will be performed using software OpenSees after the selection and primary allocation of the above three parameters. Then the constraints of the problem are controlled and the eligible designs are entered as the new population to the minimizing phase of the objective function.

A general flowchart of how to do these steps (for each island) is shown in Fig. 3. In explaining this flowchart, it can be said that in this method, first the model is defined in Opensees software and the model defined by MATLAB (software with matrix approach) is created. The optimization process is started and the initial sections are assigned to the members. The Opensees program is then summoned and analyzes the prototypes using the finite element method. The results are entered into the optimization process as data and this process is repeated until all the optimization iterations are done. Finally, the optimized structure is obtained.

Fig. 3
figure 3

General optimization flowchart for every island

Full size image

2.4 Definition of Objective, Pseudo-Objective, and Penalty Functions in Multi Meta-heuristic Algorithm Islands

The weight of structure for the optimization process of the objective function in this study has been considered as follows.

$$F\left( A \right) = \mathop \sum \limits_{1}^{Ne} \rho_{i } l_{i} a_{i}$$
(4)

where Ne is the number of structure members, \(\rho_{i}\) is density of materials for each member, \(l_{i}\) is the length of each member, and \(a_{{i{ }}}\) is the cross-section of each member.

The following relation (Eq. 5) has been also used for the modified objective function based on the objective and penalty functions.

$$\phi \left( A \right) = F \left( A \right) \left[ {1 + K\left( {\mathop \sum \limits^{nlc} \mathop \sum \limits_{q = 1}^{Q} \max \left[ {0,G_{q} } \right]} \right)} \right]$$
(5)
$$k = k_{j} \times \ln \left( {j + 1} \right);\quad j = 1, \ldots nk$$
(6)

where F(A) is the objective function of optimization problem, which has been defined in Eq. 4. \(G_{q}\) is the imperfection level of constraints and Q is the total number of constraints governing the problem. K is the penalty constant, \(k_{j}\) is a constant quantity of each migration range for total number of nk, and j is the counter of each migration interval and nlc is the number of loading compounds in the process of optimization designing.

2.5 Introducing Frames, Distribution of Seismic Force, Loading and Analysis Type

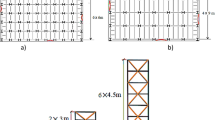
In this section, the investigating samples are two-dimensional six-story structures (height of 19.2 m) with 5 four-meter spans, 4 five-meter spans, and 3 six-meter spans, two-dimensional nine-story structures (height of 28.8 m) with 6 five-meter spans, 4 six-meter spans, and 4 seven-meter spans, and two-dimensional fifteen-story structures (height of 48 m) with 10 five-meter spans, 8 six-meter spans, and 7 seven-meter spans, representing low-, mid-, and high-rise structures.

It should be noted that the optimization process in this research was not limited to a specific structural plan. The frames were dimensioned by considering various height-to-width (h/b) ratios independent of the structural plan. It is also worth mentioning that the forces applied to the structure, which are inherently dynamic, were statically equivalent. Undoubtedly, this method is approximate and was chosen to simplify the analysis operation. Although the method seems very simple, it is based on dynamic theories. It has been observed that the buildings designed in this way have relatively good resistance and ductility against earthquakes (Paz & Leigh, 2004). Therefore, this method is recommended as a standard method in seismic design regulations enforced by different countries. In general, static analysis methods are suitable when the response of the structure during an earthquake is mainly due to the vibration of the first method.

The dead and live loads of stories are broadly distributed into the beams in stories and lateral loads are distributed into frames according to Eq. 7 (ASCE, 2013).

$$F_{i} = \left( {F_{b} - F_{t} } \right) \frac{{z_{i}^{k} m_{i} }}{{\mathop \sum \nolimits_{j = 1}^{N} z_{j}^{k} m_{j} }},i = 1,2,...,N$$
(7)

where \(z_{i}\) is the height of ith level (distance between the ceiling of ith story and the base level), \(m_{i}\) is the equivalent mass of ith story including the real mass of the ith story added by a part of live loads, N is the number of stories (above the base level), k is an exponent calculated based on the main period of the structure, \(F_{t}\), also known as whipping force, is the additional lateral force applied on the last level (Nth) and can be calculated by specific relations,\(F_{b}\) is the value of base shear, and \(F_{i}\) is the lateral force in the level of the ith story (not-roof).

The value of the base shear force and the fundamental period in Eq. 7 is equal to:

$$F_{b} = C_{s} .W$$
(8)
$$T = 0.0488H^{\frac{3}{4}}$$
(9)

Description and values for the parameters in Eq. 7 and Eq. 8 are presented in Table 1 and Table 2. The period in Eq. 9 is assigned to specific convergent bracing and simple frames (the frames studied in this research). Parameter H is the height of the story.

Table 1 Relations governing some parameters of Eq. 7
Full size table
Table 2 Description of the parameters in Eq. 8 in the seismic regulations of the United States (ASCE, 2013)
Full size table

It is necessary to mention that the seismicity zone has been considered in D area of the regulations of the United States (equivalent to I-group seismicity of Iran). The site has been considered in C-group (very-dense soil) .

A combination of the following loads was used for optimization according to the regulations (ASCE, 2013).

$$U = {1}.{2}D \pm {1}E + L$$
(10)
$$U = 0.{9}D \pm {1}E$$
(11)
$$U = {1}.{2}D + {1}.{6}L$$
(12)

Uniform live and dead loads were considered equal to Ll = 200 kg m−2 and Dl = 550 kg m−2, respectively and the amount of the compressive strength of steel has been considered equal to 2400 kg m−2.

2.6 Definition of Constraints in Multi Meta-Heuristic Algorithm Islands

To minimize the objective function, the constraints of frequency, design, drift, bracing position, and the allowed values for the tensile force of braces have been considered by the multi meta-heuristic algorithm in the optimization procedure. These constraints are mentioned in detail in the following paragraphs.

2.6.1 Design Constraint

In the regulations for designing steel structures based on LRFD, some limitations have been set for the resistance of each element, the arrangement of elements, and the stresses of each element. The limitations related to the resistance of columns are investigated having the interactive effect of axial force and bending moment in the same column. In a way that if the amount of tensile or compressive axial force in the column is violating the values in regulations and show a stress ratio above one, a penalty is considered for the column. This Eq. for the frames of research is defined as following (No. 10, 2013).

$$\frac{{P_{u} }}{{\phi_{c\left( t \right)} P_{n} }} \le 1.0$$
(13)

There is another limitation considered in the columns of frames such that the sections of columns designed for lower stories should be larger than the sections of columns in the upper stories.

It is worth noting that the bending moment is decisive in beams. Considering that the beams have no part in the lateral load, they can be designed according to maximum gravitational load bending moment. Having the above description, it can be concluded that the cross-section of beams will remain constant during the optimization process. Equation 14 is proposed to design the beams in a bending state.

$$\frac{{M_{u} }}{{\phi_{b} M_{n} }} \le 1$$
(14)

In the above relation, \(P_{u}\) is the ultimate limit of compressive strength, \(P_{n}\) is the nominal strength of the section (According to Eqs. 15 and 20), \(\phi_{c\left( t \right)}\) is the strength factor in pressure or tension, which equals 0.9, \(M_{u}\) is the ultimate limit of bending strength, Mn is the nominal bending, and \(\phi_{b}\) is the strength factor, which is equal to 0.9 for bending.

The nominal compressive strength for braces and columns is calculated according to the following equation (Eq. 15).

$$p_{n} = F_{cr} A_{g}$$
(15)

where \(\phi_{c}\) is the strength reduction factor, \(A_{g}\) is the total cross-section of bracing, \(F_{cr}\) is the compressive stress from bending buckling and is computed according to Eqs. 16 and 17.

$$\frac{{F_{y} }}{{F_{e} }} \le 2.25 \to F_{cr} = \left[ {0.658^{{\frac{{F_{y} }}{{F_{e} }}}} } \right]F_{y}$$
(16)
$$\frac{{F_{y} }}{{F_{e} }} > 2.25 \to F_{cr} = 0.877F_{e}$$
(17)

In the above two relations, \(F_{y}\) is the yield stress of bracing and \(F_{e}\) is the elastic buckling stress which are calculated according to following Eq.

$$F_{e} = \frac{{\pi^{2} E}}{{ \left( \frac{KL}{r} \right) ^{2} }}$$
(18)

where \(\left( \frac{KL}{r} \right)\) is the slenderness ratio of the member, and the maximum slenderness is limited to 200.

Of course, if the columns are IPE or IPB section, the compressive stress from bending buckling must also be checked based on elastic buckling according to Eq. 19. (torsional buckling control)

$$F_{e} = \left[ {\frac{{\pi^{2} EC_{W} }}{{\left( {K_{Z} L} \right)^{2} }} + GJ} \right]\left( {\frac{1}{{I_{X} + I_{Y} }}} \right)$$
(19)

where \(c_{w}\) is the warping constant, \(GJ\) is the torsional rigidity, and \(K_{Z}\) is the effective length factor of torsional buckling.

In the case of braces and columns under tension, the nominal tensile strength takes the following forms.

$$p_{n} = F_{y} A_{g}$$
(20)

The same parameters mentioned in Eq. 20 are also defined for braces and columns under pressure, except that the forces are in the tensile state.

2.6.2 Drift Constraint

The allowable drift of stories is as Eqs. 21 and 22 according to the loading standards of the United States (ASCE, 2013).

$${\Delta }_{a} = 0.02H$$
(21)

The method for calculating the drift of story in the regulations is obtained from the following Eq.

$${\Delta } = \frac{{C_{d} \delta_{xe} }}{{I_{e} }}$$
(22)

where \({\Delta }\) is the designing drift of the stories that shall not exceed the \({\Delta }_{a }\), \(\delta_{xe}\) is the horizontal drift of the story, and \(C_{d}\) is the drift amplification factor, which is equal to 5 in simple frames and specific convergent bracing. \(I_{e}\) is also the importance factor of building, which is equal to 1.

2.6.3 Frequency Constraint

The decrease of vibration amplitude (which causes stress and deflection in structure) and the prevention of the occurrence of resonance phenomenon in the dynamic response of the structure are among the reasons for limiting the vibration frequencies of the structure. Large drifts occur in structure due to resonance phenomenon and this factor leads to the destruction of the structure. The total response of a system with n degrees of freedom can be computed by turning the system to n systems with one degree of freedom and computation of the responses. By considering the harmonic force \({ }F_{0} \sin \overline{\omega }t\) for a system with one degree of freedom, the following response is obtained according to Eq. 23 by considering structure damping:

$${\text{U}} = \left[ {\frac{1}{{1 - \left( {\frac{{\overline{\upomega } }}{\upomega }} \right) ^{2} }}} \right]{\overline{\text{u}}}\sin \overline{{\upomega {\text{t}}}}$$
(23)

where \(\overline{\omega }\) is the load frequency and \(\upomega\) is the vibration frequency of the structure. If \(\upomega = \overline{\upomega }\), the term inside the bracket, which is the dynamic amplification factor, tends to infinity. In this case, the resonance phenomenon occurs in the structure and causes large deformations in the structure. Having that the used materials don't have enough resistance for these large deformations, the structure will disrupt (Paz & Leigh, 2004). Generally, the frequency constraint can be defined as follows:

$$1 - \omega_{i} \left( X \right)/\upomega _{{\acute{{\rm I}}}} \le 0\quad i = 1, \ldots ,\omega$$
(24)

where i is the \(\upomega _{{\acute{{\rm I}}}}\)th dominant frequency of earthquake and \(\omega_{i}\) is the ith frequency of the structure.

To constrain the frequency of the first mode in the studied frames in this paper, Table 3 is prepared, which includes three accelerograms for six-, nine-, and fifteen-story frames, and the frequency content of these accelerograms will be investigated. The dominant period of each accelerogram, peak ground acceleration, peak ground velocity, and duration of high ground motion for the suggested list (accelerograms of Kocaeli, Turkey, Zarand, Iran, and Koli Bonyabad, Iran) are presented in this table. Finally, concerning the accelerograms in Table 3 and inserting the dominant period, the frequency constraint was considered as follows: the frequency of the first mode of the structure must be above 1.5 Hz for 6-story frames, above 1.2 for 9-story frames, and above 1.11 Hz for 15-story frames. \((\omega_{1,9s} \ge 1.2\;{\text{Hz}},\;\omega_{1,6s} \ge 1.5\;{\text{Hz and}}\omega_{1,15s} \ge 1.11 Hz).\)

Table 3 Data of suggested accelerogram list
Full size table

2.6.4 Constraint of Allowable Tensile Force in Braces

The braces must be considered so that a minimum of 30% and a maximum of 70% lateral force of the axis in the direction of loading can be tolerated in the tension.

As an approximate method, it can be said that the inequality in Eq. 25 must be satisfied.

$$0.3 < \frac{T}{T + C} < 0.7$$
(25)

where

$$T = \sum (p_{nt} \cdot \cos \theta ) = \sum (\cos \theta \cdot F_{y} \cdot A_{g} )$$
(26)
$$C = \sum (p_{nc} \cdot \cos \theta ) = \sum (\cos \theta \cdot F_{cr} \cdot A_{g} )$$
(27)

In the above Eqs., T and C are the sums of nominal tensile strength values for tensile braces and nominal compressive strength for compressive braces. \(\uptheta\) is the angle of braces with a horizontal line, and the other parameters have been defined in the section of design constraint.

2.6.5 Constraint of Bracing Position in Spans and Frame Height

To avoid irregularities in the height of the frames and especially the irregularity of cutting the lateral beaing system, the position of braces is constrained so that in the first story, the span to which the bracing is assigned takes the bracing for frame height.

3 Validation of the Studied Algorithm

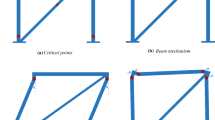
The obtained results by Safari and Maheri (2006) was used for the validation of the procedure in this research. In the above-mentioned study, two frames with 4 and 8 stories have been considered with the following geometry, which the position of X-bracing has been optimized in them using the genetic algorithm. The height of stories and the length of spans are 3 and 4 m, respectively. In this study, the objective function was considered as Eq. 28.

$${\text{Minimize:}}\;W = f\left( x \right)$$
(28)

The samples in Fig. 4 have been optimized in this research with the help of the multi meta-heuristic algorithm to be able to guarantee the validation of OpenSee modeling and also the implementation of the optimization algorithm. The results of optimization for the studied frames by the method of this research will be presented in the following (Fig. 5).

Fig. 4
figure 4

The studied samples in validation paper (Safari & Maheri, 2006)

Full size image
Fig. 5
figure 5

Optimal sections and position of braces in 4-story and 8-story frames of Safari and Maheri

Full size image

The results extracted from Table 4 shows that the codes and analyzing program are well written and implemented.

Table 4 Comparison between the optimization results of the multi meta-heuristic algorithm and genetic algorithm for the selection of optimal bracing position
Full size table

4 Weight and Typing of the Section in the Optimized Frames

In the section of comparing and calculating the weight of frames, Since the structural frame is from the type of simple building frame and the beams are of a simple type with hinge connections. Therefore, beams are designed only under the influence of gravitational loads and the forces from lateral loading have been ineffective in the design of the beams. Hence, the sections of beams have been considered equal (in all bracing arrangements of similar frames) and only the columns and braces are optimized for the distributed forces. Thus, the sum of the weights of columns and braces has been considered to compare the weight changes.

5 Results and Discussion

5.1 Results of Modeling and the Section List of the Optimized Elements

In the results, the optimization of the mentioned frames will be presented in the form of a diagram and a figure (Figs. 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 and 23). In general, it should be noted that in most standards (AISC 360-16; No.10, 2013), the focus is more on the strength limit state (strength limit state). Furthermore, earthquake control in service state or service limit state is mainly decisive in tall structures (with a height of more than 50 m and more than 15 floors which does not apply to the frames studied in this research). In this research, the frames were designed under different load combinations based on the load and resistance factors. The primary goal was to optimize the bracing members in this state. It should be noted that the level of performance obtained in the frames, due to compliance with the rules of analysis in ASCE 7 standard, is consistent with the level of life safety (ASCE, 2013).

Furthermore, the number of braced spans in the frames was specified according to the codes obtained from MATLAB program and OPENSEES software. For example, in a 6-story frame with three spans, the weight of the frame with one braced span (one of the optimal designs) was more than that of the frame with two braced spans. The reason is the determinant of the frequency constraint. In this way, in a frame with a braced span, elements with a higher cross-section are selected to meet the frequency limit, leading to an increase in the weight of the frame. Accordingly, among the optimized design sets, a frame with two braced spans was selected by the program as the final optimal design.

Finally, As it was mentioned in the previous paragraphs, this research investigates 9 frames with two types of braces for the mentioned targets. Indeed, using the MHSM algorithm in this research, 18 categories of frames have been optimized and their results have been extracted. It is worth noting that 6 categories of 9-story frames are repeated for the heuristic PSO algorithm to compare the algorithm of this research with it. The section lists of the beam, column, and bracing elements used in optimization have been extracted for 6-story and 9-story frames from the Stahl table (series UPN, IPB, IPE). The list of the beam and bracing sections existing in the Stahl table (series UPN, IPB) have been used for 15-story frames, and the section list of columns includes a hollow section made with dimensions of 20, 30, 40 and 50 cm (with specified sheet thickness in the results of frames). To increase accuracy in calculating the objective function, one type of bracing for each story and one type of column for each axis have been considered. The typing of columns with height has been also performed for every two categories.

Fig. 6
figure 6

The optimal sections, position, and convergence history of X-bracing in 3-spans 6-story frame

Full size image
Fig. 7
figure 7

The optimal sections, position, and convergence history of multi-story X-bracing in 3-spans 6-story frame

Full size image
Fig. 8
figure 8

The optimal sections, position, and convergence history of X-bracing in 4-spans 6-story frame

Full size image
Fig. 9
figure 9

The optimal sections, position, and convergence history of multi-story X-bracing in 4-spans 6-story frame

Full size image
Fig. 10
figure 10

The optimal sections, position, and convergence history of X-bracing in 5-spans 6-story frame

Full size image
Fig. 11
figure 11

The optimal sections, position, and convergence history of multi-story X-bracing in 5-spans 6-story frame

Full size image
Fig. 12
figure 12

The optimal sections, position, and convergence history of X-bracing in 4-spans 9-story frame

Full size image
Fig. 13
figure 13

The optimal sections, position, and convergence history of multi-story X-bracing in 4-spans 9-story frame

Full size image
Fig. 14
figure 14

The optimal sections, position, and convergence history of X-bracing in 5-spans 9-story frame

Full size image
Fig. 15
figure 15

The optimal sections, position, and convergence history of multi-story X-bracing in 5-spans 9-story frame

Full size image
Fig. 16
figure 16

The optimal sections, position, and convergence history of X-bracing in 6-spans 9-story frame

Full size image
Fig. 17
figure 17

The optimal sections, position, and convergence history of multi-story X-bracing in 6-spans 9-story frame

Full size image
Fig. 18
figure 18

The optimal sections, position, and convergence history of X-bracing in 7-spans 15-story frame

Full size image
Fig. 19
figure 19

The optimal sections, position, and convergence history of multi-story X-bracing in 7-spans 15-story frame

Full size image
Fig. 20
figure 20

The optimal sections, position, and convergence history of X-bracing in 8-spans 15-story frame

Full size image
Fig. 21
figure 21

The optimal sections, position, and convergence history of multi-story X-bracing in 8-spans 15-story frame

Full size image
Fig. 22
figure 22

The optimal sections, position, and convergence history of X-bracing in 10-spans 15-story frame

Full size image
Fig. 23
figure 23

The optimal sections, position, and convergence history of multi-story X-bracing in 10-spans 15-story frame

Full size image

5.2 Comparing the Optimal Results in 9-Story Frames with the MHSM Algorithm and the PSO Algorithm

As shown in Table 5, 9-story frames with X- and multi-story X-bracings have lower weights in the MHSM algorithm than in the PSO algorithm. This subject shows that the research algorithm has an appropriate performance in optimization than the meta-heuristic algorithm. The superiority level of convergence in the MHSM algorithm can be also observed by comparing convergence diagrams. In all of the 9-story frames of this research, the PSO algorithm reached the convergence almost 50 repetitions after the MHSM algorithm (a convergence mean of 148 repetitions for MHSM algorithm and 197 repetitions for PSO algorithm). The weight of frames at the beginning of optimization was 40% higher in the PSO algorithm on average compared to the MHSM algorithm. The reason is that the main population in the multi meta-heuristic algorithm has been divided into smaller sub-populations called island. Each island is responsible for the optimization of its members and the convergence velocity increases due to the smallness of the population number.

Table 5 Comparing the optimal weight of frames in MHSM and PSO algorithms
Full size table

5.3 Comparing the Optimal Results in the Frames with X-Bracing and Multi-story X-Bracing Arrangements

As shown in Table 6, multi-story X-bracing in all of the studied frames of this research has better performance considering the weight (economy-efficient design) and lowering seismic weight.

Table 6 Comparing the optimal weight of the frames with X- bracing and multi-story X-bracing by MHSM algorithm
Full size table

Figure 24 shows the weight differences in the studied frames. It can be observed in the diagrams that there is no significant weight difference in the frames that have more spans and short spans; but in the frames that have larger spans and are less in number, the weight difference between the two types of bracing is much greater.

Fig. 24
figure 24

The weight difference of the frames with X-bracing in comparison with multi-story X-bracing

Full size image

It can be concluded by investigating the results that the majority of the weight difference in high-rise and low-rise frames between the two bracing groups is due to lower column weight of multi-story X-bracing frames than X-bracing frames. In mid-rise frames, both column and brace weights have been influential, resulting in the (weight) superiority of multi-story X-bracing frames.

6 Conclusion

This study obtained the optimal design for low-, mid-, and high-rise frames with different numbers of spans and two types of bracing arrangement (X-bracing and multi-story X-bracing that is the combination of inverted V- Bracing and V- Bracing) using the multi meta-heuristic-based search method (MHSM). At the same time, a comparison with the particle swarm optimization (PSO) algorithm was performed. The reason to use and select the multi-story X-bracing system in this study is that this system has several priorities to the V- and inverted-V bracing systems in seismic aspects. As there is no unbalanced vertical force from compressive and tensile braces to beam in multi-story X-bracing frame (or there is a trivial force), no soft story can be formed due to beam collapse and story damage. However, beam damage in a story is possible in V- and inverted-V bracing systems due to the existence of this vertical unbalancing force. The main findings are as follows:

  1. 1.

    According to the results for the optimal weight of the frames in the multi meta-heuristic algorithm and comparing them with the optimal weight of frames in the particle swarm algorithm, it can be observed that the multi meta-heuristic algorithm used in this research has a more appropriate convergence trend than the other heuristic algorithms.

  2. 2.

    The effect of the parameters of meta-heuristic algorithms plays a key role because of the high number of design variables and large search space. The multi meta-heuristic algorithm reduces the impact of parameters and the relations governing the operation, as well as effectively searches through designing space until reaching the appropriate responses.

  3. 3.

    Having the results of this study, the multi-story X-bracing frame (the combination of inverted V-Bracing and V-Bracing) has economic and engineering priorities in comparison with the X-bracing frame. The Lower weight of multi-story X-bracing frame decreases the force on column hinge welding, story drift, overturning resistance moment of structure, and base shear force compared to X-bracing frame.

  4. 4.

    Considering that resonance of structure occurs when the frequencies of structure and load are equal, limiting the structure frequencies in the design can be an appropriate step to prevent probable damages due to an earthquake with the related characteristics. Even with a rather weak earthquake, which its frequency randomly gets equal to the vibration frequency of the structure, a resonant state in the structure with large deformations can occur (which the materials cannot tolerate), resulting that the building may be destroyed. Controlling frequency and limiting it to some specific value in the studied frames led to lower vibration of frames, resulting to minimum stress and deflection in structure.

  5. 5.

    About the optimal position of braces in the studied frames, it can be said with certainty that the best place to put braces is in the middle spans of frames and adjacent to each other. The reason is that the weight of the structure increases for satisfying the constraint of frequency if the spans are located with long distance in bracing. According to the results of this study, it can be suggested to put a minimum of two spans in low- and mid-rise frames and a minimum of four spans in high-rise frames for bracing.