Optimal design of seismic retrofitting of RC frames with eccentric steel bracing

Abstract

This paper focuses on optimal design for dissipative steel bracing in seismic retrofitting of gravity load designed RC frame buildings. An optimized iterative force/strength-based design procedure is presented, for simultaneous yielding of bracing of all storeys, in order to induce an global damage mechanism in the building which maximizes the hysteretic damping effect. The procedure complies with the capacity design rule, whereby the bracing system enters the plastic range before the existing RC frame. The iterative design procedure of the system is applied here to a regular RC shear frame, with various design behavior factors.

1 Introduction

In most cases, existing RC frame structures were not designed with anti-seismic criteria, but only gravity loads (GLD = gravity load design RC frames). When subjected to seismic action, these structures normally develop brittle failure, often located in a few structural elements, and mainly due to insufficient confinement of members (beams, columns, joints), sliding of longitudinal reinforcement bars of beams in joint areas, lap splicing of longitudinal reinforcement bars of columns in potential hinge areas (e.g. Kunnath et al. 1995; Aycardi et al. 1994; Bracci et al. 1995; El-Attar et al. 1997).

Various types of intervention can improve the seismic behavior of such structures (Fukuyama and Sugano 2000). They are classified as global or local interventions (Moehle 2000). Local interventions increase the ductility of elements, so that the modified displacement capacity of the structure becomes compatible with demands made on it. Global interventions include introducing new structural elements to produce a stiffer, stronger structure and reducing displacement demand, thus making such demand compatible with the original displacement capacity. Retrofitting of these structures is also important from the viewpoint of preserving historical and artistic heritage buildings, as many RC frame buildings classified as “industrial archaeology” and “pioneering concrete buildings”, are listed (Nelva and Signorelli 1990).

This work focuses on an global intervention with eccentric bracing, already amply discussed in the literature (e.g. Ghobarah and Abou Elfath 2000; Barecchia et al. 2006; Perera et al. 2004).

Ghobarah and Abou Elfath (2000) studied the performance of a non-ductile GLD three-storey office building rehabilitated with eccentric steel bracing. Two cases were analysed with a finite element model. Results showed that the link deformation angle can substantially limit inter-storey drift. Distributing eccentric bracing over the height of the building was found to have a significant effect on the characteristics of the plastic mechanism developing under lateral seismic loads. The above authors recommended that such distribution of bracing strength over the height of the building should be selected for uniform distribution of storey drift.

In the ILVA-IDEM research project headed by F.M. Mazzolani (Barecchia et al. 2006), numerical and experimental tests on RC frames with eccentric Y bracing were carried out. The efficiency of the technology used was verified, highlighting the importance of the over-resistance of bolted connections to prevent premature shear cracking of the bolts connecting diagonals and links.

Perera et al. (2004) proposed a seismic retrofitting technique for infilled masonry RC frames, based on replacing infill panels with eccentric bracing with vertical shear links. Performance was verified by experimental tests and numerical analyses.

In all these research works (e.g. Ghobarah and Abou Elfath 2000; Barecchia et al. 2006; Perera et al. 2004), the shear strength of RC elements and joints appears to be sufficient to withstand seismic action, so that the only parameter to be checked for seismic improvement was link rotation at failure (Ghobarah and Abou Elfath 2000). However, this does not often occur, since the shear strength of beams, columns and joints in existing frames is very limited (e.g. Kunnath et al. 1995; Aycardi et al. 1994; Bracci et al. 1995; El-Attar et al. 1997) and brittle failure may occur before yielding, due to the bending moment. This means that the strength and stiffness of the added bracing system, controlled by the design behavior factor, are crucial to protect existing frames.

2 Main research topics

When retrofitting existing RC frames, it should be recalled that their resistance and ductility are limited and often cannot be changed, unless local confinement is carried out. Introducing braces between frame spans also provides greater strength and stiffness, without changing the failure mode or ultimate displacement capacity of existing RC frames (Badoux and Jirsa 1990).

The bracing system must be sufficiently stiff, strong and ductile, in order to prevent brittle failure. The bracing acts as a structural fuse by producing a global failure mechanism in the system before it occurs in the existing frame (early and contemporary yielding of links to all floors) (Mastrandrea and Piluso 2009), and ensures sufficient global stiffness and strength to prevent brittle failure in existing GLD frames (e.g. Kunnath et al. 1995; Aycardi et al. 1994; Bracci et al. 1995; El-Attar et al. 1997).

In this work, a traditional force/strength-based design procedure was created to find the optimal retrofitting solution by means of an iterative linear elastic procedure.

Introducing bracing into the spans of existing RC frames modifies the magnitude and distribution of inter-storey stiffness, and thus makes the design process iterative. By setting a constrained optimization problem, as already suggested in the technical literature (Singh and Moreschi 2003), the bracing design is carried out, and ductile and global damage failure mechanism to the retrofitted structure is pursued.

An essential aspect in the design of a bracing system is the choice of the design behavior factor, which defines initial elastic stiffness and strength.

When this design behavior factor, here called $q^{d}$, is increased, the design forces for which the bracing is sized decrease, so that the bracing becomes more flexible and less effective in protecting the structure. The fraction of seismic shear force remaining in the frame increases with the $q^{d}$ adopted and, beyond a maximum acceptable value, and bracing is not sufficient to preserve the existing frame from earthquake-induced damage.

As the optimal solution is a compromise between ductility and resistance, choosing the most suitable design behavior factor is not an easy task. The optimal factor is the maximum of feasible values, i.e., by minimizing inter-storey drift, it verifies all necessary checks and restraints, ensuring minimal invasiveness to the frame at minimal cost.

Once the design procedure has produced the optimized solution, the $q^{d}$ adopted must be verified as compatible with link rotation capacity, allowable chord rotations of columns and beams, and the strength of the existing frame. This a posteriori assessment is a necessary critical step in the sizing process, as it requires static or dynamic non-linear analyses.

Theoretically, compliance with conditions such as shear capacity, allowable chord rotation, joint capacity, etc., may already be included in the iterative design optimization process. As these quantities closely depend on the non-linear behavior of the retrofitted structure, they are easier to check during the final verification phase based on non-linear analyses (whereas iterative design is conducted only by means of linear elastic calculations).

3 Design criteria for links

Research on eccentric bracing began in the late 1970s with the work of Roeder and Popov (1978). Eccentric bracing with shear inelastic performance for new steel constructions was studied by Popov and Malley (1983, 1984), Hjelmstad and Popov (1983, 1984), Kasai and Popov (1986a, b) and Engelhardt and Popov (1988, 1989a, b).

Modern anti-seismic codes cover the application of eccentric bracing systems to newly constructed steel frame buildings, requiring capacity design procedures for the various elements (links, diagonals, columns, beams, joints). In particular, by means of the formulas in section 6.8, Eurocode 8—Part 1 (2005a) establishes adequate over-resistance to non-dissipative elements and homogeneous yielding of links, for optimal dissipative behavior of the whole structure.

The bracing system must be stiff enough to withstand earthquake action and consequently reduce seismic effects in the existing frame. The design must be consistent with the strength, stiffness and ductility of the links, and diagonal elements and their connections must be properly over-designed, as specified in Mastrandrea et al. (2002).

It should be noted that, since eccentric bracing is added a posteriori to the existing frame, it is only affected by horizontal seismic actions; gravitational loads are still sustained exclusively by the frame itself.

The “inverted Y” bracing configuration can easily be used for seismic upgrading of existing RC frames, as it does not require existing beams to act as structural fuses, unlike other possible types (K, D, V, etc.) (Eurocode 8—Part 1, 2005a).

In Y bracing subjected to horizontal actions, the fixed-hinged boundary condition of the link (Fig. 1d) determines generalized stress (Fig. 1a–c). The absence of axial force in the links, together with suitable stiffeners on the link web to avoid compression buckling, provides large, stable, hysteretic dissipation loops (Kasai and Popov 1986a).

Fig. 1

a–c Generalized stresses in a Y-braced frame; d link restraint scheme; e link section

According to their length and cross-section, the links may operate in various modes:

• short links with shear yielding;

• intermediate links, with interaction between shear force and bending moment;

• long links with bending yielding.

The constancy of shear force indicates that short links should be used (Kasai and Popov 1986b), so that shear yielding spreads throughout the element. Short links also provide higher stiffness (Hjelmstad and Popov 1984), which is a mandatory characteristic for bracing efficiency when it works in parallel with the existing RC structure.

Section 6.8.2 of Eurocode 8—Part 1 (2005a) provides the formulas for link design. In particular:

• inequality, ensuring the condition of early shear yielding compared with that of bending yielding:

  $$\begin{aligned} e < e_S = 0.8 (1+\alpha ) M_p / V_p \end{aligned}$$

  (1)

  where $\alpha$ is the ratio between bending moments at the ends of links, determined by the structural detail of the connection with diagonals ($\alpha = 0$ when a perfect hinge is assumed at the bottom, as in Fig. 1d), $M_p =f_y bt_f (d-t_f )$ is the yielding bending moment, and $V_p =\left( {f_y /\sqrt{3}} \right) t_w \left( {d-t_f } \right)$ is yielding shear force (Fig. 1e);

• respect for ultimate link rotation capacity:

  $$\begin{aligned} \theta _p \le \theta _{pR} =0.08\, rad \end{aligned}$$

  (2)

  which experimental tests (e.g. Kasai and Popov 1986a; Engelhardt and Popov 1988) have demonstrated can be achieved when suitable full height stiffeners are provided. End stiffening plates thicker than $0.75 t_w$ and 10 mm, must be placed on both sides of the web, with intermediate stiffeners arranged in constant steps not exceeding a value of $({30t_w -d/5})$, and must be thicker than $t_w$ and 10 mm. If $d<600$ mm, they must be placed on only one side of the web link. The practical design criteria reported in Eurocode 8—Part 1 (2005a) come from experimental tests carried out by Engelhardt and Popov (1988) and Kasai and Popov (1986a).

4 Interaction between frame and bracing: SDOF system

Applying capacity design rule to retrofitted RC frames with eccentric bracing means that links act as structural fuses, safeguarding the integrity of the existing structure.

In order to clarify this concept, let us consider the single degree of freedom system (SDOF; Fig. 2a), subjected to horizontal seismic action. The system is composed of the RC frame, two steel diagonals, and one vertical steel link. The complex can be modelled in the elastic field as a mass connected to the ground by two springs and one damper. The two springs with stiffness $K^{d}$ and $K^{l}$ (i.e., the diagonals and the structural fuse) are arranged in series (Fig. 2b). They give the equivalent stiffness of bracing $K^{b}=\left( {K^{l}K^{d}} \right) /\left( {K^{l}+K^{d}} \right)$, which is arranged in parallel with spring $K^{f}$ representing the frame. The total stiffness of the system is therefore $K^{f+b}=K^{f}+K^{b}$.

Fig. 2

System with a single degree of freedom

Because of the increased stiffness caused by the bracing system, the structure period is reduced and becomes:

$$\begin{aligned} T^{f+b}=T(K^{f+b})=T^{f}\cdot \sqrt{{K^{f}}/{K^{f+b}}} \end{aligned}$$

(3)

$T^{f}=T({K^{f}})$ being the period of the frame alone.

The capacity design rule which drives the design of structural retrofitting states that the yield displacement of dissipation system $u_y^b$ must be less than that of original frame $u_y^f$ (Vargas and Bruneau 2004). To ensure effective retrofitting, it is also useful to provide stiffness at least comparable to or, even better, larger than the original value, in order to guarantee proper yielding strength. These concepts are shown in Fig. 3, in which elastic-perfectly plastic behavior is assumed for both frame and bracing. If $F_y^f ,F_y^b ,F_y^{f+b}$ represents the yield strength of the original frame, bracing, and braced system, respectively, then $F_p^{f+b} =F_y^f +F_y^b$ is the ultimate shear capacity of the global system. Although considerable bracing ductility is ensured, the ultimate displacement capacity of the global system is limited by the capacity of the original frame, i.e., $u_u^f =u_u^{f+b}$.

Fig. 3

Force–displacement

5 Linear elastic interaction between frame and bracing: MDOF system

The above approach for an SDOF system is now extended to structures with multiple degrees of freedom (MDOF systems) (Vargas and Bruneau 2006).

With no loss of generality, but in order to explain the frame–bracing interaction in a closed analytical form, let us consider a 2D frame with movable nodes and negligible beam deformability. Only the bending deformation of columns is taken into account; shear deformation is not.

With these simplifications, the kinematic of the system is reduced only to horizontal displacements of storeys, and then its number of degrees of freedom coincides with the storey number. Storeys are reciprocally uncoupled and the stiffness matrix becomes tri-diagonal.

Without the above simplifications, the stiffness matrix is much more complex, but the validity of the approach still holds. If beam deformability is not negligible (weak beams on strong pillars), analytical closed form solutions for 2D frames are still possible with a static condensation method (Chopra 1995). This can be generalized to any complex structure (3D frames), without any kinematic restrictions, with structural finite-element software to solve the static elastic equilibrium condition $[K] x = F$, where $[K]$ is the stiffness matrix, $x$ represents displacements and rotations vector, and $F$ is the external forces vector. In such a fully numerical approach, there is no specific prescription about ensuring in-plane diaphragm stiffness. Clearly, seismic retrofitting with added bracing can only be effective if sufficiently rigid diaphragms are in place, which is normally the case in RC frame structures designed for vertical loads only.

The relations between generalized stresses of characteristic elements and displacements of braced multi-storey frame stiffness are presented in closed form in the linear elastic field.

At each storey, RC frame stiffness works in parallel with the bracing system, the stiffness of which is again given by the stiffness of the links in series with the stiffness of diagonals. As shown in Fig. 4, $i$ indicates the $i$-th floor and $n$ is the total number of degrees of freedom. The global system can be subdivided into two subsystems: frame and bracing, the combined stiffness of which gives the stiffness matrix of the global system.

Fig. 4

Plane MDOF system with rigid beams

5.1 RC frame stiffness

Frame stiffness at level $i$ is given by:

$$\begin{aligned} K_i^f =\sum _{j=1}^{m_i } {K_{ij}^f } =\sum _{j=1}^{m_i } {\frac{12E_C J_{ij}^f }{h_i^3 }} \end{aligned}$$

(4)

where $E_C$ is the elastic modulus of the concrete, $m_i$ and $h_i$ are the number and height of columns at the $i$-th storey, and $J_{ij}^f$ is the inertia of the $j$-th column.

5.2 Bracing stiffness

At the $i$-th storey, the stiffness of the bracing system, i.e., the equivalent stiffness of links and diagonals working in series, is given by:

$$\begin{aligned} K_i^l&= \sum _{j=1}^{z_i } {K_{ij}^l } =\sum _{j=1}^{z_i } {\frac{3E_S J_{ij}^l }{e_{ij}^3 (1+\beta _{ij} )}}\end{aligned}$$

(5)

$$\begin{aligned} K_i^d&= \sum _{j=1}^{z_i } {K_{ij}^d } =\sum _{j=1}^{z_i } {\frac{2E_S A_{ij}^d }{d_{ij} }} \cos ^{2}\alpha _{ij} \end{aligned}$$

(6)

in which $j$ is the variable counter between 1 and $z_i$, where $z_i$ is the number of braced spans of the frame at the $i$-th storey; $\beta _{ij} =\left( {3E_S J_{ij}^l } \right) /\left( {G_S A_{\nu ,ij}^l e_{ij}^2 } \right)$ is the shear stiffness of the link; $E_S ,G_S$ are the normal and tangential elastic modulus of the steel; $J_{ij}^l ,A_{\nu ,ij}^l ,e_{ij}$ are inertia, reduced shear area and length of link, respectively; and $A_{ij}^d ,d_{ij}^d ,\alpha _{ij}^d$ are the area, length, and tilt angle of the diagonals, respectively. The global stiffness of the bracing system at the $i$-th storey is thus given by:

$$\begin{aligned} K_i^b =\frac{K_i^l \cdot K_i^d }{K_i^l +K_i^d } \end{aligned}$$

(7)

5.3 Overall stiffness and calculation of displacements and forces

The stiffness of the i-th storey of the retrofitted frame is the sum of the storey stiffness of the RC frame and braces:

$$\begin{aligned} K_i^{f+b} =K_i^f +K_i^b \end{aligned}$$

(8)

Assembling and imposing boundary conditions provides the following easy system:

$$\begin{aligned} -K_i^{f+b} \cdot x_{i-1} +\left( {K_i^{f+b} +K_{i+1}^{f+b} } \right) \cdot x_i -K_{i+1}^{f+b} \cdot x_{i+1} =f_i \quad \quad \forall i \end{aligned}$$

(9)

where $x_i$ is the displacement vector and $f_i$ is the seismic load vector, given by spectral analysis or equivalent static analysis (Eurocode 8—Part 1, 2005a).

Solving the tri-diagonal system gives displacement vector $x_i$ and, at each $i$-th level of the frame, the distortion of the $j$-th link can then be evaluated by:

$$\begin{aligned} \Delta x_{ij}^l =\frac{K_{ij}^d }{K_{ij}^l +K_{ij}^d }(x_i -x_{i-1}) \end{aligned}$$

(10)

The shear force in the link is given by:

$$\begin{aligned} V_{ij}^l =K_{ij}^l \cdot \Delta x_{ij}^l =K_{ij}^b (x_i -x_{i-1} ) \end{aligned}$$

(11)

Axial force on diagonals due to seismic action may be derived directly from shear on the link:

$$\begin{aligned} N_{ij}^d =\frac{V_{ij}^l \cdot \sin \alpha _{ij} }{\sin (\pi -2\alpha _{ij} )} \end{aligned}$$

(12)

In the beam sections where links are constrained, a discontinuity of the bending moment caused by horizontal load appears. Assuming that the braced span is symmetric, the two values of the beam bending moments to the right and left of these sections are given by:

$$\begin{aligned} M_{ij}^f =M_{G,ij}^f \pm \left[ {V_{ij}^l (e_{ij} +r_{ij} )} \right] /2 \end{aligned}$$

(13)

where $M_{G,ij}^f$ is the initial value of bending moment in the beam due to gravitational vertical loads, and $r_{ij}$ is the offset length between the beam axes and the top of the link.

6 Proposed optimal design method

6.1 Description of design process

The proposed design method (phase D) is an iterative process consisting of the following phases.

6.1.1 Phase D1: Choice of design data

Seismic and geomorphological characterization of the site yields the elastic design spectrum. Then, once design behavior factor $q^{d}$ has been chosen, design spectrum $S_d(T)$ is determined with the formulas supplied, for example, by Eurocode 8—Part 1 (2005a), section 3.2.2. Choosing design behavior factor $q^{d}$ plays a decisive role in retrofitting design, since it determines the stiffness and strength and therefore the effectiveness of bracing. In the examples proposed here, a $q^{d}$ value between 2 and $q^{d}= 6 = 5 \alpha _u /\alpha _1$ with $\alpha _u /\alpha _1 =1.2$ is assumed. The upper limit value is the highest recommended by Eurocode 8—Part 1 (2005a) (table 6.2) when designing new high-ductility steel buildings.

$$\begin{aligned} {Initialization} - k = 1 \end{aligned}$$

6.1.2 Phase D2: Assumption of initial geometry of bracing

The choice of initial geometry for bracing is fully arbitrary. For example, it may be based on seismic storey force distributions evaluated for the existing frame. It is better to use double T standard or welded profiles for links, provided they are in cross-section class 1 (Eurocode 3—Part 1-1, 2005). For diagonals, any type of profile may be used, but they must be designed to remain elastic and without instability.

6.1.3 Phase D3: Calculation of seismic forces

With initial geometry $k = 1$, as defined in phase D2, spectral analysis is performed with design spectrum $S_d \left( T \right)$. It is then possible to calculate storey shear force $V_i^k$. The distribution of storey forces is then determined:

$$\begin{aligned} f_i^k&= V_{i+1}^k -V_i^k\end{aligned}$$

(14)

$$\begin{aligned} \bar{{F}}^{k}&= \left[ {f_i^k } \right] ^{T} \quad \quad i=1,\ldots ,n \end{aligned}$$

(15)

These formulas only hold for regular structures with dominant first vibration mode, for which spectral analysis can be replaced by equivalent static analysis.

If the contribution of higher modes becomes relevant, the envelope of storey shear may not be suitable for deriving storey forces. In this case, these forces may be assumed equal to modal forces, as derived from spectral analysis for the relevant frequency modes.

$$\begin{aligned} \textit{Iterative }\, \textit{correction - k = k +1} \end{aligned}$$

6.1.4 Phase D4: Design of links and diagonal bracing

The storey forces determined during iteration k-1 with the analytical displacement method described in Sect. 5 or, more in general, with structural elastic F.E. Software, can identify generalized stresses on elements.

Optimal bracing design is continued through the numerical solution of a non-linear constrained optimization problem, e.g., using the “Interior Point method” (Potra and Wright 2000), shown below.

6.1.5 Free parameters

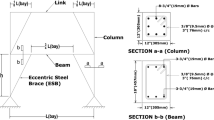
The free parameters of the problem are thickness and the width of the flanges forming the geometry of links and diagonals: length of link $e_{ij}$; link section $\left[ {t_f , t_w , b, d} \right] _{ij}$; cross-sectional area of diagonals; number of braced spans $z_i$ at floor $i$.

The position of bracing systems can also be considered as a variable. Brace positions take on importance in 3D frames, since correct positioning minimizes in-plan stiffness irregularities of the existing frame and therefore any undesired torsional effects. The position of the bracing system is not pertinent in 2D frames.

6.1.6 Imposed constraints

• At each storey, the plastic shear strength of link section $V_{p,ij}^l$must equal to shear force $V_{ij}^l$ i.e. $V_{p,ij}^l =V_{ij}^l$. If this condition is imposed, the contemporary yielding of all links on the storey is also imposed, at least as regards the distribution of design forces.

• The length of link $e_{ij}$ must be lower than the limit value identifying short links $e_{S,ij}$. If $e_{ij} < e_{S,ij} = 0.8 M_{p,ij}^l / V_{p,ij}^l$is imposed, the shear yielding of link is guaranteed. This is an optimal condition for obtaining yielding along the entire element, for the scheme of constraint chosen.

• The design axial force on diagonals must be lower than their axial strength, according to the equation in section 6.8.3 of Eurocode 8—Part 1 (2005a), which accounts for the capacity design criteria:

  $$\begin{aligned} N_{Rd,ij}^d \ge N_{Ed,ij}^d =1.1\cdot \gamma _{ov} \cdot \Omega _{ij} \cdot N_{ij}^d \end{aligned}$$

  (16)

  where $N_{Rd,ij}^d$is the axial design resistance according to Eurocode 3—Part 1.1 (2005), $N_{ij}^d$is the compressive force due to seismic action, $\gamma _{ov}$ is the coefficient of steel over-strength, i.e., 1.25, and $\Omega _{ij} =1.5 V_{p,ij}^l /V_{ij}^l =1.5$.

The diagonals must remain in the elastic range without destabilization. Equation (16) implies that the axial strength of the diagonals on the link, determined according to Eurocode 3—Part 1.1 (2005), is greater than the maximum axial action due to shear force on that link. This axial force is then multiplied by coefficients which take into account increased resistance due to link hardening in the plastic range (Eurocode 8—Part 1, 2005a) and the uncertainty of steel yield stress.

• The bending moment at the points on the beams where links intersect, is smaller than the limit value given by the following equations:

  $$\begin{aligned} \begin{array}{l} M_{Ed,ij}^{f+} =M_{G,ij}^f +\left[ {1.1 \gamma _{0v} \Omega _{ij} V_{ij}^l (e_{ij} +r_{ij} )} \right] /2\le M_{Rd,ij}^{f+} \\ M_{Ed,ij}^{f-} =M_{G,ij}^f -\left[ {1.1 \gamma _{0v} \Omega _{ij} V_{ij}^l (e_{ij} +r_{ij} )} \right] /2\ge M_{Rd,ij}^{f-} \\ \end{array} \end{aligned}$$

  (17)

  where $M_{Rd,ij}^{f+}$ and $M_{Rd,ij}^{f-}$ are the design resistant bending moments of the section, according to Eurocode 2—Part 1-1 (2005), and $M_{G,ij}^f$ is the bending moment due to non-seismic actions (i.e., gravitational vertical loads).

The design bending resistance of the RC section, determined according to Eurocode 2—Part 1-1 (2005), must be greater than the bending moment due to shear force on the link, multiplied by coefficients taking into account increased resistance due to link hardening in the plastic range (Eurocode 8—Part 1, 2005a) and the uncertainty of steel yield stress.

In particular, this check is necessary for the section of the beam in which the steel links connect, because it has a discontinuity in its bending moment, due to the effect of horizontal actions, which is binding for link design.

• The width/thickness ratio of flange link sections are compatible with the constraints of Table 5.2 of Eurocode 3—Part 1-1 (2005), for class 1 cross-sections. This ensures that the links can fully develop their rotation capacity when they enter the plastic range.

6.1.7 Optimal criterion

• Minimization of inter-storey displacements.

  The imposed optimal criterion is designed to stiffen bracing by fulfilling all constraints, in order to minimize inter-storey displacements and therefore generalized stresses and deformation demand on the frame.

6.1.8 Phase D5: Recalculation of design seismic forces

With the new $k$-th geometry, as defined in phase D4, further spectral analysis is performed and seismic loads are recalculated according to Eqs. (14) and (15). The design force concerns the bracing geometry obtained with the previous iteration. However, the new geometry causes a variation in stiffness, and the resulting variations in vibration frequencies and modes means that the forces acting on each storey are different from those used in the previous iteration.

6.1.9 Phase D6: Check for convergence of procedure

If norm $\left\| {\delta ^{k}} \right\| _\infty$ of the difference of storey forces between iteration $k$ and $k-1$, i.e.:

$$\begin{aligned} \left\| {\delta ^{k}} \right\| _\infty ={\max }_{i=1,n} \left| {\frac{f_i^k -f_i^{k-1} }{f_i^k }} \right| \le toll \end{aligned}$$

(18)

is lower than a pre-set tolerance, final geometry is achieved and the design procedure ends. Otherwise, it is necessary to return to phase D4 and carry out a new design with the new force distribution.

7 Brief mention of verification phase

After the design phase, a subsequent verification phase (phase V) to check all ductile and brittle mechanisms must be performed, to verify link rotation capacity (Eurocode 8—Part 1, 2005a), allowable chord rotations of beams and columns, and shear strength of beams, columns and nodes (Eurocode 8—Part 3, 2005b) at Ultimate Limit State (ULS). The constrains imposed by this code (Eurocode 8—Part 1, 2005a) for inter-storey drift at Damage Limit State (DLS) must also be checked. If all checks are not satisfied, retrofitting must be redesigned with a lower behavior factor.

The complete process of iterative design and verification is shown in Fig. 5.

Fig. 5

Design and verification method

Theoretically, the search for the “optimal” q-design can be directly introduced into the iterative design algorithm, but this would imply the need to perform the procedure within a non-linear approach.

At the ULS, phase V must be carried out by non-linear analyses, static or dynamic, to verify the behavior up to the ULS of both the original structure and the retrofitted bracing. Non-linear analyses are well-known to be extremely complex and time-consuming, and sometimes lead to uncontrolled results. For all these reasons, the development of easy-to-use analytical formulas to predict the inelastic behavior of retrofitted structures is highly useful in practice. Proposed analytical formulas for predicting the non-linear behavior of retrofitted frames and a different and relevant part of this study will be given in a forthcoming companion paper.

8 Application to regular 2D frames

The proposed method was applied to a regular RC shear frame. Various design solutions can be obtained by varying $q^{d}$ in the range 2–6. The proposed method was also successfully applied to the retrofitting of a irregular frame although, for the sake of brevity, the results cannot be presented here.

8.1 The existing RC frame

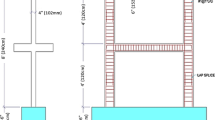
The geometries of the examined RC frame are shown in Fig. 6. The frame was designed only for vertical loads (see Table 1) in which $g$ stands for structural and non-structural dead loads and $q$ for live loads. Assuming that only 20 % of live load $q$ contributes to the mass caused by seismic action, the resulting storey masses are given in the same table (storey 3 is different because only the weight of half the columns were included).

Table 1 Design loads and storey masses of frame

Fig. 6

RC shear frame geometries

Frame vibration frequencies are listed in Table 3. The same values for the retrofitted structure designed with $q^{d}=4$ are shown in square brackets, and were obtained with an elastic modulus of concrete reduced to 50 % of its nominal value (Table 2), to take into account the bending cracking effect under seismic action. Table 2 shows the maximum compression strength of concrete $f_c$, steel elastic modulus $E_s$, and yield stress of steel reinforcement bars $f_y$.

Table 2 Table of materials

Table 3 Frequency analysis of existing frame (and retrofitted frame with q$^{d}=4$)

8.2 Pushover analysis of existing RC frame

Pushover analyses of the existing frame were carried out with the fiber model implemented in the Midas Gen code (Midas Gen, version.7.4.1, rel no. 2, 2007), with the Kent & Park model for concrete and the Menegotto & Pinto model for reinforcement bars. Assuming the two load distributions imposed by Eurocode 8—Part 1 (2005a), one proportional to the deformation given by the first vibration mode (I) and the other proportional to masses (II), yielded the two capacity curves shown in Fig. 7.

Fig. 7

Capacity curve of existing frame

These are followed by the ultimate chord rotation of columns, although this occurs after their ultimate shear strength has been reached. The ultimate chord rotation capacities of columns were calculated by the following relationship recommended by Eurocode 8—Part 3 (2005b):

$$\begin{aligned} \theta _u^{f, C} =0.85\cdot \frac{1}{\gamma _{el} }\cdot 0.016\left( {0.3^{\nu }} \right) \left[ {\frac{\max \left( {0.01;\omega ^{{\prime }}} \right) }{\max \left( {0.01;\omega } \right) }f_c } \right] ^{0.225}\left( {\frac{L_V }{h}} \right) ^{0.35}25^{\left( {\alpha \rho _{sx} \frac{f_y^r }{f_c }} \right) } \end{aligned}$$

(19)

The shear strength of columns was determined with the following Eq. 32:

$$\begin{aligned} V_R^{f, C}&= \frac{1}{\gamma _{el} } \left\{ \frac{h-x}{2L_V }\min \left( {N;0.55A_c f_c } \right) +\left[ {1-0.05\min \left( {5;\mu _\Delta ^{pl} } \right) } \right] \right. \nonumber \\&\left. \left[ {0.16\max \left( {0.5;100\rho _{tot} } \right) \left( {1-0.16\min \left( {5;\frac{L_V }{h}} \right) } \right) \sqrt{f_c }A_c +V_w } \right] \right\} \end{aligned}$$

(20)

with $\mu _\Delta ^{pl} =\frac{\theta _u^f }{\theta _y }-1 \quad e\quad \theta _y =\theta _u^f -\theta _u^{pl}$

$$\begin{aligned} \theta _u^{pl} =0.85\cdot \frac{1}{\gamma _{el} }\cdot 0.0145\left( {0.25^{\nu }} \right) \left[ {\frac{\max \left( {0.01;\omega ^{{\prime }}} \right) }{\max \left( {0.01;\omega } \right) }} \right] ^{0.3}f_c ^{0.2}\cdot \left( {\frac{L_V }{h}} \right) ^{0.35}\cdot 25^{\left( {\alpha \rho _{sx} \frac{f_y^r }{f_c }} \right) } \end{aligned}$$

(21)

The values of $\theta _u^{f, C}$ and $V_R^{f, C}$ are given in Table 4, and were obtained with $\gamma _{el} =1.5$, $f_y^r =390$ MPa, $f_c =15$ MPa and $L_V =h_{ij} /2$ (e.g. Mpampatsikos et al. 2008) and constant axial force $N$ in each column equal to that determined by gravity loads alone, i.e., about the average value to which columns are subjected during seismic action, as reported in Mpampatsikos et al. (2008).

Table 4 Columns: ultimate chord rotations and shear strength

The resulting capacity curves show very fragile behavior, and failure at both load distributions is due to the creation of a “soft storey” at ground level, which precludes the possibility of inelastic deformation in the upper storeys.

8.3 Performance Point search procedure

The procedure selected for pushover analysis and the search for the Performance Point (PP) uses the principles of equal energy and equal displacement of a bilinear hardening SDOF system (“EE-ED procedure”) (Albanesi et al. 2000).

It considers bi-linearization of the capacity curve with a plastic hardening branch defined by parameter $p$, equal to the ratio between plastic and elastic stiffness. In general, $p$ is a non-negative quantity. In RC frames, $p = 0$ is usually assumed, so that the EE-ED procedure is reduced to the standard N2 pushover procedure recommended by Eurocode 8—Part 1 (2005a), except for the Fajfar correction (Fajfar 1999) which allows continuous transition between $T^{*}<T_C$ and $T^{*}\ge T_C$.

In retrofitted frames, provided that (as in the design assumption) the RC frame remains elastic when the bracing system has largely yielded, p is equal to the elastic stiffness of RC frames divided by the elastic stiffness of the retrofitted frame (see Fig. 3):

$$\begin{aligned} p=\frac{K^{f}}{K^{f+b}}=\frac{K^{f}}{K^{f}+K^{b}}>0 \end{aligned}$$

(22)

The steps of the pushover procedure used to evaluate the PP are briefly recalled here. Mass $m^{*}$ of the equivalent SDOF system is determined by:

$$\begin{aligned} m^{*}=\sum _{i=1}^n {m_i \phi _i } \end{aligned}$$

(23)

where $m_i$ is the mass of the $i$-th storey and $\phi _i$ are normalized displacements relative to the adopted distribution of lateral loads, so that $\phi _n =1$, where $n$ stands for the control point, usually placed at the top of the building.

The coefficient of transformation from the real MDOF system to the equivalent SDOF system is given by:

$$\begin{aligned} \Gamma =\frac{m^{*}}{\sum _{i=1}^n {m_i \phi _i^2 } } \end{aligned}$$

(24)

The capacity curve of the equivalent SDOF system is defined by force $F^{*}=F/\Gamma$ and displacement $d^{*}=d_n /\Gamma$, where $F$ and $d_n$ are respectively base shear and the displacement of the control node of the system with MDOF, determined by non-linear static analysis.

The equivalent bilinear curve is determined by imposing equality of strain energy $E_u^*$ of the real capacity curve and strain energy $E^{*}$ of the idealized bilinear hardening curve, defined as follows (Fig. 8):

$$\begin{aligned} E^{*}=\frac{F_u^*}{2}\cdot \left( {d_u^*-d_y^*} \right) +\frac{F_y^*}{2}\cdot d_u^*=E_u^*\end{aligned}$$

(25)

where ultimate displacement $d_u^*$ of the equivalent SDOF system is assumed to be equal to the reduced maximum displacement derived from pushover analyses $d_{\max }^*=\frac{d_{\max } }{\Gamma }$, and ultimate strength $F_u^*$of the equivalent SDOF system is assumed to be equal to the reduced maximum base shear derived from pushover analyses $F_{\max }^*=\frac{F_{\max } }{\Gamma }$.

Fig. 8

Determination of performance point: a short period structures, b medium and long period structures

For applications to existing RC frames when $p=0$, yield strength $F_y^*$ of the equivalent SDOF system is assumed to be equal to ultimate strength $F_u^*$, as recommended by Eurocode 8—Part 1 (2005a) (Fig. 9a), which gives an elastic-perfectly plastic bilinearization criterion.

Fig. 9

Bilinearization criterion: a elastic-perfectly plastic criterion according to Eurocode 8—Part 1 (2005a); b over-estimation of period T* by elastic-perfectly plastic criterion ($p=0$) for retrofitted frame

Figure 9b shows that, using the standard pushover procedure with $p=0$ with elastic-perfectly plastic bilinearization of the retrofitted frame (Eurocode 8—Part 1, 2005a) instead of a generalized EE-ED procedure (with $p>0$), leads to over-estimation of period $T^{*}$ of the equivalent SDOF system and consequently to incorrect evaluation of the PP.

Period $T^{*}$ of the idealized equivalent SDOF system is given by $T^{*}=2\pi \sqrt{\left( {m^{*}d_y^*} \right) /F_y^*}$.

The performance displacement of the elastic structure with period $T^{*}$ is given by:

$$\begin{aligned} d_{et}^*=S_e \left( {T^{*}} \right) \left[ {\frac{T^{*}}{2\pi }} \right] ^{2} \end{aligned}$$

(26)

where $S_e \left( {T^{*}} \right)$ is the elastic acceleration response spectrum for period $T^{*}$.

Elastic and plastic stiffness and their ratio are described as follows:

$$\begin{aligned} K_e =F_y^*/d_y^*\quad K_p =\left( {F_u^*-F_y^*} \right) /\left( {d_u^*-d_y^*} \right) \quad p=K_p /K_e \end{aligned}$$

(27)

Once the force reduction factor is defined as:

$$\begin{aligned} q_{PO}^{eff} =\frac{m^{*}S_e \left( {T^{*}} \right) }{F_y^*} \end{aligned}$$

(28)

inelastic performance displacement $d_{pt}^*$ for structures with short period $T^{*}<T_C$ is calculated as follows, as a consequence of the principle of equal energy (see Fig. 8a):

$$\begin{aligned} d_{pt}^*=\left[ {{\begin{array}{l@{\quad }l} {\frac{1}{p}\left[ {\sqrt{\left( {1-p} \right) \left( {\frac{1}{q_{PO}^{eff} }} \right) ^{2}+p}-\left( {1-p} \right) \left( {\frac{1}{q_{PO}^{eff} }} \right) } \right] d_{et}^*}&{} \,{ with\, p>0 } \\ {\frac{1+\left( {1/q_{PO}^{eff} } \right) ^{2}}{2\left( {1/q_{PO}^{eff} } \right) }d_{et}^*}&{}\, { with\, p=0 } \\ \end{array} }} \right] \end{aligned}$$

(29)

For structures with medium and long periods $T^{*}\ge T_C$, inelastic performance displacement is assumed to be equal to elastic displacement (Fig. 8b), according to the principle of equal displacement:

$$\begin{aligned} d_{pt}^*=d_{et}^*\end{aligned}$$

(30)

When inelastic performance displacement has been determined, the ratio of ductility demand $\mu$ is obtained as follows:

$$\begin{aligned} \mu =\frac{d_{pt}^*}{d_y^*} \end{aligned}$$

(31)

and, for $T^{*}\ge T_C$,  $q^{eff}=\mu$.

Lastly, the inelastic performance displacement of the original MDOF structure is given by:

$$\begin{aligned} d_{pt} =\Gamma \cdot d_{pt}^*\end{aligned}$$

(32)

8.4 Determining the performance of the existing frame

Let us assume that the existing frames insists on a D ground type soil (deposits of loose to medium cohesionless soil or predominantly soft to firm cohesive soil), for which soil amplification factor S $=$ 1.35 is given. The elastic seismic design spectrum is described by following parameters, according to Eurocode 8—Part 1 (2005a): $\hbox {T}_\mathrm{B} = 0.2\, \hbox {s}$, $\hbox {T}_\mathrm{C}=0.8$ s, $\hbox {a}_\mathrm{g} = 0.3\, \hbox {g}$, B $=$ 0.2 and I $=$ 1. With this procedure, with $p = 0$ for the existing RC frame alone, the maximum compatible earthquake is calculated for the two capacity curves obtained for the two prescribed horizontal load patterns I and II.

Searching for the maximum seismic intensity for which it is still possible to determine the existence of the PP, as shown in Fig. 10, the existing building turned out to be compatible with an earthquake with maximum peak ground acceleration of $PGA\left[ g \right] =S\cdot a_g =1.35\cdot 0.15 g = 0.2 g$, provided that the columns be properly reinforced against shear. Otherwise, the maximum earthquake which does not reach the shear strength of columns would be characterized by $PGA\left[ g \right] =S\cdot a_g =1.35\cdot 0.08 g = 0.1 g$. In both cases, the load distribution which exceeds the ductility capacity or shear strength of the frame is proportional to the first vibration mode. Table 5 lists the parameters determined by pushover analyses for both force distributions for $PGA = 0.2 g$.

Fig. 10

Capacity spectrum of SDOF system

Table 5 Parameters from pushover analysis to calculate PP for limit condition PGA = 0.2g

8.5 Seismic retrofitting design with proposed optimized method

The structure described above should be retrofitted in order to withstand earthquakes with peak ground acceleration of $PGA\left[ g \right] =S\cdot a_g =1.35\cdot 0.30 g = 0.40 g$, with seismic retrofitting complete with Y bracing, following the method described here.

The design was carried out for behavior factors $q^{d} = 2$, 3, 4, 5 and 6, i.e., varying between a minimum value which nearly corresponds to that required to maintain the structure in the linear elastic range, and the maximum value allowed for new steel structures with eccentric bracing.

In order to solve the constrained optimization problem, the Generalized Reduced Gradient (GRG) algorithm (Lasdon et al. 1974) was used. It applies robust implementation of the Broyden–Fletcher–Goldafar–Shanno quasi-Newton algorithm as its default choice to determine a search direction.

Convergence is super-linear. In our applications, the number of steps required to reach the solution was always less than ten. Various minimum solutions can be found when the initial solution is changed. The closest local minimum solution consistent with the initial one was obtained. The search for the absolute optimal solution should be carried out by changing the initial solution. However, due to the constraints imposed, particularly contemporary yielding of links in all storeys, the various solutions which can be achieved do not differ very much in terms of inter-storey displacements.

Table 6 shows the results for each iteration for the design example with behavior factor $q^{d}=4$. Once the initial geometry has been established (phase D2, k $=$ 1), the iterative process stops after two iterations.

Table 6 Iterative procedure design results with q$^{d}=4$

The bracing geometry designed for $q^{d}=4$ is shown in Fig. 6. Table 7 shows that the final design result (k $=$ 3) completely fulfills the imposed constraints in terms of generalized stresses, i.e.,:

• shear force links: $V_{ij}^l \cong V_{p,ij}^l$;

• axial force on diagonal bracing: $N_{Ed,ij}^d \le N_{Rd,ij}^d$;

• bending moments on RC beams: $M_{Ed,ij}^{f+} \le M_{Rd,ij}^{f+}$ e $M_{Ed,ij}^{f-} \ge M_{Rd,ij}^{f-}$.

Respect for the limit length of links $e_{ij} \le e_{s,ij} =0.8 M_{p,ij} /V_{p,ij}$, in order to ensure short link behavior, is shown in Table 8.

Table 7 Generalized stress k = 3

Table 8 Limit length of links

The vibration frequencies of the retrofitted frame are listed in Table 3. The increase in stiffness due to bracing, accompanied by a negligible increase in mass, gives rise to a considerable reduction in the structural vibration period. Design results from all design behavior factors are listed in Table 9.

Table 9 Results from designs performed for all q$^{d}$

The increase in the behavior factor value, which coincides with the decrease in design force, clearly decreases the number and size of necessary braces. The bending resistance of existing RC beams limits the maximum shear force which the links can withstand, and therefore determines the number of frame spans to be braced.

9 Conclusions

This work contributes to the topic of designing eccentric bracing for seismic retrofitting of existing RC frames. The types of braces examined here are the eccentric inverted-Y shape, in which the link is represented by a suitably stiffened double T- shaped profile, although the concepts presented here can be directly applied to any kind of dissipative bracing.

The proposed iterative method searches for an optimized solution in the sense that:

• it maximizes energy dissipation through overall inelastic behavior of the structures, providing contemporary early yielding of the links at each floor;

• it applies a capacity design rule, imposing over-strength of RC beams and steel diagonals;

• it prevents the RC frames from entering the inelastic field before the bracing system.

Of all the possible solutions to the imposed constraints, the one which minimizes inter-storey drift is pursued and reached within a few iterations.

Although the proposed method is analytically reported only for a 2D frame with rigid beams, it may easily be generalized to more complex structures by applying condensation methods or, more in general, using elastic structural analysis software.

The proposed method applied to a regular 2D RC frame is extensively illustrated here. Preliminarily, the inadequacy of the frame to bear the design seismic load is demonstrated by pushover analysis, the procedures of which are also described.

The crucial point of the design is the choice of behavior factor $q^{d}$. Clearly, the higher $q^{d}$, the fewer seismic design forces, and the least invasive and expensive solution will be retrofitting. The choice of too high a behavior factor may lead to substantially ineffective retrofitting, since the bracing may not have the strength and stiffness sufficient to protect the existing frame from brittle and ductile failure.

Several nonlinear static and dynamic analyses were carried out on retrofitted frames to assess the effectiveness and acceptability of the retrofitting design for various values of $q^{d}$. Results from this extensive investigation will be described in a forthcoming paper.