Efficiency-Inducing Policy for Polluting Oligopolists

Abstract

This paper characterizes an efficiency-inducing policy for a polluting oligopoly when pollution abatement is technologically feasible and when environmental damage depends on the pollution stock. Using a dynamic policy game between the regulator and the oligopolists, we show that a tax–subsidy scheme can implement the efficient outcome as a regulated market equilibrium. The scheme consists of a tax on production and a subsidy that can either be on abatement efforts or on abatement costs. Both schemes prescribe a different tax rule, but both implement the efficient outcome. If firms act strategically, taking into account the evolution of the pollution stock when they decide on abatement and production, the subsidy reflects the divergence between the social and private valuation of the pollution stock associated with the abatement decision. Consequently, the tax has to correct the two market failures associated with production: the market power of the firms and the negative externality caused by pollution. Using an LQ (differential) policy game, we show that the tax increases with the pollution stock for both schemes, and that the application of a subsidy on abatement costs leads to a laxer tax rule. Interestingly, it also yields a lower fiscal deficit at the steady state. Thus, from a fiscal perspective, the policy recommendation is the application of a subsidy on abatement costs.

1 Introduction

A very influential and seminal paper by Benchekroun and Long [3] shows that there is a time-independent tax rule for polluting oligopolists that implements the efficient allocation as a regulated market equilibrium. The optimal tax increases with the pollution stock, but the authors found that it may be negative when the pollution stock is low, i.e., the optimal policy could consist of subsidizing production for an initial time interval.¹ This result is not so surprising if we consider that a polluting oligopoly is inefficient because two market failures are operating at the same time but with a different bias. On the one hand, firms have market power which causes a reduction of production below the efficient level. On the other hand, pollution is an example of a negative externality that tends to increase production above the efficient level. In the first case, the optimal policy consists of a subsidy on production to close the gap between the price and the marginal revenue of the firms. In the second case, the optimal policy is to apply a tax on emissions to drive firms to internalize the negative externality. If the first market distortion dominates the second one, the optimal policy for polluting oligopolists would be a subsidy on production. Nevertheless, Martín-Herrán and Rubio [21] have shown that if environmental damages are high enough, the optimal policy consists of taxing production for any level of the pollution stock.

The aim of this paper is to characterize the efficiency-inducing policy for polluting oligopolists if pollution abatement is technologically feasible. In this case, we have to distinguish between gross emissions linked to production and net emissions that depend on abatement efforts developed by the firms. In this framework, a tax on net emissions cannot implement the efficient solution because it penalizes production and rewards abatement at the same rate, and we would need to do it at different rates to adjust the two control variables of the model: abatement and production. Recently, Martín-Herrán and Rubio [19] addressed this issue for the case of a polluting monopoly. Following the argument we have previously presented, they showed that the regulated market equilibrium is efficient for a policy mix that combines a tax on emissions with a subsidy on production. But still in this case the tax could be negative for low values of the pollution stock.² Although a subsidy on production in this framework is a policy to recover the efficiency of the market, it could be seen by the regulatory agencies as a policy against competition and it could be questioned and difficult to apply. To avoid this criticism, in this paper we propose, following Pal and Saha [24], a policy that consists of penalizing production and rewarding abatement but a different rate, i.e., using two different instruments.³ In fact, we propose two tax–subsidy schemes that can implement the efficient allocation—one policy mix that combines a tax on production with a subsidy on abatement effort, and a second policy mix for which the subsidy is on abatement costs.⁴ Our model can be read as either an extension of Martín-Herrán and Rubio [19] for the case of a polluting oligopoly, or an extension of Benchekroun and Long [3] to incorporate an abatement technology.

For a general version of the model, we find that the subsidy will depend solely on the divergence between the social and private valuation of the pollution stock. When the subsidy is applied to abatement efforts, the subsidy is proportional to the difference between the social and private shadow price of the pollution stock. If the subsidy is on abatement costs, it is equal to the ratio between the private and social shadow prices. In both cases, the subsidy will be positive. On the other hand, the tax, as in Benchekroun and Long [3], has to correct the two market failures associated with production. Thus, we find that the optimal tax is equal to the difference between the marginal revenue and the price, which is negative, plus the difference between the social and private shadow prices, which is positive. The net effect could be negative. In any case, it is clear that the production tax rate will be lower than the abatement subsidy rate when this is applied to the abatement effort.

To advance in the analysis of the optimal policy rules, we solve, in the second part of the paper, an LQ (differential) policy game between the regulator and the oligopolists. The results confirm that, regardless of whether a subsidy is applied to abatement effort or to abatement costs, the tax could be negative for low levels of the pollution stock. Nevertheless, the tax increases with the pollution stock. A numerical exercise allows us to evaluate how the different parameters of the model influence the optimal tax rule and its steady-state value. We find that with high environmental damages, high efficiency of the resources devote to abatement, and more competition in the market, we should expect a tax that is always positive. On the other hand, the subsidies are always positive and increase with the pollution stock. Interestingly, we find that although the differential game is linear-quadratic the subsidy rule when the subsidy is for abatement costs is not linear. Moreover, we would like to highlight that the model predicts that competition is good for the environment. We show analytically that with more firms in the industry, the steady-state pollution stock decreases, and the numerical exercise shows that although each firm’s abatement and production decreases, the total production and abatement of the industry increases. Thus, total abatement monotonically increases with competition, and this increase is enough to yield decreasing total emissions compatible with an increasing total output. Finally, we compare the optimal tax rules that are obtained when the two different subsidies are applied. From this comparison, we find that the optimal tax rule is laxer when a subsidy on abatement costs is applied. In this case, both the intersection point with the vertical axis and the slope of the tax rule are lower and consequently the steady-state tax will be lower. Notice that both policy mixes implement the same efficient solution. Thus, if the tax rule is less strict, the tax at the steady state will be lower. This means that lower tax revenues will be collected by the government if the subsidy is on abatement costs. However, from a fiscal point of view, what is important is the fiscal balance of the policy mix. Unfortunately, the complexity of the fiscal balance expression prevents finding any analytical conclusion for the comparison of the fiscal balances. Nevertheless, we can indicate that the numerical exercise shows that both policies present a fiscal deficit, but that the fiscal deficit is lower when the government subsidizes the abatement costs. Therefore, we can conclude that when this type of subsidy is used both the fiscal revenues and subsidy expenses are lower and that the net effect is a lower fiscal balance. We should take this conclusion with caution, since this result is based on numerical simulations. If the criterion for selecting the type of subsidy to accompany the tax is to select the one that leads to the most favorable fiscal balance, the policy recommendation would be to opt for a subsidy on abatement costs.⁵

1.1 Literature Review$^5$

A list of papers addressing the regulation of firms with market power in the context of stock dynamics includes Bergstrom et al. [5] , Karp and Livernois [14], and Karp [13] for the case of a non-renewable resource and Benchekroun and Long [3, 4], Stimming [26], Feenstra et al. [10], and Yanase [28] for the case of polluting firms.⁶ Bergstrom et al. [5] show that there exists a continuum of tax/subsidy schedules on output that lead to a monopoly to extract efficiently a non-renewable resource. However, as these taxes/subsidies are time-dependent, they are not in general subgame perfect. Karp and Livernois [14] design a subgame-perfect tax rule that implements the efficient outcome for a monopoly. Karp [13] extends this result to the case of an oligopoly that extracts a common property non-renewable resource, and Benchekroun and Long extends this to the case of a polluting oligopoly.⁷ The two papers by Stimming [26] and Feenstra et al. [10] studying the case of a duopoly assume that environmental damages depend on current emissions and focus on investment in an abatement technology. The environmental policy in these papers is given and the analysis assesses the effects of a stricter environmental policy comparing taxes vs. emission standards. After the papers by Benchekroun and Long [3, 4], Yanase [28] is the first paper where the environmental policy is endogenously determined. The author examines a non-cooperative (differential) policy game between national governments in a model of international pollution control of a stock pollutant in which duopolists compete myopically in quantities in a third country with product differentiation and expense resources in abatement activities. The comparison of the Markov perfect Nash equilibrium of the game for different policy instruments establishes that an emission tax produces more pollution and lower welfare than those generated by a standard. This author assumes an end-of-the-pipe abatement technology like the one used in this paper.⁸

Other papers addressing environmental regulation of polluting firms with market power in a dynamic context include Benchekroun and Chaudhuri [1], Martín-Herrán and Rubio [19], and Dragone et al. [9]. Benchekroun and Chaudhuri [1] show that the imposition of a tax on emissions that depends on the pollution stock can induce stable cartelization in a polluting oligopoly, making the regulation of the market undesirable. Martín-Herrán and Rubio [19] show that a tax–subsidy scheme, consisting of taxing emissions and subsidizing production, implements the efficient outcome as a regulated market equilibrium for a polluting monopoly with an abatement technology of the type proposed by Yanase [29]. They also show that taxes and standards are equivalent in a second-best setting. In this paper, we extend this model to the case of an oligopoly, but focusing on different tax–subsidy schemes. Dragone et al. [9] study the case of a polluting oligopoly with spillovers on the abatement effort where the damages depended on the pollution stock and the total output of the industry. However, the authors considered a tax on firms’ accumulated emissions and focused mainly on the effect of competition on the aggregate abatement.

Another set of papers analyzes investment in pollution abatement capital in different settings includes Saltari and Travaglini [25], Karp and Zhang [15] , Menezes and Pereira [23] , and Martín-Herrán and Rubio [19]. Saltari and Travaglini [25] assume that uncertainty over the dynamics of pollution stock affects firm investment decisions and study, for the case of a competitive firm, how a tax–subsidy scheme based on a tax on the polluting input and a subsidy on investment influences the firm’s decisions on investment. However, in their model, there is no connection between the use of the polluting input and the evolution of the pollution stock. Karp and Zhang [15] compare emission taxes and standards when a regulator and a representative firm have asymmetric information about abatement costs, and all agents use Markov perfect decision rules. The firm can reduce future abatement costs through investment. For a linear-quadratic specification of the model and using numerical methods, they find that a tax has some advantage over a standard. Menezes and Pereira [23] study the dynamic competition of a duopoly in supply schedules that can invest in an abatement technology. In their model, damages are linear in the pollution stock and there are also technological spillovers. The focus is on the characterization of the optimal policy mix consisting of a tax on emissions and a subsidy on investment costs, assuming that the regulator can commit for the entire temporal horizon and that firms’ production, investment, and abatement capital are given by their steady-state values when the regulator decides the optimal policy. Our paper differs from this work mainly in three aspects. Firstly, we do not assume that the regulator can commit for the entire temporal horizon; instead, we look for the feedback Stackelberg equilibrium of the differential game played by the regulator and the oligopolists, i.e., the regulator maximizes net social welfare subject to best responses of the firms to the policy adopted by the regulator. Secondly, we assume quadratic environmental damages while Menezes and Pereira [23] assume a linear damage function. Thirdly, we consider two tax–subsidy schemes that are based on a tax on production instead of a tax on emissions, and we also consider a subsidy on the abatement effort. Finally, Martín-Herrán and Rubio [20] analyzed the second-best emission tax for a polluting monopoly with abatement investments investigating the consequences for investment of two different damage structures—one linear and one quadratic in the pollution stock.

Recently, Bisceglia [6] characterized the efficiency-inducing tax rule imposed on output for an oligopoly that exploits a common productive resource, and Benchekroun at al. [2] proposed for an oligopoly that extracts a common non-renewable resource, a novel tax scheme to implement the efficient outcome where the tax bill paid by a firm depends only on the current resource stock. Finally, Feichtinger et al. [11] presented a model of a polluting common renewable resource exploited by an oligopoly in which firms can invest in an abatement technology. The authors show that if the demand is linear, the extraction costs are linear, and the access is regulated to induce the industry to harvest at the maximum sustainable yield, then there exists a tax on accumulated emissions of the firm at which aggregate emissions drop to zero. Taxation induces firms to invest in the abatement technology and eliminate emissions.⁹

The remainder of the paper is organized as follows. Section 2 presents the model and derives the efficient conditions. Section 3 characterizes the first-best policy mix, distinguishing between the two tax–subsidy schemes studied in this paper. In Sect. 4 an LQ policy game is solved. Section 5 offers some concluding remarks and points out lines for future research.

2 The Model and the Efficient Conditions

We consider a Cournot oligopoly that faces a market demand represented by the decreasing inverse demand function P(Q(t)) where $Q(t)=\sum _{i=1}^{n}q_{i}(t)$ is the output of the industry at time t and $n\ge 2$ is the number of firms. Firms produce a homogeneous good using the same productive technology, described by the cost function $\,\textrm{PC}=cq_{i}(t).$The production process generates pollution emissions, but after an appropriate choice of measurement units we can say that each unit of output generates one unit of pollution. However, emissions can be reduced without declining output if the firms employ an abatement technology. The abatement technology is assumed to be the end-of-the-pipe type. For this type of abatement technology, the emission function is: $e_{i}(t)=q_{i}(t)-w_{i}(t),$ where $w_{i}(t)$ is the abatement effort of firm i.¹⁰ The abatement cost function is represented by AC$(w_{i}(t))$ with both (AC)$^{\prime }(w_{i})$ and $(\textrm{AC})^{\prime \prime }(w_{i})$ being positive. The focus of the paper is on a stock pollutant that evolves according to the following differential equation:

$$\begin{aligned} {\dot{x}}(t)=\sum _{i=1}^{n}{\left( q_{i}(t)-w_{i}(t)\right) } -\delta x(t),\quad x(0)=x_{0}\ge 0, \end{aligned}$$

(1)

where x(t) stands for the pollution stock and $\delta >0$ for the decay rate of pollution. The environmental damages are given by the function D(x(t)) and is assumed to be strictly convex. Thus, the policy game we analyze in this paper is a differential game between a welfare maximizing regulator and profit maximizing oligopolists. Before analyzing it, we first derive the first-order conditions that characterize the efficient outcome.

The efficient conditions are obtained from the maximization of the discounted present value of net social welfare defined as the difference between gross consumer surplus minus costs and environmental damages.¹¹

$$\begin{aligned} \max _{q_{1},\ldots ,q_{n},w_{1},\ldots ,w_{n}}\ \int _{0}^{\infty }e^{-rt}\left\{ \int _{0}^{Q}P(Q^{\prime }) \textrm{d}Q^{\prime }-cQ-\sum _{i=1}^{n}AC(w_{i})-D(x)\right\} \textrm{d}t \\ \text { s.t. }\ {\dot{x}}=\sum _{i=1}^{n}{\left( q_{i}-w_{i}\right) } -\delta x,\ \ \ \ x(0)=x_{0}\ge 0, \end{aligned}$$

where r is the time discount rate.

Solving by dynamic programming, the solution to this dynamic optimization problem must satisfy the following Hamilton–Jacobi–Bellman (HJB) equation:

$$\begin{aligned} rW(x)= & {} \max _{q_{1},\ldots ,q_{n},w_{1},\ldots ,w_{n}}\left\{ \int _{0}^{Q}P(Q^{\prime })dQ^{\prime }-cQ-\sum _{i=1}^{n}\textrm{AC}(w_{i})-D(x)\right. \nonumber \\{} & {} \left. +W^{\prime }(x)\left( \sum _{i=1}^{n}{\left( q_{i}-w_{i}\right) } -\delta x\right) \right\} , \end{aligned}$$

(2)

where W(x) represents the maximum discounted present value of net social welfare for the current value, x,  of the pollution stock.

The maximization of the right-hand side (RHS) of the HJB equation yields the following first-order conditions (FOCs):

$$\begin{aligned} P= & {} c-W^{\prime }(x),\ \ i=1,\ldots n, \end{aligned}$$

(3)

$$\begin{aligned} (\textrm{AC})^{\prime }(w_{i})= & {} -W^{\prime }(x),\ \ i=1,\ldots ,n. \end{aligned}$$

(4)

The first FOC establishes that the price must be equal to the marginal costs which include the marginal cost of production plus the social valuation (shadow price) of the pollution stock. The latter is given by the reduction in the present value of the net social welfare because of an increase in the pollution stock caused by an increase in production. On the other hand, the second FOC requires that the marginal cost of abatement is equal to the marginal benefit defined by the increase in the present value of the net social welfare. This increase is caused by a reduction in the stock because of an increase in abatement. Notice that $W^{\prime }(x)$ is a marginal cost when we are considering an increase in production, and it stands for a marginal benefit when we are evaluating an increase in abatement.

To implement these conditions as a regulated market equilibrium, we propose two tax–subsidy schemes. The first scheme combines a tax on gross emissions, which in our model operates as a tax on production, with an abatement subsidy. The second scheme uses a subsidy on abatement costs instead of an abatement subsidy. In the next section, we calculate the stagewise feedback Stackelberg equilibrium (SFSE) of a (differential) policy game where the regulator who selects the level of the policy instruments is the leader, and the firms that choose the levels of production and abatement are the followers. We show that using these schemes the regulated market equilibrium will be efficient.

3 The First-Best Policy

The SFSE is based on the assumption that the regulator moves first in each moment. To find the regulator’s optimal policy, we apply backward induction, substituting the firms’ reaction functions in the regulator’s HJB equation, and computing the optimal strategy by maximizing the right-hand side of this equation. The resulting outcome is a stagewise feedback Stackelberg solution, which is a Markov perfect equilibrium. For this kind of equilibria, no commitment is required for the entire temporal horizon. For our model, this equilibrium is time consistent and also satisfies subgame perfection.¹²

3.1 Tax–Subsidy Scheme I

The output and abatement selection occurs in the second stage. Firm i chooses its output and abatement to maximize the discounted present value of net profits:

$$\begin{aligned} \max _{q_{i},w_{i}}\int \limits _{0}^{\infty }e^{-rt}\left\{ P(Q)q_{i}{-}cq_{i}{-}\textrm{AC}(w_{i}){-}\tau q_{i}{+}vw_{i}\right\} \textrm{d}t, \end{aligned}$$

subject to differential equation (1) where $\tau$ is the production tax and v stands for a subsidy on abatement. Following the seminal article by Benchekroun and Long [3] and other papers in the theoretical literature on the topic, we assume that the firm acts strategically at this stage taking into account the dynamic constraint given by (1).

The solution to this dynamic optimization problem must satisfy the following HJB equation:

$$\begin{aligned} rV^{I}(x){=}\max _{q_{i},w_{i}}\left\{ P(Q)q_{i}-cq_{i}{-}\textrm{AC}(w_{i}){-}\tau q_{i}{+}vw_{i}+{(V^{I})}^{\prime }(x)\left( \sum _{i=1}^{n}{ \left( q_{i}{-}w_{i}\right) }-\delta x\right) \right\} , \end{aligned}$$

where $V^{I}(x)$ stands for the maximum discounted present value of net profits for the current value, $x,\$of the pollution stock.¹³

From the FOCs for the maximization of the right-hand side of the HJB equation, we get:

$$\begin{aligned} P^{\prime }q_{i}+P= & {} c+\tau -{(V^{I})}^{\prime }(x),\ i=1,\ldots ,n, \end{aligned}$$

(5)

$$\begin{aligned} (AC)^{\prime }(w_{i})= & {} v-{(V^{I})}^{\prime }(x),\ i=1,\ldots ,n. \end{aligned}$$

(6)

The left-hand side (LHS) of the first FOC stands for the marginal revenue of the firm and the RHS represents the marginal costs that include the marginal cost of production, the tax, and the private valuation (shadow price) of the pollution stock. The latter is given by the reduction in the present value of the firm’s net profits because of an increase in the pollution stock caused by an increase in production. On the other hand, the LHS of the second FOC represents the marginal cost of abatement while the marginal benefits appear on the RHS. These marginal benefits include the subsidy, and the increase in the present value of the firm’s profits because of the reduction in the pollution stock. Notice that ${(V^{I})}^{\prime }(x)$ is a marginal cost when we are considering an increase in production, and it stands for a marginal benefit when we are evaluating an increase in abatement. The system of reaction functions (5) implicitly defines the firm’s strategy $q_{i}(\tau ,x)$and (6) directly yields $w_{i}(v,x).$ Notice that the optimal production does not depend on the subsidy and the optimal abatement effort does not depend on the tax. This is because of the assumption that firms use an end-of-the-pipe technology and that the regulator sets up a tax on gross emissions/output instead of on net emissions.¹⁴

In the first stage, the regulator selects the emission tax rate and subsidy by unit of abatement that maximizes net social welfare defined as the sum of consumer surplus and oligopoly net profits plus tax revenues minus subsidies and environmental damages:

$$\begin{aligned} \max _{\tau ,v}\int \limits _{0}^{\infty }e^{-rt}\left\{ \int _{0}^{Q}P(Q^{\prime })\textrm{d}Q^{\prime }-PQ+\sum _{i=1}^{n}\pi _{i}+\tau Q-v\Omega -D(x)\right\} \,\textrm{d}t, \end{aligned}$$

subject to differential equation (1), where $\pi _{i}$ stands for firm i’s net profits and $\Omega =\sum _{i=1}^{n}w_{i}$. Notice that consumer expenses and firms’ revenues on one hand, and firms’ tax expenses and subsidies and regulator tax revenues and subsidy expenses on the other hand, cancel out. Therefore, this optimization problem can be rewritten as:

$$\begin{aligned} \max _{\tau ,v}\int \limits _{0}^{\infty }e^{-rt}\left\{ \int _{0}^{Q(\tau ,x)}P(Q^{\prime })\textrm{d}Q^{\prime }-cQ(\tau ,x)-\sum _{i=1}^{n}\textrm{AC}(w_{i}(v,x))-D(x)\right\} \textrm{d}t, \end{aligned}$$

where $Q(\tau ,x)=\sum _{i=1}^{n}q_{i}(\tau ,x).$

The solution to this dynamic optimization problem must satisfy the following HJB equation:¹⁵

$$\begin{aligned} rW(x) =&\max _{\tau ,v}\left\{ \int _{0}^{Q(\tau ,x)}P(Q^{\prime })\textrm{d}Q^{\prime }-cQ(\tau ,x)-\sum _{i=1}^{n} \textrm{AC}(w_{i}(v,x))-D(x)\right. \nonumber \\&+ \left. W^{\prime }(x)\left( Q(\tau ,x)-\sum _{i=1}^{n}{ w_{i}(v,x)} -\delta x\right) \right\} . \end{aligned}$$

(7)

From the FOCs for the maximization of the RHS of the HJB equation, we get:

$$\begin{aligned} \left( P-c+W^{\prime }(x)\right) \frac{\partial Q}{\partial \tau }= & {} 0, \end{aligned}$$

(8)

$$\begin{aligned} -\sum _{i=1}^{n}\left( (\textrm{AC})^{\prime }(w_{i})+W^{\prime }(x)\right) \frac{ \partial w_{i}}{\partial v}= & {} 0. \end{aligned}$$

(9)

Assuming that both output and abatement are affected by the tax and subsidy, these conditions are immediately satisfied if the efficient conditions hold. Thus, using the efficient conditions along with FOCs (5) and (6), we can characterize the first-best policy. Conditions (3 ) and (5) allow us to define the optimal tax:

$$\begin{aligned} {\tau ^{I}}^{*}(x)=P^{\prime }q_{i}-(W^{\prime }(x)-{(V^{I})}^{\prime }(x)), \end{aligned}$$

(10)

and conditions (4) and (6) the optimal subsidy:

$$\begin{aligned} {v^{I}}^{*}(x)=-(W^{\prime }(x)-{(V^{I})}^{\prime }(x)). \end{aligned}$$

(11)

Notice that in both cases the policy instrument reflects the difference between the social and private valuations of a variation in the pollution stock. In the case of the tax, the variation is due to an increase in the pollution stock caused by an increase in net emissions provoked by an increase in output. In the case of the subsidy, the variation is due to a decrease in the pollution stock explained by a decrease in net emissions as a result of an increase in the abatement effort. In the case of the tax, we find an additional term equal to the difference between the marginal revenue of the firms and the price that appears because the firms have market power. With the tax, the regulator is correcting two distortions in the market allocation: the market power of the firms and a negative externality. For this reason, the tax has two components. The first, that is negative, operates as a subsidy on production to correct the market power of the firms, closing the gap between the price and the marginal revenue. The second, that is expected to be positive, operates as a tax on emissions to correct the negative externality.¹⁶ Thus, we can state that:

Remark 1

The production tax could be negative if the distortion cause by the market power of the firms is bigger than the distortion caused by the negative externality.

Nevertheless, if the main problem in the market is pollution, we should expect the opposite result and the optimal policy would be to tax gross emissions. Observe that even with a subsidy on abatement, the tax still has to correct the two distortions associated with production as occurs in Benchekroun and Long [3].

On the other hand, if we compare the optimal levels of the two instruments, we obtain the following expression

$$\begin{aligned} {\tau ^{I}}^{*}(x)-{v^{I}}^{*}(x)=P^{\prime }q_{i}. \end{aligned}$$

Then, we can conclude that:

Remark 2

The production tax rate is lower than the abatement subsidy rate.

The difference between the two rates is due to the firms’ market power. Obviously, if the firms are price-takers, the two rates coincide.

Remark 2 suggests that we should not expect that the proposed tax–subsidy scheme to be self-financing. In fact, the difference between the tax rate and the abatement subsidy rate indicates that the government could run a fiscal deficit. Of course, whether the policy yields a fiscal surplus or deficit also depends on the levels of production and abatement, but for a given pair of total production and abatement efforts, it will more likely obtain a fiscal deficit if the subsidy rate is larger than the tax rate. The numerical exercise solved in Sect. 4 is consistent with this conjecture since for the baseline case the fiscal balance is negative. Thus, the Tax–Subsidy Scheme I would implement the efficient outcome, but it would create a fiscal deficit.

3.2 Tax–Subsidy Scheme II

With a subsidy on abatement costs, firm i chooses its output and abatement to maximize the discounted present value of net profits given in this case by:

$$\begin{aligned} \max _{q_{i},w_{i}}\int \limits _{0}^{\infty }e^{-rt}\left\{ P(Q)q_{i}-cq_{i}-(1-v)\textrm{AC}(w_{i})-\tau q_{i}\right\} \textrm{d}t, \end{aligned}$$

subject to differential equation (1) where $\tau$ again is the production tax and $v\in (0,1)$ stands for a subsidy on abatement cost. v represents the percentage of the abatement costs that are covered by the subsidy. With this scheme, FOC (5) does not change, but FOC (6) will read:¹⁷

$$\begin{aligned} (1-v)(\textrm{AC})^{\prime }(w_{i})=-{(V^{II})}^{\prime }(x). \end{aligned}$$

(12)

Then, using (4), we find that the optimal subsidy is given by the following expression:

$$\begin{aligned} 1-{v^{II}}^{*}(x)=\frac{{(V^{II})}^{\prime }(x)}{W^{\prime }(x)}. \end{aligned}$$

(13)

In this case, the subsidy is also given by the different valuation that firms give to the pollution stock, but not as a difference between the social and private shadow prices of the pollution stock, as occurs when the subsidy is on abatement effort, but as a ratio, as a percentage of the private shadow price over the social shadow price. Notice that the subsidy will be positive only if $\left| {(V^{II})}^{\prime }(x)\right| <\left| W^{\prime }(x)\right|$. This point is confirmed in the LQ policy game we analyze in the next section.

Thus, the efficient solution could be implemented as a regulated market equilibrium using these two tax–subsidy schemes. Consequently, we cannot rank them looking at the net social welfare that is achieved using the two tax–subsidy schemes because both implement the efficient solution, i.e., with both schemes the maximum net social welfare is achieved. An alternative would be to assess them from a fiscal perspective. The scheme to recommend would be the one that yields a higher/lower fiscal surplus/deficit. In the next section, we introduce an LQ policy game that allows us to advance in the analysis of these two tax–subsidy schemes.

4 The LQ Policy Game

The LQ differential game we analyze in this section considers a polluting oligopoly that faces a linear (inverse) demand function given by $P=a-Q,$ where P is the price and Q the total output of the industry with $a>c$. On the other hand, we assume a quadratic abatement cost function given by AC$(w)=\gamma w^{2}/2.$ The abatement technology has decreasing returns to scale, with the parameter $\gamma$ measuring the extent of such decreasing returns. The disutility from environmental deterioration is given by the damage function $D(x)=dx^{2}/2, d>0$. Next, we characterize the efficient solution.

4.1 The Efficient Solution

If we focus on the symmetric solution, the optimal strategies for production and abatement from (3) and (4) are:

$$\begin{aligned} q^{*}(x)= & {} \frac{1}{n}(a-c+W^{\prime }(x)), \end{aligned}$$

(14)

$$\begin{aligned} w^{*}(x)= & {} -\frac{{1}}{\gamma }W^{\prime }(x). \end{aligned}$$

(15)

Then, optimal emissions can be obtained as the difference between optimal production (gross emissions) and abatement:

$$\begin{aligned} e^{*}(x) =q^{*}(x)-w^{*}(x) =\frac{a-c}{n}+\frac{\gamma +n}{ n\gamma }W^{\prime }(x). \end{aligned}$$

(16)

Now, substituting production and abatement by the efficient strategies (14) and (15) in the regulator’s HJB equation (5) for the LQ policy game and rearranging terms, we obtain the following nonlinear differential equation:

$$\begin{aligned} rW(x)=\frac{1}{2}(s^{2}-dx^{2})+(s-\delta x)W^{\prime }(x)+\frac{\gamma + {n}}{2\gamma }(W^{\prime }(x))^{2}, \end{aligned}$$

(17)

where $s=a-c>0.$

In order to find the solution for this equation, we guess a quadratic representation for the value function W : 

$$\begin{aligned} W(x)=\frac{A_{r}}{2}x^{2}+B_{r}x+C_{r}, \end{aligned}$$

which implies that ${W}^{\prime }(x)=A_{r}x+B_{r}$ and where $A_{r},\ B_{r}$ , and $C_{r}$ are unknowns to be determined.¹⁸

The substitution of W(x) and ${W}^{\prime }(x)$ into (17) gives a system of Riccati equations that must be satisfied for every x. Selecting the stable solution of this system, which requires that $d{\dot{x}}/dx<0,\$we obtain the following values for the first two coefficients of the regulator’s value function:

$$\begin{aligned} A_{r}= & {} \frac{\gamma (r+2\delta )-(\gamma ^{2}(r+2\delta )^{2}+4d\gamma {(\gamma +n)})^{1/2}}{2{(\gamma +n)}}<0, \end{aligned}$$

(18)

$$\begin{aligned} B_{r}= & {} \frac{s\gamma A_{r}}{\gamma (r+\delta )-(\gamma +n)A_{r}}<0. \end{aligned}$$

(19)

Then, the optimal strategies for production, abatement, and emissions read:

$$\begin{aligned} q^{*}(x)= & {} \frac{s(\gamma (\delta +r)-nA_{r})}{n(\gamma (\delta +r)- {(\gamma +n)}A_{r})}+\frac{A_{r}}{n}x, \end{aligned}$$

(20)

$$\begin{aligned} w^{*}(x)= & {} \frac{{s}A_{r}}{{(\gamma +n)} A_{r}-\gamma (\delta +r)}-\frac{A_{r}}{\gamma }x, \end{aligned}$$

(21)

$$\begin{aligned} e^{*}(x)= & {} \frac{\gamma s(r+\delta )}{n(\gamma (\delta +r)- {(\gamma +n)}A_{r})}+\frac{{(\gamma +n)}A_{r}}{ n\gamma }x. \end{aligned}$$

(22)

From the optimal strategy for emissions and the differential equation (1), and taking into account the first Riccati equation for $A_{r},$ the steady-state pollution stock is obtained:

$$\begin{aligned} x^{SS}=\frac{s\gamma (r+\delta )}{(\gamma +{n})d+\gamma \delta (r+\delta )}. \end{aligned}$$

From the expression above, it can be easily shown that the steady-state pollution stock increases with s, r and $\gamma ,$ and decreases with n and d. The different parameters influence the steady-state pollution stock in different ways. On the one hand, the market size, s,  is like a scale parameter in these kinds of models so that the higher s, the higher gross and net emissions. Therefore, we should expect that the pollution stock increases with the market size as the previous expression confirms. The rate of discount, as it is well known, gives more or less weight to the future in current decisions. Thus, a higher rate of discount will reduce the importance of the future environmental damages in today’s decisions on production and emissions, resulting in a larger accumulation of emissions. Finally, we also expect that a larger $\gamma$ yields a larger steady-state pollution stock because when the marginal costs of abatement are higher, firms will reduce the abatement efforts producing more net emissions that will lead to a higher pollution stock. On the other hand, an increase in the marginal damage function caused by an increase in parameter d will cause a reduction in the pollution stock through an increase in its shadow price. Notice that an increase in the shadow price will reduce the production and increase the abatement effort resulting in lower net emissions. Finally, we find that more competition not only reduces the market power of the firms, but also reduces the long-run equilibrium pollution stock. In our model, competition is good for the environment.

According to the optimal strategies, production and emissions decrease with the pollution stock, whereas abatement increases with the pollution stock. Thus, there exists a level for the pollution stock for which emissions are zero. From equation $e^{*}(x)=0$ this value reads:

$$\begin{aligned} x_{e}=-\frac{s\gamma ^{2}(r+\delta )}{A_{r}{(\gamma +n)} \left( \gamma (\delta +r)-{(\gamma +n)}A_{r}\right) }. \end{aligned}$$

(23)

This threshold can be easily compared with the steady-state value of the pollution stock, as follows:

$$\begin{aligned} x_{e}-x^{SS}=-\frac{s\gamma ^{3}\delta (r\!+\! \delta )}{A_{r} {(\gamma +n)}\left( \gamma \delta -{(\gamma +n)}A_{r}\right) \left( \gamma (\delta \!+\!r)-{(\gamma +n)} A_{r}\right) }. \end{aligned}$$

The difference above is positive because $A_{r}$ is negative.

Proposition 1

The efficient solutions for the total output, the abatement, and the emissions are nonnegative in the interval $[0,x_{e}]$ with the steady-state pollution stock $x^{SS}$ belonging to this interval. In this interval, total output and emissions decrease and abatement increases with the pollution stock.

Finally, we characterize the dynamics of the pollution stock. Substituting emissions given by (22) in the dynamics of the pollution stock defined by (1), we obtain the following differential equation for the pollution stock:

$$\begin{aligned} {\dot{x}}=\frac{s\gamma (r+\delta )}{\gamma (r+\delta )-{( \gamma +n)}A_{r}}+\left( \frac{{(\gamma +n)}A_{r}}{\gamma } -\delta \right) x, \end{aligned}$$

whose solution is:

$$\begin{aligned} x^{*}(t)=(x_{0}-x^{SS})e^{\alpha t}+x^{SS},\text {\ with }\alpha =\frac{ {(\gamma +n)}A_{r}}{\gamma }-\delta <0, \end{aligned}$$

(24)

for $x_{0}$ in the interval $[0,x_{e}]$. Then, the dynamics of the model can be summarized as follows

Remark 3

If $x_{0}$ is lower than $x^{SS},$ abatement increases asymptotically to its steady-state value, whereas production and emissions decrease. However, if $x_{0}\ \in (x^{SS},x_{e}],$ the dynamics are the opposite and abatement decreases asymptotically to its steady-state value, whereas production and emissions increase.

Observe that the optimal strategy for emissions (22) only gives non-negative emissions in the interval of the pollution stock $[0,x_{e}]$ which includes the steady-state pollution stock. If the initial pollution stock is larger than $x_{e},$ then the non-negative constraint applies and the efficient level of emissions is zero. In this case, the pollution would decrease according to the differential equation ${\dot{x}}=-\delta x$ until $x_{e}$ were reached in a finite time. From this level, the dynamics of the pollution stock is given by (24) and the pollution stock converges asymptotically to its steady-state value.

4.2 Tax–Subsidy Scheme I

Once the efficient solution has been obtained, we calculate the optimal policy rules that implement the efficient outcome as a regulated market equilibrium. According to (10), the optimal tax for a linear demand function is ${\tau ^{I}}^{*}(x)=-q^{*}(x)-(W^{\prime }(x)-{(V^{I})} ^{\prime }(x)),$ when using (14) yields:

$$\begin{aligned} {\tau ^{I}}^{*}(x)={(V^{I})}^{\prime }(x)-\frac{s+(n+1)W^{\prime }(x)}{n} . \end{aligned}$$

(25)

Thus, in order to completely characterize the optimal tax and the optimal subsidy, we need to solve the firm’s HJB equation. With this aim, we substitute the tax and the subsidy given by (25) and (11) and substitute the production and abatement defined by (14) and (15 ), in the firm’s HJB equation:

$$\begin{aligned} rV^{I}(x)=(a-nq)q-cq-\tau q+vw-\frac{\gamma }{2}w^{2}+{(V^{I})}^{\prime }(x)( {n(q-w)}-\delta x), \end{aligned}$$

and we obtain the following differential equation

$$\begin{aligned} rV^{I}(x) =&\frac{1}{n^{2}}(s+W^{\prime }(x))^{2}+\frac{ {1}}{2\gamma }W^{\prime }(x)^{2} +(n-1)\frac{ {\gamma +n}}{\gamma n}{(V^{I})}^{\prime }(x)W^{\prime }(x)+ \nonumber \\&+ \frac{(n-1)s-\delta nx}{n}{(V^{I})}^{\prime }(x). \end{aligned}$$

(26)

In order to solve this equation, we also guess a quadratic representation:

$$\begin{aligned} V^{I}(x)=\frac{A_{f}^{I}}{2}x^{2}+B_{f}^{I}x+C_{f}^{I}, \end{aligned}$$

which yields ${(V^{I})}^{\prime }(x)=A_{f}^{I}x+B_{f}^{I}.$¹⁹

The substitution of $V^{I}(x)$ and ${(V^{I})}^{\prime }(x)$ along with ${W}^{\prime }(x)$ into (26) gives a system of Riccati equations whose solution for coefficients $A_{f}^{I}$ and $B_{f}^{I}$ is:

$$\begin{aligned} A_{f}^{I}= & {} \frac{{(2\gamma +n^{2})}A_{r}^{2}}{n(n\gamma (r+2\delta )-2(n-1){(\gamma +n)}A_{r})}>0, \nonumber \\ B_{f}^{I}= & {} \frac{n\gamma (r+2\delta )(2s\gamma +{(2\gamma +n^{2})}B_{r})A_{r}}{n(n\gamma (r+\delta )-(n-1){(\gamma +n)} A_{r})(n\gamma (r+2\delta )-2(n-1){(\gamma +n)} A_{r})} \end{aligned}$$

(27)

$$\begin{aligned}{} & {} +\frac{(n-1)(s\gamma {(n(n-4)-2\gamma )}-{( \gamma +n)(2\gamma +n^{2})}B_{r})A_{r}^{2}}{n(n\gamma (r+\delta )-(n-1) {(\gamma +n)}A_{r})(n\gamma (r+2\delta )-2(n-1) {(\gamma +n)}A_{r})}, \end{aligned}$$

(28)

where $A_{r}<0$ is given by (18)²⁰. Then, eliminating ${(V^{I})} ^{\prime }(x)$ and $W^{\prime }(x)$ in (25) using the coefficients of the value functions, the optimal tax is obtained.

Proposition 2

The optimal tax is given by the following rule:

$$\begin{aligned} {\tau ^{I}}^{*}(x)= & {} -\frac{1}{n}(s+(n+1)B_{r}-nB_{f}^{I})\nonumber \\{} & {} +\frac{ {n(2(n^{2}-1)+(1+2\gamma )n)}A_{r}^{2}-(n+1)\gamma (r+2\delta )A_{r}}{n^{2}\gamma (r+2\delta )-2(n-1)n{(n+\gamma )}A_{r}}x, \end{aligned}$$

(29)

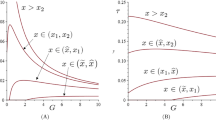
where $A_{r}$ is negative. The tax increases with the pollution stock, but it could be negative for low values of the pollution stock.

It is easy to find values of the parameters for which the intersection point with the vertical axis of the tax rule (29) is negative.²¹ When this is the case, the optimal policy consists of setting up a subsidy for low values of the pollution stock, as in Benchekroun and Long [3] and for exactly the same reasons. In our model, the subsidy only corrects the divergence between the private and social valuation of a variation in the pollution stock caused by a variation of the abatement effort. Then, the tax, as expression (10) shows, must correct the market power of the firms and the negative externality caused by production. The result is that the sign of the optimal policy given by expression (10) remains undetermined. Nevertheless, Prop. 2 establishes that the sign of the policy given by (29) also depends on the pollution stock, and that regardless of whether the tax is negative or positive when $x=0$, the tax increases with the pollution stock.

To obtain the optimal subsidy, we only need to eliminate ${(V^I)}^{\prime }(x)$ and $W^{\prime }(x)$ in (11) using the coefficients of the value functions already computed.

Proposition 3

The optimal subsidy is given by the following rule:

$$\begin{aligned} {v^{I}}^{*}(x)=B_{f}^{I}-B_{r}+\frac{{(2\gamma +n^{2}+2(n-1)n(\gamma +n))}A_{r}^{2}-n^{2}\gamma (r+2\delta )A_{r}}{ n(n\gamma (r+2\delta )-2(n-1){(\gamma +n)}A_{r})}x, \end{aligned}$$

(30)

where $A_{r}$ is negative.The subsidy increases with the pollution stock and it is positive for all $x\in [0,x_{e}].$

Proof

See Appendix. $\square$

Unlike the tax, the subsidy cannot be negative. This result establishes, according to expression (11), that the social shadow price of the pollution stock is larger than the private shadow price for all x, i.e., $\left| W^{\prime }(x)\right| >\left| {(V^I)}^{\prime }(x)\right| .\$ Then, we can confirm that the second term on the LHS of expression (10) is positive. Thus, the tax presents two components, one negative—equal to the difference between the marginal revenue and the price, and one positive—equal to the difference between the social shadow price of the pollution stock and its private valuation.

4.2.1 Numerical Example and Sensitivity Analysis

In Sect. 4.1 we analyzed the effects of the model parameters on the steady-state pollution stock. However, it is difficult to do the same exercise for the other variables of the model, because when a parameter changes not only is the pollution stock affected, but also the optimal policy rules obtained in the previous subsection. Thus, to know the effect of a change in one parameter on the variables of the model, we need to evaluate how the steady-state pollution stock is affected, and how the change affects the slope and the intersection point with the vertical axis of the optimal policy rules. The same occurs for the optimal strategies for production, abatement and emissions. The complexity of the expressions prevents obtaining analytical results. For this reason, we present a numerical exercise to get an intuition.

Let us consider the following values of the parameter as a baseline case:

$$\begin{aligned} a-c=1000,\; \delta =0.01,\;r=0.03,\;n=2,\; \gamma =3,\; d=0.025. \end{aligned}$$

(31)

From this baseline case, we carry out a sensitivity analysis with respect to the following parameters: environmental damage (d), abatement efficiency ($\gamma$), and degree of industry competition (n). For each parameter, we consider five different values. In each table (Tables 1, 2 and 3), we present the optimal policy rules and the steady-state pollution stock, as well as the regulator’s policies and the firm’s control variables, output, q, and abatement, w, as well as the net emissions, e, evaluated at the steady-state pollution stock.

First, we consider the environmental damage coefficient d: 0.01, 0.015, 0.025, 0.035, and 0.05.

Table 1 Sensitivity analysis of the optimal policies and firm’s controls with respect to changes in parameter d

An easy comparison of the emission tax and the abatement subsidy for the different entries in Table 1 allows us to conclude that as the environmental damage parameter increases, both the intersection point with the vertical axis and the slope of the tax and the subsidy increase, and hence, the tax and the subsidy also increase for any level of the pollution stock. The steady-state of the pollution stock decreases as parameter d increases. However, this fall is more than compensated by the increase in the regulator’s optimal tax and subsidy rules, implying that at the steady state both instruments augment with d. Concerning the firm’s instruments at the steady-state, any increase of the environmental damage parameter reduces output and augments abatement, and consequently net emissions are reduced. As expected, more damages imply higher taxes and subsidies leading to less net and gross emissions and a lower steady-state pollution stock.

Next, we focus on the effect of the abatement efficiency parameter ($\gamma$ ). We consider the following five values of $\gamma$: 2.5, 2.75, 3, 3.25, and 3.5.

Table 2 Sensitivity analysis of the optimal policies and firm’s controls with respect to changes in parameter $\gamma$

Table 2 states that as $\gamma$ increases and firms operate with higher abatement costs, the regulator’s optimal policies increase for any value of the pollution stock (both the intersection point with the vertical axis and the slope of the policies increase with $\gamma$) as occurs with an increase in d. But now that $\gamma ,$ has a larger value, the steady-state of the pollution stock is higher. Consequently, both the long-run emission tax and subsidy on abatement increase too. The stricter tax policy and laxer subsidy policy as $\gamma$ becomes higher reduce the output and the abatement level, with the later effect being stronger than the former and hence implying a rise in net emissions.

Next, we analyze the effect of industry competition measured by the number of firms on the optimal regulatory rules and the firms’ decisions. We start from the base case of a duopoly ($n=2$) and increase the number of firms in the industry, n: 3, 5, 7, and 9.

Table 3 Sensitivity analysis of the optimal policies and firm’s controls with respect to changes in parameter n

Table 3 shows that as industry competition increases both the optimal tax on emissions and the optimal subsidy on abatement decrease, because for both policy rules the ordinate at the origin and the slope decrease as the number of firms in the industry increases. However, there is a case for which this does not occur, when comparing a duopoly with a triopoly. In this case, the intersection point with the vertical axis increases. However, this increase is not enough as to yield a higher tax when the number of firms goes from 2 to 3 and the steady-state tax decreases when the number of firms augments. The decrease in the tax and in the subsidy comes with a reduction in the steady-state pollution stock. A laxer tax policy and less generous subsidy as competition increases lead to lower levels of output, abatement, and net emissions in the long run for firms. Thus, as we already pointed out in Sect. 4.1, competition is good for the environment since it reduces net emissions and the pollution stock. Moreover, we should highlight that competition also increases the total output and the total abatement of the industry, although the individual production and abatement decrease. The total output for the duopoly is 450.7, and when the industry is formed by 9 firms it is equal to 750.9. The total abatement is 396.2 for the duopoly, but it is equal to 747 when there are 9 firms in the industry. More firms in the industry means more production and abatement. Thus, competition, on the one hand, increases the consumer surplus and reduces the damages, and—on the other hand, increases production and abatement costs. But the net effect is a larger welfare as the last row of Table 3 shows. Then, we can conclude that competition not only improves the efficiency of resource allocation, but is also good for the environment.

4.3 Tax–Subsidy Scheme II

The efficient outcome can also be implemented combining a tax on production with a subsidy on abatement costs. However, the use of a different policy mix implies that the value function of the firm changes. Now, the HJB equation of the firm is:

$$\begin{aligned} rV^{II}(x)=(a-nq)q-cq-\tau q-(1-v)\frac{\gamma }{2}w^{2}+{(V^{II})}^{\prime }(x)({ n(q-w)}-\delta x), \end{aligned}$$

so that if we substitute the subsidy and the tax by expressions (13) and (25) and the production and the abatement by the efficient strategies given by (14) and (15), we obtain the following differential equation:

$$\begin{aligned} rV^{II}(x)= & {} \frac{1}{n^{2}}(s+W^{\prime }(x))^{2}+\left( \frac{n-1}{n}+{ \frac{ 2n-1 }{2\gamma }}\right) {(V^{II})}^{\prime }(x)W^{\prime }(x) \nonumber \\{} & {} +\frac{(n-1)s-\delta nx}{n}{(V^{II})}^{\prime }(x). \end{aligned}$$

(32)

For solving this equation, we propose a quadratic specification:

$$\begin{aligned} V^{II}(x)=\frac{A_{f}^{II}}{2}x^{2}+B_{f}^{II}x+C_{f}^{II}, \end{aligned}$$

for which ${({V^{II}})}^{\prime }(x)=A_{f}^{II}x+B_{f}^{II}.^{22}$ Substituting ${V^{II}}(x), {(V^{II})}^{\prime }(x)$, and $W^{\prime }(x)$ into (32) gives a system of Riccati equations whose solution for the first two coefficients is:²²

$$\begin{aligned} A_{f}^{II}= & {} \frac{2A_{r}^{2}}{n^{2}(r+2\delta -2\eta A_{r})}>0, \end{aligned}$$

(33)

$$\begin{aligned} B_{f}^{II}= & {} \frac{2(n(s+B_{r})(r+2\delta )+\left( (n-1)s-n\eta (2s+B_{r})\right) A_{r})A_{r}}{n^{3}(r+2\delta -2\eta A_{r})(r+\delta -\eta A_{r})}<0, \end{aligned}$$

(34)

where

$$\begin{aligned} \eta =\frac{n-1}{n}+\frac{{2n-1}}{2\gamma }>0, \end{aligned}$$

(35)

and $A_{r}<0$ is given by (18).²³ Then, substituting ${ (V^{II})}^{\prime }(x)$ and $W^{\prime }(x)$ in (25) using the coefficients of the value functions, we can calculate the optimal tax.

Proposition 4

The optimal tax is defined by the following rule:

$$\begin{aligned} {\tau ^{II}}^ *(x)=-\frac{1}{n}(s+(n+1)B_{r}-nB_{f}^{I}) +\ \frac{ 2(n(n+1)\eta +1)A_{r}^{2}-n(n+1)(r+2\delta )A_{r}}{n^{2}(r+2\delta -2\eta A_{r})}x, \nonumber \\ \end{aligned}$$

(36)

where $A_{r}$ is negative. The tax increases with the pollution stock, but it can be negative for low values of the pollution stock.

As occurs when a subsidy is applied to the abatement effort and for the same reasons, the optimal policy could consist of fixing a subsidy on production for low values of the pollution stock. Finally, eliminating ${(V^{II})} ^{\prime }(x)$ and $W^{\prime }(x)$ in (13) using the coefficients of the value functions, we obtain the optimal subsidy.

Proposition 5

The optimal subsidy is given by the following rule:

$$\begin{aligned} 1-{v^{II}}^{*}(x)=\frac{2A_{r}^{2}x+B_{f}^{II}n^{2}(r+2\delta -2\eta A_{r})}{n^{2}(r+2\delta -2\eta A_{r})(A_{r}x+B_{r})}. \end{aligned}$$

(37)

For $x\le x_{e}<x_{v}=-B_{f}^{II}n^{2}(r+2\delta -2\eta A_{r})/(2A_{r}^{2}),\ {v^{II}}^{*}(x)$ is an increasing strictly concave function of the pollution stock in the interval [0, 1].

Proof

See the Appendix. $\square$

Observe that although the policy game we have proposed is an LQ differential game, in this case the subsidy rule is not linear. The subsidy rule is an increasing and strictly concave function of the pollution stock for all $x\in [0,x_{e}]$. Thus, we find that the subsidy on abatement costs increases with the pollution stock, but at a decreasing rate.

We have also carried out a sensitivity analysis for Tax–Subsidy Scheme II, but we only report here the cases for which we have found qualitative differences with the results obtained for Tax–Subsidy Scheme I. For the rest of cases we have found the same qualitative results. For the lowest value of d, the intersection point with the vertical axis of the tax rule is negative. Thus, in this case, the optimal policy consists of subsidizing the production for low values of the pollution stock, although the taxes at the steady state are positive. This result suggests that we should expect that the lower the environmental damage parameter, d, the higher the chances that the tax rule crosses the vertical axis at a negative value. With low values of d, the market distortion caused by the market power of firms can be more serious than the one caused by the environmental externality, and then we should expect that the tax becomes a subsidy. We also find differences in the effects that the different parameters have on the subsidy. Whereas an increase in d augments the subsidy when it is applied to the abatement effort, it reduces the subsidy on the abatement costs. Finally, in the case of the number of firms, the opposite occurs. More firms in the market reduce the subsidy on the abatement effort, but increase the subsidy on abatement costs. Thus, not only can two different incentive structures implement the same outcome, but they respond in a different way to changes in the parameter values of the model.

4.4 Comparison of the Tax–Subsidy Schemes

Although, as we have just seen, the two schemes implement the efficient solution, we expect that they yield differences in fiscal terms. In this subsection we try to assess these differences. The next proposition evaluates the effect on the tax rule of using a different subsidy.

Proposition 6

The optimal taxes for the two tax–subsidy schemes compare as follows:

$$\begin{aligned} {\tau ^I}^*(x)>{\tau ^{II}}^*(x) \quad \text { for any } \; x\ge 0. \end{aligned}$$

Proof

See the Appendix. $\square$

The proposition establishes that for any value of the pollution stock, the optimal tax when the subsidy is for the abatement effort is greater than when it is for abatement costs. In the proof of this result, we show that both the slope of the optimal rule and the intersection with the vertical axis when a subsidy is applied to abatement costs are lower than when a subsidy is directly applied to abatement. As both tax–subsidy schemes implement the efficient solution, the steady-state pollution stock will be the same and consequently the steady-state tax will be higher when a subsidy is applied to abatement rather than to abatement costs. Therefore, as a direct consequence of the proposition we can conclude that:

Corollary 1

The tax revenues at the steady state are higher when the subsidy is applied to the abatement effort rather than to abatement costs.

However, from a fiscal point of view, what is relevant is the fiscal balance, i.e., the difference between the tax revenues and the subsidy expenses. For the example at hand, we can compute the fiscal balance for the two schemes. For the baseline case, if a subsidy on abatement is applied, the fiscal balance is given by the following expression:

$$\begin{aligned} {\tau ^I }^{*}(x)q^{*}(x)-{v^I }^{*}(x)w^{*}(x)= {-0.017x^{2}+1.017x-24343.0}. \end{aligned}$$

It can be easily shown that the expression above always takes negative values for any value of the pollution stock, and therefore, there is always a fiscal deficit.

For the baseline case, if instead a subsidy on abatement costs is applied the fiscal balance reads:

$$\begin{aligned} {\tau ^{II} }^{*}(x)q^{*}(x)-{v^{II} }^{*}(x)\frac{\gamma }{2} (w^{*}(x))^{2}={-0.0074x^{2}+4.426x-11798.7}. \end{aligned}$$

In this case, there is a fiscal deficit too.

Finally, if we compare the fiscal balances at the steady state, we see that the fiscal deficit is lower when the subsidy is on abatement costs which means that subsidy expenses are lower in this case, since we have already showed that the tax revenues are also lower. Thus, when Tax–Subsidy Scheme II is used, the government will collect less taxes and spend less money on subsidies for the firms, resulting in a negative fiscal balance that is lower than the fiscal deficit the government will obtain applying Tax–Subsidy Scheme I. Then, if the criterion for choosing the type of subsidy by the regulator is the one that generates the most favorable fiscal balance, the regulator will choose to subsidize the abatement costs.

5 Conclusions

This paper studies an efficiency-inducing policy for a polluting oligopoly when pollution abatement is technologically feasible and environmental damages depend on the pollution stock. Using a dynamic policy game between the regulator and the oligopolists, we show that a tax–subsidy scheme can implement the efficient outcome as a regulated market equilibrium. The scheme consists of a combination of a tax on production and a subsidy. For the subsidy, we consider two alternatives. A subsidy on the abatement effort and a subsidy on abatement costs. Both schemes yield a different tax rule, but both implement the efficient outcome. We have shown that the subsidy only reflects the divergence between the social and private valuation of the pollution stock associated with the decision on abatement, and consequently, the tax has to correct the two market failures associated with production: the market power of firms and the negative externality caused by pollution. Thus, the tax could be negative if the first distortion dominates the second. Nevertheless, if the main distortion in the market allocation is the one caused by pollution, the efficiency-inducing policy will consist of a tax on production and a subsidy either on the abatement effort or the abatement costs. Although both policies implement the efficient outcome, they yield different fiscal balances. Using an LQ policy game, we find that the application of a subsidy on abatement costs relaxes the tax rule. Interestingly, it also yields a lower fiscal deficit at the steady state. A numerical exercise shows that both tax–subsidy schemes present a negative balance at the steady state for all parameter values we have studied, but when a subsidy on abatement costs is applied, the fiscal deficit is always lower. Thus, our policy recommendation is that, from a fiscal perspective, a subsidy on abatement costs should be adopted instead of a subsidy on abatement.

A limitation of our approach is that it is assumed an emission function that is additively separable in production (gross emissions) and abatement. To overcome this limitation, a possibility would be to consider an abatement technology that could reduce the emissions to output ratio.²⁴ We could also consider that the abatement capital could be adjusted through investment.²⁵ In this case, we could analyze the dynamic interdependence between the accumulation of emissions and the investment. A further step in this line of research would be to characterize the optimal environmental policy when the pollution stock or the abatement capital are subject to a stochastic evolution.²⁶ Finally, another interesting issue to address would be to investigate which would be the optimal environmental policy with free entry in the market. All these questions are part of our research agenda.

Appendix

Proof of Proposition 3

As the subsidy increases with the pollution stock, we can conclude that the subsidy is guaranteed to be positive for all $x\ge 0$ if the intersection with the vertical axis, $B_{f}^{I}-B_{r},\$ is positive too. According to (28), this difference is given by the following expression

$$\begin{aligned}{} & {} B_{f}^{I}-B_{r} \\= & {} \frac{n\gamma (r\!+\!2\delta )(2s\gamma \!+\! {(2\gamma \!+\!n^{2})}B_{r})A_{r}\!+\!(n\!-\!1)(s\gamma {(n(n\!-\!4)\!- \!2\gamma )}\!-\!(n\!+\! \gamma )(2\gamma \!+\!n^{2})B_{r})A_{r}^{2}}{ n(n\gamma (r\!+\! \delta )\!-\!(n\!-\!1)(n\!+\! \gamma )A_{r})(n\gamma (r\!+\!2\delta )\!-\!2(n\!-\!1)(n\!+\! \gamma )A_{r})} \\{} & {} -B_{r}. \end{aligned}$$

Next, we develop this difference

$$\begin{aligned}{} & {} B_{f}^{I}-B_{r}\nonumber \\= & {} \frac{n\gamma (r+2\delta )(2s\gamma +{ (2\gamma +n^{2} )} B_{r})A_{r}}{n(n\gamma (r+\delta )-(n-1){ (n+\gamma )} A_{r})(n\gamma (r+2\delta )-2(n-1){ (n+\gamma )}A_{r})} \nonumber \\{} & {} +\frac{(n-1)(s\gamma { (n(n-4)-2\gamma )}-{ (n+\gamma )(2\gamma +n^{2})}B_{r})A_{r}^{2}}{n(n\gamma (r+\delta )-(n-1){ (n+\gamma )}A_{r})(n\gamma (r+2\delta )-2(n-1){ (n+\gamma )}A_{r})} \nonumber \\{} & {} -\frac{B_{r}n(n\gamma (r+\delta )-(n-1){ (n+\gamma )} A_{r})(n\gamma (r+2\delta )-2(n-1){ (n+\gamma )}A_{r}) }{n(n\gamma (r+\delta )-(n-1){ (n+\gamma )}A_{r})(n\gamma (r+2\delta )-2(n-1){ (n+\gamma )}A_{r})}. \end{aligned}$$

(38)

As the denominator in the expressions above is positive because $A_{r}$ is negative, we focus on the sign of the numerator. Substituting $B_{r}$ by (19) and developing the numerator yields

$$\begin{aligned} \frac{s\gamma A_{r}(f_{0}A_{r}^{2}+f_{1}A_{r}+f_{2})}{{ (n+\gamma ) }A_{r}-(r+\delta )\gamma }>0, \end{aligned}$$

since

$$\begin{aligned} f_{0}= & {} { (n-1)n(2\left( n^{2}-2\right) n+2\left( 2n^{2}-n-2\right) \gamma }+2\left( n-1\right) \gamma ^{2})>0, \\ f_{1}= & {} { -\gamma (n^{3}(n-2)(r+2\delta )+n\left( n-1\right) \left( 2n^{2}+n-4\right) (r+\delta )} \\{} & {} +n^{2}(n-1)(r+2\delta )\gamma +2\left( n+1\right) \left( n-1\right) ^{2}(r+\delta )\gamma )<0, \\ f_{2}= & {} n(r+2\delta )(r+\delta )\gamma ^{2}\left( n^{2}-2\right) >0, \end{aligned}$$

for $n\ge 2.$ Thus, the numerator of (38) is positive and hence the difference $B_{f}^{I}-B_{r}$ is positive too and we can conclude that the subsidy on abatement effort is positive for all $x\ge 0$.

Sign of Coefficient $B_{f}^{II}$

The sign of coefficient $B_{f}^{II}$ according to (34) depends on the sign of the following expression (one of the factors in the numerator) since the denominator is positive because $A_{r}$ is negative

$$\begin{aligned} n(s+B_{r})(r+2\delta )+\left( (n-1)s-n\eta (2s+B_{r})\right) A_{r}. \end{aligned}$$

(39)

Substituting $B_{r}$ by (19), expression (39) reads:

$$\begin{aligned}{} & {} \frac{s}{\gamma (\delta +r)-{ (\gamma +n)}A_{r}}\left( n\gamma (\delta +r)(r+2\delta )-{ n^{2}(r+2\delta )}A_{r}\right. \nonumber \\{} & {} \left. \hspace{1cm}+\gamma (n-1-2n\eta )(\delta +r)A_{r}+{ (n\eta (\gamma +2n)}-(n-1){ (\gamma +n)})A_{r}^{2}\right) . \end{aligned}$$

(40)

Now, we use (35) to eliminate $\eta \$resulting in

$$\begin{aligned} n-1-2n\eta =-\left( (n-1)+\frac{{ n(2n-1)}}{\gamma }\right) <0, \end{aligned}$$

and

$$\begin{aligned} n\eta { (\gamma +2n)}-(n-1){ (\gamma +n)}= (n-1)n+\frac{ n(2n-1)}{2\gamma }{ (\gamma +2n)} >0. \end{aligned}$$

Then, expression (40) is positive because $A_{r}$ is negative. Consequently (39) is positive, hence, multiplied by $A_{r}$ gives a negative value for the numerator of (34) and then we can conclude that $B_{f}^{II}$ is negative.

Proof of Proposition 5

For the subsidy rule defined by (37), the denominator is negative since $A_{r}$ and $B_{r}$ are negative. On the other hand, the numerator is an increasing linear function that takes a negative value for $x=0$, because $B_{f}^{II}$ is negative. Then, we can conclude that $1-{v^{II}}^{*}(x)$ is positive for all $x<x_{v}=-B_{f}^{II}n^{2}(r+2\delta -2\eta A_{r})/(2A_{r}^{2})$, where $x_{v}$ is the pollution stock for which the numerator is null. We have to ensure that ${v^{II}}^{*}(x)$ is in the interval (0, 1). To show this point, first we check that ${v^{II}}^{*}(0)$ belongs to this interval. As $1-{v^{II}}^{*}(0)=B_{f}^{II}/B_{r}>0,\ {v^{II}}^{*}(0)$ must be lower than 1 and it will be higher than 0 if $B_{r}<B_{f}^{II}.$ The difference between these two coefficients according to (34) is given by

$$\begin{aligned} B_{r}-B_{f}^{II}= & {} B_{r}-\frac{2(n(s+B_{r})(r+2\delta )+\left( (n-1)s-n\eta (2s+B_{r})\right) A_{r})A_{r}}{n^{3}(r+2\delta -2\eta A_{r})(r+\delta -\eta A_{r})} \nonumber \\= & {} \frac{n^{3}(r+2\delta -2\eta A_{r})(r+\delta -\eta A_{r})B_{r} }{n^{3}(r+2\delta -2\eta A_{r})(r+\delta -\eta A_{r})} \nonumber \\{} & {} -\frac{2(n(s+B_{r})(r+2\delta )+\left( (n-1)s-n\eta (2s+B_{r})\right) A_{r})A_{r}}{n^{3}(r+2\delta -2\eta A_{r})(r+\delta -\eta A_{r})} , \end{aligned}$$

(41)

where the denominator is positive because $A_{r}$ is negative. Substituting $B_{r}$ by (19) in the numerator and developing it gives

$$\begin{aligned} -\frac{sA_{r}(k_{0}A_{r}^{2}+k_{1}A_{r}+k_{2})}{{ (n+\gamma )} A_{r}-(r+\delta )\gamma }<0, \end{aligned}$$

since

$$\begin{aligned} k_{0}= & {} (n(n-1)-1)\gamma +{ \frac{n}{2}(n(2n-1)-4)}>0, \\ k_{1}= & {} -\left( \frac{{ n(2n-1)-4}}{2}+\gamma (n-1)\right) <0, \\ k_{2}= & {} n(n^{2}-2)(r+2\delta ))(r+\delta )\gamma >0, \end{aligned}$$

for $n\ge 2.$ Thus, we can establish that (41) is negative that implies $B_{r}<B_{f}^{II}.$ Then, we can conclude that ${v^{II}}^{*}(0)\in (0,1).$ Finally, we calculate the derivative of $1-{v^{II}}^{*}(x)$ with respect to the pollution stock

$$\begin{aligned} (1-{v^{II}}^{*})^{\prime }(x)= & {} \frac{2A_{r}^{2}n^{2}(r+2\delta -2\eta A_{r})(A_{r}x+B_{r})}{n^{4}(r+2\delta -2\eta A_{r})^{2}(A_{r}x+B_{r})^{2}} \\- & {} \frac{(2A_{r}^{2}x+B_{f}n^{2}(r+2\delta -2\eta A_{r}))n^{2}(r+2\delta -2\eta A_{r})A_{r}}{n^{4}(r+2\delta -2\eta A_{r})^{2}(A_{r}x+B_{r})^{2}}, \end{aligned}$$

that takes a negative value for $x<x_{v}.$ Then, we have that ${v^{II}} ^{*}(x)$ must be increasing, but as $1-{v^{II}}^{*}(x)$ is positive for all $x<x_{v},$ ${v^{II}}^{*}(x)$ cannot reach a value higher than 1 for $x\in [0,x_{v}).$ In order to find the sign of the second derivative of the subsidy, we will use (13) instead of (37). The second derivative of this expression yields

$$\begin{aligned} {{(v^{II}}^{*})}^{\prime \prime }(x)= & {} \frac{1}{\left( W^{\prime }(x)\right) ^{3}}\left\{ W^{\prime }(x)\left[ {(V^{II})}^{\prime }(x)W^{\prime \prime \prime }(x)-{(V^{II})}^{\prime \prime \prime }(x)W^{\prime }(x)\right] \right. \\{} & {} -\left. 2W^{\prime \prime }(x)\left[ {(V^{II})}^{\prime }(x)W^{\prime \prime }(x)-{(V^{II})}^{\prime \prime }(x)W^{\prime }(x)\right] \right\} , \end{aligned}$$

that for the LQDG simplifies resulting in

$$\begin{aligned} {{(v^{II}}^{*})}^{\prime \prime }(x)=-\frac{2W^{\prime \prime }(x)}{ \left( W^{\prime }(x)\right) ^{3}}\left[ {(V^{II})}^{\prime }(x)W^{\prime \prime }(x)-{(V^{II})}^{\prime \prime }(x)W^{\prime }(x)\right] , \end{aligned}$$

(42)

where $W^{\prime }(x)$ and $W^{\prime \prime }(x)$ are negative and ${ (V^{II})}^{\prime \prime }(x)$ is positive. On the other hand, we have just concluded that $1-{v^{II}}^{*}(x)$ is positive for all $x<x_{v}$ that according again to (13) implies that ${(V^{II})}^{\prime }(x)$ must be negative for those values of the pollution stock. Then, for the LQ formulation $({v^{II}}^{*})^{\prime }(x)$ is negative and ${v^{II}} ^{*}(x)$ is a strictly concave function in the pollution stock.

Finally, to conclude the proof of the proposition we prove that $x_{v}>x_{e}$ . First, we rewrite the expression of $x_{v}=-B_{f}^{II}n^{2}(r+2\delta -2\eta A_{r})/(2A_{r}^{2})$, substituting the expression of $B_{f}^{II}$ in ( 34). After some easy computations using the expressions of $\eta$ in ( 35) $x_{v}$ reads:

$$\begin{aligned} x_{v}=-s\frac{n{ (\gamma (r+\delta )-nA_{r})}(r+2\delta -2\eta A_{r})+\left( (n-1)(\gamma (r+\delta )-{(n+\gamma )} A_{r})+n\gamma \eta A_{r}\right) }{n(\gamma (r+\delta )-A_{r})(r+\delta -\eta A_{r})A_{r}}. \end{aligned}$$

Taking into account the expression of the threshold $x_{e}$ in (23), the difference $x_{v}-x_{e}$ reads:

$$\begin{aligned}{} & {} s\frac{n\gamma ^{2}(r+\delta )(r+\delta -\eta A_{r})}{n{(n+ \gamma )}(\gamma (r+\delta )-{(\gamma +n)}A_{r})(r+\delta -\eta A_{r})A_{r}} \\- & {} s\frac{(n\!+\! \gamma )\left[ n{ (\gamma (r\!+\! \delta )\!-\!nA_{r})}(r\!+\!2\delta \!-\!2\eta A_{r})\!+\!A_{r}\left( (n\!-\!1)(\gamma (r\!+\! \delta )\!-\! {(n\!+\! \gamma )} A_{r})\!+\!n\gamma \eta A_{r}\right) \right] }{n{(n\!+\! \gamma )}(\gamma (r\!+\! \delta )\!-\! {(n\!+\! \gamma )} A_{r})(r\!+\! \delta \!-\! \eta A_{r})A_{r}}. \end{aligned}$$

The denominator is negative because $A_{r}<0$; hence, the difference $x_{v}-x_{e}$ is positive if and only the numerator is negative too. The numerator can be rewritten as a second-order polynomial in variable $A_{r}$ as follows:

$$\begin{aligned} l_{0}A_{r}^{2}+l_{1}A_{r}+l_{2}, \end{aligned}$$

with

$$\begin{aligned} l_{0}= & {} -{(\gamma +n)}\left( \gamma +\gamma (\eta -1)n+{ n((2\eta -1)n+1)}\right) , \\ l_{1}= & {} (\delta +r)\left( { n^{3}}+\gamma ^{2}((\eta -1)n+1)+{ \gamma n(2\eta n+1)}\right) +\delta n^{2}{(\gamma +n)}, \\ l_{2}= & {} -\gamma n(\delta +r)\left( { \gamma \delta +n(2\delta +r)} \right) <0. \end{aligned}$$

We can conclude that $l_{0}A_{r}^{2}+l_{1}A_{r}+l_{2}<0$, and consequently, $x_{v}-x_{e}>0$, because as shown below $l_{0}<0$ and $l_{1}>0$ for any $n\ge 2$, once the expressions of $\eta$, in (35) is substituted:

$$\begin{aligned} l_{0}= & {} -{(n+\gamma )}({ 2n(2n-1)}+\gamma (4n-3)), \\ l_{1}= & {} { n}\left( \delta n\left( { \gamma +n}\right) + \frac{1}{2}(\delta +r)\left( { 2n(3n-1)}+3\gamma (2n-1)\right) \right) . \end{aligned}$$

Proof of Proposition 6

We begin with the comparison of the slope of the tax rules. From (29) and (36) we know that the difference in the slopes is given by

$$\begin{aligned}{} & {} \frac{{n\left( (1+2\gamma )n+2(n^{2}-1)\right) } A_{r}^{2}-(n+1)\gamma (r+2\delta )A_{r}}{n^{2}\gamma (r+2\delta )-2(n-1)n {(n+\gamma )}A_{r}} \\- & {} \frac{2(n(n+1)\eta +1)A_{r}^{2}-n(n+1)(r+2\delta )A_{r}}{n^{2}(r+2\delta -2\eta A_{r})}, \end{aligned}$$

that yields

$$\begin{aligned}{} & {} \frac{n^{2}({n\left( (1+2\gamma )n+2(n^{2}-1)\right) }A_{r}^{2}-(n+1)\gamma (r+2\delta )A_{r})(r+2\delta -2\eta A_{r})}{n^{3}(n\gamma (r+2\delta )-2(n-1){(n+\gamma )} A_{r})(r+2\delta -2\eta A_{r})} \nonumber \\{} & {} -\frac{n(n\gamma (r+2\delta )-2(n-1){(n+ \gamma )}A_{r})(2(n(n+1)\eta +1)A_{r}^{2}-n(n+1)(r+2\delta )A_{r})}{ n^{3}(n\gamma (r+2\delta )-2(n-1){(n+\gamma )}A_{r})(r+2\delta -2\eta A_{r})},\nonumber \\ \end{aligned}$$

(43)

where the denominator is positive because $A_{r}$ is negative. Developing the numerator and simplifying terms, we obtain the following expression

$$\begin{aligned} nA_{r}^{2}({n^{3}}(r+2\delta )-{\frac{n}{ \gamma }(n^{2}(2n-1)+2(n^{2}-n+1)\gamma )}A_{r})>0. \end{aligned}$$

(44)

Therefore, (44) is positive and we can conclude that the slope of the optimal tax rule when a subsidy is applied on abatement costs is lower than the slope of the optimal tax rule when a subsidy is applied directly on abatement.

On the other hand, the difference in the intersection point with the vertical axis is given by the difference $B_{f}^{I}-B_{f}^{II}$. The intersection point with the vertical axis for scheme I is greater than for scheme II if and only if $B_{f}^{I}>B_{f}^{II}$. From (28) and (34), one has

$$\begin{aligned} B_{f}^{I}-B_{f}^{II}=\frac{A_{r}(\Delta _{1}-\Delta _{2})}{n^{3}}, \end{aligned}$$

where

$$\begin{aligned} \Delta _{1} \!\!=\! & {} \! \frac{n^{2}(A_{r}(n\!-\!1)(\gamma s {(n^{2}\!-\!4n\!-\!2\gamma )}\!-\!B_{r}{(n\!+ \! \gamma )(2\gamma \!+\!n^{2})})\!+\! \gamma n(2\delta \!+\!r)(B_{r} {(2\gamma \!+\!n^{2})}\!+\!2\gamma s))}{(\gamma n(\delta \!+\!r)\!-\!A_{r}{(n\!+\! \gamma )}(n\!-\!1))(\gamma n(2\delta \!+\!r)\!-\!2A_{r}{(n+\gamma )}(n-1))}, \\ \Delta _{2} \!\!=\! & {} \! \frac{2(A_{r}B_{r}\eta n+n(B_{r}+s)(-2A_{r}\eta +2\delta +r)+A_{r}(n-1)s)}{(-2A_{r}\eta +2\delta +r)(-A_{r}\eta +\delta +r)}. \end{aligned}$$

Because $A_r<0$, the sign of the difference $B_{f}^{I}-B_{f}^{II}$ is the opposite to the sign of the difference $\Delta _1-\Delta _2$.

The difference $\Delta _{1}-\Delta _{2}$ can be rewritten as:

$$\begin{aligned}{} & {} \Delta _{1}-\Delta _{2} \\{} & {} \quad =\frac{\textrm{Num}(\Delta _{1}\!-\! \Delta _{2})}{(\!-\!2A_{r}\eta \!+\!2\delta \!+\!r)(\!-\!A_{r}\eta \!+\! \delta \!+\!r)(\gamma n(\delta \!+\!r)\!-\!A_{r}{(n+\gamma )}(n\!-\!1))(\gamma n(2\delta \!+\!r)\!-\!2A_{r}{(n+\gamma )}(n\!-\!1))}, \end{aligned}$$

where

$$\begin{aligned} \textrm{Num}(\Delta _{1}-\Delta _{2}) \!\!=\! & {} \!(-2A_{r}\eta +2\delta +r)(-A_{r}\eta +\delta +r)\textrm{Num}(\Delta _{1}) \\ \!&\!-\!&\!(\gamma n(\delta \!+\!r)\!-\!A_{r}{(n\!+\! \gamma )} (n\!-\!1))(\gamma n(2\delta \!+\!r)\!-\!2A_{r}(n\!+\! \gamma )(n\!-\!1))\textrm{Num}(\Delta _{2}), \end{aligned}$$

with

$$\begin{aligned} \textrm{Num}(\Delta _{1})= & {} n^{2}(A_{r}(n-1)(\gamma s{(n^{2}-4n-2 \gamma )}-B_{r}{(n+\gamma )(2\gamma +n^{2})}) \\{} & {} +\gamma n(2\delta +r)(B_{r}{(2\gamma +n^{2})}+2\gamma s)), \\ \textrm{Num}(\Delta _{2})= & {} 2(A_{r}B_{r}\eta n+n(B_{r}+s)(-2A_{r}\eta +2\delta +r)+A_{r}(n-1)s). \end{aligned}$$

The denominator of $\Delta _{1}-\Delta _{2}$ is positive because $A_{r}$ is negative, and hence, the sign of the difference $\Delta _{1}-\Delta _{2}$ is the same as the sign of its numerator, $\textrm{Num}(\Delta _{1}-\Delta _{2})$. Substituting the expression of $B_{r}$ given in (19), and after some simplifications $\textrm{Num}(\Delta _{1}-\Delta _{2})$ can be rewritten as

$$\begin{aligned} \textrm{Num}(\Delta _{1}-\Delta _{2})=\frac{A_{r}(\Lambda _{1}+\Lambda _{2}A_{r}+\Lambda _{3}A_{r}^{2}+\Lambda _{4}A_{r}^{3})}{A_{r} {(n+\gamma )}-\gamma (\delta +r)}, \end{aligned}$$

(45)

where

$$\begin{aligned} \Lambda _{1}= & {} -\gamma ^{2}n^{2}s(\delta +r)(2\delta +r)[(2\delta +r) {((2\gamma +n^{2})n+2(n+\gamma )(n+1))} \\{} & {} +(\delta +r)(2\gamma +{(2\gamma +n^{2})}(n-1))-2\gamma n(\delta (2\eta +3)+(\eta +2)r], \\ \Lambda _{2}= & {} \gamma ns[2{(n+\gamma )}(n-1)( {(2\gamma +n^{2})}n(\delta +r)(2\delta +r)+2\gamma \delta ^{2}(2-7n)+(3-7n)\gamma r^{2} \\{} & {} +(7-20n)\gamma \delta r)-\gamma \eta n({(2\gamma +n^{2})} (4\delta +3r)(\delta (1-3n)+(1-2n)r) \\{} & {} +2\gamma n(2\eta +1)(\delta +r)(2\delta +r))+2{(n+\gamma )^{2}}(n-1)(2\delta +r)((3n-2)r-2\delta (1-2n)) \\{} & {} -2\gamma \eta {(n+\gamma )}n^{2}(2\delta +r)^{2}], \\ \Lambda _{3}= & {} 2s[\gamma \eta {(n+\gamma )}n^{2}(-(n-1) {(\gamma +n^{2})}(4\delta +3r)+2\gamma \eta (2\delta (2n-1)+r(3n-2))) \\{} & {} -\gamma ^{2}{(2\gamma +n^{2})}\eta ^{2}n^{2}((n-1)(\delta +r)+n(2\delta +r))-2n{(n+\gamma )^{3}}(n-1)^{2}(2\delta +r) \\{} & {} -\gamma {(n+\gamma )^{2}}(n-1)^{2}(2(\delta +\delta (2\eta -5)n)+r((4\eta -7)n+2))], \\ \Lambda _{4}= & {} 4{(n+\gamma )}(n-1)s[\gamma (2\gamma +n^{2})\eta ^{2}n^{2}+{(n+\gamma )^{2}}(n-1)((2\eta -1)n+1) \\{} & {} -\gamma \eta n{(n+\gamma )}(n-1+2\eta n)]. \end{aligned}$$

Taking into account that $A_{r}$ is negative, the sign of $\textrm{Num}(\Delta _{1}-\Delta _{2})$ in expression (45) coincides with the sign of the third-order polynomial in variable $A_{r}$, $\Lambda _{1}+\Lambda _{2}A_{r}+\Lambda _{3}A_{r}^{2}+\Lambda _{4}A_{r}^{3}$. From the expression of $\Lambda _{1}$ it is clear that $\Lambda _{1}$ is negative for any $n\ge 2$, because $\eta$ is positive. However, to completely characterize the sign of coefficients $\Lambda _{2},\Lambda _{3},\Lambda _{4}$, we need to substitute the expressions of $\eta$ given in (35 ). After the substitution coefficient $\Lambda _{4}$ reads

$$\begin{aligned} \Lambda _{4}\!&\!=&\! \frac{1}{\gamma }(n-1){ ns}\left( { \gamma +n}\right) \left[ 2\gamma n{ (n-1)\left( 4n^{2}-2n-1\right) }+{ n^{2}(n(2n-3)(2n+1)+2)}\right. \\{} & {} \left. +2\gamma ^{2}(n-1)(2(n-1)n+1)\right] . \end{aligned}$$

Therefore, $\Lambda _{4}$ is positive for any $n\ge 2$.

Unfortunately, the expressions for coefficients $\Lambda _{2}$ and $\Lambda _{3}$ are much longer and more complicated:

$$\begin{aligned} \Lambda _{2}= & {} \gamma ns\left[ 2(n-1)(2\delta +r)\left( { \gamma +n}\right) ^{2}((3n-2)r-2\delta (n-2))\right. \\{} & {} +\left. 2(n-1)\left( { \gamma +n}\right) \left( n(\delta +r)(2\delta +r)\left( { \gamma +n^{2}}\right) -\gamma (4\delta +3r)(\delta (3n-1)+(2n-1)r)\right) \right. \\{} & {} +\left. \frac{1}{2}\left( { n(2n-1)}+2\gamma (n-1)\right) \left( -2n(2\delta +r)^{2}\left( { \gamma +n}\right) \right. \right. \\{} & {} -\left. \left. 2(\delta +r)(2\delta +r)\left( { n(2n-1)}+\gamma (3n-2)\right) \right. \right. \\{} & {} +\left. \left. (4\delta +3r)\left( { 2+n^{2}}\right) (\delta (3n-1)+(2n-1)r)\right) \right] , \\ \Lambda _{3}= & {} -\frac{1}{2}s\left( { 2\gamma \!+\!n^{2}} \right) \left( { n(2n\!-\!1)}\!+\!2\gamma (n\!-\!1)\right) ^{2}((n\!-\!1)(\delta \!+\!r)+n(2\delta \!+\!r)) \\{} & {} +s\left( { \gamma \!+\!n}\right) \left( { n(2n\!-\!1)} +2\gamma (n\!-\!1)\right) \left( (1\!-\!n)n(4\delta +3r)\left( { \gamma \!+\!n^{2}}\right) \right. \\{} & {} -\left. \left( { (1\!-\!2n)n}\!-\!2\gamma (n\!-\!1)\right) (2\delta (2n\!-\!1)+(3n\!-\!2)r)\right) \\{} & {} -2(1\!-\!n)(n\!-\!1)s\left( { \gamma \!+\!n}\right) ^{2}\left( 2(\delta \!+\!r)\left( { (1\!-\!2n)n}\!-\!2\gamma (n\!-\!1)\right) +\gamma (2\delta (5n\!-\!1)\!+\!(7n\!-\!2)r)\right) \\{} & {} -4(n\!-\!1)^{2}ns(2\delta \!+\!r)\left( { \gamma \!+\!n}\right) ^{3}. \end{aligned}$$

Given the complexity of the above expressions for $\Lambda _{2}$ and $\Lambda _{3}$, we have resorted to studying their sign with the help of the Reduce command of the mathematical software Mathematica. This command reduces expressions by solving both equations and inequalities by eliminating quantifiers. This command allows us to determine that $\Lambda _{2}$ and $\Lambda _{3}$ are positive and negative, respectively, for any $n\ge 2$. Therefore, we can conclude that the third-order polynomial in variable $A_{r}$, $\Lambda _{1}+\Lambda _{2}A_{r}+\Lambda _{3}A_{r}^{2}+\Lambda _{4}A_{r}^{3}$ is always negative for any $A_{r}<0$, and consequently, $B_{f}^{I}-B_{f}^{II}>0$.