Introduction

Nanofluids are stable colloidal deferrals of mental or non-metal element on a disreputable liquid, which heighten the heat transfer of the solution and intensify the storage aptitude. Nanoliquids are fascinating numerous researchers for their higher thermophysical assets in various industrial and engineering applications. The initiation of extraordinary heat flow developments has formed noteworthy demand for innovative technologies to heighten heat transfer. Nanoliquids have forthcoming solicitations in various crucial fields such as heating and cooling system of building, electrical machines, thermonuclear vessel, and frequent thermal scheming structures. A nanoliquid can be shaped by dispersing a unique size of less than 100 nm of metallic or non-metallic nanofibers or nanoparticles in a base liquid. The nanoliquid preparation is the essential phase to magnify the thermal conductivity of liquids. Now, numerous sorts of nanoparticles, e.g. metallic nanoparticles and ceramic nanoparticles, have been consumed in nanoliquid exploration. Abundant notional and experimental exploration of thermophysical assets of nanoliquids in different aspects have been exposed in Choi (1995), Ibrahim et al. (2013), Das (2017), Anwar and Rasheed (2017), Prasad et al. (2017), Irfan et al. (2019), Rashid et al. (2019), Venkateswarlu and Narayana (2019), Khan et al. (2019), and Dogonchi et al. (2020). The heat transfer mechanism on 3D flow of magneto nanoliquid towards shrinking surface was analyzed by Nayak (2017). The viscous dissipation and thermal radiation effects were also considered there. They established that for shrinking surface instance, the impact of viscous dissipation declines the amount of heat transferal. The structures of chemical species on nanoliquid flow influenced by rotating disc were considered by Hayat et al. (2017). They noted that the amount of surface shear stress declines for higher thickness quantity of disk although rises for volume fraction of silver-based nanoparticles. The stretched flow of radiative micropolar nanoliquid influenced with magnetic field was explored by Paul and Mandal (2017). Pryazhnikov et al. (2017) scrutinized the capacities of thermal conductivity on nanoliquid. They recognized that the lesser the thermal conductivity of the base liquid, the advanced the comparative thermal conductivity of coefficient the nanoliquid. Hsiao (2017) incorporated MHD and radiation aspect in Carreau nanofluid employing parameter control approach. Recently, the heat transport with multiple nature study on Carreau fluid was noted by Hashim (2019) Conflicting performance for velocity and temperature fields was noted for second solution by enhancing values of magnetic parameter.

Currently, non-Newtonian fluids (Khan et al. 2017; Mahanthesh et al. 2017; Alshomrani et al. 2018; Asghar et al. 2019) utilizing nanoparticles have stressed exhaustive fascination because of their industrialized and scientific applications e.g. genetic clarifications, polymers liquefies, splatters, tarmacs, and fastens. An analysis of non-Newtonian liquids is an influential sort of flow intensifying a numeral of concrete diligence, manufacturing, and organic liquid solicitations. In the periodical of its prominence, numerous contemporary exploration has been fascinated on the flow of linear and non-linear liquids. In vision of these application, numerically, the influence of magneto Casson and Williamsonn liquid was presented by Kumaran and Sandeep (2017). These result displayed that the heat and mass transferal enactment of Williamson liquid was quite lesser than the Casson liquid. Heat transfer appliance for MHD rotating flow of Jeffrey nanoliquid in a porous medium was scrutinized by Zin et al. (2017). They pragmatic that for both primary and secondary velocities, the Lorentz force impedes the liquid flow. Currently, Dufour–Soret impact on non-Newtonian liquid flow subject to MHD and radiation was scrutinized by Mahabaleshwar et al. (2020).

Enthused by above fictions, this study reports to explore the features of heat and transport on unsteady 3D Carreau nanofluid. The concept of thermal conductivity and heat sink/source is also reported in the energy equation in energetic to foresee precise manifestation of heat transport. The non-linear ODEs resolved numerically by employing vorticity–stream function preparation with an appropriate coordinate variation and then elucidated by implementing bvp4c algorithm.

Modeling

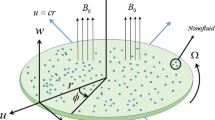
A numerical consideration is made for the study of unsteady 3D flow of a Carreau nanoliquid influenced by a bidirectional stretched surface. The flow is influenced due to stretching surface in two perpendicular x- and y-directions with velocities \(U_{w} (x,\,t) = \tfrac{ax}{{1 - \beta t}}\) and \(V_{w} (y,\,t) = \tfrac{by}{{1 - \beta t}}\), respectively, where \(a\) and \(b\) are stretching rate constants and the nanoliquid flow occupies the region in the domain, \(z > 0\) as portrayed in Fig. 1. The transport of heat is analyzed in apparition of heat source/sink and variable conductivity. Moreover, nanoparticles structures are taken by considering Brownian motion and thermophoresis. The temperature and concentration of liquid \([T_{w} (x,\,t),\,C_{w} (x,\,t)]\) of surface are considered to be higher than the ambient temperature and concentration \((T_{\infty } ,\,C_{\infty } ),\) respectively.

Fig. 1
figure 1

Schematic diagram

Full size image

The flow of Carreau nanoliquid in vision of above norms is given by Irfan et al. (2017) and Khan et al. (2018):

$$\frac{\partial u}{{\partial x}} + \frac{\partial v}{{\partial y}} + \frac{\partial w}{{\partial z}} = 0,$$
(1)
$$ \begin{aligned}& \frac{\partial u}{{\partial t}} + u\frac{\partial u}{{\partial x}} + v\frac{\partial u}{{\partial y}} + w\frac{\partial u}{{\partial z}} = \nu \frac{{\partial^{2} u}}{{\partial z^{2} }}\left[ {1 + \Gamma^{2} \left( {\frac{\partial u}{{\partial z}}} \right)^{2} } \right]^{{\tfrac{n - 1}{2}}} \\ &\quad+ \nu (n - 1)\Gamma^{2} \frac{{\partial^{2} u}}{{\partial z^{2} }}\left( {\frac{\partial u}{{\partial z}}} \right)^{2} \left[ {1 + \Gamma^{2} \left( {\frac{\partial u}{{\partial z}}} \right)^{2} } \right]^{{\tfrac{n - 3}{2}}} ,\end{aligned} $$
(2)
$$ \begin{aligned}& \frac{\partial v}{{\partial t}} + u\frac{\partial v}{{\partial x}} + v\frac{\partial v}{{\partial y}} + w\frac{\partial v}{{\partial z}} = \nu \frac{{\partial^{2} v}}{{\partial z^{2} }}\left[ {1 + \Gamma^{2} \left( {\frac{\partial v}{{\partial z}}} \right)^{2} } \right]^{{\tfrac{n - 1}{2}}} \\ &\quad+ \nu (n - 1)\Gamma^{2} \frac{{\partial^{2} v}}{{\partial z^{2} }}\left( {\frac{\partial v}{{\partial z}}} \right)^{2} \left[ {1 + \Gamma^{2} \left( {\frac{\partial v}{{\partial z}}} \right)^{2} } \right]^{{\tfrac{n - 3}{2}}} ,\end{aligned} $$
(3)
$$ \begin{aligned}& \frac{\partial T}{{\partial t}} + u\frac{\partial T}{{\partial x}} + v\frac{\partial T}{{\partial y}} + w\frac{\partial T}{{\partial z}} = \frac{1}{{\left( {\rho c} \right)_{{\text{f}}} }}\frac{\partial }{\partial z}\left( {K(T)\frac{{\partial^{} T}}{{\partial z^{} }}} \right) \\ &\quad+ \tau \left[ {D_{B} \frac{\partial C}{{\partial z}}\frac{\partial T}{{\partial z}} + \frac{{D_{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial z}}} \right)^{2} } \right] + \frac{{Q_{0} }}{{\left( {\rho c} \right)_{{\text{f}}} }}\left( {T - T_{\infty } } \right),\end{aligned} $$
(4)
$$\frac{\partial C}{{\partial t}} + u\frac{\partial C}{{\partial x}} + v\frac{\partial C}{{\partial y}} + w\frac{\partial C}{{\partial z}} = D_{B} \frac{{\partial^{2} C}}{{\partial z^{2} }} + \frac{{D_{T} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial z^{2} }}.$$
(5)

The following boundary conditions are

$$ \begin{aligned}& u = U_{w} = \frac{ax}{{1 - \beta t}},{\mkern 1mu} \, v = V_{w} = \frac{by}{{1 - \beta t}},{\mkern 1mu} \, w = 0, \, T = T_{w} (x,{\mkern 1mu} t){, }\\ &C = C_{w} (x,{\mkern 1mu} t){\text{ at }}z = 0,\end{aligned} $$
(6)
$$u \to 0,{\mkern 1mu} \, v \to 0,{\mkern 1mu} \, T \to T_{\infty } ,{\mkern 1mu} \, C \to C_{\infty } {\text{ as }}z \to \infty .$$
(7)

Here \((u,\,v,\,w)\) are the velocity components in the x-, y-, and z-directions, respectively, \(\Gamma\) the material rate constant, \(n\) the power law exponent, \(\nu\) the kinematic viscosity, \((\rho_{{\text{f}}} ,\,c_{{\text{f}}} )\) the specific density and heat respectively, \((T,C)\) the liquid temperature and nanoparticles concentrations, respectively, \(Q_{0}\) the heat source/sink coefficient, \(\tau\) the ratio of effective heat capacity of nanoparticles to heat capacity of the base liquid, \((D_{{\text{B}}} ,D_{{\text{T}}} )\) the Brownian and thermophoretic diffusion coefficients, respectively, \(\beta\) dimensional unsteadiness parameter and \(K(T)\) variable thermal conductivity.

The variable thermal conductivity \(K(T),\) temperature and concentration of wall are given by the following form

$$ \begin{aligned}&K(T) = k_{\infty } \left[ {1 + \varepsilon \left( {\frac{{T - T_{\infty } }}{\Delta T}} \right)} \right], \, T_{w} (x,{\mkern 1mu} t) = T_{\infty } + \frac{{T_{0} ax^{2} }}{{\left( {1 - \beta t} \right)^{{\tfrac{3}{2}}} }}{, }\\ &C_{w} (x,{\mkern 1mu} t) = C_{\infty } + \frac{{C_{0} ax^{2} }}{{\left( {1 - \beta t} \right)^{{\tfrac{3}{2}}} }},\end{aligned} $$
(8)

where \(\left( {\varepsilon ,\,k_{\infty } } \right)\) the thermal conductivity parameter and nanoliquid thermal conductivity far away from the stretched surface, \(\Delta T\) represents the liquid temperature difference between the stretched surface and far away from the surface, respectively, \((T_{0} ,\,C_{0} )\) the positive reference temperature and concentration of the nanoliquid.

Conversion variables

Let the conversion variables are

$$\begin{aligned} u = & \frac{ax}{{1 - \beta t}}f^{\prime}(\eta ),\, \, v = \frac{ay}{{1 - \beta t}}g^{\prime}(\eta ),\, \, w = - \sqrt {\frac{a\nu }{{1 - \beta t}}} [f(\eta ) + g(\eta )], & \\ \theta \left( \eta \right) = & \frac{{T - T_{\infty } }}{{T_{w} - T_{\infty } }},\, \, \varphi = \frac{{C - C_{\infty } }}{{C_{w} - C_{\infty } }} \, \eta = z\sqrt {\frac{a}{{\nu \left( {1 - \beta t} \right)}}} . & \\ \end{aligned}$$
(9)

The above conversions satisfied the incompressibility condition automatically and Eqs. (2)–(7) using Eq. (8), yield

$$ \begin{aligned}& f^{\prime\prime\prime}[1 + {\text{We}}_{1}^{2} f^{\prime \prime 2} ]^{{\tfrac{n - 3}{2}}} [1 + n{\text{We}}_{1}^{2} f^{\prime \prime 2} ] - S\left( {f^{\prime} + \frac{1}{2}\eta f^{\prime\prime}} \right) \\ &\quad- f^{\prime 2} + f^{\prime\prime}(f + g) = 0,\end{aligned} $$
(10)
$$ \begin{aligned}& g^{\prime\prime\prime}[1 + {\text{We}}_{2}^{2} g^{\prime \prime 2} ]^{{\tfrac{n - 3}{2}}} [1 + n{\text{We}}_{2}^{2} g^{\prime \prime 2} ] - S\left( {g^{\prime} + \frac{1}{2}\eta g^{\prime\prime}} \right) \\ &\quad- g^{\prime 2} + g^{\prime\prime}(f + g) = 0,\end{aligned} $$
(11)
$$ \begin{aligned}& \left( {1 + \varepsilon \theta } \right){\mkern 1mu} \theta^{\prime \prime } + \varepsilon \theta^{\prime 2} + \mathop {\Pr }\limits_{{}}^{{}} (f + g)\theta^{\prime } - 2\mathop {\Pr }\limits_{{}}^{{}} f^{\prime } \theta - \mathop {\Pr }\limits_{{}}^{{}} \frac{S}{2}\left( {3\theta + \eta \theta^{\prime } } \right) \\ &\quad+ \mathop {\Pr }\limits_{{}}^{{}} N_{{\text{b}}} \theta^{\prime } \varphi^{\prime } + \mathop {\Pr }\limits_{{}}^{{}} N_{{\text{t}}} \theta^{\prime 2} + \mathop {\Pr }\limits_{{}}^{{}} \delta \theta = 0,\end{aligned} $$
(12)
$$ \begin{aligned}& \phi ^{\prime\prime} + \mathop {\Pr }\limits {\text{Le}}(f + g)\phi ^{\prime} - 2\mathop {\Pr }\limits {\text{Le}}f^{\prime}\phi \\ &\quad- \mathop {\Pr }\limits {\text{Le}}\frac{S}{2}\left( {3\phi + \eta \phi ^{\prime}} \right) + \left( {\frac{{N_{{\text{t}}} }}{{N_{{\text{b}}} }}} \right)\,\theta^{\prime\prime} = 0,\end{aligned} $$
(13)
$$f(0) = 0,{\mkern 1mu} \, g(0) = 0,{\mkern 1mu} \, f^{\prime } (0) = 1,{\mkern 1mu} \, g^{\prime } (0) = \alpha ,{\mkern 1mu} \, \theta (0) = 1 \, \phi (0) = 0,$$
(14)
$$f^{\prime } \to 0,{\mkern 1mu} \, g^{\prime } \to 0,{\mkern 1mu} \, \theta \to 0 \, \phi \to 0{\text{ as }}\eta \to \infty .$$
(15)

Here, \(({\text{We}}_{1} ,\,{\text{We}}_{2} ) = \left( {\sqrt {\tfrac{{\Gamma^{2} a^3x^{2} }}{\nu (1-\beta t)^3}} ,\,\sqrt {\tfrac{{\Gamma^{2} a^3y^{2} }}{\nu (1-\beta t)^3}} } \right)\) are the local Weissenberg numbers, \(S\left( { = \tfrac{\beta }{a}} \right)\) the unsteadiness parameter, \(\delta \left( { = \tfrac{{Q_{0} (1 - \beta t)}}{{a\left( {\rho c} \right)_{f} }}} \right)\) heat generation/absorption parameter, \(N_{{\text{b}}} \left( {\tfrac{{\tau D_{B} (C_{w} - C_{\infty } )}}{\nu }} \right)\) the Brownian motion parameter, \(N_{{\text{t}}} \left( { = \tfrac{{\tau D_{T} (T_{w} - T_{\infty } )}}{{\nu T_{\infty } }}} \right)\) the thermophoresis parameter, \({\text{Le}}( = \tfrac{{\alpha_{1} }}{{D_{B} }})\;\) the Lewis number, \(\Pr \left( { = \tfrac{\nu }{{\alpha_{1} }}} \right)\) the Prandtl number, and \(\alpha \left( { = \tfrac{b}{a}} \right)\) the ratio of stretching rates parameter.

Industrial and engineering quantities of interest

The quantities of industrial and engineering interest in materials processing are the skin frictions, heat and mass transfer coefficients which may be defined by:

$$C_{fx} = \frac{{\tau_{xz} }}{{\tfrac{1}{2}\rho_{{\text{f}}} U_{w}^{2} }}{\text{ and }}C_{fy} = \frac{{\tau_{yz} }}{{\tfrac{1}{2}\rho_{{\text{f}}} U_{w}^{2} }},$$
(16)
$${\text{Nu}}_{x} = - \frac{x}{{\left( {T_{w} - T_{\infty } } \right)}}\left. {\frac{\partial T}{{\partial z}}} \right|_{z = 0} ,{\mkern 1mu} {\text{ Sh}}_{x} = - \frac{x}{{\left( {C_{w} - C_{\infty } } \right)}}\left. {\frac{\partial C}{{\partial z}}} \right|_{z = 0} .$$
(17)

The overhead expression in the dimensionless form:

$$\frac{1}{2}C_{fx} {\text{Re}}_{x}^{{\tfrac{1}{2}}} = f^{\prime \prime } (0)[1 + {\text{We}}_{1}^{2} f^{\prime \prime 2} (0)]^{{\tfrac{n - 1}{2}}} , \, \frac{1}{2}\left( {\frac{{U_{w} }}{{V_{w} }}} \right){\mkern 1mu} C_{fy} {\text{Re}}_{x}^{{\tfrac{1}{2}}} = g^{\prime \prime } (0)[1 + {\text{We}}_{2}^{2} g^{\prime \prime 2} (0)]^{{\tfrac{n - 1}{2}}} ,$$
(18)
$${\text{Re}}_{x}^{{ - \tfrac{1}{2}}} {\text{Nu}}_{x} = - \theta^{\prime } \left( 0 \right),{\mkern 1mu} {\text{ Re}}_{x}^{{ - \tfrac{1}{2}}} {\text{Sh}}_{x} = - \phi^{\prime}\left( 0 \right),$$
(19)

in which, \({\text{Re}}_{x} = xU_{w} (x,\,t)/\nu\) is local Reynolds number.

Analysis

Here the graphical and tabular depiction of influential parameters are elaborated utilizing bvp4c algorithm for Carreau nanofluid. This impartial is attained via sketch and clarification of Figs. 2, 3, 4, 5, 6, 7, 8 and 9, which are plotted for both the shear thinning \((n < 1)\) and shear thickening \((n > 1)\) circumstances. Additionally, we incorporated the following specific values of influential parameters i.e., \({\text{We}}_{1} = {\text{We}}_{2} = 3.0,\) \(N_{{\text{t}}} = 0.2\), \(S = \delta = N_{{\text{b}}} = 0.4,\) \(\alpha = \varepsilon = 0.5,\) \(\Pr = 1.7\), and \({\text{Le}} = 1.0\) except particular in graphs.

Fig. 2
figure 2

a, b \(\theta (\eta )\) for \(\varepsilon\)

Full size image
Fig. 3
figure 3

a, b \(\theta (\eta )\) for \(\Pr\)

Full size image
Fig. 4
figure 4

a, b \(\theta (\eta )\) for \(N_{{\text{b}}}\)

Full size image
Fig. 5
figure 5

a, b \(\theta (\eta )\) for \(N_{{\text{t}}}\)

Full size image
Fig. 6
figure 6

a, b \(\phi (\eta )\) for \(\;n\)

Full size image
Fig. 7
figure 7

a, b \(\phi (\eta )\) for \(\alpha\)

Full size image
Fig. 8
figure 8

a, b \(\phi (\eta )\) for \(N_{{\text{b}}}\)

Full size image
Fig. 9
figure 9

a, b \(\phi (\eta )\) for \(N_{{\text{t}}}\)

Full size image

Temperature field \(\theta (\eta )\) for \(\varepsilon\), \(\Pr ,\) \(N_{{\text{b}}}\), and \(N_{{\text{t}}}\)

Figures 2a, b and 3a, b are conscripted to picture the structures of the variable conductivity parameter \(\varepsilon\) and Prandtl number Pr on nanoliquid temperature distribution for \((n < 1)\) and \((n > 1)\). Progressive values of these parameter spectacle the conflicting behavior for both cases. Amassed values of \(\Pr\) diminish the temperature field, while it enhance for \(\varepsilon\). Physically, higher values of \(\varepsilon\) boosts the thermal conductivity of the liquid which outcomes the temperature of Carreau liquid increases. Hence, opposite performance is noted for Pr for both \((n < 1)\) and \((n > 1).\)

Figures 4a, b and 5a, b are drawn to infer the sorts of the Brownian motion \(N_{{\text{b}}}\) and thermophoresis parameters \(N_{{\text{t}}}\) on the Carreau liquid temperature field. It is famed that \(N_{{\text{b}}}\) and \(N_{{\text{t}}}\) are enhancing function of temperature profile for both shear thinning/thickening liquids. It is remarked that an improvement in \(N_{{\text{b}}}\) causes enlargements of the liquid temperature. This ensues on reason of slow expansion in nanoparticles measurement with \(N_{{\text{b}}}\). Additionally, as the difference between the wall and reference temperature growths that reasons the temperature of the liquid enhances.

Concentration field \(\phi (\eta )\) for \(n,\) \(\alpha ,\,\;N_{{\text{b}}}\) and \(N_{{\text{t}}}\)

The illustration for higher power law exponent \(n\) \({\text{(i.e.}},\,n < 1\) \(and\) \(n > 1)\) and ratio of stretching rates \(\alpha\) are envision in Figs. 6a, b and 7a, b. For both shear thinning/thickening cases, the concentration field lessen for \(n\) and analogous trend is reported for \(\alpha .\). The stretching along x-\({\text{direction}}\) intensifies as assessment with stretching along y-\({\text{direction}}\) decays the concentration field. Therefore, outcomes indicate the same performance for both parameters for both circumstances.

To picture the results of nanoliquid concentration field for the sophisticated values of \(N_{{\text{b}}}\) and \(N_{{\text{t}}} ,\) Figs. 8a, b and 9a, b are portrayed. From these depictions, the concentration field augment for larger \(N_{{\text{b}}}\) while it diminish for \(N_{{\text{t}}} ,\) for \((n = 0.5)\) and \((n = 1.5)\). For higher \(N_{{\text{b}}}\), the collision of the liquid particles rises, which consequences in decline of the concentration of Carreau liquid. Moreover, amassed values of \(N_{{\text{t}}} ,\) produces rise in thermophoretic force and this habitually transports the nanoparticles from constituency of greater to inferior temperature because of which nanoliquid concentration heightens.

Tabular illustrations

Table 1 is the assessment table of \(- f^{\prime\prime}(0)\) for two diverse approaches namely, bvp4c and HAM for distinct values of \(S\) in restrictive sense with former prose. In this analysis, the authenticity of the numerical and analytical outcomes is also presented by comparison with earlier pertinent prose as an exceptional circumstance of the problem and outstanding settlement is noticed in Tables 2 and 3.

Table 1 A comparison of \(- f^{\prime\prime}\left( 0 \right)\) for \(S\) when \({\text{We}}_{1} = {\text{We}}_{2} = \alpha = 0\) and \(n = 1\) are fixed
Full size table
Table 2 A comparison of \(f^{\prime\prime}(0)\) in limiting cases when \({\text{We}}_{1} = {\text{We}}_{2} = S = 0\) and \(n = 1\) are fixed
Full size table
Table 3 A comparison of \(g^{\prime\prime}(0)\) in limiting cases when \({\text{We}}_{1} = {\text{We}}_{2} = S = 0\) and \(n = 1\) are fixed
Full size table

Table 4 elaborates the numerical computation of \(\left( {\tfrac{1}{2}C_{fx} {\text{Re}}_{x}^{{\tfrac{1}{2}}} } \right)\) and \(\left( {\tfrac{1}{2}\left( {\tfrac{{U_{w} }}{{V_{w} }}} \right)\,C_{fy} {\text{Re}}_{x}^{{\tfrac{1}{2}}} } \right)\) for \(S\) and \(\alpha\), respectively. For both \(n = 0.7\) and \(n = 1.7\) cases, the skin friction coefficient augmented when we intensified these values. Tables 5 and 6 report the numerical outcomes of \(- \theta^{\prime}(0)\) and \(- \phi^{\prime}(0),\) respectively, for diverse value of \(\varepsilon\), \(N_{{\text{b}}}\), and \(N_{{\text{t}}} ,\) The heat transport amount decayed from higher values of these parameters for both \(n = 0.7\) and \(n = 1.7.\) Moreover, mass transport amount exaggerates for \(\varepsilon\) and \(N_{{\text{b}}}\); however, it fall-off for \(N_{{\text{t}}} .\)

Table 4 Numerical values of \(\tfrac{1}{2}C_{fx} {\text{Re}}_{x}^{{\tfrac{1}{2}}}\) and \(\tfrac{1}{2}\left( {\tfrac{{U_{w} }}{{V_{w} }}} \right)\,C_{fy} {\text{Re}}_{x}^{{\tfrac{1}{2}}}\) when \({\text{We}}_{1} = {\text{We}}_{2} = 3\) and \(n = 1\) are fixed
Full size table
Table 5 Numerical values of \(- \theta^{\prime}\left( 0 \right)\) when \({\text{We}}_{1} = {\text{We}}_{2} = 3.0,\) \(S = \delta = 0.4,\) \(\alpha = 0.5,\) \(\Pr = 1.7\) and \({\text{Le}} = 1.0\) are fixed
Full size table
Table 6 Numerical values of \(- \phi ^{\prime}\left( 0 \right)\) when \({\text{We}}_{1} = {\text{We}}_{2} = 3.0,\) \(S = \delta = 0.4,\) \(\alpha = 0.5,\) \(\Pr = 1.7\) and \({\text{Le}} = 1.0\) are fixed
Full size table

Concluding remarks

The heat and mass transport mechanisms for 3D magneto Carreau nanoliquid with variable conductivity and heat source/sink were established. The somatic reports about the attained outcomes are summarized as follows:

  • The influence of \(\varepsilon\), \(N_{{\text{t}}}\), and \(N_{{\text{b}}}\) were quite opposite to the \(\Pr\) on nanoliquid temperature for \((n < 1)\) and \((n > 1).\)

  • The analogous trend of \(n\) and \(\alpha\) was noticed for concentration field.

  • In both instances, \(N_{{\text{t}}}\) and \(N_{{\text{b}}}\) have opposed performance on concentration field.