Multiple nature analysis of Carreau nanomaterial flow due to shrinking geometry with heat transfer

Abstract

An astonishing feature of modern research in the field of fluid flow and heat transfer is the suspension of small solid particles (nanoparticle) in the working fluid to increase the low thermal conductivity of these fluids. Because of unique chemical and physical properties, nanomaterials are being progressively utilized in almost every field of science and technology. Therefore, the intent of current manuscript is to theoretically examine the magneto-hydrodynamic flow of Carreau nanofluids along with heat transport in the presence of heat generation driven by a wedge-shaped shrinking geometry. We incorporated the revised Buongiorno’s model in which nanofluids particle fraction on the boundary is passively controlled. Mathematical modeling of assumed physical problem results in a system of non-linear partial differential equations outlining the basic conservation laws. The governing problem is made dimensionless with the assistance of non-dimensional variables and numerical solutions are computed via a built-in MATLAB solver bvp4c. The computed results showed that multiple solutions (first and second) exist for the non-dimensional velocity, temperature and concentration distributions by applying the said numerical scheme. We concluded that by enhancing the magnetic parameter the nanofluid velocity increases in case of second solution while an opposite is true for temperature. Further, the outcomes indicate that higher heat generation parameter leads to enhance the temperature distributions in both solutions.

Introduction

At present, the low thermal conductivity of the ordinary liquids is a big challenge which has diverted the attention of researchers. The new heat transfer fluids called nanofluids have been developed to address this challenge. In fact, nanofluids are dilute suspension which is obtained by adding the solid particles of size less than 100 nm in ordinary liquids. Recently, several experimental studies have been devoted on this new type of heat transferring flowing fluids which witnessed improved thermo physical traits, like thermal conductivity, viscosity and density. The various solid particles employed in engineering and industrial process are metallic and non-metallic, for instance, copper, silver, gold, titanium oxide, silica, alumina, etc.

These fluids having high heat transferring properties are widely used in different practical problems, for example, in temperature reduction, cancer therapy, solar collectors, electronic cooling, peristaltic pumps for diabetic treatment, etc. The notion of nanofluids was originally introduced by Choi (1995) through the blend of base liquid with the ultra-fine solid nanoparticles.

In another experimental analysis, Lee et al. (1999) proved that the suspension of nanoparticles enhances the heat transfer characteristics of water very substantially. Afterward, Buongiorno (2006) presented another hypothesis for the mechanism of thermal conductivity of nanomaterials by considering the thermophoresis and Brownian movement. Reddy et al. (2009) examined the combined effects of double diffusion and chemical reaction on mixed convection MHD flow and heat transfer to nanofluids caused by an infinite plate. In the same way, Khan and Pop (2010) presented a numerical study to talk about the laminar flow of nanofluids generated by a stretching flat plate by considering the effects of Brownian motion and thermophoresis. Sheikholislami et al. (2013) analyzed the influence of magnetic field on ${\text{Al}}_{ 2} {\text{O}}_{ 3}$–water nanofluid flow and heat transfer in an annulus. MHD flow of nanofluids past a permeable stretching sheet in the presence of Newtonian heating has been discussed by Mutuku-Njane and Makinde (2014). Mabood et al. (2015) investigated the flow of water-based nanofluids generated by a stretching surface in the presence of magnetic field and viscous dissipation. They acquired the numerical solutions for their governing problem and presented the results for velocity, temperature and concentration distributions. Recently, multiple solutions have been computed by Khan and Hafeez (2017) for nanofluid flow and heat transfer in the presence of slip phenomenon. Khan et al. (2018) presented the MHD flow of Cu–water nanofluid by considering different shapes of nanoparticle along with heat transport analysis. Ma et al. (2019) numerically investigated the flow and convective heat transfer to nanofluids in a channel. Very recently, Hamid et al. (2019) discussed the flow of Williamson nanofluids over a vertical stretching surface and computed the numerical solutions.

For more than several decades, there has been a growing interest in magneto-hydrodynamic (MHD) flow and heat transport investigation of nanofluids past a stretching/shrinking wedge. In fact, such types of flows challenge our best engineering abilities and remain one of the most demanding problems due to their wide applications, like, geothermal systems, storage of nuclear waste, crude oil extraction, spinning of filaments, thermal insulation and the design of heat exchangers etc., The study of Falkner and Skan (1931) produces the two-dimensional laminar flow past a fixed wedge to elaborate the Prandtl boundary layer theory. They offered the well-known Falkner–Skan equations to investigate the flow past a wedge. Thereafter, this exciting problem of boundary layer flow past a stretching/shrinking wedge by the use of different physical effects has been investigated by numerous researchers; see (Hartree 1937; Yih 1999; Ishak et al. 2007; Ishaq et al. 2008; Boyd and Martin 2010). Further, Xu and Chen (2017) analyzed the MHD flow of Cu–water nanofluid flow along with heat transfer over a permeable wedge in the attendance of variable viscosity. Sayyed et al. (2018) computed the analytic solutions MHD flow over a constant wedge in the presence of porous medium and slip velocity. Awaludin et al. (2018) numerically produced the dual solutions for MHD flow and heat transfer analysis of a viscous fluid generated by a stretching/shrinking wedge. Ibrahim and Tulu (2019) investigated the flow of nanofluid past a wedge with heat transport by considering viscous dissipation and porous medium.

Over the past few years, numerous studies have been presented to investigate the boundary layer flow and heat transfer analysis of non-Newtonian Carreau fluid in the presence of nanoparticles. In most of the cases, authors consider the flow over different stretching surfaces and computed the single solutions for the flow fields. Therefore, the aim of present analysis is to compute the multiple solutions for two-dimensional flow of Carreau nanofluids over a stretching/shrinking wedge with heat generation/absorption and mass suction. The problem has been mathematically modeled with the assistance of conservation laws of mass, momentum, energy and nanoparticle concentration. The governing system of strong non-linear equations is numerically tackled through built-in MATLAB routine bvp4c. At last, the graphical review is given for velocity, temperature, concentration, skin friction and Nusselt number distributions for varying physical parameters.

Problem description

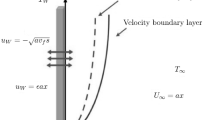
In this paper, steady, incompressible and two-dimensional flow of Carreau nanofluids over a stretching/shrinking wedge with heat and mass transfer has been explored. The physical flow model and coordinate axes are shown in Fig. 1. Herein, we choose the coordinate axes in such a way that x-axis is aligned with the surface of the wedge and y-axis is normal to wedge surface. Further, the fluid is subject to a transverse magnetic field of variable strength $B\left( x \right) = B_{0} x^{{\tfrac{m - 1}{2}}} ,$ where $B_{0}$ represents a steady strength magnetic field. The velocity distribution for stretching/shrinking wedge is denoted by $U_{\text{w}} \left( x \right) = ax^{m} ,$ where $a > 0$ represents stretching wedge while $a < 0$ means shrinking wedge. However, the outer edge of the boundary layer has non-uniform velocity $U_{\infty } \left( x \right) = bx^{m} ,$ where $b$ is a constant. In addition, $m$ is the power-law parameter or Falkner–Skan parameter $0 \le m \le 1$ where $m = \tfrac{\beta }{2 - \beta }$ and $\beta = \tfrac{\varOmega }{\pi }$ represent the wedge angle. The fluid temperature and nanoparticles concentration at the surface of the wedge are assumed to be $T_{\text{w}} ,C_{\text{w}}$ and $T_{\infty } ,C_{\infty }$ denotes the ambient temperature and concentration, respectively.

Fig. 1

Flow configuration for wedge-shaped geometry

In accordance with scale analysis and usual boundary layer approximations, the governing non-linear PDEs of mass, momentum, energy and concentration conservation using Buongiorno’s model of nanofluid are expressed in the following manner (Wang 2007)

$$\frac{{{\mathbf{\partial }}u}}{{{\mathbf{\partial }}x}} + \frac{{{\mathbf{\partial }}v}}{{{\mathbf{\partial }}y}} = 0,$$

(1)

$$u\frac{{{\mathbf{\partial }}u}}{{{\mathbf{\partial }}x}} + v\frac{{{\mathbf{\partial }}u}}{{{\mathbf{\partial }}y}} = \nu \frac{{\partial^{2} u}}{{\partial y^{2} }}\left[ {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} } \right]^{{\tfrac{n - 1}{2}}} + \nu (n - 1)\varGamma^{2} \frac{{\partial^{2} u}}{{\partial y^{2} }}\left( {\frac{\partial u}{\partial y}} \right)^{2} \left[ {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} } \right]^{{\tfrac{n - 3}{2}}} + U_{\infty } \frac{{{\text{d}}U_{\infty } }}{{{\text{d}}x}} + \frac{{\sigma B^{2} \left( x \right)}}{\rho }\left( {U_{\infty } - u} \right),$$

(2)

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \tau \left[ {D_{\text{B}} \frac{\partial T}{\partial y}\frac{\partial C}{\partial y} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\left( {\frac{\partial T}{\partial y}} \right)^{2} } \right] + \frac{{Q^{*} \left( x \right)}}{{\rho c_{\text{p}} }}\left( {T - T_{\infty } } \right),$$

(3)

$$u\frac{\partial C}{\partial x} + v\frac{\partial C}{\partial y} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial y^{2} }} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial y^{2} }},$$

(4)

The associated physical boundary conditions for the above problem are as follows:

$$u = u_{\text{w}} \left( x \right),\, \, v = v_{\text{w}} \left( x \right),\, \, T = T_{\text{w}} ,\, \, D_{\text{B}} \frac{\partial C}{\partial y} + \frac{{D_{\text{T}} }}{{T_{\infty } }}\frac{\partial T}{\partial y} = 0{\text{ at }}y = 0,$$

(5)

$$u = U_{\infty} \left( x \right),\, \, T \to T_{\infty } ,\, \, C \to C_{\infty } {\text{ as }}y \to \infty .$$

(6)

In above system, $\left( {u,v} \right)$ represents the velocity components along $\left( {x,y} \right)$ axes, $\rho ,$ $\sigma ,$ $\nu ,$ $\varGamma ,$ $n,$$\alpha \; = \frac{k}{{\rho c_{\text{p}} }},$ $k,$ $c_{p} ,$ $\tau = \tfrac{{(\rho c)_{p} }}{{(\rho c)_{f} }},$ $D_{\text{B}}$ and $D_{\text{T}}$ denotes the fluid density, electrical conductivity, kinematic viscosity, relaxation time, power-law index, thermal diffusivity, heat capacity, ratio of effective heat capacity of nanoparticle and base fluid, Brownian diffusion coefficient and thermophoretic diffusion coefficient. Further, the fluid temperature and nanoparticle concentration are denoted by $T$ and $C$. Moreover, the mass flux velocity is taken to be of the form $v_{\text{w}} \left( x \right) = v_{0} x^{{\tfrac{m - 1}{2}}}$ and we also assume that the heat generation/absorption is of the following form $Q^{*} = \frac{{Q_{0} }}{{x^{1 - m} }},$ where $Q_{0}$ is a constant coefficient.

We introduced the following non-dimensional variables:

$$\psi = \sqrt {\frac{2\nu b}{m + 1}} x^{{\tfrac{m + 1}{2}}} f\left( \xi \right),\, \, \xi = y\sqrt {\frac{{b\left( {m + 1} \right)}}{2\nu }} x^{{\tfrac{m - 1}{2}}} ,\, \, \theta = \frac{{T - T_{\infty } }}{{T_{\text{w}} - T_{\infty } }},\, \, \varphi = \frac{{C - C_{\infty } }}{{C_{\infty } }}.$$

(7)

The continuity Eq. (1) is satisfied by the stream function $\psi$ which is expressed in terms of Cauchy–Reimann equations $u = \frac{\partial \psi }{\partial y}{ , }\, v = - \frac{\partial \psi }{\partial x}.$

Now invoking Eq. (7) into the Eqs. (2), (3), (4), respectively, we get the subsequent system of coupled non-linear ODEs:

$$\left\{ {1 + nWe^{2} \left( {\frac{{d^{2} f}}{{{\text{d}}\xi^{2} }}} \right)^{2} } \right\}\,\left\{ {1 + We^{2} \left( {\frac{{d^{2} f}}{{{\text{d}}\xi^{2} }}} \right)^{2} } \right\}^{{\tfrac{n - 3}{2}}} \frac{{d^{3} f}}{{{\text{d}}\xi^{3} }} + f\frac{{d^{2} f}}{{{\text{d}}\xi^{2} }} + \frac{2m}{m + 1}\left( {1 - \left( {\frac{{{\text{d}}f}}{{{\text{d}}\xi }}} \right)^{2} } \right) + M^{2} \left( {1 - \frac{{{\text{d}}f}}{{{\text{d}}\xi }}} \right) = 0,$$

(8)

$$\frac{{d^{2} \theta }}{{{\text{d}}\xi^{2} }} + \mathop {\Pr }\limits \left[ {f\frac{{{\text{d}}\theta }}{{{\text{d}}\xi }} + Nb\frac{{{\text{d}}\theta }}{{{\text{d}}\xi }}\frac{{{\text{d}}\varphi }}{{{\text{d}}\xi }} + Nt\left( {\frac{{{\text{d}}\theta }}{{{\text{d}}\xi }}} \right)^{2} + Q\theta } \right] = 0,$$

(9)

$$\frac{{{\text{d}}^{2} \varphi }}{{{\text{d}}\xi^{2} }} + \mathop {\Pr }\limits Lef\frac{{{\text{d}}\varphi }}{{{\text{d}}\xi }} + \frac{Nt}{Nb}\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\xi^{2} }} = 0.$$

(10)

The corresponding boundary conditions (5) and (6) in dimensionless form are written as:

$$f(0) = f_{w} ,\, \, \frac{{{\text{d}}f}}{{{\text{d}}\xi }}(0) = \varepsilon ,\, \, \theta (0) = 0,\, \, Nb\frac{{{\text{d}}\varphi }}{{{\text{d}}\xi }}(0) + Nt\frac{{{\text{d}}\theta }}{{{\text{d}}\xi }}(0) = 0,$$

(11)

$$\frac{{{\text{d}}f}}{{{\text{d}}\xi }}(\infty ) \to 1,\, \, \theta (\infty ) \to 0,\, \, \varphi (\infty ) \to 0.$$

(12)

The dimensionless physical parameters employed in Eqs. (8)–(12) are given by:

The stretching/shrinking parameter $\varepsilon = \tfrac{a}{b}$, local Weissenberg number ${\text{We}} = \left( {\tfrac{{b^{3} \varGamma^{2} x^{3m - 1} }}{2\nu }} \right)^{1/2}$, the suction/injection parameter $f_{\text{w}} = - v_{0} \sqrt {\tfrac{2}{{b\left( {m + 1} \right)\,\nu }}} ,$ the magnetic parameter $M = \sqrt {\tfrac{2\sigma }{{b\left( {m + 1} \right)\,\rho }}} B_{0} ,$ the heat generation/absorption parameter $Q = \tfrac{{2Q_{0} }}{{\,\left( {m + 1} \right)b\rho c_{\text{p}} }},$ the Lewis number $Le = \tfrac{\alpha }{{D_{B} }},$ the thermophoresis parameter $Nt = \tau \tfrac{{D_{T} \left( {Tw - T_{\infty } } \right)}}{{T_{\infty } \nu }},$ the Brownian motion parameter $Nb = \tau \tfrac{{D_{\text{B}} C_{\infty } }}{\nu }$ and the Prandtl number $\Pr = \tfrac{\nu }{\alpha }$. To get the similarity solution, we fixed $m = \frac{1}{3}$ so that the Weissenberg number takes the form $We = \left( {\tfrac{{b^{3} \varGamma^{2} }}{2\nu }} \right)^{1/2}$.

In view of practical importance, the physical quantities used in several engineering and industrial applications are the skin friction coefficient and local Nusselt number, respectively. These are defined as:

$$C_{\text{fx}} = \frac{{\tau_{\text{w}} }}{{\rho U_{\text{w}}^{ 2} }},\,\;\;\;\;Nu_{x} = \frac{{xq_{\text{w}} }}{{k\left( {T_{\text{w}} - T_{\infty } } \right)}}.$$

(13)

where, the shear stress along the stretching surface $\tau_{\text{w}}$ and the surface heat flux $q_{\text{w}}$ are given by the following relations

$$\tau_{\text{w}} = \mu_{0} \frac{{{\mathbf{\partial }}u}}{{{\mathbf{\partial }}y}}\left[ {1 + \varGamma^{2} \left( {\frac{\partial u}{\partial y}} \right)^{2} } \right]_{y = 0}^{{\tfrac{n - 1}{2}}} ,\, \, q_{\text{w}} = - k\left( {\frac{\partial T}{\partial y}} \right)_{y = 0} .$$

(14)

In dimensionless form, skin friction coefficient and local Nusselt number becomes:

$$Re^{1/2} C_{fx} = \sqrt {\frac{m + 1}{2}} \frac{{{\text{d}}^{2} f}}{{{\text{d}}\xi^{2} }}(0)\left[ {1 + We^{2} \left( \frac{{{\text{d}}^{2} f}}{{{\text{d}}\xi^{2}}}(0) \right)^{2} } \right]^{{\tfrac{n - 1}{2}}} ,\,\;Re^{ - 1/2} Nu_{x} = - \sqrt {\frac{m + 1}{2}} \frac{{{\text{d}} \theta}}{{{\text{d}}\xi }}(0),$$

(15)

where the local Reynolds number is defined as $Re = \tfrac{{bx^{m + 1} }}{\nu }.$

Numerical technique

The main focus of this analysis is to compute the multiple numerical solutions for the modeled governing problem. Hence, the transformed system of coupled and non-linear ordinary differential Eqs. (8)–(10) under the boundary conditions (11) and (12) is numerically integrated for momentum, energy and concentration equations by employing MATLAB solver bvp4c. To apply this technique, we first change the leading system (8)–(10) into a first-order system of ODEs. Let us consider:

$$y_{1} = f,\, \, y_{2} = \frac{{{\text{d}}f}}{{{\text{d}}\xi }},\, \, y_{3} = \frac{{{\text{d}}^{2} f}}{{{\text{d}}\xi^{2} }},\, \, y_{4} = \theta ,\, \, y_{5} = \frac{{{\text{d}}\theta }}{{{\text{d}}\xi }},\, \, y_{6} = \varphi ,\, \, y_{7} = \frac{{{\text{d}}\varphi }}{{{\text{d}}\xi }},$$

(16)

$$\frac{{{\text{d}}^{3} f}}{{{\text{d}}\xi^{3} }} = \frac{{ - y_{1} y_{3} - \beta \left\{ {1 - \left( {y_{2} } \right)^{2} } \right\} - M^{2} \left( {1 - y_{2} } \right)}}{{\left\{ {1 + nWe^{2} \left( {y_{3} } \right)^{2} } \right\}\,\left\{ {1 + We^{2} \left( {y_{3} } \right)^{2} } \right\}^{{\tfrac{n - 3}{2}}} }},$$

(17)

$$\frac{{{\text{d}}^{2} \theta }}{{{\text{d}}\xi^{2} }} = - \mathop {\Pr }\limits \left[ {y_{1} y_{5} + Nby_{5} y_{7} + Nt\left( {y_{5} } \right)^{2} + Qy_{4} } \right],$$

(18)

$$\frac{{{\text{d}}^{2} \varphi }}{{{\text{d}}\xi^{2} }} = - \mathop {\Pr }\limits Ley_{1} y_{7} - \left( {\frac{Nt}{Nb}} \right)\,\frac{{{\text{d}}y_{5} }}{{{\text{d}}\xi }}.$$

(19)

The subsequent initial conditions are

$$y_{1} \left( 0 \right) = f_{\text{w}} ,\, \, y_{2} \left( 0 \right) = \varepsilon ,\, \, y_{4} \left( 0 \right) = 1,\, \, Nby_{7} \left( 0 \right) + Nty_{5} \left( 0 \right) = 0,$$

(20)

$$y_{2} \left( \infty \right) \to 1,\, \, y_{4} \left( \infty \right) \to 0,\, \, y_{6} \left( \infty \right) \to 0.$$

(21)

Actually, this method employs three-stage Labatto IIIa formula which is a collocation method of order-four. For the present problem, we set the tolerance of relative error to be $10^{ - 6} .$ This built-in function requires a guess for the convergent solution. Since, this problem exhibits dual solutions; therefore, a reasonable guess is required to get the desired solutions. The most significant step in this numerical strategy is to choose an approximate finite value of $\xi_{\infty }$. Since, there exist dual solutions in our problem. Hence, in case of first solution, we select $\xi_{\infty } = 8$ and for second solutions we choose $\xi_{\infty } = 10.$

Graphical results and discussion

In this segment, we investigate the effect of involved fluid and flow parameters, namely the Weissenberg number $We,$ the power-law index $n,$ the magnetic parameter $M,$ stretching/shrinking parameter $\varepsilon ,$ the mass suction parameter $f_{\text{w}} ,$ the Brownian motion parameter $Nb,$ the thermophoresis parameter $Nt,$ the heat generation/absorption parameter $Q,$ the Lewis number $Le$ and the Prandtl number $\Pr$ on nanofluid velocity distributions, nanofluid temperature distributions and nanoparticles concentration distributions. For numerical computations, the fixed values chosen for physical parameters are: $n = 0.4,$ $We = 1.0,$ $\varepsilon = - 1.6,$ $f_{w} = 1.0,$ $\Pr = 1.0,$ $Q = 0.2,$ $Nt = Nb = 0.1$ and $Le = 1.0$.

Table 1 shows the comparison of computed results obtained by bvp4c routine in this analysis with already published works of Wang (2007) and (Akbar et al. 2014). This table displays the simulated results of skin friction coefficient $f^{\prime\prime}\left( 0 \right)$ in limiting case of Newtonian fluid, i.e., $n = 1$ and $We = 0$ for varying values of stretching/shrinking parameter $\varepsilon$. It is clearly seen through this table that the numerical results obtained by the present formulation are in excellent agreement with that of Akbar et al. (2014).

Table 1 Numerical comparison of the values $f^{\prime\prime}\left( 0 \right)$ with varying values of stretching/shrinking parameter $\varepsilon$

The most important physical quantities, as far as the current research work goes, are skin friction coefficient $Re^{1/2} C_{fx}$ and Nusselt number $Re^{ - 1/2} Nu_{x}$, whose variation for different values of mass suction parameter $f_{w}$ is plotted in Figs. 2 and 3. In both the figures, skin friction coefficient and Nusselt number are sketched as a function of stretching/shrinking parameter $\varepsilon .$ It is noteworthy here that the simulated results of present problem confirm the existence of dual solutions for both the profiles of skin friction and Nusselt number. As depicted in Fig. 2 an increase in mass suction strength $f_{w}$, both the magnitude of skin friction coefficient and the solution domain for stretching/shrinking parameter $\varepsilon$ also increases. Moreover, it is interesting to note that the dual solutions for skin friction coefficient are possible in the range of $\varepsilon \left( {\varepsilon_{c} < \varepsilon < 0} \right)$ and no solution for $\varepsilon \left( {\varepsilon < \varepsilon_{c} } \right)$, where $\varepsilon_{c}$ is known as the critical value of $\varepsilon .$ We can see that both the first and second solution coincide at the critical value $\varepsilon_{c}$. This figure further emphasizes that unique solution exists for $\varepsilon \ge - 1.$ Physically, the increasing behavior of skin friction for higher suction parameter means that suction delays the separation. Moreover, the Nusselt number profiles obtained in Fig. 3 exhibit an increasing behavior for increasing values of mass suction parameter. Again, dual solutions are observed in certain range of shrinking parameter for some fixed values of mass suction.

Fig. 2

Behavior of suction parameter on the skin friction coefficient

Fig. 3

Behavior of suction parameter on the Nusselt number

The dimensionless velocity $f^{\prime}\left( \xi \right)$ and temperature profiles $\theta \left( \xi \right)$ are displayed in Figs. 4 and 5 for the same values of magnetic parameter $M$ in case of shrinking wedge $\varepsilon = - 1.6$. It is noticeable that both figures witnessed the occurrence of dual solutions for nanofluid velocity as well as the temperature profiles. For dual velocity curves, it is perceived that they increase with increase in magnetic parameter in case of first solution while an n opposite is seen for second solution. At the same time, these profiles depict that the corresponding boundary layer thickness is much lesser for first solution. The physical explanation behind this phenomenon is the Lorentz force which is produced by the application of transverse magnetic field. In fact, this is a resistive force and causes a deceleration in flow over the wedge which reduces the fluid velocity as well as momentum boundary layer thickness. On the other hand, temperature profiles displayed in Fig. 5 show a decreasing behavior for higher values of magnetic parameter in case of first solution. However, an enhancement in temperature profile is seen with higher magnetic parameter.

Fig. 4

Behavior of magnetic parameter on the velocity distributions

Fig. 5

Behavior of magnetic parameter on the temperature distributions

Figures 6 and 7 depict the velocity $f^{\prime}\left( \xi \right)$ and temperature distributions $\theta \left( \xi \right)$ within the boundary layer for distinct values of shrinking parameter $\varepsilon$ at fixed values of other parameter. In either case, the solutions profiles satisfy the far field boundary conditions asymptotically. The results shown in these figures provide that the boundary layer thickness is much smaller for the first solution than that of the second solution. It is further perceived that the fluid velocity is a decreasing function of shrinking parameter in case of first solutions while the fluid temperature shows an opposite behavior. Figures 8 and 9 present the mass suction parameter $f_{w}$ impact on the dimensionless velocity profiles and dimensionless temperature profiles for the case of shrinking wedge. It is evident from these figures that, with increasing values of mass suction parameter, the velocity profiles $f^{\prime}\left( \xi \right)$ increase along with their boundary layer thickness for second solution. However, in case of second solution we found a significant reduction in the velocity distribution when mass suction parameter rises. On the contrary to velocity profiles, the increase in mass suction parameter leads to a significant reduction in the temperature profiles $\theta \left( \xi \right)$ in case of first solution along with corresponding boundary layer thickness. Further, as expected, the temperature profiles display an increasing behavior so as the thermal boundary thickness for higher values of mass suction parameter in case of second solution.

Fig. 6

Behavior of stretching/shrinking parameter on the velocity distributions

Fig. 7

Behavior of stretching/shrinking parameter on the temperature distributions

Fig. 8

Behavior of suction parameter on the velocity distributions

Fig. 9

Behavior of suction parameter on the temperature distributions

We now discuss the various outcomes of the nanoparticle concentration profiles for varying values of magnetic parameter, shrinking parameter and mass suction parameter within the boundary layer region. Figure 10 describes the influence of magnetic parameter on concentration distributions. At the increasing values of the magnetic parameter $M$, an increment in the velocity profile is seen near the solid boundary in the first solutions, while after a certain distance from the solid surface, they exhibit a decreasing characteristic. However, quite opposite is true for the second solution. An important effect of shrinking parameter $\varepsilon$ is that it increases the concentration profiles $\varphi \left( \xi \right)$ near the solid boundary for second solution and decreases them in first solution, as seen through Fig. 11. Moreover, it has been noticed that concentration profiles decrease significantly in case of second solution but increase for first solution near the slit and asymptotically satisfy the boundary condition, as depicted in Fig. 12.

Fig. 10

Behavior of magnetic parameter on the concentration distributions

Fig. 11

Behavior of stretching/shrinking parameter on the concentration distributions

Fig. 12

Behavior of suction parameter on the concentration distributions

The influence of Prandtl number $\Pr$ on non-dimensional temperature $\theta \left( \xi \right)$ and concentration distributions $\phi \left( \xi \right)$ within the boundary layer is illustrated in Figs. 13 and 14. It is witnessed that both the temperature and thermal boundary layer thickness reduces with higher Prandtl number in case of first solution. This is attributable to the fact that increasing the Prandtl number leads to reduce the thermal diffusivity and responsible for less penetration of heat within the fluid. It is important to note that the nanoparticles’ concentration is a decreasing function of Prandtl number. Figures 15 and 16 are drawn to highlight the dependence of dimensionless temperature and concentration distributions on thermophoresis parameter $Nt.$ It is observed from these figures that the nanofluid temperature enhances with growing values of thermophoresis parameter so as the thermal boundary layer thickens in first solution. While, increasing thermophoresis parameter reduces the temperature profiles for the case of second solution. It is worth seeing that nanoparticle concentration decreases in response of increasing values of thermophoresis parameter in second solution while it increases in first solution. To visualize the effect of heat generation/absorption parameter $Q$ on dimensionless temperature profiles Fig. 17 has been drawn. Form this figure, we noticed that the temperature profiles increase with growing values of heat generation/absorption parameter in both the solutions. Further, the associated boundary layer thickness also enhances.

Fig. 13

Behavior of Prandtl number on the temperature distributions

Fig. 14

Behavior of Prandtl number on the concentration distributions

Fig. 15

Behavior of themophoresis parameter on the temperature distributions

Fig. 16

Behavior of Brownian motion parameter on the temperature distributions

Fig. 17

Behavior of heat generation/absorption parameter on the temperature distributions

Concluding remarks

Numerical simulation of MHD flow of Carreau nanofluid past a stretching/shrinking wedge has been performed employing boundary layer form of Navier–Stokes equations with MATLAB package bvp4c. The main focus of current analysis was to obtain the dual solutions in case of shrinking wedge. Based on the detailed analysis of obtained results, the key points are listed as below:

• 1. Solution domain was significantly raised by increasing the mass suction parameter.

• 2. Heat transport rate enhances with higher values of suction parameter.

• 3. Larger magnetic parameter leads to the decreasing behavior of fluid velocity.

• 4. An increment in fluid temperature is observed with higher heat generation/absorption parameter in both solutions.