Intuitionistic fuzzy transportation problem with various kinds of uncertainties in parameters and variables

Abstract

In real-life decisions usually we have to suffer through different states of uncertainties. In this article, we formulate a transportation problem in which costs, supplies and demands all are different types of real, fuzzy or intuitionistic fuzzy numbers that is the data has different types of uncertainties. We propose a ranking procedure for intuitionistic fuzzy numbers. Using the proposed ranking function intuitionistic fuzzy methods are proposed to find starting basic feasible solution in terms of trapezoidal intuitionistic fuzzy numbers. Intuitionistic fuzzy modified distribution method is proposed to find optimal solution. We illustrate the methodology by numerical examples.

1 Introduction

In most of the cases of judgements, evaluation is done by human beings where certainly there are limitations of knowledge, intellectual functionaries or availability of data due to some uncontrollable factors. Naturally, every decision-maker hesitates more or less on every evaluation activity. This is the concept of intuitionistic fuzzy set (IFS) theory introduced by Atanassov (1986). The major advantage of IFS over fuzzy set is that IFS separates the degree of membership (belongingness) and the degree of non-membership (non-belongingness) of an element in the set. IFS theory is one of the interesting generalizations of the fuzzy set theory introduced by Zadeh (1965). Because of this generalization IFS theory has much wider scope of applicability than the usual fuzzy set theory in solving various kinds of real physical problems.

The concept of mathematical programming was introduced by Bellman and Zadeh (1970). Then many researchers move towards fuzzy optimization and now it is an active area of research. Nagoorgani and Razak (2006) presented a two stage cost minimizing fuzzy transportation problem in which supplies and demands are trapezoidal fuzzy numbers. Dinager and Palanivel (2009) investigated a method to solve fuzzy transportation problem (FTP) by taking trapezoidal fuzzy numbers. Pandian and Natarajan (2010) presented a new algorithm for finding a fuzzy optimal solution for fuzzy transportation problem. Ismail and Kumar (2010) did a comparative study on transportation problem in fuzzy environment. Zangiabadi and Maleki (2013) developed fuzzy goal programming technique to solve multi-objective transportation problems with some non-linear membership functions. Singh and Yadav (2014a, b) developed algorithms to solve intuitionistic fuzzy transportation problems of type-1 and type-2.

In real life transportation problems some data may be exact that is a crisp value, some may be in fuzzy form and some may be in intuitionistic fuzzy form due to different reasons of uncertainties and hesitations. Therefore to deal with such types of data, we have developed the notion of mixed intuitionistic fuzzy transportation problem. In this paper, we have developed a new ordering procedure using accuracy function of intuitionistic fuzzy numbers (IFN) and used to obtain optimal solution of mixed intuitionistic fuzzy transportation problem (MIFTP).

The paper is organized as follows: Sect. 2 deals with some definitions and arithmetic operations on TrIFNs from literature (Kumar et al. 2011; Singh and Yadav 2014a, b). In Sect. 3, we have proposed some propositions to find the accuracy functional value of an IFN. In Sect. 4, we have defined score function and accuracy function of an IFN. In Sect. 5, we have proposed some definitions required to develop the solution algorithm for MIFBTP. Section 6 deals with MIFBTP. Section 7 deals with the proposed methods to find the starting basic feasible solution (BFS) of MIFBTP. Section 8 deals with methodology to find the optimal solution of MIFBTP. In Sect. 9, numerical examples are given to illustrate the methodology to get optimal solution for different ranking functions with results and discussion of the findings followed by conclusion in the last.

2 Some definitions

Definition 2.1

Let X be a universal set. Then a fuzzy set $\tilde{A}$ in X is defined by

$$\tilde{A}\, = \,\left\{ {(x,\,\mu_{{\tilde{A}}} (x)):\,\,x \in \,X\,} \right\},{\text{where}}\,\mu_{{\tilde{A}}} :X \to [0,1].$$

Definition 2.2

A fuzzy set $\tilde{A}\, = \,\left\{ { < x,\,\mu_{{\tilde{A}}} (x)\, > \,:\,x \in R} \right\}$ is called a fuzzy number (FN) if the following hold:

• 1. There exists m ∊ R such that $\mu_{{\tilde{A}}} (m)\, = \,1\,$(m is called the mean value of $\tilde{A}$),

• 2. $\mu_{{\tilde{A}}}$ is piecewise continuous function from R to the closed interval [0, 1], where

  $$\mu_{{\tilde{A}}} (x)\, = \left\{ {\begin{array}{ll} {g(x),} \hfill & {m - a \le x < m,} \hfill \\ {1,} \hfill & {x = m,} \hfill \\ {h(x),} \hfill & {m < x \le m + b,} \hfill \\ {0,} \hfill & {\text{otherwise,}} \hfill \\ \end{array} } \right.$$

Here, g is piecewise continuous and strictly increasing function in [m − a, m); h is piecewise continuous and strictly decreasing function in (m, m + b]. This FN $\tilde{A}$ is denoted by $\tilde{A}\, = \,(m;\,a,\,\,b).$

Definition 2.3

Let X be a universe of discourse. Then an intuitionistic fuzzy set (IFS) $\tilde{A}^{I}$ in X is defined by a set of ordered triples

$$\tilde{A}^{I} \, = \,\left\{ { < x,\,\mu_{{\tilde{A}^{I} }} (x),\,\upsilon_{{\tilde{A}^{I} }} (x)\, > \,:\,x \in X} \right\},$$

where $\mu_{{\tilde{A}^{I} }} ,\,\,\upsilon_{{\tilde{A}^{I} }} \,:X\, \to \,[0,\,1]$ are functions such that $0 \le \mu_{{\tilde{A}^{I} }} (x)\, + \,\upsilon_{{\tilde{A}^{I} }} (x)\, \le \,1,\,\forall x \in X.$ The value $\mu_{{\tilde{A}^{I} }} (x)$ represents the degree of membership and $\upsilon_{{\tilde{A}^{I} }} (x)\,$ represents the degree of non- membership of the element x ∊ X being in $\tilde{A}^{I}.$

Definition 2.4

An IFS $\tilde{A}^{I} \, = \,\left\{ { < x,\,\mu_{{\tilde{A}^{I} }} (x),\,\upsilon_{{\tilde{A}^{I} }} (x)\, > \,:\,x \in R} \right\}$ is called an IFN if the following hold:

• 1. There exists m ∊ R such that $\mu_{{\tilde{A}^{I} }} (m)\, = \,1\,\,{\text{and}}\,\,\upsilon_{{\tilde{A}^{I} }} (m)\, = \,0$ (m is called the mean value of $\tilde{A}^{I}$),

• 2. $\mu_{{\tilde{A}^{I} }}$ and $\nu_{{\tilde{A}^{I} }}$ are piecewise continuous functions from R to the closed interval [0, 1] and $0 \le \mu_{{\tilde{A}^{I} }} (x)\, + \,\upsilon_{{\tilde{A}^{I} }} (x)\, \le \,1,\,\forall x \in R$, where

  $$\mu_{{\tilde{A}^{I} }} (x)\, = \left\{ \begin{array}{ll} g_{1} (x),&\quad m - a \le x < m, \hfill \\ 1, &\quad x = m, \hfill \\ h_{1} (x),&\quad m < x \le m + b, \hfill \\ 0,&\quad {\text{otherwise}}, \hfill \\ \end{array} \right.$$

  and

  $$\upsilon_{{\tilde{A}^{I} }} (x)\, = \left\{ \begin{array}{ll} g_{2} (x),&\quad m - a^{\prime} \le x \le m;\,0 \le g_{1} (x) + g_{2} (x) \le 1, \hfill \\ 0,&\quad x = m, \hfill \\ h_{2} (x),&\quad m \le x \le m + b^{\prime};\,0 \le h_{1} (x) + h_{2} (x) \le 1, \hfill \\ 1,&\quad {\text{otherwise}}. \hfill \\ \end{array} \right.$$

Here m is the mean value of $\tilde{A}^{I}$; a and b are left and right spreads of membership function $\mu_{{\tilde{A}^{I} }}$ respectively; a′ and b′ are left and right spreads of non-membership function $\upsilon_{{\tilde{A}^{I} }}$ respectively; where g ₁ and h ₁ are piecewise continuous, strictly increasing and strictly decreasing functions in [m − a, m) and (m, m + b] respectively; g ₂ and h ₂ are piecewise continuous, strictly decreasing and strictly increasing functions in [m − a, m] and [m, m + b] respectively. The IFN $\tilde{A}^{I}$ is represented by $\tilde{A}^{I} \, = \,(m;\,a,\,\,b;\,\,a^{\prime},\,\,b^{\prime}).$

Definition 2.5

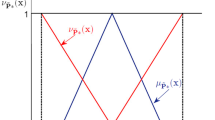
A Trapezoidal Intuitionistic Fuzzy Number (TrIFN) $\tilde{A}^{I}$ is an IFN with the membership function $\mu_{{\tilde{A}^{I} }}$ and non-membership function $\nu_{{\tilde{A}^{I} }}$ given by

$$\mu_{{\tilde{A}^{I} }} (x) = \left\{ \begin{array}{ll} \mu_{{\tilde{A}^{I} }}^{L} (x) = \frac{x - a}{b - a} ,&\quad a < x \le b, \hfill \\ 1, &\quad {\text{b}} \le x \le c, \hfill \\ \mu_{{\tilde{A}^{I} }}^{R} (x) = \frac{d - x}{d - c} ,&\quad {\text{ c}} \le x < d, \hfill \\ 0,&\quad {\text{otherwise}}, \hfill \\ \end{array} \right.\quad{\text{and}}\quad \nu_{{\tilde{A}^{I} }} (x) = \left\{ \begin{array}{ll} \nu_{{\tilde{A}^{I} }}^{L} (x) = \frac{{b^{\prime} - x}}{{b^{\prime} - a^{\prime}}} , & a^{\prime} < x \le b^{\prime}, \hfill \\ 0 ,&\quad b^{\prime} \le x \le c^{\prime}, \hfill \\ \nu_{{\tilde{A}^{I} }}^{R} (x) = \frac{{x - c^{\prime}}}{{d^{\prime} - c^{\prime}}} , &\quad c^{\prime} \le x < d^{\prime}, \hfill \\ 1,&\quad {\text{otherwise}}, \hfill \\ \end{array} \right.$$

where a′ ≤ a ≤ b′ ≤ b ≤ c ≤ c′ ≤ d ≤ d′ (Fig. 1).

Fig. 1

Membership and non-membership functions of TrIFN

This TrIFN is denoted by $\tilde{A}^{I} = (a,b,c,d;a^{\prime},b^{\prime},c^{\prime},d^{\prime}).$

2.1 Particular cases

Case 1

If b′ = b, c′ = c, then $\tilde{A}^{I}$ also represents a TrIFN. It is denoted by $\tilde{A}^{I} = (a,b,c,d;a^{\prime},b,c,d^{\prime}).$

Case 2

If b′ = b = c = c′,  then $\tilde{A}^{I}$ represents a Triangular Intuitionistic Fuzzy Number (TIFN). It is denoted by $\tilde{A}^{I} = (a,b,d;a^{\prime},b,d^{\prime}).$

Case 3

If a′ = a, b′ = b, c′ = c, d′ = d,  then $\tilde{A}^{I}$ represents Trapezoidal Fuzzy Number (TrFN). It is denoted by $\tilde{A}^{I} = (a,b,c,d).$

Case 4

If a′ = a, b′ = b = c = c′, d′ = d,  then $\tilde{A}^{I}$ represents a Triangular Fuzzy Number (TFN). It is denoted by $\tilde{A}^{I} = (a,b,d).$

Case 5

If a′ = a = b′ = b, c = c′ = d = d′, then $\tilde{A}^{I}$ represents the crisp interval [b, c].

Case 6

If a′ = a = b′ = b = c = c′ = d = d′ = m, then $\tilde{A}^{I}$ represents a real number m.

2.2 Arithmetic operations on TrIFNs

If $\tilde{A}_{1}^{I} = (a_{1} ,b_{1} ,c_{1} ,d_{1} ;a_{1}^{\prime} ,b_{1}^{\prime} ,c_{1}^{\prime} ,d_{1}^{\prime} )$ and $\tilde{A}_{2}^{I} = (a_{2} ,b_{2} ,c_{2} ,d_{2} ;a_{2}^{\prime} ,b_{2}^{\prime} ,c_{2}^{\prime} ,d_{2}^{\prime} )$ are two TrIFNs. Then

$${\text{Addition}}:\quad \tilde{A}_{1}^{i} \oplus \tilde{A}_{2}^{i} = \left( {a_{1} + a_{2} ,b_{1} + b_{2} ,c_{1} + c_{2} ,d_{1} + d_{2} ;a_{1}^{\prime} + a_{2}^{\prime} ,b_{1}^{\prime} + b_{2}^{\prime} ,c_{1}^{\prime} + c_{2}^{\prime} ,d_{1}^{\prime} + d_{2}^{\prime} } \right)$$

$${\text{Subtraction}}:\quad \tilde{A}_{1}^{i} \varTheta \tilde{A}_{2}^{i} = \left( {a_{1} - d_{2} ,b_{1} - b_{2} ,c_{1} - c_{2} ,d_{1} - a_{2} ;a_{1}^{\prime } - d_{2}^{\prime } ,b_{1}^{\prime } - b_{2}^{\prime } ,c_{1}^{\prime } - c_{2}^{\prime } ,d_{1}^{\prime } - a_{2}^{\prime } } \right)$$

$$\begin{aligned} {\text{Multiplication}}{:}\; & \tilde{A}_{1}^{I} \otimes \tilde{A}_{2}^{I} = (l_{1} ,l_{2} ,l_{3} ,l_{4} ;l_{1}^{\prime } ,l_{2}^{\prime } ,l_{3}^{\prime } ,l_{4}^{\prime } ),\;{\text{where}} \\ & l_{1} = \hbox{min} \{ a_{1} a_{2} ,a_{1} d_{2} ,d_{1} a_{2} ,d_{1} d_{2} \} ,\,\,\,l_{1}^{\prime } = \hbox{min} \{ a_{1}^{\prime } a_{2}^{\prime } ,a_{1}^{\prime } d_{2}^{\prime } ,d_{1}^{\prime } a_{2}^{\prime } ,d_{1}^{\prime } d_{2}^{\prime } \} \\ & l_{2} = \hbox{min} \{ b_{1} b_{2} ,b_{1} c_{2} ,c_{1} b_{2} ,c_{1} c_{2} \} ,\,\,\,\,\,l_{2}^{\prime } = \hbox{min} \{ b_{1}^{\prime } b_{2}^{\prime } ,b_{1}^{\prime } c_{2}^{\prime } ,c_{1}^{\prime } b_{2}^{\prime } ,c_{1}^{\prime } c_{2}^{\prime } \} , \\ & l_{3} = \hbox{max} \{ b_{1} b_{2} ,b_{1} c_{2} ,c_{1} b_{2} ,c_{1} c_{2} \} ,\,\,\,\,l_{3}^{\prime } = \hbox{max} \{ b_{1}^{\prime } b_{2}^{\prime } ,b_{1}^{\prime } c_{2}^{\prime } ,c_{1}^{\prime } b_{2}^{\prime } ,c_{1}^{\prime } c_{2}^{\prime } \} , \\ & l_{4} = \hbox{max} \{ a_{1} a_{2} ,a_{1} d_{2} ,d_{1} a_{2} ,d_{1} d_{2} \} ,\,l_{4}^{\prime } = \hbox{max} \{ a_{1}^{\prime } a_{2}^{\prime } ,a_{1}^{\prime } d_{2}^{\prime } ,d_{1}^{\prime } a_{2}^{\prime } ,d_{1}^{\prime } d_{2}^{\prime } \} . \\ \end{aligned}$$

$${\text{Scalar}}\;{\text{multiplication}}{:}\;k\tilde{A}_{1}^{I} = \left\{ \begin{aligned} (ka_{1} ,\,kb_{1} ,\,kc_{1} ,kd_{1} ;ka_{1}^{\prime } ,\,kb_{1}^{\prime } ,\,kc_{1}^{\prime } ,kd_{1}^{\prime } ),\quad k > 0, \hfill \\ (kd_{1} ,\,kc_{1} ,kb_{1} ,\,ka_{1} ;kd_{1}^{\prime } ,\,kc_{1}^{\prime } ,kb_{1}^{\prime } ,\,ka_{1}^{\prime } ),\quad k < 0. \hfill \\ \end{aligned} \right.$$

3 Propositions

Proposition 3.1

The left membership function $\mu_{{\tilde{A}^{I} }}^{L}$ and the right membership function $\mu_{{\tilde{A}^{I} }}^{R}$ are invertible.

Proof

The left membership function $\mu_{{\tilde{A}^{I} }}^{L} :[a,b] \to [0,1]$ is continuous and strictly increasing, the inverse function of $\mu_{{\tilde{A}^{I} }}^{L}$ will exists name it by $g_{{\tilde{A}^{I} }}^{L} :[0,1] \to [a,b].$ Similarly, the right membership function $\mu_{{\tilde{A}^{I} }}^{R} :[c,d] \to [0,1]$ is continuous and strictly decreasing, the inverse function of $\mu_{{\tilde{A}^{I} }}^{R}$ will exists name it by $g_{{\tilde{A}^{I} }}^{R} :[0,1] \to [c,d].$

Proposition 3.2

The left non-membership function $\nu_{{\tilde{A}^{I} }}^{L}$ and the right non-membership function $\nu_{{\tilde{A}^{I} }}^{R}$ are invertible.

Proof

The left non-membership function $\nu_{{\tilde{A}^{I} }}^{L} :[a',b'] \to [0,1]$ is continuous and strictly decreasing, the inverse function of $\nu_{{\tilde{A}^{I} }}^{L}$ will exists name it by $h_{{\tilde{A}^{I} }}^{L} :[0,1] \to [a',b'].$ Similarly, the right non-membership function $\nu_{{\tilde{A}^{I} }}^{R} :[c',d'] \to [0,1]$ is continuous and strictly increasing, the inverse function of $\nu_{{\tilde{A}^{I} }}^{R}$ will exists name it by $h_{{\tilde{A}^{I} }}^{R} :[0,1] \to [c',d'].$

Proposition 3.3

The functions $g_{{\tilde{A}^{I} }}^{L}$,$g_{{\tilde{A}^{I} }}^{R}$, $h_{{\tilde{A}^{I} }}^{L}$ and $h_{{\tilde{A}^{I} }}^{R}$ are also continuous and monotonic.

Proof

Since $\mu_{{\tilde{A}^{I} }}^{L}$, $\mu_{{\tilde{A}^{I} }}^{R}$, $\nu_{{\tilde{A}^{I} }}^{L}$ and $\nu_{{\tilde{A}^{I} }}^{R}$ are continuous and monotonic, therefore their respective inverses $g_{{\tilde{A}^{I} }}^{L}$, $g_{{\tilde{A}^{I} }}^{R}$, $h_{{\tilde{A}^{I} }}^{L}$ and $h_{{\tilde{A}^{I} }}^{R}$ are also continuous and monotonic in the closed interval [0, 1].

Proposition 3.4

The functions $g_{{\tilde{A}^{I} }}^{L}$, $g_{{\tilde{A}^{I} }}^{R}$, $h_{{\tilde{A}^{I} }}^{L}$ and $h_{{\tilde{A}^{I} }}^{R}$ are integrable.

Proof

Since $g_{{\tilde{A}^{I} }}^{L}$, $g_{{\tilde{A}^{I} }}^{R}$, $h_{{\tilde{A}^{I} }}^{L}$ and $h_{{\tilde{A}^{I} }}^{R}$ are continuous in the closed interval [0, 1], these are integrable on [0, 1]. That is,$\int\limits_{0}^{1} {g_{{\tilde{A}^{I} }}^{L} (y)dy}$, $\int\limits_{0}^{1} {g_{{\tilde{A}^{I} }}^{R} (y)dy}$,$\int\limits_{0}^{1} {h_{{\tilde{A}^{I} }}^{L} (y)dy}$ and $\int\limits_{0}^{1} {h_{{\tilde{A}^{I} }}^{R} (y)dy}$ exist.

4 Score function and accuracy function of a TrIFN

Let $\tilde{A}^{I} = (a,b,c,d;a^{\prime},b^{\prime},c^{\prime},d^{\prime})$ be a TrIFN.

Definition 4.1

The left integral and right integral values of $\tilde{A}^{I}$ for the membership function $\mu_{{\tilde{A}^{I} }}$ are denoted by $I_{L} (\mu_{{\tilde{A}^{I} }} )$ and $I_{R} (\mu_{{\tilde{A}^{I} }} )$ and defined by $I_{L} (\mu_{{\tilde{A}^{I} }} ) = \int\limits_{0}^{1} {g_{{\tilde{A}^{I} }}^{L} (y)dy}$ and $I_{R} (\mu_{{\tilde{A}^{I} }} ) = \int\limits_{0}^{1} {g_{{\tilde{A}^{I} }}^{R} (y)dy}$ respectively.

Definition 4.2

The left integral and right integral values of $\tilde{A}^{I}$ for the non-membership function $\nu_{{\tilde{A}^{I} }}$ are denoted by $I_{L} (\nu_{{\tilde{A}^{I} }} )$ and $I_{R} (\nu_{{\tilde{A}^{I} }} )$ and defined by $I_{L} (\nu_{{\tilde{A}^{I} }} ) = \int\limits_{0}^{1} {h_{{\tilde{A}^{I} }}^{L} (y)dy}$ and $I_{R} (\nu_{{\tilde{A}^{I} }} ) = \int\limits_{0}^{1} {h_{{\tilde{A}^{I} }}^{R} (y)dy}$ respectively.

Definition 4.3

The generalized score function for the membership function $\mu_{{\tilde{A}^{I} }}$ is denoted by $S^{\alpha } (\mu_{{\tilde{A}^{I} }} )$ with index of optimism α ∊ [0, 1] and is defined by $S^{\alpha } (\mu_{{\tilde{A}^{I} }} ) = \alpha \{ I_{R} (\mu_{{\tilde{A}^{I} }} ) + I_{L} (\mu_{{\tilde{A}^{I} }} )\}.$

Definition 4.4

The generalized score function for the non-membership function $\nu_{{\tilde{A}^{I} }}$ is denoted by $S^{\alpha } (\nu_{{\tilde{A}^{I} }} )$ with index of optimism α and is defined by $S^{\alpha } (\nu_{{\tilde{A}^{I} }} ) = (1 - \alpha )\{ I_{L} (\nu_{{\tilde{A}^{I} }} ) + I_{R} (\nu_{{\tilde{A}^{I} }} )\}.$

Definition 4.5

The generalized accuracy function of $\tilde{A}^{I}$ is denoted by $f^{\alpha } (\tilde{A}^{I} )$ and is defined by $f^{\alpha } (\tilde{A}^{I} )\, = \,\frac{{S^{\alpha } (\mu_{{\tilde{A}^{I} }} )\, + \,S^{\alpha } (\nu_{{\tilde{A}^{I} }} )}}{2}\, = \frac{{\alpha \{ I_{R} (\mu_{{\tilde{A}^{I} }} ) + I_{L} (\mu_{{\tilde{A}^{I} }} )\} + (1 - \alpha )\{ I_{L} (\nu_{{\tilde{A}^{I} }} ) + I_{R} (\nu_{{\tilde{A}^{I} }} )\} }}{2}.$

In case of TrIFN $\tilde{A}^{I}$, we have $\mu_{{\tilde{A}^{I} }}^{L} (x) = \frac{x - a}{b - a}$ ⇒  $g_{{\tilde{A}^{I} }}^{L} (y) = [a + (b - a)y].$

So, $I_{L} (\mu_{{\tilde{A}^{I} }} ) = \int\limits_{0}^{1} {g_{{\tilde{A}^{I} }}^{L} (y)dy} = \int\limits_{0}^{1} {[a + (b - a)y]} dy = \frac{1}{2}(a + b).$

Similarly, $I_{R} (\mu_{{\tilde{A}^{I} }} ) = \frac{1}{2}(c + d)$, $I_{L} (\nu_{{\tilde{A}^{I} }} ) = \frac{1}{2}(a' + b')$ and $I_{R} (\nu_{{\tilde{A}^{I} }} ) = \frac{1}{2}(c' + d').$

Hence,

$$f^{\alpha } (\tilde{A}^{I} )\,\, = \frac{{\alpha \{ (c + d) + (a + b)\} + (1 - \alpha )\{ (a' + b') + (c' + d')\} }}{4}$$

(1)

This gives

$$f^{0} (\tilde{A}^{I} )\,\, = \frac{a' + b' + c' + d'}{4}$$

(2)

$$f^{0.5} (\tilde{A}^{I} )\,\, = \frac{{\{ (c + d) + (a + b)\} + \{ (a' + b') + (c' + d')\} }}{8}$$

(3)

$$f^{1} (\tilde{A}^{I} )\,\, = \frac{a + b + c + d}{4}$$

(4)

Theorem

The generalized accuracy function f ^α is a linear function.

Proof

Let $\tilde{A}^{I} = (a_{1} ,a_{2} ,a_{3} ,a_{4} ;a_{1}^{'} ,a_{2}^{'} ,a_{3}^{'} ,a_{4}^{'} )\,{\text{and}}\,\tilde{B}^{I} = (b_{1} ,b_{2} ,b_{3} ,b_{4} ;b_{1}^{'} ,b_{2}^{'} ,b_{3}^{'} ,b_{4}^{'} )$ be two TrIFNs. Then

$$\begin{aligned}f^{\alpha } (\tilde{A}^{I} \oplus \tilde{B}^{I} )& = f^{\alpha } [( a_{1} ,a_{2} ,a_{3} ,a_{4} ;a_{1}^{'} ,a_{2}^{'} ,a_{3}^{'} ,a_{4}^{'} )\oplus(b_{1} ,b_{2} ,b_{3} ,b_{4} ;b_{1}^{'} ,b_{2}^{'} ,b_{3}^{'} ,b_{4}^{'} )]\\& = f^{\alpha } (a_{1} + b_{1} ,a_{2} + b_{2} ,a_{3} + b_{3} ,a_{4} + b_{4} ;a_{1}^{'} + b_{1}^{'} ,a_{2}^{'} + b_{2}^{'} ,a_{3}^{'} + b_{3}^{'} ,a_{4}^{'} + b_{4}^{'} ) \hfill \\& = \frac{{\alpha \{ (a_{1} + b_{1} ) + (a_{2} + b_{2} ) + (a_{3} + b_{3} ) + (a_{4} + b_{4} )\} + (1 - \alpha )\{ (a_{1}^{'} + b_{1}^{'} ) + (a_{2}^{'} + b_{2}^{'} ) + (a_{3}^{'} + b_{3}^{'} ) + (a_{4}^{'} + b_{4}^{'} )\} }}{4} \hfill \\&= \frac{{\alpha (a_{1} + a_{2} + a_{3} + a_{4} ) + (1 - \alpha )(a_{1}^{'} + a_{2}^{'} + a_{3}^{'} + a_{4}^{'} )}}{4} + \frac{{\alpha (b_{1} + b_{2} + b_{3} + b_{4} ) + (1 - \alpha )(b_{1}^{'} + b_{2}^{'} + b_{3}^{'} + b_{4}^{'} )}}{4}\\&=f^{\alpha } (\tilde{A}^{I} ) + f^{\alpha } (\tilde{B}^{I} ).\quad {\text{Proved}} \end{aligned}$$

Remark

α represents the degree of optimism of a decision maker (DM) (Liou and Wang 1992). A larger α indicates a higher degree of optimism because when α increases we see that the weightage of the acceptance level of the transportation cost increases. α = 0 gives non-membership value which represents a pessimistic decision maker’s viewpoint as DM is curious about the non-acceptance level of the transportation cost. α = 1 gives membership value of the transportation cost which represents an optimistic decision maker’s viewpoint as DM is curious about the acceptance level of the transportation cost. For α = 0.5, the score functional value represents a moderate decision maker’s viewpoint because the DM gives equal importance to the acceptance and non-acceptance level of the transportation cost.

5 Proposed definitions

Now, we define zero, non-negative, positive and negative TrIFNs. Ordering of TrIFNs based on accuracy function is also given here.

Definition 5.1

ATrIFN $\tilde{A}^{I} = (a,b,c,d;a^{\prime},b^{\prime},c^{\prime},d^{\prime})$ is said to be zero TrIFN if $f^{\alpha } (\tilde{A}^{I} )\, = 0.$

Definition 5.2

A TrIFN $\tilde{A}^{I} = (a,b,c,d;a^{\prime},b^{\prime},c^{\prime},d^{\prime})$ is said to be non-negative TrIFN if $f^{\alpha } (\tilde{A}^{I} )\, \ge 0.$

Definition 5.3

ATrIFN $\tilde{A}^{I} = (a,b,c,d;a^{\prime},b^{\prime},c^{\prime},d^{\prime})$ is said to be positive TrIFN if $f^{\alpha } (\tilde{A}^{I} )\, > 0.$

Definition 5.4

ATrIFN $\tilde{A}^{I} = (a,b,c,d;a^{\prime},b^{\prime},c^{\prime},d^{\prime})$ is said to be negative TrIFN if $f^{\alpha } (\tilde{A}^{I} )\, < 0.$

Definition 5.5

Let $\tilde{A}_{1}^{I} = (a_{1} ,b_{1} ,c_{1} ,d_{1} ;a_{1}^{\prime} ,b_{1}^{\prime} ,c_{1}^{\prime} ,d_{1}^{\prime} )$ and $\tilde{A}_{2}^{I} = (a_{2} ,b_{2} ,c_{2} ,d_{2} ;a_{2}^{\prime} ,b_{2}^{\prime} ,c_{2}^{\prime} ,d_{2}^{\prime} )$ be two TrIFNs. Then

• a) $\tilde{A}_{1}^{I} \ge \tilde{A}_{2}^{I}$ if $f^{\alpha } (\tilde{A}_{1}^{I} ) \ge \,f^{\alpha } (\tilde{A}_{2}^{I} )$

• b) $\tilde{A}_{1}^{I} \le \tilde{A}_{2}^{I}$ if $f^{\alpha } (\tilde{A}_{1}^{I} ) \le \,f^{\alpha } (\tilde{A}_{2}^{I} )$

• c) $\tilde{A}_{1}^{I} = \tilde{A}_{2}^{I}$ if $f^{\alpha } (\tilde{A}_{1}^{I} ) = f^{\alpha } (\tilde{A}_{2}^{I} )$

• d) $Min\,(\tilde{A}_{1}^{I} ,\tilde{A}_{2}^{I} ) = \tilde{A}_{1}^{I} \,if\,\tilde{A}_{1}^{I} \le \tilde{A}_{2}^{I} \,or\,\tilde{A}_{2}^{I} \ge \tilde{A}_{1}^{I}$

• e) $Max\,(\tilde{A}_{1}^{I} ,\tilde{A}_{2}^{I} ) = \,\tilde{A}_{1}^{I} \,if\,\tilde{A}_{1}^{I} \ge \tilde{A}_{2}^{I} \,or\,\tilde{A}_{2}^{I} \le \tilde{A}_{1}^{I}.$

Example 1

$$\tilde{A}^{I} = (2,3,4,5;1,2,4,5),\,\,\,\tilde{B}^{I} = (0,4,5,6;0,2,5,7)$$

$$\begin{aligned} f^{\alpha } (\tilde{A}^{I} )\,\, = \frac{2\alpha + 12}{4},\,f^{\alpha } (\tilde{B}^{I} )\,\, = \frac{\alpha + 14}{4} \hfill \\ \Rightarrow \, f^{0} (\tilde{A}^{I} ) = 12/4,\,\,f^{0.5} (\tilde{A}^{I} ) = 26/8,\,\,f^{1} (\tilde{A}^{I} ) = 14/4, \hfill \\ {\text{and}}\,\,\,\,f^{0} (\tilde{B}^{I} ) = 14/4,\,\,f^{0.5} (\tilde{B}^{I} ) = 29/8,\,f^{1} (\tilde{B}^{I} ) = 15/4. \hfill \\ {\text{Hence}}\,\,\,\, \, f^{0} (\tilde{A}^{I} ) < f^{0} (\tilde{B}^{I} ),\,f^{0.5} (\tilde{A}^{I} ) < f^{0.5} (\tilde{B}^{I} )\,and\,\,f^{1} (\tilde{A}^{I} ) < f^{1} (\tilde{B}^{I} ) \hfill \\ {\text{Thus}}\,{\text{in}}\,{\text{each}}\,{\text{case}}\,{\text{we}}\,{\text{have, }}\,\tilde{A}^{I} < \tilde{B}^{I} . \hfill \\ \end{aligned}$$

Example 2

$$\tilde{A}^{I} = (2,3,7,8;2,2,8,9),\,\,\,\tilde{B}^{I} = (2,4,5,7;1,4,5,8)$$

$$\begin{aligned} f^{\alpha } (\tilde{A}^{I} )\,\, = \frac{21 - \alpha }{4},\;f^{\alpha } (\tilde{B}^{I} )\,\, = \frac{18}{4} \hfill \\ \Rightarrow \,\, \, f^{0} (\tilde{A}^{I} ) = 21/4,\;f^{0.5} (\tilde{A}^{I} ) = 41/8,\,\,f^{1} (\tilde{A}^{I} ) = 20/4\,\,\,\,{\text{and}} \hfill \\ f^{0} (\tilde{B}^{I} ) = 18/4,\,\,f^{0.5} (\tilde{B}^{I} ) = 36/8,\,f^{1} (\tilde{B}^{I} ) = 18/4. \hfill \\ {\text{Hence}}\,\,\,\,f^{0} (\tilde{A}^{I} ) > f^{0} (\tilde{B}^{I} ),\,f^{0.5} (\tilde{A}^{I} ) > f^{0.5} (\tilde{B}^{I} )\,{\text{and}}\,\,f^{1} (\tilde{A}^{I} ) > f^{1} (\tilde{B}^{I} ) \hfill \\ {\text{Thus}}\;{\text{in}}\;{\text{each}}\;{\text{case}}\, \, \,\tilde{A}^{I} > \tilde{B}^{I} . \hfill \\ \end{aligned}$$

6 Balanced mixed intuitionistic fuzzy transportation problem (BMIFTP)

Usually, it is assumed that transportation costs are exactly known. However, these costs depend, in reality, on many factors, e.g., on the travelling time, which depends also on weather, on the present traffic, on the current situation of the road (traffic jams, road works etc.), Weight of the load etc. This means that in many situations such costs cannot be exactly known, but they are estimated (Dempe and Starostina 2006). Thus in estimating the transportation cost the decision maker (DM) is not very much sure. He may hesitate in predicting the transportation cost. Also, in a transportation problem the DM or the expert hesitates due to many factors from both sides that is from supplier side and demand side. Sometimes a DM is not sure that how much quantity of a particular product is available at his warehouse at a particular time by different reason. Such that, he has not a good communications to his fellows or he is not sure that how much quantity of particular product can be produced by the available row materials by that particular time. Similarly, he may hesitate from demand side. Suppose some new product is to be launch in a market then he cannot decide exactly that how much quantity of this product should transport to a particular destination. This may be due to unawareness of the customers about this product or difference in price and utility of the product to the similar one. Thus the uncertainty may occur in various parameters of a transportation problem. Also the parameters may have different types of uncertainties. So, here we consider a problem having different forms of intuitionistic fuzzy parameters to deal efficiently with the uncertainty as well as hesitation arising in prediction of transportation cost.

Let us consider a transportation problem with m origins and n destinations. Let $\tilde{c}^{I}_{ij} = (c_{ij}^{1} ,c_{ij}^{2} ,c_{ij}^{3} ,c_{ij}^{4} ;c_{ij}^{1'} ,c_{ij}^{2'} ,c_{ij}^{3'} ,c_{ij}^{4'} )$ be the IF cost of transporting one unit of the product from the ith origin to the jth destination.

Let $\tilde{a}_{i}^{I} = (a_{i}^{1} ,a_{i}^{2} ,a_{i}^{3} ,a_{i}^{4} ;a_{i}^{1'} ,a_{i}^{2'} ,a_{i}^{3'} ,a_{i}^{4'} )$ be the IF quantity (IFQ) available at the ith origin, $\tilde{b}_{j}^{I} = (b_{j}^{1} ,b_{j}^{2} ,b_{j}^{3} ,b_{j}^{4} ;b_{j}^{1'} ,b_{j}^{2'} ,b_{j}^{3'} ,b_{j}^{4'} )$ be the IFQ needed at the jth destination and $\tilde{X}_{ij}^{I} = (x_{ij}^{1} ,x_{ij}^{2} ,x_{ij}^{3} ,x_{ij}^{4} ;x_{ij}^{1'} ,x_{ij}^{2'} ,x_{ij}^{3'} ,x_{ij}^{4'} )$ be the IFQ transported from the ith origin to the jth destination. Here $\tilde{c}^{I}_{ij}$, $\tilde{a}_{i}^{I}$, $\tilde{b}_{j}^{I}$ and $\tilde{X}_{ij}^{I}$ may be any of the particular forms discussed in Definition 2.5. Then the BMIFTP is given by

$$\begin{aligned} Min\,\,\tilde{Z}^{I} \, = \,\sum\nolimits_{i = 1}^{m} {\sum\nolimits_{j = 1}^{n} {\tilde{c}^{I}_{ij} \otimes \tilde{X}^{I}_{ij} } } \,\,\, \hfill \\ s.t.\,\,\sum\nolimits_{j = 1}^{n} {\tilde{X}^{I}_{ij} } = \,\tilde{a}^{I}_{i} ,\,\,\,i = 1,2, \ldots ,m, \hfill \\ \,\,\,\,\,\,\,\,\sum\nolimits_{i = 1}^{m} {\tilde{X}^{I}_{ij} } \, = \,\tilde{b}^{I}_{j} ,\,\,\,j = 1,2, \ldots ,n, \hfill \\ \,\,\,\,\,\,\,\,\tilde{X}^{I}_{ij} \ge \,\tilde{0}^{I} ,\,\,\,i = 1,2, \ldots ,m;\,\,j = 1,2, \ldots ,n. \hfill \\ \end{aligned}$$

7 Proposed methods to find starting basic feasible solution (BFS)

First of all we transform the entries of the problem into equivalent TrIFN format. Then the following methods can be utilized to find the starting BFS of the given BMIFTP.

7.1 Intuitionistic fuzzy North West corner method (IFNWCM) for BMIFTP

The following steps are to be taken while finding the starting BFS by this method.

• Step 1 Select the North West Corner Cell (NWCC) of the BMIFTP table (BMIFTPT) and find the minimum of $\tilde{a}^{I}_{i}$ and $\tilde{b}^{I}_{j}$ using Definition 5.4. One of the following three cases will arise:

Case 1

If Min $(\tilde{a}^{I}_{i} ,\tilde{b}^{I}_{j} ) = \tilde{a}^{I}_{i}$, then allocate $\tilde{X}^{I}_{ij} = \tilde{a}^{I}_{i}$ in the NWCC of m × n BMIFTPT. Delete the ith row to obtain a new BMIFTPT of order (m − 1) × n. Replace $\tilde{b}^{I}_{j}$ by $\tilde{b}^{I}_{j} \varTheta \tilde{a}^{I}_{i}$ in the new BMIFTPT and then go to Step 2.

Case 2

If Min $(\tilde{a}_{i}^{I} ,\tilde{b}_{j}^{I} ) = \tilde{b}_{j}^{I}$, then allocate $\tilde{X}_{ij}^{I} = \tilde{b}_{j}^{I}$ in the NWCC of m × n BMIFTPT. Delete the jth column to obtain a new MIFTPT of order m × (n − 1). Replace $\tilde{a}_{i}^{I}$ by $\tilde{a}_{i}^{I} \varTheta \tilde{b}_{j}^{I}$ in the new BMIFTPT and then go to Step 2.

Case 3

If $\tilde{a}_{i}^{I} = \tilde{b}_{j}^{I}$, then follow either Case 1 or Case 2 but not both together.

• Step 2 Repeat Step 1 for new BMIFTPT until the BMIFTPT reduces to a table of order 1 × 1.

• Step 3 The starting BFS and intuitionistic fuzzy transportation cost (IFTC) are given by $\tilde{X}_{ij}^{I}$ and $\sum {\sum {\tilde{c}^{I}_{ij} } } \otimes \tilde{X}_{ij}^{I}$ respectively.

7.2 Intuitionistic fuzzy least cost method (IFLCM) for BMIFTP

The following steps are involved in this method.

• Step 1 Determine the smallest cost in the BMIFTPT using Definition 5.4. Let it be $\tilde{c}^{I}_{ij}.$ Find $\tilde{X}_{ij}^{I} = Min(\tilde{a}_{i}^{I} ,\tilde{b}_{j}^{I} ).$ One of the following three cases will arise:

Case 1

If $Min(\tilde{a}_{i}^{I} ,\tilde{b}_{j}^{I} ) = \tilde{a}_{i}^{I}$, then allocate $\tilde{X}_{ij}^{I} = \tilde{a}_{i}^{I}$ in the (i, j)th cell of m × n BMIFTPT. Ignore the ith row to obtain a new BMIFTPT of order (m − 1) × n. Replace $\tilde{b}_{j}^{I}$ by $\tilde{b}_{j}^{I} \varTheta \tilde{a}_{i}^{I}$ in the new BMIFTPT and then go to Step 2.

Case 2

If $Min(\tilde{a}_{i}^{I} ,\tilde{b}_{j}^{I} ) = \tilde{b}_{j}^{I}$, then allocate $\tilde{X}_{ij}^{I} = \tilde{b}_{j}^{I}$ in the (i, j)th cell of m × n BMIFTPT. Ignore the jth column to obtain a new BMIFTPT of order m × (n − 1). Replace $\tilde{a}_{i}^{I}$ by $\tilde{a}_{i}^{I} \varTheta \tilde{b}_{j}^{I}$ in the new BMIFTPT and then go to Step 2.

Case 3

If $\tilde{a}_{i}^{I} = \tilde{b}_{j}^{I}$, then follow either Case 1 or Case 2 but not both together.

• Step 2 Repeat Step1 for the new BMIFTPT until it reduces to an 1 × 1 BMIFTPT.

• Step 3 The starting BFS and IFTC are given by $\tilde{X}_{ij}^{I}$ and $\sum {\sum {\tilde{c}^{I}_{ij} } } \otimes \tilde{X}_{ij}^{I}$ respectively.

7.3 Intuitionistic fuzzy Vogel’s approximation method (IFVAM) for BMIFTP

The following steps are involved in this method

• Step 1 Start by taking the first row and choose its smallest cost using Definition 5.4 and subtract it from the next smallest entry. The difference is called the IF penalty (IFP) for the first row. Write it in front of the row on right. Similarly, compute the IFP for each row and write it in front of the corresponding row. In a similar fashion find the IFPs for all columns and write them in the bottom of the BMIFTPT below the corresponding columns.

• Step 2 Select the largest IFP using Definition 5.4 and find the row or column to which it corresponds. Determine the smallest cost in the selected row or column using Definition 5.4. Let it be $\tilde{c}^{I}_{ij} .$ Find $\tilde{X}_{ij}^{I} = Min(\tilde{a}_{i}^{I} ,\tilde{b}_{j}^{I} ).$ Again one of the following three cases will arise:

Case 1

If $Min(\tilde{a}_{i}^{I} ,\tilde{b}_{j}^{I} ) = \tilde{a}_{i}^{I}$, then allocate $\tilde{X}_{ij}^{I} = \tilde{a}_{i}^{I}$ in the (i, j)th cell of m × n BMIFTPT. Delete the ith row to obtain a new BMIFTPT of order(m − 1) × n. Replace $\tilde{b}_{j}^{I}$ by $\tilde{b}_{j}^{I} \varTheta \tilde{a}_{i}^{I}$ in the new BMIFTPT and then go to Step 3.

Case 2

If $Min(\tilde{a}_{i}^{I} ,\tilde{b}_{j}^{I} ) = \tilde{b}_{j}^{I}$, then allocate $\tilde{X}_{ij}^{I} = \tilde{b}_{j}^{I}$ in the (i, j)th cell of m × n BMIFTPT. Ignore the jth column to obtain a new BMIFTPT of order m × (n × 1). Replace $\tilde{a}_{i}^{I}$ by $\tilde{a}_{i}^{I} \varTheta \tilde{b}_{j}^{I}$ in the new BMIFTPT and then go to Step 3.

Case 3

If $\tilde{a}_{i}^{I} = \tilde{b}_{j}^{I}$, then either follow Case 1 or Case 2 but not both together.

• Step 3 Calculate the IFP for the reduced table obtained in Step 2. Repeat Step 2 until BMIFTPT reduces into 1 × 1.

• Step 4 The starting BFS and IFTC are given by $\tilde{X}_{ij}^{I}$ and $\sum {\sum {\tilde{c}^{I}_{ij} } } \otimes \tilde{X}_{ij}^{I}$ respectively.

8 Intuitionistic fuzzy modified distribution method (IFMODIM) to find optimal solution of BMIFTP

In this section, we develop a method based on modified distribution method (MODIM) to find optimal solution of BMIFTP. We call it as IFMODIM.

The following steps are to be taken while finding the optimal solution.

• Step 1 Find the starting BFS using any method discussed in Sect. 7.

• Step 2 Define IF dual variables $\tilde{u}^{I}_{i} = (u_{1}^{i} ,\,u_{2}^{i} ,\,u_{3}^{i} ,\,u_{4}^{i} ;\,u_{1}^{i'} ,\,u_{2}^{i'} ,\,u_{3}^{i'} ,\,u_{4}^{i'} )$ and $\tilde{v}^{I}_{j} = (v_{1}^{j} ,v_{2}^{j} ,v_{3}^{j} ,v_{4}^{j} ;v_{1}^{j'} ,v_{2}^{j'} ,v_{3}^{j'} ,v_{4}^{j'} )$ corresponding to the ith row and the jth column respectively such that $\tilde{u}^{I}_{i} = \tilde{c}^{I}_{ij} \varTheta \tilde{v}^{I}_{j} \,\,{\text{or}}\,\,\,\tilde{v}^{I}_{j} = \tilde{c}_{ij}^{I} \varTheta \tilde{u}_{i}^{I}$ for the basic cell (i, j).

• Step 3 Define $\tilde{z}^{I}_{ij} = \tilde{u}^{I}_{i} \oplus \tilde{v}^{I}_{j}.$ Find $\tilde{d}^{I}_{ij} =$ $\tilde{z}^{I}_{ij} \varTheta \tilde{c}^{I}_{ij}$ for all non-basic variables. Determine the values of $f^{\alpha } (\tilde{d}^{I}_{ij} )$ and write them in the right lower corner of the concerned cell. Any one of the following two cases will arise:

Case 1

If $f^{\alpha } (\tilde{d}^{I}_{ij} ) \le 0$ for all i, j. Then the starting BFS is optimal and stop.

Case 2

If there exists at least one $\tilde{d}^{I}_{ij}$ such that $f^{\alpha } (\tilde{d}^{I}_{ij} ) > 0$, then the BFS is not optimal. Go to step 4.

• Step 4 In MIFBTPT, choose that $f^{\alpha } (\tilde{d}^{I}_{ij} )$ which is the most positive. Let it occur for i = r and j = k.

• Step 5 Assign $\tilde{\theta }^{I}$ quantity in the (r, k)th cell. Now make a loop as follows:

• Rule for making the loop Start from the (r, k)th cell. Then move horizontally and vertically to the nearest basic cell with the restriction that the end of the loop must not lie in any non-basic cell except the (r, k)th cell. In this way return to the (r, k)th cell to complete the loop.

• Step 6 Add and subtract $\tilde{\theta }^{I}$ in concerned cell of the loop maintaining feasibility and define the value of $\tilde{\theta }^{I}$ as the minimum of $\tilde{X}_{ij}^{I}$ from which $\tilde{\theta }^{I}$ is subtracted.

• Step 7 Inserting the value of $\tilde{\theta }^{I}$ the next BFS is obtained which improves the IF transportation cost. While inserting the value of $\tilde{\theta }^{I}$, one cell assumes zero value, i.e., this cell becomes non-basic. This gives the improved BFS.

• Step 8 Repeat steps 1–7 until $f^{\alpha } (\tilde{d}^{I}_{ij} ) \le 0\,\forall \,i,j.$

• Step 9 The optimal solution and IFTC are given by $\tilde{X}_{ij}^{I}$ and $\sum {\sum {\tilde{c}^{I}_{ij} } } \otimes \tilde{X}_{ij}^{I}$ respectively, i = 1, 2, 3,…, m and j = 1, 2, 3,…, n.

9 Numerical examples

Example 1

Consider the BMIFTP given in Table 1. In this table costs, availabilities and demands are different types of numbers (crisp, fuzzy, intuitionistic fuzzy).

Table 1 BMIFTP

Changing the entries of the problem into equivalent TrIFNs, the problem is transformed as follows (Table 2).

Table 2 BMIFTP in symmetric form

Now to find the starting BFS we can apply any one of the methods discussed in Sect. 7. Here we have applied IFNWCM to find the starting BFS. The BFS obtained is given in Table 3.

Table 3 The starting BFS

Now we apply IFMODIM to test the optimality of the obtained starting BFS for pessimistic, moderate and optimistic decision maker’s viewpoint.

$$\tilde{d}_{12}^{I} = ( - 2,2,5,9; - 4,1,5,11)\varTheta (7,8,8,9;6,8,8,9) = ( - 11, - 6, - 3,2; - 13, - 7, - 3,5),\,\,$$

$$\tilde{d}_{13}^{I} = ( - 2,3,6,10; - 5,1,6,13)\varTheta (5,5,5,5;5,5,5,5) = ( - 7, - 2,1,5; - 10, - 4,1,8),\,$$

$$\tilde{d}_{31}^{I} = ( - 1,4,7,13; - 3,4,8,15)\varTheta (6,8,8,9;6,8,8,9) = ( - 10, - 4, - 1,7; - 12, - 4,0,9),\,$$

$$\tilde{d}_{32}^{I} = ( - 1,3,6,11; - 2,3,7,12)\varTheta (7,7,7,7;7,7,7,7) = ( - 8, - 4, - 1,4; - 9, - 4,0,5),\,$$

Now finding the score functional values of these deviations, we have

$$f^{0} (\tilde{d}_{12}^{I} ) = - 9/2,\,\,f^{0.5} (\tilde{d}_{12}^{I} ) = - 9/2,\,\,f^{1} (\tilde{d}_{12}^{I} ) = - 9/2.$$

$$f^{0} (\tilde{d}_{13}^{I} ) = - 5/4,\,\,f^{0.5} (\tilde{d}_{13}^{I} ) = - 1,\,\,f^{1} (\tilde{d}_{13}^{I} ) = - 3/2.$$

$$f^{0} (\tilde{d}_{31}^{I} ) = - 7/4,\,\,f^{0.5} (\tilde{d}_{31}^{I} ) = - 15/8,\,\,f^{1} (\tilde{d}_{31}^{I} ) = - 2.$$

$$f^{0} (\tilde{d}_{32}^{I} ) = - 2,\,\,f^{0.5} (\tilde{d}_{32}^{I} ) = - 17/8,\,\,f^{1} (\tilde{d}_{32}^{I} ) = - 9/4.$$

In Table 4, we find that the BFS is optimal, through each viewpoint as $f^{\alpha } (\tilde{d}_{ij}^{I} ) < 0,\,\,\,\alpha = 0,\,\,0.5\,,\,\, 1.$

Table 4 Optimality test of the starting BFS

The IFTC is $\tilde{Z}^{I}$ = (3,4,5,6;2,3,5,7) ⊗ (3,4,4,6; 2,4,4,8) ⊕ (−3,0,2,5;−6,−1,3,7) ⊗ (2,4,5,7;1,4,5,8) ⊕ (2,3,4,5;2,3,4,5) ⊗ (2,4,6,8;2,4,6,0) ⊕  (−7,−1,3,9;−11,−2,4,12) ⊗ (2,4,5,6;1,3,5,7) ⊕ (2,3,7,8;2,2,8,9) ⊗ (3,5,6,8;3,5,6,8) = (−44,38,111,229;−111,19,127,318).

9.1 Results and discussion

The IFTC $\tilde{Z}^{I}$ of the given BMIFTP is a TrIFN as given below:

$$\tilde{Z}^{I} = \left( { - 44, \, 38, \, 111, \, 229; - 111, \, 19, \, 127, \, 318} \right).$$

(5)

The result in (5) can be explained (Refer to Fig. 2) as follows:

Fig. 2

Intuitionistic fuzzy transportation cost

“The degree of acceptance of the transportation cost for the DM increases if the cost increases from −44 to 38; The DM is totally satisfied or the transportation cost is totally acceptable if the cost lie in [38, 111]. While it decreases if the cost increases from 111 to 229. Beyond (−44, 229), the level of acceptance or the level of satisfaction for the DM is zero i.e. he is not satisfied. The degree of non-acceptance of the transportation cost for the DM decreases if the cost increases from −111 to 19 while it increases if the cost increases from 127 to 318. Beyond (−111, 318), the cost is totally un-acceptable” (Table 5).

Table 5 BMIFTP

Assuming that $\mu_{{\tilde{Z}^{I} }} (c)$ is membership (acceptance) and $\nu_{{\tilde{Z}^{I} }} (c)$ is non-membership (non-acceptance) value of the transportation cost c. Then the degree of acceptance of the transportation cost c is $100\mu_{{\tilde{Z}^{I} }} (c)\;\%$ for the DM and the degree of non-acceptance is $100\nu_{{\tilde{Z}^{I} }} (c)\;\%$ for the DM. DM is not sure by $100(1 - \mu_{{\tilde{Z}^{I} }} (c) - \nu_{{\tilde{Z}^{I} }} (c))\;\%$ that he/she should accept the transportation cost c or not (Table 6).

Table 6 The starting BFS

Values of $\mu_{{\tilde{Z}^{I} }} (c)$ and $\nu_{{\tilde{Z}^{I} }} (c)$ at different values of c can be evaluated using Eqs. (5a) and (5b) respectively.

$$\mu_{{\tilde{Z}^{I} }} (c) = \left\{ \begin{array}{lll} \frac{c + 44}{82},& - 44 < c \le 38, \hfill \\ 1,& 38 \le c \le 111, \hfill \\ \frac{229 - c}{118},&111 \le c < 229, \hfill \\ 0,& {\text{otherwise,}} \hfill \\ \end{array} \right.$$

(5a)

$$\nu_{{\tilde{Z}^{I} }} (c) = \left\{ \begin{array}{lll} \frac{19 - c}{130},&7 - 111 < c \le 19, \hfill \\ 0,&\quad 19 \le c \le 127, \hfill \\ \frac{c - 127}{191},&\quad 127 \le c < 318, \hfill \\ 1,&\quad{\text{otherwise}} .\hfill \\ \end{array} \right.$$

(5b)

Example 2

Let us consider the following problem as in Table 5:

Writing the data into symmetric form we have following BFS as in Table 6.

$$\tilde{d}_{13}^{I} = ( - 1,0,1,2; - 2,0,2,3)\varTheta (2,4,4,6;2,4,4,6) = ( - 7, - 4, - 3,0; - 8, - 4, - 2,1),\,\,$$

$$\tilde{d}_{21}^{I} = (1,4,6,9; - 1,2,6,9)\varTheta (3,4,5,6;3,4,5,6) = ( - 5, - 1,2,6; - 7, - 3,2,8),\,$$

$$\tilde{d}_{31}^{I} = (1,5,7,11; - 2,3,7,14)\varTheta (2,3,3,5;1,3,3,6) = ( - 4,2,4,9; - 8,0,4,13),\,$$

$$\tilde{d}_{32}^{I} = (4,6,7,9;2,5,7,11)\varTheta (1,4,4,6;1,4,4,6) = ( - 2,2,3,8; - 4,1,3,10),\,$$

Now finding the score functional values, we have

$$f^{0} (\tilde{d}_{13}^{I} ) = - 13/4,\,\,f^{0.5} (\tilde{d}_{13}^{I} ) = - 27/8,\,\,f^{1} (\tilde{d}_{13}^{I} ) = - 13/4.$$

$$f^{0} (\tilde{d}_{21}^{I} ) = 0,\,\,f^{0.5} (\tilde{d}_{21}^{I} ) = 2/8,\,\,f^{1} (\tilde{d}_{21}^{I} ) = 2/4.$$

$$f^{0} (\tilde{d}_{31}^{I} ) = 9/4,\,\,f^{0.5} (\tilde{d}_{31}^{I} ) = 20/8,\,\,f^{1} (\tilde{d}_{31}^{I} ) = 11/4.$$

$$f^{0} (\tilde{d}_{32}^{I} ) = 10/4,\,\,f^{0.5} (\tilde{d}_{32}^{I} ) = 21/8,\,\,f^{1} (\tilde{d}_{32}^{I} ) = 11/4.$$

In Table 7, we found that the starting BFS is not optimal, through any viewpoint as some $f^{\alpha } (\tilde{d}_{ij}^{I} ) > 0,\,\,\,{\text{for}}\,\alpha = 0,\,\,0.5\,\,\,{\text{or}}\, 1.$

Table 7 Optimality test for staring BFS

In each case we see that $f^{\alpha } (\tilde{d}_{32}^{I} )$ is most positive so making a closed loop starting from (3, 2) cell and then improving the solution we have following table.

Here we have

$$f^{0} (\tilde{d}_{13}^{I} ) = - 3/4,\,\,f^{0.5} (\tilde{d}_{13}^{I} ) = - 6/8,\,\,f^{1} (\tilde{d}_{13}^{I} ) = - 3/4.$$

$$f^{0} (\tilde{d}_{21}^{I} ) = - 10/4,\,\,f^{0.5} (\tilde{d}_{21}^{I} ) = - 19/8,\,\,f^{1} (\tilde{d}_{21}^{I} ) = - 9/4.$$

$$f^{0} (\tilde{d}_{22}^{I} ) = - 10/4,\,\,f^{0.5} (\tilde{d}_{31}^{I} ) = - 21/8,\,\,f^{1} (\tilde{d}_{31}^{I} ) = - 11/4.$$

$$f^{0} (\tilde{d}_{31}^{I} ) = - 1/4,\,\,f^{0.5} (\tilde{d}_{32}^{I} ) = - 1/8,\,\,f^{1} (\tilde{d}_{32}^{I} ) = 0.$$

Thus in Table 8 $f^{\alpha } (\tilde{d}_{ij}^{I} ) \le 0,\,{\text{for}}\,\alpha = 0,0.5,1.$ So we reached the optimal solution.

Table 8 Improved BFS (Optimal Solution)

The IFTC is $\tilde{Z}^{I}$ = (1,3,4,6;0,2,4,7) ⊗ (2,3,4,5;1,2,4,6) ⊕ (4,4,4,4;4,4,4,4) ⊗ (−3,1,3,5; −4,0,4,6) ⊕ (2,2,2,2;2,2,2,2) ⊗ (−5,3,9,17; −7,1,11,19) ⊕ (1,4,4,6; 1,4,4,6) ⊗  (−3,1,4,8;−4,0,5,9) ⊕ (2,3,3,4;1,3,3,5) ⊗ (−5,0,4,10;−7,−1,6,12) = (−58,23,74,172;−68,3,92,218).

9.2 Results and discussion

The IFTC $\tilde{Z}^{I}$ of the given BMIFTP is a TrIFN as given below:

$$\tilde{Z}^{I} = \left( { - 58, \, 23, \, 74,172; - 68, \, 3, \, 92, \, 218} \right).$$

(6)

The result in (6) can be explained (Refer to Fig. 3) as explained in Example 1.

Fig. 3

Intuitionistic fuzzy transportation cost

Values of $\mu_{{\tilde{Z}^{I} }} (c)$ and $\nu_{{\tilde{Z}^{I} }} (c)$ at different values of c can be evaluated using Eqs. (6a) and (6b) respectively.

$$\mu_{{\tilde{Z}^{I} }} (c) = \left\{ \begin{array}{lll} \frac{c + 58}{81},& - 58 < c \le 23, \hfill \\ 1,& 23 \le c \le 74, \hfill \\ \frac{172 - c}{98},&74 \le c < 172, \hfill \\ 0,&{\text{otherwise,}} \hfill \\ \end{array} \right.$$

(6a)

$$\nu_{{\tilde{Z}^{I} }} (c) = \left\{ \begin{array}{ll} \frac{3 - c}{71}, & - 68 < c \le 3, \hfill \\ 0,& 3 \le c \le 92, \hfill \\ \frac{c - 92}{126},&92 \le c < 218, \hfill \\ 1,& {\text{otherwise}} .\hfill \\ \end{array} \right.$$

(6b)

10 Conclusion

The increasing complexity of the real world and the fuzziness of human thinking make it difficult to express the decision maker’s preferences over alternatives as exact numerical values. However, it is very convenient and suitable to express the preferences into FN or IFN. To express the uncertain data we have utilized different types of fuzzy numbers, which is more reliable to the real world transportation problems.

In this paper new methods are proposed to find the starting BFS and optimal solution of BMIFTP in which availabilities, demands and costs all are different types of numbers. So, the methods can be applied to solve real world transportation problems where data is not in symmetric form.