Compromising allocation for optimising agri-food supply chain distribution network: a fuzzy stochastic programming approach

Abstract

The management of Agri-food supply chains is a complex task, given the unique product characteristics, perishability, uncertain demand, and specific storage requirements. This research introduces an innovative approach to optimizing product allocation among producers, brokers, wholesalers, and retailers, focusing on minimizing transportation costs and network delivery time through multi-objective programming. To address uncertainties, supply and demand constraints are modelled using a gamma distribution, and the maximum likelihood estimation method determines their parameters with specified probabilities. The study conducts a case analysis to showcase the model’s practical effectiveness, and a numerical comparison with alternative approaches is included. The primary goal of this study is to enhance the efficiency of agri-food supply chain management practices, providing valuable insights for practitioners in the field, with a focus on cost reduction and improved delivery time.

1 Introduction

Agri-Food Supply Chains (SC) play a pivotal role in ensuring the timely and efficient delivery of agricultural and food products, especially in the context of products characterized by a shorter shelf life and high perishability. Effectively managing the distribution networks within these supply chains is critical for resilience and efficiency (Kumar and Singh 2021). Agri-food SCs encompass a complex network of facilities and distribution options that facilitate the procurement of raw materials, their transformation into finished products, and their distribution to end customers (Gupta et al. 2018a, b). This intricate network underpins the ability of organizations to provide finished goods to customers in a cost-effective and timely manner (Gupta et al. 2021a, b, c). Balancing the supply and demand within the SC is paramount for achieving profitability, yet it presents a formidable challenge for organizations (Baral et al. 2021). Effective management of resources, supplies, and the delivery of the right products to the right locations and customers at the right cost is the essence of supply chain management. In the case of agri-food SCs, this task is further complicated by the perishable nature of the products and their vulnerability to disruptions (Kumar and Singh 2021; Mishra et al. 2021).

The agri-food industry faces a multitude of challenges, including the pressures of rapid industrialization, the dynamics of oligopoly-based distribution systems, and the need to adhere to stringent food safety standards. In the face of these challenges, the efficient management of distribution networks becomes not just a necessity but a strategic imperative. Mishra et al. (2021) highlight the adaptability of agri-food SC networks in modifying their conventional procurement and inventory planning approaches to meet evolving customer demands. This shift underscores the growing importance of optimizing supply chain networks in the agri-food industry.

In this context, Lim et al. (2023) shed light on omnichannel strategies within agricultural supply chains, with a specific focus on traceability technologies, services, advertisements, and holding costs. The research by Sarkar et al. (2019; 2021) delves into sustainability, carbon emissions control, and product quality enhancement in a three-echelon supply chain. Dey et al. (2021) underscore the criticality of reducing lead time and variance within smart manufacturing systems integrated into supply chains. Ullah et al. (2021) investigate the implications of remanufacturing within closed-loop supply chains, emphasizing the significance of hybrid policies and cost-related factors. Yadav et al. (2021) address the imperatives of waste reduction and carbon emissions management within sustainable supply chains, utilizing concepts like cross-price elasticity of demand and preservation technology to maximize profit while minimizing waste.

1.1 Problem description and research objectives:

Agri-food products are usually unique and perishable, so these items cannot be stored at any node of the SCN for a very long time (Violi et al. 2019). Agri-food SCs intrinsic sources of ambiguity have a detrimental effect on performance and stability. Several authors (Borodin et al. 2016; Galal and El-Kilany 2016; Kamble et al. 2019; Banasik et al. 2019) have stated that agri-food SC development models must be updated to take an account the consequences of existing sources and consumer peregrination across the chain. Allocation of optimal order at different nodes of the agri-food SC under an uncertain environment is a challenge task. Researchers have mainly considered network optimisation for products with a long life cycle (Eskandarpour et al. 2015; Kumar et al. 2016; Banasik et al. 2017; Gupta et al. 2018a). Therefore, the focus of this study is to determine the compromised order allocations for optimising Agri-food SCN. In this study, a random and probabilistic model of agri-food SC has been developed and formulated with some imprecise input information. As we know, decision makers are often not familiar with the numerous values of shipping costs and shipment time in real-life scenarios, interpreting these as fuzzy coefficients would be more suitable. In this study, the parameters are represented through an interval type-2 triangular fuzzy parameter which are converted into a crisp form by using an appropriate ranking formula.

Additionally, when formulating real-life scenarios, circumstances may occur, when we do not understand exactly the right side of the constraints. In order to solve this condition, we regarded these parameters to be random variables following a Gamma distribution. Apart from it, we have used the maximum likelihood estimation (MLE) approach to obtain the Gamma distribution’s scale and location parameter. Different types of optimization techniques like Goal Programming, Lexicographic or Pre-emptive Goal Programming, Weighted or Mini-sum Goal programming, Fuzzy programming, Fuzzy Goal Programming, AHP, TOPSIS, VIKOR, have been used to solve the formulated Agri-Food SC problem for getting an optimal result. Researchers have found that network optimisation for optimal order allocation is a challenging task for SC managers and is not very well researched specifically in developing countries like India (Singh et al. 2018). This study aims to identify the best ordering allocation for finished goods from each producer, agent/broker, wholesaler, and retailer in the Agri-Food SCN. To demonstrate the proposed model in this study; a numerical case study has been provided.

In this study, we have identified the research objective by examining the gaps in the existing literature that need to be solved. For this study, we have conducted have conducted a literature review to identify the challenges and opportunities in the agri-food SCN. Based on the literature review, we have identified the need for an optimisation model that can address the uncertainties and complexities in the supply chain distribution network. Following the research objective of this study:

• 1. To develop a novel fuzzy stochastic programming model that can optimize the allocation of products from each stage of the SCN, including producers, agents/brokers, wholesalers, and retailers, while considering the uncertain parameters of supply and demand constraints.

• 2. To use the maximum likelihood estimation method to estimate the unknown parameters of the probabilistic distribution with a specified level of probability, thereby enhancing the accuracy of the proposed model.

• 3. To compare the performance of different optimization approaches, such as value function, ϵ-constraint, fuzzy goal programming, weighted fuzzy goal programming, and pre-emptive fuzzy goal programming, in terms of their effectiveness and computational efficiency in obtaining the optimal order allocation of products.

By achieving these objectives, the study aims to contribute to the existing literature on agri-food SCN by proposing a robust and effective approach to optimizing the allocation of products in agri-food SCN, which can enhance their overall efficiency and profitability. The remaining paper has the following structure: In Sect. 2, the SCN and Agri-food SCN literature are briefly reviewed. Section 3 describes the mathematical model formulation with fuzziness and randomness for Agri-food SCN and the proposed optimization approach used to solve the problem. Section 4 illustrates the application of the proposed framework with a case scenario. Finally, in Sects. 5, the concluding remarks are presented.

2 Literature review

Various studies have focused on using the fuzziness and randomness theories to address the ambiguity in SCN problems (Petrovic et al. 1998; Sakawa et al. 2001; Chuu 2011; Nepal et al. 2011; Cakici et al. 2012; Petridis 2015; Zokaee et al. 2017; Choi et al. 2017; Singh et al. 2018; Yaghin et al. 2020). Mishra et al. (2018) conducted a survey of the current literature on SCN performance measurements and metrics, and gave a critical evaluation of 234 publications published over the course of the previous 24 years in SC. In most real-life scenarios, parameters are assumed to take deterministic values, but sudden change in related things may lead to uncertainty. In such cases, if the uncertain prevails within the parameters but presumed to take in some set of probable values, a solution can be developed that is feasible for all uncertain parameters. Further, to solve an uncertain optimization problem, it is important to transform the problem into a deterministic form using some ranking function that could be equally generalizable to the related deterministic optimization problem. Before formulating the problem under study, a literature review was conducted and presented in the following sections.

2.1 Agri-food supply chain network design

Research in the optimization of Agri-food SCNs has taken various approaches and dimensions. Higgins et al. (2004) conducted real-world research in the Australian sugar industry, utilizing simulation to enhance production and distribution efficiency. Akkerman et al. (2010) delved into the intricacies of Agri-food SCNs and logistics, addressing processes like brand integration, packing, bundling, sealing, and stock management. The typical Agri-food SCN encompasses a range of operations spanning agriculture, processing, storage, transportation, delivery, and advertising, forming a "land-to-fork" sequence (Iakovou et al. 2012). In the agri-food SCN context, Mirabella et al. (2014) scrutinized the environmental and economic impacts of loop closings through real case studies. Eskandarpour et al. (2015) provided a comprehensive review of mathematical models applied in Agri-food SCNs, categorizing them into deterministic frameworks, such as linear programming, dynamic programming, mixed-integer linear programming, goal programming, and fuzzy programming. They underscored the need for advancements in Agri-food supply chain modeling, especially concerning biodiversity, emphasizing its unique research context. Tavana et al. (2017) contributed by developing an integrated supplier selection model for milk firms, incorporating analytic network process with quality function deployment.

Moreover, Banasik et al. (2017) conducted an analysis of financial and environmental aspects within the mushroom supply chain, emphasizing closed-loop technologies. They introduced a multi-objective (mixed-integer) linear programming method to aid decision-making for manufacturing and distribution by optimizing resource flows in closed-loop supply chains. Esteso et al. (2018) observed that existing agri-food supply chain network (SCN) development models often overlooked consumer-related factors like food quality, safety, and environmental considerations, as well as product diversity. Their two-phase approach involved devising a conceptual framework for agri-food SCN development, integrating mathematical programming models and accounting for inherent ambiguities. In a second phase, this framework was applied to evaluate established agri-food SC models. Allaoui et al. (2018) introduced a two-stage hybrid methodology for sustainable agri-food supply chain networks, combining multi-criteria and multi-objective decision-making, with a focus on sustainability aspects including carbon and water footprints, as well as overall costs. Liu et al. (2019) proposed an innovative model that integrated fuzzy numbers, Analytic Hierarchy Process, and Order Preference Model to comprehensively assess both quantitative and qualitative parameters. Sharma et al. (2020) conducted a systematic review of machine learning applications in agri-food supply chain networks, aiming to address complex issues. De and Singh (2020) and Tomasiello and Alijani (2021) established an integrated framework to assess overall supply chain performance and reviewed the application of fuzzy logic in the agri-food supply chain, considering land suitability, manufacturing techniques, water management, cold storage, transportation, waste disposal, environmental sustainability, and drought management. Recent studies have explored diverse aspects of sustainable supply chain management in the food industry, such as Kalantari and Hosseininezhad’s (2022) focus on reducing economic costs, environmental impacts, and maximizing employment in a global food supply chain with risk considerations. Alinezhad et al. (2022) proposed a methodology for designing sustainable closed-loop supply chain networks that account for customer satisfaction and carbon footprint, even under uncertain conditions. Lastly, Gholian-Jouybari et al. (2023) addressed challenges related to greenhouse gas emissions, water consumption in farmlands, and supply chain issues caused by rapid population growth. They presented a mathematical model to enhance sustainability within agricultural food supply chain networks. These studies collectively underscore the pressing need to prioritize sustainability in the food industry and offer promising strategies to tackle the intricate challenges within supply chains.

2.2 Approaches adopted for supply chain network design

The SCN is increasingly recognized as a vital driver of competitiveness in dynamic economies (Altiparmak et al. 2006). Nevertheless, its productivity and effectiveness face challenges arising from various sources of uncertainty, spanning demand, supply, manufacturing, and planning aspects. It is undeniable that supply chain instability raises concerns for every manager (Charles et al. 2019). The literature contains numerous studies addressing the design of supply chains, with Sabri and Beamon (2000) standing out for creating an integrated model capable of simultaneously addressing multi-objective supply chain challenges, encompassing both strategic and operational planning, including manufacturing costs and delivery times under uncertain demand. Lee et al. (2010) endeavored to optimize supply chain networks, focusing on objectives related to optimal location, allocation, and routing to minimize costs. Meanwhile, Peidro et al. (2010) developed an uncertain mathematical programming model for strategic supply chain management. Their objective was to centralize multiple node options to efficiently utilize available resources over time, ultimately delivering customer demands at a reduced cost.

Yeh and Chuang (2011) developed multi-objective optimzation model for partner choice in SCN. They considered four competing objectives, including optimization of overall manufacturing costs and time for manufacturing and shipping and, also tries to optimize product quality and green evaluation score, and solved them by utilizing two separate multi-objective genetic algorithms. Nasiri et al. (2014) designed the three-tier SC models for different distribution hubs, manufacturing facilities and vendors with an unpredictable stochastic demand. Trisna et al. (2016) addressed different SC issues formulated through the use of multi-objective optimization techniques. The authors provided a study of several techniques used for formulating the mathematical model for different types of SCNs and, also classified different modelling methods based on linear and non-linear programming, different kinds of techniques used for solving the multiobjective programming problems, and also categorized the models into various kinds of robust and non-robust techniques used for solving the mathematical models. Kumar et al. (2016) addressed a two-echelon integrated procurement and production model for both the producer’s and the customer's embedded SCN model. The authors proposed a new technique for evaluating the expected fuzzy shortage throughout the inventory period. Kim and Sarkar (2017) designed a SCN model that includes probabilistic demand for lead time, commercial credit policy, enhancement in product quality, lower costs for vendors and a fluctuating back-order rate. In order to handle the complicated supplier selection problem in SCM, (Pandey et al. 2017) suggested a two-phase fuzzy goal programming technique that was integrated with a hyperbolic membership function. Haddadsisakht and Ryan (2018) built a closed-loop SCN model, which incorporates forward as well as backward product flows of an item along with a change in demand of fresh and re-produced items. Gupta et al. (2018a) developed a comprehensive technique to programming the SCN issues efficiently. The author employed interactive fuzzy programming to reduce concurrently the overall transportation cost and entire delivery time in association with inventories, actual stock present at each source, as well as market demand and useable storage facilities at each site. Subsequently, Gupta et al. (2018b) formulated SCN as a two-tier programming problem with the principal purpose of identifying optimal product assignment orders for which demand and product supply was deemed to be inherently ambiguous. In hybrid uncertain conditions, including recycling and disposal operations, Farrokh et al. (2018) explored the development of a closed- loop SCN model. The authors proposed a mixed-integer programming model which optimized SCN configuration in terms of both interruption and risk management. Bhosale and Latpate (2019) took into consideration the demand of milk products for one cycle that follows probabilistic weibull distribution within the decentralized and centralizing SC for the perishable goods. Arasteh (2020) developed a three-level SC for manufacturer/distributor/customer in which the customer demand, percentage of customer returned the items and delivery time of distributors to customers were considered fuzzy variables. Qiu et al. (2021) developed a distributionally resilient optimisation strategy for retailers that buy several items from many suppliers with a limited budget in which the demand for a product is supposed to rely on the existing inventory level. Dohale et al. (2022) created a multi-product, multi-period model for aggregate production planning in order to meet the needs of customers in terms of capacity and lead time in order to achieve market competency in the aggregate industry. Table 1 summarises approach adopted by different researchers for solving SCN problem.

Table 1 Summary of approaches adopted for SCN problems

Table 1 shows that very few researchers have used the MLE technique to obtain the desired shape, scale and location value of an uncertain parameter. That can be seen as the biggest disadvantage when dealing with uncertainty that has been identified from all the previous work carried out by different researchers. However, decision makers (DMs) sometimes find it difficult to evaluate the accurate values of parameters to their full understanding in real life problems. Therefore, the novelty of this study lies in the fact that we have used the MLE approach for getting the desired shape and scale parameter of the considered probabilistic parameters. Moreover, the authors used only hypothetical numerical examples to demonstrate the proposed methodology in the past. However, in this paper, the problem of an agri-food SCN is considered with the major objective is to identify the best ordering for each manufacturer, agent/contractor, wholesaler and retailer's. The unique points of this research are as follows:

• i. In earlier studies, Agri-food SCNs were seen as a single objective programming problem, but to get the efficiency in SC process in Agri-food we have extended it to a multi-objective problem with some time constraint.

• ii. An Agri-food SCN with multi-objectives is studied with interval type-2 fuzzy variables among the shipment cost and delivery time coefficient.

• iii. Stochastic programming is used to resolve the inequalities between various supply and demand constraints.

• iv. The considered probabilistic demand and supply parameters are studied in conjunction with the use of MLE to model the best fit value for uncertainty.

After discussing the brief literature on Agri-food SCN and different approaches adopted by researchers in previous studies, the next section describes the formulation of the proposed mathematical model.

3 Proposed mathematical model

Designing suitable effective strategies to handle agri-food SC to meet consumer demand has become a complicated, demanding issue while addressing the constantly rising changes in life styles and dietary preferences. There can be no doubt that the SC management has increased the agri-food company priority significantly over the last few years. The SC is now widely recognized as having the key to both cost reduction and service enhancements in several sectors. Its function is now especially important for the food sector, due to the increasing demands of more strong retailers on suppliers. The concentration of retailers has become a way of life in many areas and increases as global merchants emerge. The suppliers need to reassess their SC strategy since they are demanding a just-in-time delivery, better product quality and tailor-made logistical solutions. Agri-food SCN comprise of farming, postharvest activities, distribution and retailing. Optimising distribution network is a challenge for managers. Here, in this section, we have formulated the multi-objective Agri-Food Supply Chain Network (MOAFSCN) model with some imprecise data. Following are the assumptions considered for the model formulation in this study:

• The system produces single type of item.

• Shipping cost and delivery time are considered as uncertain and represented by interval type-2 fuzzy number.

• Demand and supply are considered as uncertain parameter follows continuous probability distribution function.

• Order is placed only once.

• No cash discount are considered.

• No shortage and backlogging are allowed.

Nomenclature:

The following notations have been used to formulate the Agri-food supply chain problem:

Indices

$i -$ Retailers index,$\left\{ {i = 1,2,......,I} \right\}$;

$j -$ Wholesalers index, $\left\{ {j = 1,2,...,J} \right\}$;

$k -$ Agent/brokers index, $\left\{ {k = 1,2,...,K} \right\}$;

$l -$ Producers index,$\left\{ {l = 1,2,....,L} \right\}$;

$t -$ Objective index, $\left\{ {t = 1,2,....,T} \right\}$;

Parameters

$D_{i} -$ Monthly demand from the i^th Retailers,

$P_{k} -$ The prospective volume of the k^th Agent/brokers,

$S_{l} -$ The monthly supply volume of the l^th Producers,

$W_{j} -$ The prospective volume of the j^th Wholesalers,

$SC_{lk} -$ The shipping cost of a single unit from different supply sources to different agent/brokers,

$SC_{kj} -$ The producing and shipping cost of a single unit from different agent/brokers to different wholesalers,

$SC_{ki} -$ The producing and shipping cost of a single unit from different agent/brokers to different retailer,

$SC_{ji} -$ The shipping cost of a single unit from different wholesalers to different retailers,

$DT_{kj} -$ Time is taken for delivering single unit from different agent/brokers to a different wholesaler,

$DT_{ki} -$ Time is taken for delivering single unit from different agent/brokers to a different retailer,

$DT_{ji} -$ Time is taken for delivering single unit from different wholesalers to different retailers.

Decision variables

$U_{lk} -$ Amount of products to be sent to various agents/brokers from various producers,

$X_{kj} -$ Amount of product to be sent to various wholesalers from various agent/brokers,

$Y_{ki} -$ Amount of product to be sent to various retailers from various agent/brokers,

$V_{ji} -$ Amount of product to be sent to various retailers from various wholesaler.

In the case of a deterministic parameter, the mathematical model of MOAFSCN is given as follows:

In alignment with the challenges posed by the perishable nature of agricultural products, our cost objective function distinguishes itself from the aforementioned studies (Lim et al. 2023; Sarkar et al. 2021; Dey et al. 2021; Ullah et al. 2021; Yadav et al. 2021) by placing a primary focus on minimizing transportation costs within agri-food supply chains. While the previous studies consider factors like traceability technologies, carbon emissions, or lead time reduction, our research hones in on the crucial facet of transportation cost optimization. By developing strategies that specifically target cost-effective and efficient transportation of perishable goods, we aim to offer agri-food supply chain firms a dedicated solution to enhance their profitability and deliver high-quality products promptly to consumers, thereby contributing to the overall effectiveness of the supply chain. For our study, the first objective function to reduce the expenses of conveyance of the SCN, can be formulated as:

$$Min\,\,Z_{1} = \sum\limits_{l = 1}^{L} {\sum\limits_{k = 1}^{K} {SC_{lk} U_{lk} + \sum\limits_{k = 1}^{K} {\sum\limits_{j = 1}^{J} {SC_{kj} X_{kj} + \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{I} {SC_{ki} Y_{ki} + \sum\limits_{j = 1}^{J} {\sum\limits_{i = 1}^{I} {SC_{ji} } } } } } } } } V_{ji} ,$$

(1)

In the agri-food SC, timely delivery is crucial for maintaining the quality and freshness of the products. Any delay in the delivery process can result in spoilage or wastage of the produce, which ultimately affects the profitability of the businesses involved. Moreover, in the highly competitive market, customers expect prompt and reliable delivery services. Therefore, an efficient delivery system with a minimum delivery time is vital to ensure the smooth functioning of the agri-food SC and meet the growing demand for fresh and healthy food products. For our study, the second objective function, which minimizes the SCN's delivery time, can be formulated as:

$$Min\,\,Z_{2} = \sum\limits_{k = 1}^{K} {\sum\limits_{j = 1}^{J} {DT_{kj} X_{kj} + \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{I} {DT_{ki} Y_{ki} + \sum\limits_{j = 1}^{J} {\sum\limits_{i = 1}^{I} {DT_{ji} V_{ji} } } } } } } ,$$

(2)

Effective coordination and integration of different operations in the agri-food SC is crucial for ensuring optimal efficiency, reducing costs, and increasing customer satisfaction. This can involve streamlining processes such as procurement, production, logistics, and marketing, while also implementing innovative technologies and tools that facilitate real-time communication and data sharing among all stakeholders. By prioritizing coordination and integration, agri-food SCN can minimize delays, errors, and waste, while also improving product quality, safety, and traceability. Ultimately, this can help to enhance competitiveness, drive growth, and foster more sustainable and resilient SC networks in the agri-food sector. We have considered the following set of constraints for our model:

Constraint I is the complete amount shipped to the agent/broker from the producer, it can be presented as:

$$\sum\limits_{k = 1}^{K} {U_{lk} \le S_{l} } ,\;\;\;\forall l = 1,2,...,L$$

(3)

Constraint II is the manufactured quantity in the factory that cannot exceed its potential, it can be presented as:

$$\sum\limits_{i = 1}^{I} {Y_{ki} + \sum\limits_{j = 1}^{J} {X_{kj} \le P_{k} } } ,\;\;\forall k = 1,2,...,K$$

(4)

Constraint III is the amount shipped through the wholesaler which cannot exceed its capacity, it can be presented as:

$$\sum\limits_{i = 1}^{I} {V_{ji} \le W_{j,} } \;\;\forall j = 1,2,...,J$$

(5)

Constraint IV is the amount transferred to retailers that must cover the requirement of the customers, it can be presented as:

$$\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} \ge D_{i} } } ,\;\;\forall i = 1,2,...,I$$

(6)

Constraint V is the total amount shipped to the wholesaler and retailers from the agent/broker, which cannot exceed the quantity of the received raw material, it can be presented as:

$$\sum\limits_{l = 1}^{L} {U_{lk} \ge \sum\limits_{j = 1}^{J} {X_{kj} + \sum\limits_{i = 1}^{I} {Y_{ki} } } } ,\;\;\forall k = 1,2,...,K$$

(7)

Constraint VI is the amount shipped to retailers from the wholesaler that can not exceed their capacity, it can be presented as:

$$\sum\limits_{k = 1}^{K} {X_{kj} \ge \sum\limits_{i = 1}^{I} {V_{ji} } } ,\;\;\forall j = 1,2,...,J$$

(8)

with non-negative constraints:

$$\begin{gathered} U_{lk} \ge 0,\,\,\,\forall \,\,l,k, \hfill \\ X_{kj} \ge 0,\,\,\,\forall \,k,j, \hfill \\ Y_{ki} \ge 0,\,\,\,\forall \,k,i, \hfill \\ V_{ji} \ge 0,\,\,\,\forall \,j,i. \hfill \\ \end{gathered}$$

(9)

Combining all the equations, we have our model of interest:

Model (1)

$$Min\,\,Z_{1} = \sum\limits_{l = 1}^{L} {\sum\limits_{k = 1}^{K} {SC_{lk} U_{lk} + \sum\limits_{k = 1}^{K} {\sum\limits_{j = 1}^{J} {SC_{kj} X_{kj} + \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{I} {SC_{ki} Y_{ki} + \sum\limits_{j = 1}^{J} {\sum\limits_{i = 1}^{I} {SC_{ji} } } } } } } } } V_{ji} ,$$

$$Min\,\,Z_{2} = \sum\limits_{k = 1}^{K} {\sum\limits_{j = 1}^{J} {DT_{kj} X_{kj} + \sum\limits_{k = 1}^{K} {\sum\limits_{i = 1}^{I} {DT_{ki} Y_{ki} + \sum\limits_{j = 1}^{J} {\sum\limits_{i = 1}^{I} {DT_{ji} V_{ji} } } } } } } ,$$

Subject to

$$\sum\limits_{k = 1}^{K} {U_{lk} \le S_{l} } ,\;\;\forall l = 1,2,...,L$$

$$\sum\limits_{i = 1}^{I} {Y_{ki} + \sum\limits_{j = 1}^{J} {X_{kj} \le P_{k} } } ,\;\;\forall k = 1,2,...,K$$

$$\sum\limits_{i = 1}^{I} {V_{ji} \le W_{j} } ,\;\;\forall j = 1,2,...,J$$

$$\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} \ge D_{i} } } ,\;\;\forall i = 1,2,...,I$$

$$\sum\limits_{l = 1}^{L} {U_{lk} \ge \sum\limits_{j = 1}^{J} {X_{kj} + \sum\limits_{i = 1}^{I} {Y_{ki} } } } ,\;\;\forall k = 1,2,...,K$$

$$\sum\limits_{k = 1}^{K} {X_{kj} \ge \sum\limits_{i = 1}^{I} {V_{ji} } } ,\;\;\forall j = 1,2,...,J$$

$$\begin{gathered} U_{lk} \ge 0,\,\,\,\forall \,\,l,k, \hfill \\ X_{kj} \ge 0,\,\,\,\forall \,k,j, \hfill \\ Y_{ki} \ge 0,\,\,\,\forall \,k,i, \hfill \\ V_{ji} \ge 0,\,\,\,\forall \,j,i. \hfill \\ \end{gathered}$$

3.1 Uncertain mathematical model

Uncertainty in SCN refers to the decision-making process in the SC where the DMs do not know exactly what to decide due to the lack of accountability in the SC and also due to the impact of viable decisions. The parameters are assumed to take deterministic values in the above model, but they may take imprecise values in most practical situations for some of the possible reasons, as the transportation cost and delivery time of the item may not be fixed in advance. The transportation cost and delivery time of one unit transported from the source to the agent/broker, from the agent/broker to the retailer, from the agent/broker to the wholesaler, and from the wholesaler to the retailer is not exactly known to the DM and may vary during the shipping time. Increased costs are the primary reason for uncertainty in demand, most frequently in the form of surplus inventory, and excess manufacturing capacity. Typically, the firm tries to achieve a SC balance by controlling inventory, transportation and the distribution process but always tries to provide the needed quality of service to its customers. Demand is difficult to predict depending on a number of causes, including the consequences of causal variables, incidents, or lumpy demand. Some of these may be recognized, but there may also be unforeseen developments that affect the demand for items. In view of the likely above-mentioned situations, the uncertain mathematical model of agri-food SCN is typically represented by substituting all deterministic parameters with fuzzy parameters,

Model (2)

$$Min {\widetilde{Z}}_{1}=\sum_{l=1}^{L}\sum_{k=1}^{K}{\widetilde{SC}}_{lk}{U}_{lk}+\sum_{k=1}^{K}\sum_{j=1}^{J}{\widetilde{SC}}_{kj}{X}_{kj}+\sum_{k=1}^{K}\sum_{i=1}^{I}{\widetilde{SC}}_{ki}{Y}_{ki}+\sum_{j=1}^{J}\sum_{i=1}^{I}{\widetilde{SC}}_{ji}{V}_{ji}$$

$$Min {\widetilde{Z}}_{2}=\sum_{k=1}^{K}\sum_{j=1}^{J}{\widetilde{DT}}_{kj}{X}_{kj}+\sum_{k=1}^{K}\sum_{i=1}^{I}{\widetilde{DT}}_{ki}{Y}_{ki}+\sum_{j=1}^{J}\sum_{i=1}^{I}{\widetilde{DT}}_{ji}{V}_{ji}$$

Subject to

$$\sum\limits_{k = 1}^{K} {U_{lk} \le S_{l} } ,\;\;\forall l = 1,2,...,L$$

$$\sum\limits_{i = 1}^{I} {Y_{ki} + \sum\limits_{j = 1}^{J} {X_{kj} \le P_{k} } } ,\;\;\forall k = 1,2,...,K$$

$$\sum\limits_{i = 1}^{I} {V_{ji} \le W_{j} } ,\;\;\forall j = 1,2,...,J$$

$$\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} \ge D_{i} } } ,\;\;\forall i = 1,2,...,I$$

$$\sum\limits_{l = 1}^{L} {U_{lk} \ge \sum\limits_{j = 1}^{J} {X_{kj} + \sum\limits_{i = 1}^{I} {Y_{ki} } } } ,\;\;\forall k = 1,2,...,K$$

$$\sum\limits_{k = 1}^{K} {X_{kj} \ge \sum\limits_{i = 1}^{I} {V_{ji} } } ,\;\;\forall j = 1,2,...,J$$

$$\begin{gathered} U_{lk} \ge 0,\,\,\,\forall \,\,l,k, \hfill \\ X_{kj} \ge 0,\,\,\,\forall \,k,j, \hfill \\ Y_{ki} \ge 0,\,\,\,\forall \,k,i, \hfill \\ V_{ji} \ge 0,\,\,\,\forall \,j,i. \hfill \\ \end{gathered}$$

In the above-discussed model of agri-food SCN, the input parameters of both the objective function’s have been characterised with uncertainty; such uncertain parameters are as follows: shipping cost of a single unit from different supply sources to different agent/brokers, ${\widetilde{SC}}_{lk}$; producing and shipping cost of a single unit from different agent/brokers to different wholesalers,${\widetilde{SC}}_{kj}$; producing and shipping cost of a single unit from different agent/brokers to different retailer,${\widetilde{SC}}_{ki}$; shipping cost of a single unit from different wholesalers to different retailers,${\widetilde{SC}}_{ji};$ time is taken for delivering a single unit from different agent/brokers to a different wholesaler,${\widetilde{DT}}_{kj};$ time is taken for delivering a single unit from different agent/brokers to a different retailer,${\widetilde{DT}}_{ki};$ time is taken for delivering a single unit from different wholesalers to different retailers,${\widetilde{DT}}_{ji}.$ We have considered ${\widetilde{SC}}_{lk},{\widetilde{SC}}_{kj},{\widetilde{SC}}_{ki},{\widetilde{SC}}_{ji}$, ${\widetilde{DT}}_{kj},{\widetilde{DT}}_{ki}$, and ${\widetilde{DT}}_{ji}$ as interval type-2 trapezoidal fuzzy numbers.

3.2 Preliminaries

Some important definitions are provided below for the above defined imprecise parameters are as follows:

Definition 1

[Sinha et al. (2016)]: Let ${\widetilde{SC}}_{lk}$ be a type-2 fuzzy set, then ${\widetilde{SC}}_{lk}$ can be expressed as ${\widetilde{SC}}_{lk}$=$\left\{\left(\left(x,u\right),{\mu }_{{\widetilde{SC}}_{lk}}(x,u)\right)0\le {\mu }_{{\widetilde{SC}}_{lk}}\le 1\right\}$, where X is the universe of discourse and ${\mu }_{{\widetilde{SC}}_{lk}}$ denotes the membership function of${\widetilde{SC}}_{lk}$. Then, ${\widetilde{SC}}_{lk}$ can be expressed as ${\widetilde{SC}}_{lk}=$$\int\limits_{x \in X} {\int\limits_{{u \in J_{x} }} {\mu_{{\tilde{d}_{{_{ij} }}^{{}} }} (x,u)/(x,u)} }$, $u \in J_{x} \subseteq [0,1].$

Definition 2

[Sinha et al. (2016)]: For a type-2 fuzzy set${\widetilde{SC}}_{lk}$, if all ${\mu }_{{\widetilde{SC}}_{lk}}\left(x,u\right)=1$ then ${\widetilde{SC}}_{lk}$ is called an interval type-2 fuzzy set, i.e.,${\widetilde{SC}}_{lk}=$$\int\limits_{x \in X} {\int\limits_{{u \in J_{x} }} {1/(x,u)/(x,u)} }$$u \in J_{x} \subseteq [0,1].$

Definition 3

[Sinha et al. (2016)]: Uncertainty in the primary memberships of a type-2 fuzzy set, ${\widetilde{SC}}_{lk}$ consists of a bounded region that we call the footprints of uncertainty (FOU). It is the union of all primary memberships, i.e., ${FOU(\widetilde{SC}}_{lk})=$$U_{x \in X} J_{x} .$

FOU is characterized by the upper membership functions (UMF) and the lower membership function (LMF), and are denoted by ${\overline{\mu }}_{{\widetilde{SC}}_{lk}}$ and ${\underset{\_}{\mu }}_{{\widetilde{SC}}_{lk}}.$

Definition 4

[Sinha et al. (2016)]: An interval type-2 fuzzy number is called interval type-2 trapezoidal fuzzy number where the UMF and LMF are both trapezoidal fuzzy numbers, i.e.,

$$\begin{aligned} \widetilde{SC}_{lk} = & \left( {SC_{lk}^{U} ,SC_{lk}^{L} } \right) = \left( {\left( {\left( {SC_{lk}^{U} } \right)_{1} ,\left( {SC_{lk}^{U} } \right)_{2} ,\left( {SC_{lk}^{U} } \right)_{3} ,\left( {SC_{lk}^{U} } \right)_{4} } \right);H_{1} \left( {SC_{lk}^{U} } \right),H_{2} \left( {SC_{lk}^{U} } \right)} \right), \\ & \left( {\left( {\left( {SC_{lk}^{L} } \right)_{1} ,\left( {SC_{lk}^{L} } \right)_{2} ,\left( {SC_{lk}^{L} } \right)_{3} ,\left( {SC_{lk}^{L} } \right)_{4} } \right);H_{1} \left( {SC_{lk}^{L} } \right),H_{2} \left( {SC_{lk}^{L} } \right)} \right) \\ \end{aligned}$$

(10)

where,${H}_{r}\left({SC}_{lk}^{U}\right)$ and ${H}_{r}\left({SC}_{lk}^{L}\right)$, (r = 1,2) denote membership values of the corresponding elements respectively.

Definition 5

[Sinha et al. (2016)]: Defuzzification of Interval Type-2 Trapezoidal Fuzzy Number.

Let us consider an interval type-2 trapezoidal fuzzy number ${\widetilde{SC}}_{lk}$, given by Eq. (10). The expected value of interval type-2 trapezoidal fuzzy number is ${\widetilde{SC}}_{lk}$ defined as follows:

$${E(\widetilde{SC}}_{lk})=\frac{1}{2}\left(\frac{1}{4}\sum_{r=1}^{4}\left({\left({SC}_{lk}^{U}\right)}_{r}+{\left({SC}_{lk}^{L}\right)}_{r}\right)\times \frac{1}{4}\sum_{r=1}^{2}\left(\left(\left({H}_{r}\left({SC}_{lk}^{U}\right)\right)+\left({H}_{r}\left({SC}_{lk}^{L}\right)\right)\right)\right)\right)$$

(11)

Similarly, the same definition holds for other types of fuzzy parameters ${\widetilde{SC}}_{kj},{\widetilde{SC}}_{ki},{\widetilde{SC}}_{ji}$, ${\widetilde{DT}}_{kj},{\widetilde{DT}}_{ki}$, and ${\widetilde{DT}}_{ji}$ respectively. Using the above-defined definitions of Interval Type-2 Trapezoidal Fuzzy Number, the crisp transformation of the considered fuzzy parameters of objective functions can be presented as:

$$Min {\widetilde{Z}}_{1}=\sum_{l=1}^{L}\sum_{k=1}^{K}{\widetilde{SC}}_{lk}{U}_{lk}+\sum_{k=1}^{K}\sum_{j=1}^{J}{\widetilde{SC}}_{kj}{X}_{kj}+\sum_{k=1}^{K}\sum_{i=1}^{I}{\widetilde{SC}}_{ki}{Y}_{ki}+\sum_{j=1}^{J}\sum_{i=1}^{I}{\widetilde{SC}}_{ji}{V}_{ji},$$

To show the crisp transformation of the first objective function in a precise manner, we have divided the above objective function into four parts:

1st part of objective function Z₁ can be presented as:

$$=\sum_{l=1}^{L}\sum_{k=1}^{K}{\widetilde{SC}}_{lk}{U}_{lk},$$

$$=\sum_{l=1}^{L}\sum_{k=1}^{K}\left({SC}_{lk}^{U},{SC}_{lk}^{L}\right){U}_{lk},$$

$$=\sum_{l=1}^{L}\sum_{k=1}^{K}\left(\begin{array}{c}\left(\left({\left({SC}_{lk}^{U}\right)}_{1},{\left({SC}_{lk}^{U}\right)}_{2},{\left({SC}_{lk}^{U}\right)}_{3},{\left({SC}_{lk}^{U}\right)}_{4}\right);{H}_{1}\left({SC}_{lk}^{U}\right),{H}_{2}\left({SC}_{lk}^{U}\right)\right),\\ \left(\left({\left({SC}_{lk}^{L}\right)}_{1},{\left({SC}_{lk}^{L}\right)}_{2},{\left({SC}_{lk}^{L}\right)}_{3},{\left({SC}_{lk}^{L}\right)}_{4}\right);{H}_{1}\left({SC}_{lk}^{L}\right),{H}_{2}\left({SC}_{lk}^{L}\right)\right)\end{array}\right){U}_{lk},$$

$$=\sum_{l=1}^{L}\sum_{k=1}^{K}\frac{1}{2}\left(\frac{1}{4}\sum_{r=1}^{4}\left(\left({\left({SC}_{lk}^{U}\right)}_{r}+{\left({SC}_{lk}^{L}\right)}_{r}\right)\right)\times \frac{1}{4}\sum_{r=1}^{2}\left(\left(\left({H}_{r}\left({SC}_{lk}^{U}\right)\right)+\left({H}_{r}\left({SC}_{lk}^{L}\right)\right)\right)\right)\right){U}_{lk},$$

2nd part of objective function Z₁ can be presented as:

$$=\sum_{k=1}^{K}\sum_{j=1}^{J}{\widetilde{SC}}_{kj}{X}_{kj},$$

$$=\sum_{k=1}^{K}\sum_{j=1}^{J}\left({SC}_{kj}^{U},{SC}_{kj}^{L}\right){X}_{kj},$$

$$=\sum_{k=1}^{K}\sum_{J=1}^{J}\left(\begin{array}{c}\left(\left({\left({SC}_{kj}^{U}\right)}_{1},{\left({SC}_{kj}^{U}\right)}_{2},{\left({SC}_{kj}^{U}\right)}_{3},{\left({SC}_{kj}^{U}\right)}_{4}\right);{H}_{1}\left({SC}_{kj}^{U}\right),{H}_{2}\left({SC}_{kj}^{U}\right)\right),\\ \left(\left({\left({SC}_{kj}^{L}\right)}_{1},{\left({SC}_{kj}^{L}\right)}_{2},{\left({SC}_{kj}^{L}\right)}_{3},{\left({SC}_{kj}^{L}\right)}_{4}\right);{H}_{1}\left({SC}_{kj}^{L}\right),{H}_{2}\left({SC}_{kj}^{L}\right)\right)\end{array}\right){X}_{kj},$$

$$=\sum_{k=1}^{K}\sum_{j=1}^{J}\frac{1}{2}\left(\frac{1}{4}\sum_{r=1}^{4}\left(\left({\left({SC}_{kj}^{U}\right)}_{r}+{\left({SC}_{kj}^{L}\right)}_{r}\right)\right)\times \frac{1}{4}\sum_{r=1}^{2}\left(\left(\left({H}_{r}\left({SC}_{kj}^{U}\right)\right)+\left({H}_{r}\left({SC}_{kj}^{L}\right)\right)\right)\right)\right){X}_{kj},$$

3rd part of objective function Z₁ can be presented as:

$$=\sum_{k=1}^{K}\sum_{i=1}^{I}{\widetilde{SC}}_{ki}{Y}_{ki},$$

$$=\sum_{k=1}^{K}\sum_{i=1}^{I}\left({SC}_{ki}^{U},{SC}_{ki}^{L}\right){Y}_{ki},$$

$$=\sum_{k=1}^{K}\sum_{i=1}^{I}\left(\begin{array}{c}\left(\left({\left({SC}_{ki}^{U}\right)}_{1},{\left({SC}_{ki}^{U}\right)}_{2},{\left({SC}_{ki}^{U}\right)}_{3},{\left({SC}_{ki}^{U}\right)}_{4}\right);{H}_{1}\left({SC}_{ki}^{U}\right),{H}_{2}\left({SC}_{ki}^{U}\right)\right),\\ \left(\left({\left({SC}_{ki}^{L}\right)}_{1},{\left({SC}_{ki}^{L}\right)}_{2},{\left({SC}_{ki}^{L}\right)}_{3},{\left({SC}_{ki}^{L}\right)}_{4}\right);{H}_{1}\left({SC}_{ki}^{L}\right),{H}_{2}\left({SC}_{ki}^{L}\right)\right)\end{array}\right){Y}_{ki},$$

$$=\sum_{k=1}^{K}\sum_{i=1}^{I}\frac{1}{2}\left(\frac{1}{4}\sum_{r=1}^{4}\left(\left({\left({SC}_{ki}^{U}\right)}_{r}+{\left({SC}_{ki}^{L}\right)}_{r}\right)\right)\times \frac{1}{4}\sum_{r=1}^{2}\left(\left(\left({H}_{r}\left({SC}_{ki}^{U}\right)\right)+\left({H}_{r}\left({SC}_{ki}^{L}\right)\right)\right)\right)\right){Y}_{ki},$$

4th part of objective function Z₁ can be presented as:

$$=\sum_{j=1}^{J}\sum_{i=1}^{I}{\widetilde{SC}}_{ji}{V}_{ji},$$

$$=\sum_{j=1}^{J}\sum_{i=1}^{I}\left({SC}_{Ji}^{U},{SC}_{ki}^{L}\right){V}_{ji},$$

$$=\sum_{j=1}^{J}\sum_{i=1}^{I}\left(\begin{array}{c}\left(\left({\left({SC}_{ji}^{U}\right)}_{1},{\left({SC}_{ji}^{U}\right)}_{2},{\left({SC}_{ji}^{U}\right)}_{3},{\left({SC}_{ji}^{U}\right)}_{4}\right);{H}_{1}\left({SC}_{ji}^{U}\right),{H}_{2}\left({SC}_{ji}^{U}\right)\right),\\ \left(\left({\left({SC}_{ji}^{L}\right)}_{1},{\left({SC}_{ji}^{L}\right)}_{2},{\left({SC}_{ji}^{L}\right)}_{3},{\left({SC}_{ji}^{L}\right)}_{4}\right);{H}_{1}\left({SC}_{ji}^{L}\right),{H}_{2}\left({SC}_{ji}^{L}\right)\right)\end{array}\right){V}_{ji},$$

$$=\sum_{j=1}^{J}\sum_{i=1}^{I}\frac{1}{2}\left(\frac{1}{4}\sum_{r=1}^{4}\left(\left({\left({SC}_{ji}^{U}\right)}_{r}+{\left({SC}_{ji}^{L}\right)}_{r}\right)\right)\times \frac{1}{4}\sum_{r=1}^{2}\left(\left(\left({H}_{r}\left({SC}_{ji}^{U}\right)\right)+\left({H}_{r}\left({SC}_{ji}^{L}\right)\right)\right)\right)\right){V}_{ji},$$

Similarly, the 1st part of objective function Z₂ can be presented as:

$$=\sum_{k=1}^{K}\sum_{j=1}^{J}{\widetilde{DT}}_{kj}{X}_{kj},$$

$$=\sum_{k=1}^{K}\sum_{j=1}^{J}\left({DT}_{kj}^{U},{DT}_{kj}^{L}\right){X}_{kj},$$

$$=\sum_{k=1}^{K}\sum_{J=1}^{J}\left(\begin{array}{c}\left(\left({\left({DT}_{kj}^{U}\right)}_{1},{\left({DT}_{kj}^{U}\right)}_{2},{\left({DT}_{kj}^{U}\right)}_{3},{\left({DT}_{kj}^{U}\right)}_{4}\right);{H}_{1}\left({DT}_{kj}^{U}\right),{H}_{2}\left({DT}_{kj}^{U}\right)\right),\\ \left(\left({\left({DT}_{kj}^{L}\right)}_{1},{\left({DT}_{kj}^{L}\right)}_{2},{\left({DT}_{kj}^{L}\right)}_{3},{\left({DT}_{kj}^{L}\right)}_{4}\right);{H}_{1}\left({DT}_{kj}^{L}\right),{H}_{2}\left({DT}_{kj}^{L}\right)\right)\end{array}\right){X}_{kj},$$

$$=\sum_{k=1}^{K}\sum_{j=1}^{J}\frac{1}{2}\left(\frac{1}{4}\sum_{r=1}^{4}\left(\left({\left({DT}_{kj}^{U}\right)}_{r}+{\left({DT}_{kj}^{L}\right)}_{r}\right)\right)\times \frac{1}{4}\sum_{r=1}^{2}\left(\left(\left({H}_{r}\left({DT}_{kj}^{U}\right)\right)+\left({H}_{r}\left({DT}_{kj}^{L}\right)\right)\right)\right)\right){X}_{kj},$$

2nd part of objective function Z₂ can be presented as:

$$=\sum_{k=1}^{K}\sum_{i=1}^{I}{\widetilde{DT}}_{ki}{Y}_{ki},$$

$$=\sum_{k=1}^{K}\sum_{i=1}^{I}\left({DT}_{ki}^{U},{DT}_{ki}^{L}\right){Y}_{ki},$$

$$=\sum_{k=1}^{K}\sum_{i=1}^{I}\left(\begin{array}{c}\left(\left({\left({DT}_{ki}^{U}\right)}_{1},{\left({DT}_{ki}^{U}\right)}_{2},{\left({DT}_{ki}^{U}\right)}_{3},{\left({DT}_{ki}^{U}\right)}_{4}\right);{H}_{1}\left({DT}_{ki}^{U}\right),{H}_{2}\left({DT}_{ki}^{U}\right)\right),\\ \left(\left({\left({DT}_{ki}^{L}\right)}_{1},{\left({DT}_{ki}^{L}\right)}_{2},{\left({DT}_{ki}^{L}\right)}_{3},{\left({DT}_{ki}^{L}\right)}_{4}\right);{H}_{1}\left({DT}_{ki}^{L}\right),{H}_{2}\left({DT}_{ki}^{L}\right)\right)\end{array}\right){Y}_{ki},$$

$$=\sum_{k=1}^{K}\sum_{i=1}^{I}\frac{1}{2}\left(\frac{1}{4}\sum_{r=1}^{4}\left(\left({\left({DT}_{ki}^{U}\right)}_{r}+{\left({DT}_{ki}^{L}\right)}_{r}\right)\right)\times \frac{1}{4}\sum_{r=1}^{2}\left(\left(\left({H}_{r}\left({DT}_{ki}^{U}\right)\right)+\left({H}_{r}\left({DT}_{ki}^{L}\right)\right)\right)\right)\right){Y}_{ki},$$

3rd part of objective function Z₂ can be presented as:

$$=\sum_{j=1}^{J}\sum_{i=1}^{I}{\widetilde{DT}}_{ji}{V}_{ji},$$

$$=\sum_{j=1}^{J}\sum_{i=1}^{I}\left({DT}_{Ji}^{U},{DT}_{ki}^{L}\right){V}_{ji},$$

$$=\sum_{j=1}^{J}\sum_{i=1}^{I}\left(\begin{array}{c}\left(\left({\left({DT}_{ji}^{U}\right)}_{1},{\left({DT}_{ji}^{U}\right)}_{2},{\left({DT}_{ji}^{U}\right)}_{3},{\left({DT}_{ji}^{U}\right)}_{4}\right);{H}_{1}\left({DT}_{ji}^{U}\right),{H}_{2}\left({DT}_{ji}^{U}\right)\right),\\ \left(\left({\left({DT}_{ji}^{L}\right)}_{1},{\left({DT}_{ji}^{L}\right)}_{2},{\left({DT}_{ji}^{L}\right)}_{3},{\left({DT}_{ji}^{L}\right)}_{4}\right);{H}_{1}\left({DT}_{ji}^{L}\right),{H}_{2}\left({DT}_{ji}^{L}\right)\right)\end{array}\right){V}_{ji},$$

$$=\sum_{j=1}^{J}\sum_{i=1}^{I}\frac{1}{2}\left(\frac{1}{4}\sum_{r=1}^{4}\left(\left({\left({DT}_{ji}^{U}\right)}_{r}+{\left({DT}_{ji}^{L}\right)}_{r}\right)\right)\times \frac{1}{4}\sum_{r=1}^{2}\left(\left(\left({H}_{r}\left({DT}_{ji}^{U}\right)\right)+\left({H}_{r}\left({DT}_{ji}^{L}\right)\right)\right)\right)\right){V}_{ji},$$

In most of the real scenarios, we may have the difficulty of having a partial knowledge of the input values of some or all of the parameters; such a situation falls under probabilistic or stochastic programming. In this circumstance, a solution which is feasible for all potential parameters and which can serve to optimize a set of the specified objective function can be considered, if the parameters are uncertain, however presumed to be in certain potential values. Here we explored a scenario in which the demand and supply parameters of the agri-food SCN is probabilistic or random in nature and follows a gamma distribution. The importance of gamma distribution has been observed in several fields such as reliability, engineering, operational research etc. The Gamma distribution has two-parameters which belong to a continuous probability distribution. Gamma distribution has been used for modelling the aggregated volume size of the real-world problems. Gamma distribution is widely utilized for a wide range of applications, including insurance claims, forecasting of rainfall, satellite connectivity, oncology, neurology, microbial energy metabolism, genetics, etc. Many authors have been worked on this distribution in many areas such as, Harter et al. (1965) examined the parameter evaluation problem for the populations of gamma and weibull distributions with completion and censoring of the samples. Choi and Wette (1969), Coit and Jin (2000), and Zaigraev and Karakulska (2009) obtained the estimated parameter’s of the samples when the samples followed the gamma distribution. In the light of the above situations, the uncertain formulation of the agri-food SCN problem with fuzziness and randomness is conventionally expressed as:

Model (3)

$$Min {\widetilde{Z}}_{1}=\sum_{l=1}^{L}\sum_{k=1}^{K}{\widetilde{SC}}_{lk}{U}_{lk}+\sum_{k=1}^{K}\sum_{j=1}^{J}{\widetilde{SC}}_{kj}{X}_{kj}+\sum_{k=1}^{K}\sum_{i=1}^{I}{\widetilde{SC}}_{ki}{Y}_{ki}+\sum_{j=1}^{J}\sum_{i=1}^{I}{\widetilde{SC}}_{ji}{V}_{ji}$$

$$Min {\widetilde{Z}}_{2}=\sum_{k=1}^{K}\sum_{j=1}^{J}{\widetilde{DT}}_{kj}{X}_{kj}+\sum_{k=1}^{K}\sum_{i=1}^{I}{\widetilde{DT}}_{ki}{Y}_{ki}+\sum_{j=1}^{J}\sum_{i=1}^{I}{\widetilde{DT}}_{ji}{V}_{ji}$$

Subject to

$${\text{Pr}}\left( {\sum\limits_{k = 1}^{K} {U_{lk} \le S_{l} } } \right) \ge 1 - \gamma_{l} ,\;\;\forall l = 1,2,...,L$$

$$\sum\limits_{i = 1}^{I} {Y_{ki} + \sum\limits_{j = 1}^{J} {X_{kj} \le P_{k} } } ,\;\;\forall k = 1,2,...,K$$

$$\sum\limits_{i = 1}^{I} {V_{ji} \le W_{j} } ,\;\;\forall j = 1,2,...,J$$

$$\Pr \left( {\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} \ge D_{i} } } } \right) \ge 1 - \beta_{i} ,\;\;\forall i = 1,2,...,I$$

$$\sum\limits_{l = 1}^{L} {U_{lk} \ge \sum\limits_{j = 1}^{J} {X_{kj} + \sum\limits_{i = 1}^{I} {Y_{ki} } } } ,\;\;\forall k = 1,2,...,K$$

$$\sum\limits_{k = 1}^{K} {X_{kj} \ge \sum\limits_{i = 1}^{I} {V_{ji} } } ,\;\;\forall j = 1,2,...,J$$

$$\begin{gathered} U_{lk} \ge 0,\,\,\,\forall \,\,l,k, \hfill \\ X_{kj} \ge 0,\,\,\,\forall \,k,j, \hfill \\ Y_{ki} \ge 0,\,\,\,\forall \,k,i, \hfill \\ V_{ji} \ge 0,\,\,\,\forall \,j,i. \hfill \\ \end{gathered}$$

where $0 < \gamma_{l} < 1$ and $0 < \beta_{i} < 1,$ are the specified probability levels associated with demand and supply constraints. We assume that this probabilistic constraint follows a Gamma distribution. The probability density function of Gamma distribution with shape $\alpha$ and scale $\theta$ parameter is given by:

$f(x) = \frac{1}{{\theta^{\alpha } \Gamma \alpha }}x^{\alpha - 1} e^{{ - \frac{x}{\theta }}}$,$x \ge 0,\,\,\alpha > 0,\,\,\theta > 0$.

Since we have considered the problem of MOAFSCN under probabilistic environment also, two different cases occur for probabilistic constraints when it follows Gamma distribution, which can be presented as:

Case I

When Pr $\left( {\sum\limits_{k = 1}^{K} {U_{lk} \le S_{l} } } \right) \ge 1 - \gamma_{l} ,$$l = 1,2,...,L$

or, Pr $\left( {\sum\limits_{k = 1}^{K} {U_{lk} \ge S_{l} } } \right) \le \gamma_{l} ,$$l = 1,2,...,L$

The probability density function of $S_{l} \,\,(l = 1,2,...,L)$ is given by

$$f(S_{l} ,\theta_{l} ,\alpha_{l} ) = \frac{1}{{\theta_{l}^{{\alpha_{l} }} \Gamma \alpha_{l} }}S_{l}^{{\alpha_{l} - 1}} e^{{ - \frac{{S_{l} }}{{\theta_{l} }}}} ,\;\;S_{l} \ge 0,\,\,\alpha_{l} > 0,\,\,\theta_{l} > 0$$

(12)

Hence, the probabilistic constraint can be presented as:

$$\int\limits_{{\sum\limits_{k = 1}^{K} {U_{lk} } }}^{\infty } {f(S_{l} ,\theta_{l} ,\alpha_{l} )\,\,d(S_{l} )\, \le \gamma_{l} ,} \;\;l = 1,2,...,L$$

(13)

Equation (13) can be expressed in the integral form as:

$$\int\limits_{{\sum\limits_{k = 1}^{K} {U_{lk} } }}^{\infty } {\frac{1}{{\theta_{l}^{{\alpha_{l} }} \Gamma \alpha_{l} }}S_{l}^{{\alpha_{l} - 1}} e^{{ - \frac{{S_{l} }}{{\theta_{l} }}}} \,d(S_{l} ) \le \gamma_{l} ,} \;\;l = 1,2,...,L$$

(14)

Let,

$$\frac{{S_{l} }}{{\theta_{l} }} = y \Rightarrow \,\,dS_{l} = \theta_{l} dy$$

(15)

Using Eq. (15), the integral can be further presented as:

$$\int\limits_{{{{\sum\limits_{k = 1}^{K} {U_{lk} } } \mathord{\left/ {\vphantom {{\sum\limits_{k = 1}^{K} {U_{lk} } } {\theta_{l} }}} \right. \kern-0pt} {\theta_{l} }}}}^{\infty } {\frac{1}{{\theta_{l}^{{\alpha_{l} }} \Gamma \alpha_{l} }}(\theta_{l} y)_{{}}^{{\alpha_{i} - 1}} e^{ - y} \theta_{l} \,dy\, \le \gamma_{l} ,} \;\;l = 1,2,...,L$$

(16)

On rearranging, we obtain

$$\frac{1}{{\Gamma \alpha_{l} }}\int\limits_{{{{\sum\limits_{k = 1}^{K} {U_{lk} } } \mathord{\left/ {\vphantom {{\sum\limits_{k = 1}^{K} {U_{lk} } } {\theta_{l} }}} \right. \kern-0pt} {\theta_{l} }}}}^{\infty } {y_{{}}^{{\alpha_{l} - 1}} e^{ - y} dy\, \le \gamma_{l} ,} \;\;\;\;l = 1,2,...,L$$

(17)

where $\Gamma_{a} (x) = \int\limits_{x}^{\infty } {t^{a - 1} } e^{ - t} dt$ an upper incomplete Gamma function.

After simplification, we obtain

$$\frac{1}{{\Gamma \alpha_{l} }}\Gamma_{{\alpha_{l} }} \left( {\frac{{\sum\limits_{k = 1}^{K} {U_{lk} } }}{{\theta_{l} }}} \right) \le \gamma_{l} ,\;\;\;\;l = 1,2,...,L$$

After rearranging, we obtain

$$\frac{{\sum\limits_{k = 1}^{K} {U_{lk} } }}{{\theta_{l} }} \le \Gamma_{{\alpha_{l} }}^{ - 1} \,\left( {\Gamma \alpha_{l} \gamma_{l} } \right),\;\;\;\;l = 1,2,...,L$$

(18)

Finally, the probabilistic constraint can be transformed into a deterministic linear constraint as:

$$\sum\limits_{k = 1}^{K} {U_{lk} } \le \theta_{l} \Gamma_{{\alpha_{l} }}^{ - 1} \,\left( {\Gamma \alpha_{l} \gamma_{l} } \right),\;\;\;\;l = 1,2,...,L$$

(19)

where $\Gamma_{w}^{ - 1} (u) = \left\{ {x:u = \Gamma_{w} (x)} \right\}$ is an inverse gamma function solved by using R software.

Case II

When Pr $\left( {\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} \ge D_{i} } } } \right) \ge 1 - \beta_{i} ,\;\;\;\;i = 1,2,...,I$

The probability density function of $D_{i} \,\,(i = 1,2,...,I)$ is given by

$$f(D_{i} ,\theta_{i}{\prime} ,\alpha_{i}{\prime} ) = \frac{1}{{\theta{\prime}_{i}^{{\alpha_{i}{\prime} }} \Gamma \alpha_{i}{\prime} }}D_{i}^{{\alpha_{i}{\prime} - 1}} e^{{ - \frac{{D_{i} }}{{\theta_{i}{\prime} }}}} ,\;\;D_{i} \ge 0,\,\,\alpha_{i}{\prime} > 0,\,\,\theta_{i}{\prime} > 0$$

(20)

Hence, the probabilistic constraint can be presented as:

$$\int\limits_{{\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} } } }}^{\infty } {f(D_{i} ,\theta_{i}{\prime} ,\alpha_{i}{\prime} )\,\,d(D_{i} )\, \ge 1 - \beta_{i} ,} \;\;\;\;i = 1,2,...,I$$

(21)

Equation (21) can be expressed in the integral form as:

$$\int\limits_{{\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} } } }}^{\infty } {\frac{1}{{\theta{\prime}_{i}^{{\alpha_{i}{\prime} }} \Gamma \alpha_{i}{\prime} }}D_{i}^{{\alpha_{i}{\prime} - 1}} e^{{ - \frac{{D_{i} }}{{\theta_{i}{\prime} }}}} \,d(D_{i} )\, \ge 1 - \beta_{i} ,} \;\;i = 1,2,...,I$$

(22)

Let,

$$\frac{{D_{i} }}{{\theta_{i}{\prime} }} = y^{\prime } \Rightarrow \,\,dD_{i} = \theta_{i}^{\prime } dy\;\;{\text{and}}\;\;\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} = S} }$$

(23)

Using Eq. (23), the integral can be further presented as:

$$\int\limits_{{{\raise0.7ex\hbox{$S$} \!\mathord{\left/ {\vphantom {S {\theta_{i}{\prime} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\theta_{i}{\prime} }$}}}}^{\infty } {\frac{1}{{\theta{\prime}_{i}^{{\alpha_{i}{\prime} }} \Gamma \alpha_{i}{\prime} }}(y{\prime} \theta_{i}{\prime} )_{{}}^{{\alpha_{i}{\prime} - 1}} e^{{ - y{\prime} }} \,\theta_{i}{\prime} d(y{\prime} )\, \ge 1 - \beta_{i} ,} \;\;i = 1,2,...,I$$

(24)

On rearranging, we obtain

$$\frac{1}{{\Gamma \alpha_{i}{\prime} }}\int\limits_{{{\raise0.7ex\hbox{$S$} \!\mathord{\left/ {\vphantom {S {\theta_{i}{\prime} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\theta_{i}{\prime} }$}}}}^{\infty } {(y{\prime} )_{{}}^{{\alpha_{i}{\prime} - 1}} e^{{ - y{\prime} }} \,d(y{\prime} )\, \ge 1 - \beta_{i} ,} \;\;i = 1,2,...,I$$

(25)

After simplification, we get

$$\frac{1}{{\Gamma \alpha_{i}{\prime} }}\Gamma_{{\alpha_{i} }} \left( {\frac{S}{{\theta_{i}{\prime} }}} \right) \ge 1 - \beta_{i} ,\;\;i = 1,2,...,I$$

or,

$$\frac{1}{{\Gamma \alpha_{i}{\prime} }}\Gamma_{{\alpha_{i} }} \left( {\frac{{\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} } } }}{{\theta_{i}{\prime} }}} \right) \ge 1 - \beta_{i} ,\;\;i = 1,2,...,I$$

After rearranging, we obtain

$$\frac{{\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} } } }}{{\theta_{i}{\prime} }} \ge \Gamma_{{\alpha_{i} }}^{ - 1} \left( {\left( {\Gamma \alpha_{i}{\prime} \,(1 - \beta_{i} )} \right)} \right),\;\;i = 1,2,...,I$$

(26)

Thus finally, the probabilistic constraints can be transformed into a deterministic linear constraint as:

$$\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} } } \le \theta_{i}{\prime} \left( {\Gamma_{{\alpha_{i} }}^{ - 1} \left( {\Gamma \alpha_{i}{\prime} \,(1 - \beta_{i} )} \right)} \right),\;\;i = 1,2,...,I$$

(27)

where $\Gamma_{w}^{ - 1} (u) = \left\{ {x:u = \Gamma_{w} (x)} \right\}$ is an inverse Gamma function solved by using R software. The solution obtained from the MOAFSCN will be the compromised quantity to be transported from different sources to different destination i.e., different sources to different agent/brokers, different agent/brokers to different wholesalers, different wholesalers to different retailers, and from different agent/brokers to different retailers. For multi-objective, the concept of optimum with several objective functions changes because in multi-objective problems the aim is to find a good compromised solution. Belhoul et al. (2014) stated that “the compromised solution is a feasible solution, which is the closest to the ideal, and a compromised means an agreement established by mutual concessions”. In this study, we have used two different types of approach for getting the optimized result, which are discussed below.

3.3 The value function approach

The value function approach is a method that reflects the preferences of a decision-maker when dealing with objective vectors. Different decision-makers working on the same problem may have distinct value functions, and this approach provides a systematic way to order the objective functions based on these preferences. Value functions are not only explicitly used to solve multi-objective optimization problems but also play a crucial role as a theoretical framework in the development of solution methods. It is often assumed that the value function is implicitly known in many multi-objective optimization problems, and based on this knowledge, it is selected by the decision-maker (Zionts 1997a,b).

One of the primary advantages of the value function approach is that it provides a structured and intuitive means for decision-makers to express their preferences and make informed choices when faced with multiple conflicting objectives. Additionally, value functions are versatile and can accommodate various types of objective functions, making them applicable to a wide range of real-world problems. Furthermore, value functions are generally presumed to exhibit a decreasing nature, meaning that a decision-maker's preference will increase if the value of an objective function decreases, while keeping all other objective values constant (Rosenthal 1985). This inherent property of value functions simplifies the decision-making process and aids in identifying optimal solutions that align with the decision-maker's preferences. The Model (3) may be expressed as a value function approach:

Minimize $\varphi \left( {\sum\limits_{t = 1}^{T} {\tilde{Z}_{t} } } \right)$.

Subject to Pr $\left( {\sum\limits_{k = 1}^{K} {U_{lk} \le S_{l} } } \right) \ge 1 - \gamma_{l} ,$ $\forall l = 1,2,...,L$

$$\sum\limits_{i = 1}^{I} {Y_{ki} + \sum\limits_{j = 1}^{J} {X_{kj} \le P_{k} } } ,\;\;\forall k = 1,2,...,K$$

$$\sum\limits_{i = 1}^{I} {V_{ji} \le W_{j} } ,\;\;\forall j = 1,2,...,J$$

Pr $\left( {\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} \ge D_{i} } } } \right) \ge 1 - \beta_{i} ,$ $\forall i = 1,2,...,I$

$$\sum\limits_{l = 1}^{L} {U_{lk} \ge \sum\limits_{j = 1}^{J} {X_{kj} + \sum\limits_{i = 1}^{I} {Y_{ki} } } } ,$$

$$\sum\limits_{k = 1}^{K} {X_{kj} \ge \sum\limits_{i = 1}^{I} {V_{ji} } } ,\;\;\forall j = 1,2,...,J$$

$$\begin{gathered} U_{lk} \ge 0,\,\,\,\forall \,\,l,k, \hfill \\ X_{kj} \ge 0,\,\,\,\forall \,k,j, \hfill \\ Y_{ki} \ge 0,\,\,\,\forall \,k,i, \hfill \\ V_{ji} \ge 0,\,\,\,\forall \,j,i. \hfill \\ \end{gathered}$$

where $\varphi (.)$ is a scalar function which summarizes each objective function's significance. The value function $\varphi (.)$ takes an appropriate value to the nature of the optimization problem for each problem. In this article, we define $\varphi (.)$ as the weighted sum of squared of both the functions. Model (3) under this conjecture becomes:

Minimize $\sum\limits_{t = 1}^{T} {\lambda_{t} \tilde{Z}_{t} }$.

Subject to

$$\Pr \left( {\sum\limits_{k = 1}^{K} {U_{lk} \le S_{l} } } \right) \ge 1 - \gamma_{l} ,\;\;\forall l = 1,2,...,L$$

$$\sum\limits_{i = 1}^{I} {Y_{ki} + \sum\limits_{j = 1}^{J} {X_{kj} \le P_{k} } } ,\;\;\forall k = 1,2,...,K$$

$$\sum\limits_{i = 1}^{I} {V_{ji} \le W_{j} } ,\;\;\forall j = 1,2,...,J$$

$$\Pr \left( {\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} \ge D_{i} } } } \right) \ge 1 - \beta_{i} ,\;\;\forall i = 1,2,...,I$$

$$\sum\limits_{l = 1}^{L} {U_{lk} \ge \sum\limits_{j = 1}^{J} {X_{kj} + \sum\limits_{i = 1}^{I} {Y_{ki} } } } ,$$

$$\sum\limits_{k = 1}^{K} {X_{kj} \ge \sum\limits_{i = 1}^{I} {V_{ji} } } ,\;\;\forall j = 1,2,...,J$$

$$\begin{gathered} U_{lk} \ge 0,\,\,\,\forall \,\,l,k, \hfill \\ X_{kj} \ge 0,\,\,\,\forall \,k,j, \hfill \\ Y_{ki} \ge 0,\,\,\,\forall \,k,i, \hfill \\ V_{ji} \ge 0,\,\,\,\forall \,j,i. \hfill \\ \end{gathered}$$

where $\sum\limits_{t = 1}^{2} {\lambda_{t} = 1,\,\,} \lambda_{t} \ge 0,\,\forall t = 1,2,...,T$ are the weights according to the relative importance of the objective functions. The step by step procedure of using the value function approach can be easily understood from (Ghomi-Avili et al. 2019; Ghufran et al. 2020).

3.4 The ${\varvec{\epsilon}}$ constraint approach

The ε-constraint approach, as introduced by Haimes et al. (1971), involves selecting a single objective function for optimization, while imposing upper bounds on all other objectives. In this method, decision-makers are required to identify the most critical objective function. The advantage of this approach lies in its ability to simplify decision-making and provide a clear focus on the primary objective, streamlining the optimization process and facilitating more straightforward, informed choices. Additionally, by reducing the complexity associated with multi-objective optimization, it enhances the decision-maker's ability to manage and understand trade-offs among various objectives, ultimately aiding in the development of more efficient and effective solutions. The problem of acquiring a compromise solution can be expressed under this approach as:

Minimize $\tilde{Z}_{t}$, t = 1,2,…,T

Subject to

$$\tilde{Z}_{r} \le \tilde{z}_{r} ,\,\,r \ne t,\,\,r = 1,2,...,t - 1$$

$\Pr \left( {\sum\limits_{k = 1}^{K} {U_{lk} \le S_{l} } } \right) \ge 1 - \gamma_{l} ,\;\;\forall l = 1,2,...,L$

$$\sum\limits_{i = 1}^{I} {Y_{ki} + \sum\limits_{j = 1}^{J} {X_{kj} \le P_{k} } } ,\;\;\forall k = 1,2,...,K$$

$$\sum\limits_{i = 1}^{I} {V_{ji} \le W_{j} } ,\;\;\forall j = 1,2,...,J$$

$\Pr \left( {\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} \ge D_{i} } } } \right) \ge 1 - \beta_{i} ,\;\;\forall i = 1,2,...,I$

$$\sum\limits_{l = 1}^{L} {U_{lk} \ge \sum\limits_{j = 1}^{J} {X_{kj} + \sum\limits_{i = 1}^{I} {Y_{ki} } } } ,$$

$$\sum\limits_{k = 1}^{K} {X_{kj} \ge \sum\limits_{i = 1}^{I} {V_{ji} } } ,\;\;\forall j = 1,2,...,J$$

$$\begin{gathered} U_{lk} \ge 0,\,\,\,\forall \,\,l,k, \hfill \\ X_{kj} \ge 0,\,\,\,\forall \,k,j, \hfill \\ Y_{ki} \ge 0,\,\,\,\forall \,k,i, \hfill \\ V_{ji} \ge 0,\,\,\,\forall \,j,i. \hfill \\ \end{gathered}$$

where the tth objective function, $t \in \{ 1,2,...,t - 1\} ,$ is assumed to be most important and rth is a predetermined bound for the t − 1 remaining objective functions that have the least importance. In practice, $\tilde{z}_{r}$ is nothing but one of the solutions from two objective function that have the least importance according to the decision-maker, can be obtained as:

Minimize $\tilde{z}_{r}$, r = 1,2,…,t−1.

Subject to $\Pr \left( {\sum\limits_{k = 1}^{K} {U_{lk} \le S_{l} } } \right) \ge 1 - \gamma_{l} ,\;\;\forall l = 1,2,...,L$

$$\sum\limits_{i = 1}^{I} {Y_{ki} + \sum\limits_{j = 1}^{J} {X_{kj} \le P_{k} } } ,\;\;\forall k = 1,2,...,K$$

$$\sum\limits_{i = 1}^{I} {V_{ji} \le W_{j} } ,\;\;\forall j = 1,2,...,J$$

Pr $\left( {\sum\limits_{j = 1}^{J} {V_{ji} + \sum\limits_{k = 1}^{K} {Y_{ki} \ge D_{i} } } } \right) \ge 1 - \beta_{i} ,$ $\forall i = 1,2,...,I$

$$\sum\limits_{l = 1}^{L} {U_{lk} \ge \sum\limits_{j = 1}^{J} {X_{kj} + \sum\limits_{i = 1}^{I} {Y_{ki} } } } ,$$

$$\sum\limits_{k = 1}^{K} {X_{kj} \ge \sum\limits_{i = 1}^{I} {V_{ji} } } ,\;\;\forall j = 1,2,...,J$$

$$\begin{gathered} U_{lk} \ge 0,\,\,\,\forall \,\,l,k, \hfill \\ X_{kj} \ge 0,\,\,\,\forall \,k,j, \hfill \\ Y_{ki} \ge 0,\,\,\,\forall \,k,i, \hfill \\ V_{ji} \ge 0,\,\,\,\forall \,j,i. \hfill \\ \end{gathered}$$

The step by step procedure of using the ${\varvec{\epsilon}}$—constraint approach can be easily understood from (Liu and Papageorgiou 2013; Mohebalizadehgashti et al. 2020).

4 Case illustration: agri-food supply chain network design

To explain the above algorithm, we applied our proposed model to a distribution network of agricultural products in India. In the food industry, freshness and quality of products are the most important criteria to satisfy customers. Customers always opt for fresh food items at all times. In the recent past, demand for Agri-food products has been continuously increasing. The network of the Agri-food SC, which used to be marked mainly by flexibility and agent sovereignty, is now moving rapidly into integrated networks with a broad variety of complex connections. Maintaining a fresh SC in the face of rising economic and regulatory stresses is a challenge for suppliers, brokers, wholesalers and retailers. In India, linking and convergence in the SC between the different players play a very important role in making the entire SC productive and competitive. But there is a shortage of forwarding and backward alignment between the farmers and other stakeholders in the SC of the Agri-food sector in India. Higher amounts of food processing is resulting in low fruit and vegetable wastage. The agri-food SC requires a massive transportation system to ship the processed food at the minimum time to different destinations. However, as compared to other countries, food processing in India is very weak and has a huge scope for improvement.

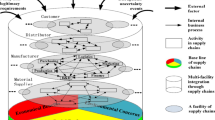
To show the efficacy of the developed model of Agri-food SCN, a numerical instance is selected with multiple producers, agent/brokers, wholesalers, and retailers respectively. We took an examples to model and optimize a problem for the Agri-food SCN with some imprecise data taken into account which is represented by the interval type-2 triangular fuzzy numbers. Based on the availability of some past research, we transformed the deterministic data into uncertainty and represented it with interval type-2 triangular fuzzy numbers. An Agri-food SCN consists of multiple producers, agent/brokers, wholesalers, and retailers, in different geographical regions or locations. In this problem, we have considered a multi-staged Agri-food SCN scenario in which a logistics company is dealing with the transportation of products from multiple producers to multiple retailers. It is assumed that five different producers are shipping the products to four different agent/brokers. Once the product reaches to agents/brokers, they deal with the further shipment of the products either to the six different wholesalers or directly to the eight different retailers. The left product at the agents/brokers is shipped to the different wholesalers and then according to the demand shipped to the different retailers. Figure 1 demonstrates a complex Agri-food SCN comprising multiple producers, agents/brokers, wholesalers and retailers. The related transportation costs and delivery time are provided for each potential route for various stages in Table 2, 3, 4, 5, 6, 7 and 8 respectively.

Fig. 1

Agri-food supply chain

Table 2 The fuzzy shipping cost of a single unit from different supply sources to different agent/brokers

Table 3 The fuzzy shipping cost of a single unit from different agents/brokers to a different retailer

Table 4 The fuzzy shipping cost of a single unit from different agents/brokers to different wholesalers

Table 5 The fuzzy shipping cost of a single unit from different wholesalers to different retailers

Table 6 The fuzzy delivery time of a single unit from the different agent/brokers to different retailers

Table 7 Fuzzy delivery time of single unit from different agent/brokers to different wholesalers

Table 8 The fuzzy delivery time of a single unit from a different wholesaler to different retailers

Let us assume a scenario in which characteristics of demand and supply are known for more than one state. Distribution centers are confronted every time with the challenge of assessing their consumers' demand. If the projected needs for distribution centers are less than those of their customers, their profit will be affected. Due to this, there will be a marginal loss because of not matching the rate of surplus demand. On the other hand, the manufacturer must constantly know how much a product it has to supply to distribution centres, in order to get rid of its losses in a worse market condition. The data in Table 9 do not expressly state how many units the producer should produce to fulfil the random demand in order to optimize its profit for future supply. In addition, the information given in Table 10 does not directly notify retailers of the number of units that they need to optimize their profit every single time. Since the DM's demand and supply patterns are partially based on more than one demand and supply points, demand and supply can be treated as a random variable in order to compute the predicted demand/supply value using a variety of probability distributions.

Table 9 Supply volume of the producers (‘000 units)

Table 10 Demand from the retailers(‘000 units)

Deterministic values of the Right Hand Side (RHS) of constraints have been obtained by using the chance-constrained programming approach as defined in the above section. We suppose that supply and demand parameters follow a Gamma distribution with a given degree of probability. We have also used a MLE approach for obtaining the shape, and scale parameters of the random variables and calculated values are given in Table 11.

Table 11 Estimated values of parameters with a specified probability level

In this study, we considered a scenario where there is no fixed or known value for the parameters of the MOAFSCN problem, but somehow, we know the range of the parameters. By using the above information, the problem can be formulated as a MOAFSCN. In order to overcome the uncertainty condition, we considered that the parameters of supply and demand of the constraints followed a Gamma distribution and maximum likelihood estimation approach has been used for getting the desired value of shape and scale parameter at a specified probability level. Using an optimization software LINGO 16.0, on a PC Core i3 2.50-GHz processor, the formulated problem has been solved after converting the probabilistic and fuzzy parameters into deterministic ones. LINGO 16.0 is the most well-known software used for solving the mathematical programming problems. The best feature of LINGO 16.0 is that it tells the decision maker about the feasibility of the model formulated. In our case, the model formulated with uncertainty is found to be feasible for the both the objective functions and after that we have checked the feasibility of the model formulated using the value function approach and $\epsilon$ constraint approach, respectively. LINGO 16.0 software solved the multi-objective problem formulated for both the value function approach and $\epsilon$ constraint approach in 81 and 104 iterations, and within a time duration of 0.461 s and 0.583 s respectively. For the given data, the MOAFSCN proposed model (Eqs. 1 to 31) is solved and the results are evaluated. Table 12 shows the optimized value of the transportation cost and delivery time along with the amount of product to be shipped from different sources to different agent/brokers; the amount of products to be shipped from different agent/brokers to different wholesalers; the amount of products to be shipped from different agents/brokers to different retailers and; the amount of products to be shipped from different wholesalers to different retailers. Figure 2 gives graphical presentation of results.

Table 12 Obtained results

Fig. 2

Graphical presentation of obtained result

For solving the formulated problem of SCN, in this study, authors have used different types of optimization approaches namely, value function approach, and $\epsilon -$ Constraint approach, and respectively compared the results with a simple additive approach, weighted additive approach and pre-emptive approach. Using the imprecise information as given in Tables 2, 3, 4, 5, 6, 7, 8, 9, and 10, and also after obtaining the crisp value of the demand and supply parameter as defined in Table 6, we obtain the final compromise solution of the MOAFSCN problem. Among all the used optimization approaches, we have found that the value function approach optimizes the formulated problem more efficiently as compared to other approaches. Relative comparison is presented in the Fig. 2. The solution to the MOAFSCN problem involves four stages of transportation. In the first stage, goods are transported from various producers to different agents/brokers. The agreed-upon allocation of shipments includes 178,000 units from producer(1) to agent/broker(4), 276,000 units from producer(2) to agent/broker(2), 70,000 units from producer(2) to agent/broker(4), 197,000 units from producer(3) to agent/broker(2), and 98,000 units from producer(4) to agent/broker(2).

In the second stage, goods are transported from the agents/brokers to different wholesalers. The agreed-upon allocation of shipments includes 52,000 units from agent/broker(2) to wholesaler(3), 188,000 units from agent/broker(4) to wholesaler(4), and 177,000 units from agent/broker(2) to wholesaler(2).

In the third stage, goods are transported from the agents/brokers to different retailers. The agreed-upon allocation of shipments includes 87,000 units from agent/broker(2) to retailer(3), 62,000 units from agent/broker(2) to retailer(5), and 95,000 units from agent/broker(2) to retailer(6).

In the fourth and final stage, goods are transported from the wholesalers to different retailers. The agreed-upon allocation of shipments includes 93,000 units from wholesaler(2) to retailer(1), 93,000 units from wholesaler(2) to retailer(1), 67,000 units from wholesaler(2) to retailer(4), 17,000 units from wholesaler(2) to retailer(8), 52,000 units from wholesaler(3) to retailer(2), 16,000 units from wholesaler(4) to retailer(6), 109,000 units from wholesaler(4) to retailer(7), and 63,000 units from wholesaler(4) to retailer(8).

The solution to the MOAFSCN problem, which involves the efficient allocation of shipments in the different stages of the SC, is crucial in the agri-food SCN. Efficient allocation of shipments in the agri-food SCN is critical to ensure that food products reach their intended destinations in a timely and cost-effective manner. Inefficient allocation of shipments can result in product waste, delay in delivery, and increased transportation costs, which can have adverse effects on the overall SC performance. Effective allocation of shipments in the agri-food SCN requires collaboration and coordination among the different stakeholders involved in the SC. It also involves the use of advanced technologies such as transportation management systems, inventory management systems, and SC analytics to optimize the allocation of shipments and improve SC efficiency.

In order to compare the proposed methodology with fuzzy goal programming, weighted fuzzy goal programming and pre-emptive fuzzy goal programming approaches, the demand and supply units have been kept constant, and the obtained result are given in Table 13. The compromise values of the first objective function (Z₁) and the second objective function (Z₂) are changes with the change in the methodology. The delivery time of the model remains almost the same for all the methodology but increases minorly with the use weighted fuzzy goal programming approach. The best value (minimum) for the first and second objective function is attained by the value function approach. This trend is observed as other presented techniques give more preference to the membership functions of objective function and less significance to feasibility degree. Figure 2 represents the change in the values of objective functions by using different methodologies presented in this study along with the fuzzy goal programming, weighted fuzzy goal programming and pre-emptive fuzzy goal programming approaches. Compared to other methods, the benefit of using the value function and ${\varvec{\epsilon}}$—constraint approach is that they significantly reduces the possibility of an infeasible solution. Although far from a panacea, the value function and ${\varvec{\epsilon}}$—constraint approach often represents a substantial improvement in the modelling and analysis of the real-life situation for a bi-criterion problems. The value function and ${\varvec{\epsilon}}$—constraint approach are not similar to the fuzzy goal programming, weighted fuzzy goal programming and pre-emptive fuzzy goal programming approach in the sense that they all use scalarization technique that uses the combination of multiple objectives into one function.

Table 13 Comparison of results

To demonstrate the impact of quantity on the numerical solution, we performed ten additional experiments by varying the demand and supply units. For each experiment, we held all certain and uncertain parameters constant, except for the change in quantity. We generated ten new compromise solutions for each experiment using the same methodology as the original problem. The results in Fig. 3 indicate that changing the quantity significantly affects transportation cost and delivery time due to the reallocation of units from one source to another destination. The uncertain change in the quantity of agri-food products can have a significant impact on the SC, particularly in terms of transportation cost and delivery time. As the demand for certain products fluctuates, it can create a mismatch between supply and demand, leading to an increase in transportation costs and delays in delivery. For instance, if the demand for a particular product suddenly increases, farmers may struggle to produce enough to meet the demand, resulting in delays in delivery and higher transportation costs as farmers transport their goods to the market. On the other hand, if the demand suddenly decreases, farmers may be left with excess stock, leading to wastage and financial losses. Therefore, it is essential for the Agri-food SCN to have proper planning and management strategies in place to minimize the impact of uncertain changes in quantity on transportation cost and delivery time.

Fig. 3

Sensitivity of result

5 Conclusions, limitations and future scope

The management of AFSCN poses significant challenges due to the unique nature of agricultural products, seasonality, and specific transportation and storage requirements (Yadav et al. 2021). These challenges are compounded by the constant threat of risks from various sources, including demand fluctuations, supply chain disruptions, production uncertainties, and planning complexities. In this study, we tackled the Multi-Objective Allocation Problem in AFSCN with fuzzy and probabilistic parameters. We employed the value function and ε-constraint approach to optimize decision-making in this intricate environment, with a primary focus on minimizing shipping costs and delivery times. The results obtained from our proposed model outperformed existing approaches, offering a promising avenue for enhancing the efficiency and competitiveness of AFSCN.

However, this study has its limitations. One notable constraint is that our model solely addresses fuzziness and probabilistic uncertainties, while real-world scenarios may involve multi-choice decision-making. Therefore, it is advisable to subject our fuzzy and probabilistic model to comprehensive testing in a true-life setting, where multiple decision alternatives are present. Additionally, future research should involve a comparative analysis of various approaches to address this problem. As cost control and efficient delivery times are crucial in today's competitive environment, the implications of this study can serve as a valuable policy framework for supply chain managers, enabling them to make more cost-effective and timely decisions. To further validate our proposed model, it should be applied to supply chain networks in other industries. Looking ahead, researchers may explore more complex probability distributions, multi-choice parameters, and the integration of intuitionistic fuzzy set theory, thereby expanding the scope of research in the field of Agri-food Supply Chain Management.