Introduction

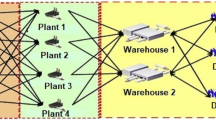
The supply chain (SC) is nowadays considered to be a significant driving factor in gaining a competitive advantage in turbulent markets. Nevertheless, its efficiency and effectiveness being threatened by various sources of uncertainty, which may originate from the demand side, supply side, manufacturing process and planning and control systems. SC consisting of a distribution network of the product, i.e., moving of a raw-material from suppliers to manufacturers, manufacturers to distributors, distributors to retailers and retailers to customers. The manufacturer receives raw material from the suppliers, and after processing it into a finished good, it is supplied to different warehouses and retailers to mark them smoothly reachable to the trades. Moreover, SC includes two main inter-related processes of (1) production planning and inventory control that deals with production, storage, and the relation between them, and (2) logistics and distribution that determine how to transport products to customers and to recycle them [1]. In the twentieth century, the SC has been gaining importance due to globalisation in the market which increased competition between the companies. Most of the companies are obliged to maintain high customer services levels while at the same time they are trying to reduce transportation cost and maintain firms/companies profit margins. Traditionally planning, purchasing, manufacturing, marketing and distribution organisations along the SC operate independently. These bodies have their specific intents, and these are often contradictory but, there is a need for an approach through which these different functions can be combined; SC is a strategy through which such incorporation can be attained. The combination of production and distribution environments is considered to be the vital part of supply chain network (SCN) [2]. To integrate such environments, we consider a multi-product echelon system with the main aim of minimizing the production cost, inventory cost, transportation cost and delivery time. This problem includes transporting products from plant facilities to the warehouse and transporting them from warehouse to retailers.

The major objective of this research is to present a fuzzy multi-objective production–distribution model with multiple products while having multiple plants and multiple warehouses. The present paper studies a special class SC consisting of minimising production cost, inventory holding cost and delivery time of a product. Here the main goal of the DM is to discover how many units of the product from start to the endpoint should be distributed so that all the produced quantity are fully used, and all the demand points are fully satisfied in such a way that the warehouse utilised fully along with initial stock available in it. Since in real-world problems, the possible values of coefficients of transportation cost, production cost, inventory holding cost, shipping time, total budget and demand are often vaguely known to the DM. Due to unknown market conditions and fluctuations, these costs, budget and demand are considered as fuzzy and are represented in terms of low, moderate, high and extremely high uncertainties respectively. Here, the parameters are represented by a trapezoidal fuzzy number and are transformed into deterministic form through graded mean integration representation method. An EFGP model has been presented in this paper that is useful in determining the quantity, shipment cost and inventory of products when parameters are not known with certainty.

The rest of the manuscript is structured as follows: a brief literature review on the production–distribution problem (PDP) is given in Sect. 2. In Sect. 3, mathematical formulation of the problem with fuzzy coefficient along with its assumptions, the indices, the parameters, and the decision variables are defined. Section 4 presents the proposed EFGP model for the problem. In Sect. 5, stepwise step algorithm of the proposed approach has been given. A mathematical example has been providing in Sect. 6 to show the competence of the presented method. Finally, in Sects. 7 conclusions are discussed based on the solutions obtained from numerical examples.

Literature Review

In this section, we have selected most relevant researchers on PDP. In recent years, academicians and practitioners have been given serious focusing on multi-objective problems which consist of PDP. There have been various articles in academic journals discussing the use of mathematical programming in PDP. It includes Martin et al. [3], Chen and Wang [4], Oh and Karimi [5] considered PDP for the multi-national glass industry, steel industry, and chemical industry and formulated it as a linear programming problem (LPP) with inventory operations. Later, Kanyalkar and Adil [6] presented PDP for a multi-product environment. Ryu et al. [7], Bredstrom and Ronnqvist [8] presented two models separately for production planning and distribution planning where they also considered multi-product environment. In the same way, Sarrafha et al. [1] extend his work by considering bi-objective mixed integer non-linear model for PDP where they have considered network from supplier to retailer. Goetschalckx et al. [9] gave a new dimension by formulating two mixed integers linear programming (MILP) models consisting of the design phase of SC and PDP with inventory and transport planning. Sabri and Beamon [10] developed an SCN model that incorporates production, delivery, and demand and trying to reduce the complication via realistic interpretations. Rizk et al. [11] formulated a MILP model for PDP consisting of single manufacture and several supply centres. Jung et al. [12] compared two linear programming problem (LPP) models based on centralised and decentralised production and transport planning system. Park [13] suggested MILP model of transportation and production cost for an environment which consists of multi-site with multi-retailer. Gen and Syarif [2] developed a genetic algorithm to minimize the system cost in such a way that the produced product in the plant should be distributed to right customers without delay in transportation. Huang et al. [14] identified the decisions made about selecting production, storage and distribution locations, and they also considered subcontracting part of production to minimize SCN costs. At the strategic level, they have acknowledged some aspects related to production level, distribution planning, transport capabilities, and managing safety inventories. Haq et al. [15] suggested a MILP model reduce the overall cost of the SCN. Their PDP model was a combination of production cost, inventory cost and transportation cost to determine the optimal production and distribution as well as inventory level. Gupta et al. [16] formulated a transportation problem under certain and uncertain environment. They used fuzziness, multi-choices and randomness for the presentation of uncertainty in the formulated transportation problem and efficiently used fuzzy goal programming approach for getting the optimal shipment.

The works referred so far for solving the PDP assume that the parameters of the problem are known precisely. However, there may be a situation when some vagueness present in the model in a precise manner. It includes, Jindal et al. [17] proposed fuzzy MILP-SCN for maximizing the profit of the whole system in an ambiguous environment. They considered a situation of multi-product with some capacitated restrictions on the network. The main aim of their model is to decide the optimal distribution of products at each source, quantity of products to be refurnished again, and amount of product to take on board from an external vendor. Selim et al. [18] developed a multi-objective linear programming model to collaborate PDP in SCN. A fuzzy goal programming (FGP) approach was considered to achieve DM imprecise aspiration levels. Chen and Lee [19] formulated mixed-integer nonlinear programming (MINLP) model for a multi-stage PDP with vagueness in demands and product prices. Aliev et al. [20] presented fully fuzzy LPP model for PDP and considered uncertainties in both the objective function and the decision variables respectively. Tang et al. [21] formulated a novel model for PDP which is a combination of quadratic and linear programming problem. The main aim of their proposed work is to minimize the total cost of the system including inventory holding cost with vague demands and supplies. Bilgen [22] presented a model formulation for assignments of products to production lines which integrate the production and distribution plans by considering vagueness in the available costs. He implements his proposed approach in the consumer goods industry consisting of multiple manufacturers, multiple production lines and multiple distributions. Also, Sel and Bilgen [23] formulated MILP model for a PDP and considered a case study of soft drink industry for the illustration of their proposed work. Their proposed work considers the formulation of single objective function which includes production cost, minor and major setup cost, transportation cost, inventory and backorder cost. Jamalnia and Soukhakian [24] formulated fuzzy multi-objective non-linear programming (MONLP) model for PDP in a qualitative and quantitative environment. They proposed a quantitative objective function optimizing the total production costs, costs of changes in workforce levels, transportation and back ordering costs, and a qualitative objective function optimizing the total customer pleasure. Two objectives are optimized regarding the inventory level, demand, labour level, machines capacity and warehouse space. Roghanian et al. [25] constructed bi-level stochastic model for PDP with multi-levels. The formulated stochastic model is first transformed into the deterministic form using the chance-constrained technique, and then fuzzy programming techniques are applied to get the compromise solution. Liang [26] presented MOPDP in a fuzzy environment and the main aim of the presented model is to minimize the total production and transportation costs, a total number of rejected items and total delivery time with subject to available production capacities, allocation flexibility and budget constraints at each source, as well as forecast demand and warehouse space at each destination. Liang and Cheng [27] applied fuzzy sets theory to integrate manufacturer decision making in distribution planning under uncertain environment. To do so, a fuzzy multi-objective linear programming model was developed to simultaneously minimize the total costs and total delivery time in an SC with reference to inventory levels, available machine capacity and labour levels at each source, as well as market demand and available warehouse space at each destination. They used a well-known FGP approach given by Hannan [28] to solve the constructed mathematical model. Gholamian et al. [29] formulated fuzzy multi-objective MINLP model to address a comprehensive multi-site, multi-period and multi-product PDP under uncertainty. Garai et al. [30] adopted the concept of intuitionistic fuzzy set theory for presenting the uncertainty in PDP and used T-sets optimization technique for solving the formulated problem. Peidro et al. [31] considered a real case study of multi-product manufacturer automobile industry and formulated PDP as a fuzzy linear programming model to integrate planning activities into a system. The relevant literature related to the work done in this paper is summarised in a tabular form in Table 1.

Table 1 Shared process information of the reviewed works
Full size table

Before formulating the problem of interest, we have noticed that all the models that have been formulated for production–distribution and modelled under different scenarios. From the Table 1, we have seen that almost authors considered production cost, transportation cost and inventory cost in their formulated models. Whereas Sarrafha et al. [1], Goetschalckx et al. [9], Peidro et al. [31], and Latpate and Bajaj [32] have considered the delivery time taken into account in their modelling, which is also the most influential factor of production–distribution. We have also noticed that almost authors formulated production–distribution problem with deterministic parameters. Motivated by such studies, we have formulated the multi-objective optimization model for production–distribution problem under fuzziness environment, which is an extended model of Latpate and Bajaj [32].

We have considered multiple products, multiple plants and multiple warehouses with some modification in the objective functions and constraints under fuzzy environment. An efficient solution procedure of fuzzy goal programming has developed for obtaining the compromise solution for the model.

Mathematical Model of MOPDP

Production–distribution planning is the most important measure in SCN. To solve this integrated PDP, we have considered an SCN with some suppliers, plants, distribution centres, warehouses and retailers in fixed locations. In SCN of this study, the used raw materials of products are supplied from suppliers to plants, and various products produced by each plant if produced in the related period, are transferred to various distributors. Here, a distributor can be understood as a logistics warehouse delivering finished products from a plant to a retailer. In this research, the allocation between distribution centres to retailers is considered to obtain the suitable amount of quantity to be distributed. The problem is to meet the production and distribution requirements at minimum costs of production, distribution and inventory, subject to various resource constraints. Minimization of total shipping cost, inventory holding cost and delivery time of products to retailers, are the objective functions of the model. We take on that minimizing delivery times between the shipments may lead to a decrease in the total cost of the network. The assumptions, notations and mathematical formulation for this SCN are presented below:

Nomenclature

Indices

\( i \)—index of the product, \( \left\{ {i = 1,2, \ldots ,I} \right\} \)

\( j \)—index of the plant, \( \left\{ {j = 1,2, \ldots ,J} \right\} \)

\( l \)—index of the customer, \( \left\{ {l = 1,2, \ldots ,L} \right\} \)

Parameters

\( V_{ij} \)—Plant warehouse space required for product i in plant j

\( U_{j} \)—Maximum plant warehouse space available for product j

\( B \)—Total Budget

\( d_{il} \)—Demand for the product i from customer l

\( P_{ij} \)—Per unit production cost for product i at plant j

\( I_{ij} \)—Per unit inventory holding cost for product i at plant j

\( S_{ijl} \)—Per unit shipping cost of product i from plant j to customer l

\( T_{ijl} \)—Per unit delivery time of product i from plant j to customer l

\( W_{ij} \)—Initial inventory of a product i at plant j

Decision variable

\( q_{ij} \)—Amount of product i produced at plant j

\( y_{ij} \)—Inventory of a product i at plant j

\( a_{ijl} \)—The amount of product i shipped from plant j to customer l.

The modified model with objective functions and constraints are formulated as follows:

The objective function (1) that minimizes production and inventory cost of PDP is given by

$$ Min\,Z_{1} = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {P_{ij} q_{ij} + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {I_{ij} y_{ij} } } } } $$
(1)

The objective function (2) that minimizes the delivery time of PDP is given by

$$ Min\,Z_{2} = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {T_{ijl} a_{ijl} } } } $$
(2)

The objective function (3) that minimizes shipping cost of PDP is given by

$$ Min\,Z_{3} = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {S_{ijl} a_{ijl} } } } $$
(3)

Subject to constraint

$$ W_{ij} + q_{ij} - \sum\limits_{l = 1}^{L} {a_{ijl} = y_{ij} } ,\quad \forall i,j $$
(4)

Constraint Eq. (4) puts restrictions on inventory balance that assures the supply of an item, at each plant is either held in inventory or shipped to a customer to meet demand.

$$ \sum\limits_{j = 1}^{J} {a_{ijl} = d_{il} ,\quad } \forall i,l $$
(5)

Constraint Eq. (5) puts restrictions on total demand from the customer.

$$ \sum\limits_{i = 1}^{I} {V_{ij} y_{ij} = U_{j} ,\quad \forall i} $$
(6)

Constraint Eq. (6) puts restrictions on godown space availability.

$$ \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {P_{ij} q_{ij} + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {I_{ij} y_{ij} } } } } + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {S_{ijl} a_{ijl} } } } \le B,\quad \forall i,j,l $$
(7)

Constraint Eq. (7) puts restrictions on a total available budget.

$$ q_{ij} ,y_{ij} ,a_{ijl} \ge 0\quad \forall i,j,l $$
(8)

Constraint Eqs. (8) enforce the non-negativity restriction on the decision variables.

In the above-discussed MOPDP, the input parameters are expected to take deterministic or known values, but in most of the real-world circumstances these may take vague value for some probable reasons as listed below:

  • The production cost of an item may vary due to change in the cost of raw-materials, unexpected labour charges, sudden break down of the machines, use of more generators and soon.

  • The cost of shipping one unit from plants to customers may vary from the predetermined shipping cost.

  • Time is taken for transporting the units also varies from the predetermined time.

  • Total budget allocated for the production distribution may change as the shipping cost, and holding cost varies.

Such vagueness in the critical information cannot be captured in a deterministic problem. Thus the optimal results obtained from this deterministic formulation may not serve the real purpose of modelling the problem. Due to this, we have considered the model with imprecise information. In light of the above-discussed possible situations in MOPDP, the fuzzy formulation of the problem by replacing the deterministic parameter \( P_{ij} ,S_{ijl} ,T_{ijl} ,I_{ij} \,\,\& \,\,B \) of the stated problem with fuzzy numbers is conventionally expressed as

Model (1)

$$ \begin{aligned} & Min\,Z_{k} = \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\tilde{P}_{ij} q_{ij} + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\tilde{I}_{ij} y_{ij} } } } } ,\sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {\tilde{T}_{ijl} a_{ijl} } } } ,\sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {\tilde{S}_{ijl} a_{ijl} } } } ,\quad k = 1,2,3 \\ & {\text{subject}}\,{\text{to}}\,{\text{constraint}} \\ & W_{ij} + q_{ij} - \sum\limits_{l = 1}^{L} {a_{ijl} = y_{ij} } ,\quad \forall i,j \\ & \sum\limits_{j = 1}^{J} {a_{ijl} = d_{il} ,} \quad \forall i,l \\ & \sum\limits_{i = 1}^{I} {V_{ij} y_{ij} = U_{j} ,\quad \forall i} \\ & \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\tilde{P}_{ij} q_{ij} + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\tilde{I}_{ij} y_{ij} } } } } + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {\tilde{S}_{ijl} a_{ijl} } } } \le \tilde{B},\quad \forall i,j,l \\ & q_{ij} ,y_{ij} ,a_{ijl} \ge 0\quad \forall i,j,l\,\& \,k = 1,2,3 \\ \end{aligned} $$

Where all the fuzzy parameter in Problem (1) are considered as the trapezoidal fuzzy number, and it can be transformed into crisp form by using the ranking function given by Vahidi & Rezvani [33]. The problem can be re-written as:

Model (2)

$$ \begin{aligned} & Min\,Z_{k} = \left( \begin{aligned} & \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\left( {\frac{{{}^{m}P_{ij} + 2{}^{n}P_{ij} + 2{}^{\alpha }P_{ij} + {}^{\beta }P_{ij} }}{6}} \right)q_{ij} } } + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\left( {\frac{{{}^{m}I_{ij} + 2{}^{n}I_{ij} + 2{}^{\alpha }I_{ij} + {}^{\beta }I_{ij} }}{6}} \right)y_{ij} ,} } \\ & \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {\left( {\frac{{{}^{m}T_{ijl} + 2{}^{n}T_{ijl} + 2{}^{\alpha }T_{ijl} + {}^{\beta }T_{ijl} }}{6}} \right)a_{ijl} } } } ,\sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {\left( {\frac{{{}^{m}S_{ijl} + 2{}^{n}S_{ijl} + 2{}^{\alpha }S_{ijl} + {}^{\beta }S_{ijl} }}{6}} \right)a_{ijl} } } } \\ \end{aligned} \right) \\ & {\text{subject}}\,{\text{to}}\,{\text{constraint}} \\ & W_{ij} + q_{ij} - \sum\limits_{l = 1}^{L} {a_{ijl} = y_{ij} } ,\quad \forall i,j \\ & \sum\limits_{j = 1}^{J} {a_{ijl} = d_{il} ,\quad } \forall i,l \\ & \sum\limits_{i = 1}^{I} {V_{ij} y_{ij} = U_{j} ,\quad \forall i} \\ & \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\left( {\frac{{{}^{m}P_{ij} + 2{}^{n}P_{ij} + 2{}^{\alpha }P_{ij} + {}^{\beta }P_{ij} }}{6}} \right)q_{ij} } } + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\left( {\frac{{{}^{m}I_{ij} + 2{}^{n}I_{ij} + 2{}^{\alpha }I_{ij} + {}^{\beta }I_{ij} }}{6}} \right)y_{ij} } } \\ & \quad + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {\left( {\frac{{{}^{m}S_{ijl} + 2{}^{n}S_{ijl} + 2{}^{\alpha }S_{ijl} + {}^{\beta }S_{ijl} }}{6}} \right)a_{ijl} } } } \le \left( {\frac{{{}^{m}B + 2{}^{n}B + 2{}^{\alpha }B + {}^{\beta }B}}{6}} \right)\quad \forall i,j,l \\ & \quad \quad q_{ij} ,y_{ij} ,a_{ijl} \ge 0\quad \forall i,j,l \\ \end{aligned} $$

Optimization Method for MOPDP: Proposed Approach

Fuzzy programming, goal programming and interactive programming is a powerful and flexible technique that can apply to a variety of decision-making problems involving multiple objectives. Several contributions have reported in the literature on goal programming, fuzzy programming, and interactive programming approach [34,35,36,37,38,39,40]. In all these literature an efficient methodology is developed for solving multi-objective programming problems by employing the FGP approach. Singh et al. [39] developed a fuzzy efficient interactive goal programming approach by extending the goal programming approach given by Waeil and Lee [40] for solving the multi-objective transportation problem. Motivated by such studies and after doing some manipulations in FGP approach, the proposed approach can be stated as with linear membership function \( \mu_{k} (Z_{k} (X)) \) [40] for the kth objective function as follows:

For the fuzzy-min, the linear membership function is defined as:

$$ \mu_{k} (Z_{k} (X)) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {if\,\,Z_{k} (X) \le l_{k} } \hfill \\ {\frac{{U_{k} - Z_{k} (X)}}{{U_{k} - l_{k} }},} \hfill & {if\,\,l_{k} \le Z_{k} (X) \le U_{k} } \hfill \\ {0,} \hfill & {if\,\,Z_{k} (X) \ge U_{k} } \hfill \\ \end{array} } \right. $$
(9)

For the fuzzy-max, the linear membership function is defined as

$$ \mu_{k} (Z_{k} (X)) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {if\,\,Z_{k} (X) \le l_{k} } \hfill \\ {\frac{{Z_{k} (X) - l_{k} }}{{U_{k} - l_{k} }},} \hfill & {if\,\,l_{k} \le Z_{k} (X) \le U_{k} } \hfill \\ {0,} \hfill & {if\,\,Z_{k} (X) \ge U_{k} } \hfill \\ \end{array} } \right. $$
(10)

where \( U_{k} \,\& \,\,\,l_{k} \) is the upper and lower tolerance limit of the objective function. The general aggregation function \( \mu_{D} :S \to [0,1] \) can be defined as

$$ \mu_{D} (X) = \mu_{D} \{ \mu_{1} (Z_{1} (X)),\mu_{2} (Z_{2} (X)),\mu_{3} (Z_{3} (X)), \ldots ,\mu_{K} (Z_{K} (X))\} $$
(11)

Once the decision vector D is known, we define \( X^{*} \in S \) to be an optimal decision if \( \mu_{D} (X^{*} ) = \hbox{max} \,\,\mu_{D} (X)\,\,\,\forall X \in S \). Another possibility could be to choose a \( \lambda_{k} \in [0,1] \) and determine all point \( x^{*} \in S \) for which \( \mu_{D} (X^{*} ) \ge \lambda . \) This decision \( X^{*} \) will have at least one lambda degree of membership grades. Following the fuzzy decision together with linear membership function, a fuzzy optimization model of MOPDP can be written as:

$$ \begin{aligned} & Max\,Min\,\mu_{k} (Z_{k} (X)),\quad k = 1,2, \ldots ,K \\ & {\text{subject}}\,{\text{to}}\,{\text{constraint}} \\ & W_{ij} + q_{ij} - \sum\limits_{l = 1}^{L} {a_{ijl} = y_{ij} } ,\quad \forall i,j \\ & \sum\limits_{j = 1}^{J} {a_{ijl} = d_{il} ,} \quad \forall i,l \\ & \sum\limits_{i = 1}^{I} {V_{ij} y_{ij} = U_{j} ,\quad \forall i} \\ & \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\tilde{P}_{ij} q_{ij} + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\tilde{I}_{ij} y_{ij} } } } } + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {\tilde{S}_{ijl} a_{ijl} } } } \le \tilde{B},\quad \forall i,j,l \\ & \quad \quad q_{ij} ,y_{ij} ,a_{ijl} \ge 0\quad \forall i,j,l \\ \end{aligned} $$

By introducing an auxiliary variable for each objective functions \( \lambda_{k} \), the above problem can be re-stated as:

$$ \begin{aligned} & Max\,\lambda_{k} ,\quad k = 1,2, \ldots ,K \\ & {\text{subject}}\,{\text{to}}\,{\text{constraint}} \\ & \lambda_{k} \le \mu_{k} (Z_{k} (X)),\quad k = 1,2,3 \\ & W_{ij} + q_{ij} - \sum\limits_{l = 1}^{L} {a_{ijl} = y_{ij} } ,\quad \forall i,j \\ & \sum\limits_{j = 1}^{J} {a_{ijl} = d_{il} ,} \quad \forall i,l \\ & \sum\limits_{i = 1}^{I} {V_{ij} y_{ij} = U_{j} ,\quad \forall i} \\ & \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\tilde{P}_{ij} q_{ij} + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\tilde{I}_{ij} y_{ij} } } } } + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {\tilde{S}_{ijl} a_{ijl} } } } \le \tilde{B},\quad \forall i,j,l \\ & \quad \quad q_{ij} ,y_{ij} ,a_{ijl} \ge 0\quad \forall i,j,l \\ \end{aligned} $$

In the above formulation, constraints \( \lambda_{k} \le \mu_{k} (Z_{k} (X)) \) can be reduced to the following form:

$$ \lambda_{k} (U_{k} - L_{K} ) + Z_{k} (X) \le U_{k} ,\quad k = 1,2, \ldots ,K $$
(12)

In many situations, a DM may not be able to determine precisely the relative importance of the goals, i.e., they minimize undesired deviations from target values. The elementary approach for EFGP is to set up a precise goal \( g_{k} \) for each \( Z_{k} (X),\,\,k = 1,2, \ldots ,K \); then the total deviation from the quantified goals \( \sum\nolimits_{k = 1}^{K} {|d_{k} |} \) is to be minimized, where \( d_{k} \) is the deviation from the set numeric goal \( g_{k} \). For formulating the absolute values, \( d_{k} \) can split into positive and negative parts such that \( |d_{k} | = d_{k}^{ + } - d_{k}^{ - } \), with \( d_{k}^{ + } \ge 0 \) and \( d_{k}^{ + } ,d_{k}^{ - } = 0 \). These negative deviations \( d_{k}^{ - } \) are known as underachievement and positive deviation \( d_{k}^{ + } \) are known as over-achievement from the goal respectively. For, EFGP model let us introduce the positive and negative deviations \( d_{k}^{ + } \) and \( d_{k}^{ - } \) respectively to the above problem, as follows:

$$ (Z_{k} (x) - g_{k} )w_{k} - (U_{k} - g_{k} )d_{k}^{ + } + (U_{k} - g_{k} )d_{k}^{ - } = 0,\quad k = 1,2, \ldots ,K $$
(13)

Using Eqs. (9)–(13), the FEGP model for MOPDP can be formulated as:

$$ \begin{aligned} & Max\,\,\,w_{k} \lambda_{k} ,\,\,\,\,k = 1,2, \ldots ,K \\ & {\text{subject}}\,{\text{to}}\,{\text{constraint}} \\ & \lambda_{k} \le \mu_{k} (Z_{k} (X)),\quad k = 1, \ldots ,s - 1 \\ & \lambda_{k} \le \mu_{k} (Z_{k} (X^{*} )),\quad k = s,s + 1, \ldots ,K \\ & (Z_{k} (X) - g_{k} )w_{k} - d_{k}^{ + } + d_{k}^{ - } = 0,\quad k = 1, \ldots ,s - 1 \\ & (Z_{k} (X^{*} ) - g_{k} )w_{k} - d_{k}^{ + } + d_{k}^{ - } = 0,\quad k = s,s + 1, \ldots ,K \\ & W_{ij} + q_{ij} - \sum\limits_{l = 1}^{L} {a_{ijl} = y_{ij} } ,\quad \forall i,j \\ & \sum\limits_{j = 1}^{J} {a_{ijl} = d_{il} ,} \quad \forall i,l \\ & \sum\limits_{i = 1}^{I} {V_{ij} y_{ij} = U_{j} ,\quad \forall i} \\ & \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\tilde{P}_{ij} q_{ij} + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\tilde{I}_{ij} y_{ij} } } } } + \sum\limits_{i = 1}^{I} {\sum\limits_{j = 1}^{J} {\sum\limits_{l = 1}^{L} {\tilde{S}_{ijl} a_{ijl} } } } \le \tilde{B},\quad \forall i,j,l \\ & \quad \quad q_{ij} ,y_{ij} ,a_{ijl} \ge 0\quad \forall i,j,l \\ \end{aligned} $$

Here, \( w_{k} = \frac{1}{{u_{k} - g_{k} }},\,\,k = 1,2, \ldots ,K \) are the relative weights attached to each objective functions. Where \( k = 1, \ldots ,s - 1 \) are the objective functions for which decision makers are satisfied and \( k = s,s + 1, \ldots ,K \) are the objective functions for which decision makers need improvement.

Model Algorithm

The solution procedure for solving MOPDP is summarised in the following steps:

Step 1 Solve the stated problem as a single objective problem using only one objective at a time and ignoring the other objective functions. The solutions thus obtained are considered to be ideal solutions for the objectives.

Step 2 The ideal solutions of each objective function is then used to calculate the value of all other objectives. Find the goal level for each objective function by calculating the maximum and a minimum value of the kth objective function. Now, we obtain the upper and lower tolerance limits for each objective function, i.e.\( U_{k} = \,Max\,\,(Z_{k} ) \) and \( L_{k} = \,Min\,\,(Z_{k} ) \); k = 1,2,…, K.

Step 3 Set up the linear membership function for the given objective functions as defined in Sect. 5.

Step 4 Construct the fuzzy programming model using the membership function and solve it for the desired allocation.

Step 5 Then the decision maker decides, whether he accepts the solution or not. If not, go to Step 6. Otherwise, go to Step 4.

Step 6 If the DM is moderately happy with the obtained solution and needs perfection or changes in the value of some objective function then replace the upper bound with the new value of objective function respectively. Keep the old one as same it is.

Step 7 Construct another membership function by introducing the deviational variables and add it to the fuzzy programming model and solve it using optimizer software LINGO 16.0. After solving the model, we get the most preferred fuzzy efficient and compromise solution for MOPDP.

Numerical Case Study

Given illustrating the proposed method, we consider the modelling and optimization of production of two types of products at different locations. Let us define the vagueness in shipping cost, inventory holding cost and production cost delivery time and customer demand in the form of the linguistic variable low, moderate, high and extremely high respectively and can be expressed as:

Product-I

Table 2 provides the information of shipping cost from different manufacturer locations to different customer’s locations.

Table 2 Shipping cost
Full size table

Table 3 provides the information of delivery time from different manufacturer locations to different customer’s locations.

Table 3 Delivery time
Full size table

Table 4 provides the information of customer’s demand from various locations.

Table 4 Customer demand
Full size table

Table 5 provides the manufacturer information with inventory holding cost and production cost along with original available stock and space required per product.

Table 5 Manufacturer information
Full size table

Product-II

Table 6 provides the information of shipping cost from different manufacturer locations to different customer’s locations.

Table 6 Shipping cost
Full size table

Table 7 provides the information of delivery time from different manufacturer locations to different customer’s locations.

Table 7 Delivery time
Full size table

Table 8 provides the information of customer’s demand from various locations.

Table 8 Customer demand
Full size table

Table 9 provides the manufacturer information with inventory holding cost and production cost along with original available stock and space required per product.

Table 9 Manufacturer information
Full size table

Table 10 provides the manufacturer information with total available storage space in different locations.

Table 10 Total available storage space
Full size table

The total available imprecise budget for the production–distribution is Rs. (150,000, 250,000, 350,000, 500,000). In Sect. 3, we have prepared our MOPDP model, and some of its parameters are considered to be fuzzy. Value of all the parameters of the formulated MOPDP model is given in Tables 2, 3, 4, 5, 6, 7, 8, 9 and 10. Before formulating the model, we have found out the equivalent crisp form of all the considered fuzzy parameters. After getting all the crisp value of parameters, the formulated MOPDP is given below:

Formulated problem

$$ \begin{aligned} & Min\,Z_{1} = 5.17q_{11} + 4.08q_{12} + 5.00q_{13} + 6.00q_{21} + 8.58q_{22} + 5.00q_{23} \\ & \quad \quad \quad \quad + \,0.65y_{11} + 0.75y_{12} + 0.85y_{13} + 1.03y_{21} + 0.93y_{22} + 1.13y_{23} \\ & Min\,\,Z_{2} = 30.00a_{111} + 49.17a_{112} + 26.67a_{113} + 40.00a_{114} + 29.17a_{121} \\ & \quad \quad \quad \quad + \,38.33a_{122} + 30.00a_{123} + 36.67a_{124} + 39.17a_{131} + 39.17a_{132} \\ &\quad \quad \quad \quad + \,31.67a_{133} + 28.33a_{134} + 25.00a_{211} + 41.67a_{212} + 37.17a_{213} \\ & \quad \quad \quad \quad + \,35.83a_{214} + 33.33a_{221} + 53.33a_{222} + 38.33a_{223} + 57.50a_{224} \\ &\quad \quad \quad \quad + \,37.50a_{231} + 53.33a_{232} + 43.33a_{233} + 24.50a_{234} \\ & Min\,\,Z_{3} = 2.17a_{111} + 3.17a_{112} + 5.42a_{113} + 3.25a_{114} + 2.67a_{121} + 7.00a_{122} \\ & \quad \quad \quad \quad + \,3.00a_{123} + 3.00a_{124} + 3.17a_{131} + 5.83a_{132} + 4.00a_{133} + 2.92a_{134} \\ & \quad \quad \quad \quad + \,3.83a_{211} + 5.00a_{212} + 6.93a_{213} + 3.83a_{214} + 4.00a_{221} + 6.08a_{222} \\ & \quad \quad \quad \quad + \,6.58a_{223} + 7.67a_{224} + 5.00a_{231} + 7.08a_{232} + 8.92a_{233} + 4.83a_{234} \\ & {\text{subject}}\,\,{\text{to}}\,\,{\text{constraint}} \\ & - q_{11} + a_{111} + a_{112} + a_{113} + a_{114} + y_{11} = 10 \\ & - q_{12} + a_{121} + a_{122} + a_{123} + a_{124} + y_{12} = 12 \\ & - q_{13} + a_{131} + a_{132} + a_{133} + a_{134} + y_{13} = 15 \\ & - q_{21} + a_{211} + a_{212} + a_{213} + a_{214} + y_{21} = 15 \\ & - q_{22} + a_{221} + a_{222} + a_{223} + a_{224} + y_{22} = 17 \\ & - q_{23} + a_{231} + a_{232} + a_{233} + a_{234} + y_{23} = 14 \\ & a_{111} + a_{121} + a_{131} = 30.8333 \\ & a_{112} + a_{122} + a_{132} = 30.8333 \\ & a_{113} + a_{123} + a_{133} = 40.0000 \\ & a_{114} + a_{124} + a_{134} = 43.3333 \\ & a_{211} + a_{221} + a_{231} = 29.1667 \\ & a_{212} + a_{222} + a_{232} = 30.8333 \\ & a_{213} + a_{223} + a_{233} = 36.6667 \\ & a_{214} + a_{224} + a_{234} = 45.8333 \\ & 0.3y_{11} + 0.6y_{21} = 5000 \\ & 0.3y_{12} + 0.6y_{22} = 2000 \\ & 0.3y_{13} + 0.6y_{23} = 3000 \\ & 5.17q_{11} + 4.08q_{12} + 5.00q_{13} + 6.00q_{21} + 8.58q_{22} + 5.00q_{23} \\ & \quad + \,0.65y_{11} + 0.75y_{12} + 0.85y_{13} + 1.03y_{21} + 0.93y_{22} + 1.13y_{23} \\ & \quad + \,2.17a_{111} + 3.17a_{112} + 5.42a_{113} + 3.25a_{114} + 2.67a_{121} + 7.00a_{122} \\ & \quad + \,3.00a_{123} + 3.00a_{124} + 3.17a_{131} + 5.83a_{132} + 4.00a_{133} + 2.92a_{134} \\ & \quad + \,3.83a_{211} + 5.00a_{212} + 6.93a_{213} + 3.83a_{214} + 4.00a_{221} + 6.08a_{222} \\ & \quad + \,6.58a_{223} + 7.67a_{224} + 5.00a_{231} + 7.08a_{232} + 8.92a_{233} + 4.83a_{234} \le 308333.3333 \\ \end{aligned} $$

Each objective of the formulated MOPDP is solved separately by using the optimising software LINGO 16.0, the values of the objective function are

$$ \begin{aligned} & Z_{1} (q_{ij}^{1} ,a_{ijl}^{1} ,y_{ij}^{1} ) = 121780.60,\quad Z_{2} (q_{ij}^{1} ,a_{ijl}^{1} ,y_{ij}^{1} ) = 10436.42,\quad Z_{3} (q_{ij}^{1} ,a_{ijl}^{1} ,y_{ij}^{1} ) = 1492.39, \\ & Z_{1} (q_{ij}^{2} ,a_{ijl}^{2} ,y_{ij}^{2} ) = 122433.50,\quad Z_{2} (q_{ij}^{2} ,a_{ijl}^{2} ,y_{ij}^{2} ) = 8875.16,\quad Z_{3} (q_{ij}^{2} ,a_{ijl}^{2} ,y_{ij}^{2} ) = 1382.81, \\ & Z_{1} (q_{ij}^{3} ,a_{ijl}^{3} ,y_{ij}^{3} ) = 122600.10,\quad Z_{2} (q_{ij}^{3} ,a_{ijl}^{3} ,y_{ij}^{3} ) = 9929.94,\quad Z_{3} (q_{ij}^{3} ,a_{ijl}^{3} ,y_{ij}^{3} ) = 1093.84 \\ \end{aligned} $$

The upper and lower bounds of each objective function can be expressed as follows:

$$ 121780.60 \le Z_{1} \le 122600.10,\quad 8875.16 \le Z_{2} \le 10436.42,\quad 1093.84 \le Z_{3} \le 1492.39 $$

The membership function of the objectives functions respectively can be constructed as:

$$ \mu_{1} (Z_{1} (X)) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {if\,\,Z_{1} (X) \le 121780.60} \hfill \\ {\frac{{122600.10 - Z_{1} (X)}}{819.50},} \hfill & {if\,\,121780.60 < Z_{1} (X) < 122600.10} \hfill \\ {0,} \hfill & {if\,\,Z_{1} (X) \ge 122600.10} \hfill \\ \end{array} } \right. $$
$$ \mu_{2} (Z_{2} (X)) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {if\,\,Z_{2} (X) \le 8875.16} \hfill \\ {\frac{{10436.42 - Z_{2} (X)}}{1561.26},} \hfill & {if\,\,8875.16 < Z_{2} (X) < 10436.42} \hfill \\ {0,} \hfill & {if\,\,Z_{2} (X) \ge 10436.42} \hfill \\ \end{array} } \right. $$
$$ \mu_{3} (Z_{3} (X)) = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {if\,\,Z_{3} (X) \le 1093.84} \hfill \\ {\frac{{1492.39 - Z_{3} (X)}}{398.55},} \hfill & {if\,\,1093.84 < Z_{3} (X) < 1492.39} \hfill \\ {0,} \hfill & {if\,\,Z_{3} (X) \ge 1492.39} \hfill \\ \end{array} } \right. $$

By Combining all the membership functions, the above-formulated problem takes the following form:

$$ \begin{aligned} & Max\, = \,\lambda_{1} + \lambda_{2} + \lambda_{3} \\ & {\text{subject}}\,{\text{to}}\,{\text{constraint of formulated problem}} \\ & 5.17q_{11} + 4.08q_{12} + 5.00q_{13} + 6.00q_{21} + 8.58q_{22} + 5.00q_{23} + 0.65y_{11} + 0.75y_{12} \\ & \quad + \,0.85y_{13} + 1.03y_{21} + 0.93y_{22} + 1.13y_{23} \le 122600.10 - 819.50\lambda_{1} \\ & 30.00a_{111} + 49.17a_{112} + 26.67a_{113} + 40.00a_{114} + 29.17a_{121} + 38.33a_{122} + 30.00a_{123} \\ & \quad + \,36.67a_{124} + 39.17a_{131} + 39.17a_{132} + 31.67a_{133} + 28.33a_{134} + 25.00a_{211} + 41.67a_{212} \\ & \quad + \,37.17a_{213} + 35.83a_{214} + 33.33a_{221} + 53.33a_{222} + 38.33a_{223} + 57.50a_{224} + 37.50a_{231} \\ & \quad + \,53.33a_{232} + 43.33a_{233} + 24.50a_{234} \le 10436.42 - 1561.26\lambda_{2} \\ & 2.17a_{111} + 3.17a_{112} + 5.42a_{113} + 3.25a_{114} + 2.67a_{121} + 7.00a_{122} + 3.00a_{123} + 3.00a_{124} \\ & \quad + \,3.17a_{131} + 5.83a_{132} + 4.00a_{133} + 2.92a_{134} + 3.83a_{211} + 5.00a_{212} + 6.93a_{213} + 3.83a_{214} \\ & \quad + \,4.00a_{221} + 6.08a_{222} + 6.58a_{223} + 7.67a_{224} + 5.00a_{231} + 7.08a_{232} + 8.92a_{233} \\ & \quad + \,4.83a_{234} \le 1492.39 - 398.55\lambda_{3} \\ & 0 \le \lambda_{i} \le 1,\,\,\,i = 1,2,3 \\ \end{aligned} $$

The above-formulated problem is solved by using the optimising software LINGO16.0; we have \( Z_{1} = 121926.00, \) with the value of \( \lambda_{1} = 0.8225615 \) that mean, we reach the achievement level of 82%. \( Z_{2} = 9342.56, \) with the value of \( \lambda_{2} = 0.7006289 \) that mean, we reach the achievement level of 70%.\( Z_{3} = 1167.93, \) with the value of \( \lambda_{3} = 0.8141164 \) that mean, we reach the achievement level of 81%.

DM assumes that the second objective function does not minimize efficiently and it further needs more improvement. Again, the upper and lower bounds of each objective function can be expressed as follows:

$$ 121780.60 \le Z_{1} \le 122600.10,\quad 8875.16 \le Z_{2} \le 9342.56,\quad 1093.84 \le Z_{3} \le 1492.39 $$

Based on the modification, the relative weights of the objective functions considered by the decision maker are \( w_{1} = 0.0012 ,\,\,{\text{w}}_{ 2} = 0.0021\,\,{\text{and}}\,\,w_{3} = 0.0025, \) then using (5), the above-formulated problem is developed as follows:

$$ \begin{aligned} & Max\, = \,0.0012\lambda_{1} + 0.0021\lambda_{2} + 0.0025\lambda_{3} \\ & {\text{subject}}\,{\text{to}}\,{\text{constraint}}\,{\text{of formulated}}\,{\text{ problem }} \\ & 5.17q_{11} + 4.08q_{12} + 5.00q_{13} + 6.00q_{21} + 8.58q_{22} + 5.00q_{23} + 0.65y_{11} + 0.75y_{12} \\ & \quad + \,0.85y_{13} + 1.03y_{21} + 0.93y_{22} + 1.13y_{23} \le 122600.10 - 819.50\lambda_{1} \\ & 30.00a_{111} + 49.17a_{112} + 26.67a_{113} + 40.00a_{114} + 29.17a_{121} + 38.33a_{122} + 30.00a_{123} \\ & \quad + \,36.67a_{124} + 39.17a_{131} + 39.17a_{132} + 31.67a_{133} + 28.33a_{134} + 25.00a_{211} \\ & \quad + \,41.67a_{212} + 37.17a_{213} + 35.83a_{214} + 33.33a_{221} + 53.33a_{222} + 38.33a_{223} \\ & \quad + \,57.50a_{224} + 37.50a_{231} + 53.33a_{232} + 43.33a_{233} + 24.50a_{234} \\ & \quad \le \,9342.56 - 467.40\lambda_{2} \\ & 2.17a_{111} + 3.17a_{112} + 5.42a_{113} + 3.25a_{114} + 2.67a_{121} + 7.00a_{122} + 3.00a_{123} + 3.00a_{124} \\ & \quad + \,3.17a_{131} + 5.83a_{132} + 4.00a_{133} + 2.92a_{134} + 3.83a_{211} + 5.00a_{212} + 6.93a_{213} \\ & \quad + \,3.83a_{214} + 4.00a_{221} + 6.08a_{222} + 6.58a_{223} + 7.67a_{224} + 5.00a_{231} + 7.08a_{232} \\ & \quad + \,8.92a_{233} + 4.83a_{234} \le 1492.39 - 398.55\lambda_{3} \\ & (5.17q_{11} + 4.08q_{12} + 5.00q_{13} + 6.00q_{21} + 8.58q_{22} + 5.00q_{23} + 0.65y_{11} + 0.75y_{12} \\ & \quad + \,0.85y_{13} + 1.03y_{21} + 0.93y_{22} + 1.13y_{23} - 121780.60) \times 0.0012 - 819.50d_{1}^{ + } \\ & \quad + \,819.50d_{1}^{ - } = 0 \\ & (30.00a_{111} + 49.17a_{112} + 26.67a_{113} + 40.00a_{114} + 29.17a_{121} + 38.33a_{122} + 30.00a_{123} \\ & \quad + \,36.67a_{124} + 39.17a_{131} + 39.17a_{132} + 31.67a_{133} + 28.33a_{134} + 25.00a_{211} \\ & \quad + \,41.67a_{212} + 37.17a_{213} + 35.83a_{214} + 33.33a_{221} + 53.33a_{222} + 38.33a_{223} \\ & \quad + \,57.50a_{224} + 37.50a_{231} + 53.33a_{232} + 43.33a_{233} + 24.50a_{234} - 8875.16) \\ & \quad \times \,0.0021 - 467.40d_{2}^{ + } + 467.40d_{2}^{ - } = 0 \\ & (2.17a_{111} + 3.17a_{112} + 5.42a_{113} + 3.25a_{114} + 2.67a_{121} + 7.00a_{122} + 3.00a_{123} + 3.00a_{124} \\ & \quad + \,3.17a_{131} + 5.83a_{132} + 4.00a_{133} + 2.92a_{134} + 3.83a_{211} + 5.00a_{212} + 6.93a_{213} + 3.83a_{214} \\ & \quad + \,4.00a_{221} + 6.08a_{222} + 6.58a_{223} + 7.67a_{224} + 5.00a_{231} + 7.08a_{232} + 8.92a_{233} + 4.83a_{234} \\ & \quad - \,1093.84) \times 0.0025 - 398.55d_{3}^{ + } + 398.55d_{3}^{ - } = 0 \\ & 0 \le \lambda_{i} \le 1,\,\,\,i = 1,2,3\quad and \\ & d_{1}^{ + } ,d_{1}^{ - } ,d_{2}^{ + } ,d_{2}^{ - } ,d_{3}^{ + } ,d_{3}^{ - } \ge 0 \\ \end{aligned} $$

Using the optimising software LINGO 16.0 on the above deterministic model, we obtain the optimal allocations which are as follows:

$$ \begin{aligned} & q_{11} = 7.50,\,q_{12} = 67.50,\,q_{13} = 25.50,\,q_{21} = 8366.493,\,q_{22} = 3316.33,\,q_{23} = 5047,\,a_{112} = 17.50, \\ & a_{113} = 27,\,a_{121} = 27.50,\,a_{123} = 26.50,\,a_{124} = 25.50,\,a_{134} = 31,\,a_{211} = 26,\,a_{212} = 16,\,a_{213} = 33, \\ & a_{234} = 36,\,y_{21} = 8333.33,\,y_{22} = 3333.33,\,y_{23} = 5000 \\ \end{aligned} $$

Let us suppose that the decision maker accepts this solution and considers it the preferred compromise solution.

\( Z_{1} = 121831.70 \) with the value of \( \lambda_{1} = 0.815652 \) that mean, we reach the achievement level of81% with deviation from the goal is d1 = 0.0069994.

\( Z_{2} = 9000.96, \) with the value of \( \lambda_{2} = 0.7308599 \) that mean, we reach the achievement level of 73% with deviation from the goal is d2 = 0.0041157.

\( Z_{3} = 1103.47, \) with the value of \( \lambda_{3} = 0.7476309 \) that mean we reach the achievement level of74% with deviation from the goal is d3 = 0.0058303.

Therefore, this solution satisfies all the termination conditions of the EFGP approach, and it becomes the satisfactory solution to the DM. We have also considered a situation when there is some deviation in demand units of product I and product II respectively. Some try-outs have been executed to inspect the sensitivity of overall demand of products on the objective functions. These try-outs have shown that as the demand varies for both the products up to finite lower and upper limits, gives the global optimal and feasible results (Table 11).

Table 11 Optimal solution for different values of demand quantity
Full size table

Conclusion

Production and distribution system are connected and interrelated to each other. The production of product quantity is entirely always depending on the amount of demand raised by the customers. It is crucial that all products manufactured in the system should be shipped to retailers or stored at storage points in the system. This paper develops a multi-objective optimization model for an SCN involving suppliers, factories, distribution centres and retailers. The nature of the logistic decisions is so strategic about to procurement of raw materials from suppliers, production of finished products at factories, distribution of finished product store retailers via distribution centres, and the storage of raw materials and end products at factories and distribution centres.

These days some researchers have shown interest in the area of fuzzy SCN, and various attempts have been made to study the solution of these types of problems. When vagueness exists in the above-defined PDP, it is not always possible to find the optimal or efficient solution for the multi-objective optimization problem. In this situation, decision maker trying to find the compromise solution using a fuzzy set theoretic approach which is acceptable to the decision maker. Therefore to overcome the shortcomings of the existing methods we introduced a new formulation of PDP involving trapezoidal fuzzy numbers for the shipping costs, inventory holding cost and delivery time of the products. We proposed an EFGP approach for solving fuzzy MOPDP by the help of graded mean integration representation method which has been used to get the crisp value of the fuzzy parameters. In our proposed method, after determining the fuzzy goals of the decision-making problem, a satisfactory solution is efficiently derived by updating the minimal satisfactory levels of decision makers with considerations of the overall satisfactory solution.

The solution procedure of proposed approach is straightforward, efficient and it is believed that by adopting the proposed approach, the company’s profits will soar and helps to achieve sufficient savings in the SCN. It is believed that the present study will increase the interest in handling multi-objective optimization problems more to other interested researchers and practitioners. In our future works, we will try to develop the solution algorithm for more large scale and complex situations of SCN problems.