1 Introduction

Quality of product is the key interest of consumers and producers. Acceptance sampling inspection plan (ASIP) is one tool of statistical quality control (SQC) to control or enhance the quality of the product. The quality of product plays an important in the decision to acceptance/rejection of the lot and various types of ASIPs are presented in literature, viz., attribute ASIP and variable ASIP. Single acceptance sampling plan (SSIP), double acceptance sampling plan (DSIP), multiple acceptance sampling plan (MSIP), sequential acceptance sampling plan (SeASIP), group acceptance sampling plan (GSIP), and skip-lot sampling plans (SkASIP) are included in the attribute ASIP. While variables sampling plans uses the accurate measurements of the quality characteristics. Moreover this, a modified chain group sampling inspection plan (MChGSIP) is also a one kind of ASIP and this can be used in several situations in the industry for decision making of process regarding the lot quality. The parameters of ASIP are known as plan parameters and determined by using acceptable quality level (AQL) and limiting quality level (LQL) and these parameters plays important role to judge the quality of manufactured products or lots of product. On a whole, the aim of researchers is to determine the plan parameters under the scenario of several sampling schemes.

The outline of the remainder of the article is as follows: Sect. 2 contained the literature review of ASIP. In Sect. 3, we have provided a quick overview of the GHND. Section 4 presented the method of MChGSIP for GHND-based time truncated life tests. Discussion over the presented tables are placed with example for better understanding of trend of findings in Sect. 5. Also, Sect. 6 included three instances of how MChGSIP for GHND can be used in the real world. At last in Sect. 7, conclusions and future research orientation are discussed.

2 Literature review

The literature of SQC enriched with the ASIPs and researchers are continuously working to add more ASIPs in the literature. Here, we have mentioned the evolution of ASIPs and researchers developed time truncated ASIPs for many probability distributions. SSIP, DSIP, and GSIP are all acronyms that are commonly used by the researchers. Many researchers have written about the time truncated SSIP, and some of them are listed here: Gupta (1962), Gupta and Groll (1961), Rosaiah and Kantam (2005), Tsai and Wu (2006), Baklizi et al. (2004), Aslam et al. (2010b), Al-Omari (2015), Tripathi et al. (2020b, 2023b) and Saha et al. (2021). Also, DSIP developed by the several authors, Rao (2011b), Ramaswamy and Anburajan (2012), Gui (2014), Gui and Xu (2015), Al-Omari et al. (2016), Al-Omari and Zamanzade (2017), Hu and Gui (2018), Tripathi et al. (2020a) and many more. An extensive works have been done on GSIP and some of them are mentioned here: Aslam et al. (2009, 2010a, 2011, 2013) for gamma, Pareto distribution of second kind, Birnbaum–Saunders and Burr type X distributions, Rao (2011a) for Marshall–Olkin extended exponential distribution, Singh and Tripathi (2017) for inverse Weibull distribution, Kanaparthi et al. (2016) for Odds exponential log-logistic distribution and many more. The ChSIP is introduced by Dodge (1955) and later several authors have done work on it and for more details, the reader may refer to Govindaraju (2006), Govindaraju and Balamurali (1998), Balamurali and Usha (2013), Govindaraju and Subramani (1993), Govindraju and Lai (1998) and Luca (2018) and Tripathi et al. (2021) and many more. Recently, Tripathi et al. (2022, 2023a) have developed a new sampling inspection plan and known as modified chain group acceptance sampling inspection plan (MChGSIP), where they have shown the benefits of MChGSIP and also shown that this plan is a good alternative of some popular exiting plans.

3 GHND

Cooray and Ananda (2008) introduced the GHND as a special case of the three-parameter generalized gamma distribution (see, Stacy 1962). The GHN distribution’s cumulative distribution function (CDF) and the probability density function (PDF) are, respectively, given as:

$$\begin{aligned} F(x,\alpha ,\theta )=2\Phi \left[ (\frac{x}{\theta })^{\alpha }\right] -1;~~~~~~~x \le 0,~~~\alpha>0,~~\theta >0 \end{aligned}$$
(3.1)

and

$$\begin{aligned} f(x,\alpha ,\theta )=\sqrt{\frac{2}{\pi }}\left( \frac{\alpha }{x}\right) \left( \frac{x}{\theta }\right) ^ {\alpha }exp^{\left( -\frac{x}{2\theta }\right) ^{2\alpha }}~~~~~~~~ x>0, \end{aligned}$$
(3.2)

where \(\Phi (\cdot )\) is the standard normal distribution’s CDF. \(\alpha\) and \(\theta\) are shape and scale parameters of the GHND, respectively. Since the CDF of the half-normal distribution and the CDF of the GHND are very close in terms of their CDFs, this density is called the GHN (see Cooray and Ananda 2008) and the kth moment of origin of GHND is

$$\begin{aligned} E(X^k)=\sqrt{\frac{2^\frac{k}{\alpha }}{\pi }}\Gamma \left( {\frac{k+\alpha }{2\alpha }}\right) \theta ^k~~;~~~~~~k=1,2,3, \ldots \end{aligned}$$
(3.3)

Now, in particular for k = 1, the mean of GHND is given as

$$\begin{aligned} \mu =\sqrt{\frac{2^\frac{1}{\alpha }}{\pi }}\Gamma \left( {\frac{1+\alpha }{2\alpha }}\right) \theta . \end{aligned}$$
(3.4)

The hazard rate function and the survival function of GHND, denoted by H(x) and S(x), respectively, for specified values of x are given as:

$$\begin{aligned} H(x,\alpha ,\theta )=\frac{\sqrt{\frac{2}{\pi }}\left( \frac{\alpha }{x}\right) \left( \frac{x}{\theta }\right) ^ {\alpha }exp^{\left( -\frac{x}{2\theta }\right) ^{2\alpha }}}{1-[{2\Phi \left[ (\frac{x}{\theta })^{\alpha }\right] -1}]} \end{aligned}$$
(3.5)

and

$$\begin{aligned} S(x,\alpha ,\theta )=1-[{2\Phi \left[ (\frac{x}{\theta })^{\alpha }\right] -1}]. \end{aligned}$$
(3.6)

The hazard rate function of GHND can be monotonically increasing, monotonically decreasing, and bathtub forms, i.e., it can be described in any pattern or shape and the range of the parameter alpha influences the hazard rate’s shape. The hazard rate function is monotonically decreases for \(0<\alpha \le .5\), monotonically increases for \(\alpha > 1\) and it posses bathtub shape curve for \(0.5< \alpha < 1\), respectively.

Fig. 1
figure 1

Block diagram of the proposed MChGSIP

Full size image

4 Method of MChGSIP

In this section, we have designed the time truncated MChGSIP plan for a pre-specified truncation time \(t_0\) and step by step procedure in the form of block diagram of the proposed plan is given in Fig. 1. The values of group size (r), truncation time (\(t_0\)), producer’s risk (\(\alpha _p\)) and consumer’s risk (\(\beta\)) are assumed to be pre-fixed. Also, the procedure of the proposed time truncated MChGSIP is as follows:

  1. 1.

    Select n items from a particular lot and allocate r items to g groups, i.e, \(n=r \times g\). Start with normal inspection for a pre-fixed experiment time \(t_0\).

  2. 2.

    Inspect all the groups simultaneously and record the number of non-conforming units (\(\Delta\)) upto pre-fixed experiment time \(t_0\).

  3. 3.

    If \(\Delta \le c\) the lot is accepted provided that there is at most 1 lot of the preceding i lots in which the number of defective units \(\Delta\) exceeds the criterion c, otherwise reject the lot.

The probability of acceptance of GSIP, denoted by \(P_a\), is given by:

$$\begin{aligned} P_a= & {} \sum \limits _{i=0}^{c}{rg \atopwithdelims ()i} p^i (1-p)^{(rg-i)} \nonumber \\= & {} \sum \limits _{i=0}^{c} f(rg,p,i) \end{aligned}$$
(4.1)

where \(p=F(t_0)\).

$$\begin{aligned} p=2\Phi \left[ \left( \frac{t/\theta _0}{\theta /\theta _0}\right) ^{\alpha }\right] -1;~~~~~~~x \le 0,~~~\alpha>0,~~\theta >0 \end{aligned}$$

We used two-point approach (at AQL and LQL) to determine the plan parameters of the proposed plan by using the following non-linear optimization problem:

$$\begin{aligned}{} & {} \text{ Minimize, } \text{ average } \text{ sample } \text{ number } \text{(ASN): }~~ n=g\times r~~~\text{ subject } \text{ to } \nonumber \\{} & {} \quad P_{acg}(p_0) \ge (1-\alpha _p) \end{aligned}$$
(4.2)
$$\begin{aligned}{} & {} \quad P_{acg}(p_1) \le \beta \end{aligned}$$
(4.3)

where

$$\begin{aligned} P_{acg}(p_0)= & {} \sum \limits _{i=0}^{c} f(rg,p_0,i)\left[ \left( \sum \limits _{i=0}^{c} f(rg,p_0,i)\right) ^i+i\left( \sum \limits _{i=0}^{c} f(rg,p_0,i)\right) ^{i-1}\left( 1-\sum \limits _{i=0}^{c} f(rg,p_0,i)\right) \right] \end{aligned}$$
(4.4)
$$\begin{aligned} P_{acg}(p_1)= & {} \sum \limits _{i=0}^{c} f(rg,p_1,i)\left[ \left( \sum \limits _{i=0}^{c} f(rg,p_1,i)\right) ^i+i\left( \sum \limits _{i=0}^{c} f(rg,p_1,i)\right) ^{i-1}\left( 1-\sum \limits _{i=0}^{c} f(rg,p_1,i)\right) \right] \end{aligned}$$
(4.5)

Based on the multiple values of both producer’s and consumer’s risks, a non-linear optimization problem is used to estimate the parameters of the plan. Tables 1, 2 and 3 provide the values of all plan parameters.

5 Discussion and results of tables

The plan parameters of proposed plan are placed in the Tables 1, 2 and 3 under the assumption that lifetime of items follows the GHND for \(\alpha =2,3,4\), respectively. Now, the presented tables are obtained for prefixed group size \(r=(5,10)\) and producer’s risk \(\alpha _p=0.05\). Along with the group size and producer’s risk, where we assumed that the consumer’s risk \(\beta =(0.25,0.10,0.05,0.01)\) and the termination ratio \(t_0/\theta _0=(0.5,0.75)\) for the computation of plan parameters of suggested plan, respectively. The acceptance probabilities of the lot \(P_{acg}(p)\) have been shown in Tables 1, 2 and 3 for the considered quality level \((\theta /\theta _0)=(2,3,4,5,6,7,8)\), respectively. It is to be noted that, important trend have been noticed from Tables 1 and 3 regarding the minimum number of groups. and the minimum number of groups increases as \(\beta\) decreases for given values of r, \(a=t_0/\theta _0\) and \(\theta /\theta _0\). In case of fixed \(\beta\), the minimum number of groups decreases when quality level increases. However, this decreasing behavior of groups are not true for all quality levels. For example, from Table 1, we got minimum number of group \(g=11\) for \(r=5,(t_0/\theta _0)=0.5,\beta =0.05,(\theta /\theta _0)=3,c=7,i=2\), but for set up \(r=5,(t_0/\theta _0)=0.5,\beta =0.05,(\theta /\theta _0)=4, c=6, i=1\), we got \(g=12\). In some cases, as we increase the quality level for this set up, the minimum number of groups are remain same. One more important result we have observed from the Tables 1, 2 and 3 that the number of groups decreases when termination ratio \((t_0/\theta _0)\) increases in both cases of group sizes \(r=5,~10\), respectively.

6 Real life examples

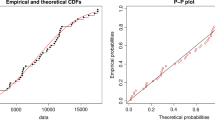
For the purpose of illustrating the proposed strategy, we looked at three real-world applications. As a first step, we must verified whether or not the data set we are examining is from the GHND or not by applying the goodness of fit test. Akaike Information Criterion (AIC) and Bayesian Information Criterion (BIC) are two of the discrimination criteria that we utilized. All the values of model fitting summary like, log-likelihood at maximum likelihood estimates (MLEs) of the parameters \(l(\hat{\Theta })\), AIC, BIC and K-S Statistic with corresponding p values are obtained and given in Table 4. We observed that the considered data sets fit our GHND very well, according to Table 4. Figures 2, 3 and 4 represent histogram-density, empirical and theoretical CDFs, and P–P plot for the model under consideration for data set I, II and III respectively. Histogram density of each chosen data sets showed that maximum area of histogram is covered by density of GHND and on other hand points of empirical-theoretical density are very near to each other with minimum K-S value, these both plots indicated that data suited well to GHND, and same conclusions can be drawn by using P–P plot. Table 5 provides a descriptive summary of all the three sets of considered data.

Data I Data I represents the Number of millions revolutions to failure for 23 ball bearings in millions and first considered by Lawless (2003).

The MLEs of data-I are \(\alpha =1.576165\) and \(\theta =90.630906\). The experimenter set the mean lifetime for ball bearing is 50 min with specific consumer’s risk 0.10 and with shape parameter \(\alpha =1.576165\). Life test would be terminated at 31.05 min by experimenter with consumer’s risk 0.10 and termination ratio is \((t_0/\mu _0)=0.5\). Hence, the optimal plan parameters for the considered specifications are \(g=4\), \(c=3\) and \(i=2\) when group size \(r=5\). Now, if the experimenter desires to set up the MChGSIP plan for the above mentioned specifications, then procedure is as follows:

  • Choose a sample of size 20 from a submitted lot. Allocate 5 items to 4 groups, i.e, \(n=r \times g\) and start with normal inspection and test the units up to truncation time 31.05 min.

  • Inspect all the groups simultaneously and record the number of non-conforming units (\(\Delta\)).

  • If \(\Delta \le 3\) the lot is accepted provided that there is at most 1 lot of the preceding 2 lots in which the number of defective units \(\Delta\) exceeds the criterion 3, otherwise reject the lot.

If true mean lifetime of the ball bearings is 150 min s, i.e., quality ratio is \((\mu /\mu _0)=3\) then probability of acceptance of lot for the considered specifications of experimenter is 0.9866054.

Data II Data II represents 100 breaking stress of carbon fibers (in Gba) and considered by Nichols and Padgett (2006).

The MLEs of data-II are \(\alpha =2.113852\) and \(\theta =3.167321\). The experimenter set the mean lifetime of breaking stress of carbon fibers is 1.5 unit with specific consumer’s risk 0.10 and with shape parameter \(\alpha =2.113852\). Life test would be terminated at 0.8164692 by experimenter with consumer’s risk 0.10 and termination ratio is \((t_0/\mu _0)=0.45\). Optimal plan parameters for the considered specifications are \(g=9\), \(c=4\) and \(i=2\) when group size \(r=5\). Now, if the experimenter desires to set up the MChGSIP plan for the above mentioned specifications, then procedure is as follows:

  • Select a sample of size 45 from a submitted lot. Allocate 5 items to 9 groups, i.e, \(n=r \times g\) and start with normal inspection and test the units up to truncation time 0.8164692 Gba.

  • Inspect all the groups simultaneously and record the number of non-conforming units (\(\Delta\)).

  • If \(\Delta \le 4\) the lot is accepted provided that there is at most 1 lot of the preceding 2 lots in which the number of defective units \(\Delta\) exceeds the criterion 4, otherwise the lot is rejected.

If true mean lifetime of breaking stress of carbon fibers is 3.00 min, i.e., quality ratio is \((\mu /\mu _0)=2\) then probability of acceptance of lot for the considered specifications of experimenter is 0.9815832.

Data III This data set represents 49 data points of the stress-rupture life of kevlar 49/epoxy strands, subjected to the constant sustained pressure at the \(70\%\) stress level until all had failed, as before we have complete data with exact time of failure and considered by Cooray and Ananda (2008).

The MLEs of data-III are \(\alpha =1.634991\) and \(\theta =10900.647977\). The experimenter set the mean lifetime of stress-rupture life of kevlar 49/epoxy strands is 2000 unit with specific consumer’s risk 0.10 and with shape parameter \(\alpha =1.634991\). Life test would be terminated at 1238.502 unit by experimenter with consumer’s risk 0.10 and termination ratio is \((t_0/\mu _0)=0.5\). Optimal plan parameters for the considered specifications are \(g=5\), \(c=4\) and \(i=2\) when group size \(r=5\). Now, if the experimenter desires to set up the MChGSIP plan for the above mentioned specifications, then procedure is as follows:

  • Select a sample of size 25 from a submitted lot. Allocate 5 items to 5 groups, i.e, \(n=r \times g\) and start with normal inspection and test the units up to truncation time 1238.502.

  • Inspect all the groups simultaneously and record the number of non-conforming units (\(\Delta\)).

  • If \(\Delta \le 4\) the lot is accepted provided that there is at most 1 lot of the preceding 2 lots in which the number of defective units \(\Delta\) exceeds the criterion 4, otherwise the lot is rejected.

If true mean lifetime of stress-rupture life of kevlar 49/epoxy strands is 6000, i.e., quality ratio is \((\mu /\mu _0)=3\) then probability of acceptance of lot for the considered specifications of experimenter is 0.9963392.

Table 1 Plan parameters of MChGSIP for GHND when \(\alpha =2\)
Full size table
Table 2 Plan parameters of MChGSIP for GHND when \(\alpha =3\)
Full size table
Table 3 Plan parameters of MChGSIP for GHND when \(\alpha =4\)
Full size table
Table 4 Model fitting summary of data sets
Full size table
Table 5 Descriptive summary of data sets
Full size table
Fig. 2
figure 2

Histogram density, empirical and theoretical CDFs and P–P plot of data I

Full size image
Fig. 3
figure 3

Histogram density, empirical and theoretical CDFs and P–P plot of data II

Full size image
Fig. 4
figure 4

Histogram density, empirical and theoretical CDFs and P–P plot of data III

Full size image

7 Conclusions and future research orientation

The MChGSIP, based on GHND has been developed in this article. The proposed plan’s minimum sample size and OC values have been calculated. The application of the proposed time truncated acceptance sampling plan has been detailed and discussed using three real-world examples. Other values of the shape parameter can be accommodated by modifying this design. The proposed method can be used in the corporate world to decide whether or not to accept or reject a large number of manufactured goods whose lifespans match the GHND pattern. Next up, we’ll develop MChGSIP for other non-normal probability distributions.