1 Introduction

Industry, aeroplanes, satellite systems, engineering activities, medical science, and all academic divisions that use computer technology all have a role in science and technology. Because the performance of a system is determined by its hardware and software, high-quality software and hardware are necessary for better outcomes. When a computer system's hardware and software operate in a logical and consistent manner, it operates at maximum capacity. As the utilisation of a computer system grows, so does the likelihood of the system failing. The system can occasionally fail owing to hardware or software problems. Economic loss is the result of system breakdowns. Hardware maintenance and software upgrades can only be performed on a single server. Redundancy provides a parallel unit that comes into existence and functioning after the failure of the operative unit. Generally, redundancy is three types such as cold standby, hot standby, and warm standby. It is considered that in cold standby mode, the chance of failure of the unit is zero. Thus, scientists and engineers always suggest a reliable computer system by considering cold standby redundancy.

Many scientists and researchers have examined reliability and standard measures of a cold-standby redundant system with a single sever for its repairing purpose under the assumption that failure and repair rates of the units are generally distributed. Srinivasan and Gopalan (1973) analysed reliability and standard measures of a cold-standby redundant system with a single sever for its repairing purpose under the assumption that failure and repair rates of the units are generally distributed. Birolini (1974) used stochastic processes and regenerating points to investigate the reliability of a warm standby system. Subramanian (1978) emphasised a different units system based on the premise that the operative unit is undergoing preventative maintenance and the backup unit is operational. Gopalan and Nagarwalla (1985) described the benefit of a redundant age replacement cold standby system with a single server to repair the failed unit. Chander (2007) discussed on economic aspects of an electric transformer subjected to inspection to perform online repair and replacement activity. Malik and Pawar (2010) evaluated a stochastic system having a single server inspect the failed unit before online repair and under an abnormal atmosphere, no repair activity was performed. Pawar and Malik (2011) threw light on a single unit system with a single server that inspected the failed unit in distinct modes working in an abnormal condition. Kadyan (2012) analyzed reliability measures of a single unit system with a single server for inspection and repair at different stages of failure under an abnormal climate.

Malik and Deswal (2012) described a repairable stochastic system of distinct units having seniority for operation and repair under normal and abnormal atmosphere. Gupta et al. (2013) evaluated a two distinct unit system having a cold standby unit with Weibull failure and repair activity with a switching device. Kumar et al. (2014) discussed the single unit system under preventive maintenance and having a repair facility subject to maximum operation. Kumar and Sirohi (2015) analyzed the profit of a two-unit cold standby system with delayed repair of partially failed unit for better utilization of unit. Kumar et al. (2015) threw light on a cold standby redundant stochastic system with preventive maintenance, seniority, and maximum repair. Yadav and Barak (2016) threw light on the semi-Markov system having identical cold standby units under the provision of a single server. Barak et al. (2016) described reliability measures under preventive maintenance of a redundant system subjected to inspection before repairing the failed unit and single server facility. Kumar et al. (2016a, b) analyzed two distinct unit redundant systems with Weibull distribution having distinct scale parameters and standard shape parameters for failure and repair activity. Kumar et al. (2016a, b) discussed the performance and economic aspect of two distinct unit redundant systems using Weibull distribution and semi Markov process for failure and repair. Barak et al. (2017) scrutinized the stochastic system having one spare unit under the conditional inability of the server. Kumar et al. (2017) described the performance of redundant systems using the regenerative point technique with Weibull failure and repair activity.

Barak et al. (2018) analyzed the two-unit redundant stochastic system having one spare unit in cold standby mode subjected to inspection with one server and its application in the water supply system. Barak et al. (2018) threw light on the two-unit cold standby system working fully under abnormal environmental conditions. Kumar and Saini (2018) threw light on comparing reliability measures of single-unit repairable systems with degradation and unconventional environment. Kumar et al. (2018) analyzed the economic aspects of a distinct warm standby system having a single server where the operative unit fails directly from normal mode, and the standby unit fails due to being unused for a long time. Singh and Poonia (2019) assessment the probability of two units parallel system with correlated lifetime under inspection using regenerative point technique. Kumar et al. (2020) analyzed reliability measures of the soft water treatment plant and its supply using the goodness of fit test. Kadyan and Barak (2020) discussed the distinct units repairable system on a seniority basis for operation and continued functioning of cold standby units. Gupta et al. (2020) discussed on benefits and availability aspects of generators in steam turbine power plants. Raghav et al. (2021) predicaiton of reliability of distribution system with homogeneity in software and server subject to different repair policies using joint probability disribution via Copula approach and a complex repairable system with n-identical units under (k-out-of-n: G) scheme and copula linguistic repair approach has been assessed by Singh et al.(2021). Saini et al. (2021) examined the behavior of two distinct redundant systems with seniority in repair and preventive maintenance with a single server facility.

2 System assumptions

  1. (a)

    The system has two units- one operative, and the second cold standby unit

  2. (b)

    The system has one cold standby unit that comes into existence and functioning after the failure of the operative unit.

  3. (c)

    The system is failed due to hardware failure or software failure.

  4. (d)

    A single repairman is required to solve the failure situations.

  5. (e)

    When the system fails due to hardware failure, the repairman comes and repairs it.

  6. (f)

    When the system fails due to software failure, the repairman comes and up-grades it.

  7. (g)

    Hardware/software failure and repair/up-gradation rates follow the Weibull distribution.

3 System notations

\(R\):

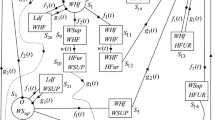
Group of regenerative states (S0, S1, S2, S3, S4)

\(O/\,Cs\):

Operative unit/cold standby unit

\(HFur/\,HFUR\):

Failure of hardware under repair/continuously from the previous stage

\(WHf/\,WHF\):

Failure of hardware waiting for repair/continuously waiting for repair from the previous state

\(Sup/\,SUP\):

Software up-gradation/continuously from the previous state

\(WSup\,/\,WSUP\):

Software up-gradation waiting for repair/continuously waiting for repair from the previous state

\(\mu_{i}\):

Mean sojourn time to the system failure \(\mu_{i} = \int\limits_{0}^{\infty } {p(T > t)dt}\), T represents the system failure time in the state Si.

\(q_{ij} (t)/Q_{ij} (t)\):

Probability density function/ cumulative density function of direct transition time from \(S_{i} \in R\) to \(S_{j} \in R\) without transit to any other regenerative state

\(q_{ij.\,k} (t)/Q_{ij.\,k} (t)\):

Probability density function/cumulative density function of first passage time from \(S_{i}\) to \(S_{j} \in R\) or a failed state \(S_{j}\) with visiting state \(S_{k}\) once in (0,t]

\(\begin{gathered} q_{ij.k(r,s)} (t)/ \hfill \\ Q_{ij.k(r,s)} (t) \hfill \\ \end{gathered}\):

Probability density function/ cumulative density function of first passage time from \(S_{i} \in R\) to \(S_{j} \in R\) or to a failed state \(S_{j}\) with visiting states \(S_{k}\), \(S_{r}\), \(S_{s}\) once in (0,t]

\(M_{i} (t)\):

Represents the probability that the system is in working state \(S_{i} \in R\) up to the time (t) without passing via any other regenerative state \(S_{i} \in R\)

\(W_{i} (t)\):

The probability that server is busy in his job at the state \(S_{i}\) up to time (t) and state transition to any other state \(S_{i} \in R\) are not allowed or transit to the same state via one or more non-regenerative states.

\(\oplus / \otimes\):

Notation for Laplace convolution/Laplace stieltjes convolution.

\(* / * * /^{\prime }\):

Notations for Laplace transform (LT)/Laplace stieltjes transform (LST)/derivative of the function.

:

Up state/failed state/regenerative state

\(f_{1} (t) = \alpha \eta t^{\eta - 1} e^{{ - \alpha t^{\eta } }}\), \(f_{2} (t) = \beta \eta t^{\eta - 1} e^{{ - \beta t^{\eta } }}\), \(g_{1} (t) = k\eta t^{\eta - 1} e^{{ - kt^{\eta } }}\), \(g_{2} (t) = l\eta t^{\eta - 1} e^{{ - lt^{\eta } }}\) and \(w(t) = h\eta t^{\eta - 1} e^{{ - ht^{\eta } }}\) are hardware failure, software failure, hardware repair, software upgradation and rate of waiting time for server arrival respectively.

4 Model description

This paper is convenient for calculating the performance and profit of a computer system with hardware repair and software up-gradation facilities in which hardware and software working simultaneously. It is assumed that out of two identical unit one unit is sufficient to opearte the system and another unit kept as cold standby as shown in the state S0, there are some probabilility to transite one stage to another stage as explain in the second and third Sections “ 2. System assumtions, and 3. Notations”. Keeping these assumtions and notations in mind construct the state transition diagram Fig. 1 which is itself expalinatory in nature.

Fig. 1
figure 1

State transition diagram

Full size image

5 Transition probabilities

The following are the probable transition probabilities:

$$ \begin{aligned} p_{01} = & \frac{\alpha }{(\alpha + \beta )},\;p_{03} = \frac{\beta }{(\alpha + \beta )},\;p_{12} = \frac{h}{(h + \alpha + \beta )},\;p_{19} = \frac{\beta }{(h + \alpha + \beta )} \\ p_{1,\,11} = & \frac{\beta }{(h + \alpha + \beta )},\;p_{20} = \frac{k}{(k + \alpha + \beta )},\;p_{2,13} = \frac{\alpha }{(k + \alpha + \beta )},\;p_{2,14} = \frac{\beta }{(k + \alpha + \beta )} \\ p_{34} = & \frac{h}{(h + \alpha + \beta )},\;p_{35} = \frac{\beta }{(h + \alpha + \beta )},\;p_{36} = \frac{\beta }{(h + \alpha + \beta )},\;p_{40} = \frac{l}{(l + \alpha + \beta )} \\ p_{47} = & \frac{\alpha }{(l + \alpha + \beta )},\;p_{48} = \frac{\beta }{(l + \alpha + \beta )} \\ p_{52} = & p_{64} = p_{72} = p_{84} = p_{9,10} = p_{10,4} = p_{11,\,12} = p_{12,\,2} = p_{13,\,2} = p_{14,\,4} = 1 \\ \end{aligned} $$
(1)

It is simply confirmed that

$$ \begin{gathered} p_{12} + p_{19} + p_{1,\,11} = p_{20} + p_{2,\,13} + p_{2,\,14} = p_{34} + p_{35} + p_{36} = p_{40} + p_{47} + p_{48} = p_{01} + p_{03} = 1 \hfill \\ p_{41} + p_{45} = p_{51} + p_{56} = p_{12} + p_{14.(9,10)} + p_{12.(11,12)} = p_{71} + p_{76} = p_{82} + p_{86} = 1 \hfill \\ p_{20} + p_{2,\,13} + p_{24.14} = p_{34} + p_{32.5} + p_{34.6} = p_{40} + p_{42.7} + p_{48} = 1 \hfill \\ \end{gathered} $$
(2)

6 Mean time of sojourn

Allow system breakdown duration is represented by the letter T, in the state Si, the average sojourn time is:

$$ \begin{aligned} \mu_{{0}} = & \int\limits_{0}^{\infty } {P(T > t)dt} = \frac{{\Gamma (1 + \frac{1}{\eta })}}{{(\alpha + \beta )^{1/\eta } }},\;\mu_{5} = \mu_{6} = \mu_{7} = \mu_{8} = \frac{{\Gamma (1 + \frac{1}{\eta })}}{{(l)^{1/\eta } }} \\ \mu_{{1}} = & \frac{{\Gamma (1 + \frac{1}{\eta })}}{{(\alpha + \beta + h)^{1/\eta } }},\;\mu_{1}^{\prime } = \Gamma (1 + \frac{1}{\eta })\left[ {\frac{1}{{(\alpha + \beta + h)^{1/\eta } }} + \frac{(\alpha + \beta )}{{(\alpha + \beta + h)(k + h)^{1/\eta } }}} \right] \\ \mu_{{2}} = & \frac{{\Gamma (1 + \frac{1}{\eta })}}{{(\alpha + \beta + k)^{1/\eta } }},\;\mu_{2}^{\prime } = \Gamma (1 + \frac{1}{\eta })\left[ {\frac{1}{{(\alpha + \beta + k)^{1/\eta } }} + \frac{(\alpha + \beta )}{{(\alpha + \beta + k)(k)^{1/\eta } }}} \right] \\ \mu_{{3}} = & \frac{{\Gamma (1 + \frac{1}{\eta })}}{{(\alpha + \beta + h)^{1/\eta } }},\;\mu_{3}^{\prime } = \Gamma (1 + \frac{1}{\eta })\left[ {\frac{1}{{(\alpha + \beta + h)^{1/\eta } }} + \frac{(\alpha + \beta )}{{(\alpha + \beta + h)(l)^{1/\eta } }}} \right] \\ \mu_{{4}} = & \frac{{\Gamma (1 + \frac{1}{\eta })}}{{(\alpha + \beta + l)^{1/\eta } }},\;\mu_{4}^{\prime } = \Gamma (1 + \frac{1}{\eta })\left[ {\frac{1}{{(\alpha + \beta + l)^{1/\eta } }} + \frac{(\alpha + \beta )}{{(\alpha + \beta + l)(l)^{1/\eta } }}} \right] \\ \mu_{9} = & \mu_{11} = \frac{{\Gamma (1 + \frac{1}{\eta })}}{{(h)^{1/\eta } }},\;\mu_{10} = \mu_{12} = \mu_{14} = \frac{{\Gamma (1 + \frac{1}{\eta })}}{{(k)^{1/\eta } }},\;\mu_{13} = \frac{{\Gamma (1 + \frac{1}{\eta })}}{{(\alpha )^{1/\eta } }} \\ \end{aligned} $$
(3)

7 Mean time to system failure (MTSF)

Let \(\phi_{i} (t)\) is the density function of the first passage time from \(S_{i} \in R\) to a failed state. And, treating the failed states as trapping states, then upcoming recursive interface for \(\phi_{i} (t)\) is:

$$ \begin{aligned} \phi_{0} (t) = & Q_{01} (t) \otimes \phi_{1} (t) + Q_{03} (t) \otimes \phi_{3} (t) \\ \phi_{1} (t) = & Q_{12} (t) \otimes \phi_{2} (t) + Q_{19} (t) + Q_{1,\,11} (t) \\ \phi_{2} (t) = & Q_{20} (t) \otimes \phi_{0} (t) + Q_{2,\,13} (t) + Q_{2,\,14} (t) \\ \phi_{3} (t) = & Q_{34} (t) \otimes \phi_{4} (t) + Q_{35} (t) + Q_{36} (t) \\ \phi_{4} (t) = & Q_{40} (t) \otimes \phi_{0} (t) + Q_{47} (t) + Q_{48} (t) \\ \end{aligned} $$
(4)

Now taking LST of the above Eq. (4) and solving for \(\phi_{0}^{**} (s)\), we have

$$ M^{*} \left( s \right) = \frac{{1 - \phi_{0}^{**} (s)}}{s} $$
(5)

Now, the system model reliability is obtained by using inverse LT of Eq. (5). We have

$$ MTSF = \lim_{s \to 0} \frac{{1 - \phi_{0}^{**} (s)}}{s} = \frac{{\mu_{0} + p_{01} (\mu_{1} + p_{02} \mu_{2} ) + p_{03} (\mu_{3} + p_{34} \mu_{4} )}}{{(1 - p_{01} p_{12} p_{20} - p_{03} p_{34} p_{40} )}} $$
(6)

8 Steady state availability

Let \(A_{i} (t)\) is the probability that the system is in up-state at the moment ‘t’ specified that the system arrives at the regenerative-state \(S_{i}\) at t = 0. And then upcoming recursive relation for \(A_{i} (t)\) is:

$$ \begin{aligned} A_{0} (t) = & M_{0} (t) + q_{01} (t) \oplus A_{1} (t) + q_{03} (t) \oplus A_{3} (t) \\ A_{1} (t) = & M_{1} (t) + [q_{12} (t) + q_{12.(11,\,12)} (t)] \oplus A_{2} (t) + q_{14.(9,\,10)} (t) \oplus A_{4} (t) \\ A_{2} (t) = & M_{2} (t) + q_{20} (t) \oplus A_{0} (t) + q_{22.13} (t) \oplus A_{2} (t) + q_{24.14} (t) \oplus A_{4} (t) \\ A_{3} (t) = & M_{3} (t) + q_{32.5} (t) \oplus A_{2} (t) + [q_{34} (t) + q_{34.6} (t)] \oplus A_{4} (t) \\ A_{4} (t) = & M_{4} (t) + q_{40} (t) \oplus A_{0} (t) + q_{42.7} (t) \oplus A_{2} (t) + q_{44.8} (t) \oplus A_{4} (t) \\ \end{aligned} $$
(7)

where, \(M_{0} (t) = e^{{ - (\alpha + \beta )t^{n} }}\), \(M_{1} (t) = e^{{ - (\alpha + \beta + h)t^{n} }}\), \(M_{2} (t) = \,e^{{ - (\alpha + \beta + k)t^{n} }}\), \(M_{3} (t) = e^{{ - (\alpha + \beta + h)t^{n} }}\), \(M_{4} (t) = e^{{ - (\alpha + \beta + l)t^{n} }}\).

Now taking LT of above Eq. (7) and solving for \(A_{0}^{*} (s)\), the steady-state availability is given by

$$ A_{0} = \lim_{s \to 0} sA_{0}^{*} (s) = \frac{{N_{A} }}{{D^{\prime } }}, $$
(8)

where, \(N_{A} = \left[ \begin{gathered} (\mu_{0} + p_{01} \mu_{1} + p_{03} \mu_{3}^{\prime } )[p_{20} (p_{40} + p_{47} ) + p_{2,\,14} p_{40} ] \hfill \\ + \mu_{2}^{\prime } [p_{47} + p_{01} \{ p_{40} (1 - p_{19} )\} + p_{03} p_{35} p_{40} \hfill \\ + \mu_{4}^{\prime } [p_{2,\,14} + p_{01} p_{20} p_{19} + p_{03} \{ p_{20} (1 - p_{35} )\} ] \hfill \\ \end{gathered} \right]\)

$$ D^{\prime } = \left[ \begin{gathered} (\mu_{0} + p_{01} \mu_{1}^{\prime } + p_{03} \mu_{3}^{\prime } )[p_{20} (p_{40} + p_{47} ) + p_{2,\,14} p_{40} ] \hfill \\ + \mu_{2}^{\prime } [p_{47} + p_{01} \{ p_{40} (1 - p_{19} )\} + p_{03} p_{35} p_{40} \hfill \\ + \mu_{4}^{\prime } [p_{2,\,14} + p_{01} p_{20} p_{19} + p_{03} \{ p_{20} (1 - p_{35} )\} ] \hfill \\ \end{gathered} \right] $$
(9)

9 Busy period of the server due to repair of the failed unit

Let \(B_{i} (t)\) is the probability that the repairman is busy due to repair of the failed unit at the moment ‘t’ specified that the system arrives at the regenerative state \(S_{i}\) at t = 0. Then the upcoming recursive interface for \(B_{i} (t)\) is:

$$ \begin{aligned} B_{0} (t) = & q_{01} (t) \oplus B_{1} (t) + q_{03} (t) \oplus B_{3} (t) \\ B_{1} (t) = & W_{1} (t) + [q_{12} (t) + q_{12.(11,\,12)} (t)] \oplus B_{2} (t) + q_{14.(9,\,10)} (t) \oplus B_{4} (t) \\ B_{2} (t) = & W_{2} (t) + q_{20} (t) \oplus B_{0} (t) + q_{22.13} (t) \oplus B_{2} (t) + q_{24.14} (t) \oplus B_{4} (t) \\ A_{3} (t) = & W_{3} (t) + q_{32.5} (t) \oplus B_{2} (t) + [q_{34} (t) + q_{34.6} (t)] \oplus B_{4} (t) \\ B_{4} (t) = & W_{4} (t) + q_{40} (t) \oplus B_{0} (t) + q_{42.7} (t) \oplus B_{2} (t) + q_{44.8} (t) \oplus B_{4} (t) \\ \end{aligned} $$
(10)

where, \(W_{1} (t) = e^{{ - (\alpha + \beta + h)t^{n} }}\), \(W_{2} (t) = \,e^{{ - (\alpha + \beta + k)t^{n} }}\), \(W_{3} (t) = e^{{ - (\alpha + \beta + h)t^{n} }}\), \(W_{4} (t) = e^{{ - (\alpha + \beta + l)t^{n} }}\).

Now taking LT of above Eq. (10) solving for \(B_{0}^{R*} (s)\), the time for which server is busy due to repair is given by

$$ B_{0} = \lim_{s \to 0} sB_{0}^{*} (s) = \frac{{N_{B} }}{{D^{\prime}}} $$
(11)
$$ {\text{where}},N_{B} = \left[ \begin{gathered} (p_{01} \mu_{1}^{\prime } + p_{03} \mu_{3}^{\prime } )[p_{20} (p_{40} + p_{47} ) + p_{2,\,14} p_{40} ] \hfill \\ + \mu_{2}^{\prime } [p_{47} + p_{01} \{ p_{40} (1 - p_{19} )\} + p_{03} p_{35} p_{40} \hfill \\ + \mu_{4}^{\prime } [p_{2,\,14} + p_{01} p_{20} p_{19} + p_{03} \{ p_{20} (1 - p_{35} )\} ] \hfill \\ \end{gathered} \right] $$
(12)

and \(D^{\prime }\) is earlier defined by Eq. (9).

10 Expected number of visit by the server

Let \(V_{i} (t)\) is the estimated no. of visits by the repairman for repair in (0, t] specified the arrival at the regenerative state \(S_{i}\) at t = 0. The upcoming recursive interface for \(V_{i} (t)\) is:

$$ \begin{aligned} V_{0} (t) = & Q_{01} (t) \oplus V_{1} (t) + Q_{03} (t) \oplus V_{3} (t) \\ V_{1} (t) = & [Q_{12} (t) + Q_{12.(11,\,12)} (t)] \oplus V_{2} (t) + Q_{14.(9,\,10)} (t) \oplus V_{4} (t) \\ V_{2} (t) = & Q_{20} (t) \oplus V_{0} (t) + Q_{22.13} (t) \oplus V_{2} (t) + Q_{24.14} (t) \oplus V_{4} (t) \\ V_{3} (t) = & Q_{32.5} (t) \oplus V_{2} (t) + [Q_{34} (t) + Q_{34.6} (t)] \oplus V_{4} (t) \\ V_{4} (t) = & Q_{40} (t) \oplus V_{0} (t) + Q_{42.7} (t) \oplus V_{2} (t) + Q_{44.8} (t) \oplus V_{4} (t) \\ \end{aligned} $$
(13)

We are now taking LST of the above Eq. (13) and solving for \(V_{0}^{**} (s)\). The expected no. of visits of the server can be obtained as:

$$ V_{0} = \lim_{s \to 0} sV_{0}^{**} (s) = \frac{{V_{r} }}{{D^{\prime } }} $$
$$ {\text{Where}}\;V_{r} = [p_{20} (p_{40} + p_{47} ) + p_{2,\,14} p_{40} ]\, $$
(14)

and \(D^{\prime }\) is earlier defined by Eq. (9).

11 Particular cases

$$ MTSF = \frac{{MTSF_{A} }}{{MTSF_{B} }} $$
(15)
$$ MTSF_{A} = \Gamma (1 + \frac{1}{\eta })\left[ \begin{gathered} \frac{1}{{(\alpha + \beta )^{1/\eta } }} + \frac{1}{{(\alpha + \beta + h)^{1/\eta } }} \hfill \\ + \frac{1}{(\alpha + \beta + h)}\left\{ {\frac{1}{{(\alpha + \beta + k)^{1/\eta } }} + \frac{1}{{(\alpha + \beta + l)^{1/\eta } }}} \right\} \hfill \\ \end{gathered} \right] $$
$$ MTSF_{B} = \left[ {1 - \frac{h}{(\alpha + \beta + h)}\left\{ {\frac{\alpha k(\alpha + \beta + l) + \beta l(\alpha + \beta + k)}{{(\alpha + \beta )(\alpha + \beta + k)(\alpha + \beta + l)}}} \right\}} \right] $$
$$ A_{0} = \frac{{A_{1} + A_{2} + A_{3} }}{{Z_{1} + Z_{2} + Z_{3} }} $$
(16)
$$ A_{1} = \Gamma (1 + \frac{1}{\eta })\left[ {\left\{ {\frac{1}{{(\alpha + \beta )^{1/\eta } }} + \frac{1}{{(\alpha + \beta + h)^{1/\eta } }} + } \right\} \times \left\{ {\frac{k(l + \alpha ) + \beta l}{{(\alpha + \beta + k)(\alpha + \beta + l)}}} \right\}} \right] $$
$$ A_{2} = \Gamma (1 + \frac{1}{\eta })\left[ {\left\{ {\frac{1}{{(\alpha + \beta + k)^{1/\eta } }} + \frac{(\alpha + \beta )}{{(\alpha + \beta + k)(k)^{1/\eta } }}} \right\} \times \left\{ {\frac{\alpha }{(\alpha + \beta + l)}\left( {1 + \frac{l}{(\alpha + \beta )}} \right)} \right\}} \right] $$
$$ A_{3} = \Gamma (1 + \frac{1}{\eta })\left[ {\left\{ {\frac{1}{{(\alpha + \beta + l)^{1/\eta } }} + \frac{(\alpha + \beta )}{{(\alpha + \beta + l)(l)^{1/\eta } }}} \right\} \times \left\{ {\frac{\alpha }{(\alpha + \beta + k)}\left( {1 + \frac{k}{(\alpha + \beta )}} \right)} \right\}} \right] $$
$$ Z_{1} = \Gamma (1 + \frac{1}{\eta })\left[ \begin{gathered} \left\{ {\frac{1}{{(\alpha + \beta )^{1/\eta } }} + \frac{1}{{(\alpha + \beta + h)^{1/\eta } }} + \frac{1}{(\alpha + \beta + h)}\left( {\frac{\alpha }{{(k + h)^{1/\eta } }} + \frac{\beta }{{(k + l)^{1/\eta } }}} \right)} \right\} \hfill \\ \times \left\{ {\frac{k(l + \alpha ) + \beta l}{{(\alpha + \beta + k)(\alpha + \beta + l)}}} \right\} \hfill \\ \end{gathered} \right] $$
$$ Z_{2} = \Gamma (1 + \frac{1}{\eta })\left[ {\left\{ {\frac{1}{{(\alpha + \beta + k)^{1/\eta } }} + \frac{(\alpha + \beta )}{{(\alpha + \beta + k)(k)^{1/\eta } }}} \right\} \times \left\{ {\frac{\alpha }{(\alpha + \beta + l)}\left( {1 + \frac{l}{(\alpha + \beta )}} \right)} \right\}} \right] $$
$$ Z_{3} = \Gamma (1 + \frac{1}{\eta })\left[ {\left\{ {\frac{1}{{(\alpha + \beta + l)^{1/\eta } }} + \frac{(\alpha + \beta )}{{(\alpha + \beta + l)(l)^{1/\eta } }}} \right\} \times \left\{ {\frac{\alpha }{(\alpha + \beta + k)}\left( {1 + \frac{k}{(\alpha + \beta )}} \right)} \right\}} \right] $$
$$ B_{0} = \frac{{B_{1} + B_{2} + B_{3} }}{{Z_{1} + Z_{2} + Z_{3} }} $$
(17)
$$ B_{1} = \Gamma (1 + \frac{1}{\eta })\left[ \begin{gathered} \left\{ {\frac{1}{{(\alpha + \beta + h)^{1/\eta } }} + \frac{1}{(\alpha + \beta + h)}\left( {\frac{\alpha }{{(k + h)^{1/\eta } }} + \frac{\beta }{{(k + l)^{1/\eta } }}} \right)} \right\} \hfill \\ \times \left\{ {\frac{k(l + \alpha ) + \beta l}{{(\alpha + \beta + k)(\alpha + \beta + l)}}} \right\} \hfill \\ \end{gathered} \right] $$
$$ B_{2} = \Gamma (1 + \frac{1}{\eta })\left[ {\left\{ {\frac{1}{{(\alpha + \beta + k)^{1/\eta } }} + \frac{(\alpha + \beta )}{{(\alpha + \beta + k)(k)^{1/\eta } }}} \right\} \times \left\{ {\frac{\alpha }{(\alpha + \beta + l)}\left( {1 + \frac{l}{(\alpha + \beta )}} \right)} \right\}} \right] $$
$$ B_{3} = \Gamma (1 + \frac{1}{\eta })\left[ {\left\{ {\frac{1}{{(\alpha + \beta + l)^{1/\eta } }} + \frac{(\alpha + \beta )}{{(\alpha + \beta + l)(l)^{1/\eta } }}} \right\} \times \left\{ {\frac{\alpha }{(\alpha + \beta + k)}\left( {1 + \frac{k}{(\alpha + \beta )}} \right)} \right\}} \right] $$

and Z1, Z2, Z3 are defined earlier.

$$ V_{0} = \frac{{V_{r} }}{{Z_{1} + Z_{2} + Z_{3} }} $$
(18)
$$ V_{r} = \left[ {\frac{k(l + \alpha ) + \beta l}{{(\alpha + \beta + k)(\alpha + \beta + l)}}} \right] $$

and Z1, Z2, Z3 are defined earlier.

12 Profit analysis

The profit analysis of the system can be done by using the profit function;

$$ P = E_{0} A_{0} - E_{1} B_{0} - E_{2} V_{0} $$
(19)

where, \(E_{0} =\) 5000 (Revenue per unit uptime of the system is available), \(E_{1} =\) 500 (Charge per unit time for which server is busy due to repair), \(E_{2} =\) 200 (Charge per unit visit by the server)

13 Discussion

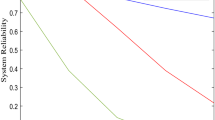
From the given Tables 1, 2, 3, it is clear that the values of MTSF, availability, and profit function having an increasing trend when software up-gradation rate (l) enhance but having decreasing trends when shape parameter (η) enhance where other parameters α = 0.003, β = 0.002, k = 1.5, h = 0.002, are hardware failure rate, software failure rate, hardware repair rate, and server waiting rate taken as constant for simplicity. When the hardware repair rate (k) changes from 1.5 to 2.5, then MTSF, availability, and profit function enhance.

Table 1 MTSF Vs. Software up-gradation rate (l)
Full size table
Table 2 Availability Vs. Software up-gradation rate (l)
Full size table
Table 3 Profit Vs. Software up-gradation rate (l)
Full size table

14 Conclusion

The table represents the numerically behavior of reliability measures which observe very small changes in the comparison of graphical behavior. It is clear that the MTSF, availability, and profit function of the computer system having two identical unit in which one unit is sufficent to operate the system and another unit kept as cold standby as an alternate unit, increases when software up-gradation rate (l) increased and the other parameters are kept as constant. But the values of reliability measures decreases when shape parameter (η) increased. Also, when the hardware repair rate increases (k), then the system’s MTSF, availability, and profit function values increases in the comparison of software upgradation by keeping other parameters has fixed constant values. Thus, system performance is improved by using timely up-gradation of the software and hardware repair of computer system.

15 Future scope

Because hardware repairs are expensive and time-consuming, it is sometimes feasible to increase the capacity of a computer system by employing a cold standby computer system and software upgrades rather than hardware repairs. Hardware repairs need a specialist, but software upgrades may be performed easily by anybody following the instructions provided.