Profit analysis of a two-unit cold standby system model operating under different weather conditions

Abstract

Generally, each machine or products are used by the human being up to its maximum capacity. If a system is performing beyond its capacity/defined conditions by the manufacturer called, the system is working under abnormal weather conditions. While, a system is performing within its capacities/stated conditions set by manufacturer called as the system working in abnormal weather conditions, for example; a car is functioning exceeding its accommodating capacity can be termed as working under abnormal weather conditions; a hydraulic machine exceeding its weight uplifting capacity of 500 tons by lifting 600 tons is termed as working under abnormal weather conditions. To overcome in such a situation, only effective maintenance strategies and suitable structure design of redundant system are the crucial factors which keep the standby system operational without failures for longer period of time. In fact, proper functioning of service mechanism and the reliability of system are strongly associated with each other. In the present paper, a water supply system simulate that is functioning of two-unit cold standby system with facilities of preventive maintenance, inspection and repair operating under different weather conditions with priority to preventive maintenance over inspection. The units are identical in nature. The single server only works under normal weather conditions capable of performing three operations inspection, repair and preventive maintenance responds to system instantly. The replacement of units is suggested if repair is impossible to perform during inspection. The operative unit undergoes for preventive maintenance after a specific time of operation. Repair of the unit is done by the server at its complete failure. All random variables are statistically independent. It is assumed that the failure rate and rate by which system undergoes for preventive maintenance are constant whereas the inspection rate, repair rate and maintenance rate follows negative exponential distribution. The expressions/graphs for several reliability measures are derived/depicted in steady state using regenerative point technique and semi-Markov process to determine the nature of the system.

1 Introduction

Proper and punctual working of water supply system is very important to all citizens of a city. The supply system works without failure behind this, the idea of inspection, preventive maintenance, priority and repair of identical or non-identical units under different weather conditions have been discussed by the researchers including, (Osaki and Asakura 1970) obtained a two-unit standby redundant system with repair and preventive maintenance. (Srinivasan and Gopalan 1973) discussed probability analysis of a two-unit system with warm standby and single repair facility. (Dhillon and Natesan 1983) analyzed stochastically outdoor power system in fluctuating environment. (Gupta and Goel 1991) obtained profit analysis of two-unit cold standby system with abnormal weather condition. (Chander 2005) analyzed reliability models with priority for operation and repair with arrival time of server. (Malik and Barak 2009) discussed reliability and economic analysis of a system operating under different weather conditions. (Kumar et al. 2012) discussed cost analysis of a two-unit cold standby system subjected to degradation, inspection and priority. (Kishan and Jain 2012) presented a two non-identical unit standby system model with repair, inspection and post-repair under classical and Bayesian viewpoints. (Kadyan and Ramniwas 2013) discussed cost–benefit analysis of a single-unit system with warranty for repair. (Deswal and Malik 2015) explained reliability measures of a system of two non-identical units with priority subject to weather conditions. Recently, (Barak and Barak 2016) discussed impact of abnormal weather conditions on various reliability measures of a repairable system with inspection. (Barak et al. 2017a, b) analyzed stochastically a cold standby system with conditional failure of server. (Barak et al. 2017a, b) discussed stochastic analysis of two-unit redundant system with priority to inspection over repair. Barak et al. 2018) analyzed stochastically a two-unit system with standby and server failure subject to inspection.

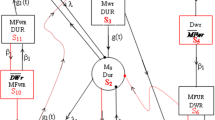
Keeping these studies in mind, a water supply system consists of two identical units (as in Fig.1) in which the unit may fail directly from normal mode. Initially, one unit is operative and other is in spare as cold standby. There is a single server who attends the system immediately whenever required. Server is capable of performing three operations i.e. preventive maintenance, inspection and repair. The preventive maintenance is carried out after a maximum operation time. Repair of unit is done at complete failure. Inspection facility is available before repair/replacement of the failed unit. Priority is given to preventive maintenance over inspection. Unit works as new after repair/preventive maintenance. Server starts, restarts or resumes its duty in normal weather only. Operations preventive maintenance and repair are stopped in abnormal weather to protect the system from unnecessary damage. It is assumed that the rate of change of weather, failure rate and the rate by which system undergoes for preventive maintenance or inspection are constant. The distributions for preventive maintenance, repair time, inspection time are taken as arbitrary with different distributions. Graphical and numerical inferences are explained in detail. All random variables are statistically independent.

Fig. 1

State transition diagram

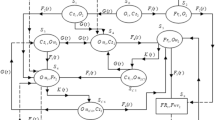
2 Transition probabilities and mean Sojourn times

Simple probabilistic consideration yields the following expressions for non-zero elements. In particular case; let $f(t) = \theta {\text{e}}^{ - \theta t}$, $g(t) = \phi e^{ - \phi t}$. The transition probabilities obtained are as follows:

$$p_{i,j} = Q_{ij} (\infty ) = \int_{0}^{\infty } {q_{i,j} (t){\text{d}}t}$$

(1)

$$\begin{aligned} p_{0,1} & = \frac{{\alpha_{0} }}{{\alpha_{0} + \lambda }},\;p_{0,2} = \frac{\lambda }{{\alpha_{0} + \lambda }},\;p_{1,0} = \frac{\theta }{{\lambda + \beta + \theta + \alpha_{0} }},\;p_{1,3} = \frac{\beta }{{\lambda + \beta + \theta + \alpha_{0} }},\;p_{1,9} = \frac{\lambda }{{\lambda + \beta + \theta + \alpha_{0} }} \\ p_{1,10} & = \frac{{\alpha_{0} }}{{\lambda + \beta + \theta + \alpha_{0} }},\;p_{2,0} = \frac{b\eta }{{\lambda + \beta + \eta + \alpha_{0} }},\;p_{2,4} = \frac{a\eta }{{\lambda + \beta + \eta + \alpha_{0} }},\;p_{2,6} = \frac{\beta }{{\lambda + \beta + \eta + \alpha_{0} }} \\ p_{2,23} & = \frac{{\alpha_{0} }}{{\lambda + \beta + \eta + \alpha_{0} }},\;p_{2,31} = \frac{\lambda }{{\lambda + \beta + \eta + \alpha_{0} }},\;p_{3,1} = p_{5,4} = p_{6,2} = \frac{{\beta_{1} }}{{\lambda + \beta_{1} + \alpha_{0} }},\;p_{3,13} = p_{5.37} = p_{6,27} = \frac{{\alpha_{0} }}{{\lambda + \beta_{1} + \alpha_{0} }} \\ p_{3,13} & = p_{5.37} = p_{6,27} = \frac{{\alpha_{0} }}{{\lambda + \beta_{1} + \alpha_{0} }},\;p_{3,15} = p_{5,36} = p_{6,29} = \frac{\lambda }{{\lambda + \beta_{1} + \alpha_{0} }} \\ \end{aligned}$$

$$\begin{aligned} p_{{4,0}} & = \frac{\phi }{{\phi + \alpha _{0} + \lambda + \beta }},\;p_{{4,5}} = \frac{\beta }{{\phi + \alpha _{0} + \lambda + \beta }},\;p_{{4,17}} = \frac{\lambda }{{\phi + \alpha _{0} + \lambda + \beta }},\;p_{{4,20}} = \frac{{\alpha _{0} }}{{\phi + \alpha _{0} + \lambda + \beta }} \\ p_{{7,2}} & = p_{{9,2}} = p{}_{{10,1}} = p_{{12,1}} = p_{{14,1}} = p_{{16,2}} = \frac{\theta }{{\theta + \beta }}, \\ p_{{7,8}} & = p_{{9,8}} = p_{{10,11}} = p_{{12,11}} = p_{{14,13}} = p_{{16,15}} = \frac{\beta }{{\theta + \beta }} \\ p_{{17,2}} & = p_{{19,2}} = p_{{20,1}} = p_{{22,1}} = p_{{26,1}} = p_{{34,2}} = p_{{35,2}} = p_{{38,1}} = \frac{\phi }{{\phi + \beta }} \\ p_{{17,18}} & = p_{{19,18}} = p_{{20,21}} = p_{{22,21}} = p_{{26,37}} = p_{{34,36}} = p_{{35,36}} = p_{{38,37}} = \frac{\beta }{{\phi + \beta }} \\ p_{{23,1}} & = p_{{25,1}} = p_{{28,1}} = p_{{30,2}} = p_{{31,2}} = p_{{33,2}} = \frac{{b\eta }}{{\eta + \beta }} \\ \end{aligned}$$

$$\begin{aligned} p_{23,24} & = p_{25,24} = p_{28,27} = p_{30,29} = p_{31,32} = p_{33,32} = \frac{\beta }{\eta + \beta } \\ p_{23,26} & = p_{25,26} = p_{28,26} = p_{30,34} = p_{31,34} = p_{33,34} = \frac{a\eta }{\eta + \beta } \\ \end{aligned}$$

$$\begin{aligned} p_{8,7} & = p_{11,12} = p_{12,13} = p_{13,14} = p_{15,16} = p_{18,19} = p_{21,22} = p_{24,25} = \\ p_{27,28} & = p_{29,30} = p_{32,33} = p_{36,35} = p_{37,38} = 1 \\ \end{aligned}$$

$$\begin{aligned} p_{1,1;10} & = \frac{{\theta \alpha_{0} }}{{(\beta + \theta )(\lambda + \theta + \beta + \alpha_{0} )}},\;p_{1,1;10(11,12)} = \frac{{\beta \alpha_{0} }}{{(\beta + \theta )(\lambda + \theta + \beta + \alpha_{0} )}}, \\ p_{1,2;9} & = \frac{\theta \lambda }{{(\beta + \theta )(\lambda + \theta + \beta + \alpha_{0} )}},\;p_{1,2;9(8,7)} = \frac{\beta \lambda }{{(\beta + \theta )(\lambda + \theta + \beta + \alpha_{0} )}}, \\ p_{2,2;23} & = \frac{{\alpha_{0} \theta }}{{(\beta + \theta )(\lambda + \eta + \beta + \alpha_{0} )}},\;p_{2,2;23(24,25)} = \frac{{\beta \alpha_{0} }}{{(\beta + \theta )(\lambda + \eta + \beta + \alpha_{0} )}}, \\ p_{2,2;28} & = \frac{b\lambda \eta }{{(\beta + \eta )(\lambda + \eta + \beta + \alpha_{0} )}},\;p_{2,2;28(29,30)} = \frac{b\lambda \beta }{{(\beta + \eta )(\lambda + \eta + \beta + \alpha_{0} )}} \\ p_{2,2;28,31} & = \frac{a\lambda \beta \phi }{{(\beta + \eta )(\beta + \phi )(\lambda + \eta + \beta + \alpha_{0} )}},\;p_{2,2;28(29,30)31} = \frac{a\lambda \beta \phi }{{(\beta + \phi )(\beta + \eta )(\lambda + \eta + \beta + \alpha_{0} )}} \\ p_{2,2;28,31(32,33)} & = \frac{a\lambda \eta \beta }{{(\beta + \phi )(\eta + \lambda + \beta + \alpha_{0} )(\eta + \beta )}} \\ p_{2,2;28(29,30)31(32,33)} & = \frac{{a\lambda \beta^{2} }}{{(\beta + \phi )(\lambda + \eta + \beta + \alpha_{0} )(\beta + \eta )}},\;p_{{3,1;(13,14)^{{}} }} = p_{5,1;(34,35)} = \frac{{\alpha_{0} }}{{\lambda + \beta_{1} + \alpha_{0} }} \\ p_{3,2;(15,16)} & = p_{5,2;(32,33)} = \frac{\lambda }{{\lambda + \beta_{1} + \alpha_{0} }} \\ \end{aligned}$$

$$\begin{aligned} p_{4,1;20} & = \frac{{\alpha_{0} \phi }}{{(\beta + \phi )(\lambda + \phi + \beta + \alpha_{0} )}},\;p_{4,2;17} = \frac{\lambda \phi }{{(\beta + \phi )(\lambda + \phi + \beta + \alpha_{0} )}} \\ p_{4,1;20(21,22)} & = \frac{{\alpha_{0} \beta }}{{(\beta + \phi )(\lambda + \phi + \beta + \alpha_{0} )}},\;p_{4,2;17(18,19)} = \frac{\lambda \beta }{{(\beta + \phi )(\lambda + \phi + \beta + \alpha_{0} )}}, \\ p_{6,2;(24,25)} & = \frac{{\alpha_{0} }}{{(\lambda + \beta_{1} + \alpha_{0} )}},\;p_{6,2;(26,27)} = \frac{{a\alpha_{0} \phi }}{{(\beta + \phi )(\alpha_{0} + \lambda + \beta_{1} )}} \\ \end{aligned}$$

$$p_{6,2;(26,27)31} = \frac{a\lambda \phi }{{(\beta + \phi )(\alpha_{0} + \lambda + \beta_{1} )}},\;p_{6,2;(26,27)31(32,33)} = \frac{a\lambda \beta }{{(\beta + \phi )(\alpha_{0} + \lambda + \beta_{1} )}}$$

(2)

The mean Sojourn times $(\mu_{i} \,{\text{and}}\,\mu^{\prime}_{i} )$ is the state S_i are

$$\mu_{0} = \frac{1}{{\alpha_{0} + \lambda }},\;\mu_{1} = \frac{1}{{\alpha_{0} + \lambda + \beta + \theta }},\;\mu_{2} = \frac{1}{{\alpha_{0} + \lambda + \beta + \eta }},\;\mu_{3} = \mu_{5} = \mu_{6} = \frac{1}{{\alpha_{0} + \lambda + \beta_{1} }}$$

$$\mu_{4} = \frac{1}{{\alpha_{0} + \lambda + \beta + \phi }}$$

(3)

and $\mu^{\prime}_{1} = \frac{{\theta \beta_{1} + (\lambda + \alpha_{0} )(\beta + \beta_{1} )}}{{\theta \beta_{1} (\lambda + \beta + \theta + \alpha_{0} )}}$, $\mu^{\prime}_{2} = \frac{{\eta \theta \phi \beta_{1} + (\alpha_{0} \eta \phi + \lambda \theta \phi + a\lambda \theta \eta )(\beta + \beta_{1} )}}{{\theta \phi \eta \beta_{1} (\lambda + \beta + \eta + \alpha_{0} )}}$

$$\mu^{\prime}_{3} = \frac{{\theta \beta_{1} + (\lambda + \alpha_{0} )(\beta + \beta_{1} + \theta )}}{{\theta \beta_{1} (\lambda + \beta_{1} + \alpha_{0} )}},\;\mu^{\prime}_{4} = \frac{{\beta_{1} \phi + (\alpha_{0} + \lambda )(\beta + \beta_{1} )}}{{\phi \beta_{1} (\lambda + \beta + \alpha_{0} + \phi )}}$$

$$\mu^{\prime}_{5} = \frac{{\phi \beta_{1} + (\lambda + \alpha_{0} )(\beta + \beta_{1} + \phi )}}{{\phi \beta_{1} (\lambda + \beta_{1} + \alpha_{0} )}},\;\mu^{\prime}_{6} = \frac{{\beta_{1} \eta \theta \phi + \alpha_{0} (\theta + \beta )\eta \phi + \lambda (\eta + \beta )\theta \phi + a\lambda (\beta + \beta_{1} )\eta \theta }}{{\theta \phi \eta \beta_{1} (\lambda + \beta_{1} + \alpha_{0} )}}$$

(4)

3 Reliability and mean time to system failure (MTSF)

Let $\phi_{i} (t)$ be the c.d.f. of first passage time from the regenerative state S_i to a failed state. Regarding the failed state as absorbing state, we have the following recursive relations for: $\phi_{i} (t)$.

$$\phi_{0} (t) = q_{0,1} (t) \otimes \phi_{1} (t) + q_{0,2} (t) \otimes \phi_{2} (t)$$

$$\phi_{1} (t) = q_{1,0} (t) \otimes \phi_{0} (t) + q_{1,3} (t) \otimes \phi_{3} (t) + q_{1,9} (t) + q_{1,10} (t)$$

$$\phi_{2} (t) =\, q_{2,0} (t) \otimes \phi_{0} (t) + q_{2,4} (t) \otimes \phi_{4} (t) + q_{2,6} (t) \otimes \phi_{6} (t) + q_{2,23} (t) + q_{2,28} (t)$$

$$\phi_{3} (t) = q_{3,1} (t) \otimes \phi_{1} (t) + q_{3,13} (t) + q_{3,15} (t)$$

$$\phi_{4} (t) = q_{4,0} (t) \otimes \phi_{0} (t) + q_{4,5} (t) \otimes \phi_{5} (t) + q_{4,17} (t) + q_{4,20} (t)$$

$$\phi_{5} (t) = q_{5,4} (t) \otimes \phi_{4} (t) + q_{5,32} (t) + q_{5,34} (t)$$

$$\phi_{6} (t) = q_{6,2} (t) \otimes \phi_{2} (t) + q_{6,24} (t) + q_{6,26} (t).$$

(5)

Taking L.T. of above relation (6.6.1) and solving for $\tilde{\phi }_{0} (t)$. We have

$$R^{*} (s) = \frac{{1 - \tilde{\phi }_{0} (s)}}{s}$$

(6)

The reliability of the system model can be obtained by taking Laplace inverse transformation of (6.6.2). The mean time to system failure (MTSF) is given by:

$$\begin{aligned} {\text{MTSF}} & = \mathop {\lim }\limits_{s \to 0} \frac{{1 - \tilde{\phi }_{0} (s)}}{s} \\ & = \frac{{\left[ {\begin{array}{*{20}l} {[\{ (\theta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} \{ (\eta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} } \hfill \\ {\{ (\phi + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} ] + [\alpha_{0} \{ (\eta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} (\lambda + \alpha_{0} + \beta_{1} + \beta )} \hfill \\ {\{ (\phi + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} ] + [\lambda \{ (\theta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} (\lambda + \alpha_{0} + \beta_{1} + \beta )\} } \hfill \\ {\{ (\phi + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} ] + [a\lambda \eta (\lambda + \alpha_{0} + \beta_{1} )(\lambda + \alpha_{0} + \beta + \beta_{1} )} \hfill \\ {\{ (\theta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} )\} ]} \hfill \\ \end{array} } \right]}}{{\left[ {\begin{array}{*{20}l} {[(\lambda + \alpha_{0} )\{ (\eta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} )\} \{ (\theta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} )\} } \hfill \\ { - \theta \alpha_{0} (\lambda + \alpha_{0} + \beta_{1} )\{ (\eta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} )\} } \hfill \\ { - b\eta \lambda (\lambda + \alpha_{0} + \beta_{1} )\{ (\theta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} )\} ] \, } \hfill \\ {[(\phi + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} ] - [a\eta \lambda \phi (\lambda + \alpha_{0} + \beta_{1} )^{2} \{ (\theta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} )]} \hfill \\ \end{array} } \right]}} \\ \end{aligned}$$

(7)

4 Steady state availability

Let $A_{i} (t)$ be the probability that the system is in up-state at instant ‘t’ given that the system entered regenerative state S_i at t = 0. The recursive relations for $A_{i} (t)$ are given as:

$$A_{0} (t) = M_{0} (t) + q_{0,1} (t) \oplus A_{1} (t) + q_{0,2} (t) \oplus A_{2} (t)$$

$$\begin{aligned} A_{1} (t) & = M_{1} (t) + q_{1,0} (t) \oplus A_{0} (t) + [q_{1,1;10} (t) + q_{1,1;10(11,12)} (t)] \oplus A_{1} (t) + [q_{1,2;9} (t) + q_{1,2;9(8,7)} (t)] \oplus A_{2} (t) \\ & \quad + q_{1,3} (t) \oplus A_{3} (t) \\ \end{aligned}$$

$$\begin{aligned} A_{2} (t) & = M_{2} (t) + q_{20} (t) \oplus A_{0} (t) + [q_{2,2;23} (t) + q_{2,2;23(24,25)} (t) + q_{2,2;28} (t) + q_{2,2;28,31} (t) + q_{2,2;28(29,30)} (t) \\ & \quad + q_{2,2;28(29,30)31} (t) + q_{2,2;28,31(32,33)} (t) + q_{2,2;28(29,30)31(32,33)} ] \oplus A_{2} (t) + q_{2,4} (t) \oplus A_{4} (t) \\ & \quad + q_{2,6} (t) \oplus A_{6} (t) \\ \end{aligned}$$

$$A_{3}^{{}} (t) = M_{3} (t) + [q_{3,1} (t) + q_{3,1;(13,14)} (t)] \oplus A_{1} (t) + q_{3,2;(15,16)} (t) \oplus A_{2} (t)$$

$$\begin{aligned} A_{4} (t) & = M_{4} (t) + q_{4,0} (t) \oplus A_{0} (t) + [q_{4,1;20} (t) + q_{4,1;20(21,22)} (t)] \oplus A_{1} (t) \\ & \quad + [q_{4,2;17} (t) + q_{4,2;17(18,19)} (t)] \oplus A_{2} (t) + q_{4,5} (t) \oplus A_{5} (t)\, \\ \end{aligned}$$

$$A_{5} (t) =\, M_{5} (t) + [q_{5,1;(34,35)} (t)] \oplus A_{1} (t) + [q_{5,2;(32,33)} (t)] \oplus A_{2} (t) + q_{5,4} (t) \oplus A_{4} (t)$$

$$\begin{aligned} A_{6} (t) & = M_{6} (t) + [ \, q_{6,2} (t) + q_{6,2;(24,25)} (t) + \,q_{6,2;(26,27)} (t) + q_{6,2;(26,27)31} (t) \\ & \quad + \, q_{6,2;(26,27)31(32,33)} ] \oplus A_{2} (t), \\ \end{aligned}$$

(8)

where $M_{i} (t)$ is the probability that the system is up initially in state $S_{i} \in E$ is up at time t without visiting to any other regenerative state, we have

$$\begin{aligned} M_{0} (t) & = {\text{e}}^{{ - (\alpha _{0} + \lambda )t}} ,\;M_{1} (t) = {\text{e}}^{{ - (\alpha _{0} + \lambda + \beta )t}} \overline{{F(t)}} ,\;M_{2} (t) = {\text{e}}^{{ - (\alpha _{0} + \beta + \lambda )t}} \overline{{H(t)}} \\ M_{4} (t) & = {\text{e}}^{{ - (\alpha _{0} + \beta + \lambda )t}} \overline{{G(t)}} \;{\text{and}}\;M_{3} (t) = M_{5} (t) = M_{6} (t) = {\text{e}}^{{ - (\alpha _{0} + \beta + \lambda )t}} \\ \end{aligned}$$

(9)

Taking Laplace transformation of above relations (8) and (9) and solving for $A_{0}^{*} (s)$, the steady state availability is given by

$$A_{0} (\infty ) = \mathop {\lim }\limits_{s \to 0} sA_{0}^{*} (s) = \mathop {\lim }\limits_{s \to 0} \frac{{sN_{0}^{*} }}{{D_{0}^{*} }} = \frac{{N_{0} }}{{D^{\prime}_{0} }}\quad \left( {\frac{0}{0}\,{\text{form}}} \right)$$

(10)

$${\text{where}}\;N_{0} = \mathop {\lim }\limits_{s \to 0} N_{0}^{*} \quad {\text{and}}\quad D_{0}^{\prime } = \mathop {\lim }\limits_{s \to 0} D_{0}^{\prime *}$$

(11)

$$N_{0} = \frac{{\left[ \begin{aligned} \{ (\phi + \lambda + \alpha_{0} + \beta_{1} )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} \{ (\theta + \lambda + \alpha_{0} + \beta_{{}} )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} \hfill \\ \{ (\eta + \lambda )(\lambda + \alpha_{0} + \beta_{1} ) + \lambda \beta \} \hfill \\ \end{aligned} \right]}}{{[(\lambda + \alpha_{0} )(\lambda + \alpha_{0} + \beta_{1} )^{3} (\lambda + \alpha_{0} + \theta + \beta )(\lambda + \alpha_{0} + \phi + \beta )(\lambda + \alpha_{0} + \eta + \beta )]}}$$

(12)

$$D^{\prime}_{0} = X + T(P_{1} + P_{2} + P_{3} )$$

(13)

where

$$X = \frac{{\left[ {\eta \{ (\theta + \alpha_{0} + \lambda + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - (\alpha_{0} (\alpha_{0} + \lambda + \beta + \beta_{1} ) + \beta \beta_{1} )} \right]}}{{(\lambda + \alpha_{0} )(\lambda + \alpha_{0} + \beta_{1} )(\lambda + \alpha_{0} + \theta + \beta )(\lambda + \alpha_{0} + \eta + \beta )}}$$

$$T = \frac{{\left[ {(\phi + \alpha_{0} + \lambda + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta_{1} \beta \} } \right]}}{{[(\lambda + \alpha_{0} + \beta_{1} )(\lambda + \alpha_{0} + \phi + \beta )]}}$$

$$\begin{aligned} P_{1} = \frac{{\left[ \begin{array}{l} [\{ (\theta + \alpha _{0} + \lambda + \beta )(\lambda + \alpha _{0} + \beta ) - \beta \beta _{1} \} - \alpha _{0} (\alpha _{0} + \lambda + \beta + \beta _{1} )\} \\ \{ (\eta + \alpha _{0} + \lambda + \beta )(\lambda + \alpha _{0} + \beta ) - \beta \beta _{1} \} - \lambda (\alpha _{0} + \lambda + \beta + \beta _{1} )\} ] - \alpha _{0} \lambda (\alpha _{0} + \lambda + \beta + \beta _{1} )^{2} \\ \end{array} \right]}}{{(\lambda + \alpha _{0} + \beta _{1} )^{2} (\theta + \alpha _{0} + \lambda + \beta )(\eta + \alpha _{0} + \lambda + \beta )}} \\ P_{3} = \frac{{\left[ \begin{array}{l} [\lambda \{(\theta+\alpha _{0}+\lambda+\beta )(\lambda + \alpha _{0} + \beta _{1} ) - \beta \beta _{1} \} ][\beta + \beta _{1} ][(\alpha _{0} + \lambda + \beta + \beta _{1} )\{ \alpha _{0} \eta \phi + \lambda \theta \phi + a\eta \theta \eta ) \\ + (\alpha _{0} + \lambda + \beta _{1} )\eta \theta \phi ] \\ \end{array} \right]}}{{[\beta _{1} \eta \phi (\lambda + \alpha _{0} )(\lambda + \alpha _{0} + \beta _{1} )^{2} (\lambda + \alpha _{0} + \theta + \beta )(\lambda + \alpha _{0} + \eta + \beta )]}} \\ P_{2} = \frac{{\left[ {\alpha _{0} \eta (\beta + \beta _{1} )\{ (\alpha _{0} + \lambda + \theta + \beta + \beta _{1} )(\alpha _{0} + \lambda ) + \beta _{1} \theta \} } \right]}}{{[\theta \beta _{1} (\lambda + \alpha _{0} )(\lambda + \alpha _{0} + \beta _{1} )(\lambda + \alpha _{0} + \theta + \beta )(\lambda + \alpha _{0} + \eta + \beta )]}} \end{aligned}$$

(14)

5 Busy period analysis for server due to preventive maintenance

(a) Let $B_{i}^{p} (t)$ be the probability that the server is busy in preventive maintenance of the unit at an instant ‘t’ given that system entered state i at t = 0. The recursive relations for $B_{i}^{p} (t)$ are as follows

$$B_{0}^{P} (t) = q_{0,1} (t) \oplus B_{1}^{P} (t) + q_{0,2} (t) \oplus B_{2}^{P} (t)$$

$$\begin{aligned} B_{1}^{P} (t) & = W_{1}^{P} (t) + q_{1,0} (t) \oplus B_{0}^{P} (t) + [q_{1,1;10} (t) + q_{1,1;10(11,12)} (t)] \oplus B_{1}^{P} (t) \\ & \quad + [q_{1,2;9} (t) + q_{1,2;9(8,7)} (t)] \oplus B_{2}^{P} (t) + q_{1,3} (t) \oplus B_{3}^{P} (t) \\ \end{aligned}$$

$$\begin{aligned} B_{2}^{P} (t) & = W_{2}^{P} (t) + q_{20} (t) \oplus B_{0}^{P} (t) + [q_{2,2;23} (t) + q_{2,2;23(24,25)} (t) + q_{2,2;28} (t) + q_{2,2;28,31} (t) + q_{2,2;28(29,30)} (t) \\ & \quad + q_{2,2;28(29,30)31} (t) + q_{2,2;28,31(32,33)} (t) + q_{2,2;28(29,30)31(32,33)} ] \oplus B_{2}^{P} (t) + q_{2,4} (t) \oplus B_{4}^{P} (t) \\ & \quad + q_{2,6} (t) \oplus B_{6}^{P} (t) \\ B_{3}^{P} (t) & = W_{3}^{P} (t) + [q_{3,1} (t) + q_{3,1;(13,14)} (t)] \oplus B_{1}^{P} (t) + q_{3,2;(15,16)} (t) \oplus B_{2}^{P} (t) \\ \end{aligned}$$

$$\begin{aligned} B_{4}^{P} (t) & = q_{4,0} (t) \oplus B_{0}^{P} (t)(t) + [q_{4,1;20} (t) + q_{4,1;20(21,22)} (t)] \oplus B_{1}^{P} (t) \\ & \quad + [q_{4,2;17} (t) + q_{4,2;17(18,19)} (t)] \oplus B_{2}^{P} (t) + q_{4,5} (t) \oplus B_{5}^{P} (t) \\ \end{aligned}$$

$$B_{5}^{P} (t) = [q_{5,1;(34,35)} (t)] \oplus B_{1}^{P} (t) + [q_{5,2;(32,33)} (t)] \oplus B_{2}^{P} (t) + q_{5,4} (t) \oplus B_{4}^{P} (t)$$

$$\begin{aligned} B_{6}^{P} (t) & = W_{6}^{P} (t) + [ \, q_{6,2} (t) + q_{6,2;(24,25)} (t) + \,q_{6,2;(26,27)} (t) + q_{6,2;(26,27)31} (t) \\ & \quad + \, q_{6,2;(26,27)31(32,33)} ] \oplus B_{2}^{P} (t), \\ \end{aligned}$$

(15)

where $W_{i} (t)$ be the probability that the server is busy in state S_i for preventive maintenance up to time ‘t’ without making any transition to any other regenerative state or before returning to the same via one or more non-regenerative states and $\;\;\;\;\mathop {\lim }\limits_{s \to 0} W_{1}^{P*} (s) = \frac{{(\alpha_{0} + \lambda + \theta )}}{{\theta (\alpha_{0} + \lambda + \theta + \beta )}}\;$, $\;\;\;\;\mathop {\lim }\limits_{s \to 0} W_{2}^{P*} (s) = \frac{{(\alpha_{0} )}}{{\theta (\alpha_{0} + \lambda + \eta + \beta )}}\;$

$$\mathop {\lim }\limits_{s \to 0} W_{3}^{P*} (s) = \frac{{(\alpha_{0} + \lambda )}}{{\theta (\alpha_{0} + \lambda + \beta_{1} )}},\;\mathop {\lim }\limits_{s \to 0} W_{6}^{P*} (s) = \frac{{\alpha_{0} }}{{\theta (\alpha_{0} + \lambda + \beta_{1} )}}$$

(16)

Solving for $B_{0}^{p*} (s)$, the time for which server is busy due to preventive maintenance is given by

$$B_{0}^{p} (\infty ) = \mathop {\lim }\limits_{s \to 0} \,\,sB_{0}^{*p} (s) = \mathop {\lim }\limits_{s \to 0} \frac{{M_{1}^{p*} }}{{D_{0}^{\prime *} }} = \frac{{M_{1}^{P} }}{{D^{\prime}_{0} }}$$

(17)

where

$$M_{1}^{P} = \mathop {\lim }\limits_{s \to 0} M_{1}^{P*} (s)\;{\text{and}}\;D^{\prime}_{0} = \mathop {\lim }\limits_{s \to 0} D_{0}^{\prime *} (s)$$

(18)

$$M_{1}^{P} (t) = \frac{\begin{aligned} \;[\alpha_{0} \{ (\theta + \lambda + \beta + \alpha_{0} )(\lambda + \beta_{1} + \alpha_{0} ) - \beta \beta_{1} \} \{ (\phi + \lambda + \beta + \alpha_{0} )(\lambda + \beta_{1} + \alpha_{0} ) - \beta \beta_{1} \} \hfill \\ \{ (\eta + \lambda )(\lambda + \beta_{1} + \alpha_{0} ) + \beta \lambda \} ] \hfill \\ \end{aligned} }{{[\theta (\lambda + \alpha_{0} )(\theta + \lambda + \beta + \alpha_{0} )(\phi + \lambda + \beta + \alpha_{0} )(\eta + \lambda + \beta + \alpha_{0} )(\lambda + \beta_{1} + \alpha_{0} )^{3} ]}}$$

(19)

and $D^{\prime}_{0}$ has already been defined in (13)

6 Busy period analyses for server due to inspection and repair

Let $B_{i}^{R} (t)$ be the probability that the server is busy in inspection or repair of the unit at an instant ‘t’ given that system entered state S_i at t = 0. The recursive relations for $B_{i}^{R} (t)$ is as follows

$$B_{0}^{R} (t) = q_{0,1} (t) \oplus B_{1}^{R} (t) + q_{0,2} (t) \oplus B_{2}^{R} (t)$$

$$\begin{aligned} B_{1}^{R} (t) & = q_{1,0} (t) \oplus B_{0}^{R} (t) + [q_{1,1;10} (t) + q_{1,1;10(11,12)} (t)] \oplus B_{1}^{R} (t) \\ & \quad + [q_{1,2;9} (t) + q_{1,2;9(8,7)} (t)] \oplus B_{2}^{R} (t) + q_{1,3} (t) \oplus B_{3}^{R} (t) \\ \end{aligned}$$

$$\begin{aligned} B_{2}^{R} (t) & = W_{2}^{R} (t) + q_{20} (t) \oplus B_{0}^{R} (t) + [q_{2,2;23} (t) + q_{2,2;23(24,25)} (t) + q_{2,2;28} (t) + q_{2,2;28,31} (t) + q_{2,2;28(29,30)} (t) \\ & \quad + q_{2,2;28(29,30)31} (t) + q_{2,2;28,31(32,33)} (t) + q_{2,2;28(29,30)31(32,33)} ] \oplus B_{2}^{R} (t) + q_{2,4} (t) \oplus B_{4}^{R} (t) \\ \, & \quad + q_{2,6} (t) \oplus B_{6}^{R} (t) \\ B_{3}^{R} (t) & = [q_{3,1} (t) + q_{3,1;(13,14)} (t)] \oplus B_{1}^{R} (t) + q_{3,2;(15,16)} (t) \oplus B_{2}^{R} (t) \\ \end{aligned}$$

$$\begin{aligned} B_{4}^{R} (t) & = W_{4}^{R} (t)(t) + q_{4,0} (t) \oplus B_{0}^{P} (t) + [q_{4,1;20} (t) + q_{4,1;20(21,22)} (t)] \oplus B_{1}^{R} (t) \\ & \quad + [q_{4,2;17} (t) + q_{4,2;17(18,19)} (t)] \oplus B_{2}^{R} (t) + q_{4,5} (t) \oplus B_{5}^{R} (t)\, \\ \end{aligned}$$

$$\begin{aligned} B_{5}^{R} (t) & = W_{5}^{R} (t) + [q_{{5,1;(34,35)}} (t)] \oplus B_{1}^{P} (t) + [q_{{5,2;(32,33)}} (t)] \oplus B_{2}^{P} (t) + q_{{5,4}} (t) \oplus B_{4}^{P} (t) \\ B_{6}^{R} (t) & = W_{6}^{R} (t) + [{\text{ }}q_{{6,2}} (t) + q_{{6,2;(24,25)}} (t) + \,q_{{6,2;(26,27)}} (t) + q_{{6,2;(26,27)31}} (t) \\ & \quad + {\text{ }}q_{{6,2;(26,27)31(32,33)}} ] \oplus B_{2}^{R} (t) \\ \end{aligned}$$

(20)

where $W_{i}^{R} (t)$ be the probability that the server is busy in state S_i due to repair up to time ‘t’ without making any transition to any other regenerative state or before returning to the same via one or more non-regenerative states and $\mathop {\lim }\limits_{s \to 0} \,W_{2}^{R*} (s) = \frac{{\phi \eta (\beta + \eta )(\beta + \phi ) + \lambda \{ a\eta^{2} (\beta + \phi ) + \beta \phi (\beta + \phi ) + a\eta \beta^{2} \} }}{{\phi \eta (\beta + \eta )(\beta + \phi )(\alpha_{0} + \lambda + \eta + \beta )}}$

$$\begin{aligned} \mathop {\lim }\limits_{s \to 0} W_{4}^{R*} (s) & = \frac{{(\alpha_{0} + \lambda + \phi )}}{{\phi (\alpha_{0} + \lambda + \beta + \phi )}},\;\mathop {\lim }\limits_{s \to 0} W_{5}^{R*} (s) = \frac{{(\alpha_{0} + \lambda )}}{{\phi (\alpha_{0} + \lambda + \beta_{1} )}} \\ \mathop {\lim }\limits_{s \to 0} W_{6}^{R*} (s) & = \frac{\lambda (\phi + a\eta )}{{\phi (\alpha_{0} + \lambda + \beta_{1} )}} \\ \end{aligned}$$

(21)

Solving for $B_{0}^{R*} (s)$, the time for which server is busy due to preventive maintenance is given by

$$B_{0}^{R} (\infty ) = \mathop {\lim }\limits_{s \to 0} \,\,sB_{0}^{R*} (s) = \mathop {\lim }\limits_{s \to 0} \frac{{M_{2}^{R*} }}{{D_{0}^{\prime *} }} = \frac{{M_{2}^{R} }}{{D^{\prime}_{0} }}$$

(22)

$$M_{2}^{R} = \mathop {\lim }\limits_{s \to 0} M_{2}^{R*} (s)\;{\text{and}}\;D^{\prime}_{0} = \mathop {\lim }\limits_{s \to 0} D_{0}^{\prime *} (s)$$

(23)

Using relations (21) and (22) into (23)

$$M_{1}^{R} = GH$$

where $G = \frac{{\left[ {\lambda [\{ (\theta + \lambda + \beta + \alpha_{0} )(\lambda + \beta_{1} + \alpha_{0} ) - \beta \beta_{1} \} ]} \right]}}{{[(\theta + \lambda + \beta + \alpha_{0} )(\lambda + \beta_{1} + \alpha_{0} )(\lambda + \alpha_{0} )]}}$

$$H = \frac{{\left[ \begin{aligned} (\phi + \alpha_{0} + \lambda + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta_{1} \beta \} [\{ (\lambda + \beta_{1} + \alpha_{0} )\eta + \lambda \beta \} (\beta + \eta )(\beta + \phi )(\phi + a\eta ) + \hfill \\ \lambda (\lambda + \beta_{1} + \alpha_{0} )\{ (a\eta^{2} + \beta \phi )(\beta + \phi ) + a\eta \beta^{2} \} ] \hfill \\ \end{aligned} \right]}}{{\phi \eta (\beta + \eta )(\beta + \phi )(\lambda + \beta + \eta + \alpha_{0} )(\lambda + \beta + \phi + \alpha_{0} )(\lambda + \beta_{1} + \alpha_{0} )^{2} }}$$

(24)

and $D^{\prime}_{0}$ has already been defined in (13).

7 Expected number of visits by the server due to preventive maintenance and due to inspection, repair

Let $N_{i}^{P} (t)$ be the expected number of preventive maintenance and repair of unit by the server in (0, t] given that the system entered the regenerative state i at t = 0. The recursive relations for $N_{i}^{P} (t)$ are given by

$$N_{0}^{P} (t) = Q_{0,1} (t) \oplus (N_{1}^{P} (t) + \delta_{PK} ) + Q_{0,2} (t) \oplus (N_{2}^{P} (t) + \delta_{RK} )$$

$$\begin{aligned} N_{1}^{P} (t) & = \,Q_{1,0} (t) \oplus N_{0}^{P} (t) + [Q_{1,1;10} (t) + q_{1,1;10(11,12)} (t)] \oplus N_{1}^{P} (t) + [Q_{1,2;9} (t) + Q_{1,2;9(8,7)} (t)] \oplus N_{2}^{P} (t) \\ & \quad + Q_{1,3} (t) \oplus N_{3}^{P} (t) \\ \end{aligned}$$

$$\begin{aligned} N_{2}^{P} (t) & = q_{20} (t) \oplus N_{0}^{P} (t) + [q_{2,2;23} (t) + q_{2,2;23(24,25)} (t) + q_{2,2;28} (t) + q_{2,2;28,31} (t) + q_{2,2;28(29,30)} (t) \\ & \quad + q_{2,2;28(29,30)31} (t) + q_{2,2;28,31(32,33)} (t) + q_{2,2;28(29,30)31(32,33)} ] \oplus N_{2}^{P} (t) + q_{2,4} (t) \oplus N_{4}^{P} (t) \\ & \quad + \;q_{2,6} (t) \oplus N_{6}^{P} (t) \\ \end{aligned}$$

$$N_{3}^{P} (t) = [q_{3,1} (t) + q_{3,1;(13,14)} (t)] \oplus N_{1}^{P} (t) + q_{3,2;(15,16)} (t) \oplus N_{2}^{P} (t)$$

$$\begin{aligned} N_{4}^{P} (t) & = q_{4,0} (t) \oplus N_{0}^{P} (t) + [q_{4,1;20} (t) + q_{4,1;20(21,22)} (t)] \oplus N_{1}^{P} (t) \\ & \quad + [q_{4,2;17} (t) + q_{4,2;17(18,19)} (t)] \oplus N_{2}^{P} (t) + q_{4,5} (t) \oplus N_{5}^{P} (t)\, \\ \end{aligned}$$

$$N_{5}^{P} (t) = [q_{5,1;(34,35)} (t)] \oplus N_{1}^{P} (t) + [q_{5,2;(32,33)} (t)] \oplus N_{2}^{P} (t) + q_{5,4} (t) \oplus N_{4}^{P} (t)$$

$$\begin{aligned} N_{6}^{P} (t) & = [{\text{ }}q_{{6,2}} (t) + q_{{6,2;(24,25)}} (t) + \,q_{{6,2;(26,27)}} (t) + q_{{6,2;(26,27)31}} (t) \\ & \quad + {\text{ }}q_{{6,2;(26,27)31(32,33)}} ] \oplus N_{2}^{P} (t) \\ \end{aligned}$$

(25)

(K = P, for preventive maintenance; K = R, for inspection and repair of the units).

Solving for $\tilde{N}_{0}^{p} (s)$. The expected no of preventive maintenance per unit time are, respectively, of given by

$$N_{0}^{P} (\infty ) = \mathop {\lim }\limits_{s \to 0} s\tilde{N}_{0}^{P} (s) = \frac{{\tilde{M}_{3}^{P} }}{{\tilde{D^{\prime}}_{0} }} = \frac{{M_{3} }}{{D^{\prime}_{0} }}$$

(26)

$$M_{3} = \mathop {\lim }\limits_{{s \to 0}} \,\tilde{M}_{3}^{p} (s) = \frac{{\left[ \begin{array}{l} [\eta \alpha _{0} \{ (\phi + \lambda + \alpha _{0} + \beta _{1} )(\lambda + \alpha _{0} + \beta _{1} ) - \beta \beta _{1} \} [\{ (\theta + \lambda + \alpha _{0} + \beta )(\lambda + \alpha _{0} + \beta _{1} ) - \beta \beta _{1} \} \\ - \{ \alpha _{0} (\alpha _{0} + \lambda + \beta + \beta _{1} )\} ] - [a\eta \lambda \{ (\theta + \lambda + \alpha _{0} + \beta )(\lambda + \alpha _{0} + \beta _{1} ) - \beta \beta _{1} \} \\ {\text{ }}(\alpha _{0} + \lambda + \beta + \beta _{1} )] \\ \end{array} \right]}}{{(\lambda + \alpha _{0} )(\lambda + \alpha _{0} + \beta _{1} )^{2} (\lambda + \alpha _{0} + \theta + \beta )(\lambda + \alpha _{0} + \phi + \beta )(\eta + \alpha _{0} + \phi + \beta )}}$$

(27)

and $D^{\prime}_{0}$ has already been defined in (13).

Solving for $\tilde{N}_{0}^{R} (s)$. The expected no of inspection and repair per unit time are, respectively, given by

$$N_{0}^{R} (\infty ) = \mathop {\lim }\limits_{s \to 0} s\tilde{N}_{0}^{R} (s) = \frac{{\tilde{M}_{4}^{R} }}{{\tilde{D^{\prime}}_{0} }} = \frac{{M_{4} }}{{D^{\prime}_{0} }}$$

(28)

where

$$M_{4} = \mathop {\lim }\limits_{s \to 0} \tilde{M}_{4}^{R} (s) = \frac{{\left[ \begin{array}{l} [\eta \lambda \{ (\phi + \lambda + \alpha_{0} + \beta_{1} )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} [\{ (\theta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} \\ - \{ \alpha_{0} (\alpha_{0} + \lambda + \beta + \beta_{1} )\} ] - [a\eta \lambda \{ (\theta + \lambda + \alpha_{0} + \beta )(\lambda + \alpha_{0} + \beta_{1} ) - \beta \beta_{1} \} \\ \, (\alpha_{0} + \lambda + \beta + \beta_{1} )] \\ \end{array} \right]}}{{(\lambda + \alpha_{0} )(\lambda + \alpha_{0} + \beta_{1} )^{2} (\lambda + \alpha_{0} + \theta + \beta )(\lambda + \alpha_{0} + \phi + \beta )(\eta + \alpha_{0} + \phi + \beta )}}$$

and $D^{\prime}_{0}$ has already been defined in (13).

8 Profit analysis

The profit incurred to the system model in steady state can be obtained as

$$P = K_{0} A_{0} - K_{1} B_{0}^{R} - K_{2} B_{0}^{P} - K_{3} N_{0}^{R} - K_{4} N_{0}^{P}$$

(29)

Let K₀ = (5000): revenue per unit up-time of the system,

K₁ = (400): cost per unit time for which server is busy due preventive maintenance,

K₂ = (500): cost per unit time for which server is busy due to repair and inspection,

K₃ = (350): cost per visit per unit time repair and inspection, and K₄ = (300): cost per visit per unit time preventive maintenance.

9 Discussion

To verify whether the cold standby system with priority to preventive maintenance over inspection is profitable or not, the numerical and graphical behavior of mean time to system failure, availability and profit function has been studied in Figs. 2, 3, 4, respectively. The application of this model in the industry as well as in the water supply system by taking particular values to the parameters like (α₀, β, β₁, λ, ϕ, η and θ).

Fig. 2

Preventive maintenance rate (θ)

Fig. 3

Preventive maintenance rate (θ)

Fig. 4

Preventive maintenance rate (θ)

Figure 2 is constructed to depict the graphical behavior of the MTSF (mean time to system failure).Thus, mean time to system failure increases swiftly with the increase of preventive maintenance rate θ. The curve L₂ indicated when the rate by which the unit goes for preventive maintenance after completions of pre-specific maximum operation time α₀ changes from 5 to 7 the MTSF declined sharply, but in increasing manner as preventive maintenance rate θ increasing.

Figure 3 highlights graphical behavior of availability of the system Vs preventive maintenance rate θ. There is relatively steep rise in values of availability against parameter β₁ in comparison to other parameters. Second line L₂ of this table shows the when the rate α₀ change from 5 to 7 then the value of availability of the system rapidly declined from the range (0.48–0.72) to (0.33–0.63) The curve name L₁(α₀ = 5, β = .45, β₁ = .55, λ = .01, ϕ = 2.5, η = 1.5) L₅(α₀ = .5, β = .45, β₁ = .55, λ = .03, ϕ = 2.5, η = 1.5) L₆(α₀ = .5, β = .45, β₁ = .55, λ = .03 and ϕ = 3.5, η = 1.5) and the curve L₇(α₀ = .5, β = .45, β₁ = .55, λ = .01 and ϕ = 3.5, η = 2) overlapping showing the similar impact of failure rate λ and repair rate ϕ and inspection rate η, on availability of system.

Figure 4 depicts the graphical behavior of the profit Vs preventive maintenance rate θ. The effect of different parameters can be observed easily from the graph. The system is more profitable if it works in controlled weather condition. The curve namely curve L₂ (α₀ = 7, β = .45, β₁ = .55, λ = .01, ϕ = 2.5, η = 1.5) indicates that the rate of the specific operation time α₀ increase 5–7 then there is steep fall in values of profit in comparison to other parameter. The curves L₅(α₀ = .5, β = .45, β₁ = .55, λ = .03, ϕ = 2.5, η = 1.5) L₆(α₀ = .5, β = .45, β₁ = .55, λ = .03, ϕ = 3.5, η = 1.5) and the curve L₇(α₀ = .5, β = .45, β₁ = .55, λ = .03, ϕ = 2.5, η = 2) are coinciding curves showing the similar impact of failure rate λ and repair rate ϕ inspection rate η on profit of system.

10 Conclusion

It is concluded that the present model can be made the water supply system more available/beneficial by enhancing the inspection rate of system. Furthermore, by increasing preventive maintenance rate, a considerable profit can be obtained from system. In normal and abnormal weather conditions it is inferred that the system becomes productive when the preventive maintenance rate increases. Consequently, modifying maintenance mechanism adapted by the server followed by prioritizing preventive maintenance over inspection does wonders to the system.