1 Introduction

For modelling lifetime data, the exponential, Weibull, and Gamma distributions have been extensively used in recent past with wide applications in reliability, economics, medical sciences, etc. However, these distributions have a number of limitations when it comes to handling diverse classes of complex data. They mainly lack the ability to analyse non-monotone hazard rate data sets. The development of new families of flexible distributions that may easily explain the complicated behaviour of the data was motivated by the limitations associated with existing classical probability models, see Gupta and Kundu (2009), Gupta et al. (2022), Kundu and Gupta (2017), Jodra et al. (2017), Sharma et al. (2022).

In 1934, the French biologist Georges Teissier developed a distribution for modelling animal species’ mortality rates as a result of ageing only. Author of Laurent (1975) discovered that Teissier’s distribution is also useful for modelling and analysing various other real-life phenomena arise in biological and demographical studies. A non-negative random variable X is said to follow the Teissier distribution (TD) with scale parameter \(\theta \), if its probability density function (PDF) is given by (see Teissier , 1934)

$$\begin{aligned} f_{X}(x,\theta )=\theta \left( e^{\theta x}-1\right) e^{\theta x-e^{\theta x}+1},\; x>0,\; \theta >0. \end{aligned}$$
(1)

We may observe that \(f_{X}(x,\theta )\) can also be expressed as follows

$$\begin{aligned} f_{X}(x,\theta )=\theta \left( e^{\theta x}-1\right) S_X(x), \end{aligned}$$

where \(S_X(x)=e^{\theta x-e^{\theta x}+1},\; x>0,\; \theta >0\) is survival function associated with the random variable X. We can easily explore that the TD is a member of the exponential family with increasing hazard rate function and may be useful in reliability analysis. Readers are encouraged to follow Muth (1977) and Jodra et al. (2015) for more information regarding its statistical properties.

Jodra et al. (2017) suggested a two-parameter TD and explored about how it may be used in reliability theory. Singh et al. (2020) proposed a family of distributions using the TD with application to the uniform, Lomax and Weibull distribution. They also presented fitting of two real data sets using the Teissier-Weibull distribution. Recently, Sharma et al. (2022) introduced a two parameter extension of the Teissier distribution which shows increasing, decreasing, and bathtub shapes for its hazard rate function. They also investigated its important statistical properties with a real application. Poonia and Azad (2022) consider an Alpha power exponentiated Teissier distribution and applied it for climate datasets. A bounded form of Teissier distribution on unit interval has also been studied by Krishna et al. (2022). The TD with location parameter is introduced by Singh et al. (2022). Recently, Sharma et al. (2023) investigated an additive hazards model based on the Teissier and Weibull distributions and they used it to model bathtub shaped hazard rate data sets.

The joint distribution is an extremely important component in the process of modeling the dependence of random variables. In this paper, we focus our attention to model bivariate random variables. In recent years, statisticians have become increasingly interested in the construction of bivariate distributions with specified marginals. Statistics literature has offered a number of cutting-edge methods for building bivariate distributions based on conventional univariate distributions. A family of bivariate distributions can be created using a variety of useful techniques, mainly those based on the marginal and conditional distributions, the cumulative hazard rate function, order statistic, transmuted transformation, etc. For further information on these methods, see the following citations: Balakrishnan and Lai (2009), Alegría and Déniz (2008), Ali Dolati, Mohammad Amini, and SM Mirhosseini (2014), Kundu and Gupta (2017), Samanthi and Sepanski (2019), Pathak and Vellaisamy (2020); Gupta et al. (2022). In addition to these methods, in recent years, copula functions have emerged as an important tool for the development of the families of multivariate distributions. Recently, a number of authors have developed a variety of bivariate distributions in order to analyse lifetime data using copula. However, the weakness of the copula approach lies in selecting a suitable copula from the data. We suggest readers to follow Balakrishnan and Lai (2009) for more information on copulas and construction of the bivariate distributions.

Dolati et al. (2014) proposed and studied a remarkable technique for building bivariate distributions based on order statistics. It is worthwhile to mention here that the marginals of bivariate distributions constructed using this technique are proportional reversed hazard rate models. Mirhosseini et al. (2015) proposed a new family of generalized bivariate exponential distributions and studied its distributional properties. Pathak and Vellaisamy (2020) proposed a new bivariate generalized linear exponential distribution and derived expressions for some of its statistical quantities. They also compared the proposed model with generalized bivariate exponential and generalized bivariate Rayleigh distribution along with a real life application. A novel bivariate generalized Weibull distribution has also been proposed and studied by Pathak et al. (2022). Recently, Arshad et al. (2023) constructed a new family of bivariate distributions using different marginals that can be useful in various real situations.

This article aims to introduce a new family of bivariate Teissier (BT) distributions via minimum order statistic approach. The proposed distribution is a three parameter absolutely continuous distribution and its marginals follow the exponentiated Teissier distribution. The suggested BT distribution has few parameters and it is capable to accommodate a variety of density shapes. To the best of our knowledge, the BT distribution under consideration has not been investigated in the literature. The BT distribution shows the positive dependence and can be effectively used for various practical applications. Several other dependence properties for the proposed distribution can be easily explored. We derive the closed form expressions for various important statistical measures such as conditional density, joint moments, regression function, and quantile function. The maximum likelihood and Bayes estimators cannot be obtained in closed algebraic forms due to the implicit form of the joint PDF. Therefore, the unknown parameters of the model are estimated numerically under both the maximum likelihood and Bayesian methodologies. The Bayes estimation was carried out using the Markov Chain Monte Carlo (MCMC) method. We also present a real data analysis to show how the suggested BT model performs better than the competing bivariate distributions.

The following is how this article is structured. Section 2 describes the model’s development with interpretation and some of its important properties. The formulae for conditional expectation, product moments, and regression functions for the BT distribution are given. The Lambert-W function (see Knuth , 1996 and Sharma et al. , 2022) is used to calculate the analytical formulation of the bivariate quantile function. Measures of dependence, reliability, and the notion of ageing are also discussed here. Section 3 deals with parameter estimation for the BT distribution. Section 4 contains extensive numerical investigations. Finally, Section 5 discusses a real-world data application of the suggested model. Section 6 brings the paper to a conclusion.

2 Proposed Bivariate Model and Interpretation

This section describes the bivariate distribution development approach. The BT distribution is introduced here, with its density and survival functions. Consider a sequence of independent Bernoulli trials with probability of \(\alpha /k, 0<\alpha <1, k=1,2,\ldots \) of the kth trail. Let N be the number of trials that are required to achieve the first success. According to Pillai and Jayakumar (1995), the random variable N follows the Mittag-Leffler distribution defined by the following probability mass function,

$$\begin{aligned} P[N=n] = \frac{(-1)^{n-1}\alpha \left( \alpha -1\right) \ldots \left( \alpha -n+1\right) }{n!}, \ n=1,2,3,\ldots \end{aligned}$$

The probability generating function of N is given by

$$\begin{aligned} g(t) = E\left( t^{N} \right) = 1-(1-t)^{\alpha }, 0<\alpha <1, t\in [0,1]. \end{aligned}$$

Let \((W_1, W_2, \ldots )\) and \((V_1, V_2, \ldots )\) be two sequences of mutually independent and identically distributed random variables. The distribution/survival function of \(W_{i}\) and \(V_{i}\), i = 1, 2, . . . are denoted by \(F_{1}/S_{1}\) and \(F_{2}/S_{2}\), respectively. Define \(X = \min \left( W_{1}, W_{2},\ldots , W_{N}\right) \) and \(Y = \min \left( V_{1}, V_{2}, \ldots , V_{N}\right) \). If N follows a Mittag-Leffler distribution, \(\left( X, Y\right) \) is said to follow a bivariate distribution proposed by Dolati et al. (2014).

The joint cumulative distribution function (CDF) of (X, Y) is derived as follows.

$$\begin{aligned} F(x,y)&= P[X\le x, Y \le y],\nonumber \\&= P[\min \left( W_{1}, W_{2},\ldots , W_{N}\right) \le x, \min \left( V_{1}, V_{2}, \ldots , V_{N}\right) \le y],\nonumber \\&= (1-(S_{1}(x))^{n})(1-(S_{2}(y))^{n}),\nonumber \\&= \sum _{n=1}^{\infty } \left( 1-S_{1}(x)^n\right) \left( 1-S_{2}(y)^n\right) P[N=n],\nonumber \\&= \sum _{n=1}^{\infty } \left( 1-S_{1}(x)^n -S_{2}(y)^n+ \left( S_{1}(x) S_{2}(y)\right) ^{n} \right) P[N=n],\nonumber \\&= \left( 1-g(S_{1}(x))-g(S_{2}(y))+ g(S_{1}(x)S_{2}(y))\right) ,\nonumber \\&= \left( 1-S_{1}(x)\right) ^{\alpha } + \left( 1-S_{2}(y)\right) ^{\alpha }-\left( 1-S_{1}(x) S_{2}(y)\right) ^{\alpha }. \end{aligned}$$
(2)

The distribution defined in equation (2) may be interpreted as the joint distribution of the survival times of series systems. We here assume that system’s components follow the Teissier distribution, \(W_i \sim \text {Teissier}(\theta _1)\) and \(V_i \sim \text {Teissier}(\theta _2)\), \(i=1,2,\ldots , N\) with the PDF given in equation (1). The joint CDF of (X, Y) is given by

$$\begin{aligned} F\left( x,y\right)&= \left( 1-e^{\theta _{1} x-e^{\theta _{1} x }+1}\right) ^{\alpha }+\left( 1-e^{\theta _{2} y-e^{\theta _{2} y }+1}\right) ^{\alpha }\nonumber \\&\quad - \left( 1-\exp \left( \theta _{1} x + \theta _{2} y -e^{\theta _{1} x} -e^{\theta _{2} y }+2\right) \right) ^{\alpha }. \end{aligned}$$
(3)

The joint PDF of (X, Y) is given by

$$\begin{aligned} f(x,y)&= \alpha \theta _{1} \theta _{2} \left( 1-e^{\theta _{1} x}\right) \left( 1-e^{\theta _{2} y}\right) e^{\phi (x,y,\nu )} \left( 1-e^{\phi (x,y,\nu )}\right) ^{\alpha -2} \left[ 1-\alpha e^{\phi (x,y,\nu )}\right] , \end{aligned}$$
(4)

where \(\phi (x,y,\nu ) = \left( \theta _{1} x -e^{\theta _{1} x}+\theta _{2} y-e^{\theta _{2} y}+2\right) , \nu =(\theta _{1}, \theta _{2}), \theta _{1}>0, \theta _{2}>0, 0<\alpha <1\). We use BT\((\theta _{1}.\theta _{2},\alpha )\) to denote the BT distribution defined in (4).

We use the following expansions to derive various mathematical/ statistical properties of the BT\((\theta _{1},\theta _{2},\alpha )\),

$$\begin{aligned} S(x,y)&= \sum _{j=1}^{\infty } \left( {\begin{array}{c}\alpha \\ j\end{array}}\right) (-1)^{j+1} e^{j \phi (x,y,\nu )},\\ f(x,y)&= \theta _{1} \theta _{2}\left( 1-e^{\theta _{1} x}\right) \left( 1-e^{\theta _{2} y}\right) \sum _{j=1}^{\infty } \left( {\begin{array}{c}\alpha \\ j\end{array}}\right) (-1)^{j+1} j^{2} e^{j \phi (x,y,\nu )}, \end{aligned}$$

where S(x, y) denotes the survival function of (X, Y).

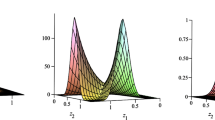
The joint CDF (3) and PDF (4) are displayed for two different parameter combinations in Fig. 1. For different choices of the model parameters, these plots have different shapes.

Fig. 1
figure 1

Surface plots of F(x, y) and f(x, y) of the BT distribution: In (a) and (b), \(\theta _1=0.25\), \(\theta _2=0.5\), \(\alpha =0.4\). In (c) and (d), \(\theta _1=1.5\), \(\theta _2=1\), \(\alpha =0.9\)

Full size image

The copula associated with the random vector (X, Y) is given by

$$\begin{aligned} C(u,v) = u+v- \left( 1-(1-u^{1/\alpha })(1-v^{1/\alpha })\right) ^{\alpha }, u,v \in (0,1), 0< \alpha < 1. \end{aligned}$$

It is introduced in Dolati et al. (2014) and also studied in Pathak and Vellaisamy (2020).

2.1 Conditional Distributions And Moments

Knowing how one variable is related to another in a bivariate situation is always important. In this section, we derive the conditional distribution along with its expected value that may be used to fit regression model. We further derive the expression of the joint moment of (X, Y). We further derive the expression of the joint moments of (X, Y). The proofs have been omitted since they are so straightforward. Results without proofs are stated below.

Proposition 1

Suppose the random vector (X, Y) follows the BT\((\theta _{1},\theta _{2},\alpha )\). The conditional PDF and CDF of \(Y|X=x\) are given by

$$\begin{aligned} f\left( y|x\right)&= \frac{\theta _{2} (e^{\theta _{2} y}-1) e^{\phi (x,y,\nu )} \left( 1-e^{\phi (x,y,\nu )}\right) ^{\alpha -2} (1-\alpha e^{\phi (x,y,\nu )})}{\left( 1-e^{\theta _{1} x-e^{\theta _{1} x}+1}\right) ^{\alpha -1}},\\ F\left( y|x\right)&=1- \frac{e^{\left( \theta _{2} y - e^{\theta _{2} y} + 1\right) } \left( 1-e^{\phi (x,y,\nu )}\right) ^{\alpha -1}}{\left( 1-e^{\left( \theta _{1}x -e^{\theta _{1} x}+1\right) }\right) ^{\alpha -1}}, \end{aligned}$$

respectively.

Proposition 2

Suppose the random vector (X, Y) follows the BT\((\theta _{1},\theta _{2},\alpha )\). The conditional expectation of \(Y|X=x\) is given by

$$\begin{aligned} E\left( Y|X=x\right) = \frac{\theta _{1} \theta _{2}\left( 1-e^{\theta _{1} x}\right) }{f_{x}(x)} \sum _{j=1}^{\infty } \left( {\begin{array}{c}\alpha \\ j\end{array}}\right) (-1)^{j+1} j^{2} e^{j \left( \theta _{1} x-e^{\theta _{1} x}+1\right) } \frac{e^{j}}{\theta _{2}^{2}} \left[ E_{1-j}^{1}(j)-E_{-j}^{1}(j)\right] , \end{aligned}$$

where \(E_{s}^{m} (z) = \frac{1}{\Gamma (m+1)} \int _{1}^{\infty } (\log u)^{m} u^{-s} e^{-zu} du\) denotes the generalised integro-exponential function (see Milgram , 1985).

Proposition 3

Suppose the random vector (X, Y) follows the BT\((\theta _{1},\theta _{2},\alpha )\). The product moment of (X, Y) is derived as follows.

$$\begin{aligned} E\left( X^{a} Y^{b}\right)= & {} \theta _{1} \theta _{2} \sum _{j=1}^{\infty } \left( {\begin{array}{c}\alpha \\ j\end{array}}\right) (-1)^{j+1} j^{2} \left[ E_{1-j}^{a}(j) -E_{-j}^{a}(j)\right] \\{} & {} \times \left[ E_{1-j}^{b}(j)-E_{-j}^{a}(j)\right] , \end{aligned}$$

where \(E_{s}^{m} (z)\) is defined in Proposition 2.

2.2 Quantile Function

Vineshkumar and Nair (2019) proposed a method of deriving bivariate quantile functions. In their approach, the quantile functions of the unconditional and conditional random variables were utilized to produce the joint quantile function. In fact, we have \(\bar{F}(x,y) = P(X>x) P(Y>y|X>x)\) for random vector (X, Y).

Definition 1

Suppose that the random vector (X, Y) follows a bivariate continuous distribution with marginals/quantiles \(F_1/Q_1\) and \(F_2/Q_2\), respectively. The bivariate quantile function of (X, Y) is defined by the pair

$$\left( Q_{1}\left( u_{1}\right) , Q_{21}\left( u_{2}|u_{1}\right) \right) , $$

where

$$Q_{1}(u_{1}) =\inf \left( {x | F_{1}(x)\ge u_{1}}, 0\le u_{1} \le 1 \right) ,$$

and

$$\begin{aligned} Q_{21}(u_{2}|u_{1}) =\inf \left[ y| P(Y\le y|X> Q_{1}(u_{1}) )\ge u_{2}, 0\le u_{2} \le 1\right] . \end{aligned}$$

Proposition 4

Let (X, Y) be the BT distributed random vector with PDF given in (4) whose marginals follow the exponentiated Teissier distribution by Sharma et al. (2022). The bivariate quantile function of the BT distribution is given by the pair

$$\left( Q_{1}\left( u_{1}\right) , Q_{21}\left( u_{2}|u_{1}\right) \right) , $$

where

$$\begin{aligned} Q_{1}(u_{1}) = -\frac{1}{\theta _{1}} + \frac{1}{\theta _{1}} \log (1-u_{1})-\frac{1}{\theta _{1}}W{-1}\left( \frac{u_{1}-1}{e}\right) , \end{aligned}$$
$$\begin{aligned} Q_{21}(u_{2}|u_{1}) = -\frac{1}{\theta _{2}} + \frac{1}{\theta _{2}} \log (1-\eta )-\frac{1}{\theta _{2}}W{-1}\left( \frac{\eta -1}{e}\right) , \end{aligned}$$

\(\frac{1-\left[ 1-(1-u_{1})(1-u_{2})\right] ^{1/\alpha }}{\left( 1-u_{1}^{1/\alpha }\right) } = (1-\eta )\) and \(W_{-1}\) denotes the Lambert-W function. The Lambert-W function provides the inverse of the function \(f(w) = we^{w}\), where w is any complex number.

2.3 Dependence, Reliability and Ageing Properties

In statistics literature, numerous concepts of dependence have been developed for the study of dependence among random variables. We start by outlining some important foundational notions of the dependence. Further information can be found in Nelsen (2007).

Definition 2

We say that (X, Y) is positive quadrant dependent (PQD) (or negative quadrant dependent (NQD)) if

$$\begin{aligned} F(x,y)\ge (\le ) F_X(x) F_Y(y)~\text {for~all}~x~\text {and}~y. \end{aligned}$$

Also, X and Y are positively correlated if \(Cov(X, Y )\ge 0\).

Definition 3

We say F(x, y) is positively regression dependent if

$$\begin{aligned} P(Y > y|X = x)~\text {is~increaing~in~x~for~all~values~of~y}. \end{aligned}$$

Definition 4

Y is left tail decreasing in X (denoted as LTD(Y|X)) if \(P(Y \le y|X \le x)\) is a non-increasing function in x for all y.

The totally positivity of order 2 (TP2) (or reverse rule of order 2 (RR2)) is a strong concept of dependence and PQD, regression dependence, and left tail decreasing properties are employed by TP2. To establish theses properties for BT distribution it is suffices to derive TP2 property for BT distribution. For a bivariate density, the TP2 property is defined by

$$\begin{aligned} f(x,y)f(x_1,y_1)-f(x_1,y)f(x,y_1)\ge (\le )~ 0,~ \text {for~ all}~x\le x_1~\text {and}~y\le y_1. \end{aligned}$$

Holland and Wang (1987) defined a local dependence function \(\gamma (x,y)\) in terms of density function for measuring dependence between X and Y as

$$\begin{aligned} \gamma (x,y)=\frac{\partial ^2}{\partial x\partial y}\ln f(x,y). \end{aligned}$$

A bivariate density f(x, y) is said to be TP2 (RR2) if and only if \(\gamma (x,y)\ge (\le )~ 0\).

For the BT distribution, we have the following result.

Proposition 5

Let \((X,Y)\sim BT(\theta _{1},\theta _{2},\alpha )\). Then, for \(0<\alpha \le 1\), f(x, y) is TP2.

Proof

Taking logarithm of (4), we get

$$\begin{aligned} \ln f(x,y)= & {} \ln (\alpha \theta _1\theta _2)+\ln (1-e^{\theta _1 x})+\ln (1-e^{\theta _2 y})+\phi (x,y,\nu )\nonumber \\{} & {} +(\alpha -2)\ln (1-e^{\phi (x,y,\nu )})+\ln (1-\alpha e^{\phi (x,y,\nu )}). \end{aligned}$$
(5)

Differentiating (5) partially with respect to x and y, we get

$$\begin{aligned} \gamma (x,y)\!=\!\theta _1\theta _2(1-e^{\theta _1 x})(1-e^{\theta _2 y})e^{\phi (x,y,\nu )}\left[ \frac{(2-\alpha )}{(1-e^{\phi (x,y,\nu )})^2}\!-\!\frac{\alpha }{(1\!-\!\alpha e^{\phi (x,y,\nu )})^2}\right] . \end{aligned}$$
(6)

For \(0<\alpha \le 1\), from (6), we see that \(\gamma (x,y)\ge 0\). This completes the proof.

For a bivariate random vector (X, Y), the hazard rate function is defined by (see Basu , 1971)

$$\begin{aligned} r(x,y)=\frac{f(x,y)}{S(x,y)}, \end{aligned}$$

where f(x, y) and S(x, y) denote the PDF and survival function, respectively.

For the BT family, the bivariate hazard rate function is

$$\begin{aligned} r(x,y)\!=\!\frac{\alpha \theta _{1} \theta _{2} \left( 1\!-\!e^{\theta _{1} x}\right) \left( 1\!-\!e^{\theta _{2} y}\right) e^{\phi (x,y,\nu )} \left( 1\!-\!e^{\phi (x,y,\nu )}\right) ^{\alpha -2} \left( 1\!-\!\alpha e^{\phi (x,y,\nu )}\right) }{\left\{ 1-\left( 1-e^{\phi (x,y,\nu )}\right) ^{\alpha }\right\} }. \end{aligned}$$

It may be observed that for \(\alpha =1\), which leads to independence of X and Y, the bivariate hazard rate function can be expressed in terms of marginal hazard rate functions as

$$\begin{aligned} r(x,y)=&\theta _{1} \theta _{2} \left( e^{\theta _{1} x}-1\right) \left( e^{\theta _{2} y}-1\right) \\ =&r^{*}(x) r^{*}(y), \end{aligned}$$

where \(r^{*}(x)=\displaystyle \frac{f_X(\cdot )}{S_X(\cdot )}\) is marginal survival hazard rate function of X.

Let (X, Y) be a bivariate random vector with joint survival function S(x, y). Define the hazard components of (X, Y) as (see Johnson and Kotz , 1975)

$$\begin{aligned} r_1(x,y)=r(y|Y>y)=-\frac{\partial }{\partial x}\ln S(x,y) \end{aligned}$$

and

$$\begin{aligned} r_2(x,y)=r(y|X>x)=-\frac{\partial }{\partial y}\ln S(x,y). \end{aligned}$$

Then the hazard gradient of a bivariate random vector (X, Y) is \((r_1(x,y), r_2(x,y))\).

For the BT distribution, we have

$$\begin{aligned} r_1(x,y)=\frac{\alpha \theta _1(1-e^{\theta _1 x}) e^{\phi (x,y,\nu )}\left( 1-e^{\phi (x,y,\nu )}\right) ^{\alpha -1}}{\left\{ 1-\left( 1-e^{\phi (x,y,\nu )}\right) ^{\alpha }\right\} } \end{aligned}$$

and

$$\begin{aligned} r_2(x,y)=\frac{\alpha \theta _2(1-e^{\theta _2 y}) e^{\phi (x,y,\nu )}\left( 1-e^{\phi (x,y,\nu )}\right) ^{\alpha -1}}{\left\{ 1-\left( 1-e^{\phi (x,y,\nu )}\right) ^{\alpha }\right\} }. \end{aligned}$$

The following result demonstrates the monotonic property of the hazard components.

Proposition 6

Let \((X,Y)\sim BT(\theta _{1},\theta _{2},\alpha )\). Then

  1. (i)

    \(r_1(x,y)\) is decreasing in y.

  2. (ii)

    \(r_2(x,y)\) is decreasing in x.

Proof

If a bivariate density f(x, y) satisfies the TP2 property, then by Shaked (1977), the conditional hazard rate \(r_1(x,y)\) is decreasing in y and \(r_2(x,y)\) is decreasing in x, respectively. Hence, considering TP2 property of BT distribution along with Shaked (1977) results, we complete the proof.

Proposition 7

The BT distribution in (3) is bivariate decreasing hazard rate.

3 Parameters Estimation

Estimating the BT distribution’s parameters might be a challenging job. In this part, we address the problem of estimation under both Bayesian and maximum likelihood estimation methodologies. The likelihood based technique becomes difficult to apply when there are several parameters. On the other hand, utilizing sophisticated sampling methods like Gibbs sampler and Metropolis-Hastings (MH) algorithm, Bayes estimates may be easily computed. In this section, we suggest applying Bayes estimation to infer about the unknown parameters of the BT distribution. The numerical computation of Bayes estimates would be achieved through the utilisation of the MH algorithm.

The log-likelihood function based on a paired data of size n from the BT distribution is given by

$$\begin{aligned} \log \ell \left( \theta _{1},\theta _{2},\alpha \right)= & {} n \left[ \log \alpha + \log \theta _{1} +\log \theta _{2}\right] + \sum _{i=1}^{n} \log (e^{\theta _{1} x_{i}}+1)\nonumber \\{} & {} +\sum _{i=1}^{n} \log (e^{\theta _{2} y_{i}}+1)\nonumber \\{} & {} +\sum _{i=1}^{n} \phi (x_{i},y_{i},\nu ) +(\alpha -1) \sum _{i=1}^{n} \log \left( 1-e^{\phi (x_{i},y_{i},\nu )}\right) \nonumber \\{} & {} +\sum _{i=1}^{n} \log \left( 1- \alpha e^{\phi (x_{i},y_{i},\nu )}\right) . \end{aligned}$$
(7)

The maximum likelihood estimates (MLEs) of the BT distribution parameters are obtained by maximizing the log-likelihood function (7) or equivalently by solving the following log-likelihood equations,

$$\begin{aligned} \frac{n}{\alpha }+ & {} \sum _{i=1}^{n} \log (1-e^{\phi _{i}}) + \sum _{i=1}^{n} \frac{-e^{\phi _{i}}}{\left( 1-\alpha e^{\phi _{i}}\right) } = 0,\end{aligned}$$
(8)
$$\begin{aligned} \frac{n}{\theta _{1}}+ & {} \sum _{i=1}^{n} \frac{x_{i} e^{\theta _{1} x_{i}}}{(1+e^{\theta _{1} x_{i}})} + \sum _{i=1}^{n} x_{i} (1-e^{\theta _{1} x_{i}})-(\alpha -2) \sum _{i=1}^{n} \frac{x_{i} (1-e^{\theta _{1} x_{i}}) e^{\phi _{i}} }{1-e^{\phi _{i}}}\nonumber \\+ & {} \alpha \sum _{i=1}^{n} \frac{x_{i} (1-e^{\theta _{1} x_{i}})e^{\phi _{i}}}{1-\alpha e^{\phi _{i}}} = 0,\end{aligned}$$
(9)
$$\begin{aligned} \frac{n}{\theta _{1}}+ & {} \sum _{i=1}^{n} \frac{y_{i} e^{\theta _{1} y_{i}}}{(1+e^{\theta _{1} y_{i}})} + \sum _{i=1}^{n} y_{i} (1-e^{\theta _{1} y_{i}})-(\alpha -2) \sum _{i=1}^{n} \frac{x_{i} (1-e^{\theta _{1} y_{i}}) e^{\phi _{i}} }{1-e^{\phi _{i}}}\nonumber \\+ & {} \alpha \sum _{i=1}^{n} \frac{y_{i} (1-e^{\theta _{2} y_{i}})e^{\phi _{i}}}{1-\alpha e^{\phi _{i}}} = 0. \end{aligned}$$
(10)

Analytical solution to the log-likelihood equations (8), (9) and (10) are not achievable under any circumstances. As a result, in order to obtain the numerical MLEs, we make use of a numerical approach like Newton-Raphson method. We suggest to use R packages namely optim() and DEoptim() for numerical maximization of the log-likelihood function given in (7).

In traditional statistical reasoning, we regarded the model parameters as constant. In practical scenarios, it is possible for the model parameters to vary over the duration of life testing. Because of this, it makes sense to think of the parameters as random variables. In the Bayesian paradigm, the parameters are viewed as a random variable following a known (Prior) distribution. The prior distribution represents the knowledge or belief about the unknown parameters. Prior to considering some data in the form of observations, we must first establish the prior distributions of the model parameters. For Bayes estimation of bivariate models, we refer the readers to Pena and Gupta (1990); Hanagal and Ahmadi (2009); Pradhan and Kundu (2016); Kundu and Gupta (2017) and articles cited therein.

In this study, we consider independent gamma prior distributions for the unknown parameters \(\theta _{1}\), \(\theta _{2}\) and beta prior distribution for \(\alpha \),

$$\begin{aligned}&\pi \left( \theta _{i}\right) \sim Gamma(a_{i}, b_{i}); b_{i}, a_{i}, \theta _{i}>0, \ \ i=1,2,\\&\pi \left( \alpha \right) \sim Beta(a_{i}, b_{i}); b_{3}, a_{3}>0, \alpha \in (0,1) , \end{aligned}$$

where \((a_{1}, a_{2}, a_{3}, b_{1}, b_{2}, b_{3})\) are the hyper-parameters and assumed to be known. The joint prior distribution of \(\theta _{1}\), \(\theta _{2}\) and \(\alpha \) is given by

$$\begin{aligned} \pi \left( \theta _{1},\theta _{2},\alpha \right) = \pi \left( \theta _{1}\right) \pi \left( \theta _{2}\right) \pi \left( \alpha \right) . \end{aligned}$$

The likelihood function and prior distribution are used to derive the joint posterior distribution of the parameters, which is given by

$$\begin{aligned} \pi \left( \theta _{1},\theta _{2},\alpha | (X,Y)\right) = \frac{\pi \left( \theta _{1},\theta _{2},\alpha \right) \ell \left( \theta _{1},\theta _{2},\alpha \right) }{\int _{0}^{\infty }\int _{0}^{\infty } \int _{0}^{\infty }\pi \left( \theta _{1},\theta _{2},\alpha \right) L\left( \theta _{1},\theta _{2},\alpha \right) d\theta _{1}d\theta _{2}d\alpha }, \end{aligned}$$
(11)

where \(\ell (.)\) is the likelihood function.

Bayes estimator of any parametric function \(s(\theta _{1},\theta _{2},\alpha )\) under squared error loss function is defined by

$$\begin{aligned} E[s(\theta _{1},\theta _{2},\alpha )] = \frac{\int _{0}^{\infty }\int _{0}^{\infty } \int _{0}^{\infty } s(\theta _{1},\theta _{2},\alpha )\pi \left( \theta _{1},\theta _{2},\alpha \right) \ell \left( \theta _{1},\theta _{2},\alpha \right) d\theta _{1}d\theta _{2}d\alpha }{\int _{0}^{\infty }\int _{0}^{\infty } \int _{0}^{\infty }\pi \left( \theta _{1},\theta _{2},\alpha \right) L\left( \theta _{1},\theta _{2},\alpha \right) d\theta _{1}d\theta _{2}d\alpha }. \end{aligned}$$
(12)

It is not possible to construct the Bayes estimators in closed-forms from the posterior distribution given in (11). We may solve the integral given above using an approximation technique to get the Bayes estimates numerically. Here, we present the use of the MH method to derive the Bayes estimates of the parameters of the BT distribution. We may draw the observations from the joint posterior distribution using the MH algorithm. These produced samples are used to get the Bayes estimates. Bayes estimates are means of the respective posterior samples under squared error loss function. We can also calculate the highest posterior density (HPD) intervals based on the quantiles of the generated posterior samples. For implementing the MH algorithm, we use the following steps,

  1. Step 1:

    Start with the initial guess as \(\Phi _{0}\) for the parameter under consideration.

  2. Step 2:

    Set j=1, generate a candidate parameter \(\Phi _{j}^{*}\) from the (asymptotically symmetric) proposal distribution \(q(\Phi _{j-1},\Phi _{j}^{*})\!=\!N(\Phi _{j}, var(\Phi _{j}))\), where \(\Phi _{j}\) and \(var(\Phi _{j})\) are suitably chosen.

  3. Step 3:

    Accept candidate parameter value \(\Phi _{j}\) as

    $$\begin{aligned} \Phi _{j}= \left\{ \begin{matrix} \Phi _{j}^{*}, \ \ \text {with probability} \ \ \phi (\Phi _{j}^{*},\Phi _{j-1}) \\ \\ \Phi _{j-1}, \ \ \text {with probability} \ \ 1-\phi (\Phi _{j}^{*},\Phi _{j-1}) \\ \end{matrix}\right. \end{aligned}$$

    where

    $$\begin{aligned} \phi (\Phi _{j}^{*},\Phi _{j-1}) = min\left( 1, \frac{\pi (\Phi ^{*}) q(\Phi _{j-1},\Phi _{j}^{*})}{\pi (\Phi ^{0}) q(\Phi _{j}^{*},\Phi _{j-1})}\right) . \end{aligned}$$
  4. Step 4:

    Set \(J=J+1\)

  5. Step 5:

    Repeat the steps \(2-4,\) m times and obtain \(\Phi _{j}\); \(j=1,2,...,m\).

  6. Step 6:

    Under the squared error loss function, Bayes estimate, say \(\hat{\Phi }_{Bayes}\) of the parameter \(\Phi \) is the mean of generated sample from the posterior distribution, which is given by

    $$\begin{aligned} \hat{\Phi }_{Bayes}= E(\Phi |data) =\frac{1}{m-m_{0}}\sum _{i=m_{0}+1}^{m} \Phi _{i} \end{aligned}$$

    where, \(m_{0}\) is the burn-in-period of the Markov chain.

  7. Step 7:

    The HPD intervals are obtained by using the approach of Chen and Shao (1999).

4 Simulation Study

This part conducts a simulation study to evaluate the effectiveness of the MLE and Bayes estimation techniques covered in the sections above. The simulation investigation is conducted for various distinct parameter combinations with varying values of the sample size. We take the following values of the parameters for simulation experiments; \(\theta _1=(0.5,1,2)\), \(\theta _2=(0.5,1,2)\) and \(\alpha =(0.3,0.5,0.7)\). For each given parameter combination, we draw different-sized observations from the BT distribution, like \(n=(30, 50, 100, 200)\). The MLEs and Bayes estimates of the BT distribution are computed for each simulated sample. For a given sample size, the mean squared error (MSE) and bias of all the estimators are computed using the 5000 simulated samples for each combination of the parameters.

Table 1 Bias and MSE of the MLEs and Bayes estimates from simulated samples for different parameter values and sample size
Full size table
Table 2 Bias and MSE of the MLEs and Bayes estimates from simulated samples for different parameter values and sample size
Full size table

We make use of the gamma and beta prior distributions in order to produce the Bayes estimates, and the primary task at hand is to select the hyper-parameters. We can notice several proposals to apply priors and elicit hyper-parameters by utilizing the moments matching approach from the past research that has been conducted and published. For simulation study, we consider prior mean (\(M_\pi \)) equals true parameter value with known prior variance (\(V_\pi \)). The prior variance gives us an indication of how confident we should be in our prior guess. A high prior variance indicates that there is less confidence in the prior assumption, and the prior distribution that results from this has a relatively flat shape. On the other hand, a low prior variance is indicative of a higher level of confidence in the prior guess.

We also study performance of the Bayes estimates with respect to the prior variance. We take prior mean as \(M_\pi (\theta _1)=\theta _1\), \(M_\pi (\theta _2)=\theta _2\) and \(M_\pi (\alpha )=\alpha \). Two combinations of the prior variance considered are {\(V_\pi (\theta _1)=1\), \(V_\pi (\theta _2)=1\), \(V_\pi (\alpha )=0.2\)} and {\(V_\pi (\theta _1)=0.1\), \(V_\pi (\theta _2)=0.1\) \(V_\pi (\alpha )=0.01\)}. These Bayes estimates are referred to as Bayes-1 and Bayes-2, respectively. The squared error loss function is assumed while calculating the Bayes estimates. We obtain 10000 samples from the posterior distribution using the MH algorithm and among which the first 1000 samples were discarded for the burn-in period.

For implementing MH algorithm, we need to consider a proposal density from which random sample is easily obtainable. There are various choices (mainly uniform and normal) considered in literature for the proposal density. In this study, we use independent normal distributions with means \((\hat{\theta _1},\hat{\theta _2},\hat{\alpha })\) with variance \((V(\hat{\theta _1}), V(\hat{\theta _2}), V(\hat{\alpha }))\) where the variances are estimated using the observed Fisher’s information matrix.

The following interpretation may be drawn from the simulations results shown in Tables 1 and 2: The MSEs of the MLEs and Bayes estimates of BT distribution parameters decrease as the sample size increase for the give parameter combination. In general, as the true value of a parameter is increased while the rest of the parameters are held constant, the MSEs of the MLE and Bayes estimates of that parameter increase. We also discovered that Bayes estimates derived from the flat prior behave similar to the MLEs. The Bayes-2 estimates (derived from the prior with low variance) outperform the MLE and Bayes-1 procedures.

Table 3 Fitting of marginals of the UEFA Champions League data
Full size table

5 Real Data Application

In this part, a real-life application of the BT distribution is shown to assess its suitability over other existing distributions in practice. We consider the UEFA Champions League data set for this purpose (see Meintanis , 2007). The bivariate data set shows the time (in minutes) of any team’s first kick goal (X) and the time of the home team’s first goal (Y). Pathak and Vellaisamy (2020) recently utilized this data set to determine the goodness of fit of the bivariate generalized linear failure rate distribution. They also looked at numerous dependent measures including Kendall’s tau, Blest’s measure, and Spearnam’s footrule coefficients. Based on these measures, it was discovered that the data set has a positive dependency.

Data modelling is accomplished in three phases. (I) First, we examine the exponential Teissier distribution (ETD)’s goodness-of-fit over its sub-model, which demonstrates the relevance of the shape parameter introduced by Sharma et al. (2022). At the reviewer’s request, we also compare the ETD’s fitting results to those of the Birnbaum-Saunders distribution (BSD) (see Balakrishnan and Kundu , 2019 and Naderi et al. , 2020) (II) Next, the bivariate families of the Teissier and linear failure rate exponential distributions are compared. (III) We then present MLE and Bayes estimates of the BT parameters for the UEFA data sets. The asymptotic and HPD intervals are also provided for the BT distribution parameters.

The joint probability of the observed data for the provided model is measured by likelihood function, and its larger value is anticipated from the best fitted model. The Kolmogorov-Smirnov (KS) test is used to determine if the data set conforms to a certain probability distribution and is based on the close agreement between empirical and fitted CDFs. We test the goodness-of-fit of all the distributions for the given data set at 5% level of significance.

For the Teissier and exponentiated Teissier distributions for X and Y individually, the MLEs, log-likelihood function, KS statistic, and associated p-value are determined. Table 3 displays the MLEs with standard errors (SEs) and marginal fitting results. We deduced from this table that the ETD offers a somewhat better fit than its sub-model. We can also see that the BSD do not fit the given data sets as evident from the p-value.

Table 4 Fitting of bivariate distributions for the UEFA Champions League data
Full size table
Table 5 The MLE and Bayes estimates of the BT distribution parameters along with CI and HPD intervals for UEFA data set
Full size table
Fig. 2
figure 2

The density and trace plots for the poeterior samples of \(\theta _{1}\), \(\theta _{2}\) and \(\alpha \) based on the real data

Full size image

Now we fit the BT and bivariate linear failure rate exponential (BLFRE) to the UEFA data set and compare their fitting results. The BLFRE distribution has five parameters and it includes bivariate exponential and Rayleigh distributions as special cases. We apply model selection selection criteria based on likelihoods, such as Akaike information criterion (AIC) and Bayesian information criteria (BIC), to select the best fitted distribution. The AIC is defined as \(-2 \log \hat{\ell } + 2p\), where \(\hat{\ell }\) represents the estimated likelihood value and p represents the number of parameters calculated using the data. Thus, it is easy to see that the AIC assesses goodness-of-fit, but it also penalizes overfitting caused by adding parameters, which is pretty sensible because increasing the number of parameters contributes to complexity in parameter estimation. The BIC is defined similarly as \(-2 \log \hat{\ell } + p \log n\), where n in the data size. Because the AIC and BIC are based on negative log-likelihood, lower values refer to a better fitting model.

Table 4 for the UEFA data set shows the MLEs, negative log-likelihood, AIC, and BIC for bivariate exponential, Rayleigh, GLFRE, and Teissier distributions. It should be noticed that the Teissier distribution has the lowest AIC and BIC values. This demonstrates the superiority of the BT distribution for the UEFA data set over the bivariate family of the GLFRE distributions.

Table 5 consists of the MLEs and Bayes estimates of the BT distribution parameters along with SEs and 95% confidence intervals. We observe that the SE of Bayes estimates is smaller than that of the MLEs. Figure 2 show the frequency distribution and simulation runs of the posterior samples of the BT distribution parameters. The figures show that the posterior sample’s distribution for each parameter is nearly bell-shaped and these MCMC samples are well-mixed.

6 Conclusions

Through the use of an order statistic, we introduced a three parameter bivariate Teissier distribution in this study. The univariate marginals of this distribution are members of the Teissier distribution. The joint and conditional moments, as well as the quantile function, are explicitly derived. The bivariate Teissier distribution is a novel addition to distribution theory because it has never been explored previously. Some notions of local dependence are thoroughly examined. The distribution exhibits positive dependency and may be beneficial in a variety of practical applications. Maximum likelihood and Bayes estimation techniques are used to estimate the model parameters. A number of numerical experiments are also carried out to analyse how the estimates behave for various parameter combinations with different sample sizes. Finally, an application to a practical data set is shown to demonstrate the bivariate Teissier distribution’s usefulness in practical situations. In future research works, the proposed bivariate model can be utilised to represent many reliability/survival analysis issues, such as stress-strength reliability, competitive risk modelling, and accelerated life testing, among others. As suggested by a referee, it may be worthwhile to undertake a research in the case of outliers, see Nooghabi and Naderi (2022).