1 Introduction

Data mining is one of the useful methods in extracting the information and hidden patterns among a huge amount of data. Generally, data mining investigates data from different perspectives and extract the useful pattern and knowledge among them. Due to high efficiency, data mining has numerous applications in medical [1, 2], wireless sensor networks [3], and vehicular ad hoc networks [4], and with the rapid growth of data in other fields [5] there is a need to extract and analyze the knowledge more than ever.

The results obtained in the literature show that the ensemble learning methods outperform the single classifiers. However, constructing an ensemble is not easy, and different important factors, including diversity [6, 7] and the accuracy of classifiers [8] play crucial roles in creating a highly accurate ensemble that should be considered [9, 10].

Accordingly, lots of used methods in the literature seek the approaches to improve the performance of ensemble learning methods, through employing the techniques to consider diversity and accuracy of classifiers, simultaneously [6, 11,12,13,14,15].

The diversity among classifiers in ensemble learning methods is a crucial factor, which has a significant effect on the performance of classification [16], and without the diversity between classifiers, one cannot obtain any benefit by hybridizing the classifiers to make ensembles [15, 17]. In other words, an ideal ensemble system must have both accurate individual classifiers and different individual classifiers errors, i.e, individual classifiers must be [18] In the literature, different methods have been proposed to improve diversity, including input manipulation, manipulated learning algorithms, partitioning, ensemble hybridization [19].

Although the diversity in ensemble learning methods is so important, there is a trade-off between diversity and accuracy [20, 21]. In other words, having diverse classifiers doesn’t necessarily always result in improving the ensemble methods [22].

In addition to the diversity and accuracy, the most important challenge in ensemble learning methods is to determine the appropriate number of classifiers, since increasing the number of classifiers has a negative effect on diversity [23]. On the other hand, it can reduce the speed of classification and increase the need for memory [7]. Since the search complexity to find the optimal number of classifiers is exponential, the pruning methods have been proposed to resolve the reduction in the number of classifiers [24, 25].

Generally, ensemble methods are categorized into two groups: sequential and non-sequential. In sequential methods, there is a dependency between classifiers, and the output of each classifier has a direct effect on building the next classifier, such as Adaboost [26], which is one of the most well-known methods in this field. In non-sequential methods, the classifiers are made independent of each other. The bagging algorithm [27] is one of the non-sequential methods in which classifiers are trained independently on the training sets generated by bootstrap. Each bootstrap is generated through random sampling without replacing a subset of training data. Each generated subset has the same number of samples [28].

Several methods have been presented in the literature so far to improve the performance of ensemble methods focusing on diversity and pruning the redundant classifiers. Akhand and Murase [29] presented a method named EIVA to improve the diversity in ensemble methods. In their proposed method, different training sets are made for each classifier. EIVA takes the main training set and then changes the attribute value of some of the samples. Antal [30] proposed approach takes the predictions of a single classifier on a training set. Then, an optimal labelling complimenting the predictions of the classifiers is created. Thus, an optimal but false labelling set is created, and the data with each false labelling is trained to a classifier, and diversity can be achieved, by using artificially created labelling.

Elyan and Gaber [31] proposed an improved random forest that uses the K-means clustering method to decompose classes of a specific dataset into subclasses. The goal was to find the within-class similarities between different samples of datasets and group them. In this method, the diversity is increased in datasets, and consequently, the classification performance is improved.

Chen et al. [32] proposed a new ensemble learning method to improve diversity through generating new samples named “neighborhood of training samples,” which are located within some of the limited neighborhoods of corresponding training samples. The generated samples are different from the original training samples. Zhang et al. [33] presented a novel algorithm termed reduced random subspace-based Bagging (RRSB). In this method, an ensemble is created by training K-Nearest Neighbor (KNN) algorithm on the new training sets generated by both random subspace and bootstrap sampling technique.

Ribeiro and Reynoso-Meza [34] presented a multi-objective evolutionary method to create an ensemble. Their proposed method includes two steps, including creating a Pareto-optimal set of ensemble candidate members and selecting the candidates to create the final optimum ensemble.

Zhang and Cao [35] defined classifier similarity as for the prediction accuracy and diversity, and then presented a classifier selection approach based on spectral clustering (SC). The SCs categorize the classifiers into two clusters, according to their similarities, and keep one cluster of classifiers in ensemble. The pruning operation could be performed in this way.

Xiao et al. [36] presented an approach so as to produce diverse classifiers for improving ensemble classifier. In their proposed approach, the supervised clustering was used to partition data samples from each class inside the cluster. The clusters are paired from different classes to form a number of training subsets. A basic classifier is then built on each of the training subset.

Seijo-Pordo et al. [37] applied two different design of feature selection ensembles. The two commonly used ensembles for are homogeneous ensemble and heterogeneous ensemble. The homogeneous ensemble is generated using the same feature selection method with different training data through distribution of the training dataset over several samplings, and the heterogeneous ensemble, which consists of using different feature selection methods for the same training data, tries to take advantage of the strengths and overcome the weaknesses of the individual methods.

Savargiv et al. [38] proposed a method named LabEL, which was based on learning automata. Their main goal was to assign the coefficient of influence to base learners in the ensemble learning approach. Assigning the coefficient of influence to base learners is performed, according to the behavior of data, and updated according to the conditions of the problem. Raza [39] presented an ensemble-based method using different machine learning classifiers to predict cardiovascular patients. Pérez-Gállego et al. [40] used the hypothesis of changing data distribution between test and training data to introduce diversity to the ensemble. The main idea of this method was to generate different training samples according to changes in expected distribution.

Cavalcanti et al. [6] used a hybrid approach based on diversity measures (Q-Statistics, Disagreement, Correlation Coefficient, Kappa-statistic, Double-fault measure), GA as well as graph coloring algorithm to prune the redundant classifiers. Mao et al. [16] proposed a novel weighted ensemble learning by maximizing the diversity and the individual accuracy simultaneously. In this method the process of combining multiple individuals is regarded as a linear transformation of them. Onam et al. [41] presented an ensemble pruning method based on clustering. In their method, the base learners are firstly selected according to the clusters’ attributes, and then two classifiers are opted based on pairwise diversity. The search space of candidate classifiers is detected by a Pareto-based multi-objective evolutionary algorithm.

Guo and Boukir [42] presented a method for pruning the classifiers in which the classifiers are firstly sorted based on their capabilities in classifying samples with low margin (those samples close to the threshold of decision-making). Then, the number of M classifiers are initially selected to form the final ensemble.

Jan and Verma [43] proposed a new diversity criterion named Misclassification Diversity (MD) and an approach named Incremental Layered Classifier Selection (ILCS) to produce an ensemble classifier. Their proposed ILCS-MD method creates an ensemble classifier with incremental classifier selection among the set of base classifiers, according to the increase in accuracy and diversity.

Zhang et al. [44] proposed a two-stage strategy to prune the bagging by combining to approaches: accuracy-based pruning (AP) and distance-based pruning (DP). These two methods, as well as their two combinations, “AP + DP” and “DP + AP” as the two-stage pruning strategy, were investigated. The experimental result depict that this two-stage pruning methods can furthermore reduce the ensemble size and improve the classification.

Guo et al. [7] proposed a criterion using “margin” and “diversity” to evaluate the importance of classifiers. By adding the ensemble members in descending order according to the criterion, the user can select the first T classifiers to form the sub-ensemble. Qun et al. [45] presented an approach to pruning the ensemble, simultaneously considering accuracy and diversity. Singh and Singh [46] presented an evolutionary multi-objective algorithm to select the base learners which maximized classifiers accuracy and minimized ensemble complexity, simultaneously.

Zouggar and Adla [47] presented a fitness function, composed of diversity and accuracy, for homogenous ensemble pruning. In their proposed method, the search process is performed using the hill climbing method. Nguyen et al. [48] proposed an ensemble selection method, which considers the base classifier’s confidence during classification and the general credibility of the base classifier in ensemble. In other words, a base classifier is selected to predict for a test sample if the confidence in its prediction is more than its credit threshold.

Bui et al. [49] proposed a new method to generate the base learners taking two objectives into account, i.e, accuracy and diversity, where the main idea of this new method was to optimize the weights of ANN using two evolutionary algorithms NSGA-II and NSDE.

In non-sequential methods such as bagging, no appropriate criterion has been presented to determine the number of classifiers, so far. Also, the presented method, such as bootstrap, has not been successful in creating diverse classifiers, since generated training sets may overlap with each other, or some of the samples may not be selected. Consequently, redundant classifiers may be produced and have a negative effect on the performance of the ensemble.

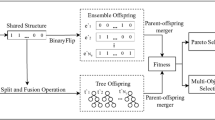
Given the performances of evolutionary algorithms, they are utilized in many problems [50, 51] In this paper, to improve non-sequential methods’ performance, the development of ensemble learning classification with density peak decomposition-based evolutionary multi-objective optimization (EDDEMO) has been proposed, which uses the concept of density peak as a new criterion to create diversity in non-sequential ensemble methods. In this regard, an evolutionary multi-objective method is presented with two objectives, i.e, accuracy and density peak, to create evolutionary training sets that result in generating diverse and accurate classifiers. In this research, the density function is used to measure the amount of data distribution in the feature space. The goal of using the objective function of the density peak criterion is to generate diverse training sets so that the classifiers are trained in different spaces of the feature space, and as a result, have different performances in relation to each other, which is the base of diversity in ensemble learning methods. Also, the accuracy function is used to measure the well-performing of training sets. In other words, through training of base classifiers over well-performing sets, their classification performance is increased. Finally, considering the obtained number of solutions in Pareto-optimal fronts, as the final solution, the number of required training sets to create the classifiers, and consequently, the required number of classifiers is obtained. In other words, the proposed method will not expose to generating redundant classifiers.

The paper structure is organized into three sections. The proposed method section includes how the training sets are generated. Section 3 presents the experimental tuning, the obtained results, and discussion. Finally, Sect. 4 presents the conclusion.

2 The proposed method

Lack of selection of appropriate criterion to improve diversity, and lack of correct selection of number of classifiers can decrease the performance of ensemble methods. In this paper, to improve the diversity, and present an appropriate approach for selecting the classifiers, a multi-objective evolutionary decomposition-based optimization algorithm (MOEA/D) [52] is used to generate diverse training sets because its complexity is less than other evolutionary methods [51, 53], such as non-dominated sorting genetic algorithm-II (NSGA-II) [54]; moreover, in terms of solution quality, MOEA/D with simple decomposition methods have outperformed or performed similarly to NSGA-II on most test instances [55]. In this method, the number of obtained solutions in the Pareto-optimal front are considered as training sets, while the number of obtained solutions determines the number of required classifiers to create the ensemble. The proposed method is able to improve non-sequential ensemble methods, such as bagging.

The proposed method includes two main steps. In the first step, the initial training sets, which are produced randomly, are converted into diverse and well-performing training sets, through an evolutionary process, and considering accuracy and density peak objectives. Finally, they are used for training the classifiers and making the final ensembles.

2.1 The proposed decomposition-based multi-objective evolutionary algorithm to generate training datasets

In this subsection, the general process of the decomposition-based multi-objective evolutionary optimization algorithm is firstly described, and then the details of objective functions are presented.

Generally, the multi-objective optimization problems could be defined as follows:

$$\begin{aligned} & minimize \, f\left( x \right) = (f_1 \left( x \right), f_2 \left( x \right), \ldots , f_m \left( x \right) \hfill \\ & subject \, to\, \;x \in \varOmega \hfill \\ \end{aligned}$$
(1)

where Ω is decision space, \(R^m\). is objective space, and \(f: \varOmega \to R^m\). includes m objective functions of real-valued.

The main goal of MOEA/D algorithm, developed by Zhang and Li [52], against Pareto-based evolutionary multi-objective optimization algorithms, is to optimize several single-objective sub-problems or several small multi-objective problems. This algorithm decomposes the multi-objective problem into some scalar optimization sub-problems and optimizes all of them, simultaneously [52]. In this approach, a weight vector is defined for each problem, and the objective functions are aggregated into a single objective function using this weight vector. The population in each generation includes the best-found solution for each sub-problem. The neighborhood relationships between these sub-problems are defined according to the distance between their aggregation coefficient vectors. The optimal solutions for two sub-problems should be so similar. Each sub-problem (i.e, scalar aggregation function) in MOEA/D is only optimized through the information of adjacent sub-problem. To convert the Pareto-front approximate problem into n scalar sub-problems, one can use different decomposition methods, including boundary intersection (BI), Tchebycheff and the weighted sum [52]. In this paper, Tchebycheff approach is used for doing so, which are described in the following.

In the Tchebycheff approach, the scalar optimization problem is stated as Eq. (2):

$$\begin{aligned} & Min \, g^{te} \left( {x|w,z^* } \right) = \mathop {\hbox{max} }\limits_{1 \le i \le m} \{ w_i \left| {f_i \left( x \right) - z_i^* } \right|\} \hfill \\ & Subject \, to \, x \in \varOmega \hfill \\ \end{aligned}$$
(2)

where \(z^* = \left( {z_1^* , \ldots , z_m^* } \right)^T\). is a reference point, i.e, \(z_i^* = \hbox{min} \{ f_i \left( x \right)|x \in \varOmega \} z_i^* = \max_{x \in \varOmega } f_i \left( x \right)\). for \(i = 1, \ldots ,{\text{m}}\).. For each Pareto-optimal point \(x^*\), there is a weight vector, where \(x^*\). is the optimal solution obtained of Eq. (2), and each optimal solution of Eq. (2) is a Pareto-optimal solution for Eq. (1).

In order to obtain a set of Pareto-optimal solutions of (1), one can solve a set of single-objective optimization problems with different weight vectors defined by (2) or other decomposition methods.

In this paper, the goal of the considered optimization problem is to reduce both the classification error and density in training sets, defined as Eq. (3).

$$minimize\, f\left( x \right) = \left( {f_1 \left( x \right), f_2 \left( x \right)} \right)$$
(3)

where, \(f_1 \left( x \right)\) measures the classification error for training sets, and \(f_2 \left( x \right)\) shows the density of sample data in training sets, and x is the produced training set. In the following, each of the objectives is explained in detail.

The first objective function (classification error) Each training set is evaluated according to the classification accuracy. To do so, the obtained accuracy from the KNN algorithm is used. The KNN algorithm does not require a training phase due to its laziness, and the results also show that it works well in dealing with various problems. The first objective function could be computed according to Eq. (4).

$$Error = 1 - \frac{1}{n}\mathop \sum \limits_{i = 1}^n \left( {Y_i = = Y'_i } \right)$$
(4)

where Y signifies the real classes, \({\text{Y'}}\) shows the predicted classes using the classifier, and n denotes the number of training samples.

The second objective function (density) Suppose that \(S_i = \left[ {s_1 , \ldots ,s_b } \right]\) is a training set, where Si is the ith training set, and b is the number of selected samples in the training set. To calculate each training set’s density, one should first calculate the distance between the samples in each training set. The distance \(d\left( {s_i , s_j } \right)\) is Euclidean distance between two points i and j in the training set S, calculated as Eq. (5), which is the output of Euclidean distance matrix E.

$$d\left( {s_i , s_j } \right) = |s_i - s_{j2}|$$
(5)

The local density of each point of each training set is first calculated using Eq. (6), to finally determine the local density of the training set [56]. To improve the accuracy of the density index, the Gaussian Kernel presented in [57] is used, stated as Eq. (6).

$$\rho_i = \sum \limits_j { \exp }\left( { - \frac{{d\left( {s_i , s_j } \right)}}{d_c }} \right)^2$$
(6)

where, \(\rho_i\) is the local density of point i, \(d\left( {s_i , s_j } \right)\) is the distance between points i and j, and \(d_c\) is the cutoff distance. To calculate \(d_c\), the upper triangular elements in matrix E are chosen and then sorted in descending order, as vector V. The value of \(d_c\) is calculated as Eq. (7).

$$d_c = V\left( k \right)$$
(7)

where k is the position determined by Eq. (8).

$$k = \left( {N_B \cdot \left( {N_B - 1} \right)} \right) \cdot P_a$$
(8)

where NB is the number of points in training set B, and Pα is a parameter showing the average percentage of neighbors in the training set. After determining the density value for each point, the average local density of a training set is calculated using Eq. (9).

$$f_2 \left( B \right) = \frac{{\sum_{i = 1}^n \rho_i }}{n}\left( {n = Number\, of\, point\, in\, each\, traiing\, set} \right)$$
(9)

The higher the average density of the training set, the fewer data samples (points) are scattered in the feature space.

The instance adjustment problem is decomposed into N single-objective sub-problems by choosing N weight vectors \(w\) and the objective function of the \(j\)th sub-problem in this paper is defined as Eq. (10).

$$minimize \, g^{te} \left( {x |w^j , z^* } \right) = \mathop {\hbox{max} }\limits_{1 \le i \le m} \left\{ {w_i^j \left| {f_i \left( x \right) - z_i^* } \right|} \right\}$$
(10)

where \(w^j = \left( {w_1^j , w_2^j } \right)\), and fi are the objective function for i = 1, 2. Since \(g^{te}\) is a continuous function of w, two sub-problems may have the same solutions if their weight vectors are close [52].

In MOEA/D, a neighborhood of weight vector \(w^i\) is defined as a set of its several closest weight vectors in \(\left\{ {w^1 , \ldots , w^N } \right\}\). The neighborhood of the \(i\)th sub-problem consists of all the sub-problems with the weight vectors from the neighborhood of \(w^i\) [52]. The population consists of the best ever found solutions for each sub-problem. Only the current solutions to its neighboring sub-problems are exploited for optimizing a sub-problem in MOEA/D.

In the following, the steps of the MOEA/D algorithm in the proposed method is explained in Algorithm 1.

figure a

At first, the number of N training sets are randomly generated, and then given to the MOEA/D algorithm as the initial population. Figure 1 represents a training set, where each training set in algorithm equals a xi.

Fig. 1
figure 1

The representation of a training set (1; signifies the presence of the sample in the training set, and 0 denotes the absence)

Full size image

In step 1.1, the number of T nearest neighbors from weight vectors w are calculated at first using Euclidean distance. Then, the F-value of the sub-problem is computed according to the two objective functions. In each iteration of step 2, T nearest neighbors of each sub-problem are considered, and two of them are randomly chosen, and an offspring y is eventually produced using a crossover operator.

In the step 2.2 a problem-specific heuristic is used to repair in the case when y invalidates any constraints. Therefore, the resultant solution \(y^{\prime}\). is feasible and very likely to have a lower function value for the neighbors of ith sub-problem.

In step 2.3, all neighbors of xi are compared with \(y^{\prime}\), and if \(y^{\prime}\). is better than the jth neighbor, i.e, \(g^{te} (y^{\prime}|w^j , z) \le g^{te} (x^j |w^j , z)\), then \(x^j = y^{\prime}\). and \(FV^j = F\left( {y^{\prime}} \right)\). Also, for j = 1, 2, if \(f_i \left( {y^{\prime}} \right) < z_j\), \(z_j = f_i \left( {y^{\prime}} \right)\). The external population (EP) in which all non-dominated solutions are saved in it, is updated. All of the existing vectors in EP which have been dominated by \(F\left( {y^{\prime}} \right)\) are removed, and if any vector in EP cannot dominate \(F\left( {y^{\prime}} \right)\), it would be added to EP.

The search process will be terminated after satisfying the stop criteria, and at the end of the optimization process, the obtained solutions, as training sets, are used to train the classifiers so as to make the ensemble. These solutions determine the number of required classifiers to make the ensemble, which makes the final ensemble needless of pruning.

3 Experimental results and discussion

In order to show the benefits of the proposed method, it has been compared with some well-known algorithms. First, the characteristics of the used datasets in experiments are stated. Then, the conducted tunings related to the experiments are presented. In the following, the obtained results are shown, and finally, non-parametric statistical analyses a conducted to analyze the existing differences between the employed methods.

3.1 Datasets

To evaluate the proposed method, 19 balanced datasets of the UCI database [58] are used. Table 1 shows a summary of the used balanced datasets in the experiments. In Table 1, the number of samples, the number of features, and the number of classes are shown for each dataset. To train the proposed model, these balanced datasets are divided using a tenfold cross-validation method.

Table 1 The features of the used datasets
Full size table

3.2 Parameter tuning

In the achievement process of an algorithm to the ideal and appropriate solutions, different factors such as used logic in developing the algorithm and assigned values to the algorithm’s parameters are effective. In this paper, the most commonly used approach in other papers in the literature to tune the parameters, i.e, trial-and-error, has been used. Through different combinations of concerned parameters in implementing an algorithm, one can obtain different solutions. Table 2 presents the used parameters in the proposed method. Also, the parameters used for other methods are set based on what the authors of each algorithm have suggested in that paper.

Table 2 The values and parameters used in the proposed method
Full size table

The used parameters in the multi-objective evolutionary algorithm are determined by trial-and-error. Table 2 presents the used parameters in the proposed method.

3.3 Results

The experiment’s purpose is to evaluate the obtained results of classification accuracy and the number of classifications produced by the proposed method. Therefore, six well-known methods which have good performance in pruning the classifiers, i.e, Spectral Clustering (SC), reduce-error pruning (RE) [59], Orientation Ordering (OO) [60], semi-definite programming (SDP) [61], Complementarity Measure (CC) [62], and Kappa pruning (Kappa) [59], as well as the bagging algorithm are used as non-sequential methods for making a comparison. In these methods, the initial number of classifiers is considered 100, and since the initial classifiers used in the bagging algorithm should be unstable, the CART tree has been used. Also, to combine the classification results, majority voting is used. In this section, the number of classifiers obtained from the proposed method is compared with the number of classifiers obtained from the pruning method. Then, the performance of methods in terms of classification accuracy is compared. Finally, non-parametric statistical tests are used to make a more accurate evaluation of the different algorithms’ performance.

3.3.1 Comparison of performance in terms of classification accuracy and the number of classifiers

3.3.1.1 Number of classifiers

The performance of different methods in handling of distinct datasets is different. So, the number of used classifiers in ensemble methods could be varied, depending on different datasets. In this subsection, the number of produced training sets, which shows the number of classifiers, are compared with the number of classifiers obtained from pruning using the EDDEMO algorithm. Figures 2, 3, 4, 5, the number of produced training sets for each dataset is depicted in a two-dimensional vector, in which x and y axes signify the error rate and density peak calculated for each dataset, respectively.

Fig. 2
figure 2

The obtained non-dominated solutions using EDDEMO method for datasets (1)

Full size image
Fig. 3
figure 3

The obtained non-dominated solutions using EDDEMO method for datasets (2)

Full size image
Fig. 4
figure 4

The obtained non-dominated solutions using EDDEMO method for datasets (3)

Full size image
Fig. 5
figure 5

The obtained non-dominated solutions using EDDEMO method for datasets (4)

Full size image

In Figs. 2, 3, 4, 5, one can observe that the proposed method generates a lesser number of training sets significantly for training the classifiers in ensemble. In order to understand the importance of the proposed method, the average number of generated training sets, indicating the number of classifiers, is compared with the pruning rate of methods in Table 3. The outcomes show that EDDEMO in this study outperforms the other methods in all cases.

Table 3 Comparison between pruning rate of algorithms and obtained average number of classifiers in EDDEMO
Full size table
3.3.1.2 Classification accuracy

To compare the algorithms, the obtained accuracy belongs to 7 algorithms, and the proposed method is compared to over 19 datasets shown in Table 4. In Table 4, each row corresponds with the accuracy of each method, where the highest accuracy is highlighted, and in the last rows, the average accuracy is presented.

Table 4 Comparison of different methods’ accuracy (the better ones are highlighted)
Full size table

According to the results of Table 4, EDDEMO has a better and equal performance over 17 and 1 datasets, respectively. The worst performance of EDDEMO is over Pendigits datasets that achieved the third rank, while for the remaining one, the differences are not significant. The average accuracy of algorithms over 19 datasets shows that EDDEMO outperforms other algorithms.

In Fig. 6, for better comparison, in the horizontal axis, the datasets have been sorted in ascending order according to the number of samples, while the vertical axis shows the difference between the accuracy of the SC method (as the second-best method in terms of performance) with the proposed method and other techniques. In the Fig. 6. Positive, negative, and zero values depict the better, worse, and equal performances, respectively.

Fig. 6
figure 6

The regression line to investigate the proposed algorithm’s performance on the datasets with different number of samples

Full size image

The regression line for the proposed method shows that the performance of the proposed method in handling the datasets with a huge amount of sample is reduced, while the simple regression line in Fig. 7, in which the datasets are sorted by increasing the number of classes, shows that the performance of the proposed method is increased.

Fig. 7
figure 7

The regression line to investigate the proposed algorithm’s performance on the datasets with different number of classes

Full size image

In Fig. 8, the bar plot of methods on different datasets is compared. The horizontal axis of these plots shows the classification accuracy. The obtained results on the Pendigits, Tic-tac-toe, segment, Votes, and Spam datasets show that except Kappa, the rest of the methods have almost the same performance, and the classification difference observed between methods is negligible. Also, EDDEMO outperforms the Australian dataset, which has the most number of classes, while the classification difference is slightly different from other methods in datasets with a high number of features and samples. According to Fig. 8, the proposed method’s best performance belongs to the Glass and Liver datasets, in which the classification difference is too much compared to other methods. Also, the worst performance happens on the Pendigits dataset.

Fig. 8
figure 8

Comparison of different algorithms’ accuracy using a bar plot based on each dataset

Full size image

3.4 Comparing the algorithms using nonparametric statistical test

In order to compare the proposed method with other methods accurately, a two-stage approach is applied proposed by Demšar [63] which are used in many recently published researches in classifying [64]. Nonparametric tests have commonly different consequences. In this context, with the goal of ensuring the accurate comparison, several nonparametric tests are applied. In Friedman test, all algorithms have equal performance, unless the null hypothesis is rejected [65]. In the second step, a post hoc test (such as [66,67,68]) can be utilized to determine the statistical differences between control (i.e, the best algorithm which gets the highest rank by Friedman test) and other algorithms.

In Friedman nonparametric statistical test, it is assumed that \(r^j_i\) shows that the algorithm k attains rank j on observation i among N observations. The goal of this test is comparing the average of the algorithms’ rank, i.e, \(R_j = \frac{1}{N}\mathop \sum \limits_{i = 1}^N r_i^j\). According to null hypothesis, the algorithms are equal in ranks. So, the Friedman test is defined as follows:

$$\rm{\mathcal{X}}_F^2 = \frac{12N}{{k\left( {k + 1} \right)}} \times \mathop \sum \limits_{j = 1}^k jR_j^2 - \frac{{k\left( {k + 1} \right)^2 }}{4}$$
(11)

\(\rm{\mathcal{X}}_F^2\) is distributed according to \(\rm{\mathcal{X}}^2\). with k-1 degree of freedom. Rejecting the null hypothesis in Friedman test does not mean the differences between algorithms, but also demonstrates the differences between the samples. In the following, a post hoc method is needed for pairwise comparison. So, a control algorithm is selected and compared with other algorithms using a post hoc method. The test statistic depends on the main nonparametric ranking for comparing the algorithms ith and jth and is as follows:

$$z = \frac{R_i - R_j }{{\sqrt {\frac{{k\left( {k + 1} \right)}}{{\delta N_{ds} }}} }}$$
(12)

where z corresponds to the probability value of Normal distribution table. Next, it is compared to an appropriate confidence level α. The post hoc test is different in terms of used method to tune α for several comparisons. Moreover, the adjusted P-values is recommended to use in order to have fair comparison of P-values. Since the post hoc tests change the significance levels for each of pairwise comparisons, the P-values are sorted as P1, P2,….P1, where \(P_1 \le P_2 \le \cdots \le P_{k - 1}\).

Bferroni-Dunn [66]: this procedure tunes the α value in each step through dividing to the number of comparisons (i.e, k − 1). The adjusted P value for this procedure is as follows:

$$APV_i = { \hbox{min} }\left( {\left( {k - 1} \right)P_i ,1} \right)$$
(13)

Li [69]: This is a two-step rejection procedure. In the first step, if P1 is less or equal than α, the null hypothesis is rejected, otherwise it is accepted and next step is continued in which the remainder hypothesis (i.e, Hi) are rejected with the probability as \(P_i \le \alpha \left( {1 - P_k - 1} \right)\left( {1 - \alpha } \right)\).

Finer method [70]: In this method, the hypothesis H1 to Hi-1 are rejected. If i be the smallest number, where \(P_i > 1 - \left( {1 - \alpha } \right)\left( {k - 1} \right)/i\).

In this research, 8 methods are applied to compare the algorithms, while the experiments are designed to investigate the statistical differences of algorithms and the number of classifiers. For this purpose, the experiments are conducted over 19 datasets to assess the accuracy of classifying and number of classifiers. In this paper, all classifying algorithms are compared in terms of accuracy. Figure 9 presents the results of Friedman test obtained from different algorithms to identify the differences in the results. These outcomes demonstrate that the different algorithms have significant different performance statistically and the null hypothesis (equal performance of algorithms) is rejected owing to both number of training sets and accuracy. According to the results, the null hypothesis is rejected for all tests which shows significant differences between algorithms. Therefore, the best algorithm with the least rank is selected as control algorithm and used to be compared with other algorithms. In Fig. 9, the proposed method (EDDEMO) has the best rank in accuracy and consequently is selected as control algorithm. In this paper, in the second step of post hoc tests, some nonparametric statistical tests are employed such as Bonferroni, Finer and Li as post hoc tests for pairwise comparisons. According to these statistical tests, the algorithms yield different performances. The presented results in Tables 5 shows that the proposed method (EDDEMO) outperforms predominantly the other algorithms.

Fig. 9
figure 9

Average ranks obtained by each algorithm in the Friedman test

Full size image
Table 5 The analysis results of the post hoc statistical test (accuracy)
Full size table

3.5 Discussion

In these section differences between EDDEMO and traditional bagging in terms of accuracy and number of classifiers is represented. The proposed method, unlike traditional bagging, improve bagging accuracy by optimizing accuracy and diversity and decreasing the number of classifiers simultaneously. Accordingly, the bagging performance with a different number of classifiers, 50, 100, 150, 200, 250, and 300, as well as EDDEMO performance with mean of the number of classifiers is given in Table 6. According to obtained results, by increasing the number of classifiers, there is no significant in bagging performance.

Table 6 Comparison between EDDEMO and Bagging performance with different number of classifiers
Full size table

A comparison between the number of classifiers and the proposed method’s accuracy shows that EDDEMO has produced a smaller number of classifiers and has higher accuracy than the bagging algorithm with a large number of classifiers.

Generally, the methods seeking for diverse classifiers cannot determine the appropriate number of those training sets that the classifiers are trained based on them. In this case, it may be considered extra number of training sets and generated redundant classifiers or it may be considered lesser number of training sets and reduced the efficiency. While, EDDEMO yield the appropriate number of training sets for training the classifiers. Furthermore, the proposed method unlike the presented methods in the literature has different nature. It focuses on two challenges simultaneously, i.e, diversity and number of classifiers and generates diverse and accurate classifiers through producing diverse training sets. Also, eliminates the need of pruning in bagging and other non-sequential ensembles, through determining the number of classifiers. Finally, according to the Friedman nonparametric statistical test, the proposed EDDEMO outperforms the other approaches statistically.

4 Conclusion

In this paper, a new approach named development of ensemble learning classification with density peak decomposition-based evolutionary multi-objective optimization (EDDEMO) was presented to improve the diversity and accuracy of the classifiers in non-sequential ensemble learning methods. In the proposed method, a multi-objective evolutionary decomposition-based optimization (MOEA/D) algorithm was used to optimize two objective functions, simultaneously, i.e, density peak and accuracy. The obtained results of optimizing these two objectives are some solutions, which are considered as final training datasets to make the ensembles. Also, the number of solutions denotes the number of required classifiers to make the ensemble. In the proposed method, the goal of using the density peak criterion is to select different samples from the feature space to build training sets to produce diverse classifiers by training the classifiers on these training sets. The accuracy objective function was also considered for producing the well-performing training sets to improve the classifiers’ accuracy through training on them. In this paper, in order to confirm the performance of the proposed method, its performance was compared with the seven existing methods in the literature on 19 datasets. The obtained results showed that the proposed method outperforms the other methods in terms of accuracy. Also, the conducted two-phase non-parametric statistical tests showed the proposed method’s dominance compared to other techniques.