A Factorization Strategy for Tensor Robust PCA

Abstract

Many kinds of real-world data, e.g., color images, videos, etc., are represented by tensors and may often be corrupted by outliers. Tensor robust principal component analysis (TRPCA) servers as a tensorial modification of the fundamental principal component analysis (PCA) which performs well in the presence of outliers. The recently proposed TRPCA model [12] based on tubal nuclear norm (TNN) has attracted much attention due to its superiority in many applications. However, TNN is computationally expensive, limiting the application of TRPCA for large tensors. To address this issue, we first propose a new TRPCA model by adopting a factorization strategy within the framework of tensor singular value decomposition (t-SVD). An algorithm based on the non-convex augmented Lagrangian method (ALM) is developed with convergence guarantee. Effectiveness and efficiency of the proposed algorithm is demonstrated through extensive experiments on both synthetic and real datasets.

This work is partially supported by the National Natural Science Foundation of China [Grant Nos. 61872188, U1713208, 61602244, 61672287, 61702262, 61773215, 61703209].

1 Introduction

PCA is arguably the most broadly applied statistical approach for high-dimensional data analysis and dimension reduction. However, it regards each data instance as a vector, ignoring the rich intro-mode and inter-mode correlations in the emerging multi-way data (tensor data). One the other hand, it is sensitive to outliers which are ubiquitous in real applications. By manipulating the tensor instance in its original multi-way form and attempting to work well against outliers, tensor robust PCA [5, 11] is a powerful extension of PCA which can overcome the above issues. TRPCA finds many applications likes image/video restoration, video surveillance, face recognition, to name a few [5, 11].

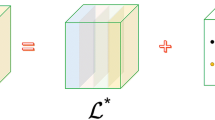
An idealized version of TRPCA aims to recover an underlying tensor ${\mathcal {L}}^*$ from measurements ${\mathcal {M}}$ corrupted by outliers represented by tensor ${\mathcal {S}}^*$, that is,

$$\begin{aligned} {\mathcal {M}}={\mathcal {L}}^*+{\mathcal {S}}^*. \end{aligned}$$

(1)

Obviously, the above decomposition is impossible without additional assumptions on the underlying tensor ${\mathcal {L}}^*$ and the outlier tensor ${\mathcal {S}}^*$. Thus, TRPCA further assumes ${\mathcal {L}}^*$ is “low-rank” and ${\mathcal {S}}^*$ sparse. Mathematically, TRPCA tries to solve a minimization problem as follows

$$\begin{aligned} \min _{{\mathcal {L}},{\mathcal {S}}}\quad \text {rank}({\mathcal {L}})+\lambda \Vert {{\mathcal {S}}} \Vert _{0}\quad \text {s.t.}~~\quad {\mathcal {L}}+{\mathcal {S}}={\mathcal {M}}, \end{aligned}$$

(2)

where $\text {rank}(\cdot )$ denotes the “rank function” of a tensor, $\Vert {\cdot } \Vert _{0}$ is the tensor $l_0$-norm (used as a sparsity measure), and $\lambda >0$ is a regularization parameter. Problem (2) is numerically very challenging, since both the tensor rank function and $l_0$-norm are neither continuous nor convex, even in their simplest matrix versions.

A mainstream approach for tackling the numerical hardness of Problem (2) is to respectively replace the rank function and $l_0$-norm with their convex surrogates $\text {conv-rank}(\cdot )$ and $l_1$-norm, leading to the following convex version of Problem (2)

$$\begin{aligned} \min _{{\mathcal {L}},{\mathcal {S}}}\quad \text {conv-rank}({\mathcal {L}})+\lambda \Vert {{\mathcal {S}}} \Vert _{\text {1}}\quad \text {s.t.}~~\quad {\mathcal {L}}+{\mathcal {S}}={\mathcal {M}}. \end{aligned}$$

(3)

The $l_1$-norm $\Vert {\cdot } \Vert _{\text {1}}$ in Problem (3) is widely used as a convex envelop of the $l_0$-norm in compressive sensing and sparse representation to impose sparsity [3].

In the 2-way version of Problem (3) where ${\mathcal {L}},{\mathcal {S}}$ and ${\mathcal {Y}}$ are matrices, tensor Robust PCA degenerates to the Robust PCA [1]. In RPCA, the matrix nuclear norm $\Vert {\cdot }\Vert _{*}$ [2] is often chosen as the convex surrogate of matrix rank. However, for general K-way $(K\ge 3)$ tensors, one may have multiple choices of $\text {conv-rank}(\cdot )$, since a tensor has many definitions of rank function due to different extensions of the matrix SVD. The most direct tensor extension of matrix rank is the tensor CP rank [6] which is the smallest number of rank-one tensors that a tensor can be decomposed into. Nevertheless, both the CP rank and its corresponding version of nuclear norm are NP hard to compute [4, 7]. Due to its computational tractability, the Tucker rank [15] defined as a vector of ranks of the unfolding matrices along each mode, is the most widely used tensor rank. Its corresponding nuclear norm (denoted by SNN in this paper) [10] is defined as the (weighted) sum of nuclear norms of the unfolding matrices along each mode, and has been used in TRPCA [5]. However, SNN is not a tight convex relaxation of sum of the Tucker rank [14], and it models the underlying tensor as simultaneously low rank along each mode, which may be too strong for some real data tensors.

Recently, the low tubal rank models have achieved better performances than low Tucker rank models in many low rank tensor recovery tasks, like tensor completion [17, 18, 23], tensor RPCA [11, 23], sample outlier robust tensor PCA [24] and tensor low rank representation [19, 20], etc. At the core of these models is the tubal nuclear norm (TNN), a version of tensor nuclear norm defined within the framework of t-SVD [9]. Using TNN as the low-rank regularization in Problem (3), the recently proposed TNN-based TRPCA model has shown better performances than traditional models [11, 12, 23]. The rationality behind the superior performance of TNN-based models lies in that TNN is the tight convex relaxation of the tensor average rank, and the low average rank assumption is weaker than the low Tucker rank and low CP rank assumption [12].

Despite its broad use, TNN is computationally expensive since it requires full matrix SVDs. The high computational complexity limits the application of TNN-based models to scale to emerging high-dimensional tensor data. By exploiting the orthogonal invariance of TNN, we come up with a factorization based model for TRPCA which can powerfully accelerate the original TNN-based TRPCA model. Extensive experiments show the superiority and efficiency of the proposed algorithm. The main contributions of this paper are as follows:

• A new model for TRPCA named TriFac is proposed in Model (11).

• An ALM algorithm (Algorithm 1) is designed to efficiently solve it.

• Convergence of the proposed algorithm is shown in Theorem 2.

The rest of the paper proceeds as follows. In Sect. 2, some preliminaries of t-SVD are introduced. The problem formulation and the algorithm are presented in Sect. 3. Experimental results are shown in Sect. 4. Proofs of the theorems and lemmas are in the supplementary material¹.

2 Notations and Preliminaries

Notations. The main notations and abbreviations are listed in Table 1 for convenience. For a 3-way tensor, a tube is a vector defined by fixing indices of the first two modes and varying the third one; A slice is a matrix defined by fixing all but two indices; $\mathrm {fft}_3({\cdot })$ denotes the fast discrete Fourier transformation (FFT) along the third mode of a 3rd order tensor, i.e., the command $\text {fft}(\cdot ,[],3)$ in Matlab; similarly, $\mathrm {ifft}_3({\cdot })$ is defined. Let $\lceil a \rceil$ denote the closest integer to $a \in \mathbb {R}^{}$ that is not smaller than a, and $\lfloor a \rfloor$ denotes the closest integer to $a \in \mathbb {R}^{}$ that is not larger than a. Let $\varvec{1}(\cdot )$ denote the indicator function which equals 1 if the condition is true and 0 otherwise. The spectral norm $\Vert {\cdot }\Vert$ and nuclear norm $\Vert {\cdot }\Vert _{*}$ of a matrix are the maximum and the sum of the singular values, respectively.

Table 1. List of notations and abbreviations

Tensor SVD. Some preliminaries of tensor SVD will be introduced.

Definition 1

(T-product [22]). Let ${\mathcal {T}}_1 \in \mathbb {R}^{d_1 \times d_2 \times d_3}$ and ${\mathcal {T}}_2 \in \mathbb {R}^{d_2\times d_4 \times d_3}$. The t-product of ${\mathcal {T}}_1$ and ${\mathcal {T}}_2$ is a tensor ${\mathcal {T}}$ of size $d_1 \times d_4 \times d_3$:

$$\begin{aligned} {\mathcal {T}}:={\mathcal {T}}_1*{\mathcal {T}}_2, \end{aligned}$$

(4)

whose $(i,j)_{th}$ tube is given by ${\mathcal {T}}(i,j,:)=\sum _{k=1}^{d_2} {\mathcal {T}}_1(i,k,:) \bullet {\mathcal {T}}_2(k,j,:)$, where $\bullet$ denotes the circular convolution between two fibers [9].

Definition 2

(Tensor transpose [22]). Let ${\mathcal {T}}$ be a tensor of size $d_1 \times d_2 \times d_3$, then ${\mathcal {T}}{}^\top$ is the $d_2 \times d_1 \times d_3$ tensor obtained by transposing each of the frontal slices and then reversing the order of transposed frontal slices 2 through $d_3$.

Definition 3

(Identity tensor [22]). The identity tensor ${\mathcal {I}} \in \mathbb {R}^{d_1 \times d_1 \times d_3}$ is a tensor whose first frontal slice is the $d_1 \times d_1$ identity matrix and all other frontal slices are zero.

Definition 4

(F-diagonal tensor [22]). A tensor is called f-diagonal if each frontal slice of the tensor is a diagonal matrix.

Definition 5

(Orthogonal tensor [22]). A tensor ${\mathcal {Q}}\in \mathbb {R}^{d_1\times d_1\times d_3}$ is orthogonal if ${\mathcal {Q}} {}^\top * {\mathcal {Q}} = {\mathcal {Q}} * {\mathcal {Q}} {}^\top = {\mathcal {I}}$.

Based on the above concepts, the tensor singular value decomposition (t-SVD) can be defined as follows.

Definition 6

(T-SVD, Tensor tubal-rank [22]). For any ${\mathcal {T}}\in \mathbb {R}^{d_1 \times d_2 \times d_3}$, the tensor singular value decomposition (t-SVD) of ${\mathcal {T}}$ is given as follows

$$\begin{aligned} {\mathcal {T}}= {\mathcal {U}}*\varvec{\underline{\varLambda }}*{\mathcal {V}}{}^\top ,\end{aligned}$$

(5)

where ${\mathcal {U}}\in \mathbb {R}^{d_1 \times d_1 \times d_3}$, $\varvec{\underline{\varLambda }}\in \mathbb {R}^{d_1 \times d_2 \times d_3}$, ${\mathcal {V}}\in \mathbb {R}^{d_2 \times d_2 \times d_3}$, ${\mathcal {U}}$ and ${\mathcal {V}}$ are orthogonal tensors, $\varvec{\underline{\varLambda }}$ is a rectangular f-diagonal tensor.

The tensor tubal rank of ${\mathcal {T}}$ is defined to be the number of non-zero tubes of $\varvec{\underline{\varLambda }}$ in the t-SVD factorization, i.e.,

$$\begin{aligned} r_{ t }({{\mathcal {T}}}):=\sum _{i}\varvec{1}(\varvec{\underline{\varLambda }}(i,i,:)\ne \varvec{0}). \end{aligned}$$

(6)

The definitions of TNN and tensor spectral norm will be given. The former has been applied as a convex relaxation of the tensor tubal rank in [11, 23, 24].

Definition 7

(Tubal nuclear norm, tensor spectral norm [12, 22]). For any ${\mathcal {T}}\in \mathbb {R}^{d_1 \times d_2 \times d_3}$, let $\overline{\varvec{T}}$ denote the block-diagonal matrix of the tensor $\widetilde{{\mathcal {T}}}:=\mathrm {fft}_3({{\mathcal {T}}})$, i.e.,

$$\begin{aligned} \begin{aligned} \overline{\varvec{T}} :=&\left[ \begin{array}{lll}\widetilde{{\varvec{T}}}(:,:,1)&{} &{} \\ &{}\ddots &{} \\ &{} &{} \widetilde{{\varvec{T}}}(:,:,d_3)\end{array} \right] \in \mathbb {C}^{d_1d_3 \times d_2d_3}. \end{aligned} \end{aligned}$$

The tubal nuclear norm $\Vert {{\mathcal {T}}} \Vert _{\star }$ and tensor spectral norm $\Vert {{\mathcal {T}}} \Vert$ of ${\mathcal {T}}$ are respectively defined as the rescaled matrix nuclear norm and the (non-rescaled) matrix spectral norm of $\overline{\varvec{T}}$, i.e.,

$$\begin{aligned} \Vert {{\mathcal {T}}} \Vert _{\star }:=\frac{\Vert {\overline{\varvec{T}}}\Vert _{*}}{d_3},\quad and ~\quad \Vert {{\mathcal {T}}} \Vert := \Vert {\overline{\varvec{T}}}\Vert . \end{aligned}$$

(7)

It has been shown in [12] that TNN is the dual norm of tensor spectral norm.

3 TriFac for Tensor Robust PCA

3.1 Model Formulation

TNN-Based TRPCA. The recently proposed TNN-based TRPCA model² [12] adopts TNN as a low rank item in Problem 3, and is formulated as follows

$$\begin{aligned} \min _{{\mathcal {L}},{\mathcal {S}}}~ \Vert {{\mathcal {L}}} \Vert _{\star }+\lambda \Vert {{\mathcal {S}}} \Vert _{\text {1}}\quad ~\text {s.t.}~~~{\mathcal {L}}+{\mathcal {S}}={\mathcal {M}}. \end{aligned}$$

(8)

In [11, 12], it is proved that when the underlying tensor ${\mathcal {L}}^*$ satisfy the tensor incoherent conditions, by solving Problem (8), one can exactly recover the underlying tensor ${\mathcal {L}}^*$ and ${\mathcal {S}}^*$ with high probability with parameter $\lambda =1/\sqrt{\max \{d_1,d_2\}d_3}$.

To solve the TNN-based TRPCA in Eq. (8), an algorithm based on the alternating directions methods of multipliers (ADMM) is proposed [11]. In each iteration, it computes a proximity operator of TNN, which requires FFT/IFFT, and $d_3$ full SVDs of $d_1$-by-$d_2$ matrices when the observed tensor ${\mathcal {M}}$ is in $\mathbb {R}^{d_1\times d_2 \times d_3}$. The one-iteration computation complexity of the ADMM-based algorithm is

$$\begin{aligned} O\big (d_1d_2d_3(\log d_3+\min \{d_1,d_2\})\big ), \end{aligned}$$

(9)

which is very expensive for large tensors.

Proposed TriFac. To reduce the cost of computing TNN in Problem (8), we propose the following lemma, indicating that TNN is orthogonal invariant.

Lemma 1

(Orthogonal invariance of TNN). Given a tensor ${\mathcal {X}}\in \mathbb {R}^{r\times r \times d_3}$, let ${\mathcal {P}}\in \mathbb {R}^{d_1\times r \times d_3}$ and ${\mathcal {Q}}\in \mathbb {R}^{d_2\times r \times d_3}$ be two semi-orthogonal tensors, i.e., ${\mathcal {P}}{}^\top *{\mathcal {P}}={\mathcal {I}}\in \mathbb {R}^{r\times r\times d_3}$ and ${\mathcal {Q}}{}^\top *{\mathcal {Q}}={\mathcal {I}}\in \mathbb {R}^{r\times r\times d_3}$, and $r\le \min \{d_1,d_2\}$. Then, we have the following relationship: $\Vert {{\mathcal {P}}*{\mathcal {X}}*{\mathcal {Q}}{}^\top } \Vert _{\star }= \Vert {{\mathcal {X}}} \Vert _{\star }$.

Equipped with Lemma 1, we decompose the low rank component in Problem 8 as follows:

$$\begin{aligned} {\mathcal {L}}={\mathcal {P}}*{\mathcal {C}}*{\mathcal {Q}}{}^\top ,\quad \text {s.t.}~~{\mathcal {P}}{}^\top *{\mathcal {P}}={\mathcal {I}}_{r},~{\mathcal {Q}}{}^\top *{\mathcal {Q}}={\mathcal {I}}_{r}, \end{aligned}$$

(10)

where ${\mathcal {I}}_{r}\in \mathbb {R}^{r\times r\times d_3}$ is an identity tensor. Further, we propose the following model based on triple factorization (TriFac) for tensor robust PCA

$$\begin{aligned} \begin{aligned} \min _{{\mathcal {P}},{\mathcal {Q}},{\mathcal {C}},{\mathcal {S}}}&~ \Vert {{\mathcal {C}}} \Vert _{\star }+\lambda \Vert {{\mathcal {S}}} \Vert _{\text {1}}\\ \text {s.t.}~~&~{\mathcal {P}}*{\mathcal {C}}*{\mathcal {Q}}{}^\top +{\mathcal {S}}={\mathcal {M}}, ~{\mathcal {P}}{}^\top *{\mathcal {P}}={\mathcal {I}}_{r},~{\mathcal {Q}}{}^\top *{\mathcal {Q}}={\mathcal {I}}_{r}, \end{aligned} \end{aligned}$$

(11)

where ${\mathcal {I}}_{r}:={\mathcal {I}}\in \mathbb {R}^{r\times r \times d_3}$, r is an upper estimation of tubal rank of the underlying tensor $r^*=r_{ t }({{\mathcal {L}}^*})$ and we set $\lambda =1/\sqrt{\max \{d_1,d_2\}d_3}$ as suggested by [12].

Different from Problem 8, the proposed TriFac is a non-convex model which may have many local minima. We establish a connection between the proposed model TriFac in Problem (11) with the TNN-based TRPCA model (8) in the following theorem.

Theorem 1

(Connection between TriFac and TRPCA). Let $({\mathcal {P}}_{*}, {\mathcal {C}}_{*}, {\mathcal {Q}}_{*},{\mathcal {S}}_{*})$ be a global optimal solution to TriFac in Problem (11). And let $({\mathcal {L}}^\star ,{\mathcal {S}}^\star )$ be the solution to TRPCA in Problem (8), and $r_{ t }({{\mathcal {L}}^\star })\le r$, where r is the initialized tubal rank. Then $({\mathcal {P}}_{*}*{\mathcal {C}}_{*}*{\mathcal {Q}}{}^\top _{*},{\mathcal {S}}_{*})$ is also the optimal solution to Problem (8).

Theorem 1 asserts that the global optimal point of the (non-convex) TriFac coincides with solution of the (convex) TNN-based TRPCA which is guaranteed to exactly recover the underlying tensor ${\mathcal {L}}^*$ under certain conditions. This phenomenon means that the accuracy of the proposed model cannot exceed TPRCA, which will be shown numerically in the experiment section.

3.2 Optimization Algorithm

The partial augmented Lagrangian of Problem (11) is as follows:

$$\begin{aligned} \begin{aligned}&L_{\mu }({\mathcal {P}},{\mathcal {C}},{\mathcal {Q}},{\mathcal {S}},{\mathcal {Y}})\\&= \Vert {{\mathcal {C}}} \Vert _{\star }+\lambda \Vert {{\mathcal {S}}} \Vert _{\text {1}}+\left\langle {\mathcal {Y}},{\mathcal {P}}*{\mathcal {C}}*{\mathcal {Q}}{}^\top +{\mathcal {S}}-{\mathcal {M}}\right\rangle +\frac{\mu }{2} \Vert {{\mathcal {P}}*{\mathcal {C}}*{\mathcal {Q}}{}^\top +{\mathcal {S}}-{\mathcal {M}}} \Vert _{\text {F}}^2,\\&\text {s.t.}~~~{\mathcal {P}}{}^\top *{\mathcal {P}}={\mathcal {I}}_{r},~{\mathcal {Q}}{}^\top *{\mathcal {Q}}={\mathcal {I}}_{r}, \end{aligned} \end{aligned}$$

(12)

where $\mu >0$ is a penalty parameter, and ${\mathcal {Y}}\in \mathbb {R}^{d_1\times d_2 \times d_3}$ is the Lagrangian multiplier. Based on the Lagrangian in Eq. (12), we update each variable by fixing the others.

The ${\mathcal {P}}$-subproblem. We update ${\mathcal {P}}$ by fixing other variables and minimize $L_{\mu }(\cdot )$:

$$\begin{aligned} {\mathcal {P}}_{t+1} =\mathop {\mathrm{argmin}}\limits _{{\mathcal {P}}{}^\top *{\mathcal {P}}={\mathcal {I}}_{r}}L_{\mu _t}({\mathcal {P}},{\mathcal {C}}_{t},{\mathcal {Q}}_{t},{\mathcal {S}}_{t},{\mathcal {Y}}_{t})=\mathop {\mathrm{argmin}}\limits _{{\mathcal {P}}{}^\top *{\mathcal {P}}={\mathcal {I}}_{r}}\frac{\mu _t}{2} \Vert {{\mathcal {P}}*{\mathcal {A}}-{\mathcal {B}}} \Vert _{\text {F}}^2 \end{aligned}$$

(13)

where ${\mathcal {A}}={\mathcal {C}}_{t}*{\mathcal {Q}}{}^\top _{t}$ and ${\mathcal {B}}={\mathcal {M}}-{\mathcal {S}}_{t}-{\mathcal {Y}}_{t}/\mu _t$. We need the following lemma to solve Problem (13).

Lemma 2

Given any tensors ${\mathcal {A}}\in \mathbb {R}^{r\times d_2 \times d_3},{\mathcal {B}}\in \mathbb {R}^{d_1\times d_2 \times d_3}$, suppose tensor ${\mathcal {B}}*{\mathcal {A}}{}^\top$ has t-SVD ${\mathcal {B}}*{\mathcal {A}}{}^\top ={\mathcal {U}}*\varvec{\underline{\varLambda }}*{\mathcal {V}}{}^\top$, where ${\mathcal {U}}\in \mathbb {R}^{d_1\times r \times d_3}$ and ${\mathcal {V}}\in \mathbb {R}^{r\times r\times d_3}$. Then, the problem

$$\begin{aligned} \min _{{\mathcal {P}}{}^\top *{\mathcal {P}}={\mathcal {I}}_{r}} \Vert {{\mathcal {P}}*{\mathcal {A}}-{\mathcal {B}}} \Vert _{\text {F}}^2 \end{aligned}$$

(14)

has a closed-form solution as

$$\begin{aligned} {\mathcal {P}}=\mathfrak {P}({\mathcal {B}}*{\mathcal {A}}{}^\top ):={\mathcal {U}}*{\mathcal {V}}{}^\top . \end{aligned}$$

(15)

The ${\mathcal {Q}}$-subproblem. By fixing other variables, we update ${\mathcal {Q}}$ as follows

$$\begin{aligned} \begin{aligned} {\mathcal {Q}}_{t+1} =&\mathop {\mathrm{argmin}}\limits _{{\mathcal {Q}}{}^\top *{\mathcal {Q}}={\mathcal {I}}_{r}}L_{\mu _t}({\mathcal {P}}_{t+1},{\mathcal {C}}_{t},{\mathcal {Q}},{\mathcal {S}}_{t},{\mathcal {Y}}_{t})\\ =&\mathop {\mathrm{argmin}}\limits _{{\mathcal {Q}}{}^\top *{\mathcal {Q}}={\mathcal {I}}_{r}}\frac{\mu _t}{2} \Vert {{\mathcal {A}}'*{\mathcal {Q}}{}^\top -{\mathcal {B}}} \Vert _{\text {F}}^2\\ =&\mathop {\mathrm{argmin}}\limits _{{\mathcal {Q}}{}^\top *{\mathcal {Q}}={\mathcal {I}}_{r}}\frac{\mu _t}{2} \Vert {({\mathcal {Q}}*{\mathcal {A}}'{}^\top )-{\mathcal {B}}{}^\top } \Vert _{\text {F}}^2\\ =&\big (\mathfrak {P}({\mathcal {B}}{}^\top *{\mathcal {A}}')\big ){}^\top , \end{aligned} \end{aligned}$$

(16)

where ${\mathcal {A}}'={\mathcal {P}}_{t+1}*{\mathcal {C}}_{t}$ and ${\mathcal {B}}={\mathcal {M}}-{\mathcal {S}}_{t}-{\mathcal {Y}}_{t}/\mu _t$, and $\mathfrak {P}(\cdot )$ is defined in Lemma 2. The last equality holds because of Eq. (15) in Lemma 2.

The ${\mathcal {C}}$-subproblem. We update ${\mathcal {C}}$ as follows

$$\begin{aligned} \begin{aligned} {\mathcal {C}}_{t+1} =&\mathop {\mathrm{argmin}}\limits _{{\mathcal {C}}}L_{\mu _t}({\mathcal {P}}_{t+1},{\mathcal {C}},{\mathcal {Q}}_{t+1},{\mathcal {S}}_{t},{\mathcal {Y}}_{t})\\ =&\mathop {\mathrm{argmin}}\limits _{{\mathcal {C}}} \Vert {{\mathcal {C}}} \Vert _{\star }+\frac{\mu _t}{2} \Vert {{\mathcal {P}}_{t+1}*{\mathcal {C}}*{\mathcal {Q}}{}^\top _{t}+{\mathcal {S}}_{t}-{\mathcal {M}}+{\mathcal {Y}}/\mu _t} \Vert _{\text {F}}^2\\ =&\mathop {\mathrm{argmin}}\limits _{{\mathcal {C}}} \Vert {{\mathcal {C}}} \Vert _{\star }+\frac{\mu _t}{2} \Vert {{\mathcal {C}}-{\mathcal {P}}_{t+1}{}^\top *({\mathcal {M}}-{\mathcal {S}}_{t}-{\mathcal {Y}}/\mu _t)*{\mathcal {Q}}_{t+1}} \Vert _{\text {F}}^2\\ =&\mathfrak {S}_{1/\mu _t}({\mathcal {P}}_{t+1}{}^\top *({\mathcal {M}}-{\mathcal {S}}_{t}-{\mathcal {Y}}/\mu _t)*{\mathcal {Q}}_{t+1}) \end{aligned} \end{aligned}$$

(17)

where $\mathfrak {S}_{\tau }(\cdot )$ is the proximity operator of TNN [16]. In [16], a closed-form expression of $\mathfrak {S}_{\tau }(\cdot )$ is given as follows:

Lemma 3

(Proximity operator of TNN [16]). For any 3D tensor ${\mathcal {A}}\in \mathbb {R}^{d_1\times d_2 \times d_3}$ with reduced t-SVD ${\mathcal {A}}={\mathcal {U}}*\varvec{\underline{\varLambda }}*{\mathcal {V}}{}^\top$, where ${\mathcal {U}}\in \mathbb {R}^{d_1 \times r \times d_3}$ and ${\mathcal {V}}\in \mathbb {R}^{d_2 \times r \times d_3}$ are orthogonal tensors and $\varvec{\underline{\varLambda }}\in \mathbb {R}^{r \times r \times d_3}$ is the f-diagonal tensor of singular tubes, the proximity operator $\mathfrak {S}_{\tau }({\mathcal {A}})$ at ${\mathcal {A}}$ can be computed by:

$$\begin{aligned} \mathfrak {S}_{\tau }({\mathcal {A}}):=&\mathop {\mathrm{argmin}}\limits _{{\mathcal {X}}}\tau \Vert {{\mathcal {X}}} \Vert _{\star }+\frac{1}{2} \Vert {{\mathcal {X}}-{\mathcal {A}}} \Vert _{\text {F}}^2 ={\mathcal {U}}*\mathrm {ifft}_3({\max (\mathrm {fft}_3({\varvec{\underline{\varLambda }}})-\tau ,0)})*{\mathcal {V}}{}^\top . \end{aligned}$$

The ${\mathcal {S}}$-subproblem. We update ${\mathcal {S}}$ as follows

$$\begin{aligned} \begin{aligned} {\mathcal {S}}_{t+1} =&\mathop {\mathrm{argmin}}\limits _{{\mathcal {S}}}L_{\mu _{t}}({\mathcal {P}}_{t+1},{\mathcal {C}}_{t+1},{\mathcal {Q}}_{t+1},{\mathcal {S}},{\mathcal {Y}}_{t})\\ =&\mathop {\mathrm{argmin}}\limits _{{\mathcal {S}}}\lambda \Vert {{\mathcal {S}}} \Vert _{\text {1}}+\frac{\rho }{2} \Vert {{\mathcal {P}}_{t+1}*{\mathcal {C}}_{t+1}*{\mathcal {Q}}{}^\top _{t+1}+{\mathcal {S}}-{\mathcal {M}}+\frac{{\mathcal {Y}}_{t}}{\mu _t}} \Vert _{\text {F}}\\ =&\mathfrak {T}_{\lambda /\rho }({\mathcal {M}}-{\mathcal {P}}_{t+1}*{\mathcal {C}}_{t+1}*{\mathcal {Q}}{}^\top _{t+1}-\frac{{\mathcal {Y}}_{t}}{\mu _t}) \end{aligned} \end{aligned}$$

(18)

where $\mathfrak {T}_{\tau }(\cdot )$ is the proximity operator of tensor $l_1$-norm given as follows:

$$\begin{aligned} \mathfrak {T}_{\tau }({\mathcal {A}}):=\mathop {\mathrm{argmin}}\limits _{{\mathcal {X}}}\tau \Vert {{\mathcal {X}}} \Vert _{\text {1}}+\frac{1}{2} \Vert {{\mathcal {X}}-{\mathcal {A}}} \Vert _{\text {F}}^2=\text {sign}({\mathcal {A}})\circledast \max \{(|{\mathcal {A}}|-\tau ,0\}, \end{aligned}$$

where $\circledast$ denotes the element-wise tensor product.

Complexity Analysis. In each iteration, the update of ${\mathcal {P}}$ involves computing FFT, IFFT and $d_3$ SVDs of $r\times d_2$ matrices, having complexity of order $O\big ( rd_2d_3\log d_3 + r^2d_2d_3\big )$. Similarly, the update of ${\mathcal {Q}}$ has complexity of order $O\big ( rd_1d_3\log d_3 + r^2d_1d_3\big )$. Updating ${\mathcal {C}}$ involves complexity of order $O\big ( r^2d_3(r+\log d_3)\big )$. Updating ${\mathcal {S}}$ costs $O\big (d_1d_2d_3\big )$. So one iteration cost of Algorithm 1 is

$$\begin{aligned} O\left( d_3\big (d_1d_2\log d_3 + r^2(r+d_1+d_2+\log d_3)+r(d_1+d_2)\log d_3\big )\right) . \end{aligned}$$

When $r\ll \min \{d_1,d_2\}$, the above cost is significantly lower than the one-iteration cost of ADMM-based TRPCA [12] in Eq. (9). Consider an extreme case in high dimensional settings where $r_{ t }({{\mathcal {L}}^*})=O(1)$, i.e., the tubal rank of the underlying tensor ${\mathcal {L}}^*$ scales like a small constant. By choosing the initialized rank $r=2r_{ t }({{\mathcal {L}}^*})=O(1)$, the one-iteration cost of Algorithm 1 scales like

$$\begin{aligned} O(d_1d_2d_3\log d_3), \end{aligned}$$

(20)

which is much cheaper than $O(d_1d_2d_3\min \{d_1,d_2\})$ of ADMM-based algorithm in high dimensional settings.

Convergence Analysis. The following theorem shows that Algorithm 1 is convergent.

Theorem 2

Letting $({\mathcal {P}}_t,{\mathcal {C}}_t,{\mathcal {Q}}_t,{\mathcal {S}}_t)$ be any sequence generated by Algorithm 1, the following statements hold

• (I) The sequences $({\mathcal {C}}_t,{\mathcal {P}}_t*{\mathcal {C}}_t*{\mathcal {Q}}_t{}^\top ,{\mathcal {S}}_{t})$ are Cauchy sequences respectively.

• (II) $({\mathcal {P}}_t,{\mathcal {C}}_t,{\mathcal {Q}}_t,{\mathcal {S}}_t)$ is a feasible solution to Problem (11) in a sense that

  $$\begin{aligned} \lim _{t\rightarrow \infty } \Vert {{\mathcal {P}}_t*{\mathcal {C}}_t*{\mathcal {Q}}{}^\top _t+{\mathcal {S}}_{t}-{\mathcal {M}}} \Vert _{\infty } \le \varepsilon . \end{aligned}$$

  (21)

4 Experiments

In this section, we experiment on both synthetic and real datasets to verify the effectiveness and the efficiency of the proposed algorithm. All codes are written in Matlab and all experiments are performed in Windows 10 based on Intel(R) Core(TM) i7-8565U 1.80-1.99 GHz CPU with 8G RAM.

4.1 Synthetic Data Experiments

In this subsection, we compare Algorithm 1 (TriFac) with the TNN-based TRPCA [11] in both accuracy and speed on synthetic datasets. Given tensor size $d_1\times d_2 \times d_3$ and tubal rank $r^*\ll \min \{d_1,d_2\}$, we first generate a tensor ${\mathcal {L}}_0\in \mathbb {R}^{d_1\times d_2 \times d_3}$ by ${\mathcal {L}}_0={\mathcal {A}}*{\mathcal {B}}$, where the elements of tensors ${\mathcal {A}}\in \mathbb {R}^{d_1\times r^*\times d_3}$ and ${\mathcal {B}}\in \mathbb {R}^{r^*\times d_2\times d_3}$ are sampled from independent and identically distributed (i.i.d.) standard Gaussian distribution. We then form ${\mathcal {L}}^*$ by ${\mathcal {L}}^*=\sqrt{d_1d_2d_3}{\mathcal {L}}_0/ \Vert {{\mathcal {L}}_0} \Vert _{\text {F}}$. Next, the support of ${\mathcal {S}}^*$ is uniformly sampled at random. For any $(i,j,k)\in \mathrm {supp}\left( {\mathcal {S}}^*\right)$, we set ${\mathcal {S}}^*_{ijk} = {\mathcal {B}}_{ijk}$, where ${\mathcal {B}}$ is a tensor with independent Bernoulli $\pm 1$ entries. Finally, we form the observation tensor ${\mathcal {M}}={\mathcal {L}}^*+{\mathcal {S}}^*$. For an estimation $\hat{{\mathcal {L}}}$ of the underlying tensor ${\mathcal {L}}^*$, the relative squared error (RSE) is used to evaluate its quality [11].

Effectiveness and Efficiency of TriFac

We first show that TriFac can exactly recover the underlying tensor ${\mathcal {L}}^*$ from corruptions faster than TRPCA. We first test the recovery performance of different tensor sizes by setting $d_1=d_2\in \{100,160,200\}$ and $d_3=30$, with $(r_{ t }({{\mathcal {L}}^*}), \Vert {{\mathcal {S}}^*} \Vert _{0})=(0.05d,0.05d^2d_3)$. Then, a more difficult setting $(r_{ t }({{\mathcal {L}}^*}), \Vert {{\mathcal {S}}^*} \Vert _{0})=(0.15d,0.1d^2d_3)$ is tested. The results are shown in Table 2. It can be seen that TriFac can perform as well as TRPCA in the sense that both of them can exactly recover the underlying tensor. However, TriFac is much faster than TRPCA.

Table 2. Comparison with TRPCA in both accuracy and speed for different tensor sizes when the outliers follow i.i.d. Bernoulli distribution.

Fig. 1.

Computation time of TRPCA [12] and the proposed TriFac versus $d\in \{100,150,\cdots ,500\}$ with $d_3=20$, when the tubal rank of the underlying tensor is 5. The RSEs of TNN and TriFac in all the setting are smaller than $1{\text {e}}{-6}$.

To further show the efficiency of the proposed TriFac, we consider a special case where the size of the underlying tensor ${\mathcal {L}}^*$ increases while the tubal rank is fixed as a constant. Specifically, we fix $r_{ t }({{\mathcal {L}}^*})=5$, and vary $d\in \{100,150,\cdots ,500\}$ with $d_3=20$. We set the parameter of initialized rank r of TriFac in Algorithm 1 by $r=30$. We test each setting 10 times and compute the averaged time. In all the runs, both TRPCA and TriFac can recover the underling tensor with RSE smaller than $1{\text {e}}{-6}$. The plot of averaged time versus the tensor size (shown in d) is given in Fig. 1. We can see that the time cost of TRPCA scales super-linearly with respect to d, whereas the proposed TriFac has approximately linear scaling.

Effects of the Initialized Tubal Rank r. The performance of TriFac heavily relies on the choice of initialized tubal rank r in Model (11). Here, we explore the effects of initialized tubal rank on the accuracy and speed of TriFac. Specifically, we consider tensors of size $100\times 100\times 30$ with four different settings of tubal rank $r^*=r_{ t }({{\mathcal {L}}^*})$ and sparsity $s^*= \Vert {{\mathcal {S}}^*} \Vert _{0}$ as $(r^*,s^*)\in \{(10,1.5{\text {e}}{4}),(10,3{\text {e}}{4}),(15,1.5{\text {e}}{4}),(10,3{\text {e}}{4})\}$, where the elements outliers follow i.i.d. $\mathcal {N}(0,1)$. By varying the initialized $r\in \{5,10,\cdots ,50\}$, we test the effects of the initialized tubal rank r on the accuracy and speed of TriFac.

Fig. 2.

Effects of initialized tubal rank r in Algorithm 1 on the recovery performance of the underlying tensor ${\mathcal {L}}^*\in \mathbb {R}^{100\times 100\times 30}$. (a): RSE of $\hat{{\mathcal {L}}}$ versus r in log scale; (b): tubal rank of $\hat{{\mathcal {L}}}$ versus r.

Fig. 3.

Effects of initialized tubal rank r in Algorithm 1 on the estimation performance of the outlier tensor ${\mathcal {S}}^*\in \mathbb {R}^{100\times 100\times 30}$. (a): RSE of $\hat{{\mathcal {S}}}$ in log scale versus r; (b): $l_0$-norm of $\hat{{\mathcal {S}}}$ versus r.

We first report the effects of initialized tubal rank r on the recovery accuracy of the underlying tensor ${\mathcal {L}}^*$, in terms of RSE and tubal rank of the final solution $\hat{{\mathcal {L}}}$. The results are shown in Fig. 2. As can be seen, there exists a phrase transition point $r_\mathrm{{pt}}$ that once the initialized rank r is larger than it, the RSE of $\hat{{\mathcal {L}}}$ will decrease rapidly. Then, the effects of initialized tubal rank r on the estimation performance of the outlier tensor ${\mathcal {S}}^*$, in terms of RSE and $l_0$-norm of the final solution $\hat{{\mathcal {S}}}$ are shown in Fig. 2. We can also see that when the initialized rank r gets larger than the same phrase transition point $r_\mathrm{{pt}}$, the RSE of $\hat{{\mathcal {S}}}$ will soon vanishes. Finally, we show the effects of initialized tubal rank r on the running time of TriFac in Fig. 4. We can see that the running time will increase, if the initialized rank r gets larger, the underlying tensor gets more complex (i.e., $r^*$ gets greater), or the corruption gets heavier (i.e., $s^*$ gets larger). That is consistent with our intuition (Fig. 3).

Fig. 4.

Effects of initialized tubal rank r on the running time of TriFac for problem size $100\times 100\times 30$.

4.2 Real Data Experiments

In this section, the efficiency of the proposed TriFac compared with TRPCA [12] is evaluated on real-world datasets. Specifically, we carry out tensor restoration experiments on point cloud data and brain MRI data. For an estimation $\hat{{\mathcal {L}}}$ of the underlying tensor ${\mathcal {L}}^*$, the peak signal-to-noise ratio (PSNR) [11] is applied to evaluate the quality of $\hat{{\mathcal {L}}}$.

Point Cloud Data. We conduct experiments on a point cloud data set acquired by a vehicle-mounted Velodyne HDL-64E LiDAR³ [13]. We extract the first 32 frames, transform and upsample the data to form two tensors in $\mathbb {R}^{512\times 800 \times 32}$ representing the distance data and the intensity data, respectively. Given a data tensor, we uniformly choose its indices with probability $\rho _s\in \{0.2,0.4\}$. We then corrupt the chosen positions with element-wise outliers from i.i.d. symmetric Bernoulli $\text {Ber}(-1,+1)$ or $\mathcal {N}(0,1)$. The proposed algorithm is also compared with SNN [8] and RPCA [1]. RPCA works on each frontal slice individually. The parameters of RPCA is set by $\lambda =1/\sqrt{\max \{d_1,d_2\}}$ [1]. The weight parameters $\varvec{\lambda }$ of SNN are chosen by $\lambda _k=\sqrt{\max \{d_k,\prod _{k'\ne k}d_{k'}\}}/3$. We set the initialized tubal rank $r=196$ in Algorithm 1.

We report the PSNR values and running time of each algorithm on the distance and intensity data in Fig. 5. It can be seen that TNN-based TRPCA has the highest PSNR values in all the settings, which is consistent with the results of tensor completion on this data that TNN outperforms SNN [17]. The proposed TriFac algorithm performs slightly worse than TNN, but it has the lowest running time. As is shown in Theorem 1, the proposed model in Eq. 11 can not outperform TNN-based RPCA model in Eq. (8) since they have the same global optimal solutions but the proposed model is non-convex. This explains why TriFac cannot achieve better performances than TRPCA.

Fig. 5.

Quantitative comparison of algorithms in PSNR and running time on point cloud data. (a): PSNR values of algorithms on the distance data; (b): running time of algorithms on the distance data; (c): PSNR values of algorithms on the intensity data; (d): running time of algorithms on the intensity data. (‘0.2, B’ means 20% of the positions are corrupted by Ber($-1,+1$) outliers, and ‘0.4,G’ means 40% of the positions are corrupted by $\mathcal {N}(0,1)$ outliers).

Brain MRI Data. To show the efficiency of the proposed TriFac, we also use the 3-way MRI data set analyzed in [21] which has good low-rank property. We extract the first 15 slices, each having a size of $181 \times 217$. To further show the efficiency of TriFac, we resize the data with scale parameter $\kappa \in \{1,1.5,2,2.5,3\}$ to form tensors in $\mathbb {R}^{\lceil 181\kappa \rceil \times \lceil 217\kappa \rceil \times 15}$. Then, we randomly choose $20\%$ of the elements in the rescaled tensor, and corrupts them by elements from i.i.d. Bernoulli distribution $\text {Ber}(-1,+1)$. We compare TriFac with TRPCA in both running time and recovery performance with respect to different sizes. The results are shown in Table 3. It can be seen that the proposed TriFac works almost as well as TRPCA but has faster speed.

Table 3. Comparison of TriFac with TRPCA in both PSNR values and running time on rescaled MRI data in $\mathbb {R}^{\lceil 181\kappa \rceil \times ~\lceil 217\kappa \rceil ~\times 15}$ with $\kappa \in \{1,1.5,2,2.5,3\}$.

5 Conclusion

In this paper, a factorization-based TRPCA model (TriFac) is first proposed to recover a 3-way data tensor from its observation corrupted by sparse outliers. Then, we come up with a non-convex ALM algorithm (Algorithm 1) to efficiently solve it. Further, the convergence of the proposed algorithm is analyzed in Theorem 2. The effectiveness and efficiency of the proposed algorithm is demonstrated in experiments on both synthetic and real datasets.