1 Introduction

In 1982, Wille first put forward the theory of formal concept analysis (FCA) which is also called concept lattice theory [12, 46] to discover, sort and display formal concepts [extent (collection of objects), intent (collection of attributes)]. Concept lattice, a model of knowledge representation, is the core data structure in FCA. Based on the dependence or causality of knowledge in the extent and intent, the concept lattice is constructed. It reflects the generalization and specialization between concepts vividly and succinctly [2, 5, 45]. FCA is a powerful formal tool for data analysis and knowledge processing, which has been successfully applied in fields such as data mining, software engineering and many other disciplines [7, 31, 36, 43]. At present, the research on FCA is mainly divided into the following aspects: basic theoretical research, concept lattice construction algorithm composed of incremental algorithm [14, 21, 30]and batch algorithm [44, 60], reduction of concept lattices [62], the relations between FCA and rough sets [32], concept lattice theory under fuzzy conditions [4, 6] and so on.

The theory of rough sets (RS)[32] is an extension of the classical set theory. FCA and RS can learn from each other and integrate with each other, and realize mutual improvement [16, 20]. In recent years, many researchers have combined the two theories and conduct deeper knowledge discovery. For instance, based on the modal-style operators, Duntsch and Gediga proposed the attribute-oriented concept lattice [10, 13]. Yao further developed the object-oriented concept lattice which enrich the research on FCA [54, 55].

The notion of granular computing (GrC) originated in the context of fuzzy sets presented by Zadeh [57]. Zadeh proposed the basic framework of GrC and emphasized the importance of granularity in reasoning. GrC is an approach for knowledge representation and data mining [28, 33]. GrC emphasizes multi-perspective and multi-level understanding and description of real-world problems. Its basic idea is to use the information on different granularity to divide the complex problem into a series of more easily handled, smaller sub-problems. Thereby, its computational cost is reduced. In recent years, GrC has been widely used in many fields such as data mining, pattern recognition, intelligent control and complex problems solving [8, 24, 26, 27, 29, 34, 37, 38, 41, 42, 58, 59].

GrC has been an emerging research focus in recent years. For example, Yao discussed the comprehensive level of granularity and the theory of GrC in [52, 53]. As one of the effective model of GrC, RS theory [56] describes the target concept, the attribute reduction, rules extraction and problem decision-making through the set of attributes [61]. In order to deal with the complex real-world problems such as multi-source information systems, Qian et al. [35] proposed a multi-granularity rough set model based on multi-granularity structures. Wu et al. [47] further studied the theory and application of granular blocks in multi-granularity decision information system. In addition, Dick et al. [9] established a new type of granular neural network. On the other hand, the selection of optimal granularity in multi-granularity labeling information systems is studied in [17, 22, 23, 40, 48]. Xu et al. further proposed the transformation of information granules for the human cognitive system [49] and studied the information fusion in multi-source database [51]. What’s more, She et al. [39] studied the acquisition of rules in the context of multi-granularity decision making.

With the development of GrC and FCA, the combination of the two theories has drawn the attention of researchers. Du et al. [11] studied the relevance between concept lattice and granularity division, concept description and concept hierarchy. Based on concept library, Kang [18] analyzed the granularity of concept lattice and proposed the upper and lower bounds when dealing with attribute granularity. The attribute reduction in concep lattice was studied in [25, 63]. Gong and Shao [15] discussed the approximation operators in the concept granular system. In [64], Zou et al. proposed a “expanding algorithm” to rapidly increase the granularity of formal concept lattices. Xu et al. [50] proposed a novel GrC method of machine learning by using formal concept description of information granules. Kang and Miao [19] discussed the relation between granularity and the algebraic structure in complex information systems. In [1, 3], based on attribute granularity tree, Belohlavek et al. proposed the transformation method of the attribute granularity level and applied zoom algorithms to control the number of concepts in the classic concept lattice.

Comparing with the studies on classical concept lattices, there are few researches on the attribute (object)-oriented multi-granularity concept lattices. Our concern in this paper is the fast construction of attribute (object)-oriented multi-granularity concept lattices. We construct the attribute granularity tree according to the experience of experts. If the attribute granularity is too fine, redundant concepts may be generated. That is, users can not extract useful knowledge easily compared with a relatively coarser granularity. According to the given attribute granularity trees, different information can be extracted from the concept lattice by dynamically changing the attribute granularity. In a multi-granularity information system, the construction of the attribute (object)-oriented concept lattices are as follows: first, for a given level of granularity, the all attribute (object)-oriented concepts are generated; then, apply the operators to the attribute (object)-oriented concepts to obtain the concept lattice.

The remainder of this paper is organized as follows: in order to make the paper self-contained, basic notions of formal context, approximation operators, attribute (object)-oriented concept and attribute granularity are briefly reviewed in Sect. 2. In Sect. 3, the zoom algorithms of attribute (object)-oriented concept lattice are provided. The transformation algorithms among three types of concept lattice are proposed in Sect. 4. In Sect. 5, it is concluded with a summary and the prospects for further research. In the end, the examples are used to demonstrate the zoom algorithms.

2 Preliminaries

In this section, the notions and properties related to attribute (object)-oriented concept lattice (see [13, 54]) are briefly reviewed. Besides, the definition of attribute granularity and its basic properties are introduced (for details, please refer to [3]).

Definition 1

[54] A triplet \(K=(G,M,I)\) is called a formal context if, G (the collection of objects) and M (the collection of attributes) are two finite nonempty sets and I (subset of cartesian product \(G\times M\)) represents the binary relation between G and M, where 1 denotes that object has attribute and 0 denotes that object does not have the attribute.

Example 1

A formal context \(K=(G,M,I)\) is presented in Table 1, where \(G=\{x_1,x_2,x_3,x_4,x_5,x_6\}\), \(M=\{a,b,c,d,e\}\).

Table 1 A formal context (G, M, I) with \(G=\{x_1,x_2,x_3,x_4,x_5,x_6\},\) and \(M=\{a,b,c,d,e\}\)
Full size table

Let \(K=(G,M,I)\) be a formal context. If \(x\in G\), \(b\in M\) and \((x,b)\in I\), it can be written as xIb. It means that object x possesses attribute b or attribute b is possessed by object x.

In addition, xIb can be replaced by its equivalence \(b\in xI\) or \(x\in Ib\). xI and Ib are described by

$$\begin{aligned} xI=\{b\in M|xIb\},\ Ib=\{x\in G|xIb\}, \end{aligned}$$

where xI represents the collection of attribute b which is possessed by object x, and Ib represents the collection of object x which has attribute b. The above relations can be extended to the subsets of \(X\subseteq G\) and \(B\subseteq M\) respectively as

$$\begin{aligned} XI=\bigcup _{x\in X}xI,\ IB=\bigcup _{b\in B}Ib. \end{aligned}$$

Definition 2

[13, 54] Let \(K=(G,M,I)\) be a formal context, \(X\subseteq G\) and \(B\subseteq M\). Operators \(^{\uparrow }\) and \(^{\downarrow }\) are defined as follows:

(1)   \(^{\uparrow }\), \(^{\downarrow }\), \(2^G\rightarrow 2^M\):

$$\begin{aligned} \begin{array}{cl} &{} X^{\uparrow }=XI=\{b\in M|\ \exists x\in G, (xIb\wedge (x\in X))\}, \\ &{} X^{\downarrow }=\{b\in M|\ \forall x\in G, (xIb\Rightarrow (x\in X))\}. \end{array} \end{aligned}$$
(1)

(2)   \(^{\uparrow }\), \(^{\downarrow }\), \(2^M\rightarrow 2^G\):

$$\begin{aligned} \begin{array}{ll} &{} B^{\uparrow }=IB=\{x\in G|\ \exists b\in M, (xIb\wedge (b\in B))\}, \\ &{} B^{\downarrow }=\{x\in G|\ \forall b\in M, (xIb\Rightarrow (b\in B))\}. \end{array} \end{aligned}$$
(2)

Let \(K=(G,M,I)\) be a formal context, \(X_1\subseteq G\) and \(X_2\subseteq G\). Operators \(^{\uparrow }\) and \(^{\downarrow }\) satisfy the following properties:

  1. (1)

    \(X_1\subseteq X_2\Rightarrow X_1^\uparrow \subseteq X_2^\uparrow , X_1^\downarrow \subseteq X_2^\downarrow ;\)

  2. (2)

    \({X_1^{\downarrow \uparrow }\subseteq } X_1\subseteq X_1^{\uparrow \downarrow };\)

  3. (3)

    \(X_1^{\downarrow \uparrow \downarrow }= X_1^\downarrow ;\)

  4. (4)

    \(X_1^{\uparrow \downarrow \uparrow }= X_1^\uparrow ;\)

  5. (5)

    \((X_1\cap X_2)^\downarrow =X_1^\downarrow \cap X_2^\downarrow ;\)

  6. (6)

    \((X_1\cup X_2)^\uparrow =X_1^\uparrow \cup X_2^\downarrow\).

Definition 3

[13, 54] Let \(K=(G,M,I)\) be a formal context. A pair (X, B) (\(X\subseteq G\), \(B\subseteq M\)) is called an attribute-oriented concept if \(X=B^\downarrow\) and \(B=X^\uparrow\). Similarly, (X, B) is called object-oriented concept if \(X=B^\uparrow\) and \(B=X^\downarrow\). X and B are called the extent and intent of the attribute(object)-oriented concept respectively.

Let \((X_1,B_1)\) and \((X_2,B_2)\) be the attribute(object)-oriented concepts. The partial order \(\le\) among them is defined by

$$\begin{aligned} (X_1,B_1)\le (X_2,B_2)\ \text{ iff }\ X_1\subseteq X_2\ (\text{ iff }\ B_1\subseteq B_2). \end{aligned}$$

Let \(K=(G,M,I)\) be a formal context. The complete set of attribute-oriented concepts form a complete lattice denoted by \(L_A(G,M,I)\) with the meet ∧ and join ∨ between the concepts given by

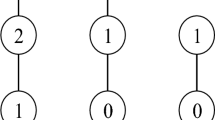
$$\begin{aligned} \begin{array}{cl} (X_1,B_1)\wedge (X_2,B_2)&{}=(X_1\cap X_2,(X_1\cap X_2)^\uparrow )\\ &{}=(X_1\cap X_2,(B_1\cap B_2)^{\downarrow \uparrow });\\ (X_1,B_1)\vee (X_2,B_2)&{}=((B_1\cup B_2)^\downarrow ,B_1\cup B_2)\\ &{}=((X_1\cup X_2)^{\uparrow \downarrow },B_1\cup B_2). \end{array} \end{aligned}$$
(3)

The Hasse diagram of \(L_A(G,M,I)\) derived from Table 1 is shown by Fig. 1

Fig. 1
figure 1

The attribute-oriented concept lattice \(L_A(G,M,I)\)

Full size image

Similarly, the complete set of object-oriented concepts forms a complete lattice denoted by \(L_O(G,M,I)\) with the meet ∧ and join ∨ between the concepts given by

$$\begin{aligned} \begin{array}{cl} (X_1,B_1)\wedge (X_2,B_2)&{}=((B_1\cap B_2)^\uparrow ,B_1\cap B_2)\\ {} &{}=((X_1\cap X_2)^{\downarrow \uparrow },B_1\cap B_2);\\ (X_1,B_1)\vee (X_2,B_2)&{}=(X_1\cup X_2,(X_1\cup X_2)^\downarrow )\\ &{}=(X_1\cup X_2,(B_1\cup B_2)^{\uparrow \downarrow }). \end{array} \end{aligned}$$
(4)

Hasse diagram of object-oriented lattice \(L_O(G,M,I)\) derived from Table 2 is shown by Fig. 2.

Fig. 2
figure 2

The object-oriented lattice \(L_O(G,M,I)\)

Full size image

In some real-life problems, granularity refers to the degree of refinement or comprehensiveness of the stored data. Its main application is to achieve the optimal granularity among different granularity levels, which enable the users to obtain interesting knowledge. The finer the attribute granularity is, the more detailed the description of the object is. For example, the attribute “Grade” ([0–100] points) can be subdivided into other level of attribute granularity: {“Fail” ([0–60) points), “Pass” ([60–100] points)}.

Definition 4

[3] A g-tree (granularity tree) for attribute b is a rooted tree with the following properties:

  1. (1)

    each node of the tree is labeled by a unique attribute name, and the root is labeled by b which is at the biggest granularity ;

  2. (2)

    to each label z of a node, \(z^*\) represents the objects to which attribute z applies;

  3. (3)

    if the nodes labeled by \(z_1,\ldots ,z_i,\ldots ,z_j,\ldots ,z_n\) are the complete successors of the node labeled by z, then \(\{z_1^*,\ldots ,z_i^*,\ldots ,z_j^*,\ldots ,z_n^*\}\) is a partition of \(z^*\) satisfying \(z_1^*\cup \cdots \cup z_i^*\cup \cdots \cup z_j^*\cup \cdots \cup z_n^*=z^{*}\), \(z_i^*\ne \emptyset\) and \(z_i^*\cap z_j^*=\emptyset\).

The set of nodes {z1,…,zi,…,zj,…,zn} which are at the same level is called a cut of the g-tree if it satisfies the following conditions:

$$\begin{aligned} z_i^*\ne \emptyset \ \text{ and }\ z_i\cap z_j=\emptyset \ \text{ and }\ z_1^*\cup \cdots \cup z_i^*\cup \cdots \cup z_j^*\cup \cdots \cup z_n^*=G \end{aligned}$$

where G is the complete set of objects.

Example 2

There are three cuts of the g-tree for attribute “Grade”: {{Grade}, {Pass, Fail}, {Worse, Bad, Good, Excellent}} (Fig. 3).

Fig. 3
figure 3

A g-tree for attribute “Grade”

Full size image

We denote the set of the cut of each attribute in M  by

$$\begin{aligned} U={\bigcup_{i=1}^{\left|M\right|}}c_i, \end{aligned}$$

where \(\left| M\right|\) represents the number of attributes in \(K=(G,M,I)\) and \(c_i\) represents the cut of the g-tree for the ith-attribute.

Suppose  \(U_1={\bigcup_{i=1}^{\left|M\right|}}c_i^1\) and \(U_2={\bigcup_{i=1}^{\left|M\right|}}c_i^2\), we denote the partial order \(\le\) between different granularity combinations by \(U_2\leq U_1 \mbox{iff}\ \forall i\in\{1,\ldots,\left|M\right|\}, c_i^{2*}\subset c_i^{1*}.\) Different formal contexts can be obtained based on different combinations of each attribute cut.

For example, suppose \(U_1=\{\{L\},\{R\},\{G\}\}\), \(U_2=\{\{L\},\{R\},\{lG,dG\}\}\). The formal contexts \(K_{U_1}=(G,M_{U_1},I_{U_1})\) and \(K_{U_2}=(G,M_{U_2},I_{U_2})\) based on \(U_1\) and \(U_2\) are represented by Table 2 respectively.

Table 2 Formal context
Full size table

3 Construction algorithms of attribute-oriented multi-granularity concept lattices

Let \(K_{U_1}=(G,M_{U_1},I_{U_1})\) and \(K_{U_2}=(G,M_{U_2},I_{U_2})\) be two formal contexts derived from \(K=(G,M,I)\). Two attribute-oriented concept lattices derived from \(K_{U_1}\) and \(K_{U_2}\) are denoted by \(L_A^1\) and \(L_A^2\), where \(K_{U_1}\) and \(K_{U_2}\) are abbreviations of \(K_{U_1}=(G,M_{U_1},I_{U_1})\) and \(K_{U_2}=(G,M_{U_2},I_{U_2})\). The change from \(L_A^1\) to \(L_A^2\) and vice versa are called attribute granularity refinement and coarsening of attribute-oriented concept lattices respectively.

It is necessary to add attribute columns with the changed granularity and delete the attribute columns with the original granularity at the same time for the selected attribute. After the change of the attribute granularity, the concepts in the induced concept lattice have certain relations with those in the original concept lattice.

Let \(K_{U_1}=(G,M_{U_1},I_{U_1})\) and \(K_{U_2}=(G,M_{U_2},I_{U_2})\) be two formal contexts derived from \(K=(G,M,I)\) and \(U_2=(U_1{\setminus } \{p\})\cup P\). p, belonging to \(U_1\), is the selected attribute the granularity of which needs to be refined. P, belonging to \(U_2\), is the complete set of the fine-granularity attributes corresponding to p satisfying \(p^*={p_1}^*\cup {p_2}^*\cup \cdots \cup {p_i}^*\cup \cdots \cup {p_n}^*=P^*\), \(p_i\)\((i=1\ldots n)\) represents the fine-granularity attribute, and \(P_s\) represents the subset of P. We denote the resulted attribute-oriented concept lattice by \(L_A^{'}\), the set of the attribute-oriented concepts by CS(L) (where L represents the lattice). The concept-generating operators of attribute-oriented concepts based on \(K_{U_1}\) and \(K_{U_2}\) are denoted by \((^{\downarrow _1},^{\uparrow _1})\) and \((^{\downarrow _2}, ^{\uparrow _2})\). Besides, the objects possessing the selected attribute can be obtained by operator \(^*\).

3.1 The knowledge related to zoom-in algorithm for attribute-oriented concept lattice

In order to find the rules of the concept changing with the granularity of attributes, different concept types are defined according to the relations between the intent of concept and the selected attribute granularity.

For simplicity, the intent and extent of concept C are abbreviated as int(C) and ext(C) respectively.

Definition 5

Let \(K_{U_1}=(G,M_{U_1},I_{U_1})\) be a formal context, and \(C_{U_1}=(X_{U_1},B_{U_1})\) be an attribute-oriented concept belonging to \(CS(L_A^1)\). If \(p\notin int(C_{U_1})\), then \(C_{U_1}\) is referred to as a reserved attribute-oriented concept.

The set of the reserved attribute-oriented concepts is denoted by \(RS(L_A^1)\).

Definition 6

Let \(K_{U_1}=(G,M_{U_1},I_{U_1})\) be a formal context, and \(C_{U_1}=(X_{U_1},B_{U_1})\) be an attribute-oriented concept belonging to \(CS(L_A^1)\). If \(p\in int(C_{U_1})\), then \(C_{U_1}\) is referred to as a modified attribute-oriented concept.

The set of the modified attribute-oriented concepts is denoted by \(MS(L_A^1)\).

By Definitions 5 and 6, it is easy to see that

$$\begin{aligned} CS(L_A^1)=RS(L_A^1)+MS(L_A^1). \end{aligned}$$
(5)

Theorem 1

Let\(K_{U_1}=(G,M_{U_1},I_{U_1})\)be a formal context, and\(C_{U_1}=(X_{U_1},B_{U_1})\)be an attribute-oriented concept belonging to\(CS(L_A^1)\). If\(C_{U_1}\in RS(L_A^1)\), then\(C_{U_1}\in CS(L_A^2)\).

Proof

By Definition 5, we then have \(p\notin int(C_{U_1})\) in the case of \(C_{U_1}\in RS(L_A^1)\). Thus, there exists \(B_{U_1}\subseteq M_{U_2}\). Since

$$\begin{aligned} X_{U_1}={B_{U_1}}^{\downarrow _1}={B_{U_1}}^{\downarrow _2}\ \text{ and }\ B_{U_1}={X_{U_1}}^{\uparrow _2}, \end{aligned}$$

therefore, we conclude that

$$\begin{aligned} C_{U_1}=(X_{U_1},B_{U_1})\in CS(L_A^2). \end{aligned}$$

\(\square\)

Theorem 2

Let\(K_{U_1}=(G,M_{U_1},I_{U_1})\)be a formal context, and\(C_{U_1}=(X_{U_1},B_{U_1})\)be an attribute-oriented concept belonging to\(CS(L_A^1)\). If\(C_{U_1}\in MS(L_A^1)\), then\(\exists \ C_{U_2}\in CS(L_A^2)\)such that

$$\begin{aligned} ext(C_{U_2})=ext(C_{U_1})\ \mathrm{{and}}\ int(C_{U_2})=(int(C_{U_1}){\setminus } \{p\})\cup ((p^*\cap ext(C_{U_1}))^{\uparrow _2}\cap P). \end{aligned}$$

Proof

By Definition 6, we have \(p\in int(C_{U_1})\) in the case of \(C_{U_1}\in MS(L_A^1)\). Since \(p^*=\{{p_1}^*\cup {p_2}^*\cup \ldots \cup {p_n}^*\}\) (each \(p_i\) represents a fine-granularity attribute), therefore the case that the extent of \(C_{U_1}\) remains unchanged when p is replaced with \(P_s\) (\(P_s=(p^*\cap ext(C_{U_1}))^{\uparrow _ 2}\cap P\)) holds. Hence, we conclude that

$$\begin{aligned} \exists C_{U_2}=(ext(C_{U_1}),(int(C_{U_1}){\setminus } \{p\})\cup ((p^*\cap ext(C_{U_1}))^{\uparrow _ 2}\cap P))\in CS(L_A^2). \end{aligned}$$

\(\square\)

3.2 The description of zoom-in algorithm for attribute-oriented concept lattices

The main idea of the zoom-in algorithm for attribute-oriented concept lattice is as follows: firstly, starting from the maximal concept of the lattice, the type of the concept is judged from top to bottom. Then, the corresponding concept generation, update, deletion and edge adjustment are performed.

The process of the algorithm is as follows: first, input \(L_A^1\), coarse-granularity attribute p and the corresponding fine-granularity attribute set P. Then, calculate the concept in top-down order. If \(p\notin int(C_{U_1})\), then \(C_{U_1}\) is reserved. Otherwise, modify the intent of \(C_{U_1}\) as

$$\begin{aligned} int(C_{U_1})=(int(C_{U_1}){\setminus } \{p\})\cup ((p^{*}\cap ext(C_{U_1}))^{\uparrow _2}\cap P). \end{aligned}$$

Meanwhile, one can judge and generate the new concept by

$$\begin{aligned} C_{new}=(((int(C_{U_1}){\setminus } \{p\})\cup (P{\setminus } P_s))^{\downarrow _2},(int(C_{U_1}){\setminus } \{p\})\cup (P{\setminus } P_s)). \end{aligned}$$

Modify the edges between the concepts at the same time. Finally, adjust edges among concepts from bottom to top and obtain fine-granularity lattice \(L_A^{'}\). The detailed algorithm is shown in Algorithm 1.

figure a

Proposition 1

The attribute-oriented concepts in\(L_A^{'}\)are in\(L_A^2\).

Proof

Note that \(L_A^{'}\) is constructed by applying zoom-in algorithm to \(L_A^1\). To prove Proposition 1, we need to prove that the concepts derived from \(L_A^1\) are in \(L_A^2\), which is equal to proving the concepts in \(L_A^{'}\) are in \(L_A^2\). Suppose \(C_{U_1}=(X_{U_1},B_{U_1})\in L_A^1\). The following three cases will be discussed:

(1)   \(p\notin B_{U_1}\). By Definition 5, we have \(C_{U_1}\in RS(L_A^1)\). It can be easily observed that \(C_{U_1}\in L_A^{'}\). From Theorem 1, we obtain \(C_{U_1}\in L_A^2\). Hence, if \(C_{U_1}\in L_A^{'}\) and \(p\notin B_{U_1}\), then \(C_{U_1}\in L_A^2\) holds.

(2)   \(p\in B_{U_1}\). By Definition 6, we have \(C_{U_1}\in MS(L_A^1)\). Besides, It can be easily verified that \(C_{U_1}\in L_A^{'}\). Followed by Theorem 2, we deduce that \(ext(C_{U_1})\) remains unchanged and

$$\begin{aligned} int(C_{U_1})=(int(C_{U_1}){\setminus } \{p\})\cup ((p^{*}\cap ext(C_{U_1}))^{\uparrow _2}\cap P)\in M_{U_2} \end{aligned}$$

after zoom-in algorithm. Therefore, if the modified concepts derived from the \(C_{U_1}\in MS(L_A^1)\) belong to \(L_A^{'}\), then they belong to \(L_A^2\).

(3)   The new concepts generated from the division of the concept whose intent includes p. It is easy to see that the new generated concepts belong to \(L_A^{'}\). Since

$$\begin{aligned} int(C_{new})=(int(C_{U_1}){\setminus } \{p\})\cup (P{\setminus } P_s)\in M_{U_2}\ \text{ and } \ ext(C_{new})=\{int(C_{new})\}^{\downarrow _2}, \end{aligned}$$

we deduce that \(C_{new}\) belongs to \(L_A^2\). That is, \(C_{new}\in L_A^2\).

For the three cases above, we conclude that the concepts in \(L_A^{'}\) belong to \(L_A^2\). \(\square\)

Proposition 2

The attribute-oriented concepts in\(L_A^2\)are in\(L_A^{'}\).

Proof

Suppose \(C_{U_2}=(X_{U_2},B_{U_2})\in L_A^2\). According to the relations between the selected fine-granularity attributes and concept intent, the following three cases will be discussed:

(1)   \(P\cap B_{U_2}=\varnothing\). It is easy to see that \(B_{U_2}\subseteq M_{U_1}\) under this situation. Therefore, we have \(C_{U_2}=(X_{U_2},B_{U_2})=({B_{U_2}}^{\downarrow _1},B_{U_2})\), that is, \(C_{U_2}\in L_A^1\). It follows from Definition 5 that \(C_{U_2}\) belongs to \(RS(L_A^1)\). Then, by Theorem 1, we know that \(C_{U_2}\) remains unchanged in \(L_A^{'}\).

(2)   \(P_s\subseteq B_{U_2}\) and \(P_s^{*}=p^{*}\). This implies \(p\in {X_{U_2}}^{\uparrow _1}\). One can check that \(C_{U_2}\) corresponds to the \(MS(L_A^1)\). In other words, \(C_{U_2}\) is derived from modifying the intent of the concept in \(L_A^1\) as replacing p with \(P_s\). Hence, we obtain \(C_{U_2}\in L_A^{'}\).

(3)   \(P_s\subseteq B_{U_2}\) and \(P_s^{*}\ne p^{*}\). In this case, it can be easily checked that \(C_{U_2}\) is obtained by the division of the concept whose intent includes p in \(L_A^1\). Therefore, we have \(C_{U_2}\in L_A^{'}\).

For the three cases above, we conclude that the concepts in \(L_A^2\) belong to \(L_A^{'}\). \(\square\)

Proposition 3

The edges in\(L_A^2\)are in\(L_A^{'}\).

Proof

Suppose \(C_1\) and \(C_2\) belong to \(L_A^2\), and \(C_2\) is the upper neighbor of \(C_1\). By Proposition 2, we know that both \(C_1\) and \(C_2\) are in \(L_A^{'}\). The following three cases will be considered:

(1)   \(C_1\) belongs to \(L_A^1\). In this condition, \(C_2\) is an upper neighbor of \(C_1\) in \(L_A^1\), or \(C_2\) is a modified concept corresponding to a concept in \(L_A^1\), or \(C_2\) is a new concept added to \(L_A^2\). For the first one, \(C_1\) and \(C_2\) are not processed by the algorithm, which means the edge between \(C_1\) and \(C_2\) is unchanged. For the second one, by Theorem 2, it is easy to see that \(int(C_1)\subseteq int(C_2)\) and \(ext(C_1)\subseteq ext(C_2)\) still hold. Ii can easily be verified that there is no new concept \(C_{new}\) s.t. \(C_1\le C_{new}\le C_2\). For the last one, the \(Upper(C_2)\) is \(Upper(Upper(C_1))\), where Upper( ) represents the upper neighbor of the concept. Therefore, \(Upper(C_2)\) is also a minimal concept satisfying \(C_1\le C_2\). Therefore, under this condition, the edge between \(C_1\) and \(C_2\) in \(L_A^2\) is also in \(L_A^{'}\).

(2)   \(C_1\) is a modified concept corresponding to a concept in \(L_A^1\), and \(C_2\) is a modified concept corresponding to a concept in \(L_A^1\). It is easy to see that the partial order between \(C_1\) and \(C_2\) is unchanged. And there is no new concept \(C_{new}\) s.t. \(C_1\le C_{new}\le C_2\). Hence, the edge between them remains unchanged.

(3)   \(C_1\) is added to \(L_A^2\) as a new concept with \(int(C_1)=(int(C_{U_1})\backslash \{p\})\cup (P\backslash P_s)\) and \(ext(C_1)={int(C_1)}^{\downarrow _2}\) corresponding to a concept in \(L_A^1\). The only upper neighbors of \(C_1\) are concepts in \(L_A^1\) with the intent changed (replace p with \(P_s\)) or the new concept generated by the division of the \(Upper(Upper(C_1))\). It can easily be observed that \(C_2\) is the minimal concept satisfying \(C_1\le C_2\). Hence, the edge between \(C_1\) and \(C_2\) is in \(L_A^{'}\).

We conclude by the three cases above that edges in \(L_A^2\) are in \(L_A^{'}\).

Proposition 4

The edges in\(L_A^{'}\)are in\(L_A^2\).

Proof

Suppose \(C_1\) and \(C_2\) belong to \(L_A^{'}\), \(C_2\) is the upper neighbor of \(C_1\). The following two conditions will be considered:

(1)   The edge is added when \(L_A^{'}\) is initialized. It is known that there is no new concept \(C^{'}\) s.t. \(C_1\le C^{'}\le C_2\). Therefore, the edges in \(L_A^{'}\) are in \(L_A^2\) in this case.

(2)   The edge is added when a new concept is created and its upper neighbors are attached. This means that \(C_2\) is either a adjoint upper neighbor of \(C_1\) or a minimal concept in \(L_A^1\) satisfying \(Upper(Upper(C_1))=Upper(C_2)\), which is achieved by adjusting edge in zoom-in algorithm. Hence, the edge between \(C_1\) and \(C_2\) is in \(L_A^2\).

We conclude by the two cases above that edges in \(L_A^{'}\) are in \(L_A^2\). \(\square\)

Theorem 3

Zoom-in algorithm is correct.

Proof

It follows immediately from Propositions 1, 2, 3 and 4. \(\square\)

3.3 The knowledge related to zoom-out algorithm for attribute-oriented concept lattice

Definition 7

Let \(K_{U_2}=(G,M_{U_2},I_{U_2})\) be a formal context and \(C_{U_2}=(X_{U_2},B_{U_2})\) be an attribute-oriented concept belonging to \(CS(L_A^2)\). If \(\forall p_i\in P\), \(p_i\notin B_{U_2}\), then \(C_{U_2}\) is referred to as a reserved attribute-oriented concept.

The set of reserved attribute-oriented concepts is denoted as \(RS(L_A^2)\).

Definition 8

Let \(K_{U_2}=(G,M_{U_2},I_{U_2})\) be a formal context and \(C_{U_2}=(X_{U_2},B_{U_2})\) be an attribute-oriented concept belonging to \(CS(L_A^2)\). If \(P_s\subseteq B_{U_2}\) and \(P_s^{*}=p^{*}\), then \(C_{U_2}\) is referred to as a modified attribute-oriented concept.

The set of modified attribute-oriented concepts is denoted as \(MS(L_A^2)\).

Definition 9

Let \(K_{U_2}=(G,M_{U_2},I_{U_2})\) be a formal context and \(C_{U_2}=(X_{U_2},B_{U_2})\) be an attribute-oriented concept belonging to \(CS(L_A^2)\). If \(P_s\subseteq B_{U_2}\) and \(P_s^{*}\ne p^{*}\), then \(C_{U_2}\) is referred to a deleted attribute-oriented concept.

The set of deleted attribute-oriented concepts is denoted as \(DS(L_A^2)\).

By Definitions 7, 8 and 9, it is easy to see that

$$\begin{aligned} CS(L_A^2)=RS(L_A^2)+MS(L_A^2)+DS(L_A^2). \end{aligned}$$
(6)

Theorem 4

Let\(K_{U_2}=(G,M_{U_2},I_{U_2})\)be a formal context and\(C_{U_2}=(X_{U_2},B_{U_2})\)be an attribute-oriented concept belonging to\(CS(L_A^2)\). If\(C_{U_2}\in RS(L_A^2)\), then\(C_{U_2}\in CS(L_A^1)\).

Proof

By Definition 7, we have \(p_i\notin B_{U_2}\) in the case of \(C_{U_2}\in RS(L_A^2)\). Thus, we have \(B_{U_2}\subseteq M_{U_2}\). On the other hand, we have

$$\begin{aligned} X_{U_2}={B_{U_2}}^{\downarrow _2}={B_{U_2}}^{\downarrow _1}\ \text{ and }\ B_{U_2}={X_{U_2}}^{\uparrow _1}. \end{aligned}$$

Hence, we conclude that

$$\begin{aligned} C_{U_2}=(X_{U_2},B_{U_2})\in CS(L_A^1). \end{aligned}$$

\(\square\)

Theorem 5

Let\(K_{U_2}=(G,M_{U_2},I_{U_2})\)be a formal context and\(C_{U_2}=(X_{U_2},B_{U_2})\)be an attribute-oriented concept belonging to\(CS(L_A^2)\). If\(C_{U_2}\in MS(L_A^2)\), then there exists\(C=(X_{U_2},(B_{U_2}{\setminus } P_s)\cup \{p\})\in CS(L_A^1)\).

Proof

By Definition 8, we have \({P_s}^{*}=p^{*}\). Then, \(P_s\) can be replaced by p, that is,

$$\begin{aligned} X_{U_2}=B^{\downarrow _2}=((B{\setminus } P_s)\cup \{p\})^{\downarrow _1}. \end{aligned}$$

Hence, we conclude that

$$\begin{aligned} \exists \ C=(X_{U_2},(B_{U_2}{\setminus } P_s)\cup \{p\})\in CS(L_A^1). \end{aligned}$$

\(\square\)

3.4 The description of zoom-out algorithm for attribute-oriented concept lattice

The main idea of the zoom-out algorithm for attribute-oriented multi-granularity concept lattice is as follows: starting from the maximal concept of the lattice, judge the type of the node from top to bottom. Then, the corresponding concept update, deletion and edge adjustment are performed.

The process of this algorithm is as follows. Firstly, input \(L_A^2\), selected fine-granularity attribute set P and the corresponding coarse-granularity attribute p. Secondly, for all concepts including \(p_i\), divide them into two classes according to whether \({P_s}^*\) is equal to \(p^{*}\) or not. If equal, modify the intent of \(C_{U_2}\) as \(int(C_{U_2})=(int(C_{U_2}){\setminus } P_s)\cup \{p\}\). Otherwise, delete \(C_{U_2}\). Finally, we obtain coarse-granularity lattice \(L_A^{'}\). The detailed algorithm is shown in Algorithm 2.

figure b

Proposition 5

The attribute-oriented concepts in\(L_A^{'}\)are in\(L_A^1\).

Proof

Note that \(L_A^{'}\) is constructed by applying zoom-out algorithm to \(L_A^2\). To prove Proposition 5, we need to prove that the concepts derived from \(L_A^2\) are in \(L_A^1\), which is equal to proving the concepts in \(L_A^{'}\) are in \(L_A^1\). Suppose \(C_{U_2}=(X_{U_2},B_{U_2})\in L_A^2\), the following three cases will be discussed:

(1)   \(p_i\notin B_{U_2}\). It is easy to see that \(C_{U_2}\in L_A^{'}\). By Theorem 4, we have

$$\begin{aligned} B_{U_2}\in M_{U_1}\ \text{ and }\ X_{U_2}={B_{U_2}}^{\downarrow _2}={B_{U_2}}^{\downarrow _1}. \end{aligned}$$

Therefore, under this condition, we conclude that \(C_{U_2}\in L_A^1\).

(2)   \(P_s\in B_{U_2}\) and \(P_s^{*}=p^{*}\). Obviously, \(C_{U_2}\in L_A^{'}\). Notice that \(C_{U_2}\) corresponds to the modified concepts in \(L_A^1\). Followed by Theorem 5, after modifying \(C_{U_2}\) as

$$\begin{aligned} (int(C_{U_2})\backslash P_s)\cup \{p\}\subseteq M_{U_1} \end{aligned}$$

and

$$\begin{aligned} ext(C_{U_2})=((int(C_{U_2})\backslash P_s)\cup \{p\})^{\downarrow _1}, \end{aligned}$$

\(C_{U_2}\in L_A^1\) holds.

(3)   \(P_s\in B_{U_2}\) and \(P_s^{*}\ne p^{*}\). Then, we deduce that this kind of concepts are deleted concepts compared to the concepts in \(L_A^1\). Therefore, \(C_{U_2}\) is deleted after applying zoom-out algorithm to \(L_A^2\), that is, \(C_{U_2}\) is not in \(L_A^{'}\) and \(L_A^1\).

For the above three cases, we conclude that the concepts in \(L_A^{'}\) are in \(L_A^1\). \(\square\)

Theorem 6

Zoom-out algorithm is correct.

Proof

It is similar to the proof of zoom-in algorithm. \(\square\)

The zoom-in and zoom-out algorithms for object-oriented multi-granularity concept lattices can be obtained in a similar way.

4 Transformation algorithms among three kinds of concept lattice

Based on the same formal context, attribute-oriented concept lattice, object-oriented concept lattice, and formal concept lattice can be obtained by using different computation operators and operation methods. Three kinds of concept lattice reveal the knowledge contained in the formal context from different perspectives. In this section, the transformation algorithms among three kinds of concept lattice are proposed.

Let \(K=(G,M,I)\) be a formal context. \(L_O(K)\) and \(L_A(K)\) represent the object-oriented concept lattice and the attribute-oriented concept lattice derived from \(K=(G,M,I)\). \(L(K^c)\) represents the formal concept lattice based on the \(K=(G,M,I^c)\), where \(I^c\) represents the complement of the binary relation I.

4.1 Transformation algorithm between \(L_A(K)\) and \(L_O(K)\)

By the properties of concept-generating operators, we know that attribute-oriented concept lattice is isomorphic to object-oriented concept lattice, that is, for each concept \(C_O\) in \(L_O(K)\), there is only one concept \(C_A\) in \(L_A(K)\) corresponding to \(C_O\).

Theorem 7

Let\(L_O(K)\)and\(L_A(K)\)be object-oriented concept lattice and attribute-oriented concept lattice derived from context\(K=(G,M,I)\). If\((X,B)\in L_O(K)\), then\((X^c,B^c)\in L_A(K)\). Similarly, if \((X,B)\in L_A(K)\), then \((X^c,B^c)\in L_O(K).\)

Proof

Since

$$\begin{aligned} (X,B)\in L_O(K), \end{aligned}$$

therefore, we obtain

$$\begin{aligned} (X,B)=(B^\uparrow ,X^\downarrow ). \end{aligned}$$

On the other hand,

$$\begin{aligned} (X^c,B^c)=(B^{\uparrow c},X^{\downarrow c})=(B^{c\downarrow },X^{c\uparrow }), \end{aligned}$$

therefore, we conclude that

$$\begin{aligned} (X^c,B^c)\in L_A(K). \end{aligned}$$

If \((X,B)\in L_A(K)\), it can be proven by the similar way. \(\square\)

Theorem 8

Suppose \(L_O(K)\) and \(L_A(K)\) are object-oriented concept lattice and attribute-oriented concept lattice derived from context \(K=(G,M,I)\). If

$$\begin{aligned} (X_1,B_1),(X_2,B_2)\in L_O(K), \end{aligned}$$

then,

$$\begin{aligned}&((X_1,B_1)\wedge (X_2,B_2))^c=({X_1}^c,{B_1}^c)\vee ({X_2}^c,{B_2}^c),\\&((X_1,B_1)\vee (X_2,B_2))^c=({X_1}^c,{B_1}^c)\wedge ({X_2}^c,{B_2}^c). \end{aligned}$$

Similarly, if \((X_1,B_1),(X_2,B_2)\in L_A(K)\), then the equations still hold.

Proof

Since

$$\begin{aligned} (X_1,B_1)\wedge (X_2,B_2)= & {} ((X_1\cap X_2)^{\downarrow \uparrow }, B_1\cap B_2),\\ (X_1\cap X_2)^{\downarrow \uparrow c}=(X_1\cap X_2)^{\downarrow c \downarrow }= & {} (X_1\cap X_2)^{c\uparrow \downarrow }=({X_1}^c\cup {X_2}^c)^{\uparrow \downarrow },\\ (B_1\cap B_2)^c= & {} {B_1}^c\cup {B_2}^c \end{aligned}$$

and

$$\begin{aligned} ({X_1}^c,{B_1}^c)\vee ({X_2}^c,{B_2}^c)=(({X_1}^c\cup {X_2}^c)^{\uparrow \downarrow }, {B_1}^c\cup {B_2}^c), \end{aligned}$$

therefore, we have

$$\begin{aligned} ((X_1,B_1)\wedge (X_2,B_2))^c=({X_1}^c,{B_1}^c)\vee ({X_2}^c,{B_2}^c). \end{aligned}$$

Similarly,

$$\begin{aligned} ((X_1,B_1)\vee (X_2,B_2))^c=({X_1}^c,{B_1}^c)\wedge ({X_2}^c,{B_2}^c). \end{aligned}$$

If \((X_1,B_1),(X_2,B_2)\in L_A(K)\), it can be proven by the similar way. \(\square\)

That is to say, the edges in \(L_O(K)\) and \(L_A(K)\) are corresponding to each other.

The main idea of the transformation algorithm between \(L_A(K)\) and \(L_O(K)\) are as follows. The concept \(C=(X,B)\) in the concept lattice is modified as \(C=(X^c,B^c)\) from top to bottom, then modify the edges among concepts: the upper neighbor relations between the original concepts become the lower neighbor relations. The detailed algorithm is shown in Algorithm 3.

figure c

Theorem 9

Algorithm 3 is correct.

Proof

It can be easily proven by Theorems 7 and 8. That is, based on the same context, all the concepts and the edges derived from the original concept lattice are also in the new generated concept lattice. \(\square\)

In addition, formal concept lattice \(L(K^c)\) derived from context \(K=(G,M,I^c)\) is isomorphic to \(L_A(K)\) and \(L_O(K)\)  derived from context \(K=(G,M,I)\).

4.2 Transformation algorithms of \(L(K^c)\)-\(L_A(K)\) and \(L(K^c)\)-\(L_O(K)\)

There are also mapping relations among concepts and edge relations between \(L(K^c)\) and \(L_A(K)\) as well as the mapping relations among edges. The relations between \(L(K^c)\) and \(L_A(K)\) also hold between \(L(K^c)\) and \(L_O(K)\). In the following, the transformation algorithms between \(L_A(K)\) and \(L(K^c)\), \(L_O(K)\) and \(L(K^c)\) will be proposed.

Theorem 10

Let\(L_A(K)\)and\(L_O(K)\)be the attribute-oriented concept lattice and object-oriented concept lattice based on\(K=(G,M,I)\), \(L(K^c)\)be concept lattice based on\(K=(G,M,I^{c})\). If

$$\begin{aligned}&(X,B)\in L_A(K), \end{aligned}$$

then

$$\begin{aligned} (X,B^c)\in L(K^c). \end{aligned}$$

Also, if \((X,B) \in L(K^c)\), then \((X,B^c) \in L_A(K)\).  If

$$\begin{aligned} (X,B)\in L_O(K), \end{aligned}$$

then

$$\begin{aligned} (X^c,B)\in L(K^c). \end{aligned}$$

And if \((X,B) \in L(K^c)\), \((X^c,B) \in L_O(K)\).

Proof

It can be proven by the similar way of Theorem 7. \(\square\)

Theorem 11

The edges in\(L_A(K)\) are the same as those in\(L(K^c)\). This rule also applies to that  between\(L_O(K)\)to\(L(K^c)\).

Proof

It can be proven by the similar way of Theorem 8. \(\square\)

The main idea of the transformation algorithm between \(L_A(K)\) and \(L(K^c)\) are as follows: the concept \(C=(X,B)\) in the concept lattice is modified as \(C=(X,B^c)\) in top-down order, and the edges between concepts remain unchanged. The detailed algorithm is shown in Algorithm 4.

figure d

Theorem 12

Algorithm 4 is correct.

Proof

It can be easily proven by Theorems 10 and 11. \(\square\)

The main idea of the transformation algorithm between \(L_O(K)\) and \(L(K^c)\) are as follows: the concept \(C=(X,B)\) in the concept lattice is modified as \(C=(X^c,B)\) in top-down order, and the edges between concepts remain unchanged. The detailed algorithm is shown in Algorithm 5.

figure e

Theorem 13

Algorithm 5 is correct.

Proof

It is similar to the proof of Theorem 12.

By using the transformation algorithm, we can get two other kinds of concept lattices from one kind of concept lattice derived from a multi-granularity formal context.

5 Conclusion

Attribute granularity has an important effect on extracting concepts and constructing the concept lattice from the data. Choosing the appropriate combination of attribute granularity levels can effectively control the number of concepts in the lattice, which in turn helps users discover interesting knowledge. The relations among the extent, intent of attribute-oriented concepts and the changes of attribute granularity are analysed separately. Based on the attribute-oriented concept lattice and the attribute granularity tree, a zoom-in algorithm is proposed to reconstruct a new concept lattice after the refinement of the attribute granularity. And the zoom-out algorithm is proposed to reconstruct a new concept lattice after the coarsening of the attribute granularity. The proposed algorithms can realize the rapid construction of the attribute (object)-oriented concept lattice on the basis of the existing concept lattice and granularity tree. It avoids the heavy workload of reconstructing the concepts using the formal context. The object-oriented, attribute-oriented and classical concepts represent the knowledge behind the data from different aspects. The transforming approaches of the three kinds of concept lattices are proposed at the end of the paper. The fast construction method of multi-granularity generalized one-sided concept lattices should be an issue for further research.