1 Introduction

Over the past decades, a lot of attention has been drawn to machine learning of which many methods have been successfully applied in substantial practical applications including protein–protein interactions prediction [1–3], image retrieval [4], and text data analysis [5]. Ordinal regression is a type of supervised machine learning problems and can be applied in a wide range of fields such as medical image analysis [6], image ranking [7], facial age estimation [8], and so on. It involves how to find an order among the different categories according to the learned rules which are used to predict order of ordinal scale [9–13]. Therefore, the key issue in ordinal regression is how to learn the prediction rules from the training data. Ordinal regression differs from traditional regression and traditional classification [14–19]. The reason is that the labels of different categories in ordinal regression are discrete and simultaneously have an ordinal relationship.

Recently, many efforts have been directed toward tackling the ordinal regression problems [20–23]. In [20], Herbrich et al., based on a threshold model in which the threshold values of each ordinal category are estimated, explored the use of support vector (SV) learning in ordinal regression. In [21], the authors employed the classification and regression trees to tackle the ordinal regression problems. This method actually first maps the ordinal variables into numeric values and then employs the traditional classification and regression methods to solve the problems. However, it is difficult to devise an appropriate mapping function in that ones can not know the true metric distances between the ordinal scales in most cases. Thus, the application of this method may be limited. In [12], based on Gaussian processes, the authors presented a probabilistic kernel method to deal with ordinal regression. In [22], Sun et al. extended the kernel discriminant analysis (kDa) [16] algorithm to handle the ordinal regression problems. In [23], through making use of the abundance of unlabeled patterns, the authors proposed a transductive learning paradigm for the ordinal regression problems.

The basic idea of support vector machine (SVM) [17], which is one of the best-known kernel learning methods [24], is also developed to deal with the ordinal regression problems. By extending the formulation of SVM to ordinal regression, Shashua and Levin [25] introduced two methods for ordinal regression. These methods embody the large margin principle, which is the intuitive idea of SVM. In [13], Chu and Keerthi improved the SVM formulation for ordinal regression by including the ordinal inequalities on the thresholds. This method is referred to as support vector ordinal regression (SVOR). It can be solved by a sequential minimal optimization (SMO)-type algorithm and achieves the encouraging experimental results. In [26], Shevade and Chu further employed minimum enclosing sphere (MEB) to handle ordinal regression. In [27], the authors proposed a called block-quantized support vector ordinal regression (BQSVOR) to tackle the large-scale ordinal regression problems. All of these methods are derived from the traditional SVM and share a common property: borrowing the idea from SVM and generalizing the SVM formulation to solve the ordinal regression problems.

However, SVM is essentially a local classifier. This is because only the so-called support vectors determine the decision hyperplane of SVM, whereas all other data points have no impact on it. Therefore, the traditional SVM does not take into consideration the distribution characteristics of the data and may receive a non-robust solution. In order to overcome the limitation of SVM, in [18] the authors proposed a modified class of SVM. This method is called minimum class variance support vector machine (MCVSVM) and motivated by Fisher discriminant analysis [16]. Similarly to SVM, MCVSVM embodies the large margin principle [19]. However, different from SVM, MCVSVM can give a more robust solution in that it further considers the distribution of the categories in its model.

In this paper, we propose a novel method to handle the ordinal regression problems. This method is referred to as minimum class variance ordinal regression (MCVSVOR). The key difference between MCVSVOR and the traditional SVOR is that the former generalizes MCVSVM to deal with the ordinal regression problems and explicitly incorporates the distribution information of the categories, whereas the latter extends SVM to tackle ordinal regression and ignores the distribution characteristics of the data. Simultaneously, as SVOR, MCVSVOR also embodies the large margin principle in that it stems from MCVSVM. Following the basic idea of SVOR, we define the primal optimization model of MCVSVOR and develop the linear and nonlinear cases of MCVSVOR. We further analyze the relationship between MCVSVOR and SVOR. The analysis shows that MCVSVOR can be solved using the existing SVOR software, which makes the solution easy to be computed. The comprehensive experimental results suggest that the proposed method is effective and can achieve superior generalization performance in contrast with SVOR.

The rest of this paper is organized as follows. The related work is reviewed in Sect. 2. In Sect. 3, the linear case of MCVSVOR is first presented, and the relationship between MCVSVOR and SVOR is then analyzed. In Sect. 4, the nonlinear case of MCVSVOR is discussed. The experimental results are reported in Sect. 5. Finally, conclusions are drawn in Sect. 6.

2 Related work

In this paper, we will address an ordinal regression problem with r ranked categories. The training dataset contains N sample points and is represented by \(\{ ({\mathbf{x}}_{i}^{j} ,{\text{y}}^{j} )|{\mathbf{x}}_{i}^{j} \in R^{d} ,{\text{y}}^{j} \in Y,i = 1, \ldots ,N\}\), where \({\mathbf{x}}_{i}^{j}\) refers to the ith sample in the j-th category and \({\text{y}}^{j}\) is its corresponding rank. Here, \(d\) is the dimension of the sample space and \(Y = \{ 1, \ldots ,r\}\) are consecutive integers and used to keep the known rank information of the training samples.

Besides, let \(N^{j}\) be the number of the samples in the j-th category and \({\mathbf{X}}{ = [}{\mathbf{x}}_{1}^{1} , \ldots ,{\mathbf{x}}_{{N^{1} }}^{1} ,{\mathbf{x}}_{1}^{2} , \ldots ,{\mathbf{x}}_{{N^{2} }}^{2} , \ldots ,{\mathbf{x}}_{1}^{r} , \ldots ,{\mathbf{x}}_{{N^{r} }}^{r} ] { = [}{\mathbf{x}}_{1} , \ldots ,{\mathbf{x}}_{N} ]\) represents the sample matrix. Note, here \(N = \sum\nolimits_{j = 1}^{r} {N^{j} }\) holds.

2.1 Support vector ordinal regression

Generally, the key step of solving the ordinal regression problems is to learn a function \(f:R \to \{ 1, \ldots ,r\}\) such that \(f({\mathbf{x}}_{i}^{j} ) = y^{j}\) from the training samples [25, 26]. Therefore, SVOR directs at constructing \(r - 1\) hyperplanes \({\mathbf{w}}^{T} {\mathbf{x}} - b_{j} = 0\;(j = 1, \ldots ,r)\) which can separate the samples of different categories. In the linear case, SVOR defines its primal optimization problem as [13]

$$\begin{aligned} \mathop {\hbox{min} }\limits_{{{\mathbf{w}},{\mathbf{b}},{\varvec{\upxi}},{\varvec{\upxi}}^{*} }} \frac{1}{2}{\mathbf{w}}^{T} {\mathbf{w}} + C\sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {(\xi_{i}^{j} + \xi_{i}^{*j} )} } \hfill \\ s.t.\;{\mathbf{w}}^{T} {\mathbf{x}}_{i}^{j} - b_{j} \le - 1 + \xi_{i}^{j} ,\;\xi_{i}^{j} \ge 0,\;\forall i,j \hfill \\ \;\;\;\;\;{\mathbf{w}}^{T} {\mathbf{x}}_{i}^{j} - b_{j - 1} \ge 1 - \xi_{i}^{*j} ,\;\xi_{i}^{*j} \ge 0,\;\forall i,j \hfill \\ \;\;\;\;\;b_{j - 1} \le b_{j} ,\;\forall i,j \hfill \\ \end{aligned}$$
(1)

where \(j = 1 \ldots ,r\) and \(i = 1, \ldots ,N^{j}\). Note, SVOR introduces two auxiliary variables \(b_{0}\) and \(b_{r}\) which are respectively set \(b_{0} = - \infty\) and \(b_{r} = { + }\infty\). This type of SVOR is with the explicit constraints on the thresholds. In [13], the authors simultaneously presented another type of SVOR with the implicit constraints on the thresholds. More details can be found in [13]. Note, SVOR is derived from SVM in which the large margin principle [17] is implements. Thus, the principle is also embodied in SVOR.

2.2 Kernel discriminant learning for ordinal regression

For the given training dataset, the within-class scatter matrix \({\mathbf{S}}_{W}\) is defined as [16]

$${\mathbf{S}}_{W} = \sum\limits_{j = 1}^{r} {\sum\limits_{{{\mathbf{x}} \in {\mathbf{X}}^{j} }} {({\mathbf{x}} - {\mathbf{u}}^{j} )({\mathbf{x}} - {\mathbf{u}}^{j} )^{T} } }$$
(2)

where \({\mathbf{X}}^{j} = \{ {\mathbf{x}}_{i}^{j} |y^{j} = j,\;i = 1, \ldots ,N^{j} \}\) is the j-th category samples, \({\mathbf{u}}^{j} = \frac{1}{{N^{j} }}\sum\nolimits_{{{\mathbf{x}} \in {\mathbf{X}}^{j} }} {\mathbf{x}}\) is the mean sample vector of \({\mathbf{X}}^{j}\) and \(T\) denotes vector transpose. Here, \(N^{j}\) is the number of the j-th category samples \({\mathbf{X}}^{j}\). KDLOR defines the following optimization [22]

$$\begin{aligned} \mathop {\hbox{min} }\limits_{{\mathbf{w}}} \;\;{\mathbf{w}}^{T} {\mathbf{S}}_{W} {\mathbf{w}} - C\rho \hfill \\ s.t.\;{\mathbf{w}}^{T} ({\mathbf{u}}^{j + 1} - {\mathbf{u}}^{j} ) \ge \rho ,\;j = 1,2, \ldots ,r - 1 \hfill \\ \end{aligned}$$
(3)

Obviously, KDLOR takes into account the distribution of the categories by introducing the within-class scatter matrix \({\mathbf{S}}_{W}\) in its objective function. However, KDLOR does not directly embody the large margin principle as SVM.

3 Minimum class variance support vector ordinal regression

In this section, we will first present the formulation of the linear SVOR and discuss how to solve it. Then, we will analyze the relationship between MCVSVOR and SVOR.

3.1 The linear case of the proposed method

By following the basic idea of SVOR and using the within-class scatter matrix \({\mathbf{S}}_{W}\) defined as (2), in the linear case, the primal optimization problem of the proposed method MCVSVOR is defined as follows

$$\begin{aligned} \mathop {\hbox{min} }\limits_{{{\mathbf{w}},{\mathbf{b}},{\varvec{\upxi}},{\varvec{\upxi}}^{*} }} \frac{1}{2}{\mathbf{w}}^{T} {\mathbf{S}}_{\text{W}} {\mathbf{w}} + C\sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {(\xi_{i}^{j} + \xi_{i}^{*j} )} } \hfill \\ s.t.\;{\mathbf{w}}^{T} {\mathbf{x}}_{i}^{j} - b_{j} \le - 1 + \xi_{i}^{j} ,\;\xi_{i}^{j} \ge 0,\;\forall i,j \hfill \\ \;\;\;\;\;{\mathbf{w}}^{T} {\mathbf{x}}_{i}^{j} - b_{j - 1} \ge 1 - \xi_{i}^{*j} ,\;\xi_{i}^{*j} \ge 0,\;\forall i,j \hfill \\ \;\;\;\;\;b_{j - 1} \le b_{j} ,\;\forall i,j \hfill \\ \end{aligned}$$
(4)

where \(j = 1 \ldots ,r\) and \(i = 1, \ldots ,N^{j}\). As SVOR, MCVSVOR actually tries to find \(r - 1\) binary classifiers with a shared mapping direction \({\mathbf{w}}\) and the additional constraint thresholds. Here, as in SVOR with the explicit threshold constraints, we explicitly include the natural ordinal inequalities on the thresholds constraints. However, in contrast with SOVR, MCVSVOR introduces the matrix \({\mathbf{S}}_{W}\) in the objective function of its primal optimization problem. In this way, MCVSVOR takes fully into account the distribution of the categories. Besides, MCVSVOR implements the large margin principle because it modifies MCVSVM, which embodies the principle, to handle the ordinal regression tasks.

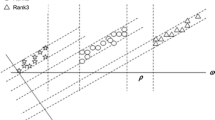
Figure 1 illustrates the difference between SOVR and MCVSVOR. Here, we consider a synthetic ordinal regression task with 3 ranked categories, each category of which consists of 100 samples. Figure 1a describes the decision hyperplanes of SOVR on the artificial dataset. As can be seen in Fig. 1a, the decision hyperplanes of SOVR actually do not reflect the characteristic of the data although it can separate or rank each category. Figure 1b shows the decision hyperplanes of MCVSVOR. Obviously, they reflect the distribution characteristic of the data and shows more reasonable in contrast with ones of SOVR. This example clearly demonstrates the limitation of SOVR and the advantage of MCVSVOR in contrast with SVOR.

Fig. 1
figure 1

Illustration of the decision hyperplanes generated by SOVR and MCVSVOR on a synthetic dataset

Full size image

It is easy to find that the primal optimization problem (4) of MCVSVOR is a quadratic programming (QP) problem and similar to one (1) of SVOR. This problem can be efficiently solved by transforming it into its dual optimization problem [28]. First, we can formulate the primal Lagrangian of (4) as follows

$$\begin{aligned} L = \frac{1}{2}{\mathbf{w}}^{T} {\mathbf{S}}_{\text{W}} {\mathbf{w}} + C\sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {(\xi_{i}^{j} + \xi_{i}^{*j} )} } - \sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {\alpha_{i}^{j} ( - 1 + \xi_{i}^{j} - {\mathbf{w}}^{T} {\mathbf{x}}_{i}^{j} + b_{j} )} } \hfill \\ \;\;\;\;\; - \sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {\alpha_{i}^{*j} ( - 1 + \xi_{i}^{*j} + {\mathbf{w}}^{T} {\mathbf{x}}_{i}^{j + 1} - b_{j - 1} )} } - \sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {\beta_{i}^{j} \xi_{i}^{j} } } - \sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {\beta_{i}^{*j} \xi_{i}^{*j} } } \hfill \\ \;\;\;\;\; - \sum\limits_{j = 1}^{r} {\gamma^{j} (b_{j} - b_{j - 1} )} \hfill \\ \end{aligned}$$
(5)

where the vectors \({\varvec{\upalpha}} = [\alpha_{1}^{1} , \ldots ,\alpha_{{N^{r} }}^{r} ]^{T}\), \({\varvec{\upalpha}}^{*} = [\alpha_{1}^{*1} , \ldots ,\alpha_{{N^{r} }}^{*r} ]^{T}\), \({\varvec{\upbeta}} = [\beta_{1}^{1} , \ldots ,\beta_{{N^{r} }}^{r} ]^{T}\), \({\varvec{\upbeta}}^{*} = [\beta_{1}^{*1} , \ldots ,\beta_{{N^{r} }}^{*r} ]^{T}\) and \({\varvec{\upgamma}} = [\gamma_{1} , \ldots ,\gamma_{r} ]^{T}\) are the Lagrangian multipliers for the constraints of (4). By differentiating with respect to \({\mathbf{w}}\), \({\varvec{\upxi}}\), \({\varvec{\upxi}}^{*}\) and \({\mathbf{b}}\), we have the following formulas

$$\begin{aligned} \frac{\partial L}{{\partial {\mathbf{w}}}} = {\mathbf{S}}_{\text{W}} {\mathbf{w}} - \sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {(\alpha_{i}^{*j} - \alpha_{i}^{j} ){\mathbf{x}}_{i}^{j} } } = 0 \hfill \\ \frac{\partial L}{{\partial \xi_{i}^{j} }} = C - \alpha_{i}^{j} - \beta_{i}^{j} = 0,\;\forall i,j \hfill \\ \frac{\partial L}{{\partial \xi_{i}^{*j} }} = C - \alpha_{i}^{*j} - \beta_{i}^{*j} = 0,\;\forall i,j \hfill \\ \frac{\partial L}{{\partial b_{j} }} = - \sum\limits_{i = 1}^{{N^{j} }} {(\alpha_{i}^{j} + \gamma^{j} )} + \sum\limits_{i = 1}^{{N^{j + 1} }} {(\alpha_{i}^{*j + 1} + \gamma^{j + 1} )} = 0,\;\forall j \hfill \\ \end{aligned}$$
(6)

Note, we implement the Karush–Kuhn–Tucker (KKT) conditions [28] of (4) in the above formulas. If \({\mathbf{S}}_{W}\) is nonsingular, according to (6), the mapping direction \({\mathbf{w}}\) can be formulated as

$${\mathbf{w}} = {\mathbf{S}}_{W}^{ - 1} \sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {(\alpha_{i}^{*j} - \alpha_{i}^{j} ){\mathbf{x}}_{i}^{j} } }$$
(7)

In the practical applications, as in MCVSVM, the matrix singularity problem may be encountered in MCVSVOR in that the inverse matrix of \({\mathbf{S}}_{W}\) is needed during the process of solving the problem (4). Once this singularity problem occurs, as in [22], ones can add a diagonal matrix to \({\mathbf{S}}_{W}\), i.e., \({\mathbf{S}}_{W} = {\mathbf{S}}_{W} + \rho {\mathbf{I}}\). Here \(\rho > 0\) and \({\mathbf{I}}\) is an identity matrix. This technique that deals with the matrix singularity problem is referred to as regularization method [29]. It is difficult to directly obtain the optimum value of \(\rho\). As determining other parameters in SVOR and MCVSVOR, we can estimate a suitable value of \(\rho\) through using the cross validation technique.

According to the KKT conditions of (4) and the formula (7), the Wolf dual problem of the primal problem (4) of MCVSVOR can be formulated as

$$\begin{aligned} \mathop {\hbox{min} }\limits_{{{\varvec{\upalpha}},{\varvec{\upalpha}}^{*} }} \sum\limits_{j,i} {\sum\limits_{{j^{'} ,i^{'} }} {(\alpha_{i}^{*j} - \alpha_{i}^{j} )(\alpha_{{i^{'} }}^{{*j^{'} }} - \alpha_{{i^{'} }}^{{j^{'} }} )({\mathbf{x}}_{i}^{j} )^{T} {\mathbf{S}}_{W}^{ - 1} {\mathbf{x}}_{{i^{'} }}^{{j^{'} }} } } - \sum\limits_{j,i} {(\alpha_{i}^{*j} + \alpha_{i}^{j} )} \hfill \\ s.t.\;0 \le \alpha_{i}^{j} \le C,\;\forall i,j \hfill \\ \;\;\;\;\;0 \le \alpha_{i}^{{*j{ + }1}} \le C,\;\forall i,j \hfill \\ \;\;\;\;\;\sum\limits_{i = 1}^{{N^{j} }} {\alpha_{i}^{j} } + \gamma^{j} = \sum\limits_{i = 1}^{{N^{j + 1} }} {\alpha_{i}^{*j + 1} } + \gamma^{j + 1} ,\;\gamma^{j} \ge 0,\forall j \hfill \\ \end{aligned}$$
(8)

where \(j\) runs over \(1, \ldots ,r - 1\). This problem is similar to the dual optimization problem of SVOR and can be solved by using the same technique as in SVOR. Suppose that \(\{ {\varvec{\upalpha}},{\varvec{\upalpha}}^{*} ,{\varvec{\upgamma}}\}\) solves the above optimization problem (8), then the mapping direction \({\mathbf{w}}\) is obtained with (7) and the discriminant function value of a new input vector \({\mathbf{x}}\) in MCVSVOR is given by

$$f({\mathbf{x}}) = {\mathbf{w}}^{T} {\mathbf{x}} = \left( {{\mathbf{S}}_{W}^{ - 1} \sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {(\alpha_{i}^{ *j} - \alpha_{i}^{j} ){\mathbf{x}}_{i}^{j} } } } \right)^{T} {\mathbf{x}} = \sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {(\alpha_{i}^{ *j} - \alpha_{i}^{j} )({\mathbf{x}}_{i}^{j} )^{T} {\mathbf{S}}_{W}^{ - 1} {\mathbf{x}}} }$$
(9)

Further, the predictive ordinal rank of the input vector \({\mathbf{x}}\) can be determined by the following decision function

$$\hbox{min} \mathop {\arg }\limits_{i} \{ i:f({\mathbf{x}}) < b_{i} \}$$
(10)

Here, as in SVOR, \(b_{j}\)’s are the thresholds and can be determined by the optimality conditions for the dual problem, which is discussed in detail in [13]. For the sake of completeness, here we offer the computation method of \(b_{j}\)’s, and more details can be found in [13]. First, we set

$$\begin{aligned} I_{0a}^{j} = \{ i \in \{ 1, \ldots ,N^{j} \} :0 < \alpha_{i}^{j} < C\} \hfill \\ I_{0b}^{j} = \{ i \in \{ 1, \ldots ,N^{j + 1} \} :0 < \alpha_{i}^{*j + 1} < C\} \hfill \\ I_{1}^{j} = \{ i \in \{ 1, \ldots ,N^{j + 1} \} :\alpha_{i}^{*j + 1} = 0\} \hfill \\ I_{2}^{j} = \{ i \in \{ 1, \ldots ,N^{j} \} :\alpha_{i}^{j} = 0\} \hfill \\ I_{3}^{j} = \{ i \in \{ 1, \ldots ,N^{j} \} :\alpha_{i}^{j} = C\} \hfill \\ I_{4}^{j} = \{ i \in \{ 1, \ldots ,N^{j + 1} \} :\alpha_{i}^{*j + 1} = C\} \hfill \\ I_{0}^{j} = I_{0a}^{j} \cup I_{0b}^{j} ,I_{up}^{j} = I_{0}^{j} \cup I_{1}^{j} \cup I_{3}^{j} ,I_{low}^{j} = I_{0}^{j} \cup I_{2}^{j} \cup I_{4}^{j} \hfill \\ \end{aligned}$$
(11)

and

$$\begin{aligned} F_{up}^{j} (\mu_{j} ) = \left\{ \begin{aligned} f({\mathbf{x}}_{i}^{j} ) + 1\;\;\;if\;i \in I_{0a}^{j} \cup I_{3}^{j} \hfill \\ f({\mathbf{x}}_{i}^{j + 1} ) - 1\;\;\;if\;i \in I_{0b}^{j} \cup I_{1}^{j} \hfill \\ \end{aligned} \right. \hfill \\ F_{low}^{j} (\mu_{j} ) = \left\{ \begin{aligned} f({\mathbf{x}}_{i}^{j} ) + 1\;\;\;if\;i \in I_{0a}^{j} \cup I_{2}^{j} \hfill \\ f({\mathbf{x}}_{i}^{j + 1} ) - 1\;\;\;if\;i \in I_{0b}^{j} \cup I_{4}^{j} \hfill \\ \end{aligned} \right. \hfill \\ b_{low}^{j} { = } \,\hbox{max} \{ F_{low}^{i} (\mu_{j} ):i \in I_{low}^{j} \} \hfill \\ b_{up}^{j} { = }\,min \{ F_{up}^{i} (\mu_{j} ):i \in I_{up}^{j} \} \hfill \\ \end{aligned}$$
(12)

Therefore, any value from the interval \(b_{j} \in [B_{low}^{j} ,B_{up}^{j} ]\) can be viewed as the feasible value of the threshold \(b_{j}\). Under the circumstances, the final value of \(b_{j}\) might encounter the non-uniqueness problem. In order to handle this problem, ones can determine the final value of \(b_{j}\) by simply taking

$$b_{j} = \frac{1}{2}(B_{low}^{j} + B_{up}^{j} )$$
(13)

where

$$B_{low}^{j} = \left\{ \begin{aligned} \tilde{B}_{low}^{j + 1} \;\;if\;\gamma^{j + 1} > 0 \hfill \\ \tilde{B}_{low}^{j} \;\;otherwise \hfill \\ \end{aligned} \right.\;\;and\;\;B_{up}^{j} = \left\{ \begin{aligned} \tilde{B}_{up}^{j - 1} \;\;if\;\gamma^{j} > 0 \hfill \\ \tilde{B}_{up}^{j} \;\;otherwise \hfill \\ \end{aligned} \right.\;$$
(14)

Here \(\tilde{B}_{low}^{j} { = }\,\hbox{max} \{ b_{low}^{k} :k = 1, \ldots ,j\}\) and \(\tilde{B}_{up}^{j} { = }\,\hbox{min} \{ b_{up}^{k} :k = j, \ldots ,r - 1\}\).

3.2 Connection to SVOR

By observing the optimization problems of MCVSVOR and SVOR, it is easy to find that they actually have a close relationship. Suppose the within-class scatter matrix \({\mathbf{S}}_{W}\) is nonsingular and let \({\mathbf{P}} = {\mathbf{S}}_{W}^{{ - \frac{1}{2}}}\), we have \({\mathbf{P}}^{T} = ({\mathbf{S}}_{W}^{{ - \frac{1}{2}}} )^{T} = {\mathbf{S}}_{W}^{{ - \frac{1}{2}}} = {\mathbf{P}}\) since \({\mathbf{S}}_{W}\) is invertible and symmetric. Therefore, the optimization problem (4) of MCVSVOR can be transformed into

$$\begin{aligned} \mathop {\hbox{min} }\limits_{{{\mathbf{v}},{\mathbf{b}},{\varvec{\upxi}},{\varvec{\upxi}}^{*} }} \frac{1}{2}{\mathbf{v}}^{T} {\mathbf{v}} + C\sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {(\xi_{i}^{j} + \xi_{i}^{*j} )} } \hfill \\ s.t.\;{\mathbf{v}}^{T} {\mathbf{y}}_{i}^{j} - b_{j} \le - 1 + \xi_{i}^{j} ,\;\xi_{i}^{j} \ge 0,\;\forall i,j \hfill \\ \;\;\;\;\;{\mathbf{v}}^{T} {\mathbf{y}}_{i}^{j} - b_{j - 1} \ge 1 - \xi_{i}^{*j} ,\xi_{i}^{*j} \; \ge 0,\forall i,j \hfill \\ \;\;\;\;\;b_{j - 1} \le b_{j} ,\;\forall i,j \hfill \\ \end{aligned}$$
(15)

where \({\mathbf{y}}_{i}^{j} = {\mathbf{P}}^{T} {\mathbf{x}}_{i}^{j}\) and \({\mathbf{v}} = {\mathbf{P}}^{ - 1} {\mathbf{w}}\). The above optimization problem is actually the same as the primal optimization problem of SVOR. This reveals the close relationship between SVOR and MCVSVOR. Further, it can be concluded that the MCVSVOR problem can be solved by using the existing SVOR software. Thus, the solution of MCVSVOR is easy to be computed.

4 The nonlinear case

In the nonlinear case, ones generally use the kernelization trick [24] to map the d-dimensional sample space into a high-dimensional feature space. In this way, a linear hyperplane in the feature space corresponds to a nonlinear hyperplane in the original sample space. Without loss of generality, the optimization problem of MCVSVOR in the feature space is defined as

$$\begin{aligned} \mathop {\hbox{min} }\limits_{{{\mathbf{w}},{\mathbf{b}},{\varvec{\upxi}},{\varvec{\upxi}}^{*} }} \frac{1}{2}{\mathbf{w}}^{T} {\mathbf{S}}_{W}^{\phi } {\mathbf{w}} + C\sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {(\xi_{i}^{j} + \xi_{i}^{*j} )} } \hfill \\ s.t.\;{\mathbf{w}}^{T} \varphi ({\mathbf{x}}_{i}^{j} ) - b_{j} \le - 1 + \xi_{i}^{j} ,\;\xi_{i}^{j} \ge 0,\;\forall i,j \hfill \\ \;\;\;\;\;{\mathbf{w}}^{T} \varphi ({\mathbf{x}}_{i}^{j} ) - b_{j - 1} \ge 1 - \xi_{i}^{*j} ,\;\xi_{i}^{*j} \ge 0,\;\forall i,j \hfill \\ \;\;\;\;\;b_{j - 1} \le b_{j} ,\;\forall i,j \hfill \\ \end{aligned}$$
(16)

where \(\varphi ({\mathbf{x}}_{i}^{j} )\) denotes the sample in the feature space and \({\mathbf{S}}_{W}^{\varphi }\) is the corresponding within-class scatter matrix. Assume

$$\begin{aligned} {\mathbf{X}}^{\varphi } { = [}\varphi ({\mathbf{x}}_{1}^{1} ), \ldots ,\varphi ({\mathbf{x}}_{{N^{1} }}^{1} ),\varphi ({\mathbf{x}}_{1}^{2} ), \ldots ,\varphi ({\mathbf{x}}_{{N^{2} }}^{2} ),\varphi ({\mathbf{x}}_{1}^{r} ), \ldots ,\varphi ({\mathbf{x}}_{{N^{r} }}^{r} ) ]\hfill \\ \;\;\;\;\;{ = [}\varphi ({\mathbf{x}}_{1} ), \ldots ,\varphi ({\mathbf{x}}_{N} ) ]\hfill \\ \end{aligned}$$
(17)

according to [30], \({\mathbf{S}}_{W}^{\varphi }\) can be further rewritten as

$${\mathbf{S}}_{W}^{\varphi } = {\mathbf{X}}^{\varphi } {\mathbf{L}}({\mathbf{X}}^{\varphi } )^{T}$$
(18)

where \({\mathbf{L}} = {\mathbf{I}} - {\mathbf{W}}\). Here \({\mathbf{I}}\) is a identity matrix and \({\mathbf{W}}\) is defined as

$${\mathbf{W}}_{ij} = \left\{ \begin{aligned} { 1\mathord{\left/ {\vphantom { 1{N^{k} }}} \right. \kern-0pt} {N^{k} }} ,\;if\;{\mathbf{x}}_{i} \;and\;{\mathbf{x}}_{j} \;belong\;to\;the\;kth\;category \hfill \\ 0,\;\;\;\;\;\;otherwise. \hfill \\ \end{aligned} \right.$$
(19)

On the other hand, according to the representation theorem for Reproducing Kernel Hilbert Spaces [28], of which the vector \({\mathbf{w}}\) can be formulated as

$${\mathbf{w}} = \sum\limits_{i = 1}^{N} {a_{i} \varphi ({\mathbf{x}}_{i} )}$$
(20)

where \(a_{i} \in {\mathbf{R}}\).

Thus, according to the above discussion and by using (18) and (20), the optimization problem (16) can be reformulated as

$$\begin{aligned} \mathop {\hbox{min} }\limits_{{{\mathbf{a}},{\mathbf{b}},{\varvec{\upxi}},{\varvec{\upxi}}^{*} }} \frac{1}{2}{\mathbf{a}}^{\text{T}} {\mathbf{KLKa}} + C\sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {(\xi_{i}^{j} + \xi_{i}^{*j} )} } \hfill \\ s.t.\;{\mathbf{a}}^{\text{T}} {\mathbf{k}}_{i}^{j} - b_{j} \le - 1 + \xi_{i}^{j} ,\;\xi_{i}^{j} \ge 0,\;\forall i,j \hfill \\ \;\;\;\;\;{\mathbf{a}}^{\text{T}} {\mathbf{k}}_{i}^{j} - b_{j - 1} \ge 1 - \xi_{i}^{*j} ,\;\xi_{i}^{*j} \ge 0,\;\forall i,j \hfill \\ \;\;\;\;\;b_{j - 1} \le b_{j} ,\;\forall i,j \hfill \\ \end{aligned}$$
(21)

where \({\mathbf{K}} = \left( {k({\mathbf{x}}_{i} ,{\mathbf{x}}_{j} )} \right)_{N \times N}\) is the kernel matrix, the vectors \({\mathbf{k}}_{i}^{j}\) and \(\;{\mathbf{a}}\) are defined as \({\mathbf{k}}_{i}^{j} = [k({\mathbf{x}}_{i}^{j} ,{\mathbf{x}}_{1} ),k({\mathbf{x}}_{i}^{j} ,{\mathbf{x}}_{2} ), \ldots ,k({\mathbf{x}}_{i}^{j} ,{\mathbf{x}}_{N} )]^{T}\) and \(\;{\mathbf{a}} = [a_{1} , \ldots ,a_{N} ]^{T}\), respectively. Here \(k({\mathbf{x}}{}_{i},{\mathbf{x}}{}_{j}) = \varphi^{T} ({\mathbf{x}}{}_{i})\varphi ({\mathbf{x}}{}_{j})\) is a predefined kernel function. Let \({\mathbf{M}} = {\mathbf{KLK}}\), the above optimization problem (21) can be further written as

$$\begin{aligned} \mathop {\hbox{min} }\limits_{{{\mathbf{a}},{\mathbf{b}},{\varvec{\upxi}},{\varvec{\upxi}}^{*} }} \frac{1}{2}{\mathbf{a}}^{\text{T}} {\mathbf{Ma}} + C\sum\limits_{j = 1}^{r} {\sum\limits_{i = 1}^{{N^{j} }} {(\xi_{i}^{j} + \xi_{i}^{*j} )} } \hfill \\ s.t.\;{\mathbf{a}}^{\text{T}} {\mathbf{k}}_{i}^{j} - b_{j} \le - 1 + \xi_{i}^{j} ,\;\xi_{i}^{j} \ge 0,\;\forall i,j \hfill \\ \;\;\;\;\;{\mathbf{a}}^{\text{T}} {\mathbf{k}}_{i}^{j} - b_{j - 1} \ge 1 - \xi_{i}^{*j} ,\;\xi_{i}^{*j} \ge 0,\;\forall i,j \hfill \\ \;\;\;\;\;b_{j - 1} \le b_{j} ,\;\forall i,j \hfill \\ \end{aligned}$$
(22)

This is the final formulation of the optimization problem of the nonlinear MCVSVOR. It should be noted that the above optimization problem (22) actually is a optimization problem defined by linear MCVSVOR since \({\mathbf{M}} = {\mathbf{KLK}}\) is the within-class scatter matrix of the dataset which consists of \({\mathbf{k}}_{i} (i = 1, \ldots ,N)\). So, according to the previous discussion about the linear MCVSVOR, it can be efficiently solved. Here, it is worthwhile to note that our method uses \({\mathbf{a}}^{\text{T}} {\mathbf{KLKa}}\) as the regularization term in the nonlinear case. Actually, here \({\mathbf{a}}^{\text{T}} {\mathbf{KLKa}}\) is employed in that it is derived form \({\mathbf{w}}^{T} {\mathbf{S}}_{W}^{\phi } {\mathbf{w}}\) in (16) by using (18) and (20). If ones used \({\mathbf{a}}^{\text{T}} {\mathbf{Ka}}\) in (21), then it is reduced to the optimization problem of the kernelized SVOR. Besides, the matrix \({\mathbf{M}} = {\mathbf{KLK}}\) may be singular. This singularity problem can be tackled as the linear case in Sect. 3.1 since the problem (22) essentially formulates a linear MCVSVOR in which the training data is represented by \({\mathbf{k}}_{i} (i = 1, \ldots ,N)\) and the matrix \({\mathbf{M}} = {\mathbf{KLK}}\) is its within-class scatter matrix.

Suppose \(\{ {\mathbf{a}},{\mathbf{b}},{\varvec{\upxi}},{\varvec{\upxi}}^{*} \}\) is the solution of the above optimization problem, the discriminant function value of a new input vector \({\mathbf{x}}\) is

$$f({\mathbf{x}}) = {\mathbf{a}}^{T} {\mathbf{k}}$$
(23)

where \({\mathbf{k}} = [k({\mathbf{x}}_{1} ,{\mathbf{x}}),k({\mathbf{x}}_{2} ,{\mathbf{x}}), \ldots ,k({\mathbf{x}}_{N} ,{\mathbf{x}})]^{T}\). Thus, the predictive ordinal decision function is given by

$$\hbox{min} \mathop {\arg }\limits_{i} \{ i:f({\mathbf{x}}) < b_{i} \}$$
(24)

Here thresholds \(b_{j}\)’s can be determined by the same strategy in Sect. 3.1.

5 Experiments

In the experiments, we first demonstrate the effectiveness of the proposed method on a synthetic dataset. Then, we conduct the experiments on a synthetic dataset with noise in which the data is non-separable. This experiments intuitionisticly illustrates the difference between SOVR and the proposed method MCVSVOR in the situation where a noisy data is encountered. After that, we conduct experiments on several benchmark datasets to evaluate its performance by comparing it with KDLOR and SVOR-EXC. Finally, we report the experimental results on several real datasets. Note, for the sake of fairness, SVOR with explicit threshold constraints (called SVOR-EXC) is considered since our method is with explicit threshold constraints.

5.1 Synthetic dataset

In order to evaluate the effectiveness of the proposed method, in this subsection we report the experimental result on a synthetic dataset. As is shown in Fig. 2, the dataset contains three ordinal categories, each ordinal category of which has 100 samples.

Fig. 2
figure 2

Illustration of the decision hyperplanes generated by MCVSVOR

Full size image

In the experiment, we used the Gaussian kernel, i.e. \(k({\mathbf{x}},{\mathbf{y}}) = \exp ( - \gamma ||{\mathbf{x}} - {\mathbf{y}}||^{2} )\). The experimental result is showed in Fig. 2. It can be found that the samples of different category can be ordinally arranged by the hyperplanes of the proposed method, i.e., the samples that have the same rank are arranged in same bin by the proposed method. The experimental result shows that the proposed method MCVSVOR is effective to handle the ordinal regression task.

5.2 Noisy dataset

In the above experiment, we validate the effectiveness of the proposed method on a synthetic dataset where the data is obviously separable. In order to further intuitionisticly demonstrate its ability of dealing with the data with noise, we create a synthetic dataset which contains noise and so the categories are not completely separable. As is shown in Fig. 3, the synthetic dataset also includes three ordinal categories and each category consists of 100 samples.

Fig. 3
figure 3

Illustration of the decision hyperplanes of SVOR and MCVSVOR on a synthetic data with noise

Full size image

In this experiment, we adopted the liner kernel function, i.e. \(k({\mathbf{x}},{\mathbf{y}}) = {\mathbf{x}}^{T} {\mathbf{y}}\). Figures 3a and b respectively show the decision hyperplanes generated by SOVR and MCVSVOR. It is easy to be observed that the decision hyperplanes of MCVSVOR reflect the characteristic of the data and show more reasonable in contrast with SOVR. This experimental results further verify the fact that incorporating the distribution information of the data in SOVR can improve its performance. The proposed method embodies this principle by using the within-class scatter matrix in SOVR.

5.3 Benchmark datasets

In order to assess the performance of MCVSVOR, we conducted the experiments on several benchmark datasets. These datasets were frequently used to test the ordinal regression methods, for example, in [13, 22]. In this section we report the experimental results. Table 1 shows a summary of the characteristics of the selected datasets. For each dataset, the target values were discretized into ten ordinal quantities through using equal-frequency binning. In the experiments, each dataset was randomly partitioned into training/test splits as specified in Table 1. Each attribute of the samples were scaled to 0 mean and 1 variance.

Table 1 Characteristics of the selected benchmark datasets
Full size table

On evaluating the ordinal regression methods, there are generally two metrics to be used to quantify the accuracy of predicted values with respect to true targets [13, 22]. One of which is mean-absolute-error (MAE) which measures how far the predicted ordinal scales of the samples differ from their true targets and is formulated as \(\frac{1}{N}\sum\nolimits_{i = 1}^{N} {|y_{i} - \tilde{y}_{i} |}\), where \(y_{i}\) and \(\tilde{y}_{i}\) are respectively the predicted ordinal scales and the true targets, and \(| \cdot |\) denotes the absolute operation. The other is mean-zero–one-error (MZE). It measures the classification error of the samples and is defined as \(\frac{1}{N}\sum\nolimits_{i = 1}^{N} {I(y_{i} \ne \tilde{y}_{i} )}\). Here \(y_{i}\) and \(\tilde{y}_{i}\) are respectively the predicted rank of the respective method and the true rank, and \(I( \cdot )\) is an indicator function that takes 1 if \(y_{i} \ne \tilde{y}\) and returns 0 otherwise.

In the experiments, we employed the Gaussian kernel, which is formulated as \(k({\mathbf{x}},{\mathbf{y}}) = \exp ( - \gamma ||{\mathbf{x}} - {\mathbf{y}}||^{2} )\). We employed fivefold cross validation to choose the appropriate values for the relevant parameters (i.e. the Gaussian kernel parameter \(\gamma\) and the regularization factor \(C\), which were chose from the sets {2−5, 2−4, 2−3, 2−2, 2−1, 20, 21, 22, 23, 24, 25} × {10−4, 10−3, 10−2, 10−1, 100,101, 102, 103, 104}) involved in the problem formulation of each method. The final test error of each method was obtained by using the selected parameters for it. The experiment on each dataset was repeated 20 times independently.

The experimental results are reported in Table 2. In comparison with KDLOR and SVOR-EXC, the proposed method has the lowest MZE and MAE on the whole. These indicate that it is competitive with the other two methods in generalization ability. The reason is that in MCVSVOR not only the distribution of the categories is explicitly considered but also the large margin principle is embodied. Actually, KDLOR also takes the distribution characteristic of the data into consideration, and so it performs better than SVOR-EXC on the whole. However, it does not explicitly embody the large margin principle but MCVSVOR does.

Table 2 The experimental results on the selected benchmark datasets
Full size table

In order to further investigate the statistical significance, we performed the paired two-tailed t-tests [31] according to MZE of these methods. The smaller the p value of a t test, the more significant the difference of the two average values is. T test usually takes a p value of 0.05 as a typical threshold which is considered statistically significant. Table 3 reports the experimental results of the t-tests. For example, the p value of the t test is 0.0207 (<0.05) when comparing KDLOR and SVOR-EXC on the Pyrimidines dataset. This means that KDLOR performs significantly better than SVOR-EXC on this dataset at the 0.05 significant level. From Table 3, although the proposed method MCVSVOR has on the whole better MZE, compared with KDLOR, its improvement is not significant. However, MCVSVOR significantly outperforms SVOR-EXC on five of eight datasets.

Table 3 P-value of t-test on the selected benchmark datasets
Full size table

We further investigated the computational cost of several methods. Table 4 reports the results. It can be observed that KDLOR has the least time consumption on the whole. The proposed method need more time consumption in contrast with the other two methods. The reason is that the inversion of \({\mathbf{S}}_{W}\) is necessary when solving the solving the optimization (8) of the proposed method. So, we need to further research more efficient method to solve the optimization problem of the proposed method in the future.

Table 4 The computational cost (in seconds) on the selected benchmark datasets
Full size table

5.4 Real datasets

In order to further evaluate the performance of the proposed method, we conducted the experiments on several real datasets including USPS [32], UMIST [33], FG-NET [8] and Mixed-Gambles [34]. The USPS dataset comprises 11,000 grayscale handwritten digit images and each image has a resolution with 16 × 16. The dataset is divided into ten ranked categories (from 0 to 9) and each category consists of 1100 images. In this experiment, our aim is to rank the data. The UMIST dataset is a multi-view face dataset. It contains 564 images of 20 individuals and the images of each individual change from profile to frontal views. We select six consecutive ordinal interval angles for ordinal regression. The FG-NET dataset is widely used for evaluating the age estimation methods. It has 1002 face images of 82 individuals. In this dataset, the age varies from 0 to 69 years. Note, the age distributions are imbalanced in the dataset. So, we divided the ages into five ranges: 0–9, 10–19, 20–29, 30–49, and 50+. The age label is ordinally denoted by 1,…, 5, respectively. Here we use the AAM algorithm [35] to extract the used features. The Mixed-Gambles task is a functional MRI dataset. In this dataset, there are 16 different rank levels. Similar to [7, 36], we also only consider gain levels and adopt the GLM regression coefficients as the used features.

For each dataset, we randomly selected 40 % samples from each category for training and the rest for testing. The relevant parameters were determined by the strategy used in Sect. 5.2. Finally, we report the averaged results over 30 runs.

Table 5 shows the ranking results of several methods on the datasets. It can be found that KDLOR and SVOR-EXC achieve comparable performance on the whole. However, the proposed method performs better in comparison with KDLOR and SVOR-EXC on three of the four datasets. The reason is, in our opinion, that MCVSVOR embodies the large margin principle as SVOR-EXC and simultaneously incorporates the distribution information of the categories as well as KDLOR.

Table 5 The experimental results on the real datasets
Full size table

6 Conclusions

In this paper, we proposed a novel ordinal regression method. This method stems from MCVSVM and is called MCVSVOR. In contrast with SVOR, it takes full use of the distribution information of the categories. At the same time, MCVSVOR embodies the large margin principle as well as SVOR. Therefore, MCVSVOR achieves better generalization performance compared with SVOR and KDLOR. The comprehensive experimental results suggest that MCVSVOR is effective to handle the ordinal regression problems and can obtain better generalization performance over SVOR and KDLOR.

Additionally, similar to SVOR, the proposed method can also be extended to the case where the threshold constraints are implicit. Moreover, according to the discussion in Sect. 3.2, MCVSVOR can be efficiently solved using the existing SVOR software and so its solution is easy to be computed. However, compared with SVOR, the proposed method is time-consuming because the inverse matrix of the within-class scatter matrix \({\mathbf{S}}_{W}\) is necessary in solving the optimization problem (4). Therefore, how to accelerate the proposed method is another important research topic.