Tackle balancing constraints in semi-supervised ordinal regression

Abstract

Semi-supervised ordinal regression (S²OR) has been recognized as a valuable technique to improve the performance of the ordinal regression (OR) model by leveraging available unlabeled samples. The balancing constraint is a useful approach for semi-supervised algorithms, as it can prevent the trivial solution of classifying a large number of unlabeled examples into a few classes. However, rapid training of the S²OR model with balancing constraints is still an open problem due to the difficulty in formulating and solving the corresponding optimization objective. To tackle this issue, we propose a novel form of balancing constraints and extend the traditional convex–concave procedure (CCCP) approach to solve our objective function. Additionally, we transform the convex inner loop (CIL) problem generated by the CCCP approach into a quadratic problem that resembles support vector machine, where multiple equality constraints are treated as virtual samples. As a result, we can utilize the existing fast solver to efficiently solve the CIL problem. Experimental results conducted on several benchmark and real-world datasets not only validate the effectiveness of our proposed algorithm but also demonstrate its superior performance compared to other supervised and semi-supervised algorithms

1 Introduction

Ordinal regression (OR) has been a subject of research for the past two decades and is commonly formulated as a multi-class problem with ordinal constraints (Berg et al., 2021; Buri & Hothorn, 2020; Garg & Manwani, 2020; Gu et al., 2023; Li et al., 2020; Pang et al., 2020). This learning task has been widely applied in various real-world scenarios such as information retrieval (Herbrich, 1999), collaborative filtering (Shashua & Levin, 2003), social sciences (Fullerton & Xu, 2012), and medical analysis (Cardoso et al., 2005). However, most of the existing ordinal regression models can only deal with labeled data, such as SVOR-IMC and SVOR-EXC (Chu & Keerthi, 2007). As a result, significant effort is required to obtain a sufficient number of labeled samples. To tackle this challenging problem, it has become necessary to incorporate unlabeled samples, which are often readily available at a low cost, into the training process (Chapelle et al., 2009). This has led to an increasing amount of attention being given to semi-supervised ordinal regression (S²OR) (Ganjdanesh et al., 2020; Gu et al., 2022; Liu et al., 2011; Seah et al., 2012; Srijith et al., 2013).

In semi-supervised problems, it is crucial to prevent the trivial solution of classifying a large number of unlabeled examples into a few classes (Chapelle et al., 2008; Xu et al., 2005; Zhu, 2005). To address this issue, the balancing constraint (Collobert et al., 2006) has been proposed as an effective solution, and several semi-supervised binary classification algorithms (Chapelle & Zien, 2005; Collobert et al., 2006; Joachims, 1999) with balancing constraints have been developed over the last two decades. Joachims (1999) enforced balancing constraints by swapping the pseudo-labels of unlabeled samples, assuming that these pseudo-labels match the class distribution of the labeled samples beforehand. Meanwhile, Chapelle and Zien (2005) directly treated balancing constraints as additional constraints, utilizing the gradient descent method to optimize the objective function. Additionally, Collobert et al. (2006) viewed balancing constraints as virtual samples, training the model with these virtual samples and other regular samples. Among these methods, the virtual samples approach is particularly efficient since it can leverage existing state-of-the-art solvers for the objective function with balancing constraints.

Efficiently training S²OR problems with balancing constraints remains a significant challenge due to the complexity of formulating and solving related problems. While ManifoldOR (Liu et al., 2011) and SSORERM (Tsuchiya et al., 2019) are both S²OR algorithms, they do not consider the influence of balancing constraints. To date, TOR (Seah et al., 2012) and SSGPOR (Srijith et al., 2013) are the only two S²OR algorithms using balancing constraints, and they achieve this by swapping the pseudo-labels of unlabeled samples. However, this approach may require a large number of iterations to make all pseudo-labels reach the optimal position. Therefore, the TOR and SSGPOR algorithms are not yet optimal S²OR algorithms using balancing constraints. Table 1 summarizes representative OR algorithms, which highlights the need for a fast S²OR algorithm using balancing constraints, as this remains an open question.

In this paper, we propose a new algorithm, called BC-S²OR, to address the challenging problem of balancing constraints in S²OR via virtual samples. Specifically, we introduce a novel form of balancing constraints for S²OR to prevent most of the unlabeled samples from being classified into a few classes. Then, we extend the traditional convex-concave procedure (CCCP) framework to solve this complex optimization problem. We transform the convex inner loop (CIL) problem with multiple equality constraints into a quadratic problem like support vector machine (SVM), where the multiple equality constraints are treated as virtual samples. This allows us to use existing solvers (Chu & Keerthi, 2007) to efficiently solve the CIL problems. Numerical experiments conducted on several benchmark and real-world datasets confirm the effectiveness of our proposed algorithm, which outperforms other supervised and semi-supervised OR algorithms.

Table 1 Several representative OR algorithms

2 Preliminaries

2.1 Ordinal regression

Ordinal regression (OR) is a significant supervised learning problem that involves learning a ranking or ordering of instances. It combines the properties of classification and metric regression. The goal of ordinal regression is to categorize data points into a set of finite ordered categories.

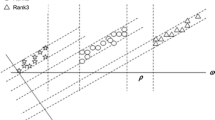
Let $S=\{(x_i,y_i) | i=1,2,\ldots ,n\}$ denote an OR dataset, where $x_i \in {\mathbb {R}}^d$ is a d-dimensional vector and $y_i \in \{ 1, 2,\ldots , r \}$ is the corresponding ordinal class label. Based on the threshold model (Crammer & Singer, 2002) illustrated in Fig. 1, the OR problem with r classes has $r-1$ ordered thresholds: $\theta _1 \le \theta _2 \le \cdots \le \theta _{r-1}$. In this threshold model, a sample x is classified as class k if its predictive output $h(x) =\langle w,\phi (x) \rangle$¹ falls within the range of $\theta _{k-1} < h(x) \le \theta _{k}$.

Fig. 1

Threshold model of OR problem

On the basis of this threshold model, Li and Lin (2007) proposed a new formulation of the OR problem. Specifically, they reduced the OR problem with r classes to $r-1$ binary classification sub-problems and defined the training set of each sub-problem as:

$$\begin{aligned} \begin{aligned}&x_i^k = x_i, \\&y_i^k = 1-2I[y_i \le k], \end{aligned} \end{aligned}$$

(1)

where I[a] denotes an indicator function that returns 1 if a is true and returns 0 if a is false, $k \in \{ 1, 2,\ldots , r-1 \}$ and $y_i^k \in \{ -1, +1 \}$. These $r-1$ sub-problems are aimed to define $r-1$ parallel decision boundaries for ordinal scales and the predictive ordinal class label $f(x_i)$ is defined as:

$$\begin{aligned} \begin{aligned}&f(x_i)=1+ \sum _{k=1}^{r-1}I[g(x_i^k)>0], \\&g(x_i^k)=h(x_i)-\theta _k, \end{aligned} \end{aligned}$$

(2)

where $h(x) =\langle w,\phi (x) \rangle$ is the predictive output, $\theta _k$ means the k-th threshold and $g(x_i^k)$ denotes the binary classifier.

2.2 Semi-supervised ordinal regression

In many cases, ordinal regression models suffer from poor performance due to a limited number of ordinal samples. To overcome this challenge, it becomes necessary to incorporate unlabeled samples into the training process. As a result, there has been a growing interest in semi-supervised ordinal regression (S²OR).

For a particular labeled sample $(x_i,y_i)$, the extended binary classification loss $\zeta _i^k$ for a particular threshold $\theta _k$ can be derived as

$$\begin{aligned} \begin{aligned} \zeta _i^k=\max \left\{ 0,1-y_i^k(w^T\phi (x_i)-\theta _k)\right\} . \end{aligned} \end{aligned}$$

(3)

Consequently, the ordinal regression loss $\zeta _i$ of the labeled sample $(x_i,y_i)$ superimposing the $r-1$ parts easily becomes

$$\begin{aligned} \begin{aligned} \zeta _i=\sum _{k=1}^{r-1}\zeta _i^k&=\sum _{k=1}^{r-1}\max \left\{ 0,1-y_i^k(w^T\phi (x_i)-\theta _k)\right\} \\&=\sum _{k=1}^{r-1} H_1(y_i^kg(x_i^k)) \end{aligned} \end{aligned}$$

(4)

where $H_s(t) = \max \{ 0, s-t \}$.

Given that n labeled samples and u unlabeled samples are available in S²OR, the objective function can be derived as:

$$\begin{aligned} \min \limits _{\bar{w}{\mathop {=}\limits ^\textrm{def}}(w,\theta )} J(\bar{w})&= \frac{1}{2}\Vert w \Vert ^2 + C \sum _{k=1}^{r-1} \sum _{i=1}^{n}H_1\left( y_i^kg\left( x_i^k\right) \right) \end{aligned}$$

(5)

$$\begin{aligned}&\quad + C^* \sum _{k=1}^{r-1} \sum _{i=n+1}^{n+u} H_1(\vert g(x_i^k) \vert ) \nonumber \\ s.t. \quad&\theta _1 \le \theta _2 \le \cdots \le \theta _{r-1}, \end{aligned}$$

(6)

where $\bar{w}=(w,\theta )$ is the parameter vector, C means the penalty coefficient of labeled samples and $C^*$ means the penalty coefficient of unlabeled samples.

The threshold order defined in Eq. (6) plays a crucial role in the OR problem and (Chu & Keerthi, 2007) proposed two approaches to ensure this order. The first approach involves calculating the loss contribution of all samples for each threshold, which automatically satisfies the ordered relations between the thresholds at the optimal solution. However, in Eq. (5), the loss term of unlabeled samples causes the objective function to lose the property of convexity. Consequently, the threshold order is not guaranteed automatically, as shown in Lemma 1. The detailed proof of Lemma 1 can be found in Appendix A.

Lemma 1

For the S²OR problem based on the threshold model, if the constraint of the threshold order (i.e., $\theta _1 \le \theta _2 \le \cdots \le \theta _{r-1}$) is not explicitly enforced, the threshold order cannot be guaranteed automatically.

Building upon the previous discussion, we adopt the second approach proposed by Chu and Keerthi (2007) to ensure the threshold order. This approach involves explicitly incorporating the constraint of the threshold order into the objective function. Although this approach may make the S²OR problem slightly more complicated, it can perfectly guarantee the threshold order.

2.3 Concave–convex procedure

The concave-convex procedure (CCCP) is a highly effective majorization-minimization algorithm that is capable of solving the non-convex program formulated as the difference of convex functions (DC) through a sequence of convex programs.

We provide a specific example of the CCCP approach. Firstly, we define the DC program as:

$$\begin{aligned} \min \limits _{w} \ \&o(w)-v(w) \nonumber \\ s.t. \ \ \ {}&a_i \le 0, i \in [A], \nonumber \\&b_j = 0, j \in [B], \end{aligned}$$

(7)

where o, v and $a_i$ are real-valued convex functions, $b_j$ is an affine function, A and B respectively represent the number of inequality constraints and equality constraints. The CCCP approach is an iterative procedure that solves the following sequence of convex programs:

$$\begin{aligned} w^{t+1} = \mathop {\mathrm {arg\,min}}\limits \limits _{w} \ \&o(w)- w \bigtriangledown v (w^t) \nonumber \\ s.t. \ \ \ {}&a_i \le 0, i \in [A], \nonumber \\&b_j = 0, j \in [B], \end{aligned}$$

(8)

where t means the iteration number. In our paper, we refer to these convex programs as the convex inner loop (CIL) problems. As demonstrated in Eq. (8), the CCCP approach involves linearizing the concave portion (i.e., $-v(w)$) to achieve a sequence of convex programs (i.e., $o(w)-w \bigtriangledown v(w^t)$).

3 Proposed algorithm

In this section, we first introduce our local balancing constraints. Then, we propose our BC-S²OR algorithm to tackle the local balancing constraints via virtual samples. Finally, we analyze the time complexity of our algorithm.

3.1 Local balancing constraints

In semi-supervised binary classification problems, a binary classifier may classify all unlabeled examples into the same class due to the large margin criterion. To address this issue, Joachims (1999) proposed a balancing constraint that ensures the proportion of different classes assigned to the unlabeled samples is the same as that found in the labeled samples. Building on this idea, Collobert et al. (2006) and Chapelle and Zien (2005) introduced a similar but slightly relaxed balancing constraint:

$$\begin{aligned} \begin{aligned} \frac{1}{u} \sum _{i=n+1}^{n+u}f(x_i)=\frac{1}{n} \sum _{i=1}^{n} y_i. \end{aligned} \end{aligned}$$

(9)

In the S²OR problem based on the threshold model, multiple binary classifiers are trained to predict the ordinal class label. However, the large margin criterion may negatively impact each extended binary classifier, resulting in poor performance of the overall S²OR problem. To address this issue, we introduce multiple similar balancing constraints as the ones mentioned above to restrict each binary classifier separately. The balancing constraint formulation for the S²OR problem is as follows:

$$\begin{aligned} \begin{aligned} \frac{1}{u} \sum _{i=n+1}^{n+u}g(x_i^k)=\frac{1}{n} \sum _{i=1}^{n} y_i^k, \end{aligned} \end{aligned}$$

(10)

where there are $r-1$ balancing constraints.

However, it should not be overlooked that the original balancing constraint defined in Eq. (10) is one slightly relaxed constraint and cannot perfectly guarantee that the proportion of positive and negative labels assigned to the unlabeled samples matches that found in the labeled samples in binary classification problems. The superposition of multiple errors of original balancing constraints can lead to the instability of the entire S²OR problem, resulting in most unlabeled samples being classified into a few categories.

To alleviate this situation, we propose a modification to the original balancing constraint. Specifically, we reduce the weights of samples that are far away from decision boundaries and only maintain the balancing constraints of samples near the decision boundaries. This modification ensures that the proportion of each class of unlabeled samples is consistent with that of labeled samples as much as possible. We introduce a novel formulation called the local balancing constraint in our S²OR, which is expressed as follows:

$$\begin{aligned} \begin{aligned} \frac{1}{Z^k} \sum _{i=n+1}^{n+u}\gamma _i^kg(x_i^k)=\frac{1}{E^k} \sum _{i=1}^{n} \gamma _i^k y_i^k, \end{aligned} \end{aligned}$$

(11)

where there are $r-1$ local balancing constraints and $\gamma _i^k$, $Z^k$ and $E^k$ can be defined as:

$$\begin{aligned} \quad \gamma _i^k= \left\{ \begin{aligned}&1 \ \ \text {if} \ \ \vert g(x_i^k) \vert < c \\&0 \quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

(12)

$$\begin{aligned} E^k=\sum _{i=1}^n I\left[ \gamma _i^k \ne 0\right] , Z^k=\sum _{i=n+1}^{n+u} I\left[ \gamma _i^k \ne 0\right] , \end{aligned}$$

(13)

where c is the constraint parameter. In practical applications, to avoid the high complexity of Eq. (11), it is common to use $\gamma _i^k$ as a constant coefficient, which is calculated in advance.

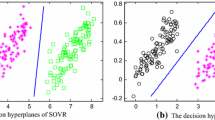
The comparison between the original balancing constraints and our local balancing constraints is presented in Fig. 2 to illustrate the difference. Specifically, we use a three-class S²OR problem as an example. The original balancing constraints defined in Eq. (10) are influenced by unlabeled samples far away from the decision boundaries, which may cause an incorrect reflection of the proportion of positive and negative labels of unlabeled samples in the binary classification sub-problem. Consequently, the superposition of multiple errors of original balancing constraints can result in a serious imbalance between the proportions of unlabeled samples in each class in the whole S²OR problem. This imbalance can lead to the classification of only a few unlabeled samples into the second class, as shown in the first picture in Fig. 2. In contrast, our proposed local balancing constraints can ignore samples far away from the decision boundaries and better ensure the proportion of unlabeled samples in each class, as shown in the second picture in Fig. 2.

Fig. 2

Contrast between original balancing constraints and our local balancing constraints

3.2 BC-S²OR algorithm

In this subsection, we discuss the transformation of our non-convex objective function into a formulation of the difference of convex functions (DC) and how we utilize the CCCP approach to solve it (Allahzadeh & Daneshifar, 2021; Oliveira & Valle, 2020; Rastgar et al., 2020; Zhai et al., 2020, 2023). We specifically focus on transferring the local balancing constraints to virtual samples and then using existing SVOR solvers (Chu & Keerthi, 2007) to efficiently solve the CIL problem.

3.2.1 DC formulation

The treatment of loss terms for unlabeled samples poses a challenging problem in semi-supervised learning, particularly in the context of S²OR. Given the large number of loss terms for each unlabeled sample at all thresholds, addressing this issue is a thorny task. To overcome this challenge, we propose to convert the unlabeled samples into artificially labeled ones. This conversion enables us to transform the non-convex objective function into a DC formulation, which is expressed as the difference between two convex functions.

Firstly, we duplicate unlabeled samples and introduce that

$$\begin{aligned} \begin{aligned} y_i=r,&\quad \forall i \in \{n+1,\ldots ,n+u\}, \\ y_i=1,&\quad \forall i \in \{n+u+1,\ldots ,n+2u\}, \\ x_i=x_{i-u}, \ \ {}&\quad \forall i \in \{n+u+1,\ldots ,n+2u\}. \end{aligned} \end{aligned}$$

(14)

Note that when $y_i=r$, we have that $\forall k \in \{1, \ldots , r-1 \}, y_i^k=+1$ according to Eq. (1), and when $y_i=1$, we have that $\forall k \in \{1, \ldots , r-1 \}, y_i^k=-1$.

Then, the original S²OR problem (i.e., Eq. (5)) can be equivalently rewritten as Eq. (15). The proof can be found in Appendix B.

$$\begin{aligned} \min _{\bar{w}{\mathop {=}\limits ^\textrm{def}}(w,\theta )}J(\bar{w})= o(\bar{w})-v(\bar{w}) \end{aligned}$$

(15)

where o and v are convex functions defined as follows:

$$\begin{aligned} o(\bar{w})&=\frac{1}{2}\Vert w \Vert ^2 +C \sum _{k=1}^{r-1} \sum _{i=1}^{n}H_1\left( y_i^kg\left( x_i^k\right) \right) \nonumber \\&\quad + C^* \sum _{k=1}^{r-1} \sum _{i=n+1}^{n+2u} H_1\left( y_i^k g\left( x_i^k\right) \right) , \nonumber \\ v(\bar{w})=&C^* \sum _{k=1}^{r-1} \sum _{i=n+1}^{n+2u} H_0\left( y_i^k g\left( x_i^k\right) \right) . \end{aligned}$$

(16)

3.2.2 CCCP for S²OR

We utilize the CCCP approach to solve the DC formulation (i.e., Eq. (15)). As shown in Eq. (8), the main process of the CCCP approach is to iteratively solve a sequence of CIL problems, which is generated by linearizing the concave part of the original DC formulation. Here, we first calculate the derivative of the concave part with respect to $\bar{w}$

$$\begin{aligned} \begin{aligned} -\bar{w} \cdot \bigtriangledown v(\bar{w})=\sum _{k=1}^{r-1} \sum _{i=n+1}^{n+2u} \beta _i^k y_i^k g\left( x_i^k\right) \end{aligned} \end{aligned}$$

(17)

$$\begin{aligned} \text {where} \quad \beta _i^k= \left\{ \begin{aligned}&C^* \ \ \text {if} \ \ y_i^k g\left( x_i^k\right) <0 \\&0 \quad \text {otherwise} \end{aligned} \right. \end{aligned}$$

(18)

Then, according Eq. (8), we obtain the following CIL problem:

$$\begin{aligned} \min \limits _{\bar{w}{\mathop {=}\limits ^\textrm{def}}(w,\theta )}\quad&\frac{1}{2}\Vert w \Vert ^2 + C \sum _{k=1}^{r-1} \sum _{i=1}^{n}\xi _i^k + C^* \sum _{k=1}^{r-1} \sum _{i=n+1}^{n+2u}\xi _i^k \nonumber \\&+ \sum _{k=1}^{r-1} \sum _{i=n+1}^{n+2u} \beta _i^k y_i^k g\left( x_i^k\right) \nonumber \\ s.t. \quad&\frac{1}{Z^k} \sum _{i=n+1}^{n+u} \gamma _i^k g(x_i^k)=\frac{1}{E^k} \sum _{i=1}^{n} \gamma _i^k y_i^k, \nonumber \\&y_i^kg(x_i^k) \ge 1- \xi _i^k,\xi _i^k \ge 0 ,\quad \forall i \in \{1,\ldots ,n+2u\},\nonumber \\&\theta _1 \le \theta _2 \le \cdots \le \theta _{r-1}. \end{aligned}$$

(19)

To solve the aforementioned CIL problem, we introduce Lagrangian variables (Bertsekas, 2014) and calculate the partial derivative with respect to primal variables. In order to simplify the dual problem, we transform our local balancing constraints to virtual samples. It should be noted that the number of virtual samples is the same as the number of local balancing constraints, both of which are $r-1$. The virtual samples are defined as follows:

$$\begin{aligned} \phi (x_0^k)=\frac{1}{Z^k}\sum _{i=n+1}^{n+u}\gamma _i^k\phi \left( x_i^k\right) , \ \ y_0^k=1 , \end{aligned}$$

(20)

where $\beta _0^k=0$. The column in kernel matrix corresponding to the example $x_0^k$ is computed as follow:

$$\begin{aligned} \left\langle \phi \left( x_0^k\right) ,\phi \left( x_i^{k'}\right) \right\rangle =\frac{1}{Z^k}\sum _{j=n+1}^{n+u}\gamma _j^k \left\langle \phi \left( x_j^k\right) ,\phi \left( x_i^{k'}\right) \right\rangle . \end{aligned}$$

(21)

Algorithm 1

BC-S²OR algorithm

Here, we directly show the final duality formulation of the CIL problem:

$$\begin{aligned}&\mathop {\mathrm {arg\,max}}\limits \limits _{\bar{\alpha }} \ \sum _{k=1}^{r-1} \sum _{i=0}^{n+2u} \varsigma _i^k \bar{\alpha } _i^k \nonumber \\&-\frac{1}{2}\sum _{k=1}^{r-1}\sum _{k'=1}^{r-1} \sum _{i=0}^{n+2u}\sum _{j=0}^{n+2u} \bar{\alpha }_i^k \bar{\alpha }_j^{k'}K\left( x_i^{k},x_j^{k'}\right) \nonumber \\&s.t. \ \underline{C}_i^k \le \bar{\alpha }_i^k \le {\overline{C}}_i^k, \sum _{i=0}^{n+2u} \bar{\alpha }_i^k - s^k +s^{k+1}=0, s^k \ge 0. \end{aligned}$$

(22)

where $\varsigma _0^k=\frac{1}{E^k}\sum _{i=1}^{n}\gamma _i^k y_i^k$ and $\varsigma _i^k=y_i^k$ when $i\ne 0$, $s^k=0$ when $k=0$ or $k=r$, $K(x_i^{k},x_j^{k'})=\langle \phi (x_i^k),\phi (x_j^{k'}) \rangle$, $\bar{\alpha }_i^k=(\alpha _i^k-\beta _i^k)y_i^k$, and $\underline{C}_i^k$ and ${\overline{C}}_i^k$ are defined as:

$$\begin{aligned}{} & {} \underline{C}_i^k = \left\{ \begin{array}{ll} \min \left\{ y_i^k C,0\right\} &{}\quad \text {if} \ \ 1\le i\le n \\ \min \left\{ y_i^k \left( C^*-\beta _i^k\right) , -y_i^k\beta _i^k\right\} &{}\quad \text {if} \ \ i\ge n+1 \end{array}{ll} \right. \\{} & {} {\overline{C}}_i^k = \left\{ \begin{array}{ll} \max \left\{ y_i^k C,0\right\} &{}\quad \text {if} \ \ 1\le i\le n \\ \max \left\{ y_i^k \left( C^*-\beta _i^k\right) , -y_i^k\beta _i^k \right\} &{}\quad \text {if} \ \ i\ge n+1 \end{array} \right. \end{aligned}$$

Equation (22) is close to the SVOR optimization problem and thus can be optimized by the standard SVOR solver (Chu & Keerthi, 2005, 2007).

When using the Lagrange multiplier method, w is formed as:

$$\begin{aligned} \begin{aligned}&w=\sum _{k=1}^{r-1} \sum _{i=0}^{n+2u}\bar{\alpha }_i^k\phi (x_i^k). \end{aligned} \end{aligned}$$

(23)

Also, $\theta$ can be obtained by the following Karush–Kuhn–Tucker (KKT) conditions (Haeser & Ramos, 2020; Su & Luu, 2020; Van Su & Hien, 2021; Zemkoho & Zhou, 2021):

If $i=0$ and $\alpha _i^k \ne 0$, we have

$$\begin{aligned} \frac{1}{Z^k} \sum _{i=n+1}^{n+u}\gamma _i^kg\left( x_i^k\right) =\frac{1}{E^k}\sum _{i=1}^{n} \gamma _i^k y_i^k , \end{aligned}$$

(24)

If $i \in \{1,\ldots ,n\}$ and $0< \alpha _i^k< C$, we have

$$\begin{aligned} y_i^kg\left( x_i^k\right) =1 , \end{aligned}$$

(25)

If $i \in \{n+1,\ldots ,n+u\}$ and $0< \alpha _i^k< C^*$, we have

$$\begin{aligned} y_i^kg\left( x_i^k\right) =1 . \end{aligned}$$

(26)

Finally, we summarize our BC-S²OR algorithm in Algorithm 1 where C means the penalty coefficient of labeled samples, $C^*$ means the penalty coefficient of unlabeled samples and k is the Gaussian kernel parameter. Moreover, the illustration of our BC-S²OR algorithm is provided in Fig. 3.

Fig. 3

Illustration of BC-S²OR

3.3 Time complexity

In this subsection, we analyze the time complexity of our BC-S²OR algorithm. In each iteration, our algorithm mainly consists of three parts: solving the CIL problem, updating the $\bar{w}$ and updating the $\beta$. To solve the CIL problem, we need to solve a SVOR problem with $N=(r-1)(n+2u)$ samples. The time complexity of solving a SVOR problem using a properly modified state-of-the-art solver (Chu & Keerthi, 2007) is $O(N^a)$, where $1<a<2.3$. Moreover, the updates of $\bar{w}$ and $\beta$ have linear time complexity. Therefore, each iteration of our BC-S²OR algorithm requires $O(N^a)$ computations.

4 Experiments

In this section, we present experimental results to demonstrate the superiority of our BC-S²OR algorithm.

4.1 Compared algorithms

We compared our algorithm with existing state-of-the-art algorithms including supervised and semi-supervised algorithms.

• SVOR-EXC/SVOR-IMC² Support vector approaches for ordinal regression, which optimize multiple thresholds to define parallel decision boundaries for ordinal scales, including two methods of explicit and implicit constraints on thresholds (Chu & Keerthi, 2007).

• TOR A transductive ordinal regression method working by a label swapping scheme that facilitates a strictly monotonic decrease in the objective function value (Seah et al., 2012).

• ManifoldOR A semi-supervised ordinal regression method projecting the original data to the one-dimensional ranking axis under the manifold learning framework (Liu et al., 2011).

• TSVM-CCCP³ A transductive classification method using convex-concave procedure framework to iteratively optimize non-convex cost functions (Collobert et al., 2006).

• TSVM-LDS⁴ A transductive classification method trying to place decision boundaries in regions with low density (Chapelle & Zien, 2005).

Specially, we utilized the TSVM-CCCP algorithm and the TSVM-LDS algorithm to handle multi-class data by the one-versus-rest approach.

Table 2 Datasets

4.2 Implementations

We implemented our BC-S²OR algorithm by building upon the SVOR-IMC code. Specifically, we introduced an outer loop based on the CCCP approach, where each iteration solves an SVM-like sub-problem. To solve the related dual problem, we modified the sequential minimal optimization (SMO) method, which has been widely used in SVMs (Chen et al., 2006; Nakanishi et al., 2020; Platt, 1998; Sornalakshmi et al., 2020). Additionally, we incorporated the shrinking technique (Chang & Lin, 2011) and a warm-start strategy to accelerate the procedure.

We utilized the open-source codes available for the TSVM-CCCP algorithm, the TSVM-LDS algorithm, the SVOR-EXC algorithm, and the SVOR-IMC algorithm. These codes were provided by their respective authors. Additionally, we implemented the TOR algorithm and the ManifoldOR algorithm by following the algorithm description provided by the authors.

Fig. 4

Mean zero–one errors of different algorithms

Fig. 5

Mean absolute errors of different algorithms

Fig. 6

Training time (s) of S²OR algorithms on large-scale datasets with fixed 1000 labeled samples

4.3 Datasets

To evaluate the performance of our proposed BC-S²OR algorithm along with other existing state-of-the-art methods, we conducted experiments on a collection of benchmark and real-world datasets, as presented in Table 2. For the benchmark datasets,⁵ we discretized the continuous target into ordinal scale using the approach of the equal-frequency bin (Sulaiman & Bakar, 2017). For the real-world datasets,⁶ we first processed the text data using the TF-IDF technique (Aizawa, 2003; Onan, 2020; Wang et al., 2020) and then reduced the dimensionality to 1000 using the PCA approach (Abdi & Williams, 2010; Chen et al., 2020). It is worth noting that we scaled all features to the range $[-1,1]$ for all datasets. To perform the experiments in a semi-supervised setting, we randomly split the labeled data into different sizes of 100, 200, 300, 400, 500, and 600, and the remaining data formed the set of unlabeled data.

4.4 Experimental setup

All the experiments were conducted on a PC with 48 2.2GHz cores and 80GB RAM, and all the results were the average of 10 trials. The penalty coefficient C of labeled samples was fixed at 10. For the kernel-based methods, we used the Gaussian kernel $k(x,x')=\exp {(\kappa ||x-x'||^2)}$ and fixed $\kappa$ at $10^{-1}$. For all compared algorithms, we followed the hyperparameter settings of their original papers. In particular, the initial penalty coefficient of unlabeled samples was set at $10^{-5}$ for the TOR algorithm. For the ManifoldOR algorithm, the nearest neighbor number is set at 50 and the value of regularization parameter is 0.5. For the TSVM-CCCP algorithm, we used the symmetric hinge loss and turned the penalty coefficient of unlabeled samples via 5-fold cross validation. For the TSVM-LDS algorithm, the exponent parameter was turned via 5-fold cross validation. And for our BC-S²OR algorithm, we used 5-fold cross validation to optimize the the penalty coefficient $C^*$ of unlabeled samples.

To compare the generalization performance of the algorithms, we employed three widely used measure criteria. The mean zero–one error was used to determine the classification error of the samples, which is defined as

$$\begin{aligned} \frac{1}{u} \sum _{i=n+1}^{n+u} I[f(x_i) \ne y_i]. \end{aligned}$$

We also used the mean absolute error to measure the deviation between the predicted and true class labels of the samples, which is defined as

$$\begin{aligned} \frac{1}{u} \sum _{i=n+1}^{n+u} \vert f(x_i)-y_i\vert . \end{aligned}$$

Furthermore, training time is an important criterion for evaluating an algorithm’s efficiency. Consuming less time to meet the requirements denotes more efficient performance. To ensure fairness, we only compare the training time among the S²OR algorithms.

4.5 Results and discussion

Figures 4 and 5 present the results of the mean zero–one error and the mean absolute error on different datasets. We would like to note that due to the excessive training time consumed by the TOR algorithm and the ManifoldOR algorithm, some of the experimental results are missing. Through careful analysis, we find that when the numbers of ordinal classes and samples are relatively small, the performance of the semi-supervised multi-classification algorithms (i.e., the TSVM-LDS algorithm and TSVM-CCCP algorithm) is better than that of the supervised OR algorithms (i.e., the SVOR-EXC algorithm and SVOR-IMC algorithm). This is because the semi-supervised algorithms can utilize unlabeled samples to improve performance. However, as the numbers of ordinal classes and samples increase, the OR algorithms start to exhibit better performance than the semi-supervised multi-classification algorithms because they make good use of the ordinal information. Importantly, our proposed BC-S²OR algorithm outperforms the above-mentioned algorithms, which is obviously due to its ability to leverage both the unlabeled samples and the ordinal information. Furthermore, our BC-S²OR algorithm also outperforms other S²OR methods (i.e., the TOR algorithm and ManifoldOR algorithm). Figure 6 compares the average training time of the S²OR algorithms. The experimental results indicate that our BC-S²OR algorithm performs better than the other S²OR algorithms in terms of training time.

5 Conclusion

In this paper, we present a novel algorithm, named BC-S²OR, that addresses the challenging issue of the balancing constraints in $\hbox {S}^2$OR using virtual samples. Firstly, we introduce a new type of the balancing constraints for S²OR that prevents the majority of unlabeled samples from being classified into only a few classes. Then, to solve our complex optimization problem, we extend the traditional convex-concave procedure (CCCP) approach. We convert the convex inner loop (CIL) problem, which includes multiple equality constraints, into a quadratic problem similar to support vector machine (SVM). In this quadratic problem, the multiple equality constraints are considered as virtual samples. This enables us to use existing solvers (Chu & Keerthi, 2007) to efficiently solve the CIL problems. Numerical experiments carried out on various benchmark and real-world datasets confirm the superiority of our proposed algorithm, which outperforms other supervised and semi-supervised algorithms.

Appendices

Appendix A: Proof of Lemma 1

Firstly, we define some data subsets where $j \in \{1,\ldots ,r\}$:

$$\begin{aligned} \begin{aligned}&I_j^{low}(\theta )\overset{\text {def}}{=}\{i \in \{1,\ldots ,n\}:y_i=j,w^T\phi (x_i)-\theta \ge -1 \}, \\&I_j^{up}(\theta )\overset{\text {def}}{=}\{i \in \{1,\ldots ,n\}:y_i=j,w^T\phi (x_i)-\theta \le 1 \}, \\&I^{low}(\theta )\overset{\text {def}}{=}\{i \in \{n+1,\ldots ,n+u\}: -1 \le w^T\phi (x_i)-\theta \le 0 \}, \\&I^{up}(\theta )\overset{\text {def}}{=}\{i \in \{n+1,\ldots ,n+u\}: 0 < w^T\phi (x_i)- \theta \le 1 \}. \end{aligned} \end{aligned}$$

It is easy to see that $\theta _k$ is optimal if it minimizes the function:

$$\begin{aligned} e_k(\theta )&=C\sum _{j=1}^{k} \sum _{i \in I_j^{low}(\theta )}(w^T\phi (x_i)-\theta +1) \nonumber \\&\quad +C\sum _{j=k+1}^{r} \sum _{i \in I_j^{up}(\theta )}(-w^T\phi (x_i)+\theta +1) \nonumber \\&\quad +C^* \sum _{i \in I^{low}(\theta )}(w^T \phi (x_i)-\theta +1) \nonumber \\&\quad +C^*\sum _{i \in I^{up}(\theta )}(-w^T\phi (x_i)+\theta +1). \end{aligned}$$

(27)

Then, we obtain the derivative of $e_k(\theta )$ with respect to $\theta$:

$$\begin{aligned} \begin{aligned} \bigtriangledown e_k(\theta )&=-C\sum _{j=1}^{k} \vert I_j^{low}(\theta )\vert + C\sum _{j=k+1}^{r} \vert I_j^{up}(\theta ) \vert \\&\quad -C^*\vert I^{low}(\theta ) \vert + C^*\vert I^{up}(\theta ) \vert :=l_k(\theta ). \end{aligned} \end{aligned}$$

(28)

And through simple calculation, we have:

$$\begin{aligned} \begin{aligned} l_{k+1}(\theta )-l_k(\theta )=-C\vert I_{k+1}^{low}(\theta )\vert -C\vert I_{k+1}^{up}(\theta )\vert < 0. \end{aligned} \end{aligned}$$

(29)

In order to prove that the order of $\theta$ is no longer guaranteed in $\hbox {S}^2$OR problem, we construct a counterexample. Firstly, we find that the derivative $l_k(\theta )$ (28) is not a monotone function. What’s more, when $\theta$ tends to be positive infinity, we have $l_k(\theta )>0$ and when $\theta$ tends to be negative infinity, we have $l_k(\theta )<0$. In this case, we assume that $l_k(\theta )$ and $l_{k+1}(\theta )$ both own three zero points, and the first derivative of these points is not zero. Next, we set the zero points of $l_k(\theta )$ from left to right as $a_1$, $a_2$ and $a_3$, and the zero points of $l_{k+1}(\theta )$ as $b_1$, $b_2$ and $b_3$. According to (29), we assume one situation that $a_1<b_1<b_2<a_2<a_3<b_3$. Under such condition, $e_k(\theta )$ and $e_{k+1}(\theta )$ both own two local minimum points $a_1, a_3$ and $b_1, b_3$. Finally, we assume that point $a_3$ and point $b_1$ are global optimal solutions of $e_k(\theta )$ and $e_{k+1}(\theta )$. Then we have $\theta _k=a_3 > \theta _{k+1}=b_1$, and this situation conflicts with the order $\theta _k \le \theta _{k+1}$ we asked for. Therefore, we conclude that the order of $\theta$ is no longer guaranteed in $\hbox {S}^2$OR problem.

Appendix B: Proof of the DC formulation

In order to handle the non-convex objective function (5) better, we rewrite the loss of unlabeled samples:

$$\begin{aligned} H_1(\vert z \vert )=R_0(z)+R_0(-z)+ \text {const} , \end{aligned}$$

(30)

where $R_s(t)=\min \{ 1-s,\max \{ 0,1-t \} \}=H_1(t)-H_s(t)$ represents a ramp loss. Further more, we rewrite the loss term of unlabeled samples in the objective function (5) with the help of the ramp loss:

$$\begin{aligned}&\sum _{k=1}^{r-1} \sum _{i=n+1}^{n+u} H_1\left( \left| g\left( x_i^k\right) \right| \right) \nonumber \\&\quad = \sum _{k=1}^{r-1} \sum _{i=n+1}^{n+u} R_0\left( g\left( x_i^k\right) \right) +\sum _{k=1}^{r-1} \sum _{i=n+1}^{n+u} R_0\left( -g\left( x_i^k\right) \right) +\text {const} \nonumber \\&\quad =\sum _{k=1}^{r-1} \sum _{i=n+1}^{n+u} H_1\left( g\left( x_i^k\right) \right) +\sum _{k=1}^{r-1} \sum _{i=n+1}^{n+u} H_1\left( -g\left( x_i^k\right) \right) \nonumber \\&\qquad -\sum _{k=1}^{r-1} \sum _{i=n+1}^{n+u} H_0\left( g\left( x_i^k\right) \right) -\sum _{k=1}^{r-1} \sum _{i=n+1}^{n+u} H_0\left( -g\left( x_i^k\right) \right) +\text {const} . \end{aligned}$$

(31)

Then, according to the artificial labeled samples (14), the expression in (31) is in the new formulation:

$$\begin{aligned} \sum _{k=1}^{r-1} \sum _{i=n+1}^{n+u} H_1\left( \left| g\left( x_i^k\right) \right| \right)&= \sum _{k=1}^{r-1} \sum _{i=n+1}^{n+2u} H_1\left( y_i^k g\left( x_i^k\right) \right) \nonumber \\&\quad -\sum _{k=1}^{r-1} \sum _{i=n+1}^{n+2u} H_0\left( y_i^kg\left( x_i^k\right) \right) +\text {const}, \end{aligned}$$

(32)

where the constant does not affect the optimization problem obviously, and we can just ignore it.

Finally, original objective function is in the formulation of

$$\begin{aligned} \begin{aligned} J(\bar{w})&=\underbrace{\frac{1}{2}\Vert w \Vert ^2 +C \sum \nolimits _{k=1}^{r-1} \sum \nolimits _{i=1}^{n}H_1\left( y_i^kg\left( x_i^k\right) \right) +C^* \sum \nolimits _{k=1}^{r-1} \sum \nolimits _{i=n+1}^{n+2u} H_1\left( y_i^k g\left( x_i^k\right) \right) }_{o(\bar{w})} \\&\quad -\underbrace{C^* \sum _{k=1}^{r-1} \sum _{i=n+1}^{n+2u} H_0\left( y_i^k g\left( x_i^k\right) \right) }_{v(\bar{w})}. \end{aligned} \end{aligned}$$

(33)