1 Introduction

Classification is one of the most widely studied problems within the field of machine learning. As one of the commonest tasks in supervised learning, it is the process of finding a model or function that learns a mapping between the set of observations and their respective classes [1, 2]. As a successful classifier, support vector machines (SVMs) have attracted much interest in theory and practice [3–6].

Respectively, let \(X = \{x_i: i \in I\}\) and \(Y = \{y_j: j \in J\}\) denote two classes of data points in \(\mathbf{R}^n\) (\(\mathbf{R}\) stands for the set of all real numbers, n for dimension), and I and J are the corresponding sets of indices. If X and Y are linearly separable, the task of a SVM is to find the maximal margin hyperplane,

$$\begin{aligned} f(x) = w^* \cdot x + b^*, \end{aligned}$$
(1)

where (\(w^*\), \(b^*\)) is the unique solution of the following quadratic model:

$$\begin{aligned}&\min \frac{1}{2}{\left\| w \right\| ^2}\nonumber \\&s.t.\,w \cdot {x_i} + b \ge 1,i \in I; w \cdot {y_j} + b \le - 1,\quad j \in J. \end{aligned}$$
(2)

It has been shown that \(M = 2/||w||\) is the maximal margin, and (\(w^*\), \(b^*\)) could be computed from the nearest point pair (\(x^*\), \(y^*\)) between the two convex hulls CH(X) and CH(Y) [7, 8],

$$\begin{aligned} {w^*} = \frac{{2({x^*} - {y^*})}}{{{{\left\| {{x^*} - {y^*}} \right\| }^2}}},\quad {b^*} = \frac{{{{\left\| {y{}^*} \right\| }^2} - {{\left\| {{x^*}} \right\| }^2}}}{{{{\left\| {{x^*} - {y^*}} \right\| }^2}}}, \end{aligned}$$

where (\(x^*\), \(y^*\)) is the solution of the following nearest point problem (NPP),

$$\begin{aligned} \min \left\| {x - y} \right\|\quad s.t.\, x \in CH(X), y \in CH(Y). \end{aligned}$$
(3)

Cross distance minimization algorithm (CDMA) [9] is an iterative algorithm for computing a hard margin SVM via the nearest point pair between CH(X) and CH(Y). The CDMA is simple to implement with fast convergence, but it works only on linearly separable data. In this paper, we first give a new version of the CDMA with clear explanation of its linear time complexity. Then we extend the new CDMA to solving the non-linear and non-separable problems, in a similar way to generalize the S-K algorithm [10].

This paper is organized as follows. Section 2 describes some related work to the CDMA. Section 3 presents a new version of the CDMA and introduces its kernel version. Section 4 provides experimental results and Sect. 5 concludes the paper.

2 Related work

2.1 Sequential minimal optimization algorithm

The basic idea of sequential minimal optimization (SMO) algorithm is to obtain an analytical solution for subproblems resulting from the working set decomposition [11]. The performance of SMO could be further improved by the maximal violating pair working set selection [12, 13]. LIBSVM [14] is a well-known SMO-type implementation, which solves a linear cost soft margin SVM below:

$$\begin{aligned} &\min \frac{1}{2}{\left\| w \right\| ^2} + C\left( {\sum \limits _{i \in I} {{\xi _i}} + \sum \limits _{j \in J} {{\zeta _j}} } \right) \nonumber \\ &s.t.\ w \cdot \phi ({x_i}) + b \ge 1 - {\xi _i},\quad{\xi _i} \ge 0,i \in I;\\ &w \cdot \phi ({y_j}) + b \le - 1 + {\zeta _j},\quad{\zeta _j} \ge 0,j \in J.\nonumber \end{aligned}$$
(4)

In Eq. (4), \(\xi _i\) and \(\zeta _j\) denote the slack variables corresponding to two classes.

2.2 Nearest point algorithm

The most similar approach to our work is the nearest point algorithm (NPA) by Keerthi et al. [7], which combines the Gilbert’s algorithm [15] and the Mitchell algorithm [16] to find the nearest points between the two convex hulls CH(X) and CH(Y). In order to deal with the non-linear and non-separable cases, the NPA solves a new nearest point problem that is equivalent to the following quadratic cost soft margin SVM [17] (QCSM-SVM),

$$\begin{aligned} \min \frac{1}{2}{\left\| w \right\| ^2} + C\left( {\sum \limits _{i \in I} {\xi _i^2} + \sum \limits _{j \in J} {\zeta _j^2} } \right) \nonumber \\ s.t.\, w \cdot \phi ({x_i}) + b \ge 1 - {\xi _i},\quad i \in I;\\ w \cdot \phi ({y_j}) + b \le - 1 + {\zeta _j},\quad j \in J.\nonumber \end{aligned}$$
(5)

Note that negative values of \({\xi _i}\) or \({\zeta _j}\) cannot occur at the optimal solution of QCSM-SVM because we may reset \(\xi _i = 0\) (\(\zeta _j = 0\)) to make the solution still feasible and also strictly decrease the total cost if \(\xi _i < 0\) (\(\zeta _j < 0\)). Thus, there is no need to include nonnegativity constraints on \(\xi _i\) and \(\zeta _j\).With a simple transformation, the QCSM-SVM model can be converted into an instance of hard margin SVM (Eq. 2) with the dimensionality of \(n + |I| + |J|\) by mapping \({x_i} \in X\) to \({x_i}^\prime \in X^\prime\) and \({y_j} \in Y\) to \(y_j^\prime \in Y^\prime\) as follows:

$$\begin{aligned} x_i^\prime = \left( {{x_i}, \frac{{{e_i}}}{{\sqrt{2C} }}} \right) = [{x_i}, 0, ..., \frac{1}{{\sqrt{2C} }}, ..., 0],\nonumber \\ y_j^\prime = \left( {{y_j}, \frac{{ - {e_{|I| + j}}}}{{\sqrt{2C} }}} \right) = [{y_j}, 0, ..., \frac{{ - 1}}{{\sqrt{2C} }}, ..., 0], \end{aligned}$$
(6)

where \({e_k}\) denotes the \(n + \left| I \right| + \left| J \right|\) dimensional vector in which the kth component is one and all other components are zero. Accordingly, \(w'\) and \(b'\) can be computed as:

$$\begin{aligned} {w'} = [w, \sqrt{2C} {\xi _1},...,\sqrt{2C} {\xi _{|I|}},\sqrt{2C} {\zeta _1},...,\sqrt{2C} {\zeta _{|J|}}], {b'} = b. \end{aligned}$$
(7)

The kernel function transformed is given by

$$\begin{aligned} {K'}({x_i},{x_j}) = K({x_i},{x_j}) + {\delta _{i,j}}\frac{1}{{2C}}, \end{aligned}$$
(8)

where K denotes the original kernel function, \({\delta _{i,j}}\) is one if \(i=j\) and zero otherwise. Thus, for any pair of \((x_i, y_j)\) the modified kernel function is easily computed.

2.3 Schlesinger-Kozinec algorithm

Another closely related approach is Schlesinger-Kozinec (SK) algorithm [10]. The original SK algorithm solves the NPP problem by computing an approximate point pair (\(x^*\), \(y^*\)) to construct a \(\varepsilon\)-optimal hyperplane \(w^* \cdot x + b^* = 0\), where \(w^* = x^* - y^*\) and \({b^*} = (\parallel {y^*}{\parallel ^2} - \parallel {x^*}{\parallel ^2})/2\). This algorithm starts from two arbitrary points \(x^* \in CH(X), y^* \in CH(Y)\) and stops when satisfying the \(\varepsilon\)-optimal criterion, namely,

$$\begin{aligned} \parallel {x^*} - {y^*}\parallel \;- \;m({v_t}) < \varepsilon , \end{aligned}$$

where \({v_t} \in X \cup Y\), \(t = \mathop {\arg \min }\limits _{i \in I \cup J} m({v_i})\), and

$$\begin{aligned} m({v_i}) = \left\{ {\begin{array}{ll} {\frac{{({v_i} - {y^*}) \cdot ({x^*} - {y^*})}}{{\parallel {x^*} - {y^*}\parallel }},\quad {v_i} \in X, i \in I}\\ {\frac{{({v_i} - {x^*}) \cdot ({y^*} - {x^*})}}{{\parallel {x^*} - {y^*}\parallel }},\quad {v_i} \in Y, i \in J} \end{array}} \right. \end{aligned}$$

The SK algorithm has been generalized to its kernel version (KSK) [10]. It should be noted that in the SK algorithm, if \({v_t} = {x_t}(t \in I)\) violates the \(\varepsilon\)-optimal criterion, \(x^*\) will be updated by the Kozinec rule \({x^{new}} = (1 - \lambda ){x^*} + \lambda {x_t}\), with \(y^*\) fixed and \(\lambda\) computed for minimizing the distance between \(x^{new}\) and \(y^*\). Otherwise, if \({v_t} = {y_t}(t \in J)\) violates the \(\varepsilon\)-optimal criterion, \(y^*\) will be updated by the Kozinec rule \({y^{new}} = (1 - \mu ){y^*} + \mu {y_t}\), with \(x^*\) fixed and \(\mu\) computed for minimizing the distance between \(y^{new}\) and \(x^*\). If \(\parallel {x^*} - {y^*}\parallel - m({v_t}) < \varepsilon\) holds, \({w^*} = {x^*} - {y^*}\) and \({b^*} = (\parallel {y^*}{\parallel ^2} - \parallel {x^*}{\parallel ^2})/2\) gives an \(\varepsilon\)-optimal solution, which coincides with the optimal hyperplane for \(\varepsilon = 0\).

3 Cross kernel distance minimization algorithm

3.1 Cross distance minimization algorithm

Let d stand for the Euclid distance function. In this subsection, we will depict a new version of the CDMA in Algorithm 2, where \(\varepsilon\) is called “precision parameter”, for controlling the convergence condition.

The original CDMA (OCDMA, see Algorithm 1) is designed to iteratively compute the nearest points of two convex hulls. If \((x^*, y^*)\) is a nearest point pair obtained by solving the NPP in (3), i.e., \(d(CH(X), CH(Y))=||x^*-y^*||\), then it can be proven that their perpendicular bisector is exactly the hard-margin SVM of X and Y [9].

figure a

The procedure of OCDMA includes two basic blocks. The steps 3–4 are to compute a nearest point pair \((x^*, y^*)\) between CH(X) and CH(Y). The steps 5–6 are to construct a SVM, \(f(x)=w^* \cdot x + b^*\).

figure b

Compared to the OCDMA, the new CDMA can reduce half an amount of distance computations needed in the case \(\lambda > 0\) by minimizing \(d(z, y^*)\) instead of \(d(x_2, y^*)\) and \(d(z, y^*)\) as well as \(d(x^*, z)\) instead of \(d(x^*, y_2)\) and \(d(x^*, z)\). The geometric meaning of z point is illustrated in Fig. 1. According to Theorem 5 in Ref. [9], if \(x_1 = x^*\) is not the nearest point from \(y^*\) to CH(X), there must exist another point \({x_2} \ne {x_1}\) in X such that \(d(z,{y^*}) < d({x^*},{y^*})\), where

$$\begin{aligned} z = {x_1} + \lambda ({x_2} - {x_1}),\\ \lambda = \min \left\{ {1,\frac{{({x_2} - {x_1})\cdot ({y^*} - {x_1})}}{{({x_2} - {x_1})\cdot ({x_2} - {x_1})}}} \right\} > 0. \end{aligned}$$
Fig. 1
figure 1

The geometric meaning of point z: (a) if \(\lambda\) =1, then \(z=x_2\) is a point in X; (b) if \(0<\lambda <1\), then \(z=x_1+\lambda (x_2-x_1)\) is actually the vertical point from \(y^*\) to the line segment \(CH\{x_1, x_2\}\). If \(x_1\) is not the nearest point from \(y^*\) to CH(X), there must exist another point \(z=x_2\) or \(z=x_1+\lambda (x_2-x_1)\) such that \(d(z, y^*)<d(x^*, y^*)\)

Full size image

Similarly, if \(y_1 = y^*\) is not the nearest point from \(x^*\) to CH(Y), there must exist another point \(y_2 \ne y_1\) in Y such that \(d({x^*},z) < d({x^*},{y^*})\), where

$$\begin{aligned} z = {y_1} + \mu ({y_2} - {y_1}), \\ \mu = \min \left\{ {1,\frac{{({y_2} - {y_1})\cdot ({x^*} - {y_1})}}{{({y_2} - {y_1})\cdot ({y_2} - {y_1})}}} \right\} > 0. \end{aligned}$$

Therefore, if (\(x^*, y^*\)) is not the nearest point pair, the CDMA can always find a nearer one until it converges.

It has been shown that CDMA converges with a rough time complexity of \(O(I(\varepsilon ) \cdot (\left| X \right| + \left| Y \right| ))\), where \(I(\varepsilon )\) is guessed a constant as an open problem [9], representing the total number of running loops for CDMA to converge at \(\varepsilon\)-precision. In fact, \(I(\varepsilon )\) can be clearly bounded by a simple constant, namely, \(I(\varepsilon ) \le L/\varepsilon\), where L may be estimated as \(L = {\max _{x \in X,y \in Y}}\left\{ {\left\| {x - y} \right\| } \right\}\), because we cannot get a cross distance decrease less than \(\varepsilon\) in each running loop until satisfying the stopping condition for CDMA.

3.2 Cross kernel distance minimization algorithm

Based on the description mentioned above, now we generalize the CDMA to its kernel extension, namely, cross kernel distance minimization algorithm (CKDMA). Given a kernel function \(K({x_i},{y_j}) = \phi ({x_i}) \cdot \phi ({y_j})\), the objective of CKDMA is to minimize the kernel distance \(kd(\tilde{x},\tilde{y})\) between \(\tilde{x} \in CH\left( {\phi (X)} \right)\) and \(\tilde{y} \in CH\left( {\phi (Y)} \right)\),

$$\begin{aligned}&\min kd(\tilde{x},\tilde{y}) = \min \left\| {\tilde{x} - \tilde{y}} \right\| \nonumber \\&s.t.\, \tilde{x} \in CH\left( {\phi (X)} \right) ,\tilde{y} \in CH\left( {\phi (Y)} \right) . \end{aligned}$$
(9)

For \({\tilde{x}^*} \in CH\left( {\phi (X)} \right)\) and \({\tilde{y}^*} \in CH\left( {\phi (Y)} \right)\), we can express them as,

$$\begin{aligned} {{\tilde{x}}^*} = \sum \limits _{i \in I} {{\alpha _i} \cdot \phi ({x_i})} = \sum \limits _{i \in I} {{\alpha _i}} \cdot {{\tilde{x}}_i}, \sum \limits _{i \in I} {{\alpha _i} \ge 0} ,{{\tilde{x}}_i} \in \phi (X),\nonumber \\ {{\tilde{y}}^*} = \sum \limits _{j \in J} {{\beta _j} \cdot \phi ({y_j})} = \sum \limits _{j \in J} {{\beta _j}} \cdot {{\tilde{y}}_j}, \sum \limits _{j \in J} {{\beta _j} \ge 0} ,{{\tilde{y}}_j} \in \phi (Y). \end{aligned}$$
(10)

If \({\tilde{x}^*}\) is not the nearest point from \({\tilde{y}^*}\) to \(CH\left( {\phi (X)} \right)\), we can find \({t_1} \in I\) to compute a new point \({\tilde{x}^{new}} = (1 - \lambda ){\tilde{x}^*} + \lambda {\tilde{x}_{{t_1}}}\), where \(\lambda = \min [1, (({\tilde{x}_{{t_1}}} - {\tilde{x}^*}) \cdot ({\tilde{y}^*} - {\tilde{x}^*}))/(({\tilde{x}_{{t_1}}} - {\tilde{x}^*}) \cdot ({\tilde{x}_{{t_1}}} - {\tilde{x}^*}))]\), such that \({\tilde{x}^{new}}\) is nearer to \({\tilde{y}^*}\) than \({\tilde{x}^*}\), i.e., \(\left\| {{{\tilde{x}}^{new}} - {{\tilde{y}}^*}} \right\| < \left\| {{{\tilde{x}}^*} - {{\tilde{y}}^*}} \right\|\).

Because \({\tilde{x}^{new}} = \sum \limits _{i \in I} {\alpha _i^{new}{{\tilde{x}}_i}} = (1 - \lambda )\sum \limits _{i \in I} {{\alpha _i}{{\tilde{x}}_i}} + \lambda {\tilde{x}_{{t_1}}} = \sum \limits _{i \in I} {[(1 - \lambda ){\alpha _i} + \lambda {\delta _{i,{t_1}}}]{{\tilde{x}}_i}}\), \({\tilde{x}^{new}}\) can be obtained by updating \({\alpha _i}\), namely,

$$\begin{aligned} \alpha _i^{new} = (1 - \lambda ){\alpha _i} + \lambda {\delta _{i,{t_1}}}, \end{aligned}$$
(11)

where \({\delta _{i,j}}\) is one if \(i = j\) and zero otherwise.

Similarly, if \({\tilde{y}^*}\) is not the nearest point from \({\tilde{x}^*}\) to \(CH\left( {\phi (Y)} \right)\), we can also find a nearer point \({\tilde{y}^{new}} = (1 - \mu ){\tilde{y}^*} + \mu {\tilde{y}_{{t_2}}},{t_2} \in J\) with the adaptation rule below,

$$\begin{aligned} \beta _j^{new} = (1 - \mu ){\beta _j} + \mu {\delta _{j,{t_2}}}. \end{aligned}$$
(12)

For convenience, we further introduce the following notations:

$$\begin{aligned}&A = {{\tilde{x}}^*} \cdot {{\tilde{x}}^*} = \sum \limits _{i \in I} {\sum \limits _{j \in J} {{\alpha _i}{\alpha _j}K({x_i},{x_j})} } ,\\&B = {{\tilde{y}}^*} \cdot {{\tilde{y}}^*} = \sum \limits _{i \in I} {\sum \limits _{j \in J} {{\beta _i}{\beta _j}K({y_i},{y_j})} } ,\\&C = {{\tilde{x}}^*} \cdot {{\tilde{y}}^*} = \sum \limits _{i \in I} {\sum \limits _{j \in J} {{\alpha _i}{\beta _j}K({x_i},{y_j})} } ,\\&\forall i \in I,{D_i} = \phi ({x_i}) \cdot {{\tilde{x}}^*} = \sum \limits _{j \in I} {{\alpha _j}K({x_i},{x_j})} ,\\&\forall i \in I,{E_i} = \phi ({x_i}) \cdot {{\tilde{y}}^*} = \sum \limits _{j \in J} {{\beta _j}K({x_i},{y_j})} ,\\&\forall j \in J,{F_j} = \phi ({y_j}) \cdot {{\tilde{x}}^*} = \sum \limits _{i \in I} {{\alpha _i}K({x_i},{y_j})} ,\\&\forall j \in J,{G_j} = \phi ({y_j}) \cdot {{\tilde{y}}^*} = \sum \limits _{i \in J} {{\alpha _i}K({y_i},{y_j})} . \end{aligned}$$

Using these notations to express the CDMA in terms of kernel inner product, it is easy to obtain the CKDMA described in Algorithm 2. Note that sqrt indicates the square root function.

figure c

In Step 6 of the CKDMA, \(A,C,{D_i},{F_j}\) are updated as follows:

$$\begin{aligned}&{A^{new}} = {(1 - \lambda )^2} A + 2(1 - \lambda )\lambda {D_{{t_1}}} + {\lambda ^2}K({x_{{t_1}}},{x_{{t_1}}}),\\&{C^{new}} = (1 - \lambda ) C + \lambda {E_{{t_1}}},\\&D_i^{new} = (1 - \lambda ) {D_i} + \lambda K({x_{{t_1}}},{x_i}),\\&F_j^{new} = (1 - \lambda ) {F_j} + \lambda K({x_{{t_1}}},{y_j}). \end{aligned}$$

And in Step 9, \(B, C, {E_i}, {G_j}\) are updated as follows:

$$\begin{aligned}&{B^{new}} = {(1 - \mu )^2} B + 2(1 - \mu )\mu {G_{{t_2}}} + {\mu ^2}K({y_{{t_2}}},{y_{{t_2}}}),\\&{C^{new}} = (1 - \mu ) C + \mu {F_{{t_2}}},\\&E_i^{new} = (1 - \mu ) {E_i} + \mu K({y_{{t_2}}},{x_i}),\\&G_j^{new} = (1 - \mu ) {G_j} + \mu K({y_{{t_2}}},{y_j}). \end{aligned}$$

Moreover, in Algorithm 2, \(d^*\) stands for the distance between the nearest points, and \(d^{new}\) for its updated value. If \(d^* - d^{new}\) is less than \(\varepsilon\), the CKDMA will return the result of a linear function in kernel space, namely, \(f(x) = {{\tilde{w}}^*} \cdot \phi (x) + {{\tilde{b}}^*}\), which can be further expressed as a kernel form below,

$$\begin{aligned} f(x)&= \left( {\sum \limits _{i \in I} {{\alpha _i}K\left( {{x_i},x} \right) } - \sum \limits _{j \in J} {{\beta _j}K\left( {{y_j},x} \right) } } \right) \\& \quad +\,\frac{1}{2}\left( {\sum \limits _{i \in J} {\sum \limits _{j \in J} {{\beta _i}{\beta _j}K\left( {{y_i},{y_j}} \right) } } - \sum \limits _{i \in I} {\sum \limits _{j \in I} {{\alpha _i}{\alpha _j}K\left( {{x_i},{x_j}} \right) } } } \right) \\&= \left( {\sum \limits _{i \in I} {{\alpha _i}K\left( {{x_i},x} \right) } - \sum \limits _{j \in J} {{\beta _j}K\left( {{y_j},x} \right) } } \right) + \frac{1}{2}\left( {B - A} \right) \end{aligned}$$

In addition, note that CKDMA can only solve separable problems in a kernel-induced feature space. After using Eq. (6) mentioned in Sect. 2.2, it can be directly applied to non-separable cases, for finding a generalized optimal hyperplane with the quadratic cost function.

Finally, it seems that the update rules of the CKDMA are very similar to that of the KSK algorithm [10]. However, there are at least two notable differences between them: (1) in each iteration the KSK algorithm updates only one of two points, either \(x^*\) or \(y^*\), whereas the CKDMA generally updates both of them; (2) Given \(x^*\) and \(y^*\), the two algorithms may pick different data points even in the same training set for updating the nearest pair. For example, suppose \(X = \{ {x_1},{x_2},{x_3}\}\) and \(Y = \{ {y_1}\}\). In Fig. 2a, the KSK algorithm will choose \(x_3 \in X\) to update \(x^*\) with \(x_{KSK}^{new} = (1 - \lambda ){x^*} + \lambda {x_3}\) . This is because

$$\begin{aligned} m({x_3}) = \left\| {q - {y^*}} \right\| = \frac{{({x_3} - {y^*}) \cdot ({x^*} - {y^*})}}{{\parallel {x^*} - {y^*}\parallel }},\\ m({x_2}) = \left\| {p - {y^*}} \right\| = \frac{{({x_2} - {y^*}) \cdot ({x^*} - {y^*})}}{{\parallel {x^*} - {y^*}\parallel }}, \end{aligned}$$

and \(m(x_3) < m(x_2)\) (see Sect. 2.3).

Fig. 2
figure 2

Different updates of the KSK algorithm and the CKDMA

Full size image

But from Fig. 2, the CKDMA will choose \(x_2 \in X\) to update \(x^*\) with \(x_{CKDMA}^{new} = (1 - \lambda ){x^*} + \lambda {x_2}\), because \(d({y^*},CH\{ {x^*},{x_2}\} ) < d({y^*},CH\{ {x^*},{x_3}\} )\) (see Sect. 3.1).

4 Experimental results

In this section, we conduct a series of numerical experiments to evaluate the classification performances of CKDMA on 17 data sets, which are listed with their code, size and dimensionality in Table 1. All these data sets are selected from the UCI repository [18], but Fourclass from THK96a [19], German.number and Heart from Statlog [20], Leukemia and Gisette from LIBSVM Data [21]. The experiments are divided into two parts. The first part compares the proposed method with KSK, NPA and LIBSVM2.9, and the second part shows the influence of precision parameter \(\varepsilon\) on CKDMA.

4.1 Comparison with other algorithms

We used 14 data sets in this experiment. The 14 data sets can be seen in Table 2. They are binary problems with features linearly scaled to [−1, 1]. Note that the “training + test” sets have been partitioned for the last four data sets, including mo1, mo2, mo3 and spl. For the sake of homogeneity in results’ presentation, we first merge the training and test sets of them. And then, we randomly split each of them into two halves for 10 times, one half for training, the other for testing. We report the average results on all the experiments, which were conducted with RBF kernel function on a Dell PC having I5-2400 3.10-GHz processors, 4-GB memory, and Windows 7.0 operation system. The two parameters, C and \(\gamma\) respectively from the candidate sets \(\{2^i|i=-4,-3,...,3,4\}\) and \(\{2^i|i=-7,-6,...,4,5\}\), were determined by 5-fold cross validation on the training sets. The precision parameter \(\varepsilon\) was chosen as \(10^{-5}\) for CKDMA, \(10^{-3}\) for KSK and NPA, and the default (i.e., \(10^{-3}\)) for LIBSVM 2.9. Note that, in experimental results, the bold values represent higher accuracies, less training time or less support vectors.

Table 1 Data sets used in the experiments
Full size table

From Table 2, it can be seen that CKDMA obtains higher accuracies on six data sets than KSK, six data sets than NPA, and seven data sets than LIBSVM2.9, respectively. Even in the case of lower accuracies, CKDMA can achieve the same level of performance with other algorithms. Moreover, CKDMA generally takes less training time and produces less support vectors than KSK and NPA, but more than LIBSVM2.9.

Table 2 Comparison of accuracies, training time (ms), and the number of support vectors
Full size table
Table 3 Comparison of four classifiers on large/high-dimensional data sets
Full size table

In addition, we also conducted experiments on three large/high-dimensional data sets (i.e., a9a, leu and gis), with the results described in Table 3. Since it take too long cross validation time to choose C and \(\gamma\) for Libsvm 2.9, we directly set the default values, namely, \(C=1\) and \(\gamma =1/dim\) (0.00813 for a9a, 0.00014 for leu, and 0.00020 for gis). From Table 3, we can get that, on the selected large/high-dimensional data sets, the CKDMA is comparable to the other three classifiers.

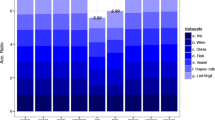
Next, we further compare the statistical significance of CKDMA with KSK, NPA, LIBSVM. Referring to [22, 23], we use Bonferroni-Dunn test for comparison over all the selected data sets. Table 4 presents the average ranking of four algorithms, and Fig. 4 provides the corresponding critical difference (CD) diagram. The test results show there are no significant differences between CKDMA and the others.

Fig. 3
figure 3

Experimental results for different precision parameters

Full size image
Table 4 Average rankings of four algorithms
Full size table

4.2 Influence of precision parameter

In this subsection we investigate influence of precision parameter \(\varepsilon\) on performance of CKDMA, with \(\varepsilon\) set from \(10^{-1}\) to \(10^{-6}\). We choose eight data sets of different dimensions (i.e., fou, mo1, hea, ger, bre, son, a9a and mus). For mo1 and a9a, we directly use the indicated training and testing sets for conducting experiments. For fou, hea, ger, bre, son and mus, we randomly split each of them into two halves only once, one half for training, the other for testing. The corresponding results are shown in Fig. 3, including testing accuracy, training time, and number of support vectors.

Fig. 4
figure 4

Comparison of CKDMA against the others with the Bonferroni-Dunn test. All classifiers with ranks outside the marked interval are significantly different (\({ \alpha } = 0.05\)) from the control

Full size image

From Fig. 3, we can see that as \(\varepsilon\) gets smaller and smaller, testing accuracies generally tend to increase and become stable. In Fig. 3a, a vertical dashed line marks a good choice of \(10^{-5}\) for CKDMA because it gives rise to satisfactory performance with relatively reasonable training time (see Fig. 3b) and number of support vectors (see Fig. 3c).

5 Conclusions

In this paper, we have explained the linear time complexity for CDMA, and further proposed a new iterative algorithm, i.e., the cross kernel distance minimization algorithm (CKDMA), to train quadratic cost support vector machines using kernel functions. Over CDMA, CKDMA can take advantages to solve non-linear and non-separable problems, preserving the simplicity in geometric meaning. Moreover, it gives a novel way to understand the nature of support vector machines. Since the basic idea of CKDMA is to express the CDMA in kernel-induced feature space, it can be implemented in a similar way to KSK and NPA, but different from LIBSVM. Experimental results show that the CKDMA is very competitive with NPA, KSK and LIBSVM2.9 on the selected data sets. As future work, we would try to introduce large margin clustering [24] for rapid generation of supports vectors.