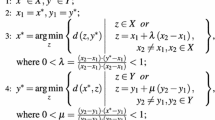Learning Distance Metric for Support Vector Machine: A Multiple Kernel Learning Approach

Abstract

Recent work in distance metric learning has significantly improved the performance in k-nearest neighbor classification. However, the learned metric with these methods cannot adapt to the support vector machines (SVM), which are amongst the most popular classification algorithms using distance metrics to compare samples. In order to investigate the possibility to develop a novel model for joint learning distance metric and kernel classifier, in this paper, we provide a new parameterization scheme for incorporating the squared Mahalanobis distance into the Gaussian RBF kernel, and formulate kernel learning into a generalized multiple kernel learning framework, gearing towards SVM classification. We demonstrate the effectiveness of the proposed algorithm on the UCI machine learning datasets of varying sizes and difficulties and two real-world datasets. Experimental results show that the proposed model achieves competitive classification accuracies and comparable execution time by using spectral projected gradient descent optimizer compared with state-of-the-art methods.

1 Introduction

Metric learning, aiming at learning an appropriate distance metric that better represents the distance between data points, which pulls the semantically similar ones closer and pushes dissimilar ones farther away, plays an important role in many machine learning and pattern recognition algorithms [4, 13, 19, 21, 38, 50]. Traditional uniformed norms, such as Euclidean distance, tend to ignore the awareness of semantic definition encoded by sample labels in supervised learning, and fail to highlight the discriminative features in varying applications. As a generalized version of Euclidean distance, Mahalanobis distance can be seen as performing a linear projection of the data points firstly and then computing the Euclidean distance in the projected space. Recent years, a surge of innovation on learning the pseudo-metric towards Mahalanobis distance has been raising. Due to the learned distance reflecting the label information, mainstream Mahalanobis distance metric learning methods are usually geared towards k-nearest neighbor (kNN) classifiers, e.g., Large Margin Nearest Neighbor (LMNN) proposed by Weinberger et al. [44], Large Margin Component Analysis (LMCA) proposed by Torresani et al. [37], and Information-Theoretic Metric Learning (ITML) proposed by Davis et al. [7]. Except for methods that are specific to k-nearest neighbors and based on Mahalanobis distance, there are some recent methods that focus on the sparse metric learning, non-linear metric learning, and regularized metric learning [5, 16, 23, 27, 30, 43, 51, 53].

Support Vector Machines (SVMs) are also amongst the most popular classifiers for various pattern recognition problems. They have been widely used not only because of their excellent predictive performance but also because of their generalization ability supported by the solid generalization error bounds defined over maximum margin philosophy. More importantly, the kernel-trick [33] allows SVM to generate higher dimensional non-linear decision boundaries with low computational burden. In order to leverage the progress on metric learning, Nguyen et al. [31] formulated the problem as a quadratic semi-definite programming problem (QSDP) with local neighborhood constraints, which is based on the SVM framework. The proposed method called MLSVM outperforms the raw kNN classifier and metric learning methods based on kNN. Xu et al. [48] investigated the efficacy of three of the most popular Mahalanobis metric learning algorithms, Neighborhood Component Analysis (NCA) [17], LMNN [44] and ITML [7], as pre-processing for SVM training and found that none of them generated metrics particularly suitable for SVM classification. To solve this problem, they incorporated the distance metric learning idea into a single kernel learning framework, and proposed an efficient kernel classifier, Support Vector Metric Learning (SVML). Instead of modeling a particular distance metric, the decomposition of squared Mahalanobis distance, i.e., ${\mathbf {M}} = {\mathbf {L}}^{{T}}{\mathbf {L}}$, was learnt for SVM classification with a single kernel learning manner, which incorporated the squared Mahalanobis distance into the RBF kernel function and iteratively optimized ${\mathbf {L}}$ via off-the-shelf SVM tools.

Many efforts have been devoted to designing kernel learning algorithms. Among them, Multiple Kernel Learning (MKL) has been considered as an effective and efficient way to achieve this goal [2, 3, 6, 24, 25, 32, 35, 40, 46], where the optimal kernel is modeled as a linear combination of a set of basis kernels. MKL based SVM methods have been used to solve kinds of classification tasks in the last decades [20, 36, 45, 52]. Lanckriet et al. [25] formulated MKL as a quadratically constrained quadratic programming problem, using a $\ell _{1}$-norm constraint to promote sparse combinations. Considering that the model in [25] is non-smooth, Bach et al. [3] proposed a smoothed version and proposed a SMO-like algorithm for solving the problem. Sonnenburg et al. [35] reformulated the problem as a semi-infinite linear program and addressed the problem by iteratively solving a classical SVM problem. Rakotomamonjy et al.  [32] further developed a SimpleMKL algorithm, and demonstrated that the training time could be further reduced by nearly an order of magnitude on some standard UCI datasets when the number of kernels was large. To further improve the representative ability of combined multiple kernels, non-linear combinations of kernels have been recently considered. Varma et al.  [40] developed the Generalized Multiple Kernel Learning (GMKL) formulation, which allowed fairly general kernel parameterization, including both linear and non-linear kernel combinations, together with general regularizations on the kernel parameters. Hirarchical multiple kernel learning [2] learned a linear combination of an exponential number of linear kernels and represented them as a product of sums, classified to a non-linear kernels combination. In [6] Cortes et al. analyze non-linear combination in the case of regression and the kernel ridge regression algorithm, making improvement for regression problem in high dimensions. Besides, to allow for robust kernel mixtures Kloft et al. [24] extended MKL to arbitrary norms, and Xu et al. [46] presented a soft margin perspective for MKL. Both of these two methods achieve an effective and sparse solution for MKL. Except for methods that focus on linear or non-linear mixture of basis kernels, efforts are made to other kinds of approaches to avoid searching for the optimal combination parameters directly. [18] proposed a methods to determine the kernels to be preserved and weighted according to the statistical significance. A radius-margin based MKL algorithm with monotone conjunctive kernels was proposed in [26]. [1] posed the problem of learning the kernel combination as a min–max problem solved by kernelized optimization of the margin distribution (KOMD) algorithm.

In this paper, we suggest a novel method to leverage the progress on multiple kernel learning and promote the classification performance of SVM from the viewpoint of metric learning, motivated by the superiority of SVML to representative metric learning methods such as ITML, NCA and LMNN. We formulate the Mahalanobis distance into the Gaussian RBF kernel, which behaves as the basis kernel inborn with the thinking of metric learning, and incorporate it into a GMKL framework. Benefitted from this formulation, we can adopt GMKL algorithm for joint learning distance metric and kernel classifier. While in the test stage we can utilize the composition of linear transformation and SVM for classification. The complexity of our model is independent with the number of basis kernels, and thus can avoid the computational burden issue of conventional MKL approach. Moreover, radius information is also incorporated as the supplement of considering the within-class distance of input data. Extensive experiments on UCI datasets and real world datasets classification clearly demonstrate the effectiveness of the proposed methods.

This algorithm, which we refer to as Metric Learning-based Multiple Kernel Classifiers (MLMKC), is particularly contributed to two aspects.

• First, by formulating the Mahalanobis distance into the Gaussian RBF kernel, which behaves as the basis kernel implanted within-class minimization via additional regularization inherited from Gaussian kernel, the involved kernel matrix can be obtained by computing the pairwise distance over given pairs of instances in the original feature space, instead of transforming to complicated high dimension feature spaces.

• Second, the learning of the distance metric kernel can be effortlessly incorporated into the Generalized MKL framework, and the flexibility of the selection of kernel size can tremendously reduce the computation overhead of whole MKL framework.

The remainder of this paper is organized as follows. We review the related work in Sect. 2. In Sect. 3, we formulate the Mahalanobis distance into the Gaussian RBF kernel and jointly learn the distance metric via GMKL framework for SVM-based classification. In Sect. 4, we evaluate the proposed algorithm on several benchmark datasets and two real-world datasets, and finally conclude this work in Sect. 5.

2 Related Work

Consider a binary classification problem in which a training set of n samples is denoted by ${\mathcal {X}}=\{({\mathbf {x}}_{i},y_{i})_{i=1}^{n}\}$, where ${\mathbf {x}}_{i}\in {\mathbb {R}}^{d}$ denotes the ith training sample, $y_{i}\in \{+1,-1\}$ denotes the class label of ${\mathbf {x}}_{i}$. SVMs learn a hyperplane $H_{{\mathbf {w}}}:{\mathbf {w}}^{T}{\mathbf {x}} + b = 0$ which maximizes the margin between the two classes. The conventional SVM model can be formulated as:

$$\begin{aligned} \begin{aligned} \min \limits _{{\mathbf {w}},b,{\xi }} \quad&\frac{1}{2}\left\| {\mathbf {w}} \right\| _{2}^{2}+C\sum \nolimits _{i}{{{\xi }_{i}}}, \\ s.t. \quad&{{y}_{i}}({{{\mathbf {w}}}^{T}}{{{\mathbf {x}}}_{i}}+b)\ge 1-{{\xi }_{i}}, \quad \forall i \end{aligned} \end{aligned}$$

(1)

where ${\xi }$ denotes the slack variable.

The performance of kernel based SVM strongly depends on the choice of kernels. A common approach developed to find the appropriate kernel function and parameters for heterogeneous data of varying applications is called MKL, where each kernel encodes a different modality of data. The same technique is suggested by other methods, e.g., dictionary learning [9], hashing based coding [10] and quantization based coding [49] in similarity search. Let $\varphi _{p}:{\mathbb {R}}^{d}\rightarrow {\mathcal {H}}_{p}$ be the pth feature mapping, inducing the corresponding basis kernel $K_{p}(\cdot ,\cdot )$ in the Hilbert space ${\mathcal {H}}_{p}$, where $p=1,\ldots ,m$. In the MKL framework based on SVM, each sample ${\mathbf {x}}$ is mapped onto m feature spaces by $\varphi ({\mathbf {x}};\varvec{\gamma })=[\sqrt{\gamma _{1}}\varphi _{1}({\mathbf {x}}),\ldots ,\sqrt{\gamma _{m}}\varphi _{m}({\mathbf {x}})]^{T}$, where $\gamma _{p}$ is the weight of the pth basis kernel. Therefore, the employed kernel can be expressed as a linear or nonlinear combination of the basis kernels, expressed as $K(\cdot ,\cdot ;\varvec{\gamma })=\sum _{p=1}^{m}\gamma _{p}K_{p}(\cdot ,\cdot )$ or $K(\cdot ,\cdot ;\varvec{\gamma })=\prod _{p=1}^{m}(K_{p}(\cdot ,\cdot ))^{\gamma _{p}}$, the formulation of which depends on the needs of different applications. To seek the optimal combination weight for each basis kernel, most MKL approaches [32, 35, 47] are suggested to solve the following objective function:

$$\begin{aligned} \begin{aligned} \min \limits _{{\mathbf {w}},b,{\xi }} \quad&\frac{1}{2}\left\| {\mathbf {w}} \right\| _{2}^{2}+C\sum \nolimits _{i}{{{\xi }_{i}}}, \\ s.t. \quad&{{y}_{i}}({{{\mathbf {w}}}^{T}}{\varphi ({{\mathbf {x}}}_{i};\varvec{\gamma }})+b)\ge 1-{{\xi }_{i}}, \quad \forall i, \\ \quad&{{\xi }_{i}} \ge 0, i=1,2,\cdots ,n, \Vert \varvec{\gamma }\Vert _{1}=1,\varvec{\gamma } \succ 0, \end{aligned} \end{aligned}$$

(2)

where ${\mathbf {w}}$ is the normal of the separating hyperplane, b is the bias term, $\xi$ is the slack variable introduced to address the linearly non-separable problem.

Some studies have been given to introduce multiple kernels into metric learning problems. Wang et al. [42] learned a distance metric in the weighted linear combinations of feature spaces by exploring the potential correlations between different kernels, the formulation of which can be seen as learning a projection from the weighted combination of mapped feature space to an embedding space. Rather than projecting to the single embedding space kernelized by the weighted combination of multiple basis feature mappings, McFee et al. [29] defined the embedding as the concatenation of different projections, allowing the algorithm to learn an ensemble of projections tailored to its corresponding domain space and jointly optimized to produce an optimal space. By restricting each projection weight matrix to be diagonal, literature [29] implicitly weighted the contribution of each kernel with respect to corresponding training point in construction of the embedding. It is claimed that the weighted combination kernels embedding formulation is much less flexible than the concatenated projection embedding formulation, as the former applies the same projection to each feature space. As a weighted version of [29], Lu et al.  [28] introduced weights to the unweighted concatenated projection formulation by jointly learning multiple metrics and weights via SVM-based SimpleMKL framework. However, the learned metrics and their corresponding weights are finally exported to a kNN classifier, which is still enduring the deficiency of having to store the entire training set during the test stage. Although the literature did not provide the results of training time, the huge computation burden can be expected.

Under the scenarios that the radius of the smallest data enclosing sphere is no longer fixed, optimizing over both the margin and the radius in an SVM-based problem can be expected to achieve a tighter generalization error bound. However, optimizing over both of them poses several difficulties since the radius is computed in a complex form [15]. Do et al. [12] proposed $\varvec{\varepsilon }$-SVM, which in addition to the margin maximization also minimized the within-class distance through the sum of the instance distances from the margin hyperplane. Except providing the interpretation that LMNN can be seen as a set of local related $\varvec{\varepsilon }$-SVMs in the quadratic space, their experimental results also demonstrated that $\varvec{\varepsilon }$-SVM performed much more pronounced in case of using Gaussian kernel, which could be attributed to its additional regularization on the within-class distance which makes it more appropriate for high dimensional spaces.

Instead of using the ratio, Do et al. [11] proved that the sum of the radius and the inverse of the margin can achieve the same optimal solution under proper parameter choices. Their R-SVM$_{\varvec{\mu }}^{+}$ is formulated as:

$$\begin{aligned} \begin{aligned} \min \limits _ {{\mathbf {w}},b,\varvec{\mu },R_{\varvec{\mu }},x_{0}} \quad&\frac{1}{2}\Vert {\mathbf {w}}\Vert ^{2}+\lambda {R_{\varvec{\mu }}^{2}}+C\sum _{i=1}^{n}{{{\xi }_{i}}},\\ s.t. \quad&{{y}_{i}}(\langle {{\mathbf {w}}},{D_{\sqrt{\varvec{\mu }}}{\mathbf {x}}}_{i}\rangle +b)\ge 1-{{\xi }_{i}}, \quad \forall i,i=1,2,\cdots ,n,\\ \quad&\sum _{k=1}^{d}{\mu _{k}}=1,\varvec{\mu },\varvec{\xi }\ge 0, \\ \quad&\Vert D_{\sqrt{\varvec{\mu }}}{\mathbf {x}}_{i}-D_{\sqrt{\varvec{\mu }}}{\mathbf {x}}_{0}\Vert \le R_{\varvec{\mu }}^{2}, \quad \forall i, \end{aligned} \end{aligned}$$

(3)

where $\sqrt{\varvec{\mu }}$ is a vector scaling the transformed feature space; $D_{\sqrt{\varvec{\mu }}}$ is a diagonal linear transformation matrix, whose diagonal elements are given by $\sqrt{\varvec{\mu }}$, thus $D_{\sqrt{\varvec{\mu }}}{\mathbf {x}}$ gives the image of an instance ${\mathbf {x}}$ in the transformed feature space; $R_{\varvec{\mu }}$ denotes the radius of the scaled feature space. Their optimization problem solves SVM from the viewpoint of metric learning, and approximated the radius of the smallest sphere enclosing the data by the maximum pairwise distance over all pairs of instances in the transformed feature space, which may result in very inefficient to solve large-scale problems.

3 Multiple Kernel Classifiers Based on Metric Learning

In this section, by extending Gaussian RBF kernel, we formulate the joint distance metric and kernel classifier learning problem into the Generalized MKL (GMKL) framework. We then present the learning algorithm for solving the proposed model, and radius information is further incorporated to impose the regularization on minimizing the enclosing ball of data in the feature space endowed with the learned kernel.

3.1 Extension of Gaussian RBF Kernel

Gaussian Radial Basis Function (RBF) kernel is a kernel function which has been widely adopted in various kernel methods. Given two samples ${\mathbf {x}}$ and ${\mathbf {y}}$, the Gaussian RBF kernel is defined as

$$\begin{aligned} \begin{aligned} K({\mathbf {x}},{\mathbf {y}})=\exp {\biggl (-\frac{\Vert {\mathbf {x}}-{\mathbf {y}}\Vert _{2}^{2}}{\sigma ^{2}}\biggr )}=\exp (-d_{\sigma }^{2}({\mathbf {x}},{\mathbf {y}})), \end{aligned} \end{aligned}$$

(4)

where $d_{\sigma }^{2}({\mathbf {x}},{\mathbf {y}})={\Vert {\mathbf {x}}-{\mathbf {y}}\Vert _{2}^{2}}/{\sigma ^{2}}$ can be explained as a scaled version of squared Euclidean distance. Here we further extend Gaussian RBF kernel by replacing the scaled Euclidean distance $d_{\sigma }({\mathbf {x}},{\mathbf {y}})$ with the Mahalanobis distance,

$$\begin{aligned} \begin{aligned} {d}_{\mathbf {M}}^{2}({\mathbf {x}},{\mathbf {y}})={({\mathbf {x}} -{\mathbf {y}})^{T}{\mathbf {M}}({\mathbf {x}}-{\mathbf {y}})}, \end{aligned} \end{aligned}$$

(5)

where the matrix ${\mathbf {M}}\in {\mathcal {R}}^{d\times d}$ is semi-positive definite. The resulting extended kernel function is then defined as follows:

$$\begin{aligned} \begin{aligned} K_{{\mathbf {M}}}({\mathbf {x}},{\mathbf {y}})=\exp {(-{d}_{{\mathbf {M}}}^{2} ({\mathbf {x}},{\mathbf {y}}))}=\exp (-({\mathbf {x}} -{\mathbf {y}})^{T}{\mathbf {M}}({\mathbf {x}}-{\mathbf {y}})) \end{aligned}, \end{aligned}$$

(6)

It is easy to see that $K_{{\mathbf {M}}}({\mathbf {x}},{\mathbf {y}})$ is a kernel function and satisfies the Mercer condition [34].

Rather than directly learning ${\mathbf {M}}$, Xu et al.  [48] parameterized ${\mathbf {M}}={\mathbf {L}}^{T}{\mathbf {L}}$, and suggested a gradient descent algorithm with respect to ${\mathbf {L}}$, which is incorporated into a single RBF kernel. Inspired by the metric learning with multiple kernel embedding proposed by Lu et al.  [28] and Doublet-SVM metric learning methods proposed by Wang et al. [41], we parameterize ${\mathbf {M}}$ as,

$$\begin{aligned} \begin{aligned} {\mathbf {M}} =&\sum _{l=1}^{{N}_{k}}{\beta _{l}({\mathbf {x}}_{l,1} -{\mathbf {x}}_{l,2})({\mathbf {x}}_{l,1}-{\mathbf {x}}_{l,2})^{T}} +\lambda _{G}{\mathbf {I}}\\ =&\sum _{l=1}^{{N}_{k}}{\beta _{l}{\mathbf {X}}_{l}}+\lambda _{G}{\mathbf {I}},\beta _{l}\ge 0,\lambda _{G}>0 \end{aligned} , \end{aligned}$$

(7)

where ${\mathbf {X}}_{l} = ({\mathbf {x}}_{l,1}-{\mathbf {x}}_{l,2})({\mathbf {x}}_{l,1}-{\mathbf {x}}_{l,2})^{T}$, $\beta _{l}$ is the weight describing the contribution of the sample pair $({\mathbf {x}}_{l,1},{\mathbf {x}}_{l,2})$ to make up the matrix ${\mathbf {M}}$. When all of $\beta _{l}=0$, $K_{{\mathbf {M}}}({\mathbf {x}},{\mathbf {y}})$ is identical to a standard Gaussian RBF kernel. With Eq. (6), the kernel can be reformulated as:

$$\begin{aligned} \begin{aligned} {K}_{{\mathbf {M}}}({\mathbf {x}},{\mathbf {y}};\varvec{\beta })&=\exp (-({\mathbf {x}} -{\mathbf {y}})^{T}\left( \sum _{l=1}^{N_{k}}\beta _{l}{\mathbf {X}}_{l} +\lambda _{G}{\mathbf {I}}\right) ({\mathbf {x}}-{\mathbf {y}}))\\&={K}_{\lambda _{G}}\prod _{l=1}^{N_{K}}(\exp (-({\mathbf {x}} -{\mathbf {y}})^{T}{\mathbf {X}}_{l}({\mathbf {x}}-{\mathbf {y}})))^{\beta _{l}} \\&={K}_{\lambda _{G}}\prod _{l=1}^{N_{K}}(K_{l}({\mathbf {x}},{\mathbf {y}}))^{\beta _{l}} \end{aligned} . \end{aligned}$$

(8)

When fixing $\lambda _{G}$, the latter denoted by $K_{\lambda _{G}}=\exp (-\lambda _{G}({\mathbf {x}}-{\mathbf {y}})^{T}({\mathbf {x}}-{\mathbf {y}}))$ can be treated as a constant. By defining the basis kernel $K_{l}=\exp (-({\mathbf {x}}-{\mathbf {y}})^{T}{\mathbf {X}}_{l}({\mathbf {x}}-{\mathbf {y}}))$, the kernel function in Eq. (8) can also be explained from the multiple kernel perspective. If we take all the sample pairs into account, the number of basis kernels is $N_{k} = n(n-1)/2$, which will be too huge for large scale dataset. To address this, one can adopt the following strategies to reduce $N_{k}$: (i) We can refer to the metric learning methods [41] by only using the nearest similar pairs and the nearest dissimilar pairs to construct the set of basis kernels. (ii) After selecting pairs based on (i), some clustering methods (e.g., k-means) can be adopted to further reduce the number of pairs for constructing basis kernels.

3.2 Formulation of Metric Learning-Based Multiple Kernel Classifier

Denote by $\varphi _{\mathbf {M}}({\mathbf {x}};\varvec{\beta })$ the feature mapping associated with the kernel function ${\mathbf {K}}_{\mathbf {M}}({\mathbf {x}},y;\varvec{\beta })$. Our objective is to learn a function of the form $f({\mathbf {x}})={\mathbf {w}}^{T}\varphi _{{\mathbf {M}}}({\mathbf {x}}_{i};\varvec{\beta })+b$. Given $\varphi _{\mathbf {M}}({\mathbf {x}};\varvec{\beta })$, one can adopt the SVM solver to learn the global optimal values of (${\mathbf {w}}$, b) from the training data $\{({\mathbf {x}}_{i},y_{i})_{i=1}^{n}\}$. If we want to jointly learn $\varvec{\beta }$ and (${\mathbf {w}}$, b), we should consider the MKL framework. Therefore, we adopt the GMKL formulation in [40],

$$\begin{aligned} \begin{aligned} \min \limits _{{\mathbf {w}},b,\varvec{\beta }} \quad&\frac{1}{2}{\mathbf {w}}^{t}{\mathbf {w}} +\sum _{i}l(y_{i},f({\mathbf {x}}_{i}))+r(\varvec{\beta })\\ s.t. \quad&\varvec{\beta }\ge 0. \end{aligned} , \end{aligned}$$

(9)

where both the regularizer $r(\varvec{\beta })$ and the kernel should be differentiable with respect to $\varvec{\beta }$, and $l(\cdot )$ could be some loss functions, e.g., hinge loss and logistic loss.

In order to learn the classifier and the Mahalanobis distance metric jointly, we formulate the problem as:

$$\begin{aligned} \begin{aligned} \{{\mathbf {w}},b,{\mathbf {M}},\varvec{\beta }\}=&\,\,\arg \min \limits _{{\mathbf {w}},b,{\mathbf {M}}} \frac{1}{2}\left\| {\mathbf {w}} \right\| _{2}^{2} +C\sum \nolimits _{i}{{{\xi }_{i}}}+\lambda r(\varvec{\beta }),\\ s.t. \quad&{{y}_{i}}(\langle {{\mathbf {w}}}, \varphi _{\mathbf {M}}({\mathbf {x}}_{i};\varvec{\beta })\rangle +b)\ge 1-{{\xi }_{i}}, \\&\quad \varvec{\beta } \ge 0,\xi _{i} \ge 0,\quad \forall i, \end{aligned} \end{aligned}$$

(10)

Reformulating above primal as a nested two step optimization, the kernel is learned by optimizing over $\varvec{\beta }$ in the outer loop, while the kernel is fixed and the SVM parameters are learnt in the inner loop. This can be achieved by rewriting the primal as follows:

$$\begin{aligned} \begin{aligned} \min \limits _{\varvec{\beta }} J(\varvec{\beta }), s.t.\ \ \beta _{l}\ge 0, \end{aligned} \end{aligned}$$

(11)

with

$$\begin{aligned} \begin{aligned} J(\varvec{\beta }) =&\max {\mathbf {1}}^{T}\varvec{\alpha }-\frac{1}{2} \varvec{\alpha }^{T}{\mathbf {Y}}{\mathbf {K}}_{\mathbf {M}} (\varvec{\beta }){\mathbf {Y}}\varvec{\alpha }+\lambda r(\varvec{\beta }),\\&\quad s.t.~ {\mathbf {1}}^{T}\mathbf {{Y}\varvec{\alpha }}=0,0\le \varvec{\alpha }\le C, \end{aligned} \end{aligned}$$

where ${\mathbf {Y}}$ is a diagonal matrix with the labels on the diagonal, $\lambda$ is a tradeoff to balance the regularization part. As to $r(\varvec{\beta })$, its derivative should exist and be continuous. For example, the non-negative $\ell _{1}$-norm regularization $r(\varvec{\beta })={\mathbf {1}}^{T}\varvec{\beta }$ could be used for learning sparse solutions, or the $\ell _{2}$-norm regularization $r(\varvec{\beta })=(\varvec{\beta }-\varvec{\mu })^{T}\varvec{\varSigma }^{-1}(\varvec{\beta }-\varvec{\mu })$ if prior knowledge is available. If $\nabla _{\varvec{\beta }}{\mathbf {K}}_{\mathbf {M}}$ and $\nabla _{\varvec{\beta }}r$ are differentiable functions of $\varvec{\beta }$, we can utilize gradient descent in the outer loop, and $J(\varvec{\beta })$ has derivatives given by

$$\begin{aligned} \begin{aligned} \frac{\partial J}{\partial \beta _{l}}=\lambda \frac{\partial r}{\partial \beta _{l}}-\frac{1}{2}\varvec{\alpha }^{*T} \frac{\partial {\mathbf {Y}}{\mathbf {K}}_{\mathbf {M}}{\mathbf {Y}}}{\partial \beta _{l}}\varvec{\alpha }^{*} \end{aligned}, \end{aligned}$$

(12)

In order to take a gradient step, in the inner loop, all we need to do is to obtain $\varvec{\alpha }^{*}$, which can be solved by any off-the-shelf SVM optimization package. To solve the non-convex formulation results from regularizing $\varvec{\beta }$, the spectral projected gradient (SPG) descent optimizer [22] can be adopted to update it. SPG iteratively approximates the objective function with a quadratic model and then optimizes the model at each iteration, which includes spectral step length and spectral projected gradient computation, the non-monotone line search and the SVM solver precision tuning. The proposed MLMKC algorithm is summarized in $\mathbf {Algorithm~1}$. From $\mathbf {Algorithm~1}$, we can see that the projection operator needs to be applied only once per iteration without the step variable, for which SPG employs a non-monotone line search criterion instead of the Armijo rule. The tolerance of the SVM solver automatically decreases as moving closer to the optimum or the step size becoming too small. These guarantee the robustness to imprecisions in calculating the objective function and the gradient, and reduce the number of SVM evaluations. The duality gap is used as a stable stopping criterion for SPG, or the projected gradient if the duality gap is unavailable.

Therefore, after we obtain the optimal $\varvec{\alpha }^{*}$, $b^{*}$ and $\varvec{\beta }$, we can write the SVM decision function as:

$$\begin{aligned} \begin{aligned} f\left( {\mathbf {x}}\right) =&\text{ sgn }\left( \sum _{i=1}^{n}{\alpha _{i}^{*}}{y_{i}}{{\mathbf {K}}_{{\mathbf {M}}}}\left( {\mathbf {x}}_{i},{\mathbf {x}};\varvec{\beta }\right) +b^{*}\right) \\ =&\text{ sgn }\left( \sum _{i=1}^{n}{\alpha _{i}^{*}}{y_{i}} \left( K_{\lambda _{G}}\prod _{l=1}^{N_{k}}\left( K_{l}\left( {\mathbf {x}}_{i}, {\mathbf {x}}\right) \right) ^{\beta _{l}}\right) +b^{*}\right) \end{aligned} . \end{aligned}$$

(13)

3.3 Computational Complexity

As illustrated in $\mathbf {Algorithm~1}$, for each training sample, $n_{1}$ similar nearest neighbors and $n_{2}$ dissimilar nearest neighbors are chosen to construct $n_{1}+n_{2}$ doublets, and in total $N(n_{1}+n_{2})$ doublets. After computing the difference of these doublets, we use k-means to find $N_{k}$ cluster centers to construct the distance matrix $\mathbf {M}$ as Eq. (7), of which the computational complexity is $O(N(n_{1}+n_{2})d)+O(N_{k}N(n_{1}+n_{2}))+O((n_{1}+n_{2})d^{2})$, where d is the dimension of the data feature. In Sect. 4 we will show that we can choose $n_{1}, n_{2}, N_{k}\ll N$ in practice, and thus, the computational cost can be reduced to $O(Nd)+O(N)+O(d^{2})$. According to Eq. (8), the computational cost of computing the kernels $K_\mathbf{{M}}$ is $O(N_{k}N^{2}d)$. For solving the alternating subproblem, the LibSVM library for SVM training is utilized, and the computational complexity of SMO-type algorithms is $O(N_{k}^{2}N^{2}d)$.

3.4 Incorporating the Radius Information

Although the Gaussian kernel implicitly imposed the regularization on minimizing the within class distance, considering the fact that the generation error of SVM is actually a function of the ratio of radius and margin [39], especially for joint learning of kernels for feature transformation and classifier, the radius information should be valuable to improve the performance of the algorithm. Due to the close relationship with the radius of minimum enclosing ball, instead of incorporating the radius directly, the trace of the total scattering matrix of training data is integrated into the proposed MLMKC framework, with the manner of summation rather than ratio as proposed in [11]. Therefore, the proposed model can be reformulated as

$$\begin{aligned} \begin{aligned} \{{\mathbf {w}},b,{\mathbf {M}},\varvec{\beta }\}=&\arg \min \limits _{{\mathbf {w}},b, {\mathbf {M}}}\frac{1}{2}\left\| {\mathbf {w}} \right\| _{2}^{2} +\rho \mathrm {tr}({\mathbf {S}}_{T}^{\varvec{\beta }})+C\sum \nolimits _{i}{{{\xi }_{i}}} +\lambda r(\varvec{\beta })\\ s.t. \quad&{{y}_{i}}(\langle {{\mathbf {w}}}, \varphi _{{\mathbf {M}}}({\mathbf {x}}_{i};\varvec{\beta })\rangle +b)\ge 1-{{\xi }_{i}}, \\ \quad&\varvec{\beta } \ge 0,\xi _{i} \ge 0,\quad \forall i, \end{aligned} \end{aligned}$$

(14)

Thus the corresponding dual problem changes to

$$\begin{aligned} \begin{aligned}&\min \limits _{\varvec{\beta }} J(\varvec{\beta }), \ \ s.t. \ \ \beta _{l}\ge 0 \\&\quad J(\varvec{\beta }) = \max {\mathbf {1}}^{T}\varvec{\alpha } -\frac{1}{2}\varvec{\alpha }^{T}{\mathbf {Y}}{\mathbf {K}}_{\mathbf {M}} (\varvec{\beta }){\mathbf {Y}}\varvec{\alpha }+\rho \mathrm {tr}({\mathbf {S}}_{T}^{\varvec{\beta }}) +{\lambda } r(\varvec{\beta })\\&\quad s.t. \ \ {\mathbf {1}}^{T}{\mathbf {Y}}\varvec{\alpha }=0,0\le \varvec{\alpha }\le C \end{aligned} , \end{aligned}$$

(15)

where $\mathrm {tr}({\mathbf {S}}_{T}^{\varvec{\beta }})$ denotes the trace of the total scatter matrix in feature space mapped via ${\mathbf {K}}_{\mathbf {M}}(\varvec{\beta })$, which can be explicitly expressed in the kernel-induced feature space as

$$\begin{aligned} \begin{aligned} \mathrm {tr}({\mathbf {S}}_{T}^{\varvec{\beta }})=\mathrm {tr}({\mathbf {K}}_{\mathbf {M}} (\varvec{\beta }))-\frac{1}{n}{\mathbf {1}}^{T}{\mathbf {K}}_{\mathbf {M}}(\varvec{\beta }) {\mathbf {1}}=\prod _{l=1}^{N_{k}}\alpha _{l}^{\beta _{l}} \end{aligned}, \end{aligned}$$

(16)

where $a_{l}\triangleq \mathrm {tr}({\mathbf {K}}_{l})-(1/n){\mathbf {1}}^{T}{\mathbf {K}}_{l}{\mathbf {1}}$, and ${\mathbf {K}}_{\mathbf {M}}(\varvec{\beta })$ is the kernel matrix formulated in Eq. (8) which can be obtained by computing the pairwise distance over all pairs or given pairs of instances in the original feature space on training set ${\mathcal {X}}$. After incorporating the radius term, the derivatives of $J(\varvec{\beta })$ in $\mathbf {Algorithm~1}$ becomes

$$\begin{aligned} \begin{aligned} \frac{\partial J}{\partial \beta _{l}}=\lambda \frac{\partial r}{\partial \beta _{l}}-\frac{1}{2}\varvec{\alpha }^{*T}\frac{\partial {\mathbf {Y}}{\mathbf {K}}_{{\mathbf {M}}}{\mathbf {Y}}}{\partial \beta _{l}}\varvec{\alpha }^{*}+\rho \frac{\partial \mathrm {tr} ({\mathbf {S}}_{T}^{\varvec{\beta }})}{\partial {\beta }_{l}} \end{aligned}, \end{aligned}$$

(17)

4 Experiments and Discussion

In this section, we first discuss the setting for $\lambda _{G}$ and $N_{k}$ in Eq. (8). Then we evaluate the proposed MLMKC algorithm using synthetic datasets with two classes whose distribution is nonlinear separable. After that, eleven datasets from UCI Machine Learning repository [14] of varying size, dimensionality and task description are used to evaluate the performance of our method and the state-of-the-art: Australian Credit Approval (ACA), Contraceptive Method Choice (CMC), Mammographic Mass (Mammo), Musk, Ionosphere (Iono), Heart, Sonar, Pima, Vote, Wpbc, and Liver. The dataset statistics are shown in Table 1. We compare the proposed methods with SVML, GMKL and other representative multiple kernel learning methods, i.e., SimpleMKL, RMKL, $\ell _{p}$-MKL, SM1MKL, EasyMKL and RM-GD in terms of classification accuracy and training time, for the reason that we incorporated distance metric into the multiple kernel learning framework. All the experiments on UCI datasets use the following setting: for each dataset, 80$\%$ of the data is used for training and the rest is used for test. All data sets have been normalized to have zero mean and unit variance on each feature. Apart from the UCI datasets, we also perform experiments on the large scale multiclass real-world datasets, i.e., handwritten digit set USPS dataset¹ and object classification set COIL20 dataset.² We use the defined training set to train the models using a 1-vs-rest strategy and calculate the classification error rates on the test set. As the dimensions of these two datasets are relatively high, PCA is utilized to reduce the feature dimension. Table 2 summarizes the basic information of the large scale real-world datasets.

Table 1 The UCI datasets used in experiments

Table 2 The real-world datasets used in experiments

We use libSVM³ to solve the SVM dual problem of our method and the parameter C is chosen from $\{0.1,1,10,10^2\}$. The regularization parameter $\lambda$ and $\rho$ are chosen from $\{1,10^2,10^3,10^4\}$, and the width $\sigma ^2$ of Gaussian kernel is settled as 1. As MLMKC is not particularly sensitive to the exact choice of $\lambda$ (i.e., the regularization parameter in Eq. (15)) when $\lambda >10^2$, and during the experiments we also find that for better results $\lambda$ and $\rho$ is often set to $10^2$, so we set them all for default. All the experiments are executed in a PC with 4 Intel Core Xeon E3-1230 V2 CPUs (3.3 GHz) and 32GB RAM.

4.1 Parameter Selection

4.1.1 A Reduced Version of MLMKC

Except for several aforementioned standard parameters, the two parameters involved in Eq. (8), i.e., $\lambda _{G}$ and $N_{k}$, tightly correlate to the classification performance of the proposed model. Here we introduce a reduced version of MLMKC by setting $\lambda _{G} = 0$, represented as R-MLMKC, the kernel of which is formulated as:

$$\begin{aligned} \begin{aligned} {K}_{{\mathbf {M}}^-}({\mathbf {x}},{\mathbf {y}};\varvec{\beta })&=\prod _{l=1}^{N_{k}}\exp (-({\mathbf {x}}-{\mathbf {y}})^{T}\beta _{l}{\mathbf {X}}_{l}({\mathbf {x}}-{\mathbf {y}})) \\&=\prod _{l=1}^{N_{k}}(\exp (-({\mathbf {x}}-{\mathbf {y}})^{T}{\mathbf {X}}_{l}({\mathbf {x}}-{\mathbf {y}})))^{\beta _{l}} \\&=\prod _{l=1}^{N_{k}}(K_{l}({\mathbf {x}},{\mathbf {y}}))^{\beta _{l}} \end{aligned} . \end{aligned}$$

(18)

${\mathbf {M}}^-$ is formulated as ${\mathbf {M}}^- = \sum _{l=1}^{{N}_{k}}{\beta _{l}({\mathbf {x}}_{l,1}-{\mathbf {x}}_{l,2})({\mathbf {x}}_{l,1}-{\mathbf {x}}_{l,2})^{T}}= \sum _{l=1}^{{N}_{k}}\beta _{l}{\mathbf {X}}_{l}$. We use this formulation to get rid of the consideration on parameter $\lambda _{G}$, and try to verify the effective working range of $N_{k}$.

Fig. 1

Classification accuracy using R-MLMKC against different number of basis kernels $N_{k}$ on three UCI datasets

In process of choosing sample pairs to construct the matrix ${\mathbf {M}}^-$, instead of using all pairs of training samples, for each training sample ${\mathbf {x}}_{i}$, we construct $n_{1}+n_{2}$ doublets $({\mathbf {x}}_{i},{\mathbf {x}}_{i,1}^{s})$,...,$({\mathbf {x}}_{i},{\mathbf {x}}_{i,n_{1}}^{s})$, $({\mathbf {x}}_{i},{\mathbf {x}}_{i,1}^{d})$,...,$({\mathbf {x}}_{i},{\mathbf {x}}_{i,n_{2}}^{d})$, where ${\mathbf {x}}_{i,k}^{s}$ denotes the kth similar nearest neighbor of ${\mathbf {x}}_{i}$, and ${\mathbf {x}}_{i,k}^{d}$ denotes the kth dissimilar nearest neighbor of ${\mathbf {x}}_{i}$. After that we compute the difference of these doublets and use k-means to find cluster centers, whose number equals to the predefined kernel size. And then we use the cluster centers to get ${\mathbf {X}}_{l}$. We initialize the R-MLMKC with different numbers of kernel size, ranging from 4 to 40, and set $n_{1} = n_{2} = 2$. We choose three UCI datasets, whose feature dimensions are of different magnitude, to test the influence on the classification accuracy when varying the size of kernel. The curves of classification accuracy versus kernel size for R-MLMKC are shown in Fig. 1. One can see that, the accuracy tends to be stable when $N_{k}\ge 20$ on all three datasets. When $\lambda _{G}>0$, we choose $4 \le N_{k}\le 20$ in experiment. If the accuracy is not very insensitive to $N_{k}$ we can choose a small number of kernels instead which can dramatically reduce the computational cost. Experiment on larger number of $N_{k}$ is needed when choosing the best size of basis kernels for large datasets, and the upper bound is decided by the execution time and memory. In Sect. 4.1.2, we will give a detailed discussion to the selection of $\lambda _{G}$ and $N_{k}$.

Fig. 2

Classification accuracy against $\lambda _{G}$ under four circumstances of different $N_{k}$ settings on different UCI datasets: a sonar, b heart, c Wpbc, and d vote

4.1.2 Selection for $\lambda _{G}$ and $N_{k}$

We first discuss the setting for $\lambda _{G}$. Leveraging the results of the observation on selecting different kernel sizes for R-MLMKC, small kernel size, i.e., $N_{k}$, which is the summation of $n_{1}$, the number of similar pairs, and $n_{2}$, the number of dissimilar pairs, can be used to observe the variation on classification performance when changing the model with varying $\lambda _{G}$. We consider four circumstances of different $N_{k}$ settings: (1) constructing the matrix ${\mathbf {M}}$ with equal small number of similar and dissimilar pairs, e.g., $N_{k}=4$, $n_{1}=n_{2}=2$; (2) constructing the matrix ${\mathbf {M}}$ with equal larger number of similar and dissimilar pairs, e.g., $N_{k}=8$, $n_{1}=n_{2}=4$; (3) constructing the matrix ${\mathbf {M}}$ with small number of similar pairs and larger number of dissimilar pairs, e.g., $N_{k}=6$, $n_{1}=2$, $n_{2}=4$; (4) constructing the matrix ${\mathbf {M}}$ with larger number of similar pairs and small number of dissimilar pairs, e.g., $N_{k}=6$, $n_{1}=4$, $n_{2}=2$. Figure 2 shows the classification accuracy against $\lambda _{G}$ on different UCI datasets, from left to right are the accuracy curve on Sonar, Heart, Wpbc and Vote datasets, respectively, when $N_{k}$ using above settings. One can observe that, for all figures the classification accuracy declined after $\lambda _{G}>0.02$, and the setting of $N_{k}$, $n_{1}$ and $n_{2}$ seems no effect on the best choice of $\lambda _{G}$, so we choose $\lambda _{G}$ within the range of [0, 0.02].

Fig. 3

Classification accuracy versus $n_{1}$ and $n_{2}$. a Results on the Wpbc dataset with $\lambda _{G}=0.005$, b classification accuracy versus $n_{1}$ for $n_{2}=3$, c classification accuracy versus $n_{2}$ for $n_{1}=2$

Fig. 4

Classification accuracy versus $n_{1}$ and $n_{2}$ with fixed $\lambda _{G}$: a results on the Heart dataset with $\lambda _{G}=0.001$, b results on the Sonar dataset with $\lambda _{G}=0.01$, and c results on the Vote dataset with $\lambda _{G}=0.01$

To further validate the effective settings of $N_{k}$, $n_{1}$ and $n_{2}$, we fixed $\lambda _{G}$ to some value within the range of [0, 0.02]. Using Wpbc dataset as an example, we get the classification accuracy on each pair of $(n_{1},n_{2})$, where $n_{1},n_{2}\in \{1,2,3,4,5,6,7,8,9\}$ and $N_{k}$ is the sum of $n_{1}$ and $n_{2}$. Figure 3 shows the classification accuracy versus $n_{1}$ and $n_{2}$ when $\lambda _{G}=0.005$, we can find that the model can approach to the highest performance several times with different combination of $n_{1}$ and $n_{2}$ for different datasets. For example, as shown in Fig. 3b, c, the model can achieve the highest accuracy when $n_{2}=3$ and $n_{1}=2$. From Fig. 3c, we can observe that, when $n_{1}=2$ and $1\le n_{2}\le 5$ the model can achieve comparatively stable performance. The classification accuracy surface for other three different datasets are also illustrated in Fig. 4. From Figs. 3 and 4, we can see that generally, the model can achieve comparable performance by choosing small number of $n_{1}$ and $n_{2}$. Therefore, we choose $n_{1},n_{2}\in \{2,3\}$ to reduce the doublets used for k-means. Besides, it seems choosing significantly different number of similar pairs and dissimilar pairs of samples is not proper when the number of $N_{k}$ is settled, especially choosing more similar ones.

Fig. 5

Two dimensional synthetic dataset

4.2 Result on the Synthetic Data Set

Two synthetic datasets with two classes whose distribution is nonlinear separable were created to evaluate our method. For the 2-dimensional dataset, feature $x_{1}$ and $x_{2}$ are drawn from a normal distribution of ${\mathcal {N}}({\mu }_{1},{\mathbf {I}})$ and ${\mathcal {N}}(\mu _{2},{\mathbf {I}})$ with equal probability, where ${\mathbf {I}}$ is an identity matrix. When $y=-1$, $\mu _{1}=[-0.75,-3]^{\mathrm{T}}$ and $\mu _{2}=[0.75,3]^{\mathrm{T}}$. When $y=+1$, $\mu _{1}=[3,-3]^{\mathrm{T}}$ and $\mu _{2}=[-3,3]^{\mathrm{T}}$. The distribution of $x_{1}$ and $x_{2}$ is shown in Fig. 5. This dataset contains 600 samples and for each sample ${\mathbf {x}}$, its label y has the equal probability of being $+1$ or $-1$. We also generated a 50-dimensional dataset using the scikit-learn tool, which can introduce interdependence between features and add further noise to the data. It contains 1000 samples and each class is composed of 5 Gaussian clusters, where the 10 independent features, 10 useless features, 10 repeated features and noise are drawn from normal Gaussian distribution. We use $m (m=10,20,\cdots ,90)$ percent of samples to form the training set and the rest to form the test set. We evaluate our MLMKC with $\ell _{1}$ regularization and radius information, namely MLMKC-$\ell _{1}$, on these nonlinear binary classification problem compared with SVML, GMKL, SimpleMKL, $\ell _{p}$-MKL and SM1MKL as baseline methods. For the first dataset we use only ten basis kernels and for the second dataset we use forty basis kernels. The basis kernels used for MKL methods are Gaussian kernels with bandwidths selected from range $\{0.1,0.2,0.5,0.7,1.0,2.0,5.0,7.0,10.0,\cdots , 20.0\}$ and polynomial kernels of degree 1 to 3. The parameter C used in SVM is chosen from a large range $\{10^{-1},\ldots ,10^{3},10^{4}\}$. Products of basis kernels are used as the combinations in GMKL framework. For $\ell _{p}$-MKL and SM1MKL, the parameters p and $\theta$ are selected according to the setting in [24, 46], respectively.

Fig. 6

Decision boundaries generated by our method with from top to bottom $N_{k}=4, N_{k}=10, N_{k}=16$ and from left to right $\lambda _{G}=0.1$, $\lambda _{G}=0.01$, $\lambda _{G}=0.001$, $\lambda _{G}=0.0$

We show the decision boundaries of the first synthetic dataset, using 50% of the samples to train and others to test, for our method with different $\lambda _{G}$ and $N_{k}$ in Fig. 6, in which setting $\lambda _{G}=0.1$ always result in over-fitting,while setting $\lambda _{G}=0.01$ can achieve the highest classification accuracy. When choosing $N_{k}=10$, the proposed MLMKC-$\ell _{1}$ can achieve the highest accuracy with non-sparse and sparse solutions for kernels combination by setting $\lambda _{G}=0.0$ and $\lambda _{G}=0.01$, respectively. It is interesting that when $N_{k}=4$, setting $\lambda _{G}=\{0.0,0.001\}$ brings poor result, while $\lambda _{G}=0.01$ provides accuracy of $97.67\%$, which demonstrates the significance of Gaussian RBF kernel. High classification accuracy no less than $97.33\%$ can be achieved by setting $\lambda _{G}=0.01$, but large $N_{k}$ (e.g., $N_{k}=16$ in Fig. 6) causes over-fitting. For the second synthetic dataset, choosing $N_{k}$ within the range of $\{20,40\}$ leads to higher accuracy, and setting larger $N_{k}$ for all settings of $\lambda _{G}$ makes no contribution to the classification accuracy. The accuracy curve with $\lambda _{G}=0.02$ exceeds $\lambda _{G}=0.0$ by nearly $10\%$ as illustrated in Fig. 7, which demonstrates that the Gaussian RBF kernel cannot be replaced in more complex classification task. Above experimental results verify the effectiveness of our proposed parameterization scheme which incorporating the squared Mahalanobis distance into the Gaussian RBF kernels, and also reveal that by properly selecting parameter $\lambda _{G}$ and $N_{k}$, the classification performance can benefit from the distance metric based kernels and the Gaussian RBF kernel in our proposed formulation.

Fig. 7

Classification accuracy of the second synthetic dataset with different $\lambda _{G}$ and $N_{k}$

We evaluate the proposed MLMKC algorithm using two synthetic datasets, and compare the proposed methods with other representative models, i.e., SVML,⁴ GMKL,⁵ SimpleMKL,⁶$\ell _{p}$-MKL,⁷ and SM1MKL⁸ in terms of classification accuracy. Experimental results are reported in Table 3, and the average number of kernels finally used in each method are reported in the last row. Comparatively, the proposed method achieves a higher accuracy compared with SVML and GMKL, especially on the first synthetic dataset. It demonstrates that utilizing the product combination framework of generalized MKL incorporated with distance metric makes our MLMKC flexible and effective for classification problem. Other MKL methods which focus on searching the optimal mixture of basis kernels, e.g., SimpleMKL, $\ell _{p}$-MKL and SM1MKL get lower accuracy with the same number of input basis kernels, especially for the second synthetic dataset, which also verifies the effectiveness of the proposed kernel formulation and the robustness of our method. Sparse solution for kernels combination is obtained using SimpleMKL, GMKL, $\ell _{p}$-MKL and our MLMKC, which we can see from the number of kernels finally used in Table 3. We find that the number of kernels finally used in our MLMKC is nearly the same as the number of features beneficial for the classification. The experimental results show that our method can get preferable results with less kernels which is more time and space efficient.

Table 3 Classification accuracy (%) comparison of SVML, GMKL, SimpleMKL, $\ell _{p}$-MKL, SM1MKL and our method on the synthetic datasets $(d = 2)$ and $(d = 50)$

4.3 Comparison with State-of-the-Art Methods

In this experiment, we evaluate the proposed MLMKC algorithm using eleven UCI datasets, and compare the proposed methods with other representative models, i.e., SVML, GMKL, SimpleMKL, $\ell _{p}$-MKL, SM1MKL, RMKL,⁹ EasyMKL$^9$and RM-GD$^9$ in terms of classification accuracy and training time. The designed RBF kernels are combined by taking their product for GMKL, and the parameters for $\ell _{p}$-MKL and SM1MKL follow the setting in [24, 46]. The parameter C used in SVM is chosen from a large range $\{10^{-3},10^{-2},\ldots ,10^{6},10^{7}\}$. Basis kernels used in SimpleMKL, $\ell _{p}$-MKL and SM1MKL include Gaussian kernel and polynomial kernel following the construction method in SimpleMKL. The bandwidths of Gaussian kernel used in RMKL and RM-GD are selected as described in [18], where 20 scales are sampled with $\sigma _{min}=0.1$ and $\sigma _{max}=20$. For EasyMKL, we construct the RBF based weak kernel following [1]. Results are all obtained by using 5-folds CV and averaging over 20 runs. The classification results of four forms of proposed MLMKC methods are reported in Table 4, which includes MLMKC in Eq. (14) with $\ell _{1}$ and $\ell _{2}$ regularization and radius information, MLMKC in Eq. (10) with $\ell _{1}$ and $\ell _{2}$ regularization but without radius information. We can observe an interesting phenomenon that the proposed MLMKC method with $\ell _{1}$ regularization but without radius information achieves good performance, which is almost the same as MLMKC with $\ell _{1}$ regularization and radius information. Without loss of generality, we take MLMKC-$\ell _{1}$ as the substitute of the proposed MLMKC in following experiments.

Table 4 Classification accuracy (mean ± SD) of different forms of MLMKC methods on the UCI datasets

Table 5 Classification accuracy comparison (mean ± SD) of different methods on the UCI datasets

The comparison results with SVML, GMKL, SimpleMKL, SM1MKL, $\ell _{p}$-MKL, RMKL, EasyMKL and RM-GD are listed in Table 5, where the highest accuracy of all are shown in solid black for each dataset, respectively. We do not report the accuracy of SVML on the Wpbc dataset, in that the released SVML code always collapsed when run on it. To compare the classification performance of these models, we list the average ranks of these models in the last row of Table 5. The average rank is defined as the mean rank of one method over the 11 datasets, which can provide a fair comparison of the algorithms [8].

In Table 5, our MLMKC-$\ell _{1}$ greatly outperforms SVML and four MKL methods including GMKL, SimpleMKL, SM1MKL, and $\ell _{p}$-MKL on most datasets with less than 10 kernels, while other methods need tens of basis kernels on small datasets and hundreds of basis kernels on large datasets. The classification accuracy of our method ranks third and is comparable with RMKL, EasyMKL and RM-GD on some datasets. These three methods solve different optimization problems instead of searching for the optimum combination directly of provided basis kernels. RMKL performs a max-variance projection-based learning, aiming at finding a low-dimensional representation which approximates the original space spanned by the basis kernels. It has capability of removing the redundancy of interscale kernel similarities, hence it is flexible with the scale of basis kernels. EasyMKL optimizes a min–max problem over probability distribution of positive and negative samples sets and the combination parameters of predefined kernel matrices, focusing on maximizing the margin. It also applies a feature selection in kernel computation, making it robust to noise features. RM-GD, a state-of-the-art margin-based MKL method, exploits a radius-margin ratio optimization based on gradient descent. It demonstrates that the minimization of the radius-margin bound achieves better results with respect to the margin maximization, while MLMKC minimizes the radius and maximizes the margin separately.

Fig. 8

Training time (s) of SVML, SimpleMKL, GMKL, $\ell _{p}$-MKL, SM1MKL, EasyMKL, RMKL, RM-GD, MLMKC-$\ell _{2}$, and MLMKC-$\ell _{1}$

The experimental results reveal that: (i) the formulation of incorporating Mahalanobis into the Gaussian RBF kernel to make up the distance metric, and jointly learning the distance metric and the corresponding kernel classifier via GMKL framework is of great efficiency for SVM-based classifiers. (ii) The optimization result without considering the radius information achieves good performance indicate that the regularizer $r(\varvec{\beta })$ related with $\varvec{\beta }$ in our kernel function also imposes constraint on the radius of training samples in the feature space. Regardless of the classification results, these MKL methods need a number of appropriate basis kernels whether seeking the optimum combination parameters directly or not, comparing with our method. SimpleMKL, SM1MKL and $\ell _{p}$-MKL methods need a large number of basis kernels, which often obtain sparse solution for kernels combination.

The training time of representative methods, and our proposed methods on several small datasets is showed in Fig. 8. All the experiments are executed in the same PC. The training time for MLMKC includes the doublets construction, k-means clustering and kernel computation. In general, we found the training time required for MLMKC-$\ell _{1}$ outperforming SVML, GMKL and SimpleMKL, and 100 times faster than RM-GD and RMKL though achieving better classification accuracy than other MKL methods. $\ell _{p}$-MKL and SM1MKL methods operate optimization in simple analytical update rules via block coordinate descent algorithm instead. The chunking optimization reduces the iteration and avoids the time consuming procedure for kernel combination coefficients in terms of the dual variable. EasyMKL replaces the kernel matrix with the sum of the predefined weak kernel matrices, making it efficient in terms of time and space. By adopting SPG optimizer, our method performs efficiently and is even comparable to EasyMKL, $\ell _{p}$-MKL and SM1MKL methods.

The classification error rates of multiclass real-world datasets are listed in Table 6. We use small number (about half of the feature dimension) of base kernels with SimpleMKL, $\ell _{p}$-MKL and SM1MKL methods to avoid memory exceptions for the real-world datasets. We do not report the result of GMKL on USPS because it require memory space that our PC can not provide with. This further validates that on the large scale dataset our proposed method is competitive with other methods with less kernels. From Table 6, we can see that our proposed MLMKC achieves the lowest error rate with small number of kernels, $N_{k}<10$, which verify the effectiveness of the method on the large scale dataset. As demonstrated by the classification results and the timing results on UCI datasets and real-world datasets, the proposed method produces overall better performance.

Table 6 Classification error rates (%) comparison of different methods on the real-world datasets

5 Conclusion

In this paper, we investigate metric learning via multiple kernel learning for SVMs. An effective MKL framework for joint learning of distance metric and kernel classifier is proposed, referred to MLMKC. We reformulate the matrix of Mahalanobis distance metric, and then incorporate it into the Gaussian RBF kernel to construct a novel kernel function formulation for the subsequent embedding to the GMKL framework. The regularization on the radius information, which shows significant improvement on MKL scenarios, although has been considered during the formulation of the proposed algorithm, shows limited ability on improving the final classification performance. Experimental results demonstrate that, dual regularizations, coming from both the regularization of distance metric imposed on the distance of samples in the original space, and regularizer $r(\varvec{\beta })$ imposed on the radius of training samples in the feature space, guarantee the reliable performance of MLMKC. On the UCI datasets we demonstrate that our algorithm achieves preferable results in terms of classification accuracy and comparable training time with state-of-the-art methods. On the handwritten digit dataset USPS and object classification dataset COIL20, we achieve competitive results and show effectiveness of our proposed method on large scale data with less number of kernels. All these aspects make MLMKC a competitive general-purpose metric learning-based multiple kernels algorithm for SVMs with Gaussian RBF kernels. The future work is to introduce efficient approximation algorithms to our proposed MLMKC model with suitable formulation, and finally make it feasible to tackle the scalability issue.