Quasi-uniform stability of Caputo-type fractional-order neural networks with mixed delay

Abstract

In this paper, a class of Caputo-type fractional-order neural networks with mixed delay is introduced. By employing known inequalities, such as Hölder inequality, Cauchy–Schwartz inequality and Gronwall inequality, sufficient conditions are presented to ensure that such neural network is quasi-uniformly stable. Finally, a numerical example is presented to prove the theoretical results.

1 Introduction

Fractional calculus’s phylogeny dated back to 1695, about 300 years ago, which was used to deal with derivatives and integrals of arbitrary. Owing to its complexity and lacking of application background, it didn’t draw much attention for a long time. Until recently, it has got increasing interests from researchers and has become a valuable tool in modeling in various field of engineering, physics, and so on [1–4], such as the fractional model of viscoelastic liquid [5], the diffusion and transmission model of ware [6], the fractional model of colored noise [7].

It has been well known that compared with classical integer-order models, fractional-order models possesses the heredity and memory, so that it provide an excellent instrument to describe the behavior of system. For instance, fractional-order models of happiness [8] and love [9] have been developed and are claimed to give a better representation than integer-order dynamical approaches. Recently, some researchers apply the characteristic of fractional calculus to neural networks to form fractional-order neural models, which can depict the complex relationship between the signal input and signal output more accurately and flexibly. In Ref. [10], it first introduced a cellular neural network with fractional-order cells. In Ref. [11], it was suggested that fractional derivatives provide neurons with a fundamental and general computation ability that can contribute to efficient information processing stimulus anticipation and frequency-independent phase shifts of oscillatory neuronal firing. Furthermore, in Refs. [12–15], it was noted that fractional-order neural networks might play a significant role in parameter estimation, therefore, it is essential to incorporate the fractional calculus into neural network models, which can said to be an important improvement.

Currently, the analyses of fractional-order artificial neural networks have received much attention and some available results about fractional-order neural networks have been obtained, especially about stability. For example, in Ref. [16], stability of fractional-order neural networks of Hopfield type is proved by the way of energy-like function analysis. Besides, employing the stability theory of fractional-order system, the asymptotically stability of fractional-order neural networks of Hopfield type is analyzed in Refs. [17, 18]. The author of Ref. [19] confirm the truth of $\alpha$-stability and $\alpha$-synchronization for fractional-order neural networks. In Ref. [20], it was pointed out that chaotic behaviors can emerge in a fractional network. What’s more, Refs. [21–23] proposed the chaos control and synchronization of some simple fractional networks by mainly using laplace transformation theory and numerical simulations. Besides, the predecessors also investigate the discrete-time Hopfield neural networks. For example, the stability and bifurcation for discrete-time Cohen-Grossberg neural network is studied in Ref. [24] and the Hopf bifurcation and stability analysis on discrete-time Hopfield neural network with delay is researched in Ref. [25].

To the best of our knowledge, much work has been done about the stability of fractional-order neural networks, such as exponential stability, Lyapunov stability, asymptotic stability and so on. In Ref. [26], it has been demonstrated the uniform stability of fractional-order neural networks. Owing to the complexity of the fractional-order neural networks, it may affected by many factors, so it is meaningful to study fractional-order neural networks with mixed delay. However, there is not exist a paper to describe the quasi-uniform stability of fractional neural networks with mixed delay. So to establish the sufficient criteria for such neural networks is quite necessary and challenging. Motivated by the above discussions, this paper devotes to presenting sufficient criterions for quasi-uniform stability of a class of fractional-order neural networks with mixed delay.

The rest of the paper is organized as follows. The fractional-order network model is introduced and some necessary definitions and lemmas are given in Sect. 2. Sufficient conditions ensuring the finite-time stability of the fractional-order neural networks are presented in Sect. 3. A numerical simulation is obtained in Sect. 4.

2 Model description and preliminaries

In this section we present some definitions, lemmas and recall some well-known results about fractional differential equations.

Definition 2.1

[1] The Riemann–Liouville fractional integral with non-integer order $\beta \in R^{+}$ of f(s) is given as follows:

$$\begin{aligned} D^{-\beta }_{0,s}f(s)=\frac{1}{\Gamma (\beta )}\int ^{s}_{0}(s-\tau )^{\beta -1}f(\tau )d\tau , \end{aligned}$$

(1)

where $\Gamma (\cdot )$ is the Gamma function $\Gamma (\xi )=\int ^{+\infty }_{0}s^{\xi -1}e^{-s}ds$.

Definition 2.2

[1] The Riemann–Liouville derivative with fractional order $\beta >0$ of f(s) is defined as

$$\begin{aligned} D_{0,s}^{\beta }f(s)=\frac{d^{n}}{dt^{n}}D^{-(n-\beta )}_{0,s}f(s)=\frac{d^{n}}{dt^{n}}\frac{1}{\Gamma (n-\beta )}\int ^{s}_{0} (s-\tau )^{n-\beta -1}f(\tau )d\tau , \end{aligned}$$

(2)

where $\beta$ is a positive number such that $n-1<\beta <n\in Z^{+}$.

Definition 2.3

[1] The Caputo derivative of fractional order $\beta >0$ of f(s) is given by

$$\begin{aligned} D_{0,s}^{\beta }f(s)=D^{-(n-\beta )}_{0,s}\frac{d^{n}}{dt^{n}}f(s)=\frac{1}{\Gamma (n-\beta )}\int ^{s}_{0} (s-\tau )^{n-\beta -1}f^{n}(\tau )d\tau , \end{aligned}$$

(3)

where $n-1<\beta <n\in Z^{+}$.

These three definitions are in general non-equivalent. Based on the definition of integral derivative and the above expressions (2) and (3), it is recognized that integral derivative of a function is only related to its nearby points, while the fractional derivative has relationship with all of the function history information. That is, the next state of a system not only depends upon its current state but also upon its historical states staring from the initial time. As a result, a model described by fractional-order equations possess memory. It is more precise to describe the state of neuron. On the another hand, from the Laplace transform of fractional derivative, the main advantage of the Caputo derivative is that it only requires initial conditions given in terms of integer-order derivatives, representing well-understood features of physical situations and thus making it more applicable to real world problems. So throughout this paper, we deal with the fractional-order neural networks involving Caputo derivative, and the notation D$^{\beta }$ is chosen as the Caputo fractional derivative operator D$^{\beta }_{o,t}$. The following properties of operator D$^{\beta }$ are provided.

Lemma 2.1

[27] If $x(s)\in C^{n}[0,\infty )$, and $n-1<\alpha ,\beta <n\in Z^{+}$, then

$$\begin{aligned}&(1) \, D^{-\alpha }D^{-\beta }x(s)=D^{-(\alpha +\beta )}x(s), \alpha ,\beta \ge 0. \nonumber \\&(2) \, D^{\beta }D^{-\beta }x(s)=x(s),\beta \ge 0. \nonumber \\&(3) \, D^{-\beta }D^{\beta }x(s)=x(s)-\sum ^{n-1}_{m=0}\frac{s^{m}}{m!}x^{(m)}(0), \beta \ge 0. \end{aligned}$$

(4)

Lemma 2.2

[28] (Hölder inequality). Suppose that $p,q>1$, and $1/p+1/q=1$, if $\mid f(\cdot )\mid ^{p}$, $\mid h(\cdot )\mid ^{q}$ $\in$ $L^{1}(E)$, then $f(\cdot )h(\cdot )\in L^{1}(E)$ and

$$\begin{aligned} \int _{E}\mid f(x)h(x)\mid dx\le \left( \int _{E}\mid f(x)\mid ^{p}dx \right) ^{\frac{1}{p}} \left( \int _{E}\mid h(x)\mid ^{q}dx \right) ^{\frac{1}{q}}, \end{aligned}$$

(5)

where $L^{1}(E)$ is the Banach space of all Lebesgue measurable functions $f: E\longrightarrow R$ with $\int _{E}\mid f(x) \mid dx < \infty$. Let $p,q=2$, it Converts to the Cauchy–Schwartz inequality as follow:

$$\begin{aligned} \int _{E}\mid f(x)h(x)\mid dx\le \left( \int _{E}\mid f(x)\mid ^{2}dx \right) ^{\frac{1}{2}} \left( \int _{E}\mid h(x)\mid ^{2}dx \right) ^{\frac{1}{2}}. \end{aligned}$$

(6)

Lemma 2.3

[29] Let $k\in N$, and let $x_{1}, x_{2},\ldots ,x_{n}$ be non-negative real numbers. Then for $\eta$ $>$1.

$$\begin{aligned} \left( \sum ^{k}_{i=1}x_{i} \right) ^{\eta }\;\le \; k^{\eta -1}\sum ^{k}_{i=1}x_{i}^{\eta }. \end{aligned}$$

(7)

Lemma 2.4

[30] (Gronwall inequality). If

$$\begin{aligned} x(t)\;\le\; f(t)+\int ^{t}_{0}g(\mu )x(\mu )d\mu . t\in [0,T), \end{aligned}$$

where all the functions involved are continuous on [0, T), $T\le$ $\infty$, and $g(t)\ge 0$, then x(t) satisfies

$$\begin{aligned} x(t) \le \, f(t)+\int ^{t}_{0}g(\mu )f(\mu )exp \left\{ \int ^{t}_{\mu }g(\nu )d\nu \right\} d\mu , t\in [0,T). \end{aligned}$$

(8)

If, in addition, f(t) is nondecreasing, then

$$\begin{aligned} x(t)\le \, f(t)exp \left\{ \int ^{t}_{0}g(\mu )d\mu \right\} , t\in [0,T). \end{aligned}$$

(9)

3 Main results

In this section, two sufficient conditions are derived for a class of fractional-order neural networks of mixed delay with order $0<\beta <0.5$ and $0.5\le \beta <1$. The dynamic behavior of a continuous fractional-order neural network with mixed delay can be described by the following differential equation.

$$\begin{aligned}&\left\{ \begin{array}{l} D^{\beta }x_{i}(t)= -c_{i}x_{i}(t)+\sum a_{ij}f_{j}(x_{j}(t))+\sum b_{ij}g_{j}(x_{j}(t-\tau ))\\ \qquad \qquad +\sum m_{ij}\int ^{t}_{t-\sigma }h_{i}(x_{i}(u))du+I_{i}(t),\\ x_{i}(t)=\psi _{i}(t), t\in [-\gamma ,0),\gamma \in max\{\tau ,\sigma \},\\ \end{array} \right. \nonumber \\ \end{aligned}$$

(10)

or equivalently

$$\begin{aligned}&\left\{ \begin{array}{l} D^{\beta }x(t)=-\mathscr {C}x(t)+\mathscr {A}F(x(t))+\mathscr {B}G(x(t-\tau ))+\mathscr {M}\int _{t-\sigma }^{t}H(x(u))du+I(t),\\ x(t)=\psi (t), t\in [-\gamma ,0),\gamma \in max\{\tau ,\sigma \},\\ \end{array} \right. \nonumber \\ \end{aligned}$$

(11)

where $0<\beta <1, i=1,2\ldots ,n,$ n corresponds to the number of units in a neural network; $x(t)=(x_{1}(t), x_{2}(t),\ldots , x_{n}(t))^{T}$ corresponds to the state vector at time t; $F(x(t))=(f_{1}(x_{1}(t)), f_{2}(x_{2}(t),\ldots , f_{n}(x_{n}(t)))^{T}$, $G(x(t))=(g_{1}(x_{1}(t)), g_{2}(x_{2}(t),$ $\ldots , g_{n}(x_{n}(t)))^{T}$ and $H(x(t))=(h_{1}(x_{1}(t)), h_{2}(x_{2}(t),\ldots , h_{n}(x_{n}(t)))^{T}$ denote the activation function of the neurons; $\mathscr {C}=diag(c_{i}>0)$, $\mathscr {A}=(a_{ij})$, $\mathscr {B}=(b_{ij})$ and $\mathscr {M}=(m_{ij})$ are constant matrices; $c_{i}$ denotes the rate with which the ith unit will reset its potential to the resting state in isolation when disconnected from the network. $\mathscr {A}=({a_{ij}})$, $\mathscr {B}=({b_{ij}})$ and $\mathscr {M}=({m_{ij}})$ are referred to the connection of the jth neuron to the ith neuron at time t, $t-\tau$ and $t-\sigma$, respectively, where $\tau$ and $\sigma$ is the transmission delay and a nonnegative constant; $I=(I_{1}(t), I_{2}(t),\ldots , I_{n}(t))^{T}$ is an external bias vector.

For the initial conditions associated with system (10),it is usually assumed that $\psi _{i}(s)\in C([-\gamma ,0],R),i\in N,$ and the norm of $C([-\gamma ,0],R)$ is denoted by $\parallel \psi \parallel$=$sup_{s\in [-\gamma ,0]}$ $\parallel \psi (s)\parallel$.

Suppose that x(t) and y(t) are any two solutions of (11) with different initial functions $\psi$ $\in$ C and $\phi$ $\in$ C, $\psi (0)=\phi (0)=0$, let $x(t)-y(t)=e(t)$=$(e_{1}(t)$, $e_{2}(t)$, ..., $e_{n}(t))^{T}$, $\varphi$ =$\psi$-$\phi$, one obtain the error system

$$\begin{aligned}&\left\{ \begin{array}{l} D^{\alpha }e(t)=-\mathscr {C}e(t)+\mathscr {A}(F(x(t))-F(y(t)))+\mathscr {B}(G(x(t-\tau ))-G(y(t-\tau )))\\ \qquad \qquad +\mathscr {M}\int ^{t}_{t-\sigma }(H(x(u))-H(y(u)))du,\\ e(t)=\varphi (t),t\in [-\gamma ,0),\gamma \in max\{\tau ,\sigma \},\\ \end{array} \right. \nonumber \\ \end{aligned}$$

(12)

where $\varphi$ $\in$ C, $\varphi$(0) = 0 is the initial function of system (11), define the norm $\parallel \varphi \parallel$ = $sup_{s\in [-\gamma ,0]}\parallel \varphi (s)\parallel$.

Definition 3.1

For any $\varepsilon >0$, if there exists two constants $0<\delta <\varepsilon , T>0$, when $\parallel e(t_{0})\parallel <\delta$, we have $\parallel e(t)\parallel <\varepsilon$, $\forall t \in J=[t_{0},t_{0}+T]$, where $t_{0}$ is the initial time of observation, then system (11) is said to be quasi-uniformly stable.

In order to obtain main results, the following assumptions are made:

• (1) Denote $\parallel x\parallel =\Sigma _{i=1}^{n}$ $\mid x_{i}\mid$ and $\parallel \mathscr {A}\parallel =max _{1\le j\le n}$ $\Sigma _{i=1}^{n}$ $\mid$a$_{ij}$ $\mid$, which are the Euclidean vector norm and matrix norm, respectively ; $x_{i}$ and $a_{ij}$ are the elements of the vector x and the matrix $\mathscr {A}$, respectively.Let $C=\parallel \mathscr {C}\parallel$, $A=\parallel \mathscr {A}\parallel$, $B=\parallel \mathscr {B}\parallel$, and $M=\parallel \mathscr {M}\parallel$.

• (2) The neuron activation functions F(x), G(x) and H(x) are Lipschitz continuous, namely, there exist positive constants F, G and H such that

$$\begin{aligned}&\parallel F(u)-F(v)\parallel \le F\parallel u-v\parallel , \parallel G(u)-G(v)\parallel \le G\parallel u-v\parallel ,\nonumber \\&\parallel H(u)-H(v)\parallel \le H\parallel u-v\parallel , \forall u, v\in R. \end{aligned}$$

(13)

Theorem 3.1

When $1/2\le \beta <1$, if assumption (1) and (2) hold and

$$\begin{aligned} \sqrt{P+Qe^{2t}+W(t)e^{(W(t)+2)t}{\left(P\frac{1-e^{-(2+W(t))t}}{2+W(t)}+Q\frac{1-e^{-W(t)t}}{W(t)}\right)}}<\frac{\varepsilon }{\delta }, \quad t\in J, \end{aligned}$$

(14)

where

$$\begin{aligned} P&=5-\frac{5M^{2}H^{2}\gamma ^{2}\Gamma (2\beta -1)}{\Gamma ^{2}(\beta )4^{\beta }},\\ Q&=\frac{5M^{2}H^{2}\gamma ^{2}\Gamma (2\beta -1)}{\Gamma ^{2}(\beta )4^{\beta }} +\frac{5B^{2}G^{2}\Gamma (2\beta -1)(1-e^{-2\gamma })}{\Gamma ^{2}(\beta )4^{\beta }},\\ L&=\frac{10\Gamma (2\beta -1)[(C+AF)^{2}+B^{2}G^{2}e^{-2\gamma }]}{\Gamma ^{2}(\beta )4^{\beta }},\\ N&=\frac{5M^{2}H^{2}}{2\beta \Gamma (\beta )},\\ W(t)&=L+Nt^{2\beta }(1-e^{-2t}), \end{aligned}$$

then system (11) is quasi-uniformly stable.

Proof

Let the initial time $t_{0}=0, e_{0}=\varphi (0)$ is the initial condition of system (12). Depend on Lemma 2.1, the solution of the system (12) can be expressed in the following form:

$$\begin{aligned} e(t)&=\varphi (0)+D^{-\beta } \left[ -\mathscr {C}e(t)+\mathscr {A}(F(x(t))-F(y(t)))+\mathscr {B}(G(x(t-\tau ))-G(y(t-\tau ))) \right. \\&\left. \quad +\mathscr {M}\int ^{t}_{t-\sigma }(H(x(u))-H(y(u)))du \right] \\&= \varphi (0)+\frac{1}{\Gamma (\beta )}\int ^{t}_{t_{0}}(t-u)^{\beta -1} \left[ -\mathscr {C}e(u)+\mathscr {A}(F(x(u))-F(y(u))) \right. \\&\left. \quad +\mathscr {B}(G(x(u-\tau ))-G(y(u-\tau )))+\mathscr {M}\int ^{t}_{t-\sigma }(H(x(s))-H(y(s)))ds \right] du. \\ \end{aligned}$$

Trough the Assumptions (1), (2) and the properties of norm $\parallel \cdot \parallel$, it obtain

$$\begin{aligned} \parallel e(t)\parallel&\le \parallel \varphi (0)\parallel +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}\left[ C\parallel e(u)\parallel +AF\parallel e(u)\parallel \right. \\&\quad \left. +\;BG\parallel e(u-\tau )\parallel +\int ^{u}_{u-\sigma }MH \parallel e(s)\parallel ds \right] du\\&= \, \parallel \varphi (0)\parallel +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}(C+AF)\parallel e(u)\parallel du\\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}BG\parallel e(u-\tau )\parallel du\\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1} \left( \int ^{u}_{u-\sigma }MH\parallel e(s)\parallel ds \right) du\\ \end{aligned}$$

$$\begin{aligned} \parallel e(t)\parallel&\le \parallel \varphi (0)\parallel +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}(C+AF)\parallel e(u)\parallel du\\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}BG\parallel e(u-\tau )\parallel du\\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1} \left( \int ^{t}_{-\sigma }MH\parallel e(s)\parallel ds \right) du\\&= \, \parallel \varphi (0)\parallel +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}(C+AF)\parallel e(u)\parallel du\\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}BG\parallel e(u-\tau )\parallel du\\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1} \left( \int ^{t}_{0}MH\parallel e(s)\parallel ds \right) du\\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1} \left( \int ^{0}_{-\sigma }MH\parallel e(s)\parallel ds \right) du\\&\le \parallel \varphi (0)\parallel +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}(C+AF)\parallel e(u)\parallel du\\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}BG\parallel e(u-\tau )\parallel du\\&\quad +\frac{MHt^{\beta }}{\beta \Gamma (\beta )}\int ^{t}_{0}\parallel e(u)\parallel du +\frac{MH\sigma \parallel \varphi \parallel }{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}du.\\ \end{aligned}$$

$\square$

According to Cauchy–Schwartz inequality (6), one gets

$$\begin{aligned} \parallel e(t)\parallel&\le \parallel \varphi \parallel +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}e^{u}(C+AF)\parallel e(u)\parallel e^{-u} du\nonumber \\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}e^{u}BG\parallel e(u-\tau )\parallel e^{-u} du\nonumber \\&\quad +\frac{MHt^{\beta }}{\beta \Gamma (\beta )}\int ^{t}_{0}e^{u}\parallel e(u)\parallel e^{-u} du\nonumber \\&\quad +\frac{MH\sigma \parallel \varphi \parallel }{\Gamma (\beta )}\int ^{t}_{0}e^{u}(t-u)^{\beta -1}e^{-u}du\nonumber \\&\le \parallel \varphi \parallel +\frac{1}{\Gamma (\beta )}\left( \int ^{t}_{0}(t-u)^{2\beta -2}e^{2u}du \right) ^{\frac{1}{2}} \left( \int ^{t}_{0}(C+AF)^{2}\parallel e(u)\parallel ^{2} e^{-2u} du \right) ^{\frac{1}{2}}\nonumber \\&\quad +\frac{1}{\Gamma (\beta )}\left( \int ^{t}_{0}(t-u)^{2\beta -2}e^{2u}du \right) ^{\frac{1}{2}} \left( \int ^{t}_{0}B^{2}G^{2}\parallel e(u-\tau )\parallel ^{2} e^{-2u} du \right) ^{\frac{1}{2}}\nonumber \\&\quad +\frac{MHt^{\beta }}{\beta \Gamma (\beta )}\left( \int ^{t}_{0}e^{2u}du \right) ^{\frac{1}{2}} \left( \int ^{t}_{0}\parallel e(u)\parallel ^{2} e^{-2u} du \right) ^{\frac{1}{2}}\nonumber \\&\quad +\frac{MH\sigma \parallel \varphi \parallel }{\Gamma (\beta )} \left( \int ^{t}_{0}e^{2u}(t-u)^{2\beta -2}du \right) ^{\frac{1}{2}} \left( \int ^{t}_{0}e^{-2u}du \right) ^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$

(15)

Since

$$\begin{aligned} \int ^{t}_{0}(t-u)^{2\beta -2}e^{2u}du&= \int ^{t}_{0}z^{2\beta -2}e^{2(t-z)}dz=e^{2t}\int ^{t}_{0}z^{2\beta -2}e^{-2z}dz\nonumber \\&= \frac{e^{2t}}{2^{2\beta -1}}\int ^{2t}_{0}u^{2\beta -2}e^{-u}du<\frac{2e^{2t}}{4^{\beta }}\Gamma (2\beta -1). \end{aligned}$$

(16)

Substituting (16) into (15), one obtains

$$\begin{aligned} \parallel e(t)\parallel&\le \parallel \varphi \parallel +\frac{1}{\Gamma (\beta )}\left( \frac{2\Gamma (2\beta -1)e^{2t}}{4^{\beta }}\right) ^{\frac{1}{2}}\left( \int ^{t}_{0}(C+AF)^{2}\parallel e(u)\parallel ^{2}e^{-2u}du \right) ^{\frac{1}{2}}\nonumber \\&\quad +\frac{1}{\Gamma (\beta )}\left( \frac{2\Gamma (2\beta -1)e^{2t}}{4^{\beta }}\right) ^{\frac{1}{2}}\left( \int ^{t}_{0}B^{2}G^{2}\parallel e(u-\tau )\parallel ^{2}e^{-2u}du\right) ^{\frac{1}{2}}\nonumber \\&\quad +\frac{MHt^{\beta }}{\beta \Gamma (\beta )}\left( \frac{e^{2t}-1}{2}\right) ^{\frac{1}{2}}\left( \int ^{t}_{0}\parallel e(u)\parallel ^{2} e^{-2u} du \right) ^{\frac{1}{2}}\nonumber \\&\quad +\frac{MH\sigma \parallel \varphi \parallel }{\Gamma (\beta )}\left( \frac{2\Gamma (2\beta -1)e^{2t}}{4^{\beta }}\right) ^{\frac{1}{2}}\left( \frac{1-e^{-2t}}{2}\right) ^{\frac{1}{2}}.\nonumber \\ \end{aligned}$$

(17)

From Lemma 2.2, let $k=5$ and $\eta =2$, it follows from (17) that

$$\begin{aligned} \parallel e(t)\parallel ^{2}&\;\le \;5\parallel \varphi \parallel ^{2}+\frac{10\Gamma (2\beta -1)e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }}\int ^{t}_{0}(C+AF)^{2}\parallel e(u)\parallel ^{2} e^{-2u} du\\&\quad +\frac{10\Gamma (2\beta -1)e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }}\int ^{t}_{0}B^{2}G^{2}\parallel e(u-\tau )\parallel ^{2}e^{-2u}du\\&\quad +\frac{5M^{2}H^{2}t^{2\beta }(e^{2t-1})}{2\beta \Gamma (\beta )}\int ^{t}_{0}\parallel e(u)\parallel ^{2} e^{-2u} du\\&\quad +\frac{5M^{2}H^{2}\sigma ^{2}\parallel \varphi \parallel ^{2}\Gamma (2\beta -1)(e^{2t}-1)}{\Gamma ^{2}(\beta )4^{\beta }}\\&\le \left[ 5+\frac{5M^{2}H^{2}\sigma ^{2}\Gamma (2\beta -1)(e^{2t}-1)}{\Gamma ^{2}(\beta )4^{\beta }}\right] \parallel \varphi \parallel ^{2}\\&\quad + \left[ \frac{10\Gamma (2\beta -1)(C+AF)^{2}e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }}+\frac{5M^{2}H^{2}t^{2\beta }(e^{2t-1})}{2\beta \Gamma (\beta )} \right] \int ^{t}_{0}\parallel e(u)\parallel ^{2} e^{-2u} du\\&\quad +\frac{10\Gamma (2\beta -1)e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }}\int ^{t}_{-\tau }B^{2}G^{2}e^{-2\tau }\parallel e(u)\parallel ^{2}e^{-2u}du\\&\le \left[ 5+\frac{5M^{2}H^{2}\sigma ^{2}\Gamma (2\beta -1)(e^{2t}-1)}{\Gamma ^{2}(\beta )4^{\beta }} \right] \parallel \varphi \parallel ^{2}\\&\quad + \left[ \frac{10\Gamma (2\beta -1)(C+AF)^{2}e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }}+\frac{5M^{2}H^{2}t^{2\beta }(e^{2t-1})}{2\beta \Gamma (\beta )} \right] \int ^{t}_{0}\parallel e(u)\parallel ^{2} e^{-2u} du\\&\quad +\frac{10\Gamma (2\beta -1)e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }}\int ^{t}_{0}B^{2}G^{2}e^{-2\tau }\parallel e(u)\parallel ^{2}e^{-2u}du\\&\quad +\frac{10\Gamma (2\beta -1)e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }}\int ^{0}_{-\tau }B^{2}G^{2}e^{-2\tau }\parallel e(u)\parallel ^{2}e^{-2u}du\\ \end{aligned}$$

$$\begin{aligned} \parallel e(t)\parallel ^{2}&\le \left[ 5+\frac{5M^{2}H^{2}\sigma ^{2}\Gamma (2\beta -1)(e^{2t}-1)}{\Gamma ^{2}(\beta )4^{\beta }}\right] \parallel \varphi \parallel ^{2}\\&\quad + \left\{ \frac{10\Gamma (2\beta -1)[(C+AF)^{2}+B^{2}G^{2}e^{-2\tau }]e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }}+\frac{5M^{2}H^{2}t^{2\beta }(e^{2t-1})}{2\beta \Gamma (\beta )} \right\} \\&\quad \times \int ^{t}_{0}\parallel e(u)\parallel ^{2} e^{-2u} du +\frac{5B^{2}G^{2}\Gamma (2\beta -1)(1-e^{-2\tau })e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }}\parallel \varphi \parallel ^{2}\\&= \left[ 5+\frac{5M^{2}H^{2}\sigma ^{2}\Gamma (2\beta -1)(e^{2t}-1)}{\Gamma ^{2}(\beta )4^{\beta }} +\frac{5B^{2}G^{2}\Gamma (2\beta -1)(1-e^{-2\tau })e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }} \right] \parallel \varphi \parallel ^{2}\\&\quad + \left\{ \frac{10\Gamma (2\beta -1)[(C+AF)^{2}+B^{2}G^{2}e^{-2\tau }]e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }}+\frac{5M^{2}H^{2}t^{2\beta }(e^{2t-1})}{2\beta \Gamma (\beta )} \right\} \\&\quad \times \int ^{t}_{0}\parallel e(u)\parallel ^{2} e^{-2u} du\\&\le \left\{ 5-\frac{5M^{2}H^{2}\gamma ^{2}\Gamma (2\beta -1)}{\Gamma ^{2}(\beta )4^{\beta }}+[\frac{5M^{2}H^{2}\gamma ^{2}\Gamma (2\beta -1)}{\Gamma ^{2}(\beta )4^{\beta }}\right. \\&\left. \quad +\;\frac{5B^{2}G^{2}\Gamma (2\beta -1)(1-e^{-2\gamma })}{\Gamma ^{2}(\beta )4^{\beta }}]e^{2t} \right\} \parallel \varphi \parallel ^{2}\\&\quad + \left\{ \frac{10\Gamma (2\beta -1)[(C+AF)^{2}+B^{2}G^{2}e^{-2\gamma }]e^{2t}}{\Gamma ^{2}(\beta )4^{\beta }} \right. \\&\left. \quad +\;\frac{5M^{2}H^{2}t^{2\beta }(e^{2t-1})}{2\beta \Gamma (\beta )} \right\} \int ^{t}_{0}\parallel e(u)\parallel ^{2} e^{-2u} du,\\ \end{aligned}$$

let

$$\begin{aligned} P&=5-\frac{5M^{2}H^{2}\gamma ^{2}\Gamma (2\beta -1)}{\Gamma ^{2}(\beta )4^{\beta }},\\ Q&=\frac{5M^{2}H^{2}\gamma ^{2}\Gamma (2\beta -1)}{\Gamma ^{2}(\beta )4^{\beta }} +\frac{5B^{2}G^{2}\Gamma (2\beta -1)(1-e^{-2\gamma })}{\Gamma ^{2}(\beta )4^{\beta }},\\ L&=\frac{10\Gamma (2\beta -1)[(C+AF)^{2}+B^{2}G^{2}e^{-2\gamma }]}{\Gamma ^{2}(\beta )4^{\beta }},\\ N&=\frac{5M^{2}H^{2}}{2\beta \Gamma (\beta )},\\ \end{aligned}$$

since

$$\begin{aligned} \parallel e(t)\parallel ^{2}&\le (P+Qe^{2t})\parallel \varphi \parallel ^{2}+(Le^{2t}+Nt^{2\beta })(e^{2t}-1)\int ^{t}_{0}\parallel e(u)\parallel ^{2}e^{-2u}du\\ \end{aligned}$$

which is equivalent to

$$\begin{aligned} \parallel e(t)\parallel ^{2}e^{-2t}&\le (Pe^{-2t}+Q)\parallel \varphi \parallel ^{2}+[(L+Nt^{2\beta })(1-e^{-2t})]\int ^{t}_{0}\parallel e(u)\parallel ^{2}e^{-2u}du. \end{aligned}$$

According to the Gronwall inequality (8), it obtain

$$\begin{aligned} \parallel e(t)\parallel ^{2}e^{-2t}&\le (Pe^{-2t}+Q)\parallel \varphi \parallel ^{2}+\int ^{t}_{0}(Pe^{-2u}+Q)\parallel \varphi \parallel ^{2}\\&\quad \times [(L+Nt^{2\beta })(1-e^{-2t})] e^{\int ^{t}_{u}(L+Nt^{2\beta })(1-e^{-2t})ds}du\\&\le (Pe^{-2t}+Q)\parallel \varphi \parallel ^{2}+[(L+Nt^{2\beta })(1-e^{-2t})]\parallel \varphi \parallel ^{2}\\&\quad \times \int ^{t}_{0}(Pe^{-2u}+Q)e^{(t-u)[(L+Nt^{2\beta })(1-e^{-2t})]}du, \end{aligned}$$

let

$$\begin{aligned} W(t)=L+Nt^{2\beta }(1-e^{-2t}), \end{aligned}$$

then

$$\begin{aligned} \parallel e(t)\parallel ^{2}e^{-2t}&\le (Pe^{-2t}+Q)\parallel \varphi \parallel ^{2}+W(t)e^{tW(t)}\parallel \varphi \parallel ^{2}\int ^{t}_{0}(Pe^{-2u}+Qe^{-W(t)u})du\\&= (Pe^{-2t}+Q)\parallel \varphi \parallel ^{2}+W(t)e^{tW(t)}\parallel \varphi \parallel ^{2}\left( \int ^{t}_{0}Pe^{-2u}du+Q\int ^{t}_{0}e^{-W(t)u}du \right) \\&\le (Pe^{-2t}+Q)\parallel \varphi \parallel ^{2}+W(t)e^{tW(t)}\left( P\frac{1-e^{-(2+W(t))t}}{2+W(t)}+Q\frac{1-e^{-W(t)t}}{W(t)}\right) \parallel \varphi \parallel ^{2}\\&= \left[ Pe^{-2t}+Q+W(t)e^{tW(t)}\left( P\frac{1-e^{-(2+W(t))t}}{2+W(t)}+Q\frac{1-e^{-W(t)t}}{W(t)}\right) \right] \parallel \varphi \parallel ^{2},\\ \end{aligned}$$

so

$$\begin{aligned} \parallel e(t)\parallel ^{2}\le \left[ P+Qe^{2t}+W(t)e^{(W(t)+2)t}\left( P\frac{1-e^{-(2+W(t))t}}{2+W(t)}+Q\frac{1-e^{-W(t)t}}{W(t)}\right) \right] \parallel \varphi \parallel ^{2},\\ \end{aligned}$$

therefore

$$\begin{aligned} \parallel e(t)\parallel \le \sqrt{P+Qe^{2t}+W(t)e^{(W(t)+2)t}\left( P\frac{1-e^{-(2+W(t))t}}{2+W(t)}+Q\frac{1-e^{-W(t)t}}{W(t)}\right) }\parallel \varphi \parallel .\nonumber \\ \end{aligned}$$

(18)

It follows that when $\parallel \varphi \parallel <\delta$, if (3.1) is satisfied, then $\parallel e(t)\parallel <\varepsilon$, from Definition 3.1, one can obtain system (11) is quasi-uniformly stable.

Theorem 3.2

When $0<\beta <1/2$, if assumption (1) and (2) hold and

$$\begin{aligned} \root q \of {\tilde{P}+\tilde{Q}e^{qt}+\frac{\tilde{W}(t)\tilde{P}(e^{(\tilde{W}(t)+q)t}-1)}{q+\tilde{W}(t)}+\frac{\tilde{W}(t)\tilde{Q}e^{(\tilde{W}(t)+q)t}(1-e^{-\tilde{W}(t)t})}{\tilde{W}(t)}}<\frac{\varepsilon }{\delta }, \quad t\in J, \end{aligned}$$

(19)

where

$$\begin{aligned}&\tilde{E}=[\frac{\Gamma (p\beta -p+1)}{\Gamma ^{p}(\beta )p^{p\beta -p+1}}]^{\frac{q}{p}},\ \ \ \tilde{P}=5^{q-1},\\&\tilde{Q}=\frac{5^{q-1}B^{q}G^{q}\tilde{E}(1-e^{-q\gamma })}{q}+5^{q-1}M^{q}H^{q}\gamma ^{q}\tilde{E},\\ \end{aligned}$$

$$\begin{aligned}&\tilde{L}=5^{q-1}\tilde{E}(C+AF)^{q}+5^{q-1}B^{q}G^{q}e^{-q\gamma }\tilde{E},\\&\tilde{N}=\frac{5^{q-1}M^{q}H^{q}}{\beta ^{q}\Gamma ^{q}(\beta )},\quad \tilde{W(t)}=\tilde{L}+\tilde{N}t^{q\beta }, \end{aligned}$$

$p=1+\beta ,q=1+1/\beta$, then system (11) is quasi-uniformly stable.

Proof

As the same in Theorem 3.1, we have the following estimate form of solution of system(12).

$$\begin{aligned} \parallel e(t)\parallel&\le \parallel \varphi (0)\parallel +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}[C\parallel e(u)\parallel +AF\parallel e(u)\parallel \\&\quad +BG\parallel e(u-\tau )\parallel +\int ^{u}_{u-\sigma }MH\parallel e(s)\parallel ds]du\\&=\;\parallel \varphi (0)\parallel +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}(C+AF)\parallel e(u)\parallel du\\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}BG\parallel e(u-\tau )\parallel du\\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}\left( \int ^{u}_{u-\sigma }MH\parallel e(s)\parallel ds \right) du.\\ \end{aligned}$$

Let $p=1+\beta ,q=1+1/\beta$, we can see that, $p,q>1$ and $1/p+1/q=1$. By using the Hölder inequality (5), one obtain

$$\begin{aligned} \parallel e(t)\parallel&\le \parallel \varphi \parallel +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}e^{u}(C+AF)\parallel e(u)\parallel e^{-u} du\\&\quad +\frac{1}{\Gamma (\beta )}\int ^{t}_{0}(t-u)^{\beta -1}e^{u}BG\parallel e(u-\tau )\parallel e^{-u} du + \frac{MHt^{\beta }}{\beta \Gamma (\beta )}\int ^{t}_{0}e^{u}\parallel e(u)\parallel e^{-u} du\\&\quad +\frac{MH\sigma \parallel \varphi \parallel }{\Gamma (\beta )}\int ^{t}_{0}e^{u}(t-u)^{\beta -1}e^{-u}du\\&\le \parallel \varphi \parallel +\frac{1}{\Gamma (\beta )}\left( \int ^{t}_{0}(t-u)^{p\beta -p}e^{pu}du \right) ^{\frac{1}{p}} \left( \int ^{t}_{0}(C+AF)^{q}\parallel e(u)\parallel ^{q} e^{-qu} du \right) ^{\frac{1}{q}}\\&\quad +\frac{1}{\Gamma (\beta )}\left( \int ^{t}_{0}(t-u)^{p\beta -p}e^{pu}du \right) ^{\frac{1}{p}} \left( \int ^{t}_{0}B^{q}G^{q}\parallel e(u-\tau )\parallel ^{q} e^{-qu} du \right) ^{\frac{1}{q}}\\&\quad +\frac{MHt^{\beta }}{\beta \Gamma (\beta )} \left( \int ^{t}_{0}e^{pu}du)^{\frac{1}{p}}(\int ^{t}_{0}\parallel e(u)\parallel ^{q} e^{-qu} du \right) ^{\frac{1}{q}}\\&\quad +\frac{MH\sigma \parallel \varphi \parallel }{\Gamma (\beta )}\left( \int ^{t}_{0}e^{pu}(t-u)^{p\beta -p}du \right) ^{\frac{1}{p}}\left( \int ^{t}_{0}e^{-qu}du \right) ^{\frac{1}{q}}\\ \end{aligned}$$

$$\begin{aligned} \parallel e(t)\parallel&\le \parallel \varphi \parallel +\frac{1}{\Gamma (\beta )}\left( \int ^{t}_{0}(t-u)^{p\beta -p}e^{pu}du \right) ^{\frac{1}{p}} \left( \int ^{t}_{0}(C+AF)^{q}\parallel e(u)\parallel ^{q} e^{-qu} du \right) ^{\frac{1}{q}}\nonumber \\&\quad +\frac{1}{\Gamma (\beta )}\left( \int ^{t}_{0}(t-u)^{p\beta -p}e^{pu}du \right) ^{\frac{1}{p}}\left( \int ^{t}_{0}B^{q}G^{q}\parallel e(u-\tau )\parallel ^{q} e^{-qu} du\right)^{\frac{1}{q}}\nonumber \\&\quad +\frac{MHt^{\beta }e^{pt}}{\beta \Gamma (\beta )}\left( \int ^{t}_{0}\parallel e(u)\parallel ^{q} e^{-qu} du \right) ^{\frac{1}{q}}\nonumber \\&\quad +\frac{MH\sigma \parallel \varphi \parallel }{\Gamma (\beta )}\left( \int ^{t}_{0}e^{pu}(t-u)^{p\beta -p}du \right) ^{\frac{1}{p}}.\nonumber \\ \end{aligned}$$

(20)

Note that

$$\begin{aligned} \int ^{t}_{0}(t-u)^{p\beta -p}e^{pu}du =&\int ^{t}_{0}z^{p\beta -p}e^{p(t-z)}dz=e^{pt}\int ^{t}_{0}z^{p\beta -p}e^{-pz}dz\nonumber \\ =\;&\frac{e^{pt}}{p^{p\beta -p+1}}\int ^{pt}_{0}u^{p\beta -p}e^{-u}du<\frac{e^{pt}}{p^{p\beta -p+1}}\Gamma (p\beta -p+1). \end{aligned}$$

(21)

$\square$

Substituting (21) into (20), we has

$$\begin{aligned} \parallel e(t)\parallel&\le \parallel \varphi \parallel +\left( \frac{e^{pt}\Gamma (p\beta -p+1)}{\Gamma ^{p}(\beta )p^{p\beta -p+1}}\right) ^{\frac{1}{p}}\left( \int ^{t}_{0}( C+AF)^{q}\parallel e(u)\parallel ^{q} e^{-qu} du \right) ^{\frac{1}{q}}\\&\quad +\left( \frac{e^{pt}\Gamma (p\beta -p+1)}{\Gamma ^{p}(\beta )p^{p\beta -p+1}}\right) ^{\frac{1}{p}}\left( \int ^{t}_{0}B^{q}G^{q}\parallel e(u-\tau )\parallel ^{q} e^{-qu}du \right) ^{\frac{1}{q}}\\&\quad +\;\frac{MHt^{\beta }e^{pt}}{\beta \Gamma (\beta )}\left( \int ^{t}_{0}\parallel e(u)\parallel ^{q} e^{-qu} du \right) ^{\frac{1}{q}}\\&\quad +\;MH\sigma \parallel \varphi \parallel \left( \frac{e^{pt}\Gamma (p\beta -p+1)}{\Gamma ^{p}(\beta )p^{p\beta -p+1}}\right) ^{\frac{1}{p}}.\\ \end{aligned}$$

Then form Lemma 2.2, let $k=5$ and $\eta =q$, one gets

$$\begin{aligned} \parallel e(t)\parallel ^{q}&\le 5^{q-1}\parallel \varphi \parallel ^{q}+5^{q-1}\left( \frac{e^{pt}\Gamma (p\beta -p+1)}{\Gamma ^{p}(\beta )p^{p\beta -p+1}}\right) ^{\frac{q}{p}} \int ^{t}_{0}(C+AF)^{q}\parallel e(u)\parallel ^{q}e^{-qu}du\\&\quad +5^{q-1}\left( \frac{e^{pt}\Gamma (p\beta -p+1)}{\Gamma ^{p}(\beta )p^{p\beta -p+1}}\right) ^{\frac{q}{p}}\int ^{t}_{0}B^{q}G^{q}\parallel e(u-\tau )\parallel ^{q} e^{-qu}du\\&\quad +\frac{5^{q-1}M^{q}H^{q}t^{q\beta }e^{pt}}{\beta ^{q}\Gamma ^{q}(\beta )}\int ^{t}_{0}\parallel e(u)\parallel ^{q}e^{-qu}du\\&\quad +(5^{q-1}M^{q}H^{q}\sigma ^{q}\parallel \varphi \parallel ^{q}) \left( \frac{e^{pt}\Gamma (p\beta -p+1)}{\Gamma ^{p}(\beta )p^{p\beta -p+1}}\right) ^{\frac{q}{p}},\\ \end{aligned}$$

let

$$\begin{aligned} \tilde{E}=\left[ \frac{\Gamma (p\beta -p+1)}{\Gamma ^{p}(\beta )p^{p\beta -p+1}}\right] ^{\frac{q}{p}}, \end{aligned}$$

then

$$\begin{aligned} \parallel e(t)\parallel ^{q}&\le \;(5^{q-1}+5^{q-1}M^{q}H^{q}\sigma ^{q}\tilde{E}e^{qt})\parallel \varphi \parallel ^{q}\\&\quad +\left[ 5^{q-1}\tilde{E}(C+AF)^{q}e^{qt}+\frac{5^{q-1}M^{q}H^{q}t^{q\beta }e^{qt}}{\beta ^{q}\Gamma ^{q}(\beta )}\right] \int ^{t}_{0}\parallel e(u)\parallel ^{q}e^{-qu}du\\&\quad +5^{q-1}\tilde{E}e^{qt}\int ^{t}_{0}B^{q}G^{q}\parallel e(u-\tau )\parallel ^{q} e^{-qu}du\\&\le\; (5^{q-1}+5^{q-1}M^{q}H^{q}\sigma ^{q}\tilde{E}e^{qt})\parallel \varphi \parallel ^{q}\\&\quad +\;\left[ 5^{q-1}\tilde{E}(C+AF)^{q}e^{qt}+\;\frac{5^{q-1}M^{q}H^{q}t^{q\beta }e^{qt}}{\beta ^{q}\Gamma ^{q}(\beta )}\right] \int ^{t}_{0}\parallel e(u)\parallel ^{q}e^{-qu}du\\&\quad +\;5^{q-1}\tilde{E}e^{qt}\int ^{t}_{0}B^{q}G^{q}e^{-q\tau }\parallel e(u)\parallel ^{q} e^{-qu}du\\&\quad +5^{q-1}\tilde{E}e^{qt}\int ^{0}_{-\tau }B^{q}G^{q}e^{-q\tau }\parallel e(u)\parallel ^{q} e^{-qu}du\\&\le \left( 5^{q-1}+5^{q-1}M^{q}H^{q}\sigma ^{q}\tilde{E}e^{qt}+ \frac{5^{q-1}B^{q}G^{q}\tilde{E}(1-e^{-q\tau })e^{qt}}{q}\right) \parallel \varphi \parallel ^{q}\\&\quad +\left[ 5^{q-1}\tilde{E}(C+AF)^{q}e^{qt}+\frac{5^{q-1}M^{q}H^{q}t^{q\beta }e^{qt}}{\beta ^{q}\Gamma ^{q}(\beta )}\right. \\&\left. \quad +5^{q-1}B^{q}G^{q}e^{-q\tau }\tilde{E}e^{qt}\right] \int ^{t}_{0}\parallel e(u)\parallel ^{q}e^{-qu}du\\&\le \left( 5^{q-1}+5^{q-1}M^{q}H^{q}\gamma ^{q}\tilde{E}e^{qt}+ \frac{5^{q-1}B^{q}G^{q}\tilde{E}(1-e^{-q\gamma })e^{qt}}{q}\right) \parallel \varphi \parallel ^{q}\\&\quad +\left[ 5^{q-1}\tilde{E}(C+AF)^{q}e^{qt}+\;\frac{5^{q-1}M^{q}H^{q}t^{q\beta }e^{qt}}{\beta ^{q}\Gamma ^{q}(\beta )}\right. \\&\left. \quad +5^{q-1}B^{q}G^{q}e^{-q\gamma }\tilde{E}e^{qt}\right] \int ^{t}_{0}\parallel e(u)\parallel ^{q}e^{-qu}du,\\ \end{aligned}$$

let

$$\begin{aligned}&\tilde{P}=5^{q-1}\\&\tilde{Q}=\frac{5^{q-1}B^{q}G^{q}\tilde{E}(1-e^{-q\gamma })}{q}+5^{q-1}M^{q}H^{q}\gamma ^{q}\tilde{E},\\&\tilde{L}=5^{q-1}\tilde{E}(C+AF)^{q}+5^{q-1}B^{q}G^{q}e^{-q\gamma }\tilde{E},\\&\tilde{N}=\frac{5^{q-1}M^{q}H^{q}}{\beta ^{q}\Gamma ^{q}(\beta )},\\ \end{aligned}$$

one gets

$$\begin{aligned} \parallel e(t)\parallel ^{q}&\le (\tilde{P}+\tilde{Q}e^{qt})\parallel \varphi \parallel ^{q} +(\tilde{L}e^{qt}+\tilde{N}t^{q\beta }e^{qt})\int ^{t}_{0}\parallel e(u)\parallel ^{q}e^{-qu}du,\\ \end{aligned}$$

then

$$\begin{aligned} \parallel e(t)\parallel ^{q}e^{-qt}&\le (\tilde{P}e^{-qt}+\tilde{Q})\parallel \varphi \parallel ^{q} +(\tilde{L}+\tilde{N}t^{q\beta })\int ^{t}_{0}\parallel e(u)\parallel ^{q}e^{-qu}du.\\ \end{aligned}$$

Form the Gronwall inequality (8),it follows that

$$\begin{aligned} \parallel e(t)\parallel ^{q}e^{-qt}&\le (\tilde{P}e^{-qt}+\tilde{Q})\parallel \varphi \parallel ^{q}+\\&\quad \times (\tilde{L}+\tilde{N}t^{q\beta })\int ^{t}_{0} (\tilde{P}e^{-qu}+ \tilde{Q})\parallel \varphi \parallel ^{q}e^{\int ^{t}_{u}(\tilde{L}+\tilde{N}t^{q\beta })ds}du.\\ \end{aligned}$$

let

$$\begin{aligned} \tilde{W}(t)=\tilde{L}+\tilde{N}t^{q\beta }, \end{aligned}$$

then

$$\begin{aligned} \parallel e(t)\parallel ^{q}e^{-qt}&\le (\tilde{P}e^{-qt}+\tilde{Q})\parallel \varphi \parallel ^{q}+\tilde{W}(t)\parallel \varphi \parallel ^{q}\int ^{t}_{0} (\tilde{P}e^{-qu}+\tilde{Q})e^{\tilde{W}(t)(t-u)}du\\ =\;&(\tilde{P}e^{-qt}+\tilde{Q})\parallel \varphi \parallel ^{q}+\tilde{W}(t)\parallel \varphi \parallel ^{q}e^{\tilde{W}(t)t}\\&\times \left[ \int ^{t}_{0}\tilde{P}e^{-qu-\tilde{W}(t)u}du+\tilde{Q}\int ^{t}_{0}e^{{-u\tilde{W}(t)}}du \right] \\ =\;&(\tilde{P}e^{-qt}+\tilde{Q})\parallel \varphi \parallel ^{q}+\tilde{W}(t)\parallel \varphi \parallel ^{q}e^{\tilde{W}(t)t}\\&\times \left( \tilde{P}\frac{1-e^{-(q+\tilde{W}(t))t}}{q+\tilde{W}(t)}+\tilde{Q}\frac{1-e^{-\tilde{W}(t)t}}{\tilde{W}(t)} \right) , \end{aligned}$$

so

$$\begin{aligned} \parallel e(t)\parallel ^{q}&\le \left[ \tilde{P}+\tilde{Q}e^{qt}+\frac{\tilde{W}(t)\tilde{P}(e^{(\tilde{W}(t)+q)t}-1)}{q+\tilde{W}(t)} \right. \\&\left. \quad +\frac{\tilde{W}(t)\tilde{Q}e^{(\tilde{W}(t)+q)t}(1-e^{-\tilde{W}(t)t})}{\tilde{W}(t)}\right] \parallel \varphi \parallel ^{q}, \end{aligned}$$

therefore

$$\begin{aligned} \parallel e(t)\parallel \le \root q \of {\tilde{P}+\tilde{Q}e^{qt}+\frac{\tilde{W}(t)\tilde{P}(e^{(\tilde{W}(t)+q)t}-1)}{q+\tilde{W}(t)}+\frac{\tilde{W}(t)\tilde{Q}e^{(\tilde{W}(t)+q)t}(1-e^{-\tilde{W}(t)t})}{\tilde{W}(t)}} \parallel \varphi \parallel . \end{aligned}$$

It follows that when $\parallel \varphi \parallel <\delta$, if (19) is satisfied, then $\parallel e(t)\parallel <\varepsilon$, from Definition 3.1, one can obtain system (11) is quasi-uniformly stable.

4 An illustrative example

In this section, a numerical example is presented to illustrate the result. Let us consider the two-state fractional-order mixed delay neural network model.

$$\begin{aligned} D^{\beta }(x_{1}(t))&=-0.1x_{1}(t)+0.2f_{1}(x_{1}(t))-0.1f_{2}(x_{2}(t))-0.5g_{1}(x_{1}(t-\tau ))\\&\quad -0.1g_{2}(x_{2}(t-\tau ))+\int ^{t}_{t-\sigma }[0.4h_{1}(x_{1}(u))-0.1h_{2}(x_{2}(u))]du\\ D^{\beta }(x_{2}(t))&=-0.1x_{2}(t)+0.1f_{1}(x_{1}(t))-0.2f_{2}(x_{2}(t))-0.2g_{1}(x_{1}(t-\tau ))\\&\quad -0.1g_{2}(x_{2}(t-\tau ))+\int ^{t}_{t-\sigma }[0.1h_{1}(x_{1}(u))+0.2h_{2}(x_{2}(u))]du \end{aligned}$$

Where the activation function is described by the function $f_{i}(x_{i}(t))$ $=g_{i}(x_{i}(t))=h_{i}(x_{i}(t))=tanhx$ $(i=1,2)$. So $F=G=H=1$.

$$\begin{aligned} \mathscr {C}=\begin{pmatrix}0.1&{}0\\ 0&{}0.1\end{pmatrix}, \quad \mathscr {A}=\begin{pmatrix}0.2&{}-0.1\\ 0.1&{}-0.2\end{pmatrix}, \quad \mathscr {B}=\begin{pmatrix}-0.5&{}-0.1\\ -0.2&{}-0.1\end{pmatrix}, \quad \mathscr {M}=\begin{pmatrix}0.4&{}-0.1\\ 0.1&{}0.2\end{pmatrix}. \end{aligned}$$

Obviously, $C=0.1$, $A=0.3$, $B=0.7$, $M=0.5$. Next is needs to verify the quasi-uniform stability. Let $t_{0}=0$, $\delta$=0.1, $\varepsilon$=1, $\sigma$=0.05.

On one hand, when $\beta$=0.7, through employing the MATLAB, it could be verified that $P=4.9938$, $Q=0.2278$, $L=2.7994$, $N=0.6878$, $W(t)=3.0884$. By the inequality $\sqrt{P+Qe^{2t}+W(t)e^{(W(t)+2)t}(P\frac{1-e^{-(2+W(t))t}}{2+W(t)}+Q\frac{1-e^{-W(t)t}}{W(t)})}<\frac{\varepsilon }{\delta }$, it could be obtained that $T=0.6690$. On the other hand, when $\beta =0.3$, by means of the MATLAB, it could be noted that $\tilde{E}=2.4949, \tilde{P}=213.7470 , \tilde{Q}=9.2269, \tilde{L}=83.7659, \tilde{N}=16.9440, \tilde{W}(t)=84.1261$, form calculating the inequality $\root q \of {\tilde{P}+\tilde{Q}e^{qt}+\frac{\tilde{W}(t)\tilde{P}(e^{(\tilde{W}(t)+q)t}-1)}{q+\tilde{W}(t)}+\frac{\tilde{W}(t)\tilde{Q}e^{(\tilde{W}(t)+q)t}(1-e^{-\tilde{W}(t)t})}{\tilde{W}(t)}}<\frac{\varepsilon }{\delta }$, it gets $T=0.0522$.

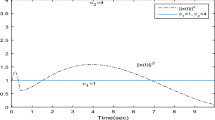
Then with fixed order $\beta$, show the trajectories of $x_{1}$ with different initial values. Here choose $\tau =0.1, \sigma =0.05, \beta =0.7$, give the time evolution of state with $x_{1}(t)=0.8, 0.5, 0.1, -0.1, -0.5, -0.8$ (see Fig. 1), and under the same conditions show the trajectories of $x_{2}$ with different initial values. Chosen to be $x_{2}(t)=0.8, 0.5, 0.1, -0.1, -0.5, -0.8$ (see Fig. 2).

Fig. 1

The trajectories of $x_{1}$ with initial values x$_{1}(t)=0.8, 0.5, 0.1, -0.1, -0.5, -0.8$

Fig. 2

The trajectories of $x_{2}$ with initial values x$_{2}(t)=0.8, 0.5, 0.1, -0.1, -0.5, -0.8$

On the other hand, with fixed order $\beta$=0.3, show the trajectories of $x_{1}$ and $x_{2}$ with the same conditions as above (see Figs. 3, 4).

Fig. 3

The trajectories of $x_{1}$ with initial values x$_{1}(t)=0.8, 0.5, 0.1, -0.1,-0.5,-0.8$

Fig. 4

The trajectories of $x_{2}$ with initial values x$_{2}(t)=0.8, 0.5, 0.1, -0.1,-0.5,-0.8$

Fig. 5

The trajectories of $x_{1}$ with the same $\sigma =0.1$, the different $\tau =0.1, 0.5, 0.8$

Furthermore, with fixed delay $\sigma =0.1$, confirmed order $\beta =0.7$, unchangeable initial values $x_{1}(t)=0.5$, $x_{2}(t)=0.5$, give the trajectories of $x_{1}$ and $x_{2}$ with different the other delay $\tau =0.1, 0.5, 0.8$ (see Figs. 5, 6).

Fig. 6

The trajectories of $x_{2}$ with the same $\sigma =0.1$, the different $\tau =0.1, 0.5, 0.8$

Following, with fixed delay $\tau =1$, confirmed order $\beta$=0.7, unchangeable initial values $x_{1}(t)=0.5$, $x_{2}(t)=0.5$, show the trajectories of $x_{1}$ and x$_{2}$ with different the other delay $\sigma =0.05, 0.1, 0.2$ (see Figs. 7, 8).

Fig. 7

The trajectories of $x_{1}$ with the same $\tau =1$, the different $\sigma =0.05, 0.1, 0.2$

Fig. 8

The trajectories of $x_{2}$ with the same $\tau =1$, the different $\sigma =0.05, 0.1, 0.2$

From the above numerical results, we could note that the neural network in this example is quasi-uniformly stable, and also the influence on quasi-uniform property with varying initial values and delays.

5 Conclusions

In this paper, quasi-uniform stability problems of a class of fractional-order neural networks with mixed delay is investigated. Not as in the integer-order delayed systems, it is very difficult to construct Lyapunov functions for fractional-order case. So by using only the inequality scaling skills in this paper, sufficient conditions ensuring quasi-uniform stability are derived. Finally, it can obtain that the fractional-order neural networks with mixed delay considered in this paper is quasi-uniformly stable through the numerical example and corresponding numerical simulation.