An efficient modified differential evolution algorithm for solving constrained non-linear integer and mixed-integer global optimization problems

Abstract

In this paper, an efficient modified Differential Evolution algorithm, named EMDE, is proposed for solving constrained non-linear integer and mixed-integer global optimization problems. In the proposed algorithm, new triangular mutation rule based on the convex combination vector of the triplet defined by the three randomly chosen vectors and the difference vectors between the best,better and the worst individuals among the three randomly selected vectors is introduced. The proposed novel approach to mutation operator is shown to enhance the global and local search capabilities and to increase the convergence speed of the new algorithm compared with basic DE. EMDE uses Deb’s constraint handling technique based on feasibility and the sum of constraints violations without any additional parameters. In order to evaluate and analyze the performance of EMDE, Numerical experiments on a set of 18 test problems with different features, including a comparison with basic DE and four state-of-the-art evolutionary algorithms are executed. Experimental results indicate that in terms of robustness, stability and efficiency, EMDE is significantly better than other five algorithms in solving these test problems. Furthermore, EMDE exhibits good performance in solving two high-dimensional problems, and it finds better solutions than the known ones. Hence, EMDE is superior to the compared algorithms.

1 Introduction

Generally, optimization is the process of finding the best result for a given problem under certain conditions. In real world problems, applications and different fields of science and engineering, the optimization problems are subject to different types of objective functions and constraints with different type of variables [1]. Thus, most of these problems can be formulated as mixed integer non-linear programming problems (MINLP) that involve continuous as well as integer decision variables. These problems are recognized as a class of NP complete problems plus due to their combinatorial nature, are considered difficult problems [2, 3]. This class of optimization problems frequently arise in various real-world problems and application fields such as mechanical design [4], Synthesis of chemical process flow sheets and design of materials [5], scheduling [6], network design [7], feature selection [8], vehicle routing [9], strategic planning [10], data classification [11] and many more [12, 13]. There are two types of MINLP according to the nature of the objective function and constraints (feasible region): convex MINLP and non-convex MINLP. The former involves minimizing a convex objective function over a convex feasible region and the latter involves minimizing an objective function and/or the continuous relaxation of the feasible region that is not convex [14]. Due to the above mentioned difficulties characteristics and such diverse area, during past decades, many attempts have been made to solve MINLP using various types of deterministic or exact approaches and stochastic or metaheuristic algorithms [15]. There are several deterministic approaches for solving convex MINLP including Branch-and-Bound Method [16, 17], Generalized Bender Decomposition [18], Outer-Approximation [19, 20], LP/NLP Based Branch-and-Bound [21], Extend Cutting Plane Method [22], Generalized Disjunctive Programming [23] and hybrid methods [24, 25] that combine classical techniques and it is considered most efficient methods [26]. On the other hand, for non-convex MINLPs, the methods are mainly based on the use of exact reformulation approach [27] or using convex envelopes or under-estimators of the non-convex feasible Region [28]. The former one allows obtaining an equivalent convex formulation of the non-convex MINLP in limited cases and all the previous techniques can be applied. The latter includes Piecewise Linear Approximations and Spatial Branch-and-Bound Methods which applies to a larger subset of non-convex MINLPs [29] and many more [30]. More details of convex MINLPs, non-convex MINLPs and their exact methods of solution are referred to the survey papers [26, 29–31]. However, the main drawbacks of these deterministic methods are such that it requires derivatives of the objective function and assumptions of continuity and convexity for the objective function and constraints. Thus, they are only applicable to problems with well-structured problems with good analytical properties. Moreover, most methods can only tackle relatively small-scale problems within a reasonable time. However, for larger problems, the global optimization method also cannot find a feasible solution within an acceptable time period [14] i.e. because MINLPs are generally NP-hard; there are no efficient exact algorithms with polynomial-time complexity for solving them. Thus there are a lot of limitations in these methods. Hence, there has been a need for developing general purpose stochastic approaches that can solve all types of MINLPs especially for handling high-dimensional, highly combinatorial and highly nonlinear problems. Metaheuristics have attracted wide attention as an alternative or hybrid methods to the exact approaches. The main advantages of these methods are that they do not require derivatives information of the objective function and constraints, or assumptions of continuity and convexity for the objective function and constraints. Besides, although these methods cannot guarantee a global solution, near-optimal solutions can often be found with reasonable computational time. However, the drawbacks of these methods are their parameter tunings. There are many stochastic approaches to solve MINLPs, such as simulated annealing algorithms [32, 33], tabu search algorithms [34], genetic algorithms [35–40], evolutionary strategies [41], evolutionary programming [42, 43], controlled random search [44], filled function techniques [45, 46], ant colony [47, 48],particle swarm optimization [49, 50], and differential evolution [51–53]. Virtually, metaheuristics have been originally proposed to overcome the challenges of global optimization problems over continuous space such as nonlinearity, non-convexity, non-continuity, non-differentiability, and/or multimodality, while traditional numerical optimization techniques had difficulties with these problems [54]. Hence, motivated by their success, more research is essentially needed trying to find solutions to MINLPs. However, from the literature, few attempts have been made to develop and extend this work in discrete space. Differential Evolution (DE) is a stochastic population-based search method, proposed by Storn and Price [55]. DE is considered the most recent evolutionary algorithms (EAs) for solving real-parameter optimization problems [56]. While DE shares similarities with other EAs, it differs significantly in the sense that in DE, distance and direction information is used to guide the search process [57]. Das and Suganthan [58] made a comprehensive review for the DE algorithm and introduced its applications to unconstrained/constrained, combinatorial, and multi-criteria optimization problems in detail. Consequently, in this article, motivated by this analysis and discussion, Constrained MINLPs are solved using an efficient modified Differential Evolution algorithm, named (EMDE). The proposed algorithm introduces a new triangular mutation rule based on the convex combination vector of the triangle and the difference vector between the best and the worst individuals among the three randomly selected vectors. The proposed novel approach to mutation operator is shown to enhance the global and local search capabilities and to increase the convergence speed of the new algorithm compared with conventional DE. EMDE uses Deb’s constraint handling technique [59] based on feasibility and the sum of constraints violations without any additional parameters. A novel triangular mutation rule without any extra parameters is proposed to balance both exploration capability and exploitation tendency and enhance the convergence speed of the algorithm. The proposed algorithm is tested and analyzed by solving a set of well-known benchmark functions. The proposed algorithm shows a superior and competitive performance to Basic DE and other recent optimization algorithms. It is worth noting that this work is an extension and modifications of our previous work in [54], there are significant differences as follows: (1) Previous work in [54] is proposed for unconstrained problems, whereas this work is proposed for constrained problems. (2) Previous work in [54] optimizes function with continuous variables only, but this work is proposed for optimizing function with mixed variables continuous and integer variables (3) The crossover rate in [54] is given by a dynamic non-linear increased probability scheme, but in this work, the crossover rate is fixed 0.5. (4) in [54], only one difference vector between the best and the worst individuals among the three randomly selected vectors with one scaling factor, uniformly random number in (0,1), is used in the mutation, but in this work, three difference vectors between the tournament best, better and worst of the selected vectors with corresponding three scaling factors, which are independently generated according to uniform distribution in (0,1), are used in the mutation scheme.(5) the triangular mutation rule is only used in this work, but in the previous work [54], The triangular mutation strategy is embedded into the DE algorithm and combined with the basic mutation strategy DE/rand/1/bin through a non-linear decreasing probability rule. (6) in previous work [54] a restart mechanism based on Random Mutation and modified BGA mutation is used to avoid stagnation or premature convergence, whereas this work does not.

The rest of the paper is organized as follows. Section 2 presents the formulation of the MINLPs. Section 3 introduces the DE algorithm. Section 4 the proposed EMDE is presented in details. Section 5 reports on the computational results of testing benchmark functions. Besides, the comparison with Basic DE and other techniques is discussed. Finally, in Sect. 6, the paper is concluded and some possible future research is pointed out.

2 Problem Statement and constraint handling

In general, Mixed Integer Nonlinear Programming problem can be expressed as follows (without loss of generality minimization is considered here [51, 52]:

$${\text{minimize }}f(\vec{x},\vec{y}),\vec{x} = (x_{1} ,x_{2} , \ldots ,x_{{n_{C} }} )\, \in \,\Re^{{n_{C} }} ,\vec{y} = (y_{1} ,y_{2} , \ldots ,y_{{n_{I} }} )\, \in \,\Re^{{n_{I} }}$$

(1)

subject to:

$$g_{j} (\vec{x},\vec{y}) \le 0\,,\,\,j = 1, \ldots ,q$$

(2)

$$h_{j\,} (\vec{x},\vec{y})\, = 0\,,\,j = q + 1, \ldots ,m$$

(3)

where $(\vec{x},\vec{y}) \in \,\varOmega \, \subseteq \,S^{{n_{C} + n_{I} }}$, n _C is the number of continuous variables, n _I is the number of integer variables, Ω is the feasible region, and Sis an (n _C  + n _I )-dimensional rectangular space in $\Re^{{n_{C} }} \cup \Re^{{n_{I} }}$ defined by the parametric constraints l _i  ≤ x _i  ≤ u _i , 1 ≤ i ≤ n _C where l _i and u _i are lower and upper bounds for a continuous decision variable x _i , l _i  ≤ y _i  ≤ u _i , 1 ≤ i ≤ n _I where l _i and u _i are lower and upper bounds for an integer decision variable y _i , respectively. For an inequality constraint that satisfies $g_{j} (\vec{x}) = 0$ (j ∊ 1, …, q)at any point $(\vec{x},\vec{y}) \in \varOmega$, we say it is active at $(\vec{x},\vec{y})$. All equality constraints $h_{j\,} (\vec{x},\vec{y}),\,(j = q + 1, \ldots ,m)$ are considered active at all points of Ω. Most constraint-handling approaches used with EAs tend to deal only with inequality constraints. Therefore equality constraints are transformed into inequality constraints of the form $\left| {h_{j} (\vec{x},\vec{y})} \right| - \varepsilon \le 0$ where ɛ is the tolerance allowed (a very small value). In order to handle constraints, we use Deb’s constraint handling procedure. Deb [59] proposed a new efficient feasibility-based rule to handle constraint for genetic algorithm where pair-wise solutions are compared using the following criteria:

• Between two feasible solutions, the one with the highest fitness values wins.

• If one solution is feasible and the other one is infeasible, the feasible solution wins.

• If both solutions are infeasible, the one with the lowest sum of constraint violation is preferred.

As a result, Deb [59] has introduced the superiority of feasible solutions selection procedure based on the idea that any individual in a constrained search space must first comply with the constraints and then with the objective function. Practically, Deb’s selection criterion does not need to fine-tune any parameter. Typically, from the problem formulation above, there are m constraints and hence the amount of constraint violation for an individual is represented by a vector of m dimensions. Using a tolerance (ɛ) allowed for equality constraints, the constraint violation of a decision vector or an individual $(\vec{x},\vec{y})$ on the jth constraint is calculated by

$$cv_{j} (\vec{x},\vec{y}) = \left\{ \begin{array}{l} \hbox{max} \,(0,g_{j} (\vec{x},\vec{y}))\,, \quad j = 1, \ldots ,q\, \hfill \\ \hbox{max} \,(0,\left| {h_{j} (\vec{x},\vec{y})} \right| - \varepsilon ), \quad j = q + 1, \ldots ,m \hfill \\ \end{array} \right.$$

(4)

If a decision vector or an individual $(\vec{x},\vec{y})$ satisfies the jth constraint, $cv_{j} (\vec{x},\vec{y})$ is set to zero, it is greater than zero. As discussed [60], in order to consider all the constraints at the same time or to treat each constraint equally, each constraint violation is then normalized by dividing it by the largest violation of that constraint in the population. Thus, the maximum violation of each constraint in the population is given by

$$cv_{\hbox{max} }^{j} = \mathop {\hbox{max} }\limits_{{\vec{x} \in s}} cv_{j} (\vec{x},\vec{y})$$

(5)

These maximum constraint violation values are used to normalize each constraint violation. The normalized constraint violations are added together to produce a scalar constraint violation $cv(\vec{x},\vec{y})$ for that individual which takes a value between 0 and 1

$$cv(\vec{x},\vec{y}) = \frac{1}{m}\sum\limits_{j = 1}^{m} {\frac{{cv_{j} (\vec{x},\vec{y})}}{{cv_{\hbox{max} }^{j} }}}$$

(6)

3 Differential evolution

This section provides a brief summary of the basic Differential Evolution (DE) algorithm. In simple DE, generally known as DE/rand/1/bin [61, 62], an initial random population consists of NP vectors $\vec{X}_{i}$,$\forall$ i = 1, 2, …, NP, is randomly generated according to a uniform distribution within the lower and upper boundaries ($x_{j}^{\text{L}} , x_{j}^{U}$). After initialization, These individuals are evolved by DE operators (mutation and crossover) to generate a trial vector. A comparison between the parent and its trial vector is then done to select the vector which should survive to the next generation [58]. DE steps are discussed below:

3.1 Initialization

In order to establish a starting point for the optimization process, an initial population must be created. Typically, each decision parameter in every vector of the initial population is assigned a randomly chosen value from the boundary constraints:

$$x_{ij}^{0} = \text{a}_{j} + rand_{j} \cdot (b_{j} - \text{a}_{j} )$$

(7)

where rand _j denotes a uniformly distributed number between [0, 1], generating a new value for each decision parameter.

3.2 Mutation

At generation G, for each target vector $x_{i}^{G}$, a mutant vector $v_{i}^{G + 1}$ is generated according to the following:

$$v_{i}^{G + 1} = x_{{r_{1} }}^{G} + F * (x_{{r_{2} }}^{G} - x_{{r_{3} }}^{G} ), \quad r_{1} \ne r_{2} \ne r_{3} \ne i$$

(8)

with randomly chosen indices r ₁, r ₂, r ₃ ∊ {1, 2, …, NP}. F is a real number to control the amplification of the difference vector $(x_{{r_{2} }}^{G} - x_{{r_{3} }}^{G} )$. According to Storn and Price [61], the range of Fis in [0, 2]. In this work, in order to verify the boundary constraints, If a component of a mutant vector goes off the search space i.e. if a component of a mutant vector violate the boundary constraints, then the new value of this component is generated using (7).

3.3 Crossover

There are two main crossover types, binomial and exponential. In the binomial crossover, the target vector is mixed with the mutated vector, using the following scheme, to yield the trial vectoru ^G+1 _i .

$$u_{ij}^{G + 1} = \left\{ {_{{x_{ij}^{G} ,\,\,\,\,rand(j) > CR\text{ and }j \ne rand(i),}}^{{v_{ij}^{G + 1} ,\,\,rand(j) \le CR\text{ }or\text{ }j = rand(i),}} } \right.$$

(9)

where j = 1, 2, …, D, rand(j) ∊ [0, 1] is the jth evaluation of a uniform random generator number. CR ∊ [0, 1] is the crossover rate, rand(i) ∊ {1, 2, …, D} is a randomly chosen index which ensures that u ^G+1 _i gets at least one element from v ^G+1 _i ; otherwise no new parent vector would be produced and the population would not alter.

In an exponential crossover, an integer value l is randomly chosen within the range {1, D}. This integer value acts as a starting point in x ^G _i , from where the crossover or exchange of components with v ^G+1 _i starts. Another integer value L (denotes the number of components) is also chosen from the interval {1, D-l}. The trial vector u ^G+1 _i is created by inheriting the values of variables in locations l to l + L from v ^G+1 _i and the remaining ones from the x ^G _i .

3.4 Selection

DE adapts a greedy selection strategy. If and only if the trial vector u ^G+1 _i yields as good as or a better fitness function value than x ^G _i , then u ^G+1 _i is set to x ^G+1 _i . Otherwise, the old vector x ^G _i is retained. The selection scheme is as follows (for a minimization problem):

$$x_{i}^{G + 1} = \left\{ {_{{x_{i}^{G} \,,\quad \text{ otherwise}}}^{{u_{i}^{G + 1} ,\quad f(u_{i}^{G + 1} ) \le f(x_{i}^{G} )}} } \right.$$

(10)

A detailed description of standard DE algorithm is given in Fig. 1.

Fig. 1

Description of standard DE algorithm. rand (0,1) is a function that returns a real number between 0 and 1. randint (min, max) is a function that returns an integer number between min and max. NP, GEN, CR and F are user-defined parameters. D is the dimensionality of the problem

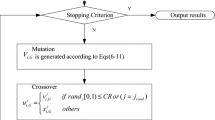
4 The proposal: EMDE

In this section, an efficient modified DE algorithm EMDE, the constraint-handling technique and handling of integer variables used in this research are described and explain the pseudo-code of the algorithm in details.

4.1 Triangular mutation scheme

DE/rand/1 is the fundamental mutation strategy developed by Storn and Price [61, 63], and it is reported to be the most successful and widely used scheme in the literature [58]. Obviously, in this strategy, the three vectors are chosen from the population at random for mutation and the base vector is then selected at random among the three. The other two vectors forms the difference vector that is added to the base vector. Consequently, it is able to maintain population diversity and global search capability with no bias to any specific search direction, but it slows down the convergence speed of DE algorithms [64]. DE/rand/2 strategy, like the former scheme with extra two vectors that forms another difference vector, which might lead to better perturbation than one-difference-vector-based strategies [64]. Furthermore, it can provide more various differential trial vectors than the DE/rand/1/bin strategy which increase its exploration ability of the search space. On the other hand, greedy strategies like DE/best/1, DE/best/2 and DE/current-to-best/1 incorporate the information of the best solution found so far in the evolutionary process to increase the local search tendency that lead to fast convergence speed of the algorithm [64]. However, the diversity of the population and exploration capability of the algorithm may deteriorate or may be completely lost through a very small number of generations i.e. at the beginning of the optimization process, that cause problems such stagnation and/or premature convergence. Consequently, in order to overcome the shortcomings of both types of mutation strategies, most of the recent successful algorithms utilize the strategy candidate pool that combines different trail vector generation strategies, that have diverse characteristics and distinct optimization capabilities, with different control parameter settings to be able to deal with a variety of problems with different features at different stages of evolution [64, 65, 66]. Contrarily, taking into consideration the weakness of existing greedy strategies, [67] introduced a new differential evolution (DE) algorithm, named JADE, to improve optimization performance by implementing a new mutation strategy “DE/current-to-p best” with optional external archive and updating control parameters in an adaptive manner. Consequently, proposing new mutations strategies that can considerably improve the search capability of DE algorithms and increase the possibility of achieving promising and successful results in complex and large scale optimization problems is still an open challenges for evolutionary computation research. Therefore, this research uses a new triangular mutation rule with a view of balancing the global exploration ability and the local exploitation tendency and enhancing the convergence rate of the algorithm. The proposed mutation strategy is based on the convex combination vector of the triplet defined by the three randomly chosen vectors and three difference vectors between the tournament best, better and worst of the selected vectors. The proposed mutation vector is generated in the following manner:

$$\nu_{i}^{G + 1} = \bar{x}_{c}^{G} + F1 \cdot (x_{best}^{G} - x_{better}^{G} ) + F2 \cdot (x_{best}^{G} - x_{worst}^{G} ) + F3 \cdot (x_{better}^{G} - x_{worst}^{G} )$$

(11)

where $\bar{x}_{c}^{G}$ is a convex combination vector of the triangle and F1, F2 and F3 are the mutation factors that are associated with x _i and are independently generated according to uniform distribution in (0,1) and $x_{best}^{G} ,x_{btter}^{G} and\;x_{worst}^{G}$ are the tournament best, better and worst three randomly selected vectors, respectively. The convex combination vector $\bar{x}_{c}^{G}$ of the triangle is a linear combination of the three randomly selected vectors and is defined as follows:

$$\bar{x}_{c}^{G} = \,w_{1} \cdot x_{best} + w_{2} \cdot x_{better} + w_{3} \cdot x_{worst}$$

(12)

where the real weights w _i satisfy w _i  ≥ 0 and $\sum\nolimits_{1 = j}^{3} {w_{i} = 1}$ . Where the real weights w _i are given by $w_{i} = p_{i} /\sum _{i = 1}^{3} p_{i}$, i = 1, 2, 3. Where p ₁ = 1, p ₂ = rand(0.75, 1) and p ₃ = rand(0.5, p(2)), rand (a,b) is a function that returns a real number between a and b, where a and b are not included. for constrained optimization problems at any generation g > 1, the tournament selection of the three randomly selected vectors and assigning weights follow one of the following three scenarios that may exist through generations, Without loss of generality, we only consider minimization problems:

Scenario 1:

If the three randomly selected vectors are feasible, then sort them in ascending according to their objective function values and assign w ₁, w ₂, w ₃ to x ^G _best , x ^G _better and x ^G _worst , respectively

Scenario 2:

If the three randomly selected vectors are infeasible, then sort them in ascending order according to their constraint violations (CV)values and assign w ₁, w ₂,w ₃to x ^G _best , x ^G _better and x ^G _worst , respectively

Scenario 3:

If the three randomly selected vectors are mixed (feasible and infeasible), then the vectors are sorted by using the three criteria: (a) Sort feasible vectors in front of infeasible solutions (b) Sort feasible solutions according to their objective function values (c) Sort infeasible solutions according to their constraint violations. Accordingly, assign w ₁, w ₂,w ₃ to x ^G _best , x ^G _better and x ^G _worst , respectively. Obviously, from mutation Eq. (11) and (12), it can be observed that the incorporation of the objective function value and constraints violation in the mutation scheme has two benefits. Firstly, the perturbation part of the mutation is formed by the three sides of the triangle in the direction of the best vector among the three randomly selected vectors. Therefore, the directed perturbation in the proposed mutation resembles the concept of gradient as the difference vector is oriented from the worst to the best vectors [68]. Thus, it is considerably used to explore the landscape of the objective function being optimized in different sub-region around the best vectors within constrained search-space through optimization process. Secondly, the convex combination vector $\bar{x}_{c}^{G}$ is a weighted sum of the three randomly selected vectors where the best vector has the highest contribution. Therefore, $\bar{x}_{c}^{G}$ is extremely affected and biased by the best vector more than the remaining two vectors. Consequently, the global solution can be easily reached if all vectors follow the direction of the best vectors besides they also follow the opposite direction of the worst vectors among the randomly selected vectors. Indeed, the new mutation process exploits the nearby region of each $\bar{x}_{c}^{G}$ in the direction of (x ^G _best  − x ^G _worst )for each mutated vector. In a nutshell, it concentrates the exploitation of some sub-regions of the search space. Thus, it has better local search tendency so it accelerates the convergence speed of the proposed algorithm. Besides, the global exploration ability of the algorithm is significantly enhanced by forming many different sizes and shapes of triangles in the feasible region through the optimization process. Thus, the proposed directed mutation balances both global exploration capability and local exploitation tendency. Illustrations of the local exploitation and global exploration capabilities of the new triangular mutation are illustrated in Figs. 2 and 3, respectively.

Fig. 2

An illustration of the new triangular mutation scheme in two-dimensional parametric space (Local Exploitation)

Fig. 3

An illustration of the new triangular mutation scheme with collection of convex combinations vectors and the newly generated donor vectors v _i corresponding to the target vectors x _i in two-dimensional parametric space (Global Exploration)

4.2 Constraint handling

In this paper, Deb’s feasibility rules [59] are used to handle the constraints. As aforementioned in Sect. 2, in the constraint-handling technique, the equality constraints are transformed to inequality constraints by a tolerance value ɛ. In the experiments, the tolerance value ɛis adopted like [69] and used in the [70]. The parameter ɛ decreases from generation to generation using the following equation:

$$\varepsilon \left( {g + 1} \right) = \left\{ {\begin{array}{ll} {\frac{\varepsilon \left( g \right)}{1.0168},} & {if \varepsilon > 10^{ - 4} } \\ {10^{ - 4} , } & {{\text{otherwise }}.} \\ \end{array} } \right.$$

(13)

where g is the generation number and the initial $\varepsilon \left( 0 \right)$ is set to 5. Regarding boundary-handling method, the re-initialization method is used (see Eq. 7), i.e. when one of the decision variable violates its boundary constraint, it is generated within the uniform distribution within the boundary, as mentioned in Sect. 3.2. The pseudo-code of NDE is presented in Fig. 4.

Fig. 4

Description of EMDE algorithm

4.3 Handling of integer variables

In its canonical form, the Differential Evolution algorithm and EMDE algorithm are only capable of optimizing unconstrained problems with continuous variables. However, there are very few attempts to transform the canonical DE and proposed EMDE algorithms to handle integer variables [51, 53, 71, 72]. In order to enhance the convergence speed and to avoid for avoiding unnecessary searches in real number field, integer variables are directly searched in the integer space, to ensure that the vector is controlled in the integer space in the evolution procedure of the EMDE. In this research, only a couple of simple modifications are required, the new generation of initial population and boundary constraints verification, the trial vector generated after novel mutation operation and the basic mutation schemes and cross over operations use rounding operator, where the operator round(x) rounds the elements of x to the nearest integers. Therefore, the initialization and mutation are as follows:

• Initialization: x ⁰ _ij  = round(l _j  + rand _j  * (u _j  - l _j )).

• Boundary constraint verification: x ^G+1 _ij  = round(l _j  + rand _j  * (u _j  - l _j )).

• New mutation: $u_{ij}^{G + 1} = round\,(\bar{x}_{c}^{G} + F1 \cdot (x_{best}^{G} - x_{better}^{G} ) + F2 \cdot (x_{best}^{G} - x_{worst}^{G} ) + F3 \cdot (x_{better}^{G} - x_{worst}^{G} ))$.

• Basic mutation: u ^G+1 _ij  = round(x ^G _r1  + F _g  * (x ^G _r2  - x ^G _r3 )).

5 Experiments and discussion

To demonstrate the feasibility and efficiency of the proposed EMDE algorithm, 18 integer and mixed integer constrained optimization problems in the literature [40] are tested. All (except problem 16) are nonlinear. The number of unknown decision variables in these problems varies from 2 to 100. However, based on self check, taking into consideration that there are few differences in problems 6, 16 and 17 in Ref. [40] from the original documents. Thus, the corrections on these problems are presented in “Appendix A”. The three main control parameters of EMDE algorithm, population size NP is 50, crossover rate Cr is fixed 0.5 and the scale factors F1, F2and F3 are uniformly random numbers in (0.1) as aforementioned. The scale factor F of the basic DE is fixed 0.5. The maximum number of generations is 1000. Thus, The maximum number of function evaluations (FEs) for all benchmark problems are set to 50,000. The experiments were executed on an Intel Pentium core i7 processor 1.6 GHz and 4 GB-RAM. EMDE algorithm is coded and realized in MATLAB. For each problem, 50 independent runs are performed and statistical results are provided including the best, median, mean, worst results and the standard deviation. Additionally, A run is considered a success if achieved value of the objective function f(x) is within 1 % of the known best solution or optimal value f(x*), where x* is the best solution or optimal value found i.e.(f(x)-f(x*)) < 0.01. For each problem, the percentage of success (obtained as the ratio of the number of successful runs to total number of runs), the statistical results about number of function evaluations (FEs) in the case of successful runs are provided including the best, median, mean, worst and standard deviation used by the algorithm in achieving the optimal solution in the case of the successful runs are also listed [40]. In order to evaluate the benefits of the proposed modifications, two experiments are conducted. Firstly, EMDE is compared with basic DE where they only differ in mutation scheme used. Then The proposed approach is compared against the following four state-of-the-art evolutionary algorithms.

• Real Coded Genetic algorithm with Laplace crossover and Power mutation (MI-LXPM) due to Deep et al. [40]. MI-LXPM algorithm is an extension of LXPM algorithm, which is efficient to solve integer and mixed integer constrained optimization problems. In MI-LXPM, Laplace crossover and Power mutation are modified and extended for integer decision variables. Moreover, a special truncation procedure for satisfaction of integer restriction on decision variables and a ‘parameter free’ penalty approach for constraint handling are used in MI-LXPM algorithm [40].

• The controlled random search technique incorporating the simulated annealing concept (the RST2ANU algorithm) due to Mohan and Nguyen [44]: this algorithm, which is primarily based on the original controlled random search approach of Price, incorporates a simulated annealing type acceptance criterion in its working so that not only downhill moves but also occasional uphill moves can be accepted. In its working it employs a special truncation procedure which not only ensures that the integer restrictions imposed on the decision variables are satisfied, but also creates greater possibilities for the search leading to a global optimal solution.

• Real Coded Genetic Algorithm with Arithmetic crossover and Non-uniform mutation (AXNUM) due to Li and Gen [73]: In AXNUM, Arithmetic crossover and Non-uniform mutation with tournament selection operator are used. It uses always rounding rule for satisfaction of integer restrictions on decision variables. Besides, a new adaptive penalty approach for the evaluation function of genetic algorithm by introducing the degree of the constraints satisfactory in order to solve constrained optimization problems.

• and Modified differential evolution algorithm of constrained nonlinear mixed integer programming (MIPDE) due to Gao et al. [51].: a variant of differential evolution (the framework is based on DE/rand/1/bin combined linearly with best solution found so far. Thus, the positions of the variation particles are self-adaptively adjusted so that the particles evolve in better direction and the feasible basis rule [59] and the dynamic constraint handling technology [74] are added to improve particles optimization’ ability.

To the best of our knowledge, It is worth noting that this is the first study compared with [40] using the complete set of test problems since its publication in 2009.

5.1 Comparison with basic DE algorithm

In this section, in order to investigate the effect of the proposed mutation, EMDE algorithm is compared with basic DE algorithm that uses DE/rand/1/bin mutation scheme. The statistical results of the EMDE and Basic DE on the benchmarks are summarized in Tables 1 and 2. It includes the known optimal solution or best solution found for each test problem and the obtained best, median, mean, worst values and the standard deviations. As shown in Table 1, EMDE is able to find the global optimal solution consistently over 50 runs with the exception of test function 8. With respect to this test function, although the optimal solutions are not consistently found, the best result achieved is very close to the global optimal solution which can be verified by the very small standard deviation. Additionally, it is able to provide the competitive results. Regarding basic DE, from Table 2, basic DE is able to find the global optimal solution consistently in the majority test functions over 30 runs with the exception of test functions 1, 7, 8, 12 and 16). EMDE and basic DE are also able to find new solution to test functions 10, 16 and 17 which is better than the best known solutions from [40]. Actually, EMDE was able to reach the new global solutions consistently for problems 10 and 16. The Better solutions obtained by EMDE and Basic DE than MI-LXPM [40] are listed in Tables 3 and 4, respectively. It is noteworthy to mentioning that problems 16 and 17 are 40 and 100 dimensions, respectively. Hence, it can be concluded that EMDE can globally optimize MINLPs with high dimensions.

Table 1 Results obtained by EMDE in 50 runs

Table 2 Results obtained by Basic DE in 50 runs

Table 3 Better solutions obtained by EMDE than MI-LXPM [40]

Table 4 Better solutions obtained by basic-DE than MI-LXPM [40]

Thus, from Table 3, it can be clearly observed that EMDE and basic DE find the global optimal value 1352439 in Problem 16. Actually, the known optimal value 1030361 is a local one. Also, a better objective function value 304153834 and 304139472 (the known one is 303062432) are found by EMDE and Basic DE, respectively, in Problem 17. However, EMDE produces better solutions than basic DE algorithm.

The computational results of EMDE and basic DE algorithm are measured by using the following two performance measures [53]:

• The success rate (SR), i.e. the proportion of convergence to the known optimal solution, which can be used to evaluate the stability and robustness of proposed algorithm.

• The mean number of fitness evaluations (FES), which can be used to assess the computational cost or efficiency of the proposed algorithm.

The statistical results about number of function evaluations (FEs) in the case of successful runs are provided including the best, median, mean, worst and standard deviation used by EMDE and basic DE algorithms in achieving the optimal solution in the case of the successful runs and the percentage of success are also listed in Tables 5 and 6, respectively. It can be obviously seen from Tables 5 and 6 that The success rate of EMDE algorithm reaches 100 % except problem 8 which is 90 %. However, the success rate of basic DE reaches 100 % with exception to problems 1,3,7,8 and 12. Besides, in terms of Number of FEs, Fig. 5 show the performance of EMDE and Basic DE algorithms in terms of Mean FEs for 18 test functions. From Fig. 5, it is clearly that mean FEs provided by EMDE is better than mean FEs provided by Basic DE in almost test problems.

Table 5 Number of FEs to achieve the fixed accuracy level (f(x)-f(x*)) < 0.01), successful rate (Ps) provided by EMDE

Table 6 Number of FEs to achieve the fixed accuracy level (f(x) − f(x*)) < 0.01), Successful rate (Ps) provided by Basic DE

Fig. 5

the performance of EMDE and Basic DE algorithms in terms of mean FEs in all test functions

Thus, in order to measure the efficiency of EMDE in solving all test problems, the sum of the mean FEs provided by Basic DE is 48221.51099 while the sum of the mean FEs produced by EMDE is 25145.36714. Therefore, on average, the improvement percentage of EMDE in terms of FEs in comparison to Basic DE is 47.85 %. Therefore, EMDE is considered the most efficient with the smallest total mean (FEs) which prove the searching ability of the proposed triangular mutation in balancing both exploration capability and exploitation tendency and enhance the convergence speed of the algorithm. Additionally, Fig. 6 show the convergence graphs of f(x)) over FEs at the median run of EMDE and Basic DE algorithms for each test problem with 50,000 FEs. From Fig. 6, it can be obviously seen that a fast convergence of both EMDE and basic DE but it shows that EMDE algorithms converge to better or global solution faster than basic DE in all cases, for function 12 the basic DE is easily trapped into local optimum, and functions can jump out of local optima with EMDE to find the global optimum, indicating that EMDE has strong searching ability and its stability is very good. From the above analysis, it can be concluded that EMDE has a fast convergence speed for these 18 test functions. Accordingly, the main benefits of the new triangular mutation are the fast convergence speed and the extreme robustness which are the weak points of all evolutionary algorithms. Therefore, the proposed EMDE algorithm is proven to be an effective and powerful approach to solve constrained mixed integer nonlinear programming problems.

Fig. 6

Convergence graph (median curves) of EMDE and Basic DE on test functions f 1–f 18

5.2 Comparison with other algorithms in the literature

To further verify the performance of EMDE, comparisons are carried out with aforementioned four competitive state-of-the-art evolutionary algorithms. Experimental results obtained by five algorithms are given in Table 7, where (ps) is success rate representing percentage of the successful runs to total runs for the algorithm, and (mean FEs) represents average number of objective function evaluations used by the algorithm in successful runs. The results provided by MI-LXPM, RST2ANU and AXNUM approaches were directly taken from Ref. [40] while for MIPDE was directly taken from Ref. [51]. Note that MIPDE algorithm solved only 14 benchmark problems with exception to problems 14, 16,17 and 18. According to the results shown in Table 7, it can be obviously seen that that EMDE algorithm can obtain the optimal solution for different kinds of linear or nonlinear mixed integer programming problems with a success rate of 100 % for all test function except problem 8 with 90 %, which verifies the stability and robustness of EMDE again, in fact, with no need for parameters to be fine-tuned. Furthermore, regarding mean FEs, it can be observed that EMDE produces 11, 14, 16 and 10 significantly better and 7, 4,2 and 4 slightly worse than MI-LXPM, RST2ANU, AXNUM and MIPDE algorithms for test problems, respectively. Thus, in order to measure the efficiency of EMDE in solving all test problems, the sum of the mean FEs provided by MI-LXPM, RST2ANU, AXNUM and MIPDE algorithms are 346575, 1913761, 804127 and 59369 while the sum of the mean FEs produced by EMDE is 25145.36714. Therefore, EMDE is considered the most efficient with the remarkable smallest total mean (FEs). Figure 7 show the performance of EMDE and MI-LXPM, RST2ANU, AXNUM and MIPDE algorithms in terms of total Mean FEs for all test functions. All in all, EMDE is superior to all compared EAs algorithms in terms of both measures success rate and efficiency.

Table 7 Results obtained by using EMDE, MI-LXPM, RST2ANU, AXNUM and MIPDE algorithms

Fig. 7

the performance of EMDE, MI-LXPM, RST2ANU, AXNUM a and MIPDE algorithms in terms of total Mean of FEs

6 Conclusion

In this paper, an efficient modified Differential Evolution algorithm EMDE is proposed for solution of constrained, integer and mixed integer optimization problems which are considered difficult optimization problems. In this algorithm new triangular mutation rule based on the convex combination vector of the triplet defined by the three randomly chosen vectors and the difference vectors between the best,better and the worst individuals among the three randomly selected vectors is introduced. The proposed novel approach to mutation operator is shown to enhance the global and local search capabilities and to increase the convergence speed of the new algorithm compared with basic DE. EMDE uses “parameter free” Deb’s constraint handling technique based on feasibility and the sum of constraints violations. Integer variables are directly searched in the integer space by using round operator, to ensure that the vector is controlled in the integer space in the evolution procedure of the EMDE. The performance of the proposed EMDE is compared with basic DE, MI-LXPM, RST2ANU, AXNUM and MIPDE algorithms on a set of 18 test problems. Our results show that the proposed EMDE algorithm outperforms remarkably other compared algorithms in terms of stability, robustness and efficiency. Accordingly, Firstly, Current research effort focuses on how to control the crossover rate by self-adaptive mechanism. Additionally, future research will investigate the performance of the EMDE algorithm in solving unconstrained and constrained multi-objective optimization problems. In future the proposed EMDE algorithm may be compared with other stochastic approaches like harmony search and particle swarm optimization, artificial bee colony, bees algorithm and ant colony optimization. Additionally, it is also worth trying to apply the present approach to the solution of real-world optimization problems.

Appendix

Corrections on problems 6, 16 and 17.

Based on self check, there are few differences in problems 6, 16 and 17 in Ref. [40] from the original documents. Thus, the corrections on these problems are as follows.

Problem	Objective function or constraints	Ref. [40]	Correction	Original references
6	Constraint	x 4	3x 4	[32]
16	Constraint 1	9x 1	8x 1	[75]
17	Objective function	$15x_{35}^{35} ,3x_{94}^{2}$	$15x_{35}^{3} ,3x_{94}^{2}$	[75]