A novel differential evolution algorithm for solving constrained engineering optimization problems

Abstract

This paper introduces a novel differential evolution (DE) algorithm for solving constrained engineering optimization problems called (NDE). The key idea of the proposed NDE is the use of new triangular mutation rule. It is based on the convex combination vector of the triplet defined by the three randomly chosen vectors and the difference vectors between the best, better and the worst individuals among the three randomly selected vectors. The main purpose of the new approach to triangular mutation operator is the search for better balance between the global exploration ability and the local exploitation tendency as well as enhancing the convergence rate of the algorithm through the optimization process. In order to evaluate and analyze the performance of NDE, numerical experiments on three sets of test problems with different features, including a comparison with thirty state-of-the-art evolutionary algorithms, are executed where 24 well-known benchmark test functions presented in CEC’2006, five widely used constrained engineering design problems and five constrained mechanical design problems from the literature are utilized. The results show that the proposed algorithm is competitive with, and in some cases superior to, the compared ones in terms of the quality, efficiency and robustness of the obtained final solutions.

Introduction

Generally, optimization is the process of finding the best results for a given problem under certain conditions. In real world problems, applications and different fields of science and engineering, most of the optimization problems are subject to different types of constraints. Thus, these problems are called constrained optimization problems (COPs) and are considered challenging and complex due to their variations in mathematical properties and structures (Mohamed and Sabry 2012; de Melo and Carosio 2012; Dong and Wang 2014; Elsayed et al. 2014; Akay and Karaboga 2012; Brajevic and Tuba 2013; Yi et al. 2016a, b; Yu et al. 2016; Mohamed 2015b). COPs can be classified in several ways depending on their mathematical properties. They can be classified based on the nature of variables, such as real, integer and discrete, and may have equality and/or inequality constraints. Another important alternative classification depends on the type of expression of objective and constraints functions. It can be classified as linear or non-linear, continuous or discontinuous and unimodal or multimodal. Furthermore, the feasible region of such problems can be either a tiny or significant portion of the search space. It can be either one single-bounded region or a collection of multiple disjoint regions.

Due to the above mentioned difficulties characteristics, over the past decade, many attempts have been made to solve COPs using various types of computational intelligence algorithms together with different constraint-handling techniques. A complete study on the most constraint-handling techniques used with evolutionary algorithms (EAs) has been discussed in details (Coello 2002). In this research, most recent studies and well-known algorithms done over the past decade are discussed. As a matter of fact, Genetic Algorithms (GAs) are considered the pioneer algorithm of EAs and have been successfully applied to solve constrained optimization problems. Tessema and Yen (2006) introduced a GA based on an adaptive penalty function. The introduced method aimed to exploit infeasible individuals with low objective function values and low constraint violations. The approach was tested on a set of 13 benchmark problems with the results showing that the approach was able to find feasible solutions in all runs. However, its performance was not robust. A multi-objective optimization based on a hybrid evolutionary algorithm to solve constrained optimization problems, named (HCOEA), was proposed by Wang et al. (2007). This method consists of two main parts: the global search model and the local search model. In the global search model, a niching genetic algorithm is proposed. The local search model performs a parallel local search operation based on clustering partition of the population. In this method, the comparison of individuals is based on multi-objective optimization technique. Recently, Elsayed et al. (2011) proposed a self-adaptive multi-operator genetic algorithm (SAMO-GA). In SAMO-GA, the population is divided into four sub-populations with individual crossover and mutation where the feasibility rules proposed by Deb (2000) were used to handle the constraints. SAMO-GA has shown significant improvement in comparison to other variants of GA with a single operator. Many optimization problems have been solved by using other branches of EAs which are evolutionary strategies (ES) and evolutionary programming (EP). Mezura-Montes and Coello (2005) proposed a simple multi membered evolution strategy to solve constrained optimization problems (SMES). Instead of using the penalty function approach, the proposed approach uses a simple diversity mechanism which allows infeasible solutions to remain in the population. The approach tested on the benchmark problems and the results obtained were very competitive when compared with other techniques in terms of the number of function evaluations used. On the other hand and as motivated by the ensemble operators technique in the literature, an ensemble of four constraint handling techniques combined with evolutionary programming algorithm, named (ECHT-EP2), is proposed by Mallipeddi and Suganthan (2010). The performance of ECHT-EP2 is competitive to the state-of-the-art algorithms. Nonetheless, since most real life problems can be mathematically formulated as optimization problems, developing another various types of efficient optimization techniques to deal with unconstrained and constrained problems has attracted much research in recent years, such as swarm intelligence which is nature-inspired algorithms that include the well-known algorithm, particle swarm optimization (PSO). Besides, latest swarm algorithms, the Firefly Algorithm (FA) was first proposed (Yang 2009), the artificial bee colony (ABC) was originally proposed (Karaboga 2005) and Seeker Optimization Algorithm (SOA) was recently proposed (Dai et al. 2006). Elsayed et al. (2014) proposed a self-adaptive mix of particle swarm methodologies (SAM-PSO). In the proposed ensemble algorithm, a set of different PSO variants are used and each of which evolves with different number of individuals from the current population. Besides, a new PSO variant is developed to balance both local and global PSO versions. SAM-PSO outperforms other PSO variants and other state-of-the-art algorithms. A modified Artificial Bee Colony algorithm (M-ABC) is proposed (Mezura-Montes and Cetina-Domínguez). Four modifications are made to improve its performance in a constrained search space. In order to improve the performance of both FA and SOA in solving constrained optimization problems, Tuba and Bacanin (2014) proposed a modified algorithm that hybridizes FA and SOA, named SOA-FS. It outperforms other state-of-the-art swarm intelligence algorithms. Similar to other Evolutionary algorithms (EAs), differential evolution (DE) is a stochastic population based search method, proposed by Storn and Price (1995). The DE algorithm coupling with the constraint-handling technique has been successfully used for solving the COPs. Becerra and Coello (2006) proposed a cultural algorithm with a differential evolution population for the COPs. In this method, this culture algorithm has used different knowledge sources to influence the variation operator of the differential evolution algorithm. Zhang et al. (2008) introduced multi-member DE with dynamic stochastic ranking to keep the feasible solutions as well as the promising infeasible solution during the evolution process. After extensive experiments studying the performance of several DE variants for solving the COPs, Mezura-Montes et al. (2010) combined two variants: DE/rand/1/bin and DE/best/1/bin into one single approach, called (DECV). Recently, a novel constrained optimization based on a modified DE algorithm (COMDE) is proposed by Mohamed and Sabry (2012), where a new directed mutation strategy and a new dynamic tolerance technique have been developed to handle equality constraints. Taking advantage of multi-objective optimization techniques, Wang and Cai (2012) presented a multi-objective optimization based on differential evolution algorithm, named (CMODE), with novel infeasible solution replacement mechanism to guide the population toward feasible region. Gong et al. (2014), presented the rank-iMDDE method, in which DE is combined with a ranking-based mutation operator to enhance the convergence speed and an improved dynamic diversity mechanism to maintain either infeasible or feasible solutions in the population. Elsayed et al. (2011) proposed self-adaptive DE algorithm with multi-operator strategy (SAMO-DE). In this algorithm, two DE variants rand-to-best and current/2/best are used for mutation and Gaussian numbers are used to generate F and CR values. Motivated by the recent success of diverse memetic approaches to solve many optimization problems, Dong and Wang (2014) proposed a new memetic DE algorithm with dynamic preference (MDEDP). In this memetic algorithm, DE is the global search and it is guided by a novel achievement scalarizing function. Simplex crossover (SPX) is used as a local search procedure to guide the search approaching the boundary of the feasible region. After performing many experimental analyses using eight different variants of the DE algorithm to solve COPs, a self-adaptive multi-strategy DE (SAMSDE) is exhibited by Elsayed et al. (2012). The proposed algorithm divides the population into a number of subpopulations, where each subpopulation evolves with its own mutation and crossover. The population size, crossover rate and scaling factor are adaptive to the search progresses. To speed up the convergence of SAMSDE, the SQP based local search is used to a randomly selected individual from the entire population. Elsayed et al. (2013) introduced an improved self-adaptive multi-operator DE algorithm (ISAMODE-CMA) that adopts a mix of different DE mutation operator. To improve the local search ability of DE, CMA-ES proposed by Hansen et al. (2003) is periodically applied. To tackle constraints of the problem, the dynamic penalty constraints-handling technique is used. Along the same lines, Asafuddoula et al. (2014), proposed an adaptive hybrid DE algorithm (AH-DEa). In this algorithm, the basic mutation strategy DE/rand/1/bin is combined with binomial and exponential crossover. Additionally, the crossover rate is adaptively controlled based on the success of the trial solutions generated. The Sequential Quadratic Programming (SQP) based local search is invoked from the best individual found to explore possibilities of further improvement. Following the same concept of parameter adaptation with different mechanisms, Sarker et al. (2014) presented a DE algorithm with dynamic parameters selection (DE-DPS), where three sets of DE parameters, amplification factor (F), crossover rate (CR) and population size (NP) are considered. Each individual is assigned a random combination of F and CR. For each combination, the success rate is recorded for a certain number of generations and the one with better performance is applied for a number of following generations. This process is repeated for many cycles. From the above discussion and analysis of the recent studies to solve COPs, it can be seen that all previous and current attempts have focused on applying ensemble operator techniques or hybridizing one or more algorithms and/or methods coupling with developing self-adaptive mechanism which lead to complicated algorithms with extra parameters. However, with the exception of Mohamed and Sabry (2012), few attempts have been made to develop a new mutation scheme to further improve the performance of DE. Consequently, motivated by this analysis and discussion, a novel triangular mutation rule without any extra parameters is proposed; the aim being to balance both the exploration capability and the exploitation tendency and enhance the convergence speed of the algorithm. The proposed algorithm is tested and analyzed by solving a set of well-known benchmark functions and engineering and mechanical design problems. The proposed algorithm shows a superior and competitive performance to other recent constrained optimization algorithms. It is worth noting that although this work is an extension and modification of our previous work in Mohamed (2015a), there are significant differences and these are as follows: (1) Previous work in Mohamed (2015a) is proposed for unconstrained problems, whereas this work is proposed for constrained problems. (2) The crossover rate in Mohamed (2015a) is given by a dynamic non-linear increased probability scheme, but in this work, the crossover rate is fixed 0.95. (3) in Mohamed (2015a), only one difference vector between the best and the worst individuals among the three randomly selected vectors with one scaling factor, uniformly random number in (0, 1), is used in the mutation, but in this work, three difference vectors between the tournament best, better and worst of the selected vectors with corresponding three scaling factors, which are independently generated according to uniform distribution in (0, 1), are used in the mutation scheme. (4) the triangular mutation rule is only used in this work, but in the previous work (Mohamed 2015a), the triangular mutation strategy is embedded into the DE algorithm and combined with the basic mutation strategy DE/rand/1/bin through a non-linear decreasing probability rule. (5) In the previous work (Mohamed 2015a) a restart mechanism based on Random Mutation and modified BGA mutation is used to avoid stagnation or premature convergence, whereas this work does not. The rest of the paper is organized as follows: “Problem formulation and constraint handling” section presents the formulation of the COPs. “Differential evolution” section introduces the DE algorithm. The fourth section proposed NDE is presented in details. “Experimental results and analysis” section reports on the computational results of testing benchmark functions and some engineering and mechanical optimization problems. Besides, the comparison with other techniques is discussed. Finally, in “Conclusion” section, the paper is concluded and some possible future research is suggested.

Problem formulation and constraint handling

In general, constrained optimization problem can be expressed as follows (without loss of generality minimization is considered here) (Mohamed and Sabry 2012):

$$\begin{aligned} \hbox {Minimize }f(\vec {x}),\vec {x}=(x_1, x_2,\ldots ,x_n ) \in \mathfrak {R}^{n} \end{aligned}$$

(1)

Subject to:

$$\begin{aligned}&g_j (\vec {x})\le 0,\quad j=1,\ldots ,q \end{aligned}$$

(2)

$$\begin{aligned}&h_{j } (\vec {x}) =0,\quad j=q+1,\ldots ,m \end{aligned}$$

(3)

where $\vec {x}\in \Omega \subseteq S, \Omega$ is the feasible region, and S is an n-dimensional rectangular space in $\mathfrak {R}^{n}$ defined by the parametric constraints $l_i \le x_i \le u_i, 1\le i\le n$ where $l_i$ and $u_i$ are lower and upper bounds for a decision variable $x_i$, respectively. For an inequality constraint that satisfies $g_j (\vec {x})=0(j\in 1,\ldots ,q)$ at any point $\vec {x}\in \Omega$, we say it is active at $\vec {x}$. All equality constraints $h_{j } (\vec {x}) (j=q+1,\ldots ,m)$ are considered active at all points of $\Omega$. Most constraint-handling approaches used with EAs tend to deal only with inequality constraints. Therefore equality constraints are transformed into inequality constraints of the form $\left| {h_j (\vec {x})} \right| -\varepsilon \le 0$ where $\varepsilon$ is the tolerance allowed (a very small value). In order to handle constraints, we use Deb’s constraint handling procedure. Deb (2000) proposed a new efficient feasibility-based rule to handle constraint for genetic algorithm where pair-wise solutions are compared using the following criteria:

• Between two feasible solutions, the one with the highest fitness values wins.

• If one solution is feasible and the other one is infeasible, the feasible solution wins.

• If both solutions are infeasible, the one with the lowest sum of constraint violation is preferred.

As a result, Deb (2000) has introduced the superiority of feasible solutions selection procedure based on the idea that any individual in a constrained search space must first comply with the constraints and then with the objective function. Practically, the Deb’s selection criterion does not need to fine-tune any parameter. Typically, from the problem formulation above, there are m constraints and hence the amount of constraint violation for an individual is represented by a vector of m dimensions. Using a tolerance $(\varepsilon )$ allowed for equality constraints, the constraint violation of a decision vector or an individual $\vec {x}$ on the jth constraint is calculated by

$$\begin{aligned} cv_j (\vec {x})=\left\{ {\begin{array}{ll} \max (0,g_j (\vec {x})),&{}\quad j=1,\ldots ,q \\ \max (0,\left| {h_j (\vec {x})} \right| -\varepsilon ),&{}\quad j=q+1,\ldots ,m\\ \end{array}} \right. \end{aligned}$$

(4)

If a decision vector or an individual $\vec {x}$ satisfies the jth constraint, $cv_j (\vec {x})$ is set to zero, otherwise it is greater than zero. Thus, in order to consider all the constraints at the same time or to treat each constraint equally, each constraint violation is then normalized by dividing it by the largest violation of that constraint in the population (Venkatraman and Yen 2005). Thus, the maximum violation of each constraint in the population is given by

$$\begin{aligned} cv_{\max }^j =\mathop {\max }\limits _{\vec {x}\in s} cv_j (\vec {x}) \end{aligned}$$

(5)

These maximum constraint violation values are used to normalize each constraint violation. The normalized constraint violations are added together to produce a scalar constraint violation $cv(\vec {x})$ for that individual which takes a value between 0 and 1

$$\begin{aligned} cv(\vec {x})=\frac{1}{m}\sum _{j=1}^m {\frac{cv_j (\vec {x})}{cv_{\max }^j }} \end{aligned}$$

(6)

Differential evolution

This section provides a brief summary of the basic Differential Evolution (DE) algorithm. In simple DE, generally known as DE/rand/1/bin (Storn and Price 1997; Fan and Lampinen 2003), an initial random population, denoted by P, consists of NP individual. Each individual is represented by the vector ${\mathrm{x}}_i =(x_{1,i},x_{2,i},\ldots ,x_{D,i} )$, where D is the number of dimensions in solution space. Since the population will be varied with the running of evolutionary process, the generation times in DE are expressed by $G=0,1,\ldots ,G_{\max }$, where $G_{\max }$ is the maximal time of generations. For the $i\hbox {th}$ individual of P at the G generation, it is denoted by ${\mathrm{x}}_i^G =(x_{1,i}^G,x_{2,i}^G ,\ldots ,x_{D,i}^G )$. The lower and upper bounds in each dimension of search space are respectively recorded by ${\mathrm{x}}_L =(x_{1,L}, x_{2,L} ,\ldots ,x_{D,L})$ and ${\mathrm{x}}_U =(x_{1,U}, x_{2,U}, \ldots ,x_{D,U} )$. The initial population $\hbox {P}^{0}$ is randomly generated according to a uniform distribution within the lower and upper boundaries $({\mathrm{x}}_L,{\mathrm{x}}_U)$. After initialization, these individuals are evolved by DE operators (mutation and crossover) to generate a trial vector. A comparison between the parent and its trial vector is then made to select the vector which should survive to the next generation (Das and Suganthan 2011). DE steps are discussed below:

Initialization

In order to establish a starting point for the optimization process, an initial population $\hbox {P}^{0}$ must be created. Typically, each $j\hbox {th}$ component $(j=1,2,\ldots ,D)$ of the $i\hbox {th}$ individuals $(i=1,2,\ldots ,NP)$ in the $\hbox {P}^{0}$ is obtained as follows:

$$\begin{aligned} x_{j,i}^0 =x_{j,L} +\hbox {rand}(0,1)\cdot (x_{j,U} -x_{j,L} ) \end{aligned}$$

(7)

where rand (0, 1) returns a uniformly distributed random number in [0, 1].

Mutation

At generation G, for each target vector $x_i^G$, a mutant vector $v_i^G$ is generated according to the following:

$$\begin{aligned} v_i^G =x_{r_1 }^G +F\cdot \left( x_{r_2 }^G -x_{r_3 }^G \right) , r_1 \ne r_2 \ne r_3 \ne i \end{aligned}$$

(8)

With randomly chosen indices $r_1, r_2, r_3 \in \{1,2,\ldots ,NP\}$. F is a real number to control the amplification of the difference vector $(x_{r_2 }^G -x_{r_3 }^G )$. According to (Storn and Price 1997), the range of F is in [0, 2]. In this work, If a component of a mutant vector violates search space, the value of this component is generated a new using (7).

Crossover

There are two main crossover types, binomial and exponential. In the binomial crossover, the target vector is mixed with the mutated vector, using the following scheme to yield the trial vector $u_i^G$.

$$\begin{aligned} u_{{j,i}}^{G} = \left\{ \begin{array}{ll} {v_{{j,i}}^{G},} &{} \quad {if\,\,(rand_{{j,i}} \le CR}\quad or\quad j = j_{{rand}} ) \\ {x_{{j,i}}^{G},} &{}\quad \hbox {otherwise} \\ \end{array} \right. \end{aligned}$$

(9)

where $rand_{j,i} (i\in [1,NP]\,\, and\,\, j\in [1,D])$ is a uniformly distributed random number in [0, 1], $CR\in [0,1]$ called the crossover rate that controls how many components are inherited from the mutant vector, $j_{rand}$ is a uniformly distributed random integer in [1, D] that makes sure at least one component of trial vector is inherited from the mutant vector.

Selection

DE adapts a greedy selection strategy. If and only if the trial vector $u_i^G$ yields as good as or a better fitness function value than $x_i^G$, then $u_i^G$ is set to $x_i^{G+1}$. Otherwise, the old vector $x_i^G$ is retained. The selection scheme is as follows (for a minimization problem):

$$\begin{aligned} x_{i}^{{G + 1}} = \left\{ \begin{array}{lll} {u_{i}^{G},} &{} {\quad f(u_{i}^{G} ) \le f(x_{i}^{G} )} \\ {x_{i}^{G},} &{} {\quad \hbox {otherwise}} \\ \end{array} \right. \end{aligned}$$

(10)

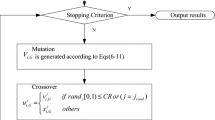
A detailed description of standard DE algorithm is given in Fig. 1.

Fig. 1

Description of standard DE algorithm. rand [0, 1) is a function that returns a real number between 0 and 1. randint (min, max) is a function that returns an integer number between min and max. NP, $G_{\max }$, CR and F are user-defined parameters. D is the dimensionality of the problem

The proposal: NDE

In this section, a novel DE algorithm NDE and the constraint-handling technique used in this research are described and they explain the pseudo-code of the algorithm in details.

Triangular mutation scheme

DE/rand/1 is the fundamental mutation strategy developed by (Storn and Price 1997; Price et al. 2005), and it is reported to be the most successful and widely used scheme in the literature (Brest et al. 2006). Obviously, in this strategy, the three vectors are chosen from the population at random for mutation and the base vector is then selected at random among the three. The other two vectors form the difference vector that is added to the base vector. Consequently, it is able to maintain population diversity and global search capability with no bias to any specific search direction, but it slows down the convergence speed of DE algorithms (Qin et al. 2009). DE/rand/2 strategy is the same as the former scheme with extra two vectors that forms another difference vector, which might lead to better perturbation than one-difference-vector-based strategies (Qin et al. 2009). Furthermore, it can provide more various differential trial vectors than the DE/rand/1/bin strategy which increases its exploration ability of the search space. On the other hand, greedy strategies like DE/best/1, DE/best/2 and DE/current-to-best/1 incorporate the information of the best solution found so far in the evolutionary process to increase the local search tendency that leading to fast convergence speed of the algorithm (Qin et al. 2009). However, the diversity of the population and exploration capability of the algorithm may deteriorate or may completely diminish through a very small number of generations i.e. at the beginning of the optimization process that causes problems such as stagnation and/or premature convergence. Consequently, in order to overcome the shortcomings of both types of mutation strategies, most of the recent successful algorithms utilize the strategy candidate pool that combines different trail vector generation strategies that have diverse characteristics and distinct optimization capabilities, with different control parameter settings to deal with a variety of problems with different features at different stages of evolution (Qin et al. 2009; Mallipeddi et al. 2011; Wang et al. 2011). Contrarily, taking into consideration the weakness of existing greedy strategies, Zhang and Sanderson (2009) introduced a new differential evolution (DE) algorithm, named JADE, to improve the optimization performance by implementing a new mutation strategy called “DE/current-to-p best” with optional external archive and updating control parameters in an adaptive manner. Consequently, proposing new mutations strategies that can considerably improve the search capability of DE algorithms and increase the possibility of achieving promising and successful results in complex and large scale optimization problems is still an open challenge for evolutionary computation research. Therefore, this research uses a new triangular mutation rule with a view of balancing the global exploration ability and the local exploitation tendency and enhancing the convergence rate of the algorithm. The proposed mutation strategy is based on the convex combination vector of the triplet defined by the three randomly chosen vectors and three difference vectors between the tournament best, better and worst of the selected vectors. The proposed mutation vector is generated in the following manner:

$$\begin{aligned} \nu _i^{G+1}= & {} \bar{{x}}_c^G + F1\cdot (x_{best}^G -x_{better}^G )+F2\cdot (x_{best}^G -x_{worst}^G )\nonumber \\&+\,F3\cdot (x_{better}^G-x_{worst}^G) \end{aligned}$$

(11)

where $\bar{{x}}_c^G$ is a convex combination vector of the triangle and F1, F2 and F3 are the mutation factors that are associated with $x_i$ and are independently generated according to uniform distribution in (0, 1) and $x_{best}^G, x_{better}^G$ and $x_{worst}^G$ are the tournament best, better and worst three randomly selected vectors, respectively. The convex combination vector $\bar{{x}}_c^G$ of the triangle is a linear combination of the three randomly selected vectors and is defined as follows:

$$\begin{aligned} \bar{{x}}_c^G = w_1 \cdot x_{best} +w_2 \cdot x_{better} +w_3 \cdot x_{worst} \end{aligned}$$

(12)

where the real weights $w_i$ satisfy $w_i \ge 0$ and $\sum \nolimits _{i=1}^3 {w_i } =1$. Where the real weights $w_i$ are given by $w_i ={p_i }/{\sum \nolimits _{i=1}^3 {p_i }},i=1,2,3.$ Where $p_1 =1, p_2=rand(0.75,1)$ and $p_3 =rand(0.5,p(2))$, $rand\left( {a,b} \right)$ is a function that returns a real number between a and b. where a and b are not included. For constrained optimization problems at any generation $\hbox {g}>1$, the tournament selection of the three randomly selected vectors and assigning weights follows one of the following three scenarios that may exist through generations. Without loss of generality, we only consider minimization problems:

Scenario 1: If the three randomly selected vectors are feasible, then sort them in ascending order according to their objective function values and assign $w_1, w_2,w_3$ to $x_{best}^G, x_{better}^G$ and $x_{worst}^G$, respectively.

Scenario 2: If the three randomly selected vectors are infeasible, then sort them in ascending order according to their constraint violations (CV)values and assign $w_1, w_2 ,w_3$ to $x_{best}^G, x_{better}^G$ and $x_{worst}^G$, respectively.

Fig. 2

An illustration of the new triangular mutation scheme in two-dimensional parametric space (local exploitation)

Scenario 3: If the three randomly selected vectors are mixed (feasible and infeasible), then the vectors are sorted by using the three criteria: (a) Sort feasible vectors in front of infeasible solutions (b) Sort feasible solutions according to their objective function values (c) Sort infeasible solutions according to their constraint violations. Accordingly, assign $w_1, w_2, w_3$ to $x_{best}^G, x_{better}^G$ and $x_{worst}^G$, respectively. Obviously, from mutation Eqs. (11) and (12), it can be observed that the incorporation of the objective function value and constraints violation in the mutation scheme has two benefits. Firstly, the perturbation part of the mutation is formed by the three sides of the triangle in the direction of the best vector among the three randomly selected vectors. Therefore, the directed perturbation in the proposed mutation resembles the concept of gradient as the difference vector is oriented from the worst to the best vectors (Feoktistov 2006). Thus, it is considerably used to explore the landscape of the objective function being optimized in different sub-region around the best vectors within constrained search-space through the optimization process. Secondly, the convex combination vector $\bar{{x}}_c^G$ is a weighted sum of the three randomly selected vectors where the best vector has the highest contribution. Therefore, $\bar{{x}}_c^G$ is extremely affected and biased by the best vector more than the remaining two vectors. Consequently, the global solution can be easily reached if all vectors follow the direction of the best vectors together with the fact that they also follow the opposite direction of the worst vectors among the randomly selected vectors. Indeed, the new mutation process exploits the nearby region of each $\bar{{x}}_c^G$ in the direction of $(x_{best}^G -x_{worst}^G)$ for each mutated vector. In a nutshell, it concentrates on the exploitation of some sub-regions of the search space. Thus, it has better local search tendency so it accelerates the convergence speed of the proposed algorithm. Besides, the global exploration ability of the algorithm is significantly enhanced by forming many different sizes and shapes of triangles in the feasible region through the optimization process. Thus, the proposed directed mutation balances both the global exploration capability and the local exploitation tendency. Illustrations of the local exploitation and global exploration capabilities of the new triangular mutation are illustrated in Figs. 2 and 3, respectively.

Fig. 3

An illustration of the new triangular mutation scheme with collection of convex combinations vectors and the newly generated donor vectors $\upnu _{i}$ corresponding to the target vectors $x_i$ in two-dimensional parametric space (global exploration)

Fig. 4

Description of NDE algorithm

Constraint handling

In this paper, Deb’s feasibility rules (Deb 2000) are used to handle the constraints. As aforementioned in “Problem formulation and constraint handling” section, in the constraint-handling technique, the equality constraints are transformed to inequality constraints by a tolerance value $\varepsilon$. In the experiments, the tolerance value $\varepsilon$ is adopted like (Mezura-Montes and Coello 2005) and is used in Yang (2009). The parameter $\varepsilon$ decreases from generation to generation using the following equation:

$$\begin{aligned} \varepsilon \left( {g+1} \right) =\left\{ \begin{array}{ll} \frac{\varepsilon (g)}{1.0168},&{}\quad if\,\,\upvarepsilon >10^{-4} \\ 10^{-4},&{}\quad otherwise. \\ \end{array} \right. \end{aligned}$$

(13)

where g is the generation number and the initial $\varepsilon (0)$ is set to 5 with all problems with exception to g17 and g23, it is set to 10. Regarding the boundary-handling method, the re-initialization method is used (see Eq. 7), i.e. when one of the decision variables violates its boundary constraint, it is generated within the uniform distribution within the boundary. The pseudo-code of NDE is presented in Fig. 4.

Experimental results and analysis

In this section, the performance of NDE is evaluated by performing comprehensive experiments using benchmark functions, engineering and mechanical design problems.

Table 1 Main characteristics of 24 benchmark problems

Table 2 The results of NDE on the benchmarks, where “–” means no feasible solution is found

Benchmark test functions and parameter settings

In this paper, 24 well-known benchmark test functions from CEC 2006 mentioned in (Liang et al. 2006) are used. The features of 24 benchmark functions are listed in Table 1. Obviously, from Table 1, n is the number of decision variables. These test functions contain several types of objective function shapes (e.g. linear, non-linear, and quadratic) as well as different types of constraints [e.g. linear inequality (LI), non-linear equality (NE), and non-linear-inequality (NI)], LI denotes the number of linear inequalities, NE denotes the number of non-linear equation, NI denotes the number of non-linear inequalities, a represents the number of active constraints at the global optimum solution, and $f\left( {x^{*}} \right)$ is the objective function value of the best known solution $x^{*}$ . $\rho ={\left| F \right| }/{\left| S \right| }$ is the feasibility ratio between the feasible region and whole search space. Note that 11 test functions (g03, g05, g11, g13, g14, g15, g17, g20, g21, g22, and g23) contain equality constraints. The $f\left( {x^{*}} \right)$ of g17 in Table 1 is different from that in (Liang et al. 2006) because NDE finds a better solution for test function g17 than the best known solutions from (Liang et al. 2006) where $x^{*}= (201.7844624935499400$, 99.9999999999995310, 383.0710348527716700, 419.9999999999993200, −10.90769795937907600000, 0.073148231208428699) with $f\left( {x^{*}} \right) = 8853.5338748064842000$. The three main control parameters of NDE algorithm, population size NP is 200, crossover rate Cr is fixed 0.95 with exception to g02 where Cr is 0.25 and the scale factors F1, F2 and F3 are uniformly random numbers in (0, 1) as mentioned before. The maximum number of function evaluations (FEs) for all benchmark problems are set to 240,000 (Gong et al. 2014; Elsayed et al. 2013). The experiments were executed on an Intel Pentium core i7 processor 1.6 GHz and 4 GB-RAM. NDE algorithm is coded and realized in MATLAB. For each problem, 30 independent runs are performed and statistical results are provided including the best, median, mean, worst results and the standard deviation. Note that two functions (g20 and g22) are highly constrained problems since they contain 14 and 19 and contain 20 and 22 decision variables, respectively. NDE cannot obtain a feasible solution over all 30 runs for both functions. Therefore, in the following experiments, the results of these two functions are not reported and the analysis is based on 22 test problems as, to the best of our knowledge, no feasible solutions have been found so far for this test function. On the other hand, to compare the solution quality from a statistical angle of different algorithms and to check the behavior of the stochastic algorithms (García et al. 2009), the results are compared using three non-parametric statistical hypothesis tests: (i) the Friedman test (to obtain the final rankings of different algorithms for all functions); (ii) Iman-Davenport test (to check the differences between all algorithms for all functions); and (iii) multi-problem Wilcoxon signed-rank test at a 0.05 significance level (Gong et al. 2013). Given k algorithms and N data sets, the Friedman test ranks the performance of algorithms for each data set (in case of equal performance, average ranks are assigned) and tests if the measured average ranks $R_j =\left( {1/N} \right) \mathop \sum \limits _{i=1}^N r_i^j\, (r_i^j$ as the rank of the j th algorithm on the $i\hbox {th}$ data set) are significantly different from the mean rank. Under the null hypothesis, which states that all the algorithms behave similarly and thus their rank should be equal, the Friedman statistic used is $\chi _F^2 =\frac{12N}{K\left( {K+1} \right) }\,\left[ {\mathop \sum \nolimits _{j=1}^k R_j^2 -\frac{k\left( {k+1} \right) ^{2}}{4}}\right]$ which follows a $\chi ^{2}$ distribution with $k-1$ degrees of freedom, and the Iman-Davenport statistic is $F_F =\frac{\left( {N-1} \right) \chi _F^2}{N\left( {k-1} \right) -\chi _F^2}$ which is distributed according to Fischer’s F-distribution with $k-1$ and $\left( {k-1} \right) \left( {N-1} \right)$ degrees of freedom (Demšar 2006). Regarding multi-problem Wilcoxon signed-rank test, $\hbox {R}^{+}$ denotes the sum of ranks for the test problems in which the first algorithm performs better than the second algorithm (in the first column), and $\hbox {R}^{-}$ represents the sum of ranks for the test problems in which the first algorithm performs worse than the second algorithm (in the first column). Larger ranks indicate larger performance discrepancy. The numbers in Better, Equal and worse columns denote the number of problems in which the first algorithm is better than, equal or worse than the second algorithm. As a null hypothesis, it is assumed that there is no significant difference between the mean results of the two samples. Whereas the alternative hypothesis is that there is significance in the mean results of the two samples, the number of test problems $\text {N}=22$ and 5% significance level. use the p value and compare it with the significance level. Reject the null hypothesis if the p-value is less than or equal to the significance level (5%). Based on the result of the test, one of three signs ($+$, −, and $\approx )$ is assigned for the comparison of any two algorithms (shown in the last column), where ($+$) sign means the first algorithm is significantly better than the second, (−) sign means the first algorithm is significantly worse than the second, and $(\approx )$ sign means that there is no significant difference between the two algorithms. All the p values in this paper were computed using SPSS (the version is 20.00).

Results of the proposed approach (NDE)

The statistical results of the NDE on the benchmarks are summarized in Table 2. It includes the known optimal solution for each test problem and the obtained best, median, mean, worst values and the standard deviations. Additionally, Figs. 5, 6, 7, 8, 9 and 10 show the convergence graphs of log10 (f(x) − f(x*)) over FEs at the median run for each test problem with 240,000 FEs, where x* is the best solution found. As shown in Table 2, NDE is able to find the global optimal solution consistently in 20 out of 22 test functions over 30 runs with the exception of test functions (g02 and g19). With respect to these test functions, although the optimal solutions are not consistently found, the best result achieved is very close to the global optimal solution which can be verified by the very small standard deviation. Additionally, it is able to provide the competitive results. NDE is also able to find new solution to test functions g17 which is better than the best known solutions from (Liang et al. 2006). From Figs. 5, 6, 7, 8, 9 and 10, it can be obviously seen that a fast convergence (less than 50,000 FES) can be achieved for the test functions (g04, g06, g08, g09, g12, g16, g18, g24). Moreover, for test functions (g01, g03, g05, g07, g10, g11, g13, g14, g15, g17), less than 150,000 FES are needed. In addition, by using about 200,000 FES, the convergence is achieved for (g19, g21, and g23). However, among those problems, g02 is multi-modal, that contains many local optima near the global minimum (Asafuddoula et al. 2014). Thus, all 240,000 FES are needed. From the above analysis, it can be concluded that NDE has a fast convergence speed for most of these 22 test functions. Accordingly, the main benefits of the new triangular mutation are the fast convergence speed and the extreme robustness which are the weak points of all evolutionary algorithms. Therefore, the proposed NDE algorithm is proven to be an effective and powerful approach to solve constrained global optimization problems.

Fig. 5

Convergence graph for g01–g04

Fig. 6

Convergence graph for g05–g08

Fig. 7

Convergence graph for g09–g12

Fig. 8

Convergence graph for g13–g16

Fig. 9

Convergence graph for g17–g19

Fig. 10

Convergence graph for g21, g23 and g24

Comparisons with current state-of-the-art competitive DE approaches

The NDE was compared to seven state-of-the-art DE approaches for COPs that were all tested on benchmark functions presented in CEC’2006 mentioned in (Liang et al. 2006). These algorithms are rank-iMDDE (Gong et al. 2014), ISAMODE-CMA (Elsayed et al. 2013), SAMO-DE (Elsayed et al. 2011), MDEDP (Dong and Wang 2014), AH-DEa (Asafuddoula et al. 2014), DE-DPS (Sarker et al. 2014), and DECV (Mezura-Montes et al. 2010). The selected algorithms had the appropriate performances available to make this comparison possible and used the same maximum number of function evaluations (FEs) (240,000). The best, the median, the mean, the worst, and the standard deviation of the objective function values of the final solutions for each algorithm are listed in Table 3. A result in boldface indicates the best result or the global optimum. NA means not available. The results provided by these approaches were directly taken from the original references for each approach. According to the results shown in Table 3, it can be obviously seen that NDE consistently exhibits high quality results in all benchmark problems as compared with other seven DE algorithms. For g02, only DE-DPS was able to find the optimal solution consistently. Besides, NDE is slightly worse than ISAMODE-CMA, MDEDP and DE-DPS in function g19. However, MDEDP, AH-DEa, DE-DPS and DECV were unable to find the global optimal solution for g17 consistently.

Table 3 Statistical features of the results obtained by of NDE, rank-iMDDE, ISAMODE-CMA, SAMO-DE, MDEDP, AH-DEa, DE-DPS and DECV

Table 4 Algorithm ranking by the objective function values for all test functions

In order to perform the Friedman test, we first rank all the algorithms according to the mean values in Table 4. From Table 4, NDE and DE-DPS get the first ranking among the eight algorithms on 22 test functions. Figure 11 shows the average ranking of the considered DE algorithm based on the Friedman test. For N $=$ 22 and $k=8$, the Friedman statistic is $\chi _F^2 =\frac{12\times 22}{8\times 9}\left[ (3.79545^{2} + 3.90909^{2}+ 4.04545^{2}+ 5.06818^{2}\right. \left. +\, 4.72727^{2}+ 4.63636^{2}+ 3.84091^{2}+5.97727^{2})-\frac{8\times 9^{2}}{4} \right] = 14.89462.$

And the Iman-Davenport statistic is $F_F =\frac{21\times 14.89462}{22\times 7-14.89462}=2.2486$.

F-distribution with $(k-1)$ and $(k-1)(N-1)$ degrees of freedom. The critical value of F (7, 147) for $\alpha =0.05$ is 2.07 . Therefore, the null-hypothesis that ranks do not significantly differ is rejected. Thus, it can be concluded that there is a significant difference between the performances of the algorithms. Additionally, due to the importance of the multiple-problem statistical analysis, Table 5 summarizes the statistical analysis results of applying Wilcoxon’s test between NDE and other seven compared algorithms. From the results shown in Table 5, we can see that NDE provides higher $\hbox {R}^{+}$ values than $\hbox {R}^{-}$ in all the cases with exception to DE-DPS case. Precisely, we can draw the following conclusions: NDE outperforms SAMO-DE, AH-DEA and DECV significantly, and it is comparable with other algorithms.

Fig. 11

Average ranking of NDE, rank-Imdde, ISAMODE-CMA, SAMO-DE, MDEDP, AH-DEa, DE-DPS and DECV by the Friedman test for the 22 functions in terms of the mean value

Table 5 Results of multiple-problem Wilcoxon’s test for NDE versus rank-iMDDE, ISAMODE-CMA, SAMO-DE, MDE-DP, AH-DEa, DE-DPS and DECV over all functions at a 0.05 significance level

Comparisons with other state-of-the-art EAs

To further verify the performance of NDE, comparisons are carried out with seven competitive state-of-the-art evolutionary algorithms. These algorithms are SAM-PSO (Elsayed et al. 2014), SAMO-GA (Elsayed et al. 2011), ECHT-EP2 (Mallipeddi and Suganthan 2010), M-ABC (Mezura-Montes and Cetina-Domínguez 2012), SOA-FS (Tuba and Bacanin 2014), HCOEA (Wang et al. 2007) and SMES (Mezura-Montes and Coello 2005). The selected algorithms had the appropriate performances available to make this comparison possible and used the same maximum number of function evaluations (FEs) (240,000). The best, the median, the mean, the worst, and the standard deviation of the objective function values of the final solutions for each algorithm are listed in Table 6. A result in boldface indicates the best result or the global optimum. NA means not available. The results provided by these approaches were directly taken from the original references for each approach. Note that SOA-FS, HCOEA and SMES algorithms solved only the first 13 benchmark problems. According to the results shown in Table 6, it can be obviously seen that almost all the eight algorithms can find the optimal solution consistently for six test functions (g01, g03, g04, g08, g11, g12). With respect to the mean results, only NDE was able to obtain the best result or global optimal in functions (g02, g19, g21, g23). Moreover, NDE had almost better performance with 0 standard deviations in most cases. All in all, NDE is superior to all compared EAs algorithms.

Table 6 Statistical features of the results obtained by of NDE, SAM-PSO, SAMO-GA, ECHT-EP2, M-ABC, SOA-FS, HCOEA and SMES

Table 7 Algorithms ranking by the objective function values for all test functions

Fig. 12

Average ranking of NDE, SAM-PSO, SAMO-GA, ECHT-EP2 and M-ABC by the Friedman test for the 22 functions in terms of the mean value

In order to perform the Friedman test, we rank all the algorithms according to the mean values in Table 7. From Table 7, NDE gets the first ranking among the five algorithms on 22 test functions. Figure 12 shows the average ranking of the considered DE algorithm based on the Friedman test. For N $=$ 22 and $=5$, the Friedman statistic is

$$\begin{aligned} \chi _F^2= & {} \frac{12\times 22}{5\times 6}\left[ (2.02273^{2}+2.63636^{2}+3.61364^{2}\right. \\&\quad +\,2.79545^{2}+3.93182^{2}) \left. -\frac{5\times 6^{2}}{4} \right] =20.89097.\\ F_F= & {} \frac{21\times 20.89097}{22\times 4-20.89097}=6.537278. \end{aligned}$$

F-distribution with $(k-1)$ and $(k-1)(N-1)$ degrees of freedom.

The critical value of $\text {F}(4, 84)$ for $\alpha =0.05$ is 2.4803. Therefore, the null-hypothesis that ranks do not significantly differ is rejected. Thus, it can be concluded that there is a significant difference between the performances of the algorithms. Additionally, due to the importance of the multiple-problem statistical analysis, Table 8 summarizes the statistical analysis results of applying Wilcoxon’s test between NDE and other four compared algorithms. From the results shown in Table 8, we can see that NDE provides higher $\hbox {R}^{+}$ values than $\hbox {R}^{-}$ in all the cases. Precisely, we can draw the following conclusions: NDE outperforms SAMO-GA, ECHT-EP2 and M-ABC significantly, and it is comparable with SAM-PSO.

In order to perform the Friedman test, we rank all the algorithms according to the mean values in Table 9. From Table 9, NDE gets the first ranking among the four algorithms on 13 test functions. Figure 13 shows the average ranking of the considered DE algorithm based on the Friedman test. For N $=\,13 \hbox {and} =\,4$, the Friedman statistic is

$$\begin{aligned} \chi _F^2= & {} \frac{12\times 13}{4\times 5}\left[ {(1.84^{2}+2.69^{2} +2.16^{2}+3.31^{2}) -\frac{4\times 5^{2}}{4}} \right] =9.69852.\\ F_F= & {} \frac{12\times 9.69852}{13\times 3-9.69852}=3.97189. \end{aligned}$$

F-distribution with $(k-1)$ and $(k-1)(N-1)$ degrees of freedom.

The critical value of F (3, 36) for $\alpha =0.05$ is 2.866. Therefore, the null-hypothesis that ranks do not significantly differ is rejected. Thus, it can be concluded that there is a significant difference between the performances of the algorithms. Additionally, due to the importance of the multiple-problem statistical analysis, Table 10 summarizes the statistical analysis results of applying Wilcoxon’s test between NDE and other four compared algorithms. From the results shown in Table 10, we can see that NDE provides higher $\hbox {R}^{+}$ values than $\hbox {R}^{-}$ in all the cases. Precisely, we can draw the following conclusions: NDE outperforms SOA-FS, HCOEA and SMES.

Table 8 Results of multiple-problem Wilcoxon’s test for NDE versus SAM-PSO, SAMO-GA, ECHT-EP2 and M-ABC over all functions at a 0.05 significance level

Table 9 Algorithm ranking by the objective function values for first 13 test functions

In the final analysis, the performance of the NDE algorithm is superior and competitive to the state-of-the-art well-known DE approaches and EAs in terms of final solution quality and robustness. Moreover, it is easily implemented and is considered a reliable approach to constrained optimization problem. In all the rankings the NDE is a powerful algorithm showing fast convergence, providing good final results and significantly outperforming most of the compared algorithms.

NDE for constrained engineering design problems

In order to study the performance of the proposed algorithm NDE on real-world constrained optimization problems, five widely used constrained engineering design problems have been solved. The five problems are: (i) welded beam design (Huang et al. 2007), (ii) tension/compression spring design (Ray and Liew 2003), (iii) speed reducer design (Ray and Liew 2003), (iv) three-bar truss design (Ray and Liew 2003), and (v) pressure vessel design (Huang et al. 2007). For reasons of (limited) space, interested readers can find the formulation of these problems in their corresponding literature. For each problem, 30 independent runs are performed and statistical results are provided including the best, median, mean and worst results and the standard deviation. Moreover, the statistical results provided by NDE were compared with some algorithms used in literature. The same settings of parameters are used. However, due to the different characteristics of different problems, NDE utilizes different population size, maximum number of generation $(G_{\max })$, and maximum number of function evaluations (FEs) for each test function and are listed in Table 11. The best values of objective function, design variables and constraints obtained by NDE in each problem are presented in Table 12. The statistical results of all engineering design problems that measure the quality of results (best, median, mean, worst, and standard deviation) are summarized in Table 13. From Table 13, it can be concluded that NDE is able to consistently find the global optimal in all engineering problems with a very small standard deviation and with a very small (FEs). This indicates that the proposed NDE has a remarkable ability to solve constrained engineering design problems with a perfect performance in terms of high quality solution, rapid convergence speed, efficiency and robustness.

Fig. 13

Average ranking of NDE, SOA-FS, HCOEA and SMES by the Friedman test for the 13 functions in terms of the mean value

Table 10 Results of multiple-problem Wilcoxon’s test for NDE versus SOA-FS, HCOEA and SMES over 13 functions at a 0.05 significance level

Welded beam design problem

This problem was previously solved by several approaches in the literature. NDE is compared with twelve optimizers: (COMDE) (Mohamed and Sabry 2012), differential evolution with level comparison (DELC) (Wang and Li 2010), multiple trial vector based DE (MDDE) (Mezura-Montes et al. 2007), particle swarm optimization (CVI-PSO) (Mazhoud et al. 2013), genetic algorithm with automatic dynamic penalization (BIANCA) (Montemurro et al. 2013), multi-view differential evolution (MVDE) (de Melo and Carosio 2013), (Rank-iMDDE) (Gong et al. 2014), hybrid particle swarm optimization (HPSO) (He and Wang 2007), co-evolutionary DE (Co-DE) (Huang et al. 2007), mine blast algorithm (MBA) (Sadollah et al. 2013), water cycle algorithm (WCA) (Eskandar et al. 2012), and social-spider algorithm (SSO-C) (Cuevas and Cienfuegos 2014). The results of these algorithms are shown in Table 14. A result in boldface means a better (or best) solution obtained. It can be obviously seen from Table 14 that NDE is able to find the optimal solution consistently and its statistical result is similar to COMDE, DELC, MDDE, Rank-iMDDE and MBA algorithms and is superior to the remaining algorithms. However, It is to be noted that the improvement percentage of NDE in terms of FEs in comparison to

COMDE, DELC, MDDE, Rank-iMDDE and MBA is 40, 40, 33.33, 46.67 and 82.77%, respectively. Therefore, NDE is considered the most efficient with the smallest (FEs) among all compared algorithms. The convergence graph of NDE for the welded beam design problem is plotted in Fig. 14.

Table 11 The required population size, maximum number of generation and number of function evaluations for engineering design problems

Table 12 Best values of objective functions, design variables and constraints for engineering design problems

Table 13 Statistical results obtained by NDE with 30 independent runs on five engineering design problems

Table 14 Results of Welded beam design problem

Tension/compression spring design problem

The approaches applied to this problem for the comparison include (COMDE), (DELC), (MDDE), (CVI-PSO), (BIANCA), (MVDE), (Rank-iMDDE), (HPSO), (Co-DE), (MBA), (WCA), (SSO-C), dynamic stochastic ranking based DE (DSS-MDE) (Zhang et al. 2008), and accelerated adaptive trade-off model based EA (AATM) (Wang et al. 2009). The results are tabulated in Table 15. It can be observed that there are seven algorithms (NDE, COMDE, DELC, DSS-MDE, Rank-iMDDE, HPSO, and SSO-C) that are able to find the optimal solution in this problem but DELC has the lower standard deviation. The mean value obtained by NDE is slightly worse than the mean values obtained by DELC and Rank-iMDDE. However, NDE performs better than the remaining algorithms in terms of the mean value. The convergence graph of NDE for the tension/compression spring design problem is plotted in Fig. 15.

Speed reducer design problem

This problem has been solved by (COMDE), (DELC), (MDDE), (MVDE), (rank-iMDDE), (MBA), (WCA), (DSS-MDE), and (AATM), and the results are shown in Table 16. It is clear that NDE, COMDE, DELC, DSS-MDE and Rank-iMDDE are able to find the optimal solution consistently in all runs but NDE has the smallest FEs among them. Note that the best result provided by MBA is slightly worse than the optimal solution although it used the least FEs. Thus, NDE is considered the most efficient with the smallest (FEs) among superior compared algorithms. The convergence graph of NDE for the speed reducer design problem is plotted in Fig. 16.

Fig. 14

Convergence graph of NDE for welded beam design problem

Table 15 Results of tension/compression spring design problem

Three-bar truss design problem

This problem has been solved by (COMDE), (DELC), (MVDE), (Rank-iMDDE), (MBA), (WCA), (DSS-MDE), and (AATM), and the results are shown in Table 17. It is clear that NDE, COMDE, DELC, and Rank-iMDDE are able to find the optimal solution consistently in all runs. Besides, the standard deviation of NDE and rank-iMDDE are equal to zero. Moreover, NDE is considered the most efficient with the smallest (FEs) among all compared algorithms. The convergence graph of NDE for the three-bar truss design problem is plotted in Fig. 17.

Fig. 15

Convergence graph of NDE for tension/compression spring design problem

Table 16 Results of speed reducer design problem

Pressure vessel design problem

This problem has been studied by several approaches in the literature, including (COMDE), (DELC), (MDDE), (CVI-PSO), (BIANCA), (MVDE), (rank-iMDDE), (HPSO), (Co-DE), (MBA), and (WCA). The statistical results of all algorithms are listed in Table 18. From the results only five algorithms (NDE, COMDE, DELC, MDDE, and rank-iMDDE) are able to solve this problem consistently in all runs but MDDE has the lower standard deviation. Moreover, NDE is considered the most efficient with the smallest (FEs) among all compared algorithms. The convergence graph of NDE for the pressure vessel design problem is plotted in Fig. 18.

Fig. 16

Convergence graph of NDE for speed reducer design problem

Table 17 Results of three-bar truss design problem

Fig. 17

Convergence graph of NDE for three-bar truss design problem

Table 18 Results of pressure vessel design problem

Based on the above analysis, results and comparisons, the proposed NDE algorithm is of better searching quality, efficiency and robustness for solving constrained engineering design problems and besides the fact that its performance is superior and competitive with all compared algorithms.

Fig. 18

Convergence graph of NDE for pressure vessel design problem

NDE for constrained mechanical design problems

To further verify the performance of NDE on solving real-world constrained optimization problems, five widely used constrained mechanical engineering design problems have been solved. The five problems are: (i) step-cone pulley (Rao et al. 2011), (ii) hydrostatic thrust bearing (Rao et al. 2011), (iii) Rolling element bearing (Rao et al. 2011), (iv)Belleville spring (Rao et al. 2011), and (v) gear train (Sadollah et al. 2013). All these problems have different

natures of objective functions, constraints and design variables (Rao et al. 2011). The objective functions of all problems are minimized herein. For reasons of space, interested readers can find the formulation of these problems in their corresponding literature. For each problem, 30 independent runs are performed and statistical results are provided including the best, median, mean and worst results and the standard deviation. Moreover, the statistical results provided by NDE were compared with some algorithms used in the literature. The same settings of parameters are used. However, due to different characteristics of different problems, NDE utilizes different population size, maximum number of generation $(G_{\max })$, and maximum number of function evaluations (FEs) for each test function that are listed in Table 19. The best values of objective function, design variables and constraints obtained by NDE in each problem are presented in Table 20. The statistical results of all mechanical design problems that measure the quality of results (best, median, mean, worst, and standard deviation) are summarized in Table 21. From Table 21, it can be concluded that NDE is able to consistently find the global optimal in rolling element bearing, Belleville spring and gear train problems with a very small standard deviation and with small (FEs). For the step-cone pulley problem and hydrostatic thrust bearing problem, although the best solution are not consistently found, the results achieved in all runs are very close to the best solution which can be verified by the small standard deviation. Clearly, it indicates that the proposed NDE algorithm is proven to be an effective and powerful approach to solve constrained mechanical design problems.

Table 19 the required population size, maximum number of generation and number of function evaluations for mechanical design problems

Table 20 Statistical results obtained by NDE with 30 independent runs on five mechanical design problems

Table 21 Values of objective functions, design variables and constraints for mechanical design problems

Table 22 Results of step-cone pulley problem

Step-cone pulley problem

This problem was previously solved using (rank-iMDDE), teaching–learning-based optimization (TLBO) (Rao et al. 2011), Artificial Bee Colony (ABC) (Rao et al. 2011). The comparison of the obtained statistical results for different algorithms is given in Table 22. From Table 22, almost NDE and rank-iMDDE obtain the same best solution. However, NDE obtains the best results compared with other optimizers in terms of mean and worst solution with the same used FEs. Thus, NDE is more robust than other compared algorithms. The convergence graph of NDE for the step-cone pulley problem is shown in Fig. 19. It can be easily seen from Fig. 19. That NDE converged to near best solutions in early generations.

Fig. 19

Convergence graph of NDE for step-cone pulley problem

Hydrostatic thrust bearing problem

This problem was previously solved using (rank-iMDDE), teaching–learning-based optimization (TLBO) (Rao et al. 2011), Artificial Bee Colony (ABC) (Rao et al. 2011). The comparison of the obtained statistical results for different algorithms is given in Table 23. From Table 23, NDE consistently obtains the best results compared with other algorithms in terms of best, mean and worst solutions with least FEs and smallest standard deviation. The convergence graph of NDE for the hydrostatic thrust bearing problem is plotted in Fig. 20. Clearly, NDE has a fast convergence speed to achieve best solutions in early generations.

Table 23 Results of hydrostatic thrust bearing problem

Rolling element bearing problem

This problem was previously solved using (rank-iMDDE), teaching–learning-based optimization (TLBO) (Rao et al. 2011), Artificial Bee Colony (ABC) (Rao et al. 2011), MBA (Sadollah et al. 2013), WCA (Eskandar et al. 2012) and Genetic Algorithm (GA) (Gupta and Tiwari 2007). The statistical results of all algorithms are listed in Table 24. Surprisingly, NDE is also able to find new solutions to this test functions which is better than the best known solutions from (Eskandar et al. 2012). Moreover, it almost obtains the best solution consistently in all runs with very small standard deviation. In fact, NDE detected the new best solution with significant difference over the previous solutions from (Sadollah et al. 2013; Eskandar et al. 2012) during the early generations as can be seen from the convergence graph of NDE for the Rolling element bearing problem in Fig. 21.

Belleville spring problem

This problem was previously solved using (rank-iMDDE), (TLBO), (ABC), and MBA. The statistical results of all algorithms are listed in Table 25. Almost all optimizers obtain the same best solution. NDE is slightly worse than Rank-iMDDE in terms of mean and worst results. However, NDE obtains the best solution consistently in all runs and it is considered the most efficient with the smallest FEs with fast convergence speed as depicted in the convergence graph of NDE for the Belleville spring problem in Fig. 22.

Fig. 20

Convergence graph of NDE for hydrostatic thrust bearing problem

Table 24 Results of Rolling element bearing problem

Gear train problem

This problem was previously solved using Unified Particle Swarm Optimization (UPSO) (Parsopoulos and Vrahatis 2005), (ABC), and MBA. The statistical results of all algorithms are listed in Table 26. Obviously, all optimizers obtain the same best solution. NDE is slightly worse than ABC in terms of mean result. NDE is better than UPSO and MBA in terms of mean and worst results. However, ABC is considered the most efficient with the smallest FEs followed by NDE, MBA and UPSO. Nonetheless, it is noteworthy that there is a remarkable difference between the FEs used by NDE and MBA algorithms and FEs used by UPSO, the ratio is (1:100) which supports the claim that NDE is highly efficient. The convergence graph of NDE for the Gear train problem is plotted in Fig. 23.

Fig. 21

Convergence graph of NDE for rolling element bearing problem

Table 25 Results of Belleville spring problem

Conclusion

Over the last decade, many EAs have been proposed to solve constrained optimization problems. However, all these algorithms including DE have the same shortcomings in solving optimization problems. These shortcoming are as follows: (i) premature convergence and stagnation due to the imbalance between the two main contradictory aspects exploration and exploitation capabilities during the evolution process, (ii) sensitivity to the choice of the control parameters which are difficult to adjust for different problems with different features, (iii) their performances decrease as search space dimensionality increases (Das et al. 2009; Wagdy Mohamed et al. 2011). Moreover, most real world optimization problems are limited by a set of constraints i.e. imposing constraints on the optimization problems. To optimize these constrained optimization problems, the optimal solution does not only taken into consideration the objective function value but it has also to satisfy the added constraints and this increases the difficulty to all EAs including DE of finding the global solution through the optimization process. Consequently, to overcome these obstacles, a considerable number of research studies have been proposed and developed to enhance the performance of DE, and they can be classified into three categories.

Fig. 22

Convergence graph of NDE for Belleville spring problem

Table 26 Results of gear train problem

• 1. Using adaptive or self-adaptive mechanisms to adapt strategies and parameters of DE combined with single search operator or multiple search operators.

• 2. Controlling the population diversity of DE by introducing new parameters to measure the diversity during the evolution process.

• 3. Hybridizing DE with another evolutionary algorithm or classical method or incorporating local search techniques.

Although all of the above method can probably enhance the performance of Basic DE, they definitely increase the complexity of the algorithm by introducing extra parameters and/or complicated mechanisms. Nonetheless, so far, there have been a few attempts in the literature to introduce novel mutations that can balance the general trade-off between the global exploration and local exploitation with fast convergence speed (Das and Suganthan 2011). Thus, in this paper, a new triangular mutation rule is proposed. It is based on the convex combination vector of the triplet defined by the three randomly chosen vectors and the difference vectors between the best, better and the worst individuals among the three randomly selected vectors. The main benefit of the proposed algorithm is that it neither adds extra parameters nor hybrids with another algorithm. Besides, no ensemble operators or complicated self-adaptive mechanism has been added. Thus, it can be obviously proven that the proposed triangular mutation represents a unique and significant step and a novel trend in developing the existing DE approaches. It also opens new research horizons in the field of global optimization. The performance of the proposed algorithm is evaluated on three well-known benchmark problem sets. The three sets are 24 well-known benchmark test functions presented in CEC’2006; five widely used constrained engineering design problems and five constrained mechanical design problems, respectively. The proposed

NDE algorithm has been compared with 30 recent Evolutionary Algorithms. The experimental results and comparisons have shown both a remarkable performance of NDE on solving all three test functions with different characteristics and superiority when compared with other recent EAs. There are five possible directions of future work. Firstly, to study the effect of adaptation techniques on the performance of NDE, NDE will combine with self-adaptive controlling parameters. Secondly, the performance of the NDE algorithm in solving unconstrained and constrained multi-objective benchmark problems will be investigated. Thirdly, the proposed triangle mutation operator will be joined with other compared DE based algorithms to study its impact on the optimization process. Moreover, Future research studies may focus on applying the algorithm to solve other complex real-world and engineering optimization problems. Finally, this would be greatly beneficial for theoretical analysis and the study of the stochastic behavior and properties of the proposed triangular mutation. The Matlab source code of NDE can be downloaded from https://sites.google.com/view/optimization-project/files.

Fig. 23

Convergence graph of NDE for gear train problem