The formation of ternary eutectic colonies in directionally solidified systems serves as an interesting platform to study pattern formation in materials science. From a theoretical perspective, this problem has already been addressed extensively by Plapp and Karma [1], but only for systems with isotropic interfacial energy. This was extended to study spiraling dendrites in three dimensions by incorporating kinetic anisotropy [2]. A recent study by Ghosh et al. [3] on the effects of interfacial energy anisotropy in eutectics, opens up a gamut of possibilities in the patterns that are possible from the instabilities during ternary eutectic colony formation. In this paper, we are going to build upon the phase field model by Plapp and Karma [1] and attempt to understand the colony formation dynamics under different relative orientations of the interfaces with respect to the direction of pulling of the sample.

1 Isotropic System

We begin by understanding the existing phase field model for the isotropic system [1] where \(\phi \) field is the one which differentiates the solid (\(\phi =1\)) and the liquid (\(\phi =0\)). It’s evolution is obtained by solving the Allen–Cahn equation [4]:

$$\begin{aligned} \tau \frac{\partial \phi }{\partial t}=W_{\phi }^{2} \nabla ^{2}\phi -g^{\prime }(\phi ) + h^{\prime }(\phi )\left( f_{liq}-f_{sol}\right) , \end{aligned}$$
(1)

where the primes indicate derivative with respect to \(\phi \) and \(W_{\phi }\) is a constant controlling the contribution of the gradient energy. \(\tau \) represents the relaxation time for \(\phi \) evolution. Time is represented by t.

Focusing on the other terms in Eq. 1, \(g(\phi )=\phi ^{2}(1-\phi )^{2}\) is a double-well potential introducing an energy barrier between the \(\phi =1\) (solid) and \(\phi =0\) (liquid). The last term in Eq. 1 denotes the driving force for solidification with \(h(\phi )=\phi ^{2}(3-2\phi )\) being an interpolation polynomial connecting solid and liquid free energy densities denoted by \(f_{sol}\) and \(f_{liq},\) respectively.

The free energy densities are functions of the mole fractions of the independent components in the system and for a ternary system there are two of them (assuming a substitutional alloy under lattice constraint). We call them u and \(\tilde{c},\) respectively. The expressions for \(f_{sol}\) and \(f_{liq}\) are given by:

$$\begin{aligned} f_{sol}=\frac{1}{8}\left( u^{2}-1\right) ^{2} + (\tilde{c} \ln \tilde{c} - \tilde{c}) - (\ln K) \tilde{c} - \frac{\Updelta T}{T_{E}}, \end{aligned}$$
(2)
$$\begin{aligned} f_{liq}=\frac{1}{2}\left( u^{2}\right) + (\tilde{c} \ln \tilde{c} - \tilde{c}), \end{aligned}$$
(3)

and, the total energy is given by:

$$\begin{aligned} f = h(\phi ) f_{sol} + (1 - h(\phi )) f_{liq}, \end{aligned}$$
(4)

where \(\Updelta T\) and \(T_{E}\) represent the undercooling in the system and the eutectic temperature, respectively in a non-dimensionalized setting. The temperature distribution in the Bridgman furnace is computed as:

$$\begin{aligned} T=T_{0} + G (z - Vt), \end{aligned}$$
(5)

where \(T_{0}\) is the temperature at the solidification interface at \(t=0,\) G is the imposed thermal gradient, z is the location of the interface, V is the pulling velocity.

From Eqs. 2 and 3, we can see that the two eutectic solids can have a minimum for \(u={\pm }1\) (the one in equilibrium for \(u=1\) is \(\alpha \) while \(u=-1\) corresponds to \(\beta \)), while \(u=0\) corresponds to an equilibrium in the liquid. u is the component which is exchanged between the solid-phases taking part in the eutectic reaction.

The component \(\tilde{c}\) is only treated in the dilute limit (see the second terms in Eqs. 2 and 3) with a partition coefficient K which is the same for both \(\alpha \) and \(\beta .\) So, \(\tilde{c}\) is an impurity component which triggers the colony formation in a manner similar to the Mullins–Sekerka instability [5] that leads to the breakdown of a planar interface into cells in the case of a binary alloy.

The evolutions of u and \(\tilde{c}\) are governed by the Cahn–Hilliard equation [6, 7], as given by:

$$\begin{aligned} \frac{\partial u}{\partial t} = M \nabla ^{2}\left( \frac{\partial f}{\partial u} -W_{u}^{2}\nabla ^{2} u\right) , \end{aligned}$$
(6)

and,

$$\begin{aligned} \frac{\partial \tilde{c}}{\partial t}=\tilde{M} \nabla ^{2}\left( \frac{\partial f}{\partial \tilde{c}} \right) , \end{aligned}$$
(7)

where we have dropped the gradient energy term in Eq. 7 keeping in mind that the gradients in impurity component are small. The mobilities M and \(\tilde{M}\) are assumed to be constant and equal in both solid and liquid.

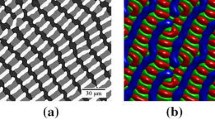
A 2D simulation of the eutectic colonies in Fig. 1 shows the random orientation of the lamellae with respect to the pulling direction which is vertically upwards. Also, the two phase fingers can be seen to be oriented randomly and no clear finger spacing is selected throughout the course of the simulation. The parameters used in this simulation were: \(G=0.001,\,V=0.1,\, \tau =0.1,\,M=1,\,\tilde{M}=1,\,dt=0.001,\,dx=1,\,dy=1,\,W_{\phi }=2.3,\,W_{u}=1.2,\,\tilde{c}_{sol}^{eq}=0.025\) and \(\tilde{c}_{liq}^{eq}=0.125.\) The initial undercooling at the solid–liquid interface was set at 0.1. No-flux boundary conditions were imposed all around the simulation box of dimensions 1440 by 1000.

Fig. 1
figure 1

Microstructures of an isotropic system at a total time of 45,000 a u field and b \(\phi \) field. Colorbars report values of the u and \(\phi \) fields, respectively

Full size image

Having introduced the model and the microstructures for an isotropic system, we can see that both \(\phi \) (changes from 1 to 0) and u (changes from \(\pm \)1 to 0) varies across a solid–liquid interface. On the other hand, across an \(\alpha \)–\(\beta \) interface, u varies (between 1 and \(-\)1) but the \(\phi \) remains constant at 1. In order to understand the influence of anisotropy there exists two possibilities: one where both solid–liquid interfaces are anisotropic but the solid–solid interface remains isotropic, which can be achieved by incorporating the anisotropy in the evolution equation of \(\phi .\) The second method is that the anisotropy is incorporated in the u field, which introduces anisotropy in the solid–solid interface.

2 Anisotropy Through the \(\phi \) Field

The evolution equation under interfacial energy anisotropy is:

$$\begin{aligned} \tau \frac{\partial \phi }{\partial t}=\left( \nabla \cdot \frac{\partial }{\partial \nabla \phi }\right) a - g^{\prime }(\phi ) + h^{\prime }(\phi )\left( f_{liq}-f_{sol}\right) , \end{aligned}$$
(8)

where the \(^{\prime }\) indicate derivative with respect to \(\phi .\) The interfacial energy term in Eq. 8 is,

$$\begin{aligned} a=\frac{1}{2} W_{\phi }^{2} a_{c}^{2}(\theta ) (\nabla \phi )^{2}, \end{aligned}$$
(9)

and, the anisotropy function \(a_{c}\) which introduces the fourfold symmetry through the interfacial energy is:

$$\begin{aligned} a_{c}=1 + \delta \cos \left( 4\left( \theta -\theta _{R}\right) \right) = 1-\delta \left( 3-4\left( \frac{{\phi _{x}^{{\prime }4}}+{\phi _{y}^{{\prime }4}}}{({\phi _{x}^{{\prime } 2}}+{\phi _{y}^{{\prime }2}})^{2}}\right) \right) , \end{aligned}$$
(10)

where the \(^{\prime }\) in Eq. 10 indicate that the derivatives (of \(\phi \) with respect to x or y as denoted by the subscripts) are evaluated in the frame of reference of the crystal, which allows us to rotate the crystal anisotropy with respect to the growing direction in the laboratory frame (the angle of rotation is defined as \(\theta _{R}\)). The magnitude of anisotropy is controlled by \(\delta \) (which is set to 0.05 in all our simulations). All other equations including the ones for the evolution of u and \(\tilde{c}\) are the same as in the isotropic situation.

To illustrate the introduction of anisotropy in the model consider the growth of an anisotropic single phase solid nuclei (\(\alpha \) in this case) for two situations: one where the reference frame of the crystal coincides with the laboratory frame (see Fig. 2) and the other where it is rotated by 30\(^{\circ }\) with respect to the laboratory frame (see Fig. 3).

Fig. 2
figure 2

Microstructures of an \(\alpha \) particle growing in liquid with anisotropy in \(\phi ,\) at a total time of 500 for \(\theta _{R}=0^{\circ }\) from a u, b \(\tilde{c},\) and c \(\phi \) fields

Full size image
Fig. 3
figure 3

Microstructures of an \(\alpha \) particle growing in liquid with anisotropy in \(\phi ,\) at a total time of 500 for \(\theta _{R}=30^{\circ }\) from a u, b \(\tilde{c},\) and c \(\phi \) fields

Full size image

At this point, it is important to note that the anisotropy by virtue of being introduced through the gradient energy in \(\phi \) can only influence the relative orientation of the solid–liquid interfaces with respect to the pulling direction and not the orientation between the two solids, (i.e., between \(\alpha \) and \(\beta ,\) both of which has \(\phi =1\)). Thus, the orientation of the \(\alpha \)–\(\beta \) interface is fixed first by force balance at the triple points (where liquid, \(\alpha \) and \(\beta \) coexist) and then modified by the growth dynamics as it cedes its position at the solidification interface and becomes a part of the colony. Furthermore, it is a competition between the orientation of the fingers as dictated by the orientation of the anisotropy and the imposed temperature gradient that determines the orientation of the global solidification envelope. The orientation that the system selects has the minimum mis-orientation with the temperature gradient. These observations can be confirmed from the microstructures (from the u field) in Figs. 4, 5, 6 and 7 where the global solidification envelope can be seen to display an orientation with respect to the pulling direction. Also, while growth, the fingers traverse the horizontal direction (as their axes are non-orthogonal to the horizontal direction), creating the appearance of a travelling wave.

The simulations shown in Figs. 4, 5, 6 and 7 were performed with no-flux boundary conditions all around. The simulation parameters were the same as in the isotropic case except for the following: \(W_{\phi }=3.2,\,W_{u}=1.7,\,\tau =1\) and \(dt=0.0025.\)

Fig. 4
figure 4

Microstructures (u field) of a system with anisotropy in \(\phi ,\) for \(\theta _{R}=0^{\circ }\) at a total time of a 30,000 and b 45,000. Colorbars report values of the u field

Full size image
Fig. 5
figure 5

Microstructures (u field) of a system with anisotropy in \(\phi ,\) for \(\theta _{R}=22.5^{\circ }\) at a total time of a 30,000 and b 45,000. Colorbars report values of the u field

Full size image
Fig. 6
figure 6

Microstructures (u field) of a system with anisotropy in \(\phi ,\) for \(\theta _{R}=45^{\circ }\) at a total time of a 40,000 and b 45,000. Colorbars report values of the u field

Full size image
Fig. 7
figure 7

Microstructures (u field) of a system with anisotropy in \(\phi ,\) for \(\theta _{R}=60^{\circ }\) at a total time of a 30,000 and b 45,000. Colorbars report values of the u field

Full size image

Another important feature of these simulations is that they have a well defined finger spacing which was not the case for the isotropic situation.

3 Anisotropy Through the u Field

In the previous section, anisotropy is introduced only in the solid–liquid interfaces. There are however alloy systems where the solid–solid interfaces are anisotropic. Therefore, in order to explore the influence of an anisotropic solid–solid interface and the effect of its orientation with respect to the growth direction on the characteristics of colony formation, we introduce anisotropy through the u field, by changing the energy of the solid phase, as:

$$\begin{aligned} f_{sol}=\frac{1}{8}\left( u^{2}-1\right) ^{2} a_{c}^{2}(\theta ) + (\tilde{c} \ln \tilde{c} - \tilde{c} ) - (\ln K) \tilde{c} - \frac{\Updelta T}{T_{E}}, \end{aligned}$$
(11)

where \(a_{c}\) has the same expression as given by Eq. 10 but with \({u^{\prime }}_{x}\) and \({u^{\prime }}_{y}\) in place of \({\phi ^{\prime }}_{x}\) and \({\phi ^{\prime }}_{y},\) respectively.

By introducing the anisotropy through the barrier potential in u we intend to restrict its effect only to the \(\alpha \)–\(\beta \) interface as they are the states which are separated by the barrier potential (see Fig. 8). However, it is to be noted that in the present model description, the shape of the solid–liquid interfaces are influenced both by the variations of the u-field as well as the \(\phi \)-field and the equilibrium shape of a solid–liquid interface is then determined by contributions of both (see Fig. 9). The parameters of the anisotropy are so adjusted that the influence of the anisotropy in the u-field weakly influences the shape of the solid phase in equilibrium with the liquid as exhibited by the \(\phi \)-field (see Fig. 10) and therefore also the \(\tilde{c}\)-field which follows the \(\phi \)-field. This construction thereby led us a system, where the anisotropy is predominantly in the solid–solid interface.

Fig. 8
figure 8

Microstructure (u field) of a system with anisotropy in u, showing a \(\beta \) particle equilibrating in \(\alpha \) at a total time of 100 for \(\theta _{R}=30^{\circ }\)

Full size image
Fig. 9
figure 9

Microstructures of a system with anisotropy in u, showing a \(\beta \) particle growing in liquid at a total time of 100 for \(\theta _{R}=0^{\circ }\) from a u, b \(\tilde{c},\) and c \(\phi \) fields

Full size image
Fig. 10
figure 10

Iso-contours at \(\phi =0.5\) for \(\delta =0.05\) (black) and \(\delta =0\) (green) with \(\theta _{R}=0^{\circ }\)

Full size image

In contrast to the simulations for the isotropic case and the ones where the anisotropy is introduced through the \(\phi \) field we can see in Figs. 12, and 14 that the lamellae do take up a very specific orientation with the solidification envelope. However, for the simulations shown in Figs. 11, and 13, the situation is a little more complex. Essentially, on incorporating an anisotropy in the solid–solid interface and giving a rotation with respect to the pulling direction, the basic steady state of the lamella pair gets tilted with respect to the growth direction. From the theory discussed in [3] a measure for the lamellae tilt can be derived and moreover the \(\alpha \)–\(\beta \) interface should remain vertical for \(\theta _{R}= 0^{\circ }\) and \(45^{\circ }\) for this choice of anisotropy function. So while in the simulations in Figs. 12 and 14 it can be seen that the colony formation results as a perturbation of the tilted lamellar state, for the simulations in Figs. 11 and 13, colony formation occurs due to a breakdown of a lamellar state that is aligned with that of the pulling velocity. The rotated lamellar orientation in Figs. 11, and 13 can be directly attributed to spinodal decomposition.

These simulations (the parameters are the same as in the case where anisotropy was introduced through the \(\phi \) field except for dt which was set to 0.001) were carried out with periodic boundary conditions on the vertical boundaries but no-flux on the horizontal ones. The implementation of a no-flux boundary condition on the vertical boundaries would have led to finger termination at the boundary towards which the fingers were moving and conversely, generation of fingers at the boundary from where the waves were receding.

Fig. 11
figure 11

Microstructures (u field) of a system with anisotropy in u, for \(\theta _{R}=0^{\circ }\) at a total time of a 30,000 and b 45,000. Colorbars report values of the u field

Full size image
Fig. 12
figure 12

Microstructures (u field) of a system with anisotropy in u, for \(\theta _{R}=22.5^{\circ }\) at a total time of a 30,000 and b 45,000. Colorbars report values of the u field

Full size image
Fig. 13
figure 13

Microstructures (u field) of a system with anisotropy in u, for \(\theta _{R}=45^{\circ }\) at a total time of a 30,000 and b 45,000. Colorbars report values of the u field

Full size image
Fig. 14
figure 14

Microstructures (u field) of a system with anisotropy in u, for \(\theta _{R}=60^{\circ }\) at a total time of a 30,000 and b 45,000. Colorbars report values of the u field

Full size image

4 Conclusions

We have tried to understand the pattern formation dynamics in ternary eutectic colonies under conditions of specific orientation relationships between the pulling direction and the different interfaces in the eutectic (namely, the \(\alpha \)-liquid, \(\beta \)-liquid and \(\alpha \)–\(\beta \) interfaces). The orientation of the \(\alpha \)-liquid and \(\beta \)-liquid interfaces were fixed by introducing anisotropy through \(\phi \) and simulations on such systems revealed tilts in the global solidification envelope enforced by the individual lamellae units. Moreover, we saw the system select a definite finger spacing which was absent in the isotropic systems. By incorporating anisotropy through the u-field, we oriented the \(\alpha \)–\(\beta \) interface at different angles to the pulling direction and the resultant eutectic colonies had a well-defined lamellae orientation quite unlike what was seen for the isotropic as well as the case where anisotropy was introduced through \(\phi .\) Furthermore, the solidification envelope appeared to be orthogonal to the constituting lamellae and a specific finger width was also selected by the system.