Introduction

Streamflow regime has been changed due to climate change and human activities (Greenwood et al. 1979), and a series of hydrologic extreme events have increased over the period of record (Obeysekera et al. 2011). As a result, some hydrologists have stated that “stationarity is dead” (Milly et al. 2008), and the hydrologic probability distribution estimation theories and methods which are based on stationary conditions are no longer helpful for studying the long-term variation pattern about water resources and flood evolution. Specifically, studies have demonstrated that hydrologic records in some rivers show non-stationarity in the form of increasing or decreasing tends (e.g., Olsen et al. 1999; Lins and Slack 1999; Douglas et al. 2000; Strupczewski et al. 2001b; Lin et al. 2014a), upward and downward shifts (e.g., Potter 1976; Salas and Boes 1980; McCabe and Wolock 2002; Fortin et al. 2004) or their combination (Villarini et al. 2009). Hence, adapting reservoir operation in a changing environment is of significant importance. Specifically, the flood limited water level (FLWL), which is the most key parameter for controlling the trade-off between activities of flood control and water conservation (Liu et al. 2008; Yun and Singh 2008; Li et al. 2010), needs to be re-established to ensure flood safety when the reservoir inflow alters.

The existing method to determine the FLWL is flood routing of design flood hydrographs by using the predetermined reservoir operating rules as follows (MWR 2006): (1) estimate the design flood hydrograph based on the maximum flood samples and (2) determine the FLWL based on the design flood hydrograph, i.e., routing the flood by setting it as the initial water level under the condition that the flood prevention risk does not increase. This approach can be conducted through a trial and error method.

The non-stationary issue of design flood has been addressed, where the most popular methods for non-stationary frequency analysis are the reductive method (Xie et al. 2009) and the time-varying moment method (Strupczewski and Kaczmarek 2001). In the reductive method, the non-stationary hydrologic series are decomposed by deterministic (a non-stationary term) and stochastic components. The stochastic component should be removed before the frequency analysis (Xie et al. 2009). Strupczewski and Kaczmarek (2001) and Strupczewski et al. (2001a, b) directly embed the linear and quadratic trinomial trend into the first and second moment of the extreme flood sequence’s distribution to describe non-stationarity, and the frequency analysis is carried out directly on the original hydrologic sequence. In order to describe the variation tendency of the hydrologic sequence, the most popular method is that the distribution parameter is expressed as a function of time, such as linear, exponential, polynomial, logarithmic, spline interpolation function (Kharin and Zwiers 2005; Rigby and Stasinopoulos 2005). It can intuitively describe the changing trend of hydrologic sequences during the observed period. Recently, some hydrologists (Villarini and Serinaldi 2012; Xiong et al. 2014) have focused on the frequency analysis of non-stationary hydrologic series which is based on physical factors, and the relation between statistical parameters and the variable is often described by using the regression equation.

The reservoir FLWL can be controlled dynamically based on hydrologic forecasting. Aiming at the problems about dynamic control of reservoir operation, the multiple near-optimal solutions (Liu et al. 2011) and a variety of calculation models (Liu et al. 2006) were proposed. Zhou et al. (2014) proposed a model for a mixed reservoir system, which consists of a dynamic control operation module for a single reservoir, a dynamic control operation module for cascade reservoirs, and a joint operation module for mixed cascade reservoir systems. Zhao and Zhao (2014) proposed an improved multiple-objective DP algorithm for reservoir operation optimization. Zhang et al. (2015) used the Bayesian model averaging model to optimize the uncertainty of reservoir operating rules. Ouyang et al. (2015) proposed an optimal design model for the FLWL to optimize the flood control risk. Diao and Wang (2011) and Wang et al. (2011) putted forward a risk control model to determine the limit scope of the FLWL. Condon et al. (2014) focused on the flood risk under non-stationary condition. However, there is no systematic research on the design of reservoir FLWL when the influence of a changing environment is considered.

The aims of this paper are: (1) to clarify the relationship between the FLWL and the reservoir inflow when statistical parameters (mean, \( C_{\text{V}} \) and \( C_{\text{S}} \)) of the design flood have a linear temporal trend and (2) to re-establish the FLWL without increasing the flood risk probability under the non-stationary condition. The paper is organized as follows: second section describes the methods on estimation of statistical parameters module, the flood risk evaluation module and the FLWL derivation module. Third section addresses a case study of China’s Three Gorges Reservoir (TGR), and then, results and discussions are given. Finally, conclusions are given in fourth section.

Methods

The steps to derive the adaptive reservoir FLWL are as follows (Fig. 1):

Fig. 1
figure 1

Flowchart of the method for adaptive reservoir FLWL

Full size image
  1. 1.

    Based on the observed data, moving average and L-moment estimation are used to fit the linear function of statistical parameters. Namely, mean, \( C_{\text{V}} \) and \( C_{\text{S}} \) of streamflow vary through time (Section estimation of statistical parameters).

  2. 2.

    The flood risk is evaluated with two scenarios, i.e., stationarity and non-stationarity, in which the FLWL keeps at the original design value (Section flood risk evaluation).

  3. 3.

    The re-establishment of FLWL is derived based on flood routing of the non-stationary design flood (Section FLWL derivation).

Estimation of statistical parameters

In order to identify the relationship of statistical parameters over time, the moving average method is used to produce sample series, and then, the L-moment method (Hosking and Wallis 1997) is used to estimate the mean, \( C_{\text{V}} \) and \( C_{\text{S}} \). Finally, functions of mean, \( C_{\text{V}} \) and \( C_{\text{S}} \) over time are quantified by using linear curve fitting method, respectively.

The L-moment method is based on the probability weighted moment (PWM) (Greenwood et al. 1979), which is defined as follows:

$$ \alpha_{r} = \int_{0}^{1} {x\left( {1 - F\left( x \right)} \right)^{r} } {\text{d}}F\left( x \right) $$
(1a)
$$ \beta_{r} = \int_{0}^{1} {xF\left( x \right)}^{r} {\text{d}}F\left( x \right) $$
(1b)

where x is a random variable, \( F\left( x \right) \) and \( f\left( x \right) \) are distribution and density functions, respectively. Hosking and Wallis (1997) define the L-moment (\( \lambda_{r} \)) based on PWM,

$$ \lambda_{\text{r}} = \int_{0}^{1} {xP_{r - 1}^{*} } \left( {F\left( x \right)} \right){\text{d}}F\left( x \right) $$
(2)

in which \( P_{r}^{*} \left( u \right) = \sum\nolimits_{k = 0}^{r} {\frac{{\left( { - 1} \right)^{r - k} \left( {r + k} \right)!}}{{\left( {k!} \right)^{2} \left( {r - k} \right)!}}} u^{k} \).

In order to facilitate the definition of the dimensionless L-moment, ratios of L-moment are as follow:

$$ \tau_{r} = \lambda_{r} /\lambda_{2} \quad r = 3,4 $$
(3a)

where \( \tau_{3} \) (which means L-skewness) reflects skewness characteristics, while \( \tau_{4} \) (which means L-kurtosis) reflects kurtosis characteristics, and L-\( C_{\text{V}} \) in Eq. (3b), which is used to reflect scale features.

$$ \tau_{2} = \lambda_{2} /\lambda_{1} $$
(3b)

Combined with the distribution density function of P-III (Eq. 4), the L-moment method can be used to estimate statistical parameters of streamflow.

$$ f\left( x \right) = \frac{{\beta^{\alpha } }}{\varGamma \left( \alpha \right)}\left( {x - a_{0} } \right)^{\alpha - 1} e^{{ - \beta \left( {x - a_{0} } \right)}} \quad \left( {\alpha ,\beta > 0;x > a_{0} } \right) $$
(4)

Specifically, \( \alpha \), \( \beta \) and \( a_{0} \) are undetermined parameters while \( \varGamma \left( \alpha \right) = \int_{0}^{\infty } {x^{\alpha - 1} } e^{ - x} {\text{d}}x \). Moreover, an approximate algorithm (Hosking and Wallis 1997) has been given in Eqs. (5), (6), (7a) and (7b),

$$ \lambda_{0} = a_{0} + \alpha /\beta $$
(5)
$$ \lambda_{2} = \sqrt \pi \varGamma \left( {\alpha + 0.5} \right)/\varGamma \left( \alpha \right)/\beta $$
(6)
$$ \tau_{3} = \alpha^{{ - \frac{1}{2}}} \frac{{A_{0} + A_{1} \alpha^{ - 1} + A_{2} \alpha^{ - 2} + A_{3} \alpha^{ - 3} }}{{1 + B_{1} \alpha^{ - 1} + B_{2} \alpha^{ - 2} }}\quad \left( {\alpha \ge 1} \right) $$
(7a)
$$ \tau_{3} = \frac{{1 + E_{1} \alpha + E_{2} \alpha^{2} + E_{3} \alpha^{3} }}{{1 + F_{1} \alpha + F_{2} \alpha^{2} + F_{3} \alpha^{3} }}\quad \left( {\alpha < 1} \right) $$
(7b)

where \( A_{0} \), \( A_{1} \), \( A_{2} \), \( A_{3} \), \( B_{1} \), \( B_{2} \), \( E_{1} \), \( E_{2} \), \( E_{3} \), \( F_{1} \), \( F_{2} \), \( F_{3} \) are constant coefficients.

It is assumed that the sample is \( x_{1:n} \le x_{2:n} \le \cdots \le x_{n:n} \), and the calculation formulas of sample moment \( l_{1} \), \( l_{2} \) and \( l_{3} \), which are corresponding to \( \lambda_{1} \), \( \lambda_{2} \) and \( \lambda_{3} \), respectively, are as follows:

$$ l_{1} = b_{0} \quad l_{2} = 2b_{1} - b_{0} \quad l_{3} = 6b_{2} - 6b_{1} + b_{0} \quad \tau_{3} = l_{3} /l_{2} $$
(8a)
$$ b_{0} = \frac{1}{n}\sum\limits_{j = 1}^{n} {x_{j:n} } \quad b_{1} = \frac{1}{n}\sum\limits_{j = 2}^{n} {\frac{{\left( {j - 1} \right)}}{{\left( {n - 1} \right)}}} x_{j:n} \quad b_{2} = \frac{1}{n}\sum\limits_{j = 3}^{n} {\frac{{\left( {j - 1} \right)\left( {j - 2} \right)}}{{\left( {n - 1} \right)\left( {n - 2} \right)}}} x_{j:n} $$
(8b)

Flood risk evaluation

The traditional methods to derive return period and flood risk should satisfy two essential conditions, namely (1) extreme events follow a stationary distribution and (2) the occurrence of extreme events is independent or weakly dependent (Gumbel 1961; Leadbetter 1983; Salas and Obeysekera 2014).

It is assumed that \( Q_{P} \) is a design flood peak value of streamflow series, and the probability of streamflow \( Q_{i} \), which is the random variable, exceeding \( Q_{P} \), is expressed as \( p_{i} \). It is assumed that \( Q_{i} \) exceeding \( Q_{P} \) would occur in the \( x^{th} \) year for the first time.

On the stationary condition, \( p_{i} \) is equal to a constant \( p \) whatever \( i \) is, and hydrologic series are independent. Hence, the probability of exceedance event occurs in year \( x \) is as follow:

$$ f\left( x \right) = P\left( {X = x} \right) = \left( {1 - p} \right)^{x - 1} p,\quad x = 1,2, \ldots $$
(9)

which follows geometric probability distribution. Then, the mathematical expectation \( E\left( X \right) \) is equal to \( 1/p \), which is known as the return period \( T \).

$$ T = E\left( X \right) = \sum\limits_{x = 1}^{\infty } {xP\left( {X = x} \right)} = \frac{1}{1 - (1 - p)} = \frac{1}{p} $$
(10)

It is assumed that the project life of a hydraulic structure is designed for \( n \) years, and the failure of the structure to facing a flood exceeding the design flood occurs before or at year \( n \) (Salas and Obeysekera 2014), and hence, the flood risk probability \( R \) is shown as follows:

$$ R = P\left( {X \le n} \right) = p\sum\limits_{x = 1}^{n} {f\left( x \right)} = p\sum\limits_{x = 1}^{n} {\left( {1 - p} \right)^{x - 1} } = 1 - \left( {1 - p} \right)^{n} $$
(11)

Due to the fact that streamflow is non-stationary in a changing environment, the exceedance probability would vary through time, namely \( p_{1} \), \( p_{2} \), \( p_{3} \), …, \( p_{t} \). Therefore, the probability of exceedance event occurs in year x is as follows:

$$ f\left( x \right) = P\left( {X = x} \right) = \left( {1 - p_{1} } \right)\left( {1 - p_{2} } \right)\left( {1 - p_{3} } \right) \cdots \left( {1 - p_{x - 1} } \right)p_{x} $$
(12a)
$$ f\left( x \right) = P\left( {X = x} \right) = \left( {1 - p_{1} } \right)\left( {1 - p_{2} } \right) \cdots \left( {1 - p_{x - 1} } \right)p_{x} ,x = 1,2, \ldots $$
(12b)

Then, the flood risk probability \( R \) is as follows:

$$ R = P\left( {X \le n} \right) = p_{1} + p_{2} \left( {1 - p_{1} } \right) + \cdots + p_{n} \left( {1 - p_{1} } \right)\left( {1 - p_{2} } \right) \cdots \left( {1 - p_{n - 1} } \right) $$
(13a)
$$ R = P\left( {X \le x} \right) = \sum\limits_{x = 1}^{n} {p_{x} \prod\limits_{t = 1}^{x - 1} {\left( {1 - p_{t} } \right)} } $$
(13b)

FLWL derivation

The FLWL derivation module is established based on flood routing of the design flood hydrographs. The steps to derive the design flood are as follows (Liu et al. 2015): (1) selection on a series of typical flood peak and flood volume values, (2) design floods based on hydrologic frequency analysis, (3) same frequency magnify method to obtain the design flood hydrograph, where the amplification coefficient of peak, the maximum flood volume for 3 days, 7 days, 15 days and 30 days are as follows:

$$ K_{Q} = \frac{{Q_{P} }}{{Q_{D} }} $$
(14a)
$$ K_{w3 - 1} = \frac{{W_{3P} - W_{1P} }}{{W_{3D} - W_{1D} }} $$
(14b)
$$ K_{w7 - 3} = \frac{{W_{7P} - W_{3P} }}{{W_{7D} - W_{3D} }} $$
(14c)
$$ K_{w15 - 7} = \frac{{W_{15P} - W_{7P} }}{{W_{15D} - W_{7D} }} $$
(14d)
$$ K_{w30 - 15} = \frac{{W_{30P} - W_{15P} }}{{W_{30D} - W_{15D} }} $$
(14e)

where \( Q_{P} \) is the design flood peak value, \( Q_{D} \) is the typical flood peak value, \( W_{iP} \) and \( W_{iD} \) are the maximum design flood volume value for i days (i = 3, 7, 15, 30) and the maximum typical flood volume value for \( i \) days, respectively.

Flood routing is formulated by the reservoir water balance equation (Deng et al. 2015) and the discharge equation, i.e., Eqs. (15a) and (15b),

$$ \frac{{Q_{1} + Q_{2} }}{2}\Delta t - \frac{{q_{1} + q_{2} }}{2}\Delta t = V_{2} - V_{1} $$
(15a)

where \( \Delta t \) is the time interval, \( Q_{\text{i}} \) and \( q_{i} \) are reservoir inflow and release, respectively, \( V_{i} \) is reservoir storage, and i = 1, 2 denote the beginning and end of the time period \( \Delta t \), respectively.

$$ q\left( t \right) = f\left[ {V\left( t \right)} \right] $$
(15b)

The discharge equation shows the relationship between the reservoir release and the reservoir storage, which is determined by reservoir operating rules. The trial and error method is used to resolve above equations.

Case study

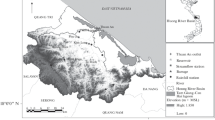
Located in Yichang, Hubei Province (Fig. 2), China’s Three Gorges Dam is 185.0 m high, the reservoir water is up to 175.0 m high. The hydropower station is equipped with 32 hydropower units, the single capacity of which is 700 MW. Overall, China’s Three Gorges Project is a large-scale hydraulic project which combines multi-purpose uses simultaneously including flood control, power generation, shipping and so on.

Fig. 2
figure 2

Location of the China’s Three Gorges Reservoir Basin

Full size image

The average annual discharge at the dam site is 14,300 m3/s, and the average annual runoff is 451 billion m3. The total area of the TGR is 1084 km2, and the TGR belongs to the channel reservoir with the length and the width of about 600 km and 1.1 km, respectively. Furthermore, the total capacity of the reservoir is about 39.3 billion m3.

Annual maximum data from 1882 to 2010 and eight historical floods (i.e., occurred in years of 1153, 1227, 1560, 1613, 1788, 1796, 1860 and 1870) are used for the case study. Furthermore, statistical parameters of the flood peak and volumes for the TGR under stationary conditions are shown in Table 1.

Table 1 Statistical parameters of TGR for stationary
Full size table

Results and discussion

Results of statistical parameters

Linear functions of statistical parameters

With the 129-year observed data, the moving average is used to sample time series for each continuous thirty years. Statistical parameters (i.e., mean, \( C_{\text{V}} \) and \( C_{\text{S}} \)) of the TGR are then estimated by using the L-moment method. Finally, the changing tendency of statistical parameters over time is derived by using linear model. In this study, statistical parameters of the flood peak and the maximum flood volume for \( i \) (\( i \) = 3, 7, 15, 30) days are estimated, respectively.

Figures 3, 4 and 5 show the result of linear fitting for statistical parameters of flood peak over time. Specifically, Fig. 3 indicates that the mean is non-stationary with the changing pattern of the mean over time declining. However, \( C_{\text{V}} \) or \( C_{\text{S}} \) does not change over time with the correlation coefficient between \( C_{\text{V}} \) and time is 0.0002, while that of \( C_{\text{S}} \) is 0.0007. Their t test statistics are 0.1217 and 0.2620, respectively. In this case, the uncorrelated hypothesis is accepted since the threshold is 1.6606 with a significance level \( \alpha = 0.95 \).

Fig. 3
figure 3

Mean of flood peak \( Ex\left( t \right) \) as a function of time \( t \) under non-stationary condition: The solid line is the linear fitting result, and the mean has a decline with time

Full size image
Fig. 4
figure 4

The \( C_{\text{V}} \) of flood peak as a function of time \( t \) under non-stationary condition: The solid line is the linear fitting result, but the amplitude of variation of \( C_{\text{V}} \) changes with time is insignificant

Full size image
Fig. 5
figure 5

The \( C_{\text{S}} \) of flood peak as a function of time \( t \) under non-stationary condition: The solid line is the linear fitting result, but the amplitude of variation of \( C_{\text{S}} \) changing with time is insignificant

Full size image

The linear fitting may not the best form, but it can simply derive the changing tendency of statistical parameters over time, which provides a foundation for the research on the adaptive FLWL under a changing environment. In order to keep consistency with design floods, the mean for 2011 year is adjusted to the designed value which is determined under stationary conditions. Table 2 lists the estimated parameter values of flood peak for the Pearson-III distribution.

Table 2 Estimated parameter values of flood peak for the Pearson-III distribution
Full size table

Similarly, statistical parameters of the maximum flood volume for \( i \) days (\( i \) = 3, 7, 15, 30) are estimated (in Fig. 6), and their results are shown in Table 3. Annual maximum data of the TGR are from 1882 to 2010, and functions of statistical parameters (in Tables 2, 3) are used to predict parameter values from 2011 to 2030. Finally, Table 4 shows the results of mean values of flood peak and maximum flood volume for \( i \) days (\( i \) = 3, 7, 15, 30).

Fig. 6
figure 6

Linear fitting results for the mean of maximum flood volume for \( i \) days (\( i \) = 3, 7, 15, 30): a the mean of maximum flood volume for 3 days, b the mean of maximum flood volume for 7 days, c the mean of maximum flood volume for 15 days, d the mean of maximum flood volume for 30 days

Full size image
Table 3 Functions for estimated parameter values of flood volume under non-stationary condition for the Pearson-III distribution
Full size table
Table 4 Means of flood peak and flood volume for the Pearson-III distribution
Full size table

Significant uncertainties in estimate of design floods arise for future projects, due to the limited data records, sampling variability and model errors (Obeysekera and Salas 2014; Lin et al. 2014b, c). This indicates that the uncertainties involved in data and methods cannot be avoided. For example, this study uses the P-III frequency curve and L-moment estimation for the frequency analysis, which leads to errors for the flood risk evaluation. However, this issue is out of our scope since the presented study aims at how to use the non-stationarity flood frequency analysis to design the reservoir FLWL.

Design flood hydrograph

Design frequencies of the TGR are 1, 0.1 and 0.01% (10% increment), and peak discharge values of four typical years (1954, 1981, 1982 and 1998.) are 66,100, 69,500, 59,000 and 61,700 m3/s, respectively.

Figure 7 shows the design flood hydrograph of the TGR for 2011, where design parameter values are shown in Table 1.

Fig. 7
figure 7

Design flood hydrograph for 2011 [there are four lines, i.e., typical year (solid line), 1% (dashed line), 0.1% (thin solid line), 0.01% (10% increment) (double dot dash line) in all the cases]: (a) the 1954 year, (b) the 1981 year, (c) the 1982 year, (d) the 1998 year

Full size image

Flood routing

The flood operating rules of the TGR are as follows: (1) When the reservoir inflow is less than a 100-year design flood, the reservoir release is no more than 53,900 m3/s to ensure that the highest reservoir water level does not exceed 175.0 m and (2) when the reservoir water level exceeds 175.0 m, the reservoir release is equal to the minimum value between the full discharge capacity and the maximum inflow (Li et al. 2010). Combined with the reservoir water balance equation (Eq. 15a), flood routing of the TGR is acquired by the trial and error method.

Estimation of flood risk

On the non-stationary condition, it is assumed that mean values of inflow decrease linearly in the forms of functions in Tables 2 and 3, and the FLWL keeps at 145.0 m. When the mean of inflow varies through time, the exceedance probability would also vary over time from 2011 to 2030. The \( p_{t} /p_{x} \) in Table 5 shows the values of \( p_{1} \), \( p_{2} \), …, \( p_{t} \) and \( p_{i} \le p = 0.01 \) (\( i = \) 1, 2, …), which is determined by flood routing. The probability distribution of the waiting time is derived from Eqs. (12a) or (12b), i.e., \( P\left( {X = x} \right) \) in Table 5. In order to distinguish the \( t \) and \( x \) in Table 5, that \( x = \) 3 is an example, and \( p_{x} = p_{3} = 0.0990\% \). The exceedance probabilities for \( t \) = 1, 2, 3 are \( p_{1} = 0.1\% \), \( p_{2} = 0.0999\% \) and \( p_{3} = 0.0990\% \), respectively. Then, Eq. (12a) gives \( f\left( 3 \right) = P\left( {X = x} \right) = \left( {1 - p_{1} } \right)\left( {1 - p_{2} } \right)p_{3} = \left( {1 - 0.1\% } \right) \times \left( {1 - 0.0999\% } \right)\,\times \left( {1 - 0.0990\% } \right) = 0.0988\% . \)

Table 5 Derivation of the return period \( T \) and flood risk \( R \) on non-stationary condition, in which the mean of inflow varies with time and FLWL keeps at 145.0 m
Full size table

Theoretically, the flood risk probability \( R \) for non-stationary conditions could be derived by Eq. (13b). It can be expected that the flood risk probability would be less than that for stationary conditions due to the decrease in \( p_{x} \) values. For example, Table 5 shows that the flood risk probability under non-stationary conditions is 0.5884% when \( n \) is six, whereas the flood risk probability for the stationary condition is equal to \( R = 1 - \left( {1 - 0.1\% } \right)^{6} = 0.5985\% \).

On stationary conditions, the exceedance probability is equal to a constant \( p_{0} \) = 0.01. The probability distribution of the waiting time is derived from Eq. (9), i.e., \( P\left( {X = x} \right) \) in Table 6. The flood risk probability \( R_{0} \) and the return period \( T_{0} \) under stationary conditions could be derived by Eqs. (11) and (10), respectively, and the return period \( T_{0} \) for stationary is 1000 years.

Table 6 Derivation of the return period \( T \) and flood risk \( R \) on stationary condition, in which the mean of inflow is equal to 51,200 m3/s
Full size table

Figure 8 reflects the difference between the non-stationary flood risk probability \( R \) and the stationary flood risk probability \( R_{0} \) with different design life. Clearly, the flood risk for stationary is greater than that of non-stationarity when the design life \( n \) of the hydraulic structure is fixed.

Fig. 8
figure 8

Flood risk probability as a function of project life \( n \) [the solid line shows the flood risk for the stationary condition, while the dashed line shows the flood risk for the non-stationary condition in which the FLWL keeps at 145.0 m]

Full size image

Results of FLWL

The FLWL of the TGR is 145.0 m based on the observed annual maximum data from 1882 to 2010 under stationary conditions; however, the FLWL needs to be re-established to ensure flood safety when the reservoir inflow is altered. In this study, the FLWL is re-set with the assumption that the flood risk probability is equal to the original design value. Means of inflow from 2011 to 2030 are derived from the functions in Tables 2 and 3.

In order to illustrate the determination method about the FLWL of the TGR, 2011 is chosen for an example. Firstly, it is assumed that the design standard (such as flood risk, design flood peak value) of the TGR does not change, and Table 7 shows engineering design parameters of the TGR. Then, statistical parameters (such as mean) of inflow are estimated, and the reservoir FLWL is assumed to 144.9, 145.0 and 145.1 m, respectively, referring to the original FLWL scheme of the TGR. Finally, the result of flood routing is shown in Table 8, and only that the FLWL is 145.0 m can satisfy all requirements for the water level. Figure 9 shows the concrete process of the flood routing.

Table 7 Engineering design parameters of TGR
Full size table
Table 8 Results of flood routing: (a) the typical year is 1954; (b) the typical year is 1981; (c) the typical year is 1982; (d) the typical year is 1998
Full size table
Fig. 9
figure 9

Flood process line when the FLWL of TGR is 145.0 m [there are three lines, i.e., inflow hydrograph (blue solid line), release (orange solid line) and water level change (green solid line)]: a design frequency is 1%, and the typical year is 1981. b Design frequency is 0.1%, and the typical year is 1982. c Design frequency is 0.01% (10% increment), and the typical year is 1954

Full size image

Table 9 shows the result of flood routing with the reservoir streamflow alters. When the mean value decreases from 2011 to 2030, the FLWL can be raised, which are shown in Fig. 10.

Table 9 Results of flood routing on non-stationary condition that the mean changes with time
Full size table
Fig. 10
figure 10

Results of the flood routing [two lines, i.e., FLWL on the non-stationary condition (blue), FLWL on the stationary condition (orange)]

Full size image

Conclusions

The FLWL is the most significant parameter for trade-off between activities of flood control and water conservation, and hence, it is necessary to re-establish FLWL to ensure flood safety when the reservoir inflow is altered. Based on results of the case study for the TGR, main conclusions are summarized as follows:

  1. 1.

    Moving average and L-moment estimation are used to fit the linear function of statistical parameters based on the observed data. Specifically, means of design flood peak, 3-day volume, 7-day volume, 15-day volume and 30-day volume yearly decrease by 33 m3/s, 0.0080 billion m3, 0.0211 billion m3, 0.0482 billion m3 and 0.0905 billion m3, respectively. However, the amplitude of variation of \( C_{\text{V}} \) or \( C_{\text{S}} \) changing with time is insignificant.

  2. 2.

    When the streamflow decreases, the flood risk for non-stationary conditions is less than that for stationary conditions with the exceedance probability varies from each year. Thus, the traditional method for designing the flood risk may not be applicable for the projects under non-stationary condition. In this case study, the cumulative flood risk probability of the reservoir water level exceeding 175.0 m during 2011 to 2030 decreases from 1.98 to 1.82% when the non-stationary design flood is used.

  3. 3.

    The FLWL is sensitive to the design flood, and when streamflow changes, the FLWL needs to be re-established without increasing the flood risk probability. The FLWL of the TGR can increase 4.7 m by 2030.

Since only linear trend has been focused in the non-stationary environment, the design flood can be improved for nonlinear and jump formulation. The FLWL, which is re-established in each year, may not conform to the practical operation and needs to be further researched.