Introduction

The blasting vibration induced by engineered blasting has an important influence on rock stability and ground structures. Many researchers analyzed the factors that effect the blasting vibration, and some field data showed that there were many factors such as delay intervals, geological conditions of the transmitting media, rock property, initiation method and total amount of explosives that had signification influence on blasting vibration except the recognized explosive weight per delay (Li et al. 2016; Roy et al. 2014; Singh et al. 2014). Some modified calculation formulas were proposed to make the vibration prediction more accurate (Birch and Pegden 2014; Hudaverdi and Akyildiz 2017). In the aspect of theory, an equivalent cavity theory of blasting source in a homogeneous elastic medium was established, and the blasting vibration wave was systematically studied and observed by Sharpe (1942a, b). Thereafter, blasting vibration theory was studied in depth along with the generation mechanism and propagation characteristics of a blasting vibration wave (Blake 1952; Duvall 1953; Favreau 1969).

Compared with spherical charge blasting, the blasting vibration of a cylindrical charge has several different characteristics. Starfield and Pugliese (1968) decomposed the cylindrical charge into an equivalent radius spherical charge and superposed an equivalent spherical charge to calculate the vibration of the cylindrical charge. However, this equivalent calculation method did not consider the effect of the axial detonation velocity. Heelan (1953) simplified the cylindrical blasting source as a load related to time that acted on the inner wall of the cylindrical cavity in order to investigate the radiation problems of a finite cylindrical explosive source. Abozena (1977) and Blair (2007) found some limits of the Heelan solution and pointed out that the Heelan solution was more in line with actual blasting vibration only in a far-field and under certain source frequencies. Additionally, Blair (2008), and Blair and Minchinton (1997) developed a nonlinear superposition model on the basis of the linear superposition model to predict the vibration waveform of the cylindrical charge blasting vibration problem. Also the nonlinear response of rock was considered by taking the medium as linear viscoelasticity material in rock blasting, and a sufficiently low-Q value was introduced to describe the viscosity of rock close to the blast hole (Blair 2010). But due to the high pressure caused by rock blasting, the rock near the blast hole had the characteristic of plastic deformation which was inaccurate to be calculated by CQ theory, so an elastic–plastic model was proposed in the calculation of stress wave close to the blast hole (Cohen et al. 2010).

With the development of simulation methods and experimental techniques, there are increasingly more research methods and means available to deal with cylindrical charge blasting vibration problems. Hildyard and Milev (2001) and Vanbrabant et al. (2002) studied cylindrical charge blasting vibration under different detonation velocities with an experimental and numerical simulation method. In their research, whether or not P-Mach and S-Mach waves appeared depended mainly on the relation between the detonation velocity and the P or S wave velocity, respectively. Wang et al. (2011) studied the stress field of cylindrical charge blasting under different initiating positions by using a holographic laser dynamic photo-elasticity experimental method. Blair (2014) studied the propagation law of P-Mach and S-Mach waves of cylindrical charge blasting and their characteristics for different charge lengths. Triviño et al. (2012) and Trivino and Mohanty (2015) analyzed cylindrical charge blasting vibration through a field experiment and numerical simulation of 2DFEM–DEM. Their research results showed that charge length, initiating detonation position and detonating direction affected the frequency and amplitude of vibration waves.

There are increasing requirements for precision in cylindrical blasting PPV prediction. Currently, most of the calculation methods employed for cylindrical charge blasting vibration were based on spherical blasting theory. This approach generally considered the charge length was less than four times its diameter and that the blasting vibration characteristics of a cylindrical charge were similar to a spherical charge (Chen 1998). However, it is not always suitable to calculate cylindrical charge blasting characteristics by using spherical charge theory. Therefore, it is necessary to further theoretically develop the understanding about the characteristics of cylindrical charge blasting and develop a specific calculation method for cylindrical charge blasting vibration.

By introducing an equivalent pressure of cylindrical charge blasting source, a superposition calculation model of long cylindrical charge blasting vibration based on Heelan solution is proposed, which is also verified by a simply Ls-Dyna simulation. Besides, by using numerical fitting method, a modified PPV calculation formula based on Sabouraud formula is proposed in this paper to provide an idea for considering the influence of charge length on blasting vibration.

Stress characteristics of a cylindrical charge blasting near blast hole

The pressure near blast hole induced by rock blasting is much higher than the rock mass strength and causes a crushed zone in rock which has the characteristics of plastic deformation. With the increase of distance from blast hole, the stress amplitude attenuates to the rock strength and then elastic–plastic boundary is emerged. Blasting vibration will be caused by the blasting load that acts on elastic–plastic boundary. In order to further explore the generation and propagation mechanism of a blasting vibration wave, researchers have attempted to find an equivalent load model to describe the blasting load on the wall of the elastic boundary. After comparing multiple source load models and analyzing actual engineering monitoring data, Schenk (1973) found that the stress change in the surrounding medium of the spherical charge blasting was in accordance with the Berlage’s equation:

$$P(t) = P_{0} t^{n} e^{ - \alpha t} \sin \left[ {(\omega + \delta t)t} \right]$$
(1)

where \(P_{0}\), n are the constants of a blasting source, and were affected by charge types, charge weight, charge density, blast hole size; α was the load attenuation coefficient and was mainly affected by the interaction of charge and blast hole; ω, δ were frequency correlation coefficients of stress waves, which were related to the distance from the measure point to the blast hole. The elastic–plastic governing equations near the blast hole were established by Cohen et al. (2010), and the approximation stress solution on elastic–plastic boundary was obtained with the characteristics of a shock wave. So the value of \(\sin \left[ {\left( {\omega + \delta t} \right)t} \right]\) in Eq. (1) could be considered to be 1. As such, the equivalent pressure load function on the blast plastic–elastic boundary can be simplified to:

$$P(t) = P_{0} t^{n} e^{ - \alpha t}$$
(2)

The derivation of P(t) shows that when t m  = n/α the pressure will reach the maximum value \(P_{m} = P_{0} \left( {\frac{n}{\alpha }} \right)^{n} e^{ - n}\), while \(P_{0} = P_{m} \left( {\frac{\alpha e}{n}} \right)^{n}\). Both sides of Eq. (2) can be divided by \(P_{m}\) for the purpose of simplify the calculation, then:

$$\frac{P(t)}{{P_{m} }} = \left( {\frac{\alpha e}{n}} \right)^{n} t^{n} e^{ - \alpha t}$$
(3)

Considering the influence of detonation velocity, the blasting load does not act on the elastic–plastic boundary at the same time, which makes cylindrical charge blasting be different from spherical charge blasting. Assuming the detonation velocity of a cylindrical charge along the axial direction is \(C_{\text{D}}\), and the axial direction is z direction, and making the charge center point as the z axial origin, the equivalent load function of cylindrical charge blasting can be shown as:

$$\frac{P(t,z)}{{P_{m} }} = \left( {\frac{\alpha e}{n}} \right)^{n} H\left[ {\tau \left( {t,z} \right)} \right]\tau^{2} \left( {t,z} \right)e^{{ - \alpha \tau \left( {t,z} \right)}}$$
(4)

where \(H\left( \tau \right)\) is the Heaviside unit step function; L is the charge length; z is the distance from cylindrical charge to the charge center; and its data range is [−L/2, L/2]. \(\tau \left( {t,z} \right)\) is a two-dimensional parameter and is decided by initiation method. Only bottom initiation is considered here, that to say \(z = - \frac{L}{2}\) means \(\tau = t\), and \(z = \frac{L}{2}\) means \(\tau = t - L/C_{\text{D}}\), so the expression of \(\tau \left( {t,z} \right)\) can be shown as:

$$\tau \left( {t,z} \right) = t - {{\left( {\frac{L}{2} + z} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{L}{2} + z} \right)} {C_{\text{D}} }}} \right. \kern-0pt} {C_{\text{D}} }}$$
(5)

If the charge length is L = 5 m, and the detonation velocity of the explosive is \(C_{\text{D}} = 5000 \,{\text{m}}/{\text{s}}\), and n is in the approximate range of 3–9 depending on the mass of experimental data of Larson (1982), and the value of α is in range of 2000–8000 which can be obtained through the work of Chen et al. (2011), the equivalent pressure load of a bottom initiation cylindrical charge blasting source can expressed as in Fig. 1 when n = 6 and α = 4000.

Fig. 1
figure 1

Equivalent pressure load of cylindrical charge blasting source with bottom initiation

Full size image

Pressure is exerted on the elastic–plastic boundary successively from an initiation point, so the assumption that blasting pressure acts on the elastic–plastic boundary along the media axis of the cylindrical charge at the same time is not suitable to reflect the characteristics of cylindrical charge blasting, especially when the length of a charge is sufficiently long. As a result, it is necessary to further consider the effects of different charge lengths in cylindrical blasting.

Vibration characteristics of a finite length cylindrical charge blasting

Heelan simplified cavity-blasting pressure to solve the cylindrical charge blasting vibration problem. The solution showed that a P wave and S wave would be produced from finite cylindrical blasting, and an elastic displacement equation for finite cylindrical blasting vibration was later obtained (Heelan 1953):

$$\left\{ {\begin{array}{*{20}c} {H_{\text{P}} = \frac{{F_{1} \left( \phi \right)}}{R}P^{\prime}\left( {t - \frac{R}{{C_{\text{P}} }}} \right)} \\ {H_{\text{S}} = \frac{{F_{2} \left( \phi \right)}}{R}P^{\prime}\left( {t - \frac{R}{{C_{S} }}} \right)} \\ \end{array} } \right.$$
(6)

where

$$\left\{ {\begin{array}{*{20}l} {F_{1} \left( \phi \right) = \frac{{r_{\text{c}}^{2} L}}{{4\mu C_{\text{P}} }}\left( {1 - \frac{{2C_{\text{s}}^{2} }}{{C_{\text{P}}^{2} }}{ \cos }^{2} \phi } \right)} \\ { F_{2} \left( \phi \right) = \frac{{r_{\text{c}}^{2} L}}{{4\mu C_{\text{s}} }}{ \sin }2\phi } \\ \end{array} } \right.$$
(7)

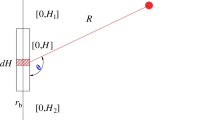
in which \(H_{\text{P}}\) and \(H_{\text{S}}\) are the displacement induced by P wave and S wave; \(r_{\text{c}}\) is the radius of the cylindrical elastic cavity; R was the distance from the measured point to the charge center; \(\phi\) is the angle between a negative z axis and the connecting line from a measured point to the origin point; \(\mu\) is the rock shear modulus; \(C_{\text{P}}\) and \(C_{\text{s}}\) are P wave and S wave propagation velocity and are expressed as follows (Guo 1982):

$$\left\{ {\begin{array}{*{20}l} {C_{\text{P}} = \sqrt {\frac{{E\left( {1 - \upsilon } \right)}}{{\rho \left( {1 + \upsilon } \right)\left( {1 - 2\upsilon } \right)}}} } \\ {C_{\text{S}} = \sqrt {\frac{E}{{2\rho \left( {1 + \upsilon } \right)}}} } \\ \end{array} } \right.$$
(8)

where \(E\) as the elastic modulus, \(\rho\) is media density and \(\upsilon\) is Poisson’s ratio.

Blair (2007) provided a numerical comparison between a Heelan solution and an exact solution for the radiation of a vibration wave and found that the Heelan solution was quite valid if the horizontal distance from the measured point to the charge center was \(r_{0} \ge 50r_{\text{c}}\), provided \(\varOmega_{A} < 0.1\), where \(\varOmega_{A} = r_{\text{c}} \omega_{A} /C_{\text{P}}\), in which \(\omega_{A}\) was a mean frequency of pressure acted on elastic cavity inner wall. For convenience of calculations, Heelan solution is used here to calculate the blasting vibration in the far field. Making \(\tau_{\text{p}} = t - R/C_{\text{p}}\), \(\tau_{\text{s}} = t - R/C_{\text{s}}\), bringing (2) into (7), and having a derivative to time, the attenuation relationship between particle velocity and the distance and time can be obtained as follows:

$$\left\{ {\begin{array}{*{20}l} {\nu_{\text{p}} = \frac{{P_{0} r_{\text{c}}^{2} L}}{{4\mu C_{\text{p}} R}}\left( {1 - \frac{{2C_{\text{s}}^{2} }}{{C_{\text{p}}^{ 2} }}{ \cos }^{2} \phi } \right)p\left( {\tau_{\text{p}} } \right)} \\ {\nu_{\text{s}} = \frac{{P_{0} r_{\text{c}}^{2} L}}{{4\mu C_{\text{s}} R}}{ \sin }2\phi p\left( {\tau_{\text{s}} } \right) } \\ \end{array} } \right.$$
(9)

where

$$p\left( \tau \right) = H\left( \tau \right)\left[ {\alpha^{2} \tau^{n} - 2\alpha n\tau^{n - 1} + n\left( {n - 1} \right)\tau^{n - 2} } \right]e^{ - \alpha \tau }$$
(10)

Analysis on \(p(\tau )\) shows that \(p(\tau )\) is a blasting vibration waveform equation, and the amplitude and the period of the particle vibration are related to the constant of the blast source \(n\) and the pressure attenuation coefficient α. Blair (2010) discussed the influence of n and found that the larger the value is, the larger the vibration period is. In this paper, making n = 6, and \({ \hbox{max} }\left[ {{\text{p}}\left( \tau \right)} \right]\) is the maximum value of \(p(\tau )\), the dimensionless vibration waveforms \(p_{d} \left( \tau \right) = {{p\left( \tau \right)} \mathord{\left/ {\vphantom {{p\left( \tau \right)} {{ \hbox{max} }\left[ {p\left( \tau \right)} \right]}}} \right. \kern-0pt} {{ \hbox{max} }\left[ {p\left( \tau \right)} \right]}}\) are illustrated in Fig. 1 for α = 3000, 4000 and 5000, respectively.

The waveforms shown in Fig. 2 are similar to some of the measured waveforms reported by Schenk (1973), which indicated that the Heelan solution and the blast source equivalent pressure are reasonable. Additionally, When the constants n and \(P_{0}\) remain unchanged, the smaller the attenuation coefficient of the cavity wall pressure is, the larger the particle vibration amplitude and the period are.

Fig. 2
figure 2

Vibration waveforms for different pressure attenuation coefficients

Full size image

Influence of charge length on cylindrical blasting vibration

Calculation model for long cylindrical charge blasting vibration

The Heelan solution is valid to solve the cylindrical charge blasting vibration problem only when the charge length is sufficiently short. Equation (9) shows that the particle velocity of cylindrical blasting vibration is a linear function of charge length L, which means that an axial linear superposition calculation model of long cylindrical blasting vibration by short cylindrical blasting is viable, and it would only cause acceptable errors in the calculation results. Cylindrical charge blasting in rock is a spatial axisymmetrical problem that can be discussed in a two-dimensional plane. A linear superposition calculation model for long cylindrical blasting vibration is shown in Fig. 3, where the center of the cylindrical charge is a coordinate origin, the charge axial is on the z axis and the charge radial is on the r axis.

Fig. 3
figure 3

Superposition calculation model of long cylindrical blasting vibration

Full size image

A long cylindrical charge can be divided into several short cylindrical charges with length d, and the interval time induced by detonation velocity is considered in order to calculate the long cylindrical blasting vibration by the superposition of short charge blasting.

Bringing (8) into (9), and the blasting vibration velocity at measure point \((r_{0} \begin{array}{*{20}c} , \\ \end{array} z_{0} )\) caused by short charge i can be expressed as follows:

$$\left\{ {\begin{array}{*{20}c} {\nu_{pi} = \frac{{P_{0} r_{\text{c}}^{2} d}}{{4\mu C_{\text{p}} }} \times \frac{{{ \sin }^{2} \phi_{i} + \left( {2{ \cos }^{2} \phi_{i} - 1} \right)\upsilon }}{{\left( {1 - \upsilon } \right)R_{i} }}p\left( {\tau_{pi} } \right)} \\ {\nu_{si} = \frac{{P_{0} r_{\text{c}}^{2} d}}{{2\mu C_{\text{s}} }} \times \frac{{{ \sin }\phi_{i} { \cos }\phi_{i} }}{{R_{i} }}p\left( {\tau_{si} } \right) } \\ \end{array} } \right.$$
(11)

where

$$\left\{ {\begin{array}{*{20}c} {\tau_{pi} = t - \left( {\frac{{\frac{L}{2} + z_{i} }}{{C_{\text{D}} }} + \frac{{R_{i} }}{{C_{\text{p}} }}} \right)} \\ {\tau_{si} = t - \left( {\frac{{\frac{L}{2} + z_{i} }}{{C_{\text{D}} }} + \frac{{R_{i} }}{{C_{\text{s}} }}} \right)} \\ \end{array} } \right.$$
(12)

As the P and S wave propagation directions are different for each short cylindrical charge, direct superposition is impossible. As such, the vibration waves are separated into horizontal and vertical directions to calculate the particle vibration velocity of short cylindrical charge blasting. It follows that:

$$\left[ {\begin{array}{*{20}c} {\nu_{ri} } \\ {\nu_{zi} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{ \sin }\phi_{i} } & {{ \cos }\phi_{i} } \\ { - { \cos }\phi_{i} } & {{ \sin }\phi_{i} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\nu_{pi} } \\ {\nu_{si} } \\ \end{array} } \right]$$
(13)

By the superposition of horizontal and vertical vibration velocities of short charges, the normalized particle vibration velocities induced by a long cylindrical charge can be obtained as follows:

$$\left\{ {\begin{array}{*{20}c} {\frac{{\nu_{r} \left( {r,z,t} \right)}}{k} = d\mathop \sum \limits_{i}^{{\frac{L}{d}}} \frac{{{ \sin }\phi_{i} }}{{R_{i} }}\left[ {2C_{\text{p}} { \cos }^{2} \phi_{i} p\left( {\tau_{si} } \right) + C_{\text{s}} \frac{{{ \sin }^{2} \phi_{i} + \left( {2{ \cos }^{2} \phi_{i} - 1} \right)\upsilon }}{{\left( {1 - \upsilon } \right)}}p\left( {\tau_{pi} } \right)} \right]} \\ {\frac{{\nu_{z} \left( {r,z,t} \right)}}{k} = d\mathop \sum \limits_{i}^{{\frac{L}{d}}} \frac{{{ \cos }\phi_{i} }}{{R_{i} }}\left[ {2C_{\text{p}} { \sin }^{2} \phi_{i} p\left( {\tau_{si} } \right) - C_{\text{s}} \frac{{{ \sin }^{2} \phi_{i} + \left( {2{ \cos }^{2} \phi_{i} - 1} \right)\upsilon }}{{\left( {1 - \upsilon } \right)}}p\left( {\tau_{pi} } \right)} \right]} \\ \end{array} } \right.$$
(14)

The parameter \(k = \frac{{P_{0} r_{\text{c}}^{2} }}{{4\mu C_{\text{P}} C_{\text{S}} }}\) depends on the type of explosive, the radius and structure of charge and the characteristics of the medium.

Discussion of long cylindrical charge blasting vibration characteristics

Equation (14) shows that the normalized particle vibration velocity depends only on the short cylindrical charge length d, the position of measure point \((r_{0} ,z_{0} )\), the detonation velocity of explosive \(C_{\text{D}}\), and the long cylindrical charge length L.

In theory, the calculation result is more accurate for a smaller short charge length. When the microcharge length d = 0.5 m, the detonation time d/C D is of the 10−4 s magnitude, which can be ignored. Therefore, a suitable microcharge length d = 0.5 m can be chosen to calculate the long charge blasting vibration in an actual situation to avoid excessive computation. In this paper, the parameters of blasting source pressure are n = 6, α = 4000, and the calculation parameters of certain surrounding rock are as shown in Table 1.

Table 1 Calculation parameters of surrounding rock
Full size table

A long charge length L = 10 m is supposed to discuss the influence of explosive detonation velocity on cylindrical blasting vibration. For C D = 3000, 4000, and 5000 m/s, the long cylindrical charge vibration of measure point with a vertical distance z 0 = 30 m and horizontal distance r 0 = 80 m, and charge length L = 10 m are as shown in Fig. 4.

Fig. 4
figure 4

Normalized velocity with different detonation velocities. a Horizontal velocity with different C D; b vertical velocity with different C D

Full size image

As shown in Fig. 4, with a decrease in detonation velocity, vibration amplitude and PPV of a long charge become small, while the duration of the blasting vibration continues to grow.

Also, the influence of horizontal distance on cylindrical charge blasting vibration is discussed. For r 0 = 40, 60, 80, 100 m, the blasting vibration waveform curves of cylindrical charge with vertical distance z 0 = 40 m, charge detonation velocity C D = 5000 m/s, and charge length L = 10 m are shown in Fig. 5.

Fig. 5
figure 5

Normalized velocity with different horizontal distances. a Horizontal velocity of different \(r_{0}\); b vertical velocity of different \(r_{0}\)

Full size image

As shown in Fig. 5, the vibration amplitude decreases, and the vibration duration increases with the increase in horizontal distance.

When detonation velocity is C D = 5000 m/s, for vertical distance z 0 = 30 m, and horizontal distance r 0 = 80 m, Fig. 6 provides the cylindrical blasting vibration waveform curves with charge length L = 5, 10, 15, and 20 m.

Fig. 6
figure 6

Normalized velocity with different charge lengths. a Horizontal velocity with different L; b vertical velocity with different L

Full size image

The influence of charge length on the cylindrical blasting vibration waveform is shown in Fig. 6. According to Fig. 6, with increasing charge length, the duration of particle vibration increases, whether it is horizontal velocity or vertical velocity. Additionally, the peak amplitude in the first half period grows with an increase in charge length. For the second half of the period, it is not so regular.

PPV characteristics of cylindrical charge blasting

PPV of cylindrical blasting vibration can be calculated through the superposition of a microcharge in an axial direction. If the detonation velocity C D = 5000 m/s, for a Heelan solution and this paper solution with d = 0.5 m, the normalized horizontal peak particle velocities are expressed as \({{{\text{PP}}v_{\text{H}} } \mathord{\left/ {\vphantom {{{\text{PP}}v_{\text{H}} } k}} \right. \kern-0pt} k}\) (Heelan) and \({{{\text{PP}}v} \mathord{\left/ {\vphantom {{{\text{PP}}v} k}} \right. \kern-0pt} k}\), which can be calculated through Eqs. (9) and (14). The calculating data are shown in Fig. 7. Due to the lack of consideration for the influence of detonation velocity, the calculation error in the Heelan formula compared with the theoretical results of this paper can be expressed as relative error R e, which is:

Fig. 7
figure 7

Horizontal peak velocity of different \(r\)

Full size image
$$R_{\text{e}} = \frac{{{{{\text{PP}}v_{\text{H}} } \mathord{\left/ {\vphantom {{{\text{PP}}v_{\text{H}} } k}} \right. \kern-0pt} k} - {{{\text{PP}}v} \mathord{\left/ {\vphantom {{{\text{PP}}v} k}} \right. \kern-0pt} k}}}{{{{{\text{PP}}v} \mathord{\left/ {\vphantom {{{\text{PP}}v} k}} \right. \kern-0pt} k}}}$$
(15)

The relative errors of horizontal and vertical velocity between a Heelan formula and formula (14) with different charge lengths and horizontal distances are shown in Fig. 8.

Fig. 8
figure 8

Horizontal and vertical velocity relative errors

Full size image

As is shown in Fig. 7, the Heelan solution is only valid for a short cylindrical charge approximation. With increasing charge length, the difference between the two calculation methods increases. Figure 8 shows that the relative error can increase to about 45%, which cannot be ignored. Also, the relative error of vertical PPV is quite similar to the horizontal peak velocity laws. As such, only horizontal PPV characteristics are discussed in the following section.

The influence of horizontal distance and charge length on particle vibration is discussed. The horizontal velocities with the change of horizontal distance and charge length are shown in Figs. 9 and 10.

Fig. 9
figure 9

Horizontal velocity for different r

Full size image
Fig. 10
figure 10

Horizontal velocity for different L

Full size image

PPV is generally a negative exponential decay with increasing horizontal distance. Peak velocity increases with increasing charge length when the charge length is less than 6 m, but not so regular when the charge length is more than 6 m. A clear rule can be found in Fig. 10, where with an increase in charge length, PPV increases and reaches a maximum value, then decreases to a constant value. The further the horizontal distance between the measure point and the blasting source, the smaller the charge length required to reach the maximum. That is to say, there is an effective charge length for the PPV of a certain measure point, and simply increasing the charge length does not significantly increase the PPV when the charge is more than a certain length. Because the charge weight is proportional to charge length in cylindrical charge blasting, the traditional calculation method, which suggests that peak vibration velocity is a positive correlation with charge weight, does not conform to the theoretical results of cylindrical charge blasting. Similar conclusions can also be found in the numerical simulation by Blair (2010), and Blair and Jiang (1995) and the blasting experiment of Grant et al. (1987).

In order to further verify the influence of charge length on blasting vibration PPV, a simple Ansys/Ls-Dyna numerical simulation model considering different charge lengths is established. The model size is 5 m × 38 m × 105 m and the surrounding rock can be obtained in Table 1, other conditions are the same as theoretical calculations. The mesh model is shown in Fig. 11.

Fig. 11
figure 11

Mesh model of long cylindrical blasting vibration

Full size image

The vertical distance is 30 m, for horizontal distance r = 20, 30, 40, 60 and 80 m; Fig. 12 provides the particle peak horizontal and vertical displacements for different charge length.

Fig. 12
figure 12

Peak particle displacement for different charge length. a Horizontal displacement; b vertical displacement

Full size image

The simulation results in Fig. 12 show that with the increase in charge length, the peak particle amplitude of cylindrical charge blasting vibration tends to be moderated. This result is the same as the theoretical calculation in this paper. Also, the simulation result further shows that the traditional vibration amplitude formula mainly considering charge weight is limited in solving the cylindrical charge blasting vibration. So, it is necessary to modify the traditional calculation method when it comes to cylindrical charge.

PPV modification of cylindrical charge blasting vibration

Commonly, a blasting vibration PPV calculation is obtained by using a semi-theoretical formula which is expressed as the Sabouraud formula (NDRC 2007):

$${\text{PPV}} = K\left( {\frac{{Q^{1/3} }}{r}} \right)^{\beta }$$
(16)

PPV is the PPV in a Sabouraud formula, cm/s; Q is the maximum charge weight per delay interval, kg; r is the distance from measured points to the center of explosion source, m; and K, β are the site coefficients. These parameters can be obtained through engineering experience or by fitting the results of field test blasting measurement data. Horizontal, vertical, and resultant velocities are all according to the Sabouraud formula based on the large amount of experimental data from Meng and Hui (1992).

As noted previously, due to the influence of explosive detonation velocity, the Sabouraud formula needs to be corrected for cylindrical charge blasting. For a cylindrical charge, if q is charge line density, L is charge length, bringing the total weight of cylindrical charge \(Q = qL\) into the Sabouraud formula, and dividing by the normalized parameters k on both sides, a normalized PPV can be express as follows:

$$\frac{\text{PPV}}{k} = K^{\prime}\left( {\frac{{\sqrt[3]{L}}}{r}} \right)^{\beta }$$
(17)

where \(K^{\prime} = \frac{K}{k}q^{{\frac{\beta }{3}}}\).

In order to facilitate analysis, only the horizontal direction velocity is calculated. If detonation velocity C D = 5000 m/s, the surrounding rock calculation parameters can be obtained in Table 1. Then the theoretical data of a normalized horizontal PPV can be obtained through Eq. (14). The fitting parameters K′ = 3.515 × 10−10, β = 1.148 can be obtained with the charge length L = 0.5 m (Fig. 13).

Fig. 13
figure 13

Fitting of the normalized horizontal PPV when \(L = 0.5\,{\text{m}}\)

Full size image

The normalized horizontal peak particle velocities \({{{\text{PP}}v_{r} } \mathord{\left/ {\vphantom {{{\text{PP}}v_{r} } k}} \right. \kern-0pt} k}\) (theoretical data) with different charge lengths can be obtained by Eq. (14), and the peak particle velocities \({{{\text{PP}}V_{r} } \mathord{\left/ {\vphantom {{{\text{PP}}V_{r} } k}} \right. \kern-0pt} k}\) with different charge lengths can be obtained by the Sabouraud formula (16). The modification factor can be obtained by \({{{\text{PP}}v_{r} } \mathord{\left/ {\vphantom {{{\text{PP}}v_{r} } k}} \right. \kern-0pt} k}\) dividing \({{{\text{PPV}}_{r} } \mathord{\left/ {\vphantom {{{\text{PPV}}_{r} } k}} \right. \kern-0pt} k}\), and the modification factor can be expressed as follows:

$$f\left( {L,r} \right) = \frac{{{\text{PP}}\nu_{r} }}{{{\text{PPV}}_{r} }}$$
(18)

The modification factor change with charge length, and horizontal distance is shown in Fig. 14.

Fig. 14
figure 14

Modification factor with different L

Full size image

The Sabouraud formula modification factor of cylindrical charge blasting vibration is a coupling equation with charge length and horizontal distance, which is shown in Fig. 14. If the charge length L < 5 m, the horizontal distance has little effect on the modification factor. When L ≥ 5 m, the farther the horizontal distance is, the smaller the modification factor is. With an increase in charge length, the modification factor first increases, reaches a maximum, and then decreases. The following equation is in accordance with the law for a modified factor curve:

$$f\left( {L,r} \right) = f_{1} \left( r \right){\text{L}}e^{{ - f_{2} \left( r \right)L}}$$
(19)

where \(f_{1} (r)\) and \(f_{2} (r)\) shown in Fig. 15 are modification functions associated with horizontal distance, and can be obtained by fitting the modification factor with charge length L in Fig. 15 and Eq. (19).

Fig. 15
figure 15

Modification factor change with horizontal distance \(r\). a Modification factor of \(f_{1} (r)\); b modification factor of \(f_{2} (r)\)

Full size image

As described in Fig. 15, \(f_{1} (r)\) is a constant, and \(f_{2} (r)\) is a function associated with horizontal distance. Their value depends on charge characteristics, site condition, etc. As discussed above, similar laws apply to vertical PPV. As such, the modification factors of the Sabouraud formula no matter in horizontal or vertical direction changes with horizontal can be expressed as follows:

$$\left\{ {\begin{array}{*{20}l} {f_{1} \left( r \right) = k_{1} } \hfill \\ {f_{2} \left( r \right) = - \frac{a}{r} + b} \hfill \\ \end{array} } \right.$$
(20)

Then the complete modification factor can be expressed as:

$$f\left( {L,r} \right) = k_{1} Le^{{\left( {\frac{a}{r} - b} \right)L}}$$
(21)

Therefore, the new modification Sabouraud formula PPV for cylindrical charge blasting is expressed as follows:

$${\text{PPV}} = Kk_{1} Le^{{\left( {\frac{a}{r} - b} \right)L}} \left( {\frac{{Q^{{\frac{1}{3}}} }}{r}} \right)^{\beta }$$
(22)

where L is charge length, m; r is the horizontal distance from measure point to blasting source, m; k 1, a, b are parameters that relate to the detonation velocity of explosive, the vertical distance of charge, site coefficients, etc. The definitions of the other parameters are the same as with Eq. (16). In the same way, PPV can be obtained for vertical and resultant velocities.

For cylindrical charge length L = 10 m, the theoretical data calculated through Eq. (14), the Sabouraud formula curve obtained by Eq. (17), and the modified Sabouraud formula curve obtain by Eq. (22) are shown in Fig. 16.

Fig. 16
figure 16

Comparison of modified Sabouraud formula when L = 10 m

Full size image

As shown in Fig. 16, the PPV of cylindrical blasting with a charge length L = 10 m calculated by the modified Sabouraud formula is very much in agreement with the theoretical results. That is to say, the modified Sabouraud formula reflects the characteristics of cylindrical blasting by considering the influence of the axial detonation velocity.

When the PPV of cylindrical blasting reaches its maximum value for a particular measure point, the corresponding charge length \(L^{\prime}\) can be obtained if the partial derivatives of the modified Sabouraud formula for L are equal to zero.

$$\frac{{\partial {\text{PPV}}}}{{\partial {\text{L}}}} = Kk_{1} \left[ {\left( {\frac{\beta }{3} + 1} \right) + \left( {\frac{a}{r} - b} \right)L} \right]e^{{\left( {\frac{a}{r} - b} \right)}} \left( {\frac{{Q^{1/3} }}{r}} \right)^{\beta } = 0$$
(23)
$$L^{\prime} = \frac{{\left( {\beta + 3} \right)r}}{{3\left( {br - a} \right)}}$$
(24)

That is to say, for a particular measure point, the PPV reaches its maximum value, when charge length \(L = L^{\prime}\). Furthermore, if \(L \ge L^{\prime}\), the PPV would not increase any more with an increase in charge length. Peak particle vibration velocity is an important criterion for characterizing blasting vibration and can be used to improve blasting design in practical engineering. Site coefficients K, β, k 1, a, b can be obtained by fitting results from measured data done in pretesting blasting at a construction site. Subsequently, PPV for cylindrical blasting can be predicted by Eq. (22).

Conclusion

A superposition model is used to calculate the vibration of cylindrical charge blasting while considering the influence of detonation velocity and charge length. The following conclusions are obtained by analyzing the calculation superposition model:

  1. 1.

    The vibration waveform of short cylindrical charge blasting is dependent on blasting source pressure function acted on the elastic–plastic boundary, with the smaller the attenuation coefficient of pressure α, the larger the vibration period and amplitude.

  2. 2.

    For a certain charge length, the smaller the detonation velocity, the smaller the vibration amplitude and the longer the duration of blasting vibration, and more complex the waveform. Therefore, the influence of charge length on cylindrical blasting vibration needs to be considered, especially for small detonation velocity.

  3. 3.

    The characteristics of cylindrical charge blasting vibration change with increase in charge length. PPV of cylindrical charge blasting increases with an increase in charge length when the charge length is small. When the length reaches a certain value, the PPV no longer increases, and even reduces. This phenomenon is quite different from the traditional calculation method currently used to determine PPV.

  4. 4.

    The traditional PPV calculation method has limitations in solving for cylindrical charge blasting vibration. A charge length modification factor for cylindrical charge blasting vibration is introduced to modify the widely applicable Sabouraud formula. The modified Sabouraud formula does well in characterizing the PPV characteristics of cylindrical charge blasting vibration, and the effective charge length can also be calculated by the modified formula.

The new calculation formula proposed in this paper is primarily based on theory and previous research and has not yet been applied in an actual project. As such, further experimental and engineering research is warranted in future.