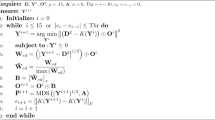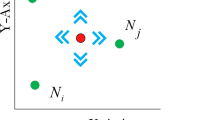T-LOC: RSSI-based, range-free, triangulation assisted localization for convex relaxation with limited node range under uncertainty skew constraint

Abstract

Triangulation uncertainty is the uncertainty associated when we try to locate an unknown target with the help of three anchor nodes resulting in formation of a triangulated region. Efficient triangulation leads to superior accuracy and lower rate of errors in sensor networks. Although sufficient work has been done to compute localization uncertainties, there is dearth of work pertaining to triangulation uncertainty. The existing problems are: first, localization incurs large computation cost, necessitating some hierarchy or clustering techniques. Second, linear, non-linear and optimization-based solvers invariably simplify the occurrence of errors during estimation of localization. To solve these problems, the present work proposes a range free assistive approach in detecting symmetric triangulations. This approach combined with semidefinite programming of the cost function is shown to exhibit improved localization performance. Numerical results show that the RMS errors is reduced by using triangulation assisted node deployment. The results are compared with the standard weighted least square method for different number of anchor nodes.

1 Introduction

Sensor nodes are meant to be deployed in groups so as to cover a large surface area. Marine environment data collection (Geetha et al. 2011) by the Argo floats system is a practical example of sensor network. Applications of sensor networks in the field of firetower placements in forests (Tekdas and Isler 2010), militarized/ security monitoring and educational setups require gathering intelligence for resource planning (Biswas et al. 2006). Localization is a crucial aspect of sensor node networks, which ensures that the nodes be aware of their physical location during the entire process of sensing, processing and communication of data. Localization may be possible through range-based or range-free methods. The advent of efficient compute nodes has enabled use of intelligent algorithms to combine both these techniques to give rise to several hybrid techniques. Triangulation (Yang et al. 2019) is a popular method of localization and ranging which helps to locate sensors and/or unknown targets in remote deployment scenarios.

1.1 Related work

Localization is being vigorously pursued by researchers so that the sensors adapt to various anomalies and ravages of nature. Some recent works which focus on the range free localization with triangulation uncertainty and employing some form of convex optimization such as semidefinite programming would be the closest to the current proposed work. The expected area of uncertainty of position per sensor has been explored using three range-free localization schemes (Stupp and Sidi 2004). Although the expected uncertainty was achieved using half the resources, yet there is a scope for improvement of approximation if convex optimization is used too. To address convex and non-convex scenarios in addition to range-free localization, (Kubo et al. 2012) propose a grid based transformation and mapping approach to locate the target. Even though their method improves upon both the positioning accuracy as well as coverage area, it misses out on the concept of triangulation uncertainty to account for the ambiguity of sensor location. An in-depth analysis about true triangulation is taken up by (Yang et al. 2019) for a 3 dimensional architecture. It could be applied to range-free localization techniques, but it falls short of the issues faced by wireless sensor networks such as the loss of anchor node and perturbations. It is triumphed by (An et al. 2020) in which larger regions are compacted into smaller triangulations. This results in a tighter control over localization as well as path planning, however, it lacks analysis of any range-free or convex optimized localization schemes. Convex triangulation is discussed in (Prateek and Arya 2021a) wherein a convex weighted approach has been applied to mathematically analyse the uncertainty behaviour. Although symmetry of triangulation has been discussed in detail, but it does not discuss how to implement semidefinite relaxation to a WSN case. The three works which closely explain the implementation of Semidefinite relaxation are, first, the twin works of Q. Shi et. al. in (Shi and He 2008; Shi et al. 2010), and third, (Salari et al. 2013). The first two attempts reveal greedy algorithm and a range free algorithm for semidefinite relaxation of the constraints to the localization cost function. While they are range-free algorithms, the third work describes range-based localization that is usually considered more resource intensive than the range free methods. Range-free is also not present in the wireless localization scheme proposed by (Zhang et al. 2016), but it discusses square of positioning uncertainty which is important if the sensor nodes or the target are in relative motion. Though it does not present a semidefinite programming approach for solving the node locations, but a geometric programming approach has been derived in detail as a proof of mathematical justification. Concept of uncertainty is extended towards the concept of estimative rectangle in (Chen et al. 2014) which decides the success or failure of localization based on overlapping regions of node communication ranges. Since rectangular region requires higher number of sensor node vertices than triangulation region, therefore, the issue of triangulation uncertainty remains wide open. This void is fulfilled partially by (Ma and Yang 2007) where they comprehensively try to achieve triangulation that is as close to equilateral triangle as possible, so that symmetry between triangulation pattern is maximized. They have named it the adaptive triangular deployment algorithm. Although it enables them to sectorize the sensing region into six parts, there is no mention of range-free mechanism that could reduce the resource requirement. Such a resource-frugal arrangement that does not require the information of reference sensor is presented with the help of the range-difference of measurements followed by numerical method, that is, source localization using majorization minimization technique (Jyothi and Babu 2020). Their work lacks triangulation methods and anchor node uncertainties, therefore, a robust triangulation method is shown to achieve accurate localization even in presence of node mobility (Hsieh and Wang 2006). It, however, lacks any form of convex triangulation, just like (Sortais et al. 2008) which incorporate range-free localization and location uncertainty without exploring the effect of convex relaxation or semidefinite optimization. Instead, they have opted for iterative evaluation that achieves accuracy at the cost of computational complexity. In particular, they have investigated the stochastic geometry of the node topology and Monte-Carlo scaling, but have refrained from using any form of convex combination for precision improvement. Convex approach is also avoided in (Sahin et al. 2015), wherein, the estimated location is derived with the help of Cramer Rao lower bound of the received signal strength of the sensor transmissions. A similar outcome in the form of localized homogenous optical wireless networks is presented by (Seguel et al. 2018), but their domain deviates significantly from the present context, into the domain of lightwave signals, therefore, the contribution by (Gopikrishnan et al. 2016) comes into the picture as they have considered convex modelling to hasten up the computation of range-free localization error identification. Further, cooperative localization has been considered to enable localization despite the random node placement and radio obstructions. However, their approach does not consider triangulation technique even though it describes a range free mode of operation. Another cooperative localization approach by (Chen et al. 2009) makes use of relay nodes to localize mobile anchor nodes and static sensor nodes. To observe both the range free and the triangulation operation working together, a cosine approach by (Zeng et al. 2012) is presented albeit with pretty scarce mathematical background. Their method claims to improve upon the traditional Approximate Point in Triangulation (APIT) but it fails to provide sufficient mathematical justification as to how it can address node perturbations. A thorough investigation is performed by (Lee et al. 2013) with the purpose of proving how to avoid multilateration, yet achieve comparable range-free localization performance. They have resorted to multidimensional support vector regression and eventually tipped towards convex optimization to train a the wireless sensor network in either isotropic or anisotropic scenario for robust performance. A new concept of “bounding boxes” is combined with convex optimized node cooperation for localized estimation in (Darakeh et al. 2017) while it misses out on triangulation uncertainty. Table lists the abbreviation used in this paper.

1.2 Major contributions

In this paper, we present an investigation into sensor network localization problem in terms of triangulation uncertainty. The scenario in which target node is affected by obstructing conditions is considered here. In an energy-limited scenario, one of the major constraints, i.e., internodal communication range is taken as a fraction of the total deployment area. Thus, location accuracy is analyzed keeping in mind that the target node is challenged both in terms of communication range as well as the unavailability of line-of-sight signal from the anchor nodes. To alleviate these issues, we develop a signal model and a range skew model to incorporate the concept of triangulation uncertainty prior to the position estimation. We prove mathematically these models by introducing a new term: “triangulation uncertainty skew” to relax the constraints of the Maximum likelihood estimation cost function into a convex semidefinite programming formulation. We take the help of parameters, namely, RMS errors and CDF plots to comment upon the accuracy aspect of the formulation. We present a convex optimization problem to localize sensor nodes by taking help of triangulation uncertainties due to limited communication range of sensor nodes. Some of the highlights of the present work are as follows:

• The present work not only considers the perturbations of the target, but also considers the perturbations of the sensor network. Therefore, two terms, namely, triangulation uncertainty and uncertainty skew have been introduced to model perturbation of the target and that of the sensor network, respectively.

• The novel concept of collective triangulation is proposed here, wherein, all the triplets of nodes (which could be anchor nodes or sensor nodes or a mixture of both) which have comparable triangulation uncertainty and enclose the target within their region, are defined as a spatial uncertainty cluster. The positioning information of the target is considered by selecting triangulating nodes from this spatial uncertainty cluster for a more precise localization.

• The concept of Apex node is defined as the node which is used to simulate the behavior of target node movement close to one of the vertex node of the triangulation concerned, to overcome the issue of edge-errors which is common in triangulation based conventional localization.

• A triangulation assisted localization (abbreviated as T-LOC) is presented here that is range-free (therefore less resource intensive), convex relaxed (thereby being applicable to even non-convex regions such as realistic terrains), semidefinite programmed (rendering the Fisher matrix solvable for accurate CRLB analysis).

  The main contributions of this paper are as follows:

• We present a scheme to attain optimal localization under radio-obstructed (R-O) and range-limited geometry. Through the introduction of skewed range, it can be shown that triangulation sensor node assisted localization achieves higher accuracy than conventional localization methods without the assistance of nodes capable of triangulation.

• We formulate an iterative method of localization aided by sensor triangulation information (T-LOC). The proposed technique can cooperatively localize unobstructed (nR-O) target nodes by taking the help of radio-obstructed (R-O) triangulation skew parameter, to improve upon the localization accuracy.

• We compare the performance of the proposed T-LOC maximum likelihood estimator (MLE) with uncertainty skew constraints and semidefinite-programming, to Weighted least squares (WLS) localization method (Wang et al. 2012; Shi et al. 2020) for different threshold sensor communication ranges.

The paper organisation is as follows: Sect. 2 proposes a signal model and a range skew model for node deployment with unobstructed (nR-O) and radio-obstructed (R-O) links, as illustrated in Fig. 1(a–d). Section 3 presents a rigorous analysis of the geometric aspect of uncertainty node skew on both spatial as well as temporal cases. Section 4 shows the numerical results and findings based on the localization uncertainty computations using the proposed methods. Finally, the conclusions are mentioned in Sect. 5.

Fig. 1

Illustration of the problem definition for different R-O and nR-O scenario

2 Problem formulation

2.1 Signal model:

In a 2D deployment scenario, suppose $N_{a}$ be the number of anchor nodes and $N_{na}$ be the number of non-anchor nodes. Then, $N_{a} + N_{na} = N$, where $N$ is the total number of nodes deployed. The positions of anchor nodes are known to be ${\mathbf{x}}_{i}$, where $i \in \alpha = \left\{ {1,2, \, \ldots \, N_{a} } \right\}$. the positions of non-anchor nodes are unknown, denoted by ${\mathbf{x}}_{j}$, where $j \in \beta = \left\{ {N_{a} + 1,N_{a} + 2, \, \ldots \, N} \right\}$. Here, $\alpha$ and $\beta$ are two sets representing the indices of the non-anchor and anchor nodes, respectively.

Triangulation is possible when three nodes are in proximity of each other’s communication range. The nodes which are involved in triangulation, and are anchors as well, will have knowledge of their node position. The nodes involved in triangulation which are non-anchor nodes do not know their exact location and may depend on the designation of neighbour nodes to determine their position. We define the term “Apex Node” and “Target Vertex Node” that shall be used throughout the manuscript.

Definition 1 (Apex Node)

Apex Node is defined as the anchor node closest to the target when the target is enclosed by at least one triangulation.

Definition 2 (Target Vertex Node)

Target Vertex Node is defined as that Apex Node which is substituted for the target node as the target node approaches the edge of a triangulation.

By using the concept of Target Vertex Node, the issue of edge errors due to range-free triangulation is reduced greatly. In illustration of target vertex node is shown in Fig. 2c. An unobstructed (nR-O) condition is simple, where two nodes can communicate directly within the triangulation. A radio-obstructed (R-O) condition can arise when there is no direct link in at least one pair of nodes within triangulation. This can happen in three ways:

Fig. 2

Illustration of the triangulation assistance for R-O scenario with (a) η = 1, (b) η = 2, and (c) Target vertex node

There is obstruction of a single link of a triangulation.

Two of the three total links of a triangulation are obstructed.

All three links of a triangulation are obstructed.

The first two cases are considered here, and the third case is ignored, assuming that triangulation would not be possible in the first place if none of the node pairs have unobstructed links at all. The range measurement $\gamma_{{ii^{\prime}}}$ in case of unobstructed and radio-obstructed links between pairs of nodes can be expressed as:

$$ \gamma_{{ii^{^{\prime}} }} = \left\{ {\begin{array}{*{20}c} {d_{{ii^{^{\prime}} }} + w_{{ii^{^{\prime}} }} ,\;nR - O\;scenario} \\ {d_{{ii^{\prime}}} + \delta_{{ii^{^{\prime}} }} + w_{{ii^{^{\prime}} }} ,\;R - O\;scenario} \\ \end{array} } \right. $$

(1)

for $i,i^{^{\prime}} \in \alpha ;\,i \ne i^{^{\prime}}$.

The l₂-norm between node i and $i^{\prime}$ is denoted by $d_{{ii^{\prime}}} \triangleq \left\| {{\mathbf{x}}_{{\mathbf{i}}} - {\mathbf{x}}_{{{\mathbf{i^{\prime}}}}} } \right\|_{2}$ and $w_{{ii^{^{\prime}} }}$ is the additive white Gaussian noise with zero mean and variance $\sigma_{{ii^{\prime}}}^{2}$. $\delta_{{ii^{\prime}}}$ denotes the range skew between node $i$ and $i^{^{\prime}}$. This range skew is not known so we keep it as unknown constant parameter. Equation (2) computes the node triangulation uncertainty $U\left( {s_{i} ,{\kern 1pt} s_{{i^{\prime}}} ,{\kern 1pt} {\kern 1pt} t_{g} } \right)$ from the known prior information of received signal strength range (RSSr) $RSSr\left( {s,t_{g} } \right)$ of the triangulations and an appropriate function $fn( \cdot )$ of internal angle of the target vertex node $\angle s_{i} t_{g} s_{{i^{\prime}}}$ in between them.

$$ U\left( {s_{i} ,{\kern 1pt} s_{{i^{^{\prime}} }} ,{\kern 1pt} {\kern 1pt} t_{g} } \right) = RSSr\left( {s_{i} ,{\kern 1pt} t_{g} } \right) \times RSSr\left( {s_{{i^{^{\prime}} }} ,{\kern 1pt} t_{g} } \right) \times \left| {fn(\angle s_{i} ,{\kern 1pt} t_{g} ,{\kern 1pt} {\kern 1pt} s_{{i^{^{\prime}} }} )} \right| $$

(2)

Triangulation uncertainty of equation (2) is related to location coordinates of the target through the Fisher Information Matrix (FIM) of the log likelihood function, which decides the Cramer Rao Lower Bound (CRLB). CRLB is the direct relation to the positioning error, which, in turn, relates to the location coordinates of the target. Further details regarding the relation of triangulation uncertainty to location coordinates of the target is mentioned in the method defined in Sect. 3.1 and Sect. 4 of (Prateek and Arya 2021a).

2.2 Range skew model:

Node environment significantly affects the extent of range skewness between radio-obstructed (R-O) links. A suitable channel model that considers close-valued range skewness due to R-O conditions between links of triangulation is discussed here. To introduce R-O range skew model, we define the notion of Spatial Uncertainty Cluster. For this definition, it is assumed that the target is triangulated by anchor nodes only, since anchor nodes store up-to date information about self-location.

Definition 3 (Spatial Uncertainty Cluster):

A Spatial uncertainty Cluster $\nu_{n}$ for $n^{th}$ target node is defined by the set of three anchor nodes ($i,i^{\prime},k \in \alpha$) in a small part of the node deployment region, such that they form the same triangulation and the uncertainty associated with each apex node is comparable, i.e.,

$$ \nu_{n} \triangleq \left\{ {N_{i,k,n} \in \alpha \, \left| { \, max\{ } \right|U_{i,k,n} - U_{{i^{\prime},k,n}} |} \right\} < \varepsilon_{U} , \, i,i^{^{\prime}} ,k \in \alpha \} $$

(3)

where, $\varepsilon_{U}$ is a positive value, $N_{i,k,n}$ represents the number ($N$) of anchor nodes (subscript $i$ and $k$) responsible for the triangulation of the $n^{th}$ target node (subscript $n$), and $U_{i,k,n}$ denotes triangulation uncertainty of $n^{th}$ target node by $i^{th}$ and $k^{th}$ anchor nodes.

Remark: The notation $N_{i}$ means $i^{th}$ anchor node, whereas $N_{i,k,n}$ means set of $i^{th}$ anchor node and $k^{th}$ anchor node used to triangulate $n^{th}$ target node.

To derive the geometric constraint of R-O range skews in a cluster, we consider the case of obstruction blocking η number of links, η ∈ {1,2}. As illustrated in Fig. 2(a, b), the common reflection point ${\mathbf{r}} = \left[ {x^{r} {\kern 1pt} y^{r} } \right]^{T}$ represents the point through which signal from a node (which faces obstruction) of a cluster bounces off to its node pair during R-O mode of communication. The range skew when η = 1 is obtained as:

$$ \begin{gathered} \delta \left( {\nu_{ir} ,\eta = 1} \right) = \left\| {x_{{i^{^{\prime}} }} - r} \right\| + \left\| {r - x_{i} } \right\| - \left\| {x_{{i^{^{\prime}} }} - x_{i} } \right\|, \hfill \\ for \, i \in \left\{ {i,i^{^{\prime}} } \right\} \hfill \\ \end{gathered} $$

(4)

The range skew when η = 2 is given by

$$ \delta \left( {\nu_{{{\mathbf{ir}}}} ,\eta = 2} \right) = \nu_{{\left( {{\mathbf{i,i^{\prime}}}} \right){\mathbf{r}}}} + \nu_{{\left( {{\mathbf{i^{\prime\prime},i^{\prime}}}} \right){\mathbf{r}}}} $$

(5)

or,

$$ \begin{gathered} \delta \left( {\nu_{ir} ,\eta = 2} \right) = \left\| {x_{{i^{\prime}}} - r} \right\| + \left\| {r - x_{{i^{\prime\prime}}} } \right\| + 2\left\| {r - x_{i} } \right\| \hfill \\ - \left\| {x_{i^{\prime}} - x_{i} } \right\| - \left\| {x_{i} - x_{{i^{\prime\prime}}} } \right\| \, ,\,\,for \, i \in \left\{ {i,i^{\prime},i^{\prime\prime}} \right\} \hfill \\ \end{gathered} $$

(6)

where, $i \in \left\{ {i,i^{^{\prime}} ,i^{^{\prime\prime}} } \right\}$ denotes that ${\text{i}}$, i' and i'', all belong to anchor nodes $\alpha$ set. An illustration of target vertex node and the geometry for the internal angle is shown in Fig. 2c, where, the internal angle may be created either by a pair of sensor node, or a pair of anchor nodes, or by one anchor and one sensor node. Suitable node is chosen based on the received signal strength values.

3 Spatial and temporal geometry of triangulation uncertainty

In this section, a localization agenda is presented that ascertains the significance of space and time variations in aiding localization through triangulation uncertainty. The assumption taken during the conversion process from triangulation uncertainty to target coordinates is as follows:

• The proposed T-LOC model does not consider energy expenditure on any other aspect besides triangulation measurement and the formation of spatial and temporal geometry.

• The target is triangulated by anchor nodes only, since anchor nodes store up-to date information about self-location

Intra triangular measurement, inter triangulation measurement:

Triangulation may be formed by three participating nodes, which may be anchor or may know some prior location information. A triangulation uncertainty $U_{{i^{\prime}}}^{{}}$ is superior to that of $U_{i}^{{}}$ if $U_{{i^{\prime}}}^{{}} < U_{i}^{{}}$. In such a setup, an intra-triangulation measurement would be:

$$ U_{{\gamma_{ii} }}^{(t)} = U_{{d_{ii} }}^{(t)} + w_{ii}^{(t)} ,\;\forall {\kern 1pt} i \in \alpha {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} t \in {\mathbf{t}} $$

(7)

where, $U_{{\gamma_{ii} }}^{\left( t \right)}$ is the measured uncertainty of ${\text{i}}^{{{\text{th}}}}$ triangulation between time $\left( {t - 1} \right)$ and $t$. $U_{{d_{ii} }}^{(t)}$ is the actual uncertainty of ${\text{i}}^{{{\text{th}}}}$ triangulation between time $\left( {t - 1} \right)$ and $t$. $w_{ii}^{(t)}$ is the additive white gaussian noise with zero mean and $\sigma_{ii}^{2}$ variance. The actual triangulation uncertainty measurement of ${\text{i}}^{{{\text{th}}}}$ triangulation between time $\left( {t - 1} \right)$ and $t$ shall be given by:

$$ U_{{d_{ii} }}^{\left( t \right)} \triangleq \left| {U_{{d_{ii} }}^{{\left( {t - 1} \right)}} - U_{{d_{ii} }}^{\left( t \right)} } \right| $$

(8)

The inter-triangulation uncertainty measurement between ${\text{i}}^{{{\text{th}}}}$ and ${\text{m}}^{{{\text{th}}}}$ triangulation at time ‘t’ in nR-O and R-O condition are given by:

$$ U_{{\gamma_{im} }}^{\left( t \right)} = \left\{ \begin{gathered} U_{{d_{im} }}^{\left( t \right)} + w_{im}^{\left( t \right)} {\text{, nR - O}} \hfill \\ U_{{d_{im} }}^{\left( t \right)} + U_{{\delta_{im} }}^{\left( t \right)} + w_{im}^{\left( t \right)} {\text{, R - O}} \hfill \\ \end{gathered} \right.{ , }\;{\text{for i}} \in \alpha {\text{, m}} \in \alpha \cup \beta {\text{, i}} \ne {\text{m, t}} \in {\mathbf{t}} $$

(9)

where, the actual triangulation uncertainty measurement between ${\text{i}}^{{{\text{th}}}}$ and $m^{{{\text{th}}}}$ triangulation is denoted by

$$ U_{{d_{im} }}^{\left( t \right)} \triangleq \left| {U_{{d_{i} }}^{\left( t \right)} - U_{{d_{m} }}^{\left( t \right)} } \right| $$

(10)

$w_{im}^{(t)}$ denotes additive white gaussian noise with zero mean and $\sigma_{im}^{\left( t \right)2}$ variance. $U_{{\delta_{im}^{{}} }}^{\left( t \right)}$ denotes the R-O triangulation uncertainty skew between ${\text{i}}^{{{\text{th}}}}$ and $m^{{{\text{th}}}}$ triangulation which is modelled as an unknown constant parameter.

3.1 Spatial geometry:

If all triangulations are afflicted with type-I (η = 1) or type-II (η = 2) obstructions, there would be some kind of R-O component in every link. We formulate Maximum Likelihood Estimator for $\left\{ {U_{j} ,{\kern 1pt} U_{{\delta_{jm} }}^{{}} :j \in \beta ,m \in \alpha \cup \beta } \right\}$

$$ \psi_{A} :\mathop {{\text{minimize}}}\limits_{{U_{j} ,U_{{d_{jm} }} ,U_{{\delta_{jm} }}^{{}} }} \sum\limits_{j \in \beta ,m \in \alpha \cup \beta } {\frac{{\left( {U_{{\gamma_{jm} }} - U_{{d_{jm} }} - U_{{\delta_{jm} }}^{{}} } \right)^{2} }}{{\sigma_{jm}^{2} }}} $$

(11)

Subject to

$$ \begin{gathered} U_{{d_{jm} }} = \left| {U_{j} - U_{m} } \right|,{\kern 1pt} \forall j \in \beta ,{\kern 1pt} m \in \alpha \cup \beta \hfill \\ U_{{\delta_{jm} }}^{{}} \ge 0{\kern 1pt} ,{\kern 1pt} \forall j \in \beta ,{\kern 1pt} m \in \alpha \cup \beta \hfill \\ \end{gathered} $$

(12)

where, $j \in \beta$ refers to those sensor nodes which can never be anchor nodes. $m \in \alpha \cup \beta$ refers to those nodes which could either be anchor nodes from the very beginning, or they could be sensor nodes with the capability to be promoted to the level of anchor nodes. As shown in Fig. 2, the sensor nodes have been denoted by $\beta_{j}$, whereas the anchor nodes by $\alpha_{i}$. Since we are dealing with spatial geometry, $t_{1}$ associated with every node denotes that time instance does not change when the measurements are taken, even though the shape of the geometry (triangulation) may vary. This notation shall contrast with the temporal geometry scenario (explained in Sect. 3.3) whereupon some nodes shall be associated with $t_{1}$ whereas some of the other nodes may be $t_{2}$, meaning that measurements were taken at different instances of time. In order to make above formulation into a relaxed convex form and more realistic, we need to introduce further constraints pertaining to uncertainty skew into $\psi_{A}$.

3.2 Convex relaxation:

We take the Uncertainty measurement equation under R-O condition and square both sides as shown in (13):

$$ \left( {U_{{\gamma_{jm} }} - U_{{\delta_{jm} }} } \right)^{2} = \left( {U_{{d_{jm} }} + w_{jm} } \right)^{2} ,{\kern 1pt} \forall j \in \beta ,{\kern 1pt} m \in \alpha \cup \beta $$

(13)

After dropping the second order noise term, we have simplified uncertainty measurement equation (14)

$$ U_{{\gamma_{jm} }}^{2} - U_{{d_{jm} }}^{2} + U_{{\delta_{jm} }}^{2} - 2U_{{\gamma_{jm} }} U_{{\delta_{jm}^{{}} }} = 2U_{{d_{jm} }} w_{jm} $$

(14)

The cost function is then modified as shown in (15)

$$ \psi_{A} :\mathop {{\text{minimize}}}\limits_{{U_{j} ,U_{{d_{jm} }} ,U_{{\delta_{jm} }} }} \sum\limits_{j \in \beta ,m \in \alpha \cup \beta } {\frac{{\left( {U_{{\gamma_{jm} }}^{2} - U_{{d_{jm} }}^{2} + U_{{\delta_{jm} }}^{2} - 2U_{{\gamma_{jm} }} U_{{\delta_{jm}^{{}} }} } \right)^{2} }}{{4U_{{d_{jm} }}^{2} \sigma_{jm}^{2} }}} $$

(15)

The cost function in (15) needs a revised constraint to work with the uncertainty matrix such that ${\mathbf{\varphi }} = {{\varvec{\upzeta}}}^{{\mathbf{T}}} {{\varvec{\upzeta}}}$, where ${{\varvec{\upzeta}}} = \left[ {{{\varvec{\upzeta}}}_{{\mathbf{a}}} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\varvec{\upzeta}}}_{{\mathbf{b}}} } \right]$, ${{\varvec{\upzeta}}}_{{\mathbf{a}}} = \left[ {U_{1} \ldots U_{{N_{a} }} } \right]$, ${{\varvec{\upzeta}}}_{{\mathbf{b}}} = \left[ {U_{{N_{a} + 1}} \ldots U_{N} } \right]$ and the actual uncertainty of triangulation pairs can be expressed by equation (16)

$$ U_{{d_{jm} }}^{2} = \left[ {\mathbf{\varphi }} \right]_{j,j} + \left[ {\mathbf{\varphi }} \right]_{m,m} - 2\left[ {\mathbf{\varphi }} \right]_{j,m} = \rho_{jm} {\kern 1pt} $$

(16)

We also need to relax the measured uncertainty constraint, since $U_{{\gamma_{jm} }}^{2} \ge U_{{d_{jm} }}^{2}$ may not always be true if the R-O skews and noise are of closely-matched magnitudes. Thus, we have equation (17) as

$$ U_{{\gamma_{jm} }}^{2} + 4U_{{\gamma_{jm} }}^{{}} \sigma_{jm} \ge \left[ {\mathbf{\varphi }} \right]_{j,j} + \left[ {\mathbf{\varphi }} \right]_{m,m} - 2\left[ {\mathbf{\varphi }} \right]_{j,m} $$

(17)

3.2.1 Uncertainty skew constraints:

The cost function proposed in (15) needs additional constraints to prevent excessive slack variables from misleading the optimization results. There are two parameters: the actual uncertainty $U_{{d_{jm} }}$ and the uncertainty skew $U_{{\delta_{jm} }}$, which need to be determined separately from the MLE cost function. With the help of Geometric arrangement of nodes as argued in (Prateek et al. 2021), we can contain the upper limit ($\overline{D}_{jm}$) of the uncertainty skew as $0 \le U_{{\delta_{jm} }} \le \overline{D}_{jm}$. In existing literature, uncertainty estimation has been linked to localization of the target through methods such as quadratic programming (Zhang et al. 2019), autonomous underwater vehicle (AUV) aided localization (Gong et al. 2018), optical wireless underwater networks (Saeed et al. 2020) etc. The issue faced in such approaches are the need for synchronization, assistance from AUV for range-based purposes, and the lack of clarity regarding the joint effect of anchor nodes and sensor nodes on the target’s whereabouts. The present work shall dwell upon uncertainties arising in a range-free triangulation scenario to determine the Fisher Information matrix that relates uncertainty to target’s coordinates in a manner similar to that of (Prateek and Arya 2021a).

The absolute difference of uncertainty skew can be confined to $\left| {U_{{\delta_{jm} }} - U_{{\delta_{{j^{\prime}m}} }} } \right| \le \Delta \tau_{{jj^{\prime}m}} {\kern 1pt} , \, {\kern 1pt} {\kern 1pt} j,j^{\prime} \in \nu_{m}$. $\Delta \tau_{{ii^{\prime}m}}$ should be the minimum acceptable non-outlier value in the Gaussian curve. Since the non-outliers are counted according to $\left( {\mu \pm 3\sigma } \right)$ rule for Gaussian distributions, therefore to diminish the Gaussian noise, the delta value is shifted to the positive side by 3σ, to obtain

$$ \Delta \tau_{{jj^{\prime}m}} = \min \left\{ {2U_{{\gamma_{{jj^{\prime}}} }} + 3\sigma_{{jj^{\prime}}} ,{\kern 1pt} {\kern 1pt} \left| {U_{{\gamma_{jm} }} - U_{{\gamma_{{j^{\prime}m}} }} } \right| + 3\sigma_{jm} } \right\} $$

(18)

Above is the Uncertainty skew constraint for uncertainties in a triangulation. The resulting semidefinite programming problem may be stated as

$$ \psi_{{\text{S1 - SDP}}} :{\text{minimize}}\sum\limits_{\begin{subarray}{l} j \in \beta , \\ m \in \alpha \cup \beta \end{subarray} } {\left\{ \begin{gathered} \left( {U_{{\gamma_{jm} }}^{2} - \rho_{jm} + g_{jm} - 2U_{{\gamma_{jm} }} U_{{\delta_{jm} }} } \right)^{2} \hfill \\ \left( {4U_{{\delta_{jm} }}^{2} \sigma_{jm}^{2} } \right)^{ - 1} \hfill \\ \end{gathered} \right\}} $$

(19)

Subject to

$$ \rho_{jm} = \left[ {\mathbf{\varphi }} \right]_{j,j} + \left[ {\mathbf{\varphi }} \right]_{m,m} - 2\left[ {\mathbf{\varphi }} \right]_{j,m} { , }\forall j \in \beta ,{\kern 1pt} m \in \alpha \cup \beta $$

(20)

$$ U_{{\gamma_{jm} }}^{2} + 4U_{{\gamma_{jm} }}^{{}} \sigma_{jm} \ge \rho_{jm} {\kern 1pt} { , }\forall j \in \beta ,{\kern 1pt} m \in \alpha \cup \beta $$

(21)

$$ \left( {\begin{array}{*{20}c} {\mathbf{\varphi }} & {{\varvec{\upzeta}}} \\ {{{\varvec{\upzeta}}}^{{\mathbf{T}}} } & {\mathbf{I}} \\ \end{array} } \right) \ge 0 $$

(22)

$$ \left( {\begin{array}{*{20}c} 1 & {U_{{d_{jm} }} } \\ {U_{{d_{jm} }} } & {\rho_{jm} } \\ \end{array} } \right) \ge 0{ , }\left( {\begin{array}{*{20}c} 1 & {U_{{\delta_{jm} }} } \\ {U_{{\delta_{jm} }} } & {g_{jm} } \\ \end{array} } \right) \ge 0{ ,}\;\forall j \in \beta ,{\kern 1pt} m \in \alpha \cup \beta $$

(23)

$$ 0 \le U_{{\delta_{jm} }} \le \overline{D}_{jm} { , }\left| {U_{{\delta_{jm} }} - U_{{\delta_{{j^{\prime}m}} }} } \right| \le \Delta \tau_{{jj^{\prime}m}} {\kern 1pt} { ,}\;\forall m \in \alpha \cup \beta { , }j,j^{\prime} \in \nu_{m} $$

(24)

where, $\rho_{jm} = U_{{d_{jm}^{{}} }}^{2}$ and $g_{jm} = U_{{\delta_{jm}^{{}} }}^{2}$ are two slack variables. The linear matrix inequality form enables us to further relax the constraints $\rho_{jm} = U_{{d_{jm}^{{}} }}^{2}$, $g_{jm} = U_{{\delta_{jm}^{{}} }}^{2}$ and ${\mathbf{\varphi }} = {{\varvec{\upzeta}}}^{{\mathbf{T}}} {{\varvec{\upzeta}}}$ as shown in equations (22, 23). To prevent misleading results, further generalization is assumed, wherein uncertainties of a common triangulation are assumed to have equal uncertainty skews, such that

$$ U_{{\delta_{jm} }} = U_{{\delta_{{j^{\prime}m}} }} = U_{{\delta_{m} }} {\text{ , m}} \in \alpha \cup \beta \, ,{\kern 1pt} \, {\kern 1pt} {\kern 1pt} j,j^{\prime} \in \nu_{m} $$

(25)

3.2.2 Temporal geometry:

Since deployed nodes could change their topology with time, this could be used as a location enhancement feature. Analysis involving anchor node uncertainties has been dealt using time of arrival estimates (Mekonnen and Wittneben 2014) and time difference of arrival approaches (Chen et al. 2020). However, in the present work, the prior location information may be used in conjunction with current location information to increase the likelihood of estimation. A proposed MLE for temporal node uncertainty is given by

$$ \psi_{B} : \, \mathop {{\text{minimize}}}\limits_{{U_{j}^{(t)} ,U_{{d_{jj} }}^{(t)} }} \, \sum\limits_{{j \in \beta ,t \in {\mathbf{t}}}} {\left( {U_{{\gamma_{jj} }}^{(t)} - U_{{d_{jj} }}^{(t)} } \right)^{2} \sigma_{jj}^{{ - 2{\kern 1pt} {\kern 1pt} {\kern 1pt} (t)}} } $$

(26)

Subject to $U_{{d_{jj} }}^{(t)} = \left| {U_{j}^{(t - 1)} - U_{j}^{(t)} } \right|,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall {\kern 1pt} j \in \beta {\kern 1pt} ,{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} t \in {\mathbf{t}}$

In order to make above formulation more feasible, we need to into transcend equation (26) into a relaxed convex form and introduce temporal uncertainty skew constraint into $\psi_{B}$. Temporal skew term is the extent of deviation of deployed nodes with time. By introducing temporal skew term, we are able to compensate for the movement of deployed nodes in addition to the usual movement of the target node. As a result, localization accuracy is expected to improve, as shall be witnessed in the upcoming subsections. One interpretation of such a temporal skew term could be “noisy prior location information” versus “less noisy current location information”.

3.2.3 Convex relaxation:

We take the uncertainty measurement and square both sides as

$$ \begin{gathered} \left( {U_{{\gamma_{jj} }}^{{}} - U_{{d_{jj} }} } \right)^{2} = w_{jj}^{2} \hfill \\ \Rightarrow w_{jj}^{2} = \left( {U_{{\gamma_{jj} }}^{2} + U_{{d_{jj} }}^{2} - 2U_{{\gamma_{jj} }} U_{{d_{jj} }} } \right) \hfill \\ \end{gathered} $$

(27)

or,

$$ \psi_{B} :{\text{ minimize}}\sum\limits_{{}} {\sigma_{jj}^{ - 2} \left( {U_{{\gamma_{jj} }}^{2} + U_{{d_{jj} }}^{2} - 2U_{{\gamma_{jj} }}^{{}} U_{{d_{jj} }}^{{}} } \right)} $$

(28)

where, equation (28) represents the formulation of cost function $\psi_{B}$. The above cost function needs a revised set of constraints to work with the uncertainty matrix such that ${\mathbf{\varphi }}_{{\mathbf{j}}}^{{\left( {{\mathbf{1:t}}} \right)}} = \left( {{{\varvec{\upzeta}}}_{{\mathbf{j}}}^{{\left( {{\mathbf{1:t}}} \right)}} } \right)^{{\mathbf{T}}} {{\varvec{\upzeta}}}_{{\mathbf{j}}}^{{\left( {{\mathbf{1:t}}} \right)}}$, where ${{\varvec{\upzeta}}}_{{\mathbf{j}}}^{{\left( {{\mathbf{1:t}}} \right)}} = \left[ {U_{{\mathbf{j}}}^{\left( 1 \right)} \, U_{{\mathbf{j}}}^{\left( 2 \right)} \ldots \, U_{{\mathbf{j}}}^{{\left( {\mathbf{t}} \right)}} } \right]$. The square of actual uncertainty of $j^{th}$ triangulation at adjacent time steps can be expressed by

$$ U_{{d_{jj} }}^{2} = {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho_{jj}^{\left( t \right)} \;(let) $$

(29)

i.e.,$\rho_{jj}^{\left( n \right)} = \left[ {{\mathbf{\varphi }}_{j}^{{\left( {1:t} \right)}} } \right]_{{\left( {t - 1} \right),\left( {t - 1} \right)}} + \left[ {{\mathbf{\varphi }}_{j}^{{\left( {1:{\mathbf{t}}} \right)}} } \right]_{t,t} - 2\left[ {{\mathbf{\varphi }}_{j}^{{\left( {1:{\mathbf{t}}} \right)}} } \right]_{{\left( {t - 1} \right),t}} { , }\forall j \in \beta$

3.2.4 Uncertainty skew constraint:

Definition 4 (Temporal Uncertainty Skew)

Temporal uncertainty skew is the extent of deviation of deployed nodes with time. It is denoted by $U_{{\delta_{jj}^{{}} }}^{\left( t \right)}$, where $\delta$ subscript denotes skew in the temporal uncertainty $U^{\left( t \right)}$.

The cost function proposed in (26) needs additional temporal constraints. There are two parameters: the actual uncertainty of $j^{th}$ triangulation at adjacent time steps $\left( {t - 1} \right)$ and $\left( t \right)$, denoted by ${\kern 1pt} \rho_{jj}^{\left( t \right)}$, and the temporal uncertainty skew $U_{{\delta_{jj}^{{}} }}^{\left( t \right)}$, which are interrelated with respect to intra triangulation uncertainty perspective, i.e.,

$$ \sqrt {\rho_{jj}^{\left( t \right)} } = \left| {U_{j}^{{\left( {t - 1} \right)}} - U_{j}^{\left( t \right)} } \right| = U_{{\delta_{jj}^{{}} }}^{\left( t \right)} $$

(30)

where, the symbol $U_{j}^{{\left( {t - 1} \right)}}$ stands for triangulation uncertainty at time $\left( {t - 1} \right)$ for $j^{th}$ sensor node, and the symbol $U_{j}^{\left( t \right)}$ denotes triangulation uncertainty at time $\left( t \right)$ for the $j^{th}$ sensor node. These two parameters need to be determined separately from the MLE cost function. The linear matrix inequality forms of ${\kern 1pt} \rho_{jj}^{\left( t \right)}$ and ${\mathbf{\varphi }}_{j}^{{\left( {1:{\mathbf{t}}} \right)}}$ form constraints to the cost function in (26). A mobility constraint $M_{jj}^{\left( t \right)}$ should be introduced, whose upper and lower bound would constrain the extent of variation of $U_{{\delta_{jj}^{{}} }}^{\left( t \right)}$. $M_{jj}^{\left( t \right)}$ can be applied to temporal skew term, as shown in (31)

$$ \underline{{M_{jj}^{\left( t \right)} }} \le \left| {U_{j}^{{\left( {t - 1} \right)}} - U_{j}^{\left( t \right)} } \right| \le \overline{{M_{jj}^{\left( t \right)} }} $$

(31)

The resulting semidefinite programming problem may be stated as

$$ \psi_{T - SDP} : \, \mathop {{\text{minimise}}}\limits_{{{{\varvec{\upzeta}}}_{j}^{{\left( {1:{\mathbf{t}}} \right)}} ,{\mathbf{\varphi }}_{j}^{{\left( {1:{\mathbf{t}}} \right)}} ,\rho_{jj}^{\left( t \right)} ,U_{jj}^{\left( t \right)} }} \, \sum\limits_{{j \in \beta ,t \in {\mathbf{t}}}} {\left( {\sigma_{jj}^{\left( t \right)} } \right)^{ - 2} \left( {\left( {U_{{\gamma_{jj} }}^{\left( t \right)} } \right)^{2} + \rho_{jj}^{\left( t \right)} - 2U_{{\gamma_{jj} }}^{\left( t \right)} U_{{d_{jj} }}^{\left( t \right)} } \right)} $$

(32)

Subject to

$$ \rho_{jj}^{\left( t \right)} = \left[ {{\mathbf{\varphi }}_{j}^{{\left( {1:{\mathbf{t}}} \right)}} } \right]_{{\left( {t - 1} \right),\left( {t - 1} \right)}} + \left[ {{\mathbf{\varphi }}_{j}^{{\left( {1:{\mathbf{t}}} \right)}} } \right]_{t,t} - 2\left[ {{\mathbf{\varphi }}_{j}^{{\left( {1:{\mathbf{t}}} \right)}} } \right]_{{\left( {t - 1} \right),t}} { , }\;\forall j \in \beta ,{\kern 1pt} t \in {\mathbf{t}} $$

(33)

$$ tr\left\{ {{\mathbf{\varphi }}_{j}^{{\left( {1:{\mathbf{t}}} \right)}} } \right\} = \sum\limits_{{}} {\left[ {{\mathbf{\varphi }}_{{}}^{\left( t \right)} } \right]}_{j,j} { , }\forall j \in \beta ,{\kern 1pt} t \in {\mathbf{t}} $$

(34)

$$ \left[ {\begin{array}{*{20}c} {{\mathbf{\varphi }}_{j}^{{\left( {1:{\mathbf{t}}} \right)}} } & {{{\varvec{\upzeta}}}_{j}^{{\left( {1:{\mathbf{t}}} \right)}} } \\ {\left( {{{\varvec{\upzeta}}}_{j}^{{\left( {1:{\mathbf{t}}} \right)}} } \right)^{T} } & {\mathbf{I}} \\ \end{array} } \right] \ge 0,\;\left[ {\begin{array}{*{20}c} 1 & {U_{jj}^{\left( t \right)} } \\ {U_{jj}^{\left( t \right)} } & {\rho_{jj}^{\left( t \right)} } \\ \end{array} } \right] \le 0,\;\forall {\text{ j}} \in \beta { , }t \in {\mathbf{t}} $$

(35)

$$ \underline{{M_{jj}^{\left( t \right)} }} \le U_{{\delta_{jj}^{{}} }}^{\left( t \right)} \le \overline{{M_{jj}^{\left( t \right)} }} ,\;\forall \, j \in \beta { , }t \in {\mathbf{t}} $$

(36)

A working example of temporal geometry may be explained through a special version of Fig. 2(a, b), whereupon the major difference would be: $\left\{ {j,t_{1} } \right\}$, $\left\{ {m,t_{1} } \right\}$ versus $\left\{ {j,t_{2} } \right\}$, $\left\{ {m,t_{2} } \right\}$ which would indicate that some measurements were taken at time instance $t_{1}$, while other measurements were carried out at a different time instance $t_{2}$. Target’s coordinates are found when uncertainty term is integrated into the calculation of Fisher Information matrix, which points towards the CRLB, which points towards the error in positioning information (Prateek and Arya 2021a). This positioning error becomes the probable radius around the estimated position of target within which actual location exists (using range free method).

3.3 Performance analysis of T-LOC method:

In this section, first a suitable detection threshold under nR-O condition and under R-O condition under presence of triangulation skew constraint condition is determined. Then, the CRLB is derived to highlight the improvement of localization accuracy from the triangulation uncertainty skew constraint.

3.3.1 Detection performance analysis

We wish to determine whether a given node is capable of getting triangulated suitably or not. To decide on this suitability, we need to compute threshold to categorize nodes as being eligible for triangulation or not. The two decision errors during triangulation may be stated as:

Missed Detection: Nodes which were suitable for triangulation, are dismissed.

False Alarm: Nodes which are not suitable for triangulation, are counted in for triangulation.

For the first kind of error, we lose vital information about nodes which assist in triangulation, so localization performance is neither benefitted nor harmed. However, in the second kind of error, when an unsuitable node is counted in for triangulation, it degrades localization by providing wrong information about the target location estimate. The following derivation details on these aspects. The hypotheses H₁ and H₀ for each node suitability for triangulation may be stated as:

$H_{1} : \, \gamma_{jm} = d_{jm} + w_{jm} ,$ no obstruction $\left( {\eta = 0} \right)$

$$ H_{0} : \, \gamma_{jm} = d_{jm} + \sum\limits_{\eta = 1,2} {\delta_{jm} \left( \eta \right) + } {\kern 1pt} w_{jm} ,\;{\text{single}}\;{\text{or}}\;{\text{ dual}}\;{\text{radio}}\;{\text{obstruction}}\;\left( {\eta = \left\{ {1,2} \right\}} \right) $$

(37)

Likelihood Ratio is written as

$$ \gamma_{jm} = \frac{{f_{\eta = 0} \left( {\gamma_{jm} ;\hat{d}_{jm} ,H_{1} } \right)}}{{f_{\eta > 0} \left( {\gamma_{jm} ;\hat{g}_{jm} ,H_{0} } \right)}} > Th_{jm} $$

(38)

where, $\hat{g}_{jm}$ is the estimate for $d_{jm} + \sum\limits_{\eta = 1,2} {\delta_{jm} \left( \eta \right)}$.

$f_{\eta = 0} \left( {\gamma_{jm} ;\hat{d}_{jm} ,H_{1} } \right)$ and $f_{\eta > 0} \left( {\gamma_{jm} ;\hat{g}_{jm} ,H_{0} } \right)$ are likelihood of no obstruction and single or multiple obstructions, respectively, their pdfs are given by ‘$eval_{\max }$’ number of evaluations:

$$ \begin{gathered} f_{\eta = 0} \left( {\gamma_{jm} ;\hat{d}_{jm} ,H_{1} } \right) \propto \prod\limits_{eval = 1}^{{eval_{\max } }} {\frac{1}{{\sqrt {2\pi \sigma_{\eta = 0}^{2} } }}} \exp \left[ { - \frac{{\left( {^{{\left( {eval} \right)}} \gamma_{jm}^{{}} - \hat{d}_{jm} } \right)^{2} }}{{2\sigma_{\eta = 0}^{2} }}} \right] \hfill \\ f_{\eta > 0} \left( {\gamma_{jm} ;\hat{g}_{jm} ,H_{0} } \right) \propto \prod\limits_{eval = 1}^{{eval_{\max } }} {\frac{1}{{\sqrt {2\pi \sigma_{\eta > 0}^{2} } }}} \exp \left[ { - \frac{{\left( {^{{\left( {eval} \right)}} \gamma_{jm}^{{}} - \hat{g}_{jm} } \right)^{2} }}{{2\sigma_{\eta > 0}^{2} }}} \right] \hfill \\ \end{gathered} $$

(39)

Thus, equation (38) becomes

$$ \begin{gathered} L.R\left( {\gamma_{jm} } \right) = \hfill \\ \frac{{\sigma_{\eta = 0}^{{ - eval_{\max } }} \exp \left[ { - \sum\limits_{eval = 1}^{{eval_{\max } }} {0.5\sigma_{\eta = 0}^{ - 2} \left( {^{{\left( {eval} \right)}} \gamma_{jm}^{{}} - \hat{d}_{jm} } \right)^{2} } } \right]}}{{\sigma_{\eta > 0}^{{ - eval_{\max } }} \exp \left[ { - \sum\limits_{eval = 1}^{{eval_{\max } }} {0.5\sigma_{\eta > 0}^{ - 2} \left( {^{{\left( {eval} \right)}} \gamma_{jm}^{{}} - \hat{g}_{jm} } \right)^{2} } } \right]}} > Th_{jm} \hfill \\ \end{gathered} $$

(40)

where, $\sigma_{\eta = 0}^{2}$ and $\sigma_{\eta > 0}^{2}$ are the noise variances corresponding to the no obstructions and some obstruction cases. Upon taking ln both sides, we have

$$ \begin{gathered} \left\{ \begin{gathered} - eval_{\max } \ln \sigma_{\eta = 0} - \sum\limits_{eval = 1}^{{eval_{\max } }} {0.5} \sigma_{{_{\eta = 0} }}^{ - 2} \left( {^{{\left( {eval_{\max } } \right)}} \gamma_{jm} - \hat{d}_{jm} } \right)^{2} \hfill \\ - \left( { - eval_{\max } \ln \sigma_{\eta > 0} } \right) - \left( { - \sum\limits_{eval = 1}^{{eval_{\max } }} {0.5} \sigma_{{_{\eta > 0} }}^{ - 2} \left( {^{{\left( {eval_{\max } } \right)}} \gamma_{jm} - \hat{g}_{jm} } \right)^{2} } \right) \hfill \\ \end{gathered} \right\} > \ln (Th_{jm} ) \hfill \\ or, \hfill \\ \left\{ \begin{gathered} \sum\limits_{eval = 1}^{{eval_{\max } }} {\sigma_{{_{\eta = 0} }}^{2} \left( {^{{\left( {eval} \right)}} \gamma_{jm} - \hat{g}_{jm} } \right)^{2} } - \hfill \\ \sum\limits_{eval = 1}^{{eval_{\max } }} {\sigma_{{_{\eta > 0} }}^{2} \left( {^{{\left( {eval} \right)}} \gamma_{jm} - \hat{d}_{jm} } \right)^{2} } \hfill \\ \end{gathered} \right\} > Th^{\prime}_{jm} \hfill \\ \end{gathered} $$

(41)

Next, we set a tolerance limit for P_FA, such as 0.01 or 0.001 etc. By following a known distribution for R-O triangulations, we can determine the threshold $Th^{\prime}_{jm}$. This distribution can be computed when we iteratively find out the skew estimate $\hat{\delta }_{jm}^{\left( t \right)}$ between measured value $\gamma_{jm}^{\left( t \right)}$ and actual value $d_{jm}^{\left( t \right)}$. Let $\hat{\delta }_{jm}^{\left( t \right)} = \sigma_{{}}^{ - 2} {\kern 1pt}^{\left( t \right)} \left( {^{{}} \gamma_{jm}^{\left( t \right)} - \hat{d}_{jm}^{\left( t \right)} } \right)^{2}$. Those iterations which yield small $\hat{\delta }_{jm}^{\left( t \right)}$ values consistently we assign such $jm$ link pair as forming nR-O triangulations. Similarly, those iterations which consistently yield large $\hat{\delta }_{jm}^{\left( t \right)}$ values, we assign such $jm$ link pair as forming $\eta$-obstructed triangulations. It is observed that $\hat{\delta }_{jm}^{\left( t \right)}$ closely approximates squared distribution with kurtosis factor ‘$a$’. Using its statistic table, we may write

$$ P_{FA} = \int\limits_{{Th^{\prime}_{jm} }}^{ + \infty } {N^{2} \left( a \right)da} $$

(42)

Upon fixing $P_{FA}$, we shall get the value of kurtosis factor ‘$a$’, which shall yield the threshold $Th^{\prime}_{jm}$. The conditional threshold for $\eta$-obstructed triangulations shall be denoted by $\left\{ {Th^{\prime}_{jm} ;U_{{\delta_{jm} }} \ne 0} \right\}$, whereas the conditional threshold for unobstructed triangulations shall be denoted by $\left\{ {Th^{\prime}_{jm} ;U_{{\delta_{jm} }} = 0} \right\}$, where $Th^{\prime}_{jm}$ is threshold. The probability of detecting unobstructed triangulations is given by

$$ \begin{gathered} P_{D} = P\left\{ {\hat{\delta }_{jm} < Th^{\prime}_{jm} ;U_{{\delta_{jm} }} = 0} \right\} \hfill \\ or, \hfill \\ P_{D} = \int\limits_{ - \infty }^{{Th^{\prime}_{jm} }} {f_{\eta = 0} \left( {U_{{\gamma_{jm} }} } \right)} dU_{{\gamma_{jm} }} \hfill \\ \end{gathered} $$

(43)

3.3.2 Verification of estimation improvement

Two unknowns are: location of the target, and the uncertainty skew associated with $\eta$-obstructed triangulations. Let the unknowns in the localization model be represented together by the vector ${{\varvec{\uptheta}}} = \left[ {{\mathbf{l}}^{T} \, {\mathbf{q}}^{T} } \right]^{T}$, where location vector ${\mathbf{l}} = \left[ {{\mathbf{x}}_{1}^{T} {\kern 1pt} {\kern 1pt} {\mathbf{x}}_{2}^{T} \ldots {\mathbf{x}}_{N}^{T} } \right]^{T}$, uncertainty skew vector ${\mathbf{q}} = \left[ {{\mathbf{U}}_{{\delta_{1} }}^{T} {\kern 1pt} {\mathbf{U}}_{{\delta_{2} }}^{T} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} {\mathbf{U}}_{{\delta_{{N_{a} }} }}^{T} } \right]^{T}$ and ${\mathbf{U}}_{{\delta_{h} }}^{{}} = \left[ {U_{{\delta_{{h_{1} }} }}^{{}} {\kern 1pt} \ldots {\kern 1pt} U_{{\delta_{{h\left( {h - 1} \right)}} }}^{{}} {\kern 1pt} U_{{\delta_{{h\left( {h + 1} \right)}} }}^{{}} \ldots U_{{\delta_{hN} }}^{{}} } \right]^{T}$. The measured location vector of target is denoted by ${{\varvec{\upgamma}}}$ and $\Delta {\tilde{\mathbf{\tau }}}$. Where,

$$ {{\varvec{\upgamma}}} = \left[ {{{\varvec{\upgamma}}}_{1}^{T} {\kern 1pt} {{\varvec{\upgamma}}}_{2}^{T} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} {{\varvec{\upgamma}}}_{{N_{a} }}^{T} } \right]^{T} \;{{\varvec{\upgamma}}}_{h} = \left[ {\gamma_{h1} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} \gamma_{{h\left( {h - 1} \right)}} {\kern 1pt} {\kern 1pt} \gamma_{{h\left( {h + 1} \right)}} {\kern 1pt} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} \gamma_{hN} } \right]^{T} $$

and, $\Delta {\tilde{\mathbf{\tau }}} = \left[ {\Delta {\tilde{\mathbf{\tau }}}_{1}^{T} {\kern 1pt} {\kern 1pt} \Delta {\tilde{\mathbf{\tau }}}_{2}^{T} {\kern 1pt} {\kern 1pt} \ldots {\kern 1pt} {\kern 1pt} {\kern 1pt} \Delta {\tilde{\mathbf{\tau }}}_{{\left( {N - N_{a} } \right)}}^{T} } \right]$ .

Let ${\hat{\mathbf{\theta }}}$ be the unbiased estimate of ${{\varvec{\uptheta}}}$, and the mean squared error be defined by $E\left\{ {\left( {{{\varvec{\uptheta}}} - {\hat{\mathbf{\theta }}}} \right)\left( {{{\varvec{\uptheta}}} - {\hat{\mathbf{\theta }}}} \right)^{T} } \right\} \ge inv\left( {{\mathbf{J}}_{\theta } } \right)$, where ‘inv’ denotes inverse of a vector, and ${\mathbf{J}}_{\theta }$ is the Fisher Information matrix (FIM) of ${{\varvec{\uptheta}}}$. ${\mathbf{J}}_{\theta }$ may be written as

$$ J_{\theta } = - E_{{\gamma ,\Delta \tilde{\tau }}} \left\{ {\frac{{\partial^{2} \ln f\left( {\gamma ,\Delta \tilde{\tau };\theta } \right)}}{{\partial \theta \partial \theta^{T} }}} \right\} $$

(44)

The log likelihood function $\ln f\left( {{{\varvec{\upgamma}}},\Delta {\tilde{\mathbf{\tau }}};{{\varvec{\uptheta}}}} \right)$ may be written as

$$ \ln f\left( {\gamma ,\Delta \tilde{\tau };\theta } \right) \propto \left\{ \begin{gathered} \sum\limits_{j \in \beta } {\sum\limits_{m \in \alpha \cup \beta } {0.5\sigma_{jm}^{ - 2} \left( {\gamma_{jm} - \tilde{d}_{jm} } \right)} }^{2} \hfill \\ + \sum\limits_{m \in \alpha \cup \beta } {0.5} \sigma_{m}^{ - 2} \left| {\Delta \tilde{\tau }_{m} - \Delta \tau_{m} } \right| \hfill \\ \end{gathered} \right\} $$

(45)

where

$$ \tilde{d}_{jm} = \left\{ \begin{gathered} d_{jm} {\text{ for unobstructed triangulation}} \hfill \\ \tilde{d}_{jm} + \delta_{jm} {\text{ for }}\eta {\text{ - obstructed triangulation}} \hfill \\ \end{gathered} \right. $$

(46)

The fisher information matrix for target and anchor locations is given by

$$ {\mathbf{J}}_{\theta } \left( {\mathbf{l}} \right) = \left[ {\begin{array}{*{20}c} {{\mathbf{L}}_{1} } & {{\mathbf{L}}_{2} } \\ {{\mathbf{L}}_{2}^{T} } & {{\mathbf{L}}_{3} } \\ \end{array} } \right] $$

(47)

where ${{\varvec{\uptheta}}} \in {\mathbf{R}}^{N}$, ${\mathbf{L}}_{1} \in {\mathbf{R}}^{{N_{a} \times N_{a} }}$, ${\mathbf{L}}_{2} \in {\mathbf{R}}^{{N_{a} \times (N - N_{a} )}}$, ${\mathbf{L}}_{3} \in {\mathbf{R}}^{{(N - N_{a} ) \times (N - N_{a} )}}$, with $\left( {N - N_{a} } \right) < N$, then the equivalent Fisher Information Matrix for ${\mathbf{l}}$ is given by ${\mathbf{J}}_{e} \left( {\mathbf{l}} \right) \triangleq {\mathbf{L}}_{1} - {\mathbf{L}}_{2} {\mathbf{L}}_{3}^{ - 1} {\mathbf{L}}_{2}^{T}$, which is the direct implementation of Schur’s complement (Shen et al. 2010; Li et al. 2020) of a matrix ${\mathbf{L}}_{3}$, and

$$ L_{1} ,{\kern 1pt} {\kern 1pt} L_{2} ,{\kern 1pt} {\kern 1pt} L_{3} = \left\{ \begin{gathered} f\left( {\sigma_{jm}^{ - 2} } \right), \, for\;unobstructed\;triangulations \hfill \\ 0, \, for \, \eta - obstructed\;triangulations \hfill \\ \end{gathered} \right. $$

(48)

The unconstrained $CRLB\left( {\mathbf{l}} \right) = \left[ {{\mathbf{L}}_{1} - {\mathbf{L}}_{2} {\mathbf{L}}_{3}^{ - 1} {\mathbf{L}}_{2}^{T} } \right]^{ - 1}$, where ${\mathbf{l}} = \left[ {x_{1}^{T} {\kern 1pt} {\kern 1pt} x_{2}^{T} {\kern 1pt} {\kern 1pt} \ldots x_{{N_{a} }}^{T} } \right]$. The triangulation-assisted CRLB shall be given by

$$ \begin{gathered} CRLB^{^{\prime}} \left( {\mathbf{l}} \right) = {\mathbf{J}}_{\theta }^{ - 1} - {\mathbf{J}}_{\theta }^{ - 1} {\mathbf{K}}^{T} \left( {{\mathbf{KJ}}_{\theta }^{ - 1} {\mathbf{K}}^{T} } \right)^{ - 1} {\mathbf{KJ}}_{\theta }^{ - 1} \hfill \\ \le {\mathbf{J}}_{\theta }^{ - 1} = CRLB\left( {\mathbf{l}} \right) \hfill \\ \end{gathered} $$

(49)

where, ${\mathbf{K}}$ is a transformation matrix for triangulation uncertainty skew constraint, derived by $U_{{\delta_{jm} }} - U_{{\delta_{{j^{\prime}m^{\prime}}} }} = 0, \, j,j^{\prime} \in \beta , \, m,m^{\prime} \in \alpha \cup \beta$. Thus, the benefit of assistance from triangulation in the form of lowering of CRLB as compared to conventional localization without triangulation skew constraints is successfully derived. A pseudocode for computing the Fisher Information Matrix is given in Appendix A for ease of understanding. A detailed description of triangulation-based localization in a sparsely deployed network has been discussed in (Prateek and Arya 2021b).

4 Numerical results

Simulations were performed by taking node communication ranges with upper bound of 10.6 m and 21.15 m, separately. Table 3 outlines the parameters used in the localization model. To observe the influence of the number of anchor nodes on the localization performance, a square deployment region of 100 × 100 m² is considered for simulation. A total of 100 sensors are uniformly deployed, and a set of 4, 8, 12, 16, 20 anchor nodes are deployed in separate trials. Out of the 100 sensor nodes, the nodes which form triangulations, are identified using l₂-norm computations for three different tolerance of triangulation uncertainties. The coordinates of these nodes are taken to have lower noise variance than those nodes which are deployed but not involved in triangulation. For triangulated nodes, a two-mode Gaussian mixture distribution (GMD) is set, one mode for the unobstructed scenario, while the other mode for radio obstructed scenario. For 100 Monte Carlo simulation trials, each set-up is run to compute the RMS errors and CDF of node position estimation errors.

Table 1 Parameters implemented in the localization model

To generate temporal data, a 2D uniform-point process is taken as the node deployment pattern, and the time duration for one complete cycle of uncertainty-based triangulation is for all the 100 sensor nodes to be scanned once. The normalized mean square temporal error is then calculated by the ratio of error due to estimated location ($\hat{\beta }_{j}$) at two consecutive time intervals ($t_{1} ,t_{2}$) and the error due to actual location ($\beta_{j}$) at two consecutive time intervals ($t_{1} ,t_{2}$).

$$ error = \frac{{\left( {\left( {\hat{\beta }_{j} ,t_{1} } \right) - \left( {\hat{\beta }_{j} ,t_{2} } \right)} \right)^{2} }}{{\left( {\left( {\beta_{j} ,t_{1} } \right) - \left( {\beta_{j} ,t_{2} } \right)} \right)^{2} }} $$

(50)

The square root of equation (50) gives us the required RMS error for temporally generated data pertaining to triangulation uncertainty. A similar approach is taken to compute the normalized mean square spatial error and the overall triangulation uncertainty is determined by the combined effect of both the temporal geometry as well as spatial geometry as stated in equation (32). In the following paragraphs, we shall be seeing the effect of such parameters on target localization.

Figure 3. denotes the outcome of simulation carried out to compute the number of sensor nodes which can be triangulated based on the tolerance value of triangulation uncertainty U. Nodes which fall within the uncertainty value (U < 200 m², U < 100 m², U < 50 m²), are counted in to be used for cooperating the anchor nodes in locating the target. The communication range is varied from 10.6 m till 28.2 m in steps of 2.5% of the maximum length of the node deployment area, i.e., 141.4 m to simulate different levels of energy available in nodes.

Fig. 3

Identification of sensor nodes participating in triangulation for different tolerances of triangulation uncertainty

Figure 4(a) depicts the RMS errors for upper threshold node range of 10.6 m. These are computed for Semidefinite programmed Gaussian Mixture Distribution (denoted by solid, dashed and dotted blue lines as “T-LOC (SDP GMD)”) and compared with weighted least squares (Wang et al. 2012; Shi et al. 2020) modified with Gaussian Mixture Distribution for both the obstructed and unobstructed cases (solid black line, as “WLS (GMD)”) and Cramer Rao-Lower Bound (CRLB) (solid red line, as “CRLB”) for the three sets of sensor nodes having different levels of triangulation uncertainty U less than 200 m², 100 m² and 50 m². The GM Model appears to consistently approach values close to CRLB, while the performance of WLS Model improves with higher number of anchor node counts. To achieve a triangulation uncertainty of $U < 50$ m² is quite a stringent requirement, as compared to $U < 100$ m² $U < 200$ m². The worse behaviour of $U < 50$ m² in Fig. 4a is explained in two ways: in terms of detection ability, and in terms of estimation accuracy. The rate of success in detecting true triangulation depends highly upon the symmetry of such triangulations. Upon restricting the triangulation uncertainty $U$ to be less than 50m², the chances of left-hand inequality of (41) crossing the threshold is low. In terms of estimation rate of targets, a sparse Fisher Information matrix of equation (47) would indicate fewer non-zero data points of matrix. With $U < 50$ m², the requirement is such that the resulting lower bound on localization error variance rises, causing poor error performance. In Fig. 4(a), this poor performance is seen for $U < 50$ m² when the number of anchor nodes are too few (for example: 4 or 6) or too many (for example: 18 to 20). Said simply, $U < 50$ m² offers fewer exploration options by being extremely selective of the number of triangulations being processed.

Fig. 4

(a) RMS error of localized node estimates for a maximum non-anchor communication range of 10.6 m. (b) CDF of estimation errors vs. anchor-sensor distance for inter-sensor communication range up to 10.6 m

Figure 4(b) depicts the cumulative distribution function (CDF) of different localization errors for triangulation uncertainty values of less than 200, 100 and 50 m². The Convex optimization-based GM model (denoted by “T-LOC (SDP GMD)”, blue coloured solid, dashed and dotted lines in the figure) once again exhibits consistently lower localization error values due to superior exploitation of optimum MLE estimates. In fact, with a tighter control on the triangulation uncertainty, both the T-LOC and the WLS (denoted by “WLS”, red coloured solid, dashed, dotted lines in the figure) models demonstrate lower localization errors for, say U < 50 than U < 200. This agrees with our theoretical derivation, according to which sensor nodes which participate in triangulations having smaller area and comparable inner angles (neither too obtuse, nor too acute) of the apex node, have higher accuracy of localization.

A similar pattern is observed for Fig. 5(a) wherein the only change is the increase of upper threshold of node communication range from 10.6 m in Fig. 4(a) to 21.15 m in Fig. 5(a). The effect observed is that the RMS errors are higher for the proposed T-LOC model with range 21.15 m as compared to the proposed T-LOC model with range 10.6 m. In this graph, we observe that once again the best performance in terms of node localization errors is found for U < 50, which agrees with the theoretical computations.

Fig. 5

(a) RMS error of localized node estimates for a maximum non-anchor communication range of 21.15 m. (b) CDF of estimation errors vs. anchor-sensor distance for inter-sensor communication range up to 21.15 m

Figure 5(b) depicts the cumulative performance of localization algorithms for node range of 21.15 m. The proposed semidefinite programmed model consistently demonstrates lower localization errors than WLS technique. Moreover, the U < 50m² constraint has the least cumulative error, which is expected, given superior node symmetry.

Figure 6 represents a realistic scenario under which numerical data has been generated by equipping the campus of National Institute of Technology Patna with anchor nodes and target nodes at various strategic positions. To interpret the physical meaning of the scenario, a satellite image of the map of the designated region has been marked with green stars denoting anchor nodes and red circles denoting target nodes. The strategic locations of the target nodes have been denoted by points A, B, C and D, respectively. To localize these targets, the anchor nodes are located at six places, as shown in Fig. 6(a). To simplify the scenario, we pick the GPS-coordinates of the sensor and anchor nodes as the actual-measurement, while the T-LOC method shall compute the estimated locations of the targets with the help from the anchor nodes for an area of 1500 × 850 m². The actual location of the anchor nodes is taken as node 1 (505, 677), node 2 (59, 423), node 3 (451, 155), node 4 (1421, 23), node 5 (1435, 807) and node 6 (827, 765).

Fig. 6

a A representation of position of Target nodes and anchor nodes in a realistic scenario. b T-LOC performance in a realistic scenario for target nodes A,B,C,D

For evaluation purpose of the proposed method, one target node is taken at a time. Based on the communication range of the triangulating nodes, the number of feasible triangulations are computed using the range skew model of equation (4, 6). Then, the triangulation uncertainty determined by intra-triangulation measurement eq (7) and inter-triangulation measurement equation (9) help to ascertain which two anchor nodes are the most suitable to triangulate the target at a time, the localization error is then worked out through the Fisher’s Information matrix for three configurations of the upper limit of triangulation uncertainty $U$. The case $U < 50$ m² considers either very short ranged triangulations (ones with short sides). The case may be extended to $U < 100$ m² and $U < 200$ m² in a similar fashion. In every case, the localization performance heavily depends upon triangulation geometry, which is evident from Fig. 6(b). For reference, the results have been compared with WLS for three sets of Gaussian Mixture Distributions (Wang et al. 2012; Shi et al. 2020), representing unobstructed Radio link as well as Radio obstructed paths to varying degrees due to measurements being taken at different times of the day.

5 Conclusion

A convex optimization-based localization approach was proposed in this paper. The uniqueness of this approach lay in intelligently identifying the nodes which triangulate a target better than the other sensor nodes. Once the semidefinite model was relaxed into a convex optimization model using triangulation uncertainty skew parameter, it exhibited a gain in localization accuracy compared to conventional methods.

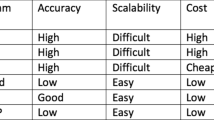
Further conclusions could be made regarding the node communication ranges, which played a critical role in identifying triangulation uncertainties: the longer the range, the higher the chance of formation of larger triangulation area, the higher the chance of error in localization of the sensor nodes. At the same time, localization error could also be worsened by formation of triangulations with highly obtuse or acute internal angles, especially the apex node. A qualitative summarization can be made in Table 1. Future directions shall include analysis of errors introduced during the conversion of actual uncertainty and uncertainty skew to target’s coordinates.

Table 2 Summary of proposed model

Appendix A

See Table 3.

Table 3 Pseudocode of fisher information matrix