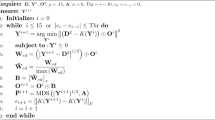1 Introduction

1.1 Motivation and applications

Sensor networks suffer from connectivity and localization issues. They require careful consideration both in time domain as well as spatial domain. Although physical dimensions can be dealt with by simply considering the coordinate space, but additional insights could be made by taking help of time–space domain together. Minkowski space is one such example that considers time space analysis. It has been used in the domain of image processing and convex-polygon geometry because of its ability to mimic convolution of different physical entities. Minkowski space and their operations have been dealt with extensively in a survey spread over multiple sections, in [1] and [2]. Minkowski triangulations are discussed in detail in [3]. Minkowski distance has been used in applications such as multi-objective optimization in [4], wireless medical sensor network systems [5] and Internet of Things (IoT) security. Sensor localization could be classified broadly as ranged, range-free or hybrid, based on whether the node is to be localized to a point, or to a region. Ranged methods are computationally complex but relatively accurate, whereas range-free methods are simple to implement and more suited to computationally constrained environments. In any case, localization parameters need to be evaluated in terms of their accuracy and inter-linkages [6] to determine how node deployment strategy affects node localization. In order to localize nodes, mechanisms such as “PG algorithm” [7], Maximum likelihood criteria for soil-air interface [8], dual beacon nodes for localization based on time difference of arrival (TDoA) and angle of arrival (AoA) [9] are proposed in the literature. To reduce the error associated with localization of nodes [10], suitable estimators are designed to achieve Cramer Rao lower bounds (CRLB) [11] under feasible conditions. Further, estimators are developed, which predict locations of target even under uncertainties [12]. There is a dearth of study that relates localization uncertainty using triangulation [13] methods. The main motivation behind pursuing triangulation-based localization, is the fact that it trades localization accuracy for computational simplicity. If methods and techniques are developed in this direction that could reduce the localization errors while still maintaining algorithmic simplicity, it would benefit wireless sensor networks (WSNs) [14] in all the three terrains: Terrestrial, underwater as well as aerial.

1.2 Literature review

In [15], a two stage Statistical Resolution Limit (SRL) has been presented. Although it could be applied to node localization, however, it does not consider the detailed impact of node geometry on triangulation uncertainty. To further dive into node geometrical topology, [16] considers Minkowski distance based k-nearest neighbourhood discovery. Although the interaction between anchor-anchor node is described in terms of virtual viscoelastic mesh, but the erroneous range & angular estimation formulation is entirely different from the concept of triangulation uncertainty as it calculates the cosine distance, the angular distance and the Minkowski distance metrics without the measurement of angle from the drop axes. Authors in [17] have considered sparse sensing technique for the retrieval of signals using a blind sensing problem. When applied to a wireless sensor network, the authors propose a ‘fractal dimension’ metric to finely discretize the Minkowski space, which may be applied to localize targets in a sparse environment. Triangulation geometry remains to be implemented, though, the solution to blind sensing problem has been rigorously derived in the context of stochastic setting. To deal with the persistent issue of dissatisfactory localization accuracy, a Minkowski Sum based estimation technique has been proposed in [18]. The technique has been established with the help of a rigorous mathematical analysis on fusion-based sensor node geometry. It foregoes the discussion about triangulation uncertainty because it considers ellipsoidal calculus under decentralized estimation. A three stage event based estimation approach in wireless sensor networks has been elaborated with the backdrop of Kalman filter in [19]. For each stage, a Minkowski sum aids in the sensor fusion and determines the boundedness of measurement. Although the relationship between sensor nodes [20] and the size of estimation means is established, their relationship with triangulation and the associated positioning uncertainty is beyond the scope of discussion. The authors in [21] address the information geometry in UAV- sensor networks. Accuracy of target localization has been improved using Minkowski determinant theorem. However, there is a scope of further investigation in terms of informational uncertainty, which will enable us to formulate techniques to combat positioning uncertainty.

1.3 Key contributions

Based on the literature review, a critical analysis reveals the follows research gaps:

  1. (a)

    Lack of sufficient works on Minkowski parameter in wireless sensor networks: One of the requirements of parameter measurement in sensor networks is the choice of norm. Appropriate norm formulation ensures non-erroneous parameter measurement. While traditional norms focus on point-to-point connectivity (such as L2-norm), real-life scenarios always require some sort of compensation or correction-factor in addition to the usual norm. Minkowski-norm promises a much-needed feature that would revolutionize the measurement of WSN parameters, hence the need for its formulation.

  2. (b)

    Geometry of triangulation uncertainty in target positioning estimation: Range-free localization heavily relies on sensor node geometry. Since triangulation uncertainty is one such parameter that quantifies the node geometry, it is a crucial tool for estimation of target position in a WSN. Formulation of a suitable positioning technique which utilizes geometric triangulation uncertainty could potentially provide a solid framework for further analysis.

  3. (c)

    Lack of Minkowski timespace based localization techniques: Minkowski timespace is used to compute the dynamic environment of topology coordinates with respect to time. When applied to localization, it could address the perennial problem of positioning task allocation when dealing with a moving target. However, its implementation requires careful planning in a multi-stage algorithm to suit the purpose.

These lacunas have been addressed strategically in the present treatment, and their major highlights are as follows:

  1. (a)

    Based on the concept of triangulation uncertainty, a proposed Minkowski-Triangulation Uncertainty (MTU) technique is formulated for a two-stage localization of unknown target node in a wireless sensor network.

  2. (b)

    the first stage formulates countLocalized algorithm to compute Minkowski distances between the sensor nodes, anchor nodes and the target node to come up with the number of localized sensor nodes.

  3. (c)

    the second stage formulates a countAnchors to determine how many of the sensor nodes are capable of acting as anchor nodes, to be used for triangulating the unknown target.

  4. (d)

    Performance analysis of the proposed MTU method in terms of localization ratio, error computation, anchor node density and network connectivity to compare with standard mature models of localization in WSNs.

1.4 Organization of paper

The rest of the paper is organized as follows: Section 2 describes the conceptual model in which “Minkowski triangulations” and “Triangulation Uncertainty” are briefly stated. Section 3 details on the methodology behind the localization framework. Next, the sources of range estimation error and interior angle estimation error are dealt with. Finally, the proposed Minkowski Triangulation Uncertainty (MTU) technique is detailed with the help of two proposed algorithms, namely the countLocalized algorithm and the countAnchor algorithm. Simulation setup parameters and the simulation environment used are discussed in Section 4. An in-depth analysis of results in the form of a comparison of the proposed work to the literature is explained in the “Results and Discussion” of Section 4. Conclusion and Future Works are summarized in Section 6.

Notations: Bold letters denote vectors and matrices. \(\left\| { \, \cdot \, } \right\|\) denotes Minkowski-distance in 2 dimensions. \(\left| { \, \cdot \, } \right|\) denotes absolute value, or, in certain cases, the count of the number of objects.

2 Conceptual model

In the present section, a conceptual framework of the Minkowski theory is presented. Minkowoski Triangulation is stated in section A and proven through Lemma 3.1. Equations (3) and (4) briefly touch upon Triangulation Uncertainty in Section B. The concepts discussed here lay the foundation of the proposed algorithms in the subsequent sections.

Localization in wireless sensor networks may be carried out by performing ranged measurements as well as range-free methods. Ranged measurements such as received signal strength information (RSSI), time of arrival (ToA), AoA, TDoA estimate the location of target node to a point, whereas range free methods such as Convex position estimation (CPE) and approximate point in triangulation (APIT) estimate the region in which the target node has the highest probability of being detected. Although range free measurements are not as pinpointed as ranged methods, but they offer significant computational simplicity and higher tolerance to scenarios with drifting nodes or non-line of sight (nLOS) localization. The current implementation of triangulation based on Minkowski spaces is used because triangle is the simplest polygon that can effectively make use of two sensor nodes to calculate the target node triangulation uncertainty. Within this paper, triangulation uncertainty, localization uncertainty, node uncertainty or simply uncertainty, all mean the same and have been used interchangeably without any change in context. The symbol notations used in this paper are enlisted in Table 1.

Table 1 Symbol notations used in this paper
Full size table

2.1 Minkowski triangulations

Minkowski Space is the multidimensional space–time region which has diverse applications in research, ranging from Minkowski Sum, Minkowski Fractal, Minkowski distance [16], Minkowski Decomposition, to name a few. Minkowski-sum is used to put an Upper and Lower bound on the number of triangulations possible with polygons. The polygons themselves may be either convex or arbitrary. The computational complexity of the Minkowski sum varies with ℝ2, ℝ3 and ℝd as shown in Table 2.

Table 2 Complexity of Minkowski sums
Full size table

The upper bound on triangulation of simple polygons P and Q with ‘m’ and ‘n’ vertices, respectively, is given by Eq. (1)

$${\text{Triangulate}}\;P = \bigcup\limits_{i = 1}^{m - 2} {T_{i}^{P} } ;\;\;{\text{Triangulate}}\;Q = \bigcup\limits_{i = 1}^{n - 2} {T_{i}^{Q} }$$
(1)

Equation (1) emphasizes that if the number of triangulations is the same for two different polygons, then the vertices could be comprised of the same set of nodes. In the subsequent sections we shall see that the error in estimation of range or of internal angles is highly dependent on the triangulation geometry of the deployed nodes.

In the domain of wireless sensor networks, the limited range of connectivity of each node means triangulations formed by linked nodes will usually be less than the Minkowski Triangulation.

Lemma 3.1

If the number of Minkowski Triangulations is denoted by \(T_{i}^{M}\) and the number of 2D Sensor Triangulations is denoted by \(T_{i}^{S}\), then \(T_{i}^{S} \subseteq T_{i}^{M}\).

Proof

We need to prove that the number of triangulations formed by Minkowski method is inclusive of those formed by l2-norm range of sensor nodes in a WSN. We know that the number of links formed by n- Minkowski distance where xi and yi are d-dimensional vectors, is given by Eq. (2).

$$M_{n} = \sqrt[n]{{\sum\limits_{i = 1}^{d} {\left| {x_{i} - y_{i} } \right|^{n} } }}, \, n \ge {1}$$
(2)

Since the number of Minkowski Triangulation considers ‘m’ vertices polygon unlike ‘m’ independent nodes of a sensor network, hence \(\left| {T_{i}^{M} } \right| \ge \left| {T_{i}^{S} } \right|\). Thus, \(T_{i}^{S} \subseteq T_{i}^{M}\).

2.2 Triangulation uncertainty

When a set of three nodes communicate in close proximity, then it is possible to triangulate an unknown target situated within the region of triangulation. The accuracy of localization under the concept of triangulation is explained by the term “Uncertainty” in triangulation. Authors in [22] have dealt with triangulation uncertainty in a great detail. According to the formulation, Triangulation Uncertainty is calculated as shown in Eq. (3).

$$\, U = {{\left( {l_{{{\text{side}}\;{1}}} \times l_{{{\text{side}}\;{2}}} } \right)} \mathord{\left/ {\vphantom {{\left( {l_{{{\text{side}}\;{1}}} \times l_{{{\text{side}}\;{2}}} } \right)} {\left( {\left| {\sin \angle \left( {l_{{{\text{side}}\;{1}}} ,l_{{{\text{side}}\;{2}}} } \right)} \right|} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\left| {\sin \angle \left( {l_{{{\text{side}}\;{1}}} ,l_{{{\text{side}}\;{2}}} } \right)} \right|} \right)}}$$
(3)

where \(l_{{{\text{side}}\;{1}}}\) and \(l_{{{\text{side}}\;{2}}}\) are the lengths of the sides of the triangle having a common third vertex as illustrated in Fig. 2. \(\sin \angle \left( {l_{{{\text{side}}\;{1}}} ,l_{{{\text{side}}\;{2}}} } \right)\) is the interior angle formed by the target vertex node at the apex position, as shall be explained in the subsequent illustrations. It may be broadly observed that triangulation uncertainty increases with decrease in the interior angle. \(U\) also increases if the target node is situated farther away from the two sensor nodes. If the communication range between the target node (represented by the Minkowski vector \({\mathbf{o}}\)) and sensor nodes (denoted by \({\mathbf{a}}\) and \({\mathbf{b}}\)) is given by the set of all points along the ray \(\left[ {{\mathbf{o}},{\mathbf{a}}} \right.\rangle\) and \(\left[ {{\mathbf{o}},{\mathbf{b}}} \right.\rangle\), respectively, then the angle measurement of the target (denoted by \(\measuredangle {\mathbf{aob}}\)) is defined by Eq. (4).

$$\measuredangle {\mathbf{aob}} = \cos^{ - 1} \left[ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \times \left( {2 - \left\| {{\hat{\mathbf{a}}} - {\hat{\mathbf{b}}}} \right\|^{2} } \right)} \right]$$
(4)

where \({\mathbf{\hat{a} = }}{{\mathbf{a}} \mathord{\left/ {\vphantom {{\mathbf{a}} {\left\| {\mathbf{a}} \right\|}}} \right. \kern-\nulldelimiterspace} {\left\| {\mathbf{a}} \right\|}}\) and \({\mathbf{\hat{b} = }}{{\mathbf{b}} \mathord{\left/ {\vphantom {{\mathbf{b}} {\left\| {\mathbf{b}} \right\|}}} \right. \kern-\nulldelimiterspace} {\left\| {\mathbf{b}} \right\|}}\) represent the unit vectors in Minkowski space of order 2. Because this uncertainty depends not only on the size of the links but also on the shape of geometry, therefore having node deployments such that the triangulations are symmetric, helps to efficiently localize any target node.

Summarizing Section 2, the concepts of Minkowski Triangulation as well as Triangulation Uncertainty shall enable the strategical formulation of the proposed methodology in Section 3.

3 Localization framework

In this section, an attempt has been made to propose a framework of localization in WSNs based on the concept of Minkowski distance and Triangulation Uncertainty. The detailed methodology for computation of triangulation uncertainty is mentioned in Section A. Sources of estimation error in a geometric sensor network topology is derived in Eqs. (13) to (32) of Section B. Based on the foundation laid down by Section A and B, a Minkowski Triangulation Uncertainty (MTU) technique for localization of unknown target in a WSN is proposed in Section C. The MTU technique comprising of two algorithms, namely countLocalized and countAnchor is explained here. The numerical computations follow in the subsequent sections.

3.1 Methodology

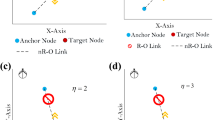
An illustration of triangulation uncertainty calculation is shown in Fig. 1. To measure interior angle of the triangulation, suppose nodes N1 and N3 act as vector nodes. Then, the node N2 shall be designated as the apex node, as shown in Fig. 2.

Fig. 1
figure 1

Pictorial representation of node deployment scenario with three anchor nodes and a target node

Full size image
Fig. 2
figure 2

Nodes N1 and N3 acting as vector nodes and N2 as apex node. U2 would denote triangulation uncertainty of the case when target node position would coincide with apex node N2

Full size image

The angular measurements are taken according to three different perspectives. For node N1 as the apex node, as in Fig. 3a, the node N2 and N3 act as vector nodes through which the location and angle measurements of the target node is to be made. For the sake of simplicity, we take that the target node location coincides with the apex node. The localization uncertainty is then calculated by the formula mentioned in Eq. (3). However, we do not know if the exact proximity of the target node is towards which anchor node (N1, N2 or N3). Hence, we individually calculate the three inner angles of the apex nodes, as shown in Eqs. (5), (6) and (7), illustrated in Figs. 2, 3a, b.

$$\left. {\measuredangle {\mathbf{aob}}} \right|_{{{\mathbf{o}} = {\mathbf{N}}_{{\mathbf{3}}} }} = \left. {\cos^{ - 1} \left[ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \times \left( {2 - \left\| {{\hat{\mathbf{a}}} - {\hat{\mathbf{b}}}} \right\|^{2} } \right)} \right]} \right|_{{{\mathbf{a}} = {\mathbf{N}}_{{\mathbf{1}}} ,{\mathbf{b}} = {\mathbf{N}}_{{\mathbf{2}}} }}$$
(5)
$$\left. {\measuredangle {\mathbf{aob}}} \right|_{{{\mathbf{o}} = {\mathbf{N}}_{{\mathbf{2}}} }} = \left. {\cos^{ - 1} \left[ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \times \left( {2 - \left\| {{\hat{\mathbf{a}}} - {\hat{\mathbf{b}}}} \right\|^{2} } \right)} \right]} \right|_{{{\mathbf{a}} = {\mathbf{N}}_{{\mathbf{1}}} ,{\mathbf{b}} = {\mathbf{N}}_{{\mathbf{3}}} }}$$
(6)
$$\left. {\measuredangle {\mathbf{aob}}} \right|_{{{\mathbf{o}} = {\mathbf{N}}_{{\mathbf{1}}} }} = \left. {\cos^{ - 1} \left[ {\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \times \left( {2 - \left\| {{\hat{\mathbf{a}}} - {\hat{\mathbf{b}}}} \right\|^{2} } \right)} \right]} \right|_{{{\mathbf{a}} = {\mathbf{N}}_{{\mathbf{3}}} ,{\mathbf{b}} = {\mathbf{N}}_{{\mathbf{2}}} }}$$
(7)

where the vector distance \(\left( {{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}} \right) \times \left( {2 - \left\| {{\hat{\mathbf{a}}} - {\hat{\mathbf{b}}}} \right\|^{2} } \right)\) lies in the interval \(\left[ {0,1} \right]\). In Eq. (5), the target node position \({\mathbf{o}}\) coincides with the apex vertex \({\mathbf{N}}_{{\mathbf{3}}}\). Subsequently, \({\mathbf{N}}_{{\mathbf{1}}}\) and \({\mathbf{N}}_{{\mathbf{2}}}\) act as the vector nodes. The target node \({\mathbf{o}}\) in Eq. (6) is overlapped with the apex vertex \({\mathbf{N}}_{2}\). The job of vector nodes is subsequently performed by the two nodes \({\mathbf{N}}_{{\mathbf{1}}}\) and \({\mathbf{N}}_{{\mathbf{3}}}\). When the vector nodes \({\mathbf{N}}_{{\mathbf{1}}}\) and \({\mathbf{N}}_{{\mathbf{2}}}\) are used to triangulate the target \({\mathbf{o}}\), the coinciding apex node is \({\mathbf{N}}_{{\mathbf{3}}}\). The triangulation uncertainties of the three prospective nodes will be given by Eqs. (8)–(10).

$$\left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{3}}} }} = {{\left( {l_{{{\mathbf{N}}_{{\mathbf{1}}} {\mathbf{,N}}_{{\mathbf{3}}} }} \cdot l_{{{\mathbf{N}}_{{\mathbf{2}}} {\mathbf{,N}}_{{\mathbf{3}}} }} } \right)} \mathord{\left/ {\vphantom {{\left( {l_{{{\mathbf{N}}_{{\mathbf{1}}} {\mathbf{,N}}_{{\mathbf{3}}} }} \cdot l_{{{\mathbf{N}}_{{\mathbf{2}}} {\mathbf{,N}}_{{\mathbf{3}}} }} } \right)} {\left( {\left| {\sin \left( {\measuredangle {\mathbf{aob}}|_{{{\mathbf{o}} = {\mathbf{N}}_{{\mathbf{3}}} }} } \right)} \right|} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\left| {\sin \left( {\measuredangle {\mathbf{aob}}|_{{{\mathbf{o}} = {\mathbf{N}}_{{\mathbf{3}}} }} } \right)} \right|} \right)}}$$
(8)
$$\left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{2}}} }} = {{\left( {l_{{{\mathbf{N}}_{{\mathbf{1}}} {\mathbf{,N}}_{{\mathbf{2}}} }} \cdot l_{{{\mathbf{N}}_{{\mathbf{3}}} {\mathbf{,N}}_{{\mathbf{2}}} }} } \right)} \mathord{\left/ {\vphantom {{\left( {l_{{{\mathbf{N}}_{{\mathbf{1}}} {\mathbf{,N}}_{{\mathbf{2}}} }} \cdot l_{{{\mathbf{N}}_{{\mathbf{3}}} {\mathbf{,N}}_{{\mathbf{2}}} }} } \right)} {\left( {\left| {\sin \left( {\left. {\measuredangle {\mathbf{aob}}} \right|_{{{\mathbf{o}} = {\mathbf{N}}_{{\mathbf{2}}} }} } \right)} \right|} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\left| {\sin \left( {\left. {\measuredangle {\mathbf{aob}}} \right|_{{{\mathbf{o}} = {\mathbf{N}}_{{\mathbf{2}}} }} } \right)} \right|} \right)}}$$
(9)
$$\left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{1}}} }} = {{\left( {l_{{{\mathbf{N}}_{{\mathbf{3}}} {\mathbf{,N}}_{{\mathbf{1}}} }} \cdot l_{{{\mathbf{N}}_{{\mathbf{2}}} {\mathbf{,N}}_{{\mathbf{1}}} }} } \right)} \mathord{\left/ {\vphantom {{\left( {l_{{{\mathbf{N}}_{{\mathbf{3}}} {\mathbf{,N}}_{{\mathbf{1}}} }} \cdot l_{{{\mathbf{N}}_{{\mathbf{2}}} {\mathbf{,N}}_{{\mathbf{1}}} }} } \right)} {\left( {\left| {\sin \left( {\left. {\measuredangle {\mathbf{aob}}} \right|_{{{\mathbf{o}} = {\mathbf{N}}_{{\mathbf{1}}} }} } \right)} \right|} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\left| {\sin \left( {\left. {\measuredangle {\mathbf{aob}}} \right|_{{{\mathbf{o}} = {\mathbf{N}}_{{\mathbf{1}}} }} } \right)} \right|} \right)}}$$
(10)

where the uncertainty \(\left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{3}}} }}\) of Eq. (8) is described by the scenario of Fig. 3b, and the triangulation uncertainty \(\left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{1}}} }}\) of Eq. (10) is represented by Fig. 3a. The target node is supposed to have an overall triangulation uncertainty associated with it. The different approaches possible are mentioned as follows:

Fig. 3
figure 3

a Nodes N2 and N3 acting as vector nodes and N1 as apex node. U1 would denote triangulation uncertainty of the case when target node position would coincide with apex node N1. b Nodes N1 and N2 acting as vector nodes and N3 as apex node. U3 would denote triangulation uncertainty of the case when target node position would coincide with apex node N3

Full size image

Approach 1: Take the average of the three uncertainties (8)–(10), since the target node is equally probable to be present towards any of the three corners. This is given by Eq. (11).

$$U_{{{\text{target}}}} = \left( {{1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-\nulldelimiterspace} 3}} \right)\sum\limits_{i = 1}^{3} {\left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{i}}} }} } = {{\left( {\left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{1}}} }} + \left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{2}}} }} + \left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{3}}} }} } \right)} \mathord{\left/ {\vphantom {{\left( {\left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{1}}} }} + \left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{2}}} }} + \left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{3}}} }} } \right)} 3}} \right. \kern-\nulldelimiterspace} 3}$$
(11)

Approach 2: Select only the peak uncertainty, since it would take into consideration, the worst-case possibility of locating the target node. The target node uncertainty would then be given by Eq. (12).

$$U_{{{\text{target}}}} = Max\left\{ {\left. U \right|_{{{\mathbf{o = N}}_{{\mathbf{i}}} }} } \right\},i \in \left\{ {1,2,3} \right\}$$
(12)

Approach 3: Consider the triangulation only if 30° < θ < 120° and \(0.5 < \left( {{{l_{i} } \mathord{\left/ {\vphantom {{l_{i} } {l_{j} }}} \right. \kern-\nulldelimiterspace} {l_{j} }}} \right) < 2\), else discard the triangulation. This approach is also called the Steiner-point approach [23].

The current paper selects Approach 2 in order to grasp the worst-case scenario of the entire proposed model.

3.2 Sources of error

During the region estimation for the target node, errors may arise in two ways:

(a) Interior angle estimation by the two vector nodes \({\mathbf{a}}\) and \({\mathbf{b}}\) incurs errors. Let us denote it by \(\Phi_{{\measuredangle {\mathbf{aob}}}}^{{{\text{error}}}}\).

(b) Range estimation error by the vector nodes, denoted by \(\Phi_{{l_{i} l_{j} }}^{{{\text{error}}}}\). These are illustrated in Fig. 4.

Fig. 4
figure 4

An illustration for sources of error during uncertainty estimation. There can be error in distance estimation or in angle estimation, or a combination of both

Full size image

Error in localization region could be modelled using the convex hull formed by Minkowski sum of the actual and projected positions of the two vector node positions, as shown in Fig. 5. Localization error due to target node uncertainty may be modelled as in Eqs. (13)–(24).

$$\Phi_{U}^{{{\text{estimated}}}} = \Phi_{U}^{{{\text{actual}}}} \pm \Delta U$$
(13)
$${\text{where}},\;\;\Delta U = f\left( {\Phi_{{\measuredangle {\mathbf{aob}}}}^{{{\text{error}}}} ,\;\Phi_{{l_{i} l_{j} }}^{{{\text{error}}}} } \right)$$
(14)
$${\text{or}},\;\;\;\Phi_{U}^{{{\text{estimated}}}} = {\raise0.7ex\hbox{${\left( {l_{i} \pm \Delta l_{i}^{{{\text{error}}}} } \right) \cdot \left( {l_{j} \pm \Delta l_{j}^{{{\text{error}}}} } \right)}$} \!\mathord{\left/ {\vphantom {{\left( {l_{i} \pm \Delta l_{i}^{{{\text{error}}}} } \right) \cdot \left( {l_{j} \pm \Delta l_{j}^{{{\text{error}}}} } \right)} {\left| {\sin \left( {\theta \pm \Delta \theta^{{{\text{error}}}} } \right)} \right|}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${\left| {\sin \left( {\theta \pm \Delta \theta^{{{\text{error}}}} } \right)} \right|}$}}$$
(15)
$$\Rightarrow \Phi_{U}^{{{\text{estimated}}}} = \frac{{\left( {l_{i} l_{j} \pm l_{i} \Delta l_{j}^{{{\text{error}}}} \pm l_{j} \Delta l_{i}^{{{\text{error}}}} + \Delta l_{i}^{{{\text{error}}}} \Delta l_{j}^{{{\text{error}}}} } \right)}}{{\left| {\sin \theta \cos \left( {\Delta \theta^{{{\text{error}}}} } \right) \pm \cos \theta \sin \left( {\Delta \theta^{{{\text{error}}}} } \right)} \right|}}$$
(16)
$$\Rightarrow \Phi_{U}^{{{\text{estimated}}}} = \frac{{\left( {l_{i} l_{j} + E_{{{\text{length}}}} } \right)}}{{\sin \theta \left| {\left( {\cos \left( {\Delta \theta^{{{\text{error}}}} } \right) \pm \cos \theta \frac{{\sin \left( {\Delta \theta^{{{\text{error}}}} } \right)}}{\sin \theta }} \right)} \right|}}$$
(17)

where,

$$E_{{{\text{length}}}} = \Delta l_{i}^{{{\text{error}}}} \Delta l_{j}^{{{\text{error}}}} \pm l_{i} \Delta l_{j}^{{{\text{error}}}} \pm l_{j} \Delta l_{i}^{{{\text{error}}}}$$
(18)
Fig. 5
figure 5

Minkowski sum of the actual and erroneous positions of the two vector node positions gives rise to four virtual locations, the convex hull of which, forms the uncertainty area for target node

Full size image

For simplification,

$$\Delta l_{i}^{{{\text{error}}}} \Delta l_{j}^{{{\text{error}}}} \approx 0.$$
(19)

Thus,

$$E_{length} = \pm l_{i} \Delta l_{j}^{error} \pm l_{j} \Delta l_{i}^{error}$$
(20)

when \(\left( {{{\Delta \theta^{{{\text{error}}}} } \mathord{\left/ {\vphantom {{\Delta \theta^{{{\text{error}}}} } \theta }} \right. \kern-\nulldelimiterspace} \theta }} \right) \ll 1,\)

$$\Rightarrow \left( {{{\sin \Delta \theta^{{{\text{error}}}} } \mathord{\left/ {\vphantom {{\sin \Delta \theta^{{{\text{error}}}} } {\sin \theta }}} \right. \kern-\nulldelimiterspace} {\sin \theta }}} \right) \ll 1$$
(21)

So, the second term in the denominator,

$$\left( {\cos \left( {\Delta \theta^{{{\text{error}}}} } \right) \pm \cos \theta \frac{{\sin \left( {\Delta \theta^{{{\text{error}}}} } \right)}}{\sin \theta }} \right) \approx \cos \left( {\Delta \theta^{{{\text{error}}}} } \right)$$
(22)

Equation (17) then becomes

$$\Phi_{U}^{{{\text{estimated}}}} = \frac{{l_{i} l_{j} \pm l_{i} \Delta l_{j}^{{{\text{error}}}} \pm l_{j} \Delta l_{i}^{{{\text{error}}}} }}{{\sin \theta \cos \left( {\Delta \theta^{{{\text{error}}}} } \right)}}$$
(23)
$${\text{or}},\;\;\Phi_{U}^{{{\text{estimated}}}} = \Phi_{U}^{{{\text{actual}}}} + \Phi_{{\theta ,l_{i} }}^{{{\text{error}}}} + \Phi_{{\theta ,l_{j} }}^{{{\text{error}}}}$$
(24)

where,

$$\begin{aligned} & \Phi_{{\theta ,l_{j} }}^{{{\text{error}}}} = {{ \pm l_{i} \Delta l_{j}^{{{\text{error}}}} } \mathord{\left/ {\vphantom {{ \pm l_{i} \Delta l_{j}^{{{\text{error}}}} } {\Phi_{{\measuredangle {\mathbf{aob}}}}^{{{\text{error}}}} }}} \right. \kern-\nulldelimiterspace} {\Phi_{{\measuredangle {\mathbf{aob}}}}^{{{\text{error}}}} }}, \\ & \Phi_{{\theta ,l_{i} }}^{{{\text{error}}}} = {{ \pm l_{j} \Delta l_{i}^{{{\text{error}}}} } \mathord{\left/ {\vphantom {{ \pm l_{j} \Delta l_{i}^{{{\text{error}}}} } {\Phi_{{\measuredangle {\mathbf{aob}}}}^{{{\text{error}}}} }}} \right. \kern-\nulldelimiterspace} {\Phi_{{\measuredangle {\mathbf{aob}}}}^{{{\text{error}}}} }} \\ & \Phi_{{\measuredangle {\mathbf{aob}}}}^{{{\text{error}}}} = \sin \theta \cos \left( {\Delta \theta^{{{\text{error}}}} } \right) \\ \end{aligned}$$
(25)

Thus, it may be seen that the estimation error in triangulation uncertainty is due to the collective errors of angle and ranging from the two vector nodes which are given the task of triangulation of the target node. Minimization of these errors shall directly benefit accuracy of the uncertainty. Taking the common approach of virtual nodes, we may attempt to provide more sets of observations to triangulate the target. A simple representation is as follows: For a triangulation, we need two vector nodes \(N_{i}\) and \(N_{j}\). Let us estimate two unknown parameters \(l\) and \(\theta\) using multiple observations from the vector nodes. The pdf of the observed data be given by \(X\sim N\left( {\mu ,\sigma^{2} } \right)\), where, observed data are \(\overline{X} = \left\{ {X_{1} ,X_{2} , \ldots ,X_{m} } \right\}\). Let \(\hat{\theta }\) be a rule by which we can guess the value of the unknown parameter \(\theta\). \(\hat{\theta }\left( {\overline{X}} \right) = \hat{\theta }\left( {X_{1} ,X_{2} , \ldots ,X_{m} } \right)\) denotes the estimator \(\hat{\theta }\). Similarly, \(\hat{l}\) be a rule by which we can guess the value of the unknown parameter \(l\). \(\hat{l}\left( {\overline{X}} \right) = \hat{l}\left( {X_{1} ,X_{2} , \ldots ,X_{m} } \right)\) denotes the estimator \(\hat{l}\). There could be two approaches to estimate \(\theta\), as outlined below:

Approach 1: Both the nodes \(N_{i}\) and \(N_{j}\) separately measure the drop-angle from the reference point (0°) till -90°, denoted by \(\hat{\theta }_{i}\) and \(\hat{\theta }_{j}\), respectively, as illustrated in Fig. 6a. The rule \(\hat{\theta }\), is then given by Eq. (26).

$$\hat{\theta } = \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}} \right)\sum\limits_{k = 1}^{m} {\left( {\hat{\theta }_{k}^{i} + \hat{\theta }_{k}^{j} } \right)}$$
(26)
Fig. 6
figure 6

a Nodes Ni and Nj measure angle from the reference drop axes. b Nodes Ni and Nj measure angle from each other

Full size image

Approach 2: Location of \(N_{i}\) is known to \(N_{j}\). So, entire \(\theta = \measuredangle {\mathbf{aob}}\) is estimated, but, at least once from each of the vector node, as illustrated in Fig. 6b. The rule \(\hat{\theta }\), is then given by Eq. (27).

$$\hat{\theta } = \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {2m}}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{${2m}$}}} \right)\sum\limits_{k = 1}^{m} {\left( {\hat{\theta }_{k}^{i} + \hat{\theta }_{k}^{j} } \right)}$$
(27)

If the mean of the estimated data is unknown and the variance is known to be σ2, then we have the joint pdf of the rule as \(\theta \left( {\overline{X}} \right)\sim N\left( {\mu_{\theta } ,\sigma_{\theta }^{2} } \right)\), where \(\mu_{\theta }\) = unknown mean of the angle to be estimated, and \(\sigma_{\theta }^{2}\) = known variance of the measured angle. A simple estimator \(\hat{\mu }_{\theta }^{1}\) that averages the first and the last observation, would be given by \(\hat{\mu }_{\theta }^{1} \left( {\overline{X}^{\theta } } \right) = \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)\left( {X_{1}^{\theta } + X_{m}^{\theta } } \right)\). Breaking down this estimator into two respective components of two vector nodes i and j, we have Eq. (28)

$${\text{and}},\;\;\begin{array}{*{20}c} {\hat{\mu }_{{\theta_{i} }}^{1} \left( {\overline{X}^{{\theta_{i} }} } \right) = \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)\left( {X_{1}^{{\theta_{i} }} + X_{m}^{{\theta_{i} }} } \right)} \\ {\hat{\mu }_{{\theta_{j} }}^{1} \left( {\overline{X}^{{\theta_{j} }} } \right) = \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)\left( {X_{1}^{{\theta_{j} }} + X_{m}^{{\theta_{j} }} } \right)} \\ {i,j \in \# \left( {{\text{feasible}}\;{\text{triangulations}}} \right)} \\ \end{array}$$
(28)

The variance of such an estimator is expressed as Eq. (29)

$$\left( {{\text{or}}} \right)\;\;\begin{array}{*{20}l} {{\text{var}} \left( {\hat{\mu }_{\theta }^{1} } \right) = {\text{var}} \left[ {\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right)\left( {X_{1}^{\theta } + X_{m}^{\theta } } \right)} \right]} \hfill \\ {{\text{var}} \left( {\hat{\mu }_{\theta }^{1} } \right) = {\raise0.7ex\hbox{${\sigma_{\theta }^{2} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\theta }^{2} } 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \hfill \\ \end{array}$$
(29)

We observe that mere two observations do not yield a very consistent estimator. So, multiple samples of the observation must be taken. The usual way forward would be an m-sample averaging estimator \(\hat{\mu }_{\theta }^{2}\), described by Eq. (30).

$${\text{and}},\;\;\begin{array}{*{20}c} {\hat{\mu }_{\theta }^{2} \left( {\overline{X}^{\theta } } \right) = \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}} \right)\sum\limits_{k = 1}^{m} {\left( {X_{k}^{\theta } } \right)} } \\ {\hat{\mu }_{l}^{2} \left( {\overline{X}^{l} } \right) = \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}} \right)\sum\limits_{k = 1}^{m} {\left( {X_{k}^{l} } \right)} } \\ \end{array}$$
(30)

The variance would then be given by Eq. (31).

$$\left( {{\text{or}}} \right)\;\;\begin{array}{*{20}l} {{\text{var}} \left( {\hat{\mu }_{\theta }^{2} } \right) = {\text{var}} \left[ {\left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}} \right)\sum\limits_{k = 1}^{m} {\left( {X_{k}^{\theta } } \right)} } \right]} \hfill \\ {{\text{var}} \left( {\hat{\mu }_{\theta }^{2} } \right) = {\raise0.7ex\hbox{${\sigma_{\theta }^{2} }$} \!\mathord{\left/ {\vphantom {{\sigma_{\theta }^{2} } m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}} \hfill \\ \end{array}$$
(31)

Similarly, variance of the range is \({\text{var}} \left( {\hat{\mu }_{l}^{2} } \right) = {\raise0.7ex\hbox{${\sigma_{l}^{2} }$} \!\mathord{\left/ {\vphantom {{\sigma_{l}^{2} } m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}\), which is more consistent than \({\text{var}} \left( {\hat{\mu }_{l}^{2} } \right) = {\raise0.7ex\hbox{${\sigma_{l}^{2} }$} \!\mathord{\left/ {\vphantom {{\sigma_{l}^{2} } 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}\). Asymptotically, these estimators would be minimum variance, and would satisfy the lower bounds of variance. The length estimator \(\hat{\mu }_{l}^{2}\) needs to be individually calculated for each of the two lengths corresponding to the two vector nodes i and j, given by Eq. (32), that is,

$$\begin{array}{*{20}l} {\hat{\mu }_{{l_{i} }}^{2} = \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}} \right)\sum\limits_{k = 1}^{m} {\left( {X_{k}^{{l_{i} }} } \right)} } \hfill \\ {\hat{\mu }_{{l_{j} }}^{2} = \left( {{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 m}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$m$}}} \right)\sum\limits_{k = 1}^{m} {\left( {X_{k}^{{l_{j} }} } \right)} } \hfill \\ \end{array} \;\; {\text{for}}\;{\text{node}}\;\;i\;\;{\text{and}}\;\;j.$$
(32)

3.3 Proposed Minkowski triangulation uncertainty (MTU) algorithm

We have used the concept of triangulation uncertainty to decide the region in which a target node is most likely present. Our version of localization, thus, depends on the relative area that a triangulation covers. A flow chart to visualize the steps of the approach taken is illustrated in Fig. 7. For this paper, we have set the criteria based on Lemma 3.1 of Section 3 that a node is said to be localized if the upper bound on its uncertainty \(U^{*}\) is given by Eq. (33).

$$U^{*} \le k \times U_{\max }$$
(33)

where \(U_{\max }\) is the upper bound on uncertainty for a given threshold range and k is a value between 0 and 1. Once the relevant nodes are localized, we designate those localized nodes which have an appreciably low bound on their uncertainty, considering the area of deployment. For this paper, we have set the criteria that a localized node is said to be an anchor node if the upper bound in its uncertainty is given by Eq. (34).

$$U^{*} \le t\% \left( {Ar\left( {{\text{deployment}}} \right)} \right)$$
(34)
$${\text{For}}\;{\text{example}},\;\;U^{*} \le 500\;{\text{m}}^{2} \;\;{\text{for}}\;t = {5}$$
(35)

where t is the tolerance set for electing an anchor node. To perform triangulation uncertainty-based localization, we propose two algorithms: countLocalized and countAnchor. The steps to be followed in the algorithm countLocalized are explained in brief as follows:

Fig. 7
figure 7

Flow chart of the proposed MTU technique

Full size image

After the nodes are deployed in the rectangular 2D area, the number of unique links, that is, sensor-to-sensor linkages are counted and stored in an array along with their corresponding sensor node IDs. From these unique links, the number of unique triangulations is counted and stored in a separate array, along with their constituent triplet of nodes. Next, the target uncertainty associated with each unique triangle is computed, and the nodes are counted as localized if the uncertainty is below certain threshold. Then, those localized nodes which are probable candidates for being apex node (that is, as target node) are counted and stored in the variable countLocalized. Their uncertainty parameter is stored as well.

 

Algorithm countLocalized

1

Deploy Nodes

2

uniqueLink.nodeID = struct_array1, uniqueLink.nodelocations = struct_array2, countLink = #rows(struct_array1)

3

uniqueTriangles.nodeID = struct_array3, uniqueTriangles.nodelocations = struct_array4

4

countTriangles = #rows(struct_array3)

5

Associated Uncertainty = \(length(side1)\times length(side2)/\left|\mathrm{sin}\angle (side1,side2)\right|\)

6

target_localized.nodeID = \(\phi\)

7

if target_U < k × Umax

8

horzcat(Uniquelocalized.nodeID, target_node)

9

uncertaintyIndex = \(\phi\)

10

if triangulation \(\in\) localized node as a target node

11

uncertaintyIndex = store uncertainties of localized target nodes

12

countLocalized = length(unique_localized_nodes)

The steps for countAnchor algorithm are as follows:

Amongst the localized nodes with their corresponding uncertainties for triangulation, those nodes are identified whose triangulation uncertainty is below the reference tolerance level. These nodes are designated as anchor nodes, and stored in the array countAnchor. Next, the number of anchor-anchor linkages, anchor-sensor linkages and sensor-sensor linkages are identified and stored in their respective arrays.

 

Algorithm countAnchor

1

Look for U* < A m2 amongst uncertaintyIndex {actually atleast one U* < A m2 for any node}

2

Designate such localized nodes as “anchor nodes”

Store their nodeIDs in “anchorID”

3

countAnchor = length(anchorID)

4

Identify

5

#anchor-anchor linkages = Na:a

6

#anchor-sensor linkages = Na:s

7

#sensor-sensor linkages = Ns:s

Thus, summarizing Section 3, the problem formulation for wireless sensor network localization under the presence of range estimation error and interior angle estimation error was described. It was found that the position of the unknown target could be safely approximated to coincide with an apex node, following which the minkowski-distance based triangulation uncertainty could be calculated. How this formulation translates quantitatively, shall be observed in Section 4 and 5.

4 Simulation

In this section, the details regarding simulation environment and simulation tool are mentioned. The justification of the simulation parameters such as localization rate, localization error, node-to-node linkages are explained through Eqs. (36)–(41). The value of simulation parameters is justified in text as well as in tabular form. The choice of standard models used for comparison of the proposed method is discussed in brief.

For computation of the Algorithms countLocalized and countAnchor, the simulation tool MATLAB is used in Windows 10 operating system. A workstation with Intel Xeon Gold 5218 CPU @2.8 GHz with 64 GB DDR4 RAM @2666 MHz is the hardware used for running the simulations. To simulate a wireless sensor network, a set of 29 sensors are deployed in a 2D-uniform point process [24] in an area of 100 × 100 m2. The maximum diagonal distance of the deployment area turns out to be 141.4 m, and is denoted by dmax. The communication range of each sensor node is set as 1% till 20% of dmax. To compare the results with mature models, a Convex Triangulation of Optimal node Localization (C-TOL) is taken [22]. In C-TOL, the computation of the algorithms countLinks and countTriangles is aided by a WeightedUncertainty technique which computes the empirical weight coefficient of the links between sensors and anchor nodes. The concept of L2-norm is preferred as opposed to the Minkowski norm of this paper. As a result, triangulations of distinct symmetry are formed and compared subsequently. The proposed Minkowski-triangulated Uncertainty based technique is abbreviated as MTU in the simulation graphs. MTU method is also compared to the Polygonal-Geometry based Weighted Least Squares technique (abbreviated as PG-WLS in the graphs), in which the sensor node geometry is responsible for non-coherent localization of target [25]. This method is significant because the WLS computation enables the authors to compute pentagonal uncertainty of both the space-based (spatial) geometry as well as time-based (temporal) geometry. The parameters for simulations are outlined in Table 3.

Table 3 Parameters implemented in the localization model
Full size table

The four primary parameters used here to justify the performance of the proposed method are as follows:

Localization Ratio: It is the ratio of number of localized nodes to that of total number of nodes. In terms of uncertainty, localized nodes are those nodes that can communicate with neighbour nodes, can form triangulations, and have a target node uncertainty of less than 20% of the maximum node uncertainty for a kind of deployment. If \(N_{{{\text{loc}}}}\) denotes number of localized nodes, \(N_{{{\text{tri}}}}\) is the nodes which can form triangulations (but may or may not be localized) and \(N\) denotes the total number of nodes deployed, then localization ratio is given by Eq. (36)

$${\text{Localization}}{\kern 1pt} \;{\text{ratio}} = {{N_{{{\text{loc}}}} } \mathord{\left/ {\vphantom {{N_{{{\text{loc}}}} } N}} \right. \kern-\nulldelimiterspace} N}$$
(36)

Localization error: In terms of triangulation uncertainty, localization error is the average difference between the actual uncertainty and the measured uncertainties, with respect to every localized target node. For the purpose of worst-case computation of the error, the peak uncertainty amongst all triangulation of a target node is chosen as the actual uncertainty. We denote \(N_{{{\text{target}}}}\) as the total number of triangulations made by a target node. If \(U^{*}\) denotes the measured uncertainty, and \(U_{{{\text{tri}}}}\) denotes the uncertainty of the triangulations made by the same target node, then localization error is given by Eqs. (37)–(39).

$$\left( {L.E.} \right)_{{{\text{abs}}}}^{i} = \left| {U^{*} - U_{{{\text{tri}}}}^{i} } \right|{, }i \in N_{{{\text{target}}}}$$
(37)
$$\left( {L.E.} \right)_{{\text{Least - squares}}}^{i} = \left| {U^{*} - U_{{{\text{tri}}}}^{i} } \right|^{2} {, }i \in N_{{{\text{target}}}}$$
(38)
$$\left( {L.E.} \right)_{{{\text{MSE}}}} = \frac{1}{{N_{{{\text{target}}}} }}\sum\limits_{i = 1}^{{N_{{{\text{target}}}} }} {\left| {U^{*} - U_{{{\text{tri}}}}^{i} } \right|^{2} }$$
(39)

where \(\left( {L.E.} \right)_{{{\text{abs}}}}^{i}\) denotes absolute localization error, \(\left( {L.E.} \right)_{{\text{Least - squares}}}^{i}\) denotes the least squared errors and \(\left( {L.E.} \right)_{{{\text{MSE}}}}\) denotes mean squared error.

Average number of neighbouring anchor nodes: Anchor nodes may be linked with other anchor nodes or sensor nodes, thus forming anchor-anchor linkages and anchor-sensor linkages. The ratio of sensors which are connectible to anchors (denoted by \(N_{s:a}\)) to the total number of sensor nodes gives us the average number of neighbouring anchor nodes, shown by Eq. (40)

$${\text{Avg}}\_{\text{neighb}}\_{\text{nodes}} = {{N_{s:a} } \mathord{\left/ {\vphantom {{N_{s:a} } N}} \right. \kern-\nulldelimiterspace} N}$$
(40)

Network connectivity: The ratio of nodes which form sensor-sensor linkages (denoted by \(N_{s:s}\)) to the total number of sensor nodes gives us the network connectivity for a given threshold range, as shown in Eq. (41)

$${\text{Net}}\_{\text{conn}} = {{N_{s:s} } \mathord{\left/ {\vphantom {{N_{s:s} } N}} \right. \kern-\nulldelimiterspace} N}$$
(41)

5 Results and discussion

In this section, a detailed technical discussion is presented for the results of the simulation. The proposed method is compared to standard models with respect to Localization ratio in Section A, root mean square error (RMSE) in localization in Section B, average number of neighbouring anchor node calculation in Section C. Section D demonstrates the performance in terms of average connectivity of sensor nodes. The effectiveness of the proposed method is tabulated in the end.

5.1 Localization ratio

Figure 8 depicts the ratio of localization for different sets of threshold communication range of each sensor node. They are compared to the percentage of nodes participating in the triangulation of target nodes. For short ranges of 10.6 m and 14.1 m, although there are nodes participating in triangulation, but there are no localized nodes, because the uncertainties associated with such triangulations must be beyond the upper bounds of localizability. The method C-TOL exhibits poor localization ratio below 21.15 m. At 21.15 m threshold, C-TOL localization ratio is 12% lower than the proposed MTU method. As node range is increased further (17.67 m till 28.2 m) the steady increase in possible triangulations results in increase in localization ratio from 20.69 to 79.31%. Throughout all threshold ranges, the number of nodes that participate in triangulation, is consistently higher than the number of nodes that are localized. Without perturbation, the PG-WLS technique is stuck at 31% at 24.748 m range and lower than the proposed MTU method by a fair margin of 36%. This means, although some nodes participate in triangulation, the triangulation themselves are very asymmetric. Most probably, the angle formed by the target node with the two sensors is very small, leading to a high value of associated uncertainty. The percentage of nodes participating in triangulation rises from 6.89% till 86.21% when the threshold range is varied from 10.6 to 28.2 m.

Fig. 8
figure 8

Localization ratio for different communication threshold ranges

Full size image

5.2 Localization error

Localization errors occur when a target node has several triangulations to its credit with different associated uncertainties. Since the peak uncertainty of them all is taken as the actual uncertainty, the RMS localization errors for each threshold consists of the RMS errors of each of the target nodes, of which there are increasingly many, as the threshold is increased. Figure 9 shows the RMS errors in localization of the triangulated targets for each triangulation possible in a deployment scenario with different sets of threshold communication range. From the graph, we may infer that large threshold range invites a large number of target nodes, each target node involves several triangulations, the RMS error of several triangulations is a single value for every target node. Thus, each point on a threshold range corresponds to the respective number of target nodes. More number of points closer to the x-axis would indicate target nodes with more accurate localization. The circles towards the upper region of the graph indicate those target nodes with poor localization accuracy. The proposed MTU technique faces slightly raised error at 0.05Umax setting as compared to the C-TOL method at 24.748 m and 28.2 m simply because the proportions of anchor nodes to that of the sensor nodes turns out to be unbalanced. At 21.15 m threshold, the proposed MTU error is at least 600m2 lower than the corresponding C-TOL error, while being 200 m2 lower than the PG-WLS error. The overall trend of the RMS error is generally more consistent for the proposed MTU technique than the compared techniques.

Fig. 9
figure 9

Localization errors for various communication threshold ranges

Full size image

5.3 Average number of neighbouring anchor nodes

The ratio of anchor-sensor linkages to that of total sensors is shown in Fig. 10. Since localization is negligible when the node communication range is highly restricted (10.6 m or 14.1 m), there are no anchor nodes to speak of. When the communication range is more expansive (17.67 m and higher) then the number of anchor-sensor linkages increase from 13.04% up till 55.55%. A higher percentage of neighbouring anchor nodes is a desirable parameter. It means that there is a higher prospect of accurate localization because of availability of a greater number of anchor nodes surrounding the target nodes. Compared to the proposed MTU method, the C-TOL performance at 0.1Umax absolutely tanks below 24.748 m, indicating the absence of anchor-sensor linkage either due to dearth of anchor nodes, or due to anchor nodes being farther than the communication region.

Fig. 10
figure 10

Average number of neighbouring anchor nodes for different communication threshold ranges

Full size image

5.4 Network connectivity

Network connectivity depends directly on the number of sensor-sensor linkages. Thus, for longer communication threshold range, there would be more sensor linkages. However, since the total number of sensors deployed here is fixed, and therefore, increasing the range results in increase of the number of anchor nodes too. After crossing certain range (21.15 m, here,) we observe a slight drop of network connectivity because some of the erstwhile sensor nodes have now become anchor nodes, hence some of the sensor-sensor linkages are now sensor-anchor linkages or even anchor-anchor linkages, which do not directly contribute to network connectivity. The peak connectivity achieved in current scenario is 78.95%. Figure 11 shows the percentage of sensor-sensor linkages amongst all other linkages for different threshold ranges. The role of Minkowski spacetime in the justification of network connectivity is as follows.

Fig. 11
figure 11

Network connectivity for different communication threshold ranges

Full size image

In terms of Minkowski spacetime \(M_{s}\) in a four dimensional real vector space [26], if any unknown target \({\mathbf{o}}\) in \(M_{s}\) shall define a triangulation \(T_{i}^{M}\), then an arbitrary future-directed timelike vector of triangulation shall be denoted by \(\Phi^{ + }\), whereas its counterpart shall be a past-directed timelike vector of triangulation \(\Phi^{ - }\) such that sensor-sensor linkages shall be formed when the unknown target \({\mathbf{o}}\) shall lie in both the triangulation \(T_{i}^{M}\) as well as a directed timelike vector \(\Phi\). In other words,

$$T_{i}^{M} \left( {x_{0} } \right) = \left\{ {x \in M_{s} :\left( {x - x_{0} } \right) \in \Phi } \right\}$$
(42)
$${\text{That}}\;{\text{is}},\;\;T_{i}^{M} \left( {x_{0} } \right) \cap \Phi^{ + } \;\;{\text{or}}\;\;T_{i}^{M} \left( {x_{0} } \right) \cap \Phi^{ - }$$
(43)
$$T_{ + }^{M} \left( {x_{0} } \right)\;\;{\text{or}}\;\;T_{ - }^{M} \left( {x_{0} } \right)$$
(44)

where \(T_{ + }^{M} \left( {x_{0} } \right) \approx T_{i}^{M} \left( {x_{0} } \right) \cap \Phi^{ + }\) and \(T_{ - }^{M} \left( {x_{0} } \right) \approx T_{i}^{M} \left( {x_{0} } \right) \cap \Phi^{ - }\).

Thus, when the triangulation \(T_{ + }^{M} \left( {x_{0} } \right)\) shall coincide with the triangulation \(T_{ - }^{M} \left( {x_{0} } \right)\), the network shall be linked by pairs of anchor node and sensor node, establishing a viable network connectivity.

It may be observed that with decrease in the number of anchor nodes, there is a complimentary increase in the number of non-anchor nodes. What counted earlier as an anchor once, is now a sensor, either a localized one or a non-localized one. Since the total number of nodes deployed in the current work and the area of deployment are fixed (29 nodes in an area of 100 × 100 m2), the percentage of anchors and non-anchor nodes merely gets redistributed upon changing the communication range of the nodes. Table 4 summarizes the four simulation results.

Table 4 Optimal parameter interval
Full size table

Summarizing Section 4 and 5, the proposed method was found to improve upon the existing techniques for an average of 28% over C-TOL method and about 30.1% over PG-WLS method which holds true in the respective optimal scenarios.

6 Conclusion and future work

This paper presents a consistent two-dimensional localization scheme that has been verified for small set of node deployment in a small, regularly shaped area. Two algorithms, namely, countLocalized and countAnchor are proposed in order to localize the sensor nodes and elect anchor nodes. A triangulation uncertainty criterion is proposed as the basis for localization. Preliminary error analysis reveals that uncertainty is dependent on the accuracy of estimation of two parameters of the target node, namely, its distance from two vector nodes and the interior angle made when the target node location coincides with the apex node position. Simulation results indicate that the proposed method is the most effective when the communication range of the nodes is 15%-17.5% of the longest diagonal of the deployment area.

The proposed MTU technique improves upon the existing methods by a margin of up to 36% in terms of localization ratio, up to 70% in terms of RMS positioning error, up to 6% in terms of anchor-sensor linkages, and up to 29% in terms of sensor-sensor linkages. This establishes the versatility of Minkowski spacetime combined with triangulation uncertainty as a dominant trait of the proposed MTU method. The proposed method needs to be investigated for scalability testing, since the current work has been restricted to a small set of nodes under a fixed area of deployment. Further parameters need to be analysed to make localization criteria more robust, and triangulations more symmetric. We are working on finding a suitable way to incorporate Steiner points criteria for optimizing the uncertainty threshold to improve localization efficiency.