Modeling and optimizing a multi-period closed-loop supply chain for pricing, warranty period, and quality management

Abstract

Nowadays, most of the researchers have focused on collecting the used products to carry out the recovery process. This paper deals with the repair process to improve the virtual age of used products and integrate to forward flow as a closed-loop supply chain (CLSC). The products can be returned to the chain several times until they have the required quality to be repaired. Here the optimal number of returning and repairing the used products for maximization of the profits are calculated. Also, the price of selling the products, the acquisition cost, and the warranty period are determined to motivate the customers to bring back their used products and increase the demand for products. For our proposed multi-period problem, an appropriate inventory control policy is taken, and in case of increasing the production amount, additional capacity can be installed by extra cost. The proposed mixed-integer non-linear model has been solved by three metaheuristic algorithms: Particle Swarm Optimization Algorithm (PSO), Genetic Algorithm (GA), Invasive Weeds Optimization algorithm (IWO). Numerical problems depicted model efficiency and by the use of the Taguchi method, qualitative parameters of proposed algorithms are calibrated. Then, the performance comparison of the methods has been done by Relative Performance Deviation.

1 Introduction

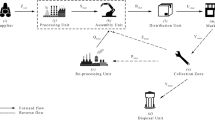
Recovery is a process of adding significant value to old or repairable products. Hence, it contributes to enterprises and governments to save costs and natural resources. In fact, innovation in the production of diverse products has led to a shorter life span, and to save energy for the future generation, the recovery process is an economic and environmentalist approach (Guide 2000). In reverse logistics, all activities are done to return the used products by users and reuse them (Fleischmann et al. 1997). The value of reusing the returned products can be more than hundreds of millions of dollars for one retailer (R Jr and Van Wassenhove 2009). Therefore, integrating the forward and reverse logistics as a closed-loop supply chain (CLSC) increases system value throughout the life cycle of products (Guide and Van Wassenhove 2009). On the other hand, this creates complications compared to its traditional forward state (Melo et al. 2009).

In terms of the quality of the products after recovery processes, it should be considered that the value added by restoring out of returned products can be as good as the new ones or not. For the lower quality, customers are willing to pay less in comparison with the new products. From this point of view, some researchers assume the quality of recovered products is the same as the new products as (Ijomah et al. 2004; Shi et al. 2011; Jing Wang et al. 2011; Kim et al. 2013; Giri and Sharma 2015; Polotski et al. 2017; As'ad et al. 2019). While others distinguish between them such as Debo et al. (2005), Ferguson and Toktay (2006), Jaber and El Saadany (2009), Hasanov et al. (2012), Gan et al. (2017). So depending on the industry and the way to reuse the returned products, the quality can be an important factor to distinguish the recovered products and also pricing decisions. It is obvious that the quality of returned products can be highly variable, illustrating the need for quality assessment procedures. For this purpose, segmentation policies for returned products with different quality grades have drawn attention in the recent decade. By compiling a proper segmentation policy, returned products might undergo different recovery policies or be disposed of. However, it can be found a general problem by reviewing the related literature that clarifies the need for the current investigation. Indeed, a classification program to head the different quality grades of returns is determined by predefined proportions which are obtained from historical data, experts’ opinions, etc. In the case of uncertainty with less available data, probability theory can be utilized to appropriately classify the returns. In this study, we bridge this gap by proposing age-dependent quality levels of used products which are uniformly distributed at multiple periods.

Based on the above discussion, the quality of returns depends on their age (when they are returned) that can be estimated from forms and registration logs/books, e-services, etc. (Chattopadhyay and Murthy 2000). Accordingly, products are collected from consumers to be sent for the recovery processes. Under an upgrade action, a reliability growth program is conducted to a certain extent. This approach was introduced by Kijima et al. (1988), and to clearly demonstrate upgrade action, Fig. 1 was adopted from Naini and Shafiee (2011) as follows:

Fig. 1

Effects of upgrade actions on the age of products and failure rate (Naini and Shafiee 2011)

With regard to the above figure, the basic observations incorporate the lifetime of products and their failure rate. Through restoring out the products by an upgrade action, the age of them decreases. This implies age-dependent quality levels of products. In this paper, age-dependent quality levels of products are considered in a multi-period CLSC problem in which an upgrade action improves the reliability of used products in each period. Although the recovery process makes some discarded products reusable, they are not as good as new products. Therefore, it is necessary to determine a proper strategy as a key for motivating customers to buy second-hand products. To this end, this paper deals with pricing, warranty period, and acquisition costs decisions along with forward-flow decisions in a supply chain. In order to fill the gaps, first, relevant literature has been presented.

In recent years, comprehensive reviews in the CLSC context are done by Govindan et al. (2015), Coenen et al. (2018), and Islam and Huda (2018) to investigate the values of numerous studies for meeting the environmental and social needs. However, this paper is provided to close the gaps in the literature via proposing a mathematical model dealing with streams in the field of price-sensitive demand, acquisition costs and warranty costs in CLSC models which are as follows:

The first stream is the tendency of researchers on topics related to price-dependent demand and acquisition costs management in the CLSC problems. In these fields, Maiti and Giri (2015) discussed different policies in a CLSC model considering the importance of the quality of products and price-dependent demand to find out the best result. Gao et al. (2016) studied a price-dependent demand in multi-structure channels to explore the low price and best performance in a CLSC model under the optimal coordination strategy. Christy et al. (2017) addressed a CLSC problem with two acceptance quality grades in the recovery process. Indeed, after the recovery process, the products may have the quality same as new ones or not. In their model, demands for products linearly depends on the quality and price of products. Masoudipour et al. (2017) investigated a multi-objective CLSC model with different recovery options for reusing the returned products and making decisions on the acquisition price. Alamdar et al. (2018) examined the performance of the price-dependent demand in a Fuzzy CLSC problem to obtain the optimal values of several presented scenarios by considering the profitability. Xu and Wang (2018) analyzed the relation between consumers and supply chain performances to tackle the price and carbon emission decision problems in two periods. They investigated the multiple structure scenarios for improving member profits. Ghomi-Avili et al. (2018) presented a new CLSC model with accounting for two objective functions attempting to maximize the total CLSC profits and minimize the carbon emissions in a fuzzy environmental and price-dependent demand. Duan et al. (2018) investigated a closed-loop policy for deteriorating products considering the inventory management to reach the maximum system profits. In their model, demand depends on the price of products with stochastic changes over the period interval. Zand et al. (2019) considered governmental limitations on the green activities for collecting and reusing the returned products. In their model, a linear function of price-dependent demand has been given to maximize the system profits. Wu et al. (2020) studied a two-echelon CLSC model to provide a structure optimizing the environmental issues in which demand is sensitive to the price decisions, and the objective function maximizes the total profits. Jian Wang et al. (2020) provided a dual-channel CLSC model with one manufacturer and one retailer. In their model, products can be purchased in an online manner from the manufacturer or purchased from the retailer in an online or a traditional way. In that, demand is sensitive to the price of products. Gu et al. (2019) proposed a multi-stage CLSC problem with recycling, repair, and refurbishing processes for reusing the returned products. In their model, optimum values of acquisition costs should be determined with the aim of maximizing the total profits wherein demand for products depends on the price of selling. Xu et al. (2019) investigated a CLSC problem for determining the optimum value of prices in terms of the retailer and the collector with available big data. Taleizadeh et al. (2019) worked on a CLSC problem with price decisions and offered a quantity discount. They studied social and environmental issues in a real case study with respect to their corresponding costs. Taleizadeh and Moshtagh (2019) investigated a multi-level CLSC problem with a focus on a consignment stock scheme. They proposed a non-linear expression to estimate the quality-dependent return rate and considered a minimum acceptance quality level to collect the used products which are good enough for the recovery process. Hassanpour et al. (2019) proposed a robust approach for a CLSC model in which the used products were collected with different quality grades. Therefore, a recovery process on the returned products was applied according to their quality grades. To solve their proposed model, metaheuristic algorithms have been utilized.

Another stream of the literature is related to the warranty in CLSC problems which is comprehensively discussed by Bhakthavatchalam et al. (2015). Afterward, Ashayeri et al. (2015) provided a distribution network for a CLSC problem considering several recovery options and warranty decisions. Gan et al. (2017) proposed a warranty contract for remanufactured products to ensure the quality of them to be upgraded to the same as the new products. Giri et al. (2018) proposed two CLSC models; in the first model, demand is sensitive to price and warranty period. In the second model, the green level is also considered. They attempted to maximize the profits regarding the revenue sharing contract in a single period. Tang et al. (2020) developed a CLSC model in which the impact of the warranty period was analyzed on customer willingness to buy both new and manufactured products. Also, a discount was offered to the customer for remanufactured products.

In this paper, a multi-period CLSC problem is proposed wherein inventory decisions, pricing and acquisition costs management for age-dependent quality levels of products are considered. Under this circumstance, a warranty contract plays a significant role in motivating the customer to buy repaired products through protection and promotion (Emons (1989)). In this regard, Table 1 is provided to illustrate the related gaps.

Table 1 Detailed information about S/N ratios for GA

In summary, the most contributions of the presented research are:

• Owing to the fact that we have a multi-period problem, the optimal number for the repair process to upgrade the quality of the used products would be calculated.

• Demand for products is a function of the length of the warranty period and the selling price. Also, the return rate of used products is a function of the acquisition cost of used products and the age of returns.

• The acquisition cost for the returned products, the selling price of products, inventory costs, and the cost of installing the additional capacity for production planning are addressed and optimized.

• We provide Genetic algorithm, Particle Swarm optimization algorithm, and Invasive Weed Optimization algorithm to solve the proposed mixed-integer non-linear (MINLP) model.

In the rest of the paper, in Sect. 2, assumptions and notations are presented. A MINLP model of a closed-loop supply chain relying on all contributions is described in Sect. 3. In Sect. 4, solution procedures are presented by three metaheuristic algorithms. Numerical examples are proposed in Sect. 5 which are solved with the aforementioned algorithms and the main parameters of them are calibrated with the Taguchi method. In Sect. 6, managerial insights are provided. Finally, the conclusion and future directions will be presented in Sect. 7.

2 Problem definition

In this proposed model, a multi-period closed-loop supply chain for a single product is investigated, in which the used products are collected from consumers to be repaired. In each period, the percentage of used products to be collected depends on the age of returned products and acquisition costs. The initial age of used products ($x$) is a stochastic variable and follows uniform distribution between the interval ($a, b$). After passing a period of time, returned products would be recovered in weaker quality compared to newly manufactured products. From this point, the initial age of the used products degrades to $(x-{x}_{m})$. Hence, repaired products retrieve over and over within the next periods if customers are willing to return them. Nevertheless, the initial age of the returned products decreases to $(x-{i}_{t}{x}_{m})$ when consumers return products for ${i}_{t}$ times from period $i$ to period $t$. On the other hand, the second variable that has a significant effect on the percentage of returned products is the acquisition cost offered to customers to motivate them to bring back their used products. In addition to collecting the used products and doing recovery operation, appropriate decisions on the price of selling and the length of warranty period lead to more demands for products. The lower selling price leads to more demands, however, this may not be profitable for the system. Besides, longer warranty periods may incur additional service costs to the system, while short warranty periods may lead to dissatisfaction and lose the customers. That’s why the selling price and the warranty period should be determined appropriately. Considering these two variables, demands for manufactured and repaired products are modeled as nonlinear functions. The main innovation of this paper is to make decisions on the number of times that the used products can be restored so the investments on the warranty contracts are affordable. To develop the model, the following notations are considered in Table 2.

Table 2 Detailed information about S/N ratios for PSO

2.1 Assumption

• A multi-period single product model is considered.

• Products have a limited age that follows the uniform distribution within the interval $[a-{i}_{t}{x}_{m}, b-{i}_{t}{x}_{m}]$. That means, newly manufactured products have an initial age in the interval $[a, b]$ which degrades in the amount of ${{i}_{t}x}_{m}$ after ${i}_{t}$ times retrieving.

• The quality of used products depends on the age of returns.

• Warranty length period ($w$) and selling price (${p}_{rt}$) affect the demand for repaired products in a non-linear form which is equal to ${D}_{rt}\left({p}_{rt},w\right)=d{p}_{rt}^{-\alpha }{w}^{\theta }$.

• Warranty length period ($w$) and selling price (${p}_{mt}$) affect the demand for new products in a non-linear form which is equal to ${D}_{t}\left({p}_{mt},w\right)={D}_{mt}{p}_{mt}^{-\alpha }{w}^{\theta }$.

• Shortages are not allowed and all types of demands should be satisfied.

• Used products are directly collected by the manufacturer.

• All products are used in the same pattern in which failures occur based on the Weibull distribution $(g\left(t\right)=\lambda \beta {(\lambda t)}^{\beta -1}{e}^{-\lambda \beta t})$ with parameters $\lambda$ and $\beta$. Where $\lambda$ indicates the scale parameter and $\beta$ is the shape parameter.

• Failures are independent.

• Repairing time during the warranty period ($w$) is negligible.

• The selling price of repaired products should be less than the selling price of new products (${p}_{rt}\le {p}_{mt}$).

3 Model formulation

In this proposed model, there are two types of customer demands. The first type is the demands for new products in each period, and the second type is for repaired products. Demands are as a function of the selling price and warranty length period. This non-linear formulation is obtained from related research such as Lee and Kim (1993), Glickman and Berger (1976), and Jung and Klein (2006). Moreover, Yazdian et al. (2016) have developed an optimization model with linear and non-linear formulas of demand for remanufactured products. In this paper, we suggested the non-linear formulation of demand in a CLSC problem due to its greater adaptation to reality, which is equal to ${D}_{rt}\left({p}_{rt},w\right)=d{p}_{rt}^{-\alpha }{w}^{\theta }$ for recovered products and ${D}_{t}\left({p}_{mt},w\right)={D}_{mt}{p}_{mt}^{-\alpha }{w}^{\theta }$ for manufactured products, where $\alpha$ and $\theta$ are positive scaling parameters. In these cases, whatever the length of the warranty period increases, it motivates customers to increase their demands while increasing selling price leads to decreases in demand for products.

The quantity of returned products for a single-period model is proposed by Yazdian et al. (2016). In this paper, the quantity of returned products from the previous periods is obtained by $R\left({v}_{t},x\right)=k{v}_{t}^{\partial }{x}^{y}$, where $k$ is a base return quantity of used products; $\partial$ and $y$ are positive scaling parameters. Accordingly, the return quantity depends on the acquisition cost of used products in each period (${v}_{t}$) and the age of them ($x$). As upgrading the age affects the quality of the products, it would be completely cleared in this section that the repairing will be permissible only for the qualified products.

In order to calculate the total returned products for this multi-period model, Eqs. (1) and (2) are presented, in which the initial age of new products is a stochastic variable ($x$) with uniform distribution in the interval $[a, b]$. During the recovery process, the age of the used products has changed to the ($x-{i}_{t}{x}_{m})$, where ${i}_{t}$ represents the returned products from period $i$ to period $t$ for ${i}_{t}$ times. In this regard, if the quality of returned products reaches the new condition, ${x}_{m}$ becomes zero. Whereas, ${x}_{m}=x$ indicates the recovery process is not able to upgrade the quality of used products. (See appendix A)

$${R}_{total}=\sum_{t(t>1)}^{T}\sum_{{i}_{t}}^{{I}_{t}}\left\{ {\int }_{a-{i}_{t}{x}_{m}}^{b-{i}_{t}{x}_{m}}R\left({v}_{t},x\right)f\left(x\right)dx\right\},$$

(1)

$${R}_{total}=\sum_{t(t>1)}^{T}\left(\sum_{{i}_{t}}^{{I}_{t}} {kv}_{{i}_{t}}^{\partial }\left\{\frac{{(b-{i}_{t}{x}_{m})}^{y+1}-{(a-{i}_{t}{x}_{m})}^{y+1}}{(y+1)(b-a)}\right\}\right).$$

(2)

3.1 Objective function

From Eq. (3), the total acquisition costs are obtained as follows:

$${TC}_{r}={R}_{total}=\sum_{t(t>1)}^{T}\left(\sum_{{i}_{t}}^{{I}_{t}} {kv}_{{i}_{t}}^{\partial +1}\left\{\frac{{(b-{i}_{t}{x}_{m})}^{y+1}-{(a-{i}_{t}{x}_{m})}^{y+1}}{(y+1)(b-a)}\right\}\right).$$

(3)

The failure time distribution function is Weibull ($\lambda , \beta$), and after upgrading the age of repaired products, the failure rate function becomes $r\left(t\right)=r(t-(x-{i}_{t}{x}_{m})$. Accordingly, the expected number of failures during the warranty period is given in Eq. (4).

$$E\left(N\right)={\int }_{x}^{x+w}r\left(t-\left(x-{i}_{t}{x}_{m}\right)\right)dt={\int }_{{i}_{t}{x}_{m}}^{{i}_{t}{x}_{m}+w}r\left(t\right)d(t).$$

(4)

From Eq. (5), the total expected warranty costs for all demands for manufactured and repaired products can be obtained as follows:

$$\begin{aligned}{TC}_{w}=&\sum_{t}^{T}{D}_{t}\left({p}_{mt},w\right)w\\ &+\sum_{t(t>1)}^{T}\sum_{{i}_{t}}^{{I}_{t}-1}{D}_{{i}_{t}}\left({p}_{r{i}_{t}},w\right)\left\{C[{\left({i}_{t}{x}_{m}+w\right)}^{\beta }+{i}_{t}^{\beta }{x}_{m}^{\beta }\right\}.\end{aligned}$$

(5)

Equation (6) represents the total costs of the manufacturing process.

$${TC}_{p}=\sum_{t}^{T}{A}_{t}{Q}_{t}.$$

(6)

To obtain more profits and prevent deficiency, additional capacity can be installed on the plant with respect to their related costs imposed on the system. These installation costs are derived from Eq. (7).

$${TC}_{ad}=\sum_{t}^{T}\sum_{j}^{J}{C}_{jt}{y}_{jt}.$$

(7)

3.1.1 Inventory holding cost

Inventory holding cost is one of the main costs of the supply chain and should be taken into account, especially when all demands should be met in each period. Since in this paper, the shortage is not allowed and all demands of new or repaired products should be satisfied, determining an appropriate inventory control policy plays an important role in the proper management of the supply chain. The stock holding procedure in this model is shown in Fig. 2:

Fig. 2

Inventory planning over the multiple periods

Equations (8) present the equality of the inventory level at the end of period $t-1$ and the inventory level at the beginning of period $t$.

$${IF}_{t-1}={IS}_{t};\, \forall t \,where\, t>1,$$

(8)

The inventory remained at the end of period $t$ is obtained from Eqs. (9), and the inventory holding cost is calculated according to Eq. (10).

$${IF}_{t}={IS}_{t}+{Q}_{t}+{R}_{t}\left({v}_{t},x\right)-{D}_{t}\left({p}_{mt},w\right)-{D}_{rt}\left({p}_{rt},w\right); \forall t,$$

(9)

$${TC}_{IN}=\sum_{t=1}^{T}{h}_{t}\left\{\frac{({IF}_{t}+{D}_{t}\left({p}_{mt},w\right)-D\left({p}_{t},w\right)+{IS}_{t}){T}_{t}}{2}+(b-{T}_{t}){IF}_{t}\right\},$$

(10)

In Eq. (10), ${T}_{t}$ is the time elapsed to produce ${Q}_{t}$ products, and is equal to $\frac{{Q}_{t}}{pr}$. Where $pr$ is the production rate.

Equations (11) determine the total revenue earned from selling new products and repaired products.

$$RE=\sum_{t}^{T}{p}_{mt}{D}_{t}+\sum_{t>1}^{T}{p}_{rt}{D}_{rt}\left({p}_{rt},w\right); \forall t.$$

(11)

Finally, the objective function is presented in Eq. (12) to maximize the total profits of the proposed CLSC model.

$$PR=RE-{TC}_{r}-{TC}_{w}-{TC}_{p}-{TC}_{ad}-{TC}_{IN}.$$

(12)

3.2 Constraints

Constraints (13) show that all demands for recovered products should be satisfied. The right term of these constraints contains the total amount of the returned products in period $t$ in addition to repaired products remained from the previous periods.

$$\begin{aligned}&{D}_{rt}\left({p}_{rt},w\right)\le {R}_{t}\left({v}_{t},x\right)\\ &\quad+\sum_{{t}^{^{\prime}}=1}^{t-1}\left({R}_{{t}^{^{\prime}}}\left({v}_{{t}^{^{\prime}}},x\right)-{D}_{r{t}^{^{\prime}}}\left({p}_{r{t}^{^{\prime}}},w\right)\right);\quad \forall t\, where\, t>1.\end{aligned}$$

(13)

Constraints (14) prevent the occurrence of deficiency in satisfying new product demands. The right term of these inequalities is the total products produced in period $t$ in addition to the products remained from the previous periods.

$${D}_{t}\le {Q}_{t}+\sum_{{t}^{^{\prime}}=1}^{t-1}\left({Q}_{{t}^{^{\prime}}}-{D}_{{t}^{^{\prime}}}\right);\quad \forall t\, where\, t>1.$$

(14)

Constraints (15) ensure that the total capacity required to produce ${Q}_{t}$ products within period $t$ should be less than the available capacity, and additional capacity can be installed if it is required.

$${Q}_{t}\le \sum_{j}^{J}{Ac}_{j}{y}_{jt}+M; \quad \forall t.$$

(15)

Constraints (16) guarantee that returned products must have the required quality for restoration and reuse. Constraints (17) ensure that the remaining life of products should be at least greater than the warranty period to be repaired.

$$a-\left({I}_{t}+1\right){x}_{m}\ge 0; \quad \forall t,$$

(16)

$$b-\left({I}_{t}+1\right){x}_{m}\ge w; \quad \forall t.$$

(17)

Constraint (18) relates to the types of variables.

$${{{IF}_{t},{IS}_{t},Q}_{t},{T}_{t},{v}_{t},{p}_{rt},{p}_{mt},w,{I}_{t},{y}_{jt}\ge 0;I}_{t}\epsilon integer, {y}_{jt}\epsilon binary.$$

(18)

In short, the complete mathematical model for the proposed CLSC is given as follows:

$$\begin{aligned}Max \,Z=& \sum_{t}^{T}{p}_{mt}{D}_{t}\left({p}_{mt},w\right)+\sum_{t>1}^{T}{p}_{rt}{D}_{rt}({P}_{rt},w)\\ &-\sum_{t(t>1)}^{T}\left(\sum_{{i}_{t}}^{{I}_{t}} k{v}_{{i}_{t}}^{\partial +1}\left\{\frac{{\left(b-{i}_{t}{x}_{m}\right)}^{y+1}-{\left(a-{i}_{t}{x}_{m}\right)}^{y+1}}{\left(y+1\right)\left(b-a\right)}\right\} \right)\\ &-\sum_{t}^{T}{D}_{t}\left({p}_{mt},w\right)w+\sum_{t\left(t>1\right)}^{T}\sum_{{i}_{t}}^{{I}_{t}-1}{D}_{{i}_{t}}\left({p}_{r{i}_{t}},w\right)\left\{C{[\left({i}_{t}{x}_{m}+w\right)}^{\beta }+{i}_{t}^{\beta }{x}_{m}^{\beta }\right\}\\ &-\sum_{t}^{T}{A}_{t}{Q}_{t}-\sum_{t}^{T}\sum_{j}^{J}{C}_{jt}{y}_{jt}\\ &-\sum_{t=1}^{T}{h}_{t}\left\{\frac{\left({IF}_{t}+{D}_{t}\left({p}_{mt},w\right)-{D}_{rt}\left({p}_{rt},w\right)+{IS}_{t}\right){T}_{t}}{2}+\left(b-{T}_{t}\right){IF}_{t}\right\}\end{aligned}$$

$$Subject To:$$

$${IF}_{t-1}={IS}_{t} \quad \forall t (t {>}1)$$

$${IF}_{t}={IS}_{t}+{Q}_{t}+\sum_{t>1}^{T}R({v}_{t},x)-{D}_{t}\left({p}_{mt},w\right)-{D}_{rt}\left({p}_{rt},w\right) \forall t$$

$${D}_{rt}\left({p}_{rt},w\right)\le {R}_{t}\left({v}_{t},x\right)+\sum_{{t}^{^{\prime}}=1}^{t-1}\left({R}_{{t}^{^{\prime}}}\left({v}_{t},x\right)-{D}_{r{t}^{^{\prime}}}\left({p}_{r{t}^{^{\prime}}},w\right)\right) \forall t (t>1) (19)$$

$${D}_{t}\left({p}_{mt},w\right)\le {Q}_{t}+\sum_{{t}^{^{\prime}}=1}^{t-1}\left({Q}_{{t}^{^{\prime}}}-{D}_{{t}^{^{\prime}}}\left({p}_{m{t}^{^{\prime}}},w\right)\right) \forall t$$

$${Q}_{t}\le \sum_{j}^{J}{Ac}_{j}{y}_{jt}+M \quad \forall t$$

$$a-\left({I}_{t}+1\right){x}_{m}\ge 0\quad \forall t$$

$$b-\left({I}_{t}+1\right){x}_{m}\ge w\quad \forall t$$

$${{{IF}_{t},{IS}_{t},Q}_{t},{T}_{t},{v}_{t},{p}_{rt},{p}_{mt},w,{I}_{t},{y}_{jt}\ge 0;I}_{t}\epsilon integer, {y}_{jt}\epsilon binary$$

4 Solution approaches

The proposed model in this study is a direct extension of the non-linear form of the proposed model by Yazdian et al. (2016). According to their investigation, the non-linear form of their model is one type of geometric program that becomes daunting to solve by increasing the size of the problem. Since this study improved their assumptions to adapt for real applications, it increases the inherent complexity making the problem difficult to solve. Moreover, most integer non-linear programming problems are called NP-complete with computational complexity (Tian et al. (1998)). In these problems, whatever the size of the problem increases, exact solutions become computationally intractable (D’Ambrosio (2010)). In this respect, since the proposed model is a mixed-integer non-linear non-convex mathematical problem with inherent complexity, metaheuristic algorithms are required to deal with NP-hardness. For this purpose, three metaheuristic algorithms have been suggested which were known as efficient algorithms in dealing with tough optimization problems namely genetic algorithm (GA), particle swarm optimization (PSO) algorithm, and Invasive Weed Optimization (IWO). The steps of proposed algorithms are described in detail as follows:

4.1 Solution representation

4.1.1 Encoding strategy for initialization

To promote the efficiency of three proposed algorithms, an encoding strategy is expressed as follows:

Step 1. Binary variable ${y}_{jt}$ is randomly generated to initialize the population of the problem. Besides, variable ${P}_{mt}$ is randomly generated in the intervals presented in Tables 3 and 4, and is considered as an upper bound for variable ${P}_{rt}$.

Table 3 Detailed information about S/N ratios for IWO

Table 4 Literature review

Step 2. Variable ${I}_{t}$ is generated in such a way to meet the following conditions.

Step 3. In this step, demands for manufactured and repaired products are generated based on the following conditions. By applying these conditions, constraints (13)–(14) can be met.

$${D}_{t}\left({p}_{mt},w\right)=Max\left(Min\left({D}_{mt}{ p}_{mt}^{-\alpha }\left({w}^{\theta }\right),{D}_{t-1}\left({p}_{mt-1},w\right)\right),0\right),$$

(20)

$${D}_{rt}\left({p}_{rt},w\right)=Max\left(Min\left(d{ p}_{rt}^{-\alpha }\left({w}^{\theta }\right),{D}_{rt-1}\left({p}_{rt-1},w\right)\right),0\right);,$$

(21)

Step 4. In this step, the quantity of production, the beginning inventory level, and the inventory at the end of periods are initialized.

Step 4.1. The production quantity in the first period is generated in the interval $({D}_{t}({p}_{mt},w), \sum_{j}^{J}{Ac}_{j}{y}_{jt}+M)$ (where $t$ is equal to 1). This approach prevents deficiency and meets the constraint (15).

Step 4.2. After calculating the total production in the first period, the demand of the customer should be satisfied. Thereafter, the extra amount of the products should be calculated as inventory at the beginning of the next period. Production quantity for other periods is generated between demand rate and total capacity with deduction of the inventory. Then, the amount of inventory for each period is updated.

Step 4.3. The time elapsed to produce ${Q}_{t}$ products is calculated from $\frac{{Q}_{t}}{pr}$.

Step 5. First, the variable ${V}_{t}$ is generated based on the Eqs. (22), (23), then ${R}_{t}\left({v}_{t},x\right)$ is calculated.

$$r=k\frac{{b}^{y}+{a}^{y+1}}{(b-a)(y+1)},$$

(22)

$${V}_{t}=unifrnd\left({\left(\frac{{D}_{rt}\left({p}_{rt},w\right)}{r}\right)}^{\frac{1}{\partial }},{\left(\frac{{D}_{t-1}}{r}\right)}^{\frac{1}{\partial }}\right).$$

(23)

4.2 Genetic algorithm (GA)

GA is a metaheuristic optimization algorithm developed by Holland (1975) and emanated from population genetics including heredity, gene frequencies, and evolution. GA is known as a powerful metaheuristic algorithm to find near-optimal solutions for many non-linear problems (He et al. (2013)) and is used to solve many engineering problems (Azimi et al. (2018)). GA superiorly performs to solve CLSC models (Guo et al. (2019)). In consideration of GA’s profitability to cope with complex problems, it has been applied in many papers in the supply chain context that some of which are Ma and Li (2018), Hassanpour et al. (2019), Chan et al. (2020), Chouhan et al. (2020), Guo et al. (2020), Mohtashami et al. (2020), Liao et al. (2020), Ren et al. (2020), Son et al. (2020), Hemmati and Pasandideh (2020).

Base on the above discussion, GA is employed in this paper as a baseline method. The steps of GA are provided and briefly explained as follows:

4.2.1 Initial population generation

Generally, each solution in this algorithm is a chromosome generated with a size of ${N}_{pop}$ to create a population.

4.2.1.1 Selection strategy

There are several strategies to select parents, some of which are rank selection strategy, random selection strategy, tournament selection strategy, and roulette wheel selection strategy. According to the investigation done by Jebari and Madiafi (2013), the limitations and advantages of these approaches are as follows.

• Roulette wheel selection strategy is a linear search method that can be easily implemented with less computational time, however, it may be trapped into local optimal.

• Rank selection strategy is similar to Roulette wheel selection strategy with robust performance. However, this strategy has a lower convergence.

• Tournament selection strategy selected parents by preserving diversity in population, implying the low speed of convergence.

• Random selection is an easy implemented strategy to select the parent by preserving diversity.

In this paper, the roulette wheel selection strategy for crossover operators outperforms others in small size instances with less computational time. Therefore, we applied it to select parents in all instances.

4.2.2 Crossover operators

4.2.2.1 Single point crossover operator

In this step, parents are selected via a roulette wheel selection strategy. In this strategy, a proportion of each wheel is assigned according to its fitness. In maximization problems, fitness has a direct relationship with the objective function value. After spinning the roulette wheel, a parent is selected.

For the discrete variables of the proposed model, the single-point crossover is applied shown in Fig. 3. The basis of this operator is to select a single point along with the parent genes. Then the genes of the right hand of one parent are replaced with the other. As a result, two offspring would be generated.

Fig. 3

Single point crossover operator for discrete chromosomes

4.2.2.2 Arithmetic crossover

For the continuous variables of the proposed model, we handle the arithmetic crossover where a uniform random number like $\theta$ is generated between (0, 1), and then the offspring are obtained as follows:

$$\mathrm{Offspring}1\hspace{0.17em}=\hspace{0.17em}(\mathrm{parent}1\times \theta +\mathrm{ parent}2\times (1-\theta ),$$

(24)

$$\mathrm{Offspring}2\hspace{0.17em}=\hspace{0.17em}(\mathrm{parent}2\times \theta +\mathrm{ parent}1\times (1-\theta ).$$

(25)

4.2.3 Mutation operators

4.2.3.1 Swap mutation

In the mutation operator for selecting the parent, the random selection method is used. Then for the discrete variables, the swap operator is applied as shown in Fig. 4. Indeed, two points are selected along with the genes of chromosomes, then they are replaced with each other.

Fig. 4

Swap mutation operator for discrete chromosomes

4.2.3.2 Arithmetic mutation

To do the mutation operation on the continuous variables, first, a uniform random number is generated ($p$). Then the standard deviation is obtained from Eq. (26). In this equation, $MaxV$ is the upper bound and $MinV$ is the lower bound of the parent.

$$\sigma =p*\left(MaxV-MinV\right).$$

(26)

Then, new offspring is obtained as follows:

$$offspring=parent+\sigma *\left(randn\right),$$

(27)

where $randn$ is a parameter generated based on the normal distribution.

4.2.4 Stopping criteria

The algorithm continues until it reaches a specified maximum iteration denoted by ${Max}_{ iteration}$.

4.3 Particle swarm optimization (PSO) algorithm

PSO is a powerful metaheuristic algorithm initially proposed by Eberhart and Kennedy (1995) to solve the problem in a continuous search space, relying on the movement and intelligence of swarms. According to Harifi et al. (2020) and Alejo-Reyes et al. (2021) PSO is known as one of the most widely used metaheuristic algorithms to solve complex problems. PSO has been successfully used in many NP-hard problems and applied in many engineering problem due to its special characteristics such as Mojtahedi et al. (2019). PSO has quick and accurate search, fast convergence, the balance between exploration and exploitation, and competent performance (Yu et al. 2017; Tirkolaee et al. 2019). To confirm these, it can be found in research done by Yaseen et al. (2019) that they used several metaheuristic algorithms among which PSO leads to better performance. Moreover, Guo and Ya (2015), Yazdian et al. (2016), Guo et al. (2017), Guo et al. (2019), and Guo et al. (2020) have utilized PSO algorithm to solve reverse logistics problem.

The essential intention of PSO is to accelerate each particle toward its local best position (${x}_{ibest}$) and the global best position of the swarm (${x}_{gbest}$) with a random weighted acceleration at each step. Since the proposed model is a mixed-integer non-linear problem, for discrete variables an Integer particle swarm optimization is applied (Del Valle et al. 2008). In this situation, discrete variables should be generated. To do this, the particles round off to the nearest discrete values.

The basic principle for PSO: we assume that ${X}_{i}=({x}_{i1}, {x}_{i2}, {x}_{i3}, \dots , {x}_{in} )$ is the current position of particle$i$, ${V}_{i}=({v}_{i1}, {v}_{i2}, {v}_{i3}, \dots , {v}_{in} )$ is the current velocity of particle$i$, ${P}_{i}=\left({p}_{i1}, {p}_{i2}, {p}_{i3}, \dots , {p}_{in}\right)$ is the best position of particle$i$. Indeed, ${P}_{i}$ is the personal best position of particle $i$ in the current iteration ($k$) and based on the Eq. (28), it will be updated in each iteration.

$$if f\left({p}_{i}^{k-1}\right)<f\left({x}_{i}^{k}\right) \to {p}_{i}^{k}={x}_{i}^{k}.$$

(28)

For the best group position, the best objective function between particles is selected in each iteration (${g}^{k}$) and will be updated based on Eq. (29).

$$if f\left({g}^{k-1}\right)<f\left({x}_{i}^{k}\right) \to {g}^{k}={x}_{i}^{k}.$$

(29)

The particle velocity will be updated according to the Eq. (30).

$${V}_{i}^{k+1}=w{V}_{i}^{k}+{c}_{1}{r}_{1}\left({p}_{i}^{k}-{x}_{i}^{k} \right)+{c}_{2}{r}_{2}\left({g}^{k}-{x}_{i}^{k}\right),$$

(30)

where ${V}_{i}^{k}$ represents the velocity of particle $i$ in iteration $k$ that should be generated within the interval $\left[-{V}_{max}, {V}_{max}\right]$ to prevent moving outside of the solution space, and $w$ is the inertia weight affecting the balance between exploitation and exploration of the PSO algorithm. In addition, ${c}_{1}$ and ${c}_{2}$ are cognitive acceleration and social acceleration factors, ${r}_{1}$ and ${r}_{2}$ are random numbers between (0, 1). By the use of Eq. (31), the new location of each particle will be updated in each iteration.

$${x}_{i}^{k+1}={x}_{i}^{k}+{V}_{i}^{k+1}.$$

(31)

It is clear the proposed algorithm is not appropriate for solving the binary particles. Thus, we used the procedure proposed by Jordehi (2019). This is the extended version of binary PSO presented by Kennedy and Eberhart (1997). In this binary PSO algorithm, a strategy is used to switch between 0 and 1. Therefore, Eq. (32) is used for this purpose.

$$TF\left({V}_{i}^{k}\right)=\left\{\begin{array}{l}{(\frac{{V}_{i}^{k}}{0.5{V}_{max}})}^{2}\, if\, {V}_{i}^{k}<0.5{V}_{max}\\ 1 if {V}_{i}^{k}>0.5{V}_{max}\end{array}\right..$$

(32)

Then the binary particle’s position is updated as follows:

$${x}_{i}^{k+1} =\left\{\begin{array}{l}\stackrel{-}{{x}_{i}^{k}}\, if\, rand<TF\left({V}_{i}^{k}\right)\\ {x}_{i}^{k} \,otherwise\end{array}\right.,$$

(33)

where $rand$ is a parameter randomly generated between 0 and 1, and $\stackrel{-}{{x}_{i}^{k}}$ represents the complement of binary particle ${x}_{i}^{k}$. In this paper, the optimal value of the model is to maximize the total profit of the proposed CLSC model. Hence, after each iteration, the particle's velocity and position should be controlled to verify and the solution procedure will continue until it reaches the stop criterion. Figures 5 and 6 represent the pseudocode and the flowchart of the proposed PSO algorithm, respectively.

Fig. 5

Pseudocode for the proposed PSO algorithm

Fig. 6

Flowchart of PSO algorithm

4.4 Invasive weed optimization (IWO) algorithm

IWO was introduced by Mehrabian and Lucas (2006), and inspired by the colonization behavior of weeds. The performance of IWO in solving many optimization problems has been taken into consideration by many researchers due to its specific characteristics such as spatial dispersal of plants, reproductive traits, and competitive exclusion (Abu-Al-Nadi et al. 2013). Besides, the efficiency and effectiveness of IWO have been measured in many recent works. For example, Niknamfar and Niaki (2018) solved their proposed model by the use of GA and IWO algorithms, concluding IWO accomplishes better than GA. Jahangir et al. (2019) applied both GA and IWO to solve their MINLP model that results indicate IWO has better convergence than GA. Goli et al. (2019) have proposed IWO algorithm for solving a multi-objective problem, and compared the obtained results from IWO with a non-dominated sorting genetic algorithm. The results in IWO are more favorable in terms of computational time and accuracy. Rahmani et al. (2020) utilized several metaheuristic algorithms among which IWO Performs better than others.

According to the above investigation, IWO algorithm is applied to solve the proposed MINLP model in this paper. The steps of IWO algorithm will be described in detail in the following and the related pseudocode is given in Fig. 7.

Fig. 7

Pseudocode for the proposed IWO algorithm

4.4.1 Initialization

First, a certain number of seeds are randomly generated to spread out over the search area in the feasible solution space.

4.4.2 Reproduction

Each weed reproduces a certain number of seeds based on its fitness. The number of seeds (${w}_{i}$) is calculated with respect to the best obtained fitness (${F}_{best}$), worst obtained fitness (${F}_{worst}$), minimum allowed number of seeds (${S}_{min})$, maximum allowed number of seeds (${S}_{max})$, and its fitness value ${(F}_{i})$. That is presented in Eq. (34).

$${w}_{i}=\frac{{F}_{i}-{F}_{worst}}{{F}_{best}-{F}_{worst}}\left({S}_{max}-{S}_{min}\right)+{S}_{min}.$$

(34)

4.4.3 Spatial dispersal

In this step, each newly generated seed should be dispersed over the feasible search space which is near the current weed using a normal distribution (N(0, ${\sigma }^{2}$). In this context, moves start from the initial standard deviation (${\sigma }_{init}$) and reduce to the final value (${\sigma }_{final}$). This non-linear motion is calculated based on Eq. (35) to perform the current standard deviation in each iteration (${\sigma }_{current}$).

$${\sigma }_{current}=\frac{{({iter}_{max}-iter)}^{n}}{{({iter}_{max})}^{n}}({\sigma }_{init}-{\sigma }_{final})+{\sigma }_{final},$$

(35)

where ${iter}_{max}$ is the maximum number of iterations, and n is the nonlinear modulation index.

4.4.4 Competitive exclusion

Finally, the abovementioned steps are repeated for building a union colony of weeds and eliminate undesirable solutions until the maximum number of iteration is reached. Besides, to generate discrete solutions by IWO algorithm, obtained solutions should round off to the nearest discrete values. For the binary invasive weed optimization, we utilized the procedure proposed by Veenhuis (2010). Figure 8 shows the flowchart of IWO algorithm.

Fig. 8

Flowchart of IWO algorithm

5 Numerical experiments

In this section, numerical test problems are presented with different sizes to depict the performance of the proposed algorithms and the application of the new CLSC model. Parameters are randomly generated in a predefined interval based on the experience of experts and related papers such as Yazdian et al. (2016) that can be seen in Tables 3 and 4. Two sets of test problems are proposed to evaluate the performance of the model under the different parameters of the Weibull distribution function, and the interval of uncertainty for the average product lifetime.

For the small size in both sets, the model is executed by GAMS 27.2.0 software using BARON solver proposed for MINLP model to validate solutions obtained by IWO, PSO, and GA algorithms (See Appendix 2). The small size instances include {(4, 4), (4, 5), (5, 5), (5, 6)} for installation capacity, and time period indices. Then for the medium and large sizes of instances, the model is executed ten times for each test problem by MATLAB 2016 software and used a computer with Core i7 CPU and 8 GB RAM. The medium and large sizes of the test problems include {(6, 6), (6, 7), (6, 8), (6, 9), (7, 9), (7, 10), (7, 10), (7, 11), (7, 12), (7, 15), (7, 16), (7, 17)} for the installation capacity and time period indices.

The validation procedure is designed for the small scale and results are summarized in Table 5.

Table 5 Description of the notations

In these cases, the optimal objective values are obtained from BARON solver with increasing computational time and an average of 656.17 s, while for three GA, PSO, and IWO are 19.49, 9.45, and 42.71 s, respectively. Furthermore, the percentage relative error (PRE) is used to compare the solution quality of applied aforementioned metaheuristic algorithms with their corresponding optimal values.

$$PRE=100\times \frac{{SOL}_{O}-{SOL}_{M}}{{SOL}_{O}},$$

(36)

where ${SOL}_{M}$ and ${SOL}_{O}$ are objective function values obtained from solving each test problem by any metaheuristic algorithm, and its corresponding optimal values obtained from BARON solver. In this regard, the results show the average PRE values for GA, PSO, and IWO are 0.04, 0.07, and 0.04, respectively. There are no significant differences between applied algorithms and their corresponding optimal values. Therefore, it can be confirmed that good quality solutions are obtained from each algorithm in small size test problems. Since the problem cannot be solved in reasonable computational time for the medium and large sizes of instances, metaheuristic algorithms are used, and compared in terms of objective function values and required CPU-times. For this purpose, the RPD values are calculated from Eq. (37) for each algorithm.

$$RPD=70\%\frac{\left({SOL}_{bes}-{SOL}_{M}\right)}{{SOL}_{best}}+30\%\frac{\left({COM}_{M}-{COM}_{best}\right)}{{COM}_{best}},$$

(37)

where ${SOL}_{M}$ denotes the objective function value obtained from solving each test problem by each proposed metaheuristic algorithm and ${SOL}_{best}$ is the best of them. Also,${COM}_{M}$ and ${COM}_{best}$ are the computational times for each algorithm and the minimum computational time among them.

5.1 Parameter setting and calibration

The Taguchi method is applied for calibration of the main parameters in metaheuristic algorithms and was used in many recent research papers. This method designs based on orthogonal arrays to deal with noise and control factors with less number of experiments compared to full experiments. Therefore, signal to noise $(S/N)$ ratio is applied to applicably calibrate the parameters of suggested algorithms and is calculated from Eq. (38) with the aim of maximizing the (S/N) ratio.

$$\left(S/N\right)=-10 log\left(\frac{S\left({Y}^{2}\right)}{n}\right),$$

(38)

where Y is the response variable and n is the number of orthogonal arrays.

Thereafter, (S/N) ratios are calculated by Minitab software for GA, PSO and IWO algorithms. Based on the obtained results, ${L}^{9}$,${L}^{9}$, and ${L}^{27}$ designs are performed for GA, PSO and IWO algorithms, respectively. (See Appendix 3).

Figures 9, 10 and 11 show S/N ratio plots for GA, PSO, and IWO algorithms, respectively. The optimal levels of all parameters are reported in Table 6.

Fig. 9

S/N ratio plots of GA

Fig. 10

S/N ratio plots of PSO

Fig. 11

S/N ratio plots of IWO

Table 6 The first set of the numerical test problems

Table 7 illustrates the average values of the objective function and computational time obtained from solving ten times each instance employing the metaheuristic algorithms. The results are graphically compared and can be seen in Figs. 12 and 13. In this respect, the computational time takes 28.11, 13.8, and 87.13 s for GA, PSO, and IWO, respectively. That indicates PSO outperforms GA and IWO in terms of computational time. While average objective function values for GA, PSO, and IWO are equal to 1,483,763, 1,464,912, and 1,486,073, respectively. The results illustrate that IWO performs better than others in terms of objective function values.

Table 7 The second set of the numerical test problems

Fig. 12

Comparison of the values of the objective function between three metaheuristic algorithms

Fig. 13

Comparison of required CPU-time between three metaheuristic algorithms

Table 8 shows the average values of RPDs based on the objective function values and computational times under the weights of 0.7 and 0.3, respectively. The results return the average RPDs for GA, PSO, and IWO which are 78.76, 3.59, and 154.21, respectively.

Table 8 Comparative results to assess the performance of GA, PSO, and IWO and their corresponding optimal values

To evaluate the performances of the proposed algorithms and compare them in terms of both objective function values and computational times, first, the normality of all RPDs were checked by the Anderson–Darling test. In all cases, at the 0.05 significance level, the normality of metrics was not rejected. Then “One-Way Analysis of Variance” (ANOVA) was applied. The results were summarized in Table 9, wherein the null hypothesis of equality of the mean of RPDs was investigated at the 0.95 confidence level. The results indicate that P-Value was obtained zero which was less than the significance level (0.05). That means there are significant differences between the obtained results from used algorithms.

Table 9 Optimal levels of all parameters for GA, PSO and IWO algorithms

In order to compare the algorithms pairwise, Tukey’s comparison test was utilized. The results are reported in Table 10 showing significant differences. Accordingly, PSO superiorly performed better than IWO and GA.

Table 10 Comparative results to assess the performance of GA, PSO, and IWO

5.2 Sensitivity analysis

The results in Table 10 indicate that the PSO outperformed GA and IWO in terms of objective function values and required CPU-times. Hence, PSO is used for sensitivity analysis of the main parameters for an instance with 6 available installation capacities and 9 time periods. Therefore, 20% decreasing and increasing are performed on the parameters at one time when the others remain constant. These parameters are the lower and upper bounds of product’s age ($a$ and $b$), parameter to upgrade the age of returned products (${x}_{m}$), maximum available capacity ($M$), cost of manufacturing new products (${A}_{t}$), inventory holding cost (${h}_{t}$). Figure 14 illustrates how the changes in parameters affect objective function values.

Fig. 14

The changes in the different terms of the objective function values obtained from the sensitivity analysis of the main parameters

In the following, observations are derived from sensitivity analysis:

• Lower bound of products age ($a$): A 20% decrease in parameter $a$ affects the profits from the repair process and total warranty costs. Decreasing in parameter $a$ causes a 29% increase in profits obtained by the repair process and a 35% increase in total warranty costs. Besides, a change in parameter $a$ can indirectly affect the acquisition costs with significant changes.

• Upper bound of products age ($b$): The efficiency of a 20% increase in the parameter $b$ is more evident in profits obtained from the repair process and total inventory costs. Wherein, this increase leads to a 7% decrease in total inventory holding costs and a 3% increase in profits from the repair process. Moreover, a 20% decrease in parameter $b$ can lead to a significant reduction in total warranty costs which is approximately 43%, and also a 59% reduction in acquisition costs.

• The parameter of upgrading the returned products (${x}_{m}$): A 20% decrease in ${x}_{m}$ would increase profits obtained from the repair process and increase the acquisition costs and warranty costs.

• Maximum available capacity ($M$): Changes in parameter $M$ have significantly direct effects on the inventory holding costs. Also, a 20% increase in $M$ affects manufacturing costs, installation; wherein, installation costs are reduced, and total manufacturing costs are increased.

• Cost of manufacturing new products (${A}_{t}$): Changes in ${A}_{t}$ have significant effects on inventory holding costs. A 20% increase in ${A}_{t}$ leads to a 29% decrease in inventory holding costs. Also a 20% increase in ${A}_{t}$ leads to a 18% increase in total manufacturing costs.

• Inventory holding cost (${h}_{t}$): A 20% increase in ${h}_{t}$ leads to a 42% decrease in total inventory holding costs.

The sensitive parameters regarding the proposed model are the inventory holding cost and the acquisition cost and the least sensitive parameter is the production cost. Finally, the changes in the objective function values are evaluated and presented in Tables 11 and 12.

Table 11 Comparative RPDs to assess the performance of GA, PSO, and IWO

Table 12 Results of One-Way Analysis of Variance (ANOVA) to compare GA, PSO, and IWO

The objective values are moderately sensitive by changing the parameters $b$, $a$, and ${x}_{m}$. Furthermore, the other changes slightly affect the objective function values.

6 Managerial insights

In manufacturing industries, the increasing amount of waste of used products with different types and quality has been a concern for companies. Broadly, many discarded products are of satisfactory quality throughout their return life cycle that can be reused after some recovery process. Repairing products is a process to transform products into the working condition that may bring profitability and sustainability for supply chains. There are several approaches carried out to upgrade the repairable products and put them into the functional states, among which the virtual age approach can be used to extend the life of products (Pérez Ramírez and Utne 2013). By applying this approach, the age of products decreases after each upgrade action. That means the repair process can extend the durability of defective products even with quality degradations. This approach can be applied in electronic industries especially for wearing-out systems (Dijoux 2009). Although the repair process makes some discarded products reusable, they are not as good as new products. Therefore, it is necessary to determine a proper strategy as a key for motivating customers to buy second-hand products. Offering a proper warranty policy and product price can be considered as effective strategies to increase demands and bring profits to the system, simultaneously (Tables 13, 14).

Table 13 Results of Tukey’s comparison test

Table 14 The obtained results from sensitivity analysis

On the other hand, there are some other critical factors affecting the performance of a CLSC problem. Inventory management is one of the critical challenges owing to increasing obsolete products and declining values of them that can efficiently control the flows of the forward and backward chain (Gan et al. 2017). To obtain optimal flows in a CLSC, not only a proper control and management of inventories should contribute to this aim, but also the production capacity planning needs to be optimized.

All these raised issues have been investigated in this paper. To do this, a multi-period CLSC problem has been proposed with the aim of maximizing the system profits considering inventory management and production capacity planning. Besides, a warranty period and price-dependent demand were suggested in a non-linear formula to be more adapted to real situations. To model the return rate of used products, a nonlinear expression was proposed depending on the acquisition costs and age of returns. In this paper, a virtual age approach was utilized to approximate the age of returns after each upgrade action. These would be valuable for managing a CLSC problem by recovering used products under satisfactory quality.

7 Conclusion and future directions

In this paper, a multi-period closed-loop supply chain is proposed with the aim of maximizing the total profit of the system. It is assumed that the reused products will be recovered until they pass the desired qualification.

Owing to the virtual age of the product, a new product has an initial age by uniform distribution, and if it breaks down in this period of time, it will be repaired to upgrade its age. In this case, the company has the ability to meet customer demands for the repaired products.

Moreover, in this paper, demands are defined as a nonlinear function of the selling price and the warranty length period, and the rate of returns is as a nonlinear function of acquisition cost and age of products. The aim of this paper is to make appropriate decisions on the number of times that used products can be returned to the system, the warranty contract for products, selling prices, and production quantity. For this purpose, additional capacity can be installed to maximize the production capacity of the plant. Owing to the complexity of the proposed MINLP model, we applied three metaheuristic algorithms GA, PSO, and IWO. Afterward, numerical examples are executed by using MATLAB software. The results of methods are compared in terms of the objective function values and required CPU-time. By applying the RPDs, the results of the objective function and CPU-time are normalized and weighted. Then, ANOVA is used to evaluate the best performing methods by testing the null hypothesis which is equality of the mean of RPDs for methods. In this problem, PSO has the best performance compared with other applied methods. Finally, sensitivity analysis is done to show the effects of the main parameters of the problem on the value of the objective function to obtain some managerial insights. The results in the sensitivity analysis revealed that the objective values are moderately sensitive by changing the lower and upper bounds of the age of products and their upgrading level.

For future directions, the following suggestions can be undertaken:

• Considering discounts to motivate customers to bring back their used products.

• Extending multi-level CLSC problem including collector, retailers, etc.

• Considering the environmental and social impacts of the proposed CLSC problem.

• Considering uncertain conditions in some parameters of the model such as the capacity of production.

• Modeling the shortages can be considered as an interesting modification to more adapt to different situations.

Appendices

Appendix 1

$${R}_{total}=\sum_{t>1}^{T}\left\{ {\int }_{a-{i}_{t}{x}_{m}}^{b-{i}_{t}{x}_{m}}R\left({v}_{t},x\right)f\left(x\right)dx\right\}$$

$${\varvec{t}}=2$$

$${\varvec{i}}{\varvec{f}} i=1\to R(t=2)={kv}_{1}^{\partial }\frac{{b}^{y+1}-{a}^{y+1}}{(b-a)(y+1)}$$

$${\varvec{t}}=3$$

$${\varvec{i}}{\varvec{f}} i=1\to R\left({i}_{t}\right)={kv}_{1}^{\partial }\frac{{\left(b-{x}_{m}\right)}^{y+1}-{\left(a-{x}_{m}\right)}^{y+1}}{\left(y+1\right)\left(b-a\right)}$$

$${\varvec{i}}{\varvec{f}} i=2\to R\left({i}_{t}\right)={kv}_{2}^{\partial }\frac{{b}^{y+1}-{a}^{y+1}}{(b-a)(y+1)}$$

$${\varvec{t}}=4$$

$${\varvec{i}}{\varvec{f}} i=1\to R\left({i}_{t}\right)={kv}_{1}^{\partial }\frac{{\left(b-{2x}_{m}\right)}^{y+1}-{\left(a-2{x}_{m}\right)}^{y+1}}{\left(y+1\right)\left(b-a\right)}$$

$${\varvec{i}}{\varvec{f}} i=2\to R\left({i}_{t}\right)={kv}_{2}^{\partial }\frac{{\left(b-{x}_{m}\right)}^{y+1}-{\left(a-{x}_{m}\right)}^{y+1}}{\left(y+1\right)\left(b-a\right)}$$

$${\varvec{i}}{\varvec{f}} i=3\to R\left({i}_{t}\right)={kv}_{3}^{\partial }\frac{{b}^{y+1}-{a}^{y+1}}{(b-a)(y+1)}$$

$${{\varvec{i}}}_{{\varvec{t}}}={\varvec{t}}-{\varvec{i}}-1$$

$${R}_{total}=\sum_{t(t>1)}^{T}\left(\sum_{{i}_{t}}^{{I}_{t}} {kv}_{{i}_{t}}^{\partial }\left\{\frac{{(b-{i}_{t}{x}_{m})}^{y+1}-{(a-{i}_{t}{x}_{m})}^{y+1}}{(y+1)(b-a)}\right\}\right)$$

$${R}_{total}=\sum_{t(t>1)}^{T}\left(\sum_{i=1}^{t-i-1\le {I}_{t}} {kv}_{{i}_{t}}^{\partial }\left\{\frac{{(b-(t-i-1){x}_{m})}^{y+1}-{(a-(t-i-1){x}_{m})}^{y+1}}{(y+1)(b-a)}\right\}\right).$$

Appendix 2

In order to solve the model by GAMS software using BARON solver, it should be noted that ${I}_{t}$ is an integer variable and must be transformed into a parameter. For that, we proposed the following procedure:

$$t-i-1\le {I}_{t}+Big{x}_{it} \forall i,t$$

$${kv}_{{i}_{t}}^{\partial }\left\{\frac{{(b-{i}_{t}{x}_{m})}^{y+1}-{(a-{i}_{t}{x}_{m})}^{y+1}}{(y+1)(b-a)}\right\}\le {Big(1- x}_{it}) \forall i,t$$

$${D}_{{i}_{t}}({p}_{r{i}_{t}},w)\left\{C[{\left({i}_{t}{x}_{m}+w\right)}^{\beta }+{i}_{t}^{\beta }{x}_{m}^{\beta }\right\}\le {Big(1- x}_{it}),$$

where ${x}_{it}$ is an auxiliary variable; equals 1 if produced products in period $i$ can be returned and repaired in period $t$.

Appendix 3

Tables 1, 2 and 3 express the obtained results from implementing ${L}^{9}$, ${L}^{9}$ and ${L}^{27}$ designs GA, PSO and IWO algorithms, respectively.