Reasoning about group social commitments in multi-agent systems

Abstract

This paper aims to analayze and reason about group communicating social commitments in Multi-Agent Systems (MASs). In fact, this paper presents Computation Tree Logic Group Commitments ($\hbox {CTL}^{GC}$), a temporal logic of group commitments for agent communications which extends computation tree logic (CTL) to reason about group social commitments and their fulfillments simultaneously. To do so, we classify groups of communicating agents into divisible and indivisible. After that, we divide group commitments into two categories: one-to-group and group-to-one commitments. Then, we advocate the necessary social accessibility relations that are needed to capture the semantics of each type of group commitments. Thereafter, we use Benthem’s Correspondence Theory for modal logics to prove the soundness and completeness of the proposed $\hbox {CTL}^{GC}$ logic. Particularly, we present a set of reasoning postulates in $\hbox {CTL}^{GC}$ and correspond them to their related classes of frames. We use the NetBill protocol, a concrete example from business domain to illustrate each reasoning postulate. Furthermore, we adopt the interpreted systems as an underlying formalism over which our developed postulates are interpreted. When correspondence exists, this confirms that the $\hbox {CTL}^{GC}$ logic generated by any subset of the proposed postulates is sound and complete with respect to models that are built on the corresponding frames. By so doing, we provide a novel, consistent, formal and computationally grounded semantic to reason about group communicating social commitments and their fulfillments in MASs and prove the soundness and completeness of the proposed logic.

1 Introduction

One of the major aspects of Multi-Agent-Systems (MASs) is communication. Using communication, agents plan their actions and behaviors to reach their target goals (Khattabi et al. 2020). Moreover, autonomous and heterogeneous agents employ Agent Communication Languages (ACLs) to interact with each other and exchange messages (Dourlens et al. 2012; Dignum and Greaves 2000; Al-Saqqar et al. 2015). Consequently, there is a crucial need to develop a formal and consistent semantics for those ACLs (El-Menshawy et al. 2012; EL Kholy et al. 2017; Marey et al. 2015).

In the literature, there have been many frameworks developed to find standards for agent communications (Singh 1998; Dignum et al. 2007; El-Menshawy et al. 2012; Wozna-Szczesniak and Szczesniak 2018; EL Kholy et al. 2017; Singh 2000; Islam and Azim 2018). In fact, Searle’s speech acts theory (Searle 1969) was the first attempt to introduce a standard semantics for ACLs. This semantic, which is known as the mental approach, attempts to investigate and provide a reasonable trade off between some agent communication aspects like: Belief-Desire-Intention (BDI) (Acay et al. 2019). Furthermore, this approach considers communications as actions that should be carried out by agents to reach their target goals. However, mental techniques concentrate on interacting agents’ minds. In fact, these approaches assume that agents can figure out how others think (Singh 1998). Consequently, mental techniques fail to investigate whether a given agent behaves based on a specific semantics or not. Therefore, those techniques suffer from a well known problem called semantics verification (Wooldridge 2002). Further, mental approaches suffer from lack of interoperability among heterogeneous systems (Singh 1998).

To fix the aforementioned problems of ACL semantics, MAS community did a major shift towards social approaches (Singh 1998; Souri et al. 2019). In fact, new formal semantics for ACLs were carried out using social approaches (Alberti et al. 2004; Fornara et al. 2008; Yolum and Singh 2004; Agha and Palmskog 2018; Kouvaros et al. 2019; Souri et al. 2019, 2019; Telang et al. 2019). More concrete, social approaches employed social commitments to provide robust frameworks that model interactions between agents in MASs (Bentahar et al. 2010; Desai et al. 2009; Günay and Yolum 2013; Singh 2000; El-Menshawy et al. 2018; Drawel et al. 2018).

Social approaches for ACLs using social commitments have a set of actions called commitment actions. These actions represent different states of commitments, such as: creation, assignment, fulfillment, violation, delegation, release and cancellation (Singh 1999). Manipulating commitments and negotiating them gives commitment-based approaches a powerful capability and flexibility to express interactions between agents in MASs (Singh 1999; Christie et al. 2018).

Social commitments have been successfully used in many real applications, such as: specifying and verifying service composition contracts (Bataineh et al. 2017), verifying security protocols (Al-humaikani et al. 2019), modeling business process (Desai et al. 2009), introducing artificial institutions (Fornara et al. 2008), developing programming languages (Günay and Chopra 2018; Winikoff 2007), Web-based applications (Venkatraman and Singh 1999; Bentahar et al. 2013), Blockchain applications (Singh 2018), modeling, specifying and verifying multi-agent interaction protocols (Baldoni et al. 2010; Desai et al. 2007; Mallya and Singh 2007; Yolum and Singh 2004; Günay et al. 2019).

Several frameworks were introduced to formalize collective (group) commitments (Castelfranchi 1995; Garion and Cholvy 2007; Wright 2012; Boella et al. 2010). However, none of them classifies groups of agents. Furthermore, none of them addresses group-to-one social commitments and its fulfillment. In Castelfranchi (1995), Castelfranchi classified commitments into internal, social and collective. He defined internal commitment as a relationship between a given agent and its action. Furthermore, he considered social commitment as a relationship between two agents. Moreover, he defined the collective (group) commitments as “a set of agents is Internally committed to a certain intention and (usually) there is mutual knowledge about that,” which makes the definition closer to the mental approaches previously explained. The other frameworks followed the same approach of Castelfranchi (Castelfranchi 1995) in their formalism of collective commitments.

Moreover, Bozena Wozna-Szczesniak and Ireneusz Szczesniak in Wozna-Szczesniak and Szczesniak (2018) extended our work in El Kholy et al. (2015) and introduced a new real-time conditional and unconditional social commitment logic called (RTCTLC). In this work, the authors defined their semantics over the Duration Communication Interpreted System (DCIS), which is a system with an arbitrary integer duration on transitions. Such transitions allow them to model various levels of deadlines and minimize the extra verification work due to the use of unit measure steps. RTCTLC has the ability to express and reason about (conditional, unconditional and group) commitments with their fulfillments and real-time constraints. For group commitments reasoning, they only investigated one-to-group conditional and unconditional commitments and their fulfillments. Moreover, the authors did not address soundness and completeness of RTCTLC.

In this article, we introduce, $\hbox {CTL}^{GC}$, a new temporal logic which extends the branching time logic CTL (Clarke and Emerson 1981) with modalities to analyze and reason about unconditional single and group commitments and their fulfillments simultaneously. To do so, we adopt Communication Interpreted Systems (CIS) (Bentahar et al. 2012; El-Menshawy et al. 2012)—an extension of the interpreted systems formalism introduced in Fagin et al. (1995) to model MASs. Particularly, we use the modified version of CISs that we have redefined in Al-Saqqar et al. (2014). Moreover, we classify groups of interacting agents into divisible and indivisible groups. In case of divisible groups, every agent can make or receive a commitment. In this context, we investigate two types of group commitments (one-to-group and group-to-one). We provide the necessary accessibility relation for each type. On the other hand, using the notion of indivisible group of agents; there is one commitment either from or towards the group. Thus, we address such commitment in a similar way to one-to-one commitment. In this framework, we only consider Unconditional Communicative Social Commitments (UCSC). To express an UCSC, we use the following notation: $C_{i\rightarrow j}\varphi$ which means that an agent i, who makes the commitment (the debtor), commits towards agent j, who receives the commitment (the creditor), that ($\varphi$), the content of the commitment, holds (Bentahar et al. 2010). Some researchers used different notations (see for example: (Desai et al. 2007, 2009; Singh 2000), but with the same meaning.

Example 1

A merchant (merch) commits to deliver the requested goods to a customer (cust). This commitment can be expressed as follows: $C_{merch \rightarrow cust} \varphi$, where $\varphi$ means deliver the requested goods.

Based on the communicative commitments notation (Bentahar et al. 2012), we introduce the notation of group social commitments. In fact, the idea of communicative commitments can be expressed as follows: if agent i asks to communicate with agent j, i and j should share a communication channel. This channel represents a shared variable between them. In this context, a communication channel is established between i and j if they have a shared variable, whereas agent i fills the channel in the current state w and agent j receives the message in the possible state $w'$. Therefore, both agents will have the same value for the shared variable which shows that the message has been delivered from i to j. Based on that, in group social commitments, for agent i to communicate with group of agents $\varOmega$, a communication channel between i and every member in $\varOmega$, if $\varOmega$ is divisible, is shared. On the other hand, if $\varOmega$ is indivisible, only one communication channel between $\varOmega$ and i is shared and information is passed through the channel. The concept of divisible and indivisible groups will be explained later in Sect. 4. By doing so, we expand communicative social commitments from handling single (one-to-one) commitment into handling a group of commitments. Furthermore, we provide the necessary accessibility relations to express the different cases of group commitments. Consequently, we introduce an intuitive semantics for group social communicative commitments.

1.1 Motivations

Nowadays, in the current settings, plenty frameworks manage interactions between agents in MASs through social commitments (Agha and Palmskog 2018; Kouvaros et al. 2019; Souri et al. 2019, 2019; Telang et al. 2019; Bentahar et al. 2012; Günay and Yolum 2013). However, none of them classify group of agents. Moreover, there is no comprehensive framework that handles all aspects of group commitment at the same time (i.e., group-to-one and one-to-group). To motivate our study in capturing and reasoning about group social commitments, let us consider the following examples:

Example 2

Assume that a merchant promises to deliver the required goods to all its requesting customers.

Example 3

All tenants in our building promise the landlord to pay their rents before the fifth day of each month.

To reason about the cases in examples 2 and 3, we need a logic that can capture and reason about a group of commitments and their fulfillments simultaneously.

1.2 Paper contribution

In this paper, we aim to enrich the area of communicative social commitments from new perspectives. In particular, we aim to introduce a new consistent, formal and computationally grounded semantic to reason about group communicating social commitments and their fulfillments. In particular, we aim to:

Fig. 1

A schematic view of the proposed approach

• Classify group of agents into divisible and indivisible groups. In divisible group, each agent can perform or receive a commitment. Where, in the case of indivisible group, one commitment can be carried out from or towards the group (i.e., the whole group can be considered as one agent).

• Redefining the social accessibility relation to reason about group commitments and their fulfillments.

• Advocate a new temporal logic of group unconditional social commitments for agent communications, $\hbox {CTL}^{GC}$, which extends computation tree logic (CTL) with modalities to reason about group unconditional social communicating commitments and their fulfillments simultaneously.

• Developing a set of reasoning postulates to reason about group commitment and their fulfillments.

• Proving the soundness and completeness of $\hbox {CTL}^{GC}$ using correspondence theory (van Benthem 1984).

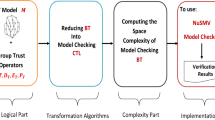
Figure 1 depicts the overall proposed approach.

1.3 Paper organization

The remainder of this paper is organized as follows. In Sect. 2, we illustrate the concept of interpreted systems (Fagin et al. 1995). After that, in Sect. 3, we explain the term “Frame Definability” that will be used later in proving the correspondence between the proposed set of reasoning postulates and certain class of frames. In Sect. 4, we first classify group of agents into divisible and indivisible. Then, we illustrate the necessary accessibility relations to handle one-to-group and group-to-one commitments. In Sect. 5, the syntax and semantics of the proposed $\hbox {CTL}^{GC}$ logic is demonstrated. In Sect. 6, the NetBill protocol is introduced as an application example. Then we develop a set of reasoning postulates to reason about group social commitments and their fulfillments and correspond them to their related classes of frames. After that, the soundness and completeness of $\hbox {CTL}^{GC}$ is proven using correspondence theory (van Benthem 1984). Finally, in Sect. 7, we present the conclusions and future directions.

2 Interpreted systems

Interpreted Systems (ISs) formalism was developed by Fagin et al. (1995) as a modeling tool to model the temporal evolution of synchronous and asynchronous MASs. Moreover, IS is exploited to model other types of agents such as autonomous and heterogeneous agents which communicate by exchanging messages (El-Menshawy et al. 2012).

IS formalism consists of a set of agents, ${AG} = \{ 1, \dots , n \}$. Every agent $i \in {AG}$ is characterized by a set of local states $LO_i$. The local state of each agent i is denoted by $lo_i \in LO_i$. At any given time, each local state has the agent complete information about the system. Every agent i owns a set of local actions $AC_i$ to reason about the temporal evolution of the MAS, and it also has a local protocol function $PR_i : LO_i \rightarrow 2^{AC_i}$ that defines the set of actions that could be carried out in a certain local state. $\tau _i$ is a local evolution function that identifies the transitions for a given agent i between its local states. The local evolution function $\tau _i$ is defined as follows: $\tau _i : LO_i \times AC_i \rightarrow LO_i$.

A given subset of the Cartesian product of all local states of n agents, $LO_1 \times \dots \times LO_n$, is the set of all global states GL in a given MAS. A global state $\mathfrak {gl} \in GL$ is a tuple $\mathfrak {gl} = ( lo_1, \dots ,lo_n)$ that shows a “snapshot” of MAS. For a given agent i, its local state in the global state $\mathfrak {gl}$ is denoted by $lo_i(\mathfrak {gl})$. $INT \subseteq GL$ is the set of initial global states. The global evolution function of MAS is denoted as: $\tau : GL \times ACT \rightarrow GL$, where $ACT = AC_1 \times \dots \times AC_n$ and each element $a \in ACT$ is a joint action, which is a tuple of actions. The set of atomic propositions is $\varPhi _p$. Finally, VL is a valuation function for those propositions such that ${VL}: GL \rightarrow 2 ^{\varPhi _p}$.

The original version of ISs formalism developed by Fagin et al. (1995) has been extended by Bentahar et al. (2012) and El-Menshawy et al. (2012). The extended version of IS allows us to reason about communicative social commitment (i.e., commitment established by communication between interacting agents in MAS). In particular, Bentahar et al. (2012) and El-Menshawy et al. (2012) introduced the notion of shared variables (i.e., interacting agents in MAS should share a communication channel (shared variable) in order to communicate and deliver messages between them). To do so, they assign a set of local variables $VAR_i$ for each agent $i \in {AG}$ . Interacting agents use these variables (communication channels) for sending and receiving messages. To have a shared variable between interacting agents i and j, $VAR_i \cap VAR_j \ne \emptyset$, indicates that there is a communication channel between the two agents. The value of a variable x in the set $VAR_i$ at local state $lo_i(\mathfrak {gl})$ is represented by $lo_i^x(\mathfrak {gl})$. For the shared variable $x \in VAR_i \cap VAR_j$, $lo_i^x(\mathfrak {gl})= lo_j^x(\mathfrak {gl})'$ means that the value of variable x for the agent i in $lo_i(\mathfrak {gl})$ is equal to the value of variable x for agent j in $lo_j(\mathfrak {gl})'$. If $lo_i(\mathfrak {gl}) = lo_i(\mathfrak {gl})'$, then $lo_i^x(\mathfrak {gl}) = lo_i^x(\mathfrak {gl})'$ for all $x \in VAR_i$. On the other hand, for the unshared variables (y), for all $y \in VAR_j - VAR_i$ we have $lo_j^y(\mathfrak {gl})=lo_j^y(\mathfrak {gl})'$.

The social accessibility relation introduced in Bentahar et al. (2012); El-Menshawy et al. (2012) has been redefined in our work (Al-Saqqar et al. 2014). In Al-Saqqar et al. (2014), we allow interacting agents to use their unshared variables also to communicate. The new definition captures the intuition that there exists some (shared variables) communication channels between agent i (the debtor) and agent j (the creditor). In other words, agent i sends the message via the channel in $(\mathfrak {gl})$, and agent j receives the message content in $(\mathfrak {gl})'$. After receiving the message, all the shared variables between the interacting agents should have the same values (i.e., $lo_i^x(\mathfrak {gl}) = lo_i^x(\mathfrak {gl})' = lo_j^x(\mathfrak {gl})'$$\forall x \in VAR_i \cap VAR_j)$.

The idea of shared and unshared variables is depicted in Figure 2, where two agents i and j are communicating using communication channel as follows: Agent i : $VAR_i$ = { $x_1, x_2, x_3, x_4$}; Agent j: $VAR_j$ = {$x_1, x_2', x_3',x_4'$}. The variable $x_1$ is the shared variable between the two interacting agents. The variables $x_2, x_3, x_4, x_2', x_3'$ and $x_4'$ are the unshared variables between i and j. When communication channel is created, the value of the shared variable $x_1$ for agent j in the global state $\mathfrak {gl}$ is modified to be equal to the value of variable $x_1$ for i in the global state $\mathfrak {gl}'$. This demonstrates the message passing via the shared channel (i.e., establishing a commitment).

Fig. 2

Typical social accessibility relation $\sim _{i \rightarrow j}$

The proposed model $\mathcal {M}$ is derived from the standard version of ISs (Fagin et al. 1995) and its extension in Al-Saqqar et al. (2014).

Definition 1

(Model of $\hbox {CTL}^{GC}$) A model $\mathcal {M}= (W, INT, R_t, \{ \sim _{i \rightarrow j} | {( i , j) \in {AG}^2} \}, {VL})$ is a tuple that belongs to the set of all models $\mathbb {M}$ , where:

• $W \subseteq LO_1 \times \dots \times LO_n$ is the set of reachable global states.

• $INT \subseteq W$ is a set of initial global states.

• $R_t \subseteq W \times W$ is the transition relation defined by $( w,w') \in R_t$ if and only if there exists a joint action $( a_1, \dots , a_n) \in AC$ such that $\tau (w, a_1, \dots , a_n) = w'$.

• For every pair $(i, j) \in {AG}^2$, $\sim _{i \rightarrow j} \subseteq W \times W$ is the social accessibility relation denoted by $w \sim _{i \rightarrow j} w'$ iff $VAR_i \cap VAR_j \ne \emptyset$ such that $\forall x \in VAR_i \cap VAR_j$ we have $lo_i^x(w) = lo_i^x(w') = lo_j^x(w')$.

• ${VL}: W \rightarrow 2 ^{\varPhi _p}$ is a valuation function.

3 Frame correspondence

Correspondence theory for modal logic (van Benthem 1984) investigates the relationship between a given classes of frames and modal languages (Al-Saqqar et al. 2016). To illustrate the idea of corresponding a class of frames to a given modal formulae, we recall the notion of frame correspondence. Similar to our work in Al-Saqqar et al. (2016), we first introduce frame, model, frame property and validity.

Definition 2

(Frame) A frame $\mathcal {FR}$ = (S, RE), where S is a nonempty set of states and RE is binary relation based on S. (Al-Saqqar et al. 2016).

Definition 3

(Model) Let $\mathcal {FR}$ = (S, RE) be a frame, a model $\mathcal {M}$ is based on the frame $\mathcal {FR}$ if $\mathcal {M} = ( \mathcal {FR}, \mathcal {VL})$ for a given valuation function $\mathcal {VL}$, where $\mathcal {VL}$ is defined as: $\mathcal {VL}: S \times \varPhi _p \rightarrow \{T,F\}$, and $\varPhi _p$ is a set of atomic propositions (Al-Saqqar et al. 2016).

Definition 4

(Frame Validity) Let $\mathcal {FR} = (S, RE)$ be a frame, a modal formula $\varphi$ is valid on $\mathcal {FR}$, defined by $\mathcal {FR} \models \varphi$, if $\mathcal {M}\models \varphi$ for all models $\mathcal {M}$ based on $\mathcal {FR}$. (Blackburn et al. 2006).

Remark 1

If a frame $\mathcal {FR}$ satisfies a certain formula $\varphi$, then $\mathcal {FR}$ satisfies every substitution instance of $\varphi$. Consequently, to prove that $\mathcal {FR} \nvDash \Box \varphi \rightarrow \varphi$, it is enough to prove that $\mathcal {FR} \nvDash \Box p \rightarrow p$ where p is any substitution instance of $\varphi$ (Huth and Ryan 2004).

Definition 5

(Frame Property) A frame $\mathcal {FR}$ = (S, RE) has property $P_r$ (e.g., serial or symmetric) with respect to a particular relation RE as long as RE has property $P_r$. (Al-Saqqar et al. 2016).

Therefore, we could have serial, symmetric, reflexive ... etc frames depending on the frame property.

4 Group social commitments

To introduce the notion of group communicative social commitment, let us consider the following motivating example. Assume that university X announced a $5 \%$ decrement in student fees starting from next semester. This means, creating a commitment from university X towards each student to deduce $5\%$ from her/his fees next semester. To reason about such commitment, we need a formalization that can reason about group social commitments. To do so, we first introduce the following classification of a group of agents.

Definition 6

(Group of Agents) Assume $\varOmega$ is a set ${\{1, ..., n}\}$ of agents. The group $\varOmega$ can be classified into:

• Divisible Group, if there exists a commitment for each member of the group.

• Indivisible Group, if there exists one commitment towards the whole group. (i.e., the whole group is considered as one agent). So, to reason about such commitment, we will use the normal (one-to-one) social commitment.

To reason about group commitments, we classify them into:

• One-to-Group Commitments.

• Group-to-One Commitments.

4.1 One-to-group commitments

In one-to-group commitment, agent i (the debtor) commits toward a group of agents $\varOmega$ that $\varphi$ (the content of the commitment) holds. Formally, $C_{i \rightarrow \varOmega } \varphi$. To reason about such commitment, we investigate the case that an agent i commits toward a divisible group of agents and the case that i commits toward an indivisible group of agents. The following motivating example illustrates the idea of committing from one agent towards a divisible group of agents.

Example 1

In a well-known company, the general manager commits to increase the salaries of his employees by $10 \%$ starting from next month.

In this example, the general manager commits toward each member of the group (company employee) to increase her/his salary by $10 \%$ starting from next month. By so doing, each member of this group will have an increment of $10 \%$ next month. We consider this commitment as committing from one agent (general manager) towards a divisible group (company employees). On the other hand, Example 2 illustrates the case that committing one agent towards an indivisible group of agents.

Example 2

In a general assembly, the chair of computer science department commits to build a new research lab next year for graduate students. In this example, all graduate students in computer science department will have a new research lab next year (i.e., one commitment from the chair towards the group). Depending on definition 6, this commitment is considered from one agent (chair of computer science department) towards indivisible group of agents (graduate students in the department).

To reason about one-to-(divisible) group commitment, we introduce the following definition.

Definition 7

(One-to-Group Commitment)

• $C_{i \rightarrow {\varOmega }} \varphi$ (read as, i commits toward everyone in $\varOmega$ that $\varphi$ holds): we say that $C_{i \rightarrow {\varOmega }} \varphi$ holds iff i commits to all members of $\varOmega$ that $\varphi$ holds. Formally, $C_{i \rightarrow {\varOmega }} \varphi$$\equiv \bigwedge \limits _{j \in \varOmega }$$C_{i \rightarrow j} \varphi$.

To capture the semantics of $C_{i \rightarrow {\varOmega }} \varphi$, we define the following accessibility relation:

Definition 8

 

• $\sim _{i \rightarrow {\varOmega }}$$= \bigcup \limits _{j \in \varOmega }$$\sim _{i \rightarrow j}$.

The social accessibility relation $\sim _{i \rightarrow {\varOmega }}$ from a global state w to another global state $w'$ (i.e., $w \sim _{i\rightarrow {\varOmega }} w'$) has the intuition that there is a communication channel between (the debtor) agent i and every (creditor) j in $\varOmega$ such that agent i fills the channel in w, and every j in $\varOmega$ receives the message (channel’s content) in $w'$. After receiving the message, the shared variables between agent i and every j will have the same values.

Figure 3 depicts the idea of committing from one agent towards a divisible group of agents $\varOmega$. In this figure, agent i (the debtor) commits towards the group $\varOmega$ that $\varphi$ holds where ($\varOmega = \{j_1, j_2\}$). To accomplish such commitments, two communication channels between i and $j_1$ and $j_2$ will be established, therefore, the message will be delivered from i to $j_1$ and $j_2$ (i.e., a separate commitment from i towards each j in $\varOmega$).

Fig. 3

An example of $C_{i \rightarrow {\varOmega }} \varphi$

4.2 Group-to-one commitments

In group-to-one commitments, a group of agents $\varOmega$ commits towards agent j that $\varphi$ holds. To investigate group-to-one commitments, we follow the same scenario in analyzing one-to-group commitments. Let us start by the following motivating example.

Example 3

Our family is planning to travel to France next summer. To book the tickets, each member of the family should pay the price of her/his ticket to the travel agency. In this example, each member of the group (our family) has a commitment towards the travel agency (agent) to pay the ticket price. Consequently, we have commitments from a group of agents $\varOmega$ to one. To reason about such commitments, we introduce the following definition:

Definition 9

(Committing from Group-to-One)

• $C_{{\varOmega } \rightarrow j} \varphi$ (read as, everyone in ${\varOmega }$ commits toward j that $\varphi$ holds): we say that $C_{{\varOmega } \rightarrow j} \varphi$ holds iff every member in group $\varOmega$ commits toward j that $\varphi$ holds. Formally, $C_{{\varOmega } \rightarrow j} \varphi$$\equiv \bigwedge \limits _{i \in \varOmega }$$C_{i \rightarrow j} \varphi$.

To capture the semantics of $C_{{\varOmega } \rightarrow j} \varphi$, we introduce the following social accessibility relation.

Definition 10

 

• $\sim _{{\varOmega } \rightarrow j}$$= \bigcup \limits _{i \in \varOmega }$$\sim _{i \rightarrow j}$.

The new social accessibility relation $(w \sim _{{\varOmega } \rightarrow j} w')$ captures the intuition that there exists a communication channel between every group member (debtor) i in $\varOmega$ and (the creditor) j where each agent i fills the communication channel in global state w, and agent j receives the message in global state $w'$. After receiving the message, all the shared variables between each agent i in $\varOmega$ and agent j will have the same values.

Figure 4 illustrates the idea of committing from a (divisible) group of agents to one. In this figure, each agent i in $\varOmega$ (which consists of two agents $\{i_1, i_2\}$) commits towards agent j that $\varphi$ holds. To accomplish such commitments, a shard channel between each i and j is established, where each i fills the channel in w and j receives the channel’s content in $w'$. Consequently, a separate message is delivered from each i to j (i.e., a separate commitment from each i towards j). Note that $\varphi$ should hold on every accessible state $w'$ from w using $\sim _{i \rightarrow j}$.

Fig. 4

An example of $C_{{\varOmega } \rightarrow j} \varphi$

On the other hand, to investigate the case of committing from an indivisible group-to-one, let us conider the following example.

Example 4

A research group in our department commits toward their supervisor to finish a research paper within three months.

In this example, all members of the research group will collaborate with each other to finish the paper in three months. Thus, Example 4 is counted as committing from indivisible group (research group) to one agent (supervisor) (i.e., one-to-one commitment).

5 The $\hbox {CTL}^{GC}$ logic

For the sake of specification and verification, Clarke and Emerson introduced a branching-time logic, called Computation Tree Logic (CTL) (Clarke and Emerson 1981). Unlike Linear Temporal Logic (LTL), where at any given time there is one possible future (Pnueli 1977), CTL has a tree-like (branching) structure, where at any given time there are different possible futures (Clarke and Emerson 1981). Moreover, CTL adds a path quantifier either A (“along all paths”) or E (“there exists one path”) before any single operator from the normal temporal operators (Clarke and Emerson 1981). However, CTL does not have the capability to reason about social communicating commitments and their fulfillments. Therefore, in this work, we extend CTL with modalities to reason about single, group unconditional commitments and their fulfillments in a new logic called $\hbox {CTL}^{GC}$.

In this section, we will discuss the $\hbox {CTL}^{GC}$ syntax and semantics. The syntax of $\hbox {CTL}^{GC}$ is defined as follows:

Definition 11

(Syntax of $\hbox {CTL}^{GC}$)

$$\begin{aligned} \varphi&{:}{:}{=} p~|~\lnot \varphi ~|~\varphi \vee \varphi ~\mid EX \varphi ~\mid E ( \varphi U \varphi ) \mid EG ~|~\mathcal {C}~|~ Fu ~\\ \mathcal {C}&{:}{:}{=} C_{i\rightarrow j}\varphi ~| ~C_{i\rightarrow {\varOmega }}\varphi ~|~C_{{\varOmega }\rightarrow j}\varphi \\ Fu&{:}{:}{=} Fu(C_{i\rightarrow j}\varphi ) ~| ~ Fu(C_{i\rightarrow {\varOmega }}\varphi ) ~| ~ Fu(C_{{\varOmega }\rightarrow j}\varphi ) \end{aligned}$$

Where:

• $p, \lnot , \vee , E, X, U$ and G are the same CTL (Clarke and Emerson 1981) modalities.

• Social commitment formulae $\mathcal {C}$, are special state formulae in $\hbox {CTL}^{GC}$ which capture social properties using the modal connectives $C_{i\rightarrow j} \varphi$, $C_{i\rightarrow {\varOmega }}$ and $C_{{\varOmega }\rightarrow j}$ standing for “commitment”, “commitment towards a divisible group” and “commitment from a divisible group” respectively.

$C_{i\rightarrow j}\varphi ~$ is read as “agent i commits towards agent j that $\varphi$” (Bentahar et al. 2012). $C_{i\rightarrow {\varOmega }}\varphi ~$ is read as agent i commits toward everyone in $\varOmega$ that $\varphi$. $C_{{\varOmega } \rightarrow j} \varphi$ is read as everyone in $\varOmega$ commits toward j that $\varphi$. Furthermore, we use the following abbreviation:

• $\bot$$\triangleq$$\varphi \wedge \lnot \varphi$.

Since the main fragment of the $\hbox {CTL}^{GC}$ logic is the CTL logic (Clarke and Emerson 1981), we only recall the semantics of single commitment, group (one-to-group and group-to-one) commitments and their fulfillments.

Definition 12

(Satisfaction of $\hbox {CTL}^{GC}$) Using the model $\mathcal {M}$, the satisfaction of a $\hbox {CTL}^{GC}$ formula $\varphi$ in a global state w, represented by $(\mathcal {M}, w) \models \varphi$, is recursively defined as follows:

• $(\mathcal {M}, w ) \models C_{i\rightarrow j} \varphi$ iff for all global states $w' \in W$ s.t. $w \sim _{i \rightarrow j} w'$, we have $(\mathcal {M}, w') \models \varphi$;

• $(\mathcal {M}, w) \models C_{i\rightarrow {\varOmega }} \varphi$ iff for all global states $w' \in W$ s.t. $w \sim _{i \rightarrow {\varOmega }} w'$, we have $(\mathcal {M}, w') \models \varphi$;

• $(\mathcal {M}, w) \models C_{{\varOmega } \rightarrow j} \varphi$ iff for all global states $w' \in W$ s.t. $w \sim _{{\varOmega } \rightarrow j} w'$, we have $(\mathcal {M}, w') \models \varphi$;

• $(\mathcal {M}, w) \models Fu (C_{i\rightarrow j} \varphi )$ iff there exists $w' \in W$ s.t. $w' \sim _{i \rightarrow j} w$ and $(\mathcal {M}, w' ) \models C_{i\rightarrow j} \varphi$;

• $(\mathcal {M}, w) \models Fu (C_{i\rightarrow \varOmega } \varphi )$ iff there exists $w' \in W$ s.t. $w' \sim _{i \rightarrow \varOmega } w$ and $(\mathcal {M}, w' ) \models C_{i\rightarrow \varOmega } \varphi$;

• $(\mathcal {M}, w) \models Fu (C_{\varOmega \rightarrow j} \varphi )$ iff there exists $w' \in W$ s.t. $w' \sim _{\varOmega \rightarrow j} w$ and $(\mathcal {M}, w' ) \models C_{\varOmega \rightarrow j} \varphi$.

The semantics of $\hbox {CTL}^{GC}$ state formulae is identified in the model $\mathcal {M}$ as the semantics of the standard CTL (Clarke and Emerson 1981) with modalities for reasoning about social commitments, group social commitments, fulfillment and group fulfillment.

The state formula $C_{i\rightarrow j} \varphi$ holds in the model $\mathcal {M}$ at the global state w if and only if the content $\varphi$ is satisfied in each accessible state $w'$ captured by the social accessibility relation $\sim _{i \rightarrow j}$. When agent i commits towards agent j that $\varphi$ holds, the social accessibility relation $\sim _{i \rightarrow j}$ from a global state w to global state $w'$ has the intuition that a commitment from i towards j exists if there is a communication channel (shared variables) between them where i fills the channel with message content at w, and j receives the message at $w'$ and the values of the shared variables for j at $w'$ equal the values of the shared variables for i at w.

The state formula $C_{i\rightarrow {\varOmega }} \varphi$ holds in the model $\mathcal {M}$ at w if and only if the content $\varphi$ is satisfied in each accessible state $w'$ captured by the social accessibility relation $\sim _{i \rightarrow {\varOmega }}$. If agent i (the debtor) commits toward a divisible group ${\varOmega }$ that $\varphi$ holds, the social accessibility relation $\sim _{i \rightarrow {\varOmega }}$ has the intuition that, a communication channels exist between agent i and every agent j in ${\varOmega }$ where i fills each channel at w and every j in ${\varOmega }$ receives the channel’s contents at $w'$. Thus, the values of the shared variables for every j at $w'$ equals the values of the shared variables for i at w which means that the message has been sent from i to every j in ${\varOmega }$ through the communication channels. When i delivers a message to every j in ${\varOmega }$, this reflects the fact that i has a commitment towards every j in the group ${\varOmega }$.

The state formula $C_{{\varOmega }\rightarrow j} \varphi$ holds in the model $\mathcal {M}$ at w if and only if the content $\varphi$ is satisfied in every accessible state $w'$ captured by the social accessibility relation $\sim _{{\varOmega }\rightarrow j}$. The social accessibility relation $\sim _{{\varOmega }\rightarrow j}$ has the intuition that, when a communication channel exists between every agent i in ${\varOmega }$ and agent j such that every i fills the channel at w and j receives the channel’s content at $w'$. Consequently, the values of the shared variables for j at $w'$ equal the values of the shared variables for every i at w which shows that the messages have been transferred from ${\varOmega }$ to j through the communication channels. Therefore, every i in ${\varOmega }$ has a commitment towards j.

The state formula $Fu(C_{i\rightarrow j} \varphi )$ holds in the model $\mathcal {M}$ if and only if, there exists a global state $w'$ satisfying the commitment from which the global state w can be reached by the social accessibility relation $\sim _{i \rightarrow j}$. The semantics of $Fu(C_{i\rightarrow j} \varphi )$ has the intuition that: if a global state w is socially accessible from a commitment global state $w'$ then w is a fulfillment state.

The state formula $Fu(C_{i\rightarrow \varOmega } \varphi )$ holds in the model $\mathcal {M}$ if and only if, there exists a global state $w'$ satisfying the group commitment $C_{i\rightarrow {\varOmega }} \varphi$ from which the global state w can be reached by the social accessibility relation $\sim _{i \rightarrow \varOmega }$. The semantics of $Fu(C_{i\rightarrow \varOmega } \varphi )$ has the intuition that: a global state w is a one-to-group fulfillment state if it is socially accessible from a one-to-group commitment global state $w'$.

The state formula $Fu (C_{\varOmega \rightarrow j} \varphi )$ holds in the model $\mathcal {M}$ if and only if, there exists a global state $w'$ satisfying the $C_{\varOmega \rightarrow j} \varphi$ from which the global w can be reached by the social accessibility relation $\sim _{\varOmega \rightarrow j}$. The semantics of $Fu (C_{\varOmega \rightarrow j} \varphi )$ has the intuition that: a global state w is a group-to-one fulfillment state if it is socially accessible from a group-to-one commitment global state $w'$.

6 Corresponding reasoning postulates

After presenting the $\hbox {CTL}^{GC}$ logic from the semantics perspective, in this section, we want to investigate $\hbox {CTL}^{GC}$ from the Soundness and Completeness perspectives. In particular, to prove the soundness and completeness of the $\hbox {CTL}^{GC}$ logic, we want to apply correspondence theory for modal logic (van Benthem 1984). To do so, we follow the following procedure:

• Develop a set of reasoning postulates in $\hbox {CTL}^{GC}$ logic to reason about group commitments and their fulfillments.

• Correspond each postulate to a certain frame and prove such correspondence.

• Use the above correspondence in proving the soundness and completeness of the $\hbox {CTL}^{GC}$ logic.

• Illustrate each postulate using an example from the NetBill payment protocol (Sirbu 1997) and show how similar these postulates are addressed in the literature.

6.1 Running example

In this section, we introduce the NetBill protocol (Sirbu 1997), taken from the business domain, for selling and buying encrypted software goods on the Internet. Figure 5 depicts the main steps of the protocol. The NetBill is a good example to illustrate how can we apply commitments in verifying and specifying protocols in business domains (Yolum and Singh 2004, 2000). This protocol mainly consists of two interacting agents: the merchant (merch) and the customer (cust).

The protocol works as follows: At the beginning, both the customer and merchant should confirm themselves using a certain public-key. After that, the customer sends a request for a special quote. The merchant replies by sending the requested quote. At this moment, the customer has two choices either accepts the quote or rejects it. In the case that the customer accepts the quote (i.e., makes a commitment to pay towards the merchant). Then, the merchant delivers the requested goods in an encrypted format withholding their key. At that moment, the customer sends an Electronic Payment Order (EPO). This EPO contains a list of the received software goods. Hereafter, the merchant verifies the EPO using the NetBill server and sends a receipt to the customer. This receipt contains the key to decrypt the received goods. Finally, when the key is received, the customer decrypts the purchased software goods.

From the previous protocol scenario, we can investigate the following commitments (Al-Saqqar et al. 2016):

• 1. $C_{cust \rightarrow merch}$Payment. This commitment implies that the customer (cust) commits toward the merchant (merch) to pay the required amount of money (Payment). When the customer actually pays the money, this means that the customer fulfills the commitment (i.e., $Fu(C_{cust \rightarrow merch} Payment))$.

• 2. $C_{merch \rightarrow cust}$Delivery. This commitment means that the merchant (merch) commits toward the customer (cust) to deliver the required software goods (Delivery) (without the key). Once the merchant sends the receipt with the key, this implies that it fulfills the commitment (i.e., $Fu(C_{merch \rightarrow cust} Delivery))$.

  Using the $\hbox {CTL}^{GC}$ logic, we can extend the above commitments to have, for example, a commitment from one customer towards a group of merchants to pay the required amount of money. Also, a commitment from a merchant towards all its customers to deliver the required goods. Further, we can express the commitment from a group of customers towards a given merchant to pay their required amounts of money and so on.

Fig. 5

The NetBill payment protocol

6.2 Correspondence

In the previous section, we introduced the NetBill protocol (Sirbu 1997) as a running example. In this section, we propose a set of reasoning postulates in $\hbox {CTL}^{GC}$ and correspond them to certain classes of frames. By doing so, we can use the correspondence theory for modal logic (van Benthem 1984) to prove the soundness and completeness of the $\hbox {CTL}^{GC}$ logic. Similar to our work in Al-Saqqar et al. (2016), at the beginning, each reasoning postulate is given a name, formalization and meaning. After that, every postulates is corresponded to a certain class of frames with the necessary proofs. Thereafter, we illustrate the crucial needs of each postulate in MASs with an example from the NetBill protocol. Further to that, we show how those postulates were tackled in the literature. For valid postulates, as they correspond to all potential frames, we will not address their correspondence.

• Pos1. [Strong consistency / single commitment]

Formalization: $C _{i\rightarrow j} \varphi \rightarrow \lnot C _{i\rightarrow j} \lnot \varphi$.

Meaning: If a commitment is satisfied, then it is not possible to commit to the negation of its content.

Correspondence: For each frame $\mathcal {FR} = (W, \sim _{i \rightarrow j})$, $\mathcal {FR} \models C _{i\rightarrow j} \varphi \rightarrow \lnot C _{i\rightarrow j} \lnot \varphi$ iff $\mathcal {FR}$ is serial.

Proof

$(\Leftarrow )$ Assume that $\mathcal {FR} = (W, \sim _{i \rightarrow j})$ is serial, and let $\mathcal {M} = ( W, \sim _{i \rightarrow j}, \mathcal {VL} )$ be a model based on $\mathcal {FR}$. Given $w_1 \in W$, we must prove that $(\mathcal {M},w_1) \models C _{i\rightarrow j} \varphi \rightarrow \lnot C _{i\rightarrow j} \lnot \varphi$. Assume that $(\mathcal {M}, w_1) \models (C _{i\rightarrow j} \varphi ) \wedge (C _{i\rightarrow j} \lnot \varphi )$. Using the semantics of $C _{i\rightarrow j} \varphi$, for all global states $w_2 \in W$ such that $w_1 \sim _{i \rightarrow j} w_2$, we have $(\mathcal {M}, w_2 ) \models \varphi \wedge \lnot \varphi$. Thus, we have contradiction. So, $(\mathcal {M},w_1) \models C _{i\rightarrow j} \varphi \rightarrow \lnot C _{i\rightarrow j} \lnot \varphi$.

$(\Rightarrow )$ Assume that $\mathcal {FR}$ is not serial. We must show $\mathcal {FR} \nvDash C _{i\rightarrow j} \varphi \rightarrow \lnot C _{i\rightarrow j} \lnot \varphi$. Since $\mathcal {FR}$ is not serial, using Remark 1, it might be the case that $(\mathcal {M}, w_1 ) \models C _{i\rightarrow j} p \wedge C _{i\rightarrow j} \lnot p$. Therefore, $\mathcal {FR} \nvDash C _{i\rightarrow j} p \rightarrow \lnot C _{i\rightarrow j} \lnot p$, as desired. $\square$

Discussion: This postulate indicates that an agent cannot commit to reason about $\varphi$ and $\lnot \varphi$ at the same time, which is reasonable and valid. This postulate is integrated in Al-Saqqar’s postulates (Al-Saqqar et al. 2016), Singh’s postulates (Singh 2008), and El Kholy’s rules (EL Kholy et al. 2014).

• Pos2. [Strong consistency / one-to-group commitment]

Formalization: $C _{i\rightarrow \varOmega } \varphi \rightarrow \lnot C _{i\rightarrow \varOmega } \lnot \varphi$.

Meaning: If a one-to-group commitment is satisfied, then it will not be possible to commit to the negation of its content.

Correspondence: For each frame $\mathcal {FR} = (W, \sim _{i \rightarrow \varOmega })$, $\mathcal {FR} \models C _{i\rightarrow \varOmega } \varphi \rightarrow \lnot C _{i\rightarrow \varOmega } \lnot \varphi$ iff $\mathcal {FR}$ is serial.

Proof

$(\Leftarrow )$ Assume that $\mathcal {FR} = (W, \sim _{i \rightarrow \varOmega })$ is serial, and let $\mathcal {M} = ( W,\sim _{i \rightarrow \varOmega }, \mathcal {VL} )$ be a model based on $\mathcal {FR}$. Given $w_1 \in W$, we need to prove that $(\mathcal {M},w_1) \models C _{i\rightarrow \varOmega } \varphi \rightarrow \lnot C _{i\rightarrow \varOmega } \lnot \varphi$. Assume that $(\mathcal {M}, w_1) \models (C _{i\rightarrow \varOmega } \varphi ) \wedge (C _{i\rightarrow \varOmega } \lnot \varphi )$. Using the semantics of $C _{i\rightarrow \varOmega } \varphi$, for all global states $w_2 \in W$ such that $w_1 \sim _{i \rightarrow \varOmega } w_2$, we have $(\mathcal {M}, w_2 ) \models \varphi \wedge \lnot \varphi$. Thus, we have contradiction. So, $(\mathcal {M},w_1) \models C _{i\rightarrow \varOmega } \varphi \rightarrow \lnot C _{i\rightarrow \varOmega } \lnot \varphi$.

$(\Rightarrow )$ Assume that $\mathcal {FR}$ is not serial. We must show $\mathcal {FR} \nvDash C _{i\rightarrow \varOmega } \varphi \rightarrow \lnot C _{i\rightarrow \varOmega } \lnot \varphi$. Since $\mathcal {FR}$ is not serial, using an argument by contraposition, then it might be the case that $(\mathcal {M}, w_1 ) \models C _{i\rightarrow \varOmega } p \wedge C _{i\rightarrow \varOmega } \lnot p$. Therefore, $\mathcal {FR} \nvDash C _{i\rightarrow \varOmega } p \rightarrow \lnot C _{i\rightarrow \varOmega } \lnot p$, as desired. $\square$

Discussion: This postulate demonstrates the fact that an agent cannot commit towards a group of agents to reason about $\varphi$ and $\lnot \varphi$ at the same time.

• Pos3. [Strong consistency / group-to-one commitment]

Formalization: $C _{\varOmega \rightarrow j} \varphi \rightarrow \lnot C _{\varOmega \rightarrow j} \lnot \varphi$.

Meaning: If a group-to-one commitment is satisfied, then it will not be possible to commit to the negation of its content.

Correspondence: For each frame $\mathcal {FR} = (W, \sim _{\varOmega \rightarrow j})$, $\mathcal {FR} \models C _{\varOmega \rightarrow j} \varphi \rightarrow \lnot C _{\varOmega \rightarrow j} \lnot \varphi$ iff $\mathcal {FR}$ is serial.

Proof

$(\Leftarrow )$ Assume that $\mathcal {FR} = (W, \sim _{\varOmega \rightarrow j})$ is serial, and let $\mathcal {M} = ( W, \sim _{\varOmega \rightarrow j}, \mathcal {VL} )$ be a model based on $\mathcal {FR}$. Given $w_1 \in W$, we need to prove that $(\mathcal {M},w_1) \models C _{\varOmega \rightarrow j} \varphi \rightarrow \lnot C _{\varOmega \rightarrow j} \lnot \varphi$. Assume that $(\mathcal {M}, w_1) \models (C _{\varOmega \rightarrow j} \varphi ) \wedge (C _{\varOmega \rightarrow j} \lnot \varphi )$. Using the semantics of $C _{\varOmega \rightarrow j} \varphi$, for all global states $w_2 \in W$ such that $w_1 \sim _{\varOmega \rightarrow j} w_2$, we have $(\mathcal {M}, w_2 ) \models \varphi \wedge \lnot \varphi$. Therefore, we have contradiction. Thus, $(\mathcal {M},w_1) \models C _{\varOmega \rightarrow j} \varphi \rightarrow \lnot C _{\varOmega \rightarrow j} \lnot \varphi$.

$(\Rightarrow )$ Assume that $\mathcal {FR}$ is not serial. We need to show that $\mathcal {FR} \nvDash C _{\varOmega \rightarrow j} \varphi \rightarrow \lnot C _{\varOmega \rightarrow j} \lnot \varphi$. Since $\mathcal {FR}$ is not serial, using Remark 1, then it might be the case that $(\mathcal {M}, w_1 ) \models C _{\varOmega \rightarrow j} p \wedge C _{\varOmega \rightarrow j} \lnot p$. So, $\mathcal {FR} \nvDash C _{\varOmega \rightarrow j} p \rightarrow \lnot C _{\varOmega \rightarrow j} \lnot p$, as desired. $\square$

Discussion: This postulate illustrates the fact that a group of agents cannot commit to reason about $\varphi$ and $\lnot \varphi$ simultaneously towards the same agent.

• Pos4. [R-Conjoin / single commitment]

Formalization: $(C _{i\rightarrow j} \varphi _1) \wedge (C _{i\rightarrow j} \varphi _2) \rightarrow C _{i\rightarrow j} (\varphi _1 \wedge \varphi _2)$.

Meaning: If agent i individually commits to reason about $\varphi _1$ and $\varphi _2$ then i would become committed to reason about both $\varphi _1$ and $\varphi _2$.

Proof

Given $w_1 \in W$, we need to prove that $(\mathcal {M},w_1) \models (C _{i\rightarrow j} \varphi _1) \wedge (C _{i\rightarrow j} \varphi _2) \rightarrow C _{i\rightarrow j} (\varphi _1 \wedge \varphi _2)$. Assume that $(\mathcal {M}, w_1 ) \models ((C _{i\rightarrow j} \varphi _1) \wedge (C _{i\rightarrow j} \varphi _2)) \wedge \lnot (C _{i\rightarrow j} (\varphi _1 \wedge \varphi _2))$. Using the semantics of single commitments, for all global states $w_2 \in W$ such that $w_1 \sim _{i \rightarrow j} w_2$, we have $(\mathcal {M}, w_2 ) \models ( \varphi _1 \wedge \varphi _2) \wedge \lnot (\varphi _1 \wedge \varphi _2)$. So, $(\mathcal {M}, w_2) \models (\varphi _1 \wedge \lnot \varphi _1) \vee (\varphi _2 \wedge \lnot \varphi _2)$. So, we have a contradiction. Therefore, $(C _{i\rightarrow j} \varphi _1) \wedge (C _{i\rightarrow j} \varphi _2) \rightarrow C _{i\rightarrow j} (\varphi _1 \wedge \varphi _2)$. $\square$

Discussion: This postulate demonstrates the fact that an agent i can have more than one commitment towards an agent j at the same time. From the NetBill, assume that the merchant commits towards the customer to send a receipt and also commits toward the same customer to deliver the goods, then the merchant would be committed towards the customer to send the receipt and deliver the goods. Formally, $(C _{merch \rightarrow cust}$Reciept ) $\wedge$$(C _{merch \rightarrow cust}$Delivery) $\rightarrow C _{merch \rightarrow cust}$$(Delivery \wedge Reciept)$. This postulate is integrated in Al-Saqqar’s postulates (Al-Saqqar et al. 2016), Singh’s postulates (Singh 2008), Chopra’s postulates (Chopra and Singh 2015), and El Kholy’s rules (EL Kholy et al. 2014).

• Pos5. [R-Conjoin / one-to-group commitment]

Formalization: $(C _{i\rightarrow \varOmega } \varphi _1) \wedge (C _{i\rightarrow \varOmega } \varphi _2) \rightarrow C _{i\rightarrow \varOmega } (\varphi _1 \wedge \varphi _2)$.

Meaning: An agent i would become committed towards a group of agents to reason about both $\varphi _1$ and $\varphi _2$ at the same time if i individually commits towards this group to reason about $\varphi _1$ and $\varphi _2$.

Proof

Given $w_1 \in W$, we need to prove that $(\mathcal {M},w_1) \models (C _{i\rightarrow \varOmega } \varphi _1) \wedge (C _{i\rightarrow \varOmega } \varphi _2) \rightarrow C _{i\rightarrow \varOmega } (\varphi _1 \wedge \varphi _2)$. Assume that $(\mathcal {M}, w_1 ) \models ((C _{i\rightarrow \varOmega } \varphi _1) \wedge (C _{i\rightarrow \varOmega } \varphi _2)) \wedge \lnot (C _{i\rightarrow \varOmega } (\varphi _1 \wedge \varphi _2))$. Using the semantics of $C _{i\rightarrow \varOmega } \varphi$, for all global states $w_2 \in W$ such that $w_1 \sim _{i\rightarrow \varOmega } w_2$, we have $(\mathcal {M}, w_2 ) \models ( \varphi _1 \wedge \varphi _2) \wedge \lnot (\varphi _1 \wedge \varphi _2)$. So, $(\mathcal {M}, w_2) \models (\varphi _1 \wedge \lnot \varphi _1) \vee (\varphi _2 \wedge \lnot \varphi _2)$. Thus, we have contradiction. Consequently, $(C _{i\rightarrow \varOmega } \varphi _1) \wedge (C _{i\rightarrow \varOmega } \varphi _2) \rightarrow C _{i\rightarrow \varOmega } (\varphi _1 \wedge \varphi _2)$. $\square$

Discussion: The idea of this postulate is that an agent i is capable to have more than one commitment towards the same group of agents $\varOmega$ at the same time. Assume that the merchant commits towards a group of customers to deliver the goods and also commits towards the same group to send a receipt, then the merchant would be committed towards the group of customers to deliver the goods and send the receipt. Formally, $(C _{merch \rightarrow \varOmega {cust}}$Delivery) $\wedge$$(C _{merch \rightarrow \varOmega cust}$Reciept) $\rightarrow C _{merch \rightarrow \varOmega cust}$$(Delivery \wedge Reciept)$.

• Pos6. [R-Conjoin / group-to-one commitment]

Formalization: $(C _{\varOmega \rightarrow j} \varphi _1) \wedge (C _{\varOmega \rightarrow j} \varphi _2) \rightarrow C _{\varOmega \rightarrow j} (\varphi _1 \wedge \varphi _2)$.

Meaning: a group of agents $\varOmega$ would become committed towards an agent j to reason about both $\varphi _1$ and $\varphi _2$ simultaneously if $\varOmega$ individually commits to reason about $\varphi _1$ and $\varphi _2$.

Proof

Given $w_1 \in W$, we need to prove that $(\mathcal {M},w_1) \models (C _{\varOmega \rightarrow j} \varphi _1) \wedge (C _{\varOmega \rightarrow j} \varphi _2) \rightarrow C _{\varOmega \rightarrow j} (\varphi _1 \wedge \varphi _2)$. Assume that $(\mathcal {M}, w_1 ) \models ((C _{\varOmega \rightarrow j} \varphi _1) \wedge (C _{\varOmega \rightarrow j} \varphi _2)) \wedge \lnot (C _{\varOmega \rightarrow j} (\varphi _1 \wedge \varphi _2))$. Using the semantics of $C _{\varOmega \rightarrow j} \varphi$, for all global states $w_2 \in W$ such that $w_1 \sim _{\varOmega \rightarrow j} w_2$, we have $(\mathcal {M}, w_2 ) \models ( \varphi _1 \wedge \varphi _2) \wedge \lnot (\varphi _1 \wedge \varphi _2)$. Thus, $(\mathcal {M}, w_2) \models (\varphi _1 \wedge \lnot \varphi _1) \vee (\varphi _2 \wedge \lnot \varphi _2)$. So, we have contradiction. Therefore, $(C _{\varOmega \rightarrow j} \varphi _1) \wedge (C _{\varOmega \rightarrow j} \varphi _2) \rightarrow C _{\varOmega \rightarrow j} (\varphi _1 \wedge \varphi _2)$. $\square$

Discussion: This postulate demonstrates the fact that a group of agents $\varOmega$ have the ability to have more than one commitment towards the same agent j at the same time. Assume that a group of merchants commits towards a given customer to deliver the goods and the same group also commits towards the same customer to send a receipt, then the group of merchants becomes committed towards the customer to deliver the goods and send the receipt. Formally, $(C _{\varOmega merch \rightarrow cust}$Delivery) $\wedge$$(C _{\varOmega merch \rightarrow cust}$Reciept) $\rightarrow C _{\varOmega merch \rightarrow cust}$$(Delivery \wedge Reciept)$.

• Pos7. [Single commitment’s chain]

Formalization: $(C_{i \rightarrow j} \varphi ) \wedge (C_{i \rightarrow j} (\varphi \rightarrow \psi )) \rightarrow C_{i \rightarrow j} \psi$.

Meaning: Single social commitments are closed under implication.

Proof

Suppose that $(\mathcal {M}, w_1 ) \models (C _{i\rightarrow j} \varphi ) \wedge (C _{i\rightarrow j} (\varphi \rightarrow \psi )) \wedge \lnot (C _{i\rightarrow j} \psi )$. Using the semantics of single commitment, for all $w_2 \in W$ such that $w_1 \sim _{i \rightarrow j} w_2$, we have $(\mathcal {M}, w_2 ) \models \varphi \wedge (\varphi \rightarrow \psi )$. Using Modus ponens, $(\mathcal {M}, w_2 ) \models \psi$. Since $w_1 \sim _{i \rightarrow j} w_2$, then $(\mathcal {M}, w_1 ) \models C _{i\rightarrow j} \psi$ which is a contradiction with our assumption. Therefore, $(C_{i \rightarrow j} \varphi ) \wedge (C_{i \rightarrow j} (\varphi \rightarrow \psi )) \rightarrow C_{i \rightarrow j} \psi$. $\square$

Discussion: This postulate demonstrates that $\hbox {CTL}^{GC}$ is closed under implication. This postulate is integrated in Al-Saqqar’s postulates (Al-Saqqar et al. 2016), Singh’s postulates (Singh 2008), and El Kholy’s rules (EL Kholy et al. 2014).

• Pos8. [One-to-Group commitment chain]

Formalization: $(C_{i \rightarrow \varOmega } \varphi ) \wedge (C_{i \rightarrow \varOmega } (\varphi \rightarrow \psi )) \rightarrow C_{i \rightarrow \varOmega } \psi$.

Meaning: One-to-Group commitments are closed under implication.

Proof

Suppose that $(\mathcal {M}, w_1 ) \models (C _{i \rightarrow \varOmega } \varphi ) \wedge (C _{i \rightarrow \varOmega } (\varphi \rightarrow \psi )) \wedge \lnot (C _{i \rightarrow \varOmega } \psi )$. Using the semantics of $(C _{i \rightarrow \varOmega } \varphi )$, for all $w_2 \in W$ such that $w_1 \sim _{i \rightarrow \varOmega } w_2$, we have $(\mathcal {M}, w_2 ) \models \varphi \wedge (\varphi \rightarrow \psi )$. Using Modus ponens, $(\mathcal {M}, w_2 ) \models \psi$. Since $w_1 \sim _{i \rightarrow \varOmega } w_2$, then $(\mathcal {M}, w_1 ) \models C _{i \rightarrow \varOmega } \psi$ which is a contradiction. Thus, $(C_{i \rightarrow \varOmega } \varphi ) \wedge (C_{i \rightarrow \varOmega } (\varphi \rightarrow \psi )) \rightarrow C_{i \rightarrow \varOmega } \psi$. $\square$

Discussion: This postulate shows that one-to-group commitments using $\hbox {CTL}^{GC}$ are closed under strict implication.

• Pos9. [Group-to-one commitment chain]

Formalization: $(C_{\varOmega \rightarrow j} \varphi ) \wedge (C_{\varOmega \rightarrow j} (\varphi \rightarrow \psi )) \rightarrow C_{\varOmega \rightarrow j} \psi$.

Meaning: Group-to-one commitments are closed under implication.

Proof

Suppose that $(\mathcal {M}, w_1 ) \models (C _{\varOmega \rightarrow j} \varphi ) \wedge (C _{\varOmega \rightarrow j} (\varphi \rightarrow \psi )) \wedge \lnot (C _{\varOmega \rightarrow j} \psi )$. From the semantics of $(C _{\varOmega \rightarrow j} \varphi )$, for all $w_2 \in W$ such that $w_1 \sim _{\varOmega \rightarrow j} w_2$, we have $(\mathcal {M}, w_2 ) \models \varphi \wedge (\varphi \rightarrow \psi )$. Using Modus ponens, $(\mathcal {M}, w_2 ) \models \psi$. Since $w_1 \sim _{\varOmega \rightarrow j} w_2$, then $(\mathcal {M}, w_1 ) \models C _{\varOmega \rightarrow j} \psi$ which is a contradiction. Therefore, $(C_{\varOmega \rightarrow j} \varphi ) \wedge (C_{\varOmega \rightarrow j} (\varphi \rightarrow \psi )) \rightarrow C_{\varOmega \rightarrow j} \psi$. $\square$

Discussion: This postulate demonstrates that group-to-one commitments using $\hbox {CTL}^{GC}$ are closed under strict implication.

• Pos10. [Weaken single commitment]

Formalization: $C _{i\rightarrow j} (\varphi _1 \wedge \varphi _2) \rightarrow C _{i\rightarrow j} \varphi _1$.

Meaning: If i commits to a conjunction of both $\varphi _1$ and $\varphi _2$, i also commits to each part of the conjunction.

Proof

Given $w_1 \in W$, we need to prove that $(\mathcal {M},w_1) \models C _{i\rightarrow j} (\varphi _1 \wedge \varphi _2) \rightarrow C _{i\rightarrow j} \varphi _1$. Let us assume that $(\mathcal {M}, w_1) \models C _{i\rightarrow j} (\varphi _1 \wedge \varphi _2) \wedge \lnot (C _{i\rightarrow j} \varphi _1)$. Using the semantics of $C _{i\rightarrow j} \varphi$, for all global states $w_2 \in W$ such that $w_1 \sim _{i \rightarrow j} w_2$, we have $(\mathcal {M}, w_2) \models (\varphi _1 \wedge \varphi _2)$. Therefoe, $(\mathcal {M}, w_2) \models \varphi _1$. Since $w_1 \sim _{i \rightarrow j} w_2$, $(\mathcal {M}, w_1) \models C _{i\rightarrow j} \varphi _1$ which is a contradiction. Thus, the postulate. $\square$

Discussion: This postulate conveys the fact that if an agent i commits to a conjunction towards agent j, i also commits to each part of the conjunction. From the NetBill, if the merchant commits to sending both the receipt and the required goods, then the merchant commits to send the receipt. Formally, $C _{merch \rightarrow cust}$ (Receipt $\wedge$Delivery) $\rightarrow C _{merch \rightarrow cust}$Receipt . This postulate is integrated in Al-Saqqar’s postulates (Al-Saqqar et al. 2016), Singh’s postulates (Singh 2008), Chopra’s postulates (Chopra and Singh 2015), and El Kholy’s rules (EL Kholy et al. 2014).

• Pos11. [Weaken one-to-group commitment]

Formalization: $C _{i\rightarrow \varOmega } (\varphi _1 \wedge \varphi _2) \rightarrow C _{i\rightarrow \varOmega } \varphi _1$.

Meaning: If an agent i commits to a conjunction towards a group of agents $\varOmega$, i also commits to each part of the conjunction.

Proof

Given $w_1 \in W$, we want to prove that $(\mathcal {M},w_1) \models C _{i\rightarrow \varOmega } (\varphi _1 \wedge \varphi _2) \rightarrow C _{i\rightarrow \varOmega } \varphi _1$. Assume that $(\mathcal {M}, w_1) \models C _{i\rightarrow \varOmega } (\varphi _1 \wedge \varphi _2) \wedge \lnot (C _{i\rightarrow \varOmega } \varphi _1)$. Using the semantics of $C _{i\rightarrow \varOmega } \varphi$, for all global states $w_2 \in W$ such that $w_1 \sim _{i\rightarrow \varOmega } w_2$, we have $(\mathcal {M}, w_2) \models (\varphi _1 \wedge \varphi _2)$. Therefoe, $(\mathcal {M}, w_2) \models \varphi _1$. Since $w_1 \sim _{i\rightarrow \varOmega } w_2$, $(\mathcal {M}, w_1) \models C _{i\rightarrow \varOmega } \varphi _1$ which is a contradiction. Thus, the postulate. $\square$

Discussion: This postulate demonstrates the fact that that if an agent i commits to a conjunction towards a group of agents $\varOmega$, i also commits to each part of this conjunction. For example, if a merchant i commits to a group $\varOmega$ to sending both the required goods and the receipt, then the merchant commits to send the goods. Formally, $C _{merch \rightarrow \varOmega cust}$ (Delivery $\wedge$Receipt) $\rightarrow C _{{merch} \rightarrow \varOmega cust}$Delivery.

• Pos12. [Weaken group-to-one commitment]

Formalization: $C _{\varOmega \rightarrow j} (\varphi _1 \wedge \varphi _2) \rightarrow C _{\varOmega \rightarrow j} \varphi _1$.

Meaning: If a group of agents $\varOmega$ commit to a conjunction, $\varOmega$ also commits to each part of the conjunction.

Proof

Given $w_1 \in W$, we need to prove that $(\mathcal {M},w_1) \models C _{\varOmega \rightarrow j} (\varphi _1 \wedge \varphi _2) \rightarrow C _{\varOmega \rightarrow j} \varphi _1$. Assume that $(\mathcal {M}, w_1) \models C _{\varOmega \rightarrow j} (\varphi _1 \wedge \varphi _2) \wedge \lnot (C _{\varOmega \rightarrow j} \varphi _1)$. Using the semantics of $C _{\varOmega \rightarrow j} \varphi$, for all global states $w_2 \in W$ such that $w_1 \sim _{\varOmega \rightarrow j} w_2$, we have $(\mathcal {M}, w_2) \models (\varphi _1 \wedge \varphi _2)$. Therefore, $(\mathcal {M}, w_2) \models \varphi _1$. Since $w_1 \sim _{\varOmega \rightarrow j} w_2$, $(\mathcal {M}, w_1) \models C _{\varOmega \rightarrow j} \varphi _1$ which contradicts our assumption. Thus, the postulate. $\square$

Discussion: This postulate coveys the fact that if a group of agents $\varOmega$ commits to a conjunction, $\varOmega$ also commits to each part of the conjunction. For example, if a group of merchants commits to sending both the required goods and the receipt towards a customer, then the merchants commit to send the goods. Formally, $C _{\varOmega _{merch} \rightarrow cust}$ (Delivery $\wedge$Receipt) $\rightarrow C _{\varOmega _{merch} \rightarrow cust}$Delivery.

• Pos13. [Single commitment consistency]

Formalization: $\lnot C _{i\rightarrow j} \bot$, where $\bot$ is read as “constant false proposition”.

Meaning: Agent i cannot commit to false.

Correspondence: For each frame $\mathcal {FR} = (W, \sim _{i \rightarrow j})$, $\mathcal {FR} \models \lnot C _{i\rightarrow j} \bot$ iff $\mathcal {FR}$ is serial.

Proof

$(\Leftarrow )$ Assume that $\mathcal {FR} = (W, \sim _{i \rightarrow j})$ is serial and let $\mathcal {M} = ( W, \sim _{i \rightarrow j}, \mathcal {VL} )$ be a model based on $\mathcal {FR}$. Given $w_1 \in W$, we need to prove that $(\mathcal {M},w_1) \models \lnot C _{i\rightarrow j} \bot$. Assume that $(\mathcal {M}, w_1) \models C_{i\rightarrow j} \bot$. Using the semantics of single commitment, for all global states $w_2 \in W$ such that $w_1 \sim _{i\rightarrow j} w_2$, we have $(\mathcal {M}, w_2) \models \bot$$(i.e., (\mathcal {M}, w_2) \models (\varphi \wedge \lnot \varphi ) )$ which is a contradiction. Therefore, $(\mathcal {M},w_1) \models \lnot C _{i\rightarrow j} \bot$.

$(\Rightarrow )$ Assume that $\mathcal {FR}$ is not serial. We must show $\mathcal {FR} \nvDash \lnot C _{i\rightarrow j} \bot$. Since $\mathcal {FR}$ is not serial, then it could be the case that $(\mathcal {M}, w_1 ) \models C _{i\rightarrow j} \bot$. Therefore, $\mathcal {FR} \nvDash \lnot C _{i\rightarrow j} \bot$. $\square$

Discussion: This postulate illustrates the fact that an agent cannot commit to false, which is reasonable. This postulate is integrated in Al-Saqqar’s postulates (Al-Saqqar et al. 2016), Singh’s postulates (Singh 2008), Chopra’s postulates (Chopra and Singh 2015), and El Kholy’s rules (EL Kholy et al. 2014).

• Pos14. [One-to-group commitment consistency]

Formalization: $\lnot C _{i\rightarrow \varOmega } \bot$.

Meaning: Agent i cannot commit to false towards a group of agents $\varOmega$.

Correspondence: For each frame $\mathcal {FR} = (W, \sim _{i \rightarrow \varOmega })$, $\mathcal {FR} \models \lnot C _{i\rightarrow \varOmega } \bot$ iff $\mathcal {FR}$ is serial.

Proof

$(\Leftarrow )$ Assume that $\mathcal {FR} = (W, \sim _{i \rightarrow \varOmega })$ is serial and let $\mathcal {M} = ( W, \sim _{i \rightarrow \varOmega }, \mathcal {VL} )$ be a model based on $\mathcal {FR}$. Given $w_1 \in W$, we need to prove that $(\mathcal {M},w_1) \models \lnot C _{i\rightarrow \varOmega } \bot$. Assume that $(\mathcal {M}, w_1) \models C_{i\rightarrow \varOmega } \bot$. Using the semantics of one-to-group commitment, for all global states $w_2 \in W$ such that $w_1 \sim _{i\rightarrow \varOmega } w_2$, we have $(\mathcal {M}, w_2) \models (\varphi \wedge \lnot \varphi ) )$ which is a contradiction. Therefore, $(\mathcal {M},w_1) \models \lnot C _{i\rightarrow \varOmega } \bot$.

$(\Rightarrow )$ Assume that $\mathcal {FR}$ is not serial. We need to show that $\mathcal {FR} \nvDash \lnot C _{i\rightarrow \varOmega } \bot$. Since $\mathcal {FR}$ is not serial, then it could be the case that $(\mathcal {M}, w_1 ) \models C _{i\rightarrow \varOmega } \bot$. Therefore, $\mathcal {FR} \nvDash \lnot C _{i\rightarrow \varOmega } \bot$. $\square$

Discussion: This postulate illustrates the fact that an agent i cannot commit to false towards a group of agents. The validity of this postulate comes from the fact that an agent cannot commit to false.

• Pos15. [Group-to-one commitment consistency]

Formalization: $\lnot C _{\varOmega \rightarrow j} \bot$.

Meaning: A group of agents $\varOmega$ cannot commit to false.

Correspondence: For each frame $\mathcal {FR} = (W, \sim _{\varOmega \rightarrow j})$, $\mathcal {FR} \models \lnot C _{\varOmega \rightarrow j} \bot$ iff $\mathcal {FR}$ is serial.

Proof

$(\Leftarrow )$ Assume that $\mathcal {FR} = (W, \sim _{\varOmega \rightarrow j})$ is serial and let $\mathcal {M} = ( W, \sim _{\varOmega \rightarrow j}, \mathcal {VL} )$ be a model based on $\mathcal {FR}$. Given $w_1 \in W$, we need to prove that $(\mathcal {M},w_1) \models \lnot C _{\varOmega \rightarrow j} \bot$. Assume that $(\mathcal {M}, w_1) \models C_{\varOmega \rightarrow j} \bot$. Using the semantics of group-to-one commitment, for all global states $w_2 \in W$ such that $w_1 \sim _{\varOmega \rightarrow j} w_2$, we have $(\mathcal {M}, w_2) \models (\varphi \wedge \lnot \varphi ) )$ which is a contradiction. Therefore, $(\mathcal {M},w_1) \models \lnot C _{\varOmega \rightarrow j} \bot$.

$(\Rightarrow )$ Assume that $\mathcal {FR}$ is not serial. We must show $\mathcal {FR} \nvDash \lnot C _{\varOmega \rightarrow j} \bot$. Since $\mathcal {FR}$ is not serial, then it could be the case that $(\mathcal {M}, w_1 ) \models C _{\varOmega \rightarrow j} \bot$. Therefore, $\mathcal {FR} \nvDash \lnot C _{\varOmega \rightarrow j} \bot$, as desired. $\square$

Discussion: This postulate demonstrates the fact that a group of agents cannot commit to false.

• Pos16. [Fulfillment for single commitment]

Formalization: $Fu (C_{i \rightarrow j}\varphi ) \rightarrow \varphi$.

Meaning: If a single commitment is fulfilled, then its content is satisfied.

Proof

The proof is straightforward from the semantics of single fulfillment. $\square$

Discussion: This postulate illustrates the fact that if an agent i fulfills its commitment, the content of this commitment is satisfied simultaneously, which is reasonable. For example, from the NetBill, when the merchant delivers the required goods, then the delivery holds. Formally, $Fu (C_{merch \rightarrow cust}$Delivery) $\rightarrow Delivery$. This postulate is integrated in Al-Saqqar’s postulates (Al-Saqqar et al. 2016), Chesani’s postulates (Chesani et al. 2013), Yolum and Singh axioms (Yolum and Singh 2004), Chopra and Singh postulates (Chopra and Singh 2015), and El Kholy’s rules (EL Kholy et al. 2014) .

• Pos17. [Fulfillment for one-to-group commitment]

Formalization: $Fu (C_{i \rightarrow \varOmega }\varphi ) \rightarrow \varphi$.

Meaning: When one-to-group commitments are fulfilled, their contents hold.

Proof

Assume that $(\mathcal {M}, w_1) \models Fu (C_{i \rightarrow \varOmega } \varphi )$. We want to prove that $(\mathcal {M}, w_1) \models \varphi$. Using the semantics of $Fu(C_{i \rightarrow \varOmega } \varphi )$, there exists $w_2 \in W$ such that $w_2 \sim _{i \rightarrow \varOmega } w_1$ and $(\mathcal {M},w_2)\models C_{i \rightarrow \varOmega } \varphi$. Using the semantics of $C_{i \rightarrow \varOmega } \varphi$, we have $(\mathcal {M}, w_1) \models \varphi$. So, we are done. $\square$

Discussion: The postulate illustrates the fact that when an agent fulfills the commitment toward a group of agents, the contents of those commitments hold at the same state. For example, once the merchant delivers the requested goods to all the customers, then the delivery holds. Formally, $Fu (C_{merch \rightarrow \varOmega {cust}}$Delivery) $\rightarrow Delivery$.

• Pos18. [Fulfillment for group-to-one commitment]

Formalization: $Fu (C_{\varOmega \rightarrow j}\varphi ) \rightarrow \varphi$.

Meaning: When a group-to-one commitments are fulfilled, their contents hold.

Proof

Assume that $(\mathcal {M}, w_1) \models Fu (C_{\varOmega \rightarrow j} \varphi )$. We want to prove $(\mathcal {M}, w_1) \models \varphi$. Using the semantics of $Fu(C_{\varOmega \rightarrow j} \varphi )$, there exists $w_2 \in W$ such that $w_2 \sim _{\varOmega \rightarrow j} w_1$ and $(\mathcal {M},w_2)\models C_{\varOmega \rightarrow j} \varphi$. Using the semantics of $C_{\varOmega \rightarrow j} \varphi$, we have $(\mathcal {M}, w_1) \models \varphi$. So, we are done. $\square$

Discussion: This postulate is reasonable because when a group of agents fulfill the commitments, the content of those commitments hold at the same state. For example, when a group of customers pays the agreed amount of money to a merchant (i.e., fulfill their commitments), then the payments hold. Formally, $Fu (C_{\varOmega _{cust} \rightarrow merch}$Pay) $\rightarrow Pay$.

• Pos19. [Weaken single fulfillment]

Formalization: $Fu(C _{i\rightarrow j} (\varphi _1 \wedge \varphi _2)) \rightarrow Fu(C _{i\rightarrow j} \varphi _1)$.

Meaning: When an agent i fulfills a conjunction towards an agent j, agent i fulfills every part of the conjunction.

Proof

Suppose that $(\mathcal {M}, w_1) \models Fu(C _{i\rightarrow j} (\varphi _1 \wedge \varphi _2)) \wedge \lnot Fu(C _{i\rightarrow j} \varphi _1)$. Using the semantics of $Fu(C _{i\rightarrow j} \varphi )$, there exists $w_2 \in W$ such that $w_2 \sim _{i \rightarrow j} w_1$ and $(\mathcal {M},w_2)\models C_{i \rightarrow j} (\varphi _1 \wedge \varphi _2)$ and for all $w \in W$ such that $w \sim _{i \rightarrow j} w_1$$(\mathcal {M}, w) \models \lnot C _{i\rightarrow j} \varphi _1$. Using Pos10, a contradiction exists when $w = w_2$. Thus, $(\mathcal {M}, w_1) \models Fu(C _{i\rightarrow j} (\varphi _1 \wedge \varphi _2)) \wedge Fu(C _{i\rightarrow j} \varphi _1)$. So, we are done. $\square$

Discussion: This postulate is reasonable, as when an agent i fulfills a conjunction, i also fulfills each part of the conjunction. From the NetBill, when the merchant fulfills the commitment of delivering both the receipt and the requested goods, then the merchant fulfills delivering the receipts. Formally, $Fu(C _{merch \rightarrow cust} (Receipt \wedge Delivery$)) $\rightarrow Fu(C _{merch \rightarrow cust}$Receipt). This postulate is integrated in Al-Saqqar’s postulates (Al-Saqqar et al. 2016).

• Pos20. [Weaken one-to-group fulfillment ]

Formalization: $Fu(C _{i\rightarrow \varOmega } (\varphi _1 \wedge \varphi _2)) \rightarrow Fu(C _{i\rightarrow \varOmega } \varphi _1)$.

Meaning: When an agent i fulfills a conjunction towards a group of agents $\varOmega$, agent i also fulfills every part of the conjunction.

Proof

Suppose that $(\mathcal {M}, w_1) \models Fu(C _{i\rightarrow \varOmega } (\varphi _1 \wedge \varphi _2)) \wedge \lnot Fu(C _{i\rightarrow \varOmega } \varphi _1)$. Using the semantics of $Fu(C _{i\rightarrow \varOmega } \varphi )$, there exists $w_2 \in W$ such that $w_2 \sim _{i \rightarrow \varOmega } w_1$ and $(\mathcal {M},w_2)\models C_{i \rightarrow \varOmega } (\varphi _1 \wedge \varphi _2)$ and for all $w \in W$ such that $w \sim _{i \rightarrow \varOmega } w_1$, $(\mathcal {M}, w) \models \lnot C _{i\rightarrow \varOmega } \varphi _1$. Using Pos11, a contradiction exists when $w = w_2$. Thus, $(\mathcal {M}, w_1) \models Fu(C _{i\rightarrow \varOmega } (\varphi _1 \wedge \varphi _2)) \wedge Fu(C _{i\rightarrow \varOmega } \varphi _1)$. $\square$

Discussion: The postulate demonstrates the fact that when agent i fulfills a conjunction towards a group of agents $\varOmega$, agent i fulfills each part of the conjunction as well. From the NetBill, when the merchant fulfills the commitments of delivering the requested goods and the receipt to all customers, then the merchant fulfills delivering the goods. Formally, $Fu(C _{merch \rightarrow \varOmega _{cust}}$ (Delivery $\wedge$Receipt)) $\rightarrow Fu(C _{merch \rightarrow \varOmega cust}$Delivery).

• Pos21. [Weaken group-to-one fulfillment]

Formalization: $Fu(C _{\varOmega \rightarrow j} (\varphi _1 \wedge \varphi _2)) \rightarrow Fu(C _{\varOmega \rightarrow j} \varphi _1)$.

Meaning: If a group of agents $\varOmega$ fulfills a conjunction towards an agent i, $\varOmega$ also fulfills every part of the conjunction.

Proof

Assume that $(\mathcal {M}, w_1) \models Fu(C _{\varOmega \rightarrow j} (\varphi _1 \wedge \varphi _2)) \wedge \lnot Fu(C _{\varOmega \rightarrow j} \varphi _1)$. Using the semantics of $Fu(C _{\varOmega \rightarrow j} \varphi )$, there exists $w_2 \in W$ such that $w_2 \sim _{\varOmega \rightarrow j} w_1$ and $(\mathcal {M},w_2)\models C_{\varOmega \rightarrow j} (\varphi _1 \wedge \varphi _2)$ and for all $w \in W$ such that $w \sim _{\varOmega \rightarrow j} w_1$$(\mathcal {M}, w) \models \lnot C _{\varOmega \rightarrow j} \varphi _1$. Using Pos12, a contradiction exists when $w = w_2$. Thus, $(\mathcal {M}, w_1) \models Fu(C _{\varOmega \rightarrow j} (\varphi _1 \wedge \varphi _2)) \wedge Fu(C _{\varOmega \rightarrow j} \varphi _1)$. $\square$

Discussion: This postulate illustrates the fact that if a group of agents $\varOmega$ fulfills a conjunction towards an agent j, $\varOmega$ also fulfill every part of the conjunction. For example, if all merchants fulfill their commitments of delivering both the required goods and the receipts to a given customer, then the merchants fulfill delivering the goods. Formally, $Fu(C _{\varOmega merch \rightarrow cust}$ (Delivery $\wedge$Receipt)) $\rightarrow Fu(C _{\varOmega merch \rightarrow cust}$Delivery).

• Pos22. [Consistency for single fulfillment]

Formalization: $\lnot Fu(C _{i\rightarrow j} \bot )$.

Meaning: A single social commitment to false cannot be fulfilled.

Proof

Assume that $(\mathcal {M}, w_1) \models Fu(C _{i\rightarrow j} \bot )$. Using the semantics of $Fu(C_{i \rightarrow j})$, there exists $w_2 \in W$ such that $w_2 \sim _{i \rightarrow j} w_1$ and $(\mathcal {M},w_2)\models C_{i \rightarrow j } \bot$ which contradicts Pos13. So, we are done. $\square$

Discussion: This postulate is reasonable since there is no possibility to fulfill a commitment that will never happen. This postulate is integrated in Al-Saqqar’s postulates (Al-Saqqar et al. 2016) and El Kholy’s rules (EL Kholy et al. 2014).

• Pos23. [Consistency for one-to-group fulfillment]

Formalization: $\lnot Fu(C _{i\rightarrow \varOmega } \bot )$.

Meaning: A one-to-group committing to false cannot be fulfilled.

Proof

Assume that $(\mathcal {M}, w_1) \models Fu(C _{i\rightarrow \varOmega } \bot )$. From the semantics of $Fu(C_{i \rightarrow \varOmega })$, there exists $w_2 \in W$ such that $w_2 \sim _{i \rightarrow \varOmega } w_1$ and $(\mathcal {M},w_2)\models (C _{i\rightarrow \varOmega } \bot )$ which is a contradiction with Pos14. Thus, we are done. $\square$

Discussion: Similar to the previuos postulate, there is no possibility to fulfill a one-to-group commitment that will never happen.

• Pos24. [Consistency for group-to-one fulfillment]

Formalization: $\lnot Fu(C _{\varOmega \rightarrow j} \bot )$.

Meaning: A group-to-one committing to false cannot be fulfilled.

Proof

Assume that $(\mathcal {M}, w_1) \models Fu(C _{\varOmega \rightarrow j} \bot )$. Using the semantics of $Fu(C _{\varOmega \rightarrow j} \bot )$, there exists $w_2 \in W$ such that $w_2 \sim _{\varOmega \rightarrow j} w_1$ and $(\mathcal {M},w_2)\models (C _{\varOmega \rightarrow j} \bot )$ which is a contradiction with Pos15. So, we are done. $\square$

Discussion: This postulate also indicates that there is no possibility to fulfill a group-to-one commitment, which will never happen.

6.3 Soundness and completeness

After introducing the reasoning postulates, in this section, we want to demonstrate how to use correspondence theory for modal logic (van Benthem 1984) to prove the soundness and completeness of the $\hbox {CTL}^{GC}$ logic. A key point of soundness and completeness of a given MAS is to show its suitability for capturing logic (Varga and Várterész 2008).

Typically, a given logic is considered semantically sound if truth theorems are derived from truth statements (Blackburn et al. 2006). Moreover, Varga (Varga and Várterész 2008) defines soundness as “whenever its decision system is solved for a given set of formulas, then this formula set has a special semantic property.” Where, an MAS system is considered complete, if any truth deduction is expressed as a formal proof in the logic (Blackburn et al. 2006). Furthermore, the relationship between modal logic and possible world semantics can be presented by the fact that modal axioms represent the properties of the accessibility relations (Blackburn et al. 2006). For instance, “A formula is provable in S4 iff it is true in all models based on frames whose accessibility relation is transitive and reflexive” is a typical modal completeness theorem (Blackburn et al. 2006).

To the best of our knowledge, Segerberg(1971) introduced the early completeness theorem in modal logic as follows: “Modal logic L is determined by a class K of Kripke frames” (van Benthem 1984). This theorem illustrates the relationship between a given modal language L represented by a set of axioms and a certain class K of Kripke frames. In this perspective, two approaches have been utilized to prove soundness and completeness. The first approach starts with a certain set K of Kripke frames looking for an axiomatisation L of its model theory, whereas the second approach starts with a given modal logic L looking for a set K of Kripke frames with respect to which it is complete (Blackburn et al. 2006).

In this context, correspondence theory (van Benthem 1984) plays a major role in the theory of modal logic during the last three decades (Al-Saqqar et al. 2016). More concretely, correspondence theory for modal logic addresses the relationship between classes of frames and modal language in a systematic way (Indrzejczak 2008). In particular, correspondence theory for modal logic reflects, in a formal way, correspondence (relation) between a given modal logic L and a certain class K of Kripke frames (Indrzejczak 2008). The existence of such correspondence yields in obtaining a set of soundness and completeness theorems (Singh 2008).

In this work, we follow the same approach of our previous work in Al-Saqqar et al. (2016) to prove the soundness and completeness of the proposed $\hbox {CTL}^{GC}$ logic. As illustrated in Al-Saqqar et al. (2016) and (Singh 2008), when correspondence between the proposed reasoning postulates and certain class of frames exists, this ensures the soundness and completeness of the $\hbox {CTL}^{GC}$ logic. Consequently, we reach the following theorem.

Theorem 1

For $\hbox {CTL}^{GC}$, the logic generated by any subset of postulates $\{Pos1-Pos24\}$ is sound and complete with respect to models that are based on the corresponding classes of frames.

By doing so, we can ensure that $\hbox {CTL}^{GC}$ is a consistent and efficient logic that can handle single and group commitments and their fulfillments. So, it can be used to design reliable MASs.

7 Conclusion and future work

In this work, we provided a new consistent, sound and complete formalism to reason about group social commitments and their fulfillments in MASs. In particular, we introduced $\hbox {CTL}^{GC}$, a new temporal logic for agent communication which extended CTL to allow reasoning about group social commitments and their fulfillment simultaneously. To do so, we first classified groups of interacting agents into divisible and indivisible. Furthermore, we introduced the necessary accessibility relations that are needed to capture the semantics of each group. After that, we provided the syntax and semantics of the proposed logic.

Then, we followed Benthem’s correspondence theory (van Benthem 1984) for modal logic to prove the soundness and completeness of the proposed $\hbox {CTL}^{GC}$ logic. In particular, we developed a set of reasoning postulates in $\hbox {CTL}^{GC}$ and corresponded them to their related classes of frames. Consequently, we proved that the $\hbox {CTL}^{GC}$ logic is sound and complete with respect to models that are built on their corresponding classes of frames. Moreover, to illustrate the proposed postulates and their importance in real life applications, we used the NetBill protocol from the business setting.

As future directions, we plan to investigate the proposed $\hbox {CTL}^{GC}$ logic in the presence of uncertainty. In addition to that, we plan to address the problem of model checking $\hbox {CTL}^{GC}$ by providing the required dedicated algorithms and implementing them on top of a symbolic model checker to gain verification results.

Finally, we plan to integrate knowledge with group commitments in one logic. Consequently, the new logic can reason about knowledge and group social commitments and analyses their interactions.