Formal verification of group and propagated trust in multi-agent systems

Abstract

While modeling trust in multi-agent systems provides a fundamental basis for promoting safe interactions and imitating agents reasoning mechanisms, exploiting model checking techniques to govern the trust relationships between group of agents and other agents is yet to be investigated. In this paper, we present a formal framework that allows individual and group of agents to reason about their trust toward other agents. In particular, we propose a branching time temporal logic BT which includes operators that express concepts such as everyone trust, distributed trust and propagated trust. We develop efficient and scalable reduction algorithms by which model checking BT logic is feasible at design time. We analyze the satisfiability and model checking problems of this logic. Moreover, we present in this manuscript BTT, a new BT Transformation tool, which is developed to automate the verification process. Finally, we demonstrate extensive experimental results, which confirm the theoretical findings and make our approach practical.

1 Introduction

Trust is a crucial basis for the development of effective Multi-Agent System (MAS) applications. It has been extensively addressed in many research contexts (e.g., peer-to-peer networks and grid computing). These researches are mainly placed under two major streams: trust computational models and logical trust formalization. The former measures the value of trust to compute the strength level in which an agent trusts other agents in order to establish future interactions [38, 47, 56]. In this stream, trust was first formalized as a measurable concept in [37]. Following this work, a number of trust models have been put forward and several proposals investigated trust propagation [8, 27]. On the other hand, the latter deals with how one agent in the system can trust that another agent behaves and will perform an action in a certain way [16, 33, 44, 46, 51].

Trust is a complex concept that is hard to be precisely defined. Different meanings of trust have been given in various domains. In the context of MASs, the authors in [7] defined trust as mental attitudes of the truster who believes that the trustee is capable to act and achieve a given goal. From a logical point of view, we can distinguish between two classes: trust that is considered as a relationship between agents in the form of trust(A, B), where A and B are two agents, and trust that is related to a content. Because it disregards the content, the first class has been largely criticised for the problems of transitivity, intentionally and unintentionally untrustworthy transmission, and negative trust multiplication as discussed in [9, 45]. In the second class, modal logics have been widely used to reason about cognitive aspects of trust by many researchers. For instance, in [25], the authors proposed a logical framework for the concept of trust where trust is basically expressed as a combination of different modalities based on the logic of action and time [24] and the BDI logic [12]. In [33], the authors presented a new dynamic logic called DL-BET for reasoning about the interaction between belief, evidence and trust. In [26], the authors considered the setting of stochastic multi-agent systems, where an automated verification framework for quantifying and reasoning about cognitive trust is proposed. Moreover, some proposals have abstracted from the cognitive stance and presented trust as a direct modality. In [16], a new branching temporal logic of preconditional trust, which extends the Computation Tree Logic (CTL) is introduced along with its model checking technique. In [51], the author provided a formal semantics for trust with various logical postulates used to reason about trust from an architectural perspective. The underlying logic is based on the idea of trust as a dependence and combines temporal modalities of linear temporal logic (LTL) [43] and a modality (C) for commitments [49] with a modality (T) for trust. However, most of these approaches focus solely on individual trust that defines trust as a relationship that only involves two agents and is not propagated to other agents.

From the formal verification point of view, the technique of model checking [10, 11] has become one of the most successful approaches widely used for verifying various aspects of MASs. Different contributions have been proposed to extend model checking techniques with the aim of verifying extended temporal logics with agent-related modalities. Several model checker tools based on these proposals have been developed over the past decades. For instance, model checking is considered in verifying epistemic properties expressed using logics of knowledge [31, 34, 36, 42], conditional and unconditional commitments [5, 19, 20, 29], the interaction between knowledge and commitments [2, 52], organizations [55] and services composition [3, 17]. Recent implementations that support more expressive languages in the context of MAS have been also presented. In [30], model checking LDLK, a logic that extends Linear Dynamic Logic (LDL) with knowledge modality, has been studied. In [35], the verification of the logic that combines the epistemic logic with the strategy alternating-time temporal logic (ATL) has been presented.

In this paper, we are interested in trust that goes beyond individuals where one individual agent trusts another agent, toward a group trust where a group of agents trusts a particular agent. We aim to capture the concepts of everyone trust and distributed trust toward a particular agent. Everyone trust is when all the members of the group agree on trusting another agent. Distributed trust is when the trust is distributed among the members of the group. We are also interested in trust that can propagate through the MAS from one agent to another. We are considering these two concepts from the logical perspective, in particular formalization, model checking and satisfiability problems.

This manuscript builds on our prior research published in [15, 16] where we proposed TCTL, a branching temporal logic extending CTL to reason about trust and time in MASs. TCTL is interpreted in a new vector-extended version of interpreted systems that captures the trust relationship between the interacting agents. Reasoning postulates and new symbolic model checking algorithms are presented to formally specify and automatically verify the system under consideration against some desirable properties expressed in TCTL. A new model checker extending MCMAS, called MCMAS-T, dedicated to TCTL, along with its new input language VISPL (Vector-extended ISPL) have been created. However, TCTL does not support group and propagated trust. Moreover, we will show in this paper that this logic cannot be extended to accommodate group and propagated trust because of its limited expressive power. The logic fails to appropriately represent nested trust formulae. We will present a branching time temporal logic named BT that refines TCTL while being expressive enough to go beyond individual trust and include operators that express the concepts of everyone trust, distributed trust and propagated trust. We will also analyze the soundness and completeness with regard to a set of postulates and constraints. Furthermore, we will investigate the model checking and satisfiability problems of this logic using a sound reduction technique.

Fig. 1

A schematic view of our approach

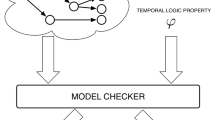
Figure 1 gives an overview of the whole framework, which consists of four parts. The logical part presents the Branching Time Temporal logic BT to reason about individual and group trust. In the transformation algorithms part, we reduce the problem of model checking BT to the problem of model checking CTL so that the use of the NuSMV model checker is made possible. In the complexity analysis part, we utilize the reduction technique to analyze the computational complexity of the problem of model checking BT. The implementation part represents the main core of this paper. We present BTT, the BT Transformation tool that automatically transforms a BT model and formulae into a standard CTL model and formulae. Moreover, the tool interacts automatically with NuSMV as a model checker for CTL.

The paper is organized as follows. We first present the syntax and semantics of TCTL and discuss its limitation in Sect. 2. In Sect. 3, we introduce the Branching Trust Logic (BT). The model checking and satisfiability problems of BT are addressed using a transformation procedure in Sect. 4. The complexity of these problems is analyzed in Sect. 5. In Sect. 6, we present the BTT tool that implements our transformation algorithms and its architecture. Section 7 reveals the experimental results obtained using the tool on two case studies. We end by concluding the paper in Sect. 8.

2 Trust computational temporal logic

2.1 Preliminaries

The semantics of TCTL formulae is interpreted using a model generated from the extended interpreted systems formalism we introduced in [16]. This formalism that extends the original formalism of interpreted systems proposed in [23] explicitly captures the trust relationship established between agents engaged in an interaction. The original formalism is composed of:

• A set $Agt = \{1,\ldots ,n\}$ of n agents where each agent $i\in Agt$ is described by:

  • A non-empty set of local states $L_{i}$, which represents the complete information that the agent can access at any time;

  • A set of local actions $Act_{i}$ to model the temporal evolution of the system;

  • A local protocol $\rho _{i} :L_{i}\rightarrow 2^{Act_{i}}$ assigning a list of enabled actions that may be performed by agent i in a given local state $l_{i}$;

  • A local evolution function $\tau _{i}$ defined as: $\tau _{i} = L_{i}\times Act_{i} \rightarrow L_{i}$, which determines the transitions for an individual agent i between local states;

• A set of global states $s \in S$, where each state represents a snapshot of all agents in the system at a given time. A global state s is a tuple $s =(l_{1}\ldots l_{n})$. The notation $l_{i}(s)$ is used to represent the local state $l_i$ of agent i in the global state s.

• A set of initial global states of the system $I\subseteq S$;

• The global evolution function of the system defined as follows: $\tau : S\times ACT \longrightarrow S$, where $ACT = Act_{1}\times \ldots \times Act_{n}$ and each component $a\in ACT$ is called a joint action, which is a tuple of actions;

• As in [23], a special agent e is used to model the environment in which the agents operate. e is modeled using a set of local states $L_{e}$, a set of actions $Act_{e}$, a protocol $\rho _{e}$, and an evolution function $\tau _{e}$.

In [16], we enriched the formalism of interpreted systems with trust function which associates to each local state $l_i \in L_{i}$ of each agent $i\in Agt$ in the global state $s \in S$ the trust vision of the truster towards other agents in the respective state. This vision is recorded in a vector-based data structure $\nu$ as values the truster associates to the other members of the system This data structure is part of each local state of every agent in the system. Specifically, the trust function gives rise to a binary relation between two states which in fact combines the reachability and compatibility of the local states with respect to the recorded values.

Our motivation behind the use of the notion of agents’ vector $\nu$ is to account for the interaction that occurs during the execution of MAS. That is, for all states $s, s' \in S$ and $i,j \in Agt$, a vector of size n, where n is the number of agents, is associated with each local state $l_{i}\in L_{i}$ of the n agents. The vector $\nu$ is used to define the trust accessibility relation $\sim _{i , j}$. The idea is, the relation $\sim _{i , j}$ relates the states that are considered to be trustful from the vision of agent i with regard to agent j. Specifically, this is obtained by comparing the element $\nu ^{i}(j)$ in the local state $l_{i}$ at the global state s (denoted by $l_{i}(s)(\nu ^{i} (j))$) with $\nu ^{i}(j)$ in the local state $l_{i}$ at the global state $s'$ (denoted by $l_{i}(s')(\nu ^{i} (j))$). Thus, the trust accessibility of agent i toward agent j does exist between two global states only if the element value that we have for agent j in the vector of the local states of agent i for both global states is the same.

Definition 1

(Model of TCTL) $M_{t} ={(S,I,R,\{\sim _{i , j}|(i,j)\in Agt^2\},V)}$ is a model of trust where: S is a non-empty set of reachable global states for the system; I $\subseteq S$ is a set of initial global states for the system; $R\subseteq$ $S\times S$ is the transition relation; $\sim _{i , j}$ $\subseteq S\times S$ is the direct trust accessibility relation for each truster-trustee pair of agents $(i,j)\in Agt^{2}$ defined by $\sim _{i , j}$ iff: (1) $l_{i}(s)(\nu ^{i} (j)) = l_{i}(s')(\nu ^{i} (j))$ and (2) $s'$ is reachable from s using transitions from the transition relation R; $V:S\rightarrow 2^{AP}$ is a labeling function, where AP is a set of atomic propositions.

Figure 2 depicts an example of a trust accessibility relation between two states s and $s'$. In this example, the solid line represents the transition relation from R, and the dashed line represents the direct trust accessibility relation $\sim _{i , j}$ between these two states. The state $s'$ is compatible with s with regard to the trust the agent i has towards agent j. In the figure, we assign a vector to each agent’s local states as follows: $\nu ^{i}$ and $\nu ^{j}$ are the vectors of i and j agents respectively. The agent i compares the element of its vector with regard to the agent j at global states s and $s'$. The particular element value of the agent i is the same in both global states (i.e., $\nu ^{i}(j)(s) = \nu ^{i}(j)(s') = 3$).

Definition 2

(Syntax of TCTL) The syntax of TCTL is defined recursively as follows:

$$\begin{aligned} \varphi {:}{:}= p \;| \; \lnot \varphi \; | \; \varphi \vee \varphi \;|\; EX\varphi \;| \; EG\varphi \; |\; E(\varphi U \varphi ) \; | \; T{(i ,j, \varphi )} \end{aligned}$$

Fig. 2

An example of trust accessibility relation $\sim _{i , j}$

The CTL fragment formulae are defined as usual (see [21]). The formula $T{(i ,j, \varphi )}$ called trust formula is read as “agent i trusts agent j to bring about $\varphi$”.

Definition 3

(Semantics of TCTL)

Given the model $M_{t}$, the satisfaction of a TCTL formula $\varphi$ in a global state s, denoted as $(M_t,s)\models \varphi$, is recursively defined. The semantics of the CTL fragment is as usual [21]. The semantics of the operator T is as follows:

$(M_{\small {t}},s) \models T(i , j, \varphi )$ iff $s \models \lnot \varphi$ and $\forall s' \ne s$ such that $s \sim _{i, j}s'$ we have $(M_{\small {t}},s') \models \varphi$.

The state formula $T(i , j, \varphi )$ is satisfied in the model $M_t$ at s iff $\varphi$ does not hold in s and all the trust accessible states $s'$ that are different from the current state satisfy the content $\varphi$.

2.2 Discussion

Although TCTL has been presented with interesting reasoning postulates [15, 16], a deep analysis of this logic reveals a major paradox resulted from the underlying assumption that complies with the first postulate in [51] stating that “when the content holds, the trust in this content is completed and is, therefore, no longer active”. Formally, the postulate is a as follows:

$$\begin{aligned} \varphi \Rightarrow \lnot T(i,j,\varphi ) \end{aligned}$$

Indeed, enforcing the condition $\lnot \varphi$ to be satisfied in the current state s for the trust to take place yields the following paradoxical postulate:

$$\begin{aligned} T(i,j,\varphi ) \Rightarrow T(i,j, \lnot T(i,j,\varphi )) \end{aligned}$$

which means if there is trust in a content, then there is no trust in this trust. The proof is straightforward since all accessible states satisfy $\lnot T(i,j,\varphi )$ because of the satisfaction of $\varphi$ in these states and the current state satisfies $T(i,j,\varphi )$.

Therefore, this logic is not suitable to reason about trust properties that need nested trust formulae to hold. We present then a refined logic that does not have this postulate, so it can express nested formulae needed for propagated trust, everyone trust and distributed trust.

However, removing the condition that the current state holds $\lnot \varphi$ entails that all tautologies are trusted. Although bringing about tautologies is counter-intuitive, as in the BIAT logic [54], in practical scenarios and applications, nested trust properties are of capital importance. For instance, we should be able to express that a patient Pat can trust the trust judgement that her physician Phy has on a radiologist Rad about recommending biopsies BiopsyRecomm. This property cannot be expressed in TCTL. In BT, it can be expressed as follows:

$$\begin{aligned} T(Pat, Phy, T(Phy, Rad, BiopsyRecomm)) \end{aligned}$$

Other examples of propagated trust, everyone trust and distributed trust are discussed in Sect. 7.

The trust accessibility relation in both TCTL and BT are transitive and not reflexive. The fact that the trust accessibility relation is not reflexive entails that if an agent i trusts an agent j about a content $\varphi$, this content doesn’t necessarily hold in the current state. Formally, $T(i,j,\varphi ) \Rightarrow \varphi$ is not a valid formula in both TCTL and BT. However, $T(i,j,\varphi ) \Rightarrow \lnot \varphi$ is a valid formula in TCTL.

3 Branching trust logic (BT)

3.1 Syntax, semantics and reasoning postulates

In this section, we start by introducing the syntax and semantics of BT, along with a set of reasoning postulates. Thereafter, we use the correspondence theory for modal logic to prove the soundness and completeness of the logic with respect to a certain constraints.

Definition 4

(Syntax of BT)

Let $G \subseteq Agt$ be a group of agents, $AP_b$ a set of atomic propositions, and p an atomic proposition from the set $AP_b$. The syntax of BT is defined recursively as follows:

$$\begin{aligned} \varphi {:}{:}= & {} p \;| \; \lnot \varphi \; |\; \varphi \vee \varphi \; |\; EX\varphi \; | \; EG\varphi \; |\; E(\varphi U \varphi ) \; | \; T\\ T {:}{:}= & {} T{(i ,j, \varphi )} \; | \; E_T{(G ,j, \varphi )} \; | \; D_T{(G ,j, \varphi )} \; | \; P_T^{\mathcal {G}}(i ,j, \varphi ) \end{aligned}$$

The formula T represents trust and three notions of group and propagated trust: $E_T$, $D_T$, and $P_T^G$. The formula $E_T$ refers to “Everyone trusts” and means that everyone in the group G trusts agent j to bring about $\varphi$. Technically, “Everyone trusts” can be seen as the conjunction of the individual trust of each agent in the group. Moreover, $D_T$ denotes “Distributed trust”. That is, the group G has its trust distributed among its member agents. Propagated trust $P_T^{\mathcal {G}}$ indicates that a new trust relationship can be derived from preexisting agent’s trust through an ordered sequence (or chain) of agents ${\mathcal {G}}$. BT formulae are evaluated over an extended Interpreted System $M_{b} ={(S_b,I_b,R_b,\{\sim _{i , j}|(i,j) \in Agt^2\},V_b)}$, which is the same as $M_t$.

The semantics of group and propagated trust is defined using new accessibility relations derived from the trust accessibility relation as follows.

Definition 5

(Group/propagation accessibility relations) The group and propagation accessibility relations are:

• $\sim ^{E}_{G,j} = \bigcup _{i\in G} \sim _{i,j}$, i.e., the union of the trust accessibility relations between every agent of the group G and the agent j.

• $\sim ^{D}_{G,j} = \bigcap _{i\in G} \sim _{i,j}$ , i.e., is the intersection of the trust accessibility relations between every agent in the group G and the agent j.

• $s \sim ^{P\{i_1,\dots ,i_{n-1}\}}_{i,j} s'$ iff there is a chain of states $s_1, \dots , s_{n-1}$ s.t. $s {\sim _{i,i_1}} s_1, s_1 {\sim _{i_1,i_2}} s_2, \dots , s_{n-1}{\sim _{i_{n-1},j}} s'$ where $\{i_1,\dots ,i_{n-1}\}$ is an ordered sequence (or chain) of agents.

Definition 6

(Satisfaction) Given the model $M_b$, the semantics of trust and group trust operators is recursively defined as follows:

• $(M_{\small {b}}, s) \models T(i , j, \varphi )$ iff $\forall s' \ne s$ such that $s \sim _{i, j} s'$, we have $(M_{\small {b}}, s')\models \varphi$.

• $(M_{\small {b}}, s) \models E_T(G , j, \varphi )$ iff $\forall s' \ne s$ such that $s \sim ^{E}_{G,j} s'$, we have $(M_{\small {b}}, s') \models \varphi$.

• $(M_{\small {b}}, s) \models D_T(G , j, \varphi )$ iff $\forall s' \ne s$ such that $s \sim ^{D}_{G,j} s'$, we have $(M_{\small {b}}, s') \models \varphi$.

• $(M_{\small {b}}, s) \models P_T^{\mathcal {G}}(i , j, \varphi )$ iff $\forall s' \ne s$ such that $s \sim ^{P{\mathcal {G}}}_{i,j} s'$ , we have $(M_{\small {b}}, s') \models \varphi$.

According to the semantics of the propagated trust, a propagated trust formula about a content $\varphi$ does not hold iff there is an accessible state that does not satisfy $\varphi$. This would happen iff there is at least an agent in the propagation chain that cannot be trusted to bring about $\varphi$.

Adding an agent $j_1$ at the tail of an ordered sequence of agents ${\mathcal {G}}$ results in an ordered sequence denoted by ${\mathcal {G}}\cup \{j_1\}$. In the same way, adding $j_1$ at the head of ${\mathcal {G}}$ results in an ordered sequence denoted by $\{j_1\} \cup {\mathcal {G}}$. ${\mathcal {G}}\cup \mathcal {G'}$ denotes the ordered sequence obtained by concatenating the elements of the ordered sequence $\mathcal {G'}$ to the tail of the ordered sequence ${\mathcal {G}}$. The following reasoning postulates hold in BT:

• P1. $T(i,j_1,T(j_1,j_2,\varphi ) )\Rightarrow P_T^{\{j_1\}}(i,j_2,\varphi )$

• P2. $P_T^{{\mathcal {G}}}(i,j_1,T(j_1,j_2, \varphi ))\Rightarrow P_T^{{\mathcal {G}}\cup \{j_1\}}(i,j_2,\varphi )$

• P3. $T(i,j_1, P_T^{{\mathcal {G}}} (j_1,j_2, \varphi ))\Rightarrow P_T^{\{j_1\}\cup {\mathcal {G}}} (i,j_2, \varphi )$

• P4. $P_T^{{\mathcal {G}}}(i,j_1, P_T^{\mathcal {G'}} (j_1,j_2, \varphi ))\Rightarrow P_T^{{\mathcal {G}}\cup \{j_1\} \cup \mathcal {G'}} (i,j_2, \varphi )$

• P5. $T(i_1,j,\varphi ) \wedge T(i_2,j,\varphi \Rightarrow \psi ) \Rightarrow D_T (\{i_1, i_2\},j, \psi )$

• P6. $\bigvee \limits _{i \in G}T(i,j,\varphi ) \Rightarrow D_T(G,j, \varphi )$

• P7. $E_T(G,j,\varphi ) \Leftrightarrow \bigwedge \limits _{i \in G} T(i,j, \varphi )$

The first four postulates ($P1 - P4$) capture the trust propagation among agents in one step (1st postulate) or many steps. Thus, P1 states that if there is a trust from i to $j_1$ about the trust that $j_1$ has on $j_2$ about $\varphi$, then there is a propagated trust from i to $j_2$ through $j_1$ about the same content $\varphi$. P2 states that if there is a propagated trust from i to $j_1$ through the chain ${\mathcal {G}}$ about the trust $j_1$ has on $j_2$, then there is a propagated trust from i to $j_2$ through the chain ${\mathcal {G}}$ augmented with the new element $j_1$ as last element. P3 states that if there is a trust from i to $j_1$ about a propagated trust from $j_1$ to $j_2$ through the chain ${\mathcal {G}}$, then there is a propagated trust from i to $j_2$ through the chain ${\mathcal {G}}$ augmented by adding $j_1$ as first element. P4 can be explained in the same way. 5th and 6th postulates ($P5-P6$) capture the properties of the distributed trust among the group members. Thus, P5 states that there is a distributed trust from a group of agents towards an agent j about $\psi$ if some members of the group have trust about $\varphi$ and others about $\varphi \Rightarrow \psi$. Consequently, even if no member has trust on j about $\psi$, as a group they can build this trust. P6 states that a distributed trust from a group towards an agent j emerges if at least one agent in the group has trust on that agent. The 7th postulate (P7) shows the everyone trust property: the group has trust on j about $\varphi$ iff every member of the group has this trust.

Fig. 3

Example (a) of a BT model

Let us assume the model depicted in Fig. 3 as an example. The state $s_0$ is labeled with the trust formula from $i_1$ to $i_2$ to bring about $\varphi$ since the unique accessible state $s_1$ via $\sim _{i_1,i_2}$ is labeled with $\varphi$. As $s_2$ is accessible from $s_1$ via $\sim _{i_2,i_3}$ and labeled with $\varphi$, the trust from $i_2$ to $i_3$ about $\varphi$ holds in $s_1$. Thus, $T(i_1,i_2,T(i_2,i_3, \varphi ))$ holds in $s_0$. Consequently, the propagated trust $P_T^{\{i_2\}}$ from $i_1$ to $i_3$ about $\varphi$ holds in $s_0$. Notice that $s_2$ is accessible from $s_0$ through $\sim ^{P\{i_2\}}_{i_1,i_3}$ because there is a chain of states $s_0, s_1$, and $s_2$ and chain of agents $i_1, i_2$, and $i_3$ linking those states through individual accessibility relations $\sim _{i_1,i_2}$ and $\sim _{i_2,i_3}$.

Another example of a BT model is illustrated in Fig. 4. The state $s_0$ is labeled with the trust formulae from $i_1$ to j and from $i_2$ to j to bring about $\varphi$ respectively. From the figure, the set of states that are accessible from $s_0$ via $\sim _{i_1,j}$ is $\{s_1\}$, and the set of states that are accessible from $s_0$ using $\sim _{i_2,j}$ is $\{s_1, s_2\}$, so the intersection is $\{s_1\}$. As a result, $\{s_1\}$ is the only accessible state from $s_0$ using the accessibility relation $\sim ^{D}_{\{i_1,i_2\},j}$. Because $s_1$ satisfies $\varphi$, $s_0$ satisfies $D_T(\{i_1,i_2\}, j, \varphi )$. Further, the everyone trust $E_T$ from $\{i_1,i_2\}$ to j about $\varphi$ holds in $s_0$ since the states $s_1$ and $s_2$ are accessible from state $s_0$ via both $\sim _{i_1,j}$ and $\sim _{i_2,j}$, and labeled with $\varphi$.

Fig. 4

Example (b) of a BT model

3.2 Soundness and completeness

BT extends the CTL logic. The soundness and completeness of the CTL fragment of BT derives then from the soundness and completeness of CTL. To prove the soundness and completeness of the trust fragment of BT with respect to the postulates introduced in Sect. 3.1, we use the correspondence theory for modal logic introduced by Benthem [6]. According to this theory, a postulate P corresponds to a constraint C iff P is satisfied in precisely those models that respect C. Each constraint C represents in fact a class of models. Thus, correspondence identifies the relationship between the semantics and the reasoning [50]. Proving the existence of the correspondence between a given set of postulates and associated constraints (i.e., related classes of models) provides the soundness and completeness for the logic under consideration with respect to any subset of the postulates [1, 50].

The following constraints define a set of model classes:

• C1. $s_1 \sim _{i,j_1} s_2$ and $s_2 \sim _{j_1,j_2} s_3$ iff $s_1 \sim ^{P\{j_1\}}_{i,j_2} s_3$

• C2. $s_1 \sim ^{P{\mathcal {G}}}_{i,j_1} s_2$ and $s_2 \sim _{j_1,j_2} s_3$ iff $s_1 \sim ^{P{\mathcal {G}}\cup \{j_1\}}_{i,j_2} s_3$

• C3. $s_1 \sim _{i,j_1} s_2$ and $s_2 \sim ^{P{\mathcal {G}}}_{j_1,j_2} s_3$ iff $s_1 \sim ^{P\{j_1\}\cup {\mathcal {G}}}_{i,j_2} s_3$

• C4. $s_1 \sim ^{P{\mathcal {G}}}_{i,j_1} s_2$ and $s_2 \sim ^{P\mathcal {G'}}_{j_1,j_2} s_3$ iff $s_1 \sim ^{P{\mathcal {G}}\cup \{j_1\} \cup \mathcal {G'}}_{i,j_2} s_3$

• C5. $s_1 \sim _{i_1,j} s_2$ and $s_1 \sim _{i_2,j} s_2$ iff $s_1 \sim ^{D}_{\{i_1,i_2\},j} s_2$

• C6. $\bigwedge \limits _{i \in G}s_1 \sim _{i,j} s_2$ iff $s_1 \sim ^{D}_{G,j} s_2$

• C7. $\bigvee \limits _{i \in G}s_1 \sim _{i,j} s_2$ iff $s_1 \sim ^{E}_{G,j} s_2$

The constraints C1 to C4 define classes of transitive models with respect to a combination of direct and propagation trust accessibility relations. Thus, C1 defines the class of models where a direct trust accessibility relation between $s_1$ and $s_2$ and another one between $s_2$ and $s_3$ yield a propagation accessibility relation between $s_1$ and $s_3$. C2 and C3 can be explained in the same way where a propagation accessibility relation is combined with a direct accessibility relation. C4 defines the class of transitive models with respect to propagation accessibility relations. C5 and C6 define the classes of distributed models with respect to a group G. In these models, a distributed trust accessibility relation with respect to G between $s_1$ and $s_2$ exists when the two states are linked by a direct accessibility relation per agent in the group G. Although the constraint C6 is a generalization of the constraint C5, we keep both of them to make the correspondence between the constraints and postulates systematic: the Constraint Ci corresponds to the Postulate Pi. Finally, the constraint C7 defines the class of models where a group accessibility relation $\sim ^{E}_{G,j}$ exists between two states $s_1$ and $s_2$ when a direct accessibility relation does exist between the two states for at least one agent from the group G.

For each correspondence between a postulate Pi and a constraint Ci, we prove the two directions: $\Rightarrow$, i.e., from the postulate to the constraint; and $\Leftarrow$, i.e., from the constraint to the postulate.

1. C1 corresponds to P1

Proof

$\Rightarrow$. This direction is straightforward from the definition of the propagation accessibility relation (Definition 5) since $p \Rightarrow q$ is equivalent to $\lnot p \vee q$.

$\Leftarrow$. Assume the constraint holds. Then, the states that are accessible from a state $s_1$ through the propagation accessibility relation $\sim ^{P\{j_1\}}_{i,j_2}$ are exactly those obtained through the chain composed of the two accessibility relations $\sim _{i,j_1}$ and $\sim _{j_1,j_2}$. Consequently, states that satisfy $T(i,j_1,T(j_1,j_2,\varphi )$ see all the states that satisfy $\varphi$ and accessible through the combination $\sim _{i,j_1}$ and then $\sim _{j_1,j_2}$. These states satisfy $\varphi$ because they are accessible from the states that satisfy $T(j_1,j_2,\varphi )$ through $\sim _{j_1,j_2}$. Thus, any state that satisfies $T(i,j_1,T(j_1,j_2,\varphi )$ satisfies $P_T^{\{j_1\}}(i,j_2,\varphi )$ as well, so the result. $\square$

2. C2 corresponds to P2

Proof

$\Rightarrow$. This direction is straightforward from the definition of the propagation accessibility relation (Definition 5).

$\Leftarrow$. Assume the constraint holds. Then, $(M_{\small {b}}, s_1) \models P_T^{{\mathcal {G}}}(i,j_1,T(j_1,j_2, \varphi ))$ iff $\forall s_2$ and $s_3$ such that $s_1 \ne s_2 \ne s_3$, $s_1 \sim ^{P{\mathcal {G}}}_{i,j_1} s_2$ and $s_2 \sim _{j_1,j_2} s_3$, we have $(M_{\small {b}}, s_3) \models \varphi$. From the constraint we obtain $(M_{\small {b}}, s_1) \models P_T^{{\mathcal {G}}\cup \{j_1\}}(i,j_2,\varphi )$, so we are done. $\square$

3. C3 corresponds to P3

Proof

$\Rightarrow$. This part is direct from Definition 5.

$\Leftarrow$. Assume the constraint holds. Then, $(M_{\small {b}}, s_1) \models T(i, j_1, P_T^{{\mathcal {G}}} (j_1,j_2, \varphi ))$ iff $\forall s_2$ such that $s_1 \ne s_2$, $s_1 \sim _{i,j_1} s_2$, we have $(M_{\small {b}}, s_2) \models P_T^{{\mathcal {G}}} (j_1,j_2, \varphi )$. This equals to $\forall s_3$ such that $s_2 \ne s_3$, $s_2 \sim ^{P{\mathcal {G}}}_{j_1,j_2} s_3$, we have $(M_{\small {b}}, s_3) \models \varphi$. Consequently, from the constraint, $(M_{\small {b}}, s_1) \models P_T^{\{j_1\}\cup {\mathcal {G}}}(i,j_2, \varphi )$ follows, so the result. $\square$

4. C4 corresponds to P4

Proof

$\Rightarrow$. This part is direct from Definition 5.

$\Leftarrow$. Assume the constraint holds. Then, $(M_{\small {b}}, s_1) \models P_T^{{\mathcal {G}}}(i,j_1, P_T^{\mathcal {G'}} (j_1,j_2, \varphi ))$ iff $\forall s_2$ and $s_3$ such that $s_1 \ne s_2 \ne s_3$, $s_1 \sim ^{P{\mathcal {G}}}_{i,j_1} s_2$ and $s_2 \sim ^{P\mathcal {G'}}_{j_1,j_2} s_3$, we have $(M_{\small {b}}, s_3) \models \varphi$. Consequently, $(M_{\small {b}}, s_1) \models P_T^{{\mathcal {G}}\cup \{j_1\} \cup \mathcal {G'}} (i,j_2, \varphi )$ follows from the constraint, so the result. $\square$

5. C5 corresponds to P5

Proof

$\Rightarrow$. This part is direct from Definition 5.

$\Leftarrow$. Assume the constraint holds. Then, $(M_{\small {b}}, s_1) \models T(i_1,j,\varphi ) \wedge T(i_2,j,\varphi \Rightarrow \psi )$ iff $\forall s_2$ such that $s_1 \ne s_2$ and $s_1 \sim _{i_1,j} s_2$, we have $(M_{\small {b}}, s_2) \models \varphi$, and $\forall s_2$ such that $s_1 \ne s_2$ and $s_1 \sim _{i_2,j} s_2$, we have $(M_{\small {b}}, s_2) \models \varphi \Rightarrow \psi$. This implies, $\forall s_2$ such that $s_1 \ne s_2$, $s_1 \sim _{i_1,j} s_2$ and $s_1 \sim _{i_2,j} s_2$, we have $(M_{\small {b}}, s_2) \models \varphi \wedge \varphi \Rightarrow \psi$, so, $(M_{\small {b}}, s_2) \models \psi$. Consequently, from the constraint we obtain $(M_{\small {b}}, s_2) \models D_T (\{i_1, i_2\},j, \psi )$, so we are done. $\square$

6. C6 corresponds to P6

Proof

$\Rightarrow$. This part follows from Definition 5.

$\Leftarrow$. Assume the constraint holds. Then, $(M_{\small {b}}, s_1) \models \bigvee \limits _{i \in G}T(i,j,\varphi )$ iff $\exists i_1 \in G$ such that $\forall s_2$ such that $s_1 \ne s_2$ and $s_1 \sim _{i_1,j} s_2$, we have $(M_{\small {b}}, s_2) \models \varphi$. This implies, $\forall s_2$ such that $s_1 \ne s_2$, $\bigwedge \limits _{i \in G}s_1 \sim _{i,j} s_2$, we have $(M_{\small {b}}, s_2) \models \varphi$. Consequently, from the constraint we obtain $(M_{\small {b}}, s_2) \models D_T(G,j, \varphi )$, so the result. $\square$

7. C7 corresponds to P7

Proof

$\Rightarrow$. This part follows from Definition 5.

$\Leftarrow$. Assume the constraint holds. Then, $(M_{\small {b}}, s_1) \models \bigwedge \limits _{i \in G} T(i,j, \varphi )$ iff $\forall i \in G$ and $\forall s_2$ such that $s_1 \ne s_2$ and $s_1 \sim _{i,j} s_2$, we have $(M_{\small {b}}, s_2) \models \varphi$. This holds iff, $\bigvee \limits _{i \in G}s_1 \sim _{i,j} s_2$, we have $(M_{\small {b}}, s_2) \models \varphi$. Consequently, from the constraint we obtain $(M_{\small {b}}, s_2) \models E_T(G,j,\varphi )$, so the result. $\square$

The existence of the previous correspondences proves the following theorem:

Theorem 1

(Soundness and completeness) The logic generated by any subset of postulates $P1-P7$ is sound and complete with respect to models that satisfy the corresponding constraints: $C1-C7$.

4 Transformation procedure

To address the model checking and satisfiability problems of BT, we introduce a transformation procedure [19] that allows us to leverage the model checking and satisfiability procedures of CTL [21, 22]. Our technique consists of applying certain reduction rules in order to transform the problem at hand to an existing model checking problem. In fact, transformation has been acknowledged as an alternative mechanism for verifying various MASs aspects. The main advantage of this technique is that it enables the designers of MASs applications to get benefit from powerful and already tested model checkers [2, 20, 36]. Indeed, we have attempted a transformation from TCTL model checking to CTL model checking in [14]. However, this approach does not capture the alignments between source and target models, which results in unsound transformations. Technically, the transformation algorithms for both the model and formulae overlook some critical cases. More precisely, the technique provided for the model consists of adding transitions to represent the accessibility relations, and so, it does not distinguish between original transitions in the original TCTL model and the transitions added in the CTL model. It turns out that some formulae with temporal operators EX and U become true in the transformed CTL model while they are false in the original example model. As a concrete example, consider the original model on the left-hand side of Fig. 5 and suppose that a proposition p is true in $s_2$ (and only in $s_2$). As a consequence, EXp is false in $s_0$ of that model. However, the translated model on the right-hand side contains a temporal transition from $s_0$ to $s_2$ resulted from transforming the accessibility relation between these two states in the original model. This transition makes the formula EXp true in the state $s_0$ of the transformed model, which should not be the case. $\alpha ^i\alpha ^j$ are fresh atomic propositions that are added in accessible states to recognize the accessibility relations is the transformed model.

Fig. 5

An example of the transformation Algorithm presented in [14]

Our new procedure avoids these problems by capturing accessibility relations through distinguishable states and transitions using atomic propositions added in the transformed CTL formulae.

4.1 From BT model to CTL model

In this section, we start by recalling the definition of the CTL model needed for the transformation algorithm.

Definition 7

(Model of CTL) A CTL formula is interpreted over a Kripke structure $M_c ={(S_c, R_c, I_c, V_c)}$, where: $S_c$ is a non-empty set of states for the system; $R_c\subseteq$ $S_c\times S_c$ is the transition relation; $I_c$ $\subseteq S_c$ is a set of possible initial global states for the system; and $V_c:S_c\rightarrow 2^{AP_c}$ is a labeling function that maps each state to the set of CTL propositional variables $AP_c$ holding in it.

Having presented the CTL model, the next step is to establish our transformation procedure. Given a BT model $M_b =(S_b , R_b , I_b ,\{\sim _{i,j}|(i,j)\in Agt^2\} , V_b )$, Algorithm 1 shows how this model, taken as input, is transformed into a CTL model $M_c ={(S_c,R_c,I_c,V_c)}$ as output. Initially, the output model $M_c$ has the same set of system states, initial states, transitions and valuation function as $M_b$ (i.e., $S_c = S_b$; $I_c = I_b$; $R_c=R_b$; and $V_c = V_b$). Thus, at the beginning, the states of $M_c$ are labeled with the same atomic propositions as the states in $M_b$. We define a new set of fresh atomic propositions Prop for the CTL logic needed to represent the trust accessibility relations to capture the semantics of trust operators. Moreover, we define a new atomic proposition $\chi$ for CTL that will be used to preserve the actual temporal transition relation by distinguishing the added states and transitions from the original ones in $M_b$. The set $AP_c$ is then defined as the set $AP_b$ augmented with $\chi$ and the atomic propositions $\alpha ^{ij}, \alpha ^{EGj}, \alpha ^{DGj}$, and $\alpha ^{P{\mathcal {G}}ij}$ for the individual, group, and propagated trust accessibility relations for all the agents i, j, groups G and chains ${\mathcal {G}}$. These atomic propositions are metavariables for the trust formulas. The algorithm proceeds to transform the trust accessibility relations for all the agents. First, it checks if there is an accessibility relation between each pair of distinct states s and $s'$. Based on the type of all the possible accessibility relations, it assigns a specific atomic proposition to the set Prop. A new state $s''$ is added to the set of system states $S_c$ along with new transitions from s to $s''$ and from $s''$ to $s'$ in $R_c$. The idea behind adding a new state along with the transitions is to capture the accessibility relations in $M_b$ through new distinguishable states, transitions and atomic propositions in the transformed CTL formulae. Thus, the trust formula $T(i, j,\varphi )$ for instance will be transformed into $AX(\alpha ^{{i}{j}} \Rightarrow AX{f}(\varphi ))$. The two next operators AX reflect the added state and the two added transitions, and the antecedent $\alpha ^{{i}{j}}$ in the implication is to insure that we are considering a new added state, which is labeled by the atomic proposition $\alpha ^{{i}{j}}$. Further, the new state $s''$ is labeled with $\chi$ and the atomic propositions in the set Prop in order to distinguish the states that are accessible from any other next state that satisfies the trust formulae without having accessibility to the current state. However, to avoid adding many states for different accessibility relations between the same two states, the algorithm checks if $s''$ is already added for another accessibility relation. If $s''$ already exists, the algorithm will only add the atomic propositions Prop to mark the accessible state for any other interacting agents.

Finally, the algorithm returns the transformed model $M_c$ after iterating over all the transitions.

Proposition 1

(Boundedness of model transformation) Let $M_c$ be the model obtained from $M_b$ using Algorithm 1 and $|M_c|$ and $|M_b|$ be the size of $M_c$ and $M_b$ respectively. $|M_c| < 3|M_b|$

Proof

Let $|A_b|$ be the number of accessibility relations in $M_b$, i.e., $|A_b| = |\{\sim _{i,j}|(i,j)\in Agt^2\}|$. We have: $|M_c| = |S_c| + |R_c|$ and $|M_b|=|S_b|+|R_b|+|A_b|$. In the worst case, each pair of distinct states $(s,s') \in R_b$ is connected by exactly one accessibility relation. Since each accessibility relation is translated into one state and two transitions in $M_c$, we obtain: $|M_c|=|S_b|+|R_b|+3|A_b|$. In the general case, more than one accessible state might exist between each pair of states. Since the other accessibility relations benefit from the already added states and transitions, we obtain: $|M_c| \le |S_b|+|R_b|+3|A_b|$. The result then follows. $\square$

4.2 From BT formulae to CTL formulae

Algorithm 2 illustrates the formulae transformation function defined over the structure of the original BT formula. The function is recursive with the propositional variables of $AP_b$ being the base case ($AP_b \subset AP_c$). For the temporal operators, we need to make sure that the transformation does not affect the CTL semantics. That is, since a new state and new transitions are added to the corresponding model $M_c$, we have to make sure that the path through which a formula is satisfied in the original model $M_b$ is still satisfied in the corresponding path of the translated model $M_c$. Indeed, this is the main reason behind the conjunction of $\lnot \chi$ for the temporal operators. This allows us to exclude the additional state and transitions when we consider the satisfaction of the formulae. For instance, the formula $EX\varphi$ is transformed into a CTL formula stating that there exist a path in the next state where the transformation of $\varphi$ and the negation of the atomic proposition $\chi$ (added to represent the temporal transition) is true in this state. For the trust, group trust, and propagated trust modalities, each formula is transformed inductively into CTL according to the defined semantics as follows: along each path, if the next state on that path satisfies the corresponding atomic proposition (from the set Prop), then the next state of the added state also satisfies the transformation of the trust content $\varphi$. The state that satisfies the fresh propositional variable is the added state to capture the corresponding accessibility, which explains the double use of AX.

Fig. 6

An example of the BT transformation Algorithm

In Fig. 6, an example illustrating the transformation of a BT model is demonstrated. On the left side of the figure (part a), the model $M_b$ consists of three global states $s_0$, $s_1$, and $s_2$. The state $s_2$ is accessible from $s_0$ via the accessibility relation $\sim _{i,j}$. Furthermore, T(i, j, p) holds in $s_0$ while the formula EXp does not hold. Using the proposed transformation technique, the model $M_b$ is transformed into the CTL model $M_c$ of the right side (part b) as follows: the temporal transitions in $M_b$ are transformed into transition relations in $M_c$. Further, the accessibility relation in $M_b$ is transformed in $M_c$ as follows: new state $s_{02}$ is added to the set of states in $M_c$ (i.e., $s_{02}$ $\in S_c$) along with two new transitions : $(s_0,s_{02})$ and $(s_{02}, s_2)$. The atomic propositions $\alpha ^{{i}{j}}$ and $\chi$ are also added to represent the accessibility relation. Moreover, each state formula in BT is transformed into a CTL formula using the transformation function f. It is easy to see that the formula EXp does not hold in $M_c$ as desired. Moreover, the formula T(i, j, p) is transformed into f(T(i, j, p) in state $s_0$. The transformed formula $AX(\alpha ^{{i}{j}} \Rightarrow AXp)$ holds in $s_0$ thanks to the added state and transitions as desired.

Proposition 2

(Boundedness of formula transformation) Let $\varphi$ be a BT formula and f the transformation function defined in Algorithm 2. There exists a constant k such that $|f(\varphi ) |< k |\varphi |$, where $|\varphi |$ is the length of $\varphi$.

Proof

The proof is by induction on the structure of the formula.

• The result holds for the base case (atomic propositions).

• For the formula $\phi = \lnot \varphi$, we have $|f(\phi ) |= |f(\varphi ) |+ 1$. Therefore, by assumption that the proposition holds for the formula $\varphi$, $\exists k_{1}$ such that $|f(\phi ) |< k_{1} |\varphi |+1$. Since $|\varphi |< |\phi |$, and $|\phi |> 1$, we get $|f(\phi ) |< (k _{1} + 1)|\phi |$, so the proposition.

• For the formula $\phi = EX \varphi$, we have $|f(\phi ) |= |f(\varphi ) |+ 4$. Therefore, by assumption that the proposition holds for the formula $\varphi$, $\exists k_{1}$ such that $|f(\phi ) |< k_{1} |\varphi |+ 4$. Since $|\varphi |< |\phi |$, and $|\phi |> 1$, we get $|f(\phi ) |< (k _{1} + 4)|\phi |$, so the proposition. The proof for $EG \varphi$ is similar.

• For the formula $\phi = E(\varphi ~\cup ~\psi )$, we have $|f(\phi ) |= |f(\varphi ) |+ |f(\psi )|+ 7$. Thus. by assumption that the proposition holds for the formulae $\varphi$ and $\psi$, $\exists k_{1}, k_{2}$ such that $|f(\phi ) |< k_{1} |\varphi |+ k_{2} |\psi |+ 7$. Because $|\varphi |< |\phi |$, $|\psi |< |\phi |$, and $|\phi |> 1$, we obtain $|f(\phi ) |< (k _{1} + k _{2} + 7)|\phi |$. The proof for $\varphi \vee \psi$ is similar ($k=k_1+k_2+1$).

• For the formula $\phi = T(i, j,\varphi )$, we have ${f} (T(i, j,\varphi ))= AX(\alpha ^{ij} \Rightarrow AX {f}(\varphi ))$. Thus, $|f(\phi ) |= |f(\varphi ) |+4$, and by assumption that the proposition holds for the formula $\varphi$, $\exists k_{1}$ such that $|f(\phi ) |< k_{1} |\varphi |+4$. Since $|\varphi |< |\phi |$, and $|\phi |> 1$, we get $|f(\phi ) |< (k _{1} + 4)|\phi |$, so the proposition. The proof is similar for the group and propagated trust formulae $E_T, D_T$, and $P_T^{\mathcal {G}}$.

$\square$

4.2.1 Model checking

Given a BT model $M_b$ representing a MAS and a BT formula $\varphi$ describing the property that the model $M_b$ has to satisfy, the problem of model checking BT is the problem of verifying whether or not $M_b \models \varphi$. The introduced transformation procedure provides a solution to this problem, by simply calling the model checking procedures of CTL as stated by the following theorem.

Theorem 2

(BT model checking) Let $M_b$ and $\varphi$ be respectively a BT model and formula and let $f(M_b)$ and $f(\varphi )$ be the CTL model and formula obtained via Algorithms 1 and 2 . We have $(M_b, s)\models \varphi$ iff $(f(M_b),s)\models f(\varphi )$.

Proof

We prove this theorem by induction on the structure of the formula $\varphi$.

• For the propositional variables from the set $AP_b$, the result is straightforward (notice that $AP_b \subset AP_c$). The result is also direct for the negation and disjunction cases.

• For the formula $\phi = EX \varphi$, we have $(M_b, s)\models EX \varphi$ iff there exists an immediate successor to s where $\varphi$ holds. Consequently, from the definition of $f(M_b)$ and $f(\varphi )$, we obtain $(M_b, s)\models EX \varphi$ iff $(M_c, s)\models EX(f(\varphi ) \wedge \lnot \chi )$. That is, we are excluding the new added path as this path will never be considered because next state (the added state) has $\chi$ and we are forcing $\lnot \chi$.

• For the formula $\phi = E(\varphi ~\cup ~\psi )$, and from the definition of f, $(f(\varphi ) \wedge \lnot \chi ) ~\cup (f( \psi ) \wedge \lnot \chi )$ captures the semantics of Until in CTL which states the existence of a path starting in the current state that satisfies $(\varphi \wedge \lnot \chi )$ until reaching a state in which $( \psi \wedge \lnot \chi )$ holds, where only original temporal transitions are considered.

• The trust formula: $T(i, j,\varphi )$. $AX(\alpha ^{ij} \Rightarrow AX{f}(\varphi ))$ captures the semantics of the trust formula where all accessible states (those satisfying $\alpha ^{ij}$ in $M_c$) should satisfy $\varphi$. The proof is similar for the group and propagated trust formulae.

$\square$

4.2.2 Satisfiability

Given a BT formula $\varphi$, the satisfiability of BT is the problem of deciding if there exists a model $M_b$ such that $M_b \models \varphi$. As for model checking problem, the transformation procedure provides also a solution for the BT satisfiability problem.

Theorem 3

(BT satisfiability) Let $\varphi$ be a BT formula and $f(\varphi )$ the CTL formula obtained via Algorithm 2. We have $\varphi$ is satisfiable iff $f(\varphi )$ is satisfiable.

Proof

The right implication is direct from Theorem 2 because if there is a model $M_b$ satisfying $\varphi$, then $f(M_b)$ that satisfies $f(\varphi )$ does exist. For the left implication, we can prove by induction on the structure of the formula that if there is a model $M_c$ that satisfies $f(\varphi )$, we can always find a model $M_c'$ that satisfies the same formula where states satisfying fresh propositional variables from $AP_c \setminus AP_b$ do not satisfy any other non-fresh propositional variable from $AP_b$. From $M_c'$ we can construct a model $M_b$ s.t. $f(M_b) =M_c'$. $\square$

5 Complexity analysis

In this section, we will first analyze the time complexity of model checking BT with regard to the size of the explicit model $M_b$ and length of the formula to be checked. Since we are using symbolic model checking of CTL, we will also analyze the space complexity of model checking BT for concurrent programs [32] with respect to the size of the components of these programs and length of the formula. The complexity of the BT satisfiability problem will end this section.

A concurrent program P as introduced in [32], is composed of n concurrent processes $P_{i}$ (modules, protocols, or agents). Each process is described by a transition system $D_{i}$ defined as follows: $D_{i}= (AP_{i},AC_{i},S_{i},\varDelta _{i},s^{0}_{i},L_{i})$ where $AP_{i}$ is a set of local atomic propositions, $AC_{i}$ is a local action alphabet, $S_{i}$ is a finite set of local states, $\varDelta _{i}\subseteq S_{i} \times AC_{i} \times S_{i}$ is a local transition relation, $s^{0}_{i} \in S_{i}$ is an initial state, and $L_{i} : S_{i} \rightarrow 2^{AP_{i}}$ is a local state labeling function.

A concurrent behavior of these processes is obtained by their product which can be described using a global transition system D. The transition actions that appear in several processes are synchronized by common actions. The transition system D is defined as follows: $D = (AP, AC, S,\varDelta ,s^{0},L)$ where:

• $AP = \bigcup ^{ n} _{i=1} AP_{i}$;

• $AC = \bigcup ^{ n} _{i=1} AC_{i}$;

• $S = \prod ^{ n} _{i=1} S_{i}$. The ith component of a state $s \in S$ is denoted by s[i];

• $(s, a, s') \in \varDelta$ iff:

  • 1. for all $1 \le i \le n$ such that $a \in AC_{i}$ we have$(s[i], a, s'[i]) \in \varDelta _{i}$, and

  • 2. for all $1 \le i \le n$ such that $a \notin AC_{i}$ we have $s[i] = s'[i]$;

• $s^0 = (s^0_1, s^0_2, s^0_3,\ldots, s^0_n)$;

• $L(s) = \prod ^{ n} _{i=1} L_{i}(s[i])$ for every $s \in S$.

As our approach is transformation-based, we start by analyzing the time complexity of transforming the BT model and formula with respect to explicit models, where all states and transitions are enumerated. Specifically, we prove that these two transformations are linear with respect to both the input BT model and the formula. The linear complexity of these two transformations entails the P-completeness of the BT model checking problem in explicit models. Given that, we proceed to analyze the space complexity of the BT model checking problem and prove its PSPACE-completeness with respect to concurrent programs where the model has the form of a synchronized product of agent programs. Indeed, our motivation behind considering the complexity of our model checking procedure for concurrent programs that provide compact representations of the systems to be checked is that in practice, existing model checking tools (e.g., MCMAS and NuSMV) do not support explicit representations where states and transitions are listed explicitly (as Kripke-like structures). In fact, only local states and transitions of each component are represented. Therefore, the actual system can still be represented by combining local states and transitions to build reachable states.

5.1 Model checking time complexity

In this subsection, we will prove that model checking BT in explicit models is P-complete, so it can be done in a polynomial running time with respect to the size of the model and length of the formula.

Theorem 4

(Explicit BT model checking: upper bound) The BT model checking problem can be solved in time $O(|M_b |\times |\varphi |)$.

Proof

BT can be reduced to CTL, and it is known from [11] that CTL model checking can be done in a linear time with respect to the size of the CTL model and formula, i.e., $O(|f(M_b)| \times |f(\varphi )|)$. From Proposition 1, $|f(M_b)| < 3|M_b|$, i.e., the size of $f(M_b)$ is linear with the size of $M_b$. Moreover, from Proposition 2, the length of $f(\varphi )$ is linear with the length of $\varphi$. Indeed, Algorithm 2 takes the BT formula $\varphi$ as input and writes recursively the corresponding CTL formula according to the structure of $\varphi$. The time complexity of transforming the BT formula is linear with respect to the length of the input formula $\varphi$. This follows from the fact that (1) the length of the recursion is bounded by the size of the input formula $\varphi$, and (2) the size of $f (\varphi )$ is bounded by the size of $\varphi$, so the theorem. $\square$

Theorem 5

(Explicit BT model checking: completeness) The BT model checking problem is P-complete.

Proof

Membership (i.e., upper bound) in P follows from Theorem 4. Hardness (i.e., lower bound) in P is a result of the polynomial reduction from model checking CTL proved to be P-complete [48]. $\square$

5.2 Model checking space complexity

In this subsection, we will prove that the complexity of BT model checking for concurrent programs is PSPACE-complete. This result means that there is an algorithm solving the problem in polynomial space in the size of the components constituting concurrent programs and the length of the formula being model checked.

Theorem 6

(Polynomial reduction of BT model checking: upper bound) Let $\sqsubseteq _{psr}$ denote the polynomial-space reduction. The problem of model checking BT can be reduced into the problem of model checking CTL in a polynomial space, i.e., $MC(BT) \sqsubseteq _{psr} MC(CTL)$.

Proof

The transformation of the BT model and BT formula into the corresponding CTL model and formula could be computed by a deterministic Turing Machine (TM) in space $O(\log n)$ where n is the size of the input BT model, and polynomial space w.r.t. the length of the BT formula. For the model, TM reads in the input tape a model of BT and produces in the output tape, one-by-one, the same states including the initial ones and the same valuations. Then, for the transitions $(s , s' )$ in the input model, it writes one-by-one, the transitions in the set $R_{c}$. It also reads the accessibility relations $\sim _{i,j}$ between two given states in the input model one-by-one and for each one, it adds an intermediate state to the set $S_{c}$ labeled with two fresh propositional variables: 1) $\alpha ^{{i}{j}}$ that depends on the accessibility relation, and 2) $\chi$, along with two transitions if such a state does not already exist; otherwise, only the propositional variable $\alpha ^{{i}{j}}$ is added. The group and propagated accessibility relations are done in the same way. All these writing operations are clearly logarithmic in space because this transformation is done on-the-fly, step-by-step. Moreover, we showed in Proposition 2 that any BT formula is transformable into a CTL formula whose length is linearly bounded by the length of the input formula. All these recursive transformations are clearly polynomial space in the length of the input formula, so the theorem. $\square$

Theorem 7

(rmBT Model Checking for Concurrent Programs: Completeness) The space complexity of the BT model checking for concurrent programs is PSPACE-complete with respect to the size of the components of these programs and the length of the formula.

Proof

Since model checking CTL is PSPACE-complete for concurrent programs [48], the lower bound of model checking BT is PSPACE as well. In fact, BT subsumes CTL as it integrates the CTL modalities and the trust modalities. The upper bound in PSPACE follows from Theorem 6, so the result. $\square$

5.3 Satisfiability complexity

Theorem 8

(BT satisfiability: completeness) The BT satisfiability problem is EXPTIME-complete.

Proof

Membership. Using the result of Theorem 3, we can imagine an EXPTIME algorithm that solves the BT satisfiability problem as follows: (1) Transform the input BT formula $\varphi$ to the CTL formula $f(\varphi )$ using Algorithm 2. As mentioned in the proof of Theorem 4, this can be done in a linear time; (2) Call the algorithm to solve the satisfiability of $f(\varphi )$ which can be done in EXPTIME [22]. Hardness. The hardness follows from the fact that BT subsumes CTL proven to be EXPTIME-complete [22]. $\square$

6 Implementation

6.1 General overview of the tool

To exemplify the theoretical complexity results and check the effectiveness and scalability of our transformation techniques, we implemented the transformation procedures and developed the BTT tool¹that automatically: (i) transforms a given BT model and formulae to a corresponding CTL model and formulae; and (ii) interacts with the NuSMV model checker in order to perform the verification process. BTT consists of modules implementing the proposed transformation algorithms (Algorithms 1 and 2). Broadly speaking, BTT takes as input a BT model and automatically generates the required SMV modules based on the given interacting agents. Then, the tool uses the NuSMV model checker engine as a core component to perform the verification process. Moreover, the tool is explicitly designed to compute the different sorts of accessibility relation and accessible states. That is, considering the various types of group and propagation accessibility relations (described in Definition 5) results in different computations and implementations by the tool.

The tool is implemented as a transformation platform that integrates the transformation algorithms and the NuSMV verification engine, with the goal of making it robust, well structured and flexible. BTT provides an integrated API (Application Programming Interface) environment organized into a set of different modules and includes several phases. Each module is responsible for a task and entirely independent of the rest to allow for more natural changes and possible extensions in the future, ranging from the underlying model checker, to the delivery mechanism (website instead of desktop application), to the supported languages. The implementation process of Algorithm 1 relies on an API that produces the target model from the input one. The challenging part of the API is the computation of the accessibility relations from the input model using the conditions in Definition 1. The API then loops over all the accessibilities calculated from the model and adds the corresponding transitions.

The implementation of Algorithm 2 is particularly challenging as it requires the design and implementation of an adequate parser. We have implemented a parser that checks the legality of the BT syntax and generates the intended transformed formulae. The parser also supports other capabilities, such as displaying error messages if the input file does not comply with the defined BT grammar. To do so, we used the provided ANother Tool for Language Recognition (ANTLR), integrated capabilities. ANTLR is a powerful parser generator that can process and translate structured text. It takes as input a simple grammar file describing the language and automatically generates a lexer and a parser that can construct parse-trees. BTT provides an extensible CTL ANTLR grammar file augmented with the definitions of the trust modalities and other modalities can be easily added. Our framework then uses the grammar files to construct a parser that would recognize these rules and apply them to the referenced language. Moreover, the ANTLR generated lexer is responsible for tokenizing the input stream. The parser then recognizes the defined rules and generates abstract syntax trees so that a tree-walker artifact can be used to browse the nodes and produce the desired application-specific behavior.

6.2 BTT architecture

The main component of BTT is the core framework, which is the back-end portion of the tool. Figure 7 gives a high level description of the BTT architecture. The core framework has three primary modules:

Fig. 7

General architecture of the BTT tool

• Transformation Module: is responsible for all the parsing and transformation from the BT logic into the CTL logic. It is also responsible for generating the SMV output file to be used with NuSMV. From a functional point of view, it consists of two different libraries: the Transformation API and the Transformation Engine. Technically, the API exposes a set of abstract classes and interfaces to allow the user to implement transformations of both the model and the formulae. The engine, on the other hand, is responsible for the actual transformation process and is made flexible so that other use-defined transformations can be integrated. Broadly specking, the engine supports ANTLR (Version 4) generated parsers, lexers, and tree-walkers. We designed the engine to support these artifacts by fully taking into account the ANTLR generation scheme meta-model. This tool also offers the added benefit of allowing the engine to support any LL(*) grammar, as well as adaptive LL(*) grammars [39,40,41].

• Accessibility Engine: offers an API for the users to define their accessibility relationships. It then uses the said definitions to calculate the accessibility relations automatically from the model.

• NuSMV Bridge Interface: communicates natively with NuSMV and offers the tool the capabilities to interact with NuSMV. It bypasses the NuSMV interactive shell by directly making calls to the core NuSMV API.

Figure 8 illustrates the main interface after invoking the BTT tool. This GUI window provides graphical access to the BT model description. BTT is designed to process models written in the VISPL language [16], the extended version of the ISPL language. It offers scalability mode that allows the designers to use a VISPL file description of the design as an input to the tool. This mode allows for the processing of large systems of multiple agents. That is, the interface enables designers to upload the BT behavioral model by selecting the Upload BT Model button. The scrolling window in the figure specifically depicts the uploaded original model description.

Once the BT model is successfully uploaded and parsed, the designers can automatically generate the corresponding SMV modules by pressing the Generate SMV Model button.

Fig. 8

A snapshot of the BTT GUI startup window

Figure 9 reports the second window where the transformation process of the model and formula is taking place. That is, the input behavioral model is processed by the tool where it configures its states, transition relations between the expected states, and the required atomic propositions and formulae. Notice from the figure that the left panel displays the generated SMV encoding modules, which constitute a CTL model. The generated model is obtained from the input encoding model using the transformation procedures presented in Algorithms 1 and 2 through the following steps:

• The set of interacting agents are extracted as a set of SMV modules instantiated in the main module using the VAR keyword along with local states and vector variables.

• Local actions in the Actions section of the BT model are transformed into input variables in the SMV module using the IVAR statement.

• The local transitions between local states are transformed using the keywords TRANS, and use the next and case expressions to define transitions by means of propositional formulae.

• The initial states of each agent in the BT model are transformed to the corresponding ones under the INIT expression.

• The DEFINE keyword declares the atomic propositions extracted from the BT model.

• Each BT formula is transformed into the corresponding CTL formula using the SPEC keyword.

To verify the constructed CTL model and temporal logic formulae, the generated model is executed using the NuSMV model checker by clicking the button Launch NuSMV. The tool provides full access to all the NuSMV features. For instance, the verification results in the right panel of the figure display the number of reachable states and total time in milliseconds. The total time is the sum of the time of transforming the behavioral model, the time of transforming the formulae, and the verification time. Furthermore, Time/Formula button gives the user an information dialog box about the transformation time of each individual formula (Fig. 10).

It is wroth mentioning that the framework is coded mainly in the JAVA programming language and its related technologies.

Fig. 9

A snapshot of the generated SMV modules and verification results

7 Evaluation and experimental results

In this section, we test the performance of the BTT tool in two application domains along with a set of experiments. In particular, we consider the computation of the set of reachable states, the time for constructing the CTL model and formulae, and the model checking processing time. Our aim is to show the capabilities of BTT in transforming, analyzing, and verifying the presented protocols.

Fig. 10

A snapshot of the information dialog box

7.1 First case study: ordering protocol

We used the well-known ordering protocol that regulates the interaction between seller and buyer agents introduced in [13] and was modelled by various authors [18, 20]. The protocol starts with the buyer requesting the price quote for one or more items from the seller, which replies with an offer. Once the former accepts the offer and the agreed payment is received, the seller starts the delivery. Trusting that the seller will deliver the items as expected (in terms of delivery time, quality of the received items, etc.) and allowing a group of buyers to work together to order complex and large items are important aspects that we consider in this paper. Our motivation is to formalize the protocol requirements using a BT model and express a set of properties using the BT logic. We also aim to check the scalability aspect of our technique.

We started by encoding two interacting agents: seller and buyer and the environment agent that facilitates the communication among these agents. We incremented gradually the number of agents to have more complicated scenarios. We encoded each agent using the VISPL input language of the MCMAS-T model checker introduced in [16]. We described each agent in the system by declaring its main components such as its local states including agent’s vector, declared by means of variables that cannot be observed by other agents to represent the accessibility relations between agents. In fact, considering the accessibility relations between agents by encoding the vector variables allows us to give a group of agents the possibility to establish the trust towards other agents. We also encoded the local actions that are performed in accordance with a local protocol, local transitions, and initial states for each agent. We have considered a certain modeling interleaved technique where each agent in the system is paired with other agents and all the resulting agents move in a parallel way. We used the Explicit interactive mode feature in the MCMAS-T tool that runs the system in interactive mode to validate our modeling and check if it functions as intended. Thereafter, we used our transformation tool to transform the VISPL-like language model and BT formulae into a standard SMV model and CTL formulae in order to start the verification process using the NuSMV model checker.

To verify the correctness of the protocol scenario at design time, we have to express a set of properties. We used the safety (something bad will never happen) and liveness (something good will eventually occur) properties along with some reachability properties. All these properties express relevant and desirable business logic properties. These classes of properties have been widely investigated in different contexts, see for instance [16, 20, 28]. Formally, the safety property $\varphi _1$ expresses the negation of a bad situation where 1) there is trust from everyone in the group Gr of buyers (e.g., $Gr = \{Buyer_1, Buyer_2,Buyer_3\}$) towards the seller with regard to deliver the requested goods as expected; and 2) the payment is fulfilled, but the delivery as expected never happened.

$$\begin{aligned} \varphi _1 = AG ~\lnot (E_T (Gr, ~Seller, ~AF~DeliverGood )~\wedge ~ Payment~\wedge ~ AG ~\lnot DeliverGood) \end{aligned}$$

The liveness property $\varphi _2$ states that in all paths globally, it is always the case that if there is distributed trust from the group Gr to the seller about a complex delivery together with the global payment that has been received, then the complex delivery as expected by the group would eventually happen in all possible executions. In this property, we can imagine that each buyer in the group may have different trust information towards the seller about some particular delivery aspects $Deliver_i$ of the complex delivery CompDeliver, but no buyer, individually, has the full trust information of the seller about the entire delivery process.

$$\begin{aligned} \varphi _2= & {} AG(D_T (Gr, ~Seller, ~AF~CompDeliver)~\wedge Payment~\Rightarrow ~AF~CompDeliver)\\ \end{aligned}$$

where:

$$\begin{aligned} CompDeliver = \bigwedge \limits _{i = 1}^n ~Deliver_i \end{aligned}$$

We also checked some reachability properties such as:

$$\begin{aligned} \varphi _3= & {} EF ~ E_T (Gr,~Seller, ~AF ~ DeliverGood)\\ \varphi _4= & {} EF ~ T(Seller, ~Buyer, ~AF ~Payment )\\ \varphi _5= & {} EF ~ D_T (Gr,~Seller, ~AF ~ CompDeliver ) \end{aligned}$$

For example, the formula $\varphi _3$ checks whether or not there exists a possibility that every member in the group trusts the seller for delivering the requested goods as expected. The properties $\varphi _4$ and $\varphi _5$ are similar. The properties that involve group trust are intuitive and desirable in many business scenarios where organizations, such as coalitions, are in place. Table 1 reports the results of 15 experiments about the verification of the order protocol against the system properties. In the table, the number of reachable states (States#) and the total transformation time of model and formulae along with the execution time in milliseconds are functions of the number of agents (Agents#).

Table 1 Verification results of ordering protocol

7.2 Second case study: breast cancer diagnosis and treatment

Our second case study is the Breast Cancer Diagnosis and Treatment (BCDT)² protocol as an illustrative application example to show how our model checking technique can efficiently be applied on a medical health care platform to check trust and group trust properties. The BCDT protocol is introduced by the Assistant Secretary for Planning and Evaluation (ASPE) project to be used for regulating the interaction between five participating parties involved in the cancer diagnosis process. These parties are: patient (Pat), physician (Phy), pathologist (Path), radiologist (Rad), and registrar. In [29, 53], the authors formalized this scenario in terms of commitments, identifying the contractual business relationships among the parties involved. Indeed, such relationships can be founded as a basic of defining trust specifications as requirements for engineering contracts among parties.

The process of the BCDT protocol starts with diagnosing the patient. If a suspicious mass is detected, the patient is immediately directed by the physician to the radiology department to do a mammography. Based on the patients’ diagnosis result, a notification is sent to the physician to recommend a biopsy if the radiologist detects calcification in the image. The physician requests then the radiologist to carry out a biopsy. The radiologist collects a tissue specimen from the patient and then sends it to the laboratory along with pertinent clinical information for further analysis by the pathologist. This latter analyzes the tissue specimen through imaging studies and determines whether a malignant disease is present or not. Both the radiologist and pathologist generate a report of their collective findings. Finally, the physician reviews the complete report with the patient to decide about a treatment plan. At the same time, the pathologist forwards the report to the registrar whose role is to insert the patient information into the cancer registry.

According to this protocol, five parties are involved in the cancer diagnosis process along with an environment agent e added to the system to model the BCDT process. In this scenario, the trust relationships between the participating parties express the system requirements that regulate the interacting agents. These requirements are specified using our BT logic. Indeed, trust relationships among parties evolve with interactions, and the following atomic propositions represent potential states in the evolution of these relationships: SuspMassDetected for suspicious mass detected, MammoRefer for mammography referral, CalcDetected for calcification detected, BiopsyRecomm for biopsy recommended, TissueAnaly for tissue analysis, BiopsyPerform for perform a biopsy, and SpecialTissueAnaly for a special (advanced) tissue analysis. The involved parties must have the possibility of reaching states in which some of these propositions hold. Thus, the trust relationships are instantiated and help prospective agents decide how should they trust other agents. Considering the same criteria of the first case study results, we report nine experiments in Table 2 for BCDT.

The following protocol properties are expressed in the BT logic to check the correctness of the process model.

$$\begin{aligned} \varphi _1&= EF~ T(Pat, ~Phy, ~SuspMassDetected \Rightarrow AF~MammoRefer) \\ \varphi _2&= EF~ E_T(GrP, ~Rad, ~CalcDetected \Rightarrow AF~BiopsyRecomm ) \\ \varphi _3&= EF~ P_T^{\{Rad\}}(Phy, ~Path, ~BiopsyRecomm \Rightarrow AF~TissueAnaly) \\ \varphi _4&= EF ~P_T^{\mathcal {R}}(Phy, ~Rad, ~EF~BiopsyPerform) \\ \varphi _5&= EF ~ D_T(GrR, ~Path, ~AF ~SpecialTissueAnaly)\\ \end{aligned}$$

These formulae express reachability and liveness properties. For example, the formula $\varphi _1$ encodes the fact that there exists a state reachable from the initial state, such that the patient trusts the physician to refer her to do a mammography upon the detection of a suspicious mass. The formula $\varphi _2$ expresses the possibility where every physician in the group GrP of physicians trusts the radiologist to recommend a biopsy for further clinical assessment when suspicious calcification is being detected. The formula $\varphi _3$ states a case where the physician trusts the pathologist through a radiologist (i.e., propagated trust) to analyze the sample tissue if an appropriate biopsy is recommended. The property $\varphi _4$ encodes a case where we have different radiologists in the system and a chain of trust ${\mathcal {R}}$ exists among them about the abilities to perform a biopsy. This trust is propagated to the physician. The property $\varphi _5$ states the case where the trust is distributed in the group GrR of radiologists towards the pathologist about the capability of the pathologist laboratory to perform an advanced tissue analysis. We can imagine the case where one of the radiologists in the group trusts the pathologist laboratory about the capability of performing this special analysis on the condition that the laboratory is equipped with some state of the art facilities, and another radiologist trusts that the pathologist laboratory has recently obtained this advanced facilities.

Table 2 Verification results of the BCDT protocol

7.3 Performance evaluation

The experimental results in Tables  1 &  2 are intended to give a comprehensive performance evaluation of the BT transformation tool. The testbed of these experiments is running on a machine Intel(R) Core(TM) i7-6700 CPU - 3.40GHZ with 16 GB memory. We considered different number of agents. Our motivation to do so is to achieve different levels of scalability that makes the problem complex enough to observe significant results. For each case study, we report the number of agents (Agent#), the number of reachable states (States#), the model transformation time that denotes the construction time needed for transforming the model in milliseconds, the formulae transformation time in milliseconds, and the total time calculated based on the transformations and verification times. The experiments revealed that all the tested formulae are satisfied. By increasing the number of agents in each experiment, we can observe that the number of reachable states are growing exponentially as we expected. However, the tool shows a significant performance in terms of verification time in each experiment for both case studies when the number of interacting agents are increased. For instance, for the standard ordering protocol scenario, we tested the satisfaction of various temporal formulae within a BT model having a large state-space of 3.51844E+13 states and aggregated from 45 agents in 1519.56 seconds execution time (i.e., the transformation time of both the models and formulae, and the time of the verification process). We were also able to check the BCDT scenario with up to 54 agents with state-space achieving 7.56681E+14 in only 1850.81 seconds. This has been achieved thanks to the high efficiency of the CTL model checking to which the model checking of BT is transformed. It is clear that the transformation times of both the models and formulae increase only logarithmically with regard to the number of states. Moreover, in both case studies, the total time shows a clear polynomial increase. Although the increase rate is much higher when the number of agents increases, it is still polynomial with the number of states. In fact, we are unable to provide a full comparison of these results to other implementations as, to the best of our knowledge, there is no model checker tool that can be used to verify properties of group and propagated trust as we do in this work.

8 Conclusion

In this paper, we presented a formal framework that allows individual and group of agents to reason about their trust toward other agents. In particular, we proposed a branching time temporal logic BT which includes operators that express concepts such as everyone trust, distributed trust and propagated trust. We analyzed the satisfiability and model checking problems of this logic using a reduction technique. We have presented a software tool developed in JAVA for the automatic transformation from BT model checking to CTL model checking. Two multi-agent systems scenarios have been encoded and experimental results have been presented confirming the effectiveness of our approach. For future work, we plan to continue improving the developed BT tool by adding some key features to enable designers to: (1) design the local system of each agent by graphically drawing the required local states, transitions, and the desirable properties; and (2) automate the analysis of counter-examples to identify and indicate the source of errors. Moreover, we plan to analyze the interaction between group commitment and trust, including quantitative group trust [4] from both, specification and model checking standpoints.