1 Introduction

Indeed, the study of non-linear wave phenomena often leads to quasilinear hyperbolic systems of partial differential equations (PDEs). While exact solutions to such non-linear systems are not always achievable, approximate analytical or numerical techniques become valuable tools for gaining insight into the physical phenomena involved. Exact solutions play a crucial role in the development, analysis, and validation of numerical methods for solving specific initial or boundary value problems. Therefore, researchers have a significant interest in obtaining exact solutions for systems of nonlinear PDEs. Indeed, the Lie group of transformations is a powerful method used to study partial differential equations (PDEs) and their solutions. This approach is particularly valuable for systems of non-linear PDEs because it allows us to find exact solutions based on the invariance of the equations under one-parameter Lie group transformations (see [1, 2]). In various fields of mechanics, mathematics, and theoretical physics, the Lie group of transformations plays a vital role in the study of continuous symmetry as it can convert complicated problems into solvable equations. In addition, it is quite difficult to obtain the analytical solution to the system of quasilinear hyperbolic partial differential equations (PDEs). While performing the Lie group of transformations, a solution of the basic equation subject to the boundary condition along with a set of curves which is known as the similarity curves, exists. Using this similarity curve, the system of PDEs can be converted into a system of ordinary differential equations (ODEs). Thereafter, the system of ODEs can be solved numerically, or particular exact solutions to the system can be obtained easily. Logan and Perez [3] investigated a time-dependent problem in shock hydrodynamics by using the Lie group analysis. Towards the study of the Lie group of transformations in various gas dynamics problems, we mention the works of Sharma and Radha [4], Sharma and Arora [5], Arora et al., Chauhan et al. [6,7,8,9,10,11].

In the realm of quasilinear hyperbolic systems of PDEs, a remarkable characteristic lies in the presence of various types of discontinuities in their solutions, such as acceleration waves, shock waves, and more. Among these, shock waves are particularly noteworthy as they generate high temperatures and pressures upon convergence. This unique property of converging shocks has led to their intriguing applications in diverse fields, including medicine and laboratory-based research. The utilization of converging shock waves in the medical field finds significance in the treatment of kidney stones. By harnessing the energy released during the shock wave’s convergence, non-invasive procedures can be employed to break down kidney stones, offering patients a safer and more efficient alternative to traditional surgical methods.

Across the wave (where a wave is defined as a moving surface), specific flow variables or their derivatives experience particular types of discontinuities that travel along the surface. On either side of this surface of discontinuity, the flow variables or their derivatives are linked by a relationship referred to as the "compatibility condition." The initial set of compatibility conditions, arising from the conservation laws applied across the discontinuity surface, is commonly known as the Rankine Hugoniot jump conditions. In continuum mechanics, singular surfaces play a crucial role in describing quasilinear hyperbolic systems by representing the relationship among the flow variables and/or their higher-order derivatives ahead and behind a shock. Thomas [8] introduced these surfaces. The evolutionary behavior of shocks in fluids, using the singular surface theory, has been discussed by many researchers namely McCarthy [13], Quintanilla and Straughan [14], Ruggeri [15], Shyam et al. [16], Sharma and Radha [17], Pandey and Sharma [18], Chadha and Jena [30], Sekhar and Sharma [20], Bira et al. [21] and Mentrelli et al. [22].

In astrophysics and cosmology, many physical phenomena, involving the collapse of self-gravitating interstellar gas clouds, are of great interest due to the description of star formation and become an interesting topic for both astronomers and physicists. Additionally, Muracchini and Ruggeri [23] have delved into the study of acceleration waves, the formation of shocks, and their stability in a gravity-involved atmosphere. An interstellar gas cloud is a complex composition of various elements. It primarily consists of atomic hydrogen in a significant proportion, along with molecular hydrogen. Additionally, there are minor percentages of carbon, oxygen, and heavy elements, some of which exist in ionized form. It is worth noting that the interstellar medium also contains different types of grains and dust [24]. In the context of understanding the behavior of these interstellar gas clouds, researchers have applied the non-linear discontinuity wave propagation theory. Virgopia and Ferraioli [26] examined the gravitational collapse in self-gravitating gaseous systems by utilizing an asymptotic wave approach. Supersonic turbulence plays a crucial role in shaping the structure within the interstellar gas. The gas components in the interstellar medium exhibit highly supersonic velocity dispersion, indicating the presence of shocks in the medium [27].

In the present work, we obtained the particular solution to the system of hyperbolic PDEs governing the one-dimensional motion of a spherically symmetric flow in an inviscid, self-gravitating, interstellar gas cloud by using the Lie group of transformation. By using the singular surface theory, a transport equation for the amplitude of the steepened wave is derived. By using a particular exact solution, the transport equation for the amplitude of the steepened wave is integrated numerically and the behavior of the steepened wave is analyzed. The effects of the exponent of ambient density, exponent of heating-cooling function, and specific heat ratio on the steepened wave are shown graphically.

2 Basic equations

The set of partial differential equations (PDEs) that characterize the one-dimensional, spherically symmetric flow within an inviscid, self-gravitating, interstellar gas cloud is expressed as [23, 25]

$$\begin{aligned} \frac{\partial \rho }{\partial t}+ u\frac{\partial \rho }{\partial r}+\rho \frac{\partial u}{\partial r}+\frac{2\rho u}{r} = 0,\nonumber \\ \frac{\partial u}{\partial t}+u \frac{\partial u}{\partial r}+\frac{1}{\rho }\frac{\partial p}{\partial r}= g, \nonumber \\ \frac{\partial p}{\partial t}+u\frac{\partial p}{\partial r}+\rho a^{2}\left( \frac{\partial u}{\partial r}+\frac{2 u}{r}\right) =-(\gamma -1)\rho L(p,\rho ),\nonumber \\ \frac{\partial g}{\partial t}+u\frac{\partial g}{\partial r}+\frac{2gu}{r}=0, \end{aligned}$$
(1)

where \(u, \rho , p\), t, r, g and \(L(p,\rho )\) denote the velocity, density, pressure, time, spatial coordinate which is radial in spherically symmetric flows, gravitational force per unit mass and energy variation per unit mass (or the cooling-heating function), respectively. The values of parameter L can be positive or negative, depending on whether the gas clouds are cooling or heating, respectively. Here, a refers to the equilibrium speed of sound in an ideal gas and is defined as \(a = (\gamma p/\rho )^{1/2}\), where \(\gamma \) is the adiabatic index. The ideal gas equation of state is given by \(p=\rho {\textbf {R}}{} {\textbf {T}}\), where \({\textbf {R}}\) is the specific gas constant, and \({\textbf {T}}\) is the absolute temperature of the gas.

The above system of PDEs (1) can be written in the matrix form as

$$\begin{aligned} {\mathcal {A}}_{t}+\mathcal {M({\mathcal {A}})}{\mathcal {A}}_{r}+\mathcal {B({\mathcal {A}})}=0, \end{aligned}$$
(2)

where \({\mathcal {A}}=(\rho , u, p, g)^{T}\) and \({\mathcal {B}}=(\frac{2\rho u}{r}, -g, \frac{2\rho u a^{2}}{r}+(\gamma -1)\rho L(\rho , p), \frac{2gu}{r})^{T}\) are the column vectors with superscript T denoting transposition while \({\mathcal {M}}\) is a \(4\times 4\) matrix with non-zero elements \({\mathcal {M}}_{11} = {\mathcal {M}}_{22} = {\mathcal {M}}_{33} = {\mathcal {M}}_{44} =u\), \({\mathcal {M}}_{12}=\rho , {\mathcal {M}}_{23}=1/\rho , {\mathcal {M}}_{32}=\rho a^{2}\). A variable as a subscript denotes the partial differentiation with respect to the indicated variable, if not mentioned.

The matrix \({\mathcal {M}}\) of hyperbolic system admits the following eigenvalues

$$\begin{aligned} \lambda ^{1}=u+a, \quad \lambda ^{2}=u \quad {\rm(double\,\, root)}, \quad \lambda ^{3}=u-a. \end{aligned}$$
(3)

Let \(L^{i}\) and \(R^{i}\) be the left and right eigenvectors corresponding to eigen value \(\lambda ^{i}, i=1, 3\) while the repeated eigenvalues \( \lambda ^{2} \) are taken as \(\lambda ^{21}\) and \(\lambda ^{22}\) with two linearly independent left eigenvectors \(L^{21}, L^{22}\) and right eigenvectors \(R^{21}, R^{22}\) and defined as

$$\begin{aligned} L^{1}= & {} \Big (0, \rho a, 1, 0\Big ), \quad R^{1}=\Big (\frac{1}{2a^{2}},\frac{1}{2\rho a}, \frac{1}{2},0\Big ), \end{aligned}$$
(4)
$$\begin{aligned} L^{21}= & {} \Big (-a^{2}, 0, 1, 0\Big ), \quad R^{21}=\Big (-\frac{1}{a^{2}},0, 0, \frac{1}{a^{2}}\Big ), \end{aligned}$$
(5)
$$\begin{aligned} L^{22}= & {} \Big (1, 0,- \frac{1}{a^{2}}, a^{2} \Big ),\quad R^{22}=\Big (0,0, 0, \frac{1}{a^{2}}\Big ), \end{aligned}$$
(6)
$$\begin{aligned} L^{3}= & {} \Big (0, -\rho a, 1, 0\Big ),\quad R^{3}=\Big (\frac{1}{2a^{2}},\frac{-1}{2\rho a}, \frac{1}{2},0\Big ). \end{aligned}$$
(7)

3 Rankine–Hugoniot conditions

The conservative forms of the system of equations (1) are as follows:

$$\begin{aligned}{} & {} \frac{\partial \rho }{\partial t}+ \frac{\partial (\rho u)}{\partial r}=-\frac{2\rho u}{r},\nonumber \\{} & {} \frac{\partial (\rho u)}{\partial t}+ \frac{\partial (\rho u^{2}+p)}{\partial r}= g\rho -\frac{2\rho u^{2}}{r}, \nonumber \\{} & {} \frac{\partial (pe)}{\partial t}+\frac{\partial (\rho e +p)u}{\partial r} =-\frac{2u(\rho e+p)}{r}\nonumber \\{} & {} \frac{\partial (\rho g)}{\partial t}+\frac{\partial (\rho gu)}{\partial r}=-\frac{4\rho ug}{r}, \end{aligned}$$
(8)

where total energy e is defined as

$$\begin{aligned} e=\frac{p}{(\gamma -1)\rho }+L+\frac{u^{2}}{2}. \end{aligned}$$
(9)

The system described above (8) can be expressed in matrix notation as follows:

$$\begin{aligned} {\mathcal {F}}_{t}(r,t,{\mathcal {A}})+{\mathcal {G}}_{r}(r,t,{\mathcal {A}})={\mathcal {H}}(r,t,{\mathcal {A}}), \end{aligned}$$
(10)

where \( {\mathcal {A}}=(\rho , u, p, g)^{tr}\), \({\mathcal {F}}=(\rho , \rho u, \rho e, \rho g)^{tr}\), \({\mathcal {G}}=(\rho u,(p+\rho u^{2}), u(p+\rho e),\rho ug)\),

\({\mathcal {H}}=(-\frac{2\rho u}{r}, g\rho -\frac{2\rho u^{2}}{r},-\frac{2u(p+\rho e)}{r},-\frac{4\rho ug}{r})\) with “tr" denoting the transpose. The Rankine-Hugoniot jump relation [28] is given by the following

$$\begin{aligned} [{\mathcal {F}}_{k}]V=[{\mathcal {G}}],\quad k=1,2,3,4. \end{aligned}$$
(11)

In this context, we define V as the shock velocity and [X] as the jump in X, represented by the difference between X and its value \(X_{0}\). The subscript 0 is used to denote the medium’s condition ahead of the shock, which is also referred to as the upstream condition whereas without the subscript is used for the medium’s condition behind the shock also referred to as the downstream condition.

Considering equations (10) and (11), the boundary conditions immediately behind the shock front can be derived from the following relationships:

$$\begin{aligned} \rho (V-u)= & {} \rho _{0}(V-u_{0}),\nonumber \\ p+\rho (V-u)^{2}= & {} p_{0}+\rho _{0}(V-u_{0})^{2},\nonumber \\ h+\frac{(V-u)^{2}}{2}= & {} h_{0}+\frac{(V-u_{0})^{2}}{2},\nonumber \\ g= & {} g_{0}, \end{aligned}$$
(12)

Here, the particle velocity relative to the shock velocity behind the wavefront is defined by \(v=V - u\), \(h=\varepsilon +p/\rho \) denotes the enthalpy, where \(\varepsilon =L+ p/((\gamma -1)\rho )\) is the internal energy.

Equations (12)\(_{1}\) and (12)\(_{2}\) imply

$$\begin{aligned} v=\frac{\rho _{0}V}{\rho }, \quad p=p_{0}+\rho _{0}V^{2}-\frac{\rho _{0}^{2}V^{2}}{\rho }. \end{aligned}$$
(13)

Using (13) into (12)\(_{3}\), we get the following quadratic equation in density \(\rho \) across the shock:

$$\begin{aligned}{} & {} \Big (-2p_{0}\gamma +\rho _{0}V^{2}(1-\gamma )\Big )\rho ^{2} -\Big ((-2p_{0}\gamma +\rho _{0}V^{2}(1-\gamma ))\rho _{0}\nonumber \\{} & {} -(\gamma +1)\rho _{0}^{2}V^{2}\Big )\rho -(\gamma +1)\rho _{0}^{3}V^{2}=0. \end{aligned}$$
(14)

The equation Eq. (14) can be readily solved to determine the density ?(R(t)) using the flow variables immediately preceding the shock. Subsequently, the other flow variables, u(R(t)), p(R(t)),  and g(R(t)), at the shock front can be obtained from Eqs. (12)–(13) in the following manner:

at shock front:

$$\begin{aligned} \begin{aligned} \rho &= \frac{(\gamma +1)\rho _{0}^{2}V^{2}}{(\gamma -1)\rho _{0}V^{2}+2\gamma p_{0}}, \quad u =\frac{2}{(\gamma +1)}\frac{\rho _{0}V^{2}-\gamma p_{0}}{\rho _{0}V},\\ p &= {} \frac{2\rho _{0}V^{2}-(\gamma -1)p_{0}}{(\gamma +1)},\quad g = g_{o}(R(t)), \end{aligned} \end{aligned}$$
(15)

and for the strong shock:

$$\begin{aligned} \begin{aligned} \rho & = \frac{(\gamma +1)}{(\gamma -1)}\rho _{0},\quad u=\frac{2}{(\gamma +1)}V,\\ p & = \frac{2}{(\gamma +1)}\rho _{0}V^{2},\quad g= g_{o}. \end{aligned} \end{aligned}$$
(16)

4 Self-similar solution using Lie group invariance analysis

In the context of multidimensional problems, the similarity method utilizes a one-parameter Lie group of transformations to successively reduce one independent variable at each step. This process results in a new equation with one fewer independent variable than the previous step. It is essential to ensure that the newly obtained equation remains invariant under the Lie group of transformations throughout each step. Once we have identified the Lie group of transformations that maintains the invariance of the system of PDEs, we can then construct a solution that is also invariant under these transformations. Our specific application of the similarity method involves the study of the motion of converging shock waves in a self-gravitating, interstellar ideal gas cloud. By employing this approach, we aim to gain insights into the behavior of the gas cloud under these conditions.

To obtain the similarity solutions for the system of partial differential equations (PDEs) described by equation (1), we investigate the one-parameter (\(\epsilon \)) Lie group of point transformations (refer to [3]). This Lie group allows us to transform the system of PDEs (1) into a system of ordinary differential equations (ODEs) expressed in a new variable, referred to as the similarity variable. For convenience, we take \(r_1 = t, r_2 = r, u_1 = \rho , u_2 = u, u_3 = p, u_4 = g\), and then, the one-parameter (\(\epsilon \)) Lie group of point transformations for the system (1) is given by

$$\begin{aligned} \begin{aligned} r^*_{l} = r_{l} + \epsilon \, \xi ^{l}_{r}(r_{1},r_{2},u_{1},u_{2},u_{3},u_{4})+O(\epsilon ^{2}), \\ u^*_{n} = u_{n} + \epsilon \, \xi ^{n}_{u}(r_{1},r_{2},u_{1},u_{2},u_{3},u_{4})+O(\epsilon ^{2}), \end{aligned} \end{aligned}$$
(17)

where \(l=1, 2\); \(n=1,2,3,4\); and \(\epsilon \) is a very small parameter. The functions \(\xi ^{l}_{r}\) and \(\xi ^{n}_{u}\) are the infinitesimal generators of the Lie group of transformations which will be determined at a later stage.

By using \(p^n_l = \frac{\partial u_n}{\partial r_l} \), the systems of equations (1) can be written in the following form:

$$\begin{aligned} H_k(r_l,u_n,p^n_l) = 0, \quad k=1,2,3,4, \end{aligned}$$

which remains invariant under the transformations (17), if there exist constants \(\alpha _{ka}(k, a = 1,2,3,4)\) such that

$$\begin{aligned} {\mathcal {L}}H_k = \alpha _{ka} H_{a}, \end{aligned}$$
(18)

which holds for all smooth surfaces \(u_n = u_n(r_l)\). Here, the repeated indices imply the summation convention and \({\mathcal {L}}\) denotes the Lie derivative and can be defined in the direction of the extended vector as

$$\begin{aligned} {\mathcal {L}} = \xi _r^l \frac{\partial }{\partial r_l} + \xi _u^n \frac{\partial }{\partial u_n} + \xi _{p_{l}}^n \frac{\partial }{\partial p_l^n}, \end{aligned}$$
(19)

with \(\xi _r^1 = T, \xi _r^2 = \chi , \xi _u^1 = S, \xi _u^2 = U, \xi _u^3 = P, \xi _u^4 = G\) and

$$\begin{aligned} \xi _{p_{l}}^n = \frac{\partial \xi _u^n}{\partial r_l} + \frac{\partial \xi _u^n}{\partial u_k} p_l^k - \frac{\partial \xi _r^i}{\partial r_l} p_{i}^{n} - \frac{\partial \xi _r^i}{\partial u_j} p_i^n p_l^j, \end{aligned}$$
(20)

where \(i = 1,2; j = 1,2,3,4\) and \(\xi _{pj}^i\) is the generalized derivative transformation.

In view of Eqs. (18)–(20), the system (1) implies

$$\begin{aligned}{} & {} \xi _r^l \frac{\partial H_k}{\partial r_l} + \xi _u^n \frac{\partial H_k}{\partial u_n} + \xi _{p_{l}}^n \frac{\partial H_k}{\partial p_l^n} = \alpha _{ka} H_a, \nonumber \\{} & {} \qquad k = 1,2,3,4; \quad a = 1,2,3,4. \end{aligned}$$
(21)

Using Eq. (20) in (21), we get a polynomial in \(p_l^n\). A system of first-order linear partial differential equations (PDEs) is derived in terms of infinitesimal generators \(T, \chi , S, U, P,\) and G. This is accomplished by equating all the coefficients of \(p_l^n\) to zero. These first-order linear PDEs are commonly referred to as the determining equations. The consistency of these equations leads to the determination of the infinitesimals \(T, \chi , S, U, P,\) and G, and the process is as follows:

$$\begin{aligned} \begin{aligned}T & = a_{1}t+b_{1},\quad \chi =(\alpha _{22}+2a_{1})r +c, S=(\alpha _{11}+a_{1})\rho , \\ U & =(\alpha _{22}+a_{1})u,\\P &= (2 \alpha _{22}+\alpha _{11}+3a_{1})p, \quad G = \alpha _{22}g +d, \quad SL_\rho + PL_p = (2\alpha _{22} + a_{1})L, \end{aligned} \end{aligned}$$
(22)

where \(a_{1}, b_{1}, c, d, \alpha _{11}, \alpha _{22}\) are all arbitrary constants.

In Eq. (22), we consider \(a_{1} \ne 0\), \((\alpha _{22}+2a_{1}) \ne 0 \) and define the new variables \(({\tilde{r}}, {\tilde{t}},{\tilde{g}})\) from (r, t, g) given as

$$\begin{aligned} {\tilde{r}}=r+\frac{c}{\alpha _{22}+2a_{1}},\quad {\tilde{t}} = t + \frac{b_{1}}{a_{1}},\quad {\tilde{g}}=g+\frac{d}{\alpha _{22}}, \end{aligned}$$
(23)

under this condition, all the fundamental equations remain unaltered. When the tilde sign is omitted, the set of infinitesimal generators in Eq. (22) can be expressed as follows:

$$\begin{aligned} \begin{aligned}&T = a_{1}t,\quad \chi = (\alpha _{22}+2a_{1})r,\quad S=(\alpha _{11}+a_{1})\rho ,\quad U =(\alpha _{22}+a_{1})u,\\&P=(2 \alpha _{22}+\alpha _{11}+3a_{1})p, \quad G = \alpha _{22}g, \quad SL_\rho + PL_p = (2\alpha _{22} + a_{1})L. \end{aligned} \end{aligned}$$
(24)

The invariant surface condition [3] yields:

$$\begin{aligned} \begin{aligned} \chi \rho _r + T \rho _t = S, \qquad \chi u_r + T u_t = U,\\ \chi p_r + T p_t = P, \qquad \chi g_r + T g_t = G, \end{aligned} \end{aligned}$$
(25)

on integrating the above conditions together with Eq. (24), the following forms of the flow variables \(\rho , u, p, g\) and L are derived:

$$\begin{aligned} \begin{aligned}\rho &= t^{1+ \frac{\alpha _{11}}{a_{1}}} {\hat{S}} (\xi ), \quad u= t^{\delta -1} {\hat{U}}(\xi ),\quad p= t^{2 \delta -1 + \frac{\alpha _{11}}{a_{1}}} {\hat{P}}(\xi ),\quad g = t^{(\delta -2)} {\hat{G}} (\xi ),\\ \end{aligned} \end{aligned}$$
(26)

where \(\delta = \frac{\alpha _{22}+2a_{1}}{a_{1}}\). The general form of L, allowing for the existence of a self-similar solution, can be expressed in terms of an arbitrary function of \(\eta \) as follows:

$$\begin{aligned} L=\rho ^{\frac{(2 \delta -3)}{\delta \nu }} l(\eta ),\quad \eta =p \rho ^{-\frac{2(\delta -1)+\delta \nu }{\delta \nu }}. \end{aligned}$$
(27)

The functions \({\hat{S}}, {\hat{U}}, {\hat{P}}\) and \({\hat{G}}\) depend on the similarity variable \(\xi =r t^{-\delta }\). Since the shock must be a similarity curve that can be normalized to be at \(\xi = 1\). Thus, the shock path R and shock velocity V are given by

$$\begin{aligned} R= t^\delta , \quad V= \frac{\delta R}{t}. \end{aligned}$$
(28)

At the shock, we have the following conditions on the flow variables \(\rho , u, p\) and g

$$\begin{aligned} \begin{aligned}&\rho |_{\xi =1}=^{(1+ \frac{\alpha _{11}}{a_{1}})} {\hat{S}}(1),\quad u|_{\xi =1} =t^{(\delta -1)} {\hat{U}}(1),\\&p|_{\xi =1}=t^{(2\delta -1 + \frac{\alpha _{11}}{a_{1}})} {\hat{P}}(1), \qquad g|_{\xi =1} = t^{(\delta -2)} {\hat{G}}(1). \end{aligned} \end{aligned}$$
(29)

In view of the invariance of the jump conditions, Eqs. (16) and (25) yield the following forms of \(\rho _0(r)\) and \(g_0(r)\):

$$\begin{aligned} \rho _0(r)=\rho _c r^\nu ,\qquad g_0(r)=g_{0c} r^\sigma . \end{aligned}$$
(30)

together with \(\sigma =\frac{\delta -2}{\delta }, \quad \nu =\frac{\alpha _{11}+a_{1}}{\delta a_{1}}\), where \(\rho _{c}\) and \(g_{0c}\) are some reference constants. In view of Eqs. (29) and (30), the jump conditions (16) for the strong shock reduce as follows:

$$\begin{aligned}{} {} {\hat{S}}(1) & = \frac{\gamma + 1}{\gamma - 1} \rho _c, \quad {\hat{U}}(1) = \frac{2 \delta }{\gamma +1}, \nonumber \\{}{\hat{P}}(1) & = \frac{2\rho _{c} \delta ^{2} }{\gamma +1}, \quad {\hat{G}}(1)=g_{0c}. \end{aligned}$$
(31)

In view of Eqs. (27)–(28) and (30), all the flow variables in Eq. (26) can be written as:

$$\begin{aligned} \begin{aligned}\rho & = \rho _0(R(t)) S^*(\xi ),\quad u =VU^*(\xi ), \\ p &= \rho _0(R(t)) V^2 P^*(\xi ), \quad g = \frac{V}{t} G^*(\xi ),\\ with \quad&L= (\rho _{0}S^{*})^{\frac{(2\delta -3)}{\delta \nu }}l(\eta ),\quad \eta = \rho _{c}\delta ^{2}P^{*} (\rho _{c}S^{*})^{\frac{(2(\delta -1) + \delta \nu )}{\delta \nu }}, \end{aligned} \end{aligned}$$
(32)

where \(S^{*}=\frac{{\hat{S}}}{\rho _{c}}, U^{*}=\frac{{\hat{U}}}{\delta }, P^{*}=\frac{{\hat{P}}}{\rho _{c}\delta ^{2}}, G^{*}=\frac{{\hat{G}}}{\delta }.\)

Using Eq. (32) together with Eqs. (28) and (30) in the system (1), we obtain the following system of ODEs in \(S^*, U^*, P^*\) and \(G^*\) (For simplicity we suppressed asterisk sign)

$$\begin{aligned} \begin{aligned}&(U-\xi )S' + S\Big (\nu + U' + \frac{2U}{\xi }\Big ) = 0,\\&\Big (\frac{\delta -1}{\delta }\Big ) U + (U-\xi )U' + \frac{P'}{S}=\frac{G}{\delta },\\&(U-\xi )P'+ \left( 2\Big (\frac{\delta -1}{\delta }\Big ) + \nu + \gamma \Big (U' + \frac{2U}{\xi }\Big )\right) P \\&+ (\gamma -1)(\rho _{c}\delta ^{3})^{-1}(\rho _{c}S)^{\frac{2\delta -3+\delta \nu }{\delta \nu }}l_*(\eta ) = 0,\\&\Big (\frac{\delta -2}{\delta }\Big ) G + (U-\xi ) G' + \frac{2UG}{\xi } = 0, \end{aligned} \end{aligned}$$
(33)

where \(l_{*}(\eta )=\rho _{c}\delta ^{2}P(\rho _{c}S)^{-({2(\delta -1)+\delta \nu })/\delta \nu }\) and the prime represents the differentiation with respect to similarity variable \(\xi \).

5 Particular solution

It is evident that obtaining the exact solution of the system (33) through analytical methods is a challenging task. As a result, any particular solution of the system holds practical significance as it provides valuable insights into the nature of the solutions. System (33) admits the particular solution of the following forms:

$$\begin{aligned} S=B_{1}\xi ^{-\zeta },\quad U=(\alpha +1)\xi ,\quad P=B_{2}\xi ^{2-\zeta },\quad G=B_{3}\xi , \quad l_{*}(\eta )=\eta ^{k}, \end{aligned}$$
(34)

where \(\alpha \) and \(B_{1}\) are the arbitrary constants. For the particular solution, all the expressions for \(\zeta , B_{2}, B_{3}\) are calculated as follows:

$$\begin{aligned} \zeta= & {} \frac{\nu +3(1+\alpha )}{\alpha },\, \nonumber \\ B_{2}= & {} \Big (\frac{(1-\gamma )(\rho _{c}\delta ^{3})^{(1-k)}\delta ^{-k}(\rho _{c}B_{1})^{(J(1-k)-(3-2k)/\mu )}}{\beta (2-\zeta )+2(\delta -1)/\delta +\nu +3\gamma (1+\beta )}\Big )^{\frac{1}{1-k}},\nonumber \\ B_{3}= & {} \frac{\delta B_{2} (2-\zeta )}{B_{1}}+\delta (\beta +1)\Big (\beta +1-\frac{1}{\delta }\Big ), \end{aligned}$$
(35)

where \(J=(\mu +2\delta )/\mu \) and \(\mu =\delta \nu \).

From Eq. (31), we get the following

$$\begin{aligned} B_{1}=\frac{\gamma +1}{\gamma -1}, \,\alpha =\frac{1-\gamma }{1+\gamma }, \, B_{2}=\frac{2}{\gamma +1},\, B_{3}=\frac{1}{\delta }. \end{aligned}$$
(36)

Using Eqs. (34) and (36) into (33)\(_{3}\), we get the following value of the similarity exponent

$$\begin{aligned} \delta =\frac{3-2k}{4(1-k)}\Big (\frac{(\gamma +1)\nu +6}{\nu +3}\Big ). \end{aligned}$$
(37)

Thus, in this way, from Eq. (32), we get the following particular solution of the system (1)

$$\begin{aligned} \begin{aligned}&\rho = \rho _0(R(t)) S(\xi ),\quad u =VU(\xi ), \quad p= \rho _0(R(t)) V^2 P(\xi ), \\&\quad g = \frac{V}{t} G(\xi ),\\&L= (\rho _{0}S)^{\frac{(2\delta -3)}{\delta \nu }}l(\eta ),\quad \eta = \rho _{c}\delta ^{2}P (\rho _{c}S)^{\frac{(2(\delta -1) + \delta \nu )}{\delta \nu }}. \end{aligned} \end{aligned}$$
(38)

The numerical values of the similarity exponent for different values of the parameters \(\gamma , k\), and \(\nu \) are shown in Table 1 as follows:

Table 1 Numerical values of similarity exponent \(\delta \) for different values of the parameters \(\gamma , k\) and \(\nu \)
Full size table

From Table 1, we can see the effects of various parameters \(\gamma , k\) and \(\nu \) on the similarity exponent \(\delta \). We see that as the value of the adiabatic index \(\gamma \) increases, the value of \(\delta \) decreases. The value of \(\delta \) decreases as we make the decrements in the values of the parameters \(\mu \) and k. As the value of \(\delta \) decreases, the shock collapses much faster. Therefore, an increment in the value of \(\gamma \) and a decrement in the value of \(\nu \) and k make the rate of shock collapse faster. From Eq. (27), the form of heating-cooling function is \(L= \rho ^{\frac{(2\delta -3)}{\delta \nu }}l(\eta )\) which shows that an increment in \(\rho \) gives rise in the the value of L. From this form of L, we must have \((2\delta -3)/\delta \nu >0\), and therefore, \(\nu \) should be negative. Also, we made the following observations on the similarity exponent \(\delta \) calculated in Eq. (37):

$$\begin{aligned} \begin{aligned} \delta &=0 \quad \text{for} \, k=3/2 \, \text{or} \, \nu =-6/(\gamma +1),\\ \delta &=\infty \quad \text{for} \, k=1 \,\,\,\text{or}\,\,\, \nu =-3 \, \text{with} \, k\ne 3/2 \,\text{and} \, \nu \ne -6/(\gamma +1),\\ \delta&<0 \quad \text{for} \, k\in (1, 3/2)\,\,\, \text{or} \,\,\,\nu \in (-6/(\gamma +1),-3),\\0 &<\delta<1 \quad \text{for} \, k>3/2, \\ \delta &>1 \quad \text{for} \,k<1. \end{aligned} \end{aligned}$$
(39)

6 Evolution of steepened wave

Let \(\sum \) be the wavefront of the steepened wave and the curve \(r={\mathcal {R}}(t)\) denote the equation of wavefront. We consider that all the flow variables \(\rho , u, p \) and g across the steepened wave, are necessarily continuous but their first and second-order derivatives are not continuous for \(r_{0}<r_{1}\), i.e., they have a jump for \(r_{0}<r_{1}\). At \(r_{0}\), a steepened wave is considered while at \(r_{1}\), a strong shock is considered. Let the front be moving with speed \({\mathcal {V}}=d{\mathcal {R}}/dt\) originated from \(r=r_{0}\). If A and \({\bar{A}}\), respectively, denote the jumps in the first and second-order space derivatives of \(\rho , u, p\) and g defined on wavefront \(\sum \), we have the following compatibility conditions for the steepened wave [12]

$$\begin{aligned} ||{\mathcal {A}}_{r}||=A,\quad ||{\mathcal {A}}_{t}||=-{\mathcal {V}}A, \quad ||{\mathcal {A}}_{rr}||={\bar{A}},\quad ||{\mathcal {A}}_{rt}||=-{\mathcal {V}}\Big (\frac{dA}{dr}-{\bar{A}}\Big ), \end{aligned}$$
(40)

together with the boundary condition \(||{\mathcal {A}}||=0\). Here, \(||X||=X_{s}-X\) denotes the jump in X across the wave front \(\sum \), where X and \(X_{s}\), respectively, denote the values just ahead and behind of \(\sum \).

Let

$$\begin{aligned} ||\rho _{r}||= & {} \zeta , \quad ||u_{r}||=\lambda ,\quad ||p_{r}||=\sigma ,\quad ||g_{r}||=\eta ,\nonumber \\ ||\rho _{t}||= & {} -{\mathcal {V}}\zeta , \quad ||u_{t}||=-{\mathcal {V}}\lambda ,\quad ||p_{t}||=-{\mathcal {V}}\sigma ,\quad ||g_{t}||=-{\mathcal {V}}\eta . \end{aligned}$$
(41)

In view of Eq. (41), the system (2) on the inner boundary of \(\sum \) gives the following relations:

$$\begin{aligned} ({\mathcal {V}}-u)\zeta =\rho \lambda ,\quad ({\mathcal {V}}-u)\rho \lambda =\sigma ,\quad ({\mathcal {V}}-u)\sigma =\rho a^{2}\lambda ,\quad ({\mathcal {V}}-u)\eta =0. \end{aligned}$$
(42)

The relations between \(\zeta , \lambda , \sigma \) and \(\eta \) are obtained from Eq. (42) as follows:

$$\begin{aligned} \lambda =\frac{a\zeta }{\rho }=\frac{\sigma }{a\rho }, \quad \eta =0. \end{aligned}$$
(43)

On differentiating the system of equation (2) with respect to r and taking jumps over the surface \(\sum \), we get the following set of equations:

$$\begin{aligned}{} & {} ||\rho _{rt}||+2||u_{r}\rho _{r}||+u||\rho _{rr}||+\rho ||u_{rr}||+\frac{2}{r}u||\rho _{r}||+\frac{2\rho }{r}||u_{rr}||=0,\nonumber \\{} & {} \rho \{||u_{tr}||+||u_{r}||^{2}+u||u_{rr}||\}+||p_{rr}||+u||\rho _{r}u_{r}||+||\rho _{r}u_{t}||-g||\rho _{r}||-\rho ||g_{r}||=0,\nonumber \\{} & {} ||p_{tr}||+\Big (1+\frac{a^{2}\rho }{p}\Big )||u_{r}p_{r}||+u||p_{rr}||+\rho a^{2}||u_{rr}||+\frac{2\rho a^{2}}{r}||u_{r}||+\frac{2u\rho a^{2}}{r p}||p_{r}|| \nonumber \\{} & {} +(\gamma -1)\{L||\rho _{r}||+\rho L_{\rho }||\rho _{r}||+\rho L_{p}||p_{r}||\}=0,\nonumber \\{} & {} ||g_{tr}||+||u_{r}g_{r}||+u||g_{rr}||+\frac{2g}{r}||u_{r}||+\frac{2u}{r}||g_{r}||=0. \end{aligned}$$
(44)

Using the notations in Eq. (40), we have

$$\begin{aligned}{} & {} ||\rho _{rr}||={\bar{\zeta }},\quad ||u_{rr}||={\bar{\lambda }},\quad ||p_{rr}||={\bar{\sigma }},\quad ||g_{rr}||={\bar{\eta }},\nonumber \\{} & {} ||\rho _{rt}||={\mathcal {V}}\Big (\frac{d\zeta }{dr}-{\bar{\zeta }}\Big ),\quad ||u_{rt}||={\mathcal {V}}\Big (\frac{d\lambda }{dr}-{\bar{\lambda }}\Big ),\nonumber \\{} & {} \quad ||p_{rt}||={\mathcal {V}}\Big (\frac{d\sigma }{dr}-{\bar{\sigma }}\Big ),\quad ||g_{rt}||={\mathcal {V}}\Big (\frac{d\eta }{dr}-{\bar{\eta }}\Big ). \end{aligned}$$
(45)

Using Eqs. (41)–(43) and (45) in (44), we get the following set of equations:

$$\begin{aligned}{} & {} {\mathcal {V}}\Big (\frac{d\zeta }{dr}-{\bar{\zeta }}\Big )+2\Big (u_{r}||\rho _{r}||+\rho _{r}||u_{r}||+||u_{r}||+||\rho _{r}||\Big )\nonumber \\{} & {} +u{\bar{\zeta }}+\rho {\bar{\lambda }}+\frac{2}{r}\Big (u\zeta +\rho \lambda \Big )=0,\nonumber \\{} & {} \rho \Big ({{\mathcal {V}}\Big (\frac{d\lambda }{dr}-{\bar{\lambda }}\Big )+\lambda ^{2}+2u_{r}\lambda +u{\bar{\lambda }}}\Big )\nonumber \\{} & {} +\Big ({\bar{\sigma }}+\lambda (u-{\mathcal {V}})(\rho _{r}+\zeta )+uu_{r}\zeta +u_{t}\zeta -g\zeta -\rho \eta \Big )=0,\nonumber \\{} & {} {\mathcal {V}}\Big (\frac{d\sigma }{dr}-{\bar{\sigma }}\Big )+\Big (1+\frac{a^{2}\rho }{p}\Big )\Big (\lambda \sigma +u_{r}\sigma +\lambda p_{r}\Big )\nonumber \\{} & {} +u{\bar{\sigma }}+\rho a^{2}\Big ({\bar{\lambda }}+\frac{2\lambda }{r}\Big )+\frac{2u\rho \sigma a^{2}}{rp}\nonumber \\{} & {} +(\gamma -1)\Big (L\zeta +\rho L_{\rho }\zeta +\rho L_{p}\sigma \Big )=0,\nonumber \\{} & {} {\mathcal {V}}\Big (\frac{d\eta }{dr}-{\bar{\eta }}\Big )+\Big (\eta \lambda +u_{r}\eta +g_{r}\lambda \Big )\nonumber \\{} & {} +u{\bar{\eta }}+\frac{2}{r}\Big (g\lambda +u\eta \Big )=0. \end{aligned}$$
(46)

\({\mathcal {V}}=d{\mathcal {R}}/dt=u+a\) is positive for advancing wave. Using \({\mathcal {V}}=u+a\) and Eq. (43) into Eq. (46) and eliminating \({\bar{\zeta }}, {\bar{\lambda }}\) and \({\bar{\sigma }}\), we get the following Bernoulli-type transport equation for \(\lambda \)

$$\begin{aligned} 2\frac{d\lambda }{dt}+\phi _{1}\lambda ^{2}+\phi _{2}\lambda =0, \end{aligned}$$
(47)

where

\(\phi _{1}=1+\frac{a^{2}\rho }{p}\),

\(\phi _{2}=\frac{u_{t}}{a}+\Big (3+\frac{u}{a}+\frac{a^{2}\rho }{p}\Big )u_{r}-\frac{g}{a}-\frac{a\rho _{r}}{\rho }+\Big (\frac{1}{\rho a}+\frac{a}{p}\Big )p_{r}+\frac{2a}{r}+\frac{2u\rho a^{2}}{rp}+(\gamma -1)\Big (\frac{L}{a^{2}}+\frac{\rho L_{\rho }}{a^{2}}+L_{p}\rho \Big ).\)

Since the jump in gradient of flow-field vector \(||{\mathcal {U}}_{r}||\) is collinear with the right eigen vector i.e. \(||{\mathcal {U}}_{r}||=\pi (t) R^{1}\), where \(\pi (t)\) is the amplitude of wave. Therefore, we get \(\pi (t)=2\rho a \lambda \) and then using it in Eq. (47), we obtain the following transport equation for the wave amplitude \(\pi (t)\):

$$\begin{aligned} \frac{d\pi }{dt}+\Phi _{1}\pi ^{2}+\frac{\Phi _{2}}{2}\pi =0, \end{aligned}$$
(48)

where

\(\Phi _{1}=\frac{\phi _{1}}{4\rho a},\)

\(\Phi _{2}=\phi _{2}-\frac{2}{\rho }\frac{d\rho }{dt}-\frac{2}{a}\frac{da}{dt}\) with \(\frac{d}{dt}=\frac{\partial }{\partial t}+(u+a)\frac{\partial }{\partial r}\).

It is worth noting that the amplitude of the wave can be described by a Bernoulli-type equation, which upon integration, yields the amplitude as follows:

$$\begin{aligned} \pi (t)=\frac{\pi _{0}\Theta _{1}(t)}{1+\pi _{0}\Theta _{2}(t)}, \end{aligned}$$
(49)

where \(\Theta _{1}(t)=exp\Big (-\int _{t_{0}}^{t}\frac{\Phi _{2}(t)}{2}dt\Big ),\quad \Theta _{2}(t)=\int _{t_{0}}^{t}\Phi _{1}(t)\Theta _{1}(t)dt,\) and \(\pi _{0}=\pi _{0}(t_{0})\).

7 Numerical results and discussion

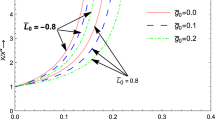
To analyze the behavior of the steepened wave, we use the exact solution of the non-linear hyperbolic system (2) obtained in Eqs. (34) and (38). By using Eqs. (34) and (38), Eq. (48) is integrated numerically and the value of the amplitude of jump in the spatial derivative of velocity is depicted in Figs. 1, 2, 3 for different values of exponent k of heating-cooling function L, ambient density exponent \(\nu \) and specific heat ratio \(\gamma \). From Eq. (49), we may note that, in a finite interval (1,t), \(\Theta _{1}(t)\) is non-zero, finite, and continuous, and \(\Theta _{1}(t)\rightarrow 0\) as \(t\rightarrow \infty \). We see that for \(\pi _{0}>0\) which corresponds to an expansion wave, \(\pi (t)\rightarrow 0\) as \(t\rightarrow \infty \), consequently the steepened wave decays first and thereafter dies out eventually. The corresponding behavior of the steepened wave is shown in Figs. 1, 2, 3 with \(\pi _{0}>0\) for the various values of \(\nu , k\) and \(\gamma \). We can see from Figs. 1 and 2 with \(\pi _{0}>0\), that the decay rate of the steepened wave increases with the decrements in the values of \(\nu \) and k. Also, from Fig. 3, with \(\pi _{0}>0\), we see that the decay rate of the steepened wave for monoatomic gases (\(\gamma =5/3\)) is greater than that of diatomic gases (\(\gamma =7/5\)). However, for \(\pi _{0}<0\) which corresponds to a compression wave, at some finite critical time \(t=t_{c}>1\) given by \(|\Theta _{2}(t_{c})|=1/\pi _{0}\), amplitude \(\pi \) is non-zero, finite and continuous in the interval \([1, t_{c})\) but for \(t\rightarrow t_{c}\), the amplitude \(\pi \rightarrow \infty \) and steepened wave culminates into shock only when \(\pi _{0}<-\pi _{c}<0\) where \(\pi _{c}=1/|\Theta _{2}(\infty )|\) . The corresponding situation is shown in Figs. 1, 2, 3 with \(\pi _{0}<-\pi _{c}<0\) for the various values of \(\nu , k\) and \(\gamma \). From Figs. 1, 2 with \(\pi _{0}<-\pi _{c}<0\), we see that decrements in the values of \(\nu \) and k, increase the decay rate of the steepened wave and speed up the formation of shock. Diatomic gases (\(\gamma =7/5\)) delay the onset of a shock, while the monoatomic (\(\gamma =5/3\)) gases go quickly for the shock formation. This situation is shown in Fig. 3 with \(\pi _{0}<-\pi _{c}<0\).

Fig. 1
figure 1

Evaluation of amplitude \(\pi \) with t for spherically symmetric flow: (a) \(\gamma =7/5, k=2, \rho _{c}=0.1\), (b) \(\gamma =7/5, \nu =-1.2, \rho _{c}=0.1\)

Full size image
Fig. 2
figure 2

Evaluation of amplitude \(\pi \) with t for spherically symmetric flow: (a) \(\gamma =5/3, k=2, \rho _{c}=0.1\), (b) \(\gamma =5/3, \nu =-1.2, \rho _{c}=0.1\)

Full size image
Fig. 3
figure 3

Evaluation of amplitude \(\pi \) with t for spherically symmetric flow: (a) \(\gamma = 7/5\) and 5/3, \(k=2, \nu =2, \rho _{c}=0.1\)

Full size image

8 Conclusions

In the present work, a particular exact solution to the system of the partial differential equation describing the one-dimensional motion of the spherically symmetric flow of an ideal gas in an interstellar gas cloud is obtained by using the group invariance properties of the system via the Lie group method. The effects of the exponent of the heating-cooling function, ambient density exponent, and specific heat ratio are shown on the similarity exponent. A transport equation for the amplitude of the steepened wave is derived by using the singular surface theory. By using a particular exact solution, the transport equation is solved numerically and the evolutionary behavior of the steepened wave is analyzed. The effects of the different values of exponent k of the heating-cooling function L, ambient density exponent \(\nu \), and specific heat ratio \(\gamma \) are shown graphically. We have shown that, for \(\pi _{0}>0\), the steepened waves decay and die out. It has also been shown that after a finite time, only when \(\pi _{0}<-\pi _{c}<0\), the compression wave culminates into a shock. It has been observed that an increase in parameters \(\nu , k\) and a decrease in \(\gamma \) enhance the decay rate of the steepened wave and delay the formation of the shock.

The study of shock wave propagation in a mixture of non-ideal gas and small solid particles has become crucial because there are several applications of it such as in environmental and industrial fields. A few applications include nozzle flow, black hole theory, lunar ash flow, and phenomena like nuclear blasts, volcanic explosions, dusty crystals formation, supersonic flight in dusty air, etc. This literature is quite vast as it is concerned with the study of shock wave propagation in dusty gas [29, 30]. In the future, the present work can be extended to the non-ideal gas with solid small dust particles , and the solutions by using the theory of self-similarity and computational methods can be obtained.