1 Introduction

Spin-orbit coupling (SOC) plays an essential role in realizing many novel phenomena such as topological superconductors and insulators [1,2,3,4], Floquet topological phases [5,6,7], nontrivial superconductors [8, 9], and so on. The realization of SOC in ultracold atomic systems [10,11,12,13] using Raman couplings has attracted a lot of interest in various physics communities. Because of advances in ultracold atomic experimental techniques, Fermi gases with SOC provide a unique and important playground to investigate various novel phases and topological phase transitions. For example, using Feshbach resonances [14, 15], one can tune interactions between atoms from the weakly interacting regime to the strongly interacting regime, driving the system from weakly interacting BCS superfluid to strongly interacting BEC regime (BCS-BEC crossover) [16]. Furthermore, the optical lattice trapping potential makes this system a perfect platform to mimic solid-state systems and related phenomena [17]. In experiments, the topological band structure has been observed by combinations of optical lattice and SOC [18, 19]. Other experimental techniques, such as spectroscopy [20,21,22], dipole interactions [23, 24], reduced dimensions [25], dynamical quench [26], open quantum systems [27], and so on, are also used to detect various phenomena related to Fermi pairing and superfluid [28, 29].

In ultracold atomic systems, one can create any kind of SOC in principle, especially the Rashba [30, 31] and Dresselhaus [32] SOC. Current experimental setup can produce SOC with an arbitrary combination of these two types of SOC [12, 13], therefore creating an anisotropic SOC. Along this line, many theoretical investigations have been performed to study effects of SOC on various superfluid properties [33,34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53]. For the balanced case with an equal number of particles in different internal states, SOC can produce a novel bound-state called Rashbons and induce a crossover from weakly correlated BCS to strongly interacting BEC regime even for very weak particle–particle interaction [43, 44]. And these new bound states have many important implications for various thermodynamic properties of the system. Especially, the opposite effect of SOC on condensation and superfluidity has been discussed in [54]. Furthermore, the combined effect of SOC and Zeeman field can host a non-trivial topological order [55,56,57,58,59,60,61,62,63,64,65,66]. Besides, the presence of a Zeeman field can create a novel FFLO phase which attracts a lot of interest in superconductors and cold atomic systems [67]. For Fermi gases with SOC, a new type of topological FFLO state has also been investigated extensively [47, 68,69,70,71]. Effects of anisotropic SOC on the ground-state properties have also been discussed in [34]. And in [60], effects of anisotropic SOC on BKT [72] transitions and collective sound velocity have been investigated. Furthermore, [73,74,75] provides an intrinsic link between the non-monotonic behavior of the superfluid density and the quantum geometry of the helicity bands.

In this paper, we conducted a detailed study on the effects of an anisotropic SOC on the condensation and superfluidity of a two-dimensional (2D) superfluid system within the framework of mean-field theory using the path-integral formalism. The coupled number and gap equations are numerically solved to obtain the chemical potentials and gap parameters. With the obtained chemical potentials and gap parameters, we calculated the condensed and superfluid fractions as functions of the interaction parameter, SOC strength, and anisotropic parameters. For the condensed fraction, we considered contributions from both the singlet and triplet pairing fields. As a function of the SOC parameters, the condensed fraction behaves non-monotonically for specific interactions, SOC strength, and anisotropic parameters. To obtain the superfluid fraction, we expanded the partition function to the quadratic order of the phase of the order parameter, from which we read off the superfluid fraction. The superfluid fraction is a tensor because of the anisotropic SOC considered in this paper. Our numerical results show that different components of the superfluid tensor behave differently as functions of the SOC and anisotropic parameters.

2 Formalism

The system we consider here is a 2D ultracold Fermi atoms or electrons interacting attractively with a contact interaction. We also consider an anisotropic SOC which can be written as an arbitrary combination of Rashba and Dresselhaus types of SOC. In the path-integral formalism, the system can be described by the finite temperature grand-partition function \(Z=\int d[\bar{ \varphi }_{\sigma },\varphi _{\sigma }]\exp \left( -S[\bar{\varphi }_{\sigma },\varphi _{\sigma }]\right)\) (\(\hbar =k_{B}=1\) through out this paper) with the action \(S[\bar{ \varphi }_{\sigma },\varphi _{\sigma }]\) being given by \(S[\bar{\varphi }_{\sigma },\varphi _{\sigma }]=\int _{0}^{\beta }d\tau \int d^{2}\textbf{r}\sum _{\sigma }[\bar{ \varphi }_{\sigma }\partial _{\tau }\varphi _{\sigma }+\mathcal {H}_{0}+\mathcal {H} _{I}]\) with \(\beta =1/T\), \(\sigma =\uparrow ,\downarrow\) denoting the two different internal states of the atoms or z component eigen states of the spin operator for electrons and \(\bar{\varphi }_{\sigma }, \varphi _{\sigma }\) being the Grassmann fields. The single-particle Hamiltonian density is \(\mathcal {H}(\bar{\psi },\psi )\mathcal {=}\bar{\psi }\left( \hat{\xi }_{\textbf{p }}+\mathcal {H}_{soc}\right) \psi\) where the kinetic operator \(\hat{\xi }_{\textbf{p}}=\hat{\textbf{p}}^{2}/(2m)-\mu\) with \(\mu\) being the chemical potential fixed by the total particle number, the spinor field reads: \(\psi \left( \textbf{r}\right) = \left[ \varphi _{\uparrow }\left( \textbf{r}\right) ,\varphi _{\downarrow }\left( \textbf{r}\right) \right] ^{T}\) and the SOC term can be written as:

$$\begin{aligned} \mathcal {H}_{soc}=\lambda _{R}\left( \sigma _{x}p_{y}-\sigma _{y}p_{x}\right) +\lambda _{D}\left( \sigma _{x}p_{y}+\sigma _{y}p_{x}\right) \end{aligned}$$
(1)

where \(\lambda _{R}\) and \(\lambda _{D}\) denote the Rashba and Dresselhaus SOC parameters, respectively, and \(\sigma _{i=x,y,z}\) are the Pauli matrices. In order to show the anisotropic character transparently, the SOC term can be re-written as: \(\mathcal {H}_{soc}=\lambda _{y}\sigma _{x}p_{y}+\lambda _{x}\sigma _{y}p_{x}\) with \(\lambda _{y}=\lambda _{D}+\lambda _{R}\) and \(\lambda _{x}=\lambda _{D}-\lambda _{R}\). From this definition, we can see that the system is isotropic when \(\lambda _{D}=0\) or \(\lambda _{R}=0\) and anisotropic for equal Rashba and Dresselhaus (ERD) SOC: \(\lambda _{D}=\lambda _{R}\). For convenience, we define the anisotropic parameter as:

$$\begin{aligned} \eta =\frac{\lambda _{D}}{\lambda _{R}} \end{aligned}$$
(2)

Without loss of generality, when \(\eta\) increases from 0 to 1, the system evolves from isotropic Rashba case to anisotropic case with ERD SOC. We denote the SOC strength by:

$$\begin{aligned} \lambda = \sqrt{\lambda _{D}^2+\lambda _{R}^2} \end{aligned}$$
(3)

Finally, the interaction between spin-up and spin-down component can be simplified by a contact interaction model:

$$\begin{aligned} \mathcal {H}_{I}= -g\int d^{2}\textbf{r}\varphi _{\uparrow }^{\dagger }\left( \textbf{r}\right) \varphi _{\downarrow }^{\dagger }\left( \textbf{r} \right) \varphi _{\downarrow }\left( \textbf{r}\right) \varphi _{\uparrow }\left( \textbf{r}\right) \end{aligned}$$
(4)

where \(g>0\) is the contact interaction parameter.

Within path integral methods, the pairing order parameter can be conveniently introduced by using the Hubbard–Stratonovich transformation [76] to decompose the four-body interaction term \(\mathcal {H}_{I}\) by introducing a pairing field \(\Delta \left( \textbf{r},\tau \right)\). After integrating out the fermionic fields, we obtain the effective action of the pairing field as \(S_{eff}\left[ \bar{\Delta },\Delta \right] =-\int _{0}^{\beta }d\tau \int d^{d}\textbf{r}\left| \Delta \left( \textbf{r},\tau \right) \right| ^{2}/g-1/2Tr\ln \left[ \mathcal {G}_{\textbf{r},\tau }^{-1}\right]\) with the inverse Greens’ function \(\mathcal {G}_{\textbf{r},\tau }^{-1}\) being:

$$\begin{aligned} \mathcal {G}_{\textbf{r},\tau }^{-1}=\left[ \begin{array}{cccc} \partial _{\tau }+\hat{\xi }_{\textbf{p}} &{} \hat{\gamma }_{_{\textbf{p}}} &{} 0 &{} \Delta \\ \hat{\gamma }_{_{\textbf{p}}}^{*} &{} \partial _{\tau }+\hat{\xi }_{\textbf{p}} &{} -\Delta &{} 0 \\ 0 &{} -\bar{\Delta } &{} \partial _{\tau }-\hat{\xi }_{\textbf{p}} &{} \hat{\gamma }_{_{\textbf{p}}}^{*} \\ \bar{\Delta } &{} 0 &{} \hat{\gamma }_{_{\textbf{p}}} &{} \partial _{\tau }-\hat{\xi }_{\textbf{p}} \end{array}\right] \end{aligned}$$
(5)

with \(\hat{\gamma }_{_{\textbf{p}}}=\lambda _{y}\hat{p}_{y}+i\lambda _{x}\hat{p}_{x}\).

At mean-field level, the pairing field can be chosen as a real constant parameter \(\Delta \left( \textbf{r},\tau \right) =\Delta _{0}\) which is referred to as the gap parameter. And the effective pairing action becomes \(S_{eff}\left[ \bar{\Delta },\Delta \right] =-\beta V\Delta _{0}^{2}/g-1/2\sum _{\textbf{p},i\omega _{n}}\ln \left[ \det \mathcal {G}_{\textbf{p},i\omega _{n}}^{-1}\right]\) where \(\mathcal {G}_{\textbf{p},i\omega _{n}}^{-1}\) is the Fourier transformation of of Eq. (5) in the momentum-frequency domain, V is the areal size of the system and \(\omega _{n}=\left( 2n+1\right) \pi /\beta\) are the Fermi Matsubara frequencies. From \(\det \mathcal {G}_{\textbf{p},E}^{-1}=0\), the quasi-particle excitation spectrum can be obtained as \(E_{ \textbf{p},\pm }=\sqrt{\left( \xi _{\textbf{p}} \pm \left| \gamma _{\textbf{p}}\right| \right) ^{2}+\Delta _{0}^{2}}\) and \(E_{\textbf{p},\pm }^{\prime }=-E_{\textbf{p},\pm }\) where \(\xi _{\textbf{p}}=\epsilon _{\textbf{p}}-\mu\) with \(\epsilon _{\textbf{p}}=\textbf{p}^{2}/2\,m\) and \(\gamma _{_{\textbf{p}}}=\lambda _{y}p_{y}+i\lambda _{x}p_{x}\). The mean-field thermodynamic potential can be obtained using \(\Omega =-1/\beta \ln Z\) and we have: \(\Omega _{0}=-V\Delta _{0}^{2}/g+1/2\sum _{\textbf{p},\delta }\left( \xi _{\textbf{p}} E_{\textbf{p,}\delta }\right) -1/\beta \sum _{\textbf{p},\delta =\pm }\ln \left( 1+e^{-\beta E_{\textbf{p},\delta }}\right)\). By variation of the thermodynamic potential with respect to the chemical potential and order parameter, we can easily obtain the mean-field gap and number equations:

$$\begin{aligned} \frac{1}{g}= & {} -\frac{1}{V}\sum _{\textbf{p,}\delta =\pm }\frac{\tanh \left( \frac{\beta E_{\textbf{p,}\delta }}{2}\right) }{4E_{\textbf{p,}\delta }}, \end{aligned}$$
(6)
$$\begin{aligned} n= & {} \frac{1}{2V}\sum _{\textbf{p,}\delta =\pm }\left[ 1-\frac{\left( \xi _{ \textbf{p}}+\delta \left| \gamma _{\textbf{p}}\right| \right) \tanh \left( \frac{\beta E_{\textbf{p,}\delta }}{2}\right) }{E_{\textbf{p,}\delta } }\right] \end{aligned}$$
(7)

As usual, divergence of the integral over momenta in Eq. (6) is removed by replacing contact interaction parameter g by binding energy \(E_{b}\) through \(V/g=\sum _{\textbf{p}}1/\left( 2\epsilon _{\textbf{p}}+E_{b}\right)\).

For anisotropic Rashba SOC, Eqs. (6) and (7) are widely used to study the ground state and finite temperature properties of this novel system. It was first shown by Gor’kov and Rashba [30, 31] that, in the presence of a weak SOC, a 2D superconductor supports both singlet and triplet pairing fields. In ultracold atomic systems, this non-trivial physics was investigated in [43, 44] and a proposal for detecting this anisotropic superfluidity was given in [77] through measurement of the momentum distribution and single-particle spectral function. On the other hand, SOC significantly enhances the pairing phenomena as demonstrated by the exact two-body solutions [43, 44] and many-body mean-field calculations [78]. The system can evolve from a BCS to a BEC state driven by SOC even for very weak interactions. Various other properties have been investigated in detail. For anisotropic SOC, however, there are not so many publications concerning the ground-state properties. In [60], they investigated the effect of anisotropic SOC on the BKT transition and collective sound velocity for a 2D Fermi gases. In this paper, we focus on the effect of anisotropic SOC on condensation and superfluidity from a different point of view presented in [73, 74].

3 Condensed density

For Fermi pairing and condensation, according to the concept of off-diagonal long-range-order, the condensed density is generally defined as [79, 80]: \(n_{c}=1/V\sum _{\textbf{p,}ss^{\prime }}\left| \left\langle \bar{\varphi }_{\textbf{p},s}\varphi _{-\textbf{p},s^{\prime }}\right\rangle \right| ^{2}\). For the system considered in this paper, the attractive interaction supports a singlet-pairing field while SOC hybridizes spin degrees of freedom and induces triplet pairing simultaneously. Within mean-field theory, spin-singlet and -triplet pairing fields are given by [77]:

$$\begin{aligned}{} & {} \left\langle \bar{\varphi }_{\textbf{p,}\uparrow }\varphi _{-\textbf{p,}\downarrow }\right\rangle =\Delta _{0}\sum _{\delta }\tanh \left( \beta E_{\textbf{p},\delta }/2\right) /\left( 4E_{\textbf{p},\delta }\right) \end{aligned}$$
(8)
$$\begin{aligned}{} & {} \left\langle \bar{\varphi }_{\textbf{p,}\uparrow }\varphi _{-\textbf{p,}\uparrow }\right\rangle =-\Delta _{0}\left( \gamma _{\textbf{p}}/\left| \gamma _{\textbf{p}}\right| \right) \sum _{\delta }\delta \tanh \left( \beta E_{\textbf{p},\delta }/2\right) /\left( 4E_{\textbf{p},\delta }\right) \end{aligned},$$
(9)

respectively. The spin-singlet contribution to the condensed fraction was first discussed in [34], where it was shown to behave non-monotonically with a minimum as a function of SOC strength for weak enough interaction parameter. In our previous investigations [54], we included both singlet and triplet contributions to the condensed density and obtained:

$$\begin{aligned} n_{c}=\frac{\Delta _{0}^{2}}{4}\frac{1}{V}\sum _{\mathbf {p,\delta }}\frac{ \tanh ^{2}\left( \frac{\beta E_{\textbf{p},\delta }}{2}\right) }{E_{\textbf{p },\delta }^{2}} \end{aligned}$$
(10)

At zero temperature, repulsive interactions between Fermi pairs (Bosons) result in the depletion of the condensate, which is a familiar phenomenon for interacting BEC systems. Therefore, the condensed fraction (condensed density divided by the total density n) is always less than 1.

4 Superfluid density

Unlike the condensed density, superfluid density is a dynamic properties of the system and a tensor in general. In Landau’s theory of superfluidity, the normal masses of the system can be obtained through the calculation of the total momentum carried by excitations when the system is subjected to a uniform flow with velocity [81] \(\textbf{v}_{s}\)

$$\begin{aligned} \textbf{P}=\sum _{\textbf{p,}\sigma }\textbf{p}f\left( E_{\textbf{p,}\sigma }-\mathbf {p\cdot v}_{s}\right) \end{aligned}$$
(11)

where \(\sigma\) is a conserved quantum number which is spin in the absence of SOC, \(f\left( x\right) =1/\left( e^{\beta x}\pm 1\right)\) is the Fermi/Bose distribution function depending on the nature of the excitations, and \(E_{\textbf{p,}\sigma }-\mathbf {p\cdot v}_{s}\) is the excitation spectrum for moving systems. At zero temperature, no excitations are created at very small \(\textbf{v}_{s}\) and the superfluid density coincides with the total density.

However, the situation is dramatically changed in the presence of SOC where the Galilean transformation is violated. As pointed out in [54], in the presence of SOC, Eq. (11) is no longer valid. Therefore, we calculate the superfluid density by the response of the system with respect to a small phase field of the order parameter: \(\Delta \left( \textbf{r},\tau \right) =\Delta _{0}e^{i\phi }\)[82]. In [83], E. Taylor proved that this method is equivalent to the definition of the superfluid tensor from the current-current correlation function. Furthermore, this method can simultaneously give the compressibility.

By substituting the ansatz \(\Delta \left( \textbf{r},\tau \right) =\Delta _{0}e^{i\phi }\) into the partition function and expanding it to the quadratic order of the phase field \(\phi\), after direct but lengthy algebraic manipulations [84], we obtain the effective action for the phase field as:

$$\begin{aligned} \mathcal {S}_{eff}\left[ \varphi , \textbf{A}\right] \simeq \mathcal {S} _{0}+\int dx\left( \sum _{i=x,y}\frac{\rho _{s}^{i}}{2m}\textbf{A}_{i}^{2}+\kappa \varphi ^{2}\right) \end{aligned}$$
(12)

with the emergent vector field \(\textbf{A}=\mathbf {\nabla }\phi\) and scalar field \(\varphi =\nabla \phi\) denoting the spatial and temporal fluctuations of the phase field of the order parameter, respectively. The superfluid tensor can be expressed as \(\rho _{s}^{i}=n - \rho _{n}^{i}\) with the normal density \(\rho _{n}^{i}\) given by:

$$\begin{aligned} \rho _{n}^{x}= & {} \frac{1}{mV}\sum _{\textbf{p,}s=\pm }p_{x}^{2}Y\left( E_{\textbf{ p},s}\right) \frac{\left( \textbf{M}^{2}+sm\lambda _{x}^{2}\xi _{\textbf{p}}\right) ^{2}}{\textbf{M}^{4}} \end{aligned}$$
(13)
$$\begin{aligned}{} & {} \quad +\frac{m\lambda _{x}^{2}}{2V}\sum _{\textbf{p,}s=\pm }\tanh \frac{\beta E_{\textbf{p},s}}{2}\frac{\left( \xi _{\textbf{p}}^{2}+\Delta _{0}^{2}+s\textbf{M}^{2}\right) \textbf{M}_{y}^{4}}{s E_{\textbf{p},s}\textbf{M}^{6}} \end{aligned}$$
(14)
$$\begin{aligned} \rho _{n}^{y}= & {} \frac{1}{mV}\sum _{\textbf{p,}s=\pm }p_{y}^{2}Y\left( E_{\textbf{ p},s}\right) \frac{\left( \textbf{M}^{2}+sm\lambda _{y}^{2}\xi _{\textbf{p} }\right) ^{2}}{\textbf{M}^{4}} \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \quad +\frac{m\lambda _{y}^{2}}{2V}\sum _{\textbf{p,}s=\pm }\tanh \frac{\beta E_{\textbf{p},s}}{2}\frac{\left( \xi _{\textbf{p}}^{2}+\Delta _{0}^{2}+s\textbf{M}^{2}\right) \textbf{M}_{x}^{4}}{s E_{\textbf{p},s}\textbf{M}^{6}} \end{aligned}$$
(16)

and the compressibility \(\kappa\) reads:

$$\begin{aligned} \kappa =\frac{1}{2V}\sum _{\textbf{p,}s=\pm }\frac{\xi _{\textbf{p}}^{2}\left( \left| \gamma _{\textbf{p}}\right| ^{2}+s\textbf{M}^{2}\right) ^{2}Y\left( E_{\textbf{p},s}\right) }{E_{\textbf{p} ,s}^{2}\textbf{M}^{4}} +\frac{\Delta _{0}^{2}}{4V}\sum _{\textbf{p,}s=\pm }\tanh \frac{\beta E_{\textbf{p},s}}{2}\frac{1}{E_{\textbf{p},s}^{3}} \end{aligned}$$
(17)

with \(\textbf{M}^{2} =\xi _{\textbf{p}}\left| \gamma _{\textbf{p} }\right|\), \(\textbf{M}_{x,y}^{2} =\xi _{\textbf{p}}\left| \gamma _{\textbf{p}}^{x,y}\right|\), \(\left| \gamma _{\textbf{p}}^{x,y}\right| =\lambda _{x,y}p_{x,y}\) and \(Y\left( x\right) =\beta f(x)[1-f(x)]\).

We first self-consistently solve Eq. (6) and Eq. (7) to obtain the chemical potential and gap parameters. Subsequently, we substitute these results into Eqs. (6) and (7) to determine the condensed fraction and superfluid fraction tensor.

5 Results and discussion

In this paper, we only consider the ground-state properties of the system. Previous investigations show that mean-field theory is qualitatively and quantitatively correct in the low-temperature regime. However, at finite temperatures, fluctuations of the order parameters become more and more important. In order to obtain qualitatively correct physics for temperatures close to the critical temperature, the most successful method is to include contributions from the lowest Gaussian fluctuations of the gap parameter to the thermodynamic potential. This is beyond the scope of this paper and will be left for future work. At the mean-field level, the superfluid density tensor has been obtained in previous research [60, 72, 74, 85]. We have checked that our results coincide with all previous calculations. However, in this paper, we focus on the opposite effect of SOC on the condensed density and superfluid density and how the anisotropic nature of the SOC influences this opposite effect, which has not been addressed in previous investigations.

Fig. 1
figure 1

(Color online) Condensed fraction defined by: \(n_{c}/n\) as functions of the SOC strength parameter \(\lambda /v_F\) with \(v_F\) being the Fermi velocity. \(E_b=0.001E_F\) and \(E_b=0.1E_F\) in (a, b), respectively

Full size image
Fig. 2
figure 2

(Color online) Condensed fraction as a function of the anisotropic parameter \(\eta =\lambda _D/\lambda _R\). \(E_b=0.001E_F\) and \(E_b=0.1E_F\) in (a, b), respectively

Full size image

In Fig. 1, we present our numerical results of the condensed fraction as a function of the SOC parameter \(\lambda /v_{F}\), with \(v_{F}=p_{F}/m\) being the Fermi velocity and \(p_{F}\) being the Fermi momentum. It is clear that SOC enhances condensation compared with cases with no SOC. However, the condensed fraction shows non-monotonic behaviors for some parameter space. In Fig. 1(a), the interaction parameter is \(E_b = 0.001E_{F}\), where \(E_F=p_F^2/2\,m\) is the Fermi energy. As one can see, in this weak interaction regime, as we increase the anisotropic parameters, the condensed fraction decreases but has a maximum value as a function of \(\lambda /v_{F}\). This means that for large enough anisotropic parameters, SOC does not necessarily enhance condensation. However, in the strong interaction limit with large enough \(E_{b}\) shown in Fig. 1(b), the condensed fraction is always a monotonic function of SOC strength. Figure 2 represents condensed fraction as functions of anisotropic parameters. And one can see that anisotropic parameters always suppress condensation. In Fig. 2(a), different lines cross with each other, which is a direct manifestation of the fact that for large enough anisotropic parameters, the condensed fraction is not a monotonic function with respect to SOC strength.

In general, as a static property, the condensed fraction has similar behaviors as the gap parameters. However, the superfluid fraction tensor becomes more complicated for the superfluid Fermi systems with anisotropic SOC. It is easily seen from Eq. 14 and Eq. 16 that SOC suppresses superfluidity, and it creates normal density even at zero temperature.

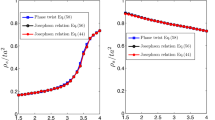
Figure 3 represents numerical results for the superfluid fraction tensor \(\rho _{s}^{x}\) and \(\rho _{s}^{y}\) as functions of the SOC strength for various interaction and anisotropic parameters. We can see from Fig. 3(a) with \(E_b=0.001E_F\) that \(\rho _{s}^{x}\) decreases with increasing SOC strength for small anisotropic parameters in the weak interaction limit. However, for large anisotropic parameters, \(\rho _{s}^{x}\) is a non-monotonic function of SOC strength with a global minimum. And this minimum for large anisotropic parameters disappears for strong interaction parameters as shown in Fig. 3(b) with \(E_b=0.1E_F\). Nonetheless, the other component of the superfluid tensor \(\rho _{s}^{y}\) has different behaviors as shown in Fig. 3(c) and (d). We have checked for various parameters and found that \(\rho _{s}^{y}\) always has a minimum regardless of the value of the anisotropic and interaction parameters. It is also clear that \(\rho _{s}^{x,y} \rightarrow n\) for \(\lambda = 0\).

We also investigated the effect of anisotropy on the superfluid fraction, and the results are shown in Fig. 4. As can be seen clearly from the results, \(\rho _{s}^{x}\) and \(\rho _{s}^{y}\) as functions of anisotropic parameters are more complicated. Firstly, in Fig. 4(a) for the weak interaction parameter \(E_b=0.001E_F\), \(\rho _{s}^{x}>\rho _{s}^{y}\) and only \(\rho _{s}^{y}\) shows a minimum for small SOC parameters. For large SOC parameters, \(\rho _{s}^{x}<\rho _{s}^{y}\), and only \(\rho _{s}^{x}\) has a minimum. Secondly, when the system enters the strong interaction regime, as shown in Fig. 4(b) with \(E_b=0.1E_F\), \(\rho _{s}^{x}>\rho _{s}^{y}\) but with no minimum for \(\rho _{s}^{y}\) for weak SOC. And for large SOC parameters, \(\rho _{s}^{x}<\rho _{s}^{y}\), and \(\rho _{s}^{x}\) still shows a minimum. And we have checked for a larger value of interaction parameters (\(E_b=1.0E_F\)), the situations are the same as shown in Fig. 4(b). \(\rho _{s}^{x}\) always has a minimum value for large SOC parameters. Finally, we noticed that \(\rho _{s}^{x}=\rho _{s}^{y}\) with \(\eta =0\), and we have the isotropic Rashba SOC case where \(\rho _{s}^{x}=\rho _{s}^{x}\). Furthermore, \(\rho _{s}^{x}=\rho _{s}^{y}=1\) for the anisotropic case with \(\eta =1\). This is true since in the ERD case, the SOC Hamiltonian density reduces to a one-dimensional SOC term. For the balanced case with an equal number of particles for spin-down and spin-up atoms, this one-dimensional SOC term can be gauged out and has no effect on the thermodynamic properties of the system. Therefore, the superfluid fraction at zero temperature goes to 1 as in the case without SOC.

A final remark: as shown in the numerical results of the superfluid fraction tensor, \(\rho _{s}^{x}\) and \(\rho _{s}^{y}\) have different behaviors. This comes from the fact that we constrain the anisotropic parameter in the domain: \(0<\eta <1\). Therefore, we never reach the regime for pure Dresselhaus limit. In the transparent anisotropic expression for the SOC part of the Hamiltonian density, \(0<\eta <1\) means \(\lambda _R > \lambda _D\) and \(\lambda _y > \lambda _x\). The other limit of pure Dresselhaus SOC can be reached by setting \(\eta \rightarrow \infty\). For symmetry considerations, thermodynamic properties should be symmetric about the two regimes: \(0<\eta <1\) and \(1<\eta <\infty\).

Fig. 3
figure 3

(Color online) Superfluid fraction \(\rho _s^{x,y}/n\) as functions of the SOC strength parameter \(\lambda /v_F\). Real black lines, dot-dashed blue lines, dashed red lines, and dotted green lines correspond to \(\eta =0.2\), \(\eta =0.3\), \(\eta =0.4\), and \(\eta =0.6\), respectively. \(E_b=0.001E_F\) in (a, c). \(E_b=0.1E_F\) in (b, d)

Full size image
Fig. 4
figure 4

(Color online) Superfluid fraction as a function of anisotropic parameters. In both figures, thick lines and thin lines correspond to \(\rho _s^{y}/n\) and \(\rho _s^{x}/n\), respectively. \(E_b=0.001E_F\) and \(E_b=0.1E_F\) in (a, b), respectively

Full size image

6 Conclusions

We performed a detailed research on the effect of an anisotropic SOC on the condensation and superfluid properties of a two-dimensional Fermi gas at zero temperature. Particularly, we found that SOC not always enhances condensation and suppresses superfluidity. The condensed fraction and superfluid tensor show many different behaviors for different parameter configurations. In this paper, we only consider the phase fluctuations of the order parameter and neglect the magnitude fluctuations. Besides, the inclusion of an optical lattice would give us many degrees of freedom and lead to more interesting phenomena such as the superfluid-Mott insulator transition. Furthermore, if we consider an imbalanced case, there will be a topological phase transition as we increase the Zeeman field across a critical value. Combinations of SOC and optical lattice provide an ideal test ground for many interesting phenomena observed in solid-state material systems.