Investigation on behavior of deceleration parameter with LRS Bianchi type-I cosmological models

Abstract

The present paper compares two LRS Bianchi type-I bulk viscous models of the universe constructed in f(R, T) theory of gravity. A parameterization of deceleration parameter (DP) is considered to find solutions of the models. This parameterization of DP reduces to both linear-varying deceleration parameter (LVDP) (Akarsu and Dereli in Int J Theor Phys 51:612–621, 2011) and bilinear-varying deceleration parameter (BVDP) (Mishra and Dua in Astrophys Space Sci 364:1–12, 2019) for specific values of model parameters. The cosmic evolution is discussed with the help of LVDP in model I and BVDP in model II. Both the models exhibit phase transition from early cosmic decelerated phase to the present accelerated phase. We discuss physical and geometrical properties of the models graphically and compare them in detail. In addition, best-fit values of model parameters are obtained using 51 values of observational Hubble parameter.

1 Introduction

Multiple research findings indicate that the present universe is experiencing accelerated expansion phase [1,2,3]. This widely accepted phenomenon is difficult to explain through Einstein’s general theory of relativity (GTR). It is believed that hypothetical matter with a negative pressure could be causing cosmic acceleration. This unknown form of matter is known as dark energy (DE). There is maximum contribution of DE in comparison with other matter such as baryonic matter and dark matter in providing an anti-gravity effect to drive the cosmic acceleration. Cosmological constant $\Lambda$ with equation of state (EoS) $\omega =-1$ is considered to be simplest candidate for DE [4,5,6,7]. However, different observations suggest an equation of state of DE different from $\omega =-1$ [8,9,10]. The other forms of DE with EoS different from $\omega =-1$ are mainly quintessence ($-1\le \omega \le -\frac{1}{3}$) [11, 12] and phantom ($\omega <-1$) [13, 14]. The most interesting thing is that the nature and origin of DE are still unknown to the scientists, and knowing the EoS of DE is a key goal in theoretical and observational cosmology. Exact information about the EoS of DE at the present epoch and its evolution will provide valuable insights into cosmic evolution leading to the late-time cosmic acceleration.

Alternatively, one may attempt to find a solution of the model using a viable parameterization of geometrical parameter and derive the EoS for possible fluid that might be driving the cosmic acceleration in the context of DE. Thereafter, one may examine whether the behavior of fluid is realistic or not and try to study the nature of DE.

Numerous attempts have been made by many cosmologists to modify the geometrical action and explain the late-time accelerated expansion phase of the universe. The most simplest geometrical modification to GTR is f(R) gravity in which action contains an arbitrary function of the Ricci scalar R rather than only R in GTR. This theory offers an explanation to the phenomenon of late-time cosmic acceleration. Harko et al. [15] proposed a theory of gravity called f(R, T) gravity in which the gravitational Lagrangian is considered as an arbitrary functional of the Ricci scalar R and trace T of energy momentum tensor $T_{\mu \nu }$. f(R, T) theory has been found to be successful in explaining various cosmological aspects such as dark matter [16], dark energy [17] and gravitational waves [18, 19]. Many authors have studied cosmological models in f(R, T) gravity and published encouraging results [20,21,22,23,24,25,26,27].

After the confirmation of the accelerated expansion of the universe, many authors have begun to investigate cosmological model with deceleration parameter (DP) as time-varying quantity [28,29,30,31,32]. DP is a dimensionless quantity and is defined as $q=-\frac{\ddot{a}a}{\dot{a}^2}$, where a is an average scale factor. $q>0$ indicates decelerated expansion phase of the universe, while $q<0$ shows accelerated cosmic expansion phase. This quantity helps in studying how acceleration varies with cosmic time. Berman [33] proposed a special law of variation for the Hubble parameter ($H=\frac{\dot{a}}{a}$), which yields constant deceleration parameter (CDP), i.e., $q=\alpha _1-1$, $\alpha _1 \ge 0$. Recently, Singh and Beesham [34] have studied LRS Bianchi-I model of universe in GTR with CDP and discussed properties of the model for different values of $\alpha _1$. Akarsu and Dereli [35] have proposed a linear-varying deceleration parameter (LVDP), i.e., $q=-\alpha _2t+\alpha _1-1$, $\alpha _1,\alpha _2>0$, and utilized it in achieving an accelerated solution of the cosmological model. This law covers Berman’s law for $\alpha _2=0$.

Further, Mishra and Chand [36] have studied a cosmological model with bilinear-varying deceleration parameter (BVDP), i.e., $q=\frac{\alpha (1-t)}{(1+t)}$, $\alpha >0$ in Brans–Dicke theory of gravity. The behavior of DP shows past cosmic deceleration followed by present cosmic acceleration, which is in good agreement with observational data. Following Mishra and Chand [36], many authors have studied the dynamics of the universe in alternate theories of gravity and achieved accelerated cosmic solutions with the help of BVDP [37,38,39,40].

Research interest in studying bulk viscous properties in cosmic fluid has seen an increase over the past few years. The concept of viscous cosmology was first given by Eckart [41]. It is believed that matter behaved like viscous fluid during early evolution of the universe when neutrino decoupling occurred. During this era, the effect of viscosity was the largest when the temperature was about 1 MeV ($10^{10}$K). Our universe at a large scale is spatially isotropic; therefore, we usually ignore shear viscosity. In view of this, bulk viscosity could play a prominent role in governing the early cosmic evolution. Several studies reported that bulk viscosity could possibly drive the early cosmic inflation [42, 43]. According to these studies, the inflation driven by bulk viscous fluid contributes a negative pressure, which in turn gives rise to repulsive gravity and cause rapid cosmic expansion. Dark energy phenomenon could also be the effect of bulk viscosity in the cosmic fluid that has been studied by Zimdahl et al. [44]. Many authors have studied the viscous cosmology and published fruitful results [45,22,46,47,48].

With this motivation, we study two LRS Bianchi type-I bulk viscous cosmological models in f(R, T) gravity. The accelerated cosmic solution has been achieved with the help of LVDP in model I and BVDP in model II. The main aim of this study is to compare physical and geometrical properties of the models in detail and constrain model parameters using observational Hubble data. The remaining paper is organized as follows: We present the metric and the field equations governing the models in Sect. 2. Section 3 deals with the parameterization of DP to find solutions of the models. In Sect. 4, we find the solutions of the models and discuss their physical and geometrical properties in detail. Section 5 is devoted to the analysis of cosmographic parameters. We also perform state finder diagnostic in this section. In Sect. 6, we constrain the model parameters $\alpha _1$ and $\alpha _2$ using observational Hubble data. Finally, in Sect. 7, we compare behavior of both the models and summarize their results.

2 Equations governing the models

For constructing cosmological models, we consider LRS Bianchi type-I metric, being defined as

$$\begin{aligned} ds^2=dt^2-a_1^2dx^2-a_2^2(dy^2+dz^2), \end{aligned}$$

(1)

where the directional scale factors $a_1$ and $a_2$ are functions of cosmic time t only. This metric is homogeneous and anisotropic in nature.

For bulk viscous fluid, the energy–momentum tensor $T_{\mu \nu }$ is defined as:

$$\begin{aligned} T_{\mu \nu }=(\rho +\bar{p})u_{\mu }u_{\nu }-\bar{p}g_{\mu \nu }, \end{aligned}$$

(2)

where $\rho$, $\bar{p}=p-3\xi H$, p, $\xi$ and H are the energy density, effective pressure, pressure, bulk viscous coefficient and Hubble parameter, respectively. $u_{\mu }=(0,0,0,1)$ is the four velocity vector in co-moving coordinate system, which agrees with $u_{\mu }u_{\nu }=1$.

The trace of energy–momentum tensor $T_{\mu \nu }$ is given by:

$$\begin{aligned} T=\rho -3\bar{p}. \end{aligned}$$

(3)

The gravitational field equations in f(R, T) gravity with $f(R,T)=f_1(R)+f_2(T)$, $f_1(R)=\lambda R$ and $f_2(T)=\lambda T$, $\lambda$ being a constant [15], are given by

$$\begin{aligned} R_{\mu \nu }-\dfrac{1}{2}R g_{\mu \nu }=\left( \dfrac{8\pi }{\mu }+1\right) T_{\mu \nu }+\left( p+\dfrac{1}{2}T\right) g_{\mu \nu }. \end{aligned}$$

(4)

The above field equations for the metric (1) and energy–momentum tensor (2) reduce to the following differential equations:

$$\begin{aligned} 2\dfrac{\ddot{a_2}}{a_2}+\left( \dfrac{\dot{a_2}}{a_2}\right) ^2=\dfrac{\rho }{2}-\left( \dfrac{8\pi }{\lambda }+\dfrac{3}{2}\right) \bar{p}, \end{aligned}$$

(5)

$$\begin{aligned} \dfrac{\ddot{a_1}}{a_1}+\dfrac{\ddot{a_2}}{a_2}+\dfrac{\dot{a_1}\dot{a_2}}{a_1a_2}=\dfrac{\rho }{2}-\left( \dfrac{8\pi }{\lambda }+\dfrac{3}{2}\right) \bar{p}, \end{aligned}$$

(6)

$$\begin{aligned} 2\dfrac{\dot{a_1}\dot{a_2}}{a_1a_2}+\left( \dfrac{\dot{a_2}}{a_2}\right) ^2=\left( \dfrac{8\pi }{\lambda }+\dfrac{3}{2}\right) \rho -\dfrac{\bar{p}}{2}. \end{aligned}$$

(7)

Here, dot in the superscript denotes the usual time derivative.

The spatial volume of LRS Bianchi type-I space-time is defined as

$$\begin{aligned} V=a_1a_2^2=\sqrt{-g} \end{aligned}$$

(8)

To solve the field Eqs. (5)–(7), we follow the technique suggested by Saha and Shikin [49] and Saha [50].

From Eqs. (5) and (6), we obtain

$$\begin{aligned} \dfrac{a_1}{a_2}=k_2 exp\left[ \int \dfrac{k_1}{a_1 a_2^2}dt\right] , \end{aligned}$$

(9)

where $k_1$ and $k_2$ are integrating constants.

Further, the scale factors $a_1$ and $a_2$ can be written as follows:

$$\begin{aligned} a_1= k_2^{\frac{2}{3}}V^{\frac{1}{3}} exp\left[ \dfrac{2}{3}k_1\int \dfrac{dt}{V}\right] , \end{aligned}$$

(10)

$$\begin{aligned} a_2= k_2^{-\frac{1}{3}}V^{\frac{1}{3}} exp\left[ -\dfrac{1}{3}k_1\int \dfrac{dt}{V}\right] , \end{aligned}$$

(11)

Using Eqs. (5)–(11), we obtain the following expressions of energy density $\rho$ and effective pressure $\bar{p}$:

$$\begin{aligned}&\rho =\dfrac{1}{A}\left[ \left( \dfrac{24\pi }{\lambda }+3\right) H^2-\dot{H}-\left( \dfrac{8\pi }{3\lambda }+\dfrac{2}{3}\right) \dfrac{k_1^2}{V^2}\right] , \end{aligned}$$

(12)

$$\begin{aligned}&\bar{p}=\dfrac{1}{A}\left[ -3\left( \dfrac{8\pi }{\lambda }+1\right) H^2-2\left( \dfrac{8\pi }{\lambda }+\dfrac{3}{2}\right) \dot{H}\right. \nonumber \\&\left. -\left( \dfrac{8\pi }{\lambda }+2\right) \dfrac{k_1^2}{3V^2}\right] , \end{aligned}$$

(13)

where $A=\left( \frac{8\pi }{\lambda }+\frac{3}{2}\right) ^2-\frac{1}{4}$.

Equations (5)–(7) are three independent differential equations containing five unknown variables, viz. $a_1$, $a_2$, $\rho$, p and $\xi$. Therefore, to find a solution of the field equations, we need two more constraints involving these parameters. We discuss the same in the next section.

3 Assumptions and some definitions

In survey of literature, it has been observed that there are multiple approaches to solve gravitational field equations. In one such approach, in order to find a solution of the field equations, either a parameterization of geometrical parameter such as a, H, q or parameterization of physical parameter such as p, $\rho$, $\rho _{de}$, $p_{de}$ is used. The first kind of parameterization helps in understanding the cosmic expansion without any knowledge of background theory and matter content of the universe. This model-independent approach provides the solution of the field equations explicitly, while the second kind of parameterization is usually considered to discuss the physical aspects of the universe such as structure formation and thermodynamics.

In this paper, we adopt model-independent approach to find a solution of the field equations.

We consider the following parameterization of DP:

$$\begin{aligned} q=\dfrac{(\alpha _1-1)-\alpha _2t}{1+\alpha _3t}, \end{aligned}$$

(14)

where $\alpha _1$, $\alpha _2$ & $\alpha _3 \ge 0$ are constants. Such form of DP is motivated from Mishra and Chand [36], where the authors have taken similar parameterization of DP and called it as bilinear-varying deceleration parameter (BVDP).

For $\alpha _2$=$\alpha _3=0$, the above form of DP (14) reduces to constant DP, i.e., $q=\alpha _1-1$ [33]. For $\alpha _3=0$, it reduces to linear-varying deceleration parameter (LVDP) [35], i.e., $q=(\alpha _1-1)-\alpha _2t$. For $\alpha _3=\alpha _2$, it reduces to the special form of BVDP, i.e., $q=\dfrac{(\alpha _1-1)-\alpha _2t}{1+\alpha _2t}$, which is similar to the form taken by Mishra and Dua [40].

• i) In this study, we find a solution of the gravitational field equations with the help of LVDP, i.e., $q=(\alpha _1-1)-\alpha _2t$, $\alpha _1, \alpha _2>0$ in model I, and BVDP, i.e., $q=\dfrac{(\alpha _1-1)-\alpha _2t}{1+\alpha _2t}$, $\alpha _1, \alpha _2>0$ in model II for solving the field equations. Table 1 shows the same.

• ii) The models assume the barotropic equation of state relating the non-viscous fluid pressure p to the energy density of fluid, i.e.,

$$\begin{aligned} p=\gamma \rho , \end{aligned}$$

(15)

where $0 \le \gamma \le 1$ is a constant. $\gamma =0$ corresponds to pressure less universe and $\gamma =\frac{1}{3}$ corresponds to radiation-dominated universe.

Using these two assumptions, we find solutions of the models in the next section.

Table 1 The models

For LRS Bianchi type-I metric, various geometrical parameters such as Hubble parameter H, directional Hubble parameters $H_\mu (\mu =1,2)$, expansion scalar $\theta$, shear scalar $\sigma$ are defined as:

$$\begin{aligned}&H=\dfrac{1}{3}\left( \dfrac{\dot{a_1}}{a_1}+2\dfrac{\dot{a_2}}{a_2}\right) , \end{aligned}$$

(16)

$$\begin{aligned}&H_\mu =\dfrac{\dot{a_\mu }}{a_\mu }, \mu =1,2, \end{aligned}$$

(17)

$$\begin{aligned}&\theta =3H=\left( \dfrac{\dot{a_1}}{a_1}+2\dfrac{\dot{a_2}}{a_2}\right) , \end{aligned}$$

(18)

$$\begin{aligned}&\sigma ^2=\dfrac{1}{2}\sigma _{\mu \nu }\sigma ^{\mu \nu }=\dfrac{1}{2}\left[ \left( \dfrac{\dot{a_1}}{a_1}\right) ^2+2\left( \dfrac{\dot{a_2}}{a_2}\right) ^2\right] -\dfrac{1}{6}\theta ^2, \end{aligned}$$

(19)

where $\sigma _{\mu \nu }$ is shear tensor.

The anisotropic parameter ${\mathcal {A}}$ is defined as

$$\begin{aligned} {\mathcal {A}}=\dfrac{1}{3}\left[ \left( \dfrac{H_1-H}{H}\right) ^2+2\left( \dfrac{H_2-H}{H}\right) ^2\right] . \end{aligned}$$

(20)

4 Solution of the models

As discussed above, we consider LVDP, i.e., $q=(\alpha _1-1)-\alpha _2t$, $\alpha _1, \alpha _2>0$ in model I, and BVDP, i.e., $q=\dfrac{(\alpha _1-1)-\alpha _2t}{1+\alpha _2t}$, $\alpha _1, \alpha _2>0$ in model II for finding a solution of the field equations.

4.1 Model I: $q=(\alpha _1-1)-\alpha _2t$, $\alpha _1, \alpha _2>0$

Here, we consider DP as

$$\begin{aligned} q=(\alpha _1-1)-\alpha _2t, \end{aligned}$$

(21)

where $\alpha _1$ and $\alpha _2$ are positive constants.

For $t=0$, $q=\alpha _1-1$. Hence, if we would like to begin the universe with decelerated expansion phase, we may choose $\alpha _1>1$.

From Eq. (21), we obtain the expressions for the Hubble parameter H and average scale factor a as follows:

$$\begin{aligned} H=\dfrac{2}{t(2\alpha _1-\alpha _2t)}, \end{aligned}$$

(22)

$$\begin{aligned} a(t)=l_0exp\left[ \dfrac{2}{\alpha _1}tanh^{-1}\left( \dfrac{\alpha _2}{\alpha _1}t-1\right) \right] , \end{aligned}$$

(23)

where $l_0$ is an integrating constant.

Further, the energy density $\rho$, effective pressure $\bar{p}$, normal pressure p and bulk viscosity coefficient $\xi$, in terms of cosmic time, are obtained as:

$$\begin{aligned}&\rho =\dfrac{1}{A}\left[ A_1(t)\left\{ \dfrac{2}{t(2\alpha _1-\alpha _2t)}\right\} ^2\right. \nonumber \\&\left. -A_2(t)l_0^{-6} exp\left\{ -\dfrac{12}{\alpha _1}tanh^{-1}\left( \dfrac{\alpha _2}{\alpha _1}t-1\right) \right\} \right] , \end{aligned}$$

(24)

where $A_1(t)=\left( \dfrac{24\pi }{\lambda }+3+\alpha _1-\alpha _2t\right)$ and $A_2(t)=k_1^2\left( \dfrac{8\pi }{3\lambda }+\dfrac{2}{3}\right)$,

$$\begin{aligned}&\bar{p}=\dfrac{1}{A}\left[ A_3(t)\left\{ \dfrac{2}{t(2\alpha _1-\alpha _2t)}\right\} ^2\right. \nonumber \\&\left. -A_4(t)l_0^{-6}exp\left\{ -\dfrac{12}{\alpha _1}tanh^{-1}\left( \dfrac{\alpha _2}{\alpha _1}t-1\right) \right\} \right] , \end{aligned}$$

(25)

where $A_3(t)=\left\{ 2\left( \dfrac{8\pi }{\lambda }+\dfrac{3}{2}\right) (\alpha _1-\alpha _2t)-3\left( \dfrac{8\pi }{\lambda }+1\right) \right\}$ and $A_4(t)=\dfrac{k_1^2}{3}\left( \dfrac{8\pi }{\lambda }+2\right)$,

$$\begin{aligned}&p=\dfrac{\gamma }{A}\left[ A_1(t)\left\{ \dfrac{2}{t(2\alpha _1-\alpha _2t)}\right\} ^2\right. \nonumber \\&\left. -A_2(t)l_0^{-6} exp\left\{ -\dfrac{12}{\alpha _1}tanh^{-1}\left( \dfrac{\alpha _2}{\alpha _1}t-1\right) \right\} \right] , \end{aligned}$$

(26)

$$\begin{aligned}&\xi =\dfrac{A_5(t)}{3A}\left\{ \dfrac{2}{t(2\alpha _1-\alpha _2t)}\right\} \nonumber \\&+\dfrac{A_6(t)}{6A}t(2\alpha _1-\alpha _2t)l_0^{-6}exp\left\{ -\dfrac{12}{\alpha _1}tanh^{-1}\left( \dfrac{\alpha _2}{\alpha _1}t-1\right) \right\} , \end{aligned}$$

(27)

where $A_5(t)=\gamma \left( \dfrac{24\pi }{\lambda }+3\right) +3\left( 1+\dfrac{8\pi }{\lambda }\right) +(\alpha _2t-\alpha _1)\left\{ 2\left( \dfrac{8\pi }{\lambda }+\dfrac{3}{2}\right) -\gamma \right\}$ and $A_6(t)=k_1^2\left\{ \dfrac{1}{3}\left( 2+\dfrac{8\pi }{\lambda }\right) -\gamma \left( \dfrac{8\pi }{3\lambda }+\dfrac{2}{3}\right) \right\}$.

The other geometrical parameters such as V, $\theta$, $\sigma$ and ${\mathcal {A}}$ are obtained as:

$$\begin{aligned}&V(t)=a_1a_2^2=l_0^3exp\left\{ \dfrac{6}{\alpha _1}tanh^{-1}\left( \dfrac{\alpha _2}{\alpha _1}t-1\right) \right\} \end{aligned}$$

(28)

$$\begin{aligned}&\theta =3H=\dfrac{6}{t(2\alpha _1-\alpha _2t)} \end{aligned}$$

(29)

$$\begin{aligned}&\sigma ^2=\dfrac{k_1^2}{3}l_0^{-6}exp\left\{ -\dfrac{12}{\alpha _1}tanh^{-1}\left( \dfrac{\alpha _2}{\alpha _1}t-1\right) \right\} \end{aligned}$$

(30)

$$\begin{aligned}&{\mathcal {A}}=\dfrac{k_1^2}{18}t^2(2\alpha _1-\alpha _2t)^2l_0^{-6}exp\left\{ -\dfrac{12}{\alpha _1}tanh^{-1}\left( \dfrac{\alpha _2}{\alpha _1}t-1\right) \right\} \end{aligned}$$

(31)

For $q_0=-0.54$ [51] and $t_0=13.8$ Gyr, Eq. (21) reduces to $13.8\alpha _2+0.46=\alpha _1$. For all the graphical representations of the cosmological parameters in model I, we make a choice of pair $(\alpha _1, \alpha _2)$ in such as way that it satisfies $13.8\alpha _2+0.46=\alpha _1$. Here, we opt $(\alpha _1,\alpha _2)=(2.216,0.127)$ for the same.

From Eq.(23), it is clear that the average scale factor $a=0$ at $t=0$ and $a\rightarrow \infty$ as $t\rightarrow \frac{2\alpha _1}{\alpha _2}$. This infers that this model of the universe starts with the Big Bang at $t=0$ and ends at $t_e=\frac{2\alpha _1}{\alpha _2}$. This is the Big Rip scenario, which was first suggested by Caldwell [14]. For chosen values of $\alpha _1$ and $\alpha _2$, $t_e=34.89$, which is found to be very close to the value given by Caldwell, i.e., $t_{rip}=35$. Similar behavior of a can be observed from Fig. 1.

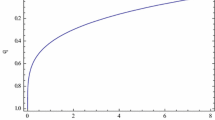
Equation (21) infers that $q=\alpha _1-1 >0$, provided $\alpha _1>1$ at $t=0$, $q \le 0$ for $t\ge \frac{\alpha _1-1}{\alpha _2}$, $q \le -1$ for $t \ge \frac{\alpha _1}{\alpha _2}$ and $q=-\alpha _1-1$ at $t_e=\frac{2\alpha _1}{\alpha _2}$. Such behavior of q indicates that the model starts with decelerated expansion phase, enters into accelerated expansion phase at $t=\frac{\alpha _1-1}{\alpha _2}$, enters into super exponential expansion phase at $t=\frac{\alpha _1}{\alpha _2}$ and ends at $t_e =\frac{2\alpha _1}{\alpha _2}$. One can observe the similar behavior of q in Fig. 2. Hubble parameter also diverges at the beginning ($t=0$) and end of the universe ($t_e=\frac{2\alpha _1}{\alpha _2}$). It remains positive throughout the evolution of the universe as observed in Fig. 3.

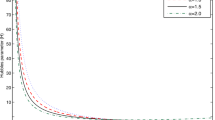
Figures 4, 5 and 6 represent the time-varying behavior of $\rho$, $\bar{p}$ and $\xi$, respectively. Here, we have used $l_0=10^3$, $\gamma =0.5$, $\lambda =1.052$ and $k_1=1$ for the pictorial representation of these parameters. It is noticed that both $\rho$ and $\xi$ remain positive throughout the cosmic evolution; however, they diverge at the beginning and end of the universe. Effective pressure $\bar{p}$ is gradually decreasing with the passage of cosmic time. Also, $\bar{p}$ is initially positive and becomes negative at present. It also diverges at the beginning and end of the universe. The negative value of $\bar{p}$ ensures the present accelerated expansion phase of the universe.

Figure 7 is a plot of the time variation of EoS parameter $\omega =\frac{\bar{p}}{\rho }$. It is observed that $\omega$ starts evolving from a non-dark region, enters into quintessence region ($-1<\omega <-\frac{1}{3}$), crosses the cosmological constant line ($w=-1$) and thereon stays in the phantom region ($w<-1$). The behavior of EoS parameter shows that the model I behaves similar to phantom DE model in future followed by the Big Rip.

Next, we explore the behavior of energy condition-dominant energy conditions (DEC): $\rho \pm \bar{p}\ge 0$, weak energy conditions (WEC): $\rho \ge 0$ and $\rho +\bar{p}\ge 0$, null energy conditions (NEC): $\rho +\bar{p}\ge 0$, strong energy conditions (SEC): $\rho +3\bar{p}\ge 0$.

Phantom matter is regarded as one of the interesting possibilities that does not satisfy NEC, i.e., $\rho +\bar{p}\ge 0$, and our model follows the same. Such property ensures that the model is physically realistic. In this model, NEC is not satisfied at late times, and hence, SEC is also violated at late time cosmic evolution. The time variation of these energy conditions is represented in Figs. 8, 9 and 10.

From Eqs. (30) and (31), it is observed that both $\sigma ^2$ & ${\mathcal {A}}\rightarrow 0$ as $t \rightarrow t_e$. Such behavior of the anisotropic parameter shows that the derived model is anisotropic in the past and it becomes isotropic at late times.

Fig. 1

Time variation of scale factor a

Fig. 2

Time variation of deceleration parameter q

Fig. 3

Time variation of Hubble parameter H

Fig. 4

Time variation of energy density $\rho$

Fig. 5

Time variation of effective pressure $\bar{p}$

Fig. 6

Time variation of bulk viscosity $\xi$

Fig. 7

Time variation of EoS parameter $\omega$

Fig. 8

Time variation of energy conditions

Fig. 9

Time variation of energy conditions

Fig. 10

Time variation of energy conditions

4.2 Model II:$q=\frac{(\alpha _{1}-1)-\alpha _{2}t}{1+\alpha _{2}t}, \alpha _{1}, \alpha _{2}>0$

Here, we consider the bilinear form of DP as

$$\begin{aligned} q=\dfrac{(\alpha _1-1)-\alpha _2t}{1+\alpha _2t}, \end{aligned}$$

(32)

where $\alpha _1$ and $\alpha _2$ are arbitrary positive constants.

Further, we write

$$\begin{aligned} \dfrac{1}{H}=\int (1+q(t))dt+k_3. \end{aligned}$$

(33)

Using Eq. (32) in the above equation, we obtain

$$\begin{aligned} H=\dfrac{1}{\dfrac{\alpha _1}{\alpha _2}log(1+\alpha _2t)+k_3}. \end{aligned}$$

(34)

Since the rate of expansion is very high during early stages of cosmic evolution, therefore, we consider $k_3=0$ so that Eq. (34) becomes

$$\begin{aligned} H=\dfrac{\alpha _2}{\alpha _1log(1+\alpha _2t)}. \end{aligned}$$

(35)

On integrating Eq. (35), the average scale factor $a=(a_1a_2^2)^{\frac{1}{3}}$ is obtained as:

$$\begin{aligned} a(t)=l_1 t^{\frac{1}{\alpha _1}}exp(A_7(t)), \end{aligned}$$

(36)

where $l_1$ is an integrating constant and $A_7(t)=\dfrac{\alpha _2t}{2\alpha _1}-\dfrac{\alpha _2^2t^2}{24\alpha _1}+\dfrac{\alpha _2^3t^3}{72\alpha _1}-\dfrac{19\alpha _2^4t^4}{2880\alpha _1}+O(t^5)$.

Further, the energy density $\rho$, effective pressure $\bar{p}$, normal pressure p and bulk viscosity coefficient $\xi$ are obtained as:

$$\begin{aligned}&\rho =\dfrac{1}{A}\left[ A_8(t)\left\{ \dfrac{\alpha _2}{\alpha _1log(1+\alpha _2t)}\right\} ^2\right. \nonumber \\&\left. -A_2(t)l_1^{-6} t^{\frac{-6}{\alpha _1}}exp(-6A_7(t))\right] , \end{aligned}$$

(37)

where $A_8(t)=\left( \dfrac{24\pi }{\lambda }+3+\dfrac{\alpha _1}{1+\alpha _2t}\right)$,

$$\begin{aligned}&\bar{p}=\dfrac{1}{A}\left[ A_9(t)\left\{ \dfrac{\alpha _2}{\alpha _1log(1+\alpha _2t)}\right\} ^2\right. \nonumber \\&\left. -A_4(t)l_1^{-6} t^{\frac{-6}{\alpha _1}}exp(-6A_7(t))\right] , \end{aligned}$$

(38)

where $A_9(t)=\left\{ 2\left( \dfrac{8\pi }{\lambda }+\dfrac{3}{2}\right) \dfrac{\alpha _1}{1+\alpha _2t}-3\left( \dfrac{8\pi }{\lambda }+1\right) \right\}$,

$$\begin{aligned}&p=\dfrac{\gamma }{A}\left[ A_8(t)\left\{ \dfrac{\alpha _2}{\alpha _1log(1+\alpha _2t)}\right\} ^2\right. \nonumber \\&\left. -A_2(t)l_1^{-6} t^{\frac{-6}{\alpha _1}}exp(-6A_7(t))\right] , \end{aligned}$$

(39)

$$\begin{aligned}&\xi =\dfrac{A_{10}(t)}{3A}\left\{ \dfrac{\alpha _2}{\alpha _1log(1+\alpha _2t)}\right\} \nonumber \\&+\dfrac{A_6(t)}{3A}\left\{ \dfrac{\alpha _1log(1+\alpha _2t)}{\alpha _2}\right\} l_1^{-6} t^{\frac{-6}{\alpha _1}}exp(-6A_7(t)), \end{aligned}$$

(40)

where $A_{10}(t)=\gamma \left( \dfrac{24\pi }{\lambda }+3\right) +3\left( 1+\dfrac{8\pi }{\lambda }\right) -\left( \dfrac{\alpha _1}{1+\alpha _2t}\right) \left\{ 2\left( \dfrac{8\pi }{\lambda }+\dfrac{3}{2}\right) -\gamma \right\}$.

The other geometrical parameters such as V, $\theta$, $\sigma$ and ${\mathcal {A}}$ are obtained as:

$$\begin{aligned}&V=l_1^3t^{\frac{3}{\alpha _1}}exp(3A_7(t)), \end{aligned}$$

(41)

$$\begin{aligned}&\theta =3H=\dfrac{3\alpha _2}{\alpha _1 log(1+\alpha _2t)}, \end{aligned}$$

(42)

$$\begin{aligned}&\sigma ^2=\dfrac{k_1^2}{3}l_1^{-6} t^{\frac{-6}{\alpha _1}}exp(-6A_7(t)), \end{aligned}$$

(43)

$$\begin{aligned}&{\mathcal {A}}=\dfrac{2k_1^2}{9}\left\{ \dfrac{\alpha _1log(1+\alpha _2t)}{\alpha _2}\right\} ^2l_1^{-6} t^{\frac{-6}{\alpha _1}}exp(-6A_7(t)), \end{aligned}$$

(44)

For $q_0=-0.54$ [51] and $t_0=13.8$ Gyr, Eq. (32) reduces to $6.34\alpha _2+0.46=\alpha _1$. For all the graphical representations of the cosmological parameters in model II, we make a choice of pair $(\alpha _1, \alpha _2)$ in such a way that it satisfies $6.34\alpha _2+0.46=\alpha _1$. Here, we opt $(\alpha _1,\alpha _2)=(1.266,0.127)$ for the same.

From Eq. (36), it is observed that the average scale factor begins with zero and approaches to infinity as $t \rightarrow \infty$. This infers that the model starts with the Big Bang singularity and continues to expand forever. Similar behavior of a can be observed from Fig. 1.

From Eq. (32), $q=\alpha _1-1 >0$ provided $\alpha _1>1$ at $t=0$, $q>0$ for $t<\frac{\alpha _1-1}{\alpha _2}$, $q<0$ for $t>\frac{\alpha _1-1}{\alpha _2}$ and $q\rightarrow -1$ as $t\rightarrow \infty$. This behavior of q infers that in this model, universe had decelerated expansion phase in the past and is currently accelerating. Such feature of the model is in line with the recent observational and theoretical data. Figure 2 represents the similar behavior of q. Hubble parameter H is a decreasing function of cosmic time t. Also, $H\rightarrow 0$ as $t\rightarrow \infty$.

The time-varying behavior of energy density $\rho$, effective pressure $\bar{p}$ and bulk viscosity coefficient $\xi$ is shown in Figs. 4, 5 and 6, respectively. Here, we have considered $l_1=10^3$, $\gamma =0.5$, $\lambda =1.052$ and $k_1=1$ for the pictorial representation of these parameters. It is clear that both $\rho$ and $\xi$ remain positive throughout the cosmic expansion. Also, both $\rho$ & $\xi \rightarrow 0$ as $t\rightarrow \infty$ and diverge at $t=0$. However, effective pressure $\bar{p}$ is negative throughout the evolution of the universe. The negative effective pressure ensures the accelerated expansion of the universe. Also, $\bar{p}\rightarrow 0$ as $t\rightarrow \infty$.

The nature of EoS parameter represented in Fig. 7 indicates that model resembles quintessence DE model ($-\frac{1}{3}<\omega <-1$) at present and $\Lambda$CDM DE model ($\omega \simeq -1$) at late times.

We examine the behavior of the energy conditions-DEC, WEC, NEC and SEC. From Figs. 8 and 9, it can be observed that all DEC, WEC and NEC are well satisfied in our model. However, SEC is violated at present and late times. In quintessence DE model, SEC needs to be violated, which is true in our case as observed from Fig. 10, and thus ensures the viability of this model.

From Eqs. (43) and (44), it is clear that both $\sigma ^2$ and $A_m \rightarrow 0$ as $t\rightarrow \infty$, i.e., model II also shows anisotropy in the past and reaches isotropization at late times.

5 Cosmographic analysis

Cosmographic analysis helps in understanding the dynamics of the observable universe without any prior knowledge of theory of gravity and matter content of the universe. This model-independent approach makes use of kinematic variables to study the evolution of the universe and dark energy.

5.1 Jerk, snap and lerk parameters

Visser [52] introduced the cosmographic parameters such as jerk, snap and lerk involving third-, fourth- and fifth-order derivatives of the scale factor a(t). Like the Hubble parameter H (involves first-order derivative of a(t)) and DP q (involves second-order derivative of a(t)), these parameters also play a significant role in studying the dynamics of the universe and are defined as:

$$\begin{aligned} j(t)=\dfrac{a^{'''}}{a}\left( \dfrac{a^{'}}{a}\right) ^{-3} \;\; s(t)=\dfrac{a^{''''}}{a}\left( \dfrac{a^{'}}{a}\right) ^{-4}\;\; l(t)=\dfrac{a^{'''''}}{a}\left( \dfrac{a^{'}}{a}\right) ^{-5}. \end{aligned}$$

(45)

We first express these parameters in terms of H and its derivatives as follows:

$$\begin{aligned}&j(t)=1+\dfrac{H^{''}}{H^3}+3\dfrac{H^{'}}{H^2}, \end{aligned}$$

(46)

$$\begin{aligned}&s(t)=1+\dfrac{H^{'''}}{H^4}+\dfrac{4H^{''}}{H^3}+3\left( \dfrac{H^{'}}{H^2}\right) ^2+\dfrac{6H^{'}}{H^2}, \end{aligned}$$

(47)

$$\begin{aligned}&l(t)=1+\dfrac{H^{''''}}{H^5}+\dfrac{5H^{'''}}{H^4}+\dfrac{10H^{''}}{H^3}+15\left( \dfrac{H^{'}}{H^2}\right) ^2\nonumber \\&+\dfrac{10H^{''}H^{'}}{H^5}+\dfrac{10H^{'}}{H^2}. \end{aligned}$$

(48)

For model I, j, s and l are obtained as:

$$\begin{aligned} j(t)=1+3T_1+2T_1^2+\dfrac{\alpha _2t}{2}(2\alpha _1-\alpha _2t), \end{aligned}$$

(49)

where $T_1=\alpha _2t-\alpha _1$,

$$\begin{aligned}&s(t)=1+6T_1+11T_1^2+6T_1^3+\alpha _2t(2\alpha _1-\alpha _2t)(2+3T_1), \end{aligned}$$

(50)

$$\begin{aligned}l(t)&=1+10T_1+35T_1^2+50T_1^3+24T_1^4+2\alpha _2t(2\alpha _1\nonumber \\&\quad-\alpha _2t)T_1(10+9T_1)+\nonumber \\&\quad\alpha _2t(2\alpha _1-\alpha _2t)\left\{ \dfrac{3}{2}\alpha _2t(2\alpha _1-\alpha _2t)+5\right\} . \end{aligned}$$

(51)

From Eqs. (49)-(51), it is noticed that $j\rightarrow 1-3\alpha _1+2\alpha _1^2$, $s\rightarrow 1-6\alpha _1+11\alpha _1^2-6\alpha _1^3$ and $l\rightarrow 1-10\alpha _1+35\alpha _1^2-50\alpha _1^3+24\alpha _1^4$ as $t\rightarrow 0$ and $j\rightarrow 1+3\alpha _1+2\alpha _1^2$, $s\rightarrow 1+6\alpha _1+11\alpha _1^2+6\alpha _1^3$ and $l\rightarrow 1+10\alpha _1+35\alpha _1^2+50\alpha _1^3+24\alpha _1^4$ as $t\rightarrow t_e$. Table 2 shows the behavior of the cosmographic parameters in model I.

Table 2 Behavior of the cosmographic parameters in Model I

For model II, these parameters are obtained as

$$\begin{aligned} j(t)=1+\left( \dfrac{\alpha _1}{1+\alpha _2t}\right) ^2(2+T_2)-\dfrac{3\alpha _1}{1+\alpha _2t}, \end{aligned}$$

(52)

where, $T_2=log(1+\alpha _2t),$

$$\begin{aligned}s(t)&=1-2\left( \dfrac{\alpha _1}{1+\alpha _2t}\right) ^3(3+3T_2+2T_2^2)+\left( \dfrac{\alpha _1}{1+\alpha _2t}\right) ^2(11+4T_2)\nonumber \\&-\dfrac{6\alpha _1}{1+\alpha _2t}, \end{aligned}$$

(53)

$$\begin{aligned}l(t)&=1+2\left( \dfrac{\alpha _1}{1+\alpha _2t}\right) ^4(12+18T_2+11T_2^2+3T_2^3)\nonumber \\&-10\left( \dfrac{\alpha _1}{1+\alpha _2t}\right) ^3 (5+4T_2+T_2^2)+5\left( \dfrac{\alpha _1}{1+\alpha _2t}\right) ^2(7+2T_2)-\dfrac{10\alpha _1}{1+\alpha _2t}. \end{aligned}$$

(54)

From Eqs. (52)–(54), its is observed that all three parameters j, s & l $\rightarrow 1$ as $t\rightarrow \infty$.

Figures 11, 12 and 13 represent the evolution of jerk, snap and lerk parameter, respectively. In model I, increasing values of all three parameters in the future show deviation from the $\Lambda$CDM model. However, in model II, all $j,s \; \& \; l \rightarrow 1$ as $t\rightarrow \infty$. Such behavior of these parameters indicates that model reaches to $\Lambda$CDM in late-time cosmic evolution. The behavior of EoS parameter in model II also shows similar feature of the model. Table 3 shows the behavior of the cosmographic parameters in model II.

Table 3 Behavior of cosmographic parameters in Model II

Fig. 11

Time variation of jerk parameter j

Fig. 12

Time variation of snap parameter s

Fig. 13

Time variation of lerk parameter l

5.2 Statefinder diagnostic

It is a model-independent approach to distinguish DE models from the standard models generally $\Lambda$CDM, Chaplygin gas (CG), quintessence and standard cold dark matter (SCDM). Sahni et al. [53] have introduced the geometrical pair (r, s), where r is same as the jerk parameter defined in Sect. 5.1 and s is the combination of r and DP q, and is defined as

$$\begin{aligned} s=\dfrac{2(r-1)}{3(2q-1)}. \end{aligned}$$

(55)

Here, we plot the trajectories of the pair (s, r) in $(s-r)$ plane and see the evolution of different DE models. In $(s-r)$ plane, the fixed point $(s,r)=(0,1)$ represents $\Lambda$CDM model and $(s,r)=(1,1)$ represents SCDM model. The region $s<0, r>1$ represents CG DE model, and $s>0,r<1$ represents quintessence DE model.

For model I, s is obtained as

$$\begin{aligned} s=\dfrac{2\left\{ 3T_1+2T_1^2+\dfrac{\alpha _2t}{2}(2\alpha _1-\alpha _2t)\right\} }{3(-2T_1-3)}. \end{aligned}$$

(56)

For model II, we obtain s as

$$\begin{aligned} s=\dfrac{2\left\{ \dfrac{\alpha _1^2}{1+\alpha _2t}(2+T_2)-3\alpha _1\right\} }{3(2\alpha _1-3\alpha _2t-3)}. \end{aligned}$$

(57)

Figure 14 shows the evolution of the (s, r) trajectories in both the models. In model I, the trajectory starts evolving in the quintessence region ($s>0,r<1$), crosses the $\Lambda$CDM fixed point and thereon stays in the CG region ($s<0, r>1$), whereas model II shows different behaviors. In model II, the trajectory starts evolving in the CG gas region, enters into the quintessence region and finally reaches to the $\Lambda CDM$ point.

Fig. 14

Plot of (s, r) trajectories

6 Best-fit values of model parameters $\alpha _1$ and $\alpha _2$

In this section, we constraint the model parameters $\alpha _1$ and $\alpha _2$ in both the models. For this purpose, we use 51 values of observed Hubble parameter measurements, complied by Magana et al. [54]. These values of H(z) are in the redshift range $0.07 \le z \le 2.36$. This Hubble data set includes 31 values of H(z) that are obtained from differential age (DA) method and 20 values of H(z) that are obtained from clustering using sound horizon at drag epoch, i.e., $r_d=152.33 \pm 1.3 Mpc$ from WMAP [55] measurements for entire data set.

The Chi-square function to find the best-fit values of the model parameters $\alpha _1$ and $\alpha _2$ is given by:

$$\begin{aligned} \chi ^2(\alpha _1,\alpha _2)=\sum _{\mu =1}^{51}\dfrac{H_{th}(\alpha _1,\alpha _2,z_{\mu })-H_{obs}(z_{\mu })}{\sigma _{\mu }^2}, \end{aligned}$$

(58)

where $H_{th}(\alpha _1,\alpha _2,z_{\mu })$ and $H_{obs}(z_{\mu })$ are the predicted and observed values of H(z), respectively. $\sigma _{\mu }$ is the standard error in observed value of H(z).

For model I, the $t-z$ relationship is obtained as

$$\begin{aligned} t(z)=\dfrac{\alpha _1}{\alpha _2}tanh\left[ -\dfrac{\alpha _1}{2}log\{l_1(1+z)\}\right] +\dfrac{\alpha _1}{\alpha _2}\approx T_3. \end{aligned}$$

(59)

Further, H in terms of redshift z is obtained as

$$\begin{aligned} H(z)=\dfrac{2}{2\alpha _1T_3-\alpha _2T_3^2}. \end{aligned}$$

(60)

Using Eq. (60), the best-fit values of $\alpha _1$ and $\alpha _2$ are obtained as $2.483 \pm 0.06$ and $0.415 \pm 0.06$, respectively, at $95 \%$ confidence level. The corresponding $\chi ^2_{red}=0.52$, and correlation coefficient is 0.97. Figure 15 represents the redshift variation of the Hubble parameter in model I.

Fig. 15

Plot of Hubble parameter H versus redshift z for model I

Fig. 16

Plot of Hubble parameter H versus redshift z for model II

Further, for model II, using the expressions of q and H as represented in Eqs. (32) and (35), respectively, we obtain

$$\begin{aligned} exp\left( -\dfrac{\alpha _2}{\alpha _1H}\right) =\dfrac{q+1}{\alpha _1}=\dfrac{1}{1+\alpha _2t} \end{aligned}$$

(61)

Further using $\dfrac{dH}{dz}=\dot{H}\left( -\dfrac{1}{H(1+z)}\right)$, one can obtain

$$\begin{aligned} \dfrac{H_z(1+z)}{H\alpha _1}= exp\left( -\dfrac{\alpha _2}{\alpha _1H}\right) =\dfrac{q+1}{\alpha _1}=\dfrac{1}{1+\alpha _2t} \end{aligned}$$

(62)

Integrating Eq. (62), we get

$$\begin{aligned} E_i\left( \dfrac{1}{\alpha _4H}\right) =-\alpha _1log(1+z)-logA, \end{aligned}$$

(63)

where $E_i$ is the exponential integral function, $\alpha _4=\frac{\alpha _1}{\alpha _2}$ and A is an integrating constant.

Using $t_0=13.8$ Gyr., we obtain the value of logA as $-Ei\left\{ log(1+13.8\alpha _2)\right\}$, so that we get

$$\begin{aligned} E_i\left( \dfrac{1}{\alpha _4H}\right) +\alpha _1log(1+z)-Ei\left\{ log(1+13.8\alpha _2)\right\} =0 \end{aligned}$$

(64)

Using Eq. (64), the best-fit values of $\alpha _1$ and $\alpha _2$ in model II are obtained as $3.145 \pm 0.08$ and $7.032 \pm 0.02$, respectively, at $95 \%$ confidence level. The corresponding $\chi ^2_{red}=0.48$, and correlation coefficient is 0.99. Figure 16 represents the redshift variation of the Hubble parameter in model II.

7 Conclusions

In this manuscript, the authors have studied two LRS Bianchi type-I bulk viscous cosmological models in f(R, T) gravity with variable DP. The parameterization of DP has been considered as $q=\dfrac{(\alpha _1-1)-\alpha _2t}{1+\alpha _3t}$, $\alpha _1,\alpha _2,\alpha _3 \ge 0$. This form of DP reduces to both LVDP [35] and BVDP [40] for specific values of model parameters. Cosmic acceleration is achieved through LVDP, i.e., $q=(\alpha _1-1)-\alpha _2t$, $\alpha _1, \alpha _2>0$ in model I, and BVDP, i.e., $q=\dfrac{(\alpha _1-1)-\alpha _2t}{1+\alpha _2t}$, $\alpha _1, \alpha _2>0$ in model II. The physical and geometrical properties of the models have been discussed and compared in detail.

In model I, the universe has finite lifetime, i.e., it starts with the Big Bang singularity $(a=0$ at $t=0)$ and ends at $t_e=\frac{2\alpha _1}{\alpha _2}$ $(a \rightarrow \infty$ as $t \rightarrow \frac{2\alpha _1}{\alpha _2} )$. Such feature is known as Big Rip scenario [14]. However in model II, the universe starts with the Big Bang singularity $(a=0$ at $t=0)$ and continues to expand forever $(a \rightarrow \infty$ as $t \rightarrow \infty$). The fastest rate of the expansion under LVDP is super-exponential expansion ($q<-1$). In model I, universe starts with decelerated expansion phase ($q=\alpha _1-1>0,$), enters into accelerated expansion phase $(q<0)$ at $t=\frac{\alpha _1-1}{\alpha _2}$ and then enters into super-exponential expansion phase ($q<-1$) at $t=\frac{\alpha _1}{\alpha _2}$ and ends with $q=-\alpha _1-1$ at $t_e =\frac{2\alpha _1}{\alpha _2}$. However, under BVDP, the fastest rate of expansion is exponential expansion $(q=-1)$. In model II, $q=\alpha _1-1 >0$ ,provided $\alpha _1>1$ at $t=0$, $q>0$ for $t<\frac{\alpha _1-1}{\alpha _2}$, $q<0$ for $t>\frac{\alpha _1-1}{\alpha _2}$ and $q\rightarrow -1$ as $t\rightarrow \infty$. Both the models show phase transition from early cosmic deceleration to the current cosmic acceleration. This feature of the models is found to be aligned with the theoretical and observational data. Both the models show anisotropy in the past and reach isotropization at late times.

Energy density $\rho$ and bulk viscosity coefficient $\xi$ remain positive throughout the evolution of the models. However, in model I, $\rho$ and $\xi$ diverge at the beginning and end of the universe, and in model II, $\rho$ and $\xi$ diverge at the beginning and $\rho$, $\xi$ $\rightarrow 0$ as $t\rightarrow \infty$. Effective pressure $\bar{p}$ alters its sign from early positive to present negative in model I. In model II, $\bar{p}$ is negative throughout the expansion of the universe. The present negative effective pressure in the models ensures the cosmic acceleration. In model I, $\omega$ starts evolving from a non-dark region, enters into quintessence region ($-1<\omega <-\frac{1}{3}$), crosses the cosmological constant line ($w=-1$) and thereon stays in the phantom region ($w<-1$). The nature of EoS parameter shows that model I behaves similar to phantom DE model in future followed by the Big Rip. However, model II resembles to quintessence DE model at present and $\Lambda$CDM model in future.

The behavior of the energy conditions—DEC, WEC, NEC and SEC—has been examined and presented graphically. Phantom matter is regarded as one of the interesting possibilities that does not satisfy NEC, i.e., $\rho +\bar{p}\ge 0$, and our model I follows the same. This ensures that the model is physically realistic. In this model, NEC is not satisfied at late times, and hence, SEC is also violated at late time cosmic evolution. In quintessence DE model, SEC needs to be violated, which is true in model II and thus ensures the viability of this model.

In model I, increasing values of jerk j, snap s and lerk l parameters in the future show deviation from the $\Lambda$CDM model. However, in model II , all $j,s \; \& \; l \rightarrow 1$ as $t\rightarrow \infty$. Such behavior of these parameters in model II indicates that model reaches to the $\Lambda$CDM in future. We have also performed statefinder diagnostic to discriminate various DE models. In model I, the trajectory starts evolving in the quintessence region, crosses the $\Lambda$CDM fixed point and thereon stays in the CG region, whereas, in model II, the trajectory starts evolving in the CG gas region, enters into the quintessence region and finally reaches to the $\Lambda$CDM point. Such feature of model II reassures that it behaves similar to the $\Lambda$CDM in late-time cosmic evolution.

In addition, we have also constrained the model parameters $\alpha _1$ and $\alpha _2$ in both the models using 51 values of observational Hubble data. The best-fit values of $\alpha _1$ and $\alpha _2$ in model I and II are obtained as $(2.483 \pm 0.06$, $0.415 \pm 0.06)$ and $(3.145 \pm 0.08, 7.032 \pm 0.02)$, respectively, at $95 \%$ confidence level.

Both the models developed in this study are significant in explaining late-time cosmic acceleration of the universe and are demonstrated to be applicable in the study of cosmic dynamics.