1 Introduction

In 1971, Professor Chua defined the fourth basic circuit component from the perspective of circuit theory [1], which established the constitutive relationship of flux and charge, named for memristor. HP Labs converted the theoretical assumptions of the memristor into an entity with the first attempt in 2008 [2]. Afterward, the unique properties of memristor attracted the attention of academia and industry. A memristor is a special element with properties such as low power consumption, memory function, and non-volatile characteristics [3]. It is crucial to overcome the bottlenecks of traditional computer architecture [4, 5]. Consequently, memristors are employed in numerous fields, such as chaotic circuits [5,6,7], image processing [8, 9], artificial neural networks [10,11,12], non-volatile memories [13, 14], and bioengineering [15, 16].

In 2014, based on the theoretical foundation of memristor, Chua proposed the definition of locally active memristor. The locally active memristor exhibits the characteristics of negative resistance or negative conductance within a specific voltage or current region, and can generate complex oscillations or even neuronal behaviors in nonlinear systems. The properties of locally active memristor are highly similar to those of neural and synaptic activities, as they possess memory and learning functions similar to synapses, and can process complex information and signals. Therefore, they provide a better platform for research in neuroscience and artificial intelligence. In recent years, numerous studies on locally active memristors have emerged. Their main work is to discover new types of memristors and study their locally active properties. Jin et al. [17] proposed a locally active memristor and combined it with capacitors and inductors to implement the simplest chaotic circuit. Li et al. [18] proposed a tristable locally active memristor, which can exist in three stable states under the same static voltage. At the same time, he proposed an s-type bistable locally active memristor model [19], which can generate two stable hysteresis loops according to different initial conditions. Xie et al. [20] proposed a fractional-order multistable locally active memristor with a wide locally active area. Ma et al. [21] proposed a new discrete memristor model, which performs discretization operations through continuous memristors and has locally active properties.

Chen et al. [22] constructed an S-type locally active memristor based on Chua's expansion theorem. The memristor has two stable equilibrium states and exhibits bistable characteristics. Gu et al. [23] proposed a novel model of current-controlled locally active memristor and found that circuits based on locally active memristors with different current biases or initial conditions can exhibit different dynamic characteristics, such as periodic oscillations and stable equilibrium points. Wheiher et al. [24] demonstrated the existence of locally active memristors from a materials science perspective.

Locally active memristors possess both local activity and non-volatility, so locally active memristive chaotic systems can exhibit more complex dynamic characteristics. They can be widely used in fields such as chaotic communication and chaotic encryption. In recent years, some research results of memristive chaotic systems have emerged. Sun et al. [25] designed an autonomous memristive chaotic system with an infinite chaotic attractor and proposed a method for designing the system. They also implemented the system in a simulated circuit. Based on the Bao system, Li et al. [26] constructed a hyperchaotic system based on memristors and designed a control method for the system, which not only allows for variable width control, but also ensures a monotonic decrease in width. The system has rich dynamic characteristics. Fu et al. [27] constructed a second-order nonlinear discrete memristor model and introduced it into a three-dimensional chaotic mapping. They designed a new four-dimensional memristive chaotic mapping, which exhibits more complex dynamic behavior and higher complexity.

Although more and more memristor chaotic systems have been designed, there are still few chaotic systems with rich dynamics. Therefore, this paper designs a new memristor jerk chaotic system based on a bistable locally active memristor. The system has the following features:

  1. 1.

    Through the simulation of the bistable locally active memristor, it can be seen that the memristor has the characteristics of low cost, easy implementation, and simple structure.

  2. 2.

    A novel memristor jerk system is constructed, which can generate four-scroll attractor under specific parameters, and has extreme multistability.

In addition, the non-volatility and local active properties of the memristor were analyzed, and the electronic components are used to realize the simulation. The generation mechanism of the memristor jerk chaotic system is explained. The multistability of the system is analyzed through the local basin of attraction. The system is implemented by circuit simulation, and the experimental results are in good agreement with the numerical simulation results.

The layout of the paper is as follows. Section 2 introduces the novel locally active memristor model, and verifies the local activity and non-volatility of the memristor through theoretical analysis and circuit simulation. Section 3 proposes a new memristive jerk chaotic system based on the novel memristor, analyzes its equilibrium point and Hoppe bifurcation point, introduces the mechanism of scroll generation, and conducts a study on the extreme multistability of the system analysis. In Sect. 4, it use analog components to simulate the memristive jerk system, which proves that the circuit simulation is consistent with the theoretical analysis, and proves the feasibility of the system. Section 5 concludes the whole paper.

2 A N-type locally-active memristor model

Chua classified memristors into four categories and first put forward the concept of the active memristor. A memristor can be divided into extended memristor, generic memristor, ideal generic memristor, and ideal memristor based on its mathematical representation. If the input is a voltage source, it is described as a voltage-controlled memristor. The mathematical model of the generic voltage-controlled memristor is defined by Eq. (1):

$$ \left\{ \begin{gathered} i = G(u)v \hfill \\ \frac{du}{{dt}} = g(u,v) \hfill \\ \end{gathered} \right. $$
(1)

where \(i\), \(v\), \(u\) are output current, input voltage, and state variable, respectively. \(G(u)\) is the memductance of a specific memristor.

2.1 Mathematical model and circuit emulator

To obtain its non-volatile memory and local activity. In this paper, a non-volatile bistable locally active memristor is proposed, and the mathematical model is defined as follows.

$$ \left\{ \begin{gathered} i = G(u)v = (3\cos u)v \hfill \\ \frac{du}{{dt}} = g(u,v) = - 2u^{3} + 4u - v \hfill \\ \end{gathered} \right. $$
(2)

where \(g(u,v)\) is the state expression of \(u\), \(v\) and \(i\) represent the output and input of the memristor.

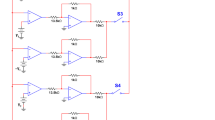
The implementation circuit of the active memristor can be designed according to the mathematical Eq. (2) as shown in Fig. 1, which is composed of a function unit \(\cos (u)\) and an integrator. The integrator consists of operational amplifiers \(U_{1} - U_{2}\), one capacitor \(C_{1}\), two analog multipliers \(A_{1} - A_{2}\), and resistors \(R_{1} - R_{5}\), in which the operational amplifier \(U_{2}\) realizes the inverse operation. Applying Kirchhoff’s law, the value of the time constant \(\tau = 1000 \, (\tau_{0} = \tau_{t} )\) is selected, and the equation of the emulator circuit is given from Eq. (3).

$$ \begin{gathered} \left\{ \begin{gathered} i_{M} = \frac{{g_{0} }}{{R_{6} }}\cos uv_{M} \hfill \\ \frac{du}{{dt}} = - \frac{{g_{1} g_{2} }}{{R_{1} C_{1} }}u^{3} + \frac{1}{{R_{2} C_{1} }}u - \frac{1}{{R_{3} C_{1} }}v_{M} \hfill \\ \end{gathered} \right. \hfill \\ \hfill \\ \end{gathered} $$
(3)

where \(v_{M}\) and \(i_{M}\) are the output voltage and input current through the memristor, respectively. \(g_{0}\), \(g_{1}\) and \(g_{2}\) are the gains of analog multipliers \(A_{3}\), \(A_{1}\) and \(A_{2}\), respectively. Let \(C_{1} = 100nF\), and the circuit parameters are identified as \(R_{1} = 2.5\,k\Omega\), \(R_{2} = 50\Omega\), \(R_{3} = 10\,k\Omega\), and \(R_{6} = 333.33\Omega\).

Fig. 1
figure 1

Simulation circuit implementation of locally active memristor

Full size image

2.2 Pinched hysteresis loops

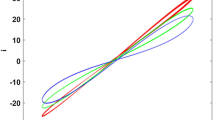
The pinched hysteresis loop (PHL) characteristics of the circuit simulator at different frequencies are explored. The signal generator is applied to generate a periodic sinusoidal voltage signal \(V = A\sin (2\pi F)\), where \(A\) and \(F\) are amplitude and frequency, respectively. When the amplitude \(A = 5{\text{V}}\) is fixed and frequencies \(F = 50\,{\text{kHz}}\), \(F = 80\,{\text{kHz}}\), \(F = 100\,{\text{kHz}}\) are selected, the PHLs are plotted in Fig. 2a. With the increase of frequency, the area of the hysteresis loop shrinks gradually. As the frequency \(F\) approaches infinity, the PHL shrinks to a single-valued function, which well verifies the characteristics of the PHL. Besides, the numerical simulation is operated to examine the validity of the circuit simulator under the same voltage signal, as shown in Fig. 2(b). According to \(\tau = 1000\), the frequency \(F\) can be derived from \(F = f\tau\).The circuit simulator is in good agreement with the numerical simulation results to certificate the fingerprint property of the proposed locally active memristor.

Fig. 2
figure 2

Simulation of the pinched hysteresis loop: a The circuit simulation diagram of pinched hysteresis loop (PHL) when the frequencies are 50 Hz, 80 Hz and 100 Hz, respectively, b the numerical simulation diagram of pinched hysteresis loop (PHL) when the frequencies are 50 Hz, 80 Hz and 100 Hz, respectively

Full size image

A memristor with two different PHLs under proper initial conditions is known as a bistable memristor. The PHL of the locally active memristor is affected not only by frequency but also depended on the initial value. When the initial values \(\varphi (0) = 0\) and \(\varphi (0) = - 1.61\) are selected with amplitude \(A = 5{\text{V}}\) and frequency \(f = 30\,{\text{Hz}}\), two identical PHLs are depicted in the \(v - i\) phase plane, as shown in Fig. 3a. It is worth noting that two different PHLs are drawn in the \(v - i\) phase plane of the initial values \(\varphi (0) = 0\) and \(\varphi (0) = 1.61\), as shown in Fig. 3b. Obviously, the initial value affects the bistability of the locally active memristor.

Fig. 3
figure 3

When a = 5V and f = 30Hz, the tightening hysteresis loop under different initial values: a The initial values are \(\varphi (0) = 0\) and \(\varphi (0) = - 1.61\), respectively, b the initial values are \(\varphi (0) = 0\) and \(\varphi (0) = - 1.61\), respectively

Full size image

2.3 Non-volatility

The non-volatile theorem proposed that ideal generic memristors have non-volatile characteristics. The nonvolatile memristor will remember its recent state of memristance by power is off. Non-volatility can be measured by POP. If the curve \(\frac{du}{{dt}}|_{{v_{M = 0} }} = 0\) has the intersection of two or more negative slopes with the \(u -\) axis, the memristor has a non-volatile memory. Let \(v_{M} = 0\) into Eq. 2, the mathematical equation of the POP can be shown in Eq. (4).

$$ \frac{du}{{dt}} = g(u,0) = - 2u^{3} + 4u $$
(4)

The POP corresponds to the proposed locally active memristor as shown in Fig. 4a, which is a dynamic route. It is obvious from Fig. 4a that there are 3 cross points with u-axis, marked as \(Q_{0} = (0,0)\), \(Q_{1} = ( - \sqrt 2 ,0)\), \(Q_{2} = (\sqrt 2 ,0)\).

Fig. 4
figure 4

Nonvolatile analysis of the memristor: a POP of a locally active memristor, b DRM diagram of five dynamic paths

Full size image

The arrowhead in Fig. 4a illustrates the moving direction of the variable u. Denoted that the initial point on the curve above (below) the u-axis must move to the right (left) alongside the pop, because \(du/dt > 0\) (\(du/dt < 0\)). From Fig. 4a, we can observe that \(Q_{1}\)\((u = - \sqrt 2 )\) and \(Q_{2}\)\((u = \sqrt 2 )\) are asymptotically stable equilibrium points with negative slopes, while \(Q_{0}\)\((u = 0)\) is unstable equilibrium points. The three equilibrium points on the \(u -\) axis will stay still. Moreover, the attraction domains of \(Q_{1}\) and \(Q_{2}\) are \([ - 1.8,0]\) and \([0,1.8]\), corresponding to blue and red curves, respectively. Thus, the memristor will judge that the state of its position tends to have two stable equilibria (\(Q_{1}\) and \(Q_{2}\)) when it is powered off. Equation (5) manifests two non-volatile memory, namely

$$ \left\{ \begin{gathered} u = u(Q_{1} ) = - \sqrt 2 {\text{ if }}x(0) < 0 \hfill \\ u = u(Q_{2} ) = \sqrt 2 {\text{ if }}x(0) > 0 \hfill \\ \end{gathered} \right. $$
(5)

The dynamic road map (DRM) of the memristor is a set of dynamic routes driven by different external voltages. The DRM is presented in Fig. 4b for five dynamic routes, each of which corresponds to voltage amplitude \(v_{M} = - 3{\text{V}}, - 1.5{\text{V}},0{\text{V}},1.5{\text{V}},3{\text{V}}\). Following the no-backtracking rule, the state variable \(u(t)\) moves along the appropriate path (from left to right or from right to left). To be sure, the direction of the arrow in DRM indicates the evolutionary direction of its asymptotically stable.

2.4 DC V–I characteristics and local activity

The DC behavior cannot be measured only by the PHL under the periodic excitation signal. It is convenient to judge the locally active characteristics of the memristor by drawing a DC V-I plot. In addition, non-volatile memristors are not all locally active. Let \(v_{M} = V\), \(i_{M} = I\) with \(du/dt = 0\), bring into Eq. (2), and we obtain Eq. (6).

$$ V = - 2U^{3} + 4U $$
(6)

where \(V\) signifies DC voltage, \(U\) represents a state variable. Combined with Eq. (2) and Eq. (6), the parametric form of the DC current \(I\) is given by

$$ I = (3\cos U)V = (3\cos U)( - 2U^{3} + 4U) $$
(7)

If \(U \in [ - 1.86,1.86]\), the U–V plot, U–I plot and the DC V–I plot established by Eq. (6) and (7) are depicted in Fig. 5. Through the U–V plot in Fig. 5a and the U–I plot in Fig. 5b, V–I plot can be shown in Fig. 5c. The red curve in Fig. 5c has negative slopes, indicating that the memristor has two locally active regions. Therefore, the proposed memristor is a bi-stable locally active memristor, which can rise chaos and even various neuromorphic patterns.

Fig. 5
figure 5

Verify the locally active function of the memristor: a U–V plot of the memristor, b U-I plot of the memristor, c V–I plot of the memristor

Full size image

3 A jerk system based on locally active memristor

The mathematical model of the Duffing system [28] is given as follows

$$ \frac{{d^{2} x}}{{dt^{2} }} + k\frac{dx}{{dt}} - x + x^{3} = 0 $$
(8)

Here \(k\) is a control parameter. Ref [29]. converted the Duffing equation into a jerk system, as follows:

$$ \frac{{d^{3} x}}{{dt^{3} }} = - \frac{{d^{2} x}}{{dt^{2} }} - k\frac{dx}{{dt}} + x - x^{3} $$
(9)

By changing the parameter k to b and adding the parameters a and c, Eq. (9) can be transformed into the form of a three-dimensional state space,

$$ \left\{ \begin{gathered} \dot{x} = y \hfill \\ \dot{y} = cz \hfill \\ z = x - ay - bz - x^{3} \hfill \\ \end{gathered} \right. $$
(10)

The proposed locally active memristor (2) are applied to Eq. (10). Thus, a four-dimension jerk chaotic system with locally active memristor is constructed as follows.

$$ \left\{ \begin{gathered} \dot{x} = y \hfill \\ \dot{y} = cz \hfill \\ z = 2x - ay - bz - x^{3} - 3\cos (u)y \hfill \\ \dot{u} = - 2u^{3} + 4u - y \hfill \\ \end{gathered} \right. $$
(11)

where a, b and c are positive parameters. The dot above variables represents differentiation concerning time.

3.1 Equilibrium point and stability analysis

The mathematical calculation is a clear manifestation of the system (11) obtains 9 equilibrium points \(E_{0} - E_{8}\) (\((x_{E} ,0,0,u_{E} )\), \((x_{E} = 0{\text{ or }} \pm \sqrt 2 ,u_{E} = 0{\text{ or }} \pm \sqrt 2 )\)), which are independent of the parameter a, b and c, are listed in Table 1. For the equilibrium points \((x_{E} ,0,0,u_{E} )\), the Jacobian matrix is given as:

$$ \left[ {\begin{array}{*{20}l} 0 \hfill &\quad 1 \hfill &\quad 0 \hfill &\quad 0 \hfill \\ 0 \hfill &\quad 0 \hfill &\quad c \hfill &\quad 0 \hfill \\ {2 - 3x_{E} ^{2} } \hfill &\quad { - a - 3\cos (u_{E} )} \hfill &\quad { - b} \hfill &\quad 0 \hfill \\ 0 \hfill &\quad { - 1} \hfill &\quad 0 \hfill &\quad { - 6u_{E} ^{2} + 4} \hfill \\ \end{array} } \right] $$
(12)
Table 1 The equilibrium points of system (11) and their stabilities
Full size table

The corresponding characteristic equation is given from the Jacobian matrix (12):

$$ (\lambda + 6u_{E}^{2} - 4)(\lambda^{3} + b\lambda^{2} + (ac + 3c\cos (u_{E} ))\lambda + 3cx_{E}^{2} - 2c){ = }0 $$
(13)

From Eq. (13), the characteristic roots are determined by the parameters a, b, c,\(x_{E}\) and \(u_{E}\). Obviously, one root \(\lambda_{1} = 4 - 6u_{E}^{2} = 4{\text{ or}} - 8\) with \(u_{E} = (0{\text{ or }} \pm \sqrt 2 )\). When selecting the parameter set:{\(a = 1\), \(b = 1\), \(c = 2\), \(x_{E} = 0{\text{ or }} \pm \sqrt 2\) }, we get the remaining three roots of the system (11), which are listed in Table 1. Equilibrium points \(E_{0} ,E_{5} ,E_{6}\) are unstable saddle focal point (USFP) of index 1, which produce the bonds and are in charge of connecting the scroll. Equilibrium points \(E_{1} ,E_{2} ,E_{3} ,E_{4}\) are unstable saddle focal point USFP) of index 2 around which the four-scroll are generated. The generation mechanism of the four scrolls will be described in detail in Sect. 3.2. Equilibrium points \(E_{7} ,E_{8}\) have a pair of complex conjugate roots which lead to Hopf bifurcation.

It is noticed that we prove the condition for the system (11) to generate Hopf bifurcation. Here, assuming the complex conjugate roots are \(\lambda_{3,4} = \pm i\omega\), the characteristic equation will satisfy Eq. (13) is given by

$$ - i\omega^{3} - b\omega^{2} + (ac + 3c\cos (u_{E} ))i\omega + 3cx_{E}^{2} - 2c = 0 $$
(14)

So that,

$$ \left\{ \begin{gathered} - b\omega^{2} + 3cx_{E}^{2} - 2c = 0 \hfill \\ (ac + 3c\cos u_{E} )\omega - \omega^{3} = 0 \hfill \\ \end{gathered} \right. $$
(15)

Thus, we get

$$ abc + 3bc\cos u_{E} - 3cx_{E}^{2} + 2c = 0 $$
(16)

Because of the parameters \(a > 0\), \(b > 0\), only the equilibrium points \(E_{1} ,E_{2} ,E_{3} ,E_{4} ,E_{7} ,E_{8}\) are suitable for Eq. (15). From Eq. (15) with \(x_{E} = \pm \sqrt 2 ,u_{E} = 0, \pm \sqrt 2\), we get two forms

$$ ab + 3bc - 4 = 0{\text{ or }}ab + 3b\cos (\sqrt 2 ) - 4 = 0 $$
(17)

Obviously, the Hopf bifurcation at equilibrium points of the system is controlled by the parameter a and b. Figure 6 plots the Hopf bifurcation trajectories for the control parameters provided in Eq. (16). It can be seen from Fig. 6, the range of selected parameters a and b is above the curve (purple or blue), the equilibrium points \(E_{1} ,E_{2} ,E_{3} ,E_{4} {\text{ or }}E_{7} ,E_{8}\) become USFP of index 1. When the range of selected parameters a and b is below the curve (purple or blue), the equilibrium points \(E_{1} ,E_{2} ,E_{3} ,E_{4} {\text{ or }}E_{7} ,E_{8}\) are converted to USFP of index 2.

Fig. 6
figure 6

Hopf bifurcation trajectories for the control parameters provided in Eq. (16)

Full size image

Considering \(a = 1\), \(b = 1\) and \(c = 2\) with initial condition \(( - 0.1, - 0.1,0.1,0.1)\), the phase portraits of system (11) are displayed in Fig. 7. The symbols “☆”, “⋄” remark the USFP of index 1 and USFP of index 2, respectively. Figure 7a exhibits the four-scroll attractor generated by the USFP of index 2 on the \(x - u\) coordinate plane.

Fig. 7
figure 7

Phase portraits of system (11) in different planes: a Phase portraits in x–u plane, b phase portraits in y–u plane, c phase portraits in z-u plane

Full size image

3.2 The generation mechanism of the scrolls

The formation mechanism of the four-scroll chaotic attractor is generated with the parameters \(a = 1\), \(b = 1\) and \(c = 2\) is analyzed qualitatively as follows.

The initial position of the system motion is located in the region \(P_{1}\), in which a scale-out scroll motion (First scroll) on the feature plane \(M^{U} (E_{1}^{ + } )\) is formed. With the scroll motion scale-out, the radius of the scroll is increasing. When reaching the boundary line \(\overline{{A_{1} C_{1} B_{1} }}\) between the two planes \(U_{1}\) and \(M^{U} (E_{1}^{ + } )\), the trajectory of the scroll will cross the plane \(U_{1}\) into the region \(P_{0}\) and lie below the feature plane \(M^{S} (E_{0} )\). After that, a downward single motion with axial tension and radial shrinkage (bond motion) is created in the region \(P_{0}\). Then, the bond passes through the plane \(U_{ - 1}\) into the region \(P_{2}\). A scale-out scroll motion (second scroll) on the feature plane \(M^{U} (E_{2}^{ - } )\) is formed again in the region \(P_{2}\). When the trajectory of the scroll reaches the boundary line \(\overline{{A_{2} C_{2} B_{2} }}\) between the two planes \(U_{2}\) and \(M^{U} (E_{2}^{ - } )\), the scroll goes through the plane \(U_{2}\) into the region \(P_{6}\). A single motion to the left with axial tension and radial shrinkage is formed. Then, the trajectory of the scroll crosses the plane \(U_{3}\) into the region \(P_{3}\). A scale-out scroll motion (Third scroll) on the feature plane \(M^{U} (E_{3}^{ + } )\) is formed in the region \(P_{3}\).

The scroll re-enters the region \(P_{6}\), when the trajectory of the scroll approaches the boundary line \(\overline{{D_{2} G_{2} F_{2} }}\) between the two planes \(U_{3}\) and \(M^{U} (E_{3}^{ + } )\). A single motion to the right with axial tension and radial shrinkage is formed and returns to the region \(P_{3}\). Thereafter, the trajectory of the scroll crosses \(U_{2}\) from the \(\overline{{D_{1} G_{1} F_{1} }}\) and arrives again in the \(P_{0}\), forming an upward bond motion. Next, the trajectory proceeds back to the region \(P_{1}\).

This stretching and folding transformation between the equilibrium points culminates in the four-scroll motion as shown in Fig. 8. Similarly, the trajectory of the scroll in the region \(P_{1}\) moves to the right, causing a scale-out scroll motion around the equilibrium point \(E_{4}\). Then, the trajectory returns to the region \(P_{1}\) again and rolls on in cycles. From Fig. 8, the direction of the scroll motion on the \(x - u\) plane is denoted by the direction of the arrow.

Fig. 8
figure 8

Diagram of stretching and folding transformation between equilibrium points in a four-scroll motion

Full size image

3.3 Local basins of attraction and symmetric dynamics

In accordance with Fig. 6, it is obvious to observe the consequences of parameters a and b on the characteristic roots. The system possesses 4 USFPs of index 2 and 3 USFPs of index 1, when the parameter \(b = 1\), \(c = 3\) and \(1 < a < 3.5320\). In this section, the multistability and symmetric dynamics attributed to the USFPs of index 2 are elaborated through the local basins of attraction.

The equilibrium points of system (11) are independent of the parameters. The USFP of index 2 is an important factor in the generation of self-excited scroll attractors. When the parameter \(a = 3.1\), two single-scroll chaotic attractors and two period-1 limit cycles about origin-symmetric that we notice cover the four attractive regions of \(E_{1} ,E_{2} ,E_{3} {\text{ and }}E_{4}\), as shown in Fig. 9a. Their initial conditions are selected as \(( - 1, - 0.1,0.1,0.1)\), \(( - 1, - 0.1,0.1, - 1)\), \((1, - 0.1,0.1, - 0.1)\) and \((1, - 0.1,0.1,1)\), respectively. When \(a = 3.285\), system (11) exhibits two coexisted single-scroll chaotic attractors, two single-scroll period-8 attractors, and two single-scroll period-1 limit cycles, as plotted in Fig. 9b. Their corresponding initial conditions are given as \(( - 1, - 0.1,0.1,0.1)\), \((0.1, - 0.1,0.1, - 0.1)\), \(( - 1, - 0.1,0.1,1)\), \((0.1, - 0.1,0.1, - 1)\), \((1, - 0.1,0.1,1)\) and \(( - 1, - 0.1,0.1, - 1)\), respectively. For \(a = 3.3\), the system (11) displays two coexisted single-scroll chaotic attractors, two single-scroll period-3 attractors, and two single-scroll period-1 limit cycles with initial conditions \(( - 1, - 0.1,0.1,0.1)\), \((0.1, - 0.1,0.1, - 0.1)\), \(( - 1, - 0.1,0.1,1)\), \((1, - 0.1,0.1, - 0.1)\), \((1, - 0.1,0.1,1)\), \(( - 1, - 0.1,0.1, - 1)\), respectively, as presented in Fig. 9c. When considering \(a = 3.4\), Fig. 9d illustrates two coexisted single-scroll period-2 attractors, two single-scroll period-1 limit cycles with initial conditions \(( - 1,0.1,0.1,0.1)\), \((1, - 0.1,0.1, - 1)\), \(( - 1, - 0.1, - 0.1,0.1)\) and \((1, - 0.1,0.1,1)\), respectively.

Fig. 9
figure 9

Attractor symmetry under different initial value conditions when a changes: a The symmetry of the four attractors when a = 3.1, b the symmetry of the six attractors when a = 3.285, c the symmetry of the six attractors when a = 3.3, d the symmetry of the four attractors when a = 3.4

Full size image

The self-excited characteristics of these coexisting attractors are discriminated by the relative position between the local attraction basins and the four equilibrium points. Consider as an example the coexisting attractors in Fig. 9a–d, whose basins of attraction cross the plane of the four equilibrium points, the four USFPs of index 2 \(E_{1} = ( - \sqrt 2 ,0,0,\sqrt 2 )\), \(E_{2} = (\sqrt 2 ,0,0, - \sqrt 2 )\), \(E_{3} = ( - \sqrt 2 ,0,0, - \sqrt 2 )\) and \(E_{4} = (\sqrt 2 ,0,0,\sqrt 2 )\), are presented in Fig. 10a–d, respectively. They are a convincing demonstration that chaotic attractors and periodic attractors are both symmetric and self-excited, in that the four USFPs of index 2 are located in their basins of attraction. The top-right and bottom-left period-1 limit cycles in Fig. 9 correspond to the orange and green regions in Fig. 10. Similarly, the self-excited attractors on the top-left and bottom-right of Fig. 9 correspond to the regions with similar colors in Fig. 10.

Fig. 10
figure 10

The local attraction basins and the relative position of the equilibrium point when a changes: a The attraction basin when a = 3.1, b The attraction basin when a = 3.285, c The attraction basin when a = 3.3, d The attraction basin when a = 3.4

Full size image

4 Circuit implementation of memristive jerk system

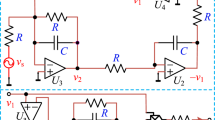
The analog circuit of the memristive jerk system is implemented based on the locally active memristor in Sect. 2 and combined with Eq. (11), as shown in Fig. 11. The actualized circuit includes analog multipliers, operational amplifiers, resistors and capacitors, which can be described by the design ideas in Ref. [3]. The operational amplifier TL084CN and the multiplier AD633AN with an external gain of 0.1 are employed in the main circuit. Applying circuit theory and the scale transformation method, the circuit state equation of (11) is written as follows:

$$ \left\{ \begin{gathered} RC_{1} \frac{{dV_{x} }}{dt} = \frac{R}{{R_{1} }}V_{y} \hfill \\ RC_{2} \frac{{dV_{y} }}{dt} = \frac{R}{{R_{2} }}V_{z} \hfill \\ RC_{3} \frac{{dV_{z} }}{dt} = \frac{R}{{R_{3} }}V_{x} - \frac{R}{{R_{4} }}V_{y} - \frac{R}{{R_{5} }}V_{z} - \frac{{g_{1} g_{2} R}}{{R_{6} }}V_{x}^{3} - \frac{{g_{3} R}}{{R_{7} }}\cos (V_{u} )V_{y} \hfill \\ RC_{4} \frac{{dV_{u} }}{dt} = - \frac{{g_{4} g_{5} R}}{{R_{8} }}V_{u}^{3} + \frac{R}{{R_{9} }}V_{u} - \frac{R}{{R_{10} }}V_{y} \hfill \\ \end{gathered} \right. $$
(18)

where the variable \(V_{x}\), \(V_{y}\), \(V_{z}\) and \(V_{u}\) denote the voltages in the integration circuit, respectively. The integration time constant is determined as \(RC_{j} = 1\) ms \((j = 1,2,3,4)\) with \(R = 10\,k\Omega\) and \(C_{j} = 100\;{\text{nF}}\), the gains of the multipliers \(g = 0.1\). From the system (11), the parameters of the jerk circuit with locally active memristor in Fig. 11 are derived in Table 2.

Fig. 11
figure 11

Simulation circuit diagram of system (11)

Full size image
Table 2 The value of the simulated circuit resistance
Full size table

Figure 12(a)-(c) displays the experimentally observed four-scroll chaotic attractor in the \(X - U\) plane, the double-scroll chaotic attractor in the \(Y - U\) plane, and the double-scroll chaotic attractor in the \(Z - U\) plane, respectively. The phase portraits of the numerical simulation in Fig. 7a–c perfectly match the results of the circuit experiments, which prove the correctness and feasibility of the system.

Fig. 12
figure 12

The circuit simulates the four—scroll chaotic attractors observed in different planes: a X–U plane, b Y–U plane, c Z–U plane

Full size image

In reality, however, analog components are not as ideal as simulation software. Changes in the external environment, such as the instability of temperature and humidity, will make the functional parameters of the analog components unstable, which is unacceptable for chaotic systems that are sensitive to initial values. Analog components also age and break over time. Therefore, in the practical application of chaotic circuits, analog circuits can only be used as experimental verification, and cannot be applied in practice.

Digital circuits become more attractive because, unlike analog components, they can provide greater stability and controllability. The signal in digital circuit exists in discrete form, and the influence of external environment changes can be reduced by accurate sampling and quantization. Problems such as temperature and humidity fluctuations and component aging have relatively little impact on digital circuits. In addition, the portability of digital circuits makes them more versatile. In summary, digital circuit is an ideal choice for hardware applications of chaotic systems.

This research uses FPGA (Field Programmable Gate Array) as the hardware realization platform, the platform chip used is cycloneIV of Altera company, and ACM9767 is used as a 14-bit dual-channel digital-to-analog converter. In order to verify the practicability of the system, the waveform of the chaotic system is displayed on the oscilloscope. Firstly, the chaotic system is discretized, which mainly includes Euler algorithm and Runge Kutta algorithm. The Runge Kutta algorithm has higher precision, but the operation occupies more resources and takes a long time, which has a greater burden on the FPGA with limited resources. Euler algorithm has faster computation speed. Therefore, the Euler algorithm is used to discretize the operation, and the specific formula is as follows:

$$ \left\{ \begin{gathered} x(n + 1) = x[n] + h * y[n] \hfill \\ y(n + 1) = y[n] + h * (c * z[n]) \hfill \\ z(n + 1) = z[n] + h * (2 * x[n] - a * y[n] - b * z[n] - x[n]^{3} - 3 * \cos (u[n]) * y[n]) \hfill \\ u(n + 1) = u[n] + h * ( - 2 * u[n]^{3} + 4u[n] - y[n]) \hfill \\ \end{gathered} \right. $$
(19)

where \(h\) is the step size of discretization,\(n\) and \(n + 1\) are two adjacent states, respectively. The specific steps of FPGA implementation are as follows:

Step1.In the VISIO software, complete the flow chart of the system iteration, which contains modules such as adders, multipliers, and integrators. This is a general understanding of discretization implementation.

Step2.Use quartus II software to write Verilog code, discretize the chaotic system through Euler algorithm, and generate iterative data. After synthesis, an RTL diagram is generated (Fig. 13).

Fig. 13
figure 13

RTL simulation diagram generated by chaotic system

Full size image

Step3.Write the testbench file and implement timing simulation in Modelsim software to ensure that the simulated waveform is chaotic. The simulated waveform is as shown in Fig. 14.

Fig. 14
figure 14

Chaos waveform simulation results in Modelsim

Full size image

Step4.After configuring the pins, connect the development board to the oscilloscope through a digital-to-analog converter. The results displayed by the oscilloscope are as shown in the figure. The results show that the discrete chaotic system iteration and numerical simulation have good consistency, which further proves the potential of the system in practical applications (Fig. 15).

Fig. 15
figure 15

Results of chaotic system implementation using FPGA a Real picture of chaotic system implementation, b phase diagram of hardware implementation

Full size image

5 Conclusion

In this paper, a novel bistable active memristor with local activity is investigated. The memristor emulator is implemented with electronic components, and the locally active characteristics and non-volatility of the memristor are demonstrated with DC \(V - I\) plot and POP, respectively. The proposed memristor has the advantages of low cost, easy implementation, and simple structure. With the proposed locally active memristor, a novel memristive jerk chaotic system is constructed. The novel system can produce complex dynamic behaviors with nine equilibria. We analyze the conditions that generate the Hopf bifurcation, which is related to the parameters \(a\) and \(b\). The memristive jerk system generates four-scroll attractors under specific parameters, and thus the generation mechanism of scrolls is revealed in detail. Furthermore, we exhibit analytically the extreme multistability of the memristive jerk system with coexisting position symmetry of six different self-excited attractors, which is demonstrated in the local attraction basins. The results achieved in analog circuit simulation and digital circuit are in good agreement with the numerical simulation results Novel dynamic behaviors in memristor-based neural models are explored in future work.