Combined action of time delay and colored cross-correlated Gaussian colored noises on dynamical characteristics for a FitzHugh–Nagumo neural system

Abstract

In this paper, we focus on the investigation of the regime shift of the steady states, the mean first-passage time (MFPT) and the stochastic resonance (SR) for a FitzHugh–Nagumo neural system with time delay perturbed by colored cross-correlated Gaussian colored noises as well as a periodic signal. By means of a series of numerical calculations, our investigation results show that time delay, the multiplicative noise and the additive one can all produce the negative influence on the maintenance of the stability for the neuronal system; while the two self-correlation times of the internal and external noises, the noise correlation strength and its correlation time can always strengthen the stability of the biological system. As for the MFPT for the FHN system, it is observed that during the recovery process from the excited state to the resting one, we should take measures to increases the noise correlation strength, two noise self-correlation times, and reduce time delay along with the noise correlation time so as to sustain the state of excitation for neuronal cells as far as possible. With respect to the SR phenomenon, it is observed that the noise correlation strength and its correlation time, two Gaussian noise correlation times $\tau_{1}$, $\tau_{2}$ can all amplify significantly the SR effect, and even stimulate the double-peaked or three-peaked phenomenon; While time delay and the additive noise will always reduce the SR effect.

1 Introduction

It is well known that the noise exists widely in every corner of the natural world [1,2,3,4,5,6,7,8,9,10]. Whereas, the noise has ever been always believed to be harmful to the signal spread, whose impact on the signal is always weakened as far as possible by people. As a significant dynamic index which is used to describe the phenomenon of system non-equilibrium phase transition, stationary probability density function (SPDF) has been applied to a large number of subjects now. In general, we apply Gaussian white noise to describing approximately the random fluctuation on a system. Whereas, the white noise is merely an ideal case. Hence, in the real model, people often use Gaussian colored noise to describe accurately the behaviors of the system [11,12,13,14,15,16,17,18]. For instance, Arnold et al. [9] investigated the impact of white and colored external noises upon the shift phenomena in nonlinear system. Castro et al. [10] discovered that a model subjected to a colored noise source can transfer from a monostable regime to a bistable one. Mangioni et al. [11] explored the disordering impacts of the color correlation in non-equilibrium phase transitions caused by multiplicative noise. Soldatov [12] discussed the phase transition in the gene selection system induced by colored noise term. Jung and Hanggi [13] investigated the bistable model evoked by the multiplicative Gaussian colored noise by means of the unified colored noise approximation. Cao et al. [18] generalized the unified colored noise approximation to a non-Markovian systems with the correlated noises. Meanwhile, they applied the general theory to the bistable dynamic system driven by cross-correlated additive and multiplicative Gaussian colored noises. Liang et al. [19] put forward a new parabolic-bistable potential system caused by an additive Gaussian color noise source, for which the SPD, the mean first-passage time (MFPT) and the SR phenomenon in were investigated. Jin et al. [20, 21] discussed the dynamics including the MFPT and stochastic resonance for a piecewise nonlinear system subjected to colored cross-correlated multiplicative and additive Gaussian colored noises.

In the 1950s, Hodgkin and Huxley [22] have ever constructed the Hodgkin–Huxley (HH) model of four dimensional nonlinear differential equation on basis of the theory of ion channels [23,24,25,26]. It depicted quantitatively the alteration process of the voltage and current on the membranes of neurons. Afterwards, FitzHugh and Nagumo [27] simplified the Hodgkin–Huxley model to a two-dimensional FitzHugh–Nagumo (FHN) model. Moreover, Alarcon [28] reduced further two-dimensional FHN neuron model and acquired one-dimensional neuron system, for which Collins et al. [29] studied the periodic stochastic resonance. Zeng et al. [30] explored the influence of time delay for the one-dimensional FHN neural model with correlations between extrinsic and intrinsic noises. Recently, there have been a great deal of work in the research of the neural system induced by non-Gaussian noise and Gaussian noise. Fuentes and Wio [31, 32] have investigated the SR phenomenon and the mean first-passage time in bistable system caused by non-Gaussian noise. Wu and Zhu [33] studied the SR effect in a in FHN neural system with non-Gaussian noise and Gaussian white noise, whose results indicated that the addition of non-Gaussian noise on FHN neuron system [34,35,36,37] is beneficial to the enhancement of the signal response and the improvement the signal-to-noise ratio (SNR). Recently, some closely related research has studied the role of noise and delays on neuronal dynamics [58,59,60]. Whereas, up to this day, there are a few works which focus on the combination of time delay and colored correlated multiplicative and additive Gaussian colored noises on the stochastic dynamics of the neural system.

In this paper, we firstly establish a stochastic FitzHugh–Nagumo neural model including time delay, colored cross-correlated multiplicative and additive Gaussian colored noises, and then derive the modified potential function and the SPDF for the FHN system in Sect. 2. Moreover, we deduce the MFPT expressions for the FNH model with time delay and different noise terms in Sect. 3. Further on, we obtain the SNR expression for the neuron system with different time delay and noise terms. Afterward, we analyze the roles of all noises and time delay on the modified potential function, the SPDF, the MFPT and the SNR for the FHN system in Sect. 5. In the final section, we summarize the main results for the FNH system (Fig. 1).

Fig. 1

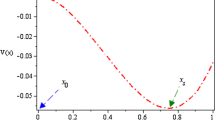
The bistable potential $\tilde{U}(v)$. The parameters take $a = 0.5,b = 0.01,\gamma = 1.0$. The unstable state is $v_{u} = \frac{1}{2}[a + 1 - \sqrt {(a - 1)^{2} - 4{b \mathord{\left/ {\vphantom {b \gamma }} \right. \kern-\nulldelimiterspace} \gamma }} ]$, the two stable states are $v_{2} = \frac{1}{2}[a + 1 + \sqrt {(a - 1)^{2} - 4{b \mathord{\left/ {\vphantom {b \gamma }} \right. \kern-\nulldelimiterspace} \gamma }} ]$(the excited state) and $v_{1} = 0$ (the resting state)

2 Stochastic FitzHugh–Nagumo neural model including colored cross-correlated Gaussian colored noise and time delay

One can describe the deterministic dynamical equations of the FitzHugh–Nagumo model as follows:

$$ \left\{ {\begin{array}{l} {\frac{{{\text{d}}v}}{{{\text{d}}t}} = v(a - v)(v - 1) - w,} \\ {\frac{{{\text{d}}w}}{{{\text{d}}t}} = bv - \gamma w,\begin{array}{*{20}c} {} & {} & {} \\ \end{array} } \\ \end{array} } \right. $$

(1)

where in the neural context, $v$ denotes a fast variable denoting the neuron membrane voltage and $w$ is a slow recovery variable, which is related to the time dependent conductance of the potassium channels in the membrane. $a$ denotes the threshold value, $b$ is on behalf of the influence of the slow variable on the neural system. $\gamma$ is a positive constant. By means of the adiabatic elimination method, the one-dimensional equation for the FHN model [40, 41] can be depicted as

$$ \frac{{{\text{d}}v}}{{{\text{d}}t}} = v(a - v)(v - 1) - \frac{b}{\gamma }v, $$

(2)

The potential function with respect to the determinative Eq. (2) is

$$ \tilde{U}(v) = \frac{{v^{4} }}{4} - \frac{a + 1}{3}v^{3} + \frac{{a + {b \mathord{\left/ {\vphantom {b \gamma }} \right. \kern-\nulldelimiterspace} \gamma }}}{2}v^{2} , $$

(3)

In the absence of the external periodic force and noise terms, Eq. (2) has two stable states which strongly depend on $a,b$ and $\gamma$:

$$ v_{1} = 0,\,\,\,v_{2} = \frac{1}{2}[a + 1 + \sqrt {(a - 1)^{2} - 4{b \mathord{\left/ {\vphantom {b \gamma }} \right. \kern-\nulldelimiterspace} \gamma }} ], $$

(4)

and an unstable state:

$$ v_{u} = \frac{1}{2}[a + 1 - \sqrt {(a - 1)^{2} - 4{b \mathord{\left/ {\vphantom {b \gamma }} \right. \kern-\nulldelimiterspace} \gamma }} ], $$

(5)

in its bistable region ${b \mathord{\left/ {\vphantom {b \gamma }} \right. \kern-\nulldelimiterspace} \gamma } < {{(a - 1)^{2} } \mathord{\left/ {\vphantom {{(a - 1)^{2} } 4}} \right. \kern-\nulldelimiterspace} 4}$. As a matter of fact, the threshold value $a$ of the neuron membrane voltage is all along perturbed by many external factors, such as temperature, drugs, social stimulation, radiotherapy and so on. It is reasonable to modify the threshold value $a$ as $a + \xi (t)$, in which $\xi (t)$ is an external noise term which describes the above fluctuations. Meanwhile, in consideration of the interaction of the neuronal cells and molecular oscillations in the human body as well as the impact from the external periodic force, an internal noise $\eta (t)$ and a weak periodic signal $A\cos (\omega t)$ (the amplitude $A$ and the pulsation $\omega$) should be introduced into the neuron system. Moreover, taking into account the fact that the external stimulus needs some time to transmit in the neural system, it is indispensable to add a time delay term $\beta$ into the neural system. When all these stochastic factors are considered, Eq. (2) can be rewritten as

$$ \frac{{{\text{d}}v}}{{{\text{d}}t}} = a(v^{2} - v(t - \beta )) + \xi (t)(v^{2} - v) - v^{2} (v - 1) - \frac{b}{\gamma }v + \eta (t) + A\cos (\omega t), $$

(6)

in which $\xi (t)$ and $\eta (t)$ are the Gaussian colored noises, which are characterized by their mean and variance, i.e.

$$ \begin{aligned} \left\langle {\xi (t)} \right\rangle &= \left\langle {\eta (t)} \right\rangle = 0,\;\; \hfill \\ \left\langle {\xi (t)\xi (t^{\prime})} \right\rangle &= \frac{Q}{{\tau_{1} }}\exp \left\{ { - \frac{{|t - t^{\prime}|}}{{\tau_{1} }}} \right\},\begin{array}{*{20}c} {} \\ \end{array} \left\langle {\eta (t)\eta (t^{\prime})} \right\rangle = \frac{M}{{\tau_{2} }}\exp \left\{ { - \frac{{|t - t^{\prime}|}}{{\tau_{2} }}} \right\}, \hfill \\ \left\langle {\xi (t)\eta (t^{\prime})} \right\rangle &= \frac{{\lambda \sqrt {QM} }}{\tau }\exp \left\{ { - \frac{{|t - t^{\prime}|}}{\tau }} \right\}, \hfill \\ \end{aligned} $$

(7)

where $Q$ and $M$ denote the strengths of the Gaussian colored noise terms $\xi (t)$ and $\eta (t)$, respectively. $\lambda \in [ - 1,1]$ represents the positive or negative correlation strength between the extrinsic noise and the intrinsic noise. $\tau_{1,2}$ denotes the self-correlation time of the multiplicative or additive noise, $\tau$ is on behalf of the correlation time of the colored cross-correlated noise.

When the delay time $\beta$ is relatively small, by means of the small time delay approximation method [12, 13, 18], we can change the equation into the following form:

$$ \frac{{{\text{d}}v(t)}}{{{\text{d}}t}} = h_{\beta } (v(t)) + g_{1} (v)\xi (t) + g_{2} (v)\eta (t),\quad v \in [ - 2,3] $$

(8)

with

$$ \begin{aligned} h_{\beta } (v(t)) & = (1 + a\beta )\left( {a(v^{2} (t) - v(t)) - v(t)^{2} (v(t) - 1) - \frac{b}{\gamma }v(t) + A\cos (\omega t)} \right), \\ g_{1} (v) & = (v^{2} - v)(1 + a\beta ),\,\,\,\,g_{2} (v) = 1 + a\beta . \\ \end{aligned} $$

(9)

By virtue of Novikov’s theorem [38] and Fox’s approach [39], the approximate Fokker–Planck equation (FPE) corresponding to Eq. (8) can be written as

$$ \begin{aligned} \frac{\partial P(v,t)}{{\partial t}} & = - \frac{\partial }{\partial v}h_{\beta } (v)P(v,t) \\ & \quad + \frac{Q}{{1 - \tau_{1} \left[ {h_{\beta }^{\prime } (v_{2} ) - \frac{{g_{1}^{\prime } (v_{2} )}}{{g_{1} (v_{2} )}}h(v_{2} )} \right]}} \times \frac{\partial }{\partial v}g_{1} (v)\frac{\partial }{\partial v}g_{1} (v)P(v,t) \\ & \quad + \frac{{\lambda \sqrt {QM} }}{{1 - \tau \left[ {h_{\beta }^{\prime } (v_{2} ) - \frac{{g_{2}^{\prime } (v_{2} )}}{{g_{2} (v_{2} )}}h(v_{2} )} \right]}} \times \frac{\partial }{\partial v}g_{1} (v)\frac{\partial }{\partial v}g_{2} (v)P(v,t) \\ & \quad + \frac{M}{{1 - \tau_{2} \left[ {h_{\beta }^{\prime } (v_{2} ) - \frac{{g_{2}^{\prime } (v_{2} )}}{{g_{2} (v_{2} )}}h(v_{2} )} \right]}} \times \frac{\partial }{\partial v}g_{2} (v)\frac{\partial }{\partial v}g_{2} (v)P(v,t) \\ & \quad + \frac{{\lambda \sqrt {QM} }}{{1 - \tau \left[ {h_{\beta }^{\prime } (v_{2} ) - \frac{{g_{1}^{\prime } (v_{2} )}}{{g_{1} (v_{2} )}}h(v_{2} )} \right]}} \times \frac{\partial }{\partial v}g_{2} (v)\frac{\partial }{\partial v}g_{1} (v)P(v,t)), \\ \end{aligned} $$

(10)

where $h(v) = v(a - v)(v - 1) - \frac{b}{\gamma }v$, $h_{\beta }^{\prime } (v)$, $g_{1}^{\prime } (v)$, $g_{2}^{\prime } (v)$ are the derivative functions of $h_{\beta } (v)$, $g_{1} (v)$, $g_{2} (v)$ with respect to $v$, respectively. It is easy to derive that

$$ \begin{aligned} & 1 - \tau_{i} \left[ {h_{\beta }^{\prime } (v_{2} ) - \frac{{g_{2}^{\prime } (v_{2} )}}{{g_{2} (v_{2} )}})h(v_{2} )} \right] = 1 - \tau_{i} \left[ {h_{\beta }^{\prime } (v_{2} ) - \frac{{g_{1}^{\prime } (v_{2} )}}{{g_{1} (v_{2} )}})h(v_{2} )} \right] \\ & \quad = 1 + (1 + a\beta )\tau_{i} \left\{ {(a - 2v_{2} )(1 - v_{2} ) - v_{2} (a - v_{2} ) + \frac{b}{\gamma }} \right\}\begin{array}{*{20}c} {} & {i = 1,2} \\ \end{array} \\ \end{aligned} $$

(11)

Therefore, the analytical Fokker–Planck equation can be written as

$$ \frac{\partial P(v,t)}{{\partial t}} = - \frac{\partial }{\partial v}\mu (v)P(v,t) + \frac{{\partial^{2} }}{{\partial v^{2} }}\sigma^{2} (v)P(v,t), $$

(12)

for which, the drift coefficient $\mu (v)$ and the diffusion coefficient $\sigma^{2} (v)$ are defined respectively by

$$ \begin{aligned} \mu (v) & = \left( {a(v^{2} - v) - v^{2} (v - 1) - \frac{b}{\gamma }v + A\cos (\omega t)} \right)(1 + a\beta ) \\ & \quad + \left( {\frac{Q}{{1 + (1 + a\beta )\tau_{1} \cdot f(v_{2} )}} \cdot v(v - 1)(2v - 1) + \frac{{\lambda \sqrt {QM} \cdot (2v - 1)}}{{1 + (1 + a\beta )\tau \cdot f(v_{2} )}}} \right)(1 + a\beta )^{2} \\ \end{aligned} $$

(13)

$$ \begin{aligned} \sigma^{2} (v) &= \left\{ {\frac{Q}{{1 + (1 + a\beta )\tau_{1} \cdot f(v_{2} )}}} \right.v^{2} (v - 1)^{2} \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} &\quad + \frac{{2\lambda \sqrt {QM} \cdot v(v - 1)}}{{1 + (1 + a\beta )\tau \cdot f(v_{2} )}} + \left. {\frac{M}{{1 + (1 + a\beta )\tau_{2} \cdot f(v_{2} )}}} \right\}(1 + a\beta )^{2} , \hfill \\ \end{aligned} $$

(14)

where $f(v_{2} ) = (a - 2v_{2} )(1 - v_{2} ) - v_{2} (a - v_{2} ) + \frac{b}{\gamma }$.

Therefore, the steady-state probability distribution can be analytically described as

$$ P_{st} (v,t) = \frac{N}{\sigma (v)}\exp \left[ {\int_{v} {\frac{{\mu (v^{\prime})}}{{\sigma^{2} (v^{\prime})}}{\text{d}}v^{\prime}} } \right] = \frac{N}{\sigma (v)}\exp \left[ { - U(v)} \right] $$

(15)

where $N$ is the normalization constant, and $U(v)$ is the modified potential function, which is calculated as

$$ \begin{aligned} U(v) & = \frac{{\arctan \left( {\frac{{Qvdd_{2} }}{{\sqrt {\left( {\lambda \sqrt {QM} d_{1} d_{2} - \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} } \right)Qdd_{2} } }}} \right)}}{{(\lambda^{2} d_{1} d_{2} - d^{2} )\sqrt {\left( {\lambda \sqrt {QM} d_{1} d_{2} - \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} } \right)Qdd_{2} } }} \times A_{1} \\ & \quad + \frac{{\ln \left( {1 + Qv^{2} dd_{2} + \lambda \sqrt {QM} d_{1} d_{2} - \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} } \right)}}{{\lambda^{2} d_{1} d_{2} - d^{2} }} \times A_{2} \\ & \quad + \frac{{\ln \left( {1 + Qv^{2} dd_{2} + \lambda \sqrt {QM} d_{1} d_{2} + \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} } \right)}}{{\lambda^{2} d_{1} d_{2} - d^{2} }} \times A_{3} \\ \end{aligned} $$

(16)

where the long coefficients $A_{1} - A_{3} ,d_{1} ,d_{2} ,d$ have been placed in the “Appendix”.

The discussion on the dynamics of the modified potential function $U(v)$ and the SPDF $P_{st} (v,t)$ will be given in the Section 5.

3 The MFPT for the neuronal system disturbed by time delay and cross-correlated Gaussian colored noise terms

With respect to the stochastic FitzHugh–Nagumo neural system, we have interest in exploring the regime shift behaviors between its stable states by exploring the mean first-passage time (MFPT) that state particle travel through a potential barrier from one steady state to another. Here, the time of the neuronal system shifting from the resting state $v_{1}$ to the excited one $v_{2}$ is called the mean excitation time, and the time of the system returns to the resting state from the excited one is named the mean resting time, whose accurate expressions of MFPT can be described as

$$ T(v_{1} \to v_{2} ) = \int_{{v_{1} }}^{{v_{2} }} {\frac{dv}{{\sigma^{2} (v)P_{st} (v)}}} \int_{0}^{v} {P_{st} (v){\text{d}}y} , $$

(17)

$$ T(v_{2} \to v_{1} ) = \int_{{v_{1} }}^{{v_{2} }} {\frac{dv}{{\sigma^{2} (v)P_{st} (v)}}} \int_{v}^{ + \infty } {P_{st} (v){\text{d}}y} , $$

(18)

However, due to the extremely complicated calculations of Eqs. (18) and (19), we have to turn to computing the approximate expressions for the mean first passage time. Under the assumption that the noise intensity is small enough relative to the energy barriers

$$ \Delta U(v) = U(v_{u} ) - U(v_{1} )\,\,\,{\text{and}}\,\,\,\Delta U(v) = U(v_{u} ) - U(v_{2} ), $$

(19)

by use of the steepest-descend approximation, by linearizing the potential profile around the minima and the maximum by Kramers [61], we can acquire the modified MFPT as follows:

$$ T(v_{1} \to v_{2} ) = \frac{2\pi }{{\sqrt {|\tilde{U}^{\prime\prime}(v_{u} )\tilde{U}^{\prime\prime}(v_{1} )|} }}\exp [U(v_{1} ) - U(v_{u} )], $$

(20)

$$ T(v_{2} \to v_{1} ) = \frac{2\pi }{{\sqrt {|\tilde{U}^{\prime\prime}(v_{u} )\tilde{U}^{\prime\prime}(v_{2} )|} }}\exp [U(v_{2} ) - U(v_{u} )], $$

(21)

in which $\tilde{U}(v)$ and $U(v)$ are defined by Eqs. (3) and (16), respectively.

4 The SNR for the neuronal system subjected to time delay, noise terms and their correlation times

When the pulsation $\omega$ and the amplitude $A$ of the input period signal are very small, the particle cannot transit from a well to the other one. Using the definition of mean first-passage time and steepest descent method, one can obtain the expression of transition rates $W_{ \pm }$ in terms of $v_{1,2}$,

$$ W_{ + } = \frac{{\sqrt {|\tilde{U}^{\prime\prime}(v_{2} )\tilde{U}^{\prime\prime}(v_{u} )|} }}{2\pi }\exp [U(v_{u} ) - U(v_{2} )], $$

(22)

$$ W_{ - } = \frac{{\sqrt {|\tilde{U}^{\prime\prime}(v_{1} )\tilde{U}^{\prime\prime}(v_{u} )|} }}{2\pi }\exp [U(v_{u} ) - U(v_{1} )], $$

(23)

in which $\tilde{U}(v)$ and $U(v)$ have been defined by Eqs. (3) and (16), respectively.

For the general asymmetric case we define the SNR as the ratio of the strength of the output signal and the broadband noise output evaluated at the signal frequency. Correspondingly, the expression of SNR is given by the two-state approach [37]

$$ {\text{SNR}} = \frac{{A^{2} \pi (\mu_{1} \alpha_{2} + \mu_{2} \alpha_{1} )^{2} }}{{4\mu_{1} \mu_{2} (\mu_{1} + \mu_{2} )}}, $$

(24)

where

$$ \begin{aligned} \mu_{1} & = \left. {W_{ - } } \right|_{A\cos (\omega t) = 0} ,\,\,\,\,\mu_{2} = \left. {W_{ + } } \right|_{A\cos (\omega t) = 0} , \\ \alpha_{1} & = \left. {\frac{{{\text{d}}W_{ - } }}{{{\text{d}}A\cos (\omega t)}}} \right|_{A\cos (\omega t) = 0} ,\,\,\,\,\,\alpha_{2} = \left. {\frac{{{\text{d}}W_{ + } }}{{{\text{d}}A\cos (\omega t)}}} \right|_{A\cos (\omega t) = 0} . \\ \end{aligned} $$

(25)

5 Results and discussion

In this section, we at first investigate the stochastic dynamics for the modified potential function and stationary probability density function induced by the colored correlated Gaussian colored noises and time delay. There are some classical references [50,51,52,53,54,55] concerning the constructive role of the noise in nonlinear systems of interdisciplinary physics far from equilibrium. On the other hand, the NES (noise-induced stability) phenomenon in metastable systems can be found in Refs. [62, 63]. For the convenience of observation, we simultaneously present the 2-dimensional and 3-dimensional plots for the modified potential function.

The 2-dimentional and 3-dimentional images of the modified function $U(v)$ as a contrast for the stochastic FitzHugh–Nagumo system are plotted in Figs. 2, 3, 4, 5 and 6, which are disturbed by all types of noise terms and time delay term. The minima of $U(v)$ corresponding to $v_{1}$ (or $v_{2}$) are stable states of the potential profile, and the maximum of $U(v)$ corresponding to $v_{u}$ is the unstable state [37]. Here, we label the depth of the left well as $d_{1} = U(v_{u} ) - U(v_{1} )$, and the one of the right well as $d_{2} = U(v_{u} ) - U(v_{2} )$. As one observes, in Figs. 2 and 3, as time delay $\beta$ and the additive noise intensity $M$ increase, the two well depths of the biological system are both decreased remarkably, which implies the attraction of two stable states $v_{1}$ and $v_{2}$ to the state particle are both weakened, and the biological stability of the FHN system is correspondingly impaired. In contrast, in Figs. 4 and 6, with the increase of two noise correlation times $\tau_{1}$ and $\tau_{1}$, the both well depths are enhanced significantly, which means that the attractions of the two stable states to the system particle are strengthened. Accordingly, the global stability of the neuron system is improved. It is very interesting that in Fig. 5 there is initially a potential well around $v = 0.5$ while the noise correlation strength $\lambda$ takes a big negative value. However, with the increase of $\lambda$ from negative to positive, there appear two potential wells on both sides of $v = 0.5$, whose depths are increased continually. The fact shows that the noise correlation strength $\lambda$ is in favor of the stability enhancement of the neuronal system.

Fig. 2

The 2D and 3D curve of the modified potential $U(v)$ versus the neuron membrane voltage $v$ and time delay $\beta$, the other relevant parameters take $\lambda = 0.5,\tau_{1} = 0.3,\tau_{2} = 0.3,\tau = 0.3,$ $Q = 0.2,M = 0.03,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0$

Fig. 3

The 2D and 3D curve of the modified potential $U(v)$ versus the neuron membrane voltage $v$ and additive noise intensity $M$, the other relevant parameters take $\lambda = 0.5,\tau_{1} = 0.3,\tau_{2} = 0.3,$ $Q = 0.2,\beta = 0.3,\tau = 0.3,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0$

Fig. 4

The 2D and 3D curve of the modified potential $U(v)$ versus the neuron membrane voltage $v$ and correlation time $\tau_{2}$ of additive noise intensity, the other relevant parameters take $\lambda = 0.5,$ $Q = 0.2,M = 0.03,\beta = 0.3,\tau_{1} = 0.3,\tau = 0.3,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0$

Fig. 5

The 2D and 3D curve of the modified potential $U(v)$ versus the neuron membrane voltage $v$ and noise correlation strength $\lambda$, the other relevant parameters take $Q = 0.2,$ $M = 0.03,$ $\tau_{1} = 0.3,\tau_{2} = 0.3,$ $\beta = 0.3,\tau = 0.3,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0$

Fig. 6

The 2D and 3D curve of the modified potential $U(v)$ versus the neuron membrane voltage $v$ and correlation time $\tau_{1}$ of multiplicative noise intensity, the other relevant parameters take $\lambda = 0.5,$ $Q = 0.2,M = 0.03,\beta = 0.3,\tau_{2} = 0.3,\tau = 0.3,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0$

The roles of the strength $Q$ of the multiplicative noise and time delay $\beta$ upon the SPDF $P_{st} (v,t)$ are depicted in Fig. 7. As one observes, the increase of $Q$ and $\beta$ can both result in the substantial reduction of the probability density at the two stable states. In a words, the biological stability of the neuron system is reduced by a wide margin because of the action of $Q$ and $\beta$.

Fig. 7

The stationary probability distribution function (SPDF) $P_{st} (v,t)$ as a function of the neuron membrane voltage $v$ for different values of $Q$ or $\beta$, and the other parameters take $\lambda = 0.5,\tau = 0.3,$ $M = 0.03,\tau_{1} = 0.3,\tau_{2} = 0.3,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0,$ (a) $\beta = 0.3$ and (b) $Q = 0.2$

In contrast to the dynamical behaviors shown in Fig. 7, the two noise correlation times $\tau$ and $\tau_{1}$ in Fig. 8 bring about the positive effect on the biological stability of the neural system. Specially speaking, the increase of $\tau$ and $\tau_{1}$ can give rise to the significant enhancement of the probability peaks at both stable states, which contributes to the reinforcement of the system stability.

Fig. 8

The stationary probability distribution function (SPDF) $P_{st} (v,t)$ as a function of the neuron membrane voltage $v$ for different values of $\tau_{1}$ or $\tau$, and the other parameters take $\lambda = 0.5,$ $Q = 0.2,\beta = 0.3,M = 0.03,\tau_{2} = 0.3,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0,$ (a) $\tau = 0.3$ and (b)$\tau_{1} = 0.3$

We describe the impact of the intensity $M$ of the additive noise and its self-correlation time $\tau_{2}$ on the SPDF in Fig. 9. As the plots show, the increase of $M$ brings about the significant reduction of the probability peaks at the two stable states. Ultimately, the heights of the two peaks reach the same value, which contributes to the information exchange between the both stable states. Conversely, an increase of $\tau_{2}$ leads to the remarkable improvement of the probability density at the resting state and the exciting one, which is in agreement with the dynamics reflected in Fig. 4. It should be noted that the probability height at the resting state surpasses far that at the exciting one, which is to the disadvantage of information exchange between stable states.

Fig. 9

The stationary probability distribution function (SPDF) $P_{st} (v,t)$ as a function of the neuron membrane voltage $v$ for different values of $M$ or $\tau_{2}$, and the other parameters take $\lambda = 0.5,$ $Q = 0.2,\beta = 0.3,\tau_{1} = 0.3,\tau = 0.3,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0$. (a) $\tau_{2} = 0.3$ and (b)$M = 0.03$

The impact of the noise correlation strength $\lambda$ upon the SPDF is revealed in Fig. 10. It is easily to see that because of the action of $\lambda$, the heights of both probability peaks are increased significantly, which indicates the corresponding biological system stability is also strengthened remarkably.

Fig. 10

The stationary probability distribution function (SPDF) $P_{st} (v,t)$ as a function of the neuron membrane voltage $v$ for different values of $\lambda$, and the other parameters take $Q = 0.2,\beta = 0.3,$ $\tau = 0.3,M = 0.03,\tau_{1} = 0.3,\tau_{2} = 0.3,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0$

Some famous works concerning noise-induced effects (as NES and stochastic resonant activation) due to non-Gaussian noise sources Lévy type can be found in Refs. [56, 57]. In accordance with Eq. (21) of the MFPT, the impacts of the time delay, the extrinsic noise, the intrinsic noise and the noise correlation between them on the mean resting time can be discussed in detail through numerical calculation as follows:

During the process of the system particle coming back to the resting state from the excited one, in order to cope with all kinds of external stimulus, we wish to prolong the mean resting time of the FHN system as far as possible. It is clear to see from Fig. 11 that as the strength $\lambda$ increases from negative to positive, the mean resting time is prolonged continually because of the improvement of peak values. That is to say, it takes more time for the neuron system to complete the transition from the excited state to the resting one. The resting process is slowed down because of the action of $\lambda$.

Fig. 11

The MFPT $T(v_{2} \to v_{1} )$ as the function of the multiplicative noise intensity $Q$ for different values of noise correlation strength $\lambda$, meanwhile the other parameters are $M = 0.03,$ $\beta = 0.3,\tau = 0.3,$ $\tau_{1} = 0.3,\tau_{2} = 0.3,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0.$

In Fig. 12, we analyze the role of time delay $\beta$ and the correlation time $\tau$ on the mean excitation time. As seen in the plot, the change of $\beta$ and $\tau$ leads to the significant reduction of the mean resting time of the neuron system, which means that the resting process is shortened greatly and the neural system can go back to the resting state quickly.

Fig. 12

The MFPT $T(v_{2} \to v_{1} )$ as the function of the multiplicative noise intensity $Q$ for different values of $\beta$ or $\tau$, meanwhile the other parameters are $\lambda = 0.5,M = 0.03,\tau_{1} = 0.3,$ $\tau_{2} = 0.3,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0.$ (a) and $\tau = 0.3,$ (b) $\beta = 0.3.$

Figure 13 demonstrates the influence of two noise self-correlation times $\tau_{1}$ and $\tau_{2}$ on the MFPT. As the figure shows, the mean resting time of the system is prolonged remarkably on account of the action of $\tau_{1}$ and $\tau_{2}$. Due to the role of resonant peaks, the neuronal system needs to spend more time in getting back from the excited state to the resting one. That is to say, on this occasion the system can maintain the excitation state longer. In addition, it’s worth noting that the peak value of the MFPT in Fig. 13b all along occurs around $Q = 0.12$.

Fig. 13

The MFPT $T(v_{2} \to v_{1} )$ as the function of the multiplicative noise intensity $Q$ for different values of $\tau_{1}$ or $\tau_{2}$, meanwhile the other parameters are $\lambda = 0.5,M = 0.03,\tau = 0.3,$ $\beta = 0.3,a = 0.5,b = 0.01,A = 0.0,\gamma = 1.0.$ (a) $\tau_{2} = 0.3,$ and (b) $\tau_{1} = 0.3.$

All above results shown in Figs. 11, 12 and 13 are due to the noise enhanced stability (NES) phenomenon, characterized by a nonmonotonic behavior of the MFPT versus the noise intensity. This is a well-known noise-induced phenomenon theoretically investigated and experimentally observed in metastable physical and biological systems [42,43,44,45]. From a physical point of view, the results shown in the figures indicate that the multiplicative noise contributes to breaking the symmetry of the bistable system.

When concerning the SR phenomenon in physical and biological systems, some well-known research [46,47,48,49, 64] has been made. In line with Eq. (24), the effects of the external force, the intensities and the correlation times of noises as well as the system parameters upon the SNR are discussed via a numerical calculation as follows.

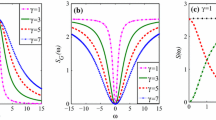
Figure 14 illustrates the influence of the noise correlation strength $\lambda$ on the SNR, which is as a function of the multiplicative noise intensity $Q$. As one can see, the strength $\lambda$ has a nice stimulating effect on the SR phenomenon. More precisely, the strength $\lambda$ excites a significant double-peak phenomenon on the SNR. As $\lambda$ increases from negative to positive, two resonant peaks simultaneously arise around $Q = 0.05$ and $Q = 0.2$. Especially, the right peak keeps moving to the large values of $Q.$

Fig. 14

The signal-to-noise ratio $SNR$ versus multiplicative noise intensity $Q$ for different values of noise correlation strength $\lambda$, and the other parameters take $M = 0.03,\tau = 0.3,\beta = 0.3,$ $\tau_{1} = 0.3,\tau_{2} = 0.3,\gamma = 1.0,a = 0.5,b = 0.01,A = 0.1,\omega = 0.01$

Figure 15 reflects truly the effect of the noise correlation time $\tau$ upon the SNR as the function of the noise correlation strength $\lambda$. As the plot shows, $\tau$ is scarcely possible to alter the height and the location of the resonant peak, which occurs around $\lambda = 0.3$. However, the increase of $\tau$ can improve the values of the SNR on both sides of the resonant peak.

Fig. 15

The signal-to-noise ratio $SNR$ versus noise correlation strength $\lambda$ for different values of noise correlation time $\tau$, and the other parameters take $Q = 0.1,M = 0.03,\beta = 0.3,\tau_{1} = 0.3,$ $\tau_{2} = 0.3,\gamma = 1.0,b = 0.01,a = 0.5,A = 0.1,\omega = 0.01$

Figure 16 shows some interesting SR phenomena caused by the correlation time $\tau_{1}$ of the multiplicative noise. It can be found that because of the stimulation of $\tau_{1}$, the resonant peak shifts from $\lambda = 1.0$ to $\lambda = 0.6$, whose height is improved continually. It’s worth mentioning in particular that all SR phenomena appear in the positive interval of $\lambda$.

Fig. 16

The signal-to-noise ratio $SNR$ versus noise correlation strength $\lambda$ for different values of noise correlation time $\tau_{1}$, and the other parameters take $Q = 0.1,M = 0.03,\beta = 0.3,\tau = 0.3,$ $\tau_{2} = 0.3,\gamma = 1.0,b = 0.01,a = 0.5,A = 0.1,\omega = 0.01$

Figure 17 portrays the stimulating role of the correlation time $\tau_{2}$ of the additive noise on the SNR as a function of $\lambda$. The fact is uncovered that the increase of $\tau_{2}$ can result in the improvement of the resonant peak, whose location moves to the small values of $\lambda$. Analogous to the fact shown in Fig. 16, there is no SR phenomenon caused by $\tau_{2}$ during the negative interval of $\lambda$.

Fig. 17

The signal-to-noise ratio $SNR$ versus noise correlation strength $\lambda$ for different values of noise correlation time $\tau_{2}$, and the other parameters take $Q = 0.1,M = 0.03,\beta = 0.3,\tau = 0.3,$ $a = 0.5,A = 0.1,\omega = 0.01,\tau_{1} = 0.3,\gamma = 1.0,b = 0.01$

Figure 18 reveals the impact of time delay $\beta$ upon the SNR while other parameters are fixed. As one can see, the small value of $\beta$ can induce a significant resonant peak. Whereas, the SR phenomenon will disappear as $\beta$ increases to 1.0. Meanwhile, the curve of the SNR degenerates into a monotone-increasing function on the strength $\lambda$. In a word, time delay $\beta$ plays a negative role in exciting the SR effect.

Fig. 18

The signal-to-noise ratio $SNR$ versus noise correlation strength $\lambda$ for different values of time delay $\beta$, and the other parameters take $Q = 0.1,M = 0.03,\tau_{1} = 0.3,\tau = 0.3,\tau_{2} = 0.3,$ $\gamma = 1.0,a = 0.5,b = 0.01,A = 0.1,\omega = 0.01$

In Fig. 19, time delay $\beta$ also illustrates the prominent inhibition effect on the SR phenomenon. To be more specific, small values of $\beta$ can stimulate a significant double-peaked phenomenon; However, with the increases of $\beta$, the two peaks drop rapidly, which shows that $\beta$ plays a critical role in reducing the SR effect.

Fig. 19

The signal-to-noise ratio $SNR$ versus multiplicative noise intensity $Q$ for different values of time delay $\beta$, and the other parameters take $\lambda = 0.6,M = 0.03,\tau_{1} = 0.3,\tau = 0.3,$ $\tau_{2} = 0.3,\gamma = 1.0,a = 0.5,b = 0.01,A = 0.1,\omega = 0.01$

Figure 20 reveals the role of the additive noise intensity $M$ upon the SNR as the function of the multiplicative noise intensity $Q$. The fact is easily found that the slight increase of $M$ can lead to the significant reduction of the resonant peak, which will verge to disappear in the end.

Fig. 20

The signal-to-noise ratio $SNR$ versus multiplicative noise intensity $Q$ for different values of additive noise intensity $M$, and the other parameters take $\lambda = 0.6,\beta = 0.3,\tau_{1} = 0.3,\tau = 0.3,$ $\tau_{2} = 0.3,\gamma = 1.0,a = 0.5,b = 0.01,A = 0.1,\omega = 0.01$

Figure 21 exhibits the complex dynamic behaviors caused by the correlation time $\tau_{1}$ of the multiplicative noise. As one watches, there appears a significant double-peaked phenomenon because of the action of $\tau_{1}$. As $\tau_{1}$ increases, the heights of the two peaks are both enhanced. Especially noteworthy is when $\tau_{1}$ increases to 2.5, there arises a distinct three-peaked phenomenon of the SNR. In particular, the left peak rises by a wide margin.

Fig. 21

The signal-to-noise ratio $SNR$ versus multiplicative noise intensity $Q$ for different values of noise correlation time $\tau_{1}$, and the other parameters take $\lambda = 0.6,M = 0.03,\beta = 0.3,$ $\tau = 0.3,\tau_{2} = 0.3,\gamma = 1.0,a = 0.5,b = 0.01,A = 0.1,\omega = 0.01$

Something interesting induced by the noise correlation time $\tau_{2}$ have also occurred in Fig. 22. Concretely speaking, initially, only one resonant peak appears around $M = 0$. Whereas, as $\tau_{2}$ increases, the height of the peak declines, together with another peak arising around $M = 0.12$, which shifts to the large values of $M$. There exists a transformation from the single peak to double peaks.

Fig. 22

The signal-to-noise ratio $SNR$ versus additive noise intensity $M$ for different values of noise correlation time $\tau_{2}$, and the other parameters take $\lambda = 0.6,Q = 0.1,\beta = 0.3,\tau = 0.3,$ $\tau_{1} = 0.3,\gamma = 1.0,b = 0.01,a = 0.5,A = 0.1,\omega = 0.01$

6 Conclusions

To sum up, we have investigated in detail the regime transition, the mean resting time between the two steady states and the stochastic resonance for a time-delayed FitzHugh–Nagumo system triggered by colored cross-correlated Gaussian colored noises. As for the stochastic stability of the neuron system, it is discovered that the extrinsic noise, the intrinsic noise and time delay can all reduce by a wide margin the probability density around the resting state and the excited one, furthermore, result in the large reduction of the stability for the whole neuronal system. Conversely, three noise self-correlation times and the noise correlation strength can all boost the probability peaks at the two stable states, which leads to the consolidation of the stability for the biological system.

On the other hand, with regard to the mean first passage time between stable states for the neuron system induced by different noise terms and delay term, the following results are uncovered: During the process of returning from the excited state to the resting one, in order to maintain excitatory state of the nerve corpuscles as far as possible, some measures should be taken to increase the values of $\lambda$, $\tau_{1}$, $\tau_{2}$, and lessen the noise correlation time $\tau$ as well as time delay $\beta$.

Finally, we discuss the SR phenomenon for the FitzHugh–Nagumo system caused by time delay and the colored correlated Gaussian colored noises. Specially speaking, the noise correlation strength $\lambda$ and its correlation time $\tau$, two correlation times $\tau_{1}$, $\tau_{2}$ of extrinsic and intrinsic noises can enhance remarkably the SR effect of the SNR. Especially, $\tau_{1}$, $\tau_{2}$ can even stimulate the double-peaked or the three-peaked phenomenon of the SNR under a certain conditions. On the contrary, time delay $\beta$ and the additive noise intensity $M$ always play a significant inhibitory role in the excitation of the SR phenomenon.

Appendix

The coefficients of the modified potential $U(x)$ are listed as follows:

$d = 1 + (1 + a\beta )\tau \cdot \left\{ {(a - 2v_{2} )(1 - v_{2} ) - v_{2} (a - v_{2} ) + \frac{b}{\gamma }} \right\}$,

$d_{1,2} = 1 + (1 + a\beta )\tau_{1,2} \cdot \left\{ {(a - 2v_{2} )(1 - v_{2} ) - v_{2} (a - v_{2} ) + \frac{b}{\gamma }} \right\}$,

$$ \begin{aligned} A_{1} &= - \frac{1}{2}\frac{{d^{2} \lambda^{2} d_{1}^{2} }}{1 + a\beta } + \frac{1}{2}\frac{{d_{2} dd_{1} a\lambda \sqrt {QM} \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} }}{(1 + a\beta )QM} - \frac{1}{2}\frac{{d_{2}^{2} d\lambda^{2} d_{1}^{2} a}}{1 + a\beta } \hfill \\ &\quad + \frac{1}{2}\frac{{d_{2} d^{3} d_{1}^{{}} }}{1 + a\beta } + \frac{1}{2}\frac{{d_{2}^{{}} d^{3} d_{1}^{{}} a}}{1 + a\beta } - \frac{1}{2}\frac{{d_{2}^{2} d\lambda^{2} d_{1}^{2} }}{1 + a\beta } - \frac{1}{2}\frac{{d_{2} dd_{1} \lambda \sqrt {QM} \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} }}{(1 + a\beta )QM} \hfill \\ &\quad + \frac{1}{2}\frac{{d_{2}^{2} d^{3} d_{1}^{{}} }}{1 + a\beta } - \frac{1}{2}\frac{{d_{2}^{2} d\lambda d_{1}^{2} a}}{1 + a\beta } - \frac{1}{2}\frac{{d_{2}^{2} dd_{1}^{2} \lambda \sqrt {QM} \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} }}{(1 + a\beta )QM} \hfill \\ &\quad + \frac{1}{2}\frac{{d_{2}^{{}} d^{3} d_{1}^{2} a}}{1 + a\beta } + \frac{1}{2}\frac{{d_{2}^{{}} d^{2} d_{1}^{{}} \lambda \sqrt {QM} \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} }}{(1 + a\beta )QM} \hfill \\ &\quad+ \frac{1}{2}\frac{{d_{2}^{2} d^{2} d_{1}^{2} a\lambda }}{1 + a\beta } + \frac{1}{2}\frac{{d_{2}^{2} d^{2} d_{1}^{{}} \lambda a\sqrt {QM} \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} }}{(1 + a\beta )QM} - \frac{1}{2}\frac{{d_{2}^{{}} d^{2} \lambda^{3} d_{1}^{{}} }}{1 + a\beta } \hfill \\ &\quad+ \frac{1}{2}\frac{{d_{2}^{{}} d^{2} \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} A\cos (\omega t)}}{(1 + a\beta )M} - \frac{1}{2}\frac{{d_{2}^{{}} d^{2} \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} A\cos (\omega t)}}{(1 + a\beta )QM} \hfill \\ \end{aligned} $$

$$ \begin{aligned} A_{2} &= \frac{1}{2}d^{2} + \frac{1}{4}\frac{{db\sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} }}{(1 + a\beta )QM} + \frac{1}{4}\frac{{da\sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} }}{(1 + a\beta )QM} \hfill \\ &\quad - \frac{1}{4}\frac{{d_{1} \lambda \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} \sqrt {QM} }}{{(1 + a\beta )Q^{2} M}} + \frac{1}{4}\frac{{d_{2} \lambda^{2} d_{1}^{2} }}{(1 + a\beta )Q} - \frac{1}{4}\frac{{d^{2} d_{1}^{{}} }}{(1 + a\beta )Q} - \frac{1}{2}\frac{{d_{2} \lambda^{2} d_{1}^{{}} }}{(1 + a\beta )QM} \hfill \\ \end{aligned} $$

$$ \begin{aligned} A_{3} &= \frac{1}{2}d^{2} + \frac{1}{4}\frac{{d_{2} \lambda^{2} d_{1}^{2} }}{(1 + a\beta )Q} - \frac{1}{4}\frac{{dd_{1}^{2} }}{(1 + a\beta )Q} - \frac{1}{4}\frac{{db\sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} }}{(1 + a\beta )QM} \hfill \\ &\quad + \frac{1}{4}\frac{{d_{1} \lambda \sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} \sqrt {QM} }}{{(1 + a\beta )Q^{2} M}} - \frac{1}{2}\frac{{d_{2} \lambda^{2} d_{1}^{{}} }}{(1 + a\beta )QM} - \frac{1}{4}\frac{{d\sqrt {QMd_{1} d_{2} (\lambda^{2} d_{1} d_{2} - d^{2} )} a}}{(1 + a\beta )QM} \hfill \\ \end{aligned} $$