Introduction

Dynamical models from cellular level to network and cortical level usually play a necessary role in cognitive neuroscience (Levin and Miller 1996; Wang et al. 2014; Déli et al. 2017; Mizraji and Lin 2017; Song et al. 2019). Due to the random release of neurotransmitter, the stochastic bombing of synaptic inputs and the random opening and closing of ion channels, noise is ubiquitous in neural systems. Various noise-induced non-equilibrium phenomena disclosed in experimental or dynamical models, such as stochastic synchronization (Kim and Lim 2018), noise induced phase transition (Lee et al. 2014) and stochastic integer multiple discharge (Gu and Pan 2015), are helpful in explaining the biophysical mechanisms underlying neural information processing and coding.

Stochastic resonance, initially proposed in exploring the periodicity of the continental ice volume in the quaternary era (Benzi et al. 1981), is such an anti-intuitive phenomenon (Gammaitoni et al. 1998; Nakamura and Tateno 2019; Xu et al. 2020; Zhao et al. 2020), where weak coherent signal can be amplified by noise through certain nonlinearity. In general, a suitable external weak signal is prerequisite for stochastic resonance. When the external weak signal is absent or replaced by an intrinsic periodicity, it is referred to as coherence resonance (Guan et al. 2020), which often appears in systems close to Hopf bifurcation. When the external weak signal is not periodic, it is called aperiodic stochastic resonance (Collins et al. 1995; 1996a, b; Tiwari et al. 2016).

Thanks to the aperiodicity of the weak signal, the spectral amplification factor or the output signal-to-noise ratio, typical for periodic signals (Liu and Kang 2018; Yan et al. 2013), is no longer suitable to be a quantifying index. In fact, for aperiodic stochastic resonance, instead of emphasizing frequency matching, shape matching should be emphasized, thus the cross-correlation measure (Collins et al. 1995; 1996a, b) and the input–output mutual information (Patel and Kosko 2005, 2008) are commonly used indexes. Although the quantification is seemingly complex, the principle of aperiodic stochastic resonance has found much significance in neural processing and coding, since the spike trains of action potential observed in hearing enhancement (Zeng et al. 2000) and visual perception experiments (Dylov and Fleischer 2010; Liu and Li 2015; Yang 1998) tend to be nonharmonic. Very recently, the principle of aperiodic stochastic resonance has been effectively applied to design visual perception algorithm using spiking networks (Fu et al. 2020).

Noise correlation is common in cortical firing activities. Nevertheless, most of the literatures took Gaussian white noise for grant, except that a few (Averbeck et al. 2006; Guo 2011; Sakai et al.1999) paid attention to the “color” of noise but far from enough. Therefore, in this paper we investigate the effect of (Orenstein-Ulunbeck type) Gaussian colored noise (Floris 2015; Wang and Wu 2016) of nonzero correlation time on the aperiodic stochastic resonance. As a starting point, we will generalize the existing zeroth order perturbation results (Freidlin et al. 2012) of nonlinear dynamical systems from Gaussian white noise to Gaussian colored noise. And then, we follow the “forbidden interval” theorem (Kosko et al. 2009) and direct simulation to explore the aperiodic stochastic resonance in bistable and excitable neural systems.

The paper is structured as follows. In “General results” section, we introduce some preliminaries and main results. In “Proof of general results”, we provide the proof for the perturbation property under global and local Lipschitz conditions, respectively. And then we predict the phenomenon of aperiodic stochastic resonance based on information theory measure through Theorem 3 in the same section. In “Numerical verification” section, numerical results based on two types of neuron models are shown to disclose the functional role of noise correlation time. Finally, conclusions are drawn in “Conclusion and discussion” section.

General results

Suppose that \(X (t )\) satisfy the general d-dimensional stochastic differential equation driven by an m-dimensional Ornstein–Ulenbeck process

$$\frac{d}{dt}X_{t} = f({X_{t}}, t) + g({X_{t}}, t)U(t),\quad X(0) = X_{0}$$
(1)

where \(X_{t} = (X^{1} (t)\;\;X^{2} (t) \;\ldots \;X^{d} (t))'\) and \(f(X_{t} ,t) = (f^{1} (X_{t} ,t)\;\;\;f^{2} (X_{t} ,t) \;\ldots\; f^{d} (X_{t} ,t))'\) is the state vector and the field vector, the function matrix \(g(X_{t} ,t) = (g_{j}^{i} (X_{t} ,t))_{d \times m}\) describes the noise intensity, and \(U(t) = (u_{1} (t)\;\;u_{2} (t) \;\ldots\; u_{m} (t)\;)'\) is the m-dimensional Ornstein–Ulenbeck process. Equation (1) is essentially shorthand for the following equations

$$\frac{d}{dt}X_{t}^{i} = f^{i} (X_{t} ,t) + \sum\limits_{j = 1}^{m} {g_{j}^{i} (X_{t} ,t)U_{j} (t)}$$
(1a)
$$du_{j} (t) = - \frac{1}{\tau }u_{j} (t)dt + \sigma dW_{j} (t)$$
(1b)

for \(i = 1,\,2, \ldots ,d\) and \(j = 1,2, \ldots ,m\). Here, each scalar Ornstein–Ulenbeck process \(u_{j} (t)\), also referred to as Gaussian colored noise, is defined on complete probability space \((\varOmega ,\mathscr{F},\{ {\mathscr{F}}_{t} \}_{t \ge 0} ,P)\) with a filtration \(\{ {\mathscr{F}}_{t} \}_{t \ge 0}\), which satisfies the usual conventions (Øksendal 2005; Mao 2007): it is increasing and right continuous and \({\mathscr{F}}_{0}\) contains all P-null sets. In Eq. (1b), where \(W_{i} (t)\)(\(1 \le i \le m\)) are statistically independent Wiener processes satisfying

$$\left\langle {W_{i} (t)} \right\rangle = 0,\,\,\left\langle {W_{i} (t )W_{j} (s )} \right\rangle = \delta_{ij} {\text{min(}}t,s ).$$

In this paper, we assume that the Ornstein–Ulenbeck process \(u_{j} (t)\) is stationary. That is, \({{u}_{j}}(t)\sim N(0,0.5\tau {{\sigma }^{2}})\) for all \(t \ge 0\). It is also known from Ito formula that

$$E\left[ {|u_{j} (t)|^{2k} } \right] = (2k - 1)!!(0.5\tau \sigma^{2} )^{k} ,\quad k = 1 ,2 ,\ldots$$

Suppose that \(\hat{X}(t)\) satisfy

$$\frac{d}{dt}\hat{X}_{t} = f(\hat{X}_{t} ,t),\;\;\hat{X}(0) = X_{0}$$
(2)

Then, the following main results in Theorems 1 and 2 state that

$$E\left[ {\;\mathop { \sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} } \right] \to 0$$
(3)

as \(\sigma \to 0\) under the global and local Lipschitz conditions, respectively.

Theorem 1

Let \(f^{i} :\;R^{d} \to R\) and \(g_{j}^{i} :\;R^{d} \to R\) in the system (1) be Borel measurable functions. Assume that there is a positive constant \(L\) such that \(f^{i}\) and \(g_{j}^{i}\) satisfy

$${\left|{f^{i}(x_{1}, \cdot) - f^{i}(x_{2}, \cdot)}\right|}^{2} \le L{\left|{x_{1} - x_{2}}\right|}^{2}, {\left|{g_{j}^{i}(x_{1}, \cdot) - g_{j}^{i}(x_{2}, \cdot)}\right|}^{2} \le L{\left|{x_{1} - x_{2}}\right|}^{2}$$
(4)

for \(\forall x_1, x_2 \in R^d\), namely, \(f^{i}\) and \(g_{j}^{i}\) are global Lipschitz continuous. Also, assume that there is a pair of positive constants \(K\) and \(\gamma \in (0,1)\) such that \(f^{i}\) and \(g_{j}^{i}\) satisfy the global growth conditions

$$\left| {f^{i} (x,t)} \right| \le K(1 + \left| x \right|),\;\;\left| {g_{j}^{i} (x,t)} \right| \le K(1 + \left| x \right|^{\gamma } )$$
(5)

for \(\forall (x,t) \in R^d \times [0, T]\). Here \(i = 1,2, \ldots ,d\) and \(j = 1,2, \ldots ,m\). Then, for every \(T > 0\), there exist positive constants \(a_{4}\) and \(b_{4}\) (see Eqs. (11) and (12) in “Proof of general results” section, respectively) such that

$$E\left[ {\;\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} } \right] \le \sigma^{2} A_{1} \exp (B_{1} T) < \infty ,$$
(6)

where \(A_{ 1} = 2dm(m + 1)T^{2} K^{2} (4\xi_{1} + \sqrt {\xi_{2} a_{4} \exp (b_{4} T)} )\), \(B_{ 1} = (m + 1)dTL\), and

$$\xi_{k} = (0.5\tau )^{k - 1} (0.5\tau + KT) + 2k\sqrt {3T(4k - 3)!!(0.5\tau )^{2k - 1} }$$
(7)

for \(k = 1,2, \ldots\).

Theorem 2

Let \(f^{i} :\;R^{d} \to R\) and \(g_{j}^{i} :\;R^{d} \to R\) in the system (1) for all \(i = 1,2,\ldots,d\) and \(j = 1,2,\ldots,m\) be Borel measurable functions, satisfying the local Lipschitz condition

$$ \left| {f^{i} (x_{1} , \cdot ) - f^{i} (x_{2} , \cdot )} \right|^{2} \le L_{N} \left| {x_{1} - x_{2} } \right|^{2} ,\;\left| {g_{j}^{i} (x_{1} , \cdot ) - g_{j}^{i} (x_{2} , \cdot )} \right|^{2} \le L_{N} \left| {x_{1} - x_{2} } \right|^{2} $$
(8)

for all \(x_{1}\),\(x_{2} \in R^{d}\) with \(\left\| {x_{1} } \right\| \le N\) and \(\left\| {x_{2} } \right\| \le N\) and the growth conditions (5) . Here \(L_{N}\) is a positive constant for any \(N > 0\). Then, for every \(T > 0\), there holds \(E\left[ {\;\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} } \right] \to 0\) as \(\sigma \to 0\).

Throughout the context, we use \(\;\left| {\; \cdot \;} \right|\) to denote the Euclidean norm in \(R^{d}\) or the trace norm of matrices, that is to say that for a vector \(X\), \(\left| X \right|^{2} = \sum\nolimits_{i} {\left| {X_{i} } \right|^{2} }\) and for a matrix \(A\), \(\left| A \right|^{2} = \sum\nolimits_{i,j} {\left| {A_{ij} } \right|^{2} }\). Here, we remark that Theorem 1 states that the solution of the perturbed system (1) satisfying global Liptschitz condition and the growth condition can be approximated by the unperturbed system when the noise intensity of the Gaussian colored noise tends to zero, while Theorem 2 states the same conclusion but relaxs the global Liptschitz condition into the local Lipschitz condition. Both of them can be regarded as the generalization of the perturbation results associated with zeroth order approximation (Freidlin et al. 2012). More exactly, the corresponding perturbation result in the book of Freidlin and Wentzell can be recovered from Theorem 1 when \(\tau \to 0\) (i.e. in the Gaussian white noise limit). By utilizing the two theorems, we can provide an assertion in the theorem 3 below for the existence of aperiodic stochastic resonance in certain nonlinear systems with Gaussian colored noise.

The aperiodic stochastic resonance phenomenon is usually referred to as a kind of special stochastic resonance where the weak drive signal is aperiodic. As pointed in the introduction section, the mutual information is more qualified as the index to quantify aperiodic stochastic resonance than the signal-to-noise ratio. To this end, we suppose that the nonlinear system receives binary random signals, denoted by \(S (t )\in \left\{ {s_{1} ,s_{2} } \right\}\) and its output \(Y (t )\in \left\{ {0 ,\;1} \right\}\) is a quantized signal as well, depending on whether the output response \(x (t )\) is below or over a certain threshold. We emphasize that this kind of quantized treatment is very common in the background of stochastic resonance and neural dynamics.

Let \(I(S,Y)\) be the Shannon mutual information of the discrete input signal \(S\) and the discrete output signal \(Y\), then it can be defined by the difference of the output’s unconditional entropy and conditional entropy (Cover and Thomas 1991), namely \(I(S,Y) = H(Y) - H(Y\left| S \right.)\). Denote by \(P_{S} (s)\) the probability density of the input signal, \(P_{Y} (y)\) the probability density of the output signal, \(P_{Y\left| S \right.} (y\left| s \right.)\) the conditional density of the output given the input, and \(P_{S,Y} (s,y)\) the joint density of the input and the output. Then,

$$\begin{aligned} I (S,Y )& = H (Y )- H (Y\left| S \right. )\\ & = - \sum\limits_{y} {P_{Y} (y ) {\text{log}}} P_{Y} (y )+ \sum\limits_{s} {\sum\limits_{y} {P_{S,Y} (s,y ) {\text{log}}} P_{Y\left| S \right.} (y\left| s \right. )} \\ & = - \sum\limits_{s} {\sum\limits_{y} {P_{S,Y} (s,y ) {\text{log}}} P_{Y} (y )} + \sum\limits_{s} {\sum\limits_{y} {P_{S,Y} (s,y ) {\text{log}}} \frac{{P{}_{S,Y} (s,y )}}{{P_{S} (s )}}} \\ & = \sum\limits_{s} {\sum\limits_{y} {P_{S,Y} (s,y ) {\text{log}}} \frac{{P_{S,Y} (s,y )}}{{P_{S} (s )P_{Y} (y )}}} \\ \end{aligned}$$
(9)

From the above final equation, it is clear to see that \(I(S,Y) = 0\) if and only if \(P_{S,Y} (s,y) = P_{S} (s)P_{Y} (y)\). Moreover, by mean of Jensen’s inequality one can find that \(I(S,Y) \ge 0\), where the equal sign holds true if and only if the input signal and the output signal are mutually independent. Hence, Shannon mutual information, capable of measuring the statistical correlation between the input and output signals, is suitable for detecting how much of the subthreshold aperiodic signal being contained in the output spike trains. Noise deteriorates the transmission performance of dynamical systems, however, when aperiodic stochastic resonance occurs, the transmission capacity can be optimally enhanced at an intermediate noise level.

Note that the nonmonotonic dependence of the input–output mutual information on noise intensity signifies the occurrence of aperiodic stochastic resonance, thus a direct proof for the existence of aperiodic stochastic resonance should contain a basic deduction of the extreme point of the mutual information. But, the explicit formulaes for mutual information are often hard to acquire, thus such a direct proof is almost impossible. In order to make our results generally applicable, we adopt an indirect proof based on the “forbidden interval” theorem (Patel and Kosko 2008), as stated by Theorem 3.

Theorem 3

Consider stochastic resonant systems of the form in Eq. (1) with \(f(X_{t} ,t) = \tilde{f}(X_{t} ) + \tilde{S}(t)\) and \(\tilde{S}(t) = [S(t)\;\;0\;\; \ldots \;\;0]'\). Suppose that \(\tilde{f}(x)\) and \(g(x)\) satisfy local Lipschitz condition and the growth condition (5). Suppose that the input signal \(S(t) \in \{ s_{1} ,s_{2} \}\) is subthreshold, that is, \(S(t) < \theta\) with \(\theta\) being some crossing threshold. Suppose that for some sufficiently larger noise intensity, there is some statistical dependence between the binary input and the impulsive output, that is to say, \(I(S,Y) > 0\) holds true for some \(\sigma_{0} > 0\). Then, the stochastic resonant systems can exhibit the aperiodic stochastic resonance effect in the sense that \(I(S,Y) \to 0\) as \(\sigma \to 0\).

Theorem 3 gives a sufficient condition for the aperiodic stochastic resonance in the system (1) with subthreshold signals. As is known from Jensen’s inequality that \(I(S,Y) \ge 0\) and \(I(S,Y) = 0\) if and only if \(S\) and \(Y\) are statistically independent. Then, we can reasonably suppose there exist some \(\sigma_{0} > 0\) such that \(I(S,Y) > 0\). The “forbidden interval” theorem states that what goes down must go up (Patel and Kosko 2005, 2008; Kosko et al. 2009), thus the assertion in Theorem 3 can be proven if one can verify that \(I(S,Y) \to 0\) as \(\sigma \to 0\). Therefore, the increase of noise intensity will lead to the increase of the mutual information and then will enhance the discriminating ability to subthreshold signals.

Proof of general results

In this section we list the proofs of the above theorems. To avoid too lengthy and tedious deduction, we only list the involving Lemmas here but move their proof to appendix.

Lemma 1

Let \(k \ge 1\) be an integer. The stationary OU process (1b) has the property that for \(\forall T \ge 0\),

$$\begin{aligned}&E\left[ {\;\mathop {\sup }\limits_{0 \le t \le T} \left| {u_{j} (t)} \right|^{2k} } \right] \le \sigma^{2k} ((0.5\tau )^{k - 1} (0.5\tau + KT) \\& \quad \quad+ 2k\sqrt {3T(4k - 3)!!(0.5\tau )^{2k - 1} } ) \\& \quad= \sigma^{2k} \xi_{k}\end{aligned}$$

Lemma 2

Let \(f^{i} :\;R^{d} \to R\) and \(g_{j}^{i} :\;R^{d} \to R\) in Eq. (1) be Borel measurable functions that satisfy the global Lipschitz condition (4) or the local Lipschitz condition (8) and the growth conditions (5). Then for any initial value \(X_{0} \in R^{d}\), Eq. (1) has a unique global solution \(X_{t}\) on \(t \ge 0\). Moreover, for any integer \(p \ge 2\), the solution has the property that

$$E\left[ {\;\mathop { \sup }\limits_{0 \le t \le T} \left| {X_{t} } \right|^{p} } \right] \le a_{p} {\text{exp(}}b_{p} T )< \infty$$
(10)

with

$$a_{p} = d^{{\frac{p}{2} + 1}} (m + 2)^{p - 1} \left( {\left| {X_{0} } \right|^{p} + T^{p} 2^{p - 1} K^{p} \left( {1 + m\sigma^{p} \xi_{p}^{{\frac{1}{2}}} + m\sigma^{{\frac{p}{1 - \gamma }}} \xi_{{\bar{k}}}^{{\frac{p}{{2(1 - \gamma )\bar{k}}}}} } \right)} \right),$$
(11)
$$b_{p} = (m + 1)d^{{\frac{p}{2} + 1}} (m + 2)^{p - 1} T^{p - 1} 2^{p - 1} K^{p} ,$$
(12)

and \(\bar{k}\) is an integer satisfying

$$\bar{k} \ge \frac{p}{2(1 - \gamma )}.$$
(13)

Proof of Theorem 1

Fix \(T > 0\) arbitrarily. Using the elementary inequality \(u^{\gamma } \le 1 + u\) for any \(u \ge 0\), we see from (5) that

$$\left| {g(x,t)} \right| \le K(2 + \left| x \right|),\;\;\forall (x,t) \in R^{d} \times \left[ {0,\infty } \right)$$
(14)

To show the assertion (6), let us start with the scalar equation

$$X_{t}^{i} - \hat{X}_{t}^{i} = \int_{0}^{t} {(f^{i} (X_{s} ,s) - f^{i} (\hat{X}_{s} ,s))ds} + \sum\limits_{j = 1}^{m} {\int_{0}^{t} {g_{j}^{i} (X_{s} ,s)u_{j} (s)ds} } ,$$

Using the inequality \((u_{1} + \cdots + u_{n} )^{2} \le n(u_{1}^{2} + \cdots + u_{n}^{2} )\), we get

$$\begin{aligned} & \left| {X_{t}^{i} - \hat{X}_{t}^{i} } \right|^{ 2} \le (m + 1)\left\{ {\left( {\int_{0}^{t} {\left| {f^{i} (X_{s} ,s) - f^{i} (\hat{X}_{s} ,s)} \right|ds} } \right)^{2} } \right. \\ & \quad \quad \left. { + \sum\limits_{j = 1}^{m} {\left| {\int_{0}^{t} {g_{j}^{i} (X_{s} ,s)u_{j} (s)ds} } \right|^{2} } } \right\} \\ & \quad \le (m + 1)\left\{ {t\int_{0}^{t} {\left| {f^{i} (X_{s} ,s) - f^{i} (\hat{X}_{s} ,s)} \right|}^{2} ds} \right. \\ &\left. { \quad \quad + \sum\limits_{j = 1}^{m} {t\int_{0}^{t} {\left| {g_{j}^{i} (X_{s} ,s)u_{j} (s)} \right|^{2} ds} } } \right\} \\ & \quad \le (m + 1)\left\{ {tL\int_{0}^{t} {\left| {X_{s} - \hat{X}_{s} } \right|}^{2} ds} \right. \\ & \left. { \quad \quad + 2tK^{2} \sum\limits_{j = 1}^{m} {\int_{0}^{t} {(4 + \left| {X_{s} } \right|^{2} )\left| {u_{j} (s)} \right|^{2} ds} } } \right\} \\ \end{aligned}$$

for \(0 < t < T\). We emphasize that the inequality (14) has been used here. As the right-hand-side terms are increasing in \(t\), we derive

$$\begin{aligned} & E\left[ {\mathop {\sup }\limits_{0 \le s \le t} \left| {X_{s}^{i} - \hat{X}_{s}^{i} } \right|^{ 2} } \right] \le (m + 1)TL\int_{0}^{t} {E\left[ {\left| {X_{s} - \hat{X}_{s} } \right|^{2} } \right]} ds \\ & \quad \quad + 2m(m + 1)T^{2} K^{2} \left( {4E\left[ {\mathop {\sup }\limits_{0 \le s \le t} \left| {u_{j} (s)} \right|^{2} } \right] + E\left[ {\mathop {\sup }\limits_{0 \le s \le t} \left| {X_{s} } \right|^{2} \mathop {\sup }\limits_{0 \le s \le t} \left| {u_{j} (s)} \right|^{2} } \right]} \right) \\ & \le (m + 1)TL\int_{0}^{t} {E\left[ {\mathop {\sup }\limits_{0 \le r \le s} \left| {X_{r} - \hat{X}_{r} } \right|^{2} } \right]} ds \\ & \quad \quad + 2\sigma^{2} m(m + 1)T^{2} K^{2} \left( {4E\left[ {\mathop {\sup }\limits_{0 \le s \le T} \left| {u_{j} (s)} \right|^{2} } \right]} \right. \\ &\left. { \quad \quad + \sqrt {E\left[ {\mathop {\sup }\limits_{0 \le s \le T} \left| {X_{s} } \right|^{4} } \right]E\left[ {\mathop {\sup }\limits_{0 \le s \le T} \left| {u_{j} (s)} \right|^{4} } \right]} } \right) \\ \end{aligned}$$

and then by Lemmas 1 and 2,

$$E\left[ {\mathop {\sup }\limits_{0 \le s \le t} \left| {X_{i} - \hat{X}_{i} } \right|^{ 2} } \right] \le (m + 1)dTL\int_{0}^{t} {E\left[ {\left| {X_{s} - \hat{X}_{s} } \right|^{2} } \right]} ds + 2\sigma^{2} dm(m + 1)T^{2} K^{2} \left( {4\xi_{1} + \sqrt {\xi_{2} a_{4} \exp (b_{4} T)} } \right).$$

An application of the Gronwall inequality implies the required assertion (6). □

Lemma 3

Let \(f^{i} :\;R^{d} \to R\) in Eq. (1) be Borel measurable functions that satisfy the local Lipschitz condition (8) and the growth condition (5). Then for any initial value \(X_{0} \in R^{d}\), Eq. (3) has a unique global solution \(\hat{X}_{t}\) on \(t \ge 0\). Moreover, for any \(T > 0\), the solution has the property that

$$\mathop {\sup }\limits_{0 \le t \le T} \left| {\hat{X}_{t} } \right|^{p} < c_{p} < \infty$$
(15)

with \(c_{p} = d^{{\frac{p}{2}}} \left( {2^{p - 1} \left| {X_{0} } \right|^{p} + T^{p} 2^{2(p - 1)} d^{{\frac{p}{2}}} K^{p} T^{p} } \right)\).

Proof of Theorem 2

The local Lipschitz condition and the growth condition ensure that the existence of the unique solution of the system (1). We are going to use the technique adapted from the work of Mao and Sababis (2003) to show the required assertion (3). For each \(N > \sqrt d (\left| {X_{0} } \right| + TK)\exp (\sqrt d KT)\), then by Lemma 3, \(\mathop {\sup }\limits_{0 \le t \le T} \left| {\hat{X}_{t} } \right| < N\) Let us define the stopping time \(\tau_{N} = \inf \{ t \ge 0:\left| {X_{t} } \right| \ge N\}\). Clearly

$$E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} } \right] = E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} 1_{{\{ \tau_{N} \le T\} }} } \right] + E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} 1_{{\{ \tau_{N} > T\} }} } \right]$$
(16)

where \(1_{A}\) is the indicator function of set \(A\).

Let us estimate the first term in the right-hand side of Eq. (16). Noting that the Young inequality (Prato and Zabczyk 1992) \(\alpha \beta \le \eta \frac{{\alpha^{\mu } }}{\mu } + \frac{{\alpha^{\mu } }}{{\mu^{{\frac{v}{\mu }}} }}\frac{{\beta^{v} }}{v}\) holds true for all \(\alpha ,\beta ,\eta ,\mu\) and \(v\) when \(u^{ - 1} + v^{ - 1} = 1\), we have

$$E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} 1_{{\{ \tau_{N} \le T\} }} } \right] \le \frac{\eta }{{{p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0pt} 2}}}E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left( {\left| {X_{t} - \hat{X}_{t} } \right|^{2} } \right)^{{{p \mathord{\left/ {\vphantom {p 2}} \right. \kern-0pt} 2}}} } \right] + E\left[ {\frac{1}{{{p \mathord{\left/ {\vphantom {p {(p - 2)}}} \right. \kern-0pt} {(p - 2)}}}}\frac{1}{{\eta^{{{2 \mathord{\left/ {\vphantom {2 {(p - 2)}}} \right. \kern-0pt} {(p - 2)}}}} }}(1_{{\{ \tau_{N} \le T\} }} )^{{{p \mathord{\left/ {\vphantom {p {(p - 2)}}} \right. \kern-0pt} {(p - 2)}}}} } \right]$$

where \(p > 2\) is an integer and \(\eta\) is a positive number from which it can be deduced that

$$E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} 1_{{\{ \tau_{N} \le T\} }} } \right] \le \frac{2\eta }{p}E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{p} } \right] + \frac{p - 2}{{p\eta^{{{2 \mathord{\left/ {\vphantom {2 {(p - 2)}}} \right. \kern-0pt} {(p - 2)}}}} }}P(\tau_{N} \le T).$$
(17)

We know

$$E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} } \right|^{p} } \right] \le a_{p} \exp (b_{p} T)$$

from Lemma 2 and

$$E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {\hat{X}_{t} } \right|^{p} } \right] \le c_{p}$$

from Lemma 3, then,

$$P(\tau_{N} \le T) = E\left[ {1_{{\{ \tau_{N} \le T\} }} \frac{{\left| {X_{{\tau_{N} }} } \right|^{p} }}{{N^{p} }}} \right] \le \frac{1}{{N^{p} }}E\left[ {\left| {X_{{\tau_{N} }} } \right|^{p} } \right] \le \frac{1}{{N^{p} }}a_{p} \exp (b_{p} T),$$
(18)
$$E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{p} } \right] \le 2^{p - 1} E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} } \right|^{p} + \mathop {\sup }\limits_{0 \le t \le T} \left| {\hat{X}_{t} } \right|^{p} } \right] \le 2^{p - 1} \left( {a_{p} \exp (b_{p} T) + c_{p} } \right).$$
(19)

Substitution of Eqs. (18) and (19) into Eq. (17) yields

$$E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} 1_{{\{ \tau_{N} < T\} }} } \right] \le \frac{{2^{p} \eta }}{p}(a_{p} \exp (b_{p} T) + c_{p} ) + \frac{p - 2}{{p\eta^{{{2 \mathord{\left/ {\vphantom {2 {(p - 2)}}} \right. \kern-0pt} {(p - 2)}}}} }}\frac{1}{{N^{p} }}a_{p} \exp (b_{p} T).$$
(20)

Next, we estimate the second term in the right-hand side of Eq. (16). The involving process is very close to the proof for Theorem 1, and here we list details to enhance the reader’s readability. Clearly,

$$E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} 1_{{\{ \tau_{N} < T\} }} } \right] = E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{{t \wedge \tau_{N} }} - \hat{X}_{{t \wedge \tau_{N} }} } \right|^{2} 1_{{\{ \tau_{N} < T\} }} } \right] \le E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{{t \wedge \tau_{N} }} - \hat{X}_{{t \wedge \tau_{N} }} } \right|^{2} } \right].$$
(21)

Noting that \(\left| {X_{{t \wedge \tau_{N} }} - \hat{X}_{{t \wedge \tau_{N} }} } \right|^{2} = \left| {\int_{0}^{{t \wedge \tau_{N} }} {(f^{i} (X_{s} ,s) - f^{i} (\hat{X}_{s} ,s))ds} + \sum\limits_{j = 1}^{m} {\int_{0}^{{t \wedge \tau_{N} }} {g_{j}^{i} (X_{s} ,s)u_{j} (s)ds} } } \right|^{2}\), then using the Hölder inequality, the local Lipschitz condition (8) and the growth condition (5) in turn arrives at

$$\begin{aligned} \left| {X_{{t \wedge \tau_{N} }} - \hat{X}_{{t \wedge \tau_{N} }} } \right|^{2} & \le (m + 1)\left\{ {\left( {\int_{0}^{{t \wedge \tau_{N} }} {\left| {f^{i} (X_{s} ,s) - f^{i} (\hat{X}_{s} ,s)} \right|ds} } \right)^{2} + \sum\limits_{j = 1}^{m} {\left| {\int_{0}^{{t \wedge \tau_{N} }} {g_{j}^{i} (X_{s} ,s)u_{j} (s)ds} } \right|^{2} } } \right\} \\ & \le (m + 1)\left\{ {t\int_{0}^{{t \wedge \tau_{N} }} {\left| {f^{i} (X_{s} ,s) - f^{i} (\hat{X}_{s} ,s)} \right|^{2} ds} + t\sum\limits_{j = 1}^{m} {\int_{0}^{{t \wedge \tau_{N} }} {\left| {g_{j}^{i} (X_{s} ,s)u_{j} (s)} \right|^{2} ds} } } \right\} \\ & \le (m + 1)\left\{ {TL_{N} \int_{0}^{{t \wedge \tau_{N} }} {\left| {X_{s} - \hat{X}_{s} } \right|^{2} ds} + 2TK^{2} \sum\limits_{j = 1}^{m} {\int_{0}^{{t \wedge \tau_{N} }} {(4 + \left| {X_{s} } \right|^{2} )\left| {u_{j} (s)} \right|^{2} ds} } } \right\} \\ \end{aligned}$$

As the right-hand-side terms are increasing in \(t\), we derive

$$\begin{aligned} E\left[ {\left| {X_{{t \wedge \tau_{N} }} - \hat{X}_{{t \wedge \tau_{N} }} } \right|^{2} } \right] & \le (m + 1 )T\left\{ {L_{N} E\left[ {\int_{0}^{{t \wedge \tau_{N} }} {\left| {X_{s} - \hat{X}_{s} } \right|^{2} ds} } \right] + 2K^{2} \sum\limits_{j = 1}^{m} {E\left[ {\int_{0}^{{t \wedge \tau_{N} }} {\left( {4 + \left| {X_{s} } \right|^{2} } \right)\left| {u_{j} (s )} \right|^{2} ds} } \right]} } \right\} \\ & = (m + 1 )T\left\{ {L_{N} \int_{0}^{t} {E\left[ {\left| {X_{{s \wedge \tau_{N} }} - \hat{X}_{{s \wedge \tau_{N} }} } \right|^{2} } \right]ds} + 2K^{2} \sum\limits_{j = 1}^{m} {\int_{0}^{t} {E\left[ {\left( {4 + \left| {X_{{s \wedge \tau_{N} }} } \right|^{2} } \right)\left| {u_{j} (s \wedge \tau_{N} )} \right|^{2} } \right]ds} } } \right\} \\ & \le (m + 1)\left\{ {L_{N} T\int_{0}^{t} {E\left[ {\mathop {\sup }\limits_{0 \le r \le s} \left| {X_{{r \wedge \tau_{N} }} - \hat{X}_{{r \wedge \tau_{N} }} } \right|^{2} } \right]ds} + 2K^{2} T^{2} m\left( {4E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {u_{j} (t)} \right|^{2} } \right] + \sqrt {E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} } \right|^{4} } \right]E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {u_{j} (t)} \right|^{4} } \right]} } \right)} \right\} \\ & \le (m + 1)\left\{ {L_{N} T\int_{0}^{t} {E\left[ {\mathop {\sup }\limits_{0 \le r \le s} \left| {X_{{r \wedge \tau_{N} }} - \hat{X}_{{r \wedge \tau_{N} }} } \right|^{2} } \right]ds} + 2\sigma^{2} K^{2} T^{2} m\left( {4\xi_{1} + \sqrt {\xi_{2} a_{4} \exp (b_{4} T)} } \right)} \right\} \\ \end{aligned}$$

and then\(E\left[ {\mathop {\sup }\limits_{0 \le s \le t} \left| {X_{{t \wedge \tau_{N} }} - \hat{X}_{{t \wedge \tau_{N} }} } \right|^{2} } \right] \le d(m + 1)\left( {TL_{N} \int_{0}^{t} {E\left[ {\mathop {\sup }\limits_{0 \le r \le s} \left| {X_{{r \wedge \tau_{N} }} - \hat{X}_{{r \wedge \tau_{N} }} } \right|^{2} } \right]ds} + 2\sigma^{2} mT^{2} K^{2} \left( {4\xi_{1} + \sqrt {\xi_{2} a_{4} \exp (b_{4} T)} } \right)} \right)\) By the Gronwall inequality we obtain

$$E\left[ {\mathop {\sup }\limits_{0 \le s \le t} \left| {X_{{t \wedge \tau_{N} }} - \hat{X}_{{t \wedge \tau_{N} }} } \right|^{2} } \right] \le 2d\sigma^{2} m(m + 1)T^{2} K^{2} \left( {4\xi_{1} + \sqrt {\xi_{2} a_{4} \exp (b_{4} T)} } \right)e^{{d(m + 1)TL_{N} }}$$
(22)

Combination of Eqs. (21) and (22) yields

$$E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} 1_{{\left\{ {\tau_{N} > T} \right\}}} } \right] \le 2d\sigma^{2} m(m + 1)T^{2} K^{2} \left( {4\xi_{1} + \sqrt {\xi_{2} a_{4} \exp (b_{4} T)} } \right)e^{{d(m + 1)TL_{N} }}$$
(23)

With Eqs. (20) and (23) substituted into Eq. (16), it is obtained that

$$\begin{aligned} & E\left[ {\mathop { \sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} } \right] \le \frac{{2^{p} \eta }}{p}\left( {a_{p} {\text{exp(}}b_{p} T )+ c_{p} } \right) \\ & \quad + \frac{p - 2}{{p\eta^{{{2 \mathord{\left/ {\vphantom {2 {(p - 2)}}} \right. \kern-0pt} {(p - 2)}}}} }}\frac{1}{{N^{p} }}a_{p} {\text{exp(}}b_{p} T )\\ & \quad + 2d\sigma^{2} m (m + 1 )T^{2} K^{2} \left( {4\xi_{1} + \sqrt {\xi_{2} a_{4} {\text{exp(}}b_{4} T )} } \right){ \exp }\left( {d (m + 1 )TL_{N} } \right) \\ \end{aligned}$$
(24)

For any \(\varepsilon > 0\), we choose \(\eta\) sufficiently small to get \(\frac{{2^{p} \eta }}{p}\left( {a_{p} \exp (b_{p} T) + c_{p} } \right) < \frac{\varepsilon }{3}\) and \(N\) sufficiently large such that \(\frac{p - 2}{{p\eta^{{{2 \mathord{\left/ {\vphantom {2 {(p - 2)}}} \right. \kern-0pt} {(p - 2)}}}} }}\frac{1}{{N^{p} }}a_{p} \exp (b_{p} T) < \frac{\varepsilon }{3}\) . Then, we can choose \(\sigma\) small enough to ensure \(2d\sigma^{2} m(m + 1)T^{2} K^{2} \left( {4\xi_{1} + \sqrt {\xi_{2} a_{4} \exp (b_{4} T)} } \right)\exp \left( {d(m + 1)TL_{N} } \right) < \frac{\varepsilon }{3}.\) Hence, there exists a critical value \(\sigma_{c}\) such that \(E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} } \right] < \varepsilon\) when \(\sigma < \sigma_{c}\). □

Lemma 4

Consider a nonlinear system with \(f(X_{t} ,t) = \tilde{f}(X_{t} ) + S(t)\) . Assume \(\tilde{f}\left( x \right)\) and \(g\left( x \right)\) satisfy the local Lipschitz condition and \(g\left( x \right)\) obey the growth condition. Suppose that the system receives a binay input \(S(t) \in \{ s_{1} ,s_{2} \}\) . Then for every \(T > 0\) and \(\varepsilon > 0\) , as \(\sigma \to 0\) there hold

$$E\left[ {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{t} - \hat{X}_{t} } \right|^{2} \left| {S = s_{i} } \right.} \right] \to 0,$$
(25)

and

$$\mathop {\lim }\limits_{k \to \infty } P\left( {\mathop {\sup }\limits_{0 \le t \le T} \left| {X_{k}(t) - \hat{X}_{k}(t) } \right| > \varepsilon \left| {S = s_{i} } \right.} \right) = 0.$$
(26)

Proof of Theorem 3

Let \(\left\{ {\sigma_{k} } \right\}_{k = 1}^{\infty }\) be arbitrary decreasing sequence of intensity parameter of Gaussian colored noise such that \(\sigma_{k} \to 0\) as \(k \to \infty\). Denote the corresponding solution process and the discrete output process of “0” and “1” by \(X_{k} (t)\) and \(Y_{k} (t)\) with Gaussian colored noise parameter \(\sigma_{k}\) instead of \(\sigma\). Recalling that \(I(S,Y) = 0\) if and only if \(S\) and \(Y\) are statistically independent, so one only needs to show that \(F_{S,Y} (s,y) = F_{S} (s)F_{Y} (y)\) or \(F_{Y\left| S \right.} (y\left| s \right.) = F_{Y} (y)\) as \(\sigma \to 0\) for signal symbols \(s \in \left\{ {s_{1} ,s_{2} } \right\}\) and for all \(y \ge 0\). Here \(F_{S,Y}\) represents for the joint distribution function and \(F_{Y\left| S \right.}\) is the conditional distribution function.

Note that \(y \ge 0\) means that \(X^{1} (t)\) is capable of crossing the firing threshold from below, then

\(P(Y_{k} (t)\left| {S = s_{i} } \right.) \le P\left( {\mathop {\sup }\limits_{{t_{1} \le t \le t_{2} }} X_{k}^{1} (t) > \theta \left| {S = s_{i} } \right.} \right)\),

and by Lemma 4,

$$\begin{aligned} \mathop { \lim }\limits_{k \to \infty } P (Y_{k} & > y\left| {S = s_{i} } \right. )\le \mathop { \lim }\limits_{k \to \infty } P\left( {\mathop { \sup }\limits_{{t_{1} \le t \le t_{2} }} X_{k}^{1} (t )> \theta \left| {S = s_{i} } \right.} \right) \\ & = \mathop { \lim }\limits_{{k \to \infty }} \mathop { \lim }\limits_{n \to \infty } P\left( {\mathop { \sup }\limits_{{t_{1} \le t \le t_{2} }} X_{k}^{1} (t )> \theta ,X_{k}^{ 1} (t )< \theta - \frac{1}{n}\left| {S = s_{i} } \right.} \right) \\ & \le \mathop { \lim }\limits_{n \to \infty } \mathop { \lim }\limits_{k \to \infty } P\left( {\mathop { \sup }\limits_{{t_{1} \le t \le t_{2} }} \left| {X_{k}^{1} (t )- X_{k}^{1} (t )} \right|^{2} > \frac{1}{n}\left| {S = s_{i} } \right.} \right) \\ \end{aligned}$$

where the first equality is owing to that the input signal is subthreshold. Thus,

$$\mathop {\lim }\limits_{k \to \infty } P(Y_{k} > y\left| {S = s_{1} } \right.) = \mathop {\lim }\limits_{k \to \infty } P\left( {Y_{k} > y\left| {S = s_{2} } \right.} \right) = 0$$

or equivalently

$$\mathop {\lim }\limits_{k \to \infty } P(Y_{k} \le y\left| {S = s_{1} } \right.) - \mathop {\lim }\limits_{k \to \infty } P\left( {Y_{k} \le y\left| {S = s_{2} } \right.} \right) = 0$$

Then, using the total probability formula,

$$\begin{aligned} F_{{Y_{k} }} (y) & = F_{{Y_{k} \left| S \right.}} (y\left| {s_{1} } \right.)P_{S} (s_{1} ) + F_{{Y_{k} \left| S \right.}} (y\left| {s_{2} } \right.)P_{S} (s_{2} ) \\ & = F_{{Y_{k} \left| S \right.}} (y\left| {s_{1} } \right.)P_{S} (s_{1} ) + F_{{Y_{k} \left| S \right.}} (y\left| {s_{2} } \right.)(1 - P_{S} (s_{1} )) \\ & = \left( {F_{{Y_{k} \left| S \right.}} (y\left| {s_{1} } \right.) - F_{{Y_{k} \left| S \right.}} (y\left| {s_{2} } \right.)} \right)P_{S} (s_{1} ) + F_{{Y_{k} \left| S \right.}} (y\left| {s_{2} } \right.) \\ \end{aligned}$$

Taking the \(k \to \infty\) limit on the both sides of this equation, we arrive at

$$F_{Y} (y) = F_{Y\left| S \right.} (y\left| {s_{2} } \right.)$$

This demonstrates that \(S\) and \(Y\) are statistically independent, and hence \(I(S,Y) = 0\) as \(\sigma \to 0\).□

Numerical verification

Theorem 3 builds a bridge between the perturbation theorem and the existence of stochastic resonance. In order to have an intuitive verification of Theorem 3, let us take two examples into account. The first example is the noisy feedback neuron models with a quantized output into account (Patel and Kosko 2008; Gao et al. 2018). Let \(x\) denote the membrane voltage, then

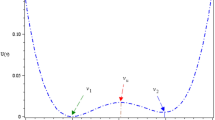
$$\left\{ {\begin{array}{*{20}l} {\frac{dx}{dt} = - x + h (x )+ S (t )+ u (t ) ,} \hfill \\ {du (t )= - \frac{1}{\tau }u (t )dt + \sigma dW (t )} \hfill \\ \end{array} } \right.$$
(27)

where the logistic function \(h(x) = (1 + e^{ - ax} )^{ - 1}\)(\(a = \text{8}\)) gives a bistable artificial neuron model, the signal \(S (t )\in \left\{ {A ,\;B} \right\}\) represents the net excitatory or inhibitory input. Here the value of \(S (t )\) is taken from the binary distribution:\(P (S (t )= A )= p\),\(P (S (t )= B )= 1 - p\), and the duration time of each value of \(S (t )\) is considerably larger than the decay time constant \(\tau\). The more details are can be found from the subsequent figures and the numerical steps for mutual information. The neuron feeds its activation back to itself through \(- x(t) + h(x(t))\) and action potential can be generated if the membrane potential (spike) is larger than zero. Here note that the vector field \(f(x) = - x(t) + h(x(t))\). According to the graphic method it can be seen in Fig. 1 that if the input signal \(S (t )\in \left\{ {A ,\;B} \right\}\) take opposite value between the two dot lines, that is, \(- 0.63 < A < B < { - }0.37\), then by linear stability analysis, the neuron has three equilibrium points, namely, two stable and one unstable. Since the neuron information is mainly transmitted by the spiking train, the quantized output \(y(t)\) can be defined as

Fig. 1
figure 1

Schemata of the vector field function of \(f(x)\) (blue solid line). The value of the above dot line is 0.63, and the value of the bottom dotted line is 0.37. In the figure, the intersection of the dash line with the S-shaped curve stands for the equilibrium points, and the one-order derivative of the vector field just is the resultant slope of tangent line. Since two of the three slopes are negative and one is positive, two of the three equilibrium points are stable, and one is unstable. (Color figure online)

Full size image
$$y(t) = \left\{ {_{0,\quad x(t) \le 0.}^{1,\quad x(t) > 0;} } \right.$$

Note that

$$\begin{aligned} & \left| {x_{2} - (1 + e^{{ - 8x_{2} }} )^{ - 1} - x_{1} + (1 + e^{{ - 8x_{1} }} )^{ - 1} } \right|^{2} \le 2\left| {x_{2} - x_{1} } \right|^{2} \\ & \quad + 2\left| {\frac{{e^{{ - 8x_{2} }} - e^{{ - 8x_{1} }} }}{{(1 + e^{{ - 8x_{1} }} )(1 + e^{{ - 8x_{2} }} )}}} \right|^{2} \le 18\left| {x_{2} - x_{1} } \right|^{2} \\ \end{aligned}$$

and

$$\left| {f(x)} \right| = \left| { - x + h(x)} \right| \le 1 + |x|.$$

The two inequalities together imply the vector field of the bistable neuron model \(f(x)\) satisfies global Lipschitz condition (4) and growth condition (5). Note that the global Lipschitz condition implies the local Lipschitz condition, which can assure the existence and uniqueness of the solution of the model, thus according to Theorem 3, the phenomenon of aperiodic stochastic resonance should exist for a subthreshold input signal. Here, by “subthreshold”, it means that the weak signal cannot spontaneously emit action potential without the help of noise. We can guarantee that when the constant value of the input signal enables the model to be bistable, the input signal is subthresold.

Before exhibiting the numerical results of aperiodic stochastic resonance, let us list the numerical steps for mutual information calculation for the sake of the reader’s reference.

  1. (I)

    Initialize the parameters A, B, p and \(x(0)\).

  2. (II)

    Given the time step-length \(\Delta t = 0.01\) and a series of the duration time \(T_{i}\)(\(i \ge 1\)).

  3. (III)

    For each time span of duration time \(T_{i}\), generate a uniformly distributed number r, and then let \(S(t) = A\) if \(r > p\). Otherwise, \(S(t) = B\).

  4. (IV)

    Apply Euler difference scheme and Box-Mueller algorithm to Eq. (27) (or Eq. (28)) to generate the output spike train \(y(t)\).

  5. (V)

    Calculate the marginal probability laws \(P(S(t))\) and \(P(y(t))\) and the joint probability law \(P(S(t),\;y(t))\).

  6. (VI)

    Substitute the above probability laws into Eq. (9) for the mutual information.

We remark that in the above Step (V), the involving probabilities (also refer to Table 1) are approximated by statistical frequencies. In all numerical implements except Fig. 4, the dimensionless duration time parameter for the input signal \(S(t)\) is fixed as \(T = 40\), and the simulating time span is taken as 50 such constant duration times. Over one time span, one membrane evolution trajectory or output spike train can be tracked, and then the mutual information can be acquired from one trial. Note that the definition in Eq. (9) can be rewritten into

Table 1 Marginal and joint probability laws
Full size table
$$I(S,Y) = E\left[ {\log \frac{{P_{SY} (s,y)}}{{P_{S} (s)P_{Y} (y)}}} \right],$$

thus the mutual information is actually the mathematical expectation of the random variable \(\log \frac{{P_{SY} (s,y)}}{{P_{S} (s)P_{Y} (y)}}\) (Patel and Kosko 2008). So, in order to improve the accuracy of the above calculation, for each set of given parameters, we employ 100 trials to obtain the averaged mutual information, as shown in all the involving figures.

The non-monotonic dependence of mutual information on noise intensity signifies the occurrence of stochastic resonance, as shown in Fig. 2. Since the binary input is subthreshold, there is no spike in absent of Gaussian colored noise (Fig. 2b). As the noise of small amount is added, the neuron starts to spike (Fig. 2c), but the output signal is much different from the binary input (Fig. 2a). When the noise is at an appropriate level, the output signal greatly resembles the input signal in shape (Fig. 2d), but the resemblance in shape is gradually broken as overmuch amount of noise could cause too frequent spikes (Fig. 2e). The non-monotonic dependence of the input–output mutual information on noise intensity exactly reflects the change in the resemblance (Fig. 2f), thus the phenomenon of stochastic resonance is confirmed.

Fig. 2
figure 2

Stochastic resonance in the bistable neuron model with quantized output. The binary signal is shown in panel (a). Here \(A = { - }0.6\), \(B = { - }0.4\) and \(p = 0.7\). Since the input signal is subthreshold, there is no 1 in the quantized output when the Gaussian colored noise is absent (\(\sigma = 0\),\(\tau = 0.4\)), as shown in panel (b). As the noise intensity of the Gaussian colored noise is introduced, more and more “1s” occur in the quantized output, as shown in panel (c) (\(\sigma = 0.1\), \(\tau = 0.4\)), (d) (\(\sigma = 0.4\), \(\tau = 0.4\)) and (e) (\(\sigma = 1\), \(\tau = 0.4\)), but obviously too much Gaussian colored noise will reduce the input–output coherence, so there is a mono-peak structure in the curves of mutual information via noise intensity as shown in panel (f): \(\tau = 0.2\)(blue dot curve),\(\tau = 0.4\)(red broken curve) and \(\tau = 0.6\) (green solid curve). (Color figure online)

Full size image

From Fig. 2f one further sees that the correlation time has a certain effect on the bell shaped curve of the input–output mutual information. That is, the peak height of the mutual information is a decreasing function of the correlation time, but at the same time, the optimal noise intensity at which the resonant peak locates shifts to a weaker noise level. In order to more systematically disclose the influence of colored noise, we plot the mutual information as function of correlation time in Fig. 3. Surprisingly, the correlation time induced aperiodic stochastic resonance is observed for given noise intensity, and there exists optimal correlation time at which the shape matching between the input signal and the output signal. Moreover, as noise intensity increases, the optimal correlation time of the maximal mutual information decreases. The similarity between Fig. 2 and Fig. 3 suggests noise intensity and correlation time play a similar role. In fact, our conjecture can be confirmed by checking the steady fluctuation of Gaussian colored noise. After a simple calculation it can be found that the steady noise variance is proportional to the correlation time and the square of noise intensity, namely \(D(u) = {{\tau \sigma^{2} } \mathord{\left/ {\vphantom {{\tau \sigma^{2} } 2}} \right. \kern-0pt} 2}\). Although this finding is a bit different from the observation related in Gaussian colored noise induced conventional (periodic) stochastic resonance (Gammaitoni et al. 1998), where the resonant peak tends to shift to a larger noise level as the correlation time increases, it is meaningful, since in neural circuit design noise intensity might be usually hard to change; one may tune the correlation time to realize the enhancement of information capacity instead. Additionally, the influence of different duration time parameter for the input signal on the aperiodic stochastic resonance is also checked in Fig. 4. It is observed that as the duration time decreases, both the effect of resonance induced by Gaussian colored noise and correlation time become weak. This is common with the conventional stochastic resonance, where only a slowly varying periodic signal can be amplified by noise rather than a high frequency signal (Kang et al. 2005).

Fig. 3
figure 3

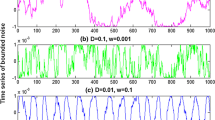
Stochastic resonance in the bistable neuron model with quantized output. The binary signal is shown in panel (a). Here \(A = { - }0.6\), \(B = { - }0.4\) and \(p = 0.7\). There is no 1 in the quantized output when the correlation time constant of Gaussian colored noise is close to zero (\(\tau = 0.001\),\(\sigma = 0.3\)), as shown in panel (b). As the correlation time constant increases, more and more “1s” occur in the quantized output, as shown in panel (c) (\(\tau = 0.2\), \(\sigma = 0.3\)) (d) (\(\tau = 0.5\), \(\sigma = 0.3\)), and (e) (\(\tau = 1.5\), \(\sigma = 0.3\)), but obviously too large correlation time constant will reduce the input–output coherence, so there is a mono-peak structure in the curves of mutual information via correlation time constant as shown in panel (f): \(\sigma = 0.3\) (blue dot curve), \(\sigma = 0.5\) (red broken curve) and \(\sigma = 0.7\)(green solid curve). (Color figure online)

Full size image
Fig. 4
figure 4

Mutual information between input signal \(S\) and quantized output signal \(Y\) as a function of (a) the noise intensity \(\sigma\) with and (b) correlation time constant \(\tau\) under different duration time parameters for the input signal. Here \(A = - 0.6\), \(B = - 0.4\) and \(p = 0.7\)

Full size image

The second example is the FitzHugh–Nagumo neuron model (Capurro et al. 1998), governed by

$$\left\{ {\begin{array}{*{20}l} {\varepsilon \frac{dv}{dt} = v(v - a)(1 - v) - w + A_{0} + S(t) + g(v)u(t),} \hfill \\ {\frac{dw}{dt} = v - w - b,} \hfill \\ {du(t) = - \frac{1}{\tau }u(t)dt + \sigma dW(t)} \hfill \\ \end{array} } \right.$$
(28)

where \(v\) stands for the transmembrane voltage, \(w\) denotes a slow recovery variable, and the input signal \(S (t )\in \left\{ {A ,\;B} \right\}\) is again taken as the subthreshold binary signal. Whenever the membrane voltage crosses the threshold value \(\theta = 0.5\) from below, the neuron emits a spike, and the output spiking train can be formulated as

$$Y(t) = \sum\limits_{i} {\delta (t - } t_{i} )$$
(29)

with \(t_{i}\) being the occurring time of the ith spike.

Note that

$$\begin{aligned} & \left| {v_{1} (v_{1} - a)(1 - v_{1} ) - w_{1} - v_{2} (v_{2} - a)(1 - v_{2} ) + w_{2} } \right|^{2} \\ & \quad = \left| {(v_{2} - v_{1} )(v_{1}^{2} + v_{1} v_{2} + v_{2}^{2} ) + (v_{1} - v_{2} )(v_{1} + v_{2} ) + a(v_{2} - v_{1} ) + w_{2} - w_{1} } \right|^{2} \\ & \quad \le 4\left| {(v_{2} - v_{1} )(v_{1}^{2} + v_{1} v_{2} + v_{2}^{2} )} \right|^{2} + 4\left| {(v_{1} - v_{2} )(v_{1} + v_{2} )} \right|^{2} \\ & \quad \quad + 4\left| {a(v_{2} - v_{1} )} \right|^{2} + 4\left| {w_{2} - w_{1} } \right|^{2} \\ & \quad \le 4(9N^{4} + 4N^{2} + a^{2} + 1)\left( {\left| {v_{2} - v_{1} } \right|^{2} + \left| {w_{2} - w_{1} } \right|^{2} } \right) \\ \end{aligned}$$

and

$$\left| {v_{1} - w_{1} - v_{2} + w_{2} } \right|^{2} \le 2\left( {\left| {v_{2} - v_{1} } \right|^{2} + \left| {w_{2} - w_{1} } \right|^{2} } \right)$$

for all \(v_{1} ,\,v_{2} \in R\) with \(\left| v \right|_{1} \le N\) and \(\left| {v_{2} } \right| \le N\). Here, the region-dependent Lipschitz constant \(L_{N} = 4(9N^{4} + 4N^{2} + a^{2} + 1)\). Thus, the vector field of the FitzHugh–Nagumo model is local Lipschitz. Actually, the local but not global Lipschitz property of the vector field has been proven by the mean value theorem (Patel and Kosko 2008). On the other hand, since the transmembrane voltage and the slow recovery variable are always bounded, one can assume that there exists constant \(C\) such that for any \(t > 0\), \(\hbox{max} (\left| v \right|,\left| w \right|) \le C\), then

$$\begin{aligned} &\left| { v(v - a)(1 - v) - w - A_{0} } \right| \le \left| {A_{0} } \right| + \left| {v(v - a)(1 - v) - w} \right| \\ & \quad \le \left| {A_{0} } \right| + \sqrt {\left| {v(v - a)(1 - v)} \right|^{2} + \left| w \right|^{2} } \\ & \quad \le (\left| {A_{0} } \right| + (1 + a)C^{2} + C^{4} + a^{2} )\left( {1 + \sqrt {v^{2} + w^{2} } } \right) \\ \end{aligned}$$

and

$$\left| {v - w - b} \right| \le \left| b \right| + \left| {v - w} \right| \le (\sqrt 2 + \left| b \right|)\left( {1 + \sqrt {v^{2} + w^{2} } } \right),$$

that is, the growth condition is satisfied. Again we can choose \(g(v) = 1\) (Figs. 5 and 6) to denote the additive intensity, or \(g(v) = \frac{{v^{2} }}{{\sqrt {1 + v^{4} } }}\) (Fig. 7) such that it stands for the multiplicative noise intensity but is easy to verify the Lipschitz and growth conditions. Then according to Theorem 3, the Gaussian colored noise induced aperiodic stochastic resonance in the neuron model can be anticipated.

Fig. 5
figure 5

Stochastic resonance in the FitzHugh–Nagumo neuron model. Here \(g (v )= 1\),\(A = { - }0.035\), \(B = { - }0.125\) and \(p = 0.7\). (a) The subthreshold binary signal. (b) Output spikes when the Gaussian colored noise is absent (\(\sigma = 0\),\(\tau = 0.4\)). (c) Output spikes when the noise intensity of Gaussian colored noise is small (\(\sigma = 0.003\), \(\tau = 0.4\)). (d) Stochastic resonance effect: Output spikes when the noise intensity of Gaussian colored noise is moderate (\(\sigma = 0.01\), \(\tau = 0.4\)). (e) Output spikes when the noise intensity of Gaussian colored noise is large (\(\sigma = 0.04\),\(\tau = 0.4\)). Obviously too much Gaussian colored noise will reduce the input–output coherence, so there is a mono-peak structure in the curves of mutual information via noise intensity as shown in panel (f): \(\tau = 0.2\) (blue dot curve),\(\tau = 0.4\)(red broken curve) and \(\tau = 0.6\) (green solid curve). (Color figure online)

Full size image
Fig. 6
figure 6

Stochastic resonance in the FitzHugh–Nagumo neuron model. Here \(g (v )= 1\), \(A = { - }0.035\), \(B = { - }0.125\) and \(p = 0.7\). (a) The subthreshold binary signal. (b) Output spikes when the correlation time constant of Gaussian colored noise is close to zero (\(\tau = 0.001\),\(\sigma = 0.03\)). (c) Output spikes when the correlation time constant is small (\(\tau = 0.01\), \(\sigma = 0.03\)). (d) Stochastic resonance effect: Output spikes when the correlation time constant is moderate (\(\tau = 0.05\), \(\sigma = 0.03\)). (e) Output spikes when the correlation time constant is large (\(\tau = 0.2\), \(\sigma = 0.03\)). Obviously too large correlation time constant will reduce the input–output coherence, so there is a mono-peak structure in the curves of mutual information via correlation time constant as shown in panel (f): \(\sigma = 0.03\) (blue dot curve), \(\sigma = 0.05\) (red broken curve) and \(\sigma = 0.07\) (green solid curve). (Color figure online)

Full size image
Fig. 7
figure 7

Mutual information between input signal \(S\) and output spike train \(Y\) as a function of (a) the noise intensity \(\sigma\) and (b) correlation time constant \(\tau\). Here \(g(v) = \frac{{v^{2} }}{{\sqrt {1 + v^{4} } }}\), \(A = - 0.035\), \(B = - 0.125\) and \(p = 0.7\). (Color figure online)

Full size image

In the numerical simulation of the second example, we take \(a = 0.5\),\(A_{0} = 0.04\),\(\varepsilon = 0.005\),\(b = 0.2466\), \(\Delta t = 0.001\) and the duration time of \(S (t )\) is again taken as 40 time units. We point out that the input binary signals in Figs. 5, 6a are still subthreshold, although a spike generation happens at the moment the signal is switched from one value to the other in Figs. 5, 6b in absence of noise, (Patel and Kosko 2005). Figures 5, 6d demonstrate again that the best shape matching can happen at a suitable noise intensity or correlation time, at which the input–output mutual information in Figs. 5, 6f attains its maximum. Thus, the aperiodic stochastic resonance induced by Gaussian colored noise is confirmed. Moreover, Fig. 7 shows that this phenomenon can also be induced by the multiplicative Gaussian colored noise. From Fig. 7, a similar effect of correlation time on resonant peak is observed. This similarity implies that increasing correlation time inhibits the aperiodic stochastic resonance effect but reduces the optimal noise intensity. This feature reflects the noise intensity and the correlation time play the same role here. Note that the “color” of the Gaussian noise always restrains the effect of conventional periodic stochastic resonance and shifts the resonant peak to larger noise intensity (Gammaitoni et al. 1998), thus the properties of aperiodic stochastic resonance seems not suitable for being directly generalized from the conventional stochastic resonance. In fact, we infer the properties of aperiodic stochastic resonance should be similar to stochastic synchronization, since they can be measured by the same quantifying index.

The above neuron models have verified the assertion in Theorem 3. In fact, Theorem 3 gives necessary conditions for aperiodic stochastic resonance effect of Gaussian colored noise in neuron models for subthreshold input signals. By utilizing the statement of Theorem 3, the investigation of the aperiodic stochastic resonance under Gaussian colored noise can be reduced to a simple task of showing that a zero limit of the input–output mutual information exists. Then, just as the theorems stated in the work of Patel and Kosko (2005, 2008) and Kosko et al. (2009), Theorem 3 again acts as a type of screening device to filter whether noise benefits in the detection of subthreshold signals based on the measurement of mutual information.

Conclusion and discussion

After proving that under certain conditions the solution of nonlinear dynamic systems perturbed by Gaussian colored noise can converge to the solution of the deterministic counterpart as noise intensity tends to zero, we theoretically predicted the occurrence of the aperiodic stochastic resonance induced by Gaussian colored noise in bistable and excitable neuron systems based on the “forbidden interval” theorem. The theoretical prediction actually presents a technical tool that screen for whether the mutual-information measured stochastic resonance occurs in the detection of subthreshold signals in the background of Gaussian colored noise. The simulated results with two typical neuron models further verified the occurrence of aperiodic stochastic resonance for weak input signals. Particularly, we disclose the novel inhibitive effect of the correlation time of Gaussian colored noise on the aperiodic stochastic resonance, and found the “color” of noise plays the same role as noise intensity. Since in the design of neural circuits, the noise intensity is not always easy to be tuned for utilizing the benefit of noise, our finding provides an alternative way to implement the effect of aperiodic stochastic resonance by adjusting the correlation time.

At the end, let us stress the main difference from the existing theoretical proofs, and let us also have some prospect. As it is known, Gaussian white noise, as the formal derivative of Wiener process of stationary independent increments, cannot describe the correlation of environmental fluctuations, the fractional Gaussian noise, as the formal derivative of fractional Brownian motion, has power-law feature in power spectral density and can model the fluctuations of long range temporal correlation, while the Gaussian colored noise, generated by the Ornstein–Ulenbeck process, is applicable for modeling the short-time correlation. Thus, the work of this paper actually shrinks the gap between the aperiodic stochastic resonance induced by Gaussian white noise (Patel and Kosko 2005) and induced by fractional Gaussian noise (Gao et al. 2018). Moreover, Levy noises are the formal derivative of the jump-diffusion Levy processes of stationary independent increments, thus the aperiodic stochastic resonance with Levy noise (Patel and Kosko 2008) did not consider the effect of “color”. Note that Gaussian colored noise is only a special member of the family of Levy colored noise (Lü and Lu 2019), which is capable of describing the subquantal release of neurotransmitter, thus it will be meaningful to explore the beneficial role of the more general Levy colored noise in neural processing in the future.