Onset of colored-noise-induced chaos in the generalized Duffing system

Abstract

The effects of colored noise, red noise and green noise, on the onset of chaos are investigated theoretically and confirmed numerically in the generalized Duffing system with a fractional-order deflection. Analytical predictions concerning the chaotic thresholds in the parameter space are derived by using the stochastic Melnikov method combined with the mean-square criterion. To qualitatively confirm the analytical results, numerical simulations obtained from the mean largest Lyapunov exponent are used as test beds. We show that colored noise can induce chaos, and the effects for the case of red noise on the onset of chaos differ from those for the case of green noise. The most noteworthy result of this work is the formula, which relates the chaotic thresholds among red, green and white noise, holds for noise-induced chaos in the Duffing system. We also show that Gaussian white noise can induce chaos more easily than colored noise.

1 Introduction

When considering the onset of chaos in a realistic system, noise in the external perturbation is inevitable present since the natural system is undeniably subject to random fluctuations [1]. As Tél and Lai [2] pointed out, noise-induced chaos is a generic phenomenon in the real world, especially in biological sciences where the concept of noise-induced chaos plays an important role in the dynamical evolution of biological systems [3, 4]. Therefore, many researchers have attempted to explore the mechanism of noise-induced chaos [5]. As a pioneering work, Crutchfield et al. [6] studied the effect of noise on the onset of chaos associated with period doubling bifurcations. They found that noise tends to smooth out the transition to chaos and lower the threshold value for the onset. By developing a renormalization approach for a noisy map, Hirsch et al. [7] derived a formulation of the transition to chaos via intermittency. Based on simulations in a Josephson system with a fractal boundary between basins of periodic attractors, Iansiti et al. [8] showed that the addition of noise pushes the orbit into the basin boundary, induces an intermittent motion, and thus leads to a strange attractor, which is similar to an interior crisis in intrinsically chaotic systems. For a nonchaotic attractor coexisting with a nonattracting chaotic saddle, Liu et al. [9, 10] discovered, under the influence of noise, the topology of the flow is destroyed due to unstable-dimension variability, and obtained in the continuous-time dynamical system a general scaling law for the largest Lyapunov exponent. The scaling law, however, is based on numerical evidence and a heuristic analysis. Based on the concept of quasi potentials [2], Tél and Lai provided a novel analytical approach to derive in such continuous flow the same scaling law, whereas they uncovered the same order of magnitude, but somewhat different, scaling law for the noisy map.

As an effective global perturbation technique to predict deterministic chaos in the sense of Smale horseshoes, the Melnikov method has been applied to homoclinic or heteroclinic chaos in noisy systems. Taking into account the effect of weak additive noise on the homoclinic threshold, Bulsara et al. [11] derived a generalized Melnikov function, which is shifted by a correction term that depends on noise characteristics. They demonstrated that, on average, additive noise elevates the threshold for chaos. In a different way, Frey and Simiu [12] defined a Melnikov process based on the fact that the stochastic excitation can be closely approximated by finite sums of harmonic excitations with random parameters, and concluded that the presence of weak noise cannot suppress chaotic motion. However, a rigorous proof of the existence of chaos via horseshoes is still to be carried out for the stochastic system. Even for the deterministic system, the standard Melnikov function only renders a necessary condition for the existence of chaos. In view of this, in order to provide an upper bound of possible chaotic domain, Lin and Yim [13] developed a generalized stochastic Melnikov method with the mean-square criterion and observed that the presence of noise lowers the threshold and enlarges the possible chaotic domain in the parameter space. Later on, this method has been employed to consider homoclinic or heteroclinic chaos in nonlinear systems driven by various types of noise [14,15,16,17,18], such as dichotomous noise, bounded noise, and red noise (Ornstein–Uhlenbeck process). In particular, Gan [19, 20] stated that the external Gaussian white noise excitation is robust for inducing chaos while the colored noise excitation is weak, implying that the former can induce chaos more easily.

Contrary to intuition, as it is now well known, stochastic excitations in nonlinear systems can interact with nonlinearities to enhance regular behaviors such as stochastic resonance, coherence resonance, and pattern [1, 21, 22]. More interestingly, Maritan and Banavar [23] showed that in a pair of chaotic systems common noise can induce synchronization. However, Pikovsky [24] pointed out that this is a numerical illusion from the insufficient precision of calculations. Sanchez et al. [25] concluded that this kind of synchronization is induced by a nonzero mean of the signal, not by its stochastic character, and claimed that unbiased noise cannot lead to synchronization. This claim was invalidated by Lai and Zhou [26]. They showed that synchronization can be achieved by zero-mean noise in a chaotic map with large convergence regions. Considering the effect of colored noise on chaotic arrays, Lorenzo and Pérez-Muñuzuri [27] uncovered for some values of the time correlation red noise can improve synchronization of the arrays. Also, Wang et al. [28] investigated synchronization among chaotic oscillators driven by colored noise, red and green noise and obtained colored-noise-induced synchronization. Importantly, they found that the onset of synchronization is different for different types of noise. More precisely, they provided a formula relating the critical noise amplitudes among red, green and white noise for synchronization. Inspired by their work on synchronization, in this study, we aim to investigate the effect of colored noise on the onset of chaos in the generalized Duffing system, since noise-induced synchronization and noise-induced chaos are two opposite transitions in terms of the sign of the largest Lyapunov exponent. We will consider whether the formula, which relates the synchronization thresholds of red, green and white noise, still holds for chaos. Instead of a heuristic analysis, this study uses the stochastic Melnikov method with the mean-square criterion to derive chaotic thresholds of colored and white noise. The remainder of this study is organized as follows. In Sect. 2, we will introduce the mathematical model and the generation of colored noise. Section 3 presents analytical estimates of chaotic thresholds in the parameter space obtained through the stochastic Melnikov method. Since the power spectrum of white noise is equivalent to the sum of spectrums of red and green noise, we prove that the formula, relating white noise and colored noise, still holds for noise-induced chaos. Subsequently, to verify the results acquired from theoretical prediction more comprehensively, numerical simulations are performed in Sect. 4, in which the algorithm for the mean largest Lyapunov exponent from Rosenstein et al. [29] is employed. Section 5 is devoted to presenting conclusions and further discussions of the major findings. Ultimately, we present the detailed steps leading to the second-order stochastic Runge–Kutta algorithm to integrate the stochastic differential equations under green noise in “Appendix”.

2 Mathematical model and colored noise

2.1 Mathematical model

In this work, we will concentrate on the effect of the onset of chaos induced by colored noise in the pervasive Duffing-type differential equation with a fractional-order nonlinear term:

$$\begin{aligned} {\ddot{x}} - x + x{\left| x \right| ^{\alpha - 1}} = \varepsilon ( - \delta {\dot{x}} + \mu G(t)). \end{aligned}$$

(1)

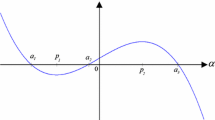
Equation (1) has a physical meaning that it can represent the oscillatory motion of the buckled beam with hinged or simply supported ends for the modal displacement x(t) [30]. The exponent $\alpha > 1$ is an integer or a fraction that depends on the bending and material properties of the beam. For example, the piano hammer is a wooden beam that coated with several layers of the compressed wool felts. The elastic force in the piano hammer is nonlinear, and the values of the exponent $\alpha$ range from 1.5 to 2.8 for new hammers and 2.2 to 3.5 for hammers taken from the pianos [31]. The phenomena in electronics can also be described with the differential Eq. (1). The nonlinearity of the restitution force plays an important role in micro-electromechanical systems like micro-actuators [32], micro-oscillators [33], and micro-filters [34]. For the micro-actuators [32], the optimal values for $\alpha$ range from 4 to 7.

By introducing a new variable $y = {\dot{x}}$ , one can rewrite Eq. (1) in the following form:

$$\begin{aligned} {\dot{x}}= & {} y,\nonumber \\ {\dot{y}}= & {} x - x{{\left| x \right| }^{\alpha - 1}} + \varepsilon ( - \delta y + \mu G(t)), \end{aligned}$$

(2)

where $0 < \varepsilon \ll 1$ is a perturbative parameter, $\delta$ is the amplitude of linear damping, and $\mu$ is the amplitude that represents the intensity of noise G(t). As discussed in Sect. 1, three types of noise, red, green and white noise, will be considered in the stochastic dynamical system (2), separately. In addition, we select the four cases, i.e. $\alpha = 5/3, 3, 11/3, 14/3$ to study the effects of colored noise on the onset of chaos. We always set $\varepsilon =0.1$, $\delta =0.15$ in the following study if there are no special statements.

Fig. 1

(Color online) The spectral density of red and green noise depicted in a and b indicates that with the growth of $\gamma$, the bandwidth of red noise become wider, i.e. its randomness becomes much stronger, whereas green noise is relatively complemented to red noise. c The sum of the spectral densities of red and green noise is always the spectrum of white noise

2.2 The generation of colored noise

It is shown that both red and green noise can be generated from a first-order linear stochastic differential equation as long as the additive stochastic component corresponds to the Gaussian white noise and violet noise separately.

Red noise can be constructed with the following equation:

$$\begin{aligned} {\dot{\xi }} = - \gamma \xi + \gamma \eta , \end{aligned}$$

(3)

where $\gamma$ is a positive parameter, $\eta (t)$ is taken as Gaussian white noise and $D$ is the amplitude of white noise. The properties for Gaussian white noise are assumed: $\langle \eta \rangle = 0$, $\langle \eta (t)\eta (t')\rangle = {D^2}\delta (t - t')$, with an initial condition $\langle \xi (0)\rangle = 0$, we obtain (for $t \rightarrow \infty$):

$$\begin{aligned}&\langle \xi \rangle = 0,\end{aligned}$$

(4)

$$\begin{aligned}&\langle \xi (t)\xi (t + \tau )\rangle = {D^2}\frac{\gamma }{2}{e^{ - \gamma \left| \tau \right| }}, \end{aligned}$$

(5)

$$\begin{aligned}&{S_R}(\omega ) = \frac{D^2}{2\pi }\frac{\gamma ^2}{\gamma ^2 + \omega ^2}, \end{aligned}$$

(6)

where the positive parameter $\gamma$ stands for the inverse correlation time of the stochastic process $\xi (t)$, and ${S_R}(\omega )$ denotes the power spectrum of $\xi (t)$. In addition, there is no denying that the autocorrelation function in Eq. (5) decays exponentially, which is just complying with the characteristic of red noise. That is to say, $\xi (t)$ is the stochastic process that generates red noise (see, for instance, Refs. [35, 36]). Note that in the past years researchers have developed different algorithms [37, 38] to simulate Langevin equations with colored noise, whose algorithms can also be introduced and utilized to integrate the set of stochastic differential equations under red noise.

Similar to the generation of red noise, green noise can be generated if the additive stochastic term $\gamma \eta$ is substituted as $- \dot{\eta }$ in Eq. (3), where $\dot{\eta }$ denotes violet noise. Owing to the reason that the numerical integration concerning the derivative term of a stochastic process is difficult to calculate, and hence, a numerically feasible way is selected to generate green noise [28]:

$$\begin{aligned} \left\{ \begin{array}{l} {\dot{z}} = f(z) + \xi - \eta .\\ {\dot{\xi }} = - \gamma \xi + \gamma \eta . \end{array} \right. \end{aligned}$$

(7)

In system (7), $\eta (t)$ is taken as Gaussian white noise. Accordingly, red noise is generated from the stochastic process $\xi (t)$. Then, we can compute the power spectrum of the stochastic process $\xi (t)-\eta (t)$ as:

$$\begin{aligned} {S_{\xi - \eta }}(\omega )= & {} \left[ {\tilde{\xi }} (\omega ) - {\tilde{\eta }} (\omega )\right] \left[ {{{\tilde{\xi }} }^ * }(\omega ) - {{{\tilde{\eta }}}^ * }(\omega )\right] \nonumber \\= & {} \dfrac{{{D^2}}}{{2\pi }}\left[ \dfrac{\gamma }{{\gamma + i\omega }} - 1\right] \times \left[ \dfrac{\gamma }{{\gamma - i\omega }} - 1\right] \nonumber \\= & {} \dfrac{{{D^2}}}{{2\pi }}\dfrac{{{\omega ^2}}}{{{\gamma ^2} + {\omega ^2}}}, \end{aligned}$$

(8)

which just obeys the characteristic of green noise. Thus, the autocorrelation function of the stochastic process can be obtained:

$$\begin{aligned} {R_{\xi - \eta }}(t,t + \tau ) = {D^2}\delta (\tau ) - {D^2}\frac{\gamma }{2}{e^{ - \gamma \left| \tau \right| }}. \end{aligned}$$

(9)

To integrate the stochastic dynamical systems under green noise numerically, the second-order Runge–Kutta algorithm is introduced and utilized, which can also be utilized to simulate dynamical systems under white noise if the system (7) contains no $\xi -$related term, and under red noise if the first equation of system (7) contains no white noise term [39], respectively. The algorithm for computing system (7) is as follows:

$$\begin{aligned} z(t + \Delta t)= & {} z(t) + {\Delta t({F_1} + {F_2})} \big /2 - D\sqrt{\Delta t} \phi ,\nonumber \\ \xi (t + \Delta t)= & {} \xi (t) + {\Delta t({H_1} + {H_2})} \big /2 + D\gamma \sqrt{\Delta t} \phi ,\nonumber \\ \end{aligned}$$

(10)

where

$$\begin{aligned} {H_1}= & {} - \gamma \xi (t),\\ {H_2}= & {} - \gamma [\xi (t) + \Delta t{H_1} + D\gamma \sqrt{\Delta t} \phi ],\\ {F_1}= & {} f[z(t)] + \xi (t),\\ {F_2}= & {} f[z(t) + \Delta t{F_1} - D\sqrt{\Delta t} \phi ] - {{{H_2}} \big / \gamma }, \end{aligned}$$

and $\phi \sim N(0,1)$ is a standard Gaussian random number. It should be noted that in this study the value of D is always set as 4.

Figure 1 displays the spectral density of colored noise for several values of parameter $\gamma$. It is confirmed clearly in Fig. 1a, b that the bandwidth of red and green noise depends mainly on $\gamma$. In addition, the larger $\gamma$ is, the wider the bandwidth could be, which means the randomness of red noise will become much stronger following with the increase of the parameter $\gamma$, whereas green noise is contrary to red noise. In fact, white noise has a flat power spectrum, i.e. ${S_\eta }=D^2/{2\pi }\equiv {S_W}$ does not depend on $\gamma$. Nonetheless, there always exists an expression between the spectral densities of the three types of noise, namely, ${S_R} + {S_G} = {S_W}$, which is verified in Fig. 1c. As a result, their effects on the onset of chaos in the Duffing system (2) should be related to each other, which will be illustrated in this work, theoretically and numerically.

3 Chaos prediction

As discussed in Sect. 1, the Melnikov method is an effective approach to detect chaotic dynamics. Moreover, the Melnikov function is introduced and extensively employed to forecast whether chaos occurs by surveying the distance between the perturbed stable and unstable manifolds of homoclinic/heteroclinic orbits. Thus, in this section we aim to apply the stochastic Melnikov method to analyze and compare the effects of the three processes above on the onset of chaos.

In order to employ the Melnikov method, Eq. (2) is primarily rewritten in the following equivalent form:

$$\begin{aligned} {\dot{X}} = f(X) + \varepsilon g(X, t), \end{aligned}$$

(11)

where

$$\begin{aligned} X = {(x, y)^\mathrm{T}}, \quad g(X, t) = \left( {\begin{array}{*{20}{c}} 0\\ {\mu G(t) - \delta y} \end{array}} \right) , \end{aligned}$$

and

$$\begin{aligned} \begin{array}{c} f(X)= {\left( {\begin{array}{*{20}{c}} {\dfrac{{\partial H(x,y)}}{{\partial y}},}&{}{ - \dfrac{{\partial H(x,y)}}{{\partial x}}} \end{array}} \right) ^\mathrm{T}}\\ = \left( {\begin{array}{*{20}{c}} y\\ {x - x{{\left| x \right| }^{\alpha - 1}}} \end{array}} \right) . \end{array} \end{aligned}$$

If we assume $\varepsilon = 0$, then the stochastic dynamical system (2) can be regarded as an unperturbed system: i.e.

$$\begin{aligned} {\dot{x}}= & {} y,\nonumber \\ {\dot{y}}= & {} x - x{{\left| x \right| }^{\alpha - 1}}. \end{aligned}$$

(12)

Meanwhile, the Hamiltonian function H(x, y) associated with the unperturbed system is obtained in the following form:

$$\begin{aligned} H(x, y) = \dfrac{1}{2}{y^2} - \dfrac{1}{2}{x^2} + \dfrac{{{x^2}{{\left| x \right| }^{\alpha - 1}}}}{{\alpha + 1}}. \end{aligned}$$

(13)

It is easy to verify that there exist three equilibrium points for $\alpha > 1$ : $O = (0,0)$ denotes the hyperbolic saddle and ${C_{1,2}} = ( \pm 1,0)$ can be considered as the centers. Then, the analytical solutions of the homoclinic orbits $\varGamma _{\hom }^ \pm$ can be expressed as:

$$\begin{aligned} \varGamma _{\hom }^ + (t)= & {} (x_ + ^0(t), y_ + ^{0}(t)),\\ \varGamma _{\hom }^{-}(t)= & {} (x_ - ^0(t), y_ - ^0(t)) = - \varGamma _{\hom }^ + (t), \end{aligned}$$

where

$$\begin{aligned} x_ + ^{0}(t)= & {} {{\left( \frac{{\alpha + 1}}{2}\right) }^{\frac{1}{{\alpha - 1}}}}{{\left( {\mathrm{sech}} \left( \frac{{\alpha - 1}}{2}t\right) \right) }^{\frac{2}{{\alpha - 1}}}},\\ y_ + ^{0}(t)= & {} - {{\left( \frac{{\alpha + 1}}{2}\right) }^{\frac{1}{{\alpha - 1}}}}{{\left( {\mathrm{sech}} \left( \frac{{\alpha - 1}}{2}t\right) \right) }^{\frac{2}{{\alpha - 1}}}}\\&\times \tanh \left( \frac{{\alpha - 1}}{2}t\right) . \end{aligned}$$

Similar to the deterministic Melnikov method, we derive the stochastic Melnikov process for system (2) in the following equation:

$$\begin{aligned} {M^ \pm }({t_0})= & {} \int _{- \infty } ^{ + \infty } {f(\varGamma _{\hom }^ \pm } (t)) \wedge g(\varGamma _{\hom }^ \pm (t),t + {t_0})\nonumber \\= & {} \int _{ - \infty }^{ + \infty } {y_ \pm ^0} (t)(\mu G(t + {t_0}) - \delta y_ \pm ^0(t))dt \\= & {} \int _{ - \infty }^{ + \infty } \mu {y_ \pm ^0} (t)G(t + {t_0})dt \nonumber \\&- \int _{ - \infty }^{ + \infty } \delta {(y_ \pm ^0} (t){)^2}dt\nonumber \\&\buildrel \Delta \over = {M_s}^ \pm + {M_d}^ \pm ,\nonumber \end{aligned}$$

(14)

where the integral ${M_s}^ \pm$ and ${M_d}^ \pm$ are given by the following relations:

$$\begin{aligned} {M_s}^ {\pm }= & {} \mu \int _{ - \infty }^{ + \infty } {y_ \pm ^{0}} (t)G(t + {t_0})dt,\\ {M_d}^{\pm }= & {} - \delta \int _{ - \infty }^{ + \infty } (y_ \pm ^{0} (t))^{2}dt. \end{aligned}$$

Meanwhile ${M_d}^ \pm$ is the deterministic part of ${M^ \pm }({t_0})$, i.e. the mean value of the Melnikov integral. And ${M_s}^ \pm$ is the corresponding stochastic portion of ${M^ \pm }({t_0})$ due to the noise excitation, where $E[{M_s}^ \pm ] = 0$. Particularly, the stochastic portion, instead of directly integrated, can be calculated by considering the convolution integral as a filtering process, i.e. a stationary process G(t) passing through a linear time-invariant filter given by the homoclinic orbit [40, 41]. Owing to the symmetry, the two homoclinic orbits will induce the same parameter sets corresponding to the onset of chaos. Thus, we only need to calculate the Melnikov function of the right homoclinic orbit. Considering G(t) an input of system (2), the function $h(t) = y_0^ + (t)$ can be taken as an impulse response function of the time-invariant linear system. Accordingly, the corresponding frequency response function can be obtained in the following form:

$$\begin{aligned} H(\omega )= & {} \int _{ - \infty }^{ + \infty } {h(t)} {e^{ - i\omega t}}dt\nonumber \\= & {} \int _{ - \infty }^{ + \infty } {y_ + ^0(t)} {e^{ - i\omega t}}dt\nonumber \\= & {} i{\left( \frac{{\alpha + 1}}{2}\right) ^{\frac{1}{{\alpha - 1}}}}\left( \frac{2}{{\alpha - 1}}\right) \nonumber \\&\times \int _{ - \infty }^{ + \infty } {\frac{{\sinh (t)}}{{{{\cosh }^{\frac{{\alpha + 1}}{{\alpha - 1}}}}(t)}}} \sin \left( \frac{{2\omega t}}{{\alpha - 1}}\right) dt. \end{aligned}$$

(15)

Thus, the mean of $M_s^2$ can be calculated as follows:

$$\begin{aligned} E[M_s^2]= & {} {\mu ^2}{\int _{ - \infty }^{ + \infty } {\left| {H(\omega )} \right| } ^2}S(\omega )d\omega \nonumber \\= & {} {\mu ^2}{\left( {\frac{{\alpha + 1}}{2}} \right) ^{\frac{2}{{\alpha - 1}}}}{\left( {\frac{2}{{\alpha - 1}}} \right) ^2}\nonumber \\&\times \int _{ - \infty }^{ + \infty } (Q_0)^2 S(\omega )d\omega . \end{aligned}$$

(16)

where

$$\begin{aligned} {Q_0} = \int _{ - \infty }^{ + \infty } {\frac{{\sinh (t)}}{{{{\cosh }^{\frac{{\alpha + 1}}{{\alpha - 1}}}}(t)}}\sin \left( \frac{{2\omega t}}{{\alpha - 1}}\right) dt}. \end{aligned}$$

Note that the mean of the stochastic Melnikov process ${M^ \pm }({t_0})$ is always negative and has no simple zero, implying that in this sense we cannot obtain the chaotic threshold. Since the standard Melnikov method only renders a necessary condition for the existence of chaos, the criterion for noisy chaotic responses can be depicted by a mean-square representation in view of energy [41]. Consequently, if $E[{M_s}^2] = {M_d}^2$, the stochastic Melnikov process will have a simple zero point under the mean-square sense. Thus, the threshold $\mu$ for the onset of chaos can be expressed as:

$$\begin{aligned} \mu = \frac{{\delta {{\left( \dfrac{{\alpha + 1}}{2}\right) }^{\frac{1}{{\alpha - 1}}}}{Q_1}}}{{\sqrt{{Q_2}} }}, \end{aligned}$$

(17)

where

$$\begin{aligned} {Q_1}= & {} \int _{ - \infty }^{ + \infty } \frac{{{{\sinh }^2}(t)}}{{{{\cosh }^{\frac{{2(\alpha + 1)}}{{\alpha {-1}}}}(t)}}} dt,\\ {Q_2}= & {} \int _{ - \infty }^{ + \infty } {(Q_0)^2S(\omega )d\omega }. \end{aligned}$$

Note that the spectral densities of red, green and white noise have been calculated as the following forms:

$$\begin{aligned} {S_R}(\omega )= & {} \frac{{{D^2}}}{{2\pi }}\frac{{{\gamma ^2}}}{{{\gamma ^2} + {\omega ^2}}}, \\ {S_G}(\omega )= & {} \frac{{{D^2}}}{{2\pi }}\frac{{{\omega ^2}}}{{{\gamma ^2} + {\omega ^2}}}, \\ {S_W}(\omega )= & {} \frac{{{D^2}}}{{2\pi }}. \end{aligned}$$

Then, the threshold $\mu$ of the three processes for the onset of chaos can be marked as ${\mu _R}$, ${\mu _G}$ and ${\mu _W}$ respectively, as follows:

Fig. 2

(Color online) The analytical threshold for the onset of chaos induced by colored noise is shown for different values of parameter $\alpha$: a red noise; b green noise. We can observe that: with the increase of $\gamma$, the chaotic threshold induced by red noise decreases, while the threshold induced by green noise increases; with the increase of $\alpha$, red noise raises the chaotic threshold, while green noise lowers it

$$\begin{aligned} {\mu _R}= & {} \frac{{\delta {{\left( \dfrac{{\alpha + 1}}{2}\right) }^{\frac{1}{{\alpha - 1}}}}{Q_1}}}{{\sqrt{Q_2^R} }}, \end{aligned}$$

(18)

$$\begin{aligned} {\mu _G}= & {} \frac{{\delta {{\left( \dfrac{{\alpha + 1}}{2}\right) }^{\frac{1}{{\alpha - 1}}}}{Q_1}}}{{\sqrt{Q_2^G} }}, \end{aligned}$$

(19)

$$\begin{aligned} {\mu _W}= & {} \frac{{\delta {{\left( \dfrac{{\alpha + 1}}{2}\right) }^{\frac{1}{{\alpha - 1}}}}{Q_1}}}{{\sqrt{Q_2^W} }}, \end{aligned}$$

(20)

where

$$\begin{aligned} Q_2^R= & {} \int _{ - \infty }^{ + \infty } {(Q_0)^2{S_R}(\omega )d\omega }, \end{aligned}$$

(21)

$$\begin{aligned} Q_2^G= & {} \int _{ - \infty }^{ + \infty } {(Q_0)^2{S_G}(\omega )d\omega }, \end{aligned}$$

(22)

$$\begin{aligned} Q_2^W= & {} \int _{ - \infty }^{ + \infty } {(Q_0)^2{S_W}(\omega )d\omega }. \end{aligned}$$

(23)

The analytical results shown in Eqs. (18–20) provide a threshold for the onset of chaos, i.e. all the three process can indeed induce chaotic responses as long as the value of $\mu$ exceeds the corresponding threshold. In addition, Fig. 2 illustrates the relation between the parameter $\gamma$ and the threshold $\mu$ for the onset of chaos induced by red and green noise, respectively. It is clear that the different stochastic excitations, red and green noise, have opposite effects on chaotic responses. We can observe that with the increase of $\gamma$, the chaotic threshold induced by red noise decreases, which means that the presence of red noise enlarges the possible chaotic domain in the parameter space, while the threshold induced by green noise increases. The reason is that the enhancement of randomness of the stochastic excitation lowers the threshold for chaotic responses in system (2) as the parameter $\gamma$ describing the inverse correlation time of red noise increases. Since green noise is relatively complemented to red noise and can be obtained by subtracting white noise from red noise, the opposite effect of green noise is expected. We can also observe that with the increase of $\alpha$, red noise raises the chaotic threshold, while green noise lowers it. When we consider white noise the stochastic excitation, the threshold ${\mu _W}$ does not depend on $\gamma$ accounting for the reason that white noise has a flat power spectrum [see Eq. (20)].

From the discussion above, it is not surprising to learn that both red and green noise can indeed induce chaos, but the onset of chaos, as characterized by the value of the critical noise amplitude above which chaos occurs, can be different for noise of different colors. Furthermore, the expressions of Eqs. (18–20) indicate that the thresholds of different stochastic excitations depend mainly on their spectrums. Just as the analysis of the spectral density shown in Sect. 2, the spectral properties of red and green noise are different, but are complementary with respect to the spectrum of white noise. Thus, according to the study of Wang et al. [28] on the onset of colored-noise-induced synchronization, we shall conjecture whether it still exists a certain relation among their impacts on the rising of chaotic responses.

Fig. 3

(Color online) The chaotic thresholds in system (2) under red, green and white noise, and the relation between them for two cases: a, b $\alpha = 5/3$; c, d $\alpha = 3$. We show that ${\mu ^*}$, which is defined by ${1}/{\mu ^*}\buildrel \Delta \over =\sqrt{{1}/{\mu _R^2}+{1}/{\mu _G^2}}$, is approximately equal to ${\mu _W}$ for all values of $\gamma$

We choose two cases, $\alpha = 5/3$ and $\alpha = 3$, in the generalized Duffing system to verify the relation between critical values of chaotic thresholds induced by red, green and white noise. To compare the effects of different stochastic excitations, we plot the chaotic thresholds in system (2) under red, green and white noise in Fig. 3a, c for $\alpha = 5/3$ and $\alpha = 3$, respectively. The results indicate that the threshold required for the onset of chaos is smaller for Gaussian white noise than for colored noise, which means Gaussian white noise can induce chaos more easily than the latter. Furthermore, when we take $\gamma = 1$, $\alpha = 5/3$ as an example, we obtain analytical threshold values of the onset of chaos ${\mu _G} \approx 0.07387$, ${\mu _R} \approx 0.04597$, and ${\mu _W} \approx 0.03903$. That is, we have the formula ${1 {/{\mu _R^2}}} + {1/ {\mu _G^2}} = {1/ {\mu _W^2}}$ approximately. In further, we define $1/{{\mu ^*}} \buildrel \Delta \over = \sqrt{{1 /{\mu _R^2}} + {{1 /{\mu _G^2}}}}$. Fig. 3b, d display the function of ${\mu ^*}$ and the analytical threshold ${\mu _W}$ versus $\gamma$. It is verified that the value of ${\mu ^*}$ is approximately equal to ${\mu _W}$ for all values of $\gamma$ in both cases. Furthermore, Eqs. (18–20) also provide the heuristic justification that for the larger values of $\gamma$, we have ${\mu _G} \rightarrow \infty$ and ${\mu _R} \rightarrow {\mu _W}$; for the smaller values of $\gamma$, ${\mu _R} \rightarrow \infty$ and ${\mu _G} \rightarrow {\mu _W}$. Therefore, we can conclude that the formula ${1/ {\mu _R^2}} + 1/ {\mu _G^2} \approx 1/{\mu _W^2}$ even holds in the limiting cases of $\gamma$.

In fact, the formula relating the chaotic thresholds of red, green, and white noise can be obtained by mathematical derivation. Based on the derivation process of the chaotic thresholds and the analysis of the expressions of Eqs. (18–20), we obtain

$$\begin{aligned} \frac{1}{{\mu _R^2}}= & {} \frac{{Q_2^R}}{{{\delta ^2}{{\left( \frac{{\alpha + 1}}{2}\right) }^{\frac{2}{{\alpha - 1}}}}Q_1^2}},\\ \frac{1}{{\mu _G^2}}= & {} \frac{{Q_2^G}}{{{\delta ^2}{{\left( \frac{{\alpha + 1}}{2}\right) }^{\frac{2}{{\alpha - 1}}}}Q_1^2}},\\ \frac{1}{{\mu _W^2}}= & {} \frac{{Q_2^W}}{{{\delta ^2}{{\left( \frac{{\alpha + 1}}{2}\right) }^{\frac{2}{{\alpha - 1}}}}Q_1^2}}. \end{aligned}$$

Since the sum of the spectral densities of red and green noise is always the spectrum of white noise, i.e. ${S_R} + {S_G} = {S_W}$, it is easy to get $Q_2^R + Q_2^G = Q_2^W.$ Finally, the formula concerning the thresholds of the three processes can be derived, i.e.

$$\begin{aligned} \frac{1}{{\mu _R^2}} + \frac{1}{{\mu _G^2}} = \frac{1}{{\mu _W^2}}. \end{aligned}$$

(24)

The Melnikov theory requires that the perturbative parameter $\varepsilon$ must be sufficiently small. In fact, the Melnikov theory is still valid when the perturbation is relatively large. In the above study, we discuss the effect of $\gamma$ on the chaotic thresholds in a generalized Duffing system with $\varepsilon = 0.1,\delta = 0.15$. In addition, the analytical threshold shown in Eq. (17) also reveals the positive correlation between the chaotic threshold and the damping coefficient $\delta$, i.e. the larger $\delta$ is, the higher the chaotic threshold will be.

4 Numerical simulations

Since the stochastic Melnikov method only renders a parameter threshold for possible chaotic responses in system (2) driven by red, green or white noise, it is necessary to employ numerical simulations to confirm the analytical predictions above.

Fig. 4

(Color online) The thresholds for numerical chaos induced by red and green noise are displayed in a–c and d–f, respectively, for $\varepsilon =0.1$, $\delta =0.15$, and $D=4$. Analytical chaotic thresholds obtained by the stochastic Melnikov method are plotted in b, c, e, f with dashed lines for comparison. We show that with the increase of $\gamma$, the numerical threshold induced by red noise decreases, while the threshold induced by green noise increases; with the increase of $\alpha$, red noise raises the numerical threshold, while green noise lowers it. The variation trend of numerical thresholds agrees well with the analytical predictions

As is well known, the most striking feature of chaos is the unpredictability for the future, which exhibits sensitive dependence on the initial conditions. It can be quantified by the Lyapunov exponent, which characterizes the asymptotic rates of exponential divergence or convergence of nearby trajectories in the state space and quantifies the strength of chaos in dynamical systems. Thus, in this section we plan to apply the mean largest Lyapunov exponent to identifying noise-induced chaos and to verifying the chaotic thresholds obtained by the stochastic Melnikov method.

The largest Lyapunov exponent for deterministic systems can be computed by using the Rosenstein’s approach [29], and the mean largest Lyapunov exponent can be obtained through averaging largest Lyapunov exponents of different orbits. Thus, we define the mean largest Lyapunov exponent as

$$\begin{aligned} L = \frac{1}{N}\sum \limits _{i = 1}^N {{L_i}}, \end{aligned}$$

(25)

where $i = 1, \ldots ,N$, ${L_i}$ denotes the largest Lyapunov exponent of orbit i , and N signifies the number of orbits.

Here, the presence of a positive Lyapunov exponent is used for diagnosing stochastic chaos and represents local instability in a particular direction. Consequently, the numerical threshold considering the onset of chaos induced by red, green and white noise can be obtained, respectively, when the mean largest Lyapunov exponent L increases from zero to positive.

Through vanishing the mean largest Lyapunov exponent, Fig. 4 depicts the thresholds for numerical chaos induced by red and green noise, respectively. It is shown that with the increase of the parameter $\gamma$, the threshold of red noise presented in Fig. 4a monotonically decreases for a fixed value of the parameter $\alpha$. Contrary to red noise, the critical values of green noise increase following the increase of the parameter $\gamma$, as displayed in Fig. 4d. Apparently, when fixing the value of the parameter $\gamma$, the threshold ${\mu _R}$ increases with the growth of the fractional-order deflection $\alpha$. When it comes to green noise, the amplitude threshold ${\mu _G}$ decreases. We verify that the numerical consequences of red noise depicted in Fig. 4a have a similar varying trend in comparison with the analytical results displayed in Fig. 2a. Meanwhile, the varying trend of threshold among numerical and analytical results for green noise is also similar by comparing Figs. 4d and 2b. Figure 4 also verifies the accuracy of the analytical results obtained in Sect. 3. For both red and green noise, we can conclude from Fig. 4b, c, e, f that the analytical thresholds calculated by the stochastic Melnikov method agree well with the numerical ones obtained through vanishing the mean largest Lyapunov exponent due to the fact that for a larger parameter $\alpha$, the relative error between numerical and analytical results is much smaller. Therefore, we confirm that the stochastic Melnikov method, together with the mean-square criterion, provides reasonable analytical results for the onset of chaos.

The results confirmed by the stochastic Melnikov method show that the effects of the three processes on the onset of chaos can be connected with each other in the form presented in Eq. (24). Then, we will verify this conclusion through vanishing the mean largest Lyapunov exponent. Note that, for large values of $\gamma$, the correlation property of red noise tends to that of white noise, while the autocorrelation function associated with green noise tends to zero. For small values of $\gamma$, the opposites occur. Thus the relation between the numerical thresholds of colored noise and white noise can be interpreted. As shown in Figs. 5a and 6a, with the increase of $\gamma$, the threshold of red noise decreases and then tends to that of white noise, while the threshold induced by green noise increases. In addition, we obtain the critical values ${\mu _R} \approx 0.08666$ and ${\mu _G} \approx 0.11333$, when we fix $\alpha = 5/3$, $\gamma = 1$. When it comes to white noise, we get the critical value: ${\mu _W} \approx 0.07333$. The three numerical thresholds satisfy the formula Eq. (24) approximately. Similarly, the relation can also be acquired for the case $\alpha = 3$ with the threshold values ${\mu _R} \approx 0.12666$, ${\mu _G} \approx 0.09333$, and ${\mu _W} \approx 0.07333$ when fixing $\gamma = 1$. Furthermore, Figs. 5b and 6b display, as $\gamma$ increases, the formula ${1 / {\mu _R^2}}+ 1/{\mu _G^2} = {1 / {\mu _W^2}}$ always holds. This agrees well with the analytical result with the stochastic Melnikov method.

Fig. 5

(Color online) a The chaotic thresholds in system (2) under red, green and white noise for $\alpha = 5/3$ through vanishing the mean largest Lyapunov exponent; b the relation between chaotic thresholds induced by colored noise and white noise, where ${1}/{\mu ^*}\buildrel \Delta \over =\sqrt{{1}/{\mu _R^2}+{1}/{\mu _G^2}}$

Fig. 6

(Color online) a The chaotic thresholds in system (2) under red, green and white noise for $\alpha = 3$ through vanishing the mean largest Lyapunov exponent; b the relation between chaotic thresholds induced by colored noise and white noise, where ${1}/{\mu ^*}\buildrel \Delta \over =\sqrt{{1}/{\mu _R^2}+{1}/{\mu _G^2}}$

Note that there exists difference between the thresholds obtained through the analytical and numerical methods. This can be comprehended accounting for the reason that simple zero points of the stochastic Melnikov method combined with the mean-square criterion just provide a necessary rising of noise-induced chaotic responses. Ultimately, we can conclude the formula relating the synchronization thresholds among red, green and white noise indeed holds for chaos in the generalized Duffing dynamical system.

Additionally, the effects of $\varepsilon$ and $\delta$ on the onset of chaos have been discussed theoretically in Sect. 3. Without loss of generality, we choose the case $\alpha = 3$ and change the values of $\varepsilon$ and $\delta$ to verify their effects on the onset of chaos in the generalized Duffing system under green noise. It is clear that, for the fixed values of the parameter $\varepsilon$ and $\delta$, the varying trends of the chaotic thresholds are similar to the conclusions obtained in the above study, i.e. with the increase of $\gamma$, the chaotic threshold induced by green noise increases. But the effects of $\varepsilon$ and $\delta$ on the onset of chaos are different. In the case of small perturbation, i.e. the perturbation parameter $\varepsilon$ satisfies $0 < \varepsilon \ll 1$, we decrease the value of $\varepsilon$ from 0.1 to 0.01 and find that the chaotic thresholds depicted in Fig. 7a have a small level of change for the fixed value of $\delta$ and $\gamma$. In theory, the parameter $\varepsilon$ has little effect on the chaotic threshold. Owing to the reason that only the first-order approximation is considered when we survey the distance between the perturbed stable and unstable manifolds of homoclinic orbits by employing the Melnikov function, the slight deviation between the numerical and the analytical results can be comprehended. Contrary to the effect of the parameter $\varepsilon$, the chaotic thresholds depicted in Fig. 7b increase for the fixed value of $\varepsilon$ and $\gamma$ when we increase the value of the parameter $\delta$ from 0.1 to 0.2. It is in accordance with the analytical result displayed in Sect. 3.

Fig. 7

(Color online) The effect of $\varepsilon$ and $\delta$ on the thresholds for numerical chaos induced by green noise are displayed in a and b, respectively. We show that the perturbation parameter $\varepsilon$ has little effect on the chaotic thresholds depicted in a for the fixed value of $\delta$ and $\gamma$, while the chaotic thresholds depicted in b increase following with the increase of $\delta$ for the fixed value of $\varepsilon$ and $\gamma$

5 Conclusion and discussion

Our focus in this study is to investigate how colored noise, especially red and green noise, influences the onset of chaos. To this aim, both the analytical and numerical methods are adopted to verify that both red and green noise can induce chaotic responses, whereas their effects on the onset of chaos are quite different. Nonetheless, in view of the energy, their critical noise amplitudes required for the onset of chaos can also be related in a certain way. Due to the fact that the sum of the power spectra of red and green noise is the spectrum of white noise, i.e. the spectrums of red and green noise are complementary to each other. Consequently, the formula, a quantitative expression relating the chaotic thresholds of red, green and white noise, has been verified by both analytical and numerical methods in the generalized Duffing differential equation, carrying with a fractional-order nonlinear term. This indicates that the critical amplitude required for chaos is generally smaller for white noise as compared to colored noise, which agrees well with the result of Gan [19, 20], implying that the Gaussian white noise excitation is beneficial to induce chaos, while the colored noise excitation is weak, namely the former can induce chaos more easily. In practical applications such as the performance optimization of circuit where chaos is undesirable, a simple control strategy is to install filters so as to make the noise source in the system as colored as possible. Another practical application is that we can place filters in the situations where chaos is desirable (such as the information security and secure communications), so as to make the noise source as white as possible. Nonetheless, understanding how these processes interact to induce chaos and employing them in practical application still remains a major challenge.

Appendix

Here, we will clarify the proposed second-order stochastic Runge–Kutta algorithm for integrating the differential equations under green noise. The basic idea of the algorithm is similar to that in [37] where white or red noise is treated.

We start with formally integrating Eq. (7) from time 0 to time $\Delta t$ :

$$\begin{aligned} z(\Delta t)= & {} {z_0} + \int _0^{\Delta t} {f(z(t'))} dt' + \int _0^{\Delta t} {\xi (t')} dt' \nonumber \\&- \int _0^{\Delta t} {\eta (t')} dt',\nonumber \\ \xi (\Delta t)= & {} {\xi _0} + \int _0^{\Delta t} {( - \gamma \xi (t'))} dt' + \int _0^{\Delta t} {\gamma \eta (t')} dt'.\nonumber \\ \end{aligned}$$

(26)

Defining

$$\begin{aligned} {\varGamma _0}(t)\equiv & {} \int _0^{t} {\eta (t')} dt',\\ {\varGamma _i}(t)\equiv & {} \int _0^{t} {{\varGamma _{i - 1}}(t')} dt',i = 1,2, \ldots , \end{aligned}$$

and using the identity [37]

$$\begin{aligned} < {\varGamma _m}(t){\varGamma _n}(t) > = {D^2}\frac{{{t^{m + n + 1}}}}{{m!n!(m + n + 1)}}, \end{aligned}$$

we can expand Eq. (26) about ${z_0}$ to ${(\Delta t)^2}$ . Then, we have

$$\begin{aligned} z(\Delta t)= & {} {z_0} + {f_0}\Delta t + \frac{1}{2}{f_0}{f'_0}{(\Delta t)^2} + \frac{1}{2}{\xi _0}{f'_0}{(\Delta t)^2}\\&+\, {\xi _0}\Delta t - \frac{1}{2}\gamma {\xi _0}{(\Delta t)^2} + {S_z},\\ \xi (\Delta t)= & {} {\xi _0} - \gamma {\xi _0}\Delta t + \frac{1}{2}{\gamma ^2}{\xi _0}{(\Delta t)^2} + {S_\xi }, \end{aligned}$$

in which ${f_0} = f({z_0})$, and

$$\begin{aligned} {S_z}= & {} - {\varGamma _0}(\Delta t) + \frac{1}{2}{f''_0}\int _0^{\Delta t} {dt'} \varGamma _0^2(t') \\&+\, \gamma {\varGamma _1}(\Delta t) - {f'_0}{\varGamma _1}(\Delta t),\\ {S_\xi }= & {} \gamma {\varGamma _0}(\Delta t) - {\gamma ^2}{\varGamma _1}(\Delta t). \end{aligned}$$

Then, we get the mean and variance of ${S_z}$ and ${S_\xi }$ to the order of ${(\Delta t)^2}$ :

$$\begin{aligned}< {S_z}>= & {} \frac{{{D^2}}}{4}{f''_0}{(\Delta t)^2},\nonumber \\< S_z^2>= & {} {D^2}\Delta t - {D^2}\gamma {(\Delta t)^2} + {D^2}{f'_0}{(\Delta t)^2},\nonumber \\< {S_\xi }>= & {} 0,\nonumber \\ < S_\xi ^2 >= & {} {D^2}{\gamma ^2}\Delta t - {D^2}{\gamma ^3}{(\Delta t)^2}. \end{aligned}$$

(27)

Parallelly, starting directly from Eq. (7) by using a second-order Runge–Kutta algorithm, we have

$$\begin{aligned} z(\Delta t)= & {} {z_0} + \frac{1}{2}({F_1} + {F_2})\Delta t - D\sqrt{\Delta t} {\phi _0},\nonumber \\ \xi (\Delta t)= & {} {\xi _0} + \frac{1}{2}({H_1} + {H_2})\Delta t + D\gamma \sqrt{\Delta t} {\phi _0}, \end{aligned}$$

(28)

in which

$$\begin{aligned} {H_1}= & {} - \gamma \left( {\xi _0} + D\gamma \sqrt{\Delta t} {\phi _1}\right) ,\\ {H_2}= & {} - \gamma \left( {\xi _0} + \Delta t{H_1} + D\gamma \sqrt{\Delta t} {\phi _2}\right) ,\\ {F_1}= & {} f\left( {z_0} - D\sqrt{\Delta t} {\phi _1}\right) + {\xi _0} + D\gamma \sqrt{\Delta t} {\phi _1},\\ {F_2}= & {} f\left( {z_0} + \Delta t{F_1} - D\sqrt{\Delta t} {\phi _2}\right) + {\xi _0} + \Delta t{H_1} \\&+\,D\gamma \sqrt{\Delta t} {\phi _2}, \end{aligned}$$

and ${\phi _0}$, ${\phi _1}$, and ${\phi _2}$ are three independent standard Gaussian random numbers, each of which has zero mean and unit variance. Expanding Eq. (28) about ${z_0}$ to order ${(\Delta t)^2}$, we obtain

$$\begin{aligned} z(\Delta t)= & {} {z_0} + {f_0}\Delta t + \frac{1}{2}{f_0}{f'_0}{(\Delta t)^2} + \frac{1}{2}{f'_0}{\xi _0}{(\Delta t)^2}\\&+ {\xi _0}\Delta t - \frac{1}{2}\gamma {\xi _0}{(\Delta t)^2} + {S'_z},\\ \xi (\Delta t)= & {} {\xi _0} - \gamma {\xi _0}\Delta t + \frac{1}{2}{\gamma ^2}{\xi _0}{(\Delta t)^2} + {S'_\xi }, \end{aligned}$$

where

$$\begin{aligned} {S'_z}= & {} - D\sqrt{\Delta t} {\phi _0} - \frac{1}{2}D({f'_0} - \gamma ){(\sqrt{\Delta t} )^3}{\phi _1} \\&+\frac{{{D^2}}}{4}{f''_0}{(\Delta t)^2}\phi _1^2 \\&- \frac{1}{2}D({f'_0} - \gamma ){(\sqrt{\Delta t} )^3}{\phi _2} + \frac{{{D^2}}}{4}{f''_0}{(\Delta t)^2}\phi _2^2,\\ {S'_\xi }= & {} D\gamma \sqrt{\Delta t} {\phi _0} - \frac{1}{2}D{\gamma ^2}{(\sqrt{\Delta t} )^3}{\phi _1} \\&- \frac{1}{2}D{\gamma ^2}{(\sqrt{\Delta t} )^3}{\phi _2}. \end{aligned}$$

The means and the variances of ${S'_z}$ and ${S'_\xi }$ are calculated to be

$$\begin{aligned}< {S'_z}>= & {} \frac{{{D^2}}}{4}{f''_0}{(\Delta t)^2}< \phi _1^2> \nonumber \\&+ \frac{{{D^2}}}{4}{f''_0}{(\Delta t)^2}< \phi _2^2> ,\nonumber \\< {S_z'^2}>= & {} {D^2}\Delta t< \phi _0^2> \nonumber \\&+ {D^2}({f'_0} - \gamma ){(\Delta t)^2}< {\phi _0}({\phi _1} + {\phi _2})> ,\nonumber \\< {S'_\xi }>= & {} 0,\nonumber \\< {S_\xi '^2}>= & {} {D^2}{\gamma ^2}\Delta t< \phi _0^2> \nonumber \\&- {D^2}{\gamma ^3}{(\Delta t)^2} < {\phi _0}({\phi _1} + {\phi _2}) > . \end{aligned}$$

(29)

Equating Eqs. (27)–(29) leads to

$$\begin{aligned}&< \phi _0^2> = 1,\\&< \phi _1^2> +< \phi _2^2> = 1,\\&< {\phi _0}({\phi _1} + {\phi _2}) > = 1. \end{aligned}$$

Due to the reason that there are three equations and three unknowns, it is possible for us to define a standard Gaussian random number $\psi$ so that ${\phi _i} = {a_i}\psi ,i = 0,1,2$. To maintain the structure, we can conveniently choose ${a_0} = {a_2} = 1$ and ${a_1} = 0$. Then, these considerations lead to the second-order stochastic Runge–Kutta algorithm as represented by Eq. (10).