1 Introduction

It is known that thermal transfer happens when there are heat differences among objects or within dissimilar parts of similar objects. Many researchers proposed heat conduction law to study heat transport phenomenon in the flow of fluids. First, Fourier [1] proposed a heat conduction theory. But its major drawback is that its energy equation is of parabolic type. To overcome this, Cattaneo [2] included relaxation time to the Fourier’s model and the new model is called the Maxwell–Cattaneo model. It was extended by Christov [3] by swapping the derivative with the Oldroyd upper convected model and then it is recognised as the Cattaneo–Christov temperature flux model. This phenomenon plays a vital role in various processes such as the sterilisation of milk, and for making microchips and electronic devises. Reddy et al [4] analysed the non-turbulent and time-dependent flow across three different geometries with an improved Fourier’s model. Ramandevi et al [5] compared the flow characteristics of the dual liquids, Casson and viscoelastic, by using the modified Fourier’s model. Irfan et al [6] obtained a numerical explanation for the three-dimensional (3D) flow of the Carreau fluid by the impact of homogeneous–heterogeneous reactions with the generalised Fourier’s model. Anantha Kumar et al [7] presented a dual solution for a magnetohydrodynamic (MHD) Cattaneo–Christov flow towards a wedge and a cone in the presence of thermal stratification. A numerical solution for the time-dependent motion of the Williamson fluid over a curved sheet with a modified Fourier’s law was obtained by Anantha Kumar et al [8].

The fluids which do not fulfil Newton’s law of viscosity are termed non-Newtonian. The Carreau liquid is a type of non-Newtonian liquid. Nowadays, many researchers have shown their interest in Carreau fluid flow due to its significances in various fields. Some examples of non-Newtonian fluids are sugar solutions, face creams, body lotions, chime, honey, glue, tooth paste, blood, chilli sauce, etc. There are so many applications of non-Newtonian fluids, motivated by which, Massoudi and Christie [9] reported a solution for the non-Newtonian liquid motion across a pipe with viscous dissipation and variable viscosity. Siddiqui et al [10] analytically explained the motion of a third-grade liquid on an inclined plane using a perturbation technique. Khan et al [11] presented the characteristics of stagnated motion of a non-Newtonian fluid such as the Carreau fluid subject to a convective boundary condition with the Runge–Kutta–Fehlberg method. The heat transfer phenomenon in 3D motion of the Carreau liquid with nonlinear radiation was observed by Khan et al [12]. Kumar et al [13] made a comparative study of the boundary layer motion due to an exponential stretched sheet. The flow characteristics of the MHD Carreau fluid with slip effects in the presence of variable thermal conductivity and frictional heat was reported by Shah et al [14].

The fluid motion across a stretched geometry with Lorentz force is significant in geophysics, medicine, aeronautics, biotechnology and astrophysics. Also it has immense significance in the manufacture of rubber dishes, missiles, polymers, strand casting and space vehicles. Magnetic field creates fluxes in the conducting fluid flow. MHD has application in droplet fitters, accelerators, magnetic drug treatment, flow meters, power production, plasma studies and MHD pumps. First, Crane [15] proposed a solution for the Blasius type of flow across a stretching plate. It was extended by Chiam [16] by considering the micropolar fluid. Chen and Char [17] determined the thermal transport characteristics of the motion across a linearly stretchable continuous surface by using Kummer’s functions. The influence of heat generation on the MHD motion of viscoelastic and incompressible liquid over a solid surface was discussed by Siddheswar and Mahabaleswar [18]. Anantha Kumar et al [19] studied the nature of the time-dependent flow of MHD non-Newtonian fluid flow over a curved surface with an irregular heat sink / source and chemical reaction. Babu and Sandeep [20] examined the effects of heat and mass transfer on the MHD flow caused by a coagulated sheet. They concluded that the performance of heat and mass transfer in Cu–water is higher than that of CuO–water. As an extension of this, Malik et al [21] considered the Carreau fluid flow by implementing an implicit finite-difference scheme. Sandeep [22] examined the characteristics of a thin film flow of a hybrid nanofluid across a stretching surface.

The phenomenon of an irregular heat sink / source has well-known implications in biomedical and many engineering activities like radial diffusers, the purpose of thrust bearing, crude oil retrieval, etc. Abel et al [23] studied the MHD boundary layer flow features of an unsteady non-Newtonian fluid over a stretched geometry under the impact of an uneven heat source / sink. It was extended to the impact of thermal radiation by Pal [24] with the aid of the Runge–Kutta–Fehlberg method. The influence of irregular heat parameters on the MHD Powell–Eyring fluid flow past a wedge was investigated by Reddy et al [25]. Further, Reddy et al [26] investigated the heat and mass transfer characteristics of Casson and Maxwell fluid flows with thermodiffusion.

The knowledge of heat and mass transfer has many applications in the engineering and paramedical fields. Power creation, heat exchangers, thermal conduction in tissues and electronic devices are a few industrial and ecological implications. Animasaun and Sandeep [27] reported the influence of Lorenz force and an irregular thermal source on a viscous fluid across a coagulated surface. A numerical study was conducted by Anantha Kumar et al [28] on the thermal transport features of MHD oblique stagnation point flow of a micropolar fluid over a stretching surface with the Runge–Kutta fifth-order method. Khan et al [29] studied the thermal and mass transport features of the Carreau nanofluid flow towards an inclined stretched cylinder under the impact of Joule heating. Ramadevi et al [30] studied the analytical solution of the effect of mass and heat transfer on Casson liquid motion affected by a wavy channel with the aid of perturbation technique. Anantha Kumar et al [31] discussed the effect of mass and thermal transfer on the viscoelastic fluid across a solid sheet with an exponential heat source.

The Joule heating is a phenomenon where the thermal energy is produced by an electric current on the conductor. It plays a vital role in huge industrial and trade applications such as in cuisines, iron manufacturing, electric coffee makers and purification. A study was conducted by Sulochana et al [32] on the influence of viscous heating and chemical response on the mixed convective motion of the Casson nanofluid across an inclined semi-infinite porous plate. For this study, they considered TiO\(_{2}\)–water and CuO–water. Lakshmi et al [33] discussed the mass transport characteristics of the chemically reacting Casson and Walters-B nanofluids across a nonlinear variable thickness stretching sheet. Anantha Kumar et al [34] gave a numerical explanation for the MHD motion of a ferrofluid towards a convective shrinking surface using the Runge–Kutta–Fehlberg technique. Mixed convective MHD third-grade liquid flow caused by an infinite sheet with radiation and convective condition was discussed by Hayat et al [35]. Furthermore, it was extended by Hayat et al [36] by considering both convective and diffusive boundary conditions. Ramadevi et al [37] and Anantha Kumar et al [38] examined the flow fields on the MHD non-Newtonian liquid across a stretching surface with a heat source / sink. The heat transfer features of particle–fluid suspension induced by a metachronal wave have been investigated by Bhatti et al [39] in the presence of Lorentz force and radiation. Khan et al [40] examined the 3D time-dependent flow of a Sisko nanofluid due to a stretching surface in the presence of nonlinear thermal radiation and chemical reaction.

To the best of our knowledge, it is clear that a few researchers concentrated on 3D MHD micropolar liquid due to the stretching of a surface. Also, to the best of our knowledge, no study was conducted on the influence of variable thermal conductivity on 3D MHD Carreau fluid flow caused by a stretching surface. Joule heating, chemical reaction, convective and diffusive boundary conditions are accounted. Similarity transmutations are applied to alter the flow governing nonlinear equations into coupled ordinary differential equations (ODEs). Runge–Kutta and shooting methods are utilised to obtain the solution. The influence of numerous physical variables on the distributions of velocity, temperature and concentration is presented using plots. Along with them, the rates of heat and mass transport and friction factors are presented in a separate table.

2 Formulation

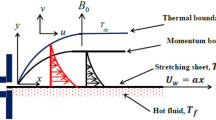
Consider the 3D flow of an incompressible MHD Carreau fluid across a bidirectional stretching sheet with Joule heating. Fluid motion is time-independent and laminar. The improved Fourier’s model is utilised to study the heat transport performance. We supposed the magnetic Reynolds number to be very small. We assumed that the surface is aligned with the xy plane and the flow is accounted in \(z>0\). The stretching velocities of the sheet are \(u_w =bx,v_w =by\), where b is a positive constant. A constant magnetic field of strength \(B_0 \) is exerted along the z-axis as shown in figure 1.

Based on the assumptions that the Carreau fluid flow is 3D, we have taken the modified Fourier’s law, variable thermal conductivity, Joule heating, irregular heat/sink and chemical reaction effects and by applying convective and diffusive boundary conditions to the boundary, the flow equations are

$$\begin{aligned}&\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0, \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial u}{\partial x}u+\frac{\partial u}{\partial y}v+\frac{\partial u}{\partial z}w\nonumber \\&\quad =\frac{\partial ^{2}u}{\partial z^{2}}\upsilon \left[ {1+\Gamma ^{2}\left( {\frac{\partial u}{\partial z}} \right) ^{2}} \right] ^{(n-1)/2} \nonumber \\&\qquad \quad +\,\Gamma ^{2}\left( {\frac{\partial u}{\partial z}} \right) ^{2}(n{-}1)\frac{\partial ^{2}u}{\partial z^{2}}\upsilon \left[ {\Gamma ^{2}\left( {\frac{\partial u}{\partial z}} \right) ^{\!\!2}{+}1} \right] ^{(n-3)/2}\nonumber \\&\qquad \quad -\,\frac{\sigma B_0^2 }{\rho }u, \end{aligned}$$
(2)
$$\begin{aligned}&\frac{\partial v}{\partial x}u+\frac{\partial v}{\partial y}v+\frac{\partial v}{\partial z}w=\frac{\partial ^{2}v}{\partial z^{2}}\upsilon \left[ {\Gamma ^{2}\left( {\frac{\partial v}{\partial z}} \right) ^{\!\!2}+1} \right] ^{(n-1)/2} \nonumber \\&\qquad +\,\Gamma ^{2}\left( {\frac{\partial v}{\partial z}} \right) ^{2}(n{-}1)\frac{\partial ^{2}v}{\partial z^{2}}\upsilon \left[ {\Gamma ^{2}\left( {\frac{\partial v}{\partial z}} \right) ^{\!\!2}+1} \right] ^{(n{-}3)/2}\nonumber \\&\qquad -\,\frac{\sigma B_0^2 }{\rho }v, \end{aligned}$$
(3)
Fig. 1
figure 1

Flow geometry.

Full size image
$$\begin{aligned}&\frac{\partial T}{\partial x}u+\frac{\partial T}{\partial y}v+\frac{\partial T}{\partial z}w= \frac{1}{\rho c_p }\frac{\partial }{\partial z}\left( {k(T)\frac{\partial T}{\partial z}} \right) +\frac{k(T) U_w }{x \upsilon }( A^{{*}}(T_w -T_\infty ){f}' \nonumber \\&\quad +B^{{*}}(T-T_\infty ) )+\,\frac{\sigma B_0^2 }{\rho c_p }( {u^{2}+v^{2}} ) \nonumber \\&\quad +\,\lambda \left( {\begin{array}{l} \dfrac{\partial ^{2}T}{\partial x^{2}}u^{2}+\dfrac{\partial ^{2}T}{\partial y^{2}}v^{2}+\dfrac{\partial ^{2}T}{\partial z^{2}}w^{2}+\dfrac{\partial ^{2}T}{\partial x\partial y}2uv \\ +\dfrac{\partial ^{2}T}{\partial y\partial z}2vw+\dfrac{\partial ^{2}T}{\partial x\partial z}2uw+\dfrac{\partial T}{\partial x}\left( {\dfrac{\partial u}{\partial x}u+\dfrac{\partial u}{\partial y}v+\dfrac{\partial u}{\partial z}w} \right) \\ +\dfrac{\partial T}{\partial y}\left( {\dfrac{\partial v}{\partial x}u+\dfrac{\partial v}{\partial y}v+\dfrac{\partial v}{\partial z}w} \right) +\dfrac{\partial T}{\partial z}\left( {\dfrac{\partial w}{\partial x}u+\dfrac{\partial w}{\partial y}v+\dfrac{\partial w}{\partial z}w} \right) \\ \end{array}} \right) , \end{aligned}$$
(4)
$$\begin{aligned}&\frac{\partial C}{\partial x}u+\frac{\partial C}{\partial y}v+\frac{\partial C}{\partial z}w=D_m \frac{\partial ^{2}C}{\partial z^{2}}-k^{*}\left( {C-C_\infty } \right) .\nonumber \\ \end{aligned}$$
(5)

The restrictions of the problem are

$$\begin{aligned} \left. {\begin{array}{ll} \left. {\begin{array}{ll} u_w (x)=u,\, \,v_w (y)=v, w=0,\,\, T=T_w ,\\ C=C_w,\, \, -\,k(T)\displaystyle \frac{\partial T}{\partial z}=h_1 \left( {T_w -T} \right) , \\ -D_m \displaystyle \frac{\partial C}{\partial z}=h_2 \left( {C_w -C} \right) , \\ \end{array}} \right\} \hbox {at} \quad z=0 \\ u\rightarrow 0, v\rightarrow 0, T\rightarrow T_\infty , C\rightarrow C_\infty \quad \hbox {as} \quad z\rightarrow \infty . \\ \end{array}} \right\} \end{aligned}$$
(6)
Fig. 2
figure 2

Impact of M on (a) the velocity field in the x direction, (b) the velocity field in the y direction, (c) thermal field and (d) concentration field.

Full size image
Fig. 3
figure 3

Impact of (a) \(W_1 \) on the velocity field in the x direction and (b) \(W_2 \) on the velocity field in the y direction.

Full size image

Here \(\left( {u,v,w} \right) \), respectively, are the velocity components along \(\left( {x,y,z} \right) \), \(\upsilon \) is the kinematic viscosity, \(\Gamma \) is the material constant, n is the velocity power index parameter, \(\sigma \) is the electrical conductivity, \(\rho \) is the Carreau fluid density, \(c_p \) is the heat capacitance, T is the temperature, \(\lambda \) is the relaxation time, \(A^{*}\,\, \hbox {and}\,B^{*}\) represent the irregular heat parameters, C is the concentration of Carreau fluid, \(D_m \) is the mass diffusivity and \(k^{*}\) is the dimensional chemical reaction variable, \(h_1 \) and \(h_2 \) are the convective components of heat and mass.

Here k(T) is the temperature-dependent thermal conductivity and it can be defined as

$$\begin{aligned} k(T)=k_\infty \left( {1+\varepsilon \left( {\frac{T-T_\infty }{T_w -T_\infty }} \right) } \right) . \end{aligned}$$
(7)

Here \(k_\infty \) is the ambient fluid thermal conductivity, \((T_w ,T_\infty )\), respectively, are the near and ambient fluid temperatures and \(\varepsilon \) is the smallest scalar quantity.

Now, we introduce suitable similarity transformations for u, v, w, T and C as

$$\begin{aligned} \left. {\begin{array}{ll} u= &{} {F}'(\eta )ax,\quad v={G}'(\eta )ay, \\ &{}w=-\left( {F(\eta )+G(\eta )} \right) \sqrt{a\upsilon }, \\ \eta = &{} \sqrt{\displaystyle \frac{a}{\upsilon }} z,T=T_\infty +\theta (\eta )\left( {T_w -T_\infty } \right) ,\\ {} &{}C=C_\infty +\phi (\eta )\left( {C_w -C_\infty } \right) . \\ \end{array}} \right\} \end{aligned}$$
(8)

From eq. (8), eq. (1) is satisfied automatically and eqs (2)–(5) become

$$\begin{aligned}&{F}'''\left[ {1+nW_1 ^{2}{F}''^{2}} \right] \left[ {1+W_1 ^{2}{F}''^{2}} \right] ^{(n-3)/2}\nonumber \\&\quad +\,{F}''(F+G)-M{F}'-{F}'^{2}=0, \end{aligned}$$
(9)
$$\begin{aligned}&\left[ {1+nW_2 ^{2}{G}''^{2}} \right] \left[ {1+W_2 ^{2}{G}''^{2}} \right] ^{(n-3)/2}{G}'''\nonumber \\&\quad +\,(F+G){G}''-M{G}'-{G}'^{2}=0, \end{aligned}$$
(10)
$$\begin{aligned}&\varepsilon {\theta }'^{2}+(1+\varepsilon \theta ){\theta }''+\Pr (F+G){\theta }' \nonumber \\&\quad +\,\beta \Pr \left( {(G+F){\theta }'({G}'+{F}')+(F+G)^{2}{\theta }''} \right) \nonumber \\&\quad +\,(1+\varepsilon \theta )\left( {A^{*}{F}'+B^{*}\theta } \right) \nonumber \\&\quad +\,M\Pr \left[ {\hbox {Ec}_1 {F}'^{2}+\hbox {Ec}_2 {G}'^{2}} \right] =0, \end{aligned}$$
(11)
$$\begin{aligned}&{\phi }''+\hbox {Sc}(F+G){\phi }'-K_l \hbox {Sc}\phi =0. \end{aligned}$$
(12)

The transformed restrictions of the boundary are

$$\begin{aligned} \left. {\begin{array}{l} F(0)=0,\quad {F}'(0)=\gamma ,\quad {G}'(0)=\gamma ,\quad G(0)=0,\\ (1+\varepsilon \theta ){\theta }'=-(1-\theta )\hbox {Bi}_\mathrm{T},\\ {\phi }'=-\hbox {Bi}_\mathrm{C} (1-\phi )\quad \hbox {at }\eta =0, \\ {F}'\rightarrow 0, \quad {G}'\rightarrow 0, \quad \theta \rightarrow 0,\quad \phi \rightarrow 0 \quad \hbox {as} \,\eta \rightarrow \infty . \\ \end{array}} \right\} \end{aligned}$$
(13)

Here \(W_1 ,W_2 \) are the Weissenberg numbers, M is a parameter related to the magnetic force, \(\Pr ,\hbox {Ec}_1 ,\hbox {Ec}_2 ,\hbox {Sc}\), respectively, are the Prandtl, Eckert and Schmidt numbers, \(\beta ,\gamma ,K_l \), respectively, the thermal relaxation, stretching ratio and chemical reaction parameters and \(\hbox {Bi}_\mathrm{C} ,\hbox {Bi}_\mathrm{T} \) are the solutal and thermal Biot numbers, respectively. These can be defined as

$$\begin{aligned} \left. {\begin{array}{ll} \displaystyle W_1 = \sqrt{\frac{\Gamma ^{2}ab^{2}x^{2}}{\upsilon }},W_2 =\sqrt{\frac{\Gamma ^{2}ab^{2}y^{2}}{\upsilon }},\\ \displaystyle M=\frac{\sigma B_0^2 }{a\rho },\quad \Pr =\frac{\mu C_p }{k_\infty },\\ \displaystyle \beta =a\lambda ,\quad \delta =\frac{Q_0 }{a\rho c_p },\quad \hbox {Sc}=\frac{\upsilon }{D_m }, \\ \displaystyle \hbox {Ec}_1 = \frac{(u_w )^{2}}{c_p \left( {T_w -T_\infty } \right) },\hbox {Ec}_2 =\frac{(v_w )^{2}}{c_p \left( {T_w -T_\infty } \right) },\\ \displaystyle K_l =\frac{k^{*}}{a},\quad \gamma =\frac{b}{a},\quad \hbox {Bi}_\mathrm{T} =\frac{h_1 }{k_\infty }\sqrt{\frac{\upsilon }{a}},\\ \displaystyle \hbox {Bi}_C =\frac{h_2 }{D_m }\sqrt{\frac{\upsilon }{a}}. \\ \end{array}} \right\} \end{aligned}$$
(14)

With regard to engineering, the physical quantities such as rates of heat and mass transport, friction factors along x, y directions can be defined as

$$\begin{aligned} C_{f_x }= & {} \frac{2\tau _{xz} }{\rho U_w^2 },\quad C_{f_y } =\frac{2\tau _{yz} }{\rho U_w^2 },\quad \hbox {Nu}=\frac{xq_w }{k_\infty \left( {T_w -T_\infty } \right) }, \nonumber \\ \hbox {Sh}= & {} \frac{xq_m }{D_m \left( {C_w -C_\infty } \right) }, \end{aligned}$$
(15)

where \(\tau _{xz} \) and \(\tau _{yz} \) are shear rates along the \(x\hbox { and }y\) directions, respectively, \(q_w =-k(T)\left( {\partial T/\partial z} \right) _{z=0} \) is the surface heat flux and \(q_m =-D_m\left( {\partial C/\partial z} \right) _{z=0} \) is the surface mass flux.

On using eq. (8), eq. (14) takes the following form:

$$\begin{aligned} \left. {\begin{array}{l} \frac{1}{2}C_{f_x } \mathrm{Re}_x^{1/2} =\left( {1+W_1 ^{2}{F}''^{2}} \right) ^{(n-1)/2}{F}''(0),\\ \frac{1}{2}C_{f_y } \mathrm{Re}_x^{1/2} =\left( {1+W_2 ^{2}{G}''^{2}} \right) ^{(n-1)/2}{G}''(0), \\ \mathrm{Re}_x^{{-1}/2} \hbox {Nu}=-(1+\varepsilon \theta ){\theta }'(0),\,\, \mathrm{Re}_x^{{-1}/2} \hbox {Sh}=-{\phi }'(0), \\ \end{array}} \right\} \end{aligned}$$
(16)

where \(\mathrm{Re}_x =ax^{2}/\upsilon \) is the local Reynolds number.

3 Discussion of results

Equations (9)–(13) are highly nonlinear and coupled ODEs. An analytical solution is not possible. Here, we use a fourth-order Runge–Kutta-based shooting technique to obtain a solution for the problem. The figures are plotted to show the behaviour of velocities, temperature and concentration with various values of flow-regulating parameters. Along with the skin-friction coefficients, the rates of heat and mass transfer are also analysed and presented with the aid of a table. For the results, we kept the parameters as constants like \(\hbox {Ec}=0.5, n=1.5, \varepsilon =0.3, \hbox {Pr}=7, \beta =0.2, A^{*}=0.2,B^{*}=0.2,\hbox {Sc}=0.7,W=2, K_l =0.5, \gamma =0.3,\hbox {Bi}_\mathrm{T} =0.5\, \mathrm{and}\, \hbox {Bi}_\mathrm{C} =0.5\). In all the plots, \({F}'(\eta ),{G}'(\eta ),\theta (\eta )\) and \(\phi (\eta )\), respectively, are the curves of velocities along \(x\, \mathrm{and} \,y\) directions, under constant temperature and concentration.

Fig. 4
figure 4

Impact of (a) \(\varepsilon \), (b) \(\hbox {Pr}\) and (c) \(\beta \) on thermal fields.

Full size image
Fig. 5
figure 5

Impact of n on (a) the velocity field in the x directiion and (b) the velocity field in the y direction.

Full size image
Fig. 6
figure 6

Impact of (a) \(A^{*}\) on the thermal field and (b) \(B^{*}\) on the thermal field.

Full size image
Fig. 7
figure 7

Impact of (a) \(\hbox {Bi}_\mathrm{T} \) on the thermal field and (b) \(\hbox {Bi}_\mathrm{C} \) on the concentration field.

Full size image
Fig. 8
figure 8

Impact of (a) \(\hbox {Sc}\) on the concentration field and (b) \(K_l \) on the concentration field.

Full size image

Figure 2 presents the plots for the profiles of velocities in the \(x\hbox { and }y\) directions, under constant temperature and concentration for different values of magnetic field. Profiles of velocities are diminished and thermal and solutal curves are enhanced with increasing values of M. An increase in magnetic field gives Lorentz force, which has the propensity to oppose the movement of the liquid atoms and that way, the fluid velocity drops in both directions. Also, it imparts heat to the particles of the fluid, so that the temperature is enhanced as it consequently hikes the concentration.

Figure 3 is depicted to discern the influence of \({F}'(\eta )\) and \({G}'(\eta )\) on the Weissenberg numbers \(W_1 \) and \(W_2 \). The curves of velocity are enhanced in the \(x \hbox { and }y\) directions with increasing values of \(W_1 \) and \(W_2 \). Actually, Weissenberg number is proportional to the time persistent and inversely proportional to the viscosity of the liquid. For a large Weissenberg number, the fluid has less viscosity. Therefore, it causes a boost in velocity profiles.

The influence of the temperature-dependent thermal conductivity parameter (\(\varepsilon )\), Pr and thermal relaxation time (\(\beta )\) on the distribution of heat is shown in figure 4. Increasing values of \(\varepsilon \) yield an enhancement in the heat function (see figure 4a). Figure 4b shows the effect of temperature on Pr and that fluid temperature is a reducing function of Pr. The effect of thermal relaxation variable on the temperature profile can be seen in figure 4c. Here, we see that the heat function is an increasing factor of \(\beta \). Generally, relaxation time is nothing but the time taken by the elements of the fluid to transmit thermal energy to the neighbouring ones. So we observe a decrement in \(\theta (\eta )\) but it shows an opposite behaviour due to the impact of other parameters.

Figure 5 is designed for profiles of velocities along with the velocity power index parameter (n). Boosting values of n raise the velocities in both directions. For accelerating values of n, the elongating velocity surpasses the unrestricted velocity. This result shows an improvement in velocity profiles.

The impacts of temperature and irregular heat parameters are portrayed in figure 6. The heat function and irregular heat factors are proportional to each other. The positive values of irregular heat parameters act as heat generators. So the the boundary layer releases a big amount of thermal energy to the flow from which, we observe an enhancement in the temperature of the fluid. Hence temperature profiles are uplifted with temperature- and space-dependent heat source / sink parameters.

Figure 7 is sketched to see the impact of temperature-dependent Biot number on temperature profiles. An elevating value of Biot number raises the temperature profiles (see figure 7a). The impact on concentration profiles with concentration-dependent Biot number can be seen in figure 7b. From this figure, it is clear that an increasing value of this number enhances the concentration profiles. Generally, temperature- and concentration-dependent Biot numbers are directly correlated with the convective solutal and thermal coefficients \(h_1 \) and \(h_2 \), respectively, and, as a result, we found an improvement in the temperature and concentration fields.

Figure 8 shows a variation in the concentration field for numerous values of \(\hbox {Sc}\) and the chemical reaction parameter (\(K_l )\). The curves of concentration are diminished with enhancing values of \(\hbox {Sc and }K_l \). Physically, \(\hbox {Sc}\) is a quotient of rate of viscous diffusion to the rate of molecular diffusion. Hence, a large Sc improves the rate of viscous diffusion. For increasing values of chemical reaction parameter, we see that there is a hike in the interfacial mass transfer. Therefore, the concentration profiles decrease with these parameters.

Fig. 9
figure 9

Impact of (a) \(\hbox {Ec}_1 \) and (b) \(\hbox {Ec}_2 \) on the thermal field.

Full size image
Fig. 10
figure 10

Impact of \(\gamma \) on (a) the velocity field in the x direction, (b) the velocity field in the y direction, (c) the thermal field and (d) the concentration field.

Full size image
Table 1 Numerical values of friction factors, heat and mass transfer coefficients with the flow-regulating parameters.
Full size table

The influence of Ec on the curves of temperature can be seen in figure 9. It is interesting to note that heat function is a growing factor of \(\hbox {Ec}_1 \hbox { and Ec}_2 \). The ratio of the kinetic energy and enthalpy change is known as Ec. So, kinetic energy improved with advanced values of the viscous heating parameter. Hence, the thermal boundary layer and its thickness are increasing factors of \(\hbox {Ec}_1 \) and \(\hbox {Ec}_2 \).

Figure 10 shows the consequence of the constraint related to the stretching ratio on the flow fields of the Carreau fluid. All the profiles are enhanced with higher values of \(\gamma \) with the exception of mass function. Actually, an enlargement in the velocity ratio parameter developed more compression on the stretching sheet and, consequently, we found that the temperature decreases and the velocity profiles improve in both directions. As a result, concentration also decreases. But, here in the case of temperature profiles we have seen an opposite outcome, which is due to the impact of other parameters.

The variation in friction factors and measure of thermal plus mass transport with various non-dimensional parameters is observed in table 1. All the four physical quantities are reduced due to the Lorentz force. Weissenberg number and the physical quantities (friction factors, heat and mass transfer rates) are proportional to each other. All the physical quantities are enhanced with the power law index parameter except the heat transfer coefficient. The heat transfer coefficient is inversely proportional to both the thermal relaxation parameter and irregular heat parameters. Also, it is directly proportional to the temperature-dependent Biot number. The mass transfer coefficient is proportional to \(\hbox {Sc},K_l ,\hbox {Bi}_\mathrm{C} \). The mass transfer rates enhance with the stretching ratio parameter and a reverse trend is noticed in all other quantities.

4 Conclusions

In this study, a numerical solution for the 3D MHD flow of the Carreau fluid over a stretching sheet with the heat and mass transfer phenomenon has been investigated. An improved heat flux model is utilised to deliberate the concept of heat transfer. The influence of an irregular heat sink / source, chemical reaction and Joule heating is considered. The converted equations are solved using shooting and fourth-order Runge–Kutta methods. The main points are given below:

  • Accelerating values of \(W_1 \hbox { and }W_2 \) decrease the fluid velocity in both directions.

  • The nature of the velocity profiles and friction factors is similar in both \(x\hbox { and }y\) directions.

  • The local Nusselt and Sherwood numbers are directly proportional to the chemical reaction parameter, Sc, power index parameter and stretching ratio parameter.

  • All the physical quantities are decelerating factors of the magnetic field parameter.

  • The irregular heat parameters play a vital role in the thermal and mass transport performance.

  • Fluid temperature is an escalating function of Ec and thermal relaxation parameter.