Estimation of multicomponent stress-strength reliability based on a bivariate Topp-Leone distribution

Abstract

In this endeavour, we study the statistical inference of multicomponent stress-strength reliability when components of the system have two paired elements experiencing common random stress. The k strength variables $(X_1,Y_1),\ldots ,(X_k,Y_k)$ follow a bivariate Topp-Leone distribution and the stress variable which follows a Topp-Leone distribution. This system is unfailing when at least $s(1\le s\le k)$ out of k components simultaneously activate. The maximum likelihood estimate along with its asymptotic confidence interval, the uniformly minimum variance unbiased estimate, and the exact Bayes estimate of stress-strength reliability are derived. Further, we determined the Bayes estimates of the stress-strength reliability via different methods such as the Tierney and Kadane approximation, Lindley’s approximation, and the Markov Chain Monte Carlo (MCMC) method, to compare their performances with the exact Bayes estimate. Also, the highest probability density credible interval is obtained using the MCMC method. Monte Carlo simulations are implemented to compare the different suggested methods. Ultimately, the analysis of one real data is investigated for illustrative purposes.

1 Introduction

The study of resistance of systems with random stress X and random strength Y in reliability literature is well-known as the stress-strength model, while the parameter $R=P(X<Y)$ assesses the reliability of the system. This system fails if $X>Y$. The problem of estimating the parameter R plays a significant role in reliability analysis. This has been discussed by a great number of authors. A comprehensive review of different stress-strength models up to 2003 has been presented in [1]. Recently, the reliability of multicomponent stress-strength models has attracted the attention of researchers. This model consists of the k independent and identical strength components and survives when at least $s(1\le s\le k)$ components persist against a common stress. The stress-strength reliability for such a system is known as the s-out-of-k: G system and it is given by $R_{s,k}$. The recent efforts in multicomponent stress-strength models are [2,3,4,5,6,7,8,9,10,11,12].

In most of the work related to the reliability of multicomponent stress-strength models, the system components have only one element, whereas in real-life each component may consist of more than one element. These types of situations may be seen in many real-life scenarios. For example, it can be used in the construction of suspended bridges, where the deck is sustained by a series of vertical cables which hang from the towers. Assume a suspension bridge is made of k pairs of vertical cables on either side of the deck. Here, each component consists of two dependent elements. The bridge will only stand when at least s number of vertical cables through the deck exceed the applied stresses such as heavy traffic, wind forces, corrosion, and so on.

In this paper, we assume that the strength variables $(X_1,Y_1),\ldots ,(X_k,Y_k)$ are independent and identically distributed random variables that following the bivariate Topp-Leone (BTL) distribution and are statistically independent with random stress that follows the Topp-Leone (TL) distribution. Recently, the estimation of multicomponent stress-strength reliability when the stress and strength variables follow Kumaraswamy and bivariate Kumaraswamy distributions, respectively, was studied in [13].

The TL distribution was first introduced by [14]. This is one of the distributions having finite support used to model percentage data, rates, and data extracted from some chemical processes. The main application of the TL distribution is when the reliability is assessed as the ratio of the number of successful experiments to the total number of experiments [15].

A random variable X has the TL distribution with the shape parameter $\theta$ if its probability density function (PDF) is specified by

$$\begin{aligned} f_X(x;\theta )=2\theta (1-x)\bigl [x(2-x)\bigr ]^{\theta -1},\qquad \theta >0,\quad 0<x<1. \end{aligned}$$

(1)

The cumulative distribution function (CDF) and survival function corresponding to Eq. (1), are

$$\begin{aligned} F_X(x;\theta )=\bigl [x(2-x)\bigr ]^{\theta }, \end{aligned}$$

(2)

and

$$\begin{aligned} {\bar{F}}_X(x;\theta )=1-\bigl [x(2-x)\bigr ]^\theta , \end{aligned}$$

(3)

respectively. From here on, the TL distribution will be signified with the PDF in Eq. (1), by $TL(\theta )$. Recently, the problem of $R_{s,k}$ in the multicomponent stress-strength model when stress and strength variables are from TL distributions considered in [16]. In this study, the MLE of $R_{s,k}$ was computed. Also, the Bayes estimates of the system reliability were determined by using the MCMC method and Lindley’s approximation. However, a UMVUE and an exact Bayes estimate of $R_{s,k}$ were not taken into consideration.

The main goal of this paper is to discuss the classical and Bayesian inferences of $R_{s,k}$ when strength variables follow the BTL distribution and the stress variable follows the TL distribution. The remainder of the paper is as follows. In Sect. 2, system reliability is determined. In Sect. 3, the MLE with the asymptotic confidence interval (ACI) and the UMVUE of $R_{s,k}$ are investigated. In Sect. 4, the Bayes estimator of $R_{s,k}$ is determined explicitly. Further, to compare other methods of the Bayesian estimates with the exact, the Tierney and Kadane method, Lindley’s approximation, and the MCMC method are used to obtain the Bayes estimates of $R_{s,k}$. Also, the highest probability density credible interval (HPDCI) is provided in this section. In Sect. 5, the proposed methods are compared via MCMC simulations. In Sect. 6, a real data is given to demonstrate the suggested approaches. In Sect. 7, we extend the studied methods to a general family of distributions. Finally, we conclude the paper in Sect. 8.

2 System reliability

In this section, we first describe the BTL distribution and then obtain $R_{s,k}$. Suppose $V_1,V_2$, and $V_3$ follow $TL(\alpha _1)$, $TL(\alpha _2)$, and $TL(\alpha _3),$ respectively and all three random variables are mutually independent. Define the random variables X and Y as

$$\begin{aligned} X=\max \{V_1,V_2\},\qquad Y=\max \{V_2,V_3\}, \end{aligned}$$

where X and Y have a common random variable $V_3$, making it clear that they are dependent. So the bivariate vector (X, Y) is the BTL distribution with the parameters $\alpha _1,\alpha _2,\alpha _3$ and it is denoted by $BTL(\alpha _1,\alpha _2,\alpha _3)$. Using the above definition, the following theorems can be easily proved.

Theorem 1

If $(X,Y)\sim BTL(\alpha _1,\alpha _2,\alpha _3)$, then their joint CDF is given by

$$\begin{aligned} F_{(X,Y)}(x,y)=\bigl [x(2-x)\bigr ]^{\alpha _1}\bigl [y(2-y)\bigr ]^{\alpha _2}\bigl [u(2-u)\bigr ]^{\alpha _3}, \end{aligned}$$

(4)

where $u=\min (x,y)$.

Proof

$$\begin{aligned} F_{(X,Y)}(x,y)&=P(X<x,Y<y)=P\bigl (\max (V_1,V_3)<x,\max (V_2,V_3)<y\bigr )\\&=P(V_1<x)P(V_2<y)P(V_3<\min (x,y))\\&=F_{V_1}(x;\alpha _1)F_{V_2}(y;\alpha _2)F_{V_1}(u;\alpha _3). \end{aligned}$$

Substituting Eq. (3) into the above equation, the proof is obtained. Note that the random variable X and Y are independent iff $\alpha _3=0$. $\square$

Theorem 2

If $(X,Y)\sim \text {BTL}(\alpha _1,\alpha _2,\alpha _3)$, then

• (a) $X\sim \text {TL}(\alpha _1)$ and $Y\sim \text {TL}(\alpha _2+\alpha _3)$.

• (b) $\max (X,Y)\sim \text {TL}(\alpha )$, where $\alpha =\alpha _1+\alpha _2+\alpha _3$.

Proof

(a)

$$\begin{aligned} F_X(x)=P(X<x)&=P\bigl [\max (V_1,V_3)<x\bigr ]\\&=P(V_1<x)P(V_3<x)=F_{V_1}(x;\alpha _1)F_{V_3}(x;\alpha _3) . \end{aligned}$$

Substituting Eq. (3) into the above equation, we get $X\sim TL\left( {{\alpha }_{1}}+{{\alpha }_{3}} \right)$. Similarly, $Y\sim TL\left( {{\alpha }_{2}}+{{\alpha }_{3}} \right)$ is proved.

(b)

$$\begin{aligned} P[\max (X,Y)<x]=P(X<x,Y<x)=F_{(X,X)}(x,x)=F_X(x;\alpha ). \end{aligned}$$

(5)

Now, we consider a system having k identical and independent strength components, creating a parallel system of dependent elements experiencing common stress. Here, the strength vectors $(X_1,Y_1),\ldots ,(X_k,Y_k)$ follow $BTL(\alpha _1,\alpha _2,\alpha _3)$ and a common stress variable T follows $TL(\beta )$. Hence the reliability in a multicomponent stress-strength model is given by

$$\begin{aligned} R_{s,k}=P\bigl (T<\max (X_i,Y_i)\bigr ),\qquad i=1,2,\ldots ,k. \end{aligned}$$

Let $Z_i=\max (X_i,Y_i),i=1,\ldots ,k$, therefore, according to Theorem 2(b), ${{Z}_{i}}\sim TL\left( \alpha \right)$ and then $R_{s,k}=P(T<Z_i),i=1,\ldots ,k$. The system works if at least s out of $k(1\le s\le k)$ of the $Z_i$ strength variables simultaneously survive. Suppose k strength $(Z_1,\ldots ,Z_k)$ components are independent and identically distributed random variables with CDF F(z) and the stress T is a random variable with the CDF F(t). Hence, the reliability of $R_{s,k}$ introduced by [17], can be obtained as

$$\begin{aligned} R_{s,k}&=P\left[ \text {at least}\ s\ \text {of}\ (Z_1,\ldots , Z_k)\ \text {exceed}\ T\right] \nonumber \\&=\sum _{i=s}^{k}\left( {\begin{array}{c}k\\ i\end{array}}\right) \int _0^\infty \bigl [1-F_Z(t)\bigr ]^{k-i}\bigl [F(t)\bigr ]^{k-i}{\text {d}}G(t)\nonumber \\&=\sum _{i=s}^{k}\sum _{j=0}^{i}\left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) \frac{(-1)^j\beta }{\alpha (k+j-i)+\beta }. \end{aligned}$$

(6)

Note that the potential data are as follows

$$\begin{aligned} \begin{bmatrix} x_{11}&{}x_{12}&{}\cdots &{}x_{1k}\\ x_{21}&{}x_{22}&{}\cdots &{}x_{2k}\\ \cdot &{}\cdot &{}\ddots &{}\cdot \\ x_{n1}&{}x_{n2}&{}\cdots &{}x_{nk}\\ \end{bmatrix}, \begin{bmatrix} y_{11}&{}y_{12}&{}\cdots &{}y_{1k}\\ y_{21}&{}y_{22}&{}\cdots &{}y_{2k}\\ \cdot &{}\cdot &{}\ddots &{}\cdot \\ y_{n1}&{}y_{n2}&{}\cdots &{}y_{nk}\\ \end{bmatrix}, \text {and} \begin{bmatrix} t_1\\ t_2\\ \cdot \\ t_n \end{bmatrix}, \end{aligned}$$

but the actual observations can be constructed as

$$\begin{aligned} \begin{bmatrix} z_{11}&{}z_{12}&{}\cdots &{}z_{1k}\\ z_{21}&{}z_{22}&{}\cdots &{}z_{2k}\\ \cdot &{}\cdot &{}\ddots &{}\cdot \\ z_{n1}&{}z_{n2}&{}\cdots &{}z_{nk}\\ \end{bmatrix}\text {and} \begin{bmatrix} t_1\\ t_2\\ \cdot \\ t_n \end{bmatrix}, \end{aligned}$$

(7)

where $z_{ij}=\max (x_{ij},y_{ij})$, $i=1,\ldots ,n$, and $j=1,\ldots ,k$. $\square$

3 Classical estimates of $R_{s,k}$

In this section, we investigate the MLE of $R_{s,k}$ along with its ACI. Also, we obtain the UMVUE of $R_{s,k}$.

3.1 MLE of $R_{s,k}$

To find the MLE of $R_{s,k}$, we need to determine the MLEs of $\alpha$ and $\beta$. The likelihood function based on Eq. (7) is

$$\begin{aligned} L(\alpha ,\beta \vert {\varvec{z}},{\varvec{t}})=&\prod _{i=1}^{n}\Bigl (\prod _{j=1}^{k}f(z_{ij})\Bigr )g(t_i)\nonumber \\ =\,&2^{n(k+1)}\alpha ^{nk}\beta ^n\Bigl (\prod _{i=1}^{n}\prod _{j=1}^{k}(1-z_{ij})\Bigr ) \Bigl (\prod _{i=1}^{n}\prod _{j=1}^{k}\bigl [z_{ij}(2-z_{ij})\bigr ]^{\alpha -1}\Bigr )\nonumber \\&\times \Bigl (\prod _{i=1}^{n}(1-t_i)\Bigr )\Bigl (\prod _{i=1}^{n}\bigl [t_i(2-t_i) \bigr ]^{\beta -1}\Bigr ), \end{aligned}$$

(8)

and the log-likelihood function is

$$\begin{aligned} l(\alpha ,\beta \vert {\varvec{z}},{\varvec{t}})=\,&nk\ln (\alpha )+n\ln (\beta )+ \sum _{i=1}^{n}\sum _{j=1}^{k}\ln (1-z_{ij})\nonumber \\&+(\alpha -1) \sum _{i=1}^{n}\sum _{j=1}^{k}\ln \bigl [z_{ij}(2-z_{ij})\bigr ]\nonumber \\&+\sum _{i=1}^{n}\ln (1-t_i)+(\beta -1)\sum _{i=1}^{n}\ln \bigl [t_i(2-t_i)\bigr ]+c, \end{aligned}$$

(9)

where c is constant. So, the MLEs of $\alpha$ and $\beta$ can be computed as the solution of the following equations

$$\begin{aligned}&\frac{\partial l}{\partial \alpha }=\frac{nk}{\alpha }+ \sum _{i=1}^{n}\sum _{j=1}^{k}\ln \bigl [z_{ij}(2-z_{ij})\bigr ]=0,\\&\frac{\partial l}{\partial \beta }=\frac{n}{\beta }+ \sum _{i=1}^{n}\ln \bigl [t_i(2-t_i)\bigr ]=0. \end{aligned}$$

Thus,

$$\begin{aligned} {\hat{\alpha }}=\frac{nk}{P},\qquad {\hat{\beta }}=\frac{n}{Q} \end{aligned}$$

(10)

where $P=\sum _{i=1}^{n}\sum _{j=1}^{k}\ln \bigl [z_{ij}(2-z_{ij})\bigr ]$ and $Q=-\sum _{i=1}^{n}\ln \bigl [t_i(2-t_i)\bigr ]$.

It should be noted that, since $0<t<1$, then $0<t(2-t)=1-(t-1)^2<1$ and $\ln \bigl [t(2-t)\bigr ]<0$, so we always have $Q>0$. In a similar process $P>0$. Therefore, ${\hat{\alpha }}$ and ${\hat{\beta }}$ are indeed the MLEs of $\alpha$ and $\beta$, respectively. Also, it can be shown that If ${{X}_{1}},...,{{X}_{n}}\sim TL\left( \alpha \right) ,$ then $-\sum \nolimits _{i=1}^{n}{\ln \left[ {{X}_{i}}\left( 2-{{X}_{i}} \right) \right] }\sim Gamma\left( n,\alpha \right) .$ For this, it is sufficient to show that $-\ln \bigl [X(2-X)\bigr ]$ has an exponential distribution with parameter $\alpha$. To find the PDF for $Y=g(X)=-\ln \bigl [X(2-X)\bigr ]$, we first find $g^{-1}(x)$. Since $y=g\left( x \right) =\ln \left[ x\left( 2-x \right) \right]$, then $x={{g}^{-1}}\left( y \right) =1-\sqrt{1-{{e}^{y}}}.$ So, by using the change of variable technique, we have

$$\begin{aligned} f_Y(y)&=\left| \frac{{\text {d}}}{{\text {d}}y} \bigl (g^{-1}(y)\bigr )\right| f_X\bigl (g^{-1}(y)\bigr )\\&=\left| -\frac{e^{-y}}{2\sqrt{1-e^{-y}}}\right| \times 2\alpha \sqrt{1-e^{-y}}(e^{-y})^{\alpha -1}\\&=\alpha e^{-\alpha y}\sim \text {exponential}(\alpha ). \end{aligned}$$

Thus, it can be concluded that $P\sim Gamma( nk,\alpha )$ and $Q\sim Gamma( n,\beta )$.

In the following, the MLE of $R_{s,k}$ is computed from Eq. (6) by the invariant property of MLEs:

$$\begin{aligned} {\hat{R}}^{MLE}_{s,k}=\sum _{i=1}^{n}\sum _{j=1}^{k} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) \frac{(-1)^j{\hat{\beta }}}{{\hat{\alpha }}(k+j-i)+{\hat{\beta }}}. \end{aligned}$$

(11)

Now, the ACI of $R_{s,k}$ can be obtained using the asymptotic distribution of $\theta =(\alpha ,\beta )$. The expected Fisher information matrix of $\theta$ is defined as

$$\begin{aligned} I(\theta )= \begin{bmatrix} -\frac{\partial ^2l}{\partial \alpha ^2}&{}-\frac{\partial ^2l}{\partial \alpha \partial \beta }\\ -\frac{\partial ^2l}{\partial \beta \partial \alpha }&{}-\frac{\partial ^2l}{\partial \beta ^2} \end{bmatrix}=E(A), \end{aligned}$$

where $a_{11}=\frac{nk}{\alpha ^2},a_{22}=\frac{n}{\beta ^2},$ and $a_{12}=a_{21}=0$.

The MLE of $R_{s,k}$ is asymptotically normal with the mean $R_{s,k}$ and variance

$$\begin{aligned} H=\sum _{i=1}^{2}\sum _{j=1}^{2} \frac{\partial R_{s,k}}{\partial \theta _i} \frac{\partial R_{s,k}}{\partial \theta _j}A^{-1}_{ij}, \end{aligned}$$

where $A^{-1}_{ij}$ is the (i, j) th element of the inverse of A.

Also,

$$\begin{aligned}&\frac{\partial R_{s,k}}{\partial \alpha }= \sum _{i=s}^{k}\sum _{j=0}^{i}\left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) \frac{(-1)^{j+1}\beta (k+j-1)}{[\alpha (k+j-i)+\beta ]^2}, \end{aligned}$$

(12)

$$\begin{aligned}&\frac{\partial R_{s,k}}{\partial \beta }= \sum _{i=s}^{k}\sum _{j=0}^{i}\left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) \frac{(-1)^{j+1}\alpha (k+j-1)}{[\alpha (k+j-i)+\beta ]^2}. \end{aligned}$$

(13)

Hence, using the delta method, the asymptotic variance is given by

$$\begin{aligned} {\hat{H}}=\frac{\alpha ^2}{nk}\left( \frac{\partial R_{s,k}}{\partial \alpha }\right) ^2+\frac{\beta ^2}{n} \left( \frac{\partial R_{s,k}}{\partial \beta }\right) ^2\Bigg \vert _{({\hat{\alpha }},{\hat{\beta }})}. \end{aligned}$$

Therefore, the $100(1-\delta )\%$ ACI of $R_{s,k}$ is obtained as follows:

$$\begin{aligned} {\hat{R}}^{MLE}_{s,k}\pm Z_{\delta /2}\sqrt{{\hat{H}}}, \end{aligned}$$

(14)

where, $Z_{\delta /2}$ is the upper $\delta /2$th quantile of the standard normal distribution.

Here, the confidence interval obtained for $R_{s,k}$ may be outside the domain (0, 1), so it is better to use the logit transformation $f(R_{s,k})=\ln \bigl [R_{s,k}/(1-R_{s,k})\bigr ]$ and then change it again to the original scale [18]. Therefore, the $100(1-\delta )\%$ ACI for $f(R_{s,k})$ is specified by

$$\begin{aligned} f(R_{s,k})\pm Z_{\alpha /2}\frac{\sqrt{{\hat{H}}}}{{\hat{R}}_{s,k}(1-{\hat{R}}_{s,k})}\equiv (L,U). \end{aligned}$$

Finally, the $100(1-\delta )\%$ ACI for $R_{s,k}$ is derived by

$$\begin{aligned} \left( \frac{e^L}{1+e^L},\frac{e^U}{1+e^U}\right) . \end{aligned}$$

(15)

3.2 UMVUE of $R_{s,k}$

In this subsection, we derive the UMVUE of $R_{s,k}$ by using an unbiased estimator of $\gamma (\alpha ,\beta )=\frac{(-1)^j\beta }{\alpha (k+j-i)+\beta }$ and a complete sufficient statistic of $\left( \alpha ,\beta \right)$. We observe from Eq. (10) that $(P,Q)=\left( -\sum _{i=1}^{n}\sum _{j=1}^{k}\ln [z_{ij}(2-z_{ij})],-\sum _{i=1}^{n}\ln \left[ t_i(2-t_i)\right] \right)$ is the complete sufficient statistic of $(\alpha ,\beta )$. In addition, as mentioned in Sect. 3.1, P and Q follow Gamma distributions with parameters $(nk,\alpha )$ and $(n,\beta )$, respectively. Let $P^*=-\ln \left[ Z_{11}(2-Z_{11})\right]$ and $Q^*=-\ln \left[ T_1(2-T_1)\right]$. It is obvious that ${{P}^{*}}$ and ${{Q}^{*}}$ are exponentially distributed with mean ${1}/{\alpha }\;$ and ${1}/{\beta },$ respectively. Hence,

$$\begin{aligned} \varphi (Q^*,P^*)= {\left\{ \begin{array}{ll} 1,&{}P^*>(k+j-i)Q^*\\ 0,&{}\text {otherwise}, \end{array}\right. } \end{aligned}$$

is an unbiased estimator of $\gamma (\alpha ,\beta )$, and so the UMVUE of $\gamma (\alpha ,\beta )$ can be derived by using the Lehmann-Scheffe Theorem. Therefore,

$$\begin{aligned} {\hat{\gamma }}_{UM}(\alpha ,\beta )&=E\left[ \varphi (Q^*,P^*)\vert P=p,Q=q\right] \nonumber \\&=\int _\omega \int f_{Q^{*}\vert Q=q }\left( q^{*}\vert q \right) f_{P^{*}\vert P= p}\left( p^{*}\vert p \right) dq^{*}dp^{*}, \end{aligned}$$

(16)

where $\omega =\{(p^*,q^*):0<p^*<p,0<q^*<q,p^*>(k+j-i)q^*\}$. This double integral can be discussed with regards to $h\le 1$ and $h>1$, where $h=\frac{(k+j-i)q}{p}$. When $h\le 1$, the integral in Eq. (16) reduces to

$$\begin{aligned} {\hat{\gamma }}_{UM}(\alpha ,\beta )&=\int _{0}^{q}\int _{p^*(k+j-i)}^{p} \frac{(n-1)(nk-1)}{qp}\left( 1-\frac{q^*}{q}\right) ^{n-2}\left( 1-\frac{p^*}{p}\right) ^{nk-2}{\text {d}}p^*{\text {d}}q^*\nonumber \\&=(n-1){\int _{0}^{1}(1-\nu )}^{n-2}(1-h\nu )^{nk-1}{\text {d}}\nu \nonumber \\&=\sum _{l=0}^{nk-1}(-1)^l(h)^l\frac{\left( {\begin{array}{c}nk-1\\ 1\end{array}}\right) }{\left( {\begin{array}{c}n+l-1\\ l\end{array}}\right) }, \end{aligned}$$

(17)

where $\nu =\frac{\tilde{q}}{q}$. When $h>1$, the integral in Eq. (16) reduces to

$$\begin{aligned} {\hat{\gamma }}_{UM}(\alpha ,\beta )&=\int _{0}^{p}\int _{0}^{\frac{p^*}{(k+j-i)}}\frac{(n-1)(nk-1)}{qp} \left( 1-\frac{q^*}{q}\right) ^{n-2} \left( 1-\frac{p^*}{p}\right) ^{nk-2} {\text {d}}q^*{\text {d}}p^*\nonumber \\&=1-(nk-1){\int _{0}^{1}(1-\nu )}^{nk-2}(1-h^{-1}\nu )^{n-1}{\text {d}}\nu \nonumber \\&=1-\sum _{l=0}^{n-1}(-1)^l(h)^l\frac{\left( {\begin{array}{c}nk-1\\ 1\end{array}}\right) }{\left( {\begin{array}{c}n+l-1\\ l\end{array}}\right) }, \end{aligned}$$

(18)

where $\nu =\frac{p^*}{p}$. Thus, the ${\hat{\gamma }}_{UM}(\alpha ,\beta )$ is obtained from Eqs. (17) and (18). Finally, the UMVUE of $R_{s,k}$ is determined by applying the linearity property of UMVUE as follows

$$\begin{aligned} {\hat{R}}_{s,k}^{UM}=\sum _{i=s}^{k}\sum _{j=0}^{i} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) (-1)^j{\hat{\gamma }}_{UM}(\alpha ,\beta ). \end{aligned}$$

(19)

4 Bayes estimation of $R_{s,k}$

In this section, we provide the Bayesian inference of $R_{s,k}$ under the squared error (SE) loss function. Assume that the parameters $\alpha$ and $\beta$ are independent random variables and have Gamma prior distributions with parameters $(a_1,b_1)$ and $(a_2,b_2)$, respectively, where $a_i,b_i>0, i=1,2$. Based on the observations, the joint posterior density function is

$$\begin{aligned} \pi (\alpha ,\beta \vert {\varvec{z}},{\varvec{t}})=&\frac{L({\varvec{z}},{\varvec{t}}\vert \alpha ,\beta )\pi _1(\alpha ) \pi _2(\beta )}{\int _{0}^{\infty }\int _{0}^{\infty }{L({\varvec{z}},{\varvec{t}}\vert \alpha ,\beta ) \pi _1(\alpha )\pi _2(\beta )d\alpha d\beta }}\\ =&\frac{(b_1+P)^{nk+a_1}(b_2+Q)^{n+a_2}}{\Gamma (nk+a_1)\Gamma (n+a_2)} \alpha ^{nk+a-1}\beta ^{n+a_2-1}\exp [-\alpha (b_1+P)\\&-\beta (b_2+Q)], \end{aligned}$$

where P and Q are shown in Eq. (10). Then, the Bayes estimate of $R_{s,k}$ is calculated by

$$\begin{aligned} {\hat{R}}_{s,k}^B&=E(R_{s,k}\vert {\varvec{z}},{\varvec{t}})\\&=\sum _{i=s}^{k}\sum _{j=0}^{i} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) (-1)^j\int _{0}^{\infty }\int _{0}^{\infty } \frac{(-1)^j\beta }{\alpha (k+j-i)+\beta }\pi (\alpha ,\beta \vert {\varvec{z}},{\varvec{t}}) {\text {d}}\alpha {\text {d}}\beta . \end{aligned}$$

Now using the computational process provided by [12], the Bayes estimate of $R_{s,k}$ can be rewritten as

$$\begin{aligned} {\hat{R}}_{s,k}^B= {\left\{ \begin{array}{ll} \sum _{i=s}^{k}\sum _{j=0}^{i} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) (-1)^j(1-\nu )^{n+a_2}\frac{n+a_2}{u} {}_2F_1(u,n+a_2+1;u+1,\nu ),\\ \qquad \vert \nu \vert<1\\ \sum _{i=s}^{k}\sum _{j=0}^{i} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) \frac{(-1)^j(n+a_2)}{u(1-\nu )^{nk+a_1}} {}_2F_1\left( u,nk+a_1+1;u+1,\frac{\nu }{\nu -1}\right) ,\\ \qquad \nu <-1 \end{array}\right. } \end{aligned}$$

(20)

where $u=nk+n+a_1+a_2$ and $\nu =1-\frac{(b_2+Q)(k+j-i)}{b_1+P}$. Notice that

$$\begin{aligned} {}_2F_1(a,b;c,x)=\frac{1}{\text {Beta}(a,c-a)} \int _{0}^{1}\nu ^{a-1}(1-\nu )^{c-a-1}(1-x\nu )^{-b}{\text {d}}\nu , \quad \vert \nu \vert <1, \end{aligned}$$

is the hypergeometric series, which is available in standard software such as R. Therefore, for this example, the Bayes estimate is derived in the closed form. However, for comparison purposes, we provide the Bayes estimate by using other techniques such as the Tierney and Kadane approximation, Lindley’s approximation, and the MCMC method.

4.1 Tierney and Kadane approximation

In this subsection, we obtain the Bayes estimator of $R_{s,k}$ via the Tierney and Kadane approximation [19]. This technique is used for the posterior expectation of the function $u(\theta )$ as follows:

$$\begin{aligned} E[u(\theta )]=\frac{\int e^{n\varphi ^*(\theta )}d\theta }{\int e^{\varphi (\theta )}{\text {d}}\theta }, \end{aligned}$$

(21)

where $\varphi (\theta )=\frac{\log {\pi }(\theta ,data)}{n}$, and $\varphi ^*(\theta )=\varphi (\theta )+\frac{\log {u}(\theta )}{n}$. Suppose ${\hat{\theta }}=({\hat{\alpha }},{\hat{\beta }})$ and ${\hat{\theta }}^*=({{\hat{\alpha }}}^*,{\hat{\beta }}^*)$ maximize the functions $\varphi (\theta )$ and $\varphi ^*(\theta )$, respectively. By employing the Tierney and Kadane approximation, Eq. (21) approximates the following expression:

$$\begin{aligned} {\hat{u}}_{TK}(\theta )=\sqrt{\frac{\vert H^*\vert }{\vert H\vert }}\exp {\left[ n(\varphi ^*({{\hat{\theta }}}^*)-\varphi ({\hat{\theta }}))\right] }, \end{aligned}$$

where $\vert H^*\vert$ and $\vert H\vert$ are the inverse determinant of the negative hessian of $\varphi (\theta )$ and $\varphi ^*(\theta )$, respectively, computed at ${\hat{\theta }}$ and ${\hat{\theta }}^*$. In our case, we have

$$\begin{aligned} \varphi (\theta )=\,&\frac{1}{n}\Biggl [(nk+a_1-1)\ln (\alpha )+(n+a_2-1)\ln (\beta )+\sum _{i=1}^{n}\sum _{j=1}^{k}\ln (1-z_{ij})\\&-b_1\alpha -b_2\beta +(\alpha -1)\sum _{i=1}^{n}\sum _{j=1}^{k}\ln [z_{ij}(2-z_{ij})]+\sum _{i=1}^{n}\ln (1-t_i)\\&+(\beta -1)\sum _{i=1}^{n}\ln [t_i(2-t_i)]\Biggr ]. \end{aligned}$$

Then, we compute ${\hat{\theta }}$ by solving following equations

$$\begin{aligned}&\frac{\partial \varphi (\theta )}{\partial \alpha }= \frac{1}{n}\left[ \frac{nk+a_1-1}{\alpha }+\sum _{i=1}^{n}\sum _{j=1}^{k}\ln [z_{ij}(2-z_{ij})]-b_1\right] =0,\\&\frac{\partial \varphi (\theta )}{\partial \beta }= \frac{1}{n}\left[ \frac{n+a_2-1}{\beta }+\sum _{i=1}^{n}\ln [t_i(2-t_i)]-b_2\right] =0. \end{aligned}$$

thus, $\varphi _{11}=\frac{nk+a_1-1}{n{\hat{\alpha }}^2}$, $\varphi _{12}=\varphi _{21}=0$, $\varphi _{22}=\frac{n+a_2-1}{n{\hat{\beta }}^2}$, and $\vert H\vert =\frac{n^2{\hat{\alpha }}^2{\hat{\beta }}^2}{(nk+a_1-1)(n+a_2-1)}$. Now, we obtain $\vert H^*\vert$ following the same arguments with $u(\theta )=\sum _{i=s}^{k}\sum _{j=0}^{i} \left( {\begin{array}{c}k\\ i\end{array}}\right) \frac{(-1)^j\beta }{\alpha (k+j-i)+\beta }$ in ${\hat{\theta }}^*$. Finally, the Bayes estimate of $R_{s,k}$ based on the Tierney and Kadane approximation is obtained as

$$\begin{aligned} {\hat{R}}_{s,k}^{B-TK}=\sqrt{\frac{\vert H^*\vert }{\vert H\vert }} \exp \left[ n(\varphi ^*({\hat{\theta }}^*)-\varphi ({\hat{\theta }}))\right] . \end{aligned}$$

(22)

4.2 Lindley’s approximation

Lindley [20] presented an approximate technique for the determination of the ratio of two integrals. Similar to the Tierney and Kadane approximation, this technique is also used to derive the posterior expectation from a function such as $u(\theta )$ as follows:

$$\begin{aligned} E[u(\theta )]=\frac{\int u(\theta )e^{l(\theta )+\varphi (\theta )}{\text {d}}\theta }{\int e^{l(\theta )+\varphi (\theta )}{\text {d}}\theta }, \end{aligned}$$

(23)

where $l(\theta )$ and $\varphi (\theta )$ are the logarithms of the likelihood function and the prior density of $\theta$, respectively. Thus, Eq. (23) can be written as follows:

$$\begin{aligned} E[u(\theta )]=\left[ u+\frac{1}{2}\sum _{i}\sum _{j}(u_{i_j}+2u_i\varphi _j) \tau _{ij}+\frac{1}{2}\sum _{i}\sum _{j}\sum _{k}\sum _{l}L_{ijk}\tau _{ij}\tau _{kl}u_l\right] \Bigg \vert _{{\hat{\theta }}}, \end{aligned}$$

where $\theta =(\theta _1,\ldots ,\theta _n),i,j,k,l=1,\ldots ,n, {\hat{\theta }}$ is the MLE of $\theta , u=u(\theta ), u_i=\frac{\partial u}{\partial \theta _i}, u_{ij}=\frac{\partial ^2u}{\partial \theta _i\partial \theta _j}, {{L_i}_j}_k=\frac{\partial ^3\,l}{\partial \theta _i}\partial \theta _j\partial \theta _k, \varphi _j=\frac{\partial \varphi }{\partial \varphi _j}$, and $\tau _{ij}=(i,j)$th element in the inverse of the matrix $[-L_{ij}]$ are all calculated at the MLEs of the parameters. In this case, Lindley’s approximation lead to

$$\begin{aligned}&E[u(\theta )]=u+(u_1c_1+u_2c_2+c_3)+\frac{1}{2}(A+B+C+D), \\&c_i=\varphi _1\tau _{i1}+\varphi _2\tau _{i2},i=1,2, \qquad c_3=\frac{1}{2}(u_{11}\tau _{11}+u_{21}\tau _{21}+u_{12}\tau _{12}+u_{22}\tau _{22}),\\&A=(L_{111}\tau _{11}+L_{211}\tau _{21}+L_{121}\tau _{12}+L_{221}\tau _{22})\tau _{11}u_1,\\&B=(L_{112}\tau _{11}+L_{212}\tau _{21}+L_{122}\tau _{12}+L_{222}\tau _{22})\tau _{21}u_1,\\&C=(L_{111}\tau _{11}+L_{211}\tau _{21}+L_{121}\tau _{12}+L_{221}\tau _{22})\tau _{12}u_2,\\&D=(L_{112}\tau _{11}+L_{212}\tau _{21}+L_{122}\tau _{12}+L_{222}\tau _{22})\tau _{22}u_2. \end{aligned}$$

Here, $\theta =(\alpha ,\beta )$ and $u=u(\alpha ,\beta )=R_{s,k}$. therefore,

$$\begin{aligned}&\varphi _1=\frac{a_1-1}{\alpha }-b_1,{} & {} \varphi _2=\frac{a_2-1}{\beta } -b_2,{} & {} L_{11}=-\frac{nk}{\alpha ^2},{} & {} L_{22}=-\frac{n}{\beta ^2},\\&L_{12}=L_{21}=0,{} & {} \tau _{11}=\frac{\alpha ^2}{nk},{} & {} \tau _{22}=\frac{\beta ^2}{n},{} & {} \tau _{12}=\tau _{21}=0,\\&L_{111}=\frac{2nk}{\alpha ^3},{} & {} L_{222}=\frac{2n}{\beta ^3},{} & {} {}{} & {} \end{aligned}$$

and the other $L_{ijk}=0$. Moreover $u_1$ and $u_2$ are presented in Eqs. (12) and (13), respectively. Also,

$$\begin{aligned}&u_{11}=\frac{\partial ^2R_{s,k}}{\partial \alpha ^2}= \sum _{i=s}^{k}\sum _{j=0}^{i} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) \frac{(-1)^j2\beta (k+j-i)^2}{\left[ \alpha (k+j-i)+\beta \right] ^3},\\&u_{22}=\frac{\partial ^2R_{s,k}}{\partial \beta ^2}=\sum _{i=s}^{k}\sum _{j=0}^{i} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) \frac{(-1)^{j+1}2\alpha (k+j-i)}{\left[ \alpha (k+j-i)+\beta \right] ^3}. \end{aligned}$$

Therefore,

$$\begin{aligned} c_3=\frac{1}{2}(u_{11}\tau _{11}+u_{22}\tau _{22}),\quad A=L_{111} {\tau _{11}}^2u_1,\quad D=L_{222}{\tau _{22}}^2u_2,\quad B=C=0. \end{aligned}$$

Hence, the Bayes estimator of $R_{s,k}$ based on Lindley’s approximation is obtained as

$$\begin{aligned} {\hat{R}}_{s,k}^{B-Lin}=\left[ u+(u_1c_1+u_2c_2+c_3)+\frac{1}{2}(A+D)\right] \Bigg \vert _{({\hat{\alpha }},{\hat{\beta }})}. \end{aligned}$$

(24)

4.3 MCMC method

In this subsection, we use the Gibbs sampling method to determine the Bayes estimate and to establish the credible interval for $R_{s,k}$. The posterior conditional density of $\alpha$ and $\beta$ can be derived as

$$\begin{aligned}&\pi ^*(\alpha \vert \beta ,{\varvec{z}},{\varvec{t}})= \frac{(b_1+P)^{nk+a_1}}{\Gamma (nk+a_1)}\alpha ^{nk+a-1}\exp \left[ -\alpha (b_1+P) \right] , \end{aligned}$$

(25)

$$\begin{aligned}&\pi ^*(\beta \vert \alpha ,{\varvec{z}},{\varvec{t}})=\frac{(b_2+Q)^{n+a_2}}{\Gamma (n+a_2)}\beta ^{n+a_2-1}\exp \left[ -\beta (b_2+Q)\right] , \end{aligned}$$

(26)

respectively. We observe from Eqs. (25) and (26) that the conditional densities of $\alpha$ and $\beta$ have Gamma distributions with parameters $(nk+a_1,b_1+P)$ and $(n+a_2,b_2+Q),$ respectively. Therefore, we can to use the Gibbs sampling algorithm steps as follows.

Algorithm 1

.

The Bayes estimate of $R_{s,k}$ based on the MCMC method is calculated by

$$\begin{aligned} {\hat{R}}_{s,k}^{B-MC}=\frac{1}{N}\sum _{l=1}^{N}R_{s,k}^{(l)}. \end{aligned}$$

Also, the highest probability density $100(1-\delta )\%$ credible interval for $R_{s,k}$ can be computed by method of [21], minimizing

$$\begin{aligned} \left( R_{s,k}^{((1-\delta )N+i)}-R_{s,k}^{(i)}\right) ,\qquad 1\le i\le \delta N, \end{aligned}$$

where, the values of $R_{s,k}$ are ranked in ascending order from 1 to N.

5 Simulation study

In this section, we performed MCMC simulations to compare the performances of the point and interval estimates of $R_{s,k}$ by using the classical and Bayesian methods for different sample sizes and different choices of parameter values. The performances of the point estimators are compared in terms of their mean squared errors (MSEs). The performances of the interval estimators are compared by the average lengths (ALs) of intervals and coverage probabilities (CPs). We have generated random samples from strength and stress populations based on different sample sizes, $n=5(10)45$, and different parameter values, $(\alpha ,\beta )=(0.5,1), (0.5,1.5), (2.5,2), (3,2)$. The true values of $R_{s,k}$ with the given $(\alpha ,\beta )$ for $(s,k)=(1,3)$ are 0.6, 0.5, 0.7895, 0.8182 and for $(s,k)=(2,4)$ are 0.4, 0.2857, 0.6579, 0.7013, respectively. To investigate the Bayes estimate, both non-informative and informative priors are considered and have been dubbed Prior 1 and Prior 2, respectively. Prior 1 is $(a_i,b_i)=(0.0001,0.0001), i=1,2$ and Prior 2 is $(a_i,b_i)=(3,1), i=1,2$. All of the calculations are obtained by using R 3.4.4 based on 50,000 replications. Further, the Bayes estimate along with its credible interval are calculated using 1000 sampling. For comparison purposes, we have considered three approximate methods of Bayes estimates, namely Lindley’s approximation, the Tierney and Kadane approximation, and the MCMC method. In Tables 1 and 2, the point estimates and the MSEs of $R_{s,k}$ are reported based on classical and Bayesian estimates. According to Tables 1 and 2, the MSEs for the estimates decrease as the sample size increases for all cases, as expected. The Bayes estimates of $R_{s,k}$ under Prior 2 have a smaller MSE than the other estimates, especially for small sample size $n=5$. Also, the MSEs of the ML estimates are smaller than the UMVUE estimates. Moreover, these MSEs are near each other as the sample size increases. According to Tables 3 and 4, the interval estimates of $R_{s,k}$ are reported based on the classical and Bayesian estimates and their ALs and CPs. As expected, the ALs of the intervals decrease as the sample size increases. The ALs of the HPDCIs are smaller than ACIs, but the CPs of ACIs are generally nearer to the nominal level of $95\%$ compared to HPDCIs. In Tables 5 and 6, the different Bayes estimates of $R_{s,k}$ and their corresponding MSEs are listed. From these tables, we observed that the MSEs in the MCMC method are generally larger than those computed from other Bayes methods for small sample sizes of $n=5$. However, as the sample size increases, all Bayes estimates and their corresponding MSEs are very close to each other.

From the Bayesian point of view, the main focus of this article is on estimating system reliability based on the SE loss function. The mentioned loss function is symmetric, which means that the same penalty is imposed for overestimation and underestimation. However, if we want to consider a higher penalty for overestimation or underestimation, we must use an asymmetric loss function. Here, we briefly examine the performance of Bayes estimation under SE loss with an asymmetric loss. The most well-known asymmetric loss function is the linear-exponential (LINEX) loss, which is defined as follows

$$\begin{aligned} L({\hat{\sigma }},\sigma )=e^{v({\hat{\sigma }}-\sigma )}-v({\hat{\sigma }}-\sigma )-1, \end{aligned}$$

where $\nu \ne 0$ and ${\hat{\sigma }}$ is an estimate of $\sigma$. The magnitude and sign of $\nu$ represents the degree and direction of asymmetry, respectively. When $\nu$ is close to zero, LINEX and SE losses are approximately equal. For $\nu <0$, underestimation is more important than overestimation, and vice versa. Calculation of Bayes estimation based on LINEX loss function is performed in a process similar to that described in Sect. 4.3, that due to the article’s length, it will not be shown here. In Table 7, the Bayes estimates of $R_{s,k}$ and their corresponding MSEs are reported based on LINEX loss function for $v=-2$ and $v=1$ as well as for both $(s,k)=(1,3)$ and (2, 4). Based on the results of Table 7 and its comparison with Tables 5 and 6, we conclude that when $\nu =1$ the performance of the Bayes estimator under LINEX loss is better than SE loss and when $\nu =-2$ the opposite is true.

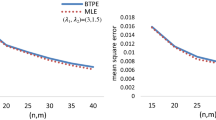
We also used graphs to compare the performances of the competing estimators when $R_{s,k}$ changes from 0.05 to 0.95. For this aim, we considered the different values of the parameters along with the different sets of hyperparameters and then calculated the MSEs of $R_{s,k}$, followed by the computation of the CPs and ALs of the interval estimates of $R_{s,k}$. Figure 1 shows the MSEs of ${\hat{R}}_{s,k}^{MLE}, {\hat{R}}_{s,k}^{UM}$, and ${\hat{R}}_{s,k}^B$ for different sample sizes, $n=5(10)35$ and $(s,k)=(1,3)$. According to Fig. 1, when $R_{s,k}$ is about 0.5, we observed that

$$\begin{aligned} MSE({\hat{R}}_{s,k}^{B-P2})<MSE( {\hat{R}}_{s,k}^{B-P1})< MSE({\hat{R}}_{s,k}^{MLE})<MSE( {\hat{R}}_{s,k}^{UM}), \end{aligned}$$

where ${\hat{R}}_{s,k}^{B-P1}$ and ${\hat{R}}_{s,k}^{B-P2}$ are Bayes estimates under non-informative and informative priors, respectively. When $R_{s,k}$ approaches the extreme values, we observed that

$$\begin{aligned} MSE({\hat{R}}_{s,k}^{B-P2})< MSE({\hat{R}}_{s,k}^{UM})< MSE({\hat{R}}_{s,k}^{MLE})< MSE({\hat{R}}_{s,k}^{B-P1}), \end{aligned}$$

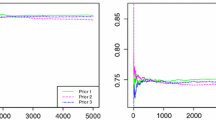
Also, the MSEs are large when $R_{s,k}$ is about 0.5 and they are small for the extreme values of $R_{s,k}$. Some of the results extracted from this figure are quite clear. It was found that the estimates obtained based on greater sample sizes have lower MSEs. Also, as the sample sizes increase, the MSEs of are near each other for all types of estimates. Figure 2 shows the ALs of interval estimates for different sample sizes, $n=5(10)35$. According to Fig. 2, we observed that the ALs of the HPDCIs under non-informative priors are almost identical with ACIs. Also, based on ALs, the performances of the HPDCIs with informative priors are the best. Furthermore, the ALs of the intervals decrease as the sample size increases, as expected. Figure 3 presents the CPs of interval estimates for different sample sizes, $n=5(10)35$. According to Fig. 3, we observed that the HPDCIs with informative priors are preferable to the ACIs in terms of CPs for case $n=5$, but as sample sizes increase, the ML estimates are nearer to the predetermined nominal level.

Table 1 The point estimates of $R_{1,3}$ and their corresponding MSEs (presented in parenthesis)

Table 2 The point estimates of $R_{2,4}$ and their corresponding MSEs (presented in parenthesis)

Table 3 The ALs of $R_{1,3}$ and their corresponding CPs (presented in parenthesis)

Table 4 The ALs of $R_{2,4}$ and their corresponding CPs (presented in parenthesis)

Table 5 Bayesian estimates of $R_{1,3}$ and their corresponding MSEs (presented in parenthesis)

Table 6 Bayesian estimates of $R_{2,4}$ and their corresponding MSEs (presented in parenthesis)

Table 7 Bayesian estimates of $R_{s,k}$ and their corresponding MSEs (presented in parenthesis) under LINEX loss function with $v=-2$ and $v=1$

Fig. 1

The MSEs of estimates of $R_{1,3}$ for sample sizes $n=5$ (a), $n=15$ (b), $n=25$ (c) and $n=35$ (d)

Fig. 2

The ALs of interval estimates of $R_{1,3}$ for sample sizes $n=5$ (a), $n=15$ (b), $n=25$ (c) and $n=35$ (d)

Fig. 3

The CPs of interval estimates of $R_{1,3}$ for sample sizes $n=5$ (a), $n=15$ (b), $n=25$ (c) and $n=$35 (d)

6 Data analysis

In this section, we conduct the analysis of real data for illustrative purposes. The issue of excessive drought is very important in agriculture because it causes a lot of damage to crops, so it needs to be managed. The following scenario is useful to understand in case of an excessive drought. In a five-year period, if at least two times, the maximum water capacity of a reservoir in August and September is more than the volume of water achieved on December of the previous year, it can be claimed that there will not be any excessive drought afterwards. Therefore, the multicomponent stress-strength reliability is the probability of non-occurrence drought. The data are taken for the months of August, September, and December from 1980 to 2015. This data was studied in [12], previously. Assuming, $k=5$ and $s=2$, $x_{11},x_{12},\ldots ,x_{15}$ and $y_{11},y_{12},\ldots ,y_{15}$ are the capacities of August and September from 1981 to 1985. $x_{21},x_{22},\ldots ,x_{25}$ and $y_{21},y_{22},\ldots ,y_{25}$ are the capacities of August and September from 1987 to 1991 and continues until $x_{61},x_{62},\ldots ,x_{65}$ and $y_{61},y_{62},\ldots ,y_{65}$ are the capacities of August and September from 2011 to 2015. Also, $t_1$ is the capacity of December 1980, $t_2$ is the capacity of December 1986 and continues until $t_6$ is the capacity of December 2010. Hence, the reliability of multicomponent can be represented as 2-out-of-5: G system. Since the support of the TL distribution is defined for $0<x<1$, we divide all the values by the total capacity of the Shasta reservoir, which is 4,552,000 acre-foot. The transformed data are as follows:

$$\begin{aligned}&X= \begin{bmatrix} 0.5597&{}0.8112&{}0.8296&{}0.7262&{}0.4238\\ 0.4637&{}0.3634&{}0.4637&{}0.3719&{}0.2912\\ 0.7540&{}0.5381&{}0.7449&{}0.7226&{}0.5612\\ 0.7552&{}0.6686&{}0.5249&{}0.6060&{}0.7159\\ 0.7188&{}0.7420&{}0.4688&{}0.3451&{}0.4253\\ 0.7951&{}0.6439&{}0.4616&{}0.2948&{}0.3929 \end{bmatrix},\\&Y= \begin{bmatrix}0.5449&{}0.7659&{}0.7946&{}0.7118&{}0.4345\\ 0.4631&{}0.3484&{}0.4605&{}0.3597&{}0.2943\\ 0.6814&{}0.4617&{}0.6890&{}0.6786&{}0.5071\\ 0.7310&{}0.6558&{}0.4832&{}0.5620&{}0.6941\\ 0.6667&{}0.7041&{}0.4128&{}0.3041&{}0.3897\\ 0.7340&{}0.5693&{}0.4187&{}0.2542&{}0.3520\\ \end{bmatrix} ,T= \begin{bmatrix} 0.7009\\ 0.6532\\ 0.4589\\ 0.7183\\ 0.5310\\ 0.7665\\ \end{bmatrix}. \end{aligned}$$

Also, let $Z_{ik}=max{(X_{ik},Y_{ik})},i=1,\ldots ,6,k=1,\ldots ,5$. Then, the actual observed data are obtained as

$$\begin{aligned} Z= \begin{bmatrix} 0.5597&{}0.8112&{}0.8296&{}0.7262&{}0.4345\\ 0.4637&{}0.3634&{}0.4637&{}0.3719&{}0.2943\\ 0.7540&{}0.5381&{}0.7449&{}0.7226&{}0.5612\\ 0.7552&{}0.6686&{}0.5249&{}0.6060&{}0.7159\\ 0.7188&{}0.7420&{}0.4688&{}0.3451&{}0.4253\\ 0.7951&{}0.6439&{}0.4616&{}0.2948&{}0.3929\\ \end{bmatrix},T =\begin{bmatrix} 0.7009\\ 0.6532\\ 0.4589\\ 0.7183\\ 0.5310\\ 0.7665\\ \end{bmatrix}. \end{aligned}$$

We first check whether or not the BTL distribution can be used to analyze these data. Unfortunately, there is no satisfactory goodness of fit test for the bivariate distributions like in univariate distributions. In this case, we can perform goodness of fit tests for X, Y,  and $Z=\max (X,Y)$, separately. Also, we use goodness of fit test to validate whether the TL distribution can be used to make an acceptable inference for the T data. The MLE of unknown parameters, the Kolmogorov-Smirnov (K-S), Andeson-Darling (A), and Cramer-von Mises (W) statistics along with the P-values for each data are reported in Table 8. Based on these results, we conclude that the TL distribution provides a good fit for the X, Y, Z, and T data. The validity of the TL distribution is also supported by P-P plot shown in Fig. 4. Here, we obtain the estimates of $R_{2,5}$ by using classical and Bayesian methods discussed in this article. First, from the above data, the ML estimates of $\alpha$ and $\beta$ are computed as ${\hat{\alpha }}=3.9496$ and ${\hat{\beta }}=6.2797$, respectively. Then, the MLE of $R_{2,5}$ along with its ACI are obtained from Eqs. (11) and (14), respectively. Also, the UMVUE of $R_{2,5}$ is determined from Eq. (19). To analyze the data from the Bayesian view, we have taken different parameters of the priors. The parameters $(a_i,b_i)=(0.0001,0.0001), i=1,2$ are selected for the non-informative prior case and the parameters $a_1=4,a_2=6, b_1=b_2=1$ are selected for the informative prior by using the MLEs of unknown parameters. Tables 9 and 10 give point and interval estimates of $R_{2,5}$. It is observed that the point estimates of $R_{2,5}$ which are obtained by the Bayesian and classical methods are about the same, but the HPDCI of $R_{2,5}$ based on the informative prior is remarkably smaller than the HPDCI based on the non-informative prior and the ACI. Therefore, if prior information is available, it should be used. Also, the estimates of $R_{2,5}$ obtained from the approximate and exact Bayes methods are near each other except that which is obtained from Lindley’s approximation under the informative prior.

Table 8 The MLE of unknown parameter and goodness of fit statistics

Table 9 Point estimates of $R_{2,5}$

Table 10 Interval estimates of $R_{2,5}$

Fig. 4

P-P plot for X, Y, Z,  and T data

7 Extension of methods to a general family of distributions

In the previous sections, we studied different methods of estimating the reliability of $R_{s,k}$ where the strength variables followed a BTL distribution and were subjected to a common random stress that had a TL distribution. Now, we extend our methods for a flexible family of distributions, namely proportional reversed hazard rate family (PRHRF) whose CDF and PDF are, respectively, defined as follows:

$$\begin{aligned}&F_X(x;\alpha )=[F_0(x)]^\alpha ,x>0,\alpha >0, \end{aligned}$$

(27)

$$\begin{aligned}&f_X(x;\alpha )=\alpha f_0(x)[F_0(x)]^{\alpha -1}, \end{aligned}$$

(28)

where $\alpha$ is the shape paramete. Also, $F_0(.)$ and $f_0(.)$ are a baseline CDF and PDF, respectively. The model given in Eqs. (27) and (28) is also known with names such as exponentiated distributions and Lehmann alternatives. This family includes several well-known lifetime distributions such as generalized Rayleigh (Burr Type X), generalized exponential, generalized Lindley, exponentiated half logistic, generalized logistic, and so on. Some of the recently introduced flexible distributions from PRHRF are: exponentiated unit Lindley [22], exponentiated Teissier [23], exponentiated XGamma [24], and exponentiated Burr-Hatke [25]. Due to the importance of PRHRF distributions in the reliability literature, many studies have been done on their properties and applications. Some of the recent efforts pertaining to this family of distributions are [26,27,28,29,30].

Now, we describe the bivariate proportional reversed hazard rate family (BPRHRF). Suppose $V_1,V_2$, and $V_3$ follow $PRHRF(\alpha _1), PRHRF(\alpha _2)$, and $PRHRF(\alpha _3)$, respectively and all three random variables are mutually independent. Define the random variables X and Y as

$$\begin{aligned} X=\max {\left\{ V_1,V_3\right\} }, \qquad Y=\max {\left\{ V_2,V_3\right\} }, \end{aligned}$$

where X and Y have a common random variable $V_3$. So the bivariate vector (X, Y) is a bivariate distribution of BPRHRF with parameters $\alpha _1,\alpha _2$, and $\alpha _3$ and it is denoted by $BPRHRF(\alpha _1,\alpha _2,\alpha _3)$. Using the above definition, the following theorems can be easily proved by applying the same argument used in Sect. 2.

Theorem 3

If $(X,Y)\sim \text {BPRHRF}(\alpha _1,\alpha _2,\alpha _3)$, then their joint CDF is given by

$$\begin{aligned} F_{(X,Y)}(x,y)=[F_0(x)]^{\alpha _1}[F_0(y)]^{\alpha _2}[F_0(u)]^{\alpha _3}, \end{aligned}$$

where $u=\min (x,y)$.

Theorem 4

If $(X,Y)\sim \text {BPRHRF}(\alpha _1,\alpha _2,\alpha _3)$, then $X\sim \text {PRHRF}(\alpha _1+\alpha _3)$ and $Y\sim \text {PRHRF}(\alpha _2+\alpha _3)$. Also, $\max (X,Y)\sim \text {PRHRF}(\alpha )$, where $\alpha =\alpha _1+\alpha _2+\alpha _3$.

Now, we assume that the strength vectors $(X_1,Y_1),\ldots ,(X_k,Y_k)$ follow $BPRHRF(\alpha _1,\alpha _2,\alpha _3)$ and a common stress variable T follows $PRHRF(\beta )$. Hence the reliability in a multicomponent stress-strength model is given by

$$\begin{aligned} R_{s,k}=P(T<\max (X_i,Y_i)),i=1,\ldots ,k. \end{aligned}$$

According to Theorem 4 and assuming $Z_i=\max (X_i,Y_i), i=1,\ldots ,k,$ we have $Z_i\sim PRHRF(\alpha )$ and then $R_{s,k}=P(T<Z_i),i=1,\ldots ,k$. Suppose k strengths $(Z_1,\ldots ,Z_k)$ be a random sample from $PRHRF(\alpha )$ and the stress T is a random sample from $PRHRF(\beta )$. Therefore, the reliability of $R_{s,k}$ is obtained as Eq. (6).

7.1 MLE of $R_{s,k}$

To find the MLE of $R_{s,k}$, we need to determine the MLEs of $\alpha$ and $\beta$. The log-likelihood function is

$$\begin{aligned} l(\alpha ,\beta \vert {\varvec{z}},{\varvec{t}})=\,&nk \ln (\alpha )+n\ln (\beta )\\&+\sum _{i=1}^{n}\sum _{j=1}^{k} \ln [f_0(z_{ij})]+(\alpha -1)\sum _{i=1}^{n}\sum _{j=1}^{k}\ln [F_0(z_{ij})]\\&+\sum _{i=1}^{n}\ln [f_0(t_i)]+(\beta -1) \sum _{i=1}^{n}\ln [F_0(t_i)]+c, \end{aligned}$$

where c is constant. So, the MLEs of $\alpha$ and $\beta$ can be easily obtained as follows

$$\begin{aligned} {\hat{\alpha }}=\frac{nk}{P}, \qquad {\hat{\beta }}=\frac{n}{Q}, \end{aligned}$$

where $P=-\sum _{i=1}^{n}\sum _{j=1}^{k}\ln [F_0(z_{ij})]$ and $Q=-\sum _{i=1}^{n}\ln [F_0(t_i)]$. Since $\ln [F_0(z)]$ and $\ln [F_0(t)]$ are negative, so we always have $P>0$ and $Q>0$. Therefore, ${\hat{\alpha }}$ and ${\hat{\beta }}$ are indeed the MLEs of $\alpha$ and $\beta$, respectively. Also, similar to what was mentioned in Sect. 3.1, it can be shown that if $X_1,\ldots ,X_n\sim PRHRF(\alpha )$, then $-\sum _{i=1}^{n}\ln [X_i(2-X_i)]\sim Gamma(n,\alpha )$. In the following, the MLE of $R_{s,k}$ is computed from Eq. (6) by the invariant property of MLEs:

$$\begin{aligned} {\hat{R}}_{s,k}^{MLE}=\sum _{i=s}^{k}\sum _{j=0}^{i} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) \frac{(-1)^j{\hat{\beta }}}{{\hat{\alpha }}(k+j-i)+{\hat{\beta }}}. \end{aligned}$$

7.2 UMVUE of $R_{s,k}$

Using same argument used in Sect. 3, the UMVUE of $R_{s,k}$ is obtained as

$$\begin{aligned} {\hat{R}}_{s,k}^{UM}=\sum _{i=s}^{k}\sum _{j=0}^{i} \left( {\begin{array}{c}k\\ i\end{array}}\right) \left( {\begin{array}{c}i\\ j\end{array}}\right) (-1)^j{\hat{\gamma }}_{UM}(\alpha ,\beta ), \end{aligned}$$

where

$$\begin{aligned} {\hat{\gamma }}_{UM}(\alpha ,\beta )= {\left\{ \begin{array}{ll} \sum _{l=0}^{nk-1}(-1)^l \left( \frac{(k+j-i)q}{p}\right) ^l \frac{\left( {\begin{array}{c}nk-1\\ l\end{array}}\right) }{\left( {\begin{array}{c}n+l-1\\ l\end{array}}\right) },&{}\frac{(k+j-i)q}{p}\le 1\\ 1-\sum _{l=0}^{n-1}(-1)^l \left( \frac{(k+j-i)q}{p}\right) ^l \frac{\left( {\begin{array}{c}nk-1\\ l\end{array}}\right) }{\left( {\begin{array}{c}n+l-1\\ l\end{array}}\right) },&\frac{(k+j-i)q}{p}> 1 \end{array}\right. } \end{aligned}$$

$p=-\sum _{i=1}^{n}\sum _{j=1}^{k}\ln [F_0(z_{ij})]$ and $q=-\sum _{i=1}^{n}\ln [F_0(t_i)]$.

7.3 Bayes estimation of $R_{s,k}$

Assume that the parameters $\alpha$ and $\beta$ are independent random variables and have Gamma prior distributions with positive parameters $(a_1,b_1)$ and $(a_2,b_2)$, respectivel. The exact and approximate Bayesian estimates of $R_{s,k}$ are obtained in a process quite similar to that mentioned in Sect. 4. It is enough to replace $P=-\sum _{i=1}^{n}\sum _{j=1}^{k}\ln [z_{ij}(2-z_{ij})]$ with $P=-\sum _{i=1}^{n}\sum _{j=1}^{k}\ln [F_0(z_{ij})]$ and $Q=-\sum _{i=1}^{n}\ln [t_i(2-t_i)]$ with $Q=-\sum _{i=1}^{n}\ln [F_0(t_i)]$.

8 Conclusions

In this endeavour, we have considered the inference of multicomponent stress-strength reliability under the bivariate Topp-Leone (BTL) distribution. Here, the strength variables follow a BTL distribution and are exposed to a common random stress that follows a Topp-Leone (TL) distribution. We have provided the MLE along with its ACI of $R_{s,k}$. Also, the UMVUE and the exact Bayes estimates of $R_{s,k}$ are computed. Moreover, we determined the Bayes estimate of $R_{s,k}$ via three methods: the Tierney and Kadane approximation, Lindley’s approximation, and the MCMC method. Additionally, we established HPDCIs of $R_{s,k}$.

The simulation results showed that the point and interval estimates of obtained from larger sample sizes have lower MSEs and lower ALs, respectively. According to the MSE and AL values, Bayesian estimators under the informative priors have the best performances among the estimators. Also, the MSEs and ALs of the all estimators are small when $R_{s,k}$ tends to the extreme value and they are large when $R_{s,k}$ tends to 0.5. Comparing the classical estimators showed that the MSEs of the UMVUE estimates are smaller than the ML estimates when $R_{s,k}$ is near extreme values, and when $R_{s,k}$ tends to 0.5, the ML estimators work better. According to the CP values, the HPDCIs with informative priors are better than ACIs for small sample sizes, but as the sample size increases, the ML estimates are nearer to the predetermined nominal level.

Comparing the different Bayesian estimation methods showed that all of the Bayes estimates and their corresponding MSEs are near each other for sample sizes of $n\ge 15$. As a general conclusion, because Bayesian estimators under the informative priors often performed better than other estimators, they should be used if information on hyerparameters is available.