Bayesian and classical estimation of reliability in a multicomponent stress-strength model under adaptive hybrid progressive censored data

Abstract

The statistical inference of multicomponent stress-strength reliability under the adaptive Type-II hybrid progressive censored samples for the Weibull distribution is considered. It is assumed that both stress and strength are two Weibull independent random variables. We study the problem in three cases. First assuming that the stress and strength have the same shape parameter and different scale parameters, the maximum likelihood estimation (MLE), approximate maximum likelihood estimation (AMLE) and two Bayes approximations, due to the lack of explicit forms, are derived. Also, the asymptotic confidence intervals, two bootstrap confidence intervals and highest posterior density (HPD) credible intervals are obtained. In the second case, when the shape parameter is known, MLE, exact Bayes estimation, uniformly minimum variance unbiased estimator (UMVUE) and different confidence intervals (asymptotic and HPD) are studied. Finally, assuming that the stress and strength have the different shape and scale parameters, ML, AML and Bayesian estimations on multicomponent reliability have been considered. The performances of different methods are compared using the Monte Carlo simulations and for illustrative aims, one data set is investigated.

1 Introduction

Among various censoring schemes, Type-I and Type-II censoring schemes are two most effective schemes. Type-I scheme finished the test at the pre-chosen time and Type-II scheme finished the test at the pre-determined number of failures. The hybrid scheme which is a mixing of Type-I and Type-II schemes has been introduced by Epstein (1954). This censoring scheme finished the test at time $T^*=\min \{X_{m:n},T\}$, where $X_{m:n}$ is the m-th failure times from n items and $T>0$. Because the above schemes cannot remove active units during the test, the progressive censoring scheme is introduced. In this scheme, the active units can be ejected during the test. Combining the Type-II and progressive schemes, the progressive Type-II censoring is obtained. Also, mixing the hybrid and progressive schemes, the progressive hybrid censoring is provided. In a progressive hybrid censoring scheme which was initiated by Kundu and Joarder (2006), N units are put on the experiment and $X_{1:n:N}\le \cdots \le X_{n:n:N}$ come from a progressive censoring scheme, with the censoring scheme $(R_1,\ldots ,R_n)$ and halting time $T^*=\min \{X_{n:n:N},T\}$, $T>0$. If $X_{n:n:N}<T$, the test finished at time $X_{n:n:N}$ and n failures happen. Also, if $X_{J:n:N}<T<X_{J+1:n:N}$, the test finished at time T and J failures happen. It is obvious that the sample size in progressive hybrid censoring is random. So, with a small number of samples, statistical inference is not applicable in practical situations. To solve this problem, Ng et al. (2009) have been provided the adaptive hybrid progressive scheme. In this paper, we work on the adaptive Type-II hybrid progressive censoring (AT-II HPC). In AT-II HPC scheme, let $X_{1:n:N}\le \cdots \le X_{n:n:N}$ be a progressive censoring sample with scheme $(R_1,\ldots ,R_n)$ and $T>0$ is fixed. If $X_{n:n:N}<T$, the experiment proceeds with the progressive censoring scheme $(R_1,\ldots ,R_n)$ and stops at the $X_{n:n:N}$ (see Fig. 1). Otherwise, once the experimental time passes time T but the number of observed failures has not reached n, we would want to terminate the experiment as soon as possible for fixed value of n, then we should leave as many surviving items on the test as possible. Suppose J is the number of failures observed before time T, i.e. $X_{J:n:N}<T<X_{J+1:n:N}$, $J=0,\cdots ,n$. After passed time T, we do not withdraw any items at all except for the time of the n-th failure where all remaining surviving items are removed. So, we set

$$\begin{aligned} R_{J+1}=\cdots =R_{n-1}=0,~ R_n=N-n-\sum \limits _{i=1}^{J}R_i. \end{aligned}$$

In Fig. 2, the schematic representation of this situation is given. From now on, a AT-II HPC sample will be denoted with $\{X_1,\ldots ,X_n\}$ under the scheme $\{N,n,T,R_1,\ldots R_n\}$ such that $X_{J}<T<X_{J+1}$. Getting the effective number of failures n is one of the most advantages of AT-II HPC scheme. Also, this scheme can be reduced to Type-II progressive censoring and Type-II censoring by setting $T=0$ and $T=\infty$, respectively. By this approach, the tester will be able to control the test. Very recently, Nassar and Abo-Kasem (2017) estimated the inverse Weibull parameters and AL Sobhi and Soliman (2016) studied the estimation of exponentiated Weibull model under this scheme.

Fig. 1

Experiment ends before time T ($X_{n:n:N}\le T$)

Fig. 2

Experiment ends after time T ($X_{n:n:N}\ge T$)

In recent years much attention has been paid to the multicomponent stress-strength model. A multicomponent system is arranged of common stress and k independent and identical strengths component. This system is reliable when s ($1\le s\le k$) or more of k components simultaneously survive. This model corresponds to the G system: s-out-of-k. Some examples can be given that is consistent with the G system. For example, in a suspension bridge, the wind loading, heavy traffic, corrosion, etc. can be regarded as stresses and the k number of vertical cable pairs, which support the bridge deck, can be considered as strengths. The bridge will only survive if a minimum s number of vertical cable through the deck is not damaged. As another example of the G system: 4-out-of-8, we can point to a V-8 engine of an automobile. As a contractor, if at least 4 cylinders are firing then the automobile may be to derive.

Bhattacharyya and Johnson (1974) improved the multicomponent reliability as

$$\begin{aligned} R_{s,k}&=P[\text{ at } \text{ least }~ s ~\text{ of }~ (X_1,\dots ,X_k) ~\text{ exceed } ~Y]\\&=\sum _{p=s}^{k}\left( {\begin{array}{c}k\\ p\end{array}}\right) \int _{-\infty }^{\infty }[1-F_X(y)]^p[F_X(y)]^{k-p}dF_Y(y), \end{aligned}$$

when the strengths $(X_1, \dots , X_k )$ are independent and identically distributed random variables with cdf $F_X(.)$ and the stress Y is a random variable with the cdf $F_Y(.)$. Estimation of the multicomponent stress-strength parameter has been studied for different distributions like for example exponential (Hanagal 1999), bivariate Kumaraswamy (Kizilaslan and Nadar 2018) and Marshall-Olkin Bivariate Weibull (Nadar and Kizilaslan 2016).

The multicomponent stress-strength parameter, in the case of complete samples, has been estimated by many authors. But, in the case of censored samples, not many studies have been done for inference about multicomponent reliability, whereas, in some practical situations, we deal with different censoring schemes. For example, we consider the following situation. If the water capacity of a reservoir in a region on December of the previous year is less than the amount of water achieved on Aguste at least two years out of the next 5 years, we claim that there will be no excessive drought afterward. In this example, it is very likely, we observe censored samples rather than complete samples from both populations.

In reliability theory, the Weibull distribution is one of the most widely used lifetime distributions with respect to other distributions. The probability density, cumulative distribution and failure rate functions of the Weibull distribution with the shape and scale parameters $\alpha$ and $\theta$, respectively, are as follows:

$$\begin{aligned} f(x)&=\frac{\alpha }{\theta } x^{\alpha -1}e^{-\frac{x^\alpha }{\theta }},~~x>0,\;\;\alpha ,\theta >0, \end{aligned}$$

(1)

$$\begin{aligned} F(x)&=1-e^{-\frac{x^\alpha }{\theta }},~~~~~~x>0,\;\;\alpha ,\theta>0,\nonumber \\ H(x)&=\frac{\alpha }{\theta }x^{\alpha -1},~~~~~~~~~x>0,\;\;\alpha ,\theta >0, \end{aligned}$$

(2)

respectively. Hereafter, we denote the Weibull distribution, with the probability distribution function in (1), by $W(\alpha ,\theta )$. As we see, the failure rate function of $W(\alpha ,\theta )$ is an increasing, constant or decreasing functions for $\alpha >1$, $\alpha =1$ and $\alpha <1$, respectively. Because of this, many researchers may be used the Weibull distribution to analyze the data sets.

In this paper, on the basis of AT-II HPC samples, we study the statistical inferences for multicomponent stress-strength reliability model $R_{s,k}=P[\text {at least}~ s ~\text {of} (X_1,\dots ,X_k) ~\text {exceed} ~Y]$. Therefore, $\{X_{i1},\ldots ,X_{ik}\},~i=1,\ldots ,n,$ and $\{Y_{1},\ldots ,Y_{n}\}$ can be considered as $n+1$ AT-II HPC samples from two different Weibull distributions, which one of them for stress and the other for strength. The censoring schemes for $\{X_{i1},\ldots ,X_{ik}\},~i=1,\ldots ,n,$ and $\{Y_{1},\ldots ,Y_{n}\}$ can be studied as $\{K,k,T_2,R_{i1},\ldots R_{in}\},~i=1\ldots ,n$ and $\{N,n,T_1,S_1,\ldots S_n\}$, respectively.

This paper is arranged as follows: In Sect. 2, we infer $R_{s,k}$ when the stress and strength have the common and unknown shape parameter $\alpha$. First, we obtain the ML estimation of $R_{s,k}$. As we will see, because the different equations to obtain the MLE cannot be solved explicitly, we derive the AMLE’s of $R_{s,k}$ which has explicit forms. Also, we provide the asymptotic and two bootstrap confidence intervals for the multicomponent stress-strength parameter. The Bayesian estimation is another estimate which we obtain for $R_{s,k}$. Because the Bayesian estimation cannot be obtained in a closed form, we use two approximation method: Lindley approximation and MCMC method. By using the MCMC method, we derive the HPD credible intervals. In Sect. 3, when the stress and strength have the common and known shape parameter $\alpha$, we derive the MLE, asymptotic confidence interval, exact Bayes estimate, HPD credible interval and UMVUE of $R_{s,k}$. In Sect. 4, when all parameters are different and unknown, we infer on $R_{s,k}$. In this section, we obtain the MLE, AMLE and Bayesian inference of multicomponent stress-strength reliability parameter. In Sect. 5, simulation results and data analysis are provided. Finally, we conclude the paper in Sect. 6.

2 Inference on $R_{s,k}$ if $\alpha$, $\theta$ and $\lambda$ are unknown

2.1 Maximum likelihood estimation of $R_{s,k}$

Suppose that $X\sim W(\alpha ,\theta )$ and $Y\sim W(\alpha ,\lambda )$ are two independent random variables with unknown common shape parameter $\alpha$ and different scale parameters $\theta$ and $\lambda$. For Weibull distribution using (1) and (2), the multicomponent stress-strength reliability is given by

$$\begin{aligned} R_{s,k}&=\sum _{p=s}^{k}\left( {\begin{array}{c}k\\ p\end{array}}\right) \frac{\alpha }{\lambda }\int _0^\infty y^{\alpha -1}e^{-y^\alpha (\frac{p}{\theta }+\frac{1}{\lambda })} (1-e^{-\frac{y^\alpha }{\theta }})^{k-p}dy~~(\text{ Put: }~ t=e^{-y^\alpha })\nonumber \\&=\sum _{p=s}^{k}\left( {\begin{array}{c}k\\ p\end{array}}\right) \frac{1}{\lambda }\int _0^1t^{\frac{p}{\theta } +\frac{1}{\lambda }-1}(1-t^{\frac{1}{\theta }})^{k-p}dt\nonumber \\&=\sum _{p=s}^{k}\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) (-1)^q \frac{1}{\lambda }\int _0^1t^{\frac{p+q}{\theta }+\frac{1}{\lambda }-1}dt\nonumber \\&=\sum _{p=s}^{k}\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) \frac{(-1)^q \theta }{\theta +\lambda (p+q)}. \end{aligned}$$

(3)

The MLE of $R_{s,k}$ will be obtained by deriving the MLE of $\theta$, $\lambda$ and $\alpha$. It is known that n systems are put on the life-testing experiment. So, to constructing the likelihood function, the samples can be shown as

$$\begin{aligned} {\mathop {\left( \begin{array}{c} Y_{1} \\ \vdots \\ Y_{n} \end{array} \right) }\limits ^{\text {Observed stress variables}}} ~~\text{ and }~~~~~ {\mathop {\left( \begin{array}{cccc} X_{11} &{}\quad \ldots &{}\quad X_{1k} \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ X_{n1} &{}\quad \ldots &{}\quad X_{nk} \end{array}\right) ,}\limits ^{\text {Observed strength variables}}} \end{aligned}$$

where $\{Y_{1},\ldots ,Y_n\}$ is a AT-II HPC sample from $W(\alpha ,\lambda )$ under the scheme $\{N,n,T_1,S_1,\ldots ,S_n)\}$ such that $Y_{J_1}<T_1<Y_{J_1+1}$. Also, $\{X_{i1},\ldots ,X_{ik}\},~i=1,\ldots ,n,$ is a AT-II HPC sample from $W(\alpha ,\theta )$ under the AT-II HPC scheme $\{K,k,T_2,R_{i1},\ldots ,R_{ik}\}$ such that $X_{iJ_2}<T_2<X_{iJ_2+1}$. Therefore, the likelihood function of $\theta$, $\lambda$ and $\alpha$ can be obtained as

$$\begin{aligned} L(\alpha ,\beta ,\lambda |\text {data})&=c_1\prod _{i=1}^{n}\left( c_2 \prod _{j=1}^{k}{f_X(x_{ij})}\prod _{j=1}^{J_2}[1-{F_X(x_{ij})}]^{R_{ij}} [1-{F_X(x_{ik})}]^{R_{ik}}\right) {f_Y(y_{i})}\\&\quad \times \prod _{i=1}^{J_1}[1-{F_Y(y_{i})}]^{S_i}[1-{F_Y(y_n)}]^{S_n}. \end{aligned}$$

Regrading the advantages of this likelihood function, this function is a general likelihood function. For example, in the case $T_1=T_2=\infty$, the likelihood function for $R_{s,k}$ in the progressive censored sample is obtained. When $k=1$ the likelihood function for $R=P(X<Y)$ in the adaptive hybrid progressive censored scheme (by making a few changes in symbols) is obtained. Also, when $k=1$ and $T_1=T_2=\infty$ the likelihood function for $R=P(X<Y)$ in the progressive censored scheme (by making a few changes in symbols) is derived. Moreover, when $T_1=T_2=\infty$ and $R_{ij}=0,~S_i=0$ the likelihood function for $R_{s,k}$ in complete sample is earned. Furthermore, when $k=1$, $T_1=T_2=\infty$ and $R_{ij}=0,~S_i=0$, the likelihood function for $R=P(X<Y)$ in complete sample is achieved.

Based on the observed data, the likelihood function is as

$$\begin{aligned} L(\alpha ,\beta ,\lambda |\text {data})&=\displaystyle c_1 c_2^n \frac{\alpha ^{n(k+1)}}{\theta ^{nk}\lambda ^n} \bigg (\prod _{i=1}^{n} y_i^{\alpha -1}\bigg ) e^{\displaystyle -\frac{1}{\lambda }\bigg [\sum \limits _{i=1}^n y_i^\alpha +\sum \limits _{i=1}^{J_1}S_iy_{i}^\alpha +S_ny_n^\alpha \bigg ]}\nonumber \\&\times \bigg (\prod _{i=1}^{n}\prod _{j=1}^k x_{ij}^{\alpha -1}\bigg )e^{\displaystyle -\frac{1}{\theta }\bigg [\sum \limits _{i=1}^n\sum \limits _{j=1}^kx_{ij}^\alpha + \sum \limits _{i=1}^n \sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^\alpha +\sum _{i=1}^nR_{ik}x_{ik}^\alpha \bigg ]}. \end{aligned}$$

(4)

The log-likelihood function ignoring the additive constant, from (4), is

$$\begin{aligned} \ell (\alpha ,\beta ,\lambda |\text {data})&=n(k+1)\log (\alpha )-nk\log (\theta ) -n\log (\lambda )\\&\quad +(\alpha -1)\bigg (\sum _{i=1}^n\log (y_i)+ \sum _{i=1}^n\sum _{j=1}^k\log (x_{ij})\bigg )\\&\quad -\frac{1}{\theta }\bigg [\sum \limits _{i=1}^n\sum \limits _{j=1}^k x_{ij}^\alpha + \sum \limits _{i=1}^n \sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^\alpha +\sum _{i=1}^nR_{ik}x_{ik}^\alpha \bigg ]\\&\quad -\frac{1}{\lambda }\bigg [\sum \limits _{i=1}^n y_i^\alpha +\sum \limits _{i=1}^{J_1}S_iy_{i}^\alpha +S_ny_n^\alpha \bigg ]. \end{aligned}$$

So, with solving the following equations, the MLE of $\theta$, $\lambda$ and $\alpha$, say $\widehat{\theta }$, $\widehat{\lambda }$ and $\widehat{\alpha }$, respectively, can be resulted

$$\begin{aligned} \frac{\partial \ell }{\partial \theta }&=-\frac{nk}{\theta }+\frac{1}{\theta ^2} \bigg [\sum \limits _{i=1}^n\sum \limits _{j=1}^kx_{ij}^\alpha + \sum \limits _{i=1}^n \sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^\alpha +\sum _{i=1}^nR_{ik}x_{ik}^\alpha \bigg ], \end{aligned}$$

(5)

$$\begin{aligned} \frac{\partial \ell }{\partial \lambda }&=-\frac{n}{\lambda }+\frac{1}{\lambda ^2} \bigg [\sum \limits _{i=1}^n y_i^\alpha +\sum \limits _{i=1}^{J_1}S_iy_{i}^\alpha +S_ny_n^\alpha \bigg ], \end{aligned}$$

(6)

$$\begin{aligned} \frac{\partial \ell }{\partial \alpha }&=\frac{n(k+1)}{\alpha }+\sum _{i=1}^n \log (y_i)-\frac{1}{\lambda }\bigg [\sum \limits _{i=1}^n y_i^\alpha \log (y_i)\nonumber \\&\quad +\;\sum \limits _{i=1}^{J_1}S_iy_{i}^\alpha \log (y_i) +S_ny_n^\alpha \log (y_n)\bigg ]\nonumber \\&\quad +\;\sum _{i=1}^n\sum _{j=1}^k\log (x_{ij})-\frac{1}{\theta }\bigg [\sum \limits _{i=1}^n \sum \limits _{j=1}^kx_{ij}^\alpha \log (x_{ij})+ \sum \limits _{i=1}^n \sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^\alpha \log (x_{ij})\nonumber \\&\quad +\;\sum _{i=1}^nR_{ik}x_{ik}^\alpha \log (x_{ik})\bigg ]=0. \end{aligned}$$

(7)

Obviously, we can obtain from (5) and (6)

$$\begin{aligned} \widehat{\theta }(\alpha )&=\frac{1}{nk}\bigg [\displaystyle \sum \limits _{i=1}^n \sum \limits _{j=1}^kx_{ij}^\alpha + \sum \limits _{i=1}^n \sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^\alpha +\sum _{i=1}^nR_{ik}x_{ik}^\alpha \bigg ],\\ \widehat{\lambda }(\alpha )&=\frac{1}{n}\bigg [\displaystyle \sum \limits _{i=1}^n y_i^\alpha +\sum \limits _{i=1}^{J_1}S_iy_{i}^\alpha +S_ny_n^\alpha \bigg ]. \end{aligned}$$

To find the solution of Eq. (7), a simple iterative procedure, for example, the Newton-Raphson method, can be applied. So, once the value of $\widehat{\alpha }$ should be derived and then $\widehat{\theta }$ and $\widehat{\lambda }$ can result. Consequently, the MLE of $R_{s,k}$ becomes

$$\begin{aligned} \widehat{R}^{MLE}_{s,k}=\sum _{p=s}^{k}\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) \frac{(-1)^q\widehat{\theta }}{\widehat{\theta }+\widehat{\lambda }(p+q)}. \end{aligned}$$

(8)

2.2 Approximate maximum likelihood estimation

As we have seen in the previous section, based on AT-II HPC samples, the MLE of $\theta$, $\lambda$, $\alpha$ and hence $R_{s,k}$ cannot be obtained in a closed form. To solve this problem, we try to obtain AMLEs of the parameters.

Let $Z''$ has Extreme value distribution, in symbols $Z''\sim EV(\mu ,\sigma )$, if it has the pdf as follows:

$$\begin{aligned} f_{Z''}(z)&=\frac{1}{\sigma }e^{\frac{z-\mu }{\sigma }-e^{\frac{z-\mu }{\sigma }}}, \quad z\in \mathbb {R},~~ \mu \in \mathbb {R},\sigma >0. \end{aligned}$$

It is obvious that if $Z'\sim W(\alpha ,\theta )$ and $Z''=\log (Z')$, then $Z''\sim EV(\mu ,\sigma )$, where $\mu =\frac{1}{\alpha }\log (\theta )$ and $\sigma =\frac{1}{\alpha }$. Now, suppose that $\{Y_{1},\ldots ,Y_n\}$ be a AT-II HPC sample from $W(\alpha ,\lambda )$ under the scheme $\{N,n,T_1,S_1,\ldots ,S_n\}$ such that $Y_{J_1}<T_1<Y_{J_1+1}$. Also, $\{X_{i1},\ldots ,X_{ik}\},~i=1,\ldots ,n,$ is a AT-II HPC sample from $W(\alpha ,\theta )$ under the AT-II HPC scheme $\{K,k,T_2,R_{i1},\ldots ,R_{ik}\}$ such that $X_{iJ_2}<T_2<X_{iJ_2+1}$. Moreover, let $U_{ij}=\log (X_{ij})$ and $V_i=\log (Y_i)$. So, $U_{ij}\sim EV(\mu _1,\sigma )$ and $V_i\sim EV(\mu _2,\sigma )$, where

$$\begin{aligned} \mu _1=\frac{1}{\alpha }\log (\theta ), \quad \mu _2=\frac{1}{\alpha }\log (\lambda ), \; \sigma =\frac{1}{\alpha }. \end{aligned}$$

So, with ignoring the constant value, based on the observed data $\{U_{i1},\ldots ,U_{ik}\}$, $i=1,\ldots ,n$ and $\{V_{1},\ldots ,V_{n}\}$, the log-likelihood function can be obtained by

$$\begin{aligned} \ell ^*(\mu _1,\mu _2,\sigma |\text {data})&=\sum _{i=1}^n\sum _{j=1}^kt_{ij} -\sum _{i=1}^n\sum _{j=1}^ke^{t_{ij}}- \sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}e^{t_{ij}}-\sum _{i=1}^nR_{ik}e^{t_{ik}}\\&\quad +\; \sum _{j=1}^nz_i-\sum _{i=1}^ne^{z_i}- \sum _{i=1}^{J_1}S_ie^{z_i}-S_ne^{z_n}-(nk+n)\log (\sigma ), \end{aligned}$$

where $\displaystyle t_{ij}=\frac{u_{ij}-\mu _1}{\sigma }$ and $\displaystyle z_i=\frac{v_i-\mu _2}{\sigma }$. The usual equations, with taking derivatives of the above equation with respect to $\mu _1$, $\mu _2$ and $\sigma$, can be derived by

$$\begin{aligned} \frac{\partial \ell ^*}{\partial \mu _1}&=-\frac{1}{\sigma }\bigg [nk -\sum _{i=1}^n\sum _{j=1}^{k}e^{t_{ij}}- \sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}e^{t_{ij}}-\sum _{i=1}^n R_{ik}e^{t_{ik}}\bigg ]=0,\\ \frac{\partial \ell ^*}{\partial \mu _2}&=-\frac{1}{\sigma }\bigg [n-\sum _{i=1}^ne^{z_i} -\sum _{i=1}^{J_1}S_ie^{z_i}-S_ne^{z_n}\bigg ]=0,\\ \frac{\partial \ell ^*}{\partial \sigma }&=-\frac{1}{\sigma }\bigg [(nk+n) +\sum _{i=1}^n\sum _{j=1}^{k}t_{ij}-\sum _{i=1}^n \sum _{j=1}^{k}t_{ij}e^{t_{ij}} -\sum _{i=1}^n\sum _{j=1}^{J_2}R_{ij}t_{ij}e^{t_{ij}}-\sum _{i=1}^nR_{ik}t_{ik} e^{t_{ik}}\\&\quad +\sum _{i=1}^nz_i-\sum _{i=1}^nz_ie^{z_i} -\sum _{i=1}^nS_iz_ie^{z_i}-S_nz_ne^{z_n}\bigg ]=0. \end{aligned}$$

We derive the AMLEs of $\theta$, $\lambda$, $\alpha$ and $R_{s,k}$, by expanding the functions $e^{t_{ij}}$ and $e^{z_i}$, in Taylor series around the points $\nu _i=\log \big (-\log (1-q_i)\big )$ and $\nu '_{ij}=\log \big (-\log (1-q'_{ij})\big )$, respectively, where

$$\begin{aligned} q_i&=1-\prod _{m=n-i+1}^{n}\frac{m+\sum \limits _{l=n-m+1}^nS_l}{m+1+\sum \limits _{l=n-m+1}^nS_l}, \quad i=1,\ldots ,n, \end{aligned}$$

and

$$\begin{aligned} q'_{ij}&=1-\prod _{m=k-j+1}^{k}\frac{m+\sum \limits _{l=k-m+1}^kR_l}{m+1 +\sum \limits _{l=k-m+1}^kR_l}, \quad j=1,\ldots ,k,~i=1,\ldots ,n. \end{aligned}$$

Then, we keep only the first-order derivatives in Taylor series and obtain the following results:

$$\begin{aligned} e^{t_{ij}}=\alpha _{ij}+\beta _{ij}t_{ij} \quad \text {and}\; e^{z_i}=\bar{\alpha }_i+\bar{\beta }_iz_i, \end{aligned}$$

where

$$\begin{aligned} \alpha _{ij}=e^{\nu '_{ij}}(1-\nu '_{ij}),~\beta _{ij}=e^{\nu '_{ij}} \quad \text {and} \quad \bar{\alpha }_i=e^{\nu _i}(1-\nu _i),~\bar{\beta }_i=e^{\nu _i}. \end{aligned}$$

The AMLEs of $\mu _1$, $\mu _2$ and $\sigma$, say $\hat{\hat{\mu }}_1$, $\hat{\hat{\mu }}_2$ and $\hat{\hat{\sigma }}$, respectively, by applying the linear approximations, can be provided as

$$\begin{aligned} \hat{\hat{\mu }}_1&=A_1+\hat{\hat{\sigma }} B_1,\quad \hat{\hat{\mu }}_2=A_2+\hat{\hat{\sigma }} B_2,\\ \hat{\hat{\sigma }}&=\frac{-(D_1+D_2)+\sqrt{(D_1+D_2)^2 +4(C_1+C_2)(E_1+E_2)}}{2(C_1+C_2)}, \end{aligned}$$

where

$$\begin{aligned} A_1&=\frac{\sum \limits _{i=1}^n\sum \limits _{j=1}^k\beta _{ij}u_{ij} +\sum \limits _{i=1}^n\sum \limits _{j=1}^{J_2}R_{ij}\beta _{ij}u_{ij} +\sum \limits _{i=1}^nR_{ik}\beta _{ik}u_{ik}}{\sum \limits _{i=1}^n \sum \limits _{j=1}^k\beta _{ij} +\sum \limits _{i=1}^n\sum \limits _{j=1}^{J_2}R_{ij}\beta _{ij} +\sum \limits _{i=1}^nR_{ik}\beta _{ik}}, \\ A_2&=\frac{\sum \limits _{i=1}^n\bar{\beta }_iv_i+\sum \limits _{i=1}^{J_1}S_i \bar{\beta }_iv_i+S_n\bar{\beta }_nv_n}{\sum \limits _{i=1}^n\bar{\beta }_i +\sum \limits _{i=1}^{J_1}S_i\bar{\beta }_i +S_n\bar{\beta }_n},\\ B_1&=\frac{-nk+\sum \limits _{i=1}^n\sum \limits _{j=1}^k\alpha _{ij} +\sum \limits _{i=1}^n\sum \limits _{j=1}^{J_2}R_{ij}\alpha _{ij} +\sum \limits _{i=1}^nR_{ik}\alpha _{ik}}{\sum \limits _{i=1}^n\sum \limits _{j=1}^k\beta _{ij} +\sum \limits _{i=1}^n\sum \limits _{j=1}^{J_2}R_{ij}\beta _{ij} +\sum \limits _{i=1}^nR_{ik}\beta _{ik}},\\ B_2&=\frac{-n+\sum \limits _{i=1}^n\bar{\alpha }_i+\sum \limits _{i=1}^{J_1} S_i\bar{\alpha }_i +S_n\bar{\alpha }_n}{\sum \limits _{i=1}^n\bar{\beta }_i+\sum \limits _{i=1}^{J_1} S_i\bar{\beta }_i +S_n\bar{\beta }_n},\\ C_1&=nk-nkB_1+B_1\sum _{i=1}^n\sum _{j=1}^k\alpha _{ij} +B_1\sum _{i=1}^n \sum _{j=1}^{J_2}R_{ij}\alpha _{ij}+B_1\sum _{i=1}^nR_{ik}\alpha _{ik}\\&\quad -B_1^2\sum _{i=1}^n\sum _{j=1}^k\beta _{ij} -B_1^2\sum _{i=1}^n\sum _{j=1}^{J_2}\beta _{ij}R_{ij} -B_1^2\sum _{i=1}^nR_{ik}\beta _{ik},\\ C_2&=n-nB_2+B_2\sum _{i=1}^n\bar{\alpha }_i +B_2\sum _{i=1}^{J_1}S_i\bar{\alpha }_i+B_2S_n\bar{\alpha }_n\\&\quad -B_2^2\sum _{i=1}^n\beta _i -B_2^2\sum _{i=1}^{J_1}\bar{\beta }_iS_i-B_2^2S_n\bar{\beta }_n,\\ D_1&=\sum _{i=1}^n\sum _{j=1}^{k}(1-\alpha _{ij})(u_{ij}-A_1)+2B_1 \sum _{i=1}^n\sum _{j=1}^k\beta _{ij}(u_{ij}-A_1)\\&\quad -\sum _{i=1}^{n} \sum _{j=1}^{J_2}R_{ij}\alpha _{ij}(u_{ij}-A_1)\\&\quad +2B_1\sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}\beta _{ij}(u_{ij}-A_1) -\sum _{i=1}^nR_{ik}\alpha _{ik}(u_{ik}-A_1)\\&\quad +2B_1\sum _{i=1}^nR_{ik}\beta _{ik} (u_{ik}-A_1),\\ D_2&=\sum _{i=1}^n(1-\bar{\alpha }_i)(v_i-A_2)+2B_2\sum _{i=1}^n\bar{\beta }_i (v_i-A_2)-\sum _{i=1}^{J_1}S_i\bar{\alpha }_i(v_i-A_2)\\&\quad +2B_2\sum _{i=1}^{J_1}S_i\bar{\beta }_i(v_i-A_2)-S_n\bar{\alpha }_n(v_n-A_2) +2B_2S_n\bar{\beta }_n(v_n-A_2),\\ E_1&=\sum _{i=1}^n\sum _{j=1}^k\beta _{ij}(u_{ij}-A_1)^2+\sum _{i=1}^{n} \sum _{j=1}^{J_2}R_{ij}\beta _{ij}(u_{ij}-A_1)^2+\sum _{i=1}^nR_{ik}\beta _{ik} (u_{ik}-A_1)^2,\\ E_2&=\sum _{i=1}^n\bar{\beta }_i(v_i-A_2)^2+\sum _{i=1}^{J_1}S_i\bar{\beta }_i (v_i-A_2)^2+S_n\bar{\beta }_n(v_n-A_2)^2. \end{aligned}$$

After deriving $\hat{\hat{\mu }}_1$, $\hat{\hat{\mu }}_2$ and $\hat{\hat{\sigma }}$, the AMLEs of $\theta$, $\lambda$, $\alpha$ and so $R_{s,k}$, say $\hat{\hat{\theta }}$, $\hat{\hat{\lambda }}$, $\hat{\hat{\alpha }}$ and $\hat{\hat{R}}_{s,k}$, respectively, can be evaluated by $\hat{\hat{\theta }}=e^{\frac{\hat{\hat{\mu }}_1}{\hat{\hat{\sigma }}}}$, $\hat{\hat{\lambda }}=e^{\frac{\hat{\hat{\mu }}_2}{\hat{\hat{\sigma }}}}$, $\hat{\hat{\alpha }}=\frac{1}{\hat{\hat{\sigma }}}$, and so

$$\begin{aligned} \hat{\hat{R}}_{s,k}=\sum _{p=s}^{k}\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) \frac{(-1)^q\hat{\hat{\theta }}}{\hat{\hat{\theta }}+\hat{\hat{\lambda }}(p+q)}. \end{aligned}$$

(9)

2.3 Confidence intervals

2.3.1 Asymptotic confidence interval

In this section, we derive the asymptotic confidence interval of $R_{s,k}$. To reach this aim, by using the multivariate central limit theorem, we obtain the asymptotic distribution of unknown parameters, i.e. $\alpha$, $\theta$, $\lambda$, and by applying the delta method, we provide the asymptotic distribution of $R_{s,k}$.

We denote the expected Fisher information matrix of $\Theta =(\theta _1,\theta _2,\theta _3)=(\alpha ,\theta ,\lambda )$ by $J(\Theta ) = -E(I(\Theta ))$, where $\displaystyle I(\Theta ) = [I_{ij}]=[{\partial ^2\ell }/{(\partial \theta _i\partial \theta _j)}]$, $i, j = 1, 2, 3$, is the observed information matrix. In our case, the observed Fisher information matrix is obtained by

$$\begin{aligned} I_{11}&=-\frac{n(k+1)}{\alpha ^2}-\frac{1}{\lambda }\bigg [\sum _{i=1}^n y_i^\alpha \log ^2(y_i)+\sum _{i=1}^{J_1}S_iy_i^\alpha \log ^2(y_i) +S_ny_n^\alpha \log ^2(y_n)\bigg ]\\&\quad -\; \frac{1}{\theta }\bigg [\sum _{i=1}^n\sum _{j=1}^k x_{ij}^\alpha \log ^2(x_{ij})+\sum _{i=1}^n\sum _{j=1}^{J_2}R_{ij} x_{ij}^\alpha \log ^2(x_{ij})+\sum _{j=1}^{n}R_{ik} x_{ik}^\alpha \log ^2(x_{ik})\bigg ],\\ I_{12}&=\frac{1}{\theta ^2}\bigg [\sum _{i=1}^{n}\sum _{j=1}^kx_{ij}^\alpha \log (x_{ij}) +\sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}x_{ij}^\alpha \log (x_{ij}) +\sum _{i=1}^{n}R_{ik}x_{ik}^\alpha \log (x_{ik})\bigg ]=I_{21},\\ I_{13}&=\frac{1}{\lambda ^2}\bigg [\sum _{i=1}^{n}y_{i}^\alpha \log (y_i) +\sum _{i=1}^{J_1}S_iy_{i}^\alpha \log (y_i) +S_ny_{n}^\alpha \log (y_n)\bigg ]=I_{31},\\ I_{22}&=\frac{nk}{\theta ^2}-\frac{2}{\theta ^3}\bigg [\sum _{i=1}^{n} \sum _{j=1}^kx_{ij}^\alpha +\sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}x_{ij}^\alpha +\sum _{i=1}^{n}R_{ik}x_{ik}^\alpha \bigg ],\\ I_{33}&=\frac{n}{\lambda ^2}-\frac{2}{\lambda ^3}\bigg [\sum _{i=1}^{n}y_{i}^\alpha +\sum _{i=1}^{J_1}S_iy_{i}^\alpha +S_ny_{n}^\alpha \bigg ],\\ I_{23}&=0=I_{32}, \end{aligned}$$

Lemma 1

Suppose that $\{Z_{1},\ldots ,Z_{n}\}$ is a AT-II HPC sample from $W(\alpha ,\theta )$ with censored scheme $\{N,n,T,R_1,\ldots ,R_n\}$, then

• (i) $\mathbb {E}(Z_i^\alpha )=\theta C_{i-1}\sum \limits _{d=1}^{i} \frac{a_{i,d}}{\eta ^2_{d}},$

• (ii) $\mathbb {E}(Z_i^\alpha \log (Z_i))=\frac{\theta C_{i-1}}{\alpha } \sum \limits _{d=1}^{i}\frac{a_{i,d}}{\eta ^2_{d}}[\psi (2) -\log (\frac{\eta _d}{\theta })]$,

• (iii) $\mathbb {E}(Z_i^\alpha \log ^2(Z_i))=\frac{\theta C_{i-1}}{\alpha ^2} \sum \limits _{d=1}^{i}\frac{a_{i,d}}{\eta ^2_{d}}\{[\psi (2) -\log (\frac{\eta _d}{\theta })]^2+\zeta (2,2)\}$,

where $\psi (x),~\zeta (x,y)$ are Euler’s psi and Riemann’s zeta functions, respectively. Also, $\eta _d=N-d+1+\sum \nolimits _{l=1}^{d-1}R_l$, $C_{i-1}=\prod \nolimits _{d=1}^i\eta _d$, $a_{i,d}=\prod \nolimits _{{\mathop {l\ne i}\limits ^{l=1}}}^d\frac{1}{\eta _l-\eta _i}$.

Proof

As given in Ng et al. (2009), if we let $\{Z_{1},\ldots ,Z_{n}\}$ be a AT-II HPC sample from $W(\alpha ,\theta )$, then the pdf of $Z_i$ is

$$\begin{aligned} f_{Z_{i}(z)}=C_{i-1}\sum _{d=1}^ia_{i,d}f_Z(z)[1-F_Z(z)]^{\eta _d-1} =\frac{\alpha }{\theta } C_{i-1}\sum _{d=1}^ia_{i,d}z^{\alpha -1}e^{-z^\alpha \frac{\eta _d}{\theta }}. \end{aligned}$$

• (i) A simple method is presented for proving this part.

• (ii) We use the table of the integrals from Gradshteyn and Ryzhik (1994) (formula 4.352(1)) and prove this part as

  $$\begin{aligned} \mathbb {E}\big (Z_i^\alpha \log (Z_i)\big )&=\int _0^\infty z^\alpha \log (z)f_{Z_i}(z)dz\\&=\frac{\alpha }{\theta } C_{i-1}\sum _{d=1}^ia_{i,d}\int _{0}^\infty z^{2\alpha -1}\log (z)e^{-z^\alpha \frac{\eta _d}{\theta }}dz\\&=\frac{\theta C_{i-1}}{\alpha }\sum \limits _{d=1}^{i}\frac{a_{i,d}}{\eta ^2_{d}}\left[ \psi (2) -\log \left( \frac{\eta _d}{\theta }\right) \right] . \end{aligned}$$

• (iii) We use the table of the integrals from Gradshteyn and Ryzhik (1994) (formula 4.358(2)) and prove this part as

  $$\begin{aligned} \mathbb {E}\big (Z_i^\alpha \log ^2(Z_i)\big )&=\int _0^\infty z^\alpha \log ^2(z)f_{Z_i}(z)dz\\&=\frac{\alpha }{\theta } C_{i-1}\sum _{d=1}^ia_{i,d}\int _{0}^\infty z^{2\alpha -1}\log ^2(z)e^{-z^\alpha \frac{\eta _d}{\theta }}dz\\&=\frac{\theta C_{i-1}}{\alpha ^2}\sum \limits _{d=1}^{i}\frac{a_{i,d}}{\eta ^2_{d}} \left\{ \left[ \psi (2)-\log \left( \frac{\eta _d}{\theta }\right) \right] ^2+\zeta (2,2)\right\} . \end{aligned}$$

  $\square$

By using Lemma 1,

$$\begin{aligned} J_{11}&=\frac{n(k+1)}{\alpha ^2}+\frac{1}{\alpha ^2}\bigg [\sum _{i=1}^nC_{i-1}\sum _{d=1}^{i} \frac{a_{i,d}}{\eta ^2_{d}}\left\{ \left[ \psi (2)-\log \left( \frac{\eta _d}{\theta }\right) \right] ^2+\zeta (2,2)\right\} \\&\quad +\sum _{i=1}^{J_1}S_iC_{i-1}\sum _{d=1}^{i} \frac{a_{i,d}}{\eta ^2_{d}}\\&\quad \times \left\{ \left[ \psi (2)-\log \left( \frac{\eta _d}{\theta }\right) \right] ^2+\zeta (2,2)\right\} +S_nC_{n-1}\\&\quad \times \; \sum _{d=1}^{n} \frac{a_{n,d}}{\eta ^2_{d}}\left\{ \left[ \psi (2)-\log \left( \frac{\eta _d}{\theta }\right) \right] ^2+\zeta (2,2)\right\} \bigg ]\\&\quad +\frac{1}{\alpha ^2}\bigg [\sum _{i=1}^n\sum \limits _{j=1}^kC_{j-1}\sum \limits _{d=1}^{j} \frac{a_{j,d}}{\eta ^2_{d}}\left\{ \left[ \psi (2)-\log \left( \frac{\eta _d}{\theta }\right) \right] ^2+\zeta (2,2)\right\} \\&\quad +\sum _{i=1}^n\sum \limits _{j=1}^{J_2}R_{ij}C_{j-1}\sum \limits _{d=1}^{j} \frac{a_{j,d}}{\eta ^2_{d}}\\&\quad \times \{[\psi (2)-\log (\frac{\eta _d}{\theta })]^2+\zeta (2,2)\} +\sum _{i=1}^nR_{ik}C_{i-1}\\&\qquad \times \; \sum \limits _{d=1}^{i} \frac{a_{i,d}}{\eta ^2_{d}}\left\{ \left[ \psi (2)-\log \left( \frac{\eta _d}{\theta }\right) \right] ^2 +\zeta (2,2)\right\} \bigg ],\\ J_{12}&=\frac{1}{\alpha \theta }\bigg [\sum \limits _{i=1}^n\sum \limits _{j=1}^kC_{j-1} \sum \limits _{d=1}^{j}\frac{a_{j,d}}{\eta ^2_{d}} \left[ \log \left( \frac{\eta _d}{\theta }\right) -\psi (2)\right] +\sum \limits _{i=1}^n\sum \limits _{j=1}^{J_2}R_{ij}C_{j-1} \sum \limits _{d=1}^{j}\frac{a_{j,d}}{\eta ^2_{d}}\\&\quad \times \left[ \log \left( \frac{\eta _d}{\theta }\right) -\psi (2)\right] +\sum \limits _{i=1}^nR_{ik}C_{i-1} \sum \limits _{d=1}^{i}\frac{a_{i,d}}{\eta ^2_{d}}\left[ \log \left( \frac{\eta _d}{\theta }\right) -\psi (2)\right] \bigg ]=J_{21},\\ J_{13}&=\frac{1}{\alpha \lambda }\bigg [\sum \limits _{i=1}^nC_{i-1} \sum \limits _{d=1}^{i}\frac{a_{i,d}}{\eta ^2_{d}}\left[ \log \left( \frac{\eta _d}{\lambda }\right) -\psi (2)\right] +\sum \limits _{i=1}^{J_1}S_iC_{i-1} \sum \limits _{d=1}^{i}\frac{a_{i,d}}{\eta ^2_{d}}\\&\quad \times \left[ \log \left( \frac{\eta _d}{\lambda }\right) -\psi (2)\right] +S_nC_{n-1} \sum \limits _{d=1}^{n}\frac{a_{n,d}}{\eta ^2_{d}}\left[ \log \left( \frac{\eta _d}{\lambda }\right) -\psi (2)\right] \bigg ]=J_{31},\\ J_{22}&=-\frac{nk}{\theta ^2}+\frac{2}{\theta ^2}\bigg [\sum \limits _{i=1}^n\sum \limits _{j=1}^kC_{j-1} \sum \limits _{d=1}^j\frac{a_{j,d}}{\eta ^2_{d}}+\sum \limits _{i=1}^n\sum \limits _{j=1}^{J_2}R_{ij}C_{j-1} \sum \limits _{d=1}^j\frac{a_{j,d}}{\eta ^2_{d}}\\&\quad +\sum \limits _{i=1}^nR_{ik}C_{i-1} \sum \limits _{d=1}^i\frac{a_{i,d}}{\eta ^2_{d}}\bigg ],\\ J_{23}&=0=J_{32},\\ J_{33}&=-\frac{n}{\lambda ^2}+\frac{2}{\lambda ^2}\bigg [\sum \limits _{i=1}^nC_{i-1}\sum \limits _{d=1}^i \frac{a_{i,d}}{\eta ^2_{d}}+\sum \limits _{i=1}^{J_1}S_iC_{i-1}\sum \limits _{d=1}^i \frac{a_{i,d}}{\eta ^2_{d}}+S_nC_{n-1}\sum \limits _{d=1}^n \frac{a_{n,d}}{\eta ^2_{d}}\bigg ]. \end{aligned}$$

By using the multivariate central limit theorem, $(\widehat{\alpha },\widehat{\theta },\widehat{\lambda }) \sim N_3((\alpha ,\theta ,\lambda ),\mathbf {J^{-1}}(\alpha ,\theta ,\lambda )),$ where $\mathbf {J^{-1}}(\alpha ,\beta ,\lambda )$ is a symmetric matrix which has the following representation:

$$\begin{aligned} \mathbf {J^{-1}}(\alpha ,\theta ,\lambda ) = \frac{1}{|\mathbf {J}(\alpha ,\theta ,\lambda )|}\left( \begin{array}{ccc} J_{22}J_{33} &{}\quad -J_{12}J_{33} &{}\quad -J_{13}J_{22} \\ &{}\quad J_{11}J_{33}-J_{13}^2 &{}\quad J_{13}J_{12} \\ &{}\quad &{}\quad J_{11}J_{22}-J_{12}^2 \end{array} \right) , \end{aligned}$$

where

$$\begin{aligned} |\mathbf {J}(\alpha ,\beta ,\lambda )|=-J_{11}J_{22}J_{33}-J_{12}^2J_{33}-J_{13}^2J_{22}. \end{aligned}$$

Also, by using the delta method, the asymptotic distribution of $\widehat{R}_{s,k}$ can be resulted as $\widehat{R}^{MLE}\sim N(R_{s,k},B)$ where $B=\mathbf {b^TJ^{-1}}(\alpha ,\theta ,\lambda )\mathbf{b}$, in which

$$\begin{aligned} \mathbf {b} = \left[ \frac{\partial R_{s,k}}{\partial \alpha }~~\frac{\partial R_{s,k}}{\partial \theta } ~~ \frac{\partial R_{s,k}}{\partial \lambda }\right] ^T=\left[ 0~~\frac{\partial R_{s,k}}{\partial \theta } ~~ \frac{\partial R_{s,k}}{\partial \lambda }\right] ^T, \end{aligned}$$

with

$$\begin{aligned} \frac{\partial R_{s,k}}{\partial \theta }&=\sum _{p=s}^{k}\sum _{q=0}^{k-p} \left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) \frac{(-1)^{q}\lambda (p+q)}{(\theta +\lambda (p+q))^2}, \end{aligned}$$

(10)

$$\begin{aligned} \frac{\partial R_{s,k}}{\partial \lambda }&=\sum _{p=s}^{k}\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) \frac{(-1)^{q+1}\theta (p+q)}{(\theta +\lambda (p+q))^2}, \end{aligned}$$

(11)

consequently,

$$\begin{aligned} B= & {} \frac{1}{|\mathbf {J}(\alpha ,\beta ,\lambda )|}\bigg [\left( \frac{\partial R_{s,k}}{\partial \theta }\right) ^2\big (J_{11}J_{33}-J^{2}_{13}\big )+\left( \frac{\partial R_{s,k}}{\partial \lambda }\right) ^2\big (J_{11}J_{22}-J^{2}_{12}\big )\\&+\,\,2\left( \frac{\partial R_{s,k}}{\partial \theta }\right) \left( \frac{\partial R_{s,k}}{\partial \lambda }\right) (J_{13}J_{12})\bigg ]. \end{aligned}$$

Therefore, a $100(1-\gamma )\%$ asymptotic confidence interval for $R_{s,k}$ is constructed as

$$\begin{aligned} \left( \widehat{R}^{MLE}_{s,k}-z_{1-\frac{\gamma }{2}}\sqrt{\widehat{B}}, \widehat{R}^{MLE}_{s,k}+z_{1-\frac{\gamma }{2}}\sqrt{\widehat{B}}\right) , \end{aligned}$$

where $z_{\gamma }$ is 100$\gamma$-th percentile of N(0, 1).

2.3.2 Bootstrap confidence interval

All we know with certainty is that the asymptotic confidence intervals, for small sample size, do not perform very well. So the asymptotic confidence intervals can be replaced by bootstrap confidence intervals as an alternative method. In this section, we propose two bootstrap parametric methods: (i) percentile bootstrap method which denoted by Boot-p, based on the original idea of Efron (1982) and (ii) bootstrap-t method which denoted by Boot-t, based on the idea of Hall (1988).

(i) Boot-p method

• 1. Provide the AT-II HPC bootstrap sample $\{y_1,\ldots ,y_{n}\}$ from $W(\alpha ,\lambda )$ under the scheme $\{N,n,T_1,S_1,\ldots ,S_n\}$, provide the AT-II HPC sample $\{x_{i1},\ldots ,x_{ik}\}$, $i=1,\ldots ,n$ from $W(\alpha ,\theta )$ under the scheme $\{K,k,T_2,R_{i1},\ldots ,R_{ik}\}$ and estimate $(\widehat{\alpha },\widehat{\theta },\widehat{\lambda })$.

• 2. Provide the AT-II HPC bootstrap sample $\{y_1^*,\ldots ,y_{n}^*\}$ from $W(\widehat{\alpha },\widehat{\lambda })$ under the scheme $\{N,n,T_1,S_1,\ldots ,S_n\}$ and provide the AT-II HPC sample $\{x_{i1},\ldots ,x_{ik}\}$, $i=1,\ldots ,n$ from $W(\widehat{\alpha },\widehat{\theta })$ under the scheme $\{K,k,T_2,R_{i1},\ldots ,R_{ik}\}$ and by them compute the bootstrap estimate $\widehat{R}^{MLE*}_{s,k}$, using (8).

• 3. Reiterate step 2 NBOOT times.

• 4. Allow $G^*(x) = P(\widehat{R}^{MLE*}_{s,k}\le x)$ be the cdf of $\widehat{R}^{MLE*}_{s,k}$ and define $\widehat{R}^{Bp}_{s,k}(x) = {G^{*}}^{-1}(x)$ for a given x. The $100(1-\gamma )\%$ Boot-p confidence interval of $R_{s,k}$ is provided by

  $$\begin{aligned} \left( \widehat{R}^{Bp}_{s,k}\left( \frac{\gamma }{2}\right) ,\widehat{R}^{Bp}_{s,k} \left( 1-\frac{\gamma }{2}\right) \right) . \end{aligned}$$

(ii) Boot-t method

• 1. Provide the AT-II HPC bootstrap sample $\{y_1,\ldots ,y_{n}\}$ from $W(\alpha ,\lambda )$ under the scheme $\{N,n,T_1,S_1,\ldots ,S_n\}$, provide the AT-II HPC sample $\{x_{i1},\ldots ,x_{ik}\}$, $i=1,\ldots ,n$ from $W(\alpha ,\theta )$ under the scheme $\{K,k,T_2,R_{i1},\ldots ,R_{ik}\}$, estimate $(\widehat{\alpha },\widehat{\theta },\widehat{\lambda })$ and compute $\widehat{R}^{MLE}_{s,k}$.

• 2. Provide the AT-II HPC bootstrap sample $\{y_1^*,\ldots ,y_{n}^*\}$ from $W(\widehat{\alpha },\widehat{\lambda })$ under the scheme $\{N,n,T_1,S_1,\ldots ,S_n\}$, provide the AT-II HPC sample $\{x_{i1},\ldots ,x_{ik}\}$, $i=1,\ldots ,n$ from $W(\widehat{\alpha },\widehat{\theta })$ under the scheme $\{K,k,T_2,R_{i1},\ldots ,R_{ik}\}$, compute the bootstrap estimate $\widehat{R}^{MLE*}_{s,k}$ and the statistic:

  $$\begin{aligned} T^*=\frac{(\widehat{R}^{MLE*}_{s,k}-\widehat{R}^{MLE}_{s,k})}{\sqrt{V(\widehat{R}^{MLE*}_{s,k})}}, \end{aligned}$$

  where $V(\widehat{R}^{MLE*}_{s,k})$ is given in the previous section.

• 3. Reiterate step 2 NBOOT times.

• 4. Allow $H(x)=P(T^*\le x)$ be the cdf of $T^*$, and define $\widehat{R}^{Bt}_{s,k}(x)= \widehat{R}^{MLE}_{s,k} + H^{-1}(x)\sqrt{V(\widehat{R}^{MLE}_{s,k} )}$, for a given x. The $100(1-\gamma )\%$ Boot-t confidence interval of $R_{s,k}$ is given by

  $$\begin{aligned} \left( \widehat{R}^{Bt}_{s,k}\left( \frac{\gamma }{2}\right) ,\widehat{R}^{Bt}_{s,k}\left( 1-\frac{\gamma }{2}\right) \right) . \end{aligned}$$

2.4 Bayes estimation of $R_{s,k}$

In this section, when the unknown parameters $\alpha$, $\theta$ and $\lambda$ are independent random variables, we improve the Bayesian inference about $R_{s,k}$. In details, the Bayes estimate and the corresponding credible intervals of $R_{s,k}$, under the squared error loss function, are derived. To reach this aim, we assume that $\alpha$ has the gamma distribution with the parameters $(a_1,b_1)$, $\theta$ and $\lambda$ have the inverse gamma distributions with the parameters $(a_2,b_2)$ and $(a_3,b_3)$, respectively, such that we show in symbols, $\alpha \sim \Gamma (a_1,b_1)$, $\theta \sim {\text{ I }}\Gamma (a_2,b_2)$ and $\lambda \sim {\text{ I }}\Gamma (a_3,b_3)$. The joint posterior density function of $\alpha$, $\theta$ and $\lambda$ is proportion with the likelihood function based on the observed sample and the prior distributions of each unknown parameters, i.e.

$$\begin{aligned} \pi (\alpha ,\theta ,\lambda |\text {data})&\propto {L(\alpha ,\theta , \lambda |\text {data})\pi _1(\alpha )\pi _2(\theta )\pi _3(\lambda )}, \end{aligned}$$

(12)

where

$$\begin{aligned} \pi _1(\alpha )\propto \alpha ^{a_1-1}e^{-b_1\alpha }, \quad \pi _2(\theta )\propto \theta ^{-a_2-1}e^{-\frac{b_2}{\theta }}, \; \pi _3(\lambda )\propto \lambda ^{-a_3-1}e^{-\frac{b_3}{\lambda }}. \end{aligned}$$

From the Eq. (12), it is obvious that the Bayes estimates of $\alpha$, $\theta$, $\lambda$ and $R_{s,k}$ cannot be obtained in a closed form. Therefore, we propose two approximation methods to obtain them:

• Lindley’s approximation,

• MCMC method.

2.4.1 Lindley’s approximation

Lindley (1980) has proposed one of the most common numerical techniques to derive the Bayes estimate, in 1980. It is known that the Bayes estimate of $U(\Theta )$ under the squared error loss function is the posterior expectation of $U(\Theta )$, such that

$$\begin{aligned} \mathbb {E}(u(\Theta )|\text{ data })=\frac{\int u(\Theta )e^{Q(\Theta )}d\Theta }{\int e^{Q(\Theta )}d\Theta }, \end{aligned}$$

where $Q(\Theta )=\ell (\Theta )+\rho (\Theta )$, $\ell (\Theta )$ and $\rho (\Theta )$ are the logarithm of the likelihood function and logarithm of the prior density of $\Theta$, respectively. Lindley suggested that $\mathbb {E}(u(\Theta )|\text{ data })$ would be approximated by

$$\begin{aligned} \mathbb {E}(u(\Theta )|\text{ data })=u+\frac{1}{2}\sum _{i}\sum _{j}(u_{ij} +2u_i\rho _j)\sigma _{ij}+\frac{1}{2}\sum _i\sum _j\sum _k\sum _p\ell _{ijk} \sigma _{ij}\sigma _{kp}u_p\bigg |_{\Theta =\widehat{\Theta }}, \end{aligned}$$

where $\Theta =(\theta _1,\dots ,\theta _m)$, $i,j,k,p=1,\dots ,m$, $\widehat{\Theta }$ is the MLE of $\Theta$, $u=u(\Theta )$, $u_i=\partial u/\partial \theta _i$, $u_{ij}=\partial ^2u/(\partial \theta _i\partial \theta _j)$, $\ell _{ijk}=\partial ^3\ell /(\partial \theta _i\partial \theta _j\partial \theta _k)$, $\rho _j=\partial \rho /\partial \theta _j$, and $\sigma _{ij}=(i,j)$th element in the inverse of matrix $[-\ell _{ij}]$ all evaluated at the MLE of the parameters. Therefore, in the case of three parameters $\Theta =(\theta _1,\theta _2,\theta _3)$, after simplifying the above equation we get

$$\begin{aligned} \mathbb {E}(u(\theta )|\text{ data })&=u+(u_1d_1+u_2d_2+u_3d_3+d_4+d_5)\nonumber \\&\quad +\frac{1}{2}[A(u_1\sigma _{11}+u_2\sigma _{12} +u_3\sigma _{13})\nonumber \\&\quad + B(u_1\sigma _{21}+u_2\sigma _{22}+u_3\sigma _{23}) +C(u_1\sigma _{31}+u_2\sigma _{32}+u_3\sigma _{33})], \end{aligned}$$

(13)

which their elements are presented in detail in “Appendix A”. Therefore, the Bayes estimate of $R_{s,k}$ is

$$\begin{aligned} \widehat{R}^{Lin}_{s,k}&=R_{s,k}+[u_2d_2+u_3d_3+d_4+d_5] +\frac{1}{2}[A(u_2\sigma _{12}+u_3\sigma _{13})\nonumber \\&\quad + B(u_2\sigma _{22}+u_3\sigma _{23})+C(u_2\sigma _{23} +u_3\sigma _{33})]. \end{aligned}$$

(14)

It is notable that all parameters are computed at $(\widehat{\alpha },\widehat{\beta },\widehat{\lambda })$.

Because by applying the Lindley’s method, constructing the credible interval is not available, so, by using the Markov Chain Monte Carlo (MCMC) method, we obtain the Bayes estimate and the corresponding HPD credible interval.

2.4.2 MCMC method

After simplifying the Eq. (12), the posterior pdfs of $\theta$, $\lambda$ and $\alpha$ can be easily obtained as

$$\begin{aligned} \theta |\alpha ,\text {data}&\sim \text {I}\Gamma \left( nk+a_2, b_2+\sum _{i=1}^{n}\sum _{j=1}^kx_{ij}^\alpha +\sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}x_{ij}^\alpha +\sum _{i=1}^{n}R_{ik}x_{ik}^\alpha \right) ,\\ \lambda |\alpha ,\text {data}&\sim \text {I}\Gamma \left( n+a_3, b_3 +\sum _{i=1}^{n}y_i^\alpha +\sum _{i=1}^{J_1}S_iy_i^\alpha +S_ny_n^\alpha \right) ,\\ \pi (\alpha |\theta ,\lambda ,\text {data})&\propto \alpha ^{n(k+1)+a_1-1} \bigg (\prod _{i=1}^{n} y_i^{\alpha -1}\bigg ) e^{\displaystyle -b_1\alpha -\frac{1}{\lambda }\bigg [\sum \limits _{i=1}^{n}y_i^\alpha +\sum \limits _{i=1}^{J_1}S_iy_i^\alpha +S_ny_n^\alpha \bigg ]} \\&\times \bigg (\prod _{i=1}^{n}\prod _{j=1}^k x_{ij}^{\alpha -1}\bigg ) e^{\displaystyle -\frac{1}{\theta }\bigg [\sum \limits _{i=1}^{n} \sum \limits _{j=1}^kx_{ij}^\alpha +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^\alpha +\sum \limits _{j=1}^{n}R_{ik}x_{ik}^\alpha \bigg ]}. \end{aligned}$$

As we see above, generating samples from the posterior pdfs of $\theta$ and $\lambda$ can be easily done. On the other hand, because the posterior pdf of $\alpha$ cannot be reduced analytically to a well-known distribution, generating a sample from $\pi (\alpha |\theta ,\lambda ,\text {data})$ is not available, directly. Consequently, with normal proposal distribution, we use the Metropolis-Hastings method to generate a sample from $\pi (\alpha |\theta ,\lambda ,\text {data})$. So, the Gibbs sampling algorithm is as follows:

• 1. Begin with an initial conjecture $(\alpha _{(0)}$, $\theta _{(0)}$, $\lambda _{(0)})$.

• 2. Set $t=1$.

• 3. Generate $\alpha _{(t)}$ from $\pi (\alpha |\theta _{(t-1)},\lambda _{(t-1)}, \text {data})$ with the $N(\alpha _{(t-1)},1)$ as the proposal distribution, using Metropolis-Hastings method.

• 4. Generate $\theta _{(t)}$ from $\text {I}\Gamma (nk+a_2, b_2+\sum \limits _{i=1}^{n}\sum \nolimits _{j=1}^kx_{ij}^{{\alpha _{(t)}}} +\sum \nolimits _{i=1}^{n}\sum \nolimits _{j=1}^{J_2}R_{ij}x_{ij}^{{\alpha _{(t)}}} +\sum \nolimits _{i=1}^{n}R_{ik}x_{ik}^{{\alpha _{(t)}}})$.

• 5. Generate $\lambda _{(t)}$ from $\text {I}\Gamma (n+a_3, b_3+\sum \limits _{i=1}^{n}y_i^{{\alpha _{(t)}}}+\sum \nolimits _{i=1}^{J_1}S_iy_i^{{\alpha _{(t)}}}+S_ny_n^{{\alpha _{(t)}}})$.

• 6. Evaluate $R_{(t)s,k}=\displaystyle \sum _{p=s}^{k}\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) \frac{(-1)^q\theta _{(t)}}{\theta _{(t)}+\lambda _{(t)}(p+q)}.$

• 7. Set $t = t +1$.

• 8. Reiterate steps 3–7, T times.

Using this algorithm, the Bayes estimate of $R_{s,k}$ is given by

$$\begin{aligned} \widehat{R}_{s,k}^{MC}=\frac{1}{T}\sum _{t=1}^{T}R_{(t)s,k}. \end{aligned}$$

(15)

Also, by applying the method of Chen and Shao (1999), the HPD $100(1-\gamma )\%$ credible interval of $R_{s,k}$ is provided.

3 Inference on $R_{s,k}$ if $\alpha$ is known, $\theta$ and $\lambda$ are unknown

3.1 Maximum likelihood estimation of $R_{s,k}$

Let $\{Y_{1},\ldots ,Y_n\}$ is a AT-II HPC sample from $W(\alpha ,\lambda )$ under the scheme $\{N,n,T_1,S_1,\ldots ,S_n\}$ such that $Y_{J_1}<T_1<Y_{J_1+1}$. Also, $\{X_{i1},\ldots ,X_{ik}\},~i=1,\ldots ,n,$ is a AT-II HPC sample from $W(\alpha ,\theta )$ under the AT-II HPC scheme $\{K,k,T_2,R_{i1},\ldots ,R_{ik}\}$ such that $X_{iJ_2}<T_2<X_{iJ_2+1}$. Now, we consider the case that the common shape parameter $\alpha$ is known. From Sect. 2.1, it can be easily obtained that the MLE of $R_{s,k}$ is as follows:

$$\begin{aligned} \widehat{R}^{MLE}_{s,k}= & {} \sum _{p=s}^{k}\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) {(-1)^q}\nonumber \\&\times \; \left( {1+\frac{k(p+q)\bigg [\sum \limits _{i=1}^{n} y_i^\alpha +\sum \limits _{i=1}^{J_1}S_iy_i^\alpha +S_ny_n^\alpha \bigg ]}{\bigg [\sum \limits _{i=1}^{n}\sum \limits _{j=1}^kx_{ij}^\alpha +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^\alpha +\sum \limits _{i=1}^{n}R_{ik}x_{ik}^\alpha \bigg ]}}\right) ^{-1}. \end{aligned}$$

(16)

By applying a similar method in Sect. 2.2, $(\widehat{R}^{MLE}_{s,k}-R_{s,k})\sim N(0,C)$, where

$$\begin{aligned} C=\left( \frac{\partial R_{s,k}}{\partial \theta }\right) ^2\frac{1}{J_{22}}+\left( \frac{\partial R_{s,k}}{\partial \lambda }\right) ^2\frac{1}{J_{33}}. \end{aligned}$$

Consequently, a $100(1-\gamma )\%$ asymptotic confidence interval for $R_{s,k}$ is constructed as

$$\begin{aligned} \left( \widehat{R}^{MLE}_{s,k}-z_{1-\gamma /2}\sqrt{\widehat{C}}, \widehat{R}^{MLE}_{s,k}+z_{1-\gamma /2}\sqrt{\widehat{C}}\right) , \end{aligned}$$

where $z_{\gamma }$ is 100$\gamma$-th percentile of N(0, 1).

3.2 Bayes estimation of $R_{s,k}$

In this section, when the unknown parameters $\theta$ and $\lambda$ are independent random variables, we improve the Bayesian inference about $R_{s,k}$. In details, the Bayes estimate and the corresponding credible intervals of $R_{s,k}$, under the squared error loss function, are derived. To reach this aim, we assume that $\theta$ and $\lambda$ have the inverse gamma distributions with the parameters $(a_2,b_2)$ and $(a_3,b_3)$, respectively. The joint posterior density function of $\theta$ and $\lambda$ is as follows:

$$\begin{aligned} \pi (\theta ,\lambda |\alpha ,\text{ data })=\frac{(V+b_2)^{nk+a_2} (U+b_3)^{n+a_3}}{\lambda ^{n+a_3+1}\theta ^{nk+a_2+1}\Gamma (nk+a_2)\Gamma (n+a_3)} e^{-\frac{1}{\theta }(V+b_2)-\frac{1}{\lambda }(U+b_3)}, \end{aligned}$$

where

$$\begin{aligned} V=\sum \limits _{i=1}^{n}\sum \limits _{j=1}^kx_{ij}^\alpha +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^\alpha +\sum \limits _{i=1}^{n}R_{ik}x_{ik}^\alpha ,\quad \text {and}\quad U=\sum \limits _{i=1}^{n}y_i^\alpha +\sum \limits _{i=1}^{J_1}S_iy_i^\alpha +S_ny_n^\alpha . \end{aligned}$$

(17)

The Bayes estimate of $R_{s,k}$, under the squared error loss function, can be obtained by solving the double integral as follows:

$$\begin{aligned} \widehat{R}^B_{s,k}&=\int _0^\infty \int _0^\infty R_{s,k}\pi (\theta , \lambda |\alpha ,\text{ data })d\theta d\lambda \\&=\sum _{p=s}^k\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) (-1)^q\int _{0}^\infty \int _{0}^\infty \frac{\theta }{\theta +\lambda (p+q)}\pi (\theta ,\lambda |\alpha , \text{ data })d\theta d\lambda . \end{aligned}$$

Using the idea of Kizilaslan and Nadar (2018), the exact Bayes estimate is

$$\begin{aligned} \widehat{R}^B_{s,k}=\left\{ \begin{array}{rl} &{}\sum \limits _{p=s}^k\sum \limits _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) \frac{(-1)^q(1-z)^{n+a_3}(n+a_3)}{w} ~_2F_1(w,n+a_3+1;w+1,z) \quad \text {if }~ |z|<1 ,\\ &{}\\ &{}\sum \limits _{p=s}^k\sum \limits _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) \frac{(-1)^q(n+a_3)}{(1-z)^{nk+a_2}w} ~_2F_1(w,nk+a_2;w+1,\frac{z}{1-z})\qquad \qquad ~ \text {if } ~z<-1, \end{array} \right. \end{aligned}$$

(18)

where $\displaystyle w=nk+n+a_2+a_3$, $\displaystyle z=1-\frac{(U+b_3)(p+q)}{V+b_2}$ and

$$\begin{aligned} {}_2F_1(\alpha ,\beta ;\gamma ,z)=\frac{1}{B(\beta ,\gamma -\beta )} \int _0^1t^{\beta -1}(1-t)^{\gamma -\beta -1}(1-tz)^{-\alpha }dt, \quad ~|z|<1. \end{aligned}$$

The function $~_2F_1(\alpha ,\beta ;\gamma ,z)$ is known as the hypergeometric series and is quickly evaluated and readily available in standard software such as Matlab. Also, by applying the method of Chen and Shao (1999), the HPD $100(1-\gamma )\%$ credible interval of $R_{s,k}$ is provided.

3.3 UMVUE of $R_{s,k}$

Let $\{Y_1,\cdots ,Y_n\}$ is a AT-II HPC sample from $W(\alpha ,\lambda )$ under the scheme $\{N,n,T_1,S_1,\cdots ,S_n\}$ such that $Y_{J_1}<T_1<Y_{J_1+1}$. Also, $\{X_{i1},\cdots ,X_{ik}\}$, $i=1,\cdots ,n$, is a AT-II HPC sample from $W(\alpha ,\theta )$ under the AT-II HPC scheme $\{K,k,T_2,R_{i1},\cdots ,R_{ik}\}$ such that $X_{iJ_2}<T_2<X_{iJ_{2}+1}$. When common shape parameter $\alpha$ is known, the likelihood function is as follows:

$$\begin{aligned} L(\alpha |\theta ,\lambda ,\text {data})&=c_1 c_2^n \frac{\alpha ^{n(k+1)}}{\theta ^{nk}\lambda ^n} \left( \prod _{i=1}^{n} y_i^{\alpha -1}\right) \left( \prod _{i=1}^{n}\prod _{j=1}^k x_{ij}^{\alpha -1}\right) e^{-\frac{1}{\theta }V-\frac{1}{\lambda }U}, \end{aligned}$$

(19)

where V and U are given in (17). From Eq. (19), when $\alpha$ is known, we conclude that V and U are the complete sufficient statistics for $\theta$ and $\lambda$, respectively. By transforming $Y^*_{i}=Y_{i}^\alpha ,~i=1,\dots ,n$, we derive one AT-II HPC sample from the exponential distribution with mean $\lambda$. Now, let

$$\begin{aligned} Z_1&=NY^*_{1},\\ Z_2&=(N-S_1-1)\big (Y^*_{2}-Y^*_{1}\big ),\\ \vdots \\ Z_{J_1}&=\left( N-\sum _{i=1}^{J_1-1}S_i-J_1+1\right) \big (Y^*_{J_1}-Y^*_{J_1-1}\big ),\\ Z_{J_1+1}&=\left( N-\sum _{i=1}^{J_1}S_i-J_1\right) \big (Y^*_{J_1+1}-Y^*_{J_1}\big ),\\ \vdots \\ Z_{n-1}&=\left( N-\sum _{i=1}^{J_1}S_i-n+2\right) \big (Y^*_{n-1}-Y^*_{n-2}\big ),\\ Z_{n}&=\left( N-\sum _{i=1}^{J_1}S_i-n+1\right) \big (Y^*_{n}-Y^*_{n-1}\big ). \end{aligned}$$

By Balakrishnan and Aggarwala (2000), we result that $Z_1,\cdots ,Z_n$ are independent and identically random variables which come from an exponential distribution with mean $\lambda$. So, $U=\sum \nolimits _{i=1}^{n}Z_i\sim \Gamma (n,\frac{1}{\lambda })$.

Lemma 2

Let $X^*_{ij}=X_{ij}^\alpha$, $j=1,\ldots ,k,~i=1,\ldots ,n$. By this notation, the conditional pdfs of $Y^*_{1}$ given $U=u$ and $X^*_{11}$ given $V=v$ are respectively as follows:

$$\begin{aligned} f_{Y^*_{1}|U=u}(y)&=N(n-1)\frac{(u-Ny)^{n-2}}{u^{n-1}}, \quad 0<y<u/N,\\ f_{X^*_{11}|V=v}(x)&=K(nk-1)\frac{(v-Kx)^{nk-2}}{v^{nk-1}}, \quad 0<x<v/K. \end{aligned}$$

Proof

By a similar method as in Kohansal (2017), we prove the lemma. $\square$

Theorem 1

$\widehat{\psi }_U(\theta ,\lambda )$, UMVUE of $\psi (\theta ,\lambda )=\frac{\theta }{\theta +\lambda (p+q)}$, based on the complete sufficient statistics V and U, for $\theta$ and $\lambda$, respectively, is as follows:

$$\begin{aligned} \widehat{\psi }_U(\theta ,\lambda )=\left\{ \begin{array}{rl} \displaystyle 1-\sum \limits _{l=0}^{n-1}(-1)^l \left( \frac{v}{u(p+q)}\right) ^l\frac{{{n-1}\atopwithdelims ()l}}{{{nk+l-1}\atopwithdelims ()l}}&{}\quad \text{ if } ~ v<u(p+q),\\ \displaystyle \sum \limits _{l=0}^{nk-1}(-1)^l \left( \frac{u(p+q)}{v}\right) ^l \frac{{{nk-1}\atopwithdelims ()l}}{{{n+l-1}\atopwithdelims ()l}}&{}\quad \text{ if } ~v>u(p+q). \end{array} \right. \end{aligned}$$

Proof

It is easy to see that $Y^*_{1}$ and $X^*_{11}$ are two random variables which come from the exponential distributions with means $\frac{\lambda }{N}$ and $\frac{\theta }{K}$, respectively. So,

$$\begin{aligned} \phi \big (X^*_{11},Y^*_{1} \big )=\left\{ \begin{array}{rl} 1&{} \quad \text {if }~ KX^*_{11}>N(p+q)Y^*_{1},\\ 0&{} \quad \text {if }~ KX^*_{11}<N(p+q)Y^*_{1}, \end{array} \right. \end{aligned}$$

is an unbiased estimate of $\psi (\theta ,\lambda )$. Therefore,

$$\begin{aligned} \widehat{\psi }_U(\theta ,\lambda )=E\big [\phi \big (X^*_{11},Y^*_{1}\big )|V=v,U=u] =\iint _{\mathcal{A}}f_{X^*_{11}|V=v}(x)f_{Y^*_{1}|U=u}(y)dxdy, \end{aligned}$$

where ${\mathcal{A}}=\{(x,y):0<x<v/K,0<y<u/N,N(p+q)y<Kx\},$ $f_{X^*_{11}|V=v}(x)$ and $f_{Y^*_{1}|U=u}(y)$ are defined in Lemma 2. For $v<u(p+q)$, we have

$$\begin{aligned} \widehat{\psi }_U(\theta ,\lambda )&=\frac{N(n-1)}{u^{n-1}}\frac{K(nk-1)}{v^{nk-1}}\int _{0}^{v/K}\int _{0}^{Kx/(N(p+q))}(u-Ny)^{n-2}(v-Kx)^{nk-2}dydx\\&=1-\frac{K(nk-1)}{u^{n-1}v^{nk-1}}\int _{0}^{v/K}(v-Kx)^{nk-2} \left( u-\frac{Kx}{p+q}\right) ^{n-1}dx~~\left\{ Put: \frac{Kx}{v}=t\right\} \\&=1-(nk-1)\int _0^1(1-t)^{nk-2}\left( 1-\frac{vt}{u(p+q)}\right) ^{n-1}dt\\&=1-(nk-1)\int _0^1(1-t)^{nk-2}\sum _{l=0}^{n-1}(-1)^l\left( {\begin{array}{c}n-1\\ l\end{array}}\right) \left( \frac{vt}{u(p+q)}\right) ^ldt\\&=1-\sum _{l=0}^{n-1}(-1)^{l}\left( \frac{v}{u(p+q)}\right) ^l\frac{\left( {\begin{array}{c}n-1\\ l\end{array}}\right) }{\left( {\begin{array}{c}nk+l-1\\ l\end{array}}\right) }. \end{aligned}$$

Similarly, for $v>u(p+q)$, we obtain $\widehat{\psi }_U\left( \theta ,\lambda \right) =\displaystyle \sum \limits _{l=0}^{nk-1}(-1)^l \left( \frac{u(p+q)}{v}\right) ^l \frac{{{nk-1}\atopwithdelims ()l}}{{{n+l-1}\atopwithdelims ()l}}$. $\square$

Consequently, $\widehat{R}^U_{s,k}$, UMVUE of $R_{s,k}$, is

$$\begin{aligned} \widehat{R}^U_{s,k}=\sum _{p=s}^{k}\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) (-1)^q\widehat{\psi }_U(\theta ,\lambda ). \end{aligned}$$

(20)

4 Inference on $R_{s,k}$ if $\alpha _1$, $\alpha _2$, $\theta$ and $\lambda$ are unknown

4.1 Maximum likelihood estimation of $R_{s,k}$

Suppose that $X\sim W(\alpha _1,\theta )$ and $Y\sim W(\alpha _2,\lambda )$ are two independent random variables with different unknown parameters. For Weibull distribution using (1) and (2), the multicomponent stress-strength reliability is given by

$$\begin{aligned} R_{s,k}&=\sum _{p=s}^{k}\left( {\begin{array}{c}k\\ p\end{array}}\right) \frac{\alpha _2}{\lambda }\int _0^\infty y^{\alpha _2-1}e^{-\frac{p}{\theta }y^{\alpha _1}-\frac{1}{\lambda }y^{\alpha _2}} \left( 1-e^{-\frac{y^{\alpha _1}}{\theta }}\right) ^{k-p}dy. \end{aligned}$$

This integral cannot be evaluated in closed form expression, so the numerical solution is required. Now, let $\{Y_{1},\ldots ,Y_n\}$ is a AT-II HPC sample from $W(\alpha _1,\lambda )$ under the scheme $\{N,n,T_1,S_1,\ldots ,S_n\}$ such that $Y_{J_1}<T_1<Y_{J_1+1}$. Also, $\{X_{i1},\ldots ,X_{ik}\},~i=1,\ldots ,n,$ is a AT-II HPC sample from $W(\alpha _2,\theta )$ under the AT-II HPC scheme $\{K,k,T_2,R_{i1},\ldots ,R_{ik}\}$ such that $X_{iJ_2}<T_2<X_{iJ_2+1}$. The likelihood function based on observed data is

$$\begin{aligned}&L(\alpha _1,\alpha _2,\theta ,\lambda |\text {data})\\&\quad =\displaystyle c_1 c_2^n \frac{\alpha _1^{nk}\alpha _2^n}{\theta ^{nk}\lambda ^n} \bigg (\prod _{i=1}^{n} y_i^{\alpha _2-1}\bigg ) e^{\displaystyle -\frac{1}{\lambda }\bigg [\sum \limits _{i=1}^n y_i^{\alpha _2}+\sum \limits _{i=1}^{J_1}S_iy_{i}^{\alpha _2}+S_ny_n^{\alpha _2}\bigg ]}\\&\qquad \times \bigg (\prod _{i=1}^{n}\prod _{j=1}^k x_{ij}^{\alpha _1-1}\bigg )e^{\displaystyle -\frac{1}{\theta } \bigg [\sum \limits _{i=1}^n\sum \limits _{j=1}^kx_{ij}^{\alpha _1}+ \sum \limits _{i=1}^n \sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^{\alpha _1}+\sum _{i=1}^nR_{ik} x_{ik}^{\alpha _1}\bigg ]}, \end{aligned}$$

and the log-likelihood function is

$$\begin{aligned}&\ell (\alpha _1,\alpha _2,\theta ,\lambda |\text {data})\\&\quad =\text {Constant} +nk\log (\alpha _1)+n\log (\alpha _2)-nk\log (\theta )-n\log (\lambda )\\&\qquad +(\alpha _2-1)\sum _{i=1}^n\log (y_i)-\frac{1}{\lambda }\bigg [\sum \limits _{i=1}^n y_i^{\alpha _2}+\sum \limits _{i=1}^{J_1}S_iy_{i}^{\alpha _2}+S_ny_n^{\alpha _2}\bigg ]\\&\qquad +(\alpha _1-1)\sum _{i=1}^n\sum _{j=1}^k\log (x_{ij})-\frac{1}{\theta } \bigg [\sum \limits _{i=1}^n\sum \limits _{j=1}^kx_{ij}^{\alpha _1}+ \sum \limits _{i=1}^n \sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^{\alpha _1}+\sum _{i=1}^nR_{ik} x_{ik}^{\alpha _1}\bigg ]. \end{aligned}$$

Therefore, the MLEs of $\theta$ and $\lambda$ denoted by $\widehat{\lambda }$ and $\widehat{\theta }$ are obtained by

$$\begin{aligned} \widehat{\theta }(\alpha _1)&=\frac{1}{nk}\bigg [\sum \limits _{i=1}^n \sum \limits _{j=1}^kx_{ij}^{\alpha _1}+ \sum \limits _{i=1}^n \sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^{\alpha _1}+\sum _{i=1}^nR_{ik} x_{ik}^{\alpha _1}\bigg ],\\ \widehat{\lambda }(\alpha _2)&=\frac{1}{n}\bigg [\sum \limits _{i=1}^n y_i^{\alpha _2}+\sum \limits _{i=1}^{J_1}S_iy_{i}^{\alpha _2}+S_ny_n^{\alpha _2}\bigg ]. \end{aligned}$$

Also, the MLEs of $\alpha _1$ and $\alpha _2$ are the solution of the following equations, respectively:

$$\begin{aligned} \frac{\partial \ell }{\partial \alpha _1}&=\frac{nk}{\alpha _1}+\sum _{i=1}^n \sum _{j=1}^k\log (x_{ij})-\frac{1}{\theta }\bigg [\sum \limits _{i=1}^n \sum \limits _{j=1}^kx_{ij}^{\alpha _1}\log (x_{ij})\\&\qquad + \sum \limits _{i=1}^n \sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^{\alpha _1}\log (x_{ij}) +\sum _{i=1}^nR_{ik}x_{ik}^{\alpha _1}\log (x_{ik})\bigg ],\\ \frac{\partial \ell }{\partial \alpha _2}&=\frac{n}{\alpha _2}+\sum _{i=1}^n \log (y_i)-\frac{1}{\lambda }\bigg [\sum \limits _{i=1}^n y_i^{\alpha _2}\log (y_i)+\sum \limits _{i=1}^{J_1}S_iy_{i}^{\alpha _2}\log (y_i) +S_ny_n^{\alpha _2}\log (y_n)\bigg ]. \end{aligned}$$

Then, in view of the MLE’s invariance property, the MLE of $R_{s,k}$ is given by

$$\begin{aligned} \widehat{R}^{MLE}_{s,k}=\sum _{p=s}^{k}\left( {\begin{array}{c}k\\ p\end{array}}\right) \frac{\widehat{\alpha }_2}{\widehat{\lambda }}\int _0^\infty y^{\widehat{\alpha }_2-1}e^{-\frac{p}{\widehat{\theta }}y^{\widehat{\alpha }_1} -\frac{1}{\widehat{\lambda }}y^{\widehat{\alpha }_2}}(1-e^{-\frac{y^{\widehat{\alpha }_1}}{\widehat{\theta }}})^{k-p}dy. \end{aligned}$$

(21)

4.2 Approximate maximum likelihood estimation of $R_{s,k}$

In this section, we obtain the AMLEs of $\theta$, $\lambda$, $\alpha _1$, $\alpha _2$ and $R_{s,k}$. Let $\{Y_{1},\ldots ,Y_n\}$ is a AT-II HPC sample from $W(\alpha _1,\lambda )$ under the scheme $\{N,n,T_1,S_1,\ldots ,S_n\}$ such that $Y_{J_1}<T_1<Y_{J_1+1}$. Also, $\{X_{i1},\ldots ,X_{ik}\},~i=1,\ldots ,n,$ is a AT-II HPC sample from $W(\alpha _2,\theta )$ under the AT-II HPC scheme $\{K,k,T_2,R_{i1},\ldots ,R_{ik}\}$ such that $X_{iJ_2}<T_2<X_{iJ_2+1}$. Moreover, let $U_{ij}=\log (X_{ij})$ and $V_i=\log (Y_i)$. So, $U_{ij}\sim EV(\mu _1,\sigma _1)$ and $V_i\sim EV(\mu _2,\sigma _2)$, where

$$\begin{aligned} \mu _1=\frac{1}{\alpha _1}\log (\theta ), \quad \mu _2=\frac{1}{\alpha _2}\log (\lambda ),\; \sigma _1=\frac{1}{\alpha _1},\; \sigma _2=\frac{1}{\alpha _2}. \end{aligned}$$

So, with ignoring the constant value, based on the observed data $\{U_{i1},\ldots ,U_{ik}\}$, $i=1,\ldots ,n$ and $\{V_{1},\ldots ,V_{n}\}$, the log-likelihood function can be obtained by

$$\begin{aligned} \ell ^*(\mu _1,\mu _2,\sigma _1,\sigma _2|\text {data})&=\sum _{i=1}^n\sum _{j=1}^k t_{ij}-\sum _{i=1}^n\sum _{j=1}^ke^{t_{ij}}- \sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}e^{t_{ij}}-\sum _{i=1}^nR_{ik}e^{t_{ik}}\\&\quad +\sum _{j=1}^nz_i-\sum _{i=1}^ne^{z_i}- \sum _{i=1}^{J_1}S_ie^{z_i}\\&\quad -S_ne^{z_n}-nk\log (\sigma _1)-n\log (\sigma _2), \end{aligned}$$

where $\displaystyle t_{ij}=\frac{u_{ij}-\mu _1}{\sigma _1}$ and $\displaystyle z_i=\frac{v_i-\mu _2}{\sigma _2}$. The usual equations, with taking derivatives of the above equation with respect to $\mu _1$, $\mu _2$, $\sigma _1$ and $\sigma _2$, can be derived by:

$$\begin{aligned} \frac{\partial \ell ^*}{\partial \mu _1}&=-\frac{1}{\sigma _1} \bigg [nk-\sum _{i=1}^n\sum _{j=1}^{k}e^{t_{ij}}- \sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}e^{t_{ij}}-\sum _{i=1}^n R_{ik}e^{t_{ik}}\bigg ]=0,\\ \frac{\partial \ell ^*}{\partial \mu _2}&=-\frac{1}{\sigma _2} \bigg [n-\sum _{i=1}^ne^{z_i}-\sum _{i=1}^{J_1}S_ie^{z_i}-S_ne^{z_n}\bigg ]=0,\\ \frac{\partial \ell ^*}{\partial \sigma _1}&=-\frac{1}{\sigma _1}\bigg [nk +\sum _{i=1}^n\sum _{j=1}^{k}t_{ij}-\sum _{i=1}^n \sum _{j=1}^{k}t_{ij}e^{t_{ij}} -\sum _{i=1}^n\sum _{j=1}^{J_2}R_{ij}t_{ij}e^{t_{ij}}-\sum _{i=1}^nR_{ik}t_{ik} e^{t_{ik}}\bigg ]=0,\\ \frac{\partial \ell ^*}{\partial \sigma _2}&=-\frac{1}{\sigma _2} \bigg [n+\sum _{i=1}^nz_i-\sum _{i=1}^nz_ie^{z_i}-\sum _{i=1}^nS_iz_ie^{z_i}-S_nz_ne^{z_n}\bigg ]=0. \end{aligned}$$

Quite similar to Sect. 2.2, we can obtain AMLEs of $\mu _1$, $\mu _2$, $\sigma _1$ and $\sigma _2$, say $\hat{\hat{\mu }}_1$, $\hat{\hat{\mu }}_2$, $\hat{\hat{\sigma }}_1$ and $\hat{\hat{\sigma }}_2$, respectively, by

$$\begin{aligned} \hat{\hat{\mu }}_1&=A_1+\hat{\hat{\sigma }}_1 B_1,\qquad \qquad \qquad \qquad \hat{\hat{\mu }}_2=A_2+\hat{\hat{\sigma }}_2 B_2,\\ \hat{\hat{\sigma }}_1&=\frac{-D_1+\sqrt{D_1^2+4C_1E_1}}{2C_1},\qquad \hat{\hat{\sigma }}_2=\frac{-D_2+\sqrt{D_2^2+4C_2E_2}}{2C_2}, \end{aligned}$$

where $A_1$, $A_2$, $B_1$, $B_2$, $C_1$, $C_2$, $D_1$, $D_2$, $E_1$ and $E_2$ are given in Sect. 2.2. After deriving $\hat{\hat{\mu }}_1$, $\hat{\hat{\mu }}_2$, $\hat{\hat{\sigma }}_1$ and $\hat{\hat{\sigma }}_2$, the values $\hat{\hat{\theta }}$, $\hat{\hat{\lambda }}$, $\hat{\hat{\alpha }}_1$, $\hat{\hat{\alpha }}_2$ and $\hat{\hat{R}}_{s,k}$ can be evaluated by $\hat{\hat{\theta }}=e^{\frac{\hat{\hat{\mu }}_1}{\hat{\hat{\sigma }}_1}}$, $\hat{\hat{\lambda }}=e^{\frac{\hat{\hat{\mu }}_2}{\hat{\hat{\sigma }}_2}}$, $\hat{\hat{\alpha }}_1=\frac{1}{\hat{\hat{\sigma }}_1}$, $\hat{\hat{\alpha }}_2=\frac{1}{\hat{\hat{\sigma }}_2}$ and

$$\begin{aligned} \hat{\hat{ R}}_{s,k}=\sum _{p=s}^{k}\left( {\begin{array}{c}k\\ p\end{array}}\right) \frac{\hat{\hat{\alpha }}_2}{\hat{\hat{\lambda }}}\int _0^\infty y^{\hat{\hat{\alpha }}_2-1}e^{-\frac{p}{\hat{\hat{\theta }}}y^{\hat{\hat{\alpha }}_1} -\frac{1}{\hat{\hat{\lambda }}}y^{\hat{\hat{\alpha }}_2}} \left( 1-e^{-\frac{y^{\hat{\hat{\alpha }}_1}}{\hat{\hat{\theta }}}}\right) ^{k-p}dy. \end{aligned}$$

(22)

4.3 Bayes estimation of $R_{s,k}$

In this section, we assume that the unknown parameters $\alpha _1$, $\alpha _2$ have the gamma distributions with the parameters $(a_1,b_1)$ and $(a_4,b_4)$ and $\theta$ and $\lambda$ have the inverse gamma distributions with the parameters $(a_2,b_2)$ and $(a_3,b_3)$, respectively. We improve the Bayesian inference about $R_{s,k}$ in this section. The joint posterior density function of $\alpha _1$, $\alpha _2$, $\theta$ and $\lambda$ is proportion with the likelihood function based on the observed sample and the prior distributions of each unknown parameters, i.e.

$$\begin{aligned} \pi (\alpha _1,\alpha _2,\theta ,\lambda |\text {data})&\propto {L(\alpha _1, \alpha _2,\theta ,\lambda |\text {data})\pi _1(\alpha _1)\pi _2(\theta ) \pi _3(\lambda )\pi _4(\alpha _2)}, \end{aligned}$$

(23)

From the Eq. (23), it is obvious that the Bayes estimates of $\alpha _1$, $\alpha _2$, $\theta$, $\lambda$ and $R_{s,k}$ cannot be obtained in a closed form. Therefore, we utilize the MCMC method. The posterior pdfs of $\theta$, $\lambda$, $\alpha _1$ and $\alpha _2$ are respectively:

$$\begin{aligned} \theta |\alpha _1,\text {data}&\sim \text {I}\Gamma \left( nk+a_2, b_2+\sum \limits _{i=1}^n\sum \limits _{j=1}^kx_{ij}^{\alpha _1}+ \sum \limits _{i=1}^n \sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^{\alpha _1} +\sum _{i=1}^nR_{ik}x_{ik}^{\alpha _1}\right) .\\ \lambda |\alpha _2,\text {data}&\sim \text {I}\Gamma \left( n+a_3, b_3 \sum \limits _{i=1}^n y_i^{\alpha _2}+\sum \limits _{i=1}^{J_1}S_iy_{i}^{\alpha _2} +S_ny_n^{\alpha _2}\right) .\\ \pi (\alpha _1|\theta ,\text {data})&\propto \alpha _1^{nk+a_1-1} \bigg (\prod _{i=1}^{n}\prod _{j=1}^k x_{ij}^{\alpha _1-1}\bigg )\\&\qquad e^{\displaystyle -b_1\alpha _1-\frac{1}{\theta }\bigg [\sum \limits _{i=1}^n \sum \limits _{j=1}^kx_{ij}^{\alpha _1}+ \sum \limits _{i=1}^n \sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^{\alpha _1} +\sum _{i=1}^nR_{ik}x_{ik}^{\alpha _1}\bigg ]}.\\ \pi (\alpha _2|\lambda ,\text {data})&\propto \alpha _2^{n+a_4-1} \bigg (\prod _{i=1}^{n} y_i^{\alpha _2-1}\bigg )\\&\qquad e^{\displaystyle -b_4\alpha _2-\frac{1}{\lambda }\bigg [\sum \limits _{i=1}^n y_i^{\alpha _2}+\sum \limits _{i=1}^{J_1}S_iy_{i}^{\alpha _2} +S_ny_n^{\alpha _2}\bigg ]}. \end{aligned}$$

As we see above, generating samples from the posterior pdfs of $\theta$ and $\lambda$ can be easily done. On the other hand, because the posterior pdfs of $\alpha _1$ and $\alpha _2$ cannot be reduced analytically to a well-known distribution, generating a sample from $\pi (\alpha _1|\theta ,\text {data})$ and $\pi (\alpha _2|\lambda ,\text {data})$ are not available, directly. Consequently, with normal proposal distribution, we use the Metropolis-Hastings method to generate a sample from $\pi (\alpha _1|\theta ,\text {data})$ and $\pi (\alpha _2|\lambda ,\text {data})$. So, the Gibbs sampling algorithm is as follows:

• 1. Begin with an initial conjecture $(\alpha _{1(0)}$, $\alpha _{2(0)}$, $\theta _{(0)}$, $\lambda _{(0)})$.

• 2. Set $t=1$.

• 3. Generate $\alpha _{1(t)}$ from $\pi (\alpha _1|\theta _{(t-1)}, \text {data})$ with the $N(\alpha _{1(t-1)},1)$ as the proposal distribution, using Metropolis-Hastings method.

• 4. Generate $\alpha _{2(t)}$ from $\pi (\alpha _2|\lambda _{(t-1)}, \text {data})$ with the $N(\alpha _{2(t-1)},1)$ as the proposal distribution, using Metropolis-Hastings method.

• 5. Generate $\theta _{(t)}$ from $\text {I}\Gamma \bigg (nk+a_2, b_2+\sum \limits _{i=1}^{n}\sum \limits _{j=1}^kx_{ij}^{{\alpha _{1(t)}}} +\sum \limits _{i=1}^{n}\sum \limits _{j=1}^{J_2}R_{ij}x_{ij}^{{\alpha _{1(t)}}} +\sum \limits _{i=1}^{n}R_{ik}x_{ik}^{{\alpha _{1(t)}}}\bigg )$.

• 6. Generate $\lambda _{(t)}$ from $\text {I}\Gamma (n+a_3, b_3+\sum \limits _{i=1}^{n}y_i^{{\alpha _{2(t)}}}+\sum \limits _{i=1}^{J_1}S_iy_i^{{\alpha _{2(t)}}} +S_ny_n^{{\alpha _{2(t)}}})$.

• 7. Evaluate $R_{(t)s,k}=\sum \limits _{p=s}^{k}\left( {\begin{array}{c}k\\ p\end{array}}\right) \frac{\alpha _{2(t)}}{\lambda _{(t)}}\int _0^\infty y^{\alpha _{2(t)}-1}e^{-\frac{p}{\theta _{(t)}}y^{\alpha _{1(t)}}-\frac{1}{\lambda _{(t)}}y^{\alpha _{2(t)}}}(1-e^{-\frac{y^{\alpha _{1(t)}}}{\theta _{(t)}}})^{k-p}dy.$

• 8. Set $t = t +1$.

• 9 Reiterate steps 3–8, T times.

Using this algorithm, the Bayes estimate of $R_{s,k}$ is given by

$$\begin{aligned} \widehat{R}_{s,k}^{MC}=\frac{1}{T}\sum _{t=1}^{T}R_{(t)s,k}. \end{aligned}$$

(24)

Also, by applying the method of Chen and Shao (1999), the HPD $100(1-\gamma )\%$ credible interval of $R_{s,k}$ is provided.

5 Data analysis and comparison study

In this section, to compare the performance of the different methods which described in the preceding sections, we display some results based on Monte Carlo simulations and real data.

5.1 Numerical experiments and discussions

In this subsection, the performance of ML, AML and Bayes estimates under different adaptive hybrid progressive censoring schemes are investigated by the Monte Carlo simulation. For this purpose, the performances of the different estimates are compared in terms of biases and mean squares errors (MSEs). Also, the different confidence intervals, namely the asymptotic confidence intervals, two bootstrap confidence intervals and the HPD credible intervals are compared in terms of the average confidence lengths, and coverage percentages. The simulation results for the different parameter values, the different hyperparameters and different sampling schemes are calculated. The utilized censoring schemes are given in Table 1. Also, we provide $T_1=T_2=2$, and we consider $s = 2$ and $s = 4$. All the results are based on 2000 replications.

Table 1 Censoring schemes

Table 2 $|\text {Biases}|$ and MSE of the MLE, AMLE and Bayes estimates of $R_{s,k}$ under various censoring schemes when $T_1=T_2=2$ and $\alpha$ is unknown

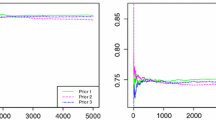
In the simulation study, when the common shape parameter $\alpha$ is unknown, the parameter value $\Theta = (\theta ,\lambda ,\alpha )=(1,1,3)$ is used to compare the MLE, AMLE and different Bayes estimators, in all cases. Three priors are assumed for computing the Bayes estimators and HPD credible intervals as follows:

$$\begin{aligned}&\text {Prior 1}: \qquad a_i=0,\qquad b_i=0, \qquad i=1,2,3. \\&\text {Prior 2}: \quad a_i=0.1,\quad b_i=0.2, \qquad i=1,2,3.\\&\text {Prior 3}: \qquad a_i=1,\qquad b_i=2, \qquad i=1,2,3. \end{aligned}$$

For different priors and different censoring schemes, the average biases, and MSEs of the MLE and AMLE using (8) and (9) and Bayes estimates of $R_{s,k}$ via Lindley’s approximation and MCMC method using (14) and (15) are derived, respectively. The results are reported in Table 2. From Table 2, it is observed that the biases and MSEs of the ML and AML estimates are almost similar in most schemes. The Bayes estimates have less MSEs. Comparing the different Bayes estimates indicates that the best performance in term of MSEs belongs to the Bayes estimates based on Prior 3. Moreover, comparing two approximate Bayes methods shows that the biases and MSEs of the MCMC method are generally smaller than those obtained from the Lindley’s approximation. Actually, with increasing n, for fixed s and k, the biases and MSEs of the ML and Bayes estimates of $R_{s,k}$ decrease in all cases. Perhaps one of the most important reasons is the fact that when n increases, some additional information is gathered and the number of observed failures increases.

Also, we calculate the $95\%$ confidence intervals for $R_{s,k}$, based on the asymptotic distribution of the MLE. Furthermore, the Boot-p, Boot-t confidence intervals and the HPD credible intervals are computed. In the simulation study, the bootstrap intervals are computed based on 350 re-sampling. Also, the Bayes estimates and the associated credible intervals are computed based on 3000 sampling, namely $T_{bayes}=3000$. These results include the average confidence or credible lengths, and the corresponding coverage percentages and they are reported in Table 3. From Table 3, we show that the bootstrap confidence intervals have the widest average confidence lengths and the HPD intervals provide the smallest average credible lengths for different censoring schemes and different priors. Also, the asymptotic confidence intervals are the second best confidence intervals. Comparing the different confidence and credible intervals show that the best performance belongs to HPD credible interval based on the Prior 3 and it is evident that the HPD intervals provide the most coverage percentages in most considered cases. Also, with increasing n, for fixed s and k, the average confidence or credible lengths decrease and the associated coverage percentages increase in all cases.

Now let us consider the case when the common shape parameter $\alpha$ is known, the parameter value $\Theta = (\theta ,\lambda ,\alpha )=(2,2,5)$ is used mainly to compare the MLEs, different Bayes estimators and UMVUEs. Three priors are assumed for computing the Bayes estimators and HPD credible intervals as follows:

$$\begin{aligned} \text {Prior 4}: \qquad a_i&=0,\qquad b_i=0, \qquad i=1,2. \\ \text {Prior 5}: \qquad a_i&=0.2,\quad b_i=0.4, \quad i=1,2.\\ \text {Prior 6}: \qquad a_i&=2,\qquad b_i=3, \qquad i=1,2. \end{aligned}$$

For different priors and different censoring schemes, the average biases, and MSEs of the MLE using (16), Bayes estimate via exact method using (18) and UMVUE of $R_{s,k}$ using (20) are derived. We reported the results in Table 4. From Table 4, it is observed that the performances of UMVU and ML estimates are quite close to those of the Bayes estimates, in most cases. Comparing the different Bayes estimates indicates that the best performance in term of MSEs belongs to the Bayes estimates based on Prior 6.

Table 3 Average confidence/credible length and coverage percentage for estimators of $R_{s,k}$ under various censoring schemes when $T_1=T_2=2$ and $\alpha$ is unknown.

Table 4 $|\text {Biases}|$ and MSE of the MLE, Bayes estimates and UMVUE of $R_{s,k}$ under various censoring schemes when $\alpha$ is known and $T_1=T_2=2$

Table 5 Average confidence/credible length and coverage percentage for estimators of $R_{s,k}$ under various censoring schemes when $\alpha$ is known.

Fig. 3

Biases and MSEs of $R_{2,5}$, when $T_1=T_2=2$, for scheme $(R_3,S_3)$ (first row) and $(R_3,S_6)$ (second row)

Also, based on the asymptotic distribution of the MLE, we computed the $95\%$ confidence intervals for $R_{s,k}$. Furthermore, we computed the HPD credible intervals. The simulation results included the average confidence or credible lengths, and the corresponding coverage percentages are reported in Table 5. The nominal level for the confidence intervals or the credible intervals is 0.95 in each case. From Table 5, we observed that the HPD intervals provide the smallest average credible lengths and the asymptotic confidence intervals are the second best confidence intervals. Also, comparing the confidence and credible intervals show that the best performance belongs to HPD credible interval based on the Prior 6 and it is evident that the HPD intervals provide the most coverage percentages in most considered cases. Same as before, with increasing n, for fixed s and k, the average confidence or credible lengths decrease and the associated coverage percentages increase in all cases.

Also, we can compare Biases and MSEs of the estimators by plotting them for some censoring plans. For this aim, we consider $\alpha =5$ and $(\lambda ,\theta )$=(6,1), (6,2), (6,3), (6,4), (6,6), (6,8), (6,10), (6,12), (6,15), (6,18), (6,20), (6,22) and (6,24). The true values of reliability in multicomponent stress-strength with the given combinations for $(s,k)=(2,5)$ are 0.1876, 0.3324, 0.4459, 0.5359, 0.6667, 0.7540, 0.8144, 0.8571, 0.9005, 0.9286, 0.9419, 0.9522 and 0.9603. Also, we study Bayesian case with $a_i=1$, $b_i=2$, $i=1$, 2, for hyperparameters. Figure 3 demonstrates the Biases and MSEs of $\widehat{R}^{MLE}_{s,k}$, $\widehat{R}^{B}_{s,k}$ and $\widehat{R}^{U}_{s,k}$, for the different schemes. We observe that with increasing sample size, the Biases and MSEs of the estimates decrease, as expected. Moreover, the MSE is large when $R_{s,k}$ is about 0.5 and it is small for the extreme values of $R_{s,k}$. Furthermore, the MSEs of UMVUE are greater than that of MLE when $R_{s,k}$ is about 0.5 and MSEs of UMVUE are small than that of MLE for the extreme values of $R_{s,k}$.

In this part, when the shape parameters $\alpha _1$ and $\alpha _2$ are different, the parameter value $\Theta = (\theta ,\lambda ,\alpha _1,\alpha _2)=(1,1,3,5)$ is used to compare the MLEs and different Bayes estimators, in all the cases. Three priors are assumed for computing the Bayes estimators as follows:

$$\begin{aligned} \text {Prior 7}: \qquad a_i&=0,\qquad b_i=0, \qquad i=1,2,3,4. \\ \text {Prior 8}: \qquad a_i&=0.1,\quad b_i=0.2, \quad i=1,2,3,4.\\ \text {Prior 9}: \qquad a_i&=1,\qquad b_i=2, \qquad i=1,2,3,4. \end{aligned}$$

In this case, the average biases, and MSEs of the MLE using (21), AMLE using (22) and Bayes estimate of $R_{s,k}$ using (24) are derived. We reported the results in Table 6. From Table 6, it is observed that the biases and MSEs of the ML estimates are quite close to those of the Bayes estimates, in most cases. Comparing the different Bayes estimates indicates that the best performance in term of MSEs belongs to the Bayes estimates based on Prior 9. Also, with increasing n, for fixed s and k, the biases and MSEs of the different estimates of $R_{s,k}$ decrease in all cases.

Table 6 $|\text {Biases}|$ and MSE of the MLE and Bayes estimates of $R_{s,k}$ under various censoring schemes when $\alpha _1$ and $\alpha _2$ are different

5.2 Data analysis

For illustrative purposes, in this section, the analysis of a pair of real data sets is provided. In agriculture, it is very important that we all understand drought. Drought occurrence has a lot of damage to production. On the other hand, there are several ways to manage these damages. One of the most important is the use of drought-insurance products. In the following, one scenario concerning the excessive drought is constructed. If the water capacity of a reservoir in a region on Aguste at least two years out of next five years is more than the amount of water achieved on December of the previous year, we demand that there will be no excessive drought afterward. So, multicomponent reliability is the probability of non-occurrence drought. Estimation of this parameter is important in agriculture. We cannot ignore the effect of drought on farm production and livestock holdings. The most immediate consequence of drought is a fall in crop production, due to inadequate and poorly distributed rainfall. Low rainfall causes poor pasture growth and may also lead to a decline in fodder supplies from crop residues. In fact, by this probability, we can plan to prevent damage from drought, which included the safety of instruments that might be damaged. In this scenario, it is very likely that the researcher confronts the censored samples from both populations rather than complete samples. There are some reasons that we can face the censored data, in water capacity. These reasons may be natural disasters, such as flood, earthquake and storm or caused by human activities, such as financial pressures, unwanted errors and etc. Many authors have studied the application of censoring data in drought and environmental conditions, for more details see Antweiler (2015), Sürücü (2015) and Tate and Freeman (2000). The data which we study in this section is the monthly water capacity of the Shasta reservoir in California, USA. We consider the months of August and December from 1975 to 2016. These data sets can be found here http://cdec.water.ca.gov/cgi-progs/queryMonthly?SHA. Some authors have been studied these data previously, for more details see Kizilaslan and Nadar (2016, 2018) and Nadar et al. (2013).

When we confront complete data, $X_{11},...,X_{15}$ are the capacities of August from 1976 to 1980, $X_{21},...,X_{25}$ are the capacities of August from 1982 to 1986 and so on $X_{71},...,X_{75}$ are the capacities of August from 2012 to 2016. Also, $Y_1$ is the capacity of December 1975, $Y_2$ is the capacity of December 1981 and so on $Y_7$ is the capacity of December 2011. Just for simplify calculations, we divide all the data points by the total capacity of Shasta reservoir which is 4,552,000 acre-foot. This work will not have any effect on statistical inference.

To implement the theoretical methods, first, we fitted the Weibull distribution on two data sets, separately. Based on the results, for X, the estimated parameters are $\alpha _1=3.5427$, $\theta =0.1891$, the Kolmogorov-Smirnov distance and associated p-value are 0.1550 and 0.3345, respectively. Also, for Y, the estimated parameters are $\alpha _2=11.0172$, $\lambda =0.0341$, the Kolmogorov-Smirnov distance and associated p-value are 0.2833 and 0.4604, respectively. From the p-values, it is obvious that the Weibull distribution is an adequate fit for these data sets. For the X and Y data sets, we provided the empirical distribution functions and the PP-plots in Figs. 4 and 5, respectively. Because the scale parameters of two data sets are not same, we consider the general case.

Fig. 4

Empirical distribution function (left) and the PP-plot (right) for X

Fig. 5

Empirical distribution function (left) and the PP-plot (right) for Y

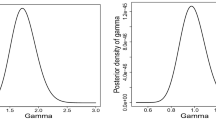
To obtain the MLE of unknown parameters $\alpha _1$ and $\alpha _2$, we use the Newton-Raphson method. The initial value for this algorithm is obtained by maximizing of profile log-likelihood function. So, we plot the profile log-likelihood function of $\alpha _1$ and $\alpha _2$ in Fig. 6 and we see that the approximate initial values for $\alpha _1$ and $\alpha _2$ should be close 3 and 11, respectively.

Fig. 6

Profile log-likelihood function of $\alpha _1$ (left) and $\alpha _2$ (right)

For the complete data sets, the MLEs of $\theta ,\lambda ,\alpha _1,\alpha _2$ are 0.1891, 0.0341, 3.5427, 11.0172, the MLE of $R_{1,5}$ is 0.6727 and the MLE of $R_{2,5}$ is 0.3333. Also, the AMLEs of $\theta ,\lambda ,\alpha _1,\alpha _2$ are 0.1277, 0.0146, 3.0498, 11.6436, the AMLE of $R_{1,5}$ is 0.4306 and the AMLE of $R_{2,5}$ is 0.1347. Moreover, the Bayes estimate of $R_{1,5}$ with non-informative priors assumption, via the MCMC method is 0.6795 and the 95$\%$ credible interval is (0.3885,0.8954). Furthermore, the Bayes estimate of $R_{2,5}$ with non-informative priors assumption, via the MCMC method is 0.5774 and the 95$\%$ credible interval is (0.3136,0.8155).

For illustrative purposes, two different AT-II HPC samples have been generated from the above data sets:

$$\begin{aligned} \text{ Scheme } \text{1: }~&R=[0,1,0,0],~S=[0,0,0,1,0,0], ~T_1=T_2=0.5~ (k=5, s=1,2).\\ \text{ Scheme } \text{2: }~&R=[1,1,0],~S=[1,0,0,0,1],~T_1=T_2=0.9~ (k=3, s=1). \end{aligned}$$

To obtain the censored data from X and Y, we perform as follows. First, using the method which has been explained in Sect. 1, we censor some elements from the Y vector and for any data of Y which has been censored, we remove the same row of X matrix. In the remaining matrix of X, we apply the censoring scheme for each row.

Based on Scheme 1, the MLEs of $\theta ,\lambda ,\alpha _1,\alpha _2$ are 0.2449, 0.0892, 2.9631, 9.0491, the MLE of $R_{1,4}$ is 0.5850 and the MLE of $R_{2,4}$ is 0.2378. Also, the AMLEs of $\theta ,\lambda ,\alpha _1,\alpha _2$ are 0.2055, 0.0861, 2.8030, 8.8085, the AMLE of $R_{1,4}$ is 0.4758 and the AMLE of $R_{2,4}$ is 0.1615. Moreover, the Bayes estimate of $R_{1,4}$ with non-informative priors assumption, via the MCMC method is 0.6348 and the 95$\%$ credible interval is (0.3322,0.8813). Furthermore, the Bayes estimate of $R_{2,4}$ with non-informative priors assumption, via the MCMC method is 0.4904 and the 95$\%$ credible interval is (0.2249,0.7482).

Similarity, based on Scheme 2, the MLEs of $\theta ,\lambda ,\alpha _1,\alpha _2$ are 0.2168, 9.2e–5, 2.9518, 25.3593 and the MLE of $R_{1,3}$ is 0.5432. Also, the AMLEs of $\theta ,\lambda ,\alpha _1,\alpha _2$ are 0.1249, 5.9e-5, 2.9740, 26.1505 and the AMLE of $R_{1,3}$ is 0.2355. Moreover, the Bayes estimate of $R_{1,3}$ with non-informative priors assumption, via the MCMC method is 0.5792 and the 95$\%$ credible interval is (2552,0.8520).

To see the effect of the hyperparameters on the Bayes estimators and also on credible intervals, we utilize the informative priors. By using the re-sampling method, the hyperparameters can be obtained as $a_1 = 46.302, b_1 = 0.0792, a_2 = 33.7983, b_2 = 0.1665, a_3 = 0.0375, b_3 =0.0001, a_4=6.3566, b_4=2.3182$. Based on this, for complete data, Bayes estimator of $R_{1,5}$ with MCMC method is 0.5373 and $95\%$ credible interval is (0.2942,0.7623). Also, Bayes estimator of $R_{2,5}$ with MCMC method is 0.4128 and $95\%$ credible interval is (0.2073,0.6443). For Scheme 1, Bayes estimator of $R_{1,4}$ with MCMC method is 0.4469 and $95\%$ credible interval is (0.2162,0.6881). Moreover, Bayes estimator of $R_{2,4}$ with MCMC method is 0.3466 and $95\%$ credible interval is (0.1459,0.5971). For Scheme 2, Bayes estimator of $R_{1,3}$ with MCMC method is 0.3605 and $95\%$ credible interval is (0.1420,0.6140). As we see, by the above scenario, the estimation of non-occurrence probability of drought, in most cases, is less than 0.6. So, in this example, we can conclude that the rainfall is not very good and dehydration may occur. Therefore, in order to avoid possible damage, planning must be done in this regard.

Comparing the two schemes with informative and non-informative priors, it is obvious that in Scheme 1, estimators have smaller standard errors than Scheme 2, as expected. Also, comparing Bayes estimators, it is observed that they depend on hyperparameters. Because the HPD credible intervals based on informative priors are slightly smaller than the corresponding length of the HPD credible intervals based on non-informative priors, therefore, if prior information is available it should be used. Moreover, comparing the estimators in the complete data set or in Scheme 1, it is observed that, in $s = 1$, estimators are smaller than $s = 2$, as expected.

6 Conclusions

In this paper, the estimation of multicomponent reliability for Weibull distribution based on AT-II HPC schemes is studied. In fact, we solved the problem in three cases. Firstly, when the common shape parameter is unknown, we derived the MLEs of the unknown parameters and $R_{s,k}$. Because the MLEs cannot be obtained in closed forms, we derived the approximate MLEs of the parameters and $R_{s,k}$. Also, by earning the asymptotic distribution of the $R_{s,k}$, we constructed the asymptotic confidence intervals. Moreover, two bootstrap confidence intervals are proposed which their performance are quite satisfactory. Furthermore, we approximated the Bayes estimate of $R_{s,k}$ by applying two methods: Lindley’s approximation and MCMC method. We constructed the HPD credible intervals by using the MCMC method. Secondly, when the common shape parameter is known, the ML, exact Bayes and UMVU estimates are computed. Also, asymptotic and HPD credible intervals are constructed in this case. Finally, in general case, when two shape parameters are different and unknown, the statistical inferences about $R_{s,k}$ such as ML, AML and Bayesian estimations are obtained and the HPD credible intervals are constructed.

From the simulation results, it is obvious that the ML and AML estimates are almost similar in most schemes. Also, comparing the Bayes estimators shows that the estimates based on informative priors perform better than the ones which obtained using the non-informative prior. Furthermore, the MCMC method approximates the Bayes estimate better than the Lindley method. Moreover, comparing the different confidence intervals indicates that HPD intervals provide the smallest credible lengths and the bootstrap intervals provide the widest lengths for different censoring schemes and different parameter values. Also, comparing two bootstrap confidence intervals shows that Boot-p intervals perform better than the Boot-t intervals.

Appendix A

For three parameters case, we compute 13 at $\widehat{\Theta }=(\widehat{\theta }_1,\widehat{\theta }_2,\widehat{\theta }_3)$, where

$$\begin{aligned} d_i&=\rho _1\sigma _{i1}+\rho _2\sigma _{i2}+\rho _3\sigma _{i3}, ~~i=1,2,3,\\ d_4&=u_{12}\sigma _{12}+u_{13}\sigma _{13}+u_{23}\sigma _{23},\\ d_5&=\frac{1}{2}(u_{11}\sigma _{11}+u_{22}\sigma _{22}+u_{33}\sigma _{33}),\\ A&=\ell _{111}\sigma _{11}+2\ell _{121}\sigma _{12}+2\ell _{131}\sigma _{13} +2\ell _{231}\sigma _{23}+\ell _{221}\sigma _{22} +\ell _{331}\sigma _{33},\\ B&=\ell _{112}\sigma _{11}+2\ell _{122}\sigma _{12}+2\ell _{132}\sigma _{13} +2\ell _{232}\sigma _{23}+\ell _{222}\sigma _{22} +\ell _{332}\sigma _{33},\\ C&=\ell _{113}\sigma _{11}+2\ell _{123}\sigma _{12}+2\ell _{133}\sigma _{13} +2\ell _{233}\sigma _{23}+\ell _{223}\sigma _{22} +\ell _{333}\sigma _{33}. \end{aligned}$$

In our case, for $(\theta _1,\theta _2,\theta _3)\equiv (\alpha ,\theta ,\lambda )$ and $u\equiv u(\alpha ,\theta ,\lambda )=R_{s,k}$ as provided in (3), we have

$$\begin{aligned} \rho _1&=\frac{a_1-1}{\alpha }-b_1,~~ \rho _2=-\frac{a_2+1}{\theta } +\frac{b_2}{\theta ^2},~~~ \rho _3=-\frac{a_3+1}{\lambda }+\frac{b_3}{\lambda ^2},\\ \ell _{11}&=-\frac{n(k+1)}{\alpha ^2}-\frac{1}{\lambda }\bigg [\sum _{i=1}^n y_i^\alpha \log ^2(y_i)+\sum _{i=1}^{J_1}S_iy_i^\alpha \log ^2(y_i) +S_ny_n^\alpha \log ^2(y_n)\bigg ]\\&\quad -\; \frac{1}{\theta }\bigg [\sum _{i=1}^n\sum _{j=1}^k x_{ij}^\alpha \log ^2(x_{ij})+\sum _{i=1}^n\sum _{j=1}^{J_2}R_{ij} x_{ij}^\alpha \log ^2(x_{ij})+\sum _{j=1}^{n}R_{ik} x_{ik}^\alpha \log ^2(x_{ik})\bigg ],\\ \ell _{12}&=\frac{1}{\theta ^2}\bigg [\sum _{i=1}^{n}\sum _{j=1}^k x_{ij}^\alpha \log (x_{ij}) +\sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}x_{ij}^\alpha \log (x_{ij}) +\sum _{i=1}^{n}R_{ik}x_{ik}^\alpha \log (x_{ik})\bigg ]=\ell _{21},\\ \ell _{13}&=\frac{1}{\lambda ^2}\bigg [\sum _{i=1}^{n}y_{i}^\alpha \log (y_i) +\sum _{i=1}^{J_1}S_iy_{i}^\alpha \log (y_i) +S_ny_{n}^\alpha \log (y_n)\bigg ]=\ell _{31},\\ \ell _{22}&=\frac{nk}{\theta ^2}-\frac{2}{\theta ^3}\bigg [\sum _{i=1}^{n} \sum _{j=1}^kx_{ij}^\alpha +\sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}x_{ij}^\alpha +\sum _{i=1}^{n}R_{ik}x_{ik}^\alpha \bigg ],\\ \ell _{23}&=0=\ell _{32},\\ \ell _{33}&=\frac{n}{\lambda ^2}-\frac{2}{\lambda ^3} \bigg [\sum _{i=1}^{n}y_{i}^\alpha +\sum _{i=1}^{J_1}S_iy_{i}^\alpha +S_ny_{n}^\alpha \bigg ]. \end{aligned}$$

Also, by using $\ell _{ij}, i,j = 1,2,3, \sigma _{ij}, i,j = 1,2,3$ can be obtained and

$$\begin{aligned} \ell _{111}&=\frac{2n(k+1)}{\alpha ^3}-\frac{1}{\lambda }\bigg [\sum _{i=1}^n y_i^\alpha \log ^3(y_i)+\sum _{i=1}^{J_1}S_iy_i^\alpha \log ^3(y_i) +S_ny_n^\alpha \log ^3(y_n)\bigg ]\\&-\frac{1}{\theta }\bigg [\sum _{i=1}^n\sum _{j=1}^k x_{ij}^\alpha \log ^3(x_{ij})+\sum _{i=1}^n\sum _{j=1}^{J_2}R_{ij} x_{ij}^\alpha \log ^3(x_{ij})+\sum _{j=1}^{n}R_{ik} x_{ik}^\alpha \log ^3(x_{ik})\bigg ],\\ \ell _{112}&=\frac{1}{\theta ^2}\bigg [\sum _{i=1}^{n}\sum _{j=1}^kx_{ij}^\alpha \log ^2(x_{ij}) +\sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}x_{ij}^\alpha \log ^2(x_{ij}) +\sum _{i=1}^{n}R_{ik}x_{ik}^\alpha \log ^2(x_{ik})\bigg ]\\&=\ell _{211}=\ell _{121},\\ \ell _{113}&=\frac{1}{\lambda ^2}\bigg [\sum _{i=1}^{n}y_{i}^\alpha \log ^2(y_i) +\sum _{i=1}^{J_1}S_iy_{i}^\alpha \log ^2(y_i) +S_ny_{n}^\alpha \log ^2(y_n)\bigg ]\\&=\ell _{311}=\ell _{131},\\ \ell _{122}&=-\frac{2}{\theta ^3}\bigg [\sum _{i=1}^{n}\sum _{j=1}^k x_{ij}^\alpha \log (x_{ij}) +\sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}x_{ij}^\alpha \log (x_{ij}) +\sum _{i=1}^{n}R_{ik}x_{ik}^\alpha \log (x_{ik})\bigg ]\\&=\ell _{221}=\ell _{212},\\ \ell _{133}&=-\frac{2}{\lambda ^3}\bigg [\sum _{i=1}^{n}y_{i}^\alpha \log (y_i) +\sum _{i=1}^{J_1}S_iy_{i}^\alpha \log (y_i) +S_ny_{n}^\alpha \log (y_n)\bigg ]=\ell _{331}=\ell _{313},\\ \ell _{222}&=-\frac{2nk}{\theta ^3}+\frac{6}{\theta ^4}\bigg [\sum _{i=1}^{n} \sum _{j=1}^kx_{ij}^\alpha +\sum _{i=1}^{n}\sum _{j=1}^{J_2}R_{ij}x_{ij}^\alpha +\sum _{i=1}^{n}R_{ik}x_{ik}^\alpha \bigg ],\\ \ell _{333}&=-\frac{2n}{\lambda ^3}+\frac{6}{\lambda ^4}\bigg [\sum _{i=1}^{n}y_{i}^\alpha +\sum _{i=1}^{J_1}S_iy_{i}^\alpha +S_ny_{n}^\alpha \bigg ], \end{aligned}$$

and other $\ell _{ijk}=0$. In addition, $u_1=\partial R_{s,k}/\partial \alpha =0$, $u_{i1}=\partial ^2 R_{s,k}/(\partial \theta _i\partial \alpha )=0$, $i=1,2,3$, and $u_2$, $u_3$ are given in (10) and (11), respectively. Also,

$$\begin{aligned} u_{22}&=\sum _{p=s}^{k}\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) \frac{(-1)^{q+1}2\lambda (p+q)}{(\theta +\lambda (p+q))^3},\\ u_{23}&=\sum _{p=s}^{k}\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) \frac{(-1)^{q+1}(p+q)(\lambda (p+q)-\theta )}{(\theta +\lambda (p+q))^3}=u_{32},\\ u_{33}&=\sum _{p=s}^{k}\sum _{q=0}^{k-p}\left( {\begin{array}{c}k\\ p\end{array}}\right) \left( {\begin{array}{c}k-p\\ q\end{array}}\right) \frac{(-1)^{q}2\theta (p+q)^2}{(\theta +\lambda (p+q))^3}. \end{aligned}$$

Hence,

$$\begin{aligned} d_4&=u_{23}\sigma _{23},\qquad d_5=\frac{1}{2}(u_{22}\sigma _{22} +u_{33}\sigma _{33}),\\ A&=\ell _{111}\sigma _{11}+2\ell _{121}\sigma _{12} +2\ell _{131}\sigma _{13}+\ell _{221}\sigma _{22}+\ell _{331}\sigma _{33},\\~~~ B&=\ell _{112}\sigma _{11}+2\ell _{122}\sigma _{12}+\ell _{222}\sigma _{22},\quad C=\ell _{113}\sigma _{11}+2\ell _{133}\sigma _{13}+\ell _{333}\sigma _{33}. \end{aligned}$$