Time-of-use pricing in the electricity markets: mathematical modelling using non-linear market demand

Abstract

We determine the gains in efficiency accruing to a monopolist producer facing a non-linear market demand under a time-of-use (TOU) pricing structure as opposed to a flat rate pricing (FRP) structure. In particular, we consider the constant elasticity of demand function and the exponential demand function for this analysis. We estimate the price and quantity demanded for these two types of functions and optimize the profit earned by the producer. A comparison of the linear, exponential, and constant elasticity of demand functions shows that in cases of linear and exponential demand, the TOU pricing works to reduce the peak demand below the installed capacity and saves on additional investment and operation costs, while no such reduction takes place in the case of constant elasticity of demand. However, profit accruing to the monopolist under the TOU pricing structure exceeds that under FRP, irrespective of the form of the demand function. Thus, we conclude that regardless of the shape of the demand function, a time-varying pricing structure is better than the traditional FRP. Finally, we study some implications for the policy maker if such a pricing structure is implemented.

1 Introduction

Considerable work has been carried out in the area of revenue management in the context of an efficient dynamic pricing scheme in electricity markets. The application of time-of-use (TOU) pricing, a specific type of dynamic pricing, can shift the high load that occurs during the peak period to off-peak periods and thus prevent demand from exceeding the capacity during the peak period. This ensures better capacity utilization during all periods by taking into account the consumers’ responsiveness to changing electricity prices. In this context, there is a need to estimate the gains of a TOU pricing scheme over that of a flat rate pricing (FRP) policy and underline the benefits arising from this shift to dynamic pricing.

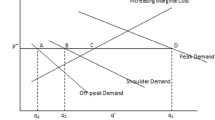
Electricity costs can be based on the average or marginal costs. In the first case, also known as FRP, the prices do not vary according to the time of the day. In the second case, also known as dynamic pricing, prices vary to balance the supply and demand at a given time. The TOU pricing scheme lies between these two extremes. Under this scheme, each day is divided into multiple periods according to consumers’ demands, and there is a demand and supply balance in all time periods, giving the right price signals to the consumers to enable them to adjust their use of electrical appliances to minimize their bills. This leads to efficiency in the market for electricity and ensures that the generation, transmission, and distribution losses are minimized. In the case of an FRP scheme, electricity required during peak periods may exceed the capacity of the generators, which then act as a constraint in the supply of electricity. The introduction of any form of dynamic pricing can help to mitigate this inefficiency by reducing demand during the peak periods as consumers respond to the high prices by readjusting their usage throughout the day. Also, the capacity which may remain idle during off-peak periods are put to better use because of a higher demand for power.

Thus, under the TOU pricing, one can expect significant gains for the electricity suppliers in the form of increased profit and benefits to the consumers in the form of reduced bill under such a scheme. In their previous study, the authors [4] used linear demand and cost functions to estimate the prices and profits of suppliers in both FRP and TOU pricing strategy under both monopolistic and oligopolistic setup. The suppliers’ profits of were found to higher under the TOU pricing scenario, which reflects the efficiency gains earned through the implementation of such a scheme. Decreasing demand during peak periods in response to higher prices leads to proper capacity utilization and minimization of losses in this situation as opposed to the case of FRP. In this paper, we extend the model to study the case when the demand function is not linear while still considering a linear cost structure under a monopolistic setup.

We use constrained optimization techniques to show that profits increase when a price structure that varies by the time of the day is adopted, even when we relax the assumption of linear demand functions. The exponential demand function and constant elasticity of demand function are considered in this study. This is followed by a comparative analysis of the results based on the three demand functions. We conclude that regardless of the form of demand function consideration, the profit under a TOU pricing is greater than that under FRP.

This paper is organized as follows. In Sect. 2, we summarize the literature on this topic and the various models used by researchers to study dynamic pricing and its forms in electricity markets. Section 3 tabulates the assumptions and economics behind the model. In Sect. 4, the model of TOU pricing is optimized under the assumption of a monopoly market condition. We summarize the computational results and analysis in Sect. 5.

2 Literature review

The pricing systems in the electricity markets have been undergoing significant changes in the past few decades. Electricity markets around the world have seen the introduction of various forms of dynamic pricing with an aim to reduce the load during periods of peak demand and use of consumers’ responsiveness to electricity prices to encourage a shift of demand from a period of high demand to a period of low demand. Several authors have modelled the electricity pricing market using experimental data and optimizing methods to understand the effects of a time-dependent pricing system on consumers’ demand.

A study exploring the residential customer response to critical peak pricing of electricity in California [3] used hourly data collected from a 15-month experiment. The high prices used were about three times the on-peak price in the TOU pricing scheme. Using descriptive statistics, the authors showed significant load reduction during critical periods, with the size of the load reduction being the highest in extreme temperatures.

Filippini [2] used the static and dynamic partial adjustment models to understand the responsiveness of residential electricity demand to prices under a TOU pricing scheme based on aggregate data for 22 Swiss cities. Using log-linear demand function, the authors calculated elasticities for both static and dynamic models. As expected, the own price elasticities are lower in the peak period than in the off-peak period. The magnitude of the elasticities suggests that residential demand for electricity is inelastic in the short run and becomes elastic in the long run. Also, the positive values of cross-price elasticities indicate that the off-peak and peak electricity demands are substitutes of each other, suggesting that the TOU price can be effective in achieving energy conservation at least in the long run that allows effective capacity utilization for producers.

While several models have examined the wholesaler’s optimization problem to determine the effect of dynamic pricing on their profits and market powers, [3] proposed a mathematical model for a retailer to determine the price to be charged to consumers on the basis of the TOU and to manage a portfolio of contracts to insure against risk.

In a study by Reiss and Matthew [6], a representative sample data of 1300 residents in California is used to estimate the aggregate and individual consequences of tariff structure changes. The authors focused on the heterogeneity in household price elasticities, how these influence their appliance holdings, how these household consumption responses are adjusted in response to complex price schedules and included these features in a model of endogenous sorting along a non-linear demand schedule. The price effects were found to vary across the appliances with all being of considerable practical significance, and the income effects were found to be almost insignificant. On estimation of households’ demand sensitivity on the margin, it was found that a change in the marginal price may change consumption within the current segment or may equivalently cause a jump to a different tier.

A framework for analysing demand, supply, and prices under real-time pricing and information asymmetry is useful [7]. Real-time pricing creates a closed-loop feedback system between the physical and market layers of the system, which is expected to increase the sensitivity and lower the robustness to demand and generation uncertainty in the absence of a designed control law. The authors allowed the consumers to adjust their consumption in response to a signal, reflecting real-time prices; In their model, they analysed the properties of a full non-linear model as opposed to first-order linear differential equations examined in previous studies. They concluded that a real-time pricing mechanism must consider demand and price variation and that it requires proper analysis of consumers’ response to price signals.

Against the background of these studies, our study focuses on using non-linear demand functions to obtain the TOU prices and efficiency gains for producers in the case of a single decision-making firm and comparing these results with those obtained using a linear demand function.

3 The model assumptions

In this model of TOU pricing, the demand function is considered non-linear and, we assume the following:

• (a) There are three time zones in a day, peak period (that has the highest demand), off-peak (with the lowest demand), and shoulder (having demand somewhere between peak and off-peak periods), with the prices being set in advance.

• (b) We do not consider the classification of consumers according to their usage and price responsiveness (say, residential and commercial). The consumers are considered as one unit, represented by a common market demand function.

• (c) The demand function is non-linear; in particular, we use an exponential demand function and a constant elasticity of demand function. The cost structures are, however, assumed to be linear.

• (d) There is a monopolistic market structure in which a single firm makes the production decisions.

• (e) The electricity is generated in a plant having capacity restrictions. That is, power generated cannot exceed the specified capacity.

• (f) The optimal price chosen by the monopolist in each period does not exceed a specified ceiling.

• (g) For calculating the efficiency gains, we consider only the variable costs for each period. The power plant can operate at constant marginal costs or variable costs that decrease as the load increases. Both these cases are discussed in our model.

• (h) The fixed cost that reflects the cost associated with setting up a generator is assumed to be a one-time cost, which does not vary between off-peak, shoulder, and peak periods. The generated power is transmitted through transmission lines, and some of it is lost in the process as transmission losses. We assume this loss is a fixed percentage of energy generated under all cases.

• (i) We do not consider the existence of externalities in our market.

• (j) A country can rely on both renewable and non-renewable resources for meeting its electricity, but we do not make this distinction in our model.

4 Mathematical model for a monopolist

This section describes the mathematical model to determine the efficiency gains in the TOU pricing vis-à-vis FRP for a monopolist using constrained optimization techniques. In Sect. 4.1, the profit maximizing prices and quantities are determined for a monopolist facing exponential demand functions, under an FRP scheme. First, we assume that the marginal cost is constant in all three periods. Then, we consider the case of decreasing marginal costs as the generation increases. In Sect. 4.2, the aforementioned exercise is repeated under a TOU pricing scheme. Sections 4.3 and 4.4 describe these cases under the assumption of a constant elasticity demand function. Section 4.5 provides a comparative summary of various cases. The model is verified by assuming three demand functions for three time periods or zones (peak, shoulder, and off-peak). The computational result, obtained from optimization using AMPL modelling languages software, is summarized under Sect. 4.6.

Each day is divided into peak, off-peak, and shoulder periods, denoted by the suffix t, where t = 1 for the peak period, t = 2 for the shoulder period, and t = 3 for the off-peak period.

We examine the price structure, quantity produced, and profit earned by the monopolist in the case of two demand functions: exponential demand function and constant elasticity of demand function.

The definitions used in this model are as follows:

${q}_{t} =$ :

Demand for energy per hour in time period t $(KWHr).$

${z}_{t} =$ :

Energy generated per hour in time period t $(KWHr).$

${A}_{t}$, ${b}_{t} =$:

Parameters of the demand function

${p}_{t} =$ :

Price charged by the monopolist at time period t in case of the TOU pricing ($Rs./KWHr$).

$p =$ :

Price charged by the monopolist in the case of uniform pricing ($Rs./KWHr$).

$C =$ :

Capacity of the power generator of the firm in power ($MW$).

$F =$ :

Fixed cost of the system (generation and distribution) of electric power ($Rs.$)

${\delta }_{t} =$ :

Marginal cost associated with an extra unit of electricity at time period t. ($Rs./KWHr$)

$\pi =$ :

Total profit earned by the monopolist ($Rs.$)

${T}_{{\varvec{l}}}\boldsymbol{\%}$ :

Percentage of energy generated that is lost while transmission.

$\therefore \left(1-{T}_{l}\%\right){z}_{t} = {q}_{t}$ :

Demand for energy per hour in time period$t$

$$ \therefore kz_{t} = q_{t} $$

where $k$ = $(1-{T}_{l}\mathrm{\%})$.

The number of hours in a day is assumed to be divided into ${n}_{1}$ hours of peak period, ${n}_{2}$ hours of shoulder period, and ${n}_{3}$ hours of off-peak period.

The energy generated in each period cannot exceed capacity; hence, ${z}_{t}\le 1000C$, $\forall t = \mathrm{1,2},3$.

In the case of flat pricing, the price $p$ that maximizes the monopolist’s profit cannot exceed a specified level $\overline{p }$. In the case of the TOU pricing, the prices ${p}_{1}, {p}_{2}$, and ${p}_{3}$ that maximize the monopolist’s profit cannot exceed a specified $\tilde{p }$.

Hence, for the flat pricing structure, we have $p\le \overline{p }$, and for the TOU pricing structure, we have ${p}_{t}\le \tilde{p }, t = \mathrm{1,2},3$

For both exponential and constant elasticity demand forms that are discussed in the subsequent sections, we assume that for both flat and TOU pricing structure

$$\overline{p } = \tilde{p } = Rs. 10.5/KWh$$

We assume that the firm faces a linear cost structure given by

$$TC = F+\sum_{t = 1}^{3}{{n}_{t}\delta }_{t}{z}_{t}$$

(1)

where ${\delta }_{t}$ represents the marginal cost of generation, and $F$ represents the fixed cost associated with electric power system.

The monopolist is assumed to be a profit maximizing agent. Thus, the monopolist maximizes,

Profit $(\pi )$ = Revenue – Cost; subject to the capacity constraints.

4.1 The monopolist faces an exponential demand function and charges the same price in all three periods

The exponential demand function is given by

$${q}_{t} = {A}_{t}{e}^{-{b}_{t}p}, t\epsilon \mathrm{1,2},3$$

(2)

The elasticity of the demand functions is given by $(-bp)$, so $b$ captures the responsiveness of quantity as the prices change. We assume that $\left|{b}_{1}\right|<\left|{b}_{2}\right|<|{b}_{3}|$ for our model.

4.1.1 Constant marginal costs

We assume that the monopolist faces a constant marginal cost, $\delta$, in all three periods.

$$ {\text{Thus}},\;{\text{ profit}}\;\pi { } = { }n_{1} pq_{1} + n_{2} pq_{2} + n_{3} pq_{3} - \frac{\delta }{k}\left( {n_{1} q_{1} + n_{2} q_{2} + n_{3} q_{3} } \right) - F $$

(3)

The monopolist’s problem, thus, reduces to

$$Maximize \pi = \left(p-\frac{\delta }{k}\right)\sum_{t = 1}^{3}{n}_{t}{A}_{t}{e}^{-{b}_{t}p}-F$$

$$subject to: {A}_{t}{e}^{-{b}_{t}p}\le 1000Ck, t = \mathrm{1,2},3$$

$$0<p\le \overline{p }$$

We use the method of Lagrange multipliers to solve this problem.

$$\mathcal{L}\boldsymbol{ }=\boldsymbol{ }\left(p-\frac{\delta }{k}\right)\sum_{t = 1}^{3}{n}_{t}{A}_{t}{e}^{-{b}_{t}p}+ \sum_{t = 1}^{3}{\lambda }_{t}\left(1000Ck-{A}_{t}{e}^{-{b}_{t}p}\right)+\mu \left(\overline{p }-p\right)-F$$

(4)

$where {\lambda }_{1},{\lambda }_{2},{\lambda }_{3} are Lagrange multipliers$. The Kaurash Kuhn Tucker (KKT) first-order necessary conditions give us

• 1.
  $$\frac{\partial \mathcal{L}}{\partial p} = 0$$
  $$\Rightarrow \sum_{t = 1}^{3}\left[{n}_{t}\left(1-\left(p-\frac{\delta }{k}\right){b}_{t}\right)+{\lambda }_{t}{b}_{t}\right]{A}_{t}{e}^{-{b}_{t}p}-\mu = 0$$

  (5)
• 2.
  $$\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 1000Ck-{A}_{t}{e}^{-{b}_{t}p}\ge 0 and {\lambda }_{t}\ge 0, t = \mathrm{1,2},3$$

  (6a)
• 3.
  $$\frac{\partial \mathcal{L}}{\partial \mu } = \overline{p }-p\ge 0 and \mu \ge 0$$

  (6b)
• 4.
  $${\lambda }_{t}\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 0, t = \mathrm{1,2},3\, and\, \mu \frac{\partial \mathcal{L}}{\partial \mu } = 0\dots $$

  (7)

As the aforementioned problem is a characterization of non-linear optimization, we might consider imposing certain regularity conditions on the constraints to ensure that the Lagrange multipliers obtained at the optimal point are positive. Hence, we check whether the constraints satisfy the linear independence constraint qualification (LICQ).

We assume that a generator can operate at full capacity during the peak periods, but a lower demand in the off-peak and shoulder periods does not require it to operate at full capacity. Thus, two cases are considered under each scenario. In the first case, there is full-capacity utilization in none of the three periods, and in the second case, full-capacity utilization occurs during the peak period but not in the off-peak or shoulder periods.

Thus, for $t = \mathrm{2,3}$, the constraint (6a) holds with strict inequality; hence, ${\lambda }_{2} = {\lambda }_{3} = 0$ for each case.

Theoretical solutions and simulations in AMPL have established that the price constraint in Eq. (6b) does not bind in deriving the optimal solution to the problem under any of the cases discussed as follows. Hence, we agree that $\mu = 0\Leftrightarrow p<\overline{p }$ for both cases 1 and 2.

Case 1

The capacity constraint is slack for all three periods. Therefore, from (6)

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{1} }}{ > }0 \Rightarrow 10000Ck{ > }A_{1} e^{{ - b_{1} p}} $$

$$\therefore {\lambda }_{1} = 0$$

Putting ${{\lambda }_{1} = \lambda }_{2} = {\lambda }_{3} = 0$ in constraint (4),

$$\sum_{t = 1}^{3}\left[{n}_{t}\left(1-\left(p-\frac{\delta }{k}\right){b}_{t}\right)\right]{A}_{t}{e}^{-{b}_{t}p} = 0$$

(8)

The aforementioned expression is non-linear in p, and hence, a solution for p cannot be obtained in the closed form. So we use Newton–Raphson’s method of iteration¹ to approximate the value of p from Eq. (8).

First, we select an interval $\left[{p}_{1, }{p}_{2}\right]$ in which a root of the function.

$f\left(p\right) = \sum_{t = 1}^{3}\left[{n}_{t}\left(1-\left(p-\frac{\delta }{k}\right){b}_{t}\right)\right]{A}_{t}{e}^{-{b}_{t}p}$ is present.

Differentiating with respect to p

$${f}^{^{\prime}}\left(p\right) = -\sum_{t = 1}^{3}\left(2-\left(p-\frac{\delta }{k}\right){b}_{t}\right){n}_{t}{A}_{t}{e}^{-{b}_{t}p}$$

(9)

It can be easily verified² that $f:[p_{1} ,p_{2} ] \to \mathbb{R}$ satisfies the following:

• (1) $f\left({p}_{1}\right).f\left({p}_{2}\right)<0\left(1\right)$

• (2) $f\left(p\right)$ is continuously differentiable for $p\in \left({p}_{1},{p}_{2}\right)$

• (3) ${f}^{^{\prime}}\left(p\right)\ne 0 \forall p\in \left({p}_{1}, {p}_{2}\right)$

• (4) $f^{{{\prime \prime }}} \left( {\text{p}} \right)$ does not change its sign in $({p}_{1,}{p}_{2})$.

These conditions ensure that the Newton–Raphson’s iterative method converges.

Next, we define the iterative procedure as

$${p}_{(j+1)} = {p}_{(j)}-\frac{f\left({p}_{\left(j\right)}\right)}{{f}^{^{\prime}}\left({p}_{\left(j\right)}\right)},$$

where ${p}_{(j)}$ denotes the ${j}^{\mathrm{th}}$ iteration of p. A starting value ${p}_{0}$ can be chosen from the interval $[{p}_{1}, {p}_{2}]$.

A stopping rule for the iterations can be defined as follows:

We fix the value of $\varepsilon = 0.005$.

Stopping Rule: $\left|\frac{f\left({p}_{\left(j\right)}\right)}{{f}^{^{\prime}}\left({p}_{\left(j\right)}\right)}\right|<\varepsilon$.

The computations were conducted using a C +  + program. The value of p thus obtained by running the C +  + code is denoted by ${{\varvec{p}}}^{\boldsymbol{*}}$.

As not all capacity constraints are assumed to be active, by the KKT conditions, the corresponding Lagrange multipliers are zeroes. Thus, the question of checking for LICQ does not arise in this case.

It can be checked that this value of $p( = {{\varvec{p}}}^{\boldsymbol{*}})$ maximizes the monopolist’s profit.³

Therefore, ${q}_{t}^{*} = {A}_{t}{e}^{-{b}_{t}{p}^{*}}, t = \mathrm{1,2},3$ and the profit earned by the monopolist

$${\pi }^{*} = \left({p}^{*}-\frac{\delta }{k}\right)\sum_{t = 1}^{3}{n}_{t}{A}_{t}{e}^{-{b}_{t}{p}^{*}}-F$$

Case 2

The capacity constraint is tight for the peak period and slack for the off-peak and shoulder periods.

Therefore, from (5)

$$ \frac{{\partial{\mathcal{L}}}}{{\partial \lambda _{1} }} = 0 \Rightarrow 10000Ck = A_{1} e^{{ - b_{1} p}} ,\lambda _{1} { > }0 $$

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{t} }}{ > }0 \Rightarrow 10000Ck{ > }A_{1} e^{{ - b_{1} p}} ,\lambda _{t} = 0,t = {\text{2}},{\text{3}} $$

Therefore, from the constraint equation for the peak period, we have

$$log 1000C{k}_{1} = log{A}_{1}-{b}_{1}p$$

Therefore, ${p}^{*} = \frac{1}{{b}_{1}}log\frac{{A}_{1}}{1000Ck}\,and\,{q}_{t}^{*} = {A}_{t}{\left[\frac{1000Ck}{{A}_{1}}\right]}^{\frac{{b}_{t}}{{b}_{1}}}, t = \mathrm{1,2},3.$

In this case, there is only one active inequality constraint at the optimal ${p}^{*}$: the capacity constraint for peak period. This is trivially linearly independent, hence LICQ is satisfied.

The total profit earned by the monopolist in this case is given by

$$\pi = \left(p-\frac{\delta }{k}\right)\sum_{t = 1}^{3}{n}_{t}{q}_{t}-F$$

$$ \Rightarrow \pi ^{*} = \left( {\frac{1}{{b_{1} }}log\frac{{A_{1} }}{{1000Ck}} - \frac{\delta }{k}} \right)\sum\limits_{{t = 1}}^{3} {n_{t} } A_{t} \left[ {\frac{{1000Ck}}{{A_{1} }}} \right]^{{\frac{{b_{t} }}{{b_{1} }}}} - F $$

4.1.2 Decreasing marginal costs

We assume that the marginal cost associated with generation of electricity decreases as more units are produced. Hence, the per unit electricity ${\delta }_{t}$ cost varies across periods with ${\delta }_{1}<{\delta }_{2}<{\delta }_{3}$ and the profit function becomes

$${\pi = n}_{1}p{q}_{1}+{n}_{2}p{q}_{2}+{n}_{3}p{q}_{3}-\frac{1}{k}\left({n}_{1}{q}_{1}{\delta }_{1}+{n}_{2}{q}_{2}{\delta }_{2}+{n}_{3}{q}_{3}{\delta }_{3}\right)-F$$

(10)

The monopolist’s problem thus reduces to

$$Maximize \pi = \sum_{t = 1}^{3}\left(p-\frac{{\delta }_{t}}{k}\right){n}_{t}{A}_{t}{e}^{-{b}_{t}p}-F$$

$$subject to: {A}_{t}{e}^{-{b}_{t}p}\le 1000Ck, t = \mathrm{1,2},3$$

$$0<p\le \overline{p }$$

We solve the constrained optimization problem with the help of Lagrange multipliers

$$\mathcal{L}\boldsymbol{ }=\boldsymbol{ }\boldsymbol{ }\sum_{t = 1}^{3}\left(p-\frac{{\delta }_{t}}{k}\right){n}_{t}{A}_{t}{e}^{-{b}_{t}p}+ \sum_{t = 1}^{3}{\lambda }_{t}\left(1000Ck-{A}_{t}{e}^{-{b}_{t}p}\right)+\mu \left(\overline{p }-p\right)-F$$

(11)

$where {\lambda }_{1},{\lambda }_{2},{\lambda }_{3} are the Lagrange multipliers$. The KKT first-order necessary conditions give us

• 1.
  $$\frac{\partial \mathcal{L}}{\partial p} = 0$$
  $$\Rightarrow \sum_{t = 1}^{3}\left[{n}_{t}\left(1-\left(p-\frac{{\delta }_{t}}{k}\right){b}_{t}\right)+{\lambda }_{t}{b}_{t}\right]{A}_{t}{e}^{-{b}_{t}p}-\mu = 0$$

  (12)
• 2.
  $$\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 1000Ck-{A}_{t}{e}^{-{b}_{t}p}\ge 0, and {\lambda }_{t}\ge 0, t = \mathrm{1,2},3$$

  (13a)
• 3.
  $$\frac{\partial \mathcal{L}}{\partial \mu } = \overline{p }-p\ge 0 \,and \,\mu \ge 0$$

  (13b)
• 4.
  $${\lambda }_{t}\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 0, t = \mathrm{1,2},3\, and\, \mu \frac{\partial \mathcal{L}}{\partial \mu } = 0$$

  (14)

For $t = \mathrm{2,3}$ the constraint (13a) always holds with strict inequality, hence in each case ${\lambda }_{2} = {\uplambda }_{3} = 0.$

As justified previously, the constraint (13b) also holds with strict inequality in all cases, hence $\mu = 0.$

Case 1

The constraint is slack in all three periods.

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{1} }}{ > }0 \Rightarrow 10000Ck{ > }A_{1} e^{{ - b_{1} p}} $$

$$\therefore {\lambda }_{1} = 0$$

Putting ${\lambda }_{1} = {\lambda }_{2} = {\uplambda }_{3} = 0$ in Eq. (12),

$$\sum_{t = 1}^{3}\left[{n}_{t}\left(1-\left(p-\frac{{\delta }_{t}}{k}\right){b}_{t}\right)\right]{A}_{t}{e}^{-{b}_{t}p} = 0$$

(15)

Like previously, the aforementioned expression is non-linear in p and, hence, a solution for p cannot be obtained in a closed form. So we use Newton–Raphson’s method of iteration to approximate the value of p from Eq. (15).

We mimic the process that was followed while solving for p in Eq. (8) in the case of constant marginal costs.

The value of p thus obtained is denoted by ${p}^{*}.$ As previously, as there are no active inequality constraints at the optimal point, LICQ is not required. In view of the facts stated about ${p}^{*}$, we proceed as follows.

Therefore, ${q}_{t}^{*} = {A}_{t}{e}^{-{b}_{t}{p}^{*}}, t = \mathrm{1,2},3$ and profit earned by the monopolist

$${\pi }^{*} = \sum_{t = 1}^{3}\left({p}^{*}-\frac{{\delta }_{t}}{k}\right){n}_{t}{A}_{t}{e}^{-{b}_{t}{p}^{*}}-F$$

Case 2

The constraint is tight for the peak period but slack for the off-peak and shoulder periods.

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{1} }} = 0 \Rightarrow 10000Ck = A_{1} e^{{ - b_{1} p}} ,\lambda _{1} { > }0 $$

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{t} }}{ > }0 \Rightarrow 10000Ck{ > }A_{1} e^{{ - b_{1} p}} ,\lambda _{t} = 0,t = {\text{2}},{\text{3}} $$

Therefore, from the constraint equation for the peak period, we have

$$log 1000C{k}_{1} = log{A}_{1}-{b}_{1}p$$

Therefore, ${p}^{*} = \frac{1}{{b}_{1}}log\frac{{A}_{1}}{1000Ck} \,and\, {q}_{t}^{*} = {A}_{t}{\left[\frac{1000Ck}{{A}_{1}}\right]}^{\frac{{b}_{t}}{{b}_{1}}}, t = \mathrm{1,2},3$

In this case, there is only one active inequality constraint at the optimal ${p}^{*}$: the capacity constraint for the peak period. This is trivially linearly independent, hence LICQ is satisfied.

The total profit earned by the monopolist in this case is given by

$$\pi = \sum_{t = 1}^{3}\left(p-\frac{{\delta }_{t}}{k}\right){n}_{t}{q}_{t}-F$$

$$ \Rightarrow \pi ^{*} = \sum\limits_{{t = 1}}^{3} {\left( {\frac{1}{{b_{1} }}log\frac{{A_{1} }}{{1000Ck}} - \frac{{\delta _{t} }}{k}} \right)} n_{t} A_{t} \left[ {\frac{{1000Ck}}{{A_{1} }}} \right]^{{\frac{{b_{t} }}{{b_{1} }}}} - F $$

4.2 The monopolist facing an exponential demand curve charges different prices in different time periods

4.2.1 Constant marginal costs

If the monopolist charges different prices in different periods but faces the same marginal costs in all three periods, then the profit function becomes

$$\pi = {n}_{1}{p}_{1}{q}_{1}+{n}_{2}{p}_{2}{q}_{2}+{n}_{3}{p}_{3}{q}_{3}-\frac{\delta }{k}\left({n}_{1}{q}_{1}+{n}_{2}{q}_{2}+{n}_{3}{q}_{3}\right)-F;$$

Thus, the optimization problem for the monopolist becomes

$$Maximize \pi = \sum_{t = 1}^{3}\left({p}_{t}-\frac{\delta }{k}\right){n}_{t}{A}_{t}{e}^{-{b}_{t}{p}_{t}}-F$$

$$subject to {A}_{t}{e}^{-{b}_{t}{p}_{t}}\le 1000Ck, t = \mathrm{1,2},3$$

$$0<{p}_{t}\le \tilde{p }, t = \mathrm{1,2},3$$

We solve the problem using the method of Lagrange multipliers.

$$\psi \boldsymbol{ }=\boldsymbol{ }\boldsymbol{ }\sum_{t = 1}^{3}\left({p}_{t}-\frac{\delta }{k}\right){n}_{t}{A}_{t}{e}^{-{b}_{t}{p}_{t}}+ \sum_{t = 1}^{3}{\varphi }_{t}\left(1000Ck-{A}_{t}{e}^{-{b}_{t}{p}_{t}}\right)+\sum_{t = 1}^{3}{\mu }_{t}(\tilde{p }-{p}_{t})-F\dots \left(16\right),$$

$where\;\varphi _{1} ,\;{\mkern 1mu}\,\varphi _{2} ,\;\varphi _{3}\;are\;the\;Lagrange\;multipliers$.

The KKT first-order necessary conditions give us

• 1.
  $$\frac{\partial \psi }{\partial {p}_{t}} = 0$$
  $$\Rightarrow \left[{n}_{t}\left(1-\left({p}_{t}-\frac{\delta }{k}\right){b}_{t}\right)+{\varphi }_{t}{b}_{t}\right]{A}_{t}{e}^{-{b}_{t}{p}_{t}}-{\mu }_{t}{p}_{t} = 0$$

  (17)
• 2.
  $$\frac{\partial \psi }{\partial {\varphi }_{t}} = 1000Ck-{A}_{t}{e}^{-{b}_{t}{p}_{t}}\ge 0 \,and\, {\varphi }_{t}\ge 0, t = \mathrm{1,2},3$$

  (18a)
• 3.
  $$\frac{\partial \psi }{\partial {\mu }_{t}} = \tilde{p }-{p}_{t}\ge 0\, and\, {\mu }_{t}\ge 0$$

  (18b)
• 4.
  $$ \varphi _{t} \frac{{\partial \psi }}{{\partial \varphi _{t} }} = 0\;\,and\;\,\mu _{t} \frac{{\partial \psi }}{{\partial \mu _{t} }} = 0,t = {\text{1}},{\text{2}},3 $$

  (19)

The constraint (18a) holds with strict inequality for $t = \mathrm{2,3}$ hence ${\varphi }_{2 } = {\varphi }_{3} = 0$ in all cases. The price constraints (18b) also hold with strict inequality in all cases, thus ${\mu }_{t} = 0 \,\forall t\, = \mathrm{1,2},3.$

Case 1

The constraints for all three periods are slack.

$$ \frac{{\partial \psi }}{{\partial \varphi _{1} }}{ > }0 \Rightarrow 10000Ck{ > }A_{1} e^{{ - b_{1} p_{1} }} $$

$$\therefore {\varphi }_{1} = 0$$

Putting ${{\varphi }_{1 } = \varphi }_{2 } = {\varphi }_{3} = 0$ in Eq. (17)

$$\left[{n}_{t}\left(1-\left({p}_{t}-\frac{\delta }{k}\right){b}_{t}\right)\right]{A}_{t}{e}^{-{b}_{t}{p}_{t}} = 0$$

(20)

Therefore, ${p}_{t}^{*} = \frac{k+\delta {b}_{t}}{k{b}_{t}}\, \mathrm{and }\,{q}_{t}^{*} = {A}_{t}{e}^{-\left(\frac{k+\delta {b}_{t}}{k}\right)}, t = \mathrm{1,2},3$

As previously, as there are no active inequality constraints at the optimal point, LICQ is not required.

The total profit of the monopolist is given by

$${\pi }^{*} = \sum_{t = 1}^{3}\left({p}_{t}^{*}-\frac{\delta }{k}\right){n}_{t}{q}_{t}^{*}-F$$

$$ \Rightarrow {\pi }^{*} = \sum_{t = 1}^{3}\frac{{n}_{t}{A}_{t}}{{b}_{t}}{e}^{-\left(\frac{k+\delta {b}_{t}}{k}\right)}-F$$

Case 2

The peak period constraint is tight

$$ \frac{{\partial \psi }}{{\partial \varphi _{1} }} = 0 \Rightarrow 10000Ck = A_{1} e^{{ - b_{1} p_{1} }} ,\varphi _{1} { > }0 $$

$$ \frac{{\partial \psi }}{{\partial \varphi _{t} }}{ > }0 \Rightarrow 10000Ck{ > }A_{t} e^{{ - b_{t} p_{t} }} ,\varphi _{t} = 0,t = {\text{2}},{\text{3}} $$

Therefore, ${p}^{*} = \frac{1}{{b}_{1}}log\frac{{A}_{1}}{1000Ck}\, and\, {q}_{1}^{*} = 1000Ck$

Putting ${{\varphi }_{2 } = \varphi }_{3} = 0$ in Eq. (17), we have

$${p}_{t}^{*} = \frac{k+\delta {b}_{t}}{k{b}_{t}} \,and\, {q}_{t}^{*} = {A}_{t}{e}^{-\left(\frac{k+\delta {b}_{t}}{k}\right)}, t = \mathrm{2,3}$$

In this case, there is only one active inequality constraint at the optimal ${p}^{*}$: the capacity constraint for peak period. This is trivially linearly independent, hence LICQ is satisfied.

The total profit earned by the monopolist becomes

$${\pi }^{*} = \sum_{t = 1}^{3}\left({p}_{t}^{*}-\frac{\delta }{k}\right){n}_{t}{q}_{t}^{*}-F$$

$$ \Rightarrow {\pi }^{*} = {n}_{1}1000Ck\left[\frac{1}{{b}_{1}}log\frac{{A}_{1}}{1000Ck}-\frac{\delta }{k}\right]+\sum_{t = 2}^{3}\frac{{n}_{t}{A}_{t}}{{b}_{t}}{e}^{-\left(\frac{k+\delta {b}_{t}}{k}\right)}-F$$

4.2.2 Decreasing marginal costs

According to the previous assumption, we have ${\delta }_{1}<{\delta }_{2}<{\delta }_{3}$. If the monopolist faces marginal costs which decrease as the load increases, the profit function becomes

$$\pi = {n}_{1}{p}_{1}{q}_{1}+{n}_{2}{p}_{2}{q}_{2}+{n}_{3}{p}_{3}{q}_{3}-\frac{1}{k}\left({n}_{1}{\delta }_{1}{q}_{1}+{n}_{2}{\delta }_{2}{q}_{2}+{n}_{3}{\delta }_{3}{q}_{3}\right)-F$$

The optimization problem for the monopolist thus becomes

$$Maximize \pi = \sum_{t = 1}^{3}\left({p}_{t}-\frac{{\delta }_{t}}{k}\right){n}_{t}{A}_{t}{e}^{-{b}_{t}{p}_{t}}-F$$

$$subject to: {A}_{t}{e}^{-{b}_{t}{p}_{t}}\le 1000Ck, t = \mathrm{1,2},3$$

$$0<{p}_{t}\le \tilde{p }, t = \mathrm{1,2},3$$

We solve the constrained optimization problem by the method of Lagrange multipliers.

$$ \psi = \mathop \sum \limits_{{t{ } = { }1}}^{3} \left( {p_{t} - \frac{{\delta_{t} }}{k}} \right)n_{t} A_{t} e^{{ - b_{t} p_{t} }} + { }\mathop \sum \limits_{{t{ } = { }1}}^{3} \varphi_{t} \left( {1000Ck - A_{t} e^{{ - b_{t} p_{t} }} } \right) + \mathop \sum \limits_{{t{ } = { }1}}^{3} \mu_{t} (\tilde{p} - p_{t} ) - F $$

(21)

$$where \, {\varphi }_{1},{\varphi }_{2},\,{\varphi }_{3} \,are\, the\, Lagrange \,multipliers$$

The KKT first-order necessary conditions give us

• 1.
  $$\frac{\partial \psi }{\partial {p}_{t}} = 0$$
  $$\Rightarrow \left[{n}_{t}\left(1-\left({p}_{t}-\frac{{\delta }_{t}}{k}\right){b}_{t}\right)+{\varphi }_{t}{b}_{t}\right]{A}_{t}{e}^{-{b}_{t}{p}_{t}}-{\mu }_{t} = 0$$

  (22)
• 2.
  $$\frac{\partial \psi }{\partial {\varphi }_{t}} = 1000Ck-{A}_{t}{e}^{-{b}_{t}{p}_{t}}\ge 0 and {\varphi }_{t}\ge 0, t = \mathrm{1,2},3$$

  (23a)
• 3.
  $$\frac{\partial \psi }{\partial {\mu }_{t}} = \tilde{p }-{p}_{t}\ge 0 and {\mu }_{t}\ge 0, t = \mathrm{1,23}$$

  (23b)
• 4.
  $${\varphi }_{t}\frac{\partial \psi }{\partial {\varphi }_{t}} = 0 and {\mu }_{t}\frac{\partial \psi }{\partial {\mu }_{t}} = 0, t = \mathrm{1,2},3$$

  (24)

The capacity constraints (23a) hold with strict inequality for $t = \mathrm{2,3}$, hence ${\varphi }_{2} = {\varphi }_{3} = 0$ in each case. The price constraints (23b) also hold with strict inequality $\forall t = \mathrm{1,2},3$ in all cases, that is, ${\mu }_{t} = 0$.

Case 1

All capacity constraints are slack.

$$ \frac{{\partial \psi }}{{\partial \varphi _{1} }}{ > }0 \Rightarrow 10000Ck{ > }A_{1} e^{{ - b_{1} p_{1} }} $$

$$\therefore {\varphi }_{1} = 0$$

Putting ${\varphi }_{1} = {\varphi }_{2} = {\varphi }_{3} = 0$ in Eq. (22), we have

$$\left[{n}_{t}\left(1-\left({p}_{t}-\frac{{\delta }_{t}}{k}\right){b}_{t}\right)\right]{A}_{t}{e}^{-{b}_{t}{p}_{t}} = 0$$

(25)

Therefore, ${p}_{t}^{*} = \frac{k+{\delta }_{t}{b}_{t}}{k{b}_{t}} \,and \,{q}_{t}^{*} = {A}_{t}{e}^{-\left(\frac{k+{\delta }_{t}{b}_{t}}{k}\right)}, t = \mathrm{1,2},3$

As previously, as there are no active inequality constraints at the optimal point, LICQ is not required.

The profit earned by the monopolist becomes

$${\pi }^{*} = \sum_{t = 1}^{3}\left({p}_{t}^{*}-\frac{{\delta }_{t}}{k}\right){n}_{t}{q}_{t}^{*}-F$$

$$ \Rightarrow {\pi }^{*} = \sum_{t = 1}^{3}\frac{{n}_{t}{A}_{t}}{{b}_{t}}{e}^{-\left(\frac{k+{\delta }_{t}{b}_{t}}{k}\right)}-F$$

Case 2

The peak period capacity constraint is tight.

$$ \frac{{\partial \psi }}{{\partial \varphi _{1} }} = 0 \Rightarrow 10000Ck = A_{1} e^{{ - b_{1} p_{1} }} ,\varphi _{1} { > }0 $$

$$ \frac{{\partial \psi }}{{\partial \varphi _{t} }}{ > }0 \Rightarrow 10000Ck{ > }A_{t} e^{{ - b_{t} p_{t} }} ,\varphi _{t} = 0,t = {\text{2}},{\text{3}} $$

Therefore, ${p}^{*} = \frac{1}{{b}_{1}}log\frac{{A}_{1}}{1000Ck} \,and\, {q}_{1}^{*} = 1000Ck$

Putting ${{\varphi }_{2 } = \varphi }_{3} = 0$ in Eq. (17), we have

$${p}_{t}^{*} = \frac{k+{\delta }_{t}{b}_{t}}{k{b}_{t}}\,and\,{q}_{t}^{*} = {A}_{t}{e}^{-\left(\frac{k+{\delta }_{t}{b}_{t}}{k}\right)}, t = \mathrm{2,3}$$

In this case, there is only one active inequality constraint at the optimal ${p}^{*}$: the capacity constraint for the peak period. This is trivially linearly independent, hence LICQ is satisfied.

The total profit earned by the monopolist becomes

$${\pi }^{*} = \sum_{t = 1}^{3}\left({p}_{t}^{*}-\frac{{\delta }_{t}}{k}\right){n}_{t}{q}_{t}^{*}-F$$

$$ \Rightarrow {\pi }^{*} = {n}_{1}1000Ck\left[\frac{1}{{b}_{1}}log\frac{{A}_{1}}{1000Ck}-\frac{{\delta }_{t}}{k}\right]+\sum_{t = 2}^{3}\frac{{n}_{t}{A}_{t}}{{b}_{t}}{e}^{-\left(\frac{k+{\delta }_{t}{b}_{t}}{k}\right)}-F$$

4.3 The monopolist faces a constant elasticity demand function and charges the same price for all three periods

We consider a constant elasticity of demand function in this section of the form

$${q}_{t} = {A}_{t}{p}^{-{b}_{t} }\,\forall t\,\,\epsilon \mathrm{1,2},3$$

(26)

The definitions used in this model are the same as those used in the model for exponential demand function. The parameters specific to this model are ${A}_{t}$ and ${b}_{t}$, where ${b}_{t}$ is the constant elasticity along the demand function for a particular period.

We assume that ${e}_{3} \ge {e}_{2}\ge {e}_{1}$, that is, the elasticity is the highest for the off-peak period followed by the shoulder and peak periods. This is consistent with the economic theory of demand, being less elastic during periods of peak demand.

4.3.1 Constant marginal costs

In this section, we assume that the monopolist faces a constant marginal cost $\delta$ in all three periods.

The profit function of the monopolist is thus

$$\pi = {n}_{1}p{q}_{1}+{n}_{2}p{q}_{2}+{n}_{3}p{q}_{3}-\delta \left({n}_{1}p{z}_{1}+{n}_{2}p{z}_{2}+{n}_{3}p{z}_{3}\right)-F$$

$${= n}_{1}p{q}_{1}+{n}_{2}p{q}_{2}+{n}_{3}p{q}_{3}-\frac{\delta }{k}\left({n}_{1}{q}_{1}+{n}_{2}{q}_{2}+{n}_{3}{q}_{3}\right)-F$$

The optimization problem of the monopolist thus reduces to

$$Maximize\, \pi = \left(p-\frac{\delta }{k}\right)\sum_{t = 1}^{3}{n}_{t}{A}_{t}{p}^{-{b}_{t}}-F$$

$$subject \,to: {A}_{t}{p}^{-{b}_{t}}\le 1000Ck, t = \mathrm{1,2},3$$

$$0<p\le \overline{p }$$

We solve this constrained optimization problem using the method of Lagrange multipliers.

$$\mathcal{L}\boldsymbol{ }=\boldsymbol{ }\boldsymbol{ }\left(p-\frac{\delta }{k}\right)\sum_{t = 1}^{3}{n}_{t}{A}_{t}{p}^{-{b}_{t}}+ \sum_{t = 1}^{3}{\lambda }_{t}\left(1000Ck-{A}_{t}{p}^{-{b}_{t}}\right)+\mu \left(\overline{p }-p\right)-F$$

(27)

where ${\lambda }_{1},\,{\lambda }_{2},\,{\lambda }_{3}$ are the Lagrange multipliers

The KKT first-order necessary conditions give us

• 1.
  $$\frac{\partial \mathcal{L}}{\partial p} = 0$$
  $$\Rightarrow \sum_{t = 1}^{3}\left[{n}_{t}\left(p-\left(p-\frac{\delta }{k}\right){b}_{t}\right)+{\lambda }_{t}{b}_{t}\right]{A}_{t}{p}^{-{b}_{t}-1}-\mu = 0$$

  (28)
• 2.
  $$\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 1000Ck-{A}_{t}{p}^{-{b}_{t}}\ge 0\, and \,{\lambda }_{t}\ge 0, t = \mathrm{1,2},3$$

  (29a)
• 3.
  $$\frac{\partial \mathcal{L}}{\partial \mu } = \overline{p }-p\ge 0\, and\, \mu \ge 0$$

  (29b)
• 4.
  $${\lambda }_{t}\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 0, t = \mathrm{1,2},3 \,and \,\mu \frac{\partial \mathcal{L}}{\partial \mu } = 0$$

  (30)

As in the previous sub-sections, we assume that the high demand during a peak period may cause the generator to operate at full capacity, but lower demands during the off-peak and shoulder periods do not require operation at full capacity. Hence, we take two cases for each of the scenarios. In the first case, the generator does not operate at full capacity in any of the three periods, and in the second, the generator operates at full capacity during the peak period but not during the off-peak or shoulder periods.

For $t = \mathrm{2,3}$ constraint (29a) holds with strict inequality, hence ${\lambda }_{2}, {\lambda }_{3} = 0$ for each case. The price constraint (29b) also holds with strict inequality for $t = \mathrm{1,2},3,$ in all the cases.

Case 1

All constraints are slack.

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{1} }}{ > }0 \Rightarrow 10000Ck{ > }A_{1} p^{{ - b_{1} }} $$

$$\therefore {\lambda }_{1} = 0$$

Putting ${\lambda }_{1} = {\lambda }_{2} = {\uplambda }_{3} = 0$ in Eq. (28)

$$\sum_{t = 1}^{3}\left[{n}_{t}\left(p-\left(p-\frac{\delta }{k}\right){b}_{t}\right)\right]{A}_{t}{p}^{-{b}_{t}-1} = 0$$

(31)

Similarly, the above expression is non-linear in p and, hence, a solution for p cannot be obtained in a closed form. So we use Newton–Raphson’s method of iteration to approximate the value of p from Eq. (31).

We mimic the process used for solving for p earlier in Eqs. (8) and (15).

The value of p thus obtained is denoted by ${p}^{*}$.

As previously, since there are no active inequality constraints at the optimal point, LICQ is not required.

Therefore, ${q}_{t}^{*} = {A}_{t}{e}^{-{b}_{t}{p}^{*}}, t = \mathrm{1,2},3$ and profit earned by the monopolist

$${\pi }^{*} = \sum_{t = 1}^{3}\left({p}^{*}-\frac{\delta }{k}\right){n}_{t}{A}_{t}{\left({p}^{*}\right)}^{-{b}_{t}}-F$$

Case 2

The peak period constraint is tight.

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{1} }} = 0 \Rightarrow 10000Ck = A_{1} p^{{ - b_{1} }} ,\lambda _{1} { > }0 $$

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{t} }}{ > }0 \Rightarrow 10000Ck{ > }A_{t} p^{{ - b_{t} }} ,\lambda _{t} = 0,t = {\text{2}},{\text{3}} $$

$$ {\text{Therefore}}\;p^{*} = [\frac{{A_{1} }}{1000Ck}]^{{\frac{1}{{b_{1} }}}} \;{\text{and}}\;q_{t}^{*} = A_{t} \left[ {\frac{1000Ck}{{A_{1} }}} \right]^{{\frac{{b_{t} }}{{b_{1} }}}} \forall t \in 1,2,3 $$

(32)

In this case, there is only one active inequality constraint at the optimal ${p}^{*}$: the capacity constraint for peak period. This is trivially linearly independent, hence LICQ is satisfied.

The profit earned by the monopolist becomes

$$\pi = \left({p}^{*}-\frac{\delta }{k}\right)\sum_{t = 1}^{3}{n}_{t}{q}_{t}^{*}-F$$

Thus

$$ \Rightarrow {\pi }^{*} = \left[{\left(\frac{{A}_{1}}{1000Ck}\right)}^{\frac{1}{{b}_{1}}}-\frac{\delta }{k}\right]\sum_{t = 1}^{3}{n}_{t}{A}_{t}{\left(\frac{1000Ck}{{A}_{1}}\right)}^{\frac{{b}_{t}}{{b}_{1}}}-F$$

4.3.2 Decreasing marginal costs

The profit function of the monopolist becomes

$$\pi = {n}_{1}p{q}_{1}+{n}_{2}p{q}_{2}+{n}_{3}p{q}_{3}-\frac{1}{k}\left({n}_{1}{\delta }_{1}{q}_{1}+{n}_{2}{\delta }_{1}{q}_{2}+{n}_{3}{\delta }_{3}{q}_{3}\right)-F$$

The optimization problem of the monopolist is

$$Maximize \pi = \sum_{t = 1}^{3}{\left(p-\frac{{\delta }_{t}}{k}\right)n}_{t}{A}_{t}{p}^{-{b}_{t}}-F$$

$$subject to {A}_{t}{p}^{-{b}_{t}}\le 1000Ck, t = \mathrm{1,2},3$$

$$0<p\le \overline{p }$$

We solve the constrained optimization problem by the method of Lagrange multipliers.

$$\mathcal{L}\boldsymbol{ }=\boldsymbol{ }\boldsymbol{ }\sum_{t = 1}^{3}{\left(p-\frac{{\delta }_{t}}{k}\right)n}_{t}{A}_{t}{p}^{-{b}_{t}}+ \sum_{t = 1}^{3}{\lambda }_{t}\left(1000Ck-{A}_{t}{p}^{-{b}_{t}}\right)+\mu \left(\overline{p }-p\right)-F$$

(33)

$where {\lambda }_{1},{\lambda }_{2},{\lambda }_{3} are theLagrange multipliers$.

The KKT first-order necessary conditions give us

• 1.
  $$\frac{\partial \mathcal{L}}{\partial p} = 0$$
  $$\Rightarrow \sum_{t = 1}^{3}\left[{n}_{t}\left(p-\left(p-\frac{{\delta }_{t}}{k}\right){b}_{t}\right)+{\lambda }_{t}{b}_{t}\right]{A}_{t}{p}^{-{b}_{t}-1}-\mu = 0$$

  (34)
• 2.
  $$\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 1000Ck-{A}_{t}{p}^{-{b}_{t}}\ge 0 and {\lambda }_{t}\ge 0, t = \mathrm{1,2},3$$

  (35a)
• 3.
  $$\frac{\partial \mathcal{L}}{\partial \mu } = \overline{p }-p\ge 0 and \mu \ge 0$$

  (35b)
• 4.
  $${\lambda }_{t}\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 0, t = \mathrm{1,2},3$$

  (36)

For $t = \mathrm{2,3}$, constraint (35) holds as strict inequality, hence ${{\lambda }_{2},\lambda }_{3} = 0$ for each case. The price constraint (35b) also holds with strict inequality for $t = \mathrm{1,2},3$ in all the cases.

Case 1

The constraint for each period is slack.

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{1} }}{ > }0 \Rightarrow 10000Ck{ > }A_{1} p^{{ - b_{1} }} $$

$$\therefore {\lambda }_{1} = 0$$

Putting ${\lambda }_{1} = {\lambda }_{2} = {\lambda }_{3} = 0$ in Eq. (34), we obtain

$$\sum_{t = 1}^{3}\left[{n}_{t}\left(p-\left(p-\frac{{\delta }_{t}}{k}\right){b}_{t}\right)\right]{A}_{t}{p}^{-{b}_{t}-1} = 0$$

(37)

Similarly, the above expression is non-linear in p and, hence, a solution for p cannot be obtained in a closed form. So we use Newton–Raphson’s method of iteration to approximate the value of p from Eq. (37).

We mimic the process that was followed while solving for p earlier in Eq. (8), (15), and (31).

The value of p thus obtained is denoted by ${p}^{*}$.

As previously, as there are no active inequality constraints at the optimal point, LICQ is not required.

Therefore, ${q}_{t}^{*} = {A}_{t}{e}^{-{b}_{t}{p}^{*}}, t = \mathrm{1,2},3$ and profit earned by the monopolist is

$${\pi }^{*} = \sum_{t = 1}^{3}\left({p}^{*}-\frac{\delta }{k}\right){n}_{t}{A}_{t}{\left({p}^{*}\right)}^{-{b}_{t}}-F$$

Case 2

The peak period constraint is tight.

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{1} }} = 0 \Rightarrow 10000Ck = A_{1} p^{{ - b_{1} }} ,\lambda _{1} { > }0 $$

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{t} }}{ > }0 \Rightarrow 10000Ck{ > }A_{t} p^{{ - b_{t} }} ,\lambda _{t} = 0,t = {\text{2}},{\text{3}} $$

$$ p^{*} = \left[ {\frac{{A_{1} }}{1000Ck}} \right]^{{\frac{1}{{b_{1} }}}} \; and\,q_{t}^{*} = A_{t} \left[ {\frac{{1000Ck_{1} }}{{A_{1} }}} \right]^{{\frac{{b_{t} }}{{b_{1} }}}} \forall t \in 1,2,3 $$

(38)

In this case, there is only one active inequality constraint at the optimal ${p}^{*}$: the capacity constraint for peak period. LICQ is trivially fulfilled.

The profit of the monopolist is

$${\pi }^{*} = \sum_{t = 1}^{3}({p}^{*}-\frac{{\delta }_{t}}{k}){n}_{t}{q}_{t}^{*}-F$$

Thus

$${\pi }^{*} = \sum_{t = 1}^{3}\left[{\left(\frac{{A}_{1}}{1000Ck}\right)}^{\frac{1}{{b}_{1}}}-\frac{{\delta }_{t}}{k}\right]{n}_{t}{A}_{t}{[\frac{1000Ck}{{A}_{1}}]}^{\frac{{b}_{t}}{{b}_{1}}}-F$$

4.4 The monopolist faces a constant elasticity demand function and charges different prices in all three periods

4.4.1 Constant marginal cost

If the monopolist charges different prices in different periods, then for constant marginal costs, the optimization problem becomes

$$\pi = {n}_{1}{p}_{1}{A}_{1}{{p}_{1}}^{-{b}_{1}}+{n}_{2}{p}_{2}{A}_{2}{{p}_{2}}^{-{b}_{2}}+{n}_{3}{p}_{3}{A}_{3}{{p}_{3}}^{-{b}_{3}}-\frac{\delta }{k}\left({n}_{1}{A}_{1}{{p}_{1}}^{{-b}_{1}}+{n}_{2}{A}_{2}{{p}_{2}}^{{-b}_{2}}+{n}_{3}{A}_{3}{{p}_{3}}^{{-b}_{3}}\right)-F$$

The optimization problem of the monopolist, thus, reduces to

$$Maximize \pi = \sum_{t = 1}^{3}\left({p}_{t}-\frac{\delta }{k}\right){n}_{t}{A}_{t}{{p}_{t}}^{-{b}_{t}}-F$$

$$subject to {A}_{t}{{p}_{t}}^{-{b}_{t}}\le 1000Ck, t = \mathrm{1,2},3$$

$$0<{p}_{t}\le \tilde{p }, t = \mathrm{1,2},3$$

We solve this constrained optimization problem by the method of Lagrange multipliers.

$$\mathcal{L}\boldsymbol{ }=\boldsymbol{ }\boldsymbol{ }\sum_{t = 1}^{3}{\left({p}_{t}-\frac{\delta }{k}\right)n}_{t}{A}_{t}{{p}_{t}}^{-{b}_{t}}+ \sum_{t = 1}^{3}{\lambda }_{t}\left(1000Ck-{A}_{t}{{p}_{t}}^{-{b}_{t}}\right)+\sum_{t = 1}^{3}{\mu }_{t}(\tilde{p }-{p}_{t})-F$$

(39)

$where {\lambda }_{1},{\lambda }_{2},{\lambda }_{3} are theLagrange multipliers$.

The KKT first-order necessary conditions give us

• 1.
  $$\frac{\partial \mathcal{L}}{\partial p} = 0$$
  $$\Rightarrow \left[{n}_{t}\left({p}_{t}-\left({p}_{t}-\frac{\delta }{k}\right){b}_{t}\right)+{\lambda }_{t}{b}_{t}\right]{A}_{t}{{p}_{t}}^{-{b}_{t}-1}-{\mu }_{t} = 0$$

  (40)
• 2.
  $$\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 1000Ck-{A}_{t}{{p}_{t}}^{-{b}_{t}}\ge 0, and {\lambda }_{t}\ge 0, t = \mathrm{1,2},3$$

  (41a)
• 3.
  $$\frac{\partial \psi }{\partial {\mu }_{t}} = \tilde{p }-{p}_{t}\ge 0 and {\mu }_{t}\ge 0, t = \mathrm{1,2},3$$

  (41b)
• 4.
  $${\lambda }_{t}\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 0 and {\mu }_{t}\frac{\partial \psi }{\partial {\mu }_{t}} = 0, t = \mathrm{1,2},3$$

  (42)

For $t = \mathrm{2,3}$, constraint (41a) holds with strict inequality, hence, ${\lambda }_{2 } = {\lambda }_{3} = 0$ in both cases. The price constraints (41b) also hold with strict inequality for $t = \mathrm{1,2},3,$ for both cases.

Case 1

The constraint is slack for all three periods.

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{1} }}{ > }0 \Rightarrow 10000Ck{ > }A_{1} p_{1} ^{{ - b_{1} }} $$

$$\therefore {\lambda }_{1} = 0$$

Putting ${\lambda }_{1} = {\lambda }_{2} = {\uplambda }_{3} = 0$ in Eq. (40)

$${n}_{t}\left({p}_{t}-\left({p}_{t}-\frac{\delta }{k}\right){b}_{t}\right){A}_{t}{{p}_{t}}^{-{b}_{t}-1} = 0$$

(43)

$$ p_{t}^{*} = \frac{{\delta b_{t} }}{{k\left( {b_{t} - 1} \right)}} \forall t \in 1,2,3\;{\text{ and}}\;q_{t}^{*} = A_{t} \left[ {\frac{{k\left( {b_{t} - 1} \right)}}{{\delta b_{t} }}} \right]^{{b_{t} }} \forall t \in 1,2,3 $$

(44)

As previously, as there are no active inequality constraints at the optimal point, LICQ is not required.

The profit of the monopolist is

$${\pi }^{*} = \sum_{t = 1}^{3}({p}_{t}^{*}-\frac{\delta }{k}){n}_{t}{q}_{t}^{*}-F$$

$${\pi }^{*} = \sum_{t = 1}^{3}\left(\frac{\delta }{k({b}_{t}-1)}\right) {n}_{t}{A}_{t}{\left[\frac{k\left({b}_{t}-1\right)}{\delta {b}_{t}}\right]}^{{b}_{t}}-F$$

Case 2

The peak period constraint is tight.

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{1} }} = 0 \Rightarrow 10000Ck = A_{1} p^{{ - b_{1} }} ,\lambda _{1} { > }0 $$

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{t} }}{ > }0 \Rightarrow 10000Ck{ > }A_{t} p^{{ - b_{t} }} ,\lambda _{t} = 0,t = {\text{2}},{\text{3}} $$

Therefore, ${p}_{1} = {[\frac{{A}_{1}}{1000Ck}]}^{\frac{1}{{b}_{1}}} and {q}_{1} = 1000Ck$

Putting ${\lambda }_{2 } = {\lambda }_{3} = 0$ in Eq. (40).

Therefore, ${p}_{t}^{*} = \frac{\delta {b}_{t}}{k\left({b}_{t}-1\right)} and {q}_{t}^{*} = {A}_{t}{\left[\frac{k\left({b}_{t}-1\right)}{\delta {b}_{t}}\right]}^{{b}_{t}} \forall t\in \mathrm{2,3}$

In this case, there is only one active inequality constraint at the optimal ${p}^{*}$: the capacity constraint for the peak period. This is trivially linearly independent, hence LICQ is satisfied.

The total profit earned by the monopolist is

$${\pi }^{*} = \sum_{t = 1}^{3}\left({p}_{t}^{*}-\frac{\delta }{k}\right){n}_{t}{q}_{t}^{*}-F$$

Thus

$${\pi }^{*} = {n}_{1}1000Ck\left[{\left(\frac{{A}_{1}}{1000Ck}\right)}^{\frac{1}{{b}_{1}}}-\frac{\delta }{k}\right]+\sum_{t = 2}^{3}\left(\frac{\delta }{k({b}_{t}-1)}\right){n}_{t}{A}_{t}{[\frac{k\left({b}_{t}-1\right)}{\delta {b}_{t}}]}^{{b}_{t}}-F$$

4.4.2 Decreasing marginal costs

If the costs faced by the monopolist are assumed to decrease as the quantity generated increases, such that ${\delta }_{1}<{\delta }_{2}<{\delta }_{3}$, then the profit function becomes

$$\pi = {n}_{1}{p}_{1}{q}_{1}+{n}_{2}{p}_{2}{q}_{2}+{n}_{3}{p}_{3}{q}_{3}-\frac{1}{k}\left({n}_{1}{\delta }_{1}{q}_{1}+{n}_{2}{\delta }_{2}{q}_{2}+{n}_{3}{\delta }_{3}{q}_{3}\right)-F$$

The monopolist’s optimization problem is

$$Maximize \pi = \sum_{t = 1}^{3}\left({p}_{t}-\frac{{\delta }_{t}}{k}\right){n}_{t}{A}_{t}{{p}_{t}}^{-{b}_{t}}-F$$

$$subject to {A}_{t}{{p}_{t}}^{-{b}_{t}}\le 1000Ck, t = \mathrm{1,2},3$$

$${0<p}_{t}\le \tilde{p }, t = \mathrm{1,2},3$$

We solve this constrained optimization problem by the method of Lagrange multipliers.

$$\mathcal{L}\boldsymbol{ }=\boldsymbol{ }\sum_{t = 1}^{3}{\left({p}_{t}-\frac{{\delta }_{t}}{k}\right)n}_{t}{A}_{t}{{p}_{t}}^{-{b}_{t}}+ \sum_{t = 1}^{3}{\lambda }_{t}\left(1000Ck-{A}_{t}{{p}_{t}}^{-{b}_{t}}\right)+\sum_{t = 1}^{3}{\mu }_{t}(\tilde{p }-{p}_{t})-F$$

(45)

$where {\lambda }_{1},{\lambda }_{2},{\lambda }_{3} are theLagrange multipliers$.

The KKT first-order necessary conditions give us

• 1.
  $$\frac{\partial \mathcal{L}}{\partial p} = 0$$
  $$\Rightarrow \left[{n}_{t}\left({p}_{t}-\left({p}_{t}-\frac{{\delta }_{t}}{k}\right){b}_{t}\right)+{\lambda }_{t}{b}_{t}\right]{A}_{t}{{p}_{t}}^{-{b}_{t}-1}-{\mu }_{t} = 0$$

  (46)
• 2.
  $$\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 1000Ck-{A}_{t}{{p}_{t}}^{-{b}_{t}}\ge 0 and {\lambda }_{t}\ge 0, t = \mathrm{1,2},3$$

  (47a)
• 3.
  $$\frac{\partial \psi }{\partial {\mu }_{t}} = \tilde{p }-{p}_{t}\ge 0 and {\mu }_{t}\ge 0, t = \mathrm{1,2},3$$

  (47b)
• 4.
  $${\lambda }_{t}\frac{\partial \mathcal{L}}{\partial {\lambda }_{t}} = 0 and {\mu }_{t}\frac{\partial \psi }{\partial {\mu }_{t}} = 0, t = \mathrm{1,2},3$$

  (48)

For $t = \mathrm{2,3},$ the constraint (47a) holds with strict inequality and hence ${\lambda }_{2 } = {\lambda }_{3} = 0$ in both cases. Price constraints (47b) also hold with strict inequality for $t = \mathrm{1,2},3,$, for both cases.

Case 1

The constraint is slack for all three periods.

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{1} }}{ > }0 \Rightarrow 10000Ck{ > }A_{1} p_{1} ^{{ - b_{1} }} $$

$$\therefore {\lambda }_{1} = 0$$

Putting ${\lambda }_{1} = {\lambda }_{2} = {\uplambda }_{3} = 0$ in Eq. (46),

$${n}_{t}\left({p}_{t}-\left({p}_{t}-\frac{{\delta }_{t}}{k}\right){b}_{t}\right){A}_{t}{{p}_{t}}^{-{b}_{t}-1} = 0$$

(49)

$$ {\text{Therefore}}\;p_{t}^{*} = \frac{{\delta b_{t} }}{{k\left( {b_{t} - 1} \right)}} \forall t \in 1,2,3 \;and\;q_{t}^{*} = A_{t} \left[ {\frac{{k\left( {b_{t} - 1} \right)}}{{\delta b_{t} }}} \right]^{{b_{t} }} \forall t \in 1,2,3 $$

(50)

As previously, as there are no active inequality constraints at the optimal point, LICQ is not required.

The total profit of the monopolist is

$${\pi }^{*} = \sum_{t = 1}^{3}\left({p}_{t}^{*}-\frac{{\delta }_{t}}{k}\right){n}_{t}{q}_{t}^{*}-F$$

Thus

$${\pi }^{*} = \sum_{t = 1}^{3}\left(\frac{{\delta }_{t}}{k({b}_{t}-1)}\right) {n}_{t}{A}_{t}{\left[\frac{k\left({b}_{t}-1\right)}{\delta {b}_{t}}\right]}^{{b}_{t}}-F$$

Case 2

The peak period constraint is tight.

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{1} }} = 0 \Rightarrow 10000Ck = A_{1} p^{{ - b_{1} }} ,\lambda _{1} { > }0 $$

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda _{t} }}{ > }0 \Rightarrow 10000Ck{ > }A_{t} p^{{ - b_{t} }} ,\lambda _{t} = 0,t = {\text{2}},{\text{3}} $$

Therefore, ${p}_{1}^{*} = {[\frac{{A}_{1}}{1000Ck}]}^{\frac{1}{{b}_{1}}} and {q}_{1}^{*} = 1000Ck$

and, ${p}_{t}^{*} = \frac{\delta {b}_{t}}{k\left({b}_{t}-1\right)} and {q}_{t}^{*} = {A}_{t}{\left[\frac{k\left({b}_{t}-1\right)}{\delta {b}_{t}}\right]}^{{b}_{t}} \forall t\in \mathrm{2,3}$

In this case, there is only one active inequality constraint at the optimal ${p}^{*}$: the capacity constraint for the peak period. This is trivially linearly independent, hence LICQ is satisfied.

The total profit earned by the monopolist in this case becomes

$${\pi }^{*} = \sum_{t = 1}^{3}\left({p}_{t}^{*}-\frac{{\delta }_{t}}{k}\right){n}_{t}{q}_{t}^{*}-F$$

$${\pi }_{t}^{*} = {n}_{1}1000Ck\left[{\left(\frac{{A}_{1}}{1000C{k}_{1}}\right)}^{\frac{1}{{b}_{1}}}-\frac{{\delta }_{t}}{k}\right]+\sum_{t = 2}^{3}\left(\frac{{\delta }_{t}}{k({b}_{t}-1)}\right){n}_{t}{A}_{t}{[\frac{k\left({b}_{t}-1\right)}{{\delta }_{t}{b}_{t}}]}^{{b}_{t}}-F$$

4.5 Comparative summary

Tables 1, 2, 3

Table 1 Monopolists profits under: linear demand curve

Table 2 Monopolists profits under: exponential demand curve

Table 3 Monopolists profits under: constant elasticity curve

4.6 Computational results

Kaicker et al. [5] estimated the linear demand functions for the peak, shoulder, and off-peak periods using the data collected from a local electricity supplier.⁴ We form those demands as the basis and estimate the exponential and constant elasticity of demand functions using specific price ranges for peak, shoulder, and off-peak periods. As the optimal prices for the peak, shoulder, and off-peak periods lie in the range of Rs. 9–9.5, Rs. 8–8.5, and Rs. 6.5–7 respectively, we use these ranges to estimate the parameters of the non-linear functions under study. We use a fairly small price interval for the estimation to obtain a better approximation of the exponential and constant elasticity of demand functions.

We use AMPL to derive the optimal prices and profits under a flat rate and TOU pricing scheme. Highest prices are observed during peak periods, followed by shoulder and off-peak periods under the TOU pricing scheme for both exponential and constant elasticity of demand functions. The peak period demand is lower than the shoulder and off-peak demands under the TOU pricing scheme because of the lower prices in the shoulder and off-peak periods. In the case of an exponential demand function, there is a gain in profit of Rs. 1,332,711 under the TOU pricing scheme over the FRP scheme assuming constant marginal costs. The corresponding increase in profits under decreasing marginal costs is Rs. 1,153,657. For constant elasticity of demand functions, we see a gain in profit of Rs. 493,235 assuming constant marginal costs and a gain in profit of Rs. 352,760 assuming decreasing marginal costs. The peak period demand for the estimated constant elasticity of demand curves remains at capacity under both the TOU and FRP scheme, which shows that differential pricing does not help to reduce demand below capacity in this case. The demands for off-peak and shoulder periods are seen to be lower under dynamic pricing as compared to FRP probably because of smaller reductions in prices observed in this case. Capacity = 500 MW.

Transmission Loss = 4%

Fixed Cost = Rs. 2,700,000.

4.6.1 Linear demand

Tables 4, 5, 6, 7, 8

Table 4 Parameters in the model

Table 5 Demand and price under constant marginal cost

Table 6 Revenue, Cost and Profit under constant marginal cost

Table 7 Demand and price under decreasing marginal cost

Table 8 Revenue, cost and profit under decreasing marginal cost

4.6.2 Exponential demand

Tables 9, 10, 11, 12, 13

Table 9 Parameters in the model

Table 10 Demand and price under constant marginal cost

Table 11 Revenue, cost and profit under constant marginal cost

Table 12 Demand and price under decreasing marginal cost

Table 13 Revenue, cost and profit under decreasing marginal cost

4.6.3 Constant elasticity demand

Tables 14, 15, 16, 17, 18

Table 14 Parameters in the model

Table 15 Demand and profit under constant marginal cost

Table 16 Revenue, cost, and profit under constant marginal cost

Table 17 Demand and price under decreasing marginal cost

Table 18 Revenue, cost, and profit under decreasing marginal cost

The profit accruing to a monopolist is higher under a differential pricing scheme as opposed to a flat rate scheme irrespective of the demand function used and the form of marginal cost. In the cases of linear and exponential demand functions, the flat rate peak period demand is above the level that can be supplied by the installed capacity and is thus constrained by the capacity level. The introduction of a TOU pricing structure helps shift the load to periods of lower demands and thus brings the peak period optimal demand below the 480,000 KWHr mark. Thus, under variable pricing scheme, installation of excess capacity for meeting the peak period market demand is not required. Under the constant elasticity of demand case, we see that the peak period demand under both forms of pricing is constrained by the installed capacity. The implementation of TOU pricing does not help to bring down the demand requirement to a level which can be generated by a 500 MW generator used in the analysis.

5 Conclusions and policy implications

The insights for the policymaker which can be drawn from this analysis relate to the efficiency gains of using dynamic pricing over any FRP scheme. Because of the higher profits that a monopolist is able to earn under a TOU pricing structure, the monopolist gains better earnings. Also, because of better capacity utilization under this type of pricing schedule, it does not require the installation of additional capacity to service the market demand during the peak period. The capacity constraint that comes into play in an FRP scheme is no longer relevant under these types of dynamic pricing structures. The consumers also respond to the higher prices during the peak period and lower prices during the off-peak and shoulder periods by reducing their peak period demand and increasing the demand during the other two periods. This shows that the introduction of such a schedule will help in the effective utilization of capacity and efficiency gains for the monopolist, which would work in favour of the acceptance of such time-varying pricing schedule.

Proper implementation of such a dynamic pricing system will, however, require installation of smart meters, an integrated method to divide the day into two or more periods, and the announcement of a time-varying pricing structure which would be predetermined. However, the gains that would emerge from this scheme are expected to be higher than the incurred costs incurred. For this, the government should undertake a proper cost–benefit analysis using real-time demand data.In this paper, we modelled the TOU pricing scheme and compared it to an FRP scheme under a monopolistic setup for non-linear market demand functions. We then performed an analytic comparison between a linear function and the two non-linear functions used in this study. It was found that irrespective of the form of the demand functions, there are efficiency gains for the producer under a time-varying pricing schedule. This form of pricing leads to a better demand–supply balance as a result of consumers responding to the higher prices during peak and lower prices during the other periods and also helps to reduce the pressure on the installed capacity. Thus, installation of additional capacity for meeting the high peak period demands is not required and investment and operating costs are reduced as result. The possibility of excess capacity remaining idle during off-peak periods is somewhat reduced due to higher demand because of low prices during these times of the day.

Under a constant elasticity of demand function, demand is above capacity under a TOU scheme as well. This means that this form of differential pricing is not effective in bringing peak demand below capacity, thus not leading to the type of load reduction seen in the other types of functions (linear and exponential), although the profit accruing to the monopolist is still higher under this pricing scheme. The implications for policymakers in the wake of higher profits for producers under the TOU pricing and better load redistribution in response to the lower prices in the off-peak and shoulder periods indicate that this type of pricing is beneficial to producers in terms of efficiency gains and for consumers in terms of reduction in their bills. Thus, acceptance of this form of pricing scheme would be easier in the wake of significant gains accruing to the public.