Time-of-use pricing of electricity in monopoly and oligopoly

Abstract

This paper discusses the efficiency gains for time-of-use pricing over flat-rate pricing in the electricity sector. The electricity market may be characterised by a monopoly in some cases, where a single firm continues to enjoy market power, or an oligopoly, where two or more firms compete against one another by strategic interaction. This study establishes the feasibility condition for efficiency gains to arise from time-of-use pricing in a monopolistic set up using constrained optimization. In an oligopolistic set-up, the strategic interaction between producers depends on the level of demand. In case of high demand, the producers compete on the basis of output they will produce, resulting in a Cournot-type competition. On the other hand, in case of low demand, an oligopolistic structure may break with only the most efficient firm operating, or results in the emergence of leader firms and follower firms, i.e. the Stackleberg model of oligopoly. The strategic behaviour of firms in a duopoly, generalizable to n firms, is modelled in this study using constrained optimization.

1 Introduction

Revenue management and dynamic pricing is one of the emerging research areas in the service industries. This paper is an attempt to study the efficiency gains for time-of-use (TOU) pricing over flat-rate pricing in the electricity sector. By application of TOU pricing, we can shift the demand from the peak period to the non-peak period and thus, may be able to avoid large capital investments. Even a reduction of 5 per cent in the peak demand can result in savings of to the tune of $9 billion¹ for India. Hence there is a need to study the efficiency gains of TOU pricing over flat-rate pricing. This paper is motivated by the application of TOU pricing in the electricity sector in different types of market structures—monopoly and oligopoly.

Electricity pricing can be based on average cost, with no variation in prices during the day, or on marginal cost, where the price adjusts to the actual demand–supply balance during the day. The former is also known as flat-rate pricing, and the latter, dynamic pricing. Between these two extremes, lies the TOU pricing, where a day is divided into two or more periods, and the price that will be charged in each period is pre-determined. In the case of flat-rate pricing, the entire price risk is borne by the producer, and in real time dynamic pricing, this risk is passed on to the consumer. Since dynamic pricing reflects the actual demand supply balance, it can give the right price signals which enable customers to decide whether the price is high enough to curtail their usage during peak hours. Not only does this bring about economic efficiency in the market for electricity, the reduction in the peak demand may lessen the power generation, transmission and distribution costs by reducing the demand–supply imbalance. It may also lead to avoidance of costs associated with building new capacities.

This paper makes fundamental contributions in the following areas in TOU pricing:

• 1. Using different prices for peak, shoulder and off-peak periods, reflecting actual demand, we determine the efficiency gains that can be captured over using a flat price throughout the day.

• 2. We observe that in the electricity market, there may be a monopoly in some cases, where a single firm continues to enjoy market power, or an oligopoly, where two or more firms compete against one another through strategic interaction. We capture the efficiency gains in both a monopolistic set-up and an oligopolistic set-up using constrained optimisation techniques.

• 3. In the case of monopoly, we demonstrate with real data, the conditions under which dynamic pricing will be beneficial compared to flat rate pricing.

• 4. In an oligopolistic set-up, the strategic interaction between producers depends on the level of demand. In case of high demand, the producers compete on the basis of the output they will produce. On the other hand, in case of low demand, an oligopolistic structure may break with only the most efficient firm operating, or result in the emergence of leader firms and follower firms. All these situations are captured in this paper.

We organise the paper as follows. Section 2 discusses related academic contributions and the techniques used in the past by researchers to model pricing in the electricity market. Section 3 describes the economics and assumptions behind our model. In Sect. 4, a model is formulated to explain the concept of TOU pricing in a monopolistic set up. In Sect. 5, the model is discussed for an oligopolistic set up, where we first take the case of a duopoly and then generalise it to n firms. Section 6 deals with the results, conclusions and future scope for research.

2 Literature review

The electricity sector is characterised by imperfect competition, strategic interaction, collective learning, asymmetric information and the occurrence of multiple equilibria. As this market is extremely complex and gradually evolving, modellers are always trying to formulate new models in order to understand the dynamics of this market. Three major classifications with respect to the modelling in electricity markets have been identified [1]. These models are Optimisation Models, Equilibrium Models, and Simulation Models. In their paper, Borenstein and Bushnell [2] simulate Cournot competition between the major electricity suppliers in California’s electricity market and conclude that under the historical industrial set-up, in the peak period, there is a possibility of significant market power. They also find out that market power can be reduced by implementing policies which promote both the consumer and the producer’s responsiveness to short run fluctuations in prices. In an extension to the above study [3], it was found that when the demand is less responsive to price changes, more market power is observed. In another study, Cardell et al. [4] analyse the strategic interactions which take place in electricity transmission networks, and find that large firms, by increasing their production, lowering prices, and using different strategic interaction techniques can foreclose competition, and hence exercise market power.

Dynamic pricing is a relatively new field which has attracted attention from researchers [5, 6]. When firms use dynamic pricing in order to match demand with the inventory or capacity, the creation of price differences between segments may cause consumers to switch (from higher priced segments to lower priced segments). Thus, there is demand leakage from the market segment with a higher priced product to the market segment with a lower priced product due to price driven substitution [7]. Cellibi and Fuller [8] build a model to estimate ex-ante TOU prices while adhering to the marginal cost principle. They illustrate it by taking four time periods, four types of generation facilities and three demand blocks into account to calculate the prices. The hourly demand derived from Ontario’s Independent Electricity System operator is grouped into 9 h of off-peak, 8 h of shoulder (or mid peak) and 7 h of on peak demand. The results show that TOU prices for some months are equal to the operating cost of the generator that serves the last unit of energy and for some months it is the weighted average of the hourly prices within a certain demand block. The authors observe a 24% increase in off-peak, an 18% increase in mid-peak and a 11% decrease in the on peak demand under TOU as compared to the historical data.

Murphy and Smeers [9] consider three models of investment in generation capacity and try to move from normal economic concepts to computable models. In their first model they assume a perfectly competitive equilibrium in line with the assumptions of a traditional capacity expansion model. The second model is an open-loop Cournot game which extends the Cournot model to allow new investments in generation capacities. The third model, the closed-loop Cournot model assumes that investment decisions are taken in the first stage and sales decision in the second. The authors assume two plants, a peak load plant and a base load plant with separate generators operating and building these plants. The results indicate that the open loop game has a unique equilibrium with market prices above marginal costs. Having a spot market decreases market power to some extent, leading to price and quantity outcomes between the closed loop and perfect competition outcomes. The peak player, due to higher operating costs, is seen to produce less in a closed-loop game than in an open-loop game even in the background of an increase in overall production. That is, in cases where the equilibrium exists, it leads to higher capacity in the closed loop game than in the open loop where all capacity is sold forward at the time of investment.

In their 2012 study, Murphy and Smeers [9] construct a model with firms specializing in a particular technology investing in the first stage, contracting a part of their output in the second and selling the remaining part of the output in a spot market in the third stage. They then compare their model to their previous model which had only two stages, investment and spot market. The authors use two load steps, peak and off-peak which are derived by changing the height of the off-peak time segment. In this context, the authors study investments in an energy-only market with an additional contracts market which is affected by market power. The authors use the Cournot model with agents competing in capacity development, contracts and supplies to the wholesale market. They observe that foreclosure in the contracts market can, under scenarios, decrease prices and increase capacity. The presence of capacity constraints on spot generation can reduce the ability of the contracts to lower market power in such a setting and as a result, investments are below the competitive level in an energy-only market leading to the requirement of additional rules to mitigate the market power resulting from under investment in capacity.

While a considerable amount of work has been done on dynamic pricing in electricity, our contribution lies in capturing the efficiency gains arising out of a special case in dynamic pricing, that is, time-of-use pricing when the market is imperfectly competitive.

3 Economics of the model

Our model for time-of-use pricing is based on the following assumptions:

• (a) Each day is divided into three periods, namely, peak period (having the highest demand), off peak period (lowest demand) and shoulder period (in between the highest and the lowest), and prices for each period are set in advance. There is no block pricing of electricity.

• (b) The consumers of electricity include households, firms, as well as the government, with each category having different demands for electricity at different points of the day and varying price sensitivity. We do not take this classification of consumers into account, and assume all consumers of electricity to be a single entity.

• (c) We assume linear demand and cost structures.

• (d) For producers of electricity, we first assume the case of monopoly. In the next case, due to de-regulation there would be more than one producer of electricity, leading to an oligopolistic market. The firms strategically interact with each other. The competitive model they follow depends on the market demand.

• (e) In the case of oligopoly, we initially take up the case of two firms, that is, the case of duopoly. Both the firms are assumed to have different cost structures depending on the technology used in the process of production and distribution of electricity. The firm using better technology faces a cost curve, which has low marginal cost, and is hence more efficient as compared to the other firm. Each firm is constrained by some capacity, beyond which it is economically not profitable to produce. We consider the capacity of the more efficient firm to be more than the less efficient one.

• (f) In calculating the efficiency gains, we look at the contribution margins in all cases, and deduct the fixed cost from the total margin. Another approach could have been to allocate all fixed costs to the peak period only; however, we do not make that distinction.

• (g) We also assume that there is government regulation, which prevents the firms in an oligopolistic setup to collude with each other and form cartels.

• (h) It is technologically possible for firms to shut down production of electricity, if the situation demands, and stop participating in the market for a period of time. However, if such a thing happens, then the costs incurred from remaining idle at that period of time must be over compensated by the profits earned by the firms when they remain active and participate in the production of electricity.

• (i) We do not take into account externalities such as pilferage of electricity. A country may rely on various sources of electricity—non renewable and renewable. We do not incorporate these differences into our model.

3.1 Technical details of the model

We assume the following with respect to the power generation plant -

• (a) The plant has a capacity restriction which is given by the maximum power that can be generated at any point. The ratio of the actual power generated and the maximum possible power generated is the plant load factor (PLF).

• (b) Some small percentage of the power generated is lost during transmission.

• (c) Production of electricity, transmission of electricity and the consumption of electricity (in terms of demand price equation) can be captured by a linear deterministic system.

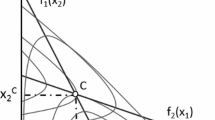
The economic rationale for TOU pricing of electricity is as follows. Figure 1 shows the case of uniform pricing. The three demand curves represent the peak, shoulder and the off-peak periods. In case of uniform pricing, a constant price $\bar{\varvec{P}}$ is charged in all the periods. The resulting quantity demanded is equal to $\varvec{q}_{1} ,\varvec{q}_{2} ,\varvec{ }{\text{and }}\varvec{q}_{3}$ respectively. However as seen from the diagram, during the peak period, there is an excess demand, given by CD. In case of the shoulder period and the off peak period, there is an excess supply given by BC and AC respectively. Thus there is an imbalance between the demand and supply of electricity due to uniform pricing.

Fig. 1

The case of flat rate pricing

Figure 2 depicts the case of TOU pricing. The main idea is to charge different prices at different periods, which reflects the true cost of electricity at that time. The price-quantity combinations are given by ($P_{1} ,q'_{1}$), ($P_{2} ,q'_{2}$), and ($P_{3} ,q'_{3}$) respectively. Suppose the capacity of the firm is given by $\bar{\varvec{q}}$, we observe that in the peak period, the quantity $q'_{1}$ exceeds the capacity. The gap by which this quantity exceeds capacity is smaller compared to the excess demand in case of flat-rate pricing. A price of P must be charged in the peak period to mitigate the excess demand. Thus TOU pricing helps to mitigate the problem of demand–supply imbalance.

Fig. 2

The case of time-of-use pricing

4 Mathematical model for a monopolist

We now look at the dynamics of the model in the following cases. Section 4.1 discusses the case of a monopolist when it charges the same price in all the three periods. We first assume the marginal costs to be constant in all the three periods, and later relax this assumption to decrease the marginal cost as production gets closer to the capacity. Section 4.2 discusses the monopolists’ case when it charges different prices in different time periods, both under the assumption of constant marginal cost, and decreasing marginal cost, as the load increases. A comparison of flat rate pricing and time-of-use pricing is done in Sect. 4.3. We verify the model by estimating three demand functions for peak, off-peak and shoulder periods each, and optimising it using AMPL software. The computational results are discussed under Sect. 4.4.

For our model, we divide each day into peak period, shoulder period, and off-peak period, denoted by a suffix t, where t = 1, for peak period, t = 2, for shoulder period, and t = 3, for off-peak period. The number of hours in a day is assumed to be divided into n₁ h of peak period, n₂ h of shoulder and n₃ h of off-peak period.

The definitions used in the model are as follows:

q_t = Energy demanded per hour in time period t ($KWHr)$

z_t = Energy generated per hour in time period t ($KWHr$)

α_t = Intercept term of the demand function at time period t

β_t = Slope of the demand curve at time period t

P_t = Price charged by the monopolist at time period t in case of time-of-use pricing ($Rs./KWHr$)

P = Price charged by the monopolist in case of uniform pricing ($Rs./KWHr$)

C = Capacity constraint of the plant ($MW$)

F = Fixed Cost associated with generation and distribution of electricity ($Rs.$)

Δt = Marginal Cost associated with an extra unit of electricity at time period t($Rs./KWHr$)

π = Total Profit earned by the monopolist ($Rs.$)

T_l % = Percentage of energy generated that is lost while transmission²

$\therefore \left( {1 - T_{l} \% } \right)z_{t} = q_{t}$ = Energy consumed/demanded per hour for time period t

If $K = \left( {1 - T_{l} \% } \right),kz_{t} = q_{t}$

4.1 Model specification

The firm faces a linear demand curve as given by:

$$ q_{t} = \alpha_{t} - \beta_{t} p_{t} \quad \forall t\,\epsilon \,1,2,3 $$

(1)

Here, we assume that,$\alpha_{1} > \alpha_{2} > \alpha_{3}$ and $\beta_{t} > 0$. $\beta_{t}$ represents the responsiveness of consumers in the period t, to a unit change in prices. We also assume that this responsiveness is the lowest in the peak period followed by the shoulder and then off-peak period. Thus, $\beta_{3} > \beta_{2} > \beta_{1} .$ Since the energy generated in each period cannot exceed the capacity constraint, $z_{t} < 1000C,\quad \forall t\epsilon 1,2,3$³

All the production, operation, transmission, and distribution costs are together termed as total cost denoted by TC. We assume that the firm faces a linear cost function of the form given by:

$$ TC = F + \mathop \sum \limits_{t = 1}^{3} n_{t} \delta_{t} z_{t} $$

(2)

The monopolist is assumed to be a profit maximizing agent. Thus, the monopolist’s problem can be stated as follows:

Maximize $\pi$ = Total Revenue- Total Costs, subject to the necessary constraints.

4.2 The monopolist charges the same price in all the three periods

• (a) Constant marginal costs

If we assume constant marginal cost in all time periods, that is, δ, the profit function is

$$ \pi = n_{1} pq_{1} + n_{2} pq_{2} + n_{3} pq_{3} - \frac{\delta }{k}\left( {n_{1} q_{1} + n_{2} q_{2} + n_{3} q_{3} } \right) - F $$

(3)

We maximise thissubject to: $q_{t} \le C \times 1000 \times k, \quad \forall t\epsilon 1,2,3$.

The optimisation problem thus becomes max,

$$ \begin{aligned} \pi & = n_{1} p\left( {\alpha_{1} - \beta_{1} p} \right) + n_{2} p(\alpha_{2} - \beta_{2} p) + n_{3} p(\alpha_{3} - \beta_{3} p) \\ & \quad - F - \frac{\delta }{k}\left[ {n_{1} \left( {\alpha_{1} - \beta_{1} p} \right) + n_{3} \left( {\alpha_{2} - \beta_{2} p} \right) + n_{3} \left( {\alpha_{3} - \beta_{3} p} \right)} \right] \\ \end{aligned} $$

(4)

subject to,

• (i) $\alpha_{1} - \beta_{1} p \le 1000Ck$

• (ii) $\alpha_{2} - \beta_{2} p \le 1000Ck$

• (iii) $\alpha_{3} - \beta_{3} p \le 1000Ck$

Taking a Lagrangian function ${\mathcal{L}}$, we solve the constrained optimisation problem as follows:

$$ \begin{aligned} {\mathcal{L}} & = \text{ }n_{1} p\left( {\alpha_{1} - \beta_{1} p} \right) + n_{2} p\left( {\alpha_{2} - \beta_{2} p} \right) + n_{3} p\left( {\alpha_{3} - \beta_{3} p} \right) - F - \frac{\delta }{k}\left[ {n_{1} \left( {\alpha_{1} - p} \right) + n_{2} \left( {\alpha_{2} - \beta_{2} p} \right) + n_{3} \left( {\alpha_{3} - \beta_{3} p} \right)} \right] \\ & \quad + \lambda_{1} \left[ {1000Ck - \left( {\alpha_{1} - \beta_{1} p} \right)} \right] + \lambda_{2} \left[ {1000Ck - \left( {\alpha_{2} - \beta_{2} p} \right)} \right] + \lambda_{3} \left[ {1000Ck - \left( {\alpha_{3} - \beta_{3} p} \right)} \right] \\ \end{aligned} $$

(5)

where $\lambda_{1} , \lambda_{2} , \lambda_{3}$ are Lagrange Multipliers.

The First Order Conditions give us the following results:

$$ \frac{{\partial {\mathcal{L}}}}{\partial p} = n_{1} \alpha_{1} + n_{2} \alpha_{2} + n_{3} \alpha_{3} - 2\beta_{1} n_{1} p - 2\beta_{2} n_{2} p - 2\beta_{3} n_{3} p + \frac{\delta }{k}\left( {n_{1} \beta_{1} + n_{2} \beta_{2} + n_{3} \beta_{3} } \right) - \lambda_{1} \beta_{1} - \lambda_{2} \beta_{2} - \lambda_{3} \beta_{3} = 0 $$

(6)

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{t} }} = 1000Ck - (\alpha_{t} - \beta_{t} p) \ge 0\quad \forall t\epsilon 1,2,3 $$

(7)

We assume that it is possible for the generator to operate at its full capacity in the peak period but lower demand in the off-peak and shoulder period does not require the generator to operate at full capacity. Thus we take two cases for each scenario in line with the Karush–Kuhn–Tucker (KKT) conditions. First, full capacity utilisation does not take place in any of the three periods and second, there is full capacity utilisation in the peak period but not in the shoulder or off-peak periods.For t = 2, 3 constraint (ii) and (iii) hold as strict inequality, hence $\lambda_{2} , \lambda_{3} = 0$ for each case.

Case 1 $1000Ck > \alpha_{1} - \beta_{1} p$(the capacity constraint is slack for all three periods).

$$ \therefore \lambda_{1} = 0 $$

Putting $\lambda_{1} = \lambda_{2} = \lambda_{3} = 0$ in Eq. (6),

$$ n_{1} \alpha_{1} + n_{2} \alpha_{2} + n_{3} \alpha_{3} - 2p\left( {n_{1} \beta_{1} + n_{2} \beta_{2} + n_{3} \beta_{3} } \right) + \frac{\delta }{k}\left( {n_{1} \beta_{1} + n_{2} \beta_{2} + n_{3} \beta_{3} } \right) = 0 $$

(8)

Solving this for the price, we get

$$ p = \frac{{\mathop \sum \nolimits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{\delta }{k}\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }}{{2\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }},{\text{and}}\;q_{t} = \alpha_{t} - \beta_{t} p = \alpha_{t} - \beta_{t} \left[ {\frac{{\mathop \sum \nolimits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{\delta }{k}\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }}{{2\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }}} \right],\forall \quad t\epsilon 1,2,3 $$

(9)

The total quantity produced is the sum of quantity supplied in each of the three periods, that is,$Q = n_{1} q_{1} + n_{2} q_{2} + n_{3} q_{3}$.

This equals,

$$ Q = \mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} - \left[ {\frac{{\mathop \sum \nolimits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{\delta }{k}\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }}{{2\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }}} \right]\mathop \sum \limits_{t = 1}^{3} n_{t} \beta_{t} $$

(10)

Thus, the total profit of the monopolist is as follows:

$$ \pi = \frac{{\left[ {\mathop \sum \nolimits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{\delta }{{k_{1} }}\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} } \right]^{2} }}{{4\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }} - F - \frac{\delta }{{k_{1} }}\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} $$

(11)

Case 2 $1000Ck = \alpha_{1} - \beta_{1} p$ (the capacity constraint for the peak period is tight and slack for off-peak and shoulder periods).

$$ p = \frac{{\alpha_{1} - 1000Ck}}{{\beta_{1} }}\;{\text{and}}\;q_{t} = \alpha_{t} - \beta_{t} \left[ {\frac{{\alpha_{1} - 1000Ck}}{{\beta_{1} }}} \right] $$

(12)

The total quantity produced will be the sum of quantities supplied in the three periods,

$$ Q = \mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} - \left[ {\frac{{\alpha_{1} - 1000Ck}}{{\beta_{1} }}} \right]\mathop \sum \limits_{t = 1}^{3} n_{t} \beta_{t} $$

(13)

The total profit of the monopolist in this case is as follows,

$$ \pi = p\left[ {\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{\delta }{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \beta_{t} - p\mathop \sum \limits_{t = 1}^{3} n_{t} \beta_{t} } \right] - F - \frac{\delta }{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} $$

(14)

Using (12), the profit in this case is:

$$ \pi = \frac{{\alpha_{1} - 1000Ck}}{{\beta_{1}^{2} }}[\beta_{1} \mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} + \left( {\frac{{\beta_{1} \delta }}{k} - \left( {\alpha_{1} - 1000Ck} \right)} \right)\mathop \sum \limits_{t = 1}^{3} n_{t} \beta_{t} ] - F - \frac{\delta }{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} . $$

(15)

• (b) Decreasing marginal costs

The marginal cost of electricity generation decreases as more units are put into use. Thus, we assume the marginal cost of producing electricity to be decreasing with the higher load, so if the per unit electricity cost varies across periods, that is, $\delta_{t}$ with $\delta_{1} < \delta_{2} < \delta_{3}$ then the profit function becomes:

$$ \pi = n_{1} pq_{1} + n_{2} pq_{2} + n_{3} pq_{3} - \frac{1}{{k_{1} }}\left( {n_{1} q_{1} \delta_{1} + n_{2} q_{2} \delta_{2} + n_{3} q_{3} \delta_{3} } \right) - F . $$

(16)

subject to,

• (i) $\alpha_{1} - \beta_{1} p \le 1000Ck$

• (ii) $\alpha_{2} - \beta_{2} p \le 1000Ck$

• (iii) $\alpha_{3} - \beta_{3} p \le 1000Ck$

Taking a Lagrangian function ${\mathcal{L}}$, we solve the constrained optimisation problem.

The First Order Conditions give us the following results:

$$ \begin{aligned} \frac{{\partial {\mathcal{L}}}}{\partial p} & = n_{1} \alpha_{1} + n_{2} \alpha_{2} + n_{3} \alpha_{3} - 2\beta_{1} n_{1} p - 2\beta_{2} n_{2} p - 2\beta_{3} n_{3} p \\ & \quad + \frac{1}{k}\left[ {n_{1} \delta_{1} \beta_{1} + n_{2} \delta_{2} \beta_{2} + n_{3} \delta_{3} \beta_{3} } \right] + \lambda_{1} \beta_{1} + \lambda_{2} \beta_{2} + \lambda_{3} \beta_{3} = 0 \\ \end{aligned} $$

(17)

$$ \frac{{\partial {\mathcal{L}}}}{{\partial \lambda_{t} }} = 1000Ck - (\alpha_{t} - \beta_{t} p) \ge 0 \quad \forall t\epsilon 1,2,3 $$

(18)

For t = 2, 3 the constraints (ii) and (iii) always hold with strict inequality, hence in each case $\lambda_{2} = \lambda_{3} = 0.$.

Case 1 $1000Ck > \alpha_{1} - \beta_{1} p$ (the capacity constraint is slack in all three periods).

$$ \therefore \lambda_{1} = 0 $$

$$ p = \frac{{\mathop \sum \nolimits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{1}{k}\mathop \sum \nolimits_{t = 1}^{3} n_{t} \delta_{t} \beta_{t} }}{{2\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }}\;{\text{and }}\;q_{t} = \alpha_{t} - \beta_{t} \left[ {\frac{{\mathop \sum \nolimits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{1}{k}\mathop \sum \nolimits_{t = 1}^{3} n_{t} \delta_{t} \beta_{t} }}{{2\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }}} \right]\forall \quad t\epsilon 1,2,3 $$

(19)

The total quantity will be the sum of quantities produced in the three periods,

$$ Q = \mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} - \left[ {\frac{{\mathop \sum \nolimits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{1}{k}\mathop \sum \nolimits_{t = 1}^{3} n_{t} \delta_{t} \beta_{t} }}{{2\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }}} \right]\mathop \sum \limits_{t = 1}^{3} n_{t} \beta_{t} $$

(20)

The total profit of the monopolist is as given by:

$$ \begin{aligned} \pi = p[\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{1}{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \delta_{t} \beta_{t} - p\mathop \sum \limits_{t = 1}^{3} n_{t} \beta_{t} ] - F - \frac{1}{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \delta_{t} \alpha_{t} \hfill \\ \pi = \frac{{\left( {\mathop \sum \nolimits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{1}{k}\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} \delta_{t} } \right)^{2} }}{{4\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }} - \frac{1}{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} \delta_{t} - F \hfill \\ \end{aligned} $$

(21)

Case 2 $1000Ck = \alpha_{1} - \beta_{1} p$ (the capacity constraint for the peak period is tight and slack for off-peak and shoulder periods).

$$ p = \frac{{\alpha_{1} - 1000Ck}}{{\beta_{1} }}\;{\text{and}}\;q_{t} = \alpha_{t} - \beta_{t} \left[ {\frac{{\alpha_{1} - 1000Ck}}{{\beta_{1} }}} \right] $$

(22)

The total quantity will be the sum of quantities produced in the three periods,

$$ Q_{t} = \mathop \sum \limits_{t = 1}^{3} \alpha_{t} - \left[ {\frac{{\alpha_{1} - 1000Ck}}{{\beta_{1} }}} \right]\mathop \sum \limits_{t = 1}^{3} \beta_{t} $$

(23)

The total profit of the monopolist in this case is as follows

$$ \pi = \frac{{\alpha_{1} - 1000Ck}}{{\beta_{1}^{2} }}[\beta_{1} \mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{{\beta_{1} }}{k}\mathop \sum \limits_{t = 1}^{3} \delta_{t} n_{t} \beta_{t} - \left( {\alpha_{1} - 1000Ck} \right)\mathop \sum \limits_{t = 1}^{3} n_{t} \beta_{t} ] - F - \frac{1}{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \delta_{t} \alpha_{t} $$

(24)

4.3 The monopolist charges different prices in different periods

• a Constant marginal costs

If the monopolist charges different prices in different periods, the profit function is:

$$ \begin{aligned} \pi & = n_{1} p_{1} \left( {\alpha_{1} - \beta_{1} p_{1} } \right) + n_{2} p_{2} \left( {\alpha_{2} - \beta_{2} p_{2} } \right) + n_{3} p_{3} \left( {\alpha_{3} - \beta_{3} p_{3} } \right) \\ & \quad - F - \frac{\delta }{k}\left[ {n_{1} \left( {\alpha_{1} - \beta_{1} p_{1} } \right) + n_{2} \left( {\alpha_{2} - \beta_{2} p_{2} } \right) + n_{3} \left( {\alpha_{3} - \beta_{3} p_{3} } \right)} \right] \\ \end{aligned} $$

(25)

The First Order Conditions using Lagrangian Optimization lead to the following results:

$$ \frac{d\psi }{{dp_{t} }} = n_{t} \alpha_{t} - 2n_{t} \beta_{t} p_{t} + \frac{\delta }{k}n_{t} \beta_{t} + \beta_{t} \varphi_{t } = 0\quad \forall t\epsilon 1,2,3 $$

(26)

$$ \frac{d\psi }{{d\varphi_{t } }} = 1000Ck - (\alpha_{t} - \beta_{t} p_{t} ) \ge 0\quad \forall t\epsilon 1,2,3 $$

(27)

The constraint (27) holds as strict inequality for t = 2, 3, hence $\varphi_{2 } = \varphi_{3} = 0$ in all cases.

Case 1 1000 $Ck > \alpha_{1} - \beta_{1} p_{1}$

$$ n_{t} \alpha_{t} + \frac{\delta }{k}n_{t} \beta_{t} = 2n_{t} \beta_{t} p_{t} , \quad \forall t\epsilon 1,2,3 $$

(28)

$$ p_{t} = \frac{{n_{t} \alpha_{t} + \frac{\delta }{k}n_{t} \beta_{t} }}{{2n_{t} \beta_{t} }},\quad \forall t\epsilon 1,2,3\;{\text{and}}\; q_{t} = \frac{{n_{t} \alpha_{t} - \frac{\delta }{k}\beta_{t} n_{t} }}{{2n_{t} }}\quad \forall t\epsilon 1,2,3 \ldots $$

(29)

The total profit of the monopolist is,

$$ \begin{aligned} \pi & = p_{1} \left[ {n_{1} \alpha_{1} + \frac{\delta }{k}n_{1} \beta_{1} - p_{1} n_{1} \beta_{1} } \right] + p_{2} \left[ {n_{2} \alpha_{2} + \frac{\delta }{k}n_{2} \beta_{2} - p_{2} n_{2} \beta_{2} } \right] \\ & \quad + p_{3} \left[ {n_{3} \alpha_{3} + \frac{\delta }{k}n_{3} \beta_{3} - p_{3} n_{3} \beta_{3} } \right] - F - \frac{\delta }{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} \\ \end{aligned} $$

$$ \pi = \mathop \sum \limits_{t = 1}^{3} p_{t} \left[ {n_{t} \alpha_{t} + \frac{{\delta n_{t} \beta_{t} }}{k} - n_{t} \beta_{t} p_{t} } \right] - F - \frac{\delta }{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} $$

$$ \pi = \frac{{n_{t} \alpha_{t} + \frac{\delta }{k}n_{t} \beta_{t} }}{{2n_{t} \beta_{t} }}\left[ {n_{t} \alpha_{t} + \frac{\delta }{k}n_{t} \beta_{t} - \frac{{n_{t} \alpha_{t} + \frac{\delta }{k}n_{t} \beta_{t} }}{{2n_{t} \beta_{t} }}\left( {n_{t} \beta_{t} } \right)} \right] - F - \frac{\delta }{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} $$

$$ {\text{Thus}},\; \pi = \mathop \sum \limits_{t = 1}^{3} \frac{{\left( {n_{t} \alpha_{t} + \frac{\delta }{k}n_{t} \beta_{t} } \right)^{2} }}{{4n_{t} \beta_{t} }} - F - \frac{\delta }{{k_{1} }}\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} $$

(30)

Case 2 $1000Ck_{1} = \alpha_{1} - \beta_{1} p_{1}$ (the constraint for the peak period is tight, and slack for the off-peak and shoulder periods).

$$ \therefore p_{1} = \frac{{\alpha_{1} - 1000Ck}}{{\beta_{1} }}\;{\text{and}}\;q_{1} = 1000Ck $$

(31)

$$ p_{t} = \frac{{n_{t} \alpha_{t} + \frac{\delta }{k}n_{t} \beta_{t} }}{{2n_{t} \beta_{t} }}\quad \forall t\epsilon 2,3\;{\text{and}} \;q_{t} = \frac{{n_{t} \alpha_{t} - \frac{\delta }{k}\beta_{t} n_{t} }}{{2n_{t} }}\quad \forall t\epsilon 2,3 $$

(32)

The total profit of the monopolist is,

$$ \pi = \mathop \sum \limits_{t = 1}^{2} \frac{{\left( {n_{t} \alpha_{t} - \frac{\delta }{{k_{1} }}n_{t} \beta_{t} } \right)^{2} }}{{4n_{t} \beta_{t} }} - \mathop \sum \limits_{t = 1}^{2} n_{t} \alpha_{t} - F + \left( {\frac{{\alpha_{1} - 1000Ck}}{{\beta_{1} }} - \frac{\delta }{k}} \right)1000Ck_{1} n_{1} $$

$$ {\text{Thus}},\;\pi = \frac{{\alpha_{1} - 1000Ck}}{{\beta_{1} }}\left[ {\frac{\delta }{k}n_{1} \beta_{1} + 1000n_{1} Ck} \right] + \mathop \sum \limits_{t = 1}^{2} \frac{{\left( {n_{t} \alpha_{t} + \frac{\delta }{k}n_{t} \beta_{t} } \right)^{2} }}{{4n_{t} \beta_{t} }} - F - \frac{\delta }{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} . $$

(33)

• b Decreasing marginal costs

If we assume that the marginal cost of producing electricity may decrease with the higher load, then the profit function is:

$$ \begin{aligned} \pi & = n_{1} p_{1} \left( {\alpha_{1} - \beta_{1} p_{1} } \right) + n_{2} p_{2} \left( {\alpha_{2} - \beta_{2} p_{2} } \right) + n_{3} p_{3} \left( {\alpha_{3} - \beta_{3} p_{3} } \right) \\ & \quad - F - \frac{1}{k}[n_{1} \delta_{1} \left( {\alpha_{1} - \beta_{1} p_{1} } \right) - n_{2} \delta_{2} (\alpha_{2} - \beta_{2} p_{2} ) - n_{3} \delta_{3} \left( {\alpha_{3} - \beta_{3} p_{3} } \right) \\ \end{aligned} $$

(34)

The First Order Conditions using Lagrangian Optimization are as follows:

$$ \frac{d\psi }{{dp_{t} }} = n_{t} \alpha_{t} - 2n_{t} \beta_{t} p_{t} + \frac{{n_{t} \delta_{t} \beta_{t} }}{k} + \beta_{t} \varphi_{t } = 0\quad \forall t\epsilon 1,2,3 $$

(35)

$$ \frac{d\psi }{{d\varphi_{t } }} = 1000Ck - (\alpha_{t} - \beta_{t} p_{t} ) \ge 0\quad \forall t\epsilon 1,2,3 $$

(36)

Case 1 $1000Ck_{1} > \alpha_{1} - \beta_{1} p_{1}$ (the constraints for all three periods are slack).

$$ p_{t} = \frac{{n_{t} \alpha_{t} + \frac{{n_{t} \delta_{t} \beta_{t} }}{k}}}{{2n_{t} \beta_{t} }},\quad \forall t\epsilon 1,2,3, \;{\text{and}}\;q_{t} = \frac{{n_{t} \alpha_{t} - \frac{{n_{t} \delta_{t} \beta_{t} }}{k}}}{{2n_{t} }}\quad \forall t\epsilon 1,2,3 \ldots $$

(37)

The total profit of the monopolist is given by,

$$ \pi = \mathop \sum \limits_{t = 1}^{3} p_{t} \left[ {n_{t} \alpha_{t} + \frac{{n_{t} \delta_{t} \beta_{t} }}{k} - n_{t} \beta_{t} p_{t} } \right] - F - \frac{1}{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \delta_{t} \alpha_{t} $$

$$ \pi = \mathop \sum \limits_{t = 1}^{3} \frac{{\left( {n_{t} \alpha_{t} + \frac{{n_{t} \delta_{t} \beta_{t} }}{k}} \right)^{2} }}{{4n_{t} \beta_{t} }} - F - \frac{1}{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \delta_{t} \alpha_{t} $$

(38)

Case 2 $1000Ck = \alpha_{1} - \beta_{1} p_{1}$ (the constraint is tight for the peak period but slack for the shoulder and off-peak periods)

$$ p_{1} = \frac{{\alpha_{1} - 1000Ck}}{{\beta_{1} }}\;{\text{and}}\;q_{1} = 1000Ck $$

(39)

$$ p_{t} = \frac{{n_{t} \alpha_{t} + \frac{{n_{t} \delta_{t} \beta_{t} }}{k}}}{{2n_{t} \beta_{t} }}\quad \forall t\epsilon 2,3\;{\text{and}}\; q_{t} = \frac{{n_{t} \alpha_{t} - \frac{{n_{t} \delta_{t} \beta_{t} }}{k}}}{{2n_{t} }}\quad \forall t\epsilon 2,3 $$

(40)

The profit function then becomes,

$$ \pi = \mathop \sum \limits_{t = 1}^{2} \frac{{\left( {n_{t} \alpha_{t} + \frac{{n_{t} \delta_{t} \beta_{t} }}{k}} \right)^{2} }}{{4n_{t} \beta_{t} }} - F - \frac{\delta }{k}\mathop \sum \limits_{t = 1}^{2} n_{t} \alpha_{t} + \left( {\frac{{\alpha_{1} - 1000Ck_{1} }}{{\beta_{1} }} - \frac{{\delta_{1} }}{k}} \right)1000n_{1} Ck_{1} $$

Thus,

$$ \pi = \frac{{\alpha_{1} - 1000Ck_{1} }}{{\beta_{1} }}\left[ {\frac{{n_{1} \delta_{1} \beta_{1} }}{k} + 1000n_{1} Ck} \right] + \mathop \sum \limits_{t = 1}^{2} \frac{{\left( {n_{t} \alpha_{t} + \frac{{n_{t} \delta_{t} \beta_{t} }}{k}} \right)^{2} }}{{4n_{t} \beta_{t} }} - F - \frac{1}{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \delta_{t} \alpha_{t} $$

(41)

4.4 Comparison of flat rate and time-of-use pricing in case of monopoly

To summarise, the profits earned by the monopolist using constrained maximisation under various conditions are given below in Tables 1 and 2.

Table 1 Flat rate versus time of use pricing when all 3 constraints are slack

Table 2 Flat rate vs Time of Use Pricing when the peak period constraint is tight and the other 2 are slack

For there to be efficiency gains from practicing time-of-use pricing, the profit should be greater than that obtained in flat rate pricing. For the first case, that is, assuming constant marginal costs, the feasibility condition thus becomes:

$$ \mathop \sum \limits_{t = 1}^{3} \frac{{\left( {n_{t} \alpha_{t} + \frac{\delta }{{k_{1} }}n_{t} \beta_{t} } \right)^{2} }}{{4n_{t} \beta_{t} }} - F - \frac{\delta }{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} > \frac{{\left[ {\mathop \sum \nolimits_{t = 1}^{3} n_{t} \alpha_{t} + \frac{\delta }{{k_{1} }}\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} } \right]^{2} }}{{4\mathop \sum \nolimits_{t = 1}^{3} n_{t} \beta_{t} }} - F - \frac{\delta }{k}\mathop \sum \limits_{t = 1}^{3} n_{t} \alpha_{t} $$

On simplifying, the feasibility condition reduces to:

$$ \Rightarrow \frac{{n_{1} \alpha_{1}^{2} }}{{\beta_{1} }} + \frac{{n_{2} \alpha_{2}^{2} }}{{\beta_{2} }} + \frac{{n_{3} \alpha_{3}^{2} }}{{\beta_{3} }} > \frac{{\left[ {n_{1} \alpha_{1} + n_{2} \alpha_{2} + n_{3} \alpha_{3} } \right]^{2} }}{{n_{1} \beta_{1} + n_{2} \beta_{2} + n_{3} \beta_{3} }} $$

(42)

Similarly, we can derive the feasibility condition for the second case, that is, with increasing marginal costs.

4.5 Computational results

We illustrate the proposed model by collecting demand data from a local supplier of electricity and by modelling a 500 MW generator in a power plant in Central India. The elasticity ranges derived from the demand data were used to create demand functions for the three periods—off-peak, shoulder and peak. For the peak period, the elasticity ranges from − 1.51 to − 1.78, for the shoulder period, the elasticity ranges from − 1.39 to − 1.93, and for the off-peak period, the elasticity ranges from − 1.5 to − 2.13. Each day is divided into 9 h of off-peak period, 8 h of shoulder period and 7 h of peak period in line with the assumptions made by Cellibi and Fuller [8]. The assumptions for the cost function are based on data taken from the report on Performance of State Power Utilities for the years 201–-12 to 2013–14 by Power Finance Corporation Limited [10]. The parameters for the demand function and cost functions are given in Table 3.

Table 3 Parameters in the model

We use AMPL [11] to derive the optimal prices under time-of-use and flat rate pricing, both for a constant and decreasing (with load) marginal cost structure. The resultant prices and demand in each of the three periods and the total profitability of the plant under the scenario of TOU pricing and flat rate pricing are given in Table 4.

Table 4 Computational results

The prices for the peak period are found to be the highest in the case of time-of-use pricing followed by shoulder and off-peak periods. The results indicate that the monopolist stands to gain under a time-of-use pricing scheme as compared to a flat rate scheme. A gain in profit of Rs. 4327,057 per day in case of constant marginal operating costs and Rs. 4068,040 per day in case of decreasing marginal cost structure is estimated in the event of a shift to time-of-use pricing from a flat rate pricing scheme. The peak demand is reduced and the shoulder and off peak demand increases under time-of-use pricing by allowing demand response by consumers in the wake of a lower off-peak and shoulder price, and a slightly increased peak price. This shows that the time of use pricing is preferable over flat rate pricing in both cases—constant and decreasing marginal costs.

5 Mathematical model for oligopolistic firms

Next, we look at time-of-use pricing in the case of an oligopoly. With increasing deregulation in the electricity market, we observe the emergence of oligopolistic firms strategically interacting among themselves. Here we first take up the case of two firms which participate in a quantity competition and then move into the general case for n number of firms, with an assumption that n should be sufficiently small so that the oligopolistic nature of the electricity market is preserved. How firms behave in an oligopolistic set up depends on the market demand. The case of the peak period is discussed in Sect. 5.1, the case of shoulder period in Sect. 5.2 and the case of off-peak period in Sect. 5.3.

We denote the firms by the suffix i such that i = 1, 2, 3,…, N. In case of duopoly, we assume that there are two firms. The index t is used to denote the time period, as earlier.

Some additional definitions for the oligopoly model are as follows:

Q_t = Hourly market demand curve for electricity at time period t $\left( {KWHr} \right)$

q_it = Electricity from firm i consumed by consumers per hour at time period t $\left( {KWHr} \right)$

q_–it = Electricity from all but firm i consumed per hour at time period t $\left( {KWHr} \right)$

Z_t = Total electricity generated per hour at time period t

Z_it = Electricity generated by firm i per hour at time period t $\left( {KWHr} \right)$

Z_–it = Electricity generated by all but firm i per hour at time period t $\left( {KWHr} \right)$

F_it = Fixed Cost for generation and distribution of electricity incurred by firm i and time period t $\left( {Rs.} \right)$

δ_t = Variable Cost for an extra unit of electricity incurred by firm i $\left( {Rs.} \right)$

C_t = Power Generation Capacity of firm i $\left( {MW} \right)$

π_it = Profit earned by firm i, in the period t $\left( {Rs.} \right)$

T_l % = Percentage of energy generated that is lost during transmission.

$\therefore \left( {1 - T_{l} \% } \right)z_{t} = q_{t}$ = Energy consumed/demanded per hour for time period $t$.

$$ \therefore kz_{it} = q_{it} $$

where $K = \left( {1 - T_{l} \% } \right)$.

Since K is assumed to be constant across firms and in all time periods, summing over the electricity generated by all firms and the electricity consumed by consumers from all firms gives us $kZ_{t} = Q_{t} .$

5.1 Model formulations

Let the linear market demand curve be denoted by

$$ Q_{t} = \alpha_{t} - \beta_{t} P_{t} \quad \forall t\epsilon 1,2,3 $$

(43)

Again, we assume that, $\alpha_{1} > \alpha_{2} > \alpha_{3}$ and $\beta_{t} > 0$.In case of N firms,

$$ \varvec{Q}_{\varvec{t}} = \varvec{ }\mathop \sum \limits_{{\varvec{i} = 1}}^{\varvec{n}} \varvec{q}_{{\varvec{it}}} = \varvec{ q}_{{\varvec{it}}} + \varvec{q}_{{ - \varvec{it}}} ,\quad \forall \varvec{ t}\epsilon 1,2,3 $$

(44)

where, $q_{it} < 1000C_{i} k$, $\forall \;t\epsilon 1,2,3$.

The unit of study in this case is 1 h and we use the relevant conversions to bring the parameters into the same unit.

In case of a duopoly, the total market demand during period t, Q_t can be catered by the two firms.

$$ \varvec{Q}_{\varvec{t}} = \varvec{ q}_{{1\varvec{t}}} + \varvec{q}_{{2\varvec{t}}} ,\quad \forall \varvec{ t}\epsilon 1,2,3 $$

(45)

$$ \varvec{ }{\text{Thus}},\;\varvec{q}_{{1\varvec{t}}} + \varvec{q}_{{2\varvec{t}}} = \varvec{ \alpha }_{\varvec{t}} -\varvec{\beta}_{\varvec{t}} \varvec{P}_{\varvec{t}} , \Rightarrow \varvec{P}_{\varvec{t}} = \frac{{\varvec{ \alpha }_{\varvec{t}} - \varvec{q}_{{1\varvec{t}}} - \varvec{q}_{{2\varvec{t}}} }}{{\varvec{\beta}_{\varvec{t}} }},\varvec{ }\quad \forall \varvec{ t}\epsilon 1,2,3 $$

(46)

$$ \Rightarrow \varvec{P}_{\varvec{t}} = \varvec{ }\frac{{\varvec{ \alpha }_{\varvec{t}} - \varvec{kz}_{{1\varvec{t}}} - \varvec{kz}_{{2\varvec{t}}} }}{{\varvec{\beta}_{\varvec{t}} }},\varvec{ }\quad \forall \varvec{ t}\epsilon 1,2,3 $$

The Cost structure faced by firm i, is given as follows:

$$ \varvec{ TC}_{\varvec{i}} = \mathop \sum \limits_{{\varvec{t} = 1}}^{3} \varvec{F}_{{\varvec{it}}} + \mathop \sum \limits_{{\varvec{t} = 1}}^{3} \varvec{n}_{\varvec{t}}\varvec{\delta}_{\varvec{i}} \varvec{z}_{{\varvec{it}}} $$

(47)

In the oligopoly model, for each firm, we assume the marginal costs to be constant in all the three periods. This assumption can be relaxed to a decrease from the off-peak period to the shoulder period to the peak period, and is left as an extension to this study. We also assumed that the Marginal Cost for producing an extra unit of electricity is greater for firm 2 than for firm 1, that is, $\delta_{2} > \delta_{1}$. In other words, Firm 1 is more efficient than Firm 2 in terms of cost advantage.

5.2 The case of peak period

In the peak period, we assume that the market demand for electricity is high enough to exceed the capacity of the individual firms. Hence no single firm can cater to the entire market demand on its own. The two firms engage in quantity competition, of the type specified by Cournot. The two firms are assumed to participate in a one stage game and they choose the amount of electricity to be supplied simultaneously. Each firm tries to maximise its profit, observing the actions of its rival firm. We obtain the reaction functions of both the firms and then solve them to obtain the respective amounts of electricity that each firm generates.

Firm 1’s optimisation problem can be stated as follows:

$$ {\text{Max}}\;\pi_{11 } = n_{1} P_{1} q_{11} - TC_{11} = n_{1} \left( {\frac{{ \alpha_{1} - q_{11} - q_{21} }}{{\beta_{1} }}} \right)q_{11} - F_{11} - n_{1} \delta_{1} z_{11} $$

(48)

The First order conditions of this optimisation problem yield the following results:

$$ \frac{{d\pi_{11 } }}{{dz_{11} }} = n_{1} k\left( {\frac{{\alpha_{1} - 2kz_{11} - kz_{21} }}{{\beta_{1} }}} \right) - n_{1} \delta_{1} $$

(49)

Equating this to zero, we obtain the Reaction Function of Firm 1 as

$$ z_{11} = \left( {\frac{{k\alpha_{1} - \delta_{1} \beta_{1} - {\text{k}}^{2} z_{21} }}{{2k^{2} }}} \right) $$

(50)

The Reaction Function of firm 1 can be defined as the best response of the firm, given that firm 2 chooses to generate Z₂₁ in the motive of profit maximisation. Similarly, firm 2’s reaction function is as follows:

$$ z_{21} = \left( {\frac{{k\alpha_{1} - \delta_{2} \beta_{1} - {\text{k}}^{2} z_{11} }}{{2 {\text{k}}^{2} }}} \right) $$

(51)

Solving the two reaction functions, the quantities consumed from firm 1 and firm 2 respectively are,

$$ q_{11}^{*} = \left( {\frac{{k\alpha_{1} - \beta_{1} \left( {2\delta_{1} - \delta_{2} } \right)}}{3k}} \right)\;{\text{and}}\;q_{21}^{*} = \left( {\frac{{k\alpha_{1} - \beta_{1} \left( {2\delta_{2} - \delta_{1} } \right)}}{3k}} \right) $$

(52)

$$ P_{1}^{*} = \frac{{ \alpha_{1} - q_{11} - q_{21} }}{{\beta_{1} }} = \frac{{k\alpha_{1} + \beta_{1} \left( {\delta_{1} + \delta_{2} } \right)}}{{3k\beta_{1} }} $$

(53)

The profits earned by the duopolists are:

$$ \pi_{11 }^{*} = \frac{{n_{1} }}{{9k^{2} \beta_{1} }}\left[ {k\alpha_{1} - \beta_{1} \left( {2\delta_{1} - \delta_{2} } \right)} \right]^{2} - F_{11} \;{\text{and}}\;\pi_{21}^{*} = \frac{{n_{1} }}{{9k^{2} \beta_{1} }}\left[ {k\alpha_{1} - \beta_{1} \left( {2\delta_{2} - \delta_{1} } \right)} \right]^{2} - F_{21} $$

(54)

5.2.1 Generalisation to the case of N firms

Here, the problem of each of the firms can be stated as follows:Maximize $\pi_{i1} = n_{1} P_{1} q_{i1} - F_{i1} - n_{1} \delta_{i} z_{i1}$

$$ = n_{1} \left[ {\frac{{\alpha_{1} - kz_{i1} - kz_{ - i1} }}{{\beta_{1} }}} \right]kz_{i1} - F_{i1} - n_{1} \delta_{i} z_{i1} . $$

(55)

The electricity generated by the ith firm is given by:

$$ z_{i1}^{*} = \frac{{k\alpha_{1} - \beta_{1} \left[ {\delta_{i} \left( {1 + N} \right) - \bar{\delta }} \right]}}{{k^{2} \left( {1 + N} \right)}} $$

(56)

The quantity supplied by the ith firm is,

$$ q_{i1}^{*} = \frac{{k\alpha_{1} - \beta_{1} \left[ {\delta_{i} \left( {1 + N} \right) - \bar{\delta }} \right]}}{{k\left( {1 + N} \right)}} $$

(57)

The total quantity of electricity supplied by all the firms taken together,

$$ Q_{1} = kZ_{1} = \frac{{Nk\alpha_{1} - \beta_{1} \bar{\delta }}}{{k\left( { 1 + N} \right)}} $$

(58)

The price of electricity and the profits of the respective firms in general are given as below:

$$ P_{1}^{*} = \frac{{k\alpha_{1} + \beta_{1} \bar{\delta }}}{{k\beta_{1} \left( {1 + N} \right)}} $$

(59)

$$ \pi_{i1 }^{*} = \frac{{n_{1} \left\{ {k \alpha_{1} - \beta_{1} \left[ {\left( {1 + N} \right)\delta_{i} - \bar{\delta }} \right]} \right\}^{2} }}{{\left( {N + 1} \right)^{2} k^{2} \beta_{1} }} - F_{i1} $$

(60)

5.3 The case of the shoulder period

In the shoulder period, though the demand for electricity is sufficiently high, it is not as high as compared to the peak period. There are three possible cases. In the first case, the capacity constraints are binding for both the firms. Since no firm can cater to the entire market alone, they strategically interact according to Cournot. In the second case and third case, the capacity constraints are non-binding. In such a situation, either only the most efficient firm operates (case ii), or both firms strategically interact according to the Stackleberg competition (case iii). These cases are described below. The model is first built for a duopoly and then generalised to an N firm case.

Case i Capacity Constraints are binding for both firms

One possibility is that the capacity constraints for each of the two firms becomes binding. Hence, no firms can cater to the entire market demand all alone, and the two firms strategically interact between themselves and compete in quantities, according to Cournot. In this case, the problem is similar to that described above for the peak period. Using the same optimisation model, we get the electricity generated by both the firms as:

$$ z_{11}^{*} = \left( {\frac{{k\alpha_{2} - \beta_{2} \left( {2\delta_{1} - \delta_{2} } \right)}}{{3k^{2} }}} \right)\;{\text{and}}\; z_{21}^{*} = \left( {\frac{{k\alpha_{2} - \beta_{2} \left( {2\delta_{2} - \delta_{1} } \right)}}{{3k^{2} }}} \right) $$

(61)

The quantity demanded from each firm is,

$$ q_{12}^{*} = \left( {\frac{{k\alpha_{2} - \beta_{2} \left( {2\delta_{1} - \delta_{2} } \right)}}{3k}} \right)\;{\text{and}}\;q_{22}^{*} = \left( {\frac{{k\alpha_{2} - \beta_{2} \left( {2\delta_{2} - \delta_{1} } \right)}}{3k}} \right) $$

(62)

The price charged in the shoulder period will be as follows:

$$ P_{2}^{*} = \frac{{k\alpha_{2} + \beta_{2} \left( {\delta_{1} + \delta_{2} } \right)}}{{3k\beta_{2} }} $$

(63)

And the respective profits earned by the duopolists are as follows:

$$ \pi_{12 }^{*} = \frac{{n_{2} }}{{9k^{2} \beta_{2} }}\left[ {k\alpha_{2} - \beta_{2} \left( {2\delta_{1} - \delta_{2} } \right)} \right]^{2} - F_{12} \;{\text{and}}\;\pi_{21}^{*} = \frac{{n_{2} }}{{9k^{2} \beta_{2} }}\left[ {k\alpha_{2} - \beta_{2} \left( {2\delta_{2} - \delta_{1} } \right)} \right]^{2} - F_{22} $$

(64)

5.3.1 Generalising to N firms

Since the capacity constraints are binding, the firms interact based on Cournot competition, similar to the case of peak period.

The quantity demanded from the ith firm and the total quantity demanded from all the firms taken together are respectively,

$$ q_{i1}^{*} = \frac{{k\alpha_{2} - \beta_{2} \left[ {\delta_{i} \left( {1 + N} \right) - \bar{\delta }} \right]}}{{k\left( {1 + N} \right)}} \;{\text{and}}\; Q_{2}^{*} = \frac{{Nk\alpha_{2} - \beta_{2} \bar{\delta }}}{{k\left( { 1 + N} \right)}} $$

(64)

The price of electricity and the profits of the respective firms in general are given as below:

$$ P_{2}^{*} = \frac{{k\alpha_{2} + \beta_{2} \bar{\delta }}}{{k\beta_{2} \left( {1 + N} \right)}} $$

(65)

$$ \pi_{i1 }^{*} = \frac{{n_{2} \left\{ {k \alpha_{2} - \beta_{2} \left[ {\left( {1 + N} \right)\delta_{i} - \bar{\delta }} \right]} \right\}^{2} }}{{\left( {N + 1} \right)^{2} k^{2} \beta_{2} }} - F_{i2} $$

(66)

Case ii Capacity Constraints are non-binding: Only the more efficient firm operates

Another possibility is that the capacity constraints become non-binding for both the firms, that is, the capacity of each firm is sufficiently more than the demand for electricity. Hence, the most efficient firm generates and distributes electricity, while the competent firm does not produce anything because of its cost disadvantage. Thus, it is technologically feasible for firm 2 (the less efficient firm) to stop generation of electricity during this time on the assumption that the profits earned by firm 2 in the peak period are sufficiently high to compensate for the loss from not operating in this period. With $z_{22} = q_{22} = 0,$ we modify the demand curve as follows:

$$ P_{2} = \left( {\frac{{ \alpha_{2} - q_{12} }}{{\beta_{2} }}} \right) = \left( {\frac{{\alpha_{2} - kz_{12} }}{{\beta_{2} }}} \right) $$

(67)

The problem of firm 1 is as follows:

$$ {\text{Max}}\;\pi_{12 } = n_{2} P_{2} q_{12} - C_{12} = kn_{2} \left( {\frac{{ \alpha_{2} - kz_{12} }}{{\beta_{2} }}} \right)z_{12} - F_{12} - n_{2} \delta_{1} z_{12} $$

(68)

The quantity demanded from the first firm would be,

$$ \Rightarrow q_{12}^{*} = \frac{{\left( {k\alpha_{2} - \delta_{1} \beta_{2} } \right)}}{2k}\;{\text{and}}\; q_{22}^{*} = 0 $$

(69)

The price charged for electricity is given by:

$$ P_{2}^{*} = \frac{{\left( {k\alpha_{2} + \beta_{2} \delta_{1} } \right)}}{{2k\beta_{2} }} $$

(70)

The profits earned by firm 1 and 2 are:

$$ \pi_{12 }^{*} = \frac{{n_{2} \left[ {k\alpha_{1} - \delta_{1} \beta_{2} } \right]^{2} }}{{4\beta_{2} k^{2} }} - F_{12} \;{\text{and}}\; \pi_{22 }^{*} = - F_{22 } $$

(71)

5.3.2 Generalising to N firms

In this case, only the most efficient firm (Firm 1) operates, and the quantity supplied by all the other firms is zero (i.e. $z_{i2} = q_{i2} = 0$ for all firms except i = 1). Thus, the problem of firm 1 is reduced to what has been discussed in case (ii) for a duopoly. The quantity consumed from firm 1 is given by:

$$ q_{12}^{*} = \left( {\frac{{k\alpha_{2} - \delta_{1} \beta_{2} }}{2k}} \right) $$

(72)

The price of electricity is given by:

$$ P_{2}^{*} = \frac{{ \alpha_{2} - q_{12} }}{{\beta_{2} }} = \frac{{k\alpha_{2} + \delta_{1} \beta_{2} }}{{2k\beta_{2} }} $$

(73)

The profits earned by the firms are:

$$ \pi_{12 }^{*} = \frac{{n_{2} \left[ {k\alpha_{1} - \delta_{1} \beta_{2} } \right]^{2} }}{{4\beta_{2} k^{2} }} - F_{12} \;{\text{and}}\; \pi_{i2 }^{*} = - F_{i2} \;{\text{for}}\,{\text{all}}\,{\text{firms}}\,{\text{except}}\;i = \, 1 $$

(74)

Case iii Capacity Constraints are nonbinding, but both firms participate

In this case, both firms participate in the market but they strategically interact between themselves sequentially, in a manner which has close proximity to Stackelberg’s oligopoly model. This is essentially a 2-stage game, where the more efficient firm (Leader) chooses its quantity of electricity to be supplied initially, and then in the next stage of the game, the rival firm (Follower), chooses its quantity, having observed the quantity chosen by the leader. In the Cournot Model, on the other hand, we saw a one period game where both firms choose the quantity of electricity to be supplied simultaneously.

In Stage 2, Firm 2’s problem is:

$$ {\text{Max}}\;\pi_{22 } = n_{2} P_{2} q_{22} - C_{22} = kn_{2} P_{2} z_{22} - F_{22} - n_{2} \delta_{2} z_{22} $$

(75)

The first order conditions yield the reaction function of Firm 2 as:

$$ z_{22} = \left( {\frac{{k\alpha_{2} - \delta_{2} \beta_{2} - k^{2} z_{12} }}{{2k^{2} }}} \right) . $$

(76)

In the first stage, firm 1 chooses its output, knowing that firm 2 will react to it in the second period according to its reaction function given by (76). Here firm 1’s problem is:

$$ \begin{aligned} {\text{Max}}\;\pi_{12 } & = n_{2} P_{ 2} q_{12} - C_{12} , = kn_{2} P_{2} z_{12} - F_{12} - n_{2} \delta_{1} z_{12} \\ & = kn_{2} \left( {\frac{{ \alpha_{2} - kz_{12} - \left( {\frac{{k\alpha_{2} - \delta_{2} \beta_{2} - k^{2} z_{12} }}{2k}} \right)}}{{\beta_{2} }}} \right)z_{12} - F_{12} - n_{2 } \delta_{1} z_{12} \\ \end{aligned} $$

(77)

On solving, the quantity of electricity generated by the Leader firm 1 is:

$$ z_{12}^{L} = \left( {\frac{{k\alpha_{2} - \beta_{2} \left( {2\delta_{1} - \delta_{2} } \right) }}{{2k^{2} }}} \right)\;{\text{and}}\;q_{12}^{L} = \left( {\frac{{k\alpha_{2} - \beta_{2} \left( {2\delta_{1} - \delta_{2} } \right) }}{2k}} \right) $$

(78)

Substituting this in the reaction function of firm 2:

$$ z_{22}^{F} = \left( {\frac{{k \alpha_{2} - \beta_{2} \left( {3\delta_{2} - 2\delta_{1} } \right) }}{{4k^{2} }}} \right)\;{\text{and}}\;q_{22}^{F} = \left( {\frac{{k\alpha_{2} - \beta_{2} \left( {3\delta_{2} - 2\delta_{1} } \right) }}{4k}} \right) $$

(79)

The respective price of electricity and the profits of the two firms may be obtained as follows:

$$ P_{2}^{*} = \frac{{k\alpha_{2} + \beta_{2} \left( {\delta_{2} + 2\delta_{1} } \right)}}{{4k\beta_{2} }} $$

(80)

The respective profits are then as follows:

$$ \pi_{12 }^{L} = \frac{{n_{2} \left\{ {k\alpha_{2} - \beta_{2} \left( {2\delta_{1} - \delta_{2} } \right)} \right\}^{2} }}{{8\beta_{2} k^{2} }} - F _{12} $$

(81)

$$ \pi_{22 }^{F} = \frac{{n_{2} \left\{ {k\alpha_{2} - \beta_{2} \left( {3\delta_{2} - 2\delta_{1} } \right)} \right\}^{2} }}{{16\beta_{2} k^{2} }} - F_{22 } $$

(82)

5.3.3 Generalising to N firms

In this case, the dynamics of the Stackelberg game can be solved by backward induction, which would result in the emergence of leader firms and follower firms in the market. The mathematical modelling is left as an extension for further work.

5.4 The case of off-peak period

We assume that the demand for electricity is in fact less than the capacity of the individual firms. Both the firms can therefore cater to the entire market demand individually, without strategically interacting with each other. The most efficient firm, due to its cost advantage as compared to its competitor, can actually charge a price which is less than the marginal cost of its competitor. Hence, the other firm cannot participate, as charging such a price would result in a loss. As a result, only the most efficient firm participates in the market, caters to the entire market demand and extracts the entire profit. The problem thus reduces to what has been discussed in Sect. 5.2, case (ii). As the entire market demand is catered by the first firm, i.e., $q_{23} = 0,$ the required electricity generated by and demanded from firm 1, using the same optimisation model, is:

$$ z_{13}^{*} = \frac{{k\alpha_{3} - \delta_{1} \beta_{3} }}{{2k^{2 } }}\;{\text{and}}\; q_{13}^{*} = \frac{{\left( {k\alpha_{3} - \beta_{3} \delta_{1} } \right)}}{2k} $$

(83)

The price charged for electricity is:

$$ P_{3}^{*} = \frac{{\left( {k\alpha_{3} + \beta_{3} \delta_{1} } \right)}}{{2k\beta_{3} }} $$

(84)

And the required profits for firm 1 and 2 are as follows:

$$ \pi_{13 }^{*} = \frac{{n_{3} \left[ {k\alpha_{3} - \delta_{1} \beta_{3} } \right]^{2} }}{{4\beta_{3} k^{2} }} - F_{13} \;{\text{and}}\;\pi_{23 }^{*} = - F_{23} $$

(85)

However, one important question is why the rival firm would choose to remain idle. A possible solution could be the payment of some side payments by the efficient firm to its rival, as a compensation for not producing. Also, as already discussed, the profits earned by the less efficient firm during the peak period and the shoulder period is sufficiently more than the loss from not producing in the off-peak period.

5.4.1 Generalization for N firms

Here, the dynamics of the model will be exactly same as that discussed in the case of a duopoly where the most efficient firm produces, while the other firms remain idle.

Thus, in the off-peak period, an oligopolistic/duopolistic structure breaks down into a monopolistic one.

6 Summary and conclusion

Table 5 summarise the various cases and presents the profits earned by the oligopolists.

Table 5 Summary: Duopolist’s profits under various demand conditions

Time-of-use pricing can not only help in containing the demand–supply imbalance, but by shifting the demand from the peak period, lower the pressure on installed capacity and thus, result in savings in investment and operating expenditure. However, time-of-use pricing affect producers depending on the market structure. In this study, we model time-of-use pricing in the context of a monopolistic set up and an oligopolistic set up.

In the presence of a single firm, that is, a monopoly, the firm operates using constrained optimisation techniques. We estimate the feasibility condition for there to be efficiency gains from practicing time-of-use pricing vis-a-vis flat rate pricing.

In an oligopolistic set up, the interaction between firms depends on the market demand. In the peak period, when the demand is very high, no single firm can cater to the demand of the entire market, and firms compete on the basis of quantity, that is, Cournot Competition. In the off shoulder period, the demand may be high enough to encourage Cournot Competition. However, if the demand is low, either only the most efficient firm operates, or there is an emergence of leaders and followers and the situation becomes similar to the Stackelberg Model. In the off-peak period, only the most efficient firm operates in the market, thus there is a breaking down of the market structure from an oligopoly to a monopoly.

7 Scope for future research

This paper can be extended in several directions. Firstly, we assume that customers are homogeneous. By segmenting the customers into different groups, say residential users and commercial users, we can derive the models considering that each group has demand curves of different elasticities, and thus varying consumer surpluses. Secondly, we can derive the optimality conditions when we move from a linear demand price relationship as assumed in this paper, to a non-linear demand price relationship, for example, the case of a constant elasticity demand curve represented by a rectangular hyperbola. We can also examine the case of non-linear (cubic) cost functions. Thirdly, as discussed in this paper, in the shoulder period, when the demand is lower, it may be possible for one firm to entirely cater to the market—the most efficient firm, or the firms to get into Stackleberg competition. Here, there is an emergence of leaders and followers, and the equilibrium can be found using a game theory approach (sequential game) and can be solved by backward induction. Modelling this for n firms could be a possible extension. Fourthly, we can take into account various externalities. Finally, in this paper, we divide the day into three periods with predetermined prices. An extension could be to look at the imperfectly competitive market structures when electricity pricing is fully dynamic, that is, it follows Real Time Pricing.